第一三章习题答案

合集下载

建筑结构抗震设计(第三版)习题解答1-5章

第一章的习题答案1. 震级是衡量一次地震强弱程度（即所释放能量的大小）的指标。

地震烈度是衡量一次地震时某地区地面震动强弱程度的尺度。

震级大时，烈度就高；但某地区地震烈度同时还受震中距和地质条件的影响。

2. 参见教材第10面。

3. 大烈度地震是小概率事件，小烈度地震发生概率较高，可根据地震烈度的超越概率确定小、中、大烈度地震；由统计关系：小震烈度＝基本烈度－1.55度；大震烈度＝基本烈度＋1.00度。

4. 概念设计为结构抗震设计提出应注意的基本原则，具有指导性的意义；抗震计算为结构或构件达到抗震目的提供具体数据和要求；构造措施从结构的整体性、锚固连接等方面保证抗震计算结果的有效性以及弥补部分情况无法进行正确、简洁计算的缺陷。

5. 结构延性好意味可容许结构产生一定的弹塑性变形，通过结构一定程度的弹塑性变形耗散地震能量，从而减小截面尺寸，降低造价；同时可避免产生结构的倒塌。

第二章的习题答案1. 地震波中与土层固有周期相一致或相近的波传至地面时，其振幅被放大；与土层固有周期相差较大的波传至地面时，其振幅被衰减甚至完全过滤掉了。

因此土层固有周期与地震动的卓越周期相近，2. 考虑材料的动力下的承载力大于静力下的承载力；材料在地震下地基承载力的安全储备可低于一般情况下的安全储备，因此地基的抗震承载力高于静力承载力。

3. 土层的地质年代；土体中的粘粒含量；地下水位；上覆非液化土层厚度；地震的烈度和作用时间。

4. a 中软场地上的建筑物抗震性能比中硬场地上的建筑物抗震性能要差（建筑物条件均同）。

b. 粉土中粘粒含量百分率愈大,则愈容易液化. c ．液化指数越小，地震时地面喷水冒砂现象越轻微。

d ．地基的抗震承载力为承受竖向荷载的能力。

5. s m v m 5.2444208.32602.82008.51802.220=+++=因m v 小于s m 250，场地为中软场地。

6. 设计地震分组为第二组，烈度为7度，取80=N砂土的临界标贯值：[])(1.09.00w s cr d d N N -+=，其中m d w 5.1=土层厚度：第i 实测标贯点所代表的土层厚度的上界取上部非液化土层的底面或第1-i 实测标贯点所代表土层的底面；其下界取下部非液化土层的顶面或相邻实测标贯点的深度的均值。

第1、2、3、4章练习题

第一章练习题1、物质能以液态形式存在的最高温度为（A）沸腾温度Tb （B）玻义耳温度TB （C）临界温度Tc2、当压缩因子Z<1时，表示该实际气体（A）易压缩（B）不易压缩（C）无法确定3、下列何种条件下真实气体可以液化（）（A）Tr>1,Pr>1 （B）Tr>1,Pr<1 （C）Tr=1,Pr<1 （D）Tr<1,Pr=14、对理想气体，压缩因子Z=1。

能否说当气体的Z=1 时，该气体必定是理想气体。

答案：（不能，因为在实际气体的等温线与理想气体的等温线交点处，Z＝1）5、当温度足够低时，任何实际气体的Z～P 曲线与理想气体的Z～P 曲线均交于两点。

试解释这种现象。

答案：（这是因为当温度足够低时，气体的玻义耳温度高于体系温度，Z～p 曲线出现极小值。

）6、从范德华方程出发并结合玻义耳温度定义，证明(1)在足够高的温度，实际气体的压缩因子Z>1 。

(2)在低温，低压下，Z<1 。

答案：（当T＜＝TB，Z＞1）(3)当a=0 ，Z 随压力p 的增加而线性增加。

答案：（当a＝0，Z＝1+bp/RT，恒温时，p 增加，Z 增大。

）7、下列说法何者正确？(1)临界压力是气体可被液化的最低压力。

(2)气体被液化的必要条件是气体温度小于波义耳温度(3)在临界点，饱和液体与饱和蒸气的密度相同。

(4)气体的临界状态与气体的性质无关。

答案：（3）8、气体A、B、C 都服从范德华方程，其范德华常数a和b的大小顺序为a(A)=a(B)>a(C);b(C)>b(B)>b(A)。

问三种气体临界温度的大小顺序。

答案：（T c(A)>T c(B)>T c(C)）9、某气体的状态方程为，式中b为常数，n为物质的量。

若该气体经一等温过程，压力自p1变至p2，则下列状态函数的变化，何者为零？（ΔU）第二章练习题1、指出下列说法的错误。

(1)因Qp =ΔH，Qv=ΔU，所以Qp 和Qv 都是状态函数。

管理学概论 (杨红娟著) 冶金工业出版社第一、三章习题与答案

复习思考题：一、名词解释1、管理2、组织3、人际技能4、概念技能5、技术技能6、管理者二、选择题1、美国管理大师彼得·德鲁克说过，如果你理解管理理论，但不具备管理技术和管理工具的运用能力，你还不是一个有效的管理者；反过来，如果你具备管理技巧和能力，而不掌握管理理论，那么充其量你只是一个技术员。

这句话说明( )。

A、有效的管理者应该既掌握管理理论，又具备管理技巧及对管理工具的运用能力B、是否掌握管理理论对管理者工作的有效性来说无足轻重C、只要理解管理理论，就能成为一名有效的管理者D、有效的管理者应该注重管理技术与工具的运用能力，而不必注重管理理论2、“三个和尚没水喝”说的是人浮于事可能不如人少好办事。

但是反过来，如果“三个和尚”都很负责，结果也许会造成水满为患。

这两种不同的说法表明( )。

A、管理工作的有效性需要考虑内外部环境各部分的整体效应B、即使管理无方，人多还是比人少好办事C、在不同的心态作用下会产生不同的群体合作结果D、纵使管理有方，也不一定是人多好办事3、一个管理者所处的层次越高，面临的问题越复杂，越无先例可循，就越需要具备（）。

A、技术技能B、领导技能C、概念技能D、人际技能4、有人说在管理中经常是“外行领导内行”，这在一定程度上说明，对管理者来说（）。

A、授权和技术一样重要B、人际关系是第一位的C、人际沟通比技术更重要D、技术不是最重要的5、下面属于基层第一线管理人员的职位是（）。

A、总裁B、厂长C、部门经理D、工长6、管理者传播者的角色属于（）。

A、人际角色B、信息角色C、决策角色D、领导角色7、人际技能对于各种层次管理者的重要性是（）。

A、对于高层管理者最重要B、对于中层管理者最重要C、对于基层管理者最重要D、对于所有层次管理者的重要性大体相同8、管理就是决策”是下面谁的观点：（）Ａ．德鲁克Ｂ．泰勒Ｃ．西蒙Ｄ．法约尔9、关于公司总经理与中层管理人员之间的区别，存在以下几种不同的说法，你认为其中哪一种说法最为贴切?( )A、总经理比中层管理人员更需要具备对环境的洞察力B、总经理比中层管理人员更有发言权C、总经理比中层管理人员更需要掌握反映公司经营问题的信息D、总经理比中层管理人员较少受约束10、管理的二重属性是指（）A、科学性与艺术性B、自然属性和科学属性C、自然属性和社会属性D、科学属性与社会属性11、关于管理有以下几种说法：①“管理就是为在集体中工作的人员谋划和保持一个能使他们完成预定目标和任务的工作环境”；②“管理就是实施计划、组织、领导、协调和控制”；③“管理就是决策”；④“管理就是通过其他人来完成工作”；⑤“管理就是由一个或多个人来协调他人活动，以便收到个人单独活动所不能收到的效果而进行的各种活动”。

电子技术基础(第二版)前三章习题答案

第一章1.1 能否将1.5V 的干电池以正向接法接到二极管两端？为什么？解：不能。

因为二极管的正向电流与其端电压成指数关系，当端电压为1.5V 时，管子会因电流过大而烧坏。

1.2已知稳压管的稳压值U Z ＝6V ，稳定电流的最小值I Zmin ＝5mA 。

求图T1.4所示电路中U O1和U O2各为多少伏。

解：U O1＝6V ，U O2＝5V 。

1.3写出图T1.3所示各电路的输出电压值，设二极管导通电压U D ＝0.7V 。

（该题与书上略有不同）解：U O1≈1.3V ，U O2＝0，U O3≈－1.3V ，U O4≈2V ，U O5≈1.3V ，U O6≈－2V 。

1.5 电路如图P1.5（a ）所示，其输入电压u I1和u I2的波形如图（b ）所示，二极管导通电压U D ＝0.7V 。

试画出输出电压u O 的波形，并标出幅值（该题与书上数据不同）解：u O 的波形如解图P1.5所示。

解图P1.51.9电路如图T1.9所示，V CC ＝15V ，β＝100，U BE ＝0.7V 。

试问：（1）R b ＝50k Ω时，u O ＝？（2）若T 临界饱和，则R b ≈？解：（1）R b ＝50k Ω时，基极电流、集电极电流和管压降分别为26bBEBB B =-=R U V I μAV2mA 6.2 C C CC CE B C =-===R I V U I I β所以输出电压U O ＝U CE ＝2V 。

1.11电路如图P1.11所示，试问β大于多少时晶体管饱和？解：取U CES ＝U BE ，若管子饱和，则Cb C BECC b BE CC R R R U V R U V ββ=-=-⋅所以，100Cb=≥R R β时，管子饱和。

图1.11 1.12 分别判断图P1.12所示各电路中晶体管是否有可能工作在放大状态第二章2.1试分析图T2.2所示各电路是否能够放大正弦交流信号，简述理由。

自考《00402学前教育史》分章节习题练习(一)(第一～三章)答案

1课程名字：自考《00402 学前教育史》分章节习题课程目录：练习（一）（第一～三章） ...................................................... 1 练习（第四～五章） ................................................................................................................................ 6 练习（第六～八章） .............................................................................................................................. 13 练习（第九～十章） (20)练习（一）（第一～三章）答案部分一、单项选择题1、【正确答案】 A【答案解析】王筠的著有《说文句读》《说文释例》《文字蒙求》《教童子法》等书。

《文字蒙求》一书则结合汉字的结构原理和儿童的思维特点，提出了蒙养识字教学的一系列方法和原则。

崔学古《幼训》; 朱熹《蒙童须知》和《小学》。

本题选 A 。

参见教材 P40。

2、【正确答案】 D【答案解析】《华容道》是世界著名的智力游戏，在国外和魔方、独立钻石棋并列，被誉为“智力游戏界三大难题”，并被编入学校的教科书。

智力游戏,是指那种将智力活动与娱乐活动巧妙地结合起来进行的游戏形式。

在我同古代智力游戏主要是通过棋艺、拼图和其他涉及数学、几何等原理变化的形式表现出来的。

比较有名的有七巧板、燕几图、包你迷、华容道等。

本题选 D 。

参见教材 P44。

3、【正确答案】 D【答案解析】《兔园册府》是中国古代的一部类书，在唐代迄五代时用作民间私塾学童的启蒙读本。

介绍有关历史、地理、博物等的浅近知识。

管理会计学习指导书习题答案(1-3)

管理会计学习指导书习题答案第一章总论一、单项选择题1．C 2.A 3.D 4.D 5.B 6.A 7.C 8.C 9.D 10.A 11.C 12.D二、多项选择题1．ABCD 2.ABCD 3.AB 4.ABC 5.ABCD 6.CD三、判断题1.√2.×3. ×4. √5.√6.√7. ×8.×9. √10. ×第二章成本习性分析一、单项选择题1．C 2.C 3.C 4.A 5.D 6.C 7.D 8.A 9.D 10.B 11.D 12.C 13.B 14.B二、多项选择题1．AD 2.ABCD 3.ABCD 4.BD 5.AB 6.BCD 7.ACD 8.BC三、判断题1. ×2.×3. ×4. ×5. ×6.√7. √8.×9. ×10. ×11. √12. √13. ×14. ×15. ×16. ×17. √18.√19. √（四）计算分析题1．（1）a=9.1875 b=0.6875 y=9.1875+0.6875x(2) y =8.6289+0.6538x(3) 高低点法下维修成本为18.81元，回归直线法下维修成本为17.78元。

2．（1）小吴的意见正确，因为计算的相关系数为0.9966，表明成本与业务量之间高度相关，而小刘计算的相关系数为0，表明不相关。

（2）y=103.33+4.375x(3) 7月份总成本为212.705万元。

3.（1）y=60000+2x（2）180000元4.（1）b=（6 ×6920－48×830）/（6×448－48×48）= 4.375a= (830 －4.375×48）/6= 103.33 y=103.33+4.375 x（2）y=103.33+4.375×18=182.085．（1）根据2月份制造费用总额组成情况可确定各月固定成本为60000元，单位变动成本为1元/件，从而可确定1至6月份混合成本分别为32500元、35000元、40000元、41250元、40000元、35000元。

(完整版)编译原理课后答案(第三版蒋立源康慕宁编)

编译原理课后答案（第三版蒋立源康慕宁编）第一章习题解答1解：源程序是指以某种程序设计语言所编写的程序。

目标程序是指编译程序（或解释程序）将源程序处理加工而得的另一种语言（目标语言）的程序。

翻译程序是将某种语言翻译成另一种语言的程序的统称。

编译程序与解释程序均为翻译程序，但二者工作方法不同。

解释程序的特点是并不先将高级语言程序全部翻译成机器代码，而是每读入一条高级语言程序语句，就用解释程序将其翻译成一段机器指令并执行之，然后再读入下一条语句继续进行解释、执行，如此反复。

即边解释边执行，翻译所得的指令序列并不保存。

编译程序的特点是先将高级语言程序翻译成机器语言程序，将其保存到指定的空间中，在用户需要时再执行之。

即先翻译、后执行。

2解：一般说来，编译程序主要由词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、目标代码生成程序、信息表管理程序、错误检查处理程序组成。

3解：C语言的关键字有：auto break case char const continue default do double else enum extern float for goto if int long register return short signed sizeof static struct switch typedef union unsigned void volatile while。

上述关键字在C语言中均为保留字。

4解：C语言中括号有三种：{}，[]，（）。

其中，{}用于语句括号；[]用于数组；（）用于函数（定义与调用）及表达式运算（改变运算顺序）。

C语言中无END关键字。

逗号在C语言中被视为分隔符和运算符，作为优先级最低的运算符，运算结果为逗号表达式最右侧子表达式的值（如：(a,b,c,d)的值为d）。

5略第二章习题解答1.（1）答：26*26=676（2）答：26*10=260（3）答：{a,b,c,...,z,a0,a1,...,a9,aa,...,az,...,zz,a00,a01,...,zzz},共26+26*36+26*36*36=34658个2.构造产生下列语言的文法（1）{anbn|n≥0}解：对应文法为G(S) = ({S},{a,b},{ S→ε| aSb },S)（2）{anbmcp|n,m,p≥0}解：对应文法为G(S) = ({S,X,Y},{a,b,c},{S→aS|X,X→bX|Y,Y→cY|ε},S)（3）{an # bn|n≥0}∪{cn # dn|n≥0}解：对应文法为G(S) = ({S,X,Y},{a,b,c,d,#}, {S→X, S→Y,X→aXb|#,Y→cYd|# },S)（4）{w#wr# | w?{0,1}*,wr是w的逆序排列}解：G(S) = ({S,W,R},{0,1,#}, {S→W#, W→0W0|1W1|# },S)（5）任何不是以0打头的所有奇整数所组成的集合解：G(S) = ({S,A,B,I,J},{-,0,1,2,3,4,5,6,7,8,9},{S→J|IBJ,B→0B|IB|e, I→J|2|4|6|8, Jà1|3|5|7|9}, S)（6）所有偶数个0和偶数个1所组成的符号串集合解：对应文法为S→0A|1B|e，A→0S|1C B→0C|1S C→1A|0B3.描述语言特点（1）S→10S0S→aAA→bAA→a解：本文法构成的语言集为：L(G)={(10)nabma0n|n, m≥0}。

高中物理必修1第三章课后的习题答案

高中物理必修1第三章课后的习题答案
高中物理必修1第三章课后的习题答案
第三章：相互作用
第1节：重力基本相互作用
1．
（1）玻璃杯从桌子上掉下，在重力作用下，运动得越来越快；被掷出去的铅球，在重力作用下沿曲线落回地面；蹦蹦床在人的压力作用下，向下凹；橡皮筋在拉力作用下变得细长。

（2）人坐在凳子上，人对凳子有一个压力，该力的施力物体是人，受力物体是凳子。

2．略。

3．是位于同一点。

第2节：弹力
1．（略）
2．钢管受到3个力作用：重力G，地面的支持力F1、绳的拉力F2（图3-11）。

重力G的'施力物体是地球，地面的支持力F1的施力物体是地面、绳的拉力F2的施力物体是绳。

【高中物理必修1第三章课后的习题答案】。

算法竞赛入门经典1-3章习题答案

第一章习题1-1#include <stdio.h>int main(){int a,b,c;double d;scanf("%d%d%d",&a,&b,&c);d=(double)(a+b+c);printf("%.3lf\n",d/3.0);return 0;}习题1-2#include<stdio.h>int main(){int f;double c;scanf("%d",&f);c=5.0*(f-32)/9;printf("%.3lf\n",c);return 0;}习题1-3#include <stdio.h>int main(){int n;scanf("%d",&n);printf("%d\n",(n*(1+n))/2);return 0;}习题1-4#include <stdio.h>#include <math.h>#define pi 4.0*atan(1.0)int main(){int n;scanf("%d",&n);printf("%lf\n",sin((pi*n)/180));printf("%lf\n",cos((pi*n)/180));return 0;}习题1-5#include<stdio.h>#include<math.h>int main(){double x1,y1,x2,y2,a;scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);a=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));printf("%lf\n",a);return 0;}习题1-6#include <stdio.h>int main(){int n;scanf("%d",&n);if(n%2==0){printf("yes\n");}else{printf("no\n");}return 0;}习题1-7#include <stdio.h>int main(){int n;double a;scanf("%d",&n);a=n*95.0;if(a<300){printf("%.2lf\n",a);}else{printf("%.2lf\n",a*0.85);}return 0;}习题1-8#include <stdio.h>#include <math.h>int main(){double n;scanf("%lf",&n);printf("%.2lf",fabs(n));return 0;}习题1-9#include <stdio.h>int main(){int a,b,c;scanf("%d%d%d",&a,&b,&c);if((a*a+b*b==c*c)||(a*a+c*c==b*b)||(b*b+c*c==a*a)) {printf("yes\n");}else{printf("no\n");}return 0;}习题1-10#include <stdio.h>int main(){int n;scanf("%d",&n);if(n%4==0){if(n%100!=0){printf("yes\n");}else{if(n%400==0){printf("yes\n");}else{printf("no\n");}}}else{printf("no\n");}return 0;}第二章习题2-1#include <stdio.h>int main(){int n,count=0;scanf("%d",&n);while(n>0){count++;n=n/10;}printf("%d\n",count);return 0;}习题2-2#include <stdio.h>int main(){int a,b,c;for(int i=100;i<=999;i++){a=i%10;b=i/10%10;c=i/100;if(i==a*a*a+b*b*b+c*c*c){printf("%d\n",i);}}return 0;}习题2-3#include <stdio.h>int main(){int i,a,b,c;scanf("%d%d%d",&a,&b,&c);for(i=10;i<=100;i++){if(i%3==a&&i%5==b&&i%7==c){printf("%d\n",i);break;}if (i==100)printf("no answer\n");}return 0;}习题2-4#include <stdio.h>int main(){int i,j,k,n;scanf("%d",&n);for(i=n;i>0;i--){for(k=0;k<n-i;k++){printf("");}for(j=0;j<2*i-1;j++){printf("#");}printf("\n");}return 0;}习题2-5文件题，南邮竞赛基本不涉及。

半导体物理导论课后习题答案第1-3章

半导体物理导论课后习题答案第1-3章1.倒格子的实际意义是什么？一种晶体的正格矢和相应的倒格矢是否有一一对应的关系？解答：倒格子的实际意义是由倒格子组成的空间，实际上是状态空间空间，在晶体的X 射线衍射照片上的斑点实际上就是倒格子所对应的点子。

由正格子的基矢(a 1,a 2,a 3)就得到倒格子的矢量(b 1,b 2,b 3)，其中其中Ω是晶格原胞的体积。

由此可以唯一地确定相应的倒格子空间。

显然，倒格子与正格子之间有如下关系：所以一种晶体的正格矢和相应的倒格矢有一一对应的关系。

Ω⨯=Ω⨯=Ω⨯=213132321222a a b a a b a a b πππ，，ij i i πδ2=⋅b a (i,j=1,2,3)2.假设有一立方晶体，画出以下各晶面（1）（100）；（2）（110）；（3）（111）；（4）（100）；（5）（110）；（6）（111）3.已知Si的晶格常数或单胞的边长a=5.43089 Å, 求：（1）Si的原子体密度。

（2）(111)面、(110)面以及(100)面的原子面密度，比较哪个晶面的面密度最大？哪个晶面的面密度最小？解:(1)每个晶胞中有8个原子，晶胞体积为a 3，每个原子所占的空间体积为a 3/8，因此每立方厘米体积中的硅原子数为：原子体密度=8/a 3=8/(5.43×108)3=5×1022（个原子/cm 3）(2)（111）面为一个边长为的等边三角形，有效原子数为等边三角形的面积为个原子（面心原子）（顶角原子）25213313=⨯+⨯4521022212a a a S =⨯⨯=2a所以，(111)面的原子面密度为(110)面为一个边长为的长方形，有效原子数为长方形的面积为所以，(110)面的原子面密度为22524525aa ==等边三角形面积有效原子数2a a ⨯个原子（体对角线原子）（面心原子）（顶角原子）42212414=+⨯+⨯222a a a S =⨯=222224aa ==等边三角形面积有效原子数(100)面为一个边长为的正方形，有效原子数为正方形的面积为所以，(100)面的原子面密度为因此，(111)面的原子面密度∶(110)面的原子面密度∶(100)面的原子面密度为 ∶ ∶ = ∶ ∶1说明(111)面的原子面密度最高，(100)面的原子面密度最低。

工程化学基础课后习题答案

[二] Qv=-二八二.0八 kJ/mol Qp=-二八五.八
第四章第一节练习题
8. △rHm θ=-二四.八 kJ/mol 9. Q=四四.九九 kJ/g
第四章第二节练习题
1. [一] × [二] √ [三] × [四] × [五] × [六 ]√
2. [一] H二O[s] ＜H二O[l] ＜H二O[g] [二] 温度越高熵值越大
1. A
2. A
3. P[O二]=二一kPa P[N二]=七八kPa P[CO二]=一 kPa
P[CO二]=0.五kPa
4. 四二.八% 八一.五%
5. 小于五.六 SO二 NO CO二 HNO二 H二CO三
H二SO三 H二SOቤተ መጻሕፍቲ ባይዱ HNO三
第三章第一节练习题
1. [a] × [b] √ [c] ×
3. pH=四.九七
4. H三PO四>HF>HAc>NH三 5. [一] pH=三.七五 [二] pH=四.七六
.二五
[三] pH=九
6. [一] pH=四.七五六 [二] pH=四.六七
7. [一] pH=九.二五 [二] pH=九.二五四四
8. V=一一.八 cm三
第五章第二节练习题
1. [一] B D [二] C 2. Ks=二.二九*一0-一三 3. AgI沉淀生成,可能后有AgCl沉淀
负极： Fe二+ == Fe三++ e
正极： Ag++e == Ag
总反应：Fe二+ +Ag+ ==Fe三+ +Ag
E一=0.0二八六
E二=-0.0八九四
第五章第一节练习题

高中数学必修1课后习题答案完整版

高中数学必修1课后习题答案第一章集合与函数概念1．1集合1．1．1集合的含义与表示练习（第5页）1．用符号“∈”或“∉”填空：（1）设A 为所有亚洲国家组成的集合，则：中国_______A ，美国_______A ，印度_______A ，英国_______A ；（2）若2{|}A x x x ==，则1-_______A ；（3）若2{|60}B x x x =+-=，则3_______B ；（4）若{|110}C x N x =∈≤≤，则8_______C ，9.1_______C ． 1．（1）中国∈A ，美国∉A ，印度∈A ，英国∉A ；中国和印度是属于亚洲的国家，美国在北美洲，英国在欧洲．（2）1-∉A 2{|}{0,1}A x x x ===．（3）3∉B 2{|60}{3,2}B x x x =+-==-．（4）8∈C ，9.1∉C 9.1N ∉． 2．试选择适当的方法表示下列集合：（1）由方程290x -=的所有实数根组成的集合；（2）由小于8的所有素数组成的集合；（3）一次函数3y x =+与26y x =-+的图象的交点组成的集合；（4）不等式453x -<的解集．2．解：（1）因为方程290x -=的实数根为123,3x x =-=，所以由方程290x -=的所有实数根组成的集合为{3,3}-；（2）因为小于8的素数为2,3,5,7，所以由小于8的所有素数组成的集合为{2,3,5,7}；（3）由326y x y x =+⎧⎨=-+⎩，得14x y =⎧⎨=⎩，即一次函数3y x =+与26y x =-+的图象的交点为(1,4)，所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)}；（4）由453x -<，得2x <，所以不等式453x -<的解集为{|2}x x <．1．1．2集合间的基本关系练习（第7页）1．写出集合{,,}a b c 的所有子集．1．解：按子集元素个数来分类，不取任何元素，得∅；取一个元素，得{},{},{}a b c ；取两个元素，得{,},{,},{,}a b a c b c ；取三个元素，得{,,}a b c ，即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅．2．用适当的符号填空：（1）a ______{,,}a b c ；（2）0______2{|0}x x =；（3）∅______2{|10}x R x ∈+=；（4）{0,1}______N ；（5）{0}______2{|}x x x =；（6）{2,1}______2{|320}x x x -+=．2．（1）{,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素；（2）20{|0}x x ∈= 2{|0}{0}x x ==；（3）2{|10}x R x ∅=∈+= 方程210x +=无实数根，2{|10}x R x ∈+==∅；（4）{0,1}N （或{0,1}N ⊆） {0,1}是自然数集合N 的子集，也是真子集；（5）{0}2{|}x x x = （或2{0}{|}x x x ⊆=） 2{|}{0,1}x x x ==；（6）2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==．3．判断下列两个集合之间的关系：（1）{1,2,4}A =，{|8}B x x =是的约数；（2）{|3,}A x x k k N ==∈，{|6,}B x x z z N ==∈；（3）{|410}A x x x N +=∈是与的公倍数,，{|20,}B x x m m N +==∈．3．解：（1）因为{|8}{1,2,4,8}B x x ==是的约数，所以AB ；（2）当2k z =时，36k z =；当21k z =+时，363k z =+，即B 是A 的真子集，BA ；（3）因为4与10的最小公倍数是20，所以A B =．1．1．3集合的基本运算练习（第11页）1．设{3,5,6,8},{4,5,7,8}A B ==，求,A B A B ．1．解：{3,5,6,8}{4,5,7,8}{5,8}A B ==， {3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}AB ==．2．设22{|450},{|1}A x x x B x x =--===，求,AB A B ．2．解：方程2450x x --=的两根为121,5x x =-=，方程210x -=的两根为121,1x x =-=，得{1,5},{1,1}A B =-=-，即{1},{1,1,5}AB A B =-=-．3．已知{|}A x x =是等腰三角形，{|}B x x =是直角三角形，求,A B A B ．3．解：{|}A B x x =是等腰直角三角形，{|}AB x x =是等腰三角形或直角三角形．4．已知全集{1,2,3,4,5,6,7}U =，{2,4,5},{1,3,5,7}A B ==，求(),()()U U U AB A B 痧?．4．解：显然{2,4,6}U B =ð，{1,3,6,7}U A =ð，则(){2,4}U AB =ð，()(){6}U U A B =痧． 1．1集合习题1．1 （第11页） A 组1．用符号“∈”或“∉”填空：（1）237_______Q ；（2）23______N ；（3）π_______Q ；（4_______R ；（5Z ；（6）2_______N ．1．（1）237Q ∈ 237是有理数；（2）23N ∈ 239=是个自然数；（3）Q π∉ π是个无理数，不是有理数；（4R（5Z3=是个整数；（6）2N ∈ 2)5=是个自然数．2．已知{|31,}A x x k k Z ==-∈，用 “∈”或“∉” 符号填空：（1）5_______A ；（2）7_______A ；（3）10-_______A ． 2．（1）5A ∈；（2）7A ∉；（3）10A -∈．当2k =时，315k -=；当3k =-时，3110k -=-； 3．用列举法表示下列给定的集合：（1）大于1且小于6的整数；（2）{|(1)(2)0}A x x x =-+=；（3）{|3213}B x Z x =∈-<-≤．3．解：（1）大于1且小于6的整数为2,3,4,5，即{2,3,4,5}为所求；（2）方程(1)(2)0x x -+=的两个实根为122,1x x =-=，即{2,1}-为所求；（3）由不等式3213x -<-≤，得12x -<≤，且x Z ∈，即{0,1,2}为所求． 4．试选择适当的方法表示下列集合：（1）二次函数24y x =-的函数值组成的集合；（2）反比例函数2y x=的自变量的值组成的集合；（3）不等式342x x ≥-的解集．4．解：（1）显然有20x ≥，得244x -≥-，即4y ≥-，得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-；（2）显然有0x ≠，得反比例函数2y x =的自变量的值组成的集合为{|0}x x ≠；（3）由不等式342x x ≥-，得45x ≥，即不等式342x x ≥-的解集为4{|}5x x ≥．5．选用适当的符号填空：（1）已知集合{|233},{|2}A x x x B x x =-<=≥，则有：4-_______B ； 3-_______A ； {2}_______B ； B _______A ；（2）已知集合2{|10}A x x =-=，则有：1_______A ； {1}-_______A ； ∅_______A ； {1,1}-_______A ；（3）{|}x x 是菱形_______{|}x x 是平行四边形； {|}x x 是等腰三角形_______{|}x x 是等边三角形．5．（1）4B -∉； 3A -∉； {2}B ； BA ；2333x x x -<⇒>-，即{|3},{|2}A x x B x x =>-=≥；（2）1A ∈； {1}-A ； ∅A ； {1,1}-=A ； 2{|10}{1,1}A x x =-==-；（3）{|}x x 是菱形{|}x x 是平行四边形；菱形一定是平行四边形，是特殊的平行四边形，但是平行四边形不一定是菱形；{|}x x 是等边三角形{|}x x 是等腰三角形．等边三角形一定是等腰三角形，但是等腰三角形不一定是等边三角形．6．设集合{|24},{|3782}A x x B x x x =≤<=-≥-，求,AB A B ．6．解：3782x x -≥-，即3x ≥，得{|24},{|3}A x x B x x =≤<=≥，则{|2}AB x x =≥，{|34}A B x x =≤<．7．设集合{|9}A x x =是小于的正整数，{1,2,3},{3,4,5,6}B C ==，求A B ，AC ，()A B C ，()A B C ．7．解：{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数，则{1,2,3}AB =，{3,4,5,6}AC =，而{1,2,3,4,5,6}B C =，{3}B C =，则(){1,2,3,4,5,6}AB C =，(){1,2,3,4,5,6,7,8}A B C =．8．学校里开运动会，设{|}A x x =是参加一百米跑的同学，{|}B x x =是参加二百米跑的同学，{|}C x x =是参加四百米跑的同学，学校规定，每个参加上述的同学最多只能参加两项，请你用集合的语言说明这项规定，并解释以下集合运算的含义：（1）AB ；（2）A C ． 8．解：用集合的语言说明这项规定：每个参加上述的同学最多只能参加两项，即为()A B C =∅．（1）{|}A B x x =是参加一百米跑或参加二百米跑的同学；（2）{|}AC x x =是既参加一百米跑又参加四百米跑的同学．9．设{|}S x x =是平行四边形或梯形，{|}A x x =是平行四边形，{|}B x x =是菱形，{|}C x x =是矩形，求BC ，A B ð，S A ð．9．解：同时满足菱形和矩形特征的是正方形，即{|}BC x x =是正方形，平行四边形按照邻边是否相等可以分为两类，而邻边相等的平行四边形就是菱形，即{|}A B x x =是邻边不相等的平行四边形ð， {|}S A x x =是梯形ð．10．已知集合{|37},{|210}A x x B x x =≤<=<<，求()R AB ð，()R A B ð，()R A B ð，()R A B ð．10．解：{|210}A B x x =<<，{|37}A B x x =≤<，{|3,7}R A x x x =<≥或ð，{|2,10}R B x x x =≤≥或ð，得(){|2,10}R A B x x x =≤≥或ð， (){|3,7}R A B x x x =<≥或ð， (){|23,710}R A B x x x =<<≤<或ð，(){|2,3710}R AB x x x x =≤≤<≥或或ð．B 组1．已知集合{1,2}A =，集合B 满足{1,2}A B =，则集合B 有个．1．4 集合B 满足AB A =，则B A ⊆，即集合B 是集合A 的子集，得4个子集．2．在平面直角坐标系中，集合{(,)|}C x y y x ==表示直线y x =，从这个角度看，集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示什么？集合,C D 之间有什么关系？2．解：集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合，即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭，点(1,1)D 显然在直线y x =上，得D C ．3．设集合{|(3)()0,}A x x x a a R =--=∈，{|(4)(1)0}B x x x =--=，求,A B A B ．3．解：显然有集合{|(4)(1)0}{1,4}B x x x =--==，当3a =时，集合{3}A =，则{1,3,4},A B A B ==∅；当1a =时，集合{1,3}A =，则{1,3,4},{1}A B A B ==；当4a =时，集合{3,4}A =，则{1,3,4},{4}AB A B ==；当1a ≠，且3a ≠，且4a ≠时，集合{3,}A a =，则{1,3,4,},AB a A B ==∅．4．已知全集{|010}U AB x N x ==∈≤≤，(){1,3,5,7}U A B =ð，试求集合B ．4．解：显然{0,1,2,3,4,5,6,7,8,9,10}U =，由U AB =，得U B A ⊆ð，即()U UAB B =痧，而(){1,3,5,7}U A B =ð，得{1,3,5,7}U B =ð，而()U UB B =痧，即{0,2,4,6,8.9,10}B =．第一章集合与函数概念1．2函数及其表示1．2．1函数的概念练习（第19页）1．求下列函数的定义域：（1）1()47f x x =+；（2）()1f x =．1．解：（1）要使原式有意义，则470x +≠，即74x ≠-，得该函数的定义域为7{|}4x x ≠-；（2）要使原式有意义，则1030x x -≥⎧⎨+≥⎩，即31x -≤≤，得该函数的定义域为{|31}x x -≤≤． 2．已知函数2()32f x x x =+，（1）求(2),(2),(2)(2)f f f f -+-的值；（2）求(),(),()()f a f a f a f a -+-的值．2．解：（1）由2()32f x x x =+，得2(2)322218f =⨯+⨯=，同理得2(2)3(2)2(2)8f -=⨯-+⨯-=，则(2)(2)18826f f +-=+=，即(2)18,(2)8,(2)(2)26f f f f =-=+-=；（2）由2()32f x x x =+，得22()3232f a a a a a =⨯+⨯=+，同理得22()3()2()32f a a a a a -=⨯-+⨯-=-，则222()()(32)(32)6f a f a a a a a a +-=++-=，即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=．3．判断下列各组中的函数是否相等，并说明理由：（1）表示炮弹飞行高度h 与时间t 关系的函数21305h t t =-和二次函数21305y x x =-；（2）()1f x =和0()g x x =．3．解：（1）不相等，因为定义域不同，时间0t >；（2）不相等，因为定义域不同，0()(0)g x x x =≠．1．2．2函数的表示法练习（第23页）1．如图，把截面半径为25cm 的圆形木头锯成矩形木料，如果矩形的一边长为xcm ，面积为2ycm ，把y 表示为x 的函数． 1，y ==，且050x <<，即(050)y x =<<．2．下图中哪几个图象与下述三件事分别吻合得最好？请你为剩下的那个图象写出一件事．（1）我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学；（2）我骑着车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．2．解：图象（A ）对应事件（2），在途中遇到一次交通堵塞表示离开家的距离不发生变化；（A ）（B ）（C ）（D ）图象（B ）对应事件（3），刚刚开始缓缓行进，后来为了赶时间开始加速；图象（D ）对应事件（1），返回家里的时刻，离开家的距离又为零；图象（C ）我出发后，以为要迟到，赶时间开始加速，后来心情轻松，缓缓行进． 3．画出函数|2|y x =-的图象．3．解：2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩，图象如下所示．{|},{0,1}A x x B ==是锐角，从A 到B 的映射是“求正弦”，4．设与A 中元素60相对应的B 中的元素是什么？与B 中的元素2相对应的A 中元素是什么？4．解：因为3sin 60=，所以与A 中元素60相对应的B ；因为2sin 452=，所以与B 中的元素2相对应的A 中元素是45． 1．2函数及其表示习题1．2（第23页）1．求下列函数的定义域：（1）3()4xf x x =-；（2）()f x =（3）26()32f x x x =-+；（4）()1f x x =-．1．解：（1）要使原式有意义，则40x -≠，即4x ≠，得该函数的定义域为{|4}x x ≠；（2）x R ∈，()f x =即该函数的定义域为R ；（3）要使原式有意义，则2320x x -+≠，即1x ≠且2x ≠，得该函数的定义域为{|12}x x x ≠≠且；（4）要使原式有意义，则4010x x -≥⎧⎨-≠⎩，即4x ≤且1x ≠，得该函数的定义域为{|41}x x x ≤≠且．2．下列哪一组中的函数()f x 与()g x 相等？（1）2()1,()1x f x x g x x=-=-；（2）24(),()f x x g x ==；（3）2(),()f x x g x ==2．解：（1）()1f x x =-的定义域为R ，而2()1x g x x=-的定义域为{|0}x x ≠，即两函数的定义域不同，得函数()f x 与()g x 不相等；（2）2()f x x =的定义域为R ，而4()g x =的定义域为{|0}x x ≥，即两函数的定义域不同，得函数()f x 与()g x 不相等；（32x =，即这两函数的定义域相同，切对应法则相同，得函数()f x 与()g x 相等．3．画出下列函数的图象，并说出函数的定义域和值域．（1）3y x =；（2）8y x=；（3）45y x =-+；（4）267y x x =-+． 3．解：（1）定义域是(,)-∞+∞，值域是(,)-∞+∞；（2）定义域是(,0)(0,)-∞+∞，值域是(,0)(0,)-∞+∞；（3）定义域是(,)-∞+∞，值域是(,)-∞+∞；（4）定义域是(,)-∞+∞，值域是[2,)-+∞．4．已知函数2()352f x x x =-+，求(f ，()f a -，(3)f a +，()(3)f a f +．4．解：因为2()352f x x x =-+，所以2(3(5(28f =⨯-⨯+=+即(8f =+同理，22()3()5()2352f a a a a a -=⨯--⨯-+=++，即2()352f a a a -=++；22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++，即2(3)31314f a a a +=++；22()(3)352(3)3516f a f a a f a a +=-++=-+，即2()(3)3516f a f a a +=-+．5．已知函数2()6x f x x +=-，（1）点(3,14)在()f x 的图象上吗？（2）当4x =时，求()f x 的值；（3）当()2f x =时，求x 的值．5．解：（1）当3x =时，325(3)14363f +==-≠-，即点(3,14)不在()f x 的图象上；（2）当4x =时，42(4)346f +==--，即当4x =时，求()f x 的值为3-；（3）2()26x f x x +==-，得22(6)x x +=-，即14x =．6．若2()f x x bx c =++，且(1)0,(3)0f f ==，求(1)f -的值．6．解：由(1)0,(3)0f f ==，得1,3是方程20x bx c ++=的两个实数根，即13,13b c +=-⨯=，得4,3b c =-=，即2()43f x x x =-+，得2(1)(1)4(1)38f -=--⨯-+=，即(1)f -的值为8．7．画出下列函数的图象：（1）0,0()1,0x F x x ≤⎧=⎨>⎩；（2）()31,{1,2,3}G n n n =+∈．7．图象如下：8．如图，矩形的面积为10，如果矩形的长为x ，宽为y ，对角线为d ，周长为l ，那么你能获得关于这些量的哪些函数？8．解：由矩形的面积为10，即10xy =，得10(0)y x x=>，10(0)x y y =>，由对角线为d ，即d =，得(0)d x =>，由周长为l ，即22l x y =+，得202(0)l x x x =+>，另外2()l x y =+，而22210,xy d x y ==+，得(0)l d ===>，即(0)l d =>．9．一个圆柱形容器的底部直径是dcm ，高是hcm ，现在以3/vcm s 的速度向容器内注入某种溶液．求溶液内溶液的高度xcm 关于注入溶液的时间ts 的函数解析式，并写出函数的定义域和值域．9．解：依题意，有2()2dx vt π=，即24v x t d π=，显然0x h ≤≤，即240v t h dπ≤≤，得204h d t v π≤≤，得函数的定义域为2[0,]4h d vπ和值域为[0,]h ． 10．设集合{,,},{0,1}A a b c B ==，试问：从A 到B 的映射共有几个？并将它们分别表示出来．10．解：从A 到B 的映射共有8个．分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩，()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩，()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩．Ｂ组1．函数()r f p =的图象如图所示．（1）函数()r f p =的定义域是什么？（2）函数()r f p =的值域是什么？（3）r 取何值时，只有唯一的p 值与之对应？1．解：（1）函数()r f p =的定义域是[5,0][2,6)-；（2）函数()r f p =的值域是[0,)+∞；（3）当5r >，或02r ≤<时，只有唯一的p 值与之对应．2．画出定义域为{|38,5}x x x -≤≤≠且，值域为{|12,0}y y y -≤≤≠的一个函数的图象．（1）如果平面直角坐标系中点(,)P x y 的坐标满足38x -≤≤，12y -≤≤，那么其中哪些点不能在图象上？（2）将你的图象和其他同学的相比较，有什么差别吗？2．解：图象如下，（1）点(,0)x 和点(5,)y 不能在图象上；（2）省略．3．函数()[]f x x =的函数值表示不超过x 的最大整数，例如，[ 3.5]4-=-，[2.1]2=．当( 2.5,3]x ∈-时，写出函数()f x 的解析式，并作出函数的图象．3．解：3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4．如图所示，一座小岛距离海岸线上最近的点P的距离是2km，从点P沿海岸正东12km处有一个城镇．（1）假设一个人驾驶的小船的平均速度为3/km h ，步行的速度是5/km h ，t （单位：h ）表示他从小岛到城镇的时间，x （单位：km ）表示此人将船停在海岸处距P 点的距离．请将t 表示为x 的函数．（2）如果将船停在距点P 4km 处，那么从小岛到城镇要多长时间（精确到1h ）？4．解：（112x -，得1235x t -=+，(012)x ≤≤，即1235x t -=+，(012)x ≤≤．（2）当4x =时，12483()355t h -=+=≈．第一章集合与函数概念1．3函数的基本性质1．3．1单调性与最大（小）值练习（第32页）1．请根据下图描述某装配线的生产效率与生产线上工人数量间的关系．1．答：在一定的范围内，生产效率随着工人数量的增加而提高，当工人数量达到某个数量时，生产效率达到最大值，而超过这个数量时，生产效率随着工人数量的增加而降低．由此可见，并非是工人越多，生产效率就越高．2．整个上午(8:0012:00)天气越来越暖，中午时分(12:0013:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后，天气转暖，直到太阳落山(18:00)才又开始转凉.画出这一天8:0020:00期间气温作为时间函数的一个可能的图象，并说出所画函数的单调区间.2．解：图象如下[8,12]是递增区间，[12,13]是递减区间，[13,18]是递增区间，[18,20]是递减区间．3．根据下图说出函数的单调区间，以及在每一单调区间上，函数是增函数还是减函数.3．解：该函数在[1,0]-上是减函数，在[0,2]上是增函数，在[2,4]上是减函数，在[4,5]上是增函数．4．证明函数()21f x x =-+在R 上是减函数.4．证明：设12,x x R ∈，且12x x <，因为121221()()2()2()0f x f x x x x x -=--=->，即12()()f x f x >，所以函数()21f x x =-+在R 上是减函数.5．设()f x 是定义在区间[6,11]-上的函数.如果()f x 在区间[6,2]--上递减，在区间[2,11]-上递增，画出()f x 的一个大致的图象，从图象上可以发现(2)f -是函数()f x 的一个 .5．最小值．1．3．2单调性与最大（小）值练习（第36页）1．判断下列函数的奇偶性：（1）42()23f x x x =+；（2）3()2f x x x =- （3）21()x f x x+=；（4）2()1f x x =+. 1．解：（1）对于函数42()23f x x x =+，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=，所以函数42()23f x x x =+为偶函数；（2）对于函数3()2f x x x =-，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-，所以函数3()2f x x x =-为奇函数；（3）对于函数21()x f x x+=，其定义域为(,0)(0,)-∞+∞，因为对定义域内每一个x 都有22()11()()x x f x f x x x-++-==-=--，所以函数21()x f x x+=为奇函数；（4）对于函数2()1f x x =+，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=，所以函数2()1f x x =+为偶函数.2.已知()f x 是偶函数，()g x 是奇函数，试将下图补充完整.2．解：()f x 是偶函数，其图象是关于y 轴对称的；()g x 是奇函数，其图象是关于原点对称的．习题1.3A 组1.画出下列函数的图象，并根据图象说出函数()y f x =的单调区间，以及在各单调区间上函数()y f x =是增函数还是减函数.（1）256y x x =--；（2）29y x =-. 1．解：（1）函数在5(,)2-∞上递减；函数在5[,)2+∞上递增；（2）函数在(,0)-∞上递增；函数在[0,)+∞上递减.2.证明：（1）函数2()1f x x =+在(,0)-∞上是减函数；（2）函数1()1f x x=-在(,0)-∞上是增函数. 2．证明：（1）设120x x <<，而2212121212()()()()f x f x x x x x x x -=-=+-，由12120,0x x x x +<-<，得12()()0f x f x ->，即12()()f x f x >，所以函数2()1f x x =+在(,0)-∞上是减函数；（2）设120x x <<，而1212211211()()x x f x f x x x x x --=-=，由12120,0x x x x >-<，得12()()0f x f x -<，即12()()f x f x <，所以函数1()1f x x=-在(,0)-∞上是增函数. 3.探究一次函数()y mx b x R =+∈的单调性，并证明你的结论.3．解：当0m >时，一次函数y mx b =+在(,)-∞+∞上是增函数；当0m <时，一次函数y mx b =+在(,)-∞+∞上是减函数，令()f x mx b =+，设12x x <，而1212()()()f x f x m x x -=-，当0m >时，12()0m x x -<，即12()()f x f x <，得一次函数y mx b =+在(,)-∞+∞上是增函数；当0m <时，12()0m x x ->，即12()()f x f x >，得一次函数y mx b =+在(,)-∞+∞上是减函数.4.一名心率过速患者服用某种药物后心率立刻明显减慢，之后随着药力的减退，心率再次慢慢升高.画出自服药那一刻起，心率关于时间的一个可能的图象（示意图）.4．解：自服药那一刻起，心率关于时间的一个可能的图象为5.某汽车租赁公司的月收益y 元与每辆车的月租金x 元间的关系为21622100050x y x =-+-，那么，每辆车的月租金多少元时，租赁公司的月收益最大？最大月收益是多少？5．解：对于函数21622100050x y x =-+-，当162405012()50x =-=⨯-时，max 307050y =（元），即每辆车的月租金为4050元时，租赁公司最大月收益为307050元．6.已知函数()f x 是定义在R 上的奇函数，当0x ≥时，()(1)f x x x =+.画出函数()f x的图象，并求出函数的解析式.6．解：当0x <时，0x ->，而当0x ≥时，()(1)f x x x =+，即()(1)f x x x -=--，而由已知函数是奇函数，得()()f x f x -=-，得()(1)f x x x -=--，即()(1)f x x x =-，所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.已知函数2()2f x x x =-，2()2([2,4])g x x x x =-∈.（1）求()f x ，()g x 的单调区间；（2）求()f x ，()g x 的最小值.1．解：（1）二次函数2()2f x x x =-的对称轴为1x =，则函数()f x 的单调区间为(,1),[1,)-∞+∞，且函数()f x 在(,1)-∞上为减函数，在[1,)+∞上为增函数，函数()g x 的单调区间为[2,4]，且函数()g x 在[2,4]上为增函数；（2）当1x =时，min ()1f x =-，因为函数()g x 在[2,4]上为增函数，所以2min ()(2)2220g x g ==-⨯=．2.如图所示，动物园要建造一面靠墙的2间面积相同的矩形熊猫居室，如果可供建造围墙的材料总长是30m ，那么宽x （单位：m ）为多少才能使建造的每间熊猫居室面积最大？每间熊猫居室的最大面积是多少？2．解：由矩形的宽为x m ，得矩形的长为3032x m -，设矩形的面积为S ，则23033(10)22x x x S x --==-，当5x =时，2max 37.5S m =，即宽5x =m 才能使建造的每间熊猫居室面积最大，且每间熊猫居室的最大面积是18.75m^2．3.已知函数()f x 是偶函数，而且在(0,)+∞上是减函数，判断()f x 在(,0)-∞上是增函数还是减函数，并证明你的判断.3．判断()f x 在(,0)-∞上是增函数，证明如下：设120x x <<，则120x x ->->，因为函数()f x 在(0,)+∞上是减函数，得12()()f x f x -<-，又因为函数()f x 是偶函数，得12()()f x f x <，所以()f x 在(,0)-∞上是增函数．复习参考题A 组1．用列举法表示下列集合：（1）2{|9}A x x ==；（2）{|12}B x N x =∈≤≤；（3）2{|320}C x x x =-+=.1．解：（1）方程29x =的解为123,3x x =-=，即集合{3,3}A =-；（2）12x ≤≤，且x N ∈，则1,2x =，即集合{1,2}B =；（3）方程2320x x -+=的解为121,2x x ==，即集合{1,2}C =．2．设P 表示平面内的动点，属于下列集合的点组成什么图形？（1）{|}P PA PB =(,)A B 是两个定点；（2）{|3}P PO cm =()O 是定点.2．解：（1）由PA PB =，得点P 到线段AB 的两个端点的距离相等，即{|}P PA PB =表示的点组成线段AB 的垂直平分线；（2）{|3}P PO cm =表示的点组成以定点O 为圆心，半径为3cm 的圆．3.设平面内有ABC ∆，且P 表示这个平面内的动点，指出属于集合{|}{|}P PA PB P PA PC ==的点是什么.3．解：集合{|}P PA PB =表示的点组成线段AB 的垂直平分线，集合{|}P PA PC =表示的点组成线段AC 的垂直平分线，得{|}{|}P PA PB P PA PC ==的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点，即ABC ∆的外心．4.已知集合2{|1}A x x ==，{|1}B x ax ==.若B A ⊆，求实数a 的值.4．解：显然集合{1,1}A =-，对于集合{|1}B x ax ==，当0a =时，集合B =∅，满足B A ⊆，即0a =；当0a ≠时，集合1{}B a =，而B A ⊆，则11a =-，或11a =，得1a =-，或1a =，综上得：实数a 的值为1,0-，或1．5.已知集合{(,)|20}A x y x y =-=，{(,)|30}B x y x y =+=，{(,)|23}C x y x y =-=，求A B ，A C ，()()A B B C .5．解：集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭，即{(0,0)}A B =；集合20(,)|23x y AC x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭，即A C =∅；集合3039(,)|{(,)}2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭；则39()(){(0,0),(,)}55A B B C =-. 6.求下列函数的定义域：（1）y =（2）||5y x =-. 6．解：（1）要使原式有意义，则2050x x -≥⎧⎨+≥⎩，即2x ≥，得函数的定义域为[2,)+∞；（2）要使原式有意义，则40||50x x -≥⎧⎨-≠⎩，即4x ≥，且5x ≠，得函数的定义域为[4,5)(5,)+∞． 7.已知函数1()1x f x x-=+，求：（1）()1(1)f a a +≠-；（2）(1)(2)f a a +≠-.7．解：（1）因为1()1x f x x-=+，所以1()1a f a a -=+，得12()1111a f a a a-+=+=++，即2()11f a a+=+；（2）因为1()1x f x x-=+，所以1(1)(1)112a a f a a a -++==-+++，即(1)2a f a a +=-+． 8.设221()1x f x x+=-，求证：50 （1）()()f x f x -=；（2）1()()f f x x=-. 8．证明：（1）因为221()1x f x x+=-，所以22221()1()()1()1x x f x f x x x+-+-===---，即()()f x f x -=；（2）因为221()1x f x x+=-，所以222211()11()()111()x x f f x x x x++===---，即1()()f f x x=-. 9.已知函数2()48f x x kx =--在[5,20]上具有单调性，求实数k 的取值范围.9．解：该二次函数的对称轴为8k x =，函数2()48f x x kx =--在[5,20]上具有单调性，则208k ≥，或58k ≤，得160k ≥，或40k ≤，即实数k 的取值范围为160k ≥，或40k ≤．10．已知函数2y x -=，（1）它是奇函数还是偶函数？（2）它的图象具有怎样的对称性？（3）它在(0,)+∞上是增函数还是减函数？（4）它在(,0)-∞上是增函数还是减函数？10．解：（1）令2()f x x -=，而22()()()f x x x f x ---=-==，即函数2y x -=是偶函数；（2）函数2y x -=的图象关于y 轴对称；（3）函数2y x -=在(0,)+∞上是减函数；（4）函数2y x -=在(,0)-∞上是增函数．B 组1.学校举办运动会时，高一（1）班共有28名同学参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳比赛和田径比赛的有3人，同时参加游泳比赛和球类比赛的有3人，没有人同时参加三项比赛.问同时参加田径和球类比赛的有多少人？只参加游泳一项比赛的有多少人？1．解：设同时参加田径和球类比赛的有x 人，则158143328x ++---=，得3x =，只参加游泳一项比赛的有15339--=（人），即同时参加田径和球类比赛的有3人，只参加游泳一项比赛的有9人．2.已知非空集合2{|}A x R x a =∈=，试求实数a 的取值范围.2．解：因为集合A ≠∅，且20x ≥，所以0a ≥．3.设全集{1,2,3,4,5,6,7,8,9}U =，(){1,3}U AB =ð，(){2,4}U A B =ð，求集合B . 3．解：由(){1,3}U AB =ð，得{2,4,5,6,7,8,9}A B =，集合A B 里除去()U A B ð，得集合B ，所以集合{5,6,7,8,9}B =.4.已知函数(4),0()(4),0x x x f x x x x +≥⎧=⎨-<⎩.求(1)f ，(3)f -，(1)f a +的值. 4．解：当0x ≥时，()(4)f x x x =+，得(1)1(14)5f =⨯+=；当0x <时，()(4)f x x x =-，得(3)3(34)21f -=-⨯--=；(1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩． 5.证明：（1）若()f x ax b =+，则1212()()()22x x f x f x f ++=；（2）若2()g x x ax b =++，则1212()()()22x x g x g x g ++≤. 5．证明：（1）因为()f x ax b =+，得121212()()222x x x x a f a b x x b ++=+=++， 121212()()()222f x f x ax b ax b a x x b ++++==++，所以1212()()()22x x f x f x f ++=；（2）因为2()g x x ax b =++，得22121212121()(2)()242x x x x g x x x x a b ++=++++， 22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()()22x x x x a b +=+++，因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤，即222212121211(2)()42x x x x x x ++≤+，所以1212()()()22x x g x g x g ++≤. 6.（1）已知奇函数()f x 在[,]a b 上是减函数，试问：它在[,]b a --上是增函数还是减函数？（2）已知偶函数()g x 在[,]a b 上是增函数，试问：它在[,]b a --上是增函数还是减函数？6．解：（1）函数()f x 在[,]b a --上也是减函数，证明如下：设12b x x a -<<<-，则21a x x b <-<-<，因为函数()f x 在[,]a b 上是减函数，则21()()f x f x ->-，又因为函数()f x 是奇函数，则21()()f x f x ->-，即12()()f x f x >，所以函数()f x 在[,]b a --上也是减函数；（2）函数()g x 在[,]b a --上是减函数，证明如下：设12b x x a -<<<-，则21a x x b <-<-<，因为函数()g x 在[,]a b 上是增函数，则21()()g x g x -<-，又因为函数()g x 是偶函数，则21()()g x g x <，即12()()g x g x >，所以函数()g x 在[,]b a --上是减函数． 7.《中华人民共和国个人所得税》规定，公民全月工资、薪金所得不超过2000元的部分不必纳税，超过2000元的部分为全月应纳税所得额.此项税款按下表分段累计计算：某人一月份应交纳此项税款为26.78元，那么他当月的工资、薪金所得是多少？7．解：设某人的全月工资、薪金所得为x 元，应纳此项税款为y 元，则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩由该人一月份应交纳此项税款为26.78元，得25004000x <≤，25(2500)10%26.78x +-⨯=，得2517.8x =，所以该人当月的工资、薪金所得是2517.8元．第三章函数的应用3．1函数与方程练习（P88）1.(1)令f(x)=-x2+3x+5,作出函数f(x)的图象(图3-1-2-7(1))，它与x轴有两个交点，所以方程-x2+3x+5=0有两个不相等的实数根.(2)2x(x-2)=-3可化为2x2-4x+3=0，令f(x)=2x2-4x+3,作出函数f(x)的图象(图3-1-2-7(2))，它与x轴没有交点，所以方程2x(x-2)=-3无实数根.(3)x2=4x-4可化为x2-4x+4=0,令f(x)=x2-4x+4,作出函数f(x)的图象(图3-1-2-7(3))，它与x轴只有一个交点(相切)，所以方程x2=4x-4有两个相等的实数根.(4)5x2+2x=3x2+5可化为2x2+2x-5=0,令f(x)=2x2+2x-5,作出函数f(x)的图象(图3-1-2-7(4))，它与x轴有两个交点，所以方程5x2+2x=3x2+5有两个不相等的实数根.图3-1-2-72.(1)作出函数图象(图3-1-2-8(1)),因为f(1)=1>0,f(1.5)=-2.875<0,所以f(x)=-x3-3x+5在区间(1,1.5)上有一个零点.又因为f(x)是(-∞,+∞)上的减函数，所以f(x)=-x3-3x+5在区间(1,1.5)上有且只有一个零点.(2)作出函数图象(图3-1-2-8(2)),因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x-2)-3在区间(3,4)上有一个零点.又因为f(x)=2x·ln(x-2)-3在(2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点.(3)作出函数图象(图3-1-2-8(3)),因为f(0)<0,f(1)>0,所以f(x)=e x-1+4x-4在区间(0,1)上有一个零点.又因为f(x)=e x-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点.(4)作出函数图象(图3-1-2-8(4)),因为f(-4)<0,f(-3)>0,f(-2)<0,f(2)<0,f(3)>0,所以f(x)=3(x+2)(x-3)(x+4)+x在(-4,-3),(-3,-2),(2,3)上各有一个零点.图3-1-2-8练习（P91）1.由题设可知f(0)=-1.4<0,f(1)=1.6>0,于是f(0)·f(1)<0,所以函数f(x)在区间(0，1)内有一个零点x0.下面用二分法求函数f(x)=x3+1.1x2+0.9x-1.4在区间(0，1)内的零点.取区间(0，1)的中点x1=0.5,用计算器可算得f(0.5)=-0.55.因为f(0.5)·f(1)<0,所以x0∈(0.5,1).再取区间(0.5，1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32.因为f(0.5)·f(0.75)<0,所以x0∈(0.5,0.75).同理,可得x0∈(0.625,0.75)，x0∈(0.625,0.687 5)，x0∈(0.656 25,0.687 5).由于|0.687 5-0.656 25|=0.031 25<0.1,所以原方程的近似解可取为0.656 25.2.原方程可化为x+lgx-3=0,令f(x)=x+lgx-3,用计算器可算得f(2)≈-0.70,f(3)≈0.48.于是f(2)·f(3)<0,所以这个方程在区间(2,3)内有一个解x0.下面用二分法求方程x=3-lgx在区间(2,3)的近似解.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)≈-0.10.因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.562 5,2.625),x0∈(2.562 5,2.593 75),x0∈(2.578 125,2.593 75),x0∈(2.585 937 5,2.59 375).由于|2.585 937 5-2.593 75|=0.007 812 5<0.01,所以原方程的近似解可取为2.593 75.习题3.1 A组（P92）1.A,C 点评：需了解二分法求函数的近似零点的条件.2.由x,f(x)的对应值表可得f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,又根据“如果函数y=f(x)在区间［a,b］上的图象是连续不断的一条曲线，并且f(a)·f(b)<0，那么函数y=f(x)在区间(a,b)内有零点.”可知函数f(x)分别在区间(2，3)，(3，4)，(4，5)内有零点.3.原方程即(x+1)(x-2)(x-3)-1=0,令f(x)=(x+1)(x-2)(x-3)-1,可算得f(-1)=-1,f(0)=5.于是f(-1)·f(0)<0,所以这个方程在区间(-1,0)内有一个解. 下面用二分法求方程(x+1)(x-2)(x-3)=1在区间(-1，0)内的近似解.取区间(-1，0)的中点x1=-0.5,用计算器可算得f(-0.5)=3.375.因为f(-1)·f(-0.5)<0,所以x0∈(-1,-0.5).再取(-1，-0.5)的中点x2=-0.75,用计算器可算得f(-0.75)≈1.58.因为f(-1)·f(-0.75)<0,所以x0∈(-1,-0.75).同理,可得x0∈(-1,-0.875)，x0∈(-0.937 5,-0.875).由于|(-0.875)-(-0.937 5)|=0.062 5<0.1,所以原方程的近似解可取为-0.937 5.4.原方程即0.8x-1-lnx=0,令f(x)=0.8x-1-lnx,f(0)没有意义，用计算器算得f(0.5)≈0.59,f(1)=-0.2.于是f(0.5)·f(1)<0,所以这个方程在区间(0.5,1)内有一个解.下面用二分法求方程0.8x-1=lnx在区间(0，1)内的近似解.取区间(0.5，1)的中点x1=0.75,用计算器可算得f(0.75)≈0.13.因为f (0.75)·f (1)<0,所以x 0∈(0.75,1).再取(0.75,1)的中点x 2=0.875,用计算器可算得f (0.875)≈-0.04.因为f (0.875)·f (0.75)<0,所以x 0∈(0.75,0.875).同理,可得x 0∈(0.812 5,0.875)，x 0∈(0.812 5,0.843 75).由于|0.812 5-0.843 75|=0.031 25<0.1,所以原方程的近似解可取为0.843 75.5.由题设有f (2)≈-0.31<0,f (3)≈0.43>0,于是f (2)·f (3)<0,所以函数f (x )在区间(2，3)内有一个零点.下面用二分法求函数f (x )=lnx x2-在区间(2，3)内的近似解. 取区间(2，3)的中点x 1=2.5,用计算器可算得f (2.5)≈0.12.因为f (2)·f (2.5)<0,所以x 0∈(2,2.5).再取(2，2.5)的中点x 2=2.25,用计算器可算得f (2.25)≈-0.08.因为f (2.25)·f (2.5)<0,所以x 0∈(2.25,2.5).同理,可得x 0∈(2.25,2.375)，x 0∈(2.312 5,2.375),x 0∈(2.343 75,2.375),x 0∈(2.343 75,2.359 375),x 0∈(2.343 75,2.351 562 5),x 0∈(2.343 75,2.347 656 25).由于|2.343 75-2.347 656 25|=0.003 906 25<0.01,所以原方程的近似解可取为2.347 656 25.B 组1.将系数代入求根公式x 得x =223(3)42(1)22±--⨯⨯-⨯=4173+, 所以方程的两个解分别为x 1=4173+,x 2=4173-.下面用二分法求方程的近似解.取区间(1.775,1.8)和(-0.3,-0.275),令f (x )=2x 2-3x -1.在区间(1.775,1.8)内用计算器可算得f (1.775)=-0.023 75,f (1.8)=0.08.于是f (1.775)·f (1.8)<0.所以这个方程在区间(1.775,1.8)内有一个解.由于|1.8-1.775|=0.025<0.1,所以原方程在区间(1.775,1.8)内的近似解可取为1.8.同理,可得方程在区间(-0.3,-0.275)内的近似解可取为-0.275.所以方程精确到0.1的近似解分别是1.8和-0.3.2.原方程即x3-6x2-3x+5=0,令f(x)=x3-6x2-3x+5,函数图象如下图所示.图3-1-2-9所以这个方程在区间(-2,0),(0,1),(6,7)内各有一个解.取区间(-2，0)的中点x1=-1,用计算器可算得f(-1)=1.因为f(-2)·f(-1)<0,所以x0∈(-2,-1).再取(-2，-1)的中点x2=-1.5,用计算器可算得f(-1.5)=-7.375.因为f(-1.5)·f(-1)<0,所以x0∈(-1.5,-1).同理,可得x0∈(-1.25,-1)，x0∈(-1.125,-1),x0∈(-1.125,-1.062 5).由于|(-1.062 5)-(-1.125)|=0.062 5<0.1,所以原方程在区间(-2，0)内的近似解可取为-1.062 5.同理,可得原方程在区间(0，1)内的近似解可取为0.7,在区间(6，7)内的近似解可取为6.3.3.(1)由题设有g(x)=2-［f(x)］2=2-(x2+3x+2)2=-x4-6x3-13x2-12x-2.(2)函数图象如下图所示.图3-1-2-10(3)由图象可知，函数g(x)分别在区间(-3，-2)和区间(-1，0)内各有一个零点.取区间(-3，-2)的中点x1=-2.5,用计算器可算得g(-2.5)=0.187 5.因为g(-3)·g(-2.5)<0,所以x0∈(-3,-2.5).再取(-3，-2.5)的中点x2=-2.75,用计算器可算得g(-2.75)≈0.28.因为g(-3)·g(-2.75)<0,所以x0∈(-3,-2.75).同理,可得x0∈(-2.875,-2.75)，x0∈(-2.812 5,-2.75).由于|-2.75-(-2.812 5)|=0.062 5<0.1,所以原方程在区间(-3，-2)内的近似解可取为-2.812 5.同样可求得函数在区间(-1,0)内的零点约为-0.2.所以函数g(x)精确到0.1的零点约为-2.8或-0.2.点评：第2、3题采用信息技术画出函数图象,并据此明确函数零点所在的区间.在教学中,如果没有信息技术条件,建议教师直接给出函数图象或零点所在区间.第三章复习参考题A组（P112）1.C2.C3.设经过时间t后列车离C地的距离为y，则y=200100,02,100200,2 5.t tt t-≤≤⎧⎨-<≤⎩图3-24.(1)圆柱形; (2)上底小、下底大的圆台形;(3)上底大、下底小的圆台形; (4)呈下大上小的两节圆柱形. 图略.图3-35.令f(x)=2x3-4x2-3x+1,函数图象如图3-3所示:函数分别在区间(-1,0)、(0,1)和区间(2,3)内各有一个零点,所以方程2x3-4x2-3x+1=0的最大的根应在区间(2,3)内.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)=-0.25.因为f(2.5)·f(3)<0,所以x0∈(2.5,3). 再取(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈4.09.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.5,2.5625),x0∈(2.5,2.53125),x0∈(2.515625,2.53125),x0∈(2.515625,2.5234375).由于|2.523 437 5-2.515 625|=0.007 812 5<0.01,所以原方程的最大根约为2.523 437 5.6.令lgx =x 1,即得方程lgx x 1-=0,再令g (x )=lgx x1-,用二分法求得交点的横坐标约为2.5.图3-47.如图,作DE ⊥AB,垂足为E.由已知可得∠ADB=90°.因为AD=x ,AB=4,于是AD 2=AE×AB,即AE=AB AD 2=42x . 所以CD=AB-2AE=4-2×42x =422x -. 于是y =AB+BC+CD+AD=4+x +422x -+x =22x -+2x +8. 由于AD>0,AE>0,CD>0,所以x >0,42x >0,422x ->0,解得0<x <22. 所以所求的函数为y =22x -+2x +8,0<x <22. 8.(1)由已知可得N=N 0(λe 1)t .因为λ是正常数,e >1,所以e λ>1,即0<λe1<1. 又N 0是正常数,所以N=N 0(λe1)t 是在于t 的减函数. (2)N=N 0e -λt ,因为e -λt =0N N ,所以-λt =ln 0N N ,即t =λ1-ln 0N N . (3)当N=20N 时,t =λ1-002N N =λ1-ln 2. 9.因为f (1)=-3+12+8=17>0,f (2)=-3×8+12×2+8=8>0,f (3)<0,所以,下次生产应在两个月后开始.B 组1.厂商希望的是甲曲线;客户希望的是乙曲线.2.函数的解析式为y=f(t)=22,01, 2(2)12,22.tt tt<≤⎪⎪⎪⎪--+<≤⎨>⎪⎩函数的图象为图3-5备课资料［备选例题］【例】对于函数f(x)=ax2+(b+1)x+b-2(a≠0)，若存在实数x0，使f(x0)=x0成立，则称x0为f(x)的不动点.（1）当a=2,b=-2时，求f(x)的不动点；（2）若对于任何实数b，函数f(x)恒有两个相异的不动点，求实数a的取值范围.解：(1)f(x)=ax2+(b+1)x+b-2(a≠0),当a=2,b=-2时,f(x)=2x2-x-4,设x为其不动点,即2x2-x-4=x，则2x2-2x-4=0,解得x1=-1,x2=2,即f(x)的不动点为-1,2．(2)由f(x)=x,得ax2+bx+b-2=0.关于x的方程有相异实根,则b2-4a(b-2)>0,即b2-4ab+8a>0.又对所有的b∈R,b2-4ab+8a>0恒成立,故有(4a)2-4·8a<0,得0<a<2.。

电路分析基础第四版课后习题第一章第二章第三章第四章答案

+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
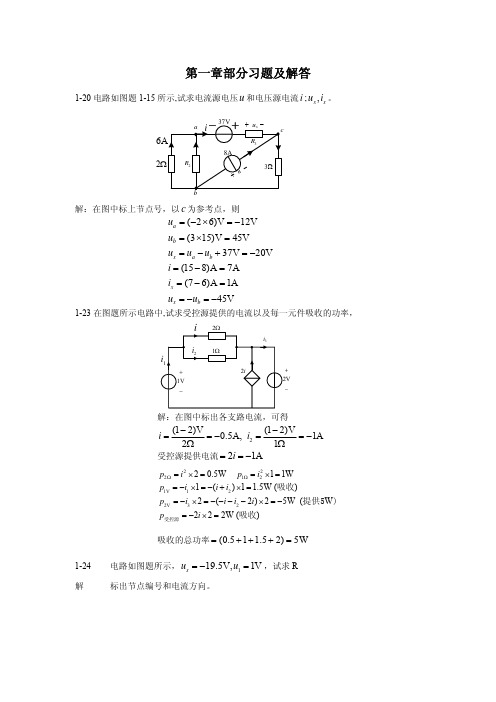
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ，列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示，试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向，
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2

软件工程课后习题_第1,2,3章

第一章：一.判断题：1.软件就程序，编软件就是编写程序。

（）2.软件危机的主要表现是软件需求增加，软件价格上升。

()3.软件工程科学出现的主要原因是软件危机的出现。

（）4.与计算机科学的理论研究不同，软件工程是一门原理性学科（）二.选择题1.在下列选项中，（）不是软件的特征A系统性与复杂性 B 可靠性与一致性C 抽象性与智能性D 有形性与可控性2.软件危机的主要原因是：A软件工具落后 B 软件生产能力不足C 对软件的认识不够D 软件本身的特点及开发方法3.下列说法正确是的是A 20世纪50年代提出了软件工程的概念B 20世纪60年代提出了软件工程的概念C 20世纪70年代提出了客户机/服务器技术D 20世纪80年代软件工程学达到成熟4.( )是将系统化的规范的可定量的方法应用于软件的开发，运行和维护的过程。

它包括方法、工具和过程三个要素A 软件生命周期B 软件测试C 软件工程D 软件过程5.在下列选项中，（）不属于软件工程学科索要研究的基本内容。

A 软件工程材料B 软件工程目标C 软件工程原理D 软件工程过程6.软件工程的三要素是（）A技术，方法和工具 B 方法，对象和类 C 方法，工具和过程 D 过程，模型和方法7.用来辅助软件开发，运行，维护，管理，支持等过程中的活动的软件成为软件开发工具，通常也称为（）工具A CADB CAIC CAMD CASE三简答题1.与计算机硬件相比，计算机软件有哪些特点？2.软件就是程序吗？如何定义软件？3.什么是软件危机？是什么原因导致了软件危机？4.为什么说软件工程的开发能在一定程度上解决软件危机的各种弊端？5.请简述软件工程的研究内容。

6.请简述软件工程的三要素。

7.请简述软件工程的目标，过程和原则。

8.请简述软件工程的基本原则。

9.请简述现代软件工程与传统软件工程显著的区别与改进。

第二章：一判断题1.瀑布模型的最大优点是将软件开发的各个阶段划分得十分清晰。

计算机导论(第3版)-1-3章参考答案

第1章习题参考答案1、简要叙述ENIAC之前计算工具的发展历程。

答案:（1）算筹；（2）算盘；（3）计算尺；（4）机械计算机；（5）机电计算机。

对于（3）—（5），列出其代表机型。

2、对比说明第一代至第四代计算机各自的主要特点。

答案:（1）第一代计算机的主要特点：用电子管作为基本元器件；用机器语言或汇编语言编写程序；使用水银延迟线、静电存储管、磁鼓和磁芯作主存储器；输入输出装置主要用穿孔卡片；主要用于科学计算。

（2）第二代计算机的主要特点：用晶体管作为基本元器件；出现了FORTRAN、ALGOL和COBOL 等高级语言；采用磁芯存储器作主存，采用磁盘与磁带作辅存；除了科学计算和数据处理外，开始进入实时过程控制领域；出现了操作系统。

（3）第三代计算机的主要特点：用集成电路作为基本元器件；高级语言得到广泛应用；用半导体存储器取代了磁芯存储器，存储容量大幅度提高；普遍采用了微程序设计技术，设计了具有兼容性的体系结构；系统软件与应用软件都有很大发展，操作系统的功能有很大的提高和完善；出现了成本较低的小型计算机。

（4）第四代计算机的主要特点：用微处理器或超大规模集成电路取代了普通集成电路；计算机的存储容量进一步扩大，开始使用光盘和激光打印机；面向对象程序设计语言得到广泛使用；微型计算机诞生；数据通信、计算机网络、分布式处理有了很大的发展，互联网得到广泛应用。

3、微型计算机是如何发展起来的？微型计算机的快速发展有什么重要意义？答案: 1971年诞生的微处理器是将运算器和控制器集成在一起的大规模/超大规模集成电路芯片，以微处理器为核心再加上存储器和接口芯片，便构成了微型计算机。

1981年IBM公司推出微型计算机IBM PC后，微型计算机得到了快速发展。

微型机的出现及快速发展，才使计算机走进了大大小小的企事业单位和千家万户，也促进了互联网的快速发展和广泛应用。

4、简要说明第五代计算机的含义，如何评价第五代计算机的研究。

基础化学第三版习题答案1-8章

习题答案第一章绪论1、求0.010kgNaOH、0.100kg（Ca2+）、0.10kg（Na2CO3）的物质的量。

解：（1）m(NaOH) = 0.010kg M(NaOH) = 40g·mol-1n(NaOH) = = 0.25 (mol)（2）m(Ca2+) = 0.100kg M(Ca2+) = 40g·mol-1n(Ca2+) = = 5.0(mol)（3）m(Na2CO3) = 0.10kg M(Na2CO3) = 53g·mol-1n(Na2CO3) = = 1.89 (mol)2、下列数值各有几位有效数字？（1）1.026 4位（2）0.0208 3位（3）0.003 1位（4）23.40 4位（5）3000 无数位（6）1.0×10-32位3、应用有效数字计算规则，计算下列各式：（1）21.10 - 0.263 + 2.3 = 23.1 （2）3.20×23.45×8.912 = 667（3）= 5.93×10-3（4）4.6×10-24、(1) 以H2SO4为基本单元，M(H2SO4)=98g/mol；(2) 以HSO4-为基本单元，M(HSO4-)=97g/mol；(3) 以3H2SO4为基本单元，M(3H2SO4)=294g/mol。

5、答：甲的报告更为合理，百分比小数点后保留两位有效数字。

第二章溶液与胶体1、在25o C时，质量分数为0.0947的稀硫酸溶液的密度为1.06g·L-1，在该温度下纯水的密度为0.997 g·L-1。

计算H2SO4的物质的量分数、物质的量浓度和质量摩尔浓度。

解：设取稀硫酸溶液1L，则n(H2SO4) = = 1.02 (mol)n(H2O) = = 53.31(mol)c(H2SO4) = = 1.02 (mol·l-1)x(H2SO4) = == 0.0188b(H2SO4) = == 0.106(mol·kg-1)2、醚的正常沸点为34.5℃，在40℃时往100g乙醚中至少加入多少摩尔不挥发溶质才能防止乙醚沸腾？解：n = 0.22mol3、苯的凝固点为5.50℃，K f = 5.12K·kg·mol-1。

(完整版)电路原理课后习题答案

，
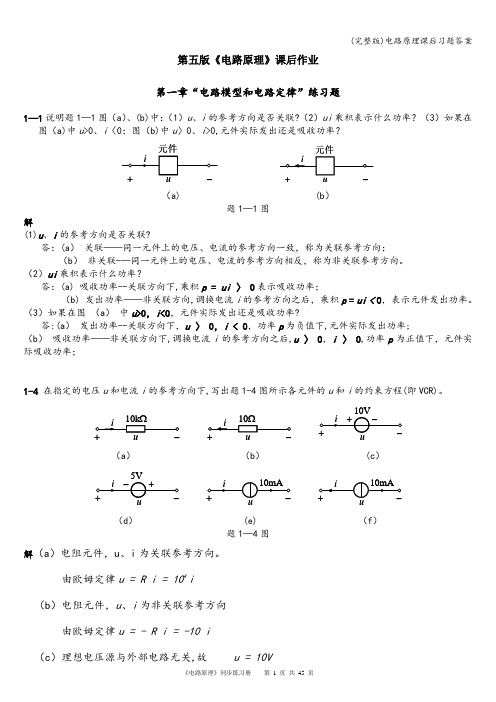
因此，时，电路的初始条件为
t〉0后，电路的方程为
设的解为
式中为方程的特解，满足
根据特征方程的根
可知，电路处于衰减震荡过程，，因此，对应齐次方程的通解为
式中。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电，所加的波形如题7—29图所示，其中 , 。求电容电压，并把：（1）用分段形式写出;（2）用一个表达式写出。
题4-17图
解:首先求出以左部分的等效电路.断开，设如题解4－17图（a）所示,并把受控电流源等效为受控电压源。由KVL可得
故开路电压
把端口短路，如题解图(b)所示应用网孔电流法求短路电流，网孔方程为
解得
故一端口电路的等效电阻
画出戴维宁等效电路，接上待求支路，如题解图（c)所示，由最大功率传输定理知时其上获得最大功率。获得的最大功率为
(a）（b）
题3—1图
解:(1)每个元件作为一条支路处理时，图(a）和(b）所示电路的图分别为题解3-1图（a1）和(b1）。
图（a1）中节点数，支路数
图(b1)中节点数，支路数
（2）电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时，图（a)和图(b）所示电路的图分别为题解图（a2）和(b2)。
电容电流
t=2 ms时
电容的储能为
7—20题7—20图所示电路，开关合在位置1时已达稳定状态，t=0时开关由位置1合向位置2，求t0时的电压 .
题7-20图
解:
用加压求流法求等效电阻
7-26题7—26图所示电路在开关S动作前已达稳态；t=0时S由1接至2，求t0时的 .
题7-26图
解：由图可知，t>0时

电磁学习题答案1-3章

第一章习题一1、电量Q 相同的四个点电荷置于正方形的四个顶点上，0点为正方形中心，欲使每个顶点的电荷所受电场力为零，则应在0点放置一个电量q ＝－(1+2√2)Q/4 的点电荷。

2、在点电荷系的电场中，任一点的电场强度等于各点电荷单独在该点产生场强的矢量和，这称为电场强度叠加原理。

3、一点电荷电场中某点受到的电场力很大，则该点的电场强度E ：( C )(A)一定很大 (B)一定很小 (C)可能大也可能小4、两个电量均为+q 的点电荷相距为2a ，O 为其连线的中点，求在其中垂线上场强具有极大值的点与O 点的距离R 。

解法一：22020214141aR qπεr q πεE E +=== 21E E E+=，θE θE θE E cos 2cos cos 121=+=2222042a R R a R q πε++=()2/32202a R R πεq +=E 有极值的条件是：()0222/522220=+-=a R R a πεq dR dE 即 0222=-R a ，解得极值点的位置为：a R 22=∵ ()2/722220223223a R a R πεqR dR E d +-=，而 0398402/222<-==aπεqdR E d a R ∴ 中垂线上场强具有极大值的点与O 点的距离为a R 22= 且 ()202/3220m a x 332/2/2aπεq a a a πεq E =+=解法二：θaq πεr q πεE E 2202021sin 4141===，21E E E +=+qθE θE θE E cos 2cos cos 121=+=θθaq πεcos sin 21220=)cos (cos 21320θθaq πε-=E 有极值的条件是：0)sin 3sin 2(2320=-=θθaπεq θd dE E 有极值时的θ满足：31cos 32sin 1cos 0sin 2211====θ，θ；θ，θ )cos 7cos 9(2)cos sin 9cos 2(232022022θθaπεq θθθa πεq θd E d -=-= 0)cos 7cos 9(22011320221>=-==aπεq θθa πεq θd E d θθ 032)cos 7cos 9(22022320222<-=-==aπεq θθa πεq θd E d θθ 可见 θ = θ2时，E 有极大值。

《热工基础》(张学学主编)第一章-第三章参考答案

《热工基础》（张学学主编）第一章-第三章参考答案第一章思考题1.平衡状态与稳定状态有何区别？热力学中为什幺要引入平衡态的概念？答：平衡状态是在不受外界影响的条件下，系统的状态参数不随时间而变化的状态。

而稳定状态则是不论有无外界影响，系统的状态参数不随时间而变化的状态。

可见平衡必稳定，而稳定未必平衡。

热力学中引入平衡态的概念，是为了能对系统的宏观性质用状态参数来进行描述。

2.表压力或真空度能否作为状态参数进行热力计算？若工质的压力不变，问测量其压力的压力表或真空计的读数是否可能变化？答：不能，因为表压力或真空度只是一个相对压力。

若工质的压力不变，测量其压力的压力表或真空计的读数可能变化，因为测量所处的环境压力可能发生变化。

3．当真空表指示数值愈大时，表明被测对象的实际压力愈大还是愈小？答：真空表指示数值愈大时，表明被测对象的实际压力愈小。

4.准平衡过程与可逆过程有何区别？答：无耗散的准平衡过程才是可逆过程，所以可逆过程一定是准平衡过程，而准平衡过程不一定是可逆过程。

准平衡过程只注重的是系统内部而可逆过程是内外兼顾！5.不可逆过程是无法回复到初态的过程，这种说法是否正确？答：不正确。

不可逆过程是指不论用任何曲折复杂的方法都不能在外界不遗留任何变化的情况下使系统回复到初态，并不是不能回复到初态。

引起其他变化时是可以回到初态的！6.没有盛满水的热水瓶，其瓶塞有时被自动顶开，有时被自动吸紧，这是什幺原因？答：水温较高时，水对热水瓶中的空气进行加热，空气压力升高，大于环境压力，瓶塞被自动顶开。

而水温较低时，热水瓶中的空气受冷，压力降低，小于环境压力，瓶塞被自动吸紧。

大气压力改变，热水能量散失，导致内部压力改变，压力平衡打破7.用U形管压力表测定工质的压力时，压力表液柱直径的大小对读数有无影响？答：严格说来，是有影响的，因为U型管越粗，就有越多的被测工质进入U型管中，这部分工质越多，它对读数的准确性影响越大。