利用随机数标准表格抽取样本的方法模板计划总结模板讲.doc
随机表法的使用方法

随机表法的使用方法
嘿,朋友们!今天咱来聊聊随机表法呀!这可是个很有意思的东西呢!
随机表法呢,简单来说就是通过随机数来进行选择或分配的一种方法。
那具体咋用呢?首先,你得有个随机数表,这就好比是你的秘密武器。
然后,根据你要解决的问题,确定选择的范围和数量。
比如说,你要从一堆物品中选几个,那就确定好这堆物品的总数。
接下来,按照随机数表中的数字,对应找到相应的物品。
哎呀,这多简单呀!但可别小瞧了它,这里面也有不少要注意的地方呢!比如,你得确保随机数表是真正随机的,不然就不灵光啦!还有,选择的时候要仔细认真,别弄混了呀!这就像是走钢丝,得小心翼翼的。
在使用随机表法的过程中,安全性和稳定性那可是杠杠的!它不会受到人为因素的过多干扰,完全就是靠随机数来决定,多公平呀!就好像是老天爷在帮你做决定,不用担心有啥猫腻。
那它都能用在啥地方呢?哎呀,那可多了去了!比如在抽样调查的时候,能保证样本的随机性和代表性。
还有在一些游戏中,决定谁先开始啥的,多有意思呀!它的优势就是简单、直接、公平,让人挑不出毛病来。
我给你说个实际例子哈!有一次学校里组织活动,要从几百个学生中选出几个代表,老师们就用了随机表法。
结果呢,选出来的同学那真是让大家心服口服,谁也没话说。
这效果,那真是立竿见影呀!
总之呢,随机表法就是个超棒的方法呀!能帮我们解决很多问题,还能保证公平公正,真的很不错呢!。
使用随机数表选取样本的方法

使用随机数表选取样本的方法嘿,你知道不?使用随机数表选取样本那可真是个超棒的方法!先说说步骤哈。
你就想象自己在一个大宝藏箱前,随机数表就是打开宝箱的神秘钥匙。
首先,确定总体范围,就像明确宝藏箱里都有啥宝贝。
然后,给每个宝贝编上号,这就好比给每个物品贴上独特的标签。
接着,从随机数表中随机选取起点,哇塞,这就像在神秘地图上随便点一个地方开始探险。
顺着起点,按照一定的规则读取随机数,对应到编号的宝贝上,这些被选中的宝贝就是咱的样本啦!
那注意事项呢?你可得小心别弄错编号呀,不然就像在迷宫里走错了路。
而且要确保随机数表的来源可靠,不然就像拿着一把不靠谱的钥匙,打不开真正的宝藏。
安全性方面,那是杠杠的!就像有个超级坚固的保险柜,随机选取让别人很难猜到你的样本是哪些,保密性超强。
稳定性也不赖,每次用同样的方法,都能得到相对稳定的结果,不会像坐过山车一样忽上忽下。
应用场景可多啦!比如市场调查,你想知道消费者对某个产品的看法,用随机数表选样本,多公平呀!就像在一场大抽奖中,每个人都有平等的机会被选中。
优势也很明显,能避免人为偏见,不像偏心的裁判。
而且操作简单,不需要复杂的技术,谁都能上手。
给你举个实际案例哈。
有个公司想了解员工对新福利政策的满意度,用随机数表选了一部分员工进行调查。
结果发现了很多有价值的意见,为公司改进政策提供了依据。
这就像在茫茫大海中找到了正确的航向。
总之,使用随机数表选取样本是个超棒的方法,既安全又稳定,应用场景广泛,优势多多。
赶紧用起来吧!。
随机数表选样法的具体步骤

随机数表选样法的具体步骤
好的呀,那咱就来说说随机数表选样法的步骤哈。
随机数表选样法呢,得先有个随机数表。
这个随机数表就像是一个装满了随机数字的大盒子。
第一步呀,得确定总体的范围。
比如说咱要从1000个小物件里选样,那就得清楚这1000个就是总体啦。
第二步呢,要给总体里的每个东西编上号。
就像给1000个小物件都贴上一个小标签,从1到1000,一个都不能落下哦。
接下来呀,从随机数表里面开始选数。
这就像是在大盒子里抓数字啦。
不过呢,选的时候得按照一定的方向,要么从左到右,要么从上到下,可不能乱抓哦。
如果选到的数字在总体编号的范围里呢,那就对应的这个编号的东西就被选中啦。
但是呢,如果选到的数字不在这个范围里,那就像这个数字是个调皮鬼,咱就不理它,再接着选下一个数字。
还有哦,如果不小心选到了重复的数字,那这个数字对应的东西咱也只选一次,不能多选,毕竟每个东西只能有一次被选中的机会嘛。
就这么一直选呀选,直到选够咱想要的样本数量为止。
比如说咱想选50个样本,那就一直按照这个方法选,直到选出50个不同的东西来。
随机数表选样法其实就像一场有趣的数字游戏,只要按照这些小规则来玩,就能选出合适的样本啦。
是不是还挺好玩的呀?。
抽样方案设计模板

抽样方案设计模板抽样调查是常见的调查方式,以下是XX收集的相关方案,仅供大家阅读参考!了解大学生使用信用卡的情况及信用卡在大学生中的分布,并据此分析信用卡在大学生中的市场潜力和需求,并预测大学生信用卡的发展趋势。
1、目标总体和调查总体目标总体指所有长沙市的大学生。
具体包括中南大学湖南大学长沙理工大学湖南农业大学湖南中医药大学湖南师范大学中南林业科技大学长沙学院长沙医学院湖南涉外经济学院湖南商学院就读的各年级在校大学生。
调查总体为根据长沙市的大学生实际情况设计形成的抽样框。
2、调查内容调查内容包括被调查人的性别和年级、大学生对信用卡的态度、大学生持有信用卡的原因、大学生在何种情况下使用信用卡、大学生期望的信用卡透支额、期望的还款日期、未持卡大学生不办卡的原因及大学生的消费支出等。
第一步:确定抽样方法调查决定采用多阶段抽样与整群抽样相结合的抽样方法进行方案设计,调查的最小单元为大学生。
决定调查的各个阶段为学校、寝室、学生,在寝室利用随机数表抽取学生。
第二步:确定样本量及各阶段样本量的配置按简单随机抽样时,在置信度为t=95%时,绝对误差为d=5%,取方差大到最大的比例,则全市的样本量应为:n0=t2*P*Q/d2≈22**/=400(人)根据以往的经验,估计回答的概率为a=90%,因此调整样本量为:n1=n0/a=400/≈445(人)由于多阶段抽样的效率比随机抽样的效率低,取设计效应deff=,则全市范围内应调查的样本学生为:n2= n0*deff=445*=600各阶段的配置分别为:初级单元:6个学校二级单元:150个寝室,每个学校抽25个寝室三级单元:600个学生,每个寝室抽4名学生1、抽样方法以全长沙市的在读大学生为总体,采用多阶段抽样方法抽取样本。
第一阶段,先以长沙市的每个高等院校为初级单元。
按不等概的PPS抽样从中抽取6个学校。
第二阶段,在每个被抽中的学校中,将全校所有的寝室依次进行编号,赋予每个寝室一个与编号一样的代码;根据所有的寝室数除以样本量25,确定抽样间距;然后对代码进行随机起点的等距抽样,则被抽中的寝室为样本寝室。
利用随机数表进行随机抽样的方法

利用随机数表进行随机抽样的方法碚究与探讨?———1}一坼数表极哆稽瞳,债爹利用随机数表进行随机抽样的方法竺秀珍庄苎7:o6,1’’一●内容提要在实施抽拌检查时,必须掌握简单随机抽样的方法.为此.文章舟绍利用随机数表获得随机数并据以进行简单随机抽样的方法.其步骤;1.将总体中的个体编号{2.确定使用随机敦衰的页数:3.确定起点数的行和列;4.确定从随机数表上读取随机敛R的位数;5.确定从总体中抽取的随机数R的三种方法.这三种方法借鉴丁国际GB1011l一88读敦方法.并修改其不够完善之处,确保了总体中N个十体都有相等的机会被抽取.实践证明它是为取得具有代袭性的样本提供另一种既科学又简便的随机抽样的方法.简单随机抽样是建立现代数理抽样检查所有理论的前提,也是各种各样随机抽样方法的基础.在实施抽样检查时,为了获得有代表性的样本,不仅需要设计合理的抽样方案,而且还需要采用随机抽样的方法.如果不能保证抽样的随机性,抽样检查的结果将降低甚至失去准确性.因此,制订和实施抽样检查的有关人员,掌握简单随机抽样的方法,也即掌握获得随机数的方法,是十分重要的.本文是利用随机数表获得随机数并据以进行简单随机抽样的方法.一,简单醴机抽样厦醴机数裹简单随机抽样是指:”从包含N个个体的总体中抽取n个个体,使包含有11个个体的所有可能的组台被抽取的可能性都相等.”按照这个定义,总体中每个个体被抽取的可能性都相等.在产品抽样检查中,个体即为”单位产品”,总体即为”批”,N为批量”,11为”样本大小”.从批中抽取作为检查的单位产品称为”样本单位”,样本单位的垒体称为”样本”.所谓随机数丧就是0~9这lO个数的1992年第3期(总7T期)随机排列,共~5000个随机数字,分成两页,每页有5O行与5O列,计有2500个随机数字.详见附表.=,随机数袭的使用方法I.将总体中.的个体编号.当总体中的个体是一个个整齐排列时,则按自然数从l到N的顺序编上号码,然后田获得的随机数对号抽取.下面将介绍如何利用随机数表获得n个琏机数,使l到N这N个自然数都有相等机会被抽取.3.确定使用的页数.随机数表分为第一,第二两页,翻到琏机数表的任何一页,闭上眼睛用一支笔指点在这一页的随机数表内,预先自行规定,若笔尖指在奇数时用第一页,指在偶数(0是偶数)用第二页.,俩如第一次指在9处,我们决定使用第一页. 3.确定起点数的行和列.当我们决定使用第一页时,为了决定起点,就是要确定起点数的行和列,若第二次笔尖指在两位数97处,由于它已超过随机数表的行数50,则97—50=47,于是起点取在第47行.若第3次笔尖捐在D7处,于是起点取在第7列.第第47行第7列交点数就为起点着取一位数起点数是3,取二位数是39,取三位数是304,取四位数是3日43,f…一?.从起数起所读取各数我们称为随机薮R...4.确定随机数R的位数.按总体大小或批量N的范围决定随机数R.的位数m如下表.r1≤N≤ll≤N≤101≤N≤1001≤N≤10001≤N≤100001≤N≤N的范围10100100010000l000o010O0000.随机数R.123I456位数Ill如果读取的随机数R.是一位或二位数.则从起点起往右边取,到达右端后移到下一行继续往右取.如果取的是三位,四位,五位或六位,先往右取够三位,四位,五位或六位数,再由下一行对应的列取第二个三位,四位,五位或六位数.如此J嘁序往下取,如到达下端不够用时,则从个位数右边紧接着的那一列的顶端开始继续往下取.例如,按随机的方法决定取第一磺,第47行,第7列,如果随机数R是取二位数,则为30,43,73,81,53,94,……J取三位数,则为394,774,181,700,636,242,656,…’’d5.确定从总体中抽取的雅机数R钧方法.根据随机数表编制的随机性,由随机数表读取的m位随机数R.从1到l0一这10m个数值出现的可能性应该相等如何由R.转换成从总体(含N个个体)中饔抽取的随机数R呢?这有三条原则必须遵循,第一,必须保证从l到N这N个个体被抽取的可能性相等J第二,尽可能减少读取的随机数R.被舍彝的机会,第三,由R转换成R时的计算要尽可能简单.按照这三条原则,建立下面三种确定抽取的随机数R的方法.方法一,如从随机数表读取的随机数R.≤N,匾【j抽取的随机数R就取R.,若R.> 8N,则舍弃不用.重复上述过程,直到取得n个不同的随机数为止这一方法适用N>5×l0s的场合,此时若R.≤M,则R就取R.,适台前述的第一条原则J若R.>N,R.数值的个数小于N,按照前述的第一条原则,应该舍弃.例l|N650,I11-:3,样本大小n=3若决定从第1页第47行第7列开始选取一系列随机数R.为394,77181,700,636.按方法一规定;R.:394<N=650,取R=394Ro=774>N=650,舍弃不用R0=181<N=650,取R:18lR.=700&g t;N=65’0,舍弃不l用R0=636<N:650,取R=636.所以,要抽取的3个个体编号便是394, 181,636方法二,如从随机数表读取的随机数Ro≤N,则抽取的随机数R就取R.}若R >N,则设R=kN+R1(其中k=[],I,D即k为的整数部分),当R=0时,取R;N,当Rl0时,如(Kl十1)N≤标璀计量与质量管理,0,取R=R,如(K+1)N>1O.舍弃不用.重复上述过程,直到获得n个不1司的随机数为止.这一方法适用于N≤5×10m且N=1.5×10一,2×10一,2.5×10一,3×1O一,3.5×10一,4×10一,4.5X10一’5×10一的场合,按照前述的第二条原则,为了利用R.>N的随机数,其思路是将1 到tO”这1Om个数值分段,每段为N个数字, 1至N为第一段,N+1至2N为第二段,2N+1至3N为第三段,…….最后一段可能是完整段.也可能是不完整段.将完整艘与N中韵个体编号对虚,不完整段则舍弃不用.为了体现这一思路,采用公式R=KN+R,将R.转换为R,R的可能取值为(0,N一1]区间,再规定RI=0时,R=N,茵而R的可能取值范围实际上为[t, N],这与总体中的个体编号是一一对应的. 对完整段能满足(Kt+1)N≤l0m,故取R:I}对不完整段则满足(K+1)N>R.被告弃不用.’按照前述的第三条原则,当N=1.5×10,2×10一’,2.5×10’,3×10’,3.5×10一,4×10,4.5×10一’,5×1O’时,按N分段由R.转换成R时,计算起来就简单得多了.侧2,N=350,m=3,样本大小n=4若决定从第1页第47行第7列开始选取一系列随机数,则R.为394,774,181,700, 636.按照方法二规定}R.=394=[i39丽4一]×350+44,Rl=440且([394]+1)×35o<10.,故取R=RI=44.1992年第3期(总77期)R.=774:【;57.4]x350+74.Rt=74{0但’([13757)+1)×35o>1o.,故舍弃不用.R.堋]×35o+0Io,取R=N:350.R.=636=[5036]×350+286,Rl=2860且([而636]+1)×35o<1o,故取R=RJ=286.所以,要抽取的4个个体编号便是44,181,3SO,286.方法三.如从随机数表读取的随机数R.≤M,刚抽取的随机数R就取R.,若R.>N,则取一个大于N的适当整数为M,一般取M;2×10m_.,2.5×l0一_.,3×10一_.,4×lD一~,5×l0设RD:KzM+R2(其中K;[{,即K;为音的整数部分),则当(K+1)M>10时,舍弃不用}当(K4+1)M≤10时,取R=Rz(若0<R≤N)或台弃不用(若R>N).重复上述过程,直到获得n不同的随机数为止.这一方法适用于N≤5×l0且N2×lO一,2.5×l0一,3×10一,4×10,5×l0的场合.按照前述的第三条原则,故采用方法三.采用方法三的思路基本与方法二相同,不再重述.倒3.N=167,m=3,取M=200,样本太小n=3.若决定从第2页第48行第7列开始选取一系列随机数,则R.为988,O34,055,9研究与探讨?t扭,粹砌匕,7}=十){},从技术先进性与经济合理性论电风扇标准的修订,,,一,问题的提出中山市百灵屯器总厂!苎堂一GB3046--82和GBn158—82的电风扇标准,自83年1月开始试行以来,根据实施经验,许多厂家对GBn152--82中几项具体指标提出了不同的意见,其中尤其以吊扇的风量,使用值指标提出修订的反映最为强烈.从87—89年,在广泛征询生产企业,商业,标准质检等部门意见的基础上,修订和通过新国标报批稿,但是至今仍来见公布实施.我国电风扇生产在八十年代初进人突飞猛进的发展,89年全国电风赢产量超过四千万台,年产量居于世界第一位.在国内市场出现供过于求的激烈竞争下,许多厂家纷纷冲出国门,把电风扇产品打进国际市场.出口电风扇绝大部分均是依据外商的订货合同或按术协议生产和交货的,并不执行国标GBat5g--82对风置和使用值的规定.根据是标准化法第十六条规定:”出口产品的技术要求, 『},fj一依照台同的约定执行”.生产企业为了适应内销和外销的要求,不得不执行两套标准体系来组织生产,给生产管理质量管理带来了许多不便,甚至出现过一些不必要的损失.例如我省一些电风扇曾因风量,使用值达不到GBn158--82的要求而被判为不合格产品,但在国际上却是适销产品.如何以技术先进性和经济合理性两方面综台平衡修订电风扇标准,更有利于合理利国家资源和积极采用国际标准.提高经济效益和社会效益,做到技术上先进,经济上合理,这就是本文所要讨论的主要内容.=,就风量使用值指标浅析技术先进性与经济合理性两者的美系风量和使用值是电风扇产品的性能标准,这两项指橱不能单一地从其指标值的高或低来衡量技术先进与否,还应考虑经济效益的综台平衡,做到既充分考虑使用要求,保761.按方法三规定}R.=988=Lg丽988J×200+188,L(L.200988]+1)×200>10.,但R2:188>N=167,故舍弃不用.R.=34<N:167,故取R=Ro=34.R.:55<N=167,故取R;R.:55.Ro=76g761]×200+161,([]+1)×200<10.,且Rz=161<N=167,故取R=R:=161.所以,要抽取的3个个体编号便是34,55,161.口参考文献1.国家标准GB101儿一88《利用随机数骰子进行随机拙样的方法2.庄友炎撰写对尉标GB10111—88读数方法的商接》标准计量与质量管理》1990年第3 期《标准计量与质量管理。
统计随机抽样简单随机抽样随机数表法ppt课件

第四步,对应以上编号找出所要回答的问题的 序号,物理题的序号为:5,8,14;化学题的序号 为:24,28,29;生物题的序号为:40,44.
[规律总结] 解答抽样问题时,要注意所抽出的 样本既要能准确地反映总体特征,又要能方便 操作.
14
Hale Waihona Puke 练习:1用随机数法进行抽样有以下几个步骤: ①将总体中的个体编号 ②获取样本号码 ③选定开始的数字 ④选定读数的方向 ⑤抽取样本 这些步骤的先后顺序应为( ) A.①②③④⑤ B.①③④②⑤ C.③②⑤①④ D.⑤④③①② [答案] B
84 26 34 91 64 57 24 55 06 88
83 92 12 06 76 16 95 55 67 19
44 39 52 38 79 78 64 56 07 82
99 66 02 79 54 09 47 27 96 54
17 37 93 23 77 04 74 47 98 10 50 71 52 42 07 44 49 17 46 097
第二个数字是637,也符合题意, 第三个数字是859,大于850,舍去, 第四个数字是169,符合题意, 第五个数字是555,符合题意, 故答案为:301,637,169,555.
11
合理运用抽样方法
例2、一个学生在一次理科综合学科竞赛中要回 答的8道题是这样产生的:从15道物理题中随机 抽取3道;从20道化学题中随机抽取3道;从12 道生物题中随机抽取2道,请选用合适的方法确 定这个学生所要回答的三门学科的题的序号(物 理题的编号为1~15,化学题的编号为16~35, 生物题的编号为36~47).
[探究] 由题意可知样本由3类组成,需分别在 物理题、化学题、生物题中抽取.由于每类总 体和样本的个数都较少,所以采用抽签法或随 机数法都可以完成.
用excel进行随机抽样
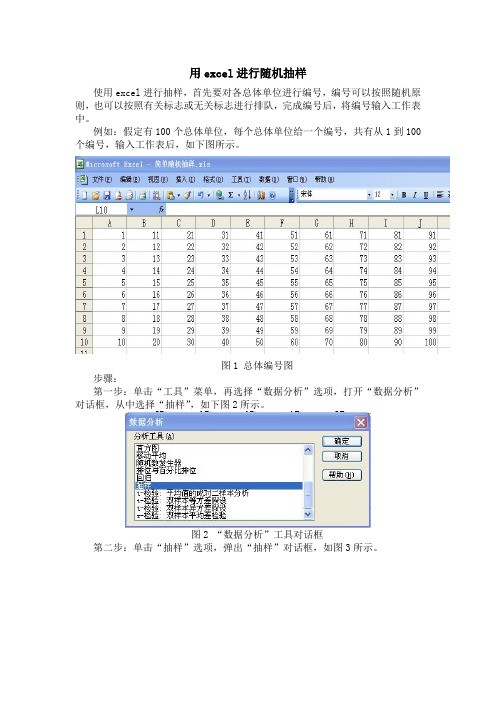
用excel进行随机抽样
使用excel进行抽样,首先要对各总体单位进行编号,编号可以按照随机原则,也可以按照有关标志或无关标志进行排队,完成编号后,将编号输入工作表中。
例如:假定有100个总体单位,每个总体单位给一个编号,共有从1到100个编号,输入工作表后,如下图所示。
图1 总体编号图
步骤:
第一步:单击“工具”菜单,再选择“数据分析”选项,打开“数据分析”对话框,从中选择“抽样”,如下图2所示。
图2 “数据分析”工具对话框
第二步:单击“抽样”选项,弹出“抽样”对话框,如图3所示。
图3 抽样选项对话框
第三步:在输入区域框中输入总体单位编号所在的单元格区域,如果输入区域的第一行或第一列为标志项(横行标题或纵列标题),可以选中“标志”复选框。
第四步:在抽样方法项下,有周期和随机两种抽样模式:
“周期”模式即所谓的等距抽样。
“随机”模式适用于纯随机抽样、分层抽样、整群抽样和多阶段抽样。
第五步:指定输出区域,单击“确定”后,即可得到抽样结果。
抽签法和随机数表法

统计是研究如何合理地收集、整理、 分析数据的学科,它可以为人们制定决 策提供依据。在日常生活中,人们常常 需要收集数据,根据所获得的数据提取 有价值的信息,作出合理的决策。
在本章中了解对数据的收集、整理和
分析,可以增强我们的社会实践能力,
培养我们解决问题的能力,增强我们学
习数学的兴趣。
5
2.1.1简单随机抽样
18
(3) 继续向下读,得到733作为第2个代号。 继续向下读,得996大于850,跳过。继 续向下读,得到131作为第3个代号。只 要3个数构成的数不大于850且不与前面 取出的数重复,就把它取出,否则跳过 不取,取到一行(列)末尾时转到下一 行(列)从左到右继续读,如此下去, 直到得到在001~850之间的50个三位数。
24
本章我们先学习简单随机抽样、系统抽 样、分层抽样这三种常用的抽样方法。
接着学习如何用样本估计总体,一是如 何用样本的频率分布估计总体分布;二是 如何用样本的某种特征数去估计总体的相 应的特征数。
最后学习两个变量之间的关系,除了函 数关系这种确定性的关系以外,还存在因 变量的取值带有一定随机性的两个变量之 间的关系——相关性。
17
例如要考察某种品牌的850颗种子的发 芽率,从中抽取50颗种子进行实验。用 随机数表抽取的步骤如下:
(1) 对850颗种子进行编号:可以编为001, 002,……,850.
(2) 在给出的随机数中取3个数一组,从 各表中任选一个数作为起始号码,例如 从第5行第7个数开始并定好方向(向 下),取出395作为抽取的第1个代号;
于是,和这10个号码对应的10个学生就 构成了一个简单随机样本 。
16
四、随机数表法
随机数表由数字0,1,2,3,……,9 这10个数字组成,并且每个数字在表中各 个位置上出现的机会一样。通过随机数生 成器,例如计算器或计算机的应用程序生 成随机数的功能,可以生成一张随机数表.
高中数学总结归纳 抽签法与随机数表法

抽签法与随机数表法常用的简单随机抽样方法有两种:抽签法和随机数表法.他们都是在总体个数不多的情况下使用.其中抽签法的操作要点是:编号、写签、搅匀、抽取.随机数表法的操作要点是:编号、选起始数、读数、获取样本.例1.北京某中学举行“元旦数理化”竞赛,每一个学生在这次竞赛中要回答的8道题是这样产生的:从15道物理题中随机抽取3道;从20道化学题中随机抽取3道;从12道数学题中随机抽取2道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为1~15,化学题的编号为16~35,数学题的编号为36~47).分析:由于题的个数较少,可以采用简单随机抽样的两种方法:抽签法及随机数表法.解法一:抽签法.第一步:将物理、化学、数学试题依次编号为1~47,分别写在一张纸条上,将纸条揉成团制成号签,并将物理、化学、数学题的号签分别放在三个不透明的袋子中,搅匀;第二步:在装有物理题的袋子中逐个抽取3个号签,装有化学题的袋子中逐个抽取3个号签,装有数学题的袋子中逐个抽取2个号签,并记录所得号签的编号,这便是所要回答的问题的序号.解法二:随机数表法.第一步:将物理题的序号对应改成01,02,…,15,共余的两科题的序号不变;第二步:在随机数表中任选一数作为开始,任选一方向作为读数方向.比如,选第10行第2个数“7”,向右读;第三步:从数“7”开始,向右读,每次读取二位,凡不在01~47中的数跳过去不读,前面已读过的也跳过去不读,从01~15中选3个号码,从16~35中选3个号码,从36~47中选2个号码,依次可得到08,24,40,44,29,05,28,14;第四步:对应以上号码找出所要回答的问题的序号,物理题的序号为5,8,14;化学题的序号为:24,28,29;数学题的序号为:40,44.点拨:当总体中个体数较少,制作号鉴比较简单时,可以用抽签法;当总体中个体数校多,制作号签比较复杂,并且把号签挽拌均匀比较困难的时候,可以用随机数表法.例2.高一(1)班有学生60人,为了了解学生对目前高考制度的看法,现要从中抽取一个容量为10的样本,问此样本若采用简单随机抽样,将如何获得?试设计抽样方案.分析:简单随机抽样方法有抽签法和随机数表法.注意到该问题中总体的个体数不多,所以采用抽签法或随机数表法都能获取样本,从而有以下两种解法:(1)采用抽签法,进行如下操作即可获得所需样本.①编号,即对这60名学生编号;②写签制签,即将这60个号码分别写在60张相同纸片上并揉成团;③搅拌均匀,即放到一盒子里搅匀;④抽签,逐个抽取,记下号码,到10个终止.(2)采用随机数表法,需完成以下三步:①编号;②选定随机数表中的起始数;③从选定的起始数开始读下去,直到取满10个为止.解法1 (抽签法):①将这60名学生按学号编号,分别为1,2, (60)②将这60个号码分别写在60张相同纸片上;③将这60张相同纸片揉成团,放到一盒子里搅拌均匀;④抽出一张,记下上面的号码,然后再搅拌均匀,接着抽取第2张,记下号码.重复这个过程直到取到10个号码为止.这样,与这10个号码对应的10名学生就构成了一个简单的随机样本.解法2 (随机数表法):①将60名学生编号,可以编为00,01,02, (59)②选定随机数表中的起始数,如指定从随机数表中的第2行第2列的数74开始;③从选定的起始数74开始向右读下去,得到24,下一个是67,由于67>59,跳过去,继续,下一个是62,由于62>59,再跳过去,继续读,得到下一个42,… 如此下去,又得到14,57,20,53,32,37,27,07(后重复出现的跳过去),至此10个样本号码已经取满.于是所要抽取的样本号码是24,42,14,57,20,53,32,37,27,07,这样,与这10个号码对应的10名学生就构成了一个简单的随机样本.点评:采用简单随机抽样(抽签法或随机数表法)时,必须先对所有个体进行编号.用抽签法时,注意“搅匀”;用随机数表抽样时,开始数和读数方向是任意的.从以上两种方法可以看出,当总体个数较少时用两种方法都可以,当样本总数较小时,解法1优于解法2.。
常规采样实验报告模板

常规采样实验报告模板一、实验目的本实验旨在通过常规采样方法,了解常规采样的原理和方法,实现对特定总体的抽样,得出样本的频数分布及抽样误差。
二、实验原理常规采样是一种简单随机抽样的方法,即从总体中随机地抽取若干个个体作为样本,以得出总体性质的估计值。
常规采样的步骤包括:1. 定义总体:明确所研究问题的总体,并确定对其进行抽样的目的。
2. 确定抽样框架:对总体中每个个体编制一个编号表,构成抽样框架。
3. 确定样本规模:根据抽样的要求和实际情况,确定所要抽取的样本数量。
4. 抽样方式:通过随机数表或随机数生成器来进行抽样,确保每个个体有相等的机会被抽到。
5. 抽取样本:依照抽样方式,从抽样框架中抽取样本。
6. 数据整理:将抽样得到的数据进行整理和归纳,以便后续数据分析和总结。
三、实验步骤1. 确定总体:以某高校的学生总体为对象,研究学生的身高分布情况。
2. 确定抽样框架:将学生总体的每个个体编制编号表,形成抽样框架。
3. 确定样本规模:根据样本容量要求和实际情况,确定从总体中抽取200名学生作为样本。
4. 抽样方式:使用随机数生成器,在抽样框架中进行抽样,确保每个学生有相等的机会被抽到。
5. 抽取样本:从抽样框架中按随机数的顺序逐个抽取学生样本,获得身高数据。
6. 数据整理:对得到的样本数据进行整理,统计开始、结束身高范围,并绘制频数分布直方图。
四、实验结果分析在本次实验中,抽样获得了200名学生的身高数据。
将这些数据根据设定的身高范围进行统计,结果如下:身高范围(cm)频数160-165 36165-170 48170-175 54175-180 42180-185 20根据频数分布可以看出,本高校学生的身高主要集中在165cm至175cm之间,频数最多。
而在180cm以上和160cm以下的身高群体数量较少。
五、实验结论通过常规采样方法,我们成功抽取了200名学生的样本数据,并对其身高进行了频数分布统计。
随机选取样本的方法

随机选取样本的方法1. 介绍在研究和实践中,为了获得对总体的全面认识和准确判断,我们需要从总体中选取一部分样本进行分析和研究。
随机选取样本的方法是一种常用的样本抽样方法,它可以确保样本的代表性和可靠性,从而提高研究和分析的可信度。
本文将详细介绍随机选取样本的方法,包括简单随机抽样、系统抽样、分层抽样和整群抽样四种常见的抽样方法,以及它们的优缺点和适用场景。
2. 简单随机抽样简单随机抽样是最基本也是最常用的一种抽样方法,它的核心思想是从总体中随机选取一部分样本,确保每个样本有相同的被选中的概率。
2.1 简单随机抽样的步骤简单随机抽样的步骤如下:1.确定总体:首先需要明确研究的总体是什么,总体可以是一个人群、一个地区或一个产品等。
2.确定样本大小:根据研究的需要和可行性确定所需样本的大小。
3.编制总体名单:将总体中的个体进行编号,构成总体名单。
4.进行随机抽样:利用随机数表、随机数生成器或抽样软件等工具,从总体名单中随机选择样本。
5.进行样本研究和分析:对选取的样本进行研究和分析,得出相应的结论。
2.2 简单随机抽样的优缺点简单随机抽样的优点如下:•简单易操作:抽样过程相对简单,不需要太多的统计学专业知识。
•代表性强:每个样本被选中的概率相同,可以保证样本的代表性。
•可信度高:样本的随机性保证了研究和分析的可信度。
简单随机抽样的缺点如下:•耗时耗力:如果总体较大,抽样时需要编制总体名单,耗时且工作量大。
•抽样误差无法估计:简单随机抽样无法估计抽样误差,对于抽样结果的置信度无法量化。
3. 系统抽样系统抽样是一种按照一定的规则从总体中选取样本的方法,它可以减少抽样过程中的主观性,确保样本的代表性。
3.1 系统抽样的步骤系统抽样的步骤如下:1.确定总体:同简单随机抽样方法一样,首先需要确定研究的总体。
2.确定样本大小:根据研究的需要和可行性确定所需样本的大小。
3.确定抽样间隔:抽样间隔是指在总体名单上每隔多少个个体选取一个样本。
利用随机数表抽取样本的方式

随机数表是由0、1、2、3……9,这十个数字随机排列成的表格,表中每个位置上出现各个数字的概率都是相等的,随机数表不是唯一的,只要一个数表各个位置上出现的数字的概率是相同的,它就可以构成一个随机数表,第一张随机数表是由铁皮特在1927年给出的,统计工作者常用计算机生成随机数表,有的多功能计算器上也设有生成随机数的按键.一、直接利用随机数表直接利用随机数表进行抽样共有三个步骤:第一步:对总体的各个个体进行编号这里所谓编号就是编数字号码,编码方法与总体中个体多少有关,具体编码方法如下:当个体数小于或等于100时,可编为两位数字号码,如:总体的个数为100,其编号为00,01,02,……99;当个体数小于或等于1000时,可编为三位数字的号码,如:总体个数为500,其编号000,001,002,……499;当个体数小于或等于10000时,可编为四位数字的号码,如:总体数为7560,其编号为0000,0001,0002,……7559;… … … … … …这样的编号是为了便于使用随机数表.第二步:选定抽样开始的数字为了保证所选数字的随机性,①要随机选,②应在面对随机数表之前就指出开始数字的纵横位置,例如:选第8行第10列位置的数字为开始抽样的数字,③根据所选数字的纵横位置,在表中查清所选的数字是几,例如:第8行第10列数字是9.第三步:抽取样本号码从选定的数字开始,按照对个体所编的号码位数〔如:两位或三位或四位……〕,沿着同一个方向向右或向左或向上或向下两位、两位或三位、三位或四位、四位……一直读下去,就会得到一系列两位数字号码或三位数字号码或四位数字号码……,在这些号码里,按抽取的顺序依次把不在编号内的号码去掉,重复号码只取一个,这个过程继续下去,直到取够样本容量为止.为了便于操作,特别是为了知道所抽取的每一个号码是否与前面得到的号码重复,可将总体中所有号码先按顺序列出,每抽出一个号码时就在其中的相应号码中做一个记号,这样就知道后面的号码是否被取出.例如:某地举行了一次数字竞赛,参加竞赛的学生300人,为了了解竞赛成绩分布情况,计划从中抽取一个容量为15的样本,其步骤如下:Ⅰ、给三百名参赛者进行三位数编号,编号为000,001,002,003……299.Ⅱ、选定开始抽样的数字,在人教版高三数学教材选修〔Ⅰ〕p25的随机数表中任选第5行第10列位置的数4为开始抽样的数字.Ⅲ、从选定的数4开始向右三位,三位读下去,得到一系列三位数号码,在得到的三位数号码中去掉大于299的,重复的号码只取一个,则得容量为15的样本号码为246,223,162,061,130,217,209,258,120,163,199,175,128,238,123.二、间接利用随机数表进行抽样当总体个数较多时,一般抽取的样本容量也较大,直接利用随机数表进行抽样,显然较为费事,如果先把总体分成几个均衡的若干部分,再利用随机数表施行抽样,则较为方便.根据总体情况和所要抽取的样本大小分两种情况来谈.1、总体已经是均衡的几部分,且样本容量与部分容量不相等对这类总体抽样方法与前面的步骤基本相同,只是第一步骤对个体编号有所不同,编号时可进行多维编号,根据每部分中个体总数的不同,可编为三维编号〔Xi;Yi;Zi;〕,或四维编号〔xi;yi;zi;ei〕等,其中第一个数字代表部分编码,第二、三位数字或二、三、四位数字等,组成的两位数或三位数等代表该个体在部分的编号,编好号码后按前面中的第二、三个步骤进行即可.例如:从某校均衡的五个班的三年级中抽出八名学生进行成绩测验编号:〔0,00〕,〔0,01〕…〔0,49〕,〔1,00〕,〔1,01〕…〔1,49〕〔2,00〕, 〔2,01〕…〔2,49〕〔3,00〕,〔3,01〕…〔3,49〕〔4,00〕,〔4,01〕…〔4,49〕〔5,00〕, 〔5,01〕…〔5,49〕选定抽样开始的数字,在人教版高三数学选修〔Ⅰ〕p25的随机数表中第3行第5列的数6为开始抽样数字.开始抽样有两种方法,第一种:从选定的数字6开始向右顺次三位、三位取,共取8个3位数〔6,22〕,〔7,66〕,〔5,65〕,〔0,26〕〔7,10〕,〔7,32〕,〔9,07〕,〔9,28〕把第一位数中大于4的用它除以5所得的余数作抽取样本编号的第一位数字,后两位数大于49的除以50所得的余数作为抽取样本的第二、三位数字,其它不动,则抽取的样本为:〔1,22〕,〔2,16〕,〔0,15〕,〔0,26〕〔2,10〕,〔2,32〕,〔4,07〕,〔4,28〕第二种:完全按前面第一大问题中的三个步骤进行即可,则抽取的样本为:026,141,012,121,014,218,176,438 2.总体个数较多时,先将总体分为均衡的几部分,然后进行抽样〔⒈〕总体中的个体数能被样本整除将总体分为均衡部分的个数可小于或等于样本容量〔这里只是谈等于,小于时可仿此法进行,但样本容量应是分成均衡的部分个数的倍数〕,然后利用随机数表法分别从每一部分抽取一个,则总共抽的个数就构成一个样本,例如:总体1000,抽取一个容量为50的样本,在抽取样本时,可将总体分为50个均等部分,再从每一部分中抽取一个,共抽取50个,构成一个样本.〔⒉〕总体中的个体数不能被样本容量整除用随机数表法,从总体中剔除一部分个体,使剩下的个体数能被样本容量整除,在按前面1的方法进行抽样.例如:总体容量为1003,抽取一个样本容量为50的样本.现用随机数表法剔除3个个体,然后将1000个个体分成50个均衡部分,再用随机数表法从每一部分中各抽取一个,共抽50个,构成一个样本容量为50的样本.。
如何从excel表中随机提取系列数据的教程

如何从excel表中随机提取系列数据的教程
在Excel中录入好数据以后,有些情况会需要抽查一些数据,因此会用到从表中随机提取系列数据的功能,如果不知道该如何操作的朋友不妨一起来学习探讨。
下面是由店铺分享的如何从excel表中随机提取系列数据的教程,以供大家阅读和学习。
如何从excel表中随机提取系列数据的教程:
从表中提取数据步骤1:如图,要随机调用表格左侧数据表中的姓名和数值。
首先在单元格中输入公式:=INDIRECT("A"&RANDBETWEEN(2,18)) 这里A代表A栏,RANDBETWEEN(2,18)代表随机选取从第二行到第18行的数据,输入公式后按enter键;(这里也可以用公式:=INDIRECT(ADDRESS(ROUNDUP(RAND()*18,1),1))来实现) 从表中提取数据步骤2:上一步骤我们得到了一个随机的姓名,如果还要调用这个姓名对应的数值,如数值3和数值1,可以利用vlookup这个公式,如下图,在单元格中输入:=VLOOKUP($G3,$A$2:$D$18,4,FALSE) 并按enter键。
这里G3代表姓名所在的单元格,这个字段就类似于定位符;$A$2:$D$18 代表表格区域即目标值所在的区域;4代表目标值所在的列,表格区域中的第四列数据就是数值3;false代表精确查询。
从表中提取数据步骤3:同理,在数值1 对应单元格中就应该输入:=VLOOKUP($G3,$A$2:$D$18,2,FALSE)
从表中提取数据步骤4:将鼠标放在单元格右下角,变十字时下拉,得到多个随机数;
从表中提取数据步骤5:同步骤4,下拉数值3和数值1,完成了系列数据的随机提取。
随机系统抽样

PPT文档演模板
随机系统抽样
例:从某厂生产的802辆轿车中随机抽取80辆测试 某项功能,请合理选择抽样方法,并写出过程。
第一步:将802辆轿车编号,号码是001,002,…,802;
第二步:用随机数表法随机抽取2个号码,如016,378, 将编号为016,378的2辆轿车剔除;
第三步:将剩下的800辆轿车重新编号,号码为1,2, …, 800,并分成80段,间隔为10;
随机、系统抽样
PPT文档演模板
2021/1/6
随机系统抽样
1.抽签法
例:某单位对口支援西部开发,现从报名的18名 志愿者中选取6人组成志愿小组到西藏工作3年, 请用抽签法设计抽样方案。
第一步:将18名志愿者编号,号码是01,02,…,18;
第二步:将号码分别写在一张纸上,制成号签;
第三步:将得到的号签放入一个容器中,并充分搅匀;
这个间隔定为10,即将编号按顺序每10个为一段, 分成10段; ③在第一段号码1~10中用简单随机抽样法抽出一个 作为起始号码,如6;
④然后从“6”开始,每隔10个号码抽取一个,得到 6,16,26,36,…,496,这样我们就得到一个 容量为50的样本。
PPT文档演模板
随机系统抽样
系统抽样的步骤:
第三步:从数“7”开始,向右读,得到一个三位数785, 由于785<799,说明号码785在总体编号内,将它取出;继 续向右读,得到916,由于916>799,将它去掉,按照这种 方法继续向右读,又取出567,199,507, …,依次下去, 直到样本的60个号码全部取出;
第四步:以上号码对应的60袋牛奶就是要抽取的对象。
共同特点:均为不放回抽样,在抽样过程中每一个个体 被抽取的机会是相等的。
利用随机数表抽取样本的方法 讲

利用随机数表抽取样本的方法随机数表是由0、1、2、3……9,这十个数字随机排列成的表格,表中每个位置上出现各个数字的概率都是相等的,随机数表不是唯一的,只要一个数表各个位置上出现的数字的概率是相同的,它就可以构成一个随机数表,第一张随机数表是由铁皮特在1927年给出的,统计工作者常用计算机生成随机数表,有的多功能计算器上也设有生成随机数的按键.一、直接利用随机数表直接利用随机数表进行抽样共有三个步骤:第一步:对总体的各个个体进行编号这里所谓编号就是编数字号码,编码方法与总体中个体多少有关,具体编码方法如下:当个体数小于或等于100时,可编为两位数字号码,如:总体的个数为100,其编号为00,01,02,……99;当个体数小于或等于1000时,可编为三位数字的号码,如:总体个数为500,其编号000,001,002,……499;当个体数小于或等于10000时,可编为四位数字的号码,如:总体数为7560,其编号为0000,0001,0002,……7559;… …… …… …这样的编号是为了便于使用随机数表.第二步:选定抽样开始的数字为了保证所选数字的随机性,①要随机选,②应在面对随机数表之前就指出开始数字的纵横位置,例如:选第8行第10列位置的数字为开始抽样的数字,③根据所选数字的纵横位置,在表中查清所选的数字是几,例如:第8行第10列数字是9.第三步:抽取样本号码从选定的数字开始,按照对个体所编的号码位数〔如:两位或三位或四位……〕,沿着同一个方向向右或向左或向上或向下两位、两位或三位、三位或四位、四位……一直读下去,就会得到一系列两位数字号码或三位数字号码或四位数字号码……,在这些号码里,按抽取的顺序依次把不在编号内的号码去掉,重复号码只取一个,这个过程继续下去,直到取够样本容量为止.为了便于操作,特别是为了知道所抽取的每一个号码是否与前面得到的号码重复,可将总体中所有号码先按顺序列出,每抽出一个号码时就在其中的相应号码中做一个记号,这样就知道后面的号码是否被取出.例如:某地举行了一次数字竞赛,参加竞赛的学生300人,为了了解竞赛成绩分布情况,计划从中抽取一个容量为15的样本,其步骤如下:Ⅰ、给三百名参赛者进行三位数编号,编号为000,001,002,003……299.Ⅱ、选定开始抽样的数字,在人教版高三数学教材选修〔Ⅰ〕p25的随机数表中任选第5行第10列位置的数4为开始抽样的数字.Ⅲ、从选定的数4开始向右三位,三位读下去,得到一系列三位数号码,在得到的三位数号码中去掉大于299的,重复的号码只取一个,则得容量为15的样本号码为246,223,162,061,130,217,209,258,120,163,199,175,128,238,123.二、间接利用随机数表进行抽样当总体个数较多时,一般抽取的样本容量也较大,直接利用随机数表进行抽样,显然较为费事,如果先把总体分成几个均衡的若干部分,再利用随机数表施行抽样,则较为方便.根据总体情况和所要抽取的样本大小分两种情况来谈.1、总体已经是均衡的几部分,且样本容量与部分容量不相等对这类总体抽样方法与前面的步骤基本相同,只是第一步骤对个体编号有所不同,编号时可进行多维编号,根据每部分中个体总数的不同,可编为三维编号〔Xi;Yi;Zi;〕,或四维编号〔xi;yi;zi;ei〕等,其中第一个数字代表部分编码,第二、三位数字或二、三、四位数字等,组成的两位数或三位数等代表该个体在部分的编号,编好号码后按前面中的第二、三个步骤进行即可.例如:从某校均衡的五个班的三年级中抽出八名学生进行成绩测验编号:〔0,00〕,〔0,01〕…〔0,49〕,〔1,00〕,〔1,01〕…〔1,49〕〔2,00〕,〔2,01〕…〔2,49〕〔3,00〕,〔3,01〕…〔3,49〕〔4,00〕,〔4,01〕…〔4,49〕〔5,00〕,〔5,01〕…〔5,49〕选定抽样开始的数字,在人教版高三数学选修〔Ⅰ〕p25的随机数表中第3行第5列的数6为开始抽样数字.开始抽样有两种方法,第一种:从选定的数字6开始向右顺次三位、三位取,共取8个3位数〔6,22〕,〔7,66〕,〔5,65〕,〔0,26〕〔7,10〕,〔7,32〕,〔9,07〕,〔9,28〕把第一位数中大于4的用它除以5所得的余数作抽取样本编号的第一位数字,后两位数大于49的除以50所得的余数作为抽取样本的第二、三位数字,其它不动,则抽取的样本为:〔1,22〕,〔2,16〕,〔0,15〕,〔0,26〕〔2,10〕,〔2,32〕,〔4,07〕,〔4,28〕第二种:完全按前面第一大问题中的三个步骤进行即可,则抽取的样本为:026,141,012,121,014,218,176,4382、总体个数较多时,先将总体分为均衡的几部分,然后进行抽样〔1〕总体中的个体数能被样本整除将总体分为均衡部分的个数可小于或等于样本容量〔这里只是谈等于,小于时可仿此法进行,但样本容量应是分成均衡的部分个数的倍数〕,然后利用随机数表法分别从每一部分抽取一个,则总共抽的个数就构成一个样本,例如:总体1000,抽取一个容量为50的样本,在抽取样本时,可将总体分为50个均等部分,再从每一部分中抽取一个,共抽取50个,构成一个样本.〔2〕总体中的个体数不能被样本容量整除用随机数表法,从总体中剔除一部分个体,使剩下的个体数能被样本容量整除,在按前面1的方法进行抽样.例如:总体容量为1003,抽取一个样本容量为50的样本.现用随机数表法剔除3个个体,然后将1000个个体分成50个均衡部分,再用随机数表法从每一部分中各抽取一个,共抽50个,构成一个样本容量为50的样本.。
利用随机数表抽取样本的方法

利用随机数表抽取样本的方法随机数表是由0、1、2、3……9,这十个数字随机排列成的表格,表中每个位置上出现各个数字的概率都是相等的,随机数表不是唯一的,只要一个数表各个位置上出现的数字的概率是相同的,它就可以构成一个随机数表,第一张随机数表是由铁皮特在1927年给出的,统计工作者常用计算机生成随机数表,有的多功能计算器上也设有生成随机数的按键.一、直接利用随机数表直接利用随机数表进行抽样共有三个步骤:第一步:对总体的各个个体进行编号这里所谓编号就是编数字号码,编码方法与总体中个体多少有关,具体编码方法如下:当个体数小于或等于100时,可编为两位数字号码,如:总体的个数为100,其编号为00,01,02,……99;当个体数小于或等于1000时,可编为三位数字的号码,如:总体个数为500,其编号000,001,002,……499;当个体数小于或等于10000时,可编为四位数字的号码,如:总体数为7560,其编号为0000,0001,0002,……7559;… …… …… …这样的编号是为了便于使用随机数表.第二步:选定抽样开始的数字为了保证所选数字的随机性,①要随机选,②应在面对随机数表之前就指出开始数字的纵横位置,例如:选第8行第10列位置的数字为开始抽样的数字,③根据所选数字的纵横位置,在表中查清所选的数字是几,例如:第8行第10列数字是9.第三步:抽取样本号码从选定的数字开始,按照对个体所编的号码位数〔如:两位或三位或四位……〕,沿着同一个方向向右或向左或向上或向下两位、两位或三位、三位或四位、四位……一直读下去,就会得到一系列两位数字号码或三位数字号码或四位数字号码……,在这些号码里,按抽取的顺序依次把不在编号内的号码去掉,重复号码只取一个,这个过程继续下去,直到取够样本容量为止.为了便于操作,特别是为了知道所抽取的每一个号码是否与前面得到的号码重复,可将总体中所有号码先按顺序列出,每抽出一个号码时就在其中的相应号码中做一个记号,这样就知道后面的号码是否被取出.例如:某地举行了一次数字竞赛,参加竞赛的学生300人,为了了解竞赛成绩分布情况,计划从中抽取一个容量为15的样本,其步骤如下:Ⅰ、给三百名参赛者进行三位数编号,编号为000,001,002,003……299.Ⅱ、选定开始抽样的数字,在人教版高三数学教材选修〔Ⅰ〕p25的随机数表中任选第5行第10列位置的数4为开始抽样的数字.Ⅲ、从选定的数4开始向右三位,三位读下去,得到一系列三位数号码,在得到的三位数号码中去掉大于299的,重复的号码只取一个,则得容量为15的样本号码为246,223,162,061,130,217,209,258,120,163,199,175,128,238,123.二、间接利用随机数表进行抽样当总体个数较多时,一般抽取的样本容量也较大,直接利用随机数表进行抽样,显然较为费事,如果先把总体分成几个均衡的若干部分,再利用随机数表施行抽样,则较为方便.根据总体情况和所要抽取的样本大小分两种情况来谈.1、总体已经是均衡的几部分,且样本容量与部分容量不相等对这类总体抽样方法与前面的步骤基本相同,只是第一步骤对个体编号有所不同,编号时可进行多维编号,根据每部分中个体总数的不同,可编为三维编号〔Xi;Yi;Zi;〕,或四维编号〔xi;yi;zi;ei〕等,其中第一个数字代表部分编码,第二、三位数字或二、三、四位数字等,组成的两位数或三位数等代表该个体在部分的编号,编好号码后按前面中的第二、三个步骤进行即可.例如:从某校均衡的五个班的三年级中抽出八名学生进行成绩测验编号:〔0,00〕,〔0,01〕…〔0,49〕,〔1,00〕,〔1,01〕…〔1,49〕〔2,00〕,〔2,01〕…〔2,49〕〔3,00〕,〔3,01〕…〔3,49〕〔4,00〕,〔4,01〕…〔4,49〕〔5,00〕,〔5,01〕…〔5,49〕选定抽样开始的数字,在人教版高三数学选修〔Ⅰ〕p25的随机数表中第3行第5列的数6为开始抽样数字.开始抽样有两种方法,第一种:从选定的数字6开始向右顺次三位、三位取,共取8个3位数〔6,22〕,〔7,66〕,〔5,65〕,〔0,26〕〔7,10〕,〔7,32〕,〔9,07〕,〔9,28〕把第一位数中大于4的用它除以5所得的余数作抽取样本编号的第一位数字,后两位数大于49的除以50所得的余数作为抽取样本的第二、三位数字,其它不动,则抽取的样本为:〔1,22〕,〔2,16〕,〔0,15〕,〔0,26〕〔2,10〕,〔2,32〕,〔4,07〕,〔4,28〕第二种:完全按前面第一大问题中的三个步骤进行即可,则抽取的样本为:026,141,012,121,014,218,176,4382、总体个数较多时,先将总体分为均衡的几部分,然后进行抽样〔1〕总体中的个体数能被样本整除将总体分为均衡部分的个数可小于或等于样本容量〔这里只是谈等于,小于时可仿此法进行,但样本容量应是分成均衡的部分个数的倍数〕,然后利用随机数表法分别从每一部分抽取一个,则总共抽的个数就构成一个样本,例如:总体1000,抽取一个容量为50的样本,在抽取样本时,可将总体分为50个均等部分,再从每一部分中抽取一个,共抽取50个,构成一个样本.〔2〕总体中的个体数不能被样本容量整除用随机数表法,从总体中剔除一部分个体,使剩下的个体数能被样本容量整除,在按前面1的方法进行抽样.例如:总体容量为1003,抽取一个样本容量为50的样本.现用随机数表法剔除3个个体,然后将1000个个体分成50个均衡部分,再用随机数表法从每一部分中各抽取一个,共抽50个,构成一个样本容量为50的样本.。
利用随机数表抽取样本的方法讲

利用随机数表抽取样本的方法讲The latest revision on November 22, 2020利用随机数表抽取样本的方法随机数表是由0、1、2、3……9,这十个数字随机排列成的表格,表中每个位置上出现各个数字的概率都是相等的,随机数表不是唯一的,只要一个数表各个位置上出现的数字的概率是相同的,它就可以构成一个随机数表,第一张随机数表是由铁皮特在1927年给出的,统计工作者常用计算机生成随机数表,有的多功能计算器上也设有生成随机数的按键.一、直接利用随机数表直接利用随机数表进行抽样共有三个步骤:第一步:对总体的各个个体进行编号这里所谓编号就是编数字号码,编码方法与总体中个体多少有关,具体编码方法如下:当个体数小于或等于100时,可编为两位数字号码,如:总体的个数为100,其编号为00,01,02,……99;当个体数小于或等于1000时,可编为三位数字的号码,如:总体个数为500,其编号000,001,002,……499;当个体数小于或等于10000时,可编为四位数字的号码,如:总体数为7560,其编号为0000,0001,0002,……7559;… … … … … …这样的编号是为了便于使用随机数表.第二步:选定抽样开始的数字为了保证所选数字的随机性,①要随机选,②应在面对随机数表之前就指出开始数字的纵横位置,例如:选第8行第10列位置的数字为开始抽样的数字,③根据所选数字的纵横位置,在表中查清所选的数字是几,例如:第8行第10列数字是9.第三步:抽取样本号码从选定的数字开始,按照对个体所编的号码位数〔如:两位或三位或四位……〕,沿着同一个方向向右或向左或向上或向下两位、两位或三位、三位或四位、四位……一直读下去,就会得到一系列两位数字号码或三位数字号码或四位数字号码……,在这些号码里,按抽取的顺序依次把不在编号内的号码去掉,重复号码只取一个,这个过程继续下去,直到取够样本容量为止.为了便于操作,特别是为了知道所抽取的每一个号码是否与前面得到的号码重复,可将总体中所有号码先按顺序列出,每抽出一个号码时就在其中的相应号码中做一个记号,这样就知道后面的号码是否被取出.例如:某地举行了一次数字竞赛,参加竞赛的学生300人,为了了解竞赛成绩分布情况,计划从中抽取一个容量为15的样本,其步骤如下:Ⅰ、给三百名参赛者进行三位数编号,编号为000,001,002,003……299.Ⅱ、选定开始抽样的数字,在人教版高三数学教材选修〔Ⅰ〕p25的随机数表中任选第5行第10列位置的数4为开始抽样的数字.Ⅲ、从选定的数4开始向右三位,三位读下去,得到一系列三位数号码,在得到的三位数号码中去掉大于299的,重复的号码只取一个,则得容量为15的样本号码为246,223,162,061,130,217,209,258,120,163,199,175,128,238,123.二、间接利用随机数表进行抽样当总体个数较多时,一般抽取的样本容量也较大,直接利用随机数表进行抽样,显然较为费事,如果先把总体分成几个均衡的若干部分,再利用随机数表施行抽样,则较为方便.根据总体情况和所要抽取的样本大小分两种情况来谈.1、总体已经是均衡的几部分,且样本容量与部分容量不相等对这类总体抽样方法与前面的步骤基本相同,只是第一步骤对个体编号有所不同,编号时可进行多维编号,根据每部分中个体总数的不同,可编为三维编号〔Xi;Yi;Zi;〕,或四维编号〔xi;yi;zi;ei〕等,其中第一个数字代表部分编码,第二、三位数字或二、三、四位数字等,组成的两位数或三位数等代表该个体在部分的编号,编好号码后按前面中的第二、三个步骤进行即可.例如:从某校均衡的五个班的三年级中抽出八名学生进行成绩测验编号:〔0,00〕,〔0,01〕…〔0,49〕,〔1,00〕,〔1,01〕…〔1,49〕〔2,00〕,〔2,01〕…〔2,49〕〔3,00〕,〔3,01〕…〔3,49〕〔4,00〕,〔4,01〕…〔4,49〕〔5,00〕,〔5,01〕…〔5,49〕选定抽样开始的数字,在人教版高三数学选修〔Ⅰ〕p25的随机数表中第3行第5列的数6为开始抽样数字.开始抽样有两种方法,第一种:从选定的数字6开始向右顺次三位、三位取,共取8个3位数〔6,22〕,〔7,66〕,〔5,65〕,〔0,26〕〔7,10〕,〔7,32〕,〔9,07〕,〔9,28〕把第一位数中大于4的用它除以5所得的余数作抽取样本编号的第一位数字,后两位数大于49的除以50所得的余数作为抽取样本的第二、三位数字,其它不动,则抽取的样本为:〔1,22〕,〔2,16〕,〔0,15〕,〔0,26〕〔2,10〕,〔2,32〕,〔4,07〕,〔4,28〕第二种:完全按前面第一大问题中的三个步骤进行即可,则抽取的样本为:026,141,012,121,014,218,176,4382、总体个数较多时,先将总体分为均衡的几部分,然后进行抽样〔1〕总体中的个体数能被样本整除将总体分为均衡部分的个数可小于或等于样本容量〔这里只是谈等于,小于时可仿此法进行,但样本容量应是分成均衡的部分个数的倍数〕,然后利用随机数表法分别从每一部分抽取一个,则总共抽的个数就构成一个样本,例如:总体1000,抽取一个容量为50的样本,在抽取样本时,可将总体分为50个均等部分,再从每一部分中抽取一个,共抽取50个,构成一个样本.〔2〕总体中的个体数不能被样本容量整除用随机数表法,从总体中剔除一部分个体,使剩下的个体数能被样本容量整除,在按前面1的方法进行抽样.例如:总体容量为1003,抽取一个样本容量为50的样本.现用随机数表法剔除3个个体,然后将1000个个体分成50个均衡部分,再用随机数表法从每一部分中各抽取一个,共抽50个,构成一个样本容量为50的样本.。
1.3抽样式方法(二)

例3 为了考查某校的教学水平,将抽查这个学校高三年级的部分 学生的本学年考试成绩进行考察。为了全面的反映实际情况,采取 以下二种形式进行抽查:(已知该校高三年级共有20个教学班,并 且每个班内的学生已经按随机方式编好了学号,假定该校每班学生 人数都相同) (1)从全年级20个班中任意抽出一个班,再从该班中任意抽取20 人,考察他们的学习成绩。 (2)把学生按成绩分成优秀、良好、普通三个级别,从其中抽取 100名学生进行考察。(若已知按成绩分,该校高三学生中优秀、 良好、普通生分别为150、600、250人) 根据上述叙述,回答下面问题 (1)上面抽取方式中,其总体、个体、样本分别指什么?样本容 量是多少? (2)上面二种抽取方式各自采用了何种抽取样本的方法? (3)试分别写出上面二种方式各自抽取样本的步骤
分层抽样定义:当已知总体由差异明显的几部分
组成时,为了使样本更充分地反映总体的情况,常 将总体分成几部分,然后按照各部分所占的比进行 抽样,这种抽取叫做分层抽样,其ቤተ መጻሕፍቲ ባይዱ所分成的各部 分叫做层。
说明: 说明 : (1)当总体由差异明显的几部分组成,采取 分层抽样。 (2)分层抽样是等概率抽样,它也是公平的。用分 层抽样从个体为N的总体中抽取一个容量为n的样本时 ,在整个抽样过程中每个个体被抽到的概率相等,都 等于 。 (3)分层抽样是建立在简单随机抽样的基础上的, 由于它充分利用了已知信息,因此它获取的样本更具 代表性,在实际应用中更为广泛。 (4)步骤:第一步求出样本容量与总体的个体数之 比m:n,第二步各层数量乘比值m:n,得各层应抽数 (需为整数时可进行四舍五入),第三步采用简单随 机抽样的方法(抽签或随机数表法)从各个层中分别 抽取,然后合在一起,就是所抽取的样本
2.三种抽样方法的比较
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用随机数表抽取样本的方法
随机数表是由0、1、2、3 9,这十个数字随机排列成的表格,表中每个位置上出现
各个数字的概率都是相等的,随机数表不是唯一的,只要一个数表各个位置上出现的数字的
概率是相同的,它就可以构成一个随机数表,第一张随机数表是由铁皮特在1927 年给出的,统计工作者常用计算机生成随机数表,有的多功能计算器上也设有生成随机数的按键.
一、直接利用随机数表
直接利用随机数表进行抽样共有三个步骤:
第一步:对总体的各个个体进行编号
这里所谓编号就是编数字号码,编码方法与总体中个体多少有关,具体编码方法如下:当个体数小于或等于100 时,可编为两位数字号码,如:总体的个数为100 ,其编号为 00 , 01, 02,99 ;
当个体数小于或等于1000 时,可编为三位数字的号码,如:总体个数为500 ,其编号000 ,001 ,002 , 499 ;
当个体数小于或等于10000 时,可编为四位数字的号码,如:总体数为7560 ,其编号为 0000 , 0001 , 0002 , 7559 ;
这样的编号是为了便于使用随机数表.
第二步:选定抽样开始的数字
为了保证所选数字的随机性,①要随机选,②应在面对随机数表之前就指出开始数字
的纵横位置,例如:选第 8 行第 10 列位置的数字为开始抽样的数字,
③根据所选数字的纵横位置,在表中查清所选的数字是几,例如:第 8 行第 10 列数字是 9 .
第三步:抽取样本号码
从选定的数字开始,按照对个体所编的号码位数〔如:两位或三位或四位〕,沿着同一个方向向右或向左或向上或向下两位、两位或三位、三位或四位、四位一直读下去,就会得到一系列两位数字号码或三位数字号码或四位数字号码,在这些号码里,按抽取的顺序依次把不在编号内的号码去掉,重复号码只取一个,这个过程继续下去,直到取够样
本容量为止.为了便于操作,特别是为了知道所抽取的每一个号码是否与前面得到的号码重
复,可将总体中所有号码先按顺序列出,每抽出一个号码时就在其中的相应号码中做一个记
号,这样就知道后面的号码是否被取出.
例如:某地举行了一次数字竞赛,参加竞赛的学生300 人,为了了解竞赛成绩分布情
况,计划从中抽取一个容量为15 的样本,其步骤如下:
Ⅰ、给三百名参赛者进行三位数编号,编号为000 ,001 , 002 ,003299 .
Ⅱ、选定开始抽样的数字,在人教版高三数学教材选修〔Ⅰ〕p25 的随机数表中任选
第 5 行第 10 列位置的数 4 为开始抽样的数字.
Ⅲ、从选定的数 4 开始向右三位,三位读下去,得到一系列三位数号码,在得到的三
位数号码中去掉大于299 的,重复的号码只取一个,则得容量为15 的样本号码为246 ,223 ,162 , 061 , 130 , 217 , 209 , 258 , 120 , 163 , 199 , 175 , 128 , 238 , 123 .
二、间接利用随机数表进行抽样
当总体个数较多时,一般抽取的样本容量也较大,直接利用随机数表进行抽样,显然
较为费事,如果先把总体分成几个均衡的若干部分,再利用随机数表施行抽样,则较为方
便.根据总体情况和所要抽取的样本大小分两种情况来谈.
1 、总体已经是均衡的几部分,且样本容量与部分容量不相等
对这类总体抽样方法与前面的步骤基本相同,只是第一步骤对个体编号有所不同,编
号时可进行多维编号,根据每部分中个体总数的不同,可编为三维编号〔Xi ; Yi ;Zi ;〕, 或四维编号〔 xi ; yi; zi; ei〕等,其中第一个数字代表部分编码,第二、三位数字或二、三、
四位数字等,组成的两位数或三位数等代表该个体在部分的编号,编好号码后按前面中的第二、三个步骤进行即可.
例如:从某校均衡的五个班的三年级中抽出八名学生进行成绩测验
编号:〔 0 , 00〕,〔 0, 01 〕〔 0 ,49 〕,
〔 1 ,00 〕,〔 1, 01〕〔1,49〕
〔 2 ,00 〕,〔2,01〕〔2,49〕
〔 3 ,00 〕,〔3,01〕〔3,49〕
〔 4 ,00 〕,〔4,01〕〔4,49〕
〔 5 ,00 〕,〔5,01〕〔5,49〕
选定抽样开始的数字,在人教版高三数学选修〔Ⅰ〕p25 的随机数表中第 3 行第 5 列的数 6 为开始抽样数字.开始抽样有两种方法,
第一种:从选定的数字 6 开始向右顺次三位、三位取,共取8 个 3 位数
〔6 ,22 〕,〔 7, 66 〕,〔 5 ,65 〕,〔0 , 26 〕
〔7 ,10 〕,〔 7, 32 〕,〔 9 ,07 〕,〔9 , 28 〕
把第一位数中大于 4 的用它除以 5 所得的余数作抽取样本编号的第一位数字,后两位数
大于 49 的除以 50 所得的余数作为抽取样本的第二、三位数字,其它不动,则抽取的样本为:
〔1 ,22 〕,〔 2, 16 〕,〔 0 ,15 〕,〔0 , 26 〕
〔2 ,10 〕,〔 2, 32 〕,〔 4 ,07 〕,〔4 , 28 〕
第二种:完全按前面第一大问题中的三个步骤进行即可,则抽取的样本为:
026 , 141 , 012 , 121 ,014 ,218 ,176 ,438
2、总体个数较多时,先将总体分为均衡的几部分,然后进行抽样
〔 1〕总体中的个体数能被样本整除
将总体分为均衡部分的个数可小于或等于样本容量〔这里只是谈等于,小于时可仿此
法进行,但样本容量应是分成均衡的部分个数的倍数〕,然后利用随机数表法分别从每一部
分抽取一个,则总共抽的个数就构成一个样本,例如:总体1000 ,抽取一个容量为50 的样本,在抽取样本时,可将总体分为50 个均等部分,再从每一部分中抽取一个,共抽取50 个,构成一个样本.
〔2〕总体中的个体数不能被样本容量整除
用随机数表法,从总体中剔除一部分个体,使剩下的个体数能被样本容量整除,在按
前面 1 的方法进行抽样.例如:总体容量为 1003 ,抽取一个样本容量为 50 的样本.现用随机数表法剔除 3 个个体,然后将 1000 个个体分成 50 个均衡部分,再用随机数表法从每一部分中各抽取一个,共抽 50 个,构成一个样本容量为 50 的样本.。
