特性阻抗计算
一直有很多人问我阻抗怎么计算的人家问多了我想给大家

⼀直有很多⼈问我阻抗怎么计算的⼈家问多了我想给⼤家⼀直有很多⼈问我阻抗怎么计算的. ⼈家问多了,我想给⼤家整理个材料,于⼰于⼈都是个⽅便.如果⼤家还有什么问题或者⽂档有什么错误,欢迎讨论与指教!在计算阻抗之前,我想很有必要理解这⼉阻抗的意义。
传输线阻抗的由来以及意义传输线阻抗是从电报⽅程推导出来(具体可以查询微波理论)如下图,其为平⾏双导线的分布参数等效电路:从此图可以推导出电报⽅程取传输线上的电压电流的正弦形式得推出通解定义出特性阻抗⽆耗线下r=0, g=0 得注意,此特性阻抗和波阻抗的概念上的差异(具体查看平⾯波的波阻抗定义)特性阻抗与波阻抗之间关系可从此关系式推出.Ok,理解特性阻抗理论上是怎么回事情,看看实际上的意义,当电压电流在传输线传播的时候,如果特性阻抗不⼀致所求出的电报⽅程的解不⼀致,就造成所谓的反射现象等等.在信号完整性领域⾥,⽐如反射,串扰,电源平⾯切割等问题都可以归类为阻抗不连续问题,因此匹配的重要性在此展现出来.叠层(stackup)的定义我们来看如下⼀种stackup,主板常⽤的8 层板(4 层power/ground 以及4 层⾛线层,sggssggs,分别定义为L1, L2…L8)因此要计算的阻抗为L1,L4,L5,L8下⾯熟悉下在叠层⾥⾯的⼀些基本概念,和⼚家打交道经常会使⽤的Oz 的概念Oz 本来是重量的单位Oz(盎司)=28.3 g(克)在叠层⾥⾯是这么定义的,在⼀平⽅英尺的⾯积上铺⼀盎司的铜的厚度为1Oz,对应的单位如下介电常数(DK)的概念电容器极板间有电介质存在时的电容量Cx 与同样形状和尺⼨的真空电容量Co之⽐为介电常数:-ε"ε = Cx/Co = ε'Prepreg/Core 的概念pp 是种介质材料,由玻璃纤维和环氧树脂组成,core 其实也是pp 类型介质,只不过他两⾯都覆有铜箔,⽽pp 没有.传输线特性阻抗的计算⾸先,我们来看下传输线的基本类型,在计算阻抗的时候通常有如下类型: 微带线和带状线,对于他们的区分,最简单的理解是,微带线只有 1 个参考地,⽽带状线有2个参考地,如下图所⽰对照上⾯常⽤的8 层主板,只有top 和bottom ⾛线层才是微带线类型,其他的⾛线层都是带状线类型在计算传输线特性阻抗的时候, 主板阻抗要求基本上是:单线阻抗要求55 或者60Ohm,差分线阻抗要求是70~110Ohm,厚度要求⼀般是1~2mm,根据板厚要求来分层得到各厚度⾼度. 在此假设板厚为 1.6mm,也就是63mil 左右, 单端阻抗要求60Ohm,差分阻抗要求100Ohm,我们假设以如下的叠层来⾛线先来计算微带线的特性阻抗,由于top 层和bottom 层对称,只需要计算top 层阻抗就好的,采⽤polar si6000,对应的计算图形如下:在计算的时候注意的是:1,你所需要的是通过⾛线阻抗要求来计算出线宽W(⽬标)2,各⼚家的制程能⼒不⼀致,因此计算⽅法不⼀样,需要和⼚家进⾏确认3,表层采⽤coated microstrip 计算的原因是,⼚家会有覆绿漆,因⽽没⽤surface microstrip 计算,但是也有⼚家采⽤surface microstrip 来计算的,它是经过校准的4,w1 和w2 不⼀样的原因在于pcb 板制造过程中是从上到下⽽腐蚀,因此腐蚀出来有梯形的感觉(当然不完全是)5,在此没计算出精确的60Ohm 阻抗,原因是实际制程的时候⼚家会稍微改变参数,没必要那么精确,在1,2ohm 范围之内我是觉得没问题6,h/t 参数对应你可以参照叠层来看再计算出L5 的特性阻抗如下图记得当初有各版本对于stripline 还有symmetrical stripline 的计算图,实际上的差异从字⾯来理解就是symmetrical stripline 其实是offset stripline 的特例H1=H2在计算差分阻抗的时候和上⾯计算类似,除所需要的通过⾛线阻抗要求来计算出线宽的⽬标除线宽还有线距,在此不列出选⽤的图是在计算差分阻抗注意的是:1,在满⾜DDR2 clock 85Ohm~1394 110Ohm 差分阻抗的同时⼜满⾜其单端阻抗,因此我通常选择的是先满⾜差分阻抗(很多是电流模式取电压的)再考虑单端阻抗(通常板⼚是不考虑的,实际做很多板⼦,问题确实不算⼤,看样⼦差分线还是⾛线同层同via 同间距要求⼀定要符合)特性阻抗公式(含微带线,带状线的计算公式)a.微带线(microstrip)Z={87/[sqrt(Er+1.41)]}ln[5.98H/(0.8W+T)] 其中,W为线宽,T为⾛线的铜⽪厚度,H为⾛线到参考平⾯的距离,Er是PCB板材质的介电常数(dielectric constant)。
pcb阻抗板‘特性阻抗;基础知识
4.2.2.2 T1/B1 分别相连的测试线长一般为 100mm,线宽与板内生产板内阻抗线宽度一致,且线面盖阻焊 油墨;
d 4.2.2.3 T1-T2/T2-B2/B2-B1/B1-T1 的两个相邻孔中心距一般为 2.54mm; e 4.2.2.4 其中,T1 仅与 TOP 层阻抗测试线相连,T2 仅与 TOP 面第 2 层内层相连;B1 仅与 BOT 层阻抗测 r 试线相连,B2 仅与 BOT 层第 2 层相连。 te 阻抗条的设计图例:
深圳顺易捷科技有限公司
Shenzhen ShunYiJie Technology Co., Ltd.
5.3 CPU 载板的 TDR 测试
d Hioki 公司 2001 年六月才在 JPCA 推出的“1109 Hi Tester”,为了对 1.7GHz 高速传输 FC/PGA 载板在 Z0 方
面的正确量测起见,已不再使用飞针式(Flying probe)快速移动的触测,也放弃了 SMA 探棒式的 TDR 手动
3.3 但当上述微带线中 Z0 的四种变数(w、t、h、 r)有任一项发生异常,例如图中的讯号线出现缺口
e 时,将使得原来的 Z0 突然上升(见上述公式中之 Z0 与 W 成反比的事实),而无法继续维持应有的稳 UnRegister 定均匀(Continuous)时,则其讯号的能量必然会发生部分前进,而部分却反弹反射的缺失
4. 2 示意图说明:
4.2.1 阻抗线的位置
一般加在生产板 PNL 边上或在客户允许的前提下加在 SET 边上
4.2.2 阻抗线的规格说明
4.2.2.1 T1、T2/B1、B2 为四个 PTH 孔,一般为喷锡成形孔,成品孔径为 1.00mm 左右,RING(成品 焊环)要求为 0.16-0.20mm;
PCB线路板阻抗计算公式

PCB线路板阻抗计算公式1. 传输线模型:PCB线路板可以近似看作是由两个导体平行排列组成的传输线。
当高频信号传输时,需要考虑传输线的特性阻抗。
常用的传输线模型有微带线(microstrip)和同轴线(coplanar)。
2.微带线模型:微带线是一种将信号层与地层通过电介质层相连的结构。
计算微带线的阻抗需要考虑的参数包括信号层宽度W、信号层与地层之间的介电常数Er、信号层厚度H1以及介电层厚度H2等。
微带线的阻抗计算公式为:Z0 = 87 / sqrt(Er + 1.41) * (W/H1 + 1.38/H2) + 0.8 * W其中Z0为微带线的特性阻抗,单位为欧姆。
3.同轴线模型:同轴线由内导体、绝缘层和外导体组成。
计算同轴线的阻抗需要考虑的参数包括内导体半径R1、绝缘层厚度H2、外导体半径R2以及介电常数Er等。
同轴线的阻抗计算公式为:Z0 = 60 * ln(R2/R1) / sqrt(Er) + 138 / sqrt(Er)其中Z0为同轴线的特性阻抗,单位为欧姆。
4.其他影响因素:在使用上述公式计算阻抗时,还需要考虑以下一些因素。
-线路板堆叠结构:多层线路板的堆叠结构会对阻抗产生影响。
通常情况下,带有地层的堆叠结构会使阻抗变小,而带有电源或信号层的堆叠结构会使阻抗变大。
-信号引线长度:信号引线的长度对阻抗也会有一定影响。
根据传输线理论,当信号引线长度小于1/10波长时,可以忽略这种影响。
-裸板材料:PCB线路板的裸板材料及其特性参数(如介电常数)也会对阻抗产生影响。
在选择裸板材料时需要根据设计需求和成本考虑。
总之,PCB线路板的阻抗计算需要综合考虑以上因素,利用适当的公式和参数进行计算。
对于复杂的线路板设计,可以借助专业的PCB设计软件来计算和优化阻抗。
AppCAD计算天线信号线的特性阻抗
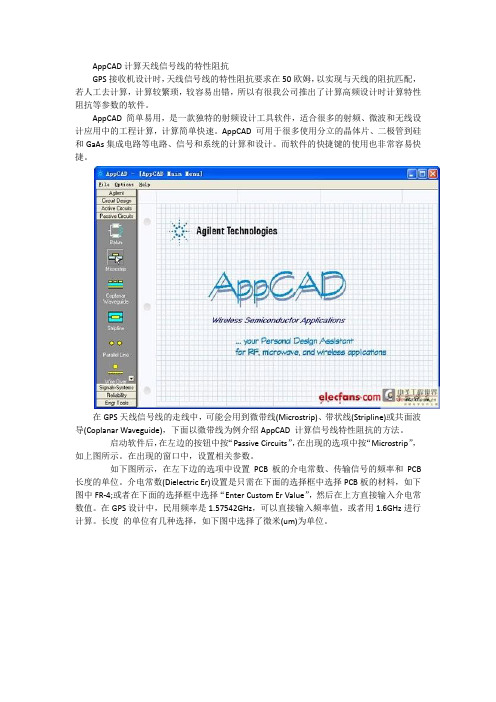
AppCAD计算天线信号线的特性阻抗GPS接收机设计时,天线信号线的特性阻抗要求在50欧姆,以实现与天线的阻抗匹配,若人工去计算,计算较繁琐,较容易出错,所以有很我公司推出了计算高频设计时计算特性阻抗等参数的软件。
AppCAD 简单易用,是一款独特的射频设计工具软件,适合很多的射频、微波和无线设计应用中的工程计算,计算简单快速。
AppCAD 可用于很多使用分立的晶体片、二极管到硅和GaAs集成电路等电路、信号和系统的计算和设计。
而软件的快捷键的使用也非常容易快捷。
在GPS天线信号线的走线中,可能会用到微带线(Microstrip)、带状线(Stripline)或共面波导(Coplanar Waveguide),下面以微带线为例介绍AppCAD 计算信号线特性阻抗的方法。
启动软件后,在左边的按钮中按“Passive Circuits”,在出现的选项中按“Microstrip”,如上图所示。
在出现的窗口中,设置相关参数。
如下图所示,在左下边的选项中设置PCB板的介电常数、传输信号的频率和PCB 长度的单位。
介电常数(Dielectric Er)设置是只需在下面的选择框中选择PCB板的材料,如下图中FR-4;或者在下面的选择框中选择“Enter Custom Er Value”,然后在上方直接输入介电常数值。
在GPS设计中,民用频率是1.57542GHz,可以直接输入频率值,或者用1.6GHz进行计算。
长度的单位有几种选择,如下图中选择了微米(um)为单位。
在上图中左上边需设置以下参数:线宽“W”,如图中为254微米;单层PCB板的厚度“H”,如8层板的厚度是1.2mm,则每层约150微米,如图中输入为150。
线的厚度“T”,1OUNCE 线厚度约35微米,0.5OUNCE线厚约18微米,如图中输入为18微米,若镀金或镀锡,则需再加25微米。
线的长度“L”线对特性阻抗影响不大,所以可以不考虑线的长度,用默认值就可以了。
阻抗的有关计算公式

影响高频测试的因素一、影响特性阻抗的主要因素即电容与电感间的关系(公式见图)从阻抗公式看影响特性阻抗值的只有外径(外径可以看成和导线间距α相等)、总的绞合系数(λ)、组合绝缘介质的等效相对介电常数(εr)。
而且,Z正比于α和λ,反比于εr。
所以只要控制好了α、λ、εr的值,也就能控制好了Z。
一般来说节距越小Z越小,稳定性也越好,ZC 的波动越小。
1导体外径:绝缘外径越小阻抗越大。
2电容:电容越小发泡度越大同时阻抗也越大;3绝缘外观:绝缘押出不能偏心,同心度控制在90%以上;外观要光滑均匀无杂质,椭圆度在85%以上。
电线押完护套后基本上阻抗是不会再出现变化的,生产过程中的随机缺陷较小时造成的阻抗波动很小,除非在生产过程有过大的外部压力致使发泡线被压伤或压变形。
当较严重的周期性不均匀缺陷时,且相邻点间的距离等于电缆传输信号波长的一半时,在此频率点及其整数倍频率点上将出现显着的尖峰(即突掉现象),这时不但阻抗不过,衰减也过不了。
二、各工序影响衰减的主要因素a衰减=a金属衰减+a介质材料衰减+a阻抗不均匀时反射引起的附加衰减1.导体:导体外径下公差,电阻增大,影响传输效果及阻抗;所以一般都采用上公差的导体做发泡线。
高频时信号传输会出现集肤效应,信号只是在导体的表面流过,所以要求导体表面要平滑,绞合绝对不能出现跳股现象,单支导体及绞合后的圆整度要好。
导体束绞、绝缘押出及芯线对绞时张力都不能过大,以防拉细导体。
2.绝缘:在绝缘时影响衰减的因素主要有绝缘材料、绝缘线径稳定性、发泡电容值及气泡匀密度、同心度(发泡层及结皮的同心度)、芯线的圆整度。
在测试频率越高时对发泡材料的要求越高,但现在所用的DGDA3485是现在高频线用得最广泛的化学发泡料。
控制绝缘主要有以下几项:A.外径要控制在工艺要求偏差±0.02mm之内;B.发泡要均匀致密,电容要控制在工艺要求偏差±1.0PF之内;C.绝缘外结皮厚度控制在0.05mm以内;D.色母配比不能过大,越少越好,在1.5%左右;E.外观:外观要光滑均匀,无杂质,椭圆度在85%以上。
矩形同轴线特性阻抗

矩形同轴线特性阻抗一、计算方法对于TEM 传输线来说,由表达式Z 1'0)(-=cC 知要计算矩形同轴线的特性阻抗,只需算得其单位长度内的电容即可。
内外导体之间相对平行部分的电容很容易求得,然而要计算四个拐角处的角电容则很难。
Skiles and Higgins 通过使用一种数学上的计算方法解决了这个难题——正交模块分析法。
该方法将待分析的区域划分为互相重叠的小区域,然后分别算出各个小区域内的量,最后予以叠加。
在计算矩形同轴线的特性阻抗时,实际只需要计算其中四分之一部分的量,如图(a )所示。
正交模块分析方法将次区域划分为了1和2两个区域,其中的量分别用1ψ和2ψ表示,如图(b )所示。
通过对所求区域内电位函数所满足的拉普拉斯方程 的求解,再结合特殊边界条件,解出各个待求的量。
二、计算过程1、目标函数:由所求区域中的电位函数满足拉普拉斯方程,得1ψ、2ψ、1φ和2φ的正交解形式:∑∞==11)/sin()(),(k k h y k x f y x πψ OBCG∑∞==12)/sin()(),(k k g x k y v y x πψ OAEF∑∞==11)/sin()(),(k k h y k x y x πφφ OADG∑∞==12)/sin()(),(k k g x k y y x πωφ OADG其中,k f 、k v 、k φ和k ω是由边界条件确定的待定常数。
),(),(11y x y x U U ψ== ABCD 2/ω+<<g x g h y <<0),(),(),(111y x y x y x U U φψ+== OADG g x <<0 h y <<0 ),(),(22y x y x U U ψ== DEFG g x <<0 2/b h y h +<< ),(),(),(222y x y x y x U U φψ+== OADG g x <<0 h y <<02、边界条件:X 方向上:(一)、在X=0处:(1)、),0(),0(),0(222y y y U φψ+= 2/0b h y +<< (2)、0),0(0),0(22=⇒=y y φψ(3)、0),0(),0(),0(111=+=y y y U φψ h y <<0(二)、在X=g 处:(1)、02),(U y g =ψ 2/0b h y +<< (2)、),(),(202y g U y g U φ+= h y <<0(3)、0),(1=y g φ h y <<0 (),(1y x ψ在g x =处连续,由上述U 等式组前两式得) (4)、),(),(21y g U y g U = h y <<0 (5)、01=∂∂=gx xφ h y <<0(三)、在2/ω+=g x 处:02/1=∂∂+=ωψg x xh y <<0Y 方向上:(一)、在0=y 处:(1)、)0,()0,()0,(111x x x U φψ+= 2/0ω+<<g x (2)、0)0,(0)0,(11=⇒=x x φψ(3)、0)0,()0,()0,(222=+=x x x U φψ g x <<0(二)、在h y =处:(1)、01),(U h x =ψ 2/0ω+<<g x (2)、),(),(101h x U h x U φ+= g x <<0(3)、0),(2=h x φ g x <<0 (),(2y x ψ在h y =处连续,由上述U 等式组前两式得) (4)、),(),(21h x U h x U = g x <<0 (5)、02=∂∂=hy yφ g x <<0(三)、在2/b h y +=处:02/2=∂∂+=b h x yψ g x <<03、通过边界条件解得系数:0')1(2)cosh()sinh()(U k h x k B h x k A x f k k k k --+=πππ0)1(2)cosh()sinh()(U k g y k N g y k M y v k k k k --+=πππ11220')(2)1()1(2)cosh()sinh()(-∞=∑⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-+-++=p p k k k k k k g h p h v U k h x k C h x k D x ππππφ ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛∙g x p k h x k g h p ππsin sinh11220)(2)1()1(2)cosh()sinh()(-∞=∑⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-+-++=p p k k k k k k h g p g f U k g y k F g y k L y ππππω ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛∙h y p k g y k h g p ππsin sinh利用特殊边界条件,将相同项约去并化简,得:⎪⎪⎩⎪⎪⎨⎧+=+=∑∑∞=∞=k p p kp k k p p kp k D X c Y B Y a X 11)sinh()1('hkg g B h k X k k k -=)sinh()1(g h k g N h k Y kk k π-=2222k p g h m g hk a p kp+⎪⎪⎭⎫ ⎝⎛=π ;222⎪⎪⎭⎫ ⎝⎛=g h k B k π 2222k p h g n h g k c p kp +⎪⎭⎫ ⎝⎛=π ;22πk D k = ⎥⎦⎤⎢⎣⎡+=g h g b p g b p g h p m p )2(cosh )2cosh()sinh(πππ⎥⎦⎤⎢⎣⎡+=)2(cosh )2cosh()sinh(h g h p h g p h g p n p ωπππ4、得出目标函数表达式:()⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡+-+=∑∞=h g x k h g h k h h g k h y k k Y h g U h y U k k k 2cosh )2(sec )sinh()sin()1(1001ωπωπππψ()⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡+-+=∑∞=g b h y k g h g b k h g h k g x k k Y h g U g x U k k k 2cosh )2(sec )sinh()sin()1(1002ππππψ利用ds n U U C ss ⎰⎪⎭⎫⎝⎛∂∂=0'ε得: ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-⎥⎦⎤⎢⎣⎡+++=∑∑∞=∞=12122'131224p p pp p p n p X m p Y h g h g g h g b h C πωε三、计算结果 136.054.500±=Z ohms。
特性阻抗

五、影响同轴电缆特性阻抗(Zc)的因素
5.1 影响同轴电缆特性阻抗的因素及比例关系:
影响Zc的因素 影响因素与Zc的变化关系 影响因素的变化 ↑ 等效介电常数ε e ↓ ↑ 内导体直径d ↓ ↑ 外导体内/外径D ↓ ↑ 编织导体直径Dw ↓ ↓ ↓ ↑ 正比 ↑ ↑ 正比 ↑ ↓ 反比 Zc的随之变化 ↓ 反比 比例关系
特性阻抗是指当电缆无限长时该电缆所具有的阻抗,是阻止电流通过导体的一
种电阻名称,它不是常规意义上的直流电阻。 一条电缆的特性阻抗是由电缆的电导率、电容以及阻值组合后的综合特性。假设 一根均匀电缆无限延伸,其发射端在某一频率下的阻抗称为特性阻抗 (Characteristic Impedance)。它由诸如导体的集合尺寸、导体间的中心距离、传输 线本身的结构、电缆绝缘材料的介电常数等因素决定,与数据传输线的长短无关。 数据传输线的瞬间阻抗或者是特征阻抗是影响信号品质及完整性的最重要的因素 。如果信号传播过程中,相邻的信号传播间隔之间阻抗保持一致,那么信号就可以十 分平稳地向前传播,因而情况变得十分简单。如果相邻的信号传播间隔之间存在差异 ,或者说阻抗发生了改变,信号中能量的一部分就会往回反射,信号传输的连续性也 会被破坏,由此会带来诸如回波损耗偏大、信号传输辐射增大、信号传输完整性不足 等问题。
解析特性阻抗 Characteristic Resistance
目
一. 特性阻抗的定义
录
二. 对称电缆的特性阻抗计算 三. 影响对称电缆特性阻抗的因素
四. 同轴电缆的特性阻抗计算
五. 影响同轴电缆特性阻抗的因素 六. NB Cable特性阻抗控制的实验数据分析
一、特性阻抗(Zc)的定义
1. 特性阻抗(Zc)的定义
4.1.2.编织外导体,绞线内导体同轴电缆的特性阻抗计算如下:
同轴电缆的特性阻抗计算

同轴电缆的特性阻抗计算同轴电缆特性阻抗拉普拉斯方程矩形网格同轴电缆的横截面可以看做是两个同心圆。
外圆半径为2,内圆半径为1。
外圆上的电势为1,内圆上的电势为0。
我们依据这些条件,通过编写matlab程序来计算出同轴缆线的特性阻抗。
首先介绍一下计算中所用到的物理学公式。
特性阻抗的公式为如下所示,C 为电容,C0为光速。
由这两个公式,我们可将求解阻抗的问题转化为求解电量的问题。
此时我们可以使用高斯公式。
为了处理截面上的问题,我们将面积分化为线积分。
本次计算过程中编程采用的方法是逐次超松弛迭代法。
先将同轴电缆的截面按矩形网格进行划分。
由于同轴电缆截面具有对称性,为了缩短程序运行时间,我们可以先计算四分之一截面内的电位分布。
电位的迭代公式如下。
由于这个程序采用矩形网格来处理圆的问题,所以处理精度和处理速度都没有采用极坐标处理理想。
如果希望得到跟极坐标情况下同样误差的结果,则需要耗费更多的计算时间。
图一为基本算法。
图二、图三、图四分别是将代误差率为百万分之一时的特性阻抗、电势分布图和电场分布图。
在文章的最后附有程序的代码。
建立一个所有元素均是nan的矩阵U在U中将1/4个圆环离散化(圆环所包括的点取0)将所有点的c1 c2 c3c4分别存入四个与U同维的矩阵C1 C2C3 C4中U(i,j)=0时上下左右是否有nan有没有U(i,j)为边界点计算c1 c2 c3 c4中不等于1的值U(i,j)不为边界c1=c2=c3=c4=1将边界上的电势值和C1 C2 C3 C4带入迭代公式开始反复迭代矩阵U若干次迭代后便得出在四分之一个圆环内的电势分布图一图二图三图四程序代码:clcclear all;ticr1=2;r2=1;n=.01;c=299792458;%err=8.854e-12;wuchalv=.0001;x=-r1:n:r1;y=r1:-n:-r1;l=length(x);dones=ones((l+1)/2);dlens=n*dones;dianwei_1=NaN((l+1)/2);[X,Y]=meshgrid(x,y);for i=1:(l+1)/2for j=1:(l+1)/2if X(i,j)^2+Y(i,j)^2<=4&&X(i,j)^2+Y(i,j)^2>=1dianwei_1(i,j)=0;elseendendenddianwei_2=isnan(dianwei_1);len3=dlens;for i=1:(l+1)/2for j=1:(l+1)/2-1if dianwei_2(i,j)==1&&dianwei_2(i,j+1)==0len3(i,j+1)=abs(abs(sqrt(r1^2-Y(i,j+1)^2))-abs(X(i,j+1)));elseendendendlen3((l+1)/2,1)=0;len2=len3';len1=dlens;for i=1:(l+1)/2for j=1:(l+1)/2-1if dianwei_2(i,j)==0&&dianwei_2(i,j+1)==1len1(i,j)=abs(abs(sqrt(r2^2-Y(i,j)^2))-abs(X(i,j)));elseendendendlen4=len1';c1=len1./n;c2=len2./n;c3=len3./n;c4=len4./n;dianwei_3=[dianwei_1 dianwei_1(:,(l+1)/2);dianwei_1((l+1)/2,:) NaN]; dianwei_4=dianwei_3;dianwei_5=dianwei_3;maxerl=1;en=1;while maxerl>=0for i=1:(l+1)/2for j=1:(l+1)/2if c1(i,j)==1&&c2(i,j)==0&&c3(i,j)==0&&c4(i,j)==1dianwei_3(i,j)=1;elseifc1(i,j)==1&&c2(i,j)<1&&c2(i,j)>0&&c3(i,j)==0&&c4(i,j)==1dianwei_3(i,j)=1;elseifc1(i,j)==1&&c3(i,j)<1&&c3(i,j)>0&&c2(i,j)==0&&c4(i,j)==1dianwei_3(i,j)=1;elseif c1(i,j)==0&&c2(i,j)==1&&c3(i,j)==1&&c4(i,j)==0dianwei_3(i,j)=0;elseifc1(i,j)==0&&c2(i,j)==1&&c3(i,j)==1&&c4(i,j)<1&&c4(i,j)>0dianwei_3(i,j)=0;elseifc1(i,j)<1&&c1(i,j)>0&&c2(i,j)==1&&c3(i,j)==1&&c4(i,j)==0dianwei_3(i,j)=0;endendendfor i=2:(l+1)/2forj=2:(l+1)/2 %c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c3(i,j)*dianwei_3(i,j +1)+c1(i,j)*dianwei_3(i,j-1))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+(( c4(i,j)*dianwei_3(i-1,j)+c2(i,j)*dianwei_3(i+1,j))/(c2(i,j)*c4(i,j)*( c2(i,j)+c4(i,j)))))/((c1(i,j)*c3(i,j))+(c2(i,j)*c4(i,j)));ifc1(i,j)==1&&c2(i,j)==1&&c3(i,j)<1&&c3(i,j)>0&&c4(i,j)==1dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c3(i,j)*dianwei_3(i ,j+1)+c1(i,j))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+((c4(i,j)*dianwei _3(i-1,j)+c2(i,j)*dianwei_3(i+1,j))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j) ))))/((c1(i,j)*c3(i,j))+(c2(i,j)*c4(i,j)));elseifc1(i,j)==1&&c2(i,j)<1&&c2(i,j)>0&&c3(i,j)==1&&c4(i,j)==1dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c3(i,j)*dianwei_3(i ,j+1)+c1(i,j)*dianwei_3(i,j-1))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+ ((c4(i,j)+c2(i,j)*dianwei_3(i+1,j))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j) ))))/((c1(i,j)*c3(i,j))+(c2(i,j)*c4(i,j)));elseifc1(i,j)<1&&c1(i,j)>0&&c2(i,j)==1&&c3(i,j)==1&&c4(i,j)==1dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c1(i,j)*dianwei_3(i ,j-1))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+((c4(i,j)*dianwei_3(i-1,j )+c2(i,j)*dianwei_3(i+1,j))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j)))))/((c 1(i,j)*c3(i,j))+(c2(i,j)*c4(i,j)));elseifc1(i,j)==1&&c2(i,j)==1&&c3(i,j)==1&&c4(i,j)<1&&c4(i,j)>0dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c3(i,j)*dianwei_3(i ,j+1)+c1(i,j)*dianwei_3(i,j-1))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+ ((c4(i,j)*dianwei_3(i-1,j))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j)))))/((c 1(i,j)*c3(i,j))+(c2(i,j)*c4(i,j)));elseifc1(i,j)==1&&c2(i,j)<1&&c2(i,j)>0&&c3(i,j)<1&&c3(i,j)>0&&c4(i,j)==1dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c3(i,j)*dianwei_3(i ,j+1)+c1(i,j))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+((c4(i,j)+c2(i,j) *dianwei_3(i+1,j))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j)))))/((c1(i,j)*c3 (i,j))+(c2(i,j)*c4(i,j)));elseifc1(i,j)<1&&c1(i,j)>0&&c4(i,j)<1&&c4(i,j)>0&&c2(i,j)==1&&c3(i,j)==1dianwei_4(i,j)=c1(i,j)*c2(i,j)*c3(i,j)*c4(i,j)*(((c1(i,j)*dianwei_3(i ,j-1))/(c1(i,j)*c3(i,j)*(c1(i,j)+c3(i,j))))+((c4(i,j)*dianwei_3(i-1,j ))/(c2(i,j)*c4(i,j)*(c2(i,j)+c4(i,j)))))/((c1(i,j)*c3(i,j))+(c2(i,j)* c4(i,j)));elseif c1(i,j)==c2(i,j)==c3(i,j)==c4(i,j)dianwei_4(i,j)=0.25*(dianwei_3(i-1,j)+dianwei_3(i+1,j)+dianwei_3(i,j+ 1)+dianwei_3(i,j-1));endendenddianwei_4((l+1)/2+1,:)=dianwei_3((l+1)/2-1,:);dianwei_4(:,(l+1)/2+1)=dianwei_3(:,(l+1)/2-1);dianwei_5=dianwei_4;dianwei_4=dianwei_3;dianwei_3=dianwei_5;er=abs(dianwei_3-dianwei_4);maxer=max(max(er));[q,w]=find(er==maxer);e=length(q);erl=zeros(1,e);for o=1:eerl(1,o)=er(q(o),w(o))-(wuchalv)*dianwei_3(q(o),w(o));endmaxerl=max(max(erl));for i=2:(l-1)/2p(i-1)=(dianwei_3(i-1,i-1)-dianwei_3(i,i))/(n*sqrt(2))*2*pi*(2-(i-1)* n)*sqrt(2);endk1=1;for k=1:(l-1)/2-1if ~isnan(p(k))==1Q(k1)=p(k);k1=k1+1;endendQ1=mean(Q');for i=2:(l-1)/4p1(i)=(dianwei_3((l+1)/2,i-1)-dianwei_3((l+1)/2,i))/(n)*2*pi*(2-(i-1) *n);endP1=mean(p1');R1=[Q1 P1];dianrong=mean(R1)*err;Z(en)=1/(c*dianrong);en=en+1;endplot(Z);hold onM=1/c/(2*pi*err/log(r1/r2));plot(M*ones(1,length(Z)),'-r');xlabel('迭代次数');ylabel('特性阻抗');text(1000,M,'理论值')hold offdianwei_6_1=fliplr(dianwei_3);dianwei_6_2=dianwei_3;dianwei_6_3=flipud(dianwei_3);dianwei_6_4=fliplr(dianwei_6_3);figure(2)dianwei_6=[dianwei_6_2(1:(l+1)/2,1:(l+1)/2)dianwei_6_1(1:(l+1)/2,3:(l+1)/2+1);dianwei_6_3(3:(l+1)/2+1,1:(l+1)/2) dianwei_6_4(3:(l+1)/2+1,3:(l+1)/2+1)];contourf(X,Y,dianwei_6);figure(3)[cc ch]=contour(X,Y,dianwei_6,15);clabel(cc);hold on[FX,FY]=gradient(dianwei_6,1,-1);quiver(X(1:20:401,1:20:401),Y(1:20:401,1:20:401),-FX(1:20:401,1:20:40 1),-FY(1:20:401,1:20:401));hold offtoc个人总结a) 本次作业的主要目的是练习一下用计算机处理FDM 。
阻抗计算公式、polarsi9000[教程]
![阻抗计算公式、polarsi9000[教程]](https://img.taocdn.com/s3/m/abe2f55979563c1ec5da71a9.png)
一直有很多人问我阻抗怎么计算的. 人家问多了,我想给大家整理个材料,于己于人都是个方便.如果大家还有什么问题或者文档有什么错误,欢迎讨论与指教!在计算阻抗之前,我想很有必要理解这儿阻抗的意义。
传输线阻抗的由来以及意义传输线阻抗是从电报方程推导出来(具体可以查询微波理论)如下图,其为平行双导线的分布参数等效电路:从此图可以推导出电报方程取传输线上的电压电流的正弦形式得推出通解定义出特性阻抗无耗线下r=0, g=0 得注意,此特性阻抗和波阻抗的概念上的差异(具体查看平面波的波阻抗定义)特性阻抗与波阻抗之间关系可从此关系式推出.Ok,理解特性阻抗理论上是怎么回事情,看看实际上的意义,当电压电流在传输线传播的时候,如果特性阻抗不一致所求出的电报方程的解不一致,就造成所谓的反射现象等等.在信号完整性领域里,比如反射,串扰,电源平面切割等问题都可以归类为阻抗不连续问题,因此匹配的重要性在此展现出来.叠层(stackup)的定义我们来看如下一种stackup,主板常用的8 层板(4 层power/ground 以及4 层走线层,sggssggs,分别定义为L1, L2…L8)因此要计算的阻抗为L1,L4,L5,L8下面熟悉下在叠层里面的一些基本概念,和厂家打交道经常会使用的Oz 的概念Oz 本来是重量的单位Oz(盎司 )=28.3 g(克)在叠层里面是这么定义的,在一平方英尺的面积上铺一盎司的铜的厚度为1Oz,对应的单位如下介电常数(DK)的概念电容器极板间有电介质存在时的电容量Cx 与同样形状和尺寸的真空电容量Co之比为介电常数:ε = Cx/Co = ε'-ε"Prepreg/Core 的概念pp 是种介质材料,由玻璃纤维和环氧树脂组成,core 其实也是pp 类型介质,只不过他两面都覆有铜箔,而pp 没有.传输线特性阻抗的计算首先,我们来看下传输线的基本类型,在计算阻抗的时候通常有如下类型: 微带线和带状线,对于他们的区分,最简单的理解是,微带线只有1 个参考地,而带状线有2个参考地,如下图所示对照上面常用的8 层主板,只有top 和bottom 走线层才是微带线类型,其他的走线层都是带状线类型在计算传输线特性阻抗的时候, 主板阻抗要求基本上是:单线阻抗要求55 或者60Ohm,差分线阻抗要求是70~110Ohm,厚度要求一般是1~2mm,根据板厚要求来分层得到各厚度高度. 在此假设板厚为1.6mm,也就是63mil 左右, 单端阻抗要求60Ohm,差分阻抗要求100Ohm,我们假设以如下的叠层来走线先来计算微带线的特性阻抗,由于top 层和bottom 层对称,只需要计算top 层阻抗就好的,采用polar si6000,对应的计算图形如下:在计算的时候注意的是:1,你所需要的是通过走线阻抗要求来计算出线宽W(目标)2,各厂家的制程能力不一致,因此计算方法不一样,需要和厂家进行确认3,表层采用coated microstrip 计算的原因是,厂家会有覆绿漆,因而没用surface microstrip 计算,但是也有厂家采用surface microstrip 来计算的,它是经过校准的4,w1 和w2 不一样的原因在于pcb 板制造过程中是从上到下而腐蚀,因此腐蚀出来有梯形的感觉(当然不完全是)5,在此没计算出精确的60Ohm 阻抗,原因是实际制程的时候厂家会稍微改变参数,没必要那么精确,在1,2ohm 范围之内我是觉得没问题6,h/t 参数对应你可以参照叠层来看再计算出L5 的特性阻抗如下图记得当初有各版本对于stripline 还有symmetrical stripline 的计算图,实际上的差异从字面来理解就是symmetrical stripline 其实是offset stripline 的特例H1=H2在计算差分阻抗的时候和上面计算类似,除所需要的通过走线阻抗要求来计算出线宽的目标除线宽还有线距,在此不列出选用的图是在计算差分阻抗注意的是:1,在满足DDR2 clock 85Ohm~1394 110Ohm 差分阻抗的同时又满足其单端阻抗,因此我通常选择的是先满足差分阻抗(很多是电流模式取电压的)再考虑单端阻抗(通常板厂是不考虑的,实际做很多板子,问题确实不算大,看样子差分线还是走线同层同via 同间距要求一定要符合)特性阻抗公式(含微带线,带状线的计算公式)a.微带线(microstrip)Z={87/[sqrt(Er+1.41)]}ln[5.98H/(0.8W+T)] 其中,W为线宽,T为走线的铜皮厚度,H为走线到参考平面的距离,Er是PCB板材质的介电常数(dielectric constant)。
射频同轴连接器特性阻抗的计算

工 业 技 术
射频 同轴连接器特性 阻抗 的计算
岳 磊
( 天津 市德 力电子仪 器有限公 司, 天津 3 0 0 3 9 2 )
摘 要: 文章介绍 了射频同轴连接器特性阻抗的计算方法之一, 快速 简便 的获得 阻抗值 , 方便采购与检验等环节。 关键 词 : 同轴 连接 器 ; 射 频转 接 器 ; 特性 阻抗 ; 阻抗 匹配
频同轴连接器显得至关重要, 选择匹配的连接器可以提高系统的. 眭能。 述条件可以计算出 N型连接器的特性阻抗。下面是计算结果。 而作为选择连接器的重要因素 , 阻抗匹配显得很重要 , 了解和掌握阻抗 内导体外直径为 3 . 0 2 a r m , 外导体内直径为 6 . 9 6 m m是阻抗为 5 0 . 1 ; 的计算方法可以一定程度的保证器件选择、 产品进货检验等。 当两者分别是 3 . 1 5 m m和 7 . 0 6 m m时结果为 4 8 A 2射频 同轴连接器简介 让我们一起来计算—个例子 : 用于射频同轴馈线系统的连接器通称为射频同轴连接器。 以外导体内直径为 6 . 9 6 m m, 内导体外直径为 3 . 0 2 m m为例由于 8 射频 同轴连接器按 连接方式 分类为 :螺纹式连 接器 ,卡 口式连接 1 , 我们将这些数据代人公式( 4 ) 就得到 器, 推人 式连接器 , 推 人锁 紧式连接 器。 Z 0 = 5 9 . 9 5 7 6 L n - - 5 9 . 9 5 7 6 0 . 8 3 4 9 —5 0 . 1  ̄5 0 2 1 常用的射频 同轴连接器有 S M A型 、 S M B型、 S S M B型 、 N型 、 B N C 型、 T N C型等 。 3 _ 3实例 2 射频同轴连接器电气陛能方面包括特性阻抗 、 耐压、 最高工作频率 B N C 型连接器 的特性阻抗 : B N C型连接器使用于低功率 , 按特f 生 阻抗分为 5 0 1 2 和7 5 l l 两种。 等因素 , 特性阻抗是连接器与传输系统及电缆的阻抗匹配, 是选择射频 同轴连接器的主要指标 , 阻抗不匹配会导致系统l 生 能的很大下降。 通过 不 同于其 它类型 连接器 的特 点是 5 0 f l 与7 5 2 的 内导体 与外导 体 的尺 1 构成特 l 生 阻抗不 同的 区别 在是否 填充介质 , 也 就是说 有一种 阻 计算的阻抗来选择匹配的连接器 , 方便采购、 检验及设计。利用射频同 寸一样 , 抗 的连接器 的填充 是空气 。 7 5 1 2 特l 生阻抗的连接器 没有填充介 质 , 即空 轴连接器的结构尺寸计算其阻抗值的方法, 快速简便。 3射频 同 气介质( £ 1 ) 。 5 0 1 1 特陛阻抗的在内外导体之间填充的是常见的聚四氟 £ r 大约在 2 2 _ 之间。B N C型连接器外导体的内直径的标 射频同轴连接器的特『 生 阻抗主要依据其外导体的内直径和内导体 乙烯介质, 称值是 6 . 5 a r m, 内导体的外直径是 2 . 0 6 - 2 . 2 1 m m 。同样对于外导体内直 的外直径以及和填充的介质共同决定的。如图 1 所示 径的标称值由于机加工过程所造成的± 0 . 0 5 a r m的误差范围,这样就可 以算出在有无介质条件下的B N C型射频同轴连接器的特 陛阻抗。 下面 是有 填充介质 时的特 陛阻抗 。 7 5 n( 填充 介质 为空气 , e r = 1 ) : 内导体 外 直径 为 2 . 0 6 m m , 外 导体 内 直径为 6 A 5 是 阻抗为 6 8 A ; 当两 者分 别是 2 . 2 1 mm和 6 . 5 5 m m时结 果为
特性阻抗计算公式推导过程

特性阻抗计算公式推导过程特性阻抗是指电磁波在介质界面上传播时的电磁特性。
它描述了电磁波在界面上的电场和磁场之间的关系。
特性阻抗的计算方法可以通过推导沿法线传播的电磁波的电场和磁场分别与其幅度、相位之间的关系而得到。
假设电磁波在介质边界上沿法线传播,具有电场E和磁场H,介质1的特性阻抗为Z1,介质2的特性阻抗为Z2、根据电磁场的麦克斯韦方程组,可以得到以下关系:1.电场E的分布具有以下形式:E1=E11*e^(-jβ1z)+E12*e^(jβ1z)E2=E21*e^(-jβ2z)+E22*e^(jβ2z)其中,E11和E21分别为E的入射分量,E12和E22分别为E的反射分量,β1和β2为介质1和介质2的相位常数,z为沿法线方向的传播距离。
2.磁场H的分布具有以下形式:H1=H11*e^(-jβ1z)+H12*e^(jβ1z)H2=H21*e^(-jβ2z)+H22*e^(jβ2z)其中,H11和H21分别为H的入射分量,H12和H22分别为H的反射分量。
在介质边界上,满足以下边界条件:1.平行电场分量的边界条件:E1+E2=E32.平行磁场分量的边界条件:H1+H2=H3其中,E3和H3分别为介质1和介质2中电磁波传播方向的电场和磁场。
通过将电场和磁场的分布式代入边界条件,可以得到以下关系:E11+E12=E21+E22H11+H12=H21+H22(E11-E12)/Z1=(E21-E22)/Z2(H11-H12)/Z1=(H21-H22)/Z2将第一个和第二个等式相加,可以得到:E11+E12+H11+H12=E21+E22+H21+H22根据能量守恒定律,入射电磁波和反射电磁波的总功率应该相等,即:1/2*(,E11,^2+,E12,^2+,H11,^2+,H12,^2)=1/2*(,E21,^2+,E22,^2+,H21,^2+,H22,^2)将上述等式代入最后一个等式中,可以得到:(Z1/Z2)*(,E11,^2+,E12,^2-,H11,^2-,H12,^2)=,E21,^2+,E22,^2-,H21,^2-,H22,^2由于左边的表达式实际上是电场与磁场之比的平方,因此可以将上述等式化简为:(Z1/Z2)*(,E1,^2-,H1,^2)=,E2,^2-,H2,^2根据电磁波的特性,我们知道E/H=Zc,其中Zc为电磁波在介质中的传播速度(Z1/Z2)*(,E1,^2-,H1,^2)=(,E2,^2-,H2,^2)*(Zc^2/Z1Z2)将上式中的E和H分别替换为E的入射和反射分量的平方和H的入射和反射分量的平方之和,得到:(Z1/Z2)*(,E11+E12,^2-,H11+H12,^2)=(,E21+E22,^2-,H21+H22,^2)*(Zc^2/Z1Z2)最后,我们再根据特性阻抗的定义,即入射波和反射波之比的平方为特性阻抗的平方,可以得到:(Z1/Z2)*(,E11+E12,^2-,H11+H12,^2)=(,E21+E22,^2-,H21+H22,^2)经过推导,我们得到了特性阻抗计算的公式。
特性阻抗计算

对特性阻抗的一种浅显易懂的解释抽象又复杂的数位高速逻辑原理,与传输线中方波讯号的如何传送,以及如何确保其讯号完整性(Signal Integrity),降低其杂讯(Noise)减少之误动作等专业表达,若能以简单的生活实例加以说明,而非动则搬来一堆数学公式与难懂的物理语言者,则对新手或隔行者之启迪与造福,实有事半功倍举重若轻之受用也。
然而,众多本科专业者,甚至杏坛为师的博士教授们,不知是否尚未真正进入情况不知其所以然?亦或是刻意卖弄所知以慑服受教者则不得而知,或是二者心态兼有之!坊间大量书籍期刊文章,多半也都言不及义缺图少例,确实让人雾里看花,看懂了反倒奇怪呢!笔者近来获得一份有关阻抗控制的简报资料,系电性测试之专业日商HIOKI所提供。
其内容堪称文要图简一看就懂,令人爱不释手。
正是笔者长久以来所追求的境界,大喜之下乃征得原著“问港建”公司的同意,并经由港建公司廖丰莹副总的大力协助,以及原作者山崎浩(Hiroshi Yamazaki)及其上司金井敏彦(Toshihiko Kanai)等解惑下,得以完成此文,在此一并感谢。
并欢迎所有前辈先进们,多多慨赐类似资料嘉惠学子读者,则功在业界善莫大焉。
一 .将讯号的传输看成软管送水浇花1.1 数位系统之多层板讯号线(Signal Line)中,当出现方波讯号的传输时,可将之假想成为软管(hose)送水浇花。
一端于手握处加压使其射出水柱,另一端接在水龙头。
当握管处所施压的力道恰好,而让水柱的射程正确洒落在目标区时,则施与受两者皆欢而顺利完成使命,岂非一种得心应手的小小成就?1.2 然而一旦用力过度水注射程太远,不但腾空越过目标浪费水资源,甚至还可能因强力水压无处宣泄,以致往来源反弹造成软管自龙头上的挣脱!不仅任务失败横生挫折,而且还大捅纰漏满脸豆花呢!1.3反之,当握处之挤压不足以致射程太近者,则照样得不到想要的结果。
过犹不及皆非所欲,唯有恰到好处才能正中下怀皆大欢喜。
阻抗和容抗的计算公式

阻抗感抗容抗计算公式
容抗感抗阻抗计算,公式如下:
1、容抗计算公式
容抗=1/(2×π×频率×容值)。
2、感抗计算公式
感抗=2×π×频率×电感值。
3、阻抗
阻抗=频率×感抗+容抗÷频率+电阻。
电阻电抗阻抗容抗的区别:
1、定义不同
电阻由导体两端的电压U与通过导体的电流I的比值来定义。
电抗用于表示电感及电容对电流的阻碍作用。
阻抗是表示元件性能或一段电路电性能的物理量,也是电阻与电抗的总合。
容抗反映了交流电可以通过电容器这一特性。
2、代表作用不同
电阻代表了导体对电流阻碍作用的大小。
电抗随着交流电路频率而变化,并引起电路电流与电压的相位变化。
阻抗代表交流电路中一段无源电路两端电压峰值((或有效值)Um与通过该电路电流峰值(或有效值)Im之比。
容交流电频率越高,容抗越小,即电容的阻碍作用越小。
容抗同样会引起电流与电容两端电压的相位差。
当频率等于零,容抗无限大,即直流电不能流过电容器。
3、公式中的字母表达不同
电阻是描述导体导电性能的物理量,用R表示。
在交流电路分析中,电抗用X表示,是复数阻抗的虚数部分。
阻抗用z表示,单位为欧姆((Ω)。
容抗用Xc表示,国际单位制单位为欧姆(Ω)。
1特性阻抗

.1特性阻抗特性阻抗也称波阻抗,是电缆的二次参数,它描述了电磁波沿均匀线路传播而没有反射时所遇到的阻抗,即线路终端匹配时,线路内任一点的电压波(U)和电流波(I)的比值。
特性阻抗可以用一个复数表示,当电缆线芯的材料、直径、绝缘形式确定后,特性阻抗只随频率的变化而变化。
特性阻抗Zc为回路上任意点电压波和电流波之比并有R、L、G、C分别为对绞回路的电阻、电感、电导、电容,虚部相位角Φ从零开始到频率f =800Hz时接近-45°,然后逐渐接近零。
可以看出传播常数和特性阻抗Zc均与电缆的一次参数R、L、G、C有关,TIA/EIA---568---A规定5类缆的特性阻抗为对于局部网布线系统来说,传输媒介具有稳定的阻抗值是很重要的,否则连接器硬件就会和电缆失配。
从而引起信号反射导致传输效率下降,甚至网络无法工作。
对于高频对称电缆,由于频率增加时,集肤效应增加,使内电感减小,而外电感与频率无关,所以随频率的增加,总电感近似于外电感,式中,为等效介电常数;a为绝缘线心外径;d为导体直径由式子可以看出特性阻抗和导体类型和直径,绝缘的类型和厚度有关,在某种程度上也与线对的绞合性能有关(因等效介电常数εr和绞合有关)。
由于一般的标准中都规定了导体的直径d=24(AWG),而且从实际情况中看来,此d值也是最理想值。
这样从上式看来影响特性阻抗的只有外径(外径可以看成和导线间距α相等)、组合绝缘介质的等效相对介电常数(εr)。
而且,Zc正比于α和λ,反比于εr。
所以只要控制好了α、λ、εr的值,也就能控制好。
在实际中常用输入阻抗Zin来表述电缆的特性阻抗。
其定义式中:Z0为终端开路时的阻抗测量值;Zs为终端短路时的阻抗测量值。
3.2 回波损耗回波损耗是数字电缆产品的一项重要指标,回波损耗合并了两种反射的影响,包括对标称阻抗(如:100Ω)的偏差以及结构影响,用于表征链路或信道的性能。
它是由于电缆长度上特性阻抗的不均匀性引起的,归根到底是由于电缆结构的不均匀性所引起的。
利用HFSS计算微带线的特性阻抗

学生实验报告一、实验目的和任务1、 了解微带线的特性阻抗计算公式;2、 通过计算微带线的特性阻抗,熟悉二、实验原理介绍a.导带厚度为零时以w e / h 代替w/h 代入前述零厚度特性阻抗计算公式,即可得非零厚度特性阻抗。
(2) HFSS 软件是一个基丁有限元法计算电磁结构的交互软件包。
它将几何结构自动剖分成大 量的四面体,计算模拟器包括在分析电磁结构细节问题时的后续处理命令。
使用 Ansoft HFSS, 你可以计算:♦基本电磁场量和开边界问题的辐射近远场 ♦端口特性阻抗和传输常数♦ S 参数和相应端口阻抗的归一化 S 参数♦一种结构的本征模或谐振解经过二十多年的发展,HFS 羽其无以伦比的仿真精度和可靠性,快捷的仿真速度,方便易用的操HFSSBM 设计。
(1)微带线的特性阻抗公式:Z oZ °a8h w59.952ln(), w/h 1w 4h119.904w/ h 2.42 0.44h/w(1 6,w/h 1h/w)61 (112h)其中w 是微带的导带宽度,b.导带厚度不为零时r1 2 (1h 是介质基片的厚度。
w 20.041(1 ) ,w/h 1h12,w/h 1 12h )w et h (1 t1 h2h w ln t ), h ,4 w w ln , t h1 212作界面,稳定成熟的自适应网格部分技术使其成为高频结构设计的首选工具和行业标准,已经广泛地应用丁航空、航天、电子、半导体、计算机、通信等多个领域,帮助工程师们高效地设计各种高频结构,包括:射频和微波部件、天线和天线阵及天线罩,高速互连结构、电真空器件,研究目标特性和系统/部件的电磁兼容/电磁干扰特性,从而降低设计成本,减少设计周期,增强党争力。
三、实验内容和数据记录1、令w 1mm,h 0.6mm, r 4.4或「2.2 ,其中t 0或t 0.05mm代入上面公式分别求出特性阻抗。
2、利用HFSS求微带线的特性阻抗(1) 进入执行命令窗口,选择单位mm(2) 画介质基片:点击solids box 选择x 0, y 0, z 0 Enter z 在Enter box size 命令下x 10, y 20,z 0.6 ,在Nam命令下写box1 Enter;点击图标Sel box1 ok Arrange / Move 在Enter vector 命令下x 5, y 0, z 0 Enter (3)画微带线:点击solids box 选择x 0, y 0, z 0 Enter z 在Enter box size 命令下x 1,y 20, z 0.05,在Nam命令下写box2 Enter ;占八、、击图标Sel box2 ok Arrange / Move 在Enter vector 命令下x 0.5, y 0,z 0.6 Enter(4) 画仿真区域:点击solids box 选择x 0, y 0, z 0 Enter z 在Enter box size 命令下 x 10, y 20, z 10 ,在Nam命令下写box3 Enter ;点击图标Sel box3 ok Arrange / Move 在Enter vector 命令下x 5, y 0,z 0 Enter(5) 点击File / Save Exit , 乂回到命令窗口,在Draw后打勾,表示完成Draw(6) Setup Materials:点击Setup Materials ,选择box1 , D 在materials 中选择FR4_epoxy Assign ;选择box2,在Materials 中选择Per conductor Assign ;选择box3,在Material 中选择vacumm Assign ;Exit 在Save changes before closing? 命令下ok(7) Setup Boundaries/Sources: 点击Setup Boundaries/Sources 选择 source port1 点击红色网格的面Assign 单击右键 Rotate 旋转物体 选择source port 2 选择与port1相对应的面为红色网格 Assign , 点击File / Save Exit , 乂回到命令窗口 (8)Setup solution: 按如下设置, (9) solve:即PC 机进入计算 (10) Post Process:post processpost process (Port:m1,port:m1 (11)在 Setup Materials 然后点击ok Matrix Data S Matrix 和 Port ZO plot New plot Data Type ( S matrix ) ,Quantity VSWR Plot Matrix ),component(Magnitude) 在将box1选择为Teflon,其它不变再进行计算解答过程: 1、a.导带厚度为零时 w/h 1.67 1 所以: a ZO w/ h 119.904 119.904所以: 2.42 0.44h/w (1 h/w)61.672.42 0.44R 98.350.6 (1 0.6)6 4.4时,e22 Z Z !Z 0e98.35 3.29 2.2 时, r 1 r 1r 所以:e 2 Z o a 2 (1 r 1 1 (1 12h ) w 54.22 12h、 —) w ZO98.35 1.809573.11 b.导带厚度不为零时 w/h 1.67 1/2(即导带厚度为0.16 所以: w e w h hln2ht1 0.6w e / h 1.78084.4 122.2 12 0.05)0.05 0.64.4 1 2(112 0.6)1123.292.2 1212 0.6) 1121.8095ln 2 °.6 0.051.7808以w e/h代替w/h代入前述零厚度特性阻抗计算公式,得:Z°a119.904 119.904所以: 所以: w e/h 2.42 0.44h/w e (1 h/w e)6 1.7808 2.42 0.44 0.5615 (1---------- 695.0510.5615)4.4时,r 1M(112h)w4.4 1 4.4 1 12 0.5615、『1 ^)12 3.311Z。
CadencePCBSI分析特性阻抗教程

1、概要在进行PCB SI的设计时,理解特性阻抗是非常重要的。
这次,我们对特性阻抗进行基础说明之外,还说明Allegro的阻抗计算原理以及各参数和阻抗的关系。
2、什么是特性阻抗?2.1、传送线路的电路特性在高频率(MHz)信号中,把传送回路作为电路。
2.1.1、电阻R电阻R是指普通的导线带有的欧姆电阻。
R = ρ・L / S[Ω] (S:横截面面积[m2],L:导体长[m],ρ:金属(铜)的电阻率[Ω*m])。
在高频频域范围内的话,根据表面效果和集合效果的影响,集中在导体表面电流流动,会使上面公式中的阻值变得更大。
2.1.2、电容C电容C是指积蓄在导体间电荷的量。
C = ε(S / d)[F](ε:介电常数,S:导体的横截面积,d:导体间的距离)2.1.3、电感L电流流动的导线必定有磁通量发生,根据这个产生的自感。
L=0.002S[2.3lg(2s/w+t)+0.5][µH]S:导线长度(cm) W:导线宽度(cm) t:导线厚度(cm)2.1.4、电导G物体传导电流的本领叫做电导。
对导体间的介电特性的反抗成分,表示容易电流的程度。
G = 1 / R2.2、阻抗和特性阻抗的不同?阻抗表示电路部分对交变电信号流通产生的阻力,是传输线上输入电压对输入电流的比率值Z = V(x)/ I(x)特性阻抗特征阻抗是指信号沿传输线传播时,信号看到的瞬间阻抗的值。
简单地讲,无限长传输线上各处的电压与电流的比值定义为传输线的特性阻抗。
Z0 = √( (R + jωL) / (G + jωC) ) ≒√(L / C)(R<<ωL,G<<ωC)3、Allegro的特性阻抗计算原理3.1、在Layout Cross Section中阻抗计算PCB SI菜单的Setup >Cross-section<单线的特性阻抗计算方法>1、设定层结构和材料物质。
2、Width栏输入线宽的话,在Impedance栏会计算出特性阻抗。
1.3传输线的特性参量

传输线的特性参量主要包括:传播常 数、特性阻抗、相速和相波长、输入阻 抗、反射系数、驻波比 ( 行波系数 ) 和传 输功率等。
1.3 传输线特性参量
一、特性阻抗
V ( z ) A1e z + A2e z 1 I ( z ) ( A1e z A2e z ) Z0
min max
1.3 传输线特性参量
I I
min max
1 1+
1
传输线上反射波的大小,可用反射系数的 模、驻波比和行波系数三个参量来描述。
反射系数模的变化范围为 驻波比的变化范围为 行波系数的变化范围为
对于微波传输线,由于, L1C1
vp 1 L1C1
所以有:
(2.3-7)
双导线和同轴线上行波的相速度均为:
vp 1
1
0 0 r
v0
r
1.3 传输线特性参量
定 义 相波长,为波在一个周期 T 内等相位
面沿传输线移动的距离,即:
0 p v pT f r
(1)传输线上任一点的阻抗与该点的位置和负载阻 抗有关,分布于沿线各点,是一种分布参数阻抗 。 (2)传输线段具有阻抗变换作用,Z L 通过线段 d变换成 Z in (d ) ,或相反。
( 3 ) 无 耗 线 的 阻 抗 呈 周 期 性 变 化 , 具 有 / 4 变换性和 / 2 阻抗重复性。
(3) 由于在微波频率下,电压和电流缺乏明 确的物理意义,不能直接测量,故传输线阻抗 也不能直接测量,但可以间接测量。
没有反射波,则:Zin(d)=Zo。
1.3 传输线特性参量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对特性阻抗的一种浅显易懂的解释抽象又复杂的数位高速逻辑原理,与传输线中方波讯号的如何传送,以及如何确保其讯号完整性(Signal Integrity),降低其杂讯(Noise)减少之误动作等专业表达,若能以简单的生活实例加以说明,而非动则搬来一堆数学公式与难懂的物理语言者,则对新手或隔行者之启迪与造福,实有事半功倍举重若轻之受用也。
然而,众多本科专业者,甚至杏坛为师的博士教授们,不知是否尚未真正进入情况不知其所以然?亦或是刻意卖弄所知以慑服受教者则不得而知,或是二者心态兼有之!坊间大量书籍期刊文章,多半也都言不及义缺图少例,确实让人雾里看花,看懂了反倒奇怪呢!笔者近来获得一份有关阻抗控制的简报资料,系电性测试之专业日商HIOKI所提供。
其内容堪称文要图简一看就懂,令人爱不释手。
正是笔者长久以来所追求的境界,大喜之下乃征得原著“问港建”公司的同意,并经由港建公司廖丰莹副总的大力协助,以及原作者山崎浩(Hiroshi Yamazaki)及其上司金井敏彦(Toshihiko Kanai)等解惑下,得以完成此文,在此一并感谢。
并欢迎所有前辈先进们,多多慨赐类似资料嘉惠学子读者,则功在业界善莫大焉。
一 .将讯号的传输看成软管送水浇花1.1 数位系统之多层板讯号线(Signal Line)中,当出现方波讯号的传输时,可将之假想成为软管(hose)送水浇花。
一端于手握处加压使其射出水柱,另一端接在水龙头。
当握管处所施压的力道恰好,而让水柱的射程正确洒落在目标区时,则施与受两者皆欢而顺利完成使命,岂非一种得心应手的小小成就?1.2 然而一旦用力过度水注射程太远,不但腾空越过目标浪费水资源,甚至还可能因强力水压无处宣泄,以致往来源反弹造成软管自龙头上的挣脱!不仅任务失败横生挫折,而且还大捅纰漏满脸豆花呢!1.3反之,当握处之挤压不足以致射程太近者,则照样得不到想要的结果。
过犹不及皆非所欲,唯有恰到好处才能正中下怀皆大欢喜。
1.4 上述简单的生活细节,正可用以说明方波(Square Wave)讯号(Signal)在多层板传输线(Transmission Line,系由讯号线、介质层、及接地层三者所共同组成)中所进行的快速传送。
此时可将传输线(常见者有同轴电缆Coaxial Cable,与微带线Microstrip Line或带线Strip Line等)看成软管,而握管处所施加的压力,就好比板面上“接受端”(Receiver)元件所并联到Gnd的电阻器一般(是五种终端技术之一,请另见TPCA会刊第13期“内嵌式电阻器之发展”一文之详细说明),可用以调节其终点的特性阻抗(Characteristic Impedance),使匹配接受端元件内部的需求。
二. 传输线之终端控管技术(Termination)2.1由上可知当“讯号”在传输线中飞驰旅行而到达终点,欲进入接受元件(如CPU或Meomery等大小不同的IC)中工作时,则该讯号线本身所具备的“特性阻抗”,必须要与终端元件内部的电子阻抗相互匹配才行,如此才不致任务失败白忙一场。
用术语说就是正确执行指令,减少杂讯干扰,避免错误动作”。
一旦彼此未能匹配时,则必将会有少许能量回头朝向“发送端”反弹,进而形成反射杂讯(Noise)的烦恼。
2.2当传输线本身的特性阻抗(Z0)被设计者订定为28ohm时,则终端控管的接地的电阻器(Zt)也必须是28ohm,如此才能协助传输线对Z0的保持,使整体得以稳定在28ohm的设计数值。
也唯有在此种Z0=Zt的匹配情形下,讯号的传输才会最具效率,其“讯号完整性”(Signal Integrity,为讯号品质之专用术语)也才最好。
三.特性阻抗(Characteristic Impedance)3.1 当某讯号方波,在传输线组合体的讯号线中,以高准位(High Level)的正压讯号向前推进时,则距其最近的参考层(如接地层)中,理论上必有被该电场所感应出来的负压讯号伴随前行(等于正压讯号反向的回归路径Return Path),如此将可完成整体性的回路(Loop)系统。
该“讯号”前行中若将其飞行时间暂短加以冻结,即可想象其所遭受到来自讯号线、介质层与参考层等所共同呈现的瞬间阻抗值(Instantanious Impedance),此即所谓的“特性阻抗”。
是故该“特性阻抗”应与讯号线之线宽(w)、线厚(t)、介质厚度(h)与介质常数(Dk)都扯上了关系。
此种传输线之一的微带线其图示与计算公式如下:【笔者注】Dk(Dielectric Constant)之正确译词应为介质常数,原文中之...r其实应称做“相对容电率”(Relative Permitivity )才对。
后者是从平行金属板电容器的立场看事情。
由于其更接近事实,因而近年来许多重要规范(如IPC-6012、IPC-4101、IPC-2141与IEC-326)等都已改称为...r了。
且原图中的E并不正确,应为希腊字母(Episolon)才对。
3.2 阻抗匹配不良的后果由于高频讯号的“特性阻抗”(Z0)原词甚长,故一般均简称之为“阻抗”。
读者千万要小心,此与低频AC交流电(60Hz)其电线(并非传输线)中,所出现的阻抗值(Z)并不完全相同。
数位系统当整条传输线的Z0都能管理妥善,而控制在某一范围内(±10﹪或±5﹪)者,此品质良好的传输线,将可使得杂讯减少而误动作也可避免。
但当上述微带线中Z0的四种变数(w、t、h、r)有任一项发生异常,例如图中的讯号线出现缺口时,将使得原来的Z0突然上升(见上述公式中之Z0与W成反比的事实),而无法继续维持应有的稳定均匀(Continuous)时,则其讯号的能量必然会发生部分前进,而部分却反弹反射的缺失。
如此将无法避免杂讯及误动作了。
下图中的软管突然被山崎的儿子踩住,造成软管两端都出现异常,正好可说明上述特性阻抗匹配不良的问题。
3.3 阻抗匹配不良造成杂讯上述部分讯号能量的反弹,将造成原来良好品质的方波讯号,立即出现异常的变形(即发生高准位向上的Overshoot,与低准位向下的Undershoot,以及二者后续的Ringing;详细内容另见TPCA会刊第13期“嵌入式电容器”之内文)。
此等高频杂讯严重时还会引发误动作,而且当时脉速度愈快时杂讯愈多也愈容易出错。
四. 特性阻抗的测试4.1 采TDR的量测由上述可知整体传输线中的特性阻抗值,不但须保持均匀性,而且还要使其数值落在设计者的要求的公差范围内。
其一般性的量测方法,就是使用“时域反射仪”(Time Domain Reflectometer;TDR )。
此TDR可产生一种梯阶波(StepPulse或Step Wave),并使之送入待测的传输线中而成为入射波(Incident Wave)。
于是当其讯号线在线宽上发生宽窄的变化时,则萤光幕上也会出现Z0欧姆值的上下起伏振荡。
4.2 低频无须量测Z0,高速才会用到TDR当讯号方波的波长(λ读音Lambda)远超过板面线路之长度时,则无需考虑到反射与阻抗控制等高速领域中的麻烦问题。
例如早期1989年速度不快的CPU,其时脉速率仅10MHz而已,当然不会发生各种讯号传输的复杂问题。
然而,目前的Pentium Ⅳ其内频却已高达1.7GHz自然就会问题丛生,相较当年之巨大差异,岂仅是霄壤云泥而已!由波动公式可知上述当年10MHz方波之波长为:但当DRAM晶片组的时脉速率已跃升到800MHz,其方波之波长亦将缩短到37.5cm;而P-4 CPU之速度更高达1.7GHz其波长更短到17.6cm,则其PCB母板上两者之间传输的外频,也将加速到400MHz与波长75cm之境界。
可知此等封装载板(Substrate)中的线长,甚至母板上的的线长等,均已*近到了讯号的波长,当然就必须要重视传输线效应,也必须要用到TDR的测量了。
4.3 TDR由来已久利用时域反射仪量测传输线的特性阻抗(Z0)值,此举并非新兴事物。
早年即曾用以监视海底电缆(Submarine Cable)的安全,随时注意其是否发生传输品质上的“不连续(Disconnection)的问题。
目前才逐渐使用于高速电脑领域与高频通讯范畴中。
4.4 CPU载板的TDR测试主动元件之封装(Packaging)技术近年来不断全面翻新加速进步,70年代的C-DIP与P-DIP双排脚的插孔焊装(PTH),目前几已绝迹。
80年金属脚架(LeadFrame)的QFP(四边伸脚)或PLCC(四边勾脚)者,亦渐从HDI板类或手执机种中迅速减少。
代之而起的是有机板材的底面格列(Area Array)球脚式的BGA或CSP,或无脚的LGA。
甚至连晶片(Chip)对载板(Substract)的彼此互连(Interconnection),也从打金线(Wire Bond)进步到路径更短更直接的“覆晶”(Flip Chip; FC)技术,整体电子工业冲锋之快几乎已到了瞬息万变!Hioki公司2001年六月才在JPCA推出的“1109 Hi Tester”,为了对1.7GHz高速传输FC/PGA载板在Z0方面的正确量测起见,已不再使用飞针式(Flying probe)快速移动的触测,也放弃了SMA探棒式的TDR手动触测(Press-type)的做法。
而改采固定式高频短距连缆,与固定式高频测针的精准定位,而在自动移距及接触列待测之落点处,进行全无人为因素干扰的高精密度自动测试。
在CCD摄影镜头监视平台的XY位移,及Laser高低感知器督察Z方向的落差落点,此等双重精确定位与找点,再加上可旋转式接触式测针之协同合作下,得以避免再使用传统缆线、连接器、与开关等仲介的麻烦,大幅减少TDR量测的误差。
如此已使得“1109HiTESTER”在封装载板上对Z0的量测,远比其他方法更为精确。
实际上其测头组合,是采用一种四方向的探针组(每个方向分别又有1个Signal及2个Gnd)。
在CCD一面监视一面进行量测下,其数据当然就会更为准确。
且温度变化所带来的任何误差,也可在标准值陶瓷卡板的自动校正下减到最低。
4.5 精确俐落大小咸宜此款最新上市的1109,不但能对最高阶封装载板的CPU进行Z0量测,且对其余的高价位CSP、BGA、FC等,也都能在游刃有余下完成逐一精测。
其之待测尺寸更可从10mm×10mm的微小,一跃而至到500mm×600mm的巨大,剧变情势下均能应对裕如令人激赏。
未来业界也许还要对Coupon以外的实际讯号线要求量测Z0,此高难度的TDR技术,目前亦正在研发中.兴森快捷公司的常规物料列表0.13mm 1/1OZ0.13mm H/H OZ0.21 mm 1/1 OZ0.25 mm 1/1 OZ 厚度数值不包括铜厚0.36 mm 1/1 OZ0.45 mm 1/1 OZ0.51 mm 1/1 OZ0.71 mm 1/1 OZ H/H代表双面18um1.0 mm 1/1 OZ 1/1代表双面35um1.2 mm 1/1 OZ 2/2代表双面70um1.6 mm H/H OZ1.6 mm 1/1 OZ1.6 mm 2/2 OZ 厚度数值包括铜厚2.0 mm 1/1 OZ2.0 mm 2/2 OZ2.5 mm 1/1 OZ3.0 mm 1/1 OZ3.2 mm 1/1 OZ1080---------4.33313---------4.42116---------4.57628---------4.7半固化片组合的介电常数为各半固化片介电常数的算数平均值例如1080+2116的介电常数为(4.3+4.5)/2=4.47628+2116---(4.5+4.7)/2=4.6默认板材的介电常数为4.0。
