数字逻辑第四版第二章答案
数字逻辑第四版课后练习题含答案

数字逻辑第四版课后练习题含答案1. 第一章1.1 课后习题1. 将十进制数22转换为二进制数。
答:22 = 101102. 将二进制数1101.11转换为十进制数。
答:1101.11 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 1 x 2^(-1) + 1 x 2^(-2) = 13.753. 将二进制数1101.01101转换为十进制数。
答:1101.01101 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 0 x 2^(-1)+ 1 x 2^(-2) + 1 x 2^(-4) + 0 x 2^(-5) + 1 x 2^(-6) = 13.406251.2 实验习题1. 合成与门电路设计一个合成与门电路,使得它的输入A,B和C,只有当A=B=C=1时输出为1,其他情况输出为0。
答:下面是一个合成与门电路的示意图。
合成与门电路示意图其中,S1和S2是两个开关,当它们都被打开时,电路才会输出1。
2. 第二章2.1 课后习题1. 将十进制数168转换为八进制数和二进制数。
答:168 = 2 x 8^3 + 1 x 8^2 + 0 x 8^1 + 0 x 8^0 = 250(八进制)。
168 = 10101000(二进制)。
2. 将八进制数237转换为十进制数和二进制数。
答:237 = 2 x 8^2 + 3 x 8^1 + 7 x 8^0 = 159(十进制)。
237 = 010111111(二进制)。
2.2 实验习题1. 全加器电路设计一个全加器电路,它有三个输入A,B和C_in,两个输出S和C_out。
答:下面是一个全加器电路的示意图。
C_in|/ \\/ \\/ \\/ \\/ \\A|________ \\| | AND Gate______| |B|__| XOR |_| S\\\\ /\\ /\\ /\\ /| | OR Gate| ||_| C_out其中,AND Gate表示与门,XOR Gate表示异或门,OR Gate表示或门。
数字逻辑欧阳星明第四版华科出版17全答案

解答: (1)
F (A ,B ,C ,D ) B C D A B AC D B BC
AB
CD
00
00
01
11 10 2021/1/4
01
11
10
1
1
1
1
1
1
1
所以,F() = m(4-7,12-15) = M(0-3,8-11)
21
习题课
解答: (2)
AB
CD
00
00
01
F (A ,B ,C ,D )(A B AB )(D B C)D ABABD(BCD ) (A B )A (B D )(B C)D ABCD
(4)(785.4)16=7×162+8×161+5×160+4×16-1+10×8-2
+
15×16-3
2021/1/4
5
习题课
1.6 将下列二进制数转换成十进制数、八进制数和十六进制数。 (1)1110101 (2)0.1110101 (3) 10111.01
解答: (1) (1110101)2=1×26+1×25+1×24+0×23+ 1×22+0×21+1×20 =64+32+16+0+4+0+1 =(117)10 =(165)8 =(75)16
=
AB=ABCBC
AB(ABB)C
AB(AB)C ABACBC
AB AC
(2) F= =
AB= =BBCD ABB(1CD)
ABB
AB
2021/1/4
19
习题课
解答:
(3) F= = =
(A B C )A (B )A (B C ) (AB)(AB)
B
(4) F= = = = =
《数字逻辑》第四版部分习题答案_khdaw

⑴真值表:
⑵真值表:
∴Y3=AB,Y2= AB ,Y1=0,Y0= AB + AB =B,逻辑电路为:
⑵ Y = X 3 ,(Y 也用二进制数表示)
因为一个两位二进制正整数的立方的二进制数最多有五位,故输入端用A、B两个变量, 输出端用Y4、Y3、Y2、Y1、Y0五个变量。可列出真值表⑵
∴Y4=AB,Y3= AB + AB= A ,Y2=0,Y1= AB ,Y0= AB + AB =B,逻辑电路如上图。
F3
(
A,B,C , D
)
=
A⋅
BC
+
ABC
⋅
D+
ABCD
第8页
《数字逻辑》习题解答
习题三
3.1 将下列函数简化,并用“与非”门和“或非”门画出逻辑电路。 ⑴ F ( A, B,C ) = ∑m(0,2,3,7)= A ⋅ C + BC = A ⋅ C ⋅ BC Q F = AC + BC ∴ F = A + C + B + C
2.9 用卡诺图判断函数 F ( A, B,C , D ) 和 G( A, B,C , D ) 有何关系。 F( A,B,C , D ) =
= B ⋅ D + A ⋅ D + C ⋅ D + AC D G( A,B,C , D ) =
= BD + CD + A ⋅ + ABD 可见, F = G
= ∏M(5,6,7,8,9,10,11,12,13,14,15) (如下卡诺图 3)
第6页
《数字逻辑》习题解答
2.8 用卡诺图化简下列函数,并写出最简“与-或”表达式和最简“或-与”表达式: ⑴ F ( A, B,C ) = ( A + B )( AB + C ) = AC + BC = C( A + B )
数字电路与逻辑设计 (第四版)1--4章答案

第一章1.4(1)10101=1∗104+1∗102+1∗100(2)0.10101=1∗10−1+1∗10−3+1∗10−5(3)1010.101=1∗103+1∗101+1∗10−1+1∗10−31.5(1)(163)10=(10100011)2(2)(0.525)10=(0.100001)2(3)(41.41)10=(101001.01101000111)21.6(123)8=(1∗82+2∗8+3)10=(83)10 1.76n<(0.3)3⇒n log6<3(log3−1)⇒n<3(log3−1)log6=−2.016⇒n≤−3(8.705)10≈(12.412)61.8A(B+C+D)+BC(A̅+D̅)+D̅⇒A+A BC+D̅1.9A̅+BA+C+DA⇒A̅+B+C+D 1.10(1)F(A,B,C)|B=1&C=1=(AB+A̅C)|B=1&C=1=1(2)F(A,B,C)|A̅=1&B=1&C=1=A̅BC|A̅=1&B=1&C=1=11.11(1)1.12A̅+C ̅̅̅̅̅̅̅+D ∙(A +C ̅)(A +B )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅= 1.13(1)F =A (B̅+C +D )(B +D ̅)=ABC +A (B⨀D ) (2)F =A̅⋅B ̅+(AB +AB ̅+A ̅B )C =A ̅⋅B ̅+C (3)F =A +A ⋅B̅⋅C ̅+AC ̅D +(C ̅+D ̅)E =A +C ̅E +D ̅E (4)F =AB̅(C +D )+BC ̅+A ̅∙B ̅+A ̅C +BC +B ̅⋅C ̅⋅D ̅=A ̅+B ̅ (5)F =(A +B )(A +C )(A +C̅)=A (6)F =(A +BC̅)(A ̅+D ̅B)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B ̅+A ̅C +AD (7)F =A (A +B̅+C ̅)(A ̅+C +D )(E +C ̅⋅D ̅)=ACE +ADE 1.14(1)F (A,B,C )=∑m(2,3,6,7)=A BC +A BC +ABC +ABC =B(2)F (A,B,C,D,E )=∏M (0,4,8,12,16,20,24,28)=A ⋅B̅⋅C ⋅D ̅⋅E ̅+A ⋅B ̅⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ̅⋅C ⋅D ̅⋅E ̅+A ⋅B̅⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅+A ⋅B ⋅C ⋅D ̅⋅E ̅=D ̅E ̅ 1.15(1)F (A,B,C )=∑m (1,3,7)=∏M (0,2,4,5,6)(2)F (A,B,C,D )=∑m(0,2,6,12,13,14)=∏M(1,3,4,5,7,8,9,10,11,15)1.16(1)F (A,B,C )=∏M(0,3,6,7)=∑m(1,2,4,5)(2)F (A,B,C,D )=∏M(0,1,2,3,4,6,12)∑m(5,7,8,9,10,11,13,14,15)1.17(1)F (A,B,C,D )=AB +A̅B ̅+CD ̅=ABC D ̅+ABC D +ABCD ̅+ABCD +A B ̅C D ̅+A B ̅C D +A B̅CD ̅+A B ̅CD +AB ̅CD ̅+A BCD ̅=∑m(0,1,2,3,6,10,12,13,14,15) (2)F (A,B,C )=(A +B )(B̅+C )=∏M(6,7,5,1)=∑m(0,2,3,4) 1.18(1)F (A,B,C )=A ⊕B +AC̅=A B +AB ̅+A C =A BC +A BC +AB ̅C +AB ̅C +A B ̅C +A BC =∑m (2,3,4,5,1)=∏M(0,6,7)(2)F (A,B,C,D )=(A +B̅+C )(A +B ̅)(A +C ̅+D ̅)(B +C ̅+D ̅)=∏M(10,11,8,9,12,4) 1.19(1)F =(AB +A B̅)(C +D )(E +C D ̅)⇒F ̅=A ⊕B +C D ̅+E ̅ (2)F =A +B +C ̅+D +E ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅⇒F ̅=A(B +C ̅+D +E ̅̅̅̅̅̅̅̅)=AB +AC +AD̅E 1.20(1)F =AB +CD +A̅C ⇒F ∗=(A +B )(C +D )(A +C )=A BC +AC +A BD (2)F =A (B̅C +BC ̅)+AC ̅⇒F ∗=(A +(B ̅+C )(B +C ))(A +C )=A +B ̅C (3)F =(A ̅+B)(B +A ̅C)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅⇒F ∗=A B +B(A +C)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅+AC 1.21(1)A ̅⊕B =A ⊕B ̅=A ⊕B ̅̅̅̅̅̅̅̅A̅⊕B =A ̅B ̅+AB =A⨀B A ⊕B̅=AB +A ̅B ̅=A⨀B A ⊕B ̅̅̅̅̅̅̅̅=A⨀B(2)A̅B ̅C +A ̅BC ̅+AB ̅C ̅+ABC =A ⊕B ⊕C A ⊕B ⊕C =(A ̅B +AB ̅)⊕C =(A ̅B +AB ̅)C +(A ̅B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅C =A BC +AB ̅C +A B ̅C +ABC (3)AB +BC +CA =(A +B)(B +C)(C +A)(A+B)(B+C)(C+A)=(B+AC)(C+A)=AB+BC+CA (4)AB̅+BC̅+CA̅=A̅B+B̅C+C̅A令:AB̅+BC̅+CA̅=K,K=1或0{A⟶A̅B⟶B̅C⟶C⇒A̅B+B̅C+C̅A=KAB̅+BC̅+CA̅=K=A̅B+B̅C+C̅A1.22(2)1.23(1)F(A,B,C,D)=∏M(1,3,5,7,13,15)=∑m(0,2,4,6,8,9,10,11,12,14)(2)F(A,B,C,D,E)=∏M(0,1,2,3,4,6,8,10,12,13,14)1.24(1)F(A,B,C,D)=∑m(3,5,6,9,12,13,14,15)+∑ϕ(0,1,7)()∑∑(4)F(A,B,C,D,E)=A̅̅̅̅̅̅(5)F(A,B,C,D)=A̅̅̅1.25̅̅12(2)F̅̅12(3)F1(A,B,C,D)=∑m(1,3,4,5,6,7,15)F2(A,B,C,D)=∑m(1,3,10,14,15)12第二章2.1关门电平V off=1.3V:保持电路输出高电平状态所允许的输入低电平的最大值开门电平V on=1.5V:保持电路输出低电平状态所允许的输入高电平的最小值≈1.4V:V off至V on这一段狭窄转折的中值阈值电压VT输入高电平时的抗干扰容限VNH=VOHmin−V on=2.4−1.5=0.9V输入低电平时的抗干扰容限VNL=V off−VOLmax=1.3−0.7=0.6V高电平:V OH(2.4~5.0V),标称值3.6V 低电平:V OL(0~0.7V),标称值0.3V2.2TTL与非门:高电平:V OH(2.4~5.0V),标称值3.6V 低电平:V OL(0~0.7V),标称值0.3V 关门电平V off=1.3V开门电平V on=1.5V阈值电压VT≈1.4V输入高电平时的抗干扰容限VNH=VOHmin−V on=2.4−1.5=0.9V输入低电平时的抗干扰容限VNL=V off−VOLmax=1.3−0.7=0.6V输出低电平的工作状态:N0L=I OLmax(驱动门)I IL(负载门)输出高电平的工作状态:N0H=I OH(驱动门)I IH(负载门)N I≤5V1:输入信号,V0:反相输出信号;V0下降到V m/2相对应于V1上升到V m/2之间的延迟时间称为导通延迟t PLHV0上升到V m/2相对应于V1下降到V m/2之间的延迟时间称为截止延时t PHLt PLH>t PHLt pd=(t PLH+t PHL)/2平均功耗小,速度快不能并联OC门方便线与逻辑,可并联,主要应用(1)实现与或非逻辑(2)电平转换(3)实现数据采集三态与非门(TSL)具有一个使能状态CMOS与非门抗干扰容限低,负载高,速度接近TTL,可并联2.3将与门、与非门的闲置端接1电平,而将或门、或非门闲置端接接0电平。
数字逻辑第四版华科出版1~7全答案

11
习题课
第 二 章 逻辑代数基础
2.1 假定一个电路中,指示灯F和开关A、B、C的关系为: F = (A+B)C,试画出相应的电路图。
解答:
A
U
B
C
F
精选ppt
12
习题课
2.2 用逻辑代数的公理、定理和规则证明下列表达式。
(1) (AB AC)ABAC
(2) A B A B A B A B 1 (3) A AB A B C C A B C AC B
1.7 将下列十进制数转换成二进制数、八进制数和十六进制 数(精确到小数点后4位)。
(1) 29 (2) 0.27 (3) 33.33
解答: (1) 29 = (11101)2=(65)8=(1D)16 (2) 0.27 = (0.0100)2=(0.21)8=(0.4 )16
(3)33.33 = (100001.0101)2 = (41.24)8= (41.2508)8= (41.2507)8 = (21.5)16 = (21.547B)16=(21.547A)16
20
习题课
2.7 将下列逻辑函数表示成“最小项之和”及“最大项之 积”形式 。
(1) F (A ,B ,C ,D ) B C D A B AC D B BC (2) F (A ,B ,C ,D )(A B AB )(B D C)D
解答: (1) F (A ,B ,C ,D ) B C D A B AC D B BC
精选ppt
3
习题课
1.4 最简电路是否一定最佳?为什么?
解答: 最简电路并不一定是最佳电路。最佳电路应满足全面的
性能指标和实际应用要求。
精选ppt
4
数字电子技术基础(第4版)_课后习题答案

第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1)=+(解:1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解:(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解:CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解:)(D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解: (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解: (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解:D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=)(2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解:)((4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式:(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止,负值,悬空时,都行)饱和-=时,=当截止时,=当都行)=饱和,,-=悬空时,都行)饱和。
大学_数字逻辑第四版(欧阳星明著)课后习题答案下载

数字逻辑第四版(欧阳星明著)课后习题答案下载数字逻辑第四版(欧阳星明著)课后答案下载第1章基础概念11.1概述11.2基础知识21.2.1脉冲信号21.2.2半导体的导电特性41.2.3二极管开关特性81.2.4三极管开关特性101.2.5三极管3种连接方法131.3逻辑门电路141.3.1DTL门电路151.3.2TTL门电路161.3.3CML门电路181.4逻辑代数与基本逻辑运算201.4.1析取联结词与正“或”门电路201.4.2合取联结词与正“与”门电路211.4.3否定联结词与“非”门电路221.4.4复合逻辑门电路221.4.5双条件联结词与“同或”电路241.4.6不可兼或联结词与“异或”电路241.5触发器基本概念与分类251.5.1触发器与时钟271.5.2基本RS触发器271.5.3可控RS触发器291.5.4主从式JK触发器311.5.5D型触发器341.5.6T型触发器37习题38第2章数字编码与逻辑代数392.1数字系统中的编码表示392.1.1原码、补码、反码412.1.2原码、反码、补码的运算举例472.1.3基于计算性质的几种常用二-十进制编码48 2.1.4基于传输性质的几种可靠性编码512.2逻辑代数基础与逻辑函数化简572.2.1逻辑代数的基本定理和规则572.2.2逻辑函数及逻辑函数的表示方式592.2.3逻辑函数的标准形式622.2.4利用基本定理简化逻辑函数662.2.5利用卡诺图简化逻辑函数68习题74第3章数字系统基本概念763.1数字系统模型概述763.1.1组合逻辑模型773.1.2时序逻辑模型773.2组合逻辑模型结构的数字系统分析与设计81 3.2.1组合逻辑功能部件分析813.2.2组合逻辑功能部件设计853.3时序逻辑模型下的数字系统分析与设计923.3.1同步与异步933.3.2同步数字系统功能部件分析943.3.3同步数字系统功能部件设计993.3.4异步数字系统分析与设计1143.4基于中规模集成电路(MSI)的数字系统设计1263.4.1中规模集成电路设计方法1263.4.2中规模集成电路设计举例127习题138第4章可编程逻辑器件1424.1可编程逻辑器件(PLD)演变1424.1.1可编程逻辑器件(PLD)1444.1.2可编程只读存储器(PROM)1464.1.3现场可编程逻辑阵列(FPLA)1484.1.4可编程阵列逻辑(PAL)1494.1.5通用阵列逻辑(GAL)1524.2可编程器件设计1604.2.1可编程器件开发工具演变1604.2.2可编程器件设计过程与举例1604.3两种常用的HDPLD可编程逻辑器件164 4.3.1按集成度分类的可编程逻辑器件164 4.3.2CPLD可编程器件1654.3.3FPGA可编程器件169习题173第5章VHDL基础1755.1VHDL简介1755.2VHDL程序结构1765.2.1实体1765.2.2结构体1805.2.3程序包1835.2.4库1845.2.5配置1865.2.6VHDL子程序1875.3VHDL中结构体的描述方式190 5.3.1结构体的行为描述方式190 5.3.2结构体的数据流描述方式192 5.3.3结构体的结构描述方式192 5.4VHDL要素1955.4.1VHDL文字规则1955.4.2VHDL中的数据对象1965.4.3VHDL中的数据类型1975.4.4VHDL的运算操作符2015.4.5VHDL的预定义属性2035.5VHDL的顺序描述语句2055.5.1wait等待语句2055.5.2赋值语句2065.5.3转向控制语句2075.5.4空语句2125.6VHDL的并行描述语句2125.6.1并行信号赋值语句2125.6.2块语句2175.6.3进程语句2175.6.4生成语句2195.6.5元件例化语句2215.6.6时间延迟语句222习题223第6章数字系统功能模块设计2556.1数字系统功能模块2256.1.1功能模块概念2256.1.2功能模块外特性及设计过程2266.2基于组合逻辑模型下的VHDL设计226 6.2.1基本逻辑门电路设计2266.2.2比较器设计2296.2.3代码转换器设计2316.2.4多路选择器与多路分配器设计2326.2.5运算类功能部件设计2336.2.6译码器设计2376.2.7总线隔离器设计2386.3基于时序逻辑模型下的VHDL设计2406.3.1寄存器设计2406.3.2计数器设计2426.3.3并/串转换器设计2456.3.4串/并转换器设计2466.3.5七段数字显示器(LED)原理分析与设计247 6.4复杂数字系统设计举例2506.4.1高速传输通道设计2506.4.2多处理机共享数据保护锁设计257习题265第7章系统集成2667.1系统集成基础知识2667.1.1系统集成概念2667.1.2系统层次结构模式2687.1.3系统集成步骤2697.2系统集成规范2717.2.1基于总线方式的互连结构2717.2.2路由协议2767.2.3系统安全规范与防御2817.2.4时间同步2837.3数字系统的非功能设计2867.3.1数字系统中信号传输竞争与险象2867.3.2故障注入2887.3.3数字系统测试2907.3.4低能耗系统与多时钟技术292习题295数字逻辑第四版(欧阳星明著):内容提要点击此处下载数字逻辑第四版(欧阳星明著)课后答案数字逻辑第四版(欧阳星明著):目录本书从理论基础和实践出发,对数字系统的基础结构和现代设计方法与设计手段进行了深入浅出的论述,并选取作者在实际工程应用中的一些相关实例,来举例解释数字系统的设计方案。
数字设计-原理与实践(第四版)课后习题答案

第1 章习题参考答案:1-6 一个电路含有一个2 输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化解:电路图和真值表如下:由真值表可以看出,该电路与一个2 输入或门(OR2)相同。
第2 章习题参考答案:将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C16(b) 1746378=1 111 100 110 011 1112=F99F16(c) 3655178=11 110 101 101 001 1112=1EB4F16(d) =10 101 011 101 011 010 0012=ABAD116(e) =111 100 011 0012=(f) =100 101 011 001 100 111 12=将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A16=111 1110 0110 10102=771528(c) ABCD16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)=1001 1110 10102=(f)=1101 1110 1010 1110 1110 11112=将下面的数转换成十进制数。
(a) =107 (b) 1740038=63491 (c) 2=183(d) = (e)= (f)F3A516=62373(g) 120103=138 (h) AB3D16=43837 (i) 71568=3694(j) =完成下面的数制转换。
(a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012(d) 9714= 227628 (e) 132= 10 000 1002 (f) 23851= 5D2B16(g) 727= 104025 (h) 57190=DF6616 (i) 1435=26338(j) 65113=FE5916将下面的二进制数相加,指出所有的进位:(a) S:1001101 C:100100(b) S: 1010001 C: 1011100(c) S: 0 C: 0(d) S: C:利用减法而不是加法重复训练题,指出所有的借位而不是进位:(a) D:011 001 B:110000 (b) D:111 101 B:1110000(c) D: B:00111000 (d) D:1101101 B:写出下面每个十进制数的8 位符号-数值,二进制补码,二进制反码表示。
习题册答案-《数字逻辑电路(第四版)》-A05-3096
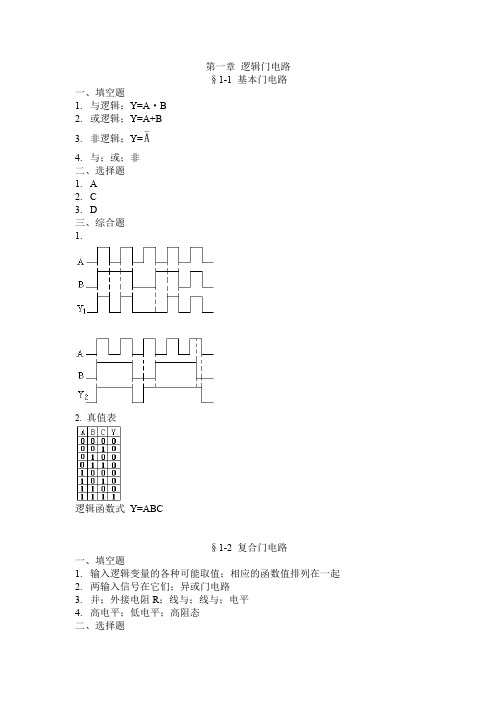
第一章逻辑门电路§1-1 基本门电路一、填空题1.与逻辑;Y=A·B2.或逻辑;Y=A+B3.非逻辑;Y=4.与;或;非二、选择题1. A2. C3. D三、综合题1.2.真值表逻辑函数式Y=ABC§1-2 复合门电路一、填空题1.输入逻辑变量的各种可能取值;相应的函数值排列在一起2.两输入信号在它们;异或门电路3.并;外接电阻R;线与;线与;电平4.高电平;低电平;高阻态二、选择题1. C2. B3. C4. D5. B三、综合题1.2.真值表逻辑表达式Y1=ABY2=Y3==A+B 逻辑符号3.第二章组合逻辑电路§2-1 组合逻辑电路的分析和设计一、填空题1.代数;卡诺图2.n;n;原变量;反变量;一;一3.与或式;1;04.组合逻辑电路;组合电路;时序逻辑电路;时序电路5.该时刻的输入信号;先前的状态二、选择题1. D2. C3. C4. A5. A三、判断题1. ×2. √3. √4. √5. ×6. √四、综合题1.略2.(1)Y=A+B(2)Y=A B+A B(3) Y=ABC+A+B+C+D=A+B+C+D3. (1) Y=A B C+A B C+ A B C + ABC=A C+AC(2) Y=A CD+A B D+AB D+AC D(3) Y=C+A B+ A B4. (a)逻辑函数式Y= Y=AB+A B真值表逻辑功能:相同出1,不同出0 (b)逻辑函数式Y=AB+BC+AC真值表逻辑功能:三人表决器5.状态表逻辑功能:相同出1,不同出0逻辑图1. 6.Y=A ABC+B ABC+C ABC判不一致电路,输入不同,输出为1,;输入相同,输出为0。
§2-2 加法器一、填空题1.加数与被加数;低位产生的进位2.加数与被加数;低位产生的进位3.加法运算二、选择题1. A2. C三、综合题1.略2.略3.§2-3 编码器与比较器一、填空题1. 编码2. 101011;010000113. 十;二;八;十六4. 0;1;逢二进一;10;逢十进一5. 二进制编码器;二—十进制编码器6. 两个数大小或相等7. 高位二、选择题1. A2. B3. C4. B三、综合题1.略2.(1)10111;00100011(2)00011001;19(3)583. (1)三位二进制(2)1,1,0(3)1,1,14.§2-4 译码器与显示器一、填空题1. 编码器;特定含意的二进制代码按其原意;输出信号;电位;解码器2. 二进制译码器;二—十进制译码器;显示译码器3. LED数字显示器;液晶显示器;荧光数码管显示器4. 1.5~3;10mA/段左右5. 共阴极显示译码器;共阳极显示译码器;液晶显示译码器二、选择题1. A;D2. A三、判断题1.√2.×3.×4.√5.√四、综合题七段显示译码器真值表f=D C B A +D C B A +D C B A+D CB A +D C B A +D C B A =D+B A +C A +C B =DB AC AC B§2-5 数据选择器与分配器一、填空题1.多路调制器;一只单刀多掷选择开关;地址输入;数字信息;输出端2.从四路数据中,选择一路进行传输的数据选择器3.地址选择;输出端二、选择题1. D2. A;C三、判断题1. √2. ×四、综合题1.略2. Y=A B D0+A BD1+A B D2+ABD3第三章触发器§3-1 基本RS触发器与同步RS触发器一、填空题1.两个;已转换的稳定状态2.R S+RSQ n;R+S=13. R S Q n+ R S;RS=04.置0;置15.相同;低电平;高电平6.时钟信号CP7.D触发器8.空翻二、选择题1.D2.B3.A4.B5.B6.D三、判断题1. ×2. ×3. √4. ×5. ×6. ×四、综合题1.略2.3.4.5.略§3-2主从触发器与边沿触发器一、填空题1.空翻2.置0、置1、保持、翻转3.D、J Q n+K Q n4.保持、置1、清0、翻转5.电平、主从6.一次变化7.边沿触发器8.不同、做成9.置0、置1、时钟脉冲二、选择题1.A2.A3.D4.B5.A6.C7.D8.B9.A10.D三、判断题1. √2. ×3. ×4. ×5. √6. ×7. √8. √四、综合题1.2.3.4.略5.略6.§3-3触发器的分类与转换一、填空题1.T、T'2. T Q n+ T Q n、Q n3.1、04. Q n、Q n5. 16. T'7. T8. T'二、选择题1.D2.D3.D4.B5.B三、判断题1. ×2. ×3. ×4. ×四、分析解答题1.2.3.略4.略5.略第四章时序逻辑电路§4-1 寄存器一、填空题1.输入信号;锁存信号2.接收;暂存;传递;数码;移位二、选择题1. C2. B;A三、判断题1. √2. ×3. √四、综合题1.JK触发器构成D触发器,即Q n+1= D。
数字逻辑与数字系统第四版课后答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++ (4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字设计原理与实践_第四版_课后习题答案

第1章习题参考答案:1-6一个电路含有一个2输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化?解:电路图和真值表如下:由真值表可以看出,该电路与一个2输入或门(OR2)相同。
第2章习题参考答案:2.2将下面的八进制数转换成二进制数和十六进制数。
(a)12348=10100111002=29C16(b)1746378=11111001100111112=F99F16(c)3655178=111101011010011112=1EB4F16(d)25353218=101010111010110100012=ABAD116(e)7436.118=111100011110.0010012=F1E.2416(f)45316.74748=100101011001110.11110011112=4ACE.F2C162.3将下面的十六进制数转换为二进制数和八进制数。
(a)102316=10000001000112=100438(b)7E6A16=1111110011010102=771528(c)ABCD16=10101011110011012=1257158(d)C35016=11000011010100002=1415208(e)9E36.7A16=1001111000110110.011110102=117066.3648(f)DEAD.BEEF16=1101111010101101.10111110111011112 =157255.57567482.5将下面的数转换成十进制数。
(a)11010112=107(b)1740038=63491(c)101101112=183 (d)67.248=55.3125(e)10100.11012=20.8125(f)F3A516= 62373(g)120103=138(h)AB3D16=43837(i)71568=3694(j)15C.3816=348.218752.6完成下面的数制转换。
数字逻辑第二章作业参考答案1

F AB AC AC AB
• 在只有原变量,没有反变量的输入条件下,采用与 非门设计的函数为:
F ABB ACC A AC A AB
电路图略
第二种方案: • (2) 化简F,得F的与或式:(卡诺图略)
F AC BC AB
• 在只有原变量,没有反变量的输入条件下,采用与 非门设计的函数为:
F ( A C D)(A B)(C B D)
• 在有原变量又有反变量的输入条件下,采用或非门 设计的函数为:
F ( A C D) ( A B) (C B D)
电路图略
P108,5(1)
• 解: 本题有两种设计方案。 • 第一种设计方案 • (1) 化简F,得F的与或式:(卡诺图略)
真值表(略) 由真值表可以看出,若将A、B分别作为一位二进制数,同 时A为被加数,B为加数,C为来自低位的进位,则F1为本 位和,F2为本位向高位的进位,该电路称作“全加器”, 它能实现两个一位二进制数加法运算。
P107,2
F ABS 3 ABS 4 BS1 BS 0 A
从真值表可知,当S0,S1 给定时,函数F的 0 0
S2 0 0 1
S4 0 1 0
F
0
0 0 0 0
0
1 1 1 1
1
0 0 1 1
1
0 1 0 1
A A A A
AB
AB
AB AB AB AB AB AB
0 0 0 0
1
1 1 1 1 1 1 1
0
0 0 0 1 1 1 1
0
0 1 1 0 0 1 1
0
1 0 1 0 1 0 1
数字逻辑欧阳星明第四版华科出版全答案课件

数字逻辑欧阳星明第四版华科出版全答案
3
习题课
1.4 最简电路是否一定最佳?为什么?
解答: 最简电路并不一定是最佳电路。最佳电路应满足全面的
性能指标和实际应用要求。
数字逻辑欧阳星明第四版华科出版全答案
4
习题课
1.5 把下列不同进制数写成按权展开形式。
(1)(4517.293)10 (2)(10110.0101)2
解答:
原码 反码 补码
0.1011
0.1011 0.1011 0.1011
-10110
110110 101001 101010
数字逻辑欧阳星明第四版华科出版全答案
9
习题课
1.10 已知[N]补=1.0110,求[N]原、[N]反和N.
解答: 原码:1.1010 反码:1.0101 N=-0.1010
第 一 章 基本知识
1.1 什么是数字信号?什么是模拟信号?试各举一例。
在时间上和数值上均作离散变化的物理信号称为离 散信号,离散信号的变化可以用不同的数字反映,所以 又称为数字信号,如学生的成绩单、电路开关等等。
在时间上和数值上均作连续变化的物理信号称为连 续信号,在工程应用中,为了处理和传送方便,通常用 一种连续信号去模拟另一种连续信号,因此习惯将连续 信号称为模拟信号,如温度、压力等等。
数字逻辑欧阳星明第四版华科出版全答案
7
习题课
1.8 如何判断一个二进制数B=b6b5b4b3b2b1b0能否被(4)整除?
解答: 因 为 B= b6b5b4b3b2b1b0 , 所 以 ( B)2= b6×26+
b5×25
+b4×24+b3×23+b2×22+b1×21+b0×20, 很 显 然 , b6×26
数字逻辑与数字系统(第四版)课后答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++ (4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
