AlphaBeta剪枝算法
Alpha-Beta剪枝算法

注意,由于示例问 题格局数非常少, 我们可以给出完整 的格局树。这种情
况下我可以找到 Minimax算法的全 局最优解。而真实 情况中,格局树非 常庞大,即使是计 算机也不可能给出 完整的树,因此我 们往往只搜索一定 深度,这时只能找
到局部最优解。
这些轮到甲 方的节点叫 做max节点, max节点的 值是其子节 点最大值。 Min节点则
Alpha-Beta 剪枝算法
什么是Alpha-Beta 剪枝算法
• Alpha——beta修剪是一种搜索算法,它试图减少在搜索树中由极 小极大算法评估的节点数量。它是一种对抗性的搜索算法,通常用 于两玩家游戏(井字游戏、棋类、围棋等)的机器游戏。当至少有 一种可能性被发现时,它就会停止完全评估一个动作,这证明了这 一举动比之前检查过的动作更糟糕。这些举措不需要进一步评估。 当应用到标准的极小极大树时,它会返回与minimax相同的移动, 但是去掉那些不可能影响最终决策的分支。
相反。 最终完整赋 值的格局树
如下:
在上面的例子 中,根节点的 价值为20,表 示如果对方每 一步都完美决 策,则我方按 照上述算法可 最终拿到20元, 这是我方在 Minimax算法 下最好的决策。 格局转换路径 如下图红色路
径所示:
• 那这跟alpha-beta剪枝算法有什么关系呢?
• 由于Minimax算法有一个很大的问题就是计算复杂性。它所需 搜索的节点数随最大深度呈指数膨胀,而算法的效果往往和深 度相关,因此这极大限制了算法的效果。
• Alpha-beta算法可以看成变种的Minimax,基本方法是从根节点 开始采用深度优先的方式构造格局树,在构造每个节点时,都 会读取此节点的alpha和beta两个值,其中alpha表示搜索到当 前节点时已知的最好选择的下界,而beta表示从这个节点往下 搜索最坏结局的上界。由于我们假设对手会将局势引入最坏结 局之一,因此当beta小于等于alpha时,表示从此处开始不论最 终结局是哪一个,其上限价值也要低于已知的最优解,也就是 说已经不可能此处向下找到更好的解,所以就会剪枝。
ab剪枝算法

ab剪枝算法在人工智能和搜索算法领域中,剪枝是一种常用的技术,它可以在搜索过程中减少不必要的计算,从而提高搜索效率。
ab剪枝算法就是其中的一种常见算法,它能够在搜索树中快速剪掉一些不必要的分支,从而减少搜索空间,提高搜索效率。
ab剪枝算法是一种基于最小-最大算法的剪枝技术。
在搜索树中,每个节点都代表一个状态,通过搜索树的遍历,可以找到最优解。
ab剪枝算法通过设置上界和下界来剪掉一些不可能产生最优解的节点,从而减少搜索空间。
ab剪枝算法的核心思想是在搜索树的遍历过程中,维护两个值,alpha和beta。
其中alpha表示当前节点的最佳选择,即当前节点的最大值;beta表示当前节点的最差选择,即当前节点的最小值。
在搜索树的遍历过程中,如果某个节点的最佳选择(即alpha)大于上界(即beta),则可以剪掉该节点及其子树,因为当前节点的最佳选择已经超出了上界,不可能产生最优解。
同样,如果某个节点的最差选择(即beta)小于下界(即alpha),则也可以剪掉该节点及其子树,因为当前节点的最差选择已经小于下界,不可能产生最优解。
通过不断地更新alpha和beta的值,ab剪枝算法可以逐渐缩小搜索空间,最终找到最优解。
与传统的搜索算法相比,ab剪枝算法能够大幅减少搜索时间,提高搜索效率。
ab剪枝算法的应用非常广泛,特别是在博弈树搜索、人工智能和优化问题求解等领域。
通过使用ab剪枝算法,可以在较短的时间内找到最优解或接近最优解,从而帮助决策者做出更好的决策。
总结一下,ab剪枝算法是一种通过设置上界和下界来剪掉不必要分支的搜索算法。
它利用最小-最大算法的思想,在搜索树的遍历过程中动态调整上界和下界,以减少搜索空间,提高搜索效率。
ab剪枝算法在人工智能和搜索算法领域有着广泛的应用,可以帮助决策者在较短的时间内找到最优解或接近最优解。
象棋AI程序的设计和优化

象棋AI程序的设计和优化一、引言象棋AI程序是人工智能领域的重要应用之一,其研发能够帮助人们更好地了解人工智能和算法优化。
本文将对象棋AI程序的设计和优化进行详细分析,力求给读者带来更多有用的知识。
二、象棋AI程序的设计1. 算法选择象棋AI程序的设计中,最重要的是算法选择。
目前比较好的算法包括蒙特卡洛树搜索算法、alpha-beta剪枝算法、深度学习算法。
蒙特卡洛树搜索算法较为适合在复杂性较高的棋类游戏中应用,alpha-beta剪枝算法适合用于对弈棋类游戏,深度学习算法则适用于一些较为简单、直观的棋类游戏。
2. 棋盘表示棋盘表示是象棋AI程序设计中比较重要的一环。
象棋的棋子可以表示为一个数字,每个数字代表一个明确的棋子,如车、马、象、士、将、炮、兵等。
通过数字来对每个棋子的位置进行表示,可以大大简化程序设计的工作量,也能够更加方便地实现算法优化。
要注意的是,棋子的数字表示需要与人们所理解的棋子相对应。
3. 算法优化算法优化是人工智能程序设计的关键部分。
在象棋AI程序设计中,可以采取的一种优化方法是对程序的运行时间进行优化。
这一方面可以通过设计一些高效的数据结构来进行实现,例如哈希表、Trie树、B+树等。
另一方面还可以通过并行计算的方法来提高程序的效率,例如GPU并行计算、多核CPU计算等。
三、象棋AI程序的优化1. alpha-beta剪枝算法的优化alpha-beta剪枝算法是目前在象棋AI程序设计中最流行、最适用的一种算法。
要使算法能够获得更好的效果,则需要对其进行一些优化。
首先,可以通过设置一个合适的搜索深度来将程序的运行时间缩短。
另外,还可以通过设计一些高效的数据结构来提高运算速度。
2. 蒙特卡洛树搜索算法的优化蒙特卡洛树搜索算法是在复杂性较高的棋类游戏中应用比较广泛的一种算法。
要提高算法的效率,则需要对其进行更加精细的调整。
一种常用的优化方法是使用动态规划,通过利用之前的搜索结果来进行快速采样,以得到更加准确的结果。
alphabeta剪枝例题

alphabeta剪枝例题Alpha-Beta剪枝算法是一种在搜索博弈树的过程中,通过维护两个值(α和β)来减少搜索的节点数的方法。
以下是一个简单的Alpha-Beta剪枝算法的例子:假设我们正在玩一个简单的井字棋游戏,现在轮到玩家X下棋。
使用Alpha-Beta剪枝算法可以帮助玩家X决定在哪个位置下棋。
Alpha-Beta剪枝算法的步骤如下:1. 初始化:设置当前玩家为玩家X,设置α和β的值,通常α设为负无穷,β设为正无穷。
2. 开始递归搜索:从当前节点开始,递归地搜索子节点。
对于每个子节点,根据当前玩家是最大化还是最小化来更新α和β的值。
3. 判断是否需要剪枝:如果β小于等于α,表示对手已经找到了一个更好的选择,我们可以剪掉当前节点的搜索分支,不再继续搜索。
4. 返回最佳走法:如果当前节点是叶子节点,则返回该节点的值;否则,返回最佳子节点的值。
以下是这个算法的伪代码表示:```pythonfunction alphabeta(node, depth, α, β, maximizingPlayer):if depth = 0 or node is a terminal node:return the heuristic value of nodeif maximizingPlayer:value = -∞for each child of node:value = max(value, alphabeta(child, depth - 1, α, β, FALSE))α = max(α, value)if β ≤ α:breakreturn valueelse:value = +∞for each child of node:value = min(value, alphabeta(child, depth - 1, α, β, TRUE))β = min(β, value)if β ≤ α:breakreturn value```在上述代码中,`node`表示当前节点,`depth`表示当前节点的深度,`α`和`β`分别表示当前玩家的最好选择和对手的最好选择,`maximizingPlayer`表示当前玩家是最大化还是最小化。
α-β剪枝技术解题过程

4.15
• 设有如图4.35所示的博弈树,其中最下面的 数字是假设的估值,请对该博弈树做如下 工作:
– 计算各节点的倒退值; – 利用α-β剪枝技术剪去不必要的分支。
4.15
S0 A C D E B F
G
H
I
J
K
L
M
N
0
5
-3
3
3
6
-2
3
5
4
-3
0
6
8
9
-3
4.15 解答
S0 A C ≥0 D E B F
G
0
H
≤-3
I
J
K
L
M
N
0
5
-3
3
3
6
-2
3
5
4
-3
0
6
8
9
-3
4.15 解答
S0 A C ≥0 0 ≤0 D ≥3 E B F
G
0
H
≤-3
I
3
J
K
L
M
N
0
5
-3
*
3
6
-2
3
5
4
-3
0
6
8
9
-3
4.15 解答
≥0 S0 A C 0 ≤0 D ≥3 E ≥4 B F
G
0
H
≤-3
I
3
*
K
4
L
-3
M
N
α-β剪枝技术 知识点 剪枝技术-剪枝技术
• α-β剪枝技术 剪枝技术 首先分析极小极大分析法效率,上述的极小极大分析法,实际是先生成一棵博弈树,然后再计 算其倒推值,至使极小极大分析法效率较低。于是在极小极大分析法的基础上提出了α-β剪枝技术 。 α-β剪枝技术的基本思想或算法是,边生成博弈树边计算评估各节点的倒推值,并且根据评估 出的倒推值范围,及时停止扩展那些已无必要再扩展的子节点,即相当于剪去了博弈树上的一些分 枝,从而节约了机器开销,提高了搜索效率。具体的剪枝方法如下: (1) 对于一个与节点MIN,若能估计出其倒推值的上确界β,并且这个β值不大于 MIN的父节点( 一定是或节点)的估计倒推值的下确界α,即α≥β,则就不必再扩展该 MIN节点的其余子节点了(因为 这些节点的估值对MIN父节点的倒推值已无任何影响 了)。这一过程称为α剪枝。 (2) 对于一个或节点MAX,若能估计出其倒推值的下确界α,并且这个α值不小于 MAX的父节点( 一定是与节点)的估计倒推值的上确界β,即α≥β,则就不必再扩展该MAX节点的其余子节点了(因为 这些节点的估值对MAX父节点的倒推值已无任何影响 了)。这一过程称为β剪枝。 从算法中看到: (1) MAX节点(包括起始节点)的α值永不减少; (2) MIN节点(包括起始节点)的β值永不增加。 在搜索期间,α和β值的计算如下: (1) 一个MAX节点的α值等于其后继节点当前最大的最终倒推值。 (2) 一个MIN节点的β值等于其后继节点当前最小的最终倒推值。
Minimax极大极小算法、Alpha-BetaPruning剪枝算法
Minimax极⼤极⼩算法、Alpha-BetaPruning剪枝算法这篇博客分为两部分。
⾸先我会先讲极⼤极⼩算法,然后在此基础上进⾏改进给出进阶版的Alpha-Beta剪枝算法以及代码实现。
⽂中配备b站讲解的视频,感兴趣的可以看⼀下视频讲解,然后复习的时候拿着⽂章当作参考。
Minimax算法(极⼤极⼩算法)概念是⼀种找出最⼩失败的可能的算法。
意思就是两个⼈下棋,A和B下棋,A想要⾃⼰的利益最⼤化(失败的可能性最⼩),B想要A的利益最⼩化(B想要A输)。
这个算法以及接下来的Alpha-Beta剪枝都是⼀种对抗性搜索算法(两个⼈互相对抗着下棋,俩⼈都想赢),是⼀种⼈⼯智能搜索的算法。
掌握此算法后可以⽤来写井字棋、五⼦棋等⼈⼯智能⼈机对抗下棋程序。
具体步骤给你⼀颗⼆叉树。
告诉你⼩紫和⼩⿊玩游戏。
紫⾊和⿊⾊圆圈代表他们两个。
我们是站在⼩紫的⾓度来描述的。
⼩紫想要他⾃⼰的得分最⼤所以⼩紫玩的时候,⼆叉树的那⼀层叫MAX层。
⼩⿊想要⼩紫的得分最⼩化,⼩⿊的叫做MIN层。
我们总是让⼩紫第⼀个开始,假设下⾯这个⼆叉树,我们只知道叶⼦节点的值(别管为啥,先学好算法原理,后续如何应⽤这个算法我还打算继续写博客和录视频讲解。
):在这⾥给出定义,MAX层的节点的值是什么??是它的⼦节点⾥⾯的最⼤值,MIN层的值是它的⼦节点⾥⾯的最⼩值。
直接上图。
MIN层是选择其孩⼦节点中最⼩值。
MAX层选择其孩⼦节点中的最⼤值。
算法概念就是这个样⼦。
算法的输⼊是构造的这⼀棵满⼆叉树,输出是最上层MAX节点的值。
代码实现class Node{ //结点类public:const int value;Node *left;Node *right;Node(int v,Node* l,Node* r):value(v),left(l),right(r) {};};为了遍历这棵树,⾸先我们得创建出来这棵树对吧?但是你的代码⾥没有创建⼆叉树这⼀部分啊。
alphabeta剪枝算法原理

alphabeta剪枝算法原理Alpha-Beta剪枝算法原理一、引言Alpha-Beta剪枝算法是一种用于搜索树的算法,用于提高搜索效率。
在博弈树等搜索问题中,搜索空间往往非常庞大,传统的搜索算法需要遍历所有可能的节点,耗费大量时间和计算资源。
而Alpha-Beta剪枝算法通过剪去不必要的节点,大大减少了搜索空间,提高了搜索效率。
二、算法原理Alpha-Beta剪枝算法是基于Minimax算法的改进。
Minimax算法是一种博弈树搜索算法,用于在双方对抗的情况下选择最优的决策。
它通过递归地遍历博弈树,计算每个节点的值,然后根据节点的深度和玩家角色选择最优的决策。
Alpha-Beta剪枝算法在Minimax算法的基础上,引入了Alpha和Beta两个参数,用于剪枝。
具体来说,Alpha表示玩家1(Max玩家)当前的最佳选择值,Beta表示玩家2(Min玩家)当前的最佳选择值。
在搜索过程中,如果某个节点的值超出了Alpha或Beta的范围,就可以剪掉该节点及其子树,因为对当前玩家来说,该节点及其子树的值不会被选择。
三、算法步骤1. 初始化Alpha和Beta为负无穷和正无穷,分别表示玩家1和玩家2的最佳选择值;2. 对于当前节点,递归地遍历其子节点。
如果当前节点是Max节点,遍历所有子节点,并更新Alpha值;如果当前节点是Min节点,遍历所有子节点,并更新Beta值;3. 在遍历子节点的过程中,进行剪枝操作。
如果某个节点的值超出了Alpha或Beta的范围,就可以剪掉该节点及其子树;4. 根据Alpha和Beta的更新情况,判断是否进行剪枝。
如果Beta 小于等于Alpha,说明已找到最佳决策,可以提前终止搜索;5. 递归地返回父节点,并将当前节点的值传递给父节点。
如果当前节点是Max节点,返回最大值;如果是Min节点,返回最小值;6. 重复步骤2-5,直到搜索完成。
四、优势与应用领域Alpha-Beta剪枝算法在搜索空间庞大的问题中具有明显优势。
alpha-beta算法 zillmer修正方法

文章标题:深入探讨Alpha-Beta算法及Zillmer修正方法一、引言在计算机科学领域中,Alpha-Beta算法是一种用于减少博弈树搜索的一种优化技术。
Zillmer修正方法是对Alpha-Beta算法的一种改进,能够更好地提高搜索效率和性能。
本文将从简单到复杂,由浅入深地探讨Alpha-Beta算法及Zillmer修正方法,以便读者能更全面地理解这一主题。
二、Alpha-Beta算法的基本概念1. 什么是Alpha-Beta算法Alpha-Beta算法是一种用于减少博弈树搜索的一种优化技术,它通过剪枝的方式来避免搜索不必要的分支,从而提高搜索效率。
2. Alpha-Beta算法的原理在搜索过程中,Alpha-Beta算法会维护两个变量:Alpha和Beta。
其中,Alpha表示当前最好的选择,Beta表示对手的最好选择。
通过比较Alpha和Beta的值,可以确定是否进行剪枝,从而减少搜索的分支。
3. Alpha-Beta算法的应用及局限性Alpha-Beta算法在博弈树搜索、人工智能等领域得到了广泛的应用,但也存在一些局限性,比如对于某些特定的游戏状态,它可能无法有效地剪枝。
三、Zillmer修正方法的改进1. Zillmer修正方法的提出Zillmer修正方法是对Alpha-Beta算法的一种改进,它通过引入额外的修正值来提高搜索效率和性能。
2. Zillmer修正方法的原理在搜索过程中,Zillmer修正方法会根据当前搜索的情况,动态地计算并更新修正值,从而更加准确地评估当前的搜索情况,提高搜索效率。
3. Zillmer修正方法的应用及改进效果Zillmer修正方法在实际的应用中能够显著提高Alpha-Beta算法的搜索效率和性能,特别是对于一些复杂的游戏状态,它能够更好地优化搜索过程。
四、个人观点及总结个人观点:Alpha-Beta算法及Zillmer修正方法对于优化博弈树搜索具有重要的意义。
AlphaBeta剪枝算法

AlphaBeta剪枝算法关于AlphaBeta剪枝的⽂章太多,这个⽅法是所有其它搜索⽅法的基础,得多花些时间认真地理解。
先把基本概念再回顾⼀遍:节点:在中国象棋中就是⼀个棋盘的当前局⾯Board,当然该轮到谁⾛棋也是确定的。
这⾥的圆形节点表⽰终⽌节点,在中国象棋⾥就是⼀⽅被将死的情况(或者到达了搜索的最⼤深度),后续不会再有着法产⽣,游戏如果⾛到这⾥就会结束。
在引擎⾥通常给红⽅⼀个很⼤的评估值,如+30000,给⿊⽅⼀个很⼩的评估值,如-30000,来⽅便地判断这种结束局⾯。
(胜利局⾯有稍微不同的表⽰法,⽤-30000+层数ply来表⽰)连线:表⽰⼀步着法Move,通过这步着法后,局⾯发⽣变化,先后⼿也要交换。
层:通常的术语是ply,复数形式是plies,也有称为levels,当然与depth也是对应的。
这个术语是为了与⽐赛⾥常说的回合相区分,⼀个回合通常包含2步,这个ply就表⽰某⼀⽅⾛了⼀步。
根节点记为0层,以下的层数递增。
深度depth:要注意是从下到上的,还是从上到下的。
(1)通常的算法书中都是从下到上递增的,即根节点为最⼤搜索深度,⾛到最底部的叶⼦结点为0,这种算法只要记住⼀个depth值就可以了。
(2)⽽另⼀种记法是根部结点为0,越向下depth增加,这时在搜索时就要传递2个参数值,depth和maxDepth,稍微有点啰嗦,应该也会影响⼀点效率。
另外在探查置换表中的结点时,⽤第(1)种记法也⽅便⼀些,因为要知道从当前节点迭代的深度值,否则还要在置换表中保存depth和maxDepth两个值。
AlphaBeta剪枝⽅法是对Minimax⽅法的优化,它们产⽣的结果是完全相同的,只不过运⾏效率不⼀样。
这种⽅法的前提假设与Minimax也是⼀样的:1)双⽅都按⾃⼰认为的最佳着法⾏棋。
2)对给定的盘⾯⽤⼀个分值来评估,这个评估值永远是从⼀⽅(搜索程序)来评价的,红⽅有利时给⼀个正数,⿊⽅有利时给⼀个负数。
alphabeta剪枝算法原理

alphabeta剪枝算法原理Alpha-Beta剪枝算法原理引言:在人工智能领域,博弈树搜索是一种常见的算法,用于解决两个对手之间的决策问题。
而Alpha-Beta剪枝算法则是一种优化博弈树搜索的方法,它通过剪去不必要的搜索分支,大大减少了搜索的时间复杂度,提高了搜索效率。
本文将详细介绍Alpha-Beta剪枝算法的原理及其应用。
一、博弈树搜索博弈树搜索是通过构建一棵树来表示博弈的决策过程。
树的每个节点表示一个决策点,树的边表示决策的选项。
对于每个节点,可以根据某种评估函数来确定它的分值。
通过搜索博弈树,可以找到最优的决策序列。
二、极小极大算法极小极大算法是一种常用的博弈树搜索算法,它在树上进行深度优先搜索,通过对叶子节点进行评估,逐层向上选择最优的决策。
该算法中的每个节点都有一个值,对于极大节点,它的值是其子节点中最大的值;对于极小节点,它的值是其子节点中最小的值。
三、Alpha-Beta剪枝算法的原理Alpha-Beta剪枝算法是对极小极大算法的一种优化方法,它通过剪去不必要的搜索分支,减少了搜索的时间复杂度。
具体来说,Alpha-Beta剪枝算法引入了两个参数:alpha和beta。
其中,alpha表示当前搜索路径中极大节点已经找到的最优值,beta表示当前搜索路径中极小节点已经找到的最优值。
在搜索过程中,当某个极大节点的值大于等于beta时,可以直接剪去该极大节点的所有子节点,因为极小节点不会选择这个极大节点。
同理,当某个极小节点的值小于等于alpha时,可以直接剪去该极小节点的所有子节点,因为极大节点不会选择这个极小节点。
通过递归地进行搜索,并不断更新alpha和beta的值,可以逐渐缩小搜索范围,从而大大减少搜索时间。
四、Alpha-Beta剪枝算法的应用Alpha-Beta剪枝算法广泛应用于博弈领域,特别是各种棋类游戏。
在这些游戏中,博弈树的规模往往非常庞大,而Alpha-Beta剪枝算法能够有效地减少搜索时间,提高计算机对手的决策速度。
α-β 剪枝
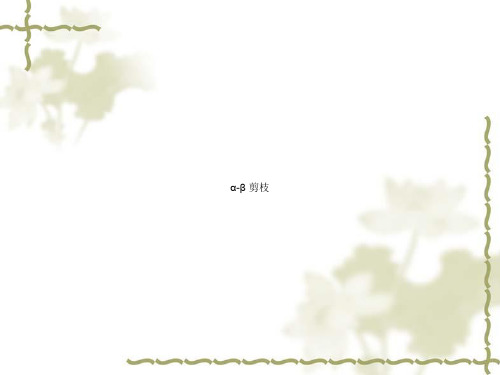
对于B(第四层)而已,尽量使得A 获利最小,因此当遇到使得A获利 更小的情况,则需要修改β。这里 3小于正无穷大,所以β修改为3
(第四层)这里17大于3,不用修பைடு நூலகம்β
对于A(第三层)而言,自
己获利越大越好,因此遇 到利益值大于α的时候, 需要α进行修改,这里3大 于负无穷大,所以α修改
选择第二个方案.
A(第一层)使自己利益最大,也就是A(第一层)的第二个方案不能差于第一个方案, 但是A(第三层)的一个 方案会导致利益为2, 小于3, 所以A(第三层)不会选择第一个方案, 因此B(第四层)也不用考虑第二个方
案.
S0 0 5 -3 3 3 -3 0 2 2 -3 0 -2 3 5 4 1 -3 0 6 8 9 -3
α-β 剪枝
Alpha-Beta剪枝用于裁剪搜索树中没有 意义的不需要搜索的树枝,以提高运算 速度
假设α为下界,β为上界,对于α
≤ N ≤ β: 若 α ≤ β 则N有解。 若 α > β 则N无解
❖ 图为整颗搜索树。这里使用极小 极大算法配合Alpha-Beta剪枝算 法,正方形为自己(A),圆为 对手(B)
为3
B(第四层)拥有一个方案使得A获利只有2,α=3, β=2, α > β, 说明A(第三层)只要选择第二个方案, 则B 必然可以使得A的获利少于A(第三层)的第一个方案,这样就不再需要考虑B(第四层)的其他候选方案了
,因为A(第三层)根本不会选取第二个方案,多考虑也是浪费.
B(第二层)要使得A利益最小,则B(第二层)的第二个方案不能使得A的获利大于β, 也就 是3. 但是若B(第二层)选择第二个方案, A(第三层)可以选择第一个方案使得A获利为 15, α=15, β=3, α > β, 故不需要再考虑A(第三层)的第二个方案, 因为B(第二层)不会
组合游戏1:详解Minimax和AlphaBeta剪枝算法

组合游戏1:详解Minimax和AlphaBeta剪枝算法本系列,我们来看看在⼀种常见的组合游戏——回合制棋盘类游戏中,如何⽤算法来解决问题。
⾸先,我们会介绍并解决搜索空间较⼩的问题,引⼊经典的博弈算法和相关理论,最终实现在⼤搜索空间中的Deep RL近似算法。
在此基础上可以理解AlphaGo的原理和⼯作⽅式。
本系列的第⼀篇,我们介绍3个Leetcode中的零和回合制游戏,从最初的暴⼒解法,到动态规划最终演变成博弈论⾥的经典算法:minimax 以及 alpha beta 剪枝。
获得最好的阅读体验,请点击最下⽅阅读原⽂,并在电脑上打开第⼀篇 [Leetcode中的Minimax 和 Alpha Beta剪枝]第⼆篇: ⼀些组合游戏的理论第三篇: 连接N个点的OpenAI Gym GUI环境第四篇: 蒙特卡洛树搜索(MCTS)和时间差分学习(TD learning)Leetcode 292 Nim Game (简单)简单题 Leetcode 292 Nim Game。
你和你的朋友,两个⼈⼀起玩 Nim游戏:桌⼦上有⼀堆⽯头,每次你们轮流拿掉 1 - 3 块⽯头。
拿掉最后⼀块⽯头的⼈就是获胜者。
你作为先⼿。
你们是聪明⼈,每⼀步都是最优解。
编写⼀个函数,来判断你是否可以在给定⽯头数量的情况下赢得游戏。
⽰例:输⼊: 4输出: false解释: 如果堆中有 4 块⽯头,那么你永远不会赢得⽐赛;因为⽆论你拿⾛ 1 块、2 块还是 3 块⽯头,最后⼀块⽯头总是会被你的朋友拿⾛。
定义为有个⽯头并采取最优策略的游戏结果,的值只有可能是赢或者输。
考察前⼏个结果:,然后来计算。
因为玩家采取最优策略(只要有⼀种⾛法让对⽅必输,玩家获胜),对于4来说,玩家能⾛的可能是拿掉1块、2块或3块,但是⽆论剩余何种局⾯,对⽅都是必赢,因此,4就是必输。
总的说来,递归关系如下:这个递归式可以直接翻译成Python 3代码# TLE# Time Complexity: O(exponential)class Solution_BruteForce:def canWinNim(self, n: int) -> bool:if n <= 3:return Truefor i in range(1, 4):if not self.canWinNim(n - i):return Truereturn False以上的递归公式和代码很像fibonacci数的递归定义和暴⼒解法,因此对应的时间复杂度也是指数级的,提交代码以后会TLE。
算法笔记--极大极小搜索及alpha-beta剪枝

算法笔记--极⼤极⼩搜索及alpha-beta剪枝极⼩极⼤搜索算法即minimax搜索算法主要应⽤于零和博弈(⾮胜即负,如围棋,象棋,井⼦棋等),完全信息(玩家知道之前所有的步骤。
象棋就是完全信息,因为玩家是交替着落⼦,且之前的步骤都能在棋盘上体现)这个算法采⽤搜索算法递归实现,⼀层为先⼿,记为a, ⼀层为后⼿,记为b, 交替出现对于最终局⾯,有⼀个分数(⽐如:先⼿胜分数为1,平局分数为0,先⼿输分数为-1)先⼿a想要让这个分数越⼤越好,后⼿b想要让这个分数越⼩越好,于是搜索到先⼿这⼀层,取最⼤返回,搜索到后⼿这⼀层,取最⼩返回如下图:于是伪代码为:int MaxMin(position,int d){int bestvalue,value;if(game over) //检查游戏是否结束return evaluation(p);// 游戏结束,返回估值if(depth<=0) //检查是否是叶⼦节点return evaluation(p);//叶⼦节点,返回估值if(max) //极⼤值点bestvalue=-INFINTY;else//极⼩值点bestvalue=INFINTY;for(each possibly move m){MakeMove(m); //⾛棋value=MaxMin(p,d-1);UnMakeMove(m); //恢复当前局⾯if(max)bestvalue=max(value,bestvalue);//取最⼤值elsebestvalue=min(value,bestvalue);//取最⼩值}return bestvalue;}关于alpha-beta剪枝:如果当前层为取最⼩,如果取最⼩后⽐上⼀层当前最⼤值还⼩,则不需要往下搜索,因为上⼀层根本不会选择当前节点往下搜,还有更好的选择同理,如果当前层为取最⼤,如果取最⼤后⽐上⼀层当前最⼩值还⼤,则不需要往下搜索,因为上⼀层根本不会选择当前节点往下搜具体推荐看最上⾯的知乎链接点赞最多的回答。
零和博弈算法

零和博弈算法
零和博弈(zero-sum game)是一种博弈理论中的概念,表示在博弈参与者之间的总收益为零。
在零和博弈中,一个参与者的收益的增加必然导致其他参与者的收益减少,反之亦然。
针对零和博弈,可以应用不同的算法来寻求最优策略。
以下是两种常见的零和博弈算法:
1. 极小化极大算法(Minimax Algorithm):
极小化极大算法是一种用于求解零和博弈最优策略的算法。
它采用递归的方式,在博弈树上进行搜索。
算法的基本思想是,假设对手会选择对己方最不利的策略,而自己会选择对己方最有利的策略。
因此,在每个节点上,交替进行极小化和极大化操作,直到达到叶子节点,然后根据叶子节点的收益值进行逐层回溯,得到最优策略。
2. Alpha-Beta剪枝算法(Alpha-Beta Pruning):
Alpha-Beta剪枝算法是对极小化极大算法的改进,用于减少搜索空间,提高搜索效率。
它利用了博弈树上的剪
枝操作,减少了不必要的搜索,从而加快算法的执行速度。
算法通过维护两个值,即alpha和beta,来表示已知的最好收益范围。
在搜索过程中,如果某个节点的收益范围超出了已知的alpha和beta范围,则可以停止搜索该节点的子树,从而减少了搜索的深度和复杂度。
这些算法可以应用于各种零和博弈场景,例如棋类游戏(如国际象棋、围棋)、博弈论问题等。
它们通过搜索博弈树,评估不同策略的收益,并选择最优的策略来应对零和博弈的挑战。
极大极小算法 剪枝

极大极小算法剪枝极大极小算法是一种经典的博弈树搜索算法,用于解决两人零和博弈问题。
在这种算法中,玩家轮流进行移动,目标是找到最佳的移动策略,使得自己在每一步都能获得最大的收益,同时让对手获得最小的收益。
剪枝则是在搜索树的过程中,通过一些条件判断,提前终止一些不必要的搜索分支,从而减少搜索的时间和空间复杂度。
极大极小算法的基本思想是通过递归地搜索博弈树,对每一层轮流进行极大化(MAX层)和极小化(MIN层)操作,直到达到叶子节点,然后通过评估函数来计算叶子节点的估值,并逐层向上传递这些估值。
在搜索的过程中,剪枝技术可以应用于减少搜索树的规模,提高搜索效率。
常见的剪枝技术包括Alpha-Beta剪枝和其他启发式剪枝方法。
Alpha-Beta剪枝是一种经典的剪枝技术,通过在搜索树的过程中动态地维护两个值alpha和beta,来减少搜索的分支。
当搜索到某个节点时,如果发现对于当前玩家来说已经存在一个更好的选择(即alpha值),则可以剪掉该节点的搜索分支,因为对手不会选择这个分支。
同样,如果对手已经有了一个更好的选择(即beta值),则当前玩家也不会选择这个分支,可以进行剪枝。
通过这种方式,可以减少搜索的分支数量,提高搜索效率。
除了Alpha-Beta剪枝外,还有一些其他的启发式剪枝方法,如历史启发式剪枝、Killer启发式剪枝等,它们通过一些特定的规则或者经验来进行剪枝,从而加速搜索过程。
总的来说,极大极小算法结合剪枝技术能够有效地解决博弈树搜索的效率问题,提高搜索的速度和效果。
然而,剪枝技术的应用需要根据具体的问题和搜索树的特点来选择合适的方法,并且需要注意剪枝条件的正确性,以避免影响最终的搜索结果。
人工智能---最清晰的α-β剪枝算法

⼈⼯智能---最清晰的α-β剪枝算法基本思想:根据倒推值的计算⽅法,或中取⼤,与中取⼩,在扩展和计算过程中,能剪掉不必要的分枝,提⾼效率。
定义:α值:有或后继的节点,取当前⼦节点中的最⼤倒推值为其下界,称为α值。
节点倒推值>=α;β值:有与后继的节点,取当前⼦节点中的最⼩倒推值为其上界,称为β值。
节点倒推值<=β;α-β剪枝:(1)β剪枝:节点x的α值不能降低其⽗节点的β值,x以下的分⽀可停⽌搜索,且x的倒推值为α ;(2)α剪枝:节点x的β值不能升⾼其⽗节点的α值,x以下的分⽀可停⽌搜索,且x的倒推值为β ;再上个例题图,⽅便⼤家理解:先做个说明:有画弧线的是与,取较⼩值,没有的是或,去最⼤值。
第⼀步:2、9、3做⽐较,取最⼩值2,I点确定为2第⼆步:J点的1和I点2⼤⼩进⾏⽐较,如果1是J点的最⼩值,由于J的⽗节点是取较⼤值,1<2,⽆法升⾼D的值,所以J点的-1可以点可停⽌搜索,我们划掉该值。
第三步:I点2接着与K点的左值-1进⾏⽐较,如果-1是最⼩值,由于K的⽗节点取较⼤值,-1<2,⽆法升⾼D的取值,所以K点的右值可以停⽌搜索。
第四步:D的值可以确定为2第五步:L点的作⽤值进⾏⽐较,取较⼩值6,D值与L值相⽐较,由于E去较⼤值,假设L就是最⼤值,E=6,⼆B点取得是D和E的较⼩值,2<6,E的结果值⽆法降低B的取值,所以E的右枝可以截掉。
第六步:B的值可以确定为2第七步:N的左右值进⾏⽐较,取0,N点在和O点的左值-5进⾏⽐较,假设-5是最⼩值,0>-5,O点的取值⽆法升⾼⽗节点F的值,所以可以停⽌搜索O点的右枝。
第⼋步:F确定为0.第九步:F点假设是C的最⼩值,它和B点的值⽐较,2>0,也就是说C点的取值⽆法升⾼A点的取值,所以G和H都停⽌搜索。
第⼗步:A点取2.-----------------------------------------------------------------------------------------------【转】。
α-β剪枝算法

α-β剪枝算法α-β剪枝算法 前⾯介绍的基本搜索算法,在实际应⽤是是⼗分费时的,因为它需要考虑所有可能的棋步。
有研究表明,在⿊⽩棋的中盘阶段,平均每个局⾯⼤约有10步棋可供选择[1]。
如果程序前瞻10步(搜索深度为10),就需要考虑⼤约100亿个局⾯。
假设计算机以每秒1000万个局⾯的速度进⾏运算,每下⼀步棋⼤约需要运算⼗⼏分钟。
因此,在有限的时间内,程序⽆法进⾏很深的搜索,这就⼤⼤制约了程序的棋⼒。
有没有更⾼效的搜索⽅法呢?Edwards、Timothy(1961年)[2]、Brudno(1963年)[3]等⼈相继在研究中发现,程序搜索过程中有很多局⾯是完全可以忽略的,并提出了α-β剪枝算法(Alpha-beta Pruning)。
我们就仍以图1所⽰的局⾯为例,简要说明剪枝算法的原理。
图1 ⽩先,当前最佳估值为0 假设⽩棋已经搜索了D6的后续变化,得出这步棋的估值为0。
接着开始搜索F4这步棋,⽩棋下F4后形成图2所⽰的局⾯。
图2 ⿊先,当前最佳估值为 6 在这⼀局⾯中,⿊棋相继搜索了C3、D3、E3三步棋,当前最佳估值是E3的 6。
作为⿊棋⽅,他是很乐意看到有E3这样的好棋,他也很希望尚未进⾏搜索的F3和G3能有更好的表现。
但问题是,⿊棋能遇上E3这样好棋的前提是⽩棋要先下出F4,下F4的决定权在于⽩棋⽅。
⽽对于⽩棋⽽⾔,⿊棋的这步E3回应显然对他太不利了。
在他看来,F4这步棋的估值最多只有-6,甚⾄有可能更差。
当⽩棋知道⿊棋将有⼀步好棋E3在等着他时,他是绝对不会去下F4的,因为他完全可以选择下D6,或者等待后续搜索中可能出现的更好棋步。
换句话说,⿊棋根本没有机会⾯对图2所⽰的局⾯,F3和G3这两步棋的结果已经⽆关紧要了,⿊棋没有必要再继续搜索下去。
我们将这种现象称为剪枝(Pruning)。
这看上去是个相当诡异的现象,⿊棋从⾃⼰的利益出发,努⼒寻找尽可能好的棋步,但是⼀旦他的棋步好过头了,对于当前局⾯的搜索⼯作就瞬间变成是多余的。
alpha-beta剪枝算法
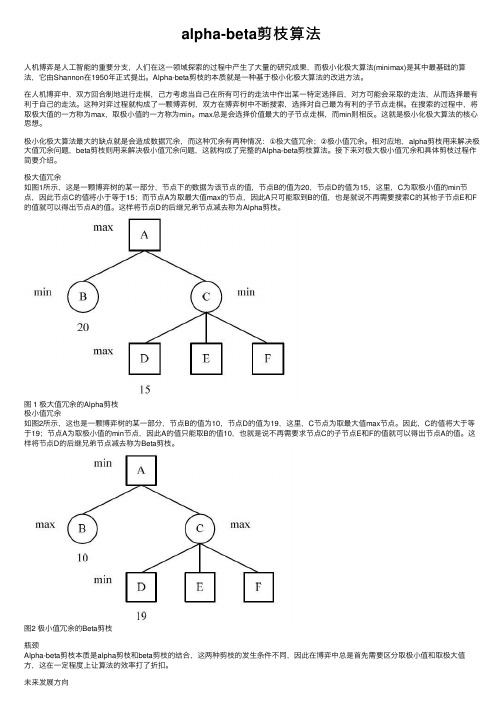
alpha-beta剪枝算法⼈机博弈是⼈⼯智能的重要分⽀,⼈们在这⼀领域探索的过程中产⽣了⼤量的研究成果,⽽极⼩化极⼤算法(minimax)是其中最基础的算法,它由Shannon在1950年正式提出。
Alpha-beta剪枝的本质就是⼀种基于极⼩化极⼤算法的改进⽅法。
在⼈机博弈中,双⽅回合制地进⾏⾛棋,⼰⽅考虑当⾃⼰在所有可⾏的⾛法中作出某⼀特定选择后,对⽅可能会采取的⾛法,从⽽选择最有利于⾃⼰的⾛法。
这种对弈过程就构成了⼀颗博弈树,双⽅在博弈树中不断搜索,选择对⾃⼰最为有利的⼦节点⾛棋。
在搜索的过程中,将取极⼤值的⼀⽅称为max,取极⼩值的⼀⽅称为min。
max总是会选择价值最⼤的⼦节点⾛棋,⽽min则相反。
这就是极⼩化极⼤算法的核⼼思想。
极⼩化极⼤算法最⼤的缺点就是会造成数据冗余,⽽这种冗余有两种情况:①极⼤值冗余;②极⼩值冗余。
相对应地,alpha剪枝⽤来解决极⼤值冗余问题,beta剪枝则⽤来解决极⼩值冗余问题,这就构成了完整的Alpha-beta剪枝算法。
接下来对极⼤极⼩值冗余和具体剪枝过程作简要介绍。
极⼤值冗余如图1所⽰,这是⼀颗博弈树的某⼀部分,节点下的数据为该节点的值,节点B的值为20,节点D的值为15,这⾥,C为取极⼩值的min节点,因此节点C的值将⼩于等于15;⽽节点A为取最⼤值max的节点,因此A只可能取到B的值,也是就说不再需要搜索C的其他⼦节点E和F 的值就可以得出节点A的值。
这样将节点D的后继兄弟节点减去称为Alpha剪枝。
图 1 极⼤值冗余的Alpha剪枝极⼩值冗余如图2所⽰,这也是⼀颗博弈树的某⼀部分,节点B的值为10,节点D的值为19,这⾥,C节点为取最⼤值max节点。
因此,C的值将⼤于等于19;节点A为取极⼩值的min节点,因此A的值只能取B的值10,也就是说不再需要求节点C的⼦节点E和F的值就可以得出节点A的值。
这样将节点D的后继兄弟节点减去称为Beta剪枝。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AlphaBeta剪枝算法关于AlphaBeta剪枝的文章太多,这个方法是所有其它搜索方法的基础,得多花些时间认真地理解。
先把基本概念再回顾一遍:节点:在中国象棋中就是一个棋盘的当前局面Board,当然该轮到谁走棋也是确定的。
这里的圆形节点表示终止节点,在中国象棋里就是一方被将死的情况(或者到达了搜索的最大深度),后续不会再有着法产生,游戏如果走到这里就会结束。
在引擎里通常给红方一个很大的评估值,如+30000,给黑方一个很小的评估值,如-30000,来方便地判断这种结束局面。
(胜利局面有稍微不同的表示法,用-30000+层数ply来表示)连线:表示一步着法Move,通过这步着法后,局面发生变化,先后手也要交换。
层:通常的术语是ply,复数形式是plies,也有称为levels,当然与depth也是对应的。
这个术语是为了与比赛里常说的回合相区分,一个回合通常包含2步,这个ply就表示某一方走了一步。
根节点记为0层,以下的层数递增。
深度depth:要注意是从下到上的,还是从上到下的。
(1)通常的算法书中都是从下到上递增的,即根节点为最大搜索深度,走到最底部的叶子结点为0,这种算法只要记住一个depth 值就可以了。
(2)而另一种记法是根部结点为0,越向下depth增加,这时在搜索时就要传递2个参数值,depth和maxDepth,稍微有点啰嗦,应该也会影响一点效率。
另外在探查置换表中的结点时,用第(1)种记法也方便一些,因为要知道从当前节点迭代的深度值,否则还要在置换表中保存depth和maxDepth两个值。
AlphaBeta剪枝方法是对Minimax方法的优化,它们产生的结果是完全相同的,只不过运行效率不一样。
这种方法的前提假设与Minimax也是一样的:1)双方都按自己认为的最佳着法行棋。
2)对给定的盘面用一个分值来评估,这个评估值永远是从一方(搜索程序)来评价的,红方有利时给一个正数,黑方有利时给一个负数。
(如果红方有利时返回正数,当轮到黑方走棋时,评估值又转换到黑方的观点,如果认为黑方有利,也返回正数,这种评估方法都不适合于常规的算法描述)3)从我们的搜索程序(通常把它称为Max)看来,分值大的数表示对己方有利,而对于对方Min来说,它会选择分值小的着法。
但要注意:用Negamax风格来描述的AlphaBeta中的评估函数,对轮到谁走棋是敏感的。
也就是说:在Minimax风格的AlphaBeta算法中,轮红方走棋时,评估值为100,轮黑方走棋评估值仍是100。
但在Negamax风格的AlphaBeta算法中,轮红方走棋时,评估值为100,轮黑方走棋时评估值要为-100。
贴一段伪代码:def ABNegaMax (board, depth, maxDepth, alpha, beta)if ( board.isGameOver() or depth == maxDepth )return board.evaluate(), nullbestMove = nullbestScore = -INFINITYfor move in board.getMoves()newBoard = board.makeMove(move)score = ABNegaMax(newBoard, maxDepth, depth+1, -beta, -max(alpha, bestScore))score = -scoreif ( score > bestScore )bestScore = scorebestMove = move# early loop exit (pruning)if ( bestScore >= beta ) return bestScore, bestMovereturn bestScore, bestMove用下列语句开始调用:ABNegaMax(board, player, maxDepth, 0, -INFINITY, INFINITY)// method call with depth 5 and minimum and maximum boundaries// minimaxValue = alphaBeta(board, 5, -MATE, +MATE)int alphaBeta(ChessBoard board, int depth, int alpha, int beta){int value;if( depth == 0 || board.isEnded()){value = evaluate(board);return value;}board.getOrderedMoves();int best = -MATE-1;int move;ChessBoard nextBoard;while (board.hasMoreMoves()){move = board.getNextMove();nextBoard = board.makeMove(move);value = -alphaBeta(nextBoard, depth-1,-beta,-alpha);if(value > best)best = value;if(best > alpha)alpha = best;if(best >= beta)break;}return best;}下面这个PDF更清楚地说明了Negamax风格的alphabeta算法的过程:/~anderson/cs440/index.html/lib/exe/fetch.php? media=notes:negamax2.pdf为了更准确地理解minmax和negamax两种不同风格的搜索执行过程,画出了详细的图解,发现negamax更容易理解了,代码也确实精练了不少。
当采用了置换表算法后,还需要对PV-Nodes, Cut-Nodes和All-Nodes三种类型结点的含义以及如何变化有更准确地了解。
可以发现,Negamax风格的算法有下面的特点(代码来自象棋巫师):int AlphaBeta(int depth, int alpha, int beta) {int hashf = hashfALPHA; //开始时的结点类型应该是All-Nodes,有些地方称为ALPHA类型结点//这里要探查置换表if (depth == 0) { // 叶子结点,评估,写入置换表,返回即可val = Evaluate();RecordHash(depth, val, hashfEXACT); // 叶子结点肯定是PV-Nodesreturn val;}GenerateLegalMoves();while (MovesLeft()) {MakeNextMove();//注意Negamax风格的调用方式,前面有个负号,后面的参数是-beta和-alpha// Negamax的含义中Nega就是指这里的负号val = -AlphaBeta(depth - 1, -beta, -alpha);UnmakeMove();if (val >= beta) { // 剪枝情况判断RecordHash(depth, beta, hashfBETA); //这时的结点类型是Cut-Nodesreturn beta;}if (val > alpha) { // Negamax中的max就是指的这一段,要记录最大的评估值,这里没有引入一个新变量,直接就用了alpha变量hashf = hashfEXACT; // 只要alpha值一发生变化,这个结点类型就是PV-Nodes了!alpha = val;}}RecordHash(depth, alpha, hashf);return alpha; // 此时的alpha就是记录了当前结点的所有子结点的最大的负评估值!}这面的代码在置换表探查方面感觉有点问题,又从Marek Strejczek的论文《Some aspects of chess programming》的第87页上找到一段代码,感觉这段代码充分利用了置换表中存储的信息。
chSCORE alphabetaWithTT(chPOSITION node,chSCORE alpha,beta) {if (isLeaf(node) ) return evaluate(node);if ( (entry = getFromHash(node) ) != NULL) {if (TT_entry_deep_enough) {// data in hash table comes from a search to the// same depth as current or deeper – so it is reliableif (entry.flag == UPPER) {if (entry.score <= alpha) {return alpha}if (entry.score < beta)beta = flag.score;}}if (entry.flag == LOWER) {if (entry.score >= beta) {return beta;}if (entry.score > alpha) {alpha = flag.score;}}if (entry.flag == EXACT) {return entry.score}}else {// TT entry represents results of a shallower// depth search – no cutoffs possible, but still// a valuable move to try first can be usedif (entry.move != NULL) {try_hash_move_first = true;}}}g = alpha;x = left_most_child(node);hash_flag = UPPER;best_move = NULL;while (isNotNull (x) ) {g = -alphabeta(x, -beta, -alpha);if (g > alpha) {alpha = g;if (g >= beta) {hash_flag = LOWER;best_move = current_move;saveHash(node,g,hash_flag,best_move);return beta;}hash_flag = EXACT;best_move = current_move;}x = next_brother(x);}putToHash(node, g, hash_flag, best_move)return alpha;} // end of alphabetaWithTT。
