余弦定理课件-PPT课件
合集下载
余弦定理ppt课件

边.
a 2 b 2 c 2 2bc cos A
b 2 a 2 c 2 2ac cos B
c 2 a 2 b 2 2ab cos C
利用余弦定理可以解决:
b2 c2 a 2
cos A
2bc
a 2 c2 b2
cos B
2ac
a 2 b2 c2
3
3.△ABC 的三内角 A,B,C 所对边的长分别为 a,b,c,设
向量 p =(a+c,b), q =(b-a,c-a),若 p ∥ q ,则 C 的大
小为( A )
π
π
π
2π
A.
B.
C.
D.
6
3
2
3
三 判断三角形的形状
例3:设△ABC 的内角 A,B,C 所对的边分别为 a,b,c.
若 bcosC+ccosB=asinA,则△ABC 的形状为( )
C.( 8,10)
D.( 10,8)
谢 谢 பைடு நூலகம் 看
B.-1
C.1
D.−
B
)
跟踪训练
1、△ABC 中,若 a:b:c=3:5:7,则这个三角形的最
大内角为( C )
A.60°
B.90°
C.120°
D.150°
二
例2
利用余弦定理进行边角互化
在△ 中,,,分别是内角,,的对边,且
= + + ,则角的大小为( D )
A.
B.
C.
D.
跟踪训练
1. 在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A= ( B )
a 2 b 2 c 2 2bc cos A
b 2 a 2 c 2 2ac cos B
c 2 a 2 b 2 2ab cos C
利用余弦定理可以解决:
b2 c2 a 2
cos A
2bc
a 2 c2 b2
cos B
2ac
a 2 b2 c2
3
3.△ABC 的三内角 A,B,C 所对边的长分别为 a,b,c,设
向量 p =(a+c,b), q =(b-a,c-a),若 p ∥ q ,则 C 的大
小为( A )
π
π
π
2π
A.
B.
C.
D.
6
3
2
3
三 判断三角形的形状
例3:设△ABC 的内角 A,B,C 所对的边分别为 a,b,c.
若 bcosC+ccosB=asinA,则△ABC 的形状为( )
C.( 8,10)
D.( 10,8)
谢 谢 பைடு நூலகம் 看
B.-1
C.1
D.−
B
)
跟踪训练
1、△ABC 中,若 a:b:c=3:5:7,则这个三角形的最
大内角为( C )
A.60°
B.90°
C.120°
D.150°
二
例2
利用余弦定理进行边角互化
在△ 中,,,分别是内角,,的对边,且
= + + ,则角的大小为( D )
A.
B.
C.
D.
跟踪训练
1. 在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A= ( B )
余弦定理ppt课件

(1)求∠A(用角度制表示); (2)当 a= 3,△ABC 的面积 S= 23时,求 b 和∠B.
❖ 分析:(1)由平面向量共线定理可得出关于各 角的一个关系式,化简之后便可求出∠A;(2) 分别利用三角形面积公式及余弦定理列出关 于b,c的方程,求出b,c的值,进而求出∠B.
解析:(1)∵m∥n,
3
2 3
=12,
∴∠BAC=30°,所求角为 30°+45°=75°.
∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能
与乙船相遇.
[例 5] 在△ABC 中,a、b、c 分别是∠A、∠B、∠C
的对边,若 m=(sin2B+2 C,1),n=(cos2A+72,4),且 m∥n.
即(281)2=9+y2-3y,整理得: (y-185)(y-98)=0, ∴y=185或 y=98(舍去),∴AD 的长为185.
❖ [例3] 在△ABC中,a·cosA=b·cosB,试确 定此三角形的外形.
解析:解法 1:由 a·cosA=b·cosB 以及余弦定理得 a·b2+2cb2c-a2=b·a2+2ca2c-b2, 得 a2(b2+c2-a2)=b2(a2+c2-b2), a2b2+a2c2-a4-a2b2-b2c2+b4=0,即(a2-b2)(c2-a2 -b2)=0. ∴a2=b2 或 c2=a2+b2, ∴a=b 或 c2=a2+b2.
❖ 二、余弦定理的运用
❖ 利用余弦定理可以处理两类斜三角形问题:
❖ 1.知三边,求⑪________. ❖ 2.知两边和它们的夹角,求⑫________
和⑬________.
❖ 友谊提示:了解运用余弦定理应留意以下 四点:
❖ (1)余弦定理提示了恣意三角形边角之间的 客观规律,是解三角形的重要工具;
❖ 分析:(1)由平面向量共线定理可得出关于各 角的一个关系式,化简之后便可求出∠A;(2) 分别利用三角形面积公式及余弦定理列出关 于b,c的方程,求出b,c的值,进而求出∠B.
解析:(1)∵m∥n,
3
2 3
=12,
∴∠BAC=30°,所求角为 30°+45°=75°.
∴甲船应沿北偏东 75°方向航行.
答:甲船应沿北偏东 75°方向航行半小时后才能
与乙船相遇.
[例 5] 在△ABC 中,a、b、c 分别是∠A、∠B、∠C
的对边,若 m=(sin2B+2 C,1),n=(cos2A+72,4),且 m∥n.
即(281)2=9+y2-3y,整理得: (y-185)(y-98)=0, ∴y=185或 y=98(舍去),∴AD 的长为185.
❖ [例3] 在△ABC中,a·cosA=b·cosB,试确 定此三角形的外形.
解析:解法 1:由 a·cosA=b·cosB 以及余弦定理得 a·b2+2cb2c-a2=b·a2+2ca2c-b2, 得 a2(b2+c2-a2)=b2(a2+c2-b2), a2b2+a2c2-a4-a2b2-b2c2+b4=0,即(a2-b2)(c2-a2 -b2)=0. ∴a2=b2 或 c2=a2+b2, ∴a=b 或 c2=a2+b2.
❖ 二、余弦定理的运用
❖ 利用余弦定理可以处理两类斜三角形问题:
❖ 1.知三边,求⑪________. ❖ 2.知两边和它们的夹角,求⑫________
和⑬________.
❖ 友谊提示:了解运用余弦定理应留意以下 四点:
❖ (1)余弦定理提示了恣意三角形边角之间的 客观规律,是解三角形的重要工具;
余弦定理(55张PPT)

2.在解三角形的过程中,求某一个角有时既可以用余 弦定理,也可以用正弦定理,两种方案有什么利弊呢?
提示:用余弦定理求角时,运算量较大,但角与余弦 值是一一对应的,无须讨论;而用正弦定理求角时,运算 量较小,但由于在区间(0,π)上角与正弦值不是一一对应 的,一般情况下一个正弦值可对应两个角,往往要依据角 的范围讨论解的情况.
新知初探
1.余弦定理 三角形中任何一边的平方等于其他两边的平方的和减 去这两边与它们的夹角的余弦的积的两倍.即
2.余弦定理的推论 余弦定理揭示了三角形中两边及其夹角与对边之间的 关系,它的另一种表达形式是 b2+c2-a2 cosA=_____________ , 2bc
a2+c2-b2 2ac cosB=_____________ , a2+b2-c2 2ab cosC=_____________.
类型二 [例2]
判断三角形的形状 在△ABC中,已知(a+b+c)(b+c-a)=3bc且
sinA=2sinBcosC,试确定△ABC的形状. [分析] 首先根据条件(a+b+c)(b+c-a)=3bc,利
用余弦定理求出一个角,再利用另一个条件,得到另外两 个角的关系,即可判断.
[解]
∵(a+b+c)(b+c-a)=3bc,
须知余弦定理是勾股定理的推广,勾股定理是余弦定
2 2 2 a > b + c 理的特例.角A为钝角⇔_____________,角A为直角⇔ 2 2 2 2 2 2 a = b + c a < b + c ____________,角A为锐角⇔____________.
3.利用余弦定理可解决的两类问题 余弦定理的每一个等式中都包含四个不同的量,它们 分别是三角形的三边和一个角,知道其中的三个量,代入 等式,便可求出第四个量来. 利用余弦定理可以解决以下两类解斜三角形的问题:
余弦定理PPT课件

c
C
aB
探索探究
联系已经学过的知识和方法,可用 什么途径来解决这个问题?
即:如图,在△ABC中,
设BC=a, AC=b, AB=c.
A
已知a, b和∠C,求边c? b
c
C
aB
探索探究
联系已经学过的知识和方法,可用 什么途径来解决这个问题?
用向量来研究这问题. A
即:如图,在△C ABC中, B
设BC=a, AC=b, AB=c.
巩经典固例知题识 典型例题
例 在△ABC中,a = 6,b = 7,c = 10,求△ABC 中的 最大角和最小角(精确到1°).
解 由于a<b<c,所以C最大,A最小,由公式(1.12),有
cos C a2 b2 c2 62 72 102 0.1786,
2ab
267
所以 C ≈ 100°,
a2 b2 c2 2cbcos A. b2 a2 c2 2ac cos B,c2 a2 b2 2ab cosC.
可以证明,上述结论对于任意三角形都成立.于是得到余弦 定理.
思考2:
a2 b2 c2 2bc cos A b2 a2 c2 2ac cos B c2 a2 b2 2ab cos C
1.3.2余弦定理
复习引入
运用正弦定理能解怎样的三角形?
A C
B
复习引入
运用正弦定理能解怎样的三角形?
①已知三角形的任意两角及其一边;
②已知三角形的任意两边A 与其中一边
的对角.
C B
情境设置
问题1:
如果已知三角形的两边及其夹角, 根据三角形全等的判定方法,这个三
A
角形是大小、形状完全确定的三角形. C
6.4.2 余弦定理PPT课件(人教版)

类型二
已知三角形两边及一角解三角形
[例 2] (1)在△ABC 中,已知 b=3,c=2 3,A=30°,求 a; (2)已知在△ABC 中,A=60°,最大边和最小边的长是方程 3x2-27x+32=0 的两实根,求边 BC 的长. [分析] (1)已知两边及其夹角,可直接利用余弦定理求出第三条边; (2)利用余弦定理、根与系数的关系进行求解.
知识点二 余弦定理及其推论的应用
[填一填] 一般地,三角形的三个角 A,B,C 和它们的对边 a,b,c 叫做三角形的元素.已 知三角形的几个元素求其他元素的过程叫做解三角形. 余弦定理及其推论可解决两类基本的解三角形的问题:一类是已知两__边__及__夹__角_ 解三角形;另一类是已知___三__边____解三角形.
解析:由余弦定理可知 cosA =AB2+2AABC·A2-C BC2=25+2×AC5A2-C 39=-12, 解得 AC=2 或-7(舍去).
类型三
判断三角形的形状
[例 3] 在△ABC 中,若(a+b+c)(a+b-c)=3ab,且 sinC=2cosAsinB,试判 断△ABC 的形状.
[分析] 判断三角形的形状时,一般有两种思路:一种是考虑三角形的三边关 系;另一种是考虑三角形的内角关系.当然有时可将边和角巧妙结合,同时考虑.
解:5x2+7x-6=0 可化为(5x-3)(x+2)=0. ∴x1=35,x2=-2(舍去).∴cosC=35.根据余弦定理, c2=a2+b2-2abcosC =52+32-2×5×3×35=16.∴c=4,即第三边长为 4.
——本课须掌握的四大问题 1.适用范围:余弦定理对任意的三角形都成立. 2.结构特征:“平方”、“夹角”、“余弦”. 3.揭示的规律:余弦定理指的是三角形中三条边与其中一个角的余弦之间的 关系式,它描述了任意三角形中边与角的一种数量关系. 4.主要功能:余弦定理的主要功能是实现三角形中边角关系的互化.
第4章第6节正弦定理余弦定理课件共47张PPT

=
6+ 4
2 .
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
点评:在△ABC中,若A=m,则B+C=π-m.从而B=π-m-C 或C=π-m-B,由此可消去B或C.
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
[跟进训练]
=4或b=5.]
1234
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
02
细研考点·突破题型
考点一 考点二 考点三
利用正、余弦定理解三角形 利用正、余弦定理解决三角形面积问题 判断三角形的形状
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
2.三角形常用面积公式
(1)S=12a·ha(ha 表示边 a 上的高);
(2)S=12absin
1
1
C=___2_a_c_s_in__B___=____2_b_c_s_in__A__;
(3)S=12r(a+b+c)(r 为内切圆半径).
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
因此,选条件②时问题中的三角形存在,此时c=2 3.
第六节 正弦定理、余弦定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课后限时集训
方案三:选条件③.
由C=π6和余弦定理得a2+2ba2b-c2=
3 2.
6.4.3 第1课时 余弦定理PPT课件(人教版)

课前篇自主预习
一
二
3.做一做
(1)在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,若 a=1,b= 7,c= 3,
则 B=
.
5π
答案: 6
解析:由已知 a=1,b= 7,c= 3,根据余弦定理,得 cos
1+3-7
3
=- .
2
2 3
5π
∵0<B<π,∴B= 6 .
2
2 +2 -
B= 2
=
课前篇自主预习
一
二
(2)判断下列说法是否正确,正确的在后面的括号内画“√”,错误
的画“×”.
①在△ABC中,若a2+b2<c2,则△ABC是钝角三角形.(
)
②在△ABC中,若△ABC是钝角三角形,则必有a2+b2<c2.(
)
③在△ABC中,若△ABC是锐角三角形,则必有a2+b2>c2.(
)
答案:①√ ②× ③√
B,BD=acos B,AD=AB-BD=c-acos B,b2=CD2+AD2=(asin B)2+(cacos B)2=a2+c2-2acos B;
同理可证:c2=a2+b2-2abcos C,a2=b2+c2-2bccos A.
图(2)
课堂篇探究学习
探究一
探究二
探究三
思维辨析
随堂演练
(3)在钝角△ABC中,如图(3),作CD⊥AB,交AB的延长线于点D,则
形.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 1.利用三角形的边角关系判断三角形的形状时,需要从
《高一数学余弦定理》课件

《高一数学余弦定理》ppt课件
• 余弦定理的引入 • 余弦定理的证明 • 余弦定理的应用 • 余弦定理的拓展 • 习题与解答
01 余弦定理的引入
三角形的边角关系
三角形的基本性质
三角形有三条边和三个角,这些 边和角之间存在一定的关系,这 是三角形的基本性质。
边角关系的重要性
理解三角形的边角关系是解决三 角形问题的关键,对于后续学习 余弦定理等知识点至关重要。
基础习题2
在三角形ABC中,已知A=45°, B=60°,a=2,求b的值。
基础习题3
已知三角形ABC中,a=2, b=2√3, B=60°,求角A的大小
。
提升习题
提升习题1
在三角形ABC中,已知A=45°,a=3, c=√13,求 b的值。
提升习题2
已知三角形ABC中,a=4, b=5, C=120°,求边c 的大小。
推论三
若三角形ABC的两边AB、 AC与平面α所成的角相等 ,且三角形ABC的两角相 等,则三角形ABC的两边 AB、AC与平面α所成的角 相等。
余弦定理在空间几何中的应用
应用一
在空间几何中,余弦定理可以用来解 决与角度和距离有关的问题,例如计 算点到平面的距离、两平面之间的夹 角等。
应用二
应用三
详细描述
首先,我们知道三角形的面积公式为S=1/2ab*sinC,其中a、b为三角形两边, C为两边之间的夹角。然后,利用三角形的面积公式和余弦定理的关系,我们可 以推导出余弦定理的表达式。
利用勾股定理证明余弦定理
总结词
勾股定理证明余弦定理是通过勾股定理和余弦定理的关系来推导余弦定理的表达式。
详细描述
应用二
在工程学中,余弦定理可以用来解 决与结构工程和机械工程有关的问 题,例如计算结构的承载能力、判 断结构的稳定性等。
• 余弦定理的引入 • 余弦定理的证明 • 余弦定理的应用 • 余弦定理的拓展 • 习题与解答
01 余弦定理的引入
三角形的边角关系
三角形的基本性质
三角形有三条边和三个角,这些 边和角之间存在一定的关系,这 是三角形的基本性质。
边角关系的重要性
理解三角形的边角关系是解决三 角形问题的关键,对于后续学习 余弦定理等知识点至关重要。
基础习题2
在三角形ABC中,已知A=45°, B=60°,a=2,求b的值。
基础习题3
已知三角形ABC中,a=2, b=2√3, B=60°,求角A的大小
。
提升习题
提升习题1
在三角形ABC中,已知A=45°,a=3, c=√13,求 b的值。
提升习题2
已知三角形ABC中,a=4, b=5, C=120°,求边c 的大小。
推论三
若三角形ABC的两边AB、 AC与平面α所成的角相等 ,且三角形ABC的两角相 等,则三角形ABC的两边 AB、AC与平面α所成的角 相等。
余弦定理在空间几何中的应用
应用一
在空间几何中,余弦定理可以用来解 决与角度和距离有关的问题,例如计 算点到平面的距离、两平面之间的夹 角等。
应用二
应用三
详细描述
首先,我们知道三角形的面积公式为S=1/2ab*sinC,其中a、b为三角形两边, C为两边之间的夹角。然后,利用三角形的面积公式和余弦定理的关系,我们可 以推导出余弦定理的表达式。
利用勾股定理证明余弦定理
总结词
勾股定理证明余弦定理是通过勾股定理和余弦定理的关系来推导余弦定理的表达式。
详细描述
应用二
在工程学中,余弦定理可以用来解 决与结构工程和机械工程有关的问 题,例如计算结构的承载能力、判 断结构的稳定性等。
第五章第六节正弦定理和余弦定理课件共58张PPT

A,bsin
C=csin
B,
cos
C=a2+2ba2b-c2
2.三角形中常用的面积公式
(1)S=12 ah(h 表示边 a 上的高);
(2)S=12
1
1
bcsin A=___2__a_c_s_in_B____=__2__a_b_si_n_C___;
(3)S=12 r(a+b+c)(r 为三角形的内切圆半径).
解析: 在△ABC 中, 由余弦定理及 a=2 2 ,b=5,c= 13 ,有 cos
C=a2+2ba2b-c2
=
2 2
π .又因为 C∈(0,π),所以 C= 4
.
π 在△ABC 中,由正弦定理及 C= 4 ,a=2 2 ,c= 13 ,可得 sin A=
a sin C c
=2 1313
.
答案:
π 4
变形
(1)a=2R sin A,b=_2_R_s_in_B___,c= __2_R_s_in_C___;
cos A=b2+2cb2c-a2
;
(2)a∶b∶c=_si_n_A_∶__s_i_n_B_∶__s_in_C___; cos B=c2+2aa2c-b2 ;
(3)asin B=bsin asin C=csin A
考点·分类突破
⊲学生用书 P84
利用正弦、余弦定理解三角形
(1)(2020·全国卷Ⅲ)在△ABC 中,cos C=23 ,AC=4,BC=3,则
tan B=( )
A. 5
B.2 5
C.4 5
D.8 5
(2)(2020·广东省七校联考)若△ABC 的内角 A,B,C 所对的边分别为 a,
b,c,已知 2b sin 2A=3a sin B,且 c=2b,则ab 等于( )
余弦定理课件
例 3:ABC三个顶点坐标为(6,5)、
(-2,8)、(4,1),求A. 解法一:
∵ AB =√[6-(-2)]2+(5-8)2 =√73 ,
BC =√(-2-4)2+(8-1)2 =√85 ,
AC =√(6-4)2+(5-1)2=2√5 ,
∴ cosA=
AB
2+ AC 2- 2 AB AC
BC
2
A(b cosC,bsin C), B(a,0),C(0,0)
AB2 (b cosC a)2 (b sin C 0)2 b2 cos2 C 2ab cosC a 2 b2 sin 2 C a2 b2 2ab cosC
c2 a2 b2 2abcosC
例 1:在ABC中,已知a=7,b=10,
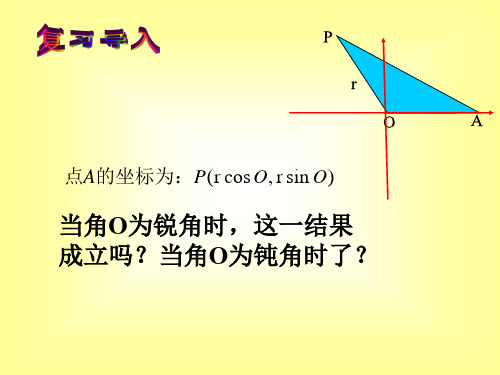
点A的坐标为:P(r cos O, r sin O)
当角O为锐角时,这一结果 成立吗?当角O为钝角时了?
余弦定理
勾股定理:
A
a2 b2 c2
证明: AB AC CB b
c
AB AB (AC CB)(AC CB)C
B
a
AC AC 2 AC CB CB CB
2
2
2
AB AC CB
C
AC AC 2AC CB CB CB
a
B
2
2
2
AB AC 2 AC CB cos(1800 C) CB
c2 a2 b2 2abcosC
余弦定理
定理:三角形任何一边的平方等于其他两边平方的和减
去这两边与它们夹角的余弦的积的两倍。
a2 b2 c2 2bc cos A b2 a2 c2 2ac cosB c2 a2 b2 2abcosC
余弦定理优秀课件

三角形的角度与边长的关系
角度与边长的关系
在三角形中,角度和边长之间存在一定的关系,如正弦定理和余弦定理。
余弦定理的引入
余弦定理是三角形边角关系的一个重要定理,它可以帮助我们解决与三角形边 长和角度相关的问题。
余弦定理的引入
余弦定理的定义
余弦定理是三角形边角关系的一个重 要定理,它描述了三角形三边与其对 应角的余弦值之间的关系。
应用二
在解决立体几何问题时,余弦定理可以用来计算空间几何体 的表面积和体积,例如球体、圆锥体等。
余弦定理与其他定理的关系
关系一
余弦定理与正弦定理密切相关,它们 在解决三角形的边角关系问题时常常 相互转换。
关系二
余弦定理与勾股定理也有一定的联系, 勾股定理是余弦定理的一个特例,即 当三角形ABC为直角三角形时,有 a^2+b^2=c^2。
题目4
在三角形ABC中,已知A = 45°,B = 60°, a = 15, 求边c的大小。
综合习题
题目5
在三角形ABC中,已知a = 14, b = 16, C = 120°,求 角B的大小以及边c的大小。
题目6
在三角形ABC中,已知A = 30°,B = 45°,a = 10, 求 边c的大小以及角C的大小。
推论三
若三角形ABC中,角A和角B为锐 角,且满足cosA=√(1-sin^2A), cosB=√(1-sin^2B),则三角形
ABC为锐角三角形。
余弦定理在空间几何中的应用
应用一
在三维空间中,余弦定理可以用来解决与平面、直线和点相 关的问题,例如判断点、线、面的位置关系,计算点到平面 的距离等。
05
习题与解答
基础习题
题目1
人教版高中数学必修2《余弦定理》PPT课件

[微思考] 勾股定理和余弦定理有什么关系? 提示:余弦定理是勾股定理的推广,勾股定理是余弦定理的特例. 2.解三角形的定义:
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形 的_元__素__.已知三角形的几个元素求其他元素的过程叫做_解__三__角__形__.
(二)基本知能小试
1.判断正误:
2×( 6+ 2)×2 3×cos 45°=8,
所以 b=2 2. 由 cos A=b2+2cb2c-a2,
得 cos A=2
22+ 6+ 2×2 2×
22-2 6+ 2
32=12.
因为 0°<A<180°,所以 A=60°.
(2)由余弦定理,得 a2=b2+c2-2bccos A =(b+c)2-2bc(1+cos A), 所以 49=64-2bc1-12,即 bc=15. 由bbc+=c1=58, 解得bc==53, 或cb==35.,
二、应用性——强调学以致用 2. 在古希腊数学家海伦的著作《测地术》中记载了著名的海伦公式,利用
三角形的三边长求三角形的面积.若三角形的三边长分别为 a,b,c, 则其面积 S= pp-ap-bp-c,这里 p=a+2b+c.已知在△ABC 中, BC=6,AB=2AC,求当△ABC 的面积最大时,sin A 的值. [析题建模] 由海伦公式,结合基本不等式,求出△ABC 的面积最大时 边 AB 及 AC 的长.再由余弦定理求出 cos A,进而求出 sin A.
6.4.3 余弦定理、正弦定理
明确目标
发展素养
1.借助向量的运算,探索三角 1.通过对余弦定理、正弦定理的学习及运
形边长与角度的关系,掌握 用,提升直观想象、数学抽象和逻辑推
余弦定理、正弦定理.
高中数学1.1.2余弦定理课件3新人教A必修5.ppt

问5:解决长度和角度问题的手段有什么?
C
baA源自cB余弦定理
问题解决
B
?
C
(精确到0.1米)
96°
B C 2 A B 2 A C 2 2 A B A C c o s A A
3 .6 2 4 .8 2 2 3 .6 4 .8 c o s 9 6
1 2 .9 6 2 3 .0 4 3 4 .5 6 0 .1 0 4 5
二.思想方法: 数形结合的思想,化归与转化的思想, 分类讨论的思想,特殊到一般的思想
• 作业 • 1.复习 • 2.必做题:书P8---P9 • 选做题:已知一钝角三角形的边长是三个
连续自然数,求该三角形的三边长。
• 3.预习
猜字谜游戏:
• 留得琴丝调宫商(打一数学名词)
39.6125
BC6.3
答:B,C两处的距离约为6.3米。
一、余弦定理:
问6:公式应该要如何记忆呢? 问7:可将公式如何变形? 问8:公式变形的目标是什么?
观察可能导致发现,观察将揭示 某种规则-------波利亚
定理应用 --------------类比的方法
----------请同学们自己编题---------解三角形问题:SSS SAS
情境引入
C B
A
情境引入
情境引入
C B
96° A
提出问题
B
?
C
96° A
问3:用正弦定理能否直接求出B,C两处的距离?
问4:如何解决这已知三角形两边c和b, 和两边的夹角A,求第三边a的问题?
公式推导 --------------特殊到一般的思想
如何由已知两边和它们的夹角求三角形的另一边?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巩 固
练习2:在△ABC中,已知b=3, c 3 3
,
知 B=30°,解三角形
识
随 练习3:在△ABC中,已知a=5,b=7,c=8, 堂 则△ABC( ) 练 A.锐角三角形 B.直角三角形 习 C.钝角三角形 D.以上都有可能
思考
在解三角形的过程中,求某一个角 有时既可以用余弦定理,也可以用正弦定理, 两种方法有什么利弊呢? 在已知三边和一个角的情况下:求另一个角正余弦弦定定理理
若a2 b2 c2,则C为锐角;
若a2 b2 c2,则C为钝角;
(2)已知两边和它们的夹角,求 第三边和其它两角;
(3)判断三角形的形状。
读书部分:阅读课本第8、9页探究与发现
八
、
优化设计第4页例题与反思
课
后 作
书面作业:优化设计第5页(必做)
业
谢谢!
从余弦定理,可以得到它的推论
四
、 余
a2 b2 c2 2bccos A
弦
定 理
b2 a2 c2 2accosB
的
推
论 c2 a2 b2 2abcosC
b2 c2 a2 cos A
2bc a2 c2 b2 cos B
2ac
a2 b2 c2
cos C 2ab
余弦定理的推论:
C
300m
兴
趣
A
?
B
导
入
500m
120° 300m
C
二 1、如何用初中的三角方法来求AB的长 、 创 设 情 2、如何边、角为一般的结论是否成立 境
兴 趣 导 入
?
三 如图,由向量的减法,A
B
、
向 AB CB CA
量
C
法 AB AB (CB CA) (CB CA)
证 明 AB AB CB CB CACA 2CB CA
余弦定理:三角形任何一边的平方等于其它两边 平方的和减去这两边与它们夹角的余弦的积的两 倍。
a2 =b2 +c2-2bccosA
b2 =c2+a2-2cacosB
c2 =a2+b2-2abcosC
应用余弦定理,我们就可以从已知的两 边和夹角计算出三角形的第三条边。
思考 如果已知三角形的三边,如何确定三个角?
1、回顾正弦定理以及正弦定理能解决的解三角形 问题的类型。
一
正弦定理: a b c 2R
sin A sin B sin C
、
复
正弦定理能解决的问题类型:
习
(1)已知两个角和一条边
回
(2)已知两条边和一边的对角
顾
二
、
创
设
·B
情 A·
境
兴 趣 导 入
二 、
A.
创
设
500m
情
境
.B
. 120°
四 、
b2 c2 a2 cos A
余
2bc
弦
a2 c2 b2
定 理
cos B 2ac
的
a2 b2 c2
推 论
cos C 2ab
应用余弦定理的推论,我们就可以从三角 形的三边计算出三角形的三个角。
勾股定理指出了直角三角形中三边平方 之间的关系,余弦定理则指出了一般三角 形中三边平方之间的关系,如何看这两个 定理之间的关系?
余 弦
2
2
2
AB CB CA 2CB CA cosC
定 理
c2 a2 b2 2ab cosC
1的、对若边已边知长△c。ABC中A两边长a,b和角C,求角C
自
c
b
主
探
B
C
a
究 2、若已知△ABC中两边长b , c和角A,求角A
的对边边长a。
3、若已知△ABC中两边长a , c和角B,求角B 的对边边长b 。
(1)用正弦定理,计算相对简单,但解不唯一,要 进行判断取舍。
(2)用余弦定理推论,解唯一,可以免去判断取舍。
思考
我们讨论的解三角形的问题可以分为几种
类型?分别是怎样求解的?
1.余弦定理
a2=b 2+c-22bccosA
2 22
七 、
b =c +-2accosB
c2=a2
2
+b-2abcosC
a2 b2 c2
cos C 2ab
C为锐角 cosC>0 a2 b2 c2
C为直角 C为钝角
cosC=0 cosC<0
a2 b2 c2
a2 b2 c2
余弦定理可以看作是勾股定理的推广, 勾股定理是余弦定理的特例
情景题
五 例1:在三角形ABC中,C=120°,b=500,
、 a=300,求c及sinA,sinB
小 结
3.余弦定理及勾股定理关系
在ABC中,
2.余弦定理的推论
cos A b2 c2 a2 , 2bc
cos B c2 a2 b2 , 2ca
cos C a2 b2 c2 。 2ab
4.余弦定理可以解决有关 三角形的问题:
若a2 b2 c2,则C为直角; (1)已知三边,求三个角;
巩
固 知
?
A
B
识
500
300
典 型
120°
C
例
题
例2:在△ABC中,已知a=2, b 2 ,
c 3 1 ,求A。
A
c 3 1
b 2
B
C
a=2
例3:在△ABC中,已知a=2, b 2 ,
c 3 1 ,解三角形。
A
c 3 1
b 2
B
C
a=2
六 、
练习1:在△ABC中,c=3,A=45°, B=75°,求a
