正余弦定理习题加答案详解超级详细
高考正弦定理和余弦定理练习题及复习资料

高考正弦定理和余弦定理练习题与答案一、选择题1.已知△中, a=c=2, A=30°, 则b=( )A. B.2C.3.D. +1答案:B解析: ∵a=c=2, ∴A=C=30°, ∴B=120°.由余弦定理可得b=2.2.△中, a= , b= , = , 则符合条件的三角形有( )A.1.B.2个C.3.D.0个答案:B解析: ∵= ,∴<b= <a= ,∴符合条件的三角形有2个.3.(2010·天津卷)在△中, 内角A, B, C的对边分别是a, b, c.若a2-b2= , =2 , 则A=( )A. 30°B. 60°C. 120°D. 150°答案:A解析: 利用正弦定理, =2 可化为c=2 b.又∵a2-b2= ,∴a2-b2= b×2 b=6b2, 即a2=7b2, a= b.在△中, === ,∴A=30°.4. (2010·湖南卷)在△中, 角A, B, C所对的边长分别为a, b, c, 若∠C=120°, c= a, 则( )A. a>bB. a<bC. a=bD. a与b的大小关系不能确定答案:A解析: 由正弦定理, 得= ,∴==>.∴A>30°.∴B=180°-120°-A<30°.∴a>b.5.如果等腰三角形的周长是底边长的5倍, 则它的顶角的余弦值为( )A..B.C..D.答案:D解析: 方法一: 设三角形的底边长为a, 则周长为5a,∴腰长为2a, 由余弦定理知α== .方法二:如图, 过点A作⊥于点D,则=2a, = , ∴= ,∴α=1-22=1-2×=.6.(2010·泉州模拟)△中, = , =1, ∠B=30°, 则△的面积等于( )A..B.C. 或.D. 或解析: ∵= ,∴=·30°=.∴C=60°或C=120°.当C=60°时, A=90°, S△=×1×= ,当C=120°时, A=30°, S△=×1× 30°= .即△的面积为或.二、填空题7. 在△中, 若b=1, c= , ∠C= , 则a=.答案:1解析: 由正弦定理= , 即= , = .又b<c, ∴B= , ∴A= .∴a=1.8.(2010·山东卷)在△中, 角A, B, C所对的边分别为a, b, c.若a = , b=2, += , 则角A的大小为.答案:解析: ∵+= ,∴(B+)=1.又0<B<π, ∴B= .由正弦定理, 知= , ∴= .又a<b, ∴A<B, ∴A= .9.(2010·课标全国卷)在△中,D为边上一点,=,∠=120°,=2.若△的面积为3-,则∠=.答案: 60°解析: S△=×2××=3- ,解得=2( -1),∴=-1, =3( -1).在△中, 2=4+( -1)2-2×2×( -1)×120°=6,在△中, 2=4+[2( -1)]2-2×2×2( -1)×60°=24-12 ,∴= ( -1),则∠=== ,∴∠=60°.三、解答题10.如图, △是等边三角形, ∠=45°, = , A.B.C三点共线.(1)求∠的值;(2)求线段的长.解: (1)∵△是等边三角形, ∠=45°,∴∠=45°+60°,∴∠=(45°+60°)=45°60°+45°60°=.(2)在△中, = ,∴=∠×=×=1+.11.(2010·全国Ⅱ卷)△中, D为边上的一点, =33, = , ∠= , 求. 解: 由∠= >0知B< ,由已知得= , ∠= ,从而∠=(∠-B)=∠-∠=×-×=.由正弦定理得= ,===25.12.(2010·安徽卷)设△是锐角三角形, a, b, c分别是内角A, B, C 所对边长, 并且2A=+2B.(1)求角A的值;(2)若·=12, a=2 , 求b, c(其中b<c).解: (1)因为2A=+2B= 2B- 2B+2B= ,所以=±.又A为锐角, 所以A= .(2)由·=12, 可得=12.①由(1)知A= , 所以=24.②由余弦定理知a2=c2+b2-2, 将a=2 与①代入, 得c2+b2=52, ③③+②×2, 得(c+b)2=100,所以c+b=10.因此c, b是一元二次方程t2-10t+24=0的两个根.解此方程并由c>b知c=6, b=4.。
完整版正弦定理余弦定理应用实例练习含答案

后,就可以计算出A 、B 两点的距离为( )课时作业3应用举例时间:45分钟 满分:100分1. 海上有A 、B 两个小岛相距10海里,从A 岛望C 岛和B 岛成 60°勺视角,从B 岛望C 岛和A 岛成75°的视角,贝J B 、C 间的距离是 ()A . 10^3海里 C . 5迈海里【答案】 D【解析】 如图,/A = 60° /B = 75° 贝JZC = 45 °, 由正弦定理得:BCAB si nA 10x sin60 BC= sinC = sin452. 如图所示,设A 、B 两点在河的两岸,一测量者在 A 所在的河岸边选定一点 C ,测出AC 的距离为50m , / ACB = 45° / CAB = 105°B . 10/6海里 D . 5^6海里课堂训练—30 =150 ° ZCBO = 45 ° AB=35 ,【答案】 A【解析】 因为ZACB = 45° ZCAB = 105°所以ZABC = 30°根 据正弦定理可知'sin%=sin 監,即爲=馬,解得AB=5072m ,选 A.3. 从某电视塔的正东方向的A 处,测得塔顶仰角是60°从电视 塔的西偏南30°的B 处,测得塔顶仰角为45° A , B 间距离是35m ,【答案】 如图所示,塔高为0C ,贝JZOAC = 60° 从OB = 180°A . 5Oj2m C . 25 辺m则此电视塔的高度是m.【解析】A设电视塔高度为hm,则OA=^h, OB= h,在△KOB中由余弦定理可得AB2= OA2+ OB2—2OA OB cos/AOB,即352=(誓h)2 + h2—2x¥hx hx (—乎)解得h= 5佰.4.如图所示,海中小岛A周围38海里内有暗礁,一船正向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛在船的南偏东45° °如果此船不改变航向,继续向南航行, 有无触礁的危险?【分析】船继续向南航行,有无触礁的危险,取决于A到直线BC的距离与38海里的大小,于是我们只要先求出AC或AB的大小,再计算出A到BC的距离,将它与38海里比较大小即可.【解析】 在△ABC 中,BC= 30,ZB= 30°,ZACB= 135°,•••zBAC = 15「「亠亠5 BC AC 卄30 AC 由正弦疋理snB ,即:sin15匸sin30/.AC = 60COS15 =°0cos(45 — 30 )=60(cos45 coS30 斗 sin45 sin30 ) = 15(V 6+V 2),•••A 到 BC 的距离为 d = ACsin45 = 15&3 + 1)〜40.98 海里 >38 海 里,所以继续向南航行,没有触礁危险.课后作业、选择题(每小题5分,共40分)1. 已知两座灯塔A 和B 与海洋观察站C 的距离相等,灯塔A 在观察站C 的北偏东40°灯塔B 在观察站C 的南偏东60°,则灯塔A 在灯塔B 的( )A .北偏东10°B .北偏西10°C .南偏东10°D .南偏西10°如图所示,/ ECA = 40° ZFCB = 60°, ZACB = 180°—40 -60 = 80 :180 ° — 80••AC= BC ,.・.ZA=/ABC = ------ 2 --- = 50°,.・.ZABG= 180 —Z CBH-ZCBA = 180°— 120°— 50°= 10°.故选 B.2. 某市在“旧城改造”工程中,计划在如下图所示的一块三角形空地上种植草皮以美化环境.已知这种草皮价格为a 元/m 2,则购买这【答案】 C1 1 1【解析】 $△= 2^ 20X 30X sin150 =十 20X 30X=150(m 2),•••购买这种草皮需要150a 元,故选C.【答案】【解析】 EGCH种草皮需要A . 450a 元C . 150a 元3. 有一长为10m 的斜坡,倾斜角为75°.在不改变坡高和坡顶的 前提下,通过加长坡面的方法将它的倾斜角改为 30。
专题11必考必刷解答题之正余弦定理(解析版)

专题11必考必刷解答题之正余弦定理1.【安徽省六安市霍邱县第一中学2019-2020学年高一下学期期末】在ABC 中,,,a b c 分别为内角,,A B C所对的边长,a b =,12cos()0B C ++=.(1)求角C 的大小; (2)求ABC 的面积. 【答案】(1)512π ;(2) (1)由内角和定理得()()cos cos cos B C A A π+=-=-, 因为12cos()0B C ++=,故1cos 2A =, 因为()0,A π∈,所以3A π=.所以根据正弦定理sin sin a bA B=得:sin sin 2b A B a===因为a b >=()0,B π∈,所以4B π=,所以()512C A B ππ=-+=. (2)由(1)得a b ==,512C π=, 所以1156sin 32sin sin 2212234ABCS ab C πππ△6321266262333222222484.2.在锐角ABC 中,角,,A B C 所对的边分别是a ,b ,c ,2222sin 6b c a bc A π⎛⎫+-=+ ⎪⎝⎭.(1)求角A 的大小;(2)求sin cos B C ⋅的取值范围. 【答案】(1)6π;(2)10,2⎛⎫ ⎪⎝⎭. 解:(1)∵2222sin 6b c a bc A π⎛⎫+-=+⎪⎝⎭,结合余弦定理,可得:cos sin 6A A π⎛⎫=+ ⎪⎝⎭,∴1cos cos 2A A A =+,∴tan A =又∵0A π<<,∴6A π=(2)因为A B C π++=,6A π=,所以56B C π+=,所以56B C π=-, 所以5sin cos sin cos 6B C C C π⎛⎫⋅=-⋅⎪⎝⎭1cos cos 2C C C ⎫=+⋅⎪⎪⎝⎭21cos cos 22C C C =+1cos 21222C C +=+⋅112cos 244C C =++ 11sin 2264C π⎛⎫=++ ⎪⎝⎭ ∵ABC 是锐角三角形,所以506202C C πππ⎧<-<⎪⎪⎨⎪<<⎪⎩,解得32C ππ<<∴,32C ππ⎛⎫∈⎪⎝⎭, ∴572,666C πππ⎛⎫+∈ ⎪⎝⎭∴11sin 2,622C π⎛⎫⎛⎫+∈- ⎪ ⎪⎝⎭⎝⎭, ∴111sin 20,2642C π⎛⎫⎛⎫++∈ ⎪ ⎪⎝⎭⎝⎭综上,sin cos B C ⋅的取值范围是10,2⎛⎫ ⎪⎝⎭3.【内蒙古赤峰市2018-2019学年高一下学期期末】在ABC 的中,角A ,B ,C 的对边分别为a b c ,,,且sin (sin sin )sin 0a A b A B c C ++-= (1)求角C ;(2)若2c =,求+a b 的取值范围.【答案】(1)23C π=;(2)2⎛ ⎝⎦. 解:(1)由sin (sin sinB)sin 0a A b A c C ++-=,及正弦定理得2220a ab b c ++-=,由余弦定理得2221cos 222a b c ab C ab ab +--===-,又0C π<<,所以23C π=; (2)由2220a ab b c ++-=及2c =,得224a ab b ++=,即2()4a b ab +-=,所以221()4()4ab a b a b =+-≤+,所以a b +≤,当且仅当a b ==成立,又2a b c +>=,所以23a b <+≤,所以+a b 的取值范围为23⎛ ⎝⎦,.4.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若2222sin sin sin sin sin 3A CB AC +-=,2c =.(1)求sin B 的值;(2)设D 在BC 边上,且2BD AD DC ==,求ABC 的面积.【答案】(1)sin 3B =;(2) (1)△ABC 中,sin 2A +sin 2C ﹣sin 2B =23sin A sin C ,由正弦定理得,a 2+c 2﹣b 2=23ac ,所以cos B =2222a c b ac+-=22ac =13;又B ∈(0,π),所以sin B =;(2)如图所示,设BD =AD =2DC =x ,由c =AB =2,利用余弦定理得,AD 2=AB 2+BD 2﹣2AB •BD •cos B , 即x 2=22+x 2﹣2×2×x ×13,解得x =3,CD =12x =32,所以△ABC 的面积为S △ABC =12AB •BC •sin B =12×2×(3+32) 5.已知ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,且()22b c b c a +-=. (1)求A 的大小;(2)若ABC 的面积等于,5b =,求sin sin B C 的值. 【答案】(1)3A π=;(2)57. 解:(1)∵222b c bc a +-=,由余弦定理得2221cos 22b c a A bc +-==,∵0A π<<,∴3A π=.(2)因为1sin 2S bc A ===, 所以20bc =,又5b =,故4c =,于是2222cos 21a b c bc A =+-=,∴a =2sin sin 3a R A π=== 所以()25sin sin 72bcB C R ==. 6.【北京市西城区2019-2020学年高一下学期期末】在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且34C π=,sin A =. (1)求sin B 的值;(2)若5c a -=ABC 的面积. 【答案】(1;(2)52.解:(1)因为34C π=,sin 5A =,所以cos 5A ==. 由已知得4B A π=-.所以sin sin sin cos cos sin 444252510B A A A πππ⎛⎫=-=-=⋅-=⎪⎝⎭. (2)由(1)知34C π=,所以sin C =且sin B =.由正弦定理得sin sin a A c C ==.又因为5c a -=,所以5c =,a =所以15sin 52102ABC S ac B ==⋅=△. 7.【北京市中国人民大学附属中学2019-2020学年高一下学期期末】在ABC 中,1b =,2c =,ABC(1)求A ∠;(2)求sin B 的值. 【答案】(1)3A π∠=或23A π∠=;(2)12或14. (1)因为1b =,2c =,ABC所以有121sin 2A ⨯⨯⨯=sin A =,因为(0,)A π∈,所以3A π∠=或23A π∠=; (2)由余弦定理可得: 当3A π=时,22212cos 1421232a b c b c A =+-⋅⋅=+-⨯⨯⨯=,所以a =由正弦定理,sin sin b a B A=,得1sin 1sin 2b A B a ===, 当23A π=时,22212cos 14212()72a b c b c A =+-⋅⋅=+-⨯⨯⨯-=,所以a =由正弦定理,sin sin b a B A=,得1sin sin b A B a ⨯===, 所以sin B 的值为12或14. 8.【北京二十中2019-2020学年高一下学期期末】在ABC 中,1a =,b =c =(1)求角B 的大小; (2)求ABC 的面积.【答案】(1)7;(2)1.(1)在ABC 中,1a =,b =c =222cos2a c b B ac +-===(2)ABC 的面积,11sin 61222S ac B ==⨯⨯=. 9.【湖北省武汉市江岸区2019-2020学年高一下学期期末】如图,某自行车手从O 点出发,沿折线O ﹣A ﹣B ﹣O 匀速骑行,其中点A 位于点O 南偏东45°且与点O 相距20千米.该车手于上午8点整到达点A ,8点20分骑至点C ,其中点C 位于点O 南偏东(45°﹣α)(其中sinα=,0°<α<90°)且与点O 相距5 千米(假设所有路面及观测点都在同一水平面上). (1)求该自行车手的骑行速度;(2)若点O 正西方向27.5千米处有个气象观测站E ,假定以点E 为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.【答案】(1)2)会进入(1)由题意知:OA=2OC =, ∠AOC=α,由于0°<α<90°,所以cos α==.在△AOC 中,由余弦定理得222222cos226 AC OC OA OC OA AOC=+-⋅⋅∠=+-⨯125=,所以AC=3=/小时).(2)如图,设直线OE与AB相交于点M.在△AOC中,由余弦定理得cos∠OAC222222210OA AC OCOC AC+-===⋅从而sin∠OAC==在△AOM中,由正弦定理得sin sinOA OMOMA OAM=∠∠,所以sin20sin(45)OA OAMOMOAM⋅∠===︒-∠,由于OE=27.5>40=OM,所以点M位于点O和点E之间,且ME=OE﹣OM=7.5.过点E作EH AB于点H,则EH为点E到直线AB的距离.在Rt△EHM中,EH=EM•sin∠EMH=EM•sin(45°﹣∠OAC)7.5 3.5==<.所以该自行车手会进入降雨区.10.【北京市一零一中学2019-2020学年高一第二学期期末】已知ABC 的角A ,B ,C 所对的边分别为a ,b ,c ,且1cos 2a C cb +=. (1)求角A 的大小;(2)若1a =,求ABC 周长l 的最大值. 【答案】(1)3A π=;(2)3.解:(1)ABC 中,∵cos 12a cC b b+=, ∴由正弦定理可得()1sin cos sin sin sin sin cos cos sin 2A C CB AC A C A C +==+=+,∴1sin cos sin 2C A C =,∴1cos 2A =. 结合()0,A π∈,可得3A π=.(2)由正弦定理得sinsin B a B A b ==,c C =,∴周长)()11sin sin 1sin sina b c B C B A B =++=++=+++⎤⎦112cos 12sin 226B B B π⎛⎫⎛⎫=++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭. ∵3A π=,∴20,3B π⎛⎫∈ ⎪⎝⎭,5,666B πππ⎛⎫+∈ ⎪⎝⎭, ∴1sin ,162B π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦,故ABC 的周长l 的最大值为3. 11.【山东省日照市2019-2020学年高一下学期期末】在①3sin 4cos a C c A =;①2sinsin 2B Cb B +=这两个条件中任选一个,补充在下面问题中.然后解答补充完整的题,在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知______,a =.(1)求sin A ;(2)如图,M 为边AC 上一点,MC MB =,2ABM π∠=,求边c .【答案】(1)45;(2.若选择条件①,则答案为:(1)在ABC 中,由正弦定理得3sin sin 4sin cos A C C A =, sin 0C ≠∴3sin 4cos A A =,两边平方可得:229sin 16cos A A =则()229sin 161sin A A =-∴225sin 16A =,sin 0A >,∴4sin 5A =. (2)设BM MC m ==易知4cos cos sin 5BMC BMA A ∠=-∠=-=-在BMC △中,由余弦定理,得22418225m m ⎛⎫=-⋅- ⎪⎝⎭,解得m 或m =去)在直角三角形ABM 中,4sin 5A =,BM =,2ABM π∠=,∴c =.若选择条件②,则答案为:(1)2sinsin 2B Cb B +=,∴2sinsin 2Ab B π-=,由正弦定理得2sin cossin sin 2Ab B A B =, sin 0B ≠,∴2cos2A A =,cos cos 222A A A = cos2A≠, ∴sin2A =, 由22sin cos 122A A ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,解得:cos =2A ± 022A π<< cos2A ∴=∴4sin 2sincos 225A A A == (2)同选择①的答案.12.【天津市滨海新区大港太平村中学2019-2020学年高一下学期期末】在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,7a =,8c =.(1)若sin C =A ;(2)若b a <,且ABC 的面积为b . 【答案】(1)3π;(2)5.(1)由已知条件可知,7a =,8c =,sin 7C =根据正弦定理可得sin sin a cA C=,∴sin 7sin 8a A c C ===, ∵a c <,∴A C <,∴π0,2A ⎛⎫∈ ⎪⎝⎭,∴π3A =.(2)因为ABC 的面积为7a =,8c =. 顶点A 到BC 的距离为h ,∴11sin 28sin 22ABC S ah ac B B ====△∴sin 14B =∴11s 14c o B ==±. ∵b a <,∴2πB <,∴11cos 14B =,由余弦定理得,2222cos b a c ac B =+-,2211782782514=+-⨯⨯⨯= ∴5b =13.【安徽省宣城市2019-2020学年高一下学期期末】已知在平面四边形ABCD 中,对角线AC 与BD 交于点E ,ADE 为正三角形,1CE =,ACD △ (1)求CD 的长; (2)若12BAC π∠=,求ABC 的面积.【答案】(1)CD =(2)94-解:(1)根据题意,如图所示:平面四边形ABCD 中,对角线AC 与BD 交于点E ,ADE 为正三角形,1CE =,ACD △ 设AD x =,则()11sin 6022ACD S x x =⋅⋅+⋅︒=△2x =或3-(负值舍去), 故2AD =.利用余弦定理:2222212cos120122122CD CE DE CE DE =+-⋅⋅⋅︒=++⨯⨯⨯,解得CD =(2)在BAD 中,33124ABD πππππ∠=---=,利用正弦定理sin sin AD AB ABD ADB =∠∠,解得AB =所以193sin2124ABC S π-=⨯=△. 14.【河北省石家庄市第二中学2019-2020学年高一下学期期末】ABC ∆的内角,,A B C 的对边分别为,,a b c ,4A π=,32a b =. (1)求sin B 的值;(2)若6a =,求ABC ∆的面积.【答案】(1)3;(2)4+ (1)因为sin sin a b A B =,32a b =,所以3sin sin 2A B =因为4A π=,所以2sin 323B =⨯=(2)因为6a =,所以4b =因为b a <,所以B A <,B 为锐角,因为sin B =cos B =所以()2sin sin sin cos cos sin 23236C A B A B A B +=+=+=+⨯=故ABC ∆的面积为112sin 644226ab C =⨯⨯⨯=+ 15.【四川省宜宾市2019-2020学年高一下学期期末】在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,向量(,)m a c b =+,(,)n c a b =-,且m n ⊥. (1)求A 的大小;(2)若ABC 为锐角三角形,且a =AD BC ⊥,AD 交BC 于D ,求AD 的取值范围.【答案】(1)4π;(2). (1)因为 m n ⊥,所以0m n ⋅=,即()()()0a c c a b b +-+=,所以222c b a +-=,由余弦定理得222cos 2c b a A bc +-==,又0A π<<,所以π4A =. (2)在ABC ∆中,由正弦定理得sin sin AB BCC BAC=∠,所以sin 4sin sin sin2BC C C AB CBAC ⋅====∠π, 因为AD BC ⊥,在Rt ABD △中,sin 4sin sin AD AB B C B ==,又34C B π+=, 所以34sin sin 4sin sin()4AD C B C C ==-π,4sin ()22C C C =+2cos sin )C C C =⋅+1cos 2cos 2CC C -=+)cos cos21)C C C -+2C C =2(sin 22)22C C =-+2sin(2)4C =-+π因为ABC 为锐角三角形,所以02C <<π,2C A π+>,因为4A π=,所以42C ππ<<,所以32444C <-<πππ,sin(2)14C <-≤π,所以2AD ≤ 所以AD的取值范围.16.【黑龙江省佳木斯市第二中学2019-2020学年高一下学期期末】在ABC 中,三个内角的对边分别为a ,b ,c,cos 10A =sin sin sin sin 5a A b B c C a B +-=.()1求B 的值;()2设10b =,求ABC 的面积S .【答案】(1);(2)60.【解析】(1)sin sin sinC sin 5a Ab Bc a B +-=,∴222a b c +-=.∴222cos 2a b c C ab +-==. 又A B C 、、是ABC ∆的内角,∴sin A C ==()cos cos cos sin sin1051052A C A C A C +=-=-=-又A B C 、、是ABC ∆的内角,∴0A C π<+<, ∴34A C π+=. ∴()4B AC ππ=-+=.(2)sin sin c bC B =,∴sin sin bc C B=⨯=∴ABC ∆的面积11sin 10602210S bc A ==⨯⨯=17.【山东省日照市青山学校2017-2018学年高一下学期期末】已知函数()()sin 0? 2f x M x M ,πωϕϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示.(1)求函数()f x 的解析式;(2)在ABC 中,角 A B C ,,的对边分别是 a b c ,,,若()2cos cos a c B b C -=,求2A f ⎛⎫⎪⎝⎭的取值范围. 【答案】(1)()sin 26f x x π⎛⎫=+ ⎪⎝⎭;(2)1 1?22A f ⎛⎫⎛⎤∈ ⎪ ⎥⎝⎭⎝⎦,. 【解析】(1)由图象知A 1=,5ππT 4π,ω2126⎛⎫=-==⎪⎝⎭, 将点π,16⎛⎫ ⎪⎝⎭代入解析式得πsin φ13⎛⎫+= ⎪⎝⎭,因为πφ2<,所以πφ6=,所以()πf x sin 2x 6⎛⎫=+ ⎪⎝⎭. (2)由()2a c cosB bcosC -=得:()2sinA sinC cosB sinBcosC -=,所以()2sinAcosB sin B C =+,2sinAcosB sinA =,因为()A 0π∈,,所以sinA 0≠,所以1cosB 2=,πB 3=,2πAC 3+=, A πf sin A 26⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,2π0A 3<<,ππ5πA 666<+<,所以π1sin A 162⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦,, 所以A 1f 122⎛⎫⎛⎤∈⎪ ⎥⎝⎭⎝⎦,. 18.【四川省广安市2018-2019学年高一下学期期末】在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c 且sin cos 6a B b A π⎛⎫=- ⎪⎝⎭.(1)求角A 的大小;(2)若a =3b c +=,求ABC 的面积.【答案】(1)3A π=(2)2(1)由正弦定理得sin sin sin cos 6A B B A π⎛⎫=- ⎪⎝⎭, ∵sin 0B >, ∴sin cos cos cos sin sin 666A A A A πππ⎛⎫=-=+ ⎪⎝⎭, 即cos cossin sin066A A ππ-=,∴cos 06A π⎛⎫+= ⎪⎝⎭又∵0A π<<,∴3A π=.(2)∵222cos 2b c a A bc+-=∴22()29231222b c bc a bc bc bc +----==.∴2bc =,∴ 1sin 2ABC S bc A ==△ 19.【河北省保定市2017-2018学年高一下学期期末调研】在ABC ∆中,3B π=,点D 在边AB 上,1BD =,且DA DC =.(1)若BCD ∆CD ;(2)设DCA θ∠=,若AC θ.【答案】(1)2cos CD θ=;(2)6πθ=或18πθ=.解法一:(1)因为BCD S ∆=1sin 2BC BD B ⋅⋅=又因为3B π=,1BD =,所以4BC =.在BDC ∆中,由余弦定理得,2222cos CD BC BD BC BD B =+-⋅⋅即21161241132CD =+-⨯⨯⨯=,解得CD = (2)在ACD ∆中,DA DC =,因为A DCA θ∠=∠=,则2ADC πθ∠=-,又AC =,由正弦定理,有sin 2sin AC CDθθ=,所以2cos CD θ=. 在BDC ∆中,2BDC θ∠=,223BCD πθ∠=-, 由正弦定理得,sin sin CD BD B BCD =∠,即12cos 2sin sin 233θππθ=⎛⎫- ⎪⎝⎭,化简得2cos sin 23πθθ⎛⎫=-⎪⎝⎭因为02πθ<<,所以2sin sin 223ππθθ⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭022ππθ<-<,222333πππθ-<-<, 所以2223θθππ-=-或2223ππθθπ-+-=, 解得6πθ=或18πθ=.解法二:(1)同解法一.(2)证明:因为DA DC =,所以A DCA ∠=∠. 取AC 中点E ,连结DE , 所以DE AC ⊥.设DCA A θ∠=∠=,因为AC EA EC ==.在Rt CDE ∆中,cos CE CD DCA =∠ 以下同解法一.20.【四川省广元市2019-2020学年高一(下)期末】在ABC ∆中,角A,B,C ,的对应边分别为,,a b c ,且2cos cos a c Cb B-=. (①)求角B 的大小;(①)若ABC ∆a c +=,D 为AC 的中点,求BD 的长. 【答案】(I )3B π=;(II)3BD =(I )2cos cos a c C b B -=,由正弦定理得2sin sin cos sin cos A C C B B-= 整理得2sin cos sin cos cos sin sin()A B B C B C B C =+=+B C A π+=-,则2sin cos sin A B A =(0,)A π∈,sin 0A ∴≠1cos 2B ∴=(0,)B π∈,3B π∴=.(II)1sin 23ac π=4ac ∴= 1()2BD BA BC =+,两边平方得2221(2)4BD BA BC BA BC =++⋅ 222211||()[()]944BD a c ac a c ac ∴=++=+-= 3BD ∴=21.【广东省深圳市红岭中学2019-2020学年高一下学期第二学段期末】如图,在平面四边形ABCD 中,AB AD ⊥,1AB =,AD =BC =(1)若1CD =ABCD 的面积;(2)若sin BCD ∠=0,2ADC π⎛⎫∠∈ ⎪⎝⎭,求sin ADC ∠.【答案】(1)12+2)410+ 解:(1)连接BD ,在Rt △ABD 中,由勾股定理得:2224BD AB AD =+=,所以2BD =,在BCD 中,由余弦定理知:222cos 2BC CD BD C BC CD +-==⋅, 因为()0,C π∈,所以4Cπ,所以12ABD S AB AD =⋅=11sin 22ABD S BC CD C +=⋅⋅=,所以ABCD 的面积12ABD BCD S S S =+=+(2)在BCD 中,由正弦定理知:sin sin BC BD BDC BCD=∠∠, 所以sin 3sin 5BC BCD BDC BD ⋅∠∠==. 因为0,2ADC π⎛⎫∠∈ ⎪⎝⎭, 所以0,2BDC π⎛⎫∠∈ ⎪⎝⎭,4cos 5BDC ∠=.在Rt △ABD 中,tan AB ADB AD ∠== 所以6ADB π∠=,所以341sin sin 6552ADC BDC π⎛⎫∠=∠+=+⨯= ⎪⎝⎭. 22.【广东省佛山市南海区2019-2020学年高一下学期期末】在ABC 中,已知45A =︒,D 是AC 上一点,6DC =,14BC =,120BDC ∠=︒.(1)求BD 的长;(2)求ABD △的面积.【答案】(1) 10BD =;(2. (1)在BDC 中,由余弦定理得:2222cos BC DC DB DC DB BDC =+-⋅⋅∠,化简得:261600BD BD +-=,解得 10BD =或16-(舍去); (2)在ABD △中,由120BDC ∠=︒,得60BDA ∠=︒,由正弦定理得sin sin BD AB A BDA=∠∠,解得AB = 又()()sin sin 18sin 0ABD BAD BDA BAD BDA ∠=∠-∠=∠+∠︒-,()sin 6sin 645045cos 0cos 45sin 60︒︒︒︒+=︒=+=︒,所以ABD △的面积175sin 22ABD S BA BD ABD +=⋅⋅∠= 23.【广东省云浮市2019-2020学年高一下学期期末】在①ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知b sin(A +C )=a sin C ,且a=2c.(1)求sin B ;(2)若①ABC 的面积为①ABC 的周长.【答案】(1(2) (1)因为b sin(A +C )=a sin C ,所以b 2=ac.因为a=2c ,所以cos B=222-2a c b ac +=22-ac 2a c ac+=22224-24c c c c +=34,因为0<B<π,所以sin .(2)因为△ABC 的面积为12ac sin B=4c 2=4c=4. 因为a=2c ,所以a=8.因为b 2=ac=32,所以b=故△ABC 的周长为a +b +c= 24.【湖南省长沙市雨花区2018-2019学年高一下学期期末】在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,向量()()sin sin ,sin sin ,sin sin ,sin m B C A B n B C A =++=-,且m n ⊥.(1)求角C 的大小;(2)若c =2a b +的取值范围.【答案】(1)2C 3π=;(2). (1)∵m n ⊥∴0m n ⋅=∴22sin sin (sin sin )sin 0B C A B B -++=∴222c a b ab =++ ∴1cos 2C =- 又()0,C π∈ . ∴23C π=.(2)∵23C π=,c = ∴△ABC 外接圆直径2R=2∴24sin 2sin a b A B +=+4sin 2sin 3A A π⎛⎫=+- ⎪⎝⎭4sin sin A A A =-3sin A A =6A π⎛⎫=+ ⎪⎝⎭ ∵0,3A π⎛⎫∈ ⎪⎝⎭ ∴,662A πππ⎛⎫+∈ ⎪⎝⎭∴1sin ,162A π⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭∴2a b + 的取值范围是 . 25.【云南省昆明市2019-2020学年高一下学期期末质量检测】ABC 的角A ,B ,C 的对边分别为a ,b ,c ,已知sin a b A =.(1)求B ;(2)若2c =,a =D 是AC 边上异于A 的点,且2BD =,求BCD 的面积.【答案】(1)90;(2 (1)在ABC 中,sin a b A =,由正弦定理得sin sin sin A A B =,因为sin 0A >,所以sin 1B =,因为0B π<<,所以90B =.(2)在ABC 中,3b =,cos C =, 在BCD 中,由余弦定理得2222cos BD BC CD BC CD C =+-⋅,所以245CD CD =+-,即231030CD CD -+=,解得13CD =或3CD =. 因为D 不与A 重合,所以13CD =,所以BCD 的面积111sin 2239S BC CD C =⋅==.。
高考数学《正弦定理、余弦定理及解三角形》真题练习含答案

高考数学《正弦定理、余弦定理及解三角形》真题练习含答案一、选择题1.设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,若a =2 ,b =3 ,B =π3,则A =( )A .π6B .56 πC .π4D .π4 或34 π答案:C解析:由正弦定理得a sin A =b sin B ,∴sin A =a sin B b =2×323=22 ,又a <b ,∴A为锐角,∴A =π4.2.在△ABC 中,b =40,c =20,C =60°,则此三角形解的情况是( ) A .有一解 B .有两解C .无解D .有解但解的个数不确定 答案:C解析:由正弦定理b sin B =c sin C ,∴sin B =b sin Cc =40×3220 =3 >1,∴角B 不存在,即满足条件的三角形不存在.3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =2,b =3,c =7 ,则角C =( )A .π6B .π4C .π3D .π2答案:C解析:由余弦定理得c 2=a 2+b 2-2ab cos C ,得cos C =a 2+b 2-c 22ab =4+9-72×2×3 =12,又C 为△ABC 内角,∴C =π3 .4.已知△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若a 2=b 2+c 2-bc ,bc =4,则△ABC 的面积为( )A .12 B .1 C .3 D .2答案:C解析:由余弦定理得a 2=b 2+c 2-2bc cos A ,又a 2=b 2+c 2-bc ,∴2cos A =1,cos A =12 ,∴sin A =1-cos 2A =32 ,∴S △ABC =12 bc sin A =12 ×4×32=3 . 5.在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边.若b sin A =3c sin B ,a =3,cos B =23,则b =( )A.14 B .6 C .14 D .6 答案:D解析:∵b sin A =3c sin B ,由正弦定理得ab =3bc ,∴a =3c ,又a =3,∴c =1,由余弦定理得b 2=a 2+c 2-2ac ·cos B =9+1-2×3×23=6,∴b =6 .6.设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .不确定 答案:B解析:∵b cos C +c cos B =a sin A ,∴sin B cos C +sin C cos B =sin 2A ,∴sin A =1,又A 为△ABC 的内角,∴A =90°,∴△ABC 为直角三角形.7.钝角三角形ABC 的面积是12,AB =1,BC =2 ,则AC =( )A .5B .5C .2D .1 答案:B解析:∵S △ABC =12 AB ×BC ×sin B =22 sin B =12 ,∴sin B =22,若B =45°,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC ·cos 45°=1+2-2×2 ×22 =1,则AC =1,则AB 2+AC 2=BC 2,△ABC 为直角三角形,不合题意;当B =135°时,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos 135°=1+2+2×2 ×22=5,∴AC =5 .8.如图,设A ,B 两点在河的两岸,一测量者在A 所在的同侧河岸边选定一点C ,测出AC 的距离为50 m ,∠ACB =45°,∠CAB =105°后,就可以计算出A ,B 两点的距离为( )A .502 mB .503 mC .252 mD .2522m答案:A解析:由正弦定理得AC sin B =ABsin C,∴AB =AC ·sin Csin B =50×22sin (180°-45°-105°) =502 .9.[2024·全国甲卷(理)]记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知B =60°,b 2=94ac ,则sin A +sin C =( )A .32 B .2C .72D .32答案:C解析:∵b 2=94 ac ,∴由正弦定理可得sin 2B =94sin A sin C .∵B =60°,∴sin B =32 ,∴34 =94 sin A sin C ,∴sin A sin C =13.由余弦定理可得b 2=a 2+c 2-2ac cos B =a 2+c 2-ac ,将b 2=94 ac 代入整理得,a 2+c 2=134ac ,∴由正弦定理得sin 2A +sin 2C =134 sin A sin C ,则(sin A +sin C )2=sin 2A +sin 2C +2sin A sin C =134 sin A sin C+2sin A sin C =214 sin A sin C =214 ×13 =74 ,∴sin A +sin C =72 或-72(舍).故选C.二、填空题10.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若(a +b +c )(a -b +c )=ac ,则B =________.答案:23π解析:由(a +b +c )(a -b +c )=ac 得a 2+c 2-b 2+ac =0.由余弦定理得cos B =a 2+c 2-b 22ac =-12 ,又B 为△ABC 的内角,∴B =23π.11.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且c =a cos B ,①则A =________;②若sin C =13,则cos (π+B )=________.答案:①90° ②-13解析:①∵c =a ·cos B ,∴c =a ·a 2+c 2-b 22ac,得a 2=b 2+c 2,∴∠A =90°;②∵cos B =cos (π-A -C )=sin C =13 .∴cos (π+B )=-cos B =-sin C =-13 .12.[2023·全国甲卷(理)]在△ABC 中,∠BAC =60°,AB =2,BC =6 ,∠BAC 的角平分线交BC 于D ,则AD =________.答案:2 解析:方法一 由余弦定理得cos 60°=AC 2+4-62×2AC ,整理得AC 2-2AC -2=0,得AC=1+3 .又S △ABC =S △ABD +S △ACD ,所以12 ×2AC sin 60°=12 ×2AD sin 30°+12 AC ×AD sin30°,所以AD =23AC AC +2 =23×(1+3)3+3=2.方法二 由角平分线定理得BD AB =CD AC ,又BD +CD =6 ,所以BD =26AC +2,CD =6AC AC +2 .由角平分线长公式得AD 2=AB ×AC -BD ×CD =2AC -12AC(AC +2)2 ,又由方法一知AC =1+3 ,所以AD 2=2+23 -12×(1+3)(3+3)2=2+23 -(23 -2)=4,所以AD =2.[能力提升]13.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,a =8,b <4,c =7,且满足(2a -b )cos C =c ·cos B ,则下列结论正确的是( )A .C =60°B .△ABC 的面积为63 C .b =2D .△ABC 为锐角三角形 答案:AB解析:∵(2a -b )cos C =c cos B ,∴(2sin A -sin B )cos C =sin C cos B ,∴2sin A cos C =sin B cos C +cos B sin C ,即2sin A cos C =sin (B +C ),∴2sin A cos C =sin A .∵在△ABC 中,sin A ≠0,∴cos C =12 ,∴C =60°,A 正确.由余弦定理,得c 2=a 2+b 2-2ab cos C ,得49=64+b 2-2×8b cos 60°,即b 2-8b +15=0,解得b =3或b =5,又b <4,∴b =3,C 错误.∴△ABC 的面积S =12 ab sin C =12 ×8×3×32 =63 ,B 正确.又cos A =b 2+c 2-a 22bc=9+49-642×3×7<0,∴A 为钝角,△ABC 为钝角三角形,D 错误. 14.[2023·全国甲卷(理)]已知四棱锥P ABCD 的底面是边长为4的正方形,PC =PD =3,∠PCA =45°,则△PBC 面积为( )A .22B .32C .42D .62 答案:C解析:如图,过点P 作PO ⊥平面ABCD ,垂足为O ,取DC 的中点M ,AB 的中点N ,连接PM ,MN ,AO ,BO .由PC =PD ,得PM ⊥DC ,又PO ⊥DC ,PO ∩PM =P ,所以DC ⊥平面POM ,又OM ⊂平面POM ,所以DC ⊥OM .在正方形ABCD 中,DC ⊥NM ,所以M ,N ,O 三点共线,所以OA =OB ,所以Rt △P AO ≌Rt △PBO ,所以PB =P A .在△P AC 中,由余弦定理,得P A =PC 2+AC 2-2PC ·AC cos 45° =17 ,所以PB =17 .在△PBC 中,由余弦定理,得cos ∠PCB =PC 2+BC 2-BP 22PC ·BC =13 ,所以sin ∠PCB =223 ,所以S △PBC =12 PC ·BCsin ∠PCB =42 ,故选C.15.[2022·全国甲卷(理),16]已知△ABC 中,点D 在边BC 上,∠ADB =120°,AD =2,CD =2BD .当ACAB取得最小值时,BD =________.答案:3 -1解析:以D 为坐标原点,DC 所在的直线为x 轴,DC →的方向为x 轴的正方向,过点D 且垂直于DC 的直线为y 轴,建立平面直角坐标系(图略),易知点A 位于第一象限.由AD =2,∠ADB =120°,得A (1,3 ).因为CD =2BD ,所以设B (-x ,0),x >0,则C (2x ,0).所以AC=(2x -1)2+(0-3)2=4x 2-4x +4,AB =(-x -1)2+(0-3)2=x 2+2x +4 ,所以⎝⎛⎭⎫AC AB 2=4x 2-4x +4x 2+2x +4.令f (x )=4x 2-4x +4x 2+2x +4,x >0,则f ′(x )=(4x 2-4x +4)′(x 2+2x +4)-(4x 2-4x +4)(x 2+2x +4)′(x 2+2x +4)2=(8x -4)(x 2+2x +4)-(4x 2-4x +4)(2x +2)(x 2+2x +4)2=12(x 2+2x -2)(x 2+2x +4)2 .令x 2+2x -2=0,解得x =-1-3 (舍去)或x =3 -1.当0<x <3 -1时,f ′(x )<0,所以f (x )在(0,3 -1)上单调递减;当x >3 -1时,f ′(x )>0,所以f (x )在(3 -1,+∞)上单调递增.所以当x =3 -1时,f (x )取得最小值,即ACAB 取得最小值,此时BD =3 -1.16.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为S ,且6S =(a +b )2-c 2,则tan C =________.答案:125解析:由余弦定理得2ab cos C =a 2+b 2-c 2,又6S =(a +b )2-c 2,所以6×12 ab sin C =(a +b )2-c 2=a 2+b 2-c 2+2ab =2ab cos C +2ab ,化简得3sin C =2cos C +2,结合sin 2C +cos 2C =1,解得sin C =1213 ,cos C =513 ,所以tan C =125.。
高考数学复习、高中数学 正弦定理和余弦定理附答案解析

第6节 正弦定理和余弦定理课标要求:借助向量的运算,探索三角形边长与角度的关系,掌握余弦定理、正弦定理.知 识 梳 理1.正弦定理____=____=____=2R ,其中R 是三角形外接圆的半径.2.余弦定理a 2=________________,b 2=________________,c 2=________________.3.在△ABC 中,a =b cos C +c cos B ,b =__________,c =__________.(此定理称作“射影定理”,亦称第一余弦定理)4.三角形面积公式S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R 、r .5.在△ABC 中,已知a ,b 和A 时,解的情况如下:[1.由正弦定理可以变形为:(1)a :b :c =_______:_______:_______;(2)a =2R sin A ,b =2R sin B ,c =__________;(3)sin A =a 2R ,sin B =b 2R,sin C =______等形式,以解决不同的三角形问题. 2.余弦定理可以变形为:cos A =b 2+c 2-a 22bc,cos B =______________,cos C =______________. 3. S △ABC =abc 4R =12(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R 、r .基 础 自 测1.判断下列说法是否正确(请在括号中打“√”或“×”).(1)在△ABC 中,A >B 必有sin A >sin B . ( )(2)在△ABC 中,若b 2+c 2>a 2,则△ABC 为锐角三角形. ( )(3)在△ABC 中,若A =60°,a =43,b =42,则∠B =45°或∠B =135°. ( )(4)若满足条件C =60°,AB =3,BC =a 的△ABC 有两个,则实数a 的取值范围是(3,2).( )(5)在△ABC 中,若a cos B =b cos A ,则△ABC 是等腰三角形. ( )(6)在△ABC 中,若tan A =a 2,tan B =b 2,则△ABC 是等腰三角形. ( )2.在△ABC 中中,如果4:3:2sin :sin :sin =C B A ,那么=C cos .3.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a =5,c =2,cos A =23,则b =( ). A. 2 B. 3 C .2 D .34.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,cos2A =sin A ,bc =2,则△ABC 的面积为( ).A.12B.14C .1D .2 5.在ABC △中,角A B C ,,所对的边分别为a b c ,,,若bc a c b c b a 3))((=-+++,则=A .6.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B =a cos C +c cos A ,则B =________.考点1应用正弦、余弦定理解三角形【例1】已知△ABC 的面积为S ,且22BC CA CB S =⋅+. (1)求B 的大小; (2)若12S =,且1BC BA -=,试求△ABC 最长边的长度.[规律方法]破解平面向量与“三角”相交汇题的常用方法是“化简转化法”,即先活用诱导公式、同角三角函数的基本关系式、倍角公式、辅助角公式等对三角函数进行巧“化简”;然后把以向量共线、向量垂直形式出现的条件转化为“对应坐标乘积之间的关系”;再活用正、余弦定理,对三角形的边、角进行互化.【训练1】(1)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.(2)在△ABC 中,cos C 2=55,BC =1,AC =5,则AB =( ). A .42 B.30 C.29 D .25考点2三角形解得个数问题【例2】在△ABC 中,如果A =60°,c =4,a =______个解.[规律方法]解三角形问题首先要判断是否会出现多解或无解的情况:对于“已知两角与任一边,求其他两边和一角”的题型不可能有多个解,也不可能无解;对于“已知两边与其中一边的对角,求另一边的对角(从而进一步求出其他边和角)”的题型,可能出现多解或无解的情况. 验证解的情况可用数形结合法.【训练2】在△ABC 中, c b a ,,分别是△ABC 中角C B A ,,的对边,若︒===45,2,B b x a ,且此三角形有两解,则x 的取值范围( ).A .2B .52C .1D .考点3利用正弦、余弦定理判定三角形的【例3】1.若△ABC 中,满足222sin sin sin C A B =+,则该三角形的形状是 三角形.2在△ABC 中,角,,A B C 的对边分别为,,a b c ,若,,a b c 成等比数列,且3B π=,则△ABC的形状为 三角形.[规律方法]常见的三角变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”,这是使问题获得解决的突破口.【训练3】在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,若c -a cos B =(2a -b )cos A ,则△ABC 的形状为( ).A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形考点4与三角形面积有关的问题【例4】 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且∠A =π3,c =37a . (1)求sin C 的值; (2)若a =7,求△ABC 的面积.[规律方法]高考中主要涉及利用正弦、余弦定理求三角形的边长、角、面积等基本计算,或将两个定理与三角恒等变换相结合综合解三角形.【训练4】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b sin C +c sin B =4a sin B sin C ,b 2+c 2-a 2=8,则△ABC 的面积为________.[思维升华](1)在解三角形中,如果表达式中含有角的余弦或边的二次式时,则优先考虑使用余弦定理。
(完整版)正余弦定理及解三角形整理(有答案)

正余弦定理考点梳理:1.直角三角形中各元素间的关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
(1)三边之间的关系:a 2+b 2=c 2。
(勾股定理) A(2)锐角之间的关系:A +B =90°; c (3)边角之间的关系:(锐角三角函数定义) b sin A =cos B =,cos A =sin B =,tan A =。
C B c a c b ba2.2.斜三角形中各元素间的关系: a如图6-29,在△ABC 中,A 、B 、C 为其内角,a 、b 、c 分别表示A 、B 、C 的对边。
(1)三角形内角和:A +B +C =_____(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
(R 为外接圆半径)R CcB b A a 2sin sin sin ===3.正弦定理:===2R 的常见变形:asin A b sin B csin C (1)sin A ∶sin B ∶sin C =a ∶b ∶c ;(2)====2R ;a sin Ab sin B csin C a +b +csin A +sin B +sin C (3)a =2R sin_A ,b =2R sin_B ,c =2R sin_C ;(4)sin A =,sin B =,sin C =.a 2Rb 2R c2R 4.三角形面积公式:S =ab sin C =bc sin A =ca sin B .1212125.余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
余弦定理的公式: 或.2222222222cos 2cos 2cos a b c bc A b a c ac B c b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩6.(1)两类正弦定理解三角形的问题:1、已知两角和任意一边,求其他的两边及一角. 2、已知两边和其中一边的对角,求其他边角. (2)两类余弦定理解三角形的问题:1、已知三边求三角.2、已知两边和他们的夹角,求第三边和其他两角.7.判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式.8.解题中利用中,以及由此推得的一些基本关系式进行三角变换ABC ∆A B C π++=的运算,如:sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-.sincos ,cos sin ,tan cot222222A B C A B C AB C+++===9. 解斜三角形的主要依据是:设△ABC 的三边为a 、b 、c ,对应的三个角为A 、B 、C 。
(完整版)正余弦典型例题及详细答案
正余弦典型例题及详细答案一、解答题(题型注释)1(1(2【答案】(2【解析】试题分析:(1;(2)利用(1),值.试题解析:(1(2考点:正余弦定理的综合应用及面积公式。
2,(1(2【答案】((2【解析】试题分析:(1)利用正弦定理,(2试题解析:(1(2=”考点:解三角形,正余弦定理,基本不等式.3(1(2【答案】(1(2【解析】试题分析:(1)等差数列再由正弦定理6sin(3045)4+=+=,再由正弦定理2245sin60sin7526224b a==⇒=+,,则11sin2(22ABCS ac B∆==⨯2分sin 6032A =4分 120,∴6分 675sin(3045)4+=+=分 245sin 60sin 752322b a b==⇒=2(31)6(31)b -=-,, 10分12分4.已知A 、B 、C 为三角形ABC 的三内角,其对应边分别为a ,b ,c,若有2acosC=2b+c 成立. (1)求A 的大小;(2)ABC 的面积. 【答案】(1(2【解析】 试题分析:(1)A 的余弦值,从而求出角A ;(2,,再结合上题中求得的角A试题解析:(1(2)考点:正弦定理,余弦定理,三角形两边一夹角的面积公式,化归与转化的数学思想.。
正弦定理和余弦定理知识点讲解+例题讲解(含解析)

导数的概念及运算一、知识梳理1.正、余弦定理在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则2.S △ABC =2ab sin C =2bc sin A =2ac sin B =4R =2(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R ,r .3.在△ABC 中,已知a ,b 和A 时,解的情况如下:4.三角形中的三角函数关系(1)sin(A +B )=sin C ;(2)cos(A +B )=-cos C ; (3)sin A +B 2=cos C 2;(4)cos A +B 2=sin C2.5.三角形中的射影定理在△ABC 中,a =b cos C +c cos B ;b =a cos C +c cos A ;c =b cos A +a cos B . 3.在△ABC 中,两边之和大于第三边,两边之差小于第三边, A >B ⇔a >b ⇔sin A >sin B ⇔cos A <cos B .二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)三角形中三边之比等于相应的三个内角之比.( ) (2)在△ABC 中,若sin A >sin B ,则A >B .( )(3)在△ABC 的六个元素中,已知任意三个元素可求其他元素.( )(4)当b 2+c 2-a 2>0时,△ABC 为锐角三角形;当b 2+c 2-a 2=0时,△ABC 为直角三角形;当b 2+c 2-a 2<0时,△ABC 为钝角三角形.( ) 解析 (1)三角形中三边之比等于相应的三个内角的正弦值之比. (3)已知三角时,不可求三边.(4)当b 2+c 2-a 2>0时,三角形ABC 不一定为锐角三角形. 答案 (1)× (2)√ (3)× (4)×2.在△ABC 中,AB =5,AC =3,BC =7,则∠BAC =( ) A.π6B.π3C.2π3D.5π6解析 在△ABC 中,设AB =c =5,AC =b =3,BC =a =7,由余弦定理得cos ∠BAC =b 2+c 2-a 22bc =9+25-4930=-12,由A ∈(0,π),得A =2π3,即∠BAC =23π. 答案 C3.在△ABC 中,a cos A =b cos B ,则这个三角形的形状为________. 解析 由正弦定理,得sin A cos A =sin B cos B , 即sin 2A =sin 2B ,所以2A =2B 或2A =π-2B , 即A =B 或A +B =π2,所以这个三角形为等腰三角形或直角三角形. 答案 等腰三角形或直角三角形4.(2018·烟台质检)已知△ABC 中,A =π6,B =π4,a =1,则b 等于( ) A.2B.1C. 3D.2解析 由正弦定理a sin A =b sin B ,得1sin π6=bsin π4,∴112=b22,∴b = 2.答案 D5.(2018·全国Ⅱ卷)在△ABC 中,cos C 2=55,BC =1,AC =5,则AB =( ) A.4 2B.30C.29D.25解析 由题意得cos C =2cos 2 C 2-1=2×⎝ ⎛⎭⎪⎫552-1=-35.在△ABC 中,由余弦定理得AB 2=AC 2+BC 2-2AC ×BC ×cos C =52+12-2×5×1×⎝ ⎛⎭⎪⎫-35=32,所以AB =4 2.答案 A6.(2019·荆州一模)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =22,cos A =34,sin B =2sin C ,则△ABC 的面积是________. 解析 由sin B =2sin C ,cos A =34,A 为△ABC 一内角, 可得b =2c ,sin A =1-cos 2A =74, ∴由a 2=b 2+c 2-2bc cos A , 可得8=4c 2+c 2-3c 2, 解得c =2(舍负),则b =4.∴S △ABC =12bc sin A =12×2×4×74=7. 答案 7考点一 利用正、余弦定理解三角形【例1】 (1)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.(2)(2019·枣庄二模)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若 (a +b )(sin A -sin B )=(c -b )sin C ,则A =( ) A.π6 B.π3 C.5π6 D.2π3(3)(2018·全国Ⅲ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为a 2+b 2-c 24,则C =( )A.π2B.π3C.π4D.π6解析 (1)由正弦定理,得sin B =b sin C c =6×323=22, 结合b <c 得B =45°,则A =180°-B -C =75°. (2)∵(a +b )(sin A -sin B )=(c -b )sin C ,∴由正弦定理得(a +b )(a -b )=c (c -b ),即b 2+c 2-a 2=bc . 所以cos A =b 2+c 2-a 22bc =12,又A ∈(0,π),所以A =π3.(3)因为a 2+b 2-c 2=2ab cos C ,且S △ABC =a 2+b 2-c24,所以S △ABC =2ab cos C 4=12ab sin C ,所以tan C =1.又C ∈(0,π),故C =π4. 答案 (1)75° (2)B (3)C【训练1】 (1)(2017·全国Ⅰ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin B +sin A (sin C -cos C )=0,a =2,c =2,则C =( ) A.π12B.π6C.π4D.π3(2)(2019·北京海淀区二模)在△ABC 中,A ,B ,C 的对边分别为a ,b ,c .若2cos 2A +B2-cos 2C =1,4sin B =3sin A ,a -b =1,则c 的值为( )A.13B.7C.37D.6(3)在△ABC 中,已知a =2,b =6,A =45°,则满足条件的三角形有( ) A.1个 B.2个 C.0个 D.无法确定解析 (1)由题意得sin(A +C )+sin A (sin C -cos C )=0, ∴sin A cos C +cos A sin C +sin A sin C -sin A cos C =0,则sin C (sin A +cos A )=2sin C sin ⎝ ⎛⎭⎪⎫A +π4=0,因为C ∈(0,π),所以sin C ≠0,所以sin ⎝ ⎛⎭⎪⎫A +π4=0,又因为A ∈(0,π),所以A +π4=π,所以A =3π4.由正弦定理a sin A =c sin C ,得2sin 3π4=2sin C ,则sin C =12,又C ∈(0,π),得C =π6.(2)由2cos 2A +B 2-cos 2C =1,可得2cos 2A +B 2-1-cos 2C =0,则有cos 2C +cos C =0,即2cos 2C +cos C -1=0,解得cos C =12或cos C =-1(舍),由4sin B =3sin A ,得4b =3a ,① 又a -b =1,②联立①,②得a =4,b =3, 所以c 2=a 2+b 2-2ab cos C =16+9-12=13,则c =13.(3)∵b sin A =6×22=3,∴b sin A <a <b . ∴满足条件的三角形有2个. 答案 (1)B (2)A (3)B 考点二 判断三角形的形状【例2】 (1)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若cb <cos A ,则△ABC 为( ) A.钝角三角形 B.直角三角形 C.锐角三角形D.等边三角形(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若b cos C+c cos B=a sin A,则△ABC的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.不确定解析(1)由cb<cos A,得sin Csin B<cos A,又B∈(0,π),所以sin B>0,所以sin C<sin B cos A,即sin(A+B)<sin B cos A,所以sin A cos B<0,因为在三角形中sin A>0,所以cos B<0,即B为钝角,所以△ABC为钝角三角形.(2)由正弦定理得sin B cos C+sin C cos B=sin2A,∴sin(B+C)=sin2A,即sin A=sin2A.∵A∈(0,π),∴sin A>0,∴sin A=1,即A=π2,∴△ABC为直角三角形.答案(1)A(2)B【训练2】若将本例(2)中条件变为“c-a cos B=(2a-b)cos A”,判断△ABC的形状.解∵c-a cos B=(2a-b)cos A,C=π-(A+B),∴由正弦定理得sin C-sin A cos B=2sin A cos A-sin B cos A,∴sin A cos B+cos A sin B-sin A cos B=2sin A cos A-sin B cos A,∴cos A(sin B-sin A)=0,∴cos A=0或sin B=sin A,∴A=π2或B=A或B=π-A(舍去),∴△ABC为等腰或直角三角形.考点三 和三角形面积、周长有关的问题 角度1 与三角形面积有关的问题【例3-1】 (2017·全国Ⅲ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin A +3cos A =0,a =27,b =2. (1)求c ;(2)设D 为BC 边上一点,且AD ⊥AC ,求△ABD 的面积. 解 (1)由sin A +3cos A =0及cos A ≠0, 得tan A =-3,又0<A <π,所以A =2π3.由余弦定理,得28=4+c 2-4c ·cos 2π3.即c 2+2c -24=0,解得c =-6(舍去),c =4.(2)由题设可得∠CAD =π2,所以∠BAD =∠BAC -∠CAD =π6. 故△ABD 与△ACD 面积的比值为12AB ·AD sin π612AC ·AD=1.又△ABC 的面积为12×4×2sin ∠BAC =23,所以△ABD 的面积为 3. 角度2 与三角形周长有关的问题【例3-2】 (2018·上海嘉定区模拟)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足a sin B =3b cos A .若a =4,则△ABC 周长的最大值为________. 解析 由正弦定理a sin A =bsin B ,可将a sin B =3b cos A 转化为sin A sin B =3sin B cos A . 又在△ABC 中,sin B >0,∴sin A =3cos A , 即tan A = 3. ∵0<A <π,∴A =π3.由余弦定理得a 2=16=b 2+c 2-2bc cos A =(b +c )2-3bc ≥(b +c )2-3⎝⎛⎭⎪⎫b +c 22,则(b+c)2≤64,即b+c≤8(当且仅当b=c=4时等号成立),∴△ABC周长=a+b+c=4+b+c≤12,即最大值为12.答案12【训练3】(2019·潍坊一模)△ABC的内角A,B,C的对边分别为a,b,c,已知(a+2c)cos B+b cos A=0.(1)求B;(2)若b=3,△ABC的周长为3+23,求△ABC的面积.解(1)由已知及正弦定理得(sin A+2sin C)cos B+sin B cos A=0,(sin A cos B+sin B cos A)+2sin C cos B=0,sin(A+B)+2sin C cos B=0,又sin(A+B)=sin C,且C∈(0,π),sin C≠0,∴cos B=-12,∵0<B<π,∴B=23π.(2)由余弦定理,得9=a2+c2-2ac cos B.∴a2+c2+ac=9,则(a+c)2-ac=9.∵a+b+c=3+23,b=3,∴a+c=23,∴ac=3,∴S△ABC =12a a c sin B=12×3×32=334.三、课后练习1.△ABC的内角A,B,C的对边分别为a,b,c,若cos C=223,b cos A+a cosB=2,则△ABC的外接圆面积为()A.4πB.8πC.9πD.36π解析由题意及正弦定理得2R sin B cos A+2R sin A cos B=2R sin(A+B)=2(R为△ABC的外接圆半径).即2R sin C=2.又cos C=223及C∈(0,π),知sin C=13.∴2R=2sin C=6,R=3.故△ABC 外接圆面积S =πR 2=9π. 答案 C2.(2019·武汉模拟)在△ABC 中,C =2π3,AB =3,则△ABC 的周长为( ) A.6sin ⎝ ⎛⎭⎪⎫A +π3+3 B.6sin ⎝ ⎛⎭⎪⎫A +π6+3 C.23sin ⎝ ⎛⎭⎪⎫A +π3+3D.23sin ⎝ ⎛⎭⎪⎫A +π6+3解析 设△ABC 的外接圆半径为R ,则2R =3sin 2π3=23,于是BC =2R sin A =23sin A ,AC =2R sin B =23sin ⎝ ⎛⎭⎪⎫π3-A .于是△ABC 的周长为23⎣⎢⎡⎦⎥⎤sin A +sin ⎝ ⎛⎭⎪⎫π3-A +3=23sin ⎝ ⎛⎭⎪⎫A +π3+3. 答案 C3.(2019·长春一模)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,若⎝ ⎛⎭⎪⎫12b -sin C cos A =sin A cos C ,且a =23,则△ABC 面积的最大值为________. 解析 因为⎝ ⎛⎭⎪⎫12b -sin C cos A =sin A cos C , 所以12b cos A -sin C cos A =sin A cosC ,所以12b cos A =sin(A +C ),所以12b cos A =sin B , 所以cos A 2=sin Bb , 又sin B b =sin A a ,a =23, 所以cos A 2=sin A 23,得tan A =3,又A ∈(0,π),则A =π3, 由余弦定理得(23)2=b 2+c 2-2bc ·12=b 2+c 2-bc ≥2bc -bc =bc ,即bc ≤12(当且仅当b =c =23时取等号), 从而△ABC 面积的最大值为12×12×32=3 3. 答案 334.(2018·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b sin A =a cos ⎝ ⎛⎭⎪⎫B -π6.(1)求角B 的大小;(2)设a =2,c =3,求b 和sin(2A -B )的值.解 (1)在△ABC 中,由正弦定理a sin A =bsin B , 得b sin A =a sin B , 又由b sin A =a cos ⎝ ⎛⎭⎪⎫B -π6, 得a sin B =a cos ⎝ ⎛⎭⎪⎫B -π6,即sin B =cos ⎝ ⎛⎭⎪⎫B -π6,可得tan B = 3. 又因为B ∈(0,π),可得B =π3.(2)在△ABC 中,由余弦定理及a =2,c =3,B =π3, 有b 2=a 2+c 2-2ac cos B =7,故b =7. 由b sin A =a cos ⎝ ⎛⎭⎪⎫B -π6,可得sin A =37. 因为a <c ,故cos A =27. 因此sin 2A =2sin A cos A =437, cos 2A =2cos 2A -1=17.所以,sin(2A -B )=sin 2A cos B -cos 2A sin B =437×12-17×32=3314.5.我国南宋著名数学家秦九韶发现了由三角形三边求三角形面积的“三斜公式”,设△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,则“三斜求积”公式为S =14⎣⎢⎡⎦⎥⎤a 2c 2-⎝ ⎛⎭⎪⎫a 2+c 2-b 222.若a 2sin C =4sin A ,(a +c )2=12+b 2,则用“三斜求积”公式求得△ABC 的面积为________. 解析 根据正弦定理及a 2sin C =4sin A ,可得ac =4, 由(a +c )2=12+b 2,可得a 2+c 2-b 2=4, 所以S △ABC =14⎣⎢⎡⎦⎥⎤a 2c 2-⎝ ⎛⎭⎪⎫a 2+c 2-b 222=14×(16-4)= 3. 答案3。
正余弦定理知识点+经典题(有答案)

正余弦定理1.定理内容:(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即2sin sin sin a b cR A B C=== (2)余弦定理:三角形中任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的两倍。
即:2222cos a b c bc A =+- 2222cos b a c ac B =+- 2222cos c a b ab C =+-(3)面积定理:111sin sin sin 222ABC S ab C bc A ac B ∆=== 2.利用正余弦定理解三角形: (1)已知一边和两角:(2)已知两边和其中一边的对角: (3)已知两边和它们所夹的角: (4)已知三边:正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .262.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 63.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定 解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6.5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .26.在△ABC 中,若cos A cos B =ba ,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形 7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或328.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .29.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________. 10.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.11.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________. 12.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.13.在△ABC 中,A =60°,a =63,b =12,S △ABC =183,则a +b +csin A +sin B +sin C =________,c =________.14.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.15.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________. 16.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .2 6C .3 6D .46 2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( )D .2 3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( )A .60°B .45°C .120°D .150°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( )或5π6 或2π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( )A .2B .-2C .4D .-4 8.在△ABC 中,b =3,c =3,B =30°,则a 为( )B .2 3 或2 3 D .29.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________. 10.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数.11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________. 12.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.14.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.15.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________. 16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -π4)的值.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .26解析:选A.应用正弦定理得:a sin A =b sin B ,求得b =a sin Bsin A = 6. 2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6解析:选=45°,由正弦定理得b =a sin Bsin A =4 6.3.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对解析:选C.由正弦定理a sin A =b sin B 得:sin B =b sin A a =22,又∵a >b ,∴B <60°,∴B =45°. 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6.5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .2解析:选=180°-105°-45°=30°,由b sin B =c sin C 得c =2×sin 30°sin45°=1.6.在△ABC 中,若cos A cos B =ba ,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形解析:选D.∵b a =sin B sin A ,∴cos A cos B =sin Bsin A , sin A cos A =sin B cos B ,∴sin2A =sin2B即2A =2B 或2A +2B =π,即A =B ,或A +B =π2.7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或32解析:选=AC sin B ,求出sin C =32,∵AB >AC ,∴∠C 有两解,即∠C =60°或120°,∴∠A =90°或30°.再由S △ABC =12AB ·AC sin A 可求面积.8.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .2解析:选D.由正弦定理得6sin120°=2sin C ,∴sin C =12.又∵C 为锐角,则C =30°,∴A =30°, △ABC 为等腰三角形,a =c = 2.9.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________.解析:由正弦定理得:a sin A =csin C ,所以sin A =a ·sin C c =12.又∵a <c ,∴A <C =π3,∴A =π6.答案:π610.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.解析:由正弦定理得a sin A =bsin B⇒sin B =b sin A a =4×12433=32.答案:3211.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________.解析:C =180°-120°-30°=30°,∴a =c ,由a sin A =b sin B 得,a =12×sin30°sin120°=43,∴a +c =8 3. 答案:8312.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.解析:由正弦定理,得a =2R ·sin A ,b =2R ·sin B , 代入式子a =2b cos C ,得 2R sin A =2·2R ·sin B ·cos C , 所以sin A =2sin B ·cos C , 即sin B ·cos C +cos B ·sin C =2sin B ·cos C , 化简,整理,得sin(B -C )=0. ∵0°<B <180°,0°<C <180°, ∴-180°<B -C <180°, ∴B -C =0°,B =C . 答案:等腰三角形13.在△ABC 中,A =60°,a =63,b =12,C=30°则a +b +csin A +sin B +sin C =________,c =________.解析:由正弦定理得a +b +c sin A +sin B +sin C=a sin A =63sin60°=12,又S △ABC =12bc sin A ,∴12×12×sin60°×c =183,∴c =6.答案:12 614.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.解析:由∠A ∶∠B ∶∠C =1∶2∶3得,∠A =30°,∠B =60°,∠C =90°,∴2R =a sin A =1sin30°=2,又∵a =2R sin A ,b =2R sin B ,c =2R sin C ,∴a -2b +c sin A -2sin B +sin C =2R sin A -2sin B +sin Csin A -2sin B +sin C =2R =2. 答案:215.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________.解析:依题意,sin C =223,S △ABC =12ab sin C =43,解得b =2 3. 答案:2316.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.解析:∵b sin C =43×12=23且c =2, ∴c <b sin C ,∴此三角形无解. 答案:0 17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少解:在△ABC 中,BC =40×12=20, ∠ABC =140°-110°=30°,∠ACB =(180°-140°)+65°=105°, 所以∠A =180°-(30°+105°)=45°, 由正弦定理得AC =BC ·sin ∠ABC sin A =20sin30°sin45°=102(km).即货轮到达C 点时,与灯塔A 的距离是10 2 km.18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .解:由sin C 2cos C 2=14,得sin C =12,又C ∈(0,π),所以C =π6或C =5π6.由sin B sin C =cos 2A2,得sin B sin C =12[1-cos(B +C )], 即2sin B sin C =1-cos(B +C ),即2sin B sin C +cos(B +C )=1,变形得 cos B cos C +sin B sin C =1,即cos(B -C )=1,所以B =C =π6,B =C =5π6(舍去),A =π-(B +C )=2π3.由正弦定理a sin A =b sin B =csin C ,得b =c =a sin Bsin A =23×1232=2.故A =2π3,B =π6,b =c =2.19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值. 解:(1)∵A 、B 为锐角,sin B =1010,∴cos B =1-sin 2B =31010.又cos 2A =1-2sin 2A =35,∴sin A =55,cos A =255, ∴cos(A +B )=cos A cos B -sin A sin B =255×31010-55×1010=22.又0<A +B <π,∴A +B =π4.(2)由(1)知,C =3π4,∴sin C =22.由正弦定理:a sin A =b sin B =csin C 得5a =10b =2c ,即a =2b ,c =5b .∵a -b =2-1,∴2b -b =2-1,∴b =1. ∴a =2,c = 5.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.解:由S =12ab sin C 得,153=12×603×sin C ,∴sin C =12,∴∠C =30°或150°. 又sin B =sin C ,故∠B =∠C .当∠C =30°时,∠B =30°,∠A =120°.又∵ab =603,a sin A =bsin B ,∴b =215. 当∠C =150°时,∠B =150°(舍去). 故边b 的长为215.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .26C .3 6D .46 解析:选A.由余弦定理,得 AC =AB 2+BC 2-2AB ·BC cos B= 42+62-2×4×6×13=6.2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( ) D .2解析:选B.由余弦定理,得c 2=a 2+b 2-2ab cos C =22+(3-1)2-2×2×(3-1)cos30° =2, ∴c = 2.3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( ) A .60° B .45° C .120° D .150°解析:选∠A =b 2+c 2-a 22bc =-3bc 2bc =-32, ∵0°<∠A <180°,∴∠A =150°. 4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( ) 或5π6 或2π3解析:选D.由(a 2+c 2-b 2)tan B =3ac ,联想到余弦定理,代入得cos B =a 2+c 2-b 22ac =32·1tan B =32·cos B sin B .显然∠B ≠π2,∴sin B =32.∴∠B =π3或2π3.5.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( ) A .a B .b C .c D .以上均不对解析:选·a 2+c 2-b 22ac +b ·b 2+c 2-a 22bc =2c 22c =c .6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .由增加的长度决定 解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2. 设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m +2m 2>c 2+2cm +m 2=(c +m )2, ∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( ) A .2 B .-2 C .4 D .-4解析:选△ABC =3=12|AB →|·|AC →|·sin A =12×4×1×sin A ,∴sin A =32,又∵△ABC 为锐角三角形,∴cos A =12,∴AB →·AC →=4×1×12=2.8.在△ABC 中,b =3,c =3,B =30°,则a 为( ) B .23 或2 3 D .2解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-33a , ∴a 2-33a +6=0,解得a =3或2 3.9.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B =π3. 在△ABD 中,AD =AB 2+BD 2-2AB ·BD cos B= 1+4-2×1×2×12= 3. 答案:310.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数. 解:∵sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10, ∴a ∶b ∶c =(3-1)∶(3+1)∶10.设a =(3-1)k ,b =(3+1)k ,c =10k (k >0), ∴c 边最长,即角C 最大.由余弦定理,得cos C =a 2+b 2-c 22ab =-12, 又C ∈(0°,180°),∴C =120°. 11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________.解析:S =12ab sin C ,sin C =32,∴C =60°或120°.∴cos C =±12,又∵c 2=a 2+b 2-2ab cos C ,∴c 2=21或61,∴c =21或61. 答案:21或6112.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________. 解析:由正弦定理a ∶b ∶c =sin A ∶sin B ∶sin C =2∶3∶4, 设a =2k (k >0),则b =3k ,c =4k ,cos B =a 2+c 2-b 22ac =2k 2+4k 2-3k 22×2k ×4k=1116, 同理可得:cos A =78,cos C =-14,∴cos A ∶cos B ∶cos C =14∶11∶(-4). 答案:14∶11∶(-4)13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.解析:∵cos C =13,∴sin C =223.又S △ABC =12ab sin C =43,即12·b ·32·223=43,∴b =2 3.答案:2314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.解析:在△ABC 中,cos B =AB 2+BC 2-AC 22AB ·BC=49+25-362×7×5=1935,∴AB →·BC →=|AB →|·|BC →|·cos(π-B )=7×5×(-1935)=-19.答案:-1915.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________. 解析:12ab sin C =S =a 2+b 2-c 24=a 2+b 2-c 22ab ·ab 2 =12ab cos C ,∴sin C =cos C ,∴tan C =1,∴C =45°.答案:45°16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 解析:设三边长为k -1,k ,k +1(k ≥2,k ∈N ),则⎩⎪⎨⎪⎧ k 2+k -12-k +12<0k +k -1>k +1⇒2<k <4,∴k =3,故三边长分别为2,3,4,∴最小角的余弦值为32+42-222×3×4=78.答案:7817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=12,即cos C =-12.又∵a ,b 是方程x 2-23x +2=0的两根,∴a +b =23,ab =2. ∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-12)=a 2+b 2+ab =(a +b )2-ab=(23)2-2=10,∴AB =10. 18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.解:(1)由题意及正弦定理得 AB +BC +AC =2+1,BC +AC =2AB ,两式相减,得AB =1.(2)由△ABC 的面积12BC ·AC ·sin C =16sin C ,得BC ·AC =13,由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC=AC +BC 2-2AC ·BC -AB 22AC ·BC=12, 所以C =60°.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值; (2)求sin(2A -π4)的值.解:(1)在△ABC 中,由正弦定理AB sin C =BC sin A ,得AB =sin C sin A BC =2BC =2 5.(2)在△ABC 中,根据余弦定理,得cos A =AB 2+AC 2-BC 22AB ·AC=255, 于是sin A =1-cos 2A =55.从而sin 2A =2sin A cos A =45,cos 2A =cos 2 A -sin 2 A =35.所以sin(2A -π4)=sin 2A cos π4-cos 2A sin π4=210.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.解:由正弦定理,得sin C sin B =c b .由2cos A sin B =sin C ,有cos A =sin C 2sin B =c 2b .又根据余弦定理,得cos A =b 2+c 2-a 22bc ,所以c 2b =b 2+c 2-a 22bc ,即c 2=b 2+c 2-a 2,所以a =b .又因为(a +b +c )(a +b -c )=3ab ,所以(a +b )2-c 2=3ab ,所以4b 2-c 2=3b 2,所以b =c ,所以a =b =c ,因此△ABC 为等边三角形.。
高考复习 第4篇 第6讲 正弦定理和余弦定理知识点+例题+练习 含答案

第6讲正弦定理和余弦定理知识梳理1.正弦定理和余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,则正弦定理余弦定理内容asin A=bsin B=csin C=2R(R为△ABC外接圆半径)a2=b2+c2-2bc cos Ab2=a2+c2-2ac cos Bc2=a2+b2-2ab cos C常见变形(1)a=2R sin A,b=2R sinB,c=2R sin C;(2)sin A=a2R,sin B=b2R,sin C=c2R;(3)a∶b∶c=sin A∶sinB∶sin Ccos A=b2+c2-a22bc;cos B=a2+c2-b22ac;cos C=a2+b2-c22ab解决的问题(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边和其他两角(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两角2.在△ABC中,已知a,b和A时,解的情况A为锐角A为钝角或直角图形关系式a=b sin A b sin A<a<b a≥b a>b解的个数一解两解一解一解(1)S=12ah(h表示边a上的高).(2)S=12bc sin A=12ab sin C=12ac sin B.(3)S=12r(a+b+c)(r为△ABC内切圆半径).辨析感悟1.三角形中关系的判断(1)在△ABC中,sin A>sin B的充分不必要条件是A>B.(×)(2)(教材练习改编)在△ABC中,a=3,b=2,B=45°,则A=60°或120°.(√) 2.解三角形(3)(2013·北京卷改编)在△ABC中,a=3,b=5,sin A=13,则sin B=59.(√)(4)(教材习题改编)在△ABC中,a=5,c=4,cos A=916,则b=6.(√)3.三角形形状的判断(5)在△ABC中,若sin A sin B<cos A cos B,则此三角形是钝角三角形.(√)(6)在△ABC中,若b2+c2>a2,则此三角形是锐角三角形.(×)[感悟·提升]一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC中,A>B⇔a>b⇔sin A>sin B,如(1).判断三角形形状的两种途径一是化边为角;二是化角为边,并常用正弦(余弦)定理实施边、角转换.考点一利用正弦、余弦定理解三角形【例1】(1)(2013·湖南卷改编)在锐角△ABC中,角A,B所对的边长分别为a,b.若2a sin B=3b,则角A等于______.(2)(2014·杭州模拟)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,c=42,B=45°,则sin C=________.解析(1)在△ABC中,由正弦定理及已知得2sin A·sin B=3sin B,∵B 为△ABC 的内角,∴sin B ≠0. ∴sin A =32.又∵△ABC 为锐角三角形, ∴A ∈⎝ ⎛⎭⎪⎫0,π2,∴A =π3.(2)由余弦定理,得b 2=a 2+c 2-2ac cos B =1+32-82×22=25,即b =5. ∴sin C =C sin B b =42×225=45. 答案 (1)π3 (2)45规律方法 已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.【训练1】 (1)在△ABC 中,a =23,c =22,A =60°,则C =________. (2)在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若a 2-b 2=3bc ,sin C =23sin B ,则A =________.解析 (1)由正弦定理,得23sin 60°=22sin C ,解得:sin C =22,又c <a ,所以C <60°,所以C =45°. (2)∵sin C =23sin B ,由正弦定理,得c =23b ,∴cos A =b 2+c 2-a 22bc =-3bc +c 22bc =-3bc +23bc 2bc =32,又A 为三角形的内角,∴A =30°.答案 (1)45° (2)30°考点二 判断三角形的形状【例2】 (2014·临沂一模)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b -c )sin B +(2c -b )sin C .(1)求角A 的大小;(2)若sin B +sin C =3,试判断△ABC 的形状. 解 (1)由2a sin A =(2b -c )sin B +(2c -b )sin C , 得2a 2=(2b -c )b +(2c -b )c ,即bc =b 2+c 2-a 2, ∴cos A =b 2+c 2-a 22bc =12,∴A =60°.(2)∵A +B +C =180°,∴B +C =180°-60°=120°. 由sin B +sin C =3,得sin B +sin(120°-B )=3, ∴sin B +sin 120°cos B -cos 120°sin B = 3. ∴32sin B +32cos B =3,即sin(B +30°)=1. ∵0°<B <120°,∴30°<B +30°<150°. ∴B +30°=90°,B =60°.∴A =B =C =60°,△ABC 为等边三角形.规律方法 解决判断三角形的形状问题,一般将条件化为只含角的三角函数的关系式,然后利用三角恒等变换得出内角之间的关系式;或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系.另外,在变形过程中要注意A ,B ,C 的范围对三角函数值的影响.【训练2】 (1)(2013·山东省实验中学诊断)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2c 2=2a 2+2b 2+ab ,则△ABC 的形状是________三角形.(填“直角”、“钝角”或“锐角”等)(2)在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,则△ABC 的形状是________三角形.(填“锐角”、“直角”、“等腰”或“等腰或直角”)解析 (1)由2c 2=2a 2+2b 2+ab ,得a 2+b 2-c 2=-12ab ,所以cos C =a 2+b 2-c 22ab =-12ab2ab =-14<0,所以90°<C <180°,即△ABC 为钝角三角形. (2)由已知(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,得b 2[sin(A -B )+sin C ]=a 2[sin C -sin(A -B )], 即b 2sin A cos B =a 2cos A sin B , 即sin 2 B sin A cos B =sin 2 A cos A sin B ,所以sin 2B =sin 2A ,由于A ,B 是三角形的内角, 故0<2A <2π,0<2B <2π. 故只可能2A =2B 或2A =π-2B , 即A =B 或A +B =π2.故△ABC 为等腰三角形或直角三角形. 答案 (1)钝角 (2)等腰或直角考点三 与三角形面积有关的问题【例3】 (2013·浙江卷)在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2a sin B =3b . (1)求角A 的大小;(2)若a =6,b +c =8,求△ABC 的面积.审题路线 (1)把2a sin B =3b 变形为2a =3b sin B ⇒利用正弦定理a sin A =bsin B ⇒得到sin A =?⇒A 为锐角,得出A =?(2)由(1)知cos A 的值⇒利用余弦定理⇒又b +c =8,求bc 的值⇒利用三角形面积公式S =12bc sin A 求得.解 (1)由2a sin B =3b ,得2a =3bsin B ,又由正弦定理a sin A =b sin B ,得a sin A =2a 3,所以sin A =32,因为A 为锐角,所以A =π3.(2)由(1)及a 2=b 2+c 2-2bc cos A ,得b 2+c 2-bc =(b +c )2-3bc =36,又b +c =8,所以bc =283,由S =12bc sin A ,得△ABC 的面积为733.规律方法 在解决三角形问题中,面积公式S =12ab sin C =12bc sin A =12ac sin B 最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来. 【训练3】 (2013·湖北卷)在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c .已知cos 2A -3cos(B +C )=1. (1)求角A 的大小;(2)若△ABC 的面积S =53,b =5,求sin B sin C 的值. 解 (1)由cos 2A -3cos(B +C )=1, 得2cos 2A +3cos A -2=0,即(2cos A -1)(cos A +2)=0,解得cos A =12或cos A =-2(舍去).因为0<A <π,所以A =π3.(2)由S =12 bc sin A =12bc ·32=34bc =53,得bc =20. 又b =5,所以c =4.由余弦定理,得a 2=b 2+c 2-2bc cos A =25+16-20=21, 故a =21.又由正弦定理,得sin B sin C =b a sin A ·ca sin A =bc a 2sin 2A =2021×34=57.1.在解三角形的问题中,三角形内角和定理起着重要作用,在解题时要注意根据这个定理确定角的范围及三角函数值的符号,防止出现增解或漏解. 2.正、余弦定理在应用时,应注意灵活性,尤其是其变形应用时可相互转化.如a 2=b 2+c 2-2bc cos A 可以转化为sin 2 A =sin 2 B +sin 2 C -2sin B sin C cos A ,利用这些变形可进行等式的化简与证明.答题模板6——解三角形问题【典例】 (13分)(2013·重庆卷)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2=b 2+c 2+3bc . (1)求A ;(2)设a =3,S 为△ABC 的面积,求S +3cos B cos C 的最大值,并指出此时B 的值.[规范解答] (1)由余弦定理, 得cos A =b 2+c 2-a 22bc =-3bc 2bc =-32. 又因为0<A <π,所以A =5π6.(4分) (2)由(1)得sin A =12, 又由正弦定理及a =3,得S =12bc sin A =12·a sin B sin A ·a sin C =3sin B sin C ,(6分) 因此,S +3cos B cos C =3(sin B sin C +cos B cos C )= 3cos(B -C ).(9分)所以,当B =C ,即B =π-A 2=π12时, S +3cos B cos C 取最大值3.(13分)[反思感悟] (1)在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.(2)在本题第(2)问中,不会结合正弦定理表达S 的角的形式是失分的主要原因.答题模板 第一步:定已知.即梳理已知条件,确定三角形中已知的边与角;第二步:选定理.即根据已知的边角关系灵活地选用定理和公式;第三步:代入求值. 【自主体验】已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,c =3a sin C -c cos A . (1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c . 解 (1)由c =3a sin C -c cos A 及正弦定理,得 3sin A sin C -cos A ·sin C -sin C =0, 由于sin C ≠0,所以sin ⎝ ⎛⎭⎪⎫A -π6=12,又0<A <π,所以-π6<A -π6<5π6,故A =π3. (2)△ABC 的面积S =12bc sin A =3,故bc =4. 而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8,解得b =c =2.基础巩固题组 (建议用时:40分钟)一、填空题1.(2013·盐城模拟)在△ABC 中,若a 2-c 2+b 2=3ab ,则C =________. 解析 由a 2-c 2+b 2=3ab ,得cos C =a 2+b 2-c 22ab =3ab 2ab =32,所以C =30°. 答案 30°2.(2014·合肥模拟)在△ABC 中,A =60°,AB =2,且△ABC 的面积为32,则BC 的长为________.解析 S =12×AB ·AC sin 60°=12×2×32AC =32,所以AC =1,所以BC 2=AB 2+AC 2-2AB ·AC cos 60°=3,所以BC = 3. 答案33.(2013·新课标全国Ⅱ卷改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =2,B =π6,C =π4,则△ABC 的面积为________. 解析 由正弦定理b sin B =csin C 及已知条件得c =22, 又sin A =sin(B +C )=12×22+32×22=2+64. 从而S △ABC =12bc sin A =12×2×22×2+64=3+1. 答案3+14.(2013·山东卷改编)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若B =2A ,a =1,b =3,则c =________.解析 由a sin A =b sin B ,得a sin A =b sin 2A ,所以1sin A =32sin A cos A ,故cos A =32,又A ∈(0,π),所以A =π6,B =π3,C =π2,c =a 2+b 2=12+(3)2=2.答案 25.(2013·陕西卷改编)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为________三角形(填“直角”、“锐角”或“钝角”).解析 由正弦定理及已知条件可知sin B cos C +cos B sin C =sin 2 A ,即sin(B +C )=sin 2 A ,而B +C =π-A ,所以sin(B +C )=sin A ,所以sin 2 A =sin A ,又0<A <π,sin A >0,∴sin A =1,即A =π2. 答案 直角6.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =2,b =2,sin B +cos B =2,则角A 的大小为________.解析 由题意知,sin B +cos B =2,所以2sin ⎝ ⎛⎭⎪⎫B +π4=2,所以B =π4,根据正弦定理可知a sin A =b sin B ,可得2sin A =2sin π4,所以sin A =12,又a <b ,故A =π6.答案 π67.(2014·惠州模拟)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为________.解析 由余弦定理,得a 2+c 2-b 22ac =cos B ,结合已知等式得cos B ·tan B =32,∴sin B =32,∴B =π3或2π3. 答案π3或2π38.(2013·烟台一模)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =1,b =2,cos C =14,则sin B 等于________.解析 由余弦定理,得c 2=a 2+b 2-2ab cos C =4,即c =2.由cos C =14得sin C =154.由正弦定理b sin B =c sin C ,得sin B =b sin C c =22×154=154(或者因为c =2,所以b =c =2,即三角形为等腰三角形,所以sin B =sin C =154). 答案154二、解答题9.(2014·扬州质检)在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,且a =12c +b cos C . (1)求角B 的大小;(2)若S △ABC =3,b =13,求a +c 的值. 解 (1)由正弦定理,得sin A =12sin C +sin B cos C , 又因为A =π-(B +C ),所以sin A =sin(B +C ), 可得sin B cos C +cos B sin C =12sin C +sin B cos C , 即cos B =12,又B ∈(0,π),所以B =π3.(2)因为S △ABC =3,所以12ac sin π3=3,所以ac =4,由余弦定理可知b 2=a 2+c 2-ac ,所以(a +c )2=b 2+3ac =13+12=25,即a +c =5.10.(2013·深圳二模)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知a =3,b =5,c =7.(1)求角C 的大小;(2)求sin ⎝ ⎛⎭⎪⎫B +π3的值. 解 (1)由余弦定理,得cos C =a 2+b 2-c 22ab =32+52-722×3×5=-12.∵0<C <π,∴C =2π3.(2)由正弦定理b sin B =c sin C ,得sin B =b sin C c =5sin 2π37=5314,∵C =2π3,∴B 为锐角, ∴cos B =1-sin 2 B =1-⎝ ⎛⎭⎪⎫53142=1114. ∴sin ⎝ ⎛⎭⎪⎫B +π3=sin B cos π3+cos B sin π3 =5314×12+1114×32=437.能力提升题组(建议用时:25分钟)一、填空题1.(2014·温岭中学模拟)在锐角△ABC 中,若BC =2,sin A =223,则A B →·A C →的最大值为________.解析 由余弦定理,得a 2=b 2+c 2-2bc ×13=4,由基本不等式可得4≥43bc ,即bc≤3,又∵sin A=223,∴cos A=13,所以A B→·A C→=bc cos A=13bc≤1.答案 12.(2013·青岛一中调研)在△ABC中,三边长a,b,c满足a3+b3=c3,那么△ABC的形状为________三角形.(填“锐角”、“钝角”或“直角”).解析由题意可知c>a,c>b,即角C最大,所以a3+b3=a·a2+b·b2<ca2+cb2,即c3<ca2+cb2,所以c2<a2+b2.根据余弦定理,得cos C=a2+b2-c22ab>0,所以0<C<π2,即三角形为锐角三角形.答案锐角3.在△ABC中,B=60°,AC=3,则AB+2BC的最大值为________ .解析由正弦定理知ABsin C=3sin 60°=BCsin A,∴AB=2sin C,BC=2sin A.又A+C=120°,∴AB+2BC=2sin C+4sin(120°-C)=2(sin C+2sin 120°cos C-2cos 120°sin C)=2(sin C+3cos C+sin C)=2(2sin C+3cos C)=27sin(C+α),其中tan α=32,α是第一象限角,由于0°<C<120°,且α是第一象限角,因此AB+2BC有最大值27.答案27二、解答题4.(2013·长沙模拟)在△ABC中,边a,b,c分别是角A,B,C的对边,且满足b cos C=(3a-c)cos B.(1)求cos B;(2)若B C →·B A →=4,b =42,求边a ,c 的值. 解 (1)由正弦定理和b cos C =(3a -c )cos B , 得sin B cos C =(3sin A -sin C )cos B ,化简,得sin B cos C +sin C cos B =3sin A cos B , 即sin(B +C )=3sin A cos B ,故sin A =3sin A cos B ,所以cos B =13.(2)因为B C →·B A →=4,所以B C →·B A →=|B C →|·|B A →|· cos B =4,所以|B C →|·|B A →|=12,即ac =12.①又因为cos B =a 2+c 2-b 22ac =13,整理得,a 2+c 2=40.②联立①②⎩⎨⎧ a 2+c 2=40,ac =12,解得⎩⎨⎧ a =2,c =6或⎩⎨⎧ a =6,c =2.。
高三复习:正弦定理、余弦定理含解析答案(教师版+学生版)

§4.7 正弦定理、余弦定理错误!未找到引用源。
1.正弦、余弦定理在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则定理正弦定理余弦定理 内容_______________________________a 2=______________;b =______________;;c 2=______________变形(1)a =2R sin A ,b =_________,c =_________;(2)sin A =a 2R ,sin B =b 2R ,sin C =c2R ;(3)a ∶b ∶c =_________; (4)a sin B =b sin A ,b sin C =c sin B ,a sin C =c sin A(5)cos A =_________ cos B =_________;cos C =_________2.S △ABC =_________=12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (r 是三角形内切圆的半径)3.在△ABC 中,已知a 、b 和A 时,解的情况如下: A 为锐角A 为钝角或直角 图形关系式 a =b sin Ab sin A <a <ba ≥b a >b 解的个数【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)在△ABC 中,A >B 必有sin A >sin B .( √ )(2)若满足条件C =60°,AB =3,BC =a 的△ABC 有两个,那么a 的取值范围是(3,2).( √ )(3)若△ABC 中,a cos B =b cos A ,则△ABC 是等腰三角形.( √ ) (4)在△ABC 中,tan A =a 2,tan B =b 2,那么△ABC 是等腰三角形.( × )(5)当b 2+c 2-a 2>0时,三角形ABC 为锐角三角形;当b 2+c 2-a 2=0时,三角形为直角三角形;当b 2+c 2-a 2<0时,三角形为钝角三角形.( × ) (6)在△ABC 中,AB =3,AC =1,B =30°,则△ABC 的面积等于32.( × )题型一 利用正弦定理、余弦定理解三角形例1 设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且a +c =6,b =2,cos B =79.(1)求a ,c 的值; (2)求sin(A -B )的值.(1)(2014·天津)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .已知b-c =14a,2sin B =3sin C ,则cos A 的值为 .(2)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且cos A =35,cos B =513,b =3,则c = .题型二 利用正弦、余弦定理判定三角形的形状例2 在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且2a sin A =(2b -c )sin B +(2c -b )sin C .(1)求角A 的大小;(2)若sin B +sin C =3,试判断△ABC 的形状. (3)在本例条件下,若sin B ·sin C =sin 2A ,试判断△ABC 的形状变式 在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)·sin(A +B ),试判断△ABC 的形状.题型三 和三角形面积有关的问题例3 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a ≠b ,c =3,cos 2A -cos 2B =3sin A cos A -3sin B cos B . (1)求角C 的大小;(2)若sin A =45,求△ABC 的面积.课堂练习1.在锐角△ABC 中,角A ,B 所对的边长分别为a ,b ,若2a sin B =3b ,则角A = . 2.在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是 三角形.3.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC的面积是 .4、如果满足∠ABC =60°,AB =8,AC =k 的△ABC 有两个,那么实数k 的取值范围是________.5、在△ABC 中,(2)(2014·山东)在△ABC 中,已知AB →·AC →=tan A ,当A =π6时,△ABC 的面积为 .6、角A ,B ,C 所对应的边分别为a ,b ,c ,已知b cos C +c cos B =2b ,则ab = .4.7 正弦定理、余弦定理作业1.在△ABC 中,若A =60°,B =45°,BC =32,则AC = .2.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a ,则ba= . 3.在△ABC 中,A ∶B =1∶2,sin C =1,则a ∶b ∶c = . 4、在△ABC中,若b =5,B =π4,tan A =2,则a= .5.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若a sin B cos C +c sin B cos A =12b ,且a >b ,则B = .6.若△ABC 的内角满足sin A +2sin B =2sin C ,则cos C 的最小值是 .7.△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高为 .8、在△ABC 中,C =90°,M 是BC 的中点.若sin ∠BAM =13,则sin ∠BAC = .9.钝角三角形ABC 的面积是12,AB =1,BC =2,则AC = .10.在△ABC 中,若b =5,B =π4,sin A =13,则a = .11.在△ABC 中,若AB =5,AC =5,且cos C =910,则BC = .12.在△ABC 中,A =60°,AC =4,BC =23,则△ABC 的面积等于 .13.在△ABC 中,a =3,b =26,B =2A . (1)求cos A 的值; (2)求c 的值.14.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a >c ,已知BA →·BC →=2,cos B =13,b =3.求: (1)a 和c 的值; (2)cos(B -C )的值.15.已知△ABC 的三个内角A ,B ,C 成等差数列,角B 所对的边b =3,且函数f (x )=23sin 2x +2sin x cos x -3在x =A 处取得最大值. (1)求f (x )的值域及周期; (2)求△ABC 的面积.§4.7 正弦定理、余弦定理错误!未找到引用源。
(完整版)正余弦定理习题加答案详解超级详细

正余弦定理高中数学组卷一.选择题(共9小题)1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若,a=2,,则b的值为()A.B. C. D.2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.(2016•岳阳校级模拟)在△ABC中,A:B:C=1:2:3,则a:b:c等于()A.1:2:3 B.3:2:1 C.1::2 D.2::14.(2016•大连一模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形 D.等腰直角三角形5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且,则∠B=()A.B.C.D.6.(2016•宝鸡一模)在△ABC,a=,b=,B=,则A等于()A.B.C.D.或7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2 B.2C.D.8.(2016•新余二模)在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.角B的值为()A.B.C.D.9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则等于()A.B.C.D.二.填空题(共7小题)10.(2016•上海二模)△ABC中,,BC=3,,则∠C=.11.(2016•丰台区一模)在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,若b=2asinB,则角A等于.12.(2016•焦作一模)在△ABC中,已知a=8,∠B=60°,∠C=75°,则b等于.13.(2016•潍坊一模)已知△ABC中,a,b,c分别为内角A,B,C的对边,且a•cosB+b•cosA=3c•cosC,则cosC=.14.(2016•抚顺一模)已知△ABC的周长为+1,且sinA+sinB=sinC,则边AB的长为.15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于.16.(2016•湖南校级模拟)设△ABC的内角A,B,C的对边分别为a,b,c.若,,则b=.三.解答题(共4小题)17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知=(1)求角C的大小,(2)若c=2,求使△ABC面积最大时a,b的值.18.(2016•安徽校级一模)在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)求角A的值;(2)若∠B=,BC边上中线AM=,求△ABC的面积.19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b ﹣2c)cosA=a﹣2acos2.(1)求角A的值;(2)若a=,则求b+c的取值范围.20.(2016•鹰潭一模)已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosc=2a ﹣c(Ⅰ)求B;(Ⅱ)若△ABC的面积为,求b的取值范围.正余弦定理高中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若,a=2,,则b的值为()A.B. C. D.【解答】解:∵在锐角△ABC中,sinA=,S△ABC=,∴bcsinA=bc=,∴bc=3,①又a=2,A是锐角,∴cosA==,∴由余弦定理得:a2=b2+c2﹣2bccosA,即(b+c)2=a2+2bc(1+cosA)=4+6(1+)=12,∴b+c=2②由①②得:,解得b=c=.故选A.2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【解答】解:当sinA=sinB时,则有A=B,则△ABC为等腰三角形,故sinA=sinB是△ABC 为等腰三角形的充分条件,反之,当△ABC为等腰三角形时,不一定是A=B,若是A=C≠60时,则sinA≠sinB,故sinA=sinB是△ABC为等腰三角形的不必要条件.故选A.3.(2016•岳阳校级模拟)在△ABC中,A:B:C=1:2:3,则a:b:c等于()A.1:2:3 B.3:2:1 C.1::2 D.2::1【解答】解:在△ABC中,若∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=π所以∠A=,∠B=,∠C=.由正弦定理可知:a:b:c=sin∠A:sin∠B:sin∠C=sin:sin:sin=1::2.故选:C.4.(2016•大连一模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形 D.等腰直角三角形【解答】解:根据正弦定理可知∵bcosB=acosA,∴sinBcosB=sinAcosA∴sin2A=sin2B∴A=B,或2A+2B=180°即A+B=90°,即有△ABC为等腰或直角三角形.故选C.5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且,则∠B=()A.B.C.D.【解答】解:已知等式利用正弦定理化简得:=,即c2﹣b2=ac﹣a2,∴a2+c2﹣b2=ac,∴cosB==,∵B为三角形的内角,∴B=.故选:C.6.(2016•宝鸡一模)在△ABC,a=,b=,B=,则A等于()A.B.C.D.或【解答】解:由正弦定理可得:sinA===∵a=<b=∴∴∠A=,故选:B.7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2 B.2C.D.【解答】解:∵△ABC中,asinAsinB+bcos2A=a,∴根据正弦定理,得sin2AsinB+sinBcos2A=sinA,可得sinB(sin2A+cos2A)=sinA,∵sin2A+cos2A=1,∴sinB=sinA,得b=,可得=.故选:C.8.(2016•新余二模)在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.角B的值为()A.B.C.D.【解答】解:由条件及正弦定理得sinBcosC+sinCcosB=﹣2sinAcosB.即sin(B+C)=﹣2sinAcosB.∵A+B+C=π,A>0∴sin(B+C)=sinA,又sinA≠0,∴cosB=﹣,而B∈(0,π),∴B=.故选:C.9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则等于()A.B.C.D.【解答】解:∵A+B+C=π,A=2B,∴===.再结合正弦定理得:.故选:D.二.填空题(共7小题)10.(2016•上海二模)△ABC中,,BC=3,,则∠C=.【解答】解:由,a=BC=3,c=,根据正弦定理=得:sinC==,又C为三角形的内角,且c<a,∴0<∠C<,则∠C=.故答案为:11.(2016•丰台区一模)在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,若b=2asinB,则角A等于30°.【解答】解:利用正弦定理化简b=2asinB得:sinB=2sinAsinB,∵sinB≠0,∴sinA=,∵A为锐角,∴A=30°.故答案为:30°12.(2016•焦作一模)在△ABC中,已知a=8,∠B=60°,∠C=75°,则b等于4.【解答】解:∵a=8,B=60°,C=75°,即A=45°,∴由正弦定理,得:b===4.故答案为:413.(2016•潍坊一模)已知△ABC中,a,b,c分别为内角A,B,C的对边,且a•cosB+b•cosA=3c•cosC,则cosC=.【解答】解:∵a•cosB+b•cosA=3c•cosC,∴利用余弦定理可得:a×+b×=3c×,整理可得:a2+b2﹣c2=,∴由余弦定理可得:cosC===.故答案为:.14.(2016•抚顺一模)已知△ABC的周长为+1,且sinA+sinB=sinC,则边AB的长为1.【解答】解:由题意及正弦定理,得:AB+BC+AC=+1.BC+AC=AB,两式相减,可得AB=1.故答案为:1.15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于1.【解答】解:设△ABC的三边分别为a,b,c,外接圆半径为R,由正弦定理得,∴a=2RsinA,b=2RsinB,c=2RsinC,∵a+b+c=2(sinA+sinB+sinC),∴2RsinA+2RsinB+2RsinC=2(sinA+sinB+sinnC),∴R=1.故答案为:1.16.(2016•湖南校级模拟)设△ABC的内角A,B,C的对边分别为a,b,c.若,,则b=2.【解答】解:B=π﹣A﹣C=,△ABC中,由正弦定理可得,∴b=2,故答案为:2.三.解答题(共4小题)17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知=(1)求角C的大小,(2)若c=2,求使△ABC面积最大时a,b的值.【解答】解:(1)∵A+C=π﹣B,即cos(A+C)=﹣cosB,∴由正弦定理化简已知等式得:=,整理得:2sinAcosC+sinBcosC=﹣sinCcosB,即﹣2sinAcosC=sinBcosC+cosBsinC=sin(B+C)=sinA,∵sinA≠0,∴cosC=﹣,∵C为三角形内角,∴C=;(Ⅱ)∵c=2,cosC=﹣,∴由余弦定理得:c2=a2+b2﹣2abcosC,即4=a2+b2+ab≥2ab+ab=3ab,∴ab≤,(当且仅当a=b时成立),∵S=absinC=ab≤,∴当a=b时,△ABC面积最大为,此时a=b=,则当a=b=时,△ABC的面积最大为.18.(2016•安徽校级一模)在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)求角A的值;(2)若∠B=,BC边上中线AM=,求△ABC的面积.【解答】解:(1)∵.∴由正弦定理,得,化简得cosA=,∴A=;(2)∵∠B=,∴C=π﹣A﹣B=,可知△ABC为等腰三角形,在△AMC中,由余弦定理,得AM2=AC2+MC2﹣2AC•MCcos120°,即7=,解得b=2,∴△ABC的面积S=b2sinC==.19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b ﹣2c)cosA=a﹣2acos2.(1)求角A的值;(2)若a=,则求b+c的取值范围.【解答】解:(1)在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2=a﹣2a•,利用正弦定理可得(sinB﹣2sinC)cosA=sinA(﹣cosB),即sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,即sinC=2sinCcosA,∴cosA=,∴A=.(2)若a=,则由正弦定理可得==2,∴b+c=2(sinB+sinC)=2[sinB+sin(﹣B)]=3sinB+cosB=2sin(B+).由于,求得<B<,∴<B+<.∴sin(B+)∈(,1],∴b+c∈(3,2].20.(2016•鹰潭一模)已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosc=2a ﹣c(Ⅰ)求B;(Ⅱ)若△ABC的面积为,求b的取值范围.【解答】解:(1)由正弦定理,得2sinBcosC=2sinA﹣sinC,﹣﹣﹣﹣(2分)在△ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC,∴2cosBsinC=sinC,又∵C是三角形的内角,可得sinC>0,∴2cosB=1,可得cosB=,∵B是三角形的内角,B∈(0,π),∴B=.﹣﹣﹣﹣﹣(6分)(2)∵S△ABC==,B=∴,解之得ac=4,﹣﹣﹣﹣(8分)由余弦定理,得b2=a2+c2﹣2accosB=a2+c2﹣ac≥2ac﹣ac=ac=4,(当且仅当a=c=2时,“=”成立)∴当且仅当a=c=2时,b的最小值为2.﹣﹣﹣﹣(12分)综上所述,边b的取值范围为[2,+∞)﹣﹣﹣﹣(13分)。
高一数学必修5解三角形-正弦-余弦知识点和练习题(含答案)

1.正弦定理:2sin sin sin a b cR A B C===或变形:::sin :sin :sin a b c A B C =. 2.余弦定理: 2222222222cos 2cos 2cos a b c bc A b a c ac B c b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩ 或 222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩.3.(1)两类正弦定理解三角形的问题:1、已知两角和任意一边,求其他的两边及一角.2、已知两角和其中一边的对角,求其他边角. (2)两类余弦定理解三角形的问题:1、已知三边求三角.2、已知两边和他们的夹角,求第三边和其他两角. 4.判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式.5.解题中利用ABC ∆中A B C π++=,以及由此推得的一些基本关系式进行三角变换的运算,如:sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=- sin cos ,cos sin ,tan cot 222222A B C A B C A B C+++===.、 已知条件 定理应用 一般解法一边和两角 (如a 、B 、C ) 正弦定理由A+B+C=180˙,求角A ,由正弦定理求出b 与c ,在有解时 有一解。
两边和夹角 (如a 、b 、c) 余弦定理由余弦定理求第三边c ,由正弦定理求出小边所对的角,再 由A+B+C=180˙求出另一角,在有解时有一解。
三边 (如a 、b 、c) 余弦定理 由余弦定理求出角A 、B ,再利用A+B+C=180˙,求出角C 在有解时只有一解。
1、ΔABC 中,a=1,b=3, ∠A=30°,则∠B 等于 ( )A .60°B .60°或120°C .30°或150°D .120°2、符合下列条件的三角形有且只有一个的是 ( )A .a=1,b=2 ,c=3B .a=1,b=2 ,∠A=30°C .a=1,b=2,∠A=100°C .b=c=1, ∠B=45°3、在锐角三角形ABC 中,有( )A .cosA>sinB 且cosB>sinA B .cosA<sinB 且cosB<sinAC .cosA>sinB 且cosB<sinAD .cosA<sinB 且cosB>sinA4、若(a+b+c)(b+c -a)=3abc,且sinA=2sinBcosC, 那么ΔABC 是 ( )A .直角三角形B .等边三角形C .等腰三角形D .等腰直角三角形5、设A 、B 、C 为三角形的三内角,且方程(sinB -sinA)x 2+(sinA -sinC)x +(sinC -sinB)=0有等根,那么角B( )A .B>60°B .B ≥60°C .B<60°D .B ≤60°6、满足A=45°,c=6 ,a=2的△ABC 的个数记为m,则a m 的值为 ( )A .4B .2C .1D .不定7、如图:D,C,B 三点在地面同一直线上,DC=a,从C,D 两点测得A 点仰角分别是β, α(α<β),则A点离地面的高度AB 等于( )A .)sin(sin sin αββα-aB .)cos(sin sin βαβα-⋅aC .)sin(cos sin αββα-a D .)cos(sin cos βαβα-a9、A 为ΔABC 的一个内角,且sinA+cosA=127, 则ΔABC 是______三角形. 11、在ΔABC 中,若S ΔABC =41 (a 2+b 2-c 2),那么角∠C=______. 12、在ΔABC 中,a =5,b = 4,cos(A -B)=3231,则cosC=_______.13、在ΔABC 中,求分别满足下列条件的三角形形状: ①B=60°,b 2=ac ; ②b 2tanA=a 2tanB ;③sinC=BA BA cos cos sin sin ++④ (a 2-b 2)sin(A+B)=(a 2+b 2)sin(A -B).1、在ABC △中,已知内角A π=3,边23BC =.设内角B x =,周长为y .(1)求函数()y f x =的解析式和定义域;(2)求y 的最大值.2、在ABC 中,角,,A B C 对应的边分别是,,a b c ,若1sin ,2A =3sin 2B =,求::a b c 3、在ABC 中,,a b c 分别为,,A B C ∠∠∠的对边,若2sin (cos cos )3(sin sin )A B C B C +=+,A BD Cαβ(1)求A 的大小;(2)若61,9a b c =+=,求b 和c 的值。
考点17 正余弦定理(讲解)(解析版)
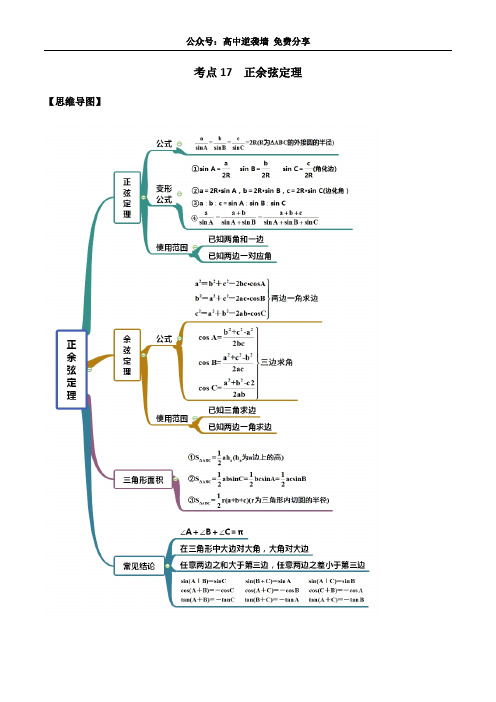
考点17 正余弦定理【思维导图】【常见考法】考法一:正余弦定理选择1.ABC ∆中,角,,A B C 所对的边分别为,,a b c.若3,60a b A ===︒,则边c = 。
【答案】4【解析】2222cos a c b cb A =+-213923cos60c c ⇒=+-⨯⨯︒,即2340c c --=,解得4c =或1c =-(舍去).2.在ABC中,2c =,75A =︒,45B =︒,则ABC 的外接圆面积为 。
【答案】4π 【解析】因为在ABC 中,75A =︒,45B =︒,所以60C =︒,又c =r,则21sin c r C ===,因此ABC 的外接圆面积为214S r ππ==.3.在△ABC 中,A =60°,asin sin sin a b cA B C++++等于 。
【解析】由正弦定理a b c sinA sinB sinC ==,a sinA=3∴sinA ,sinB ,sinC 则a b c sinA sinB sinC ++++=)3sinA sinB sinC sinA sinB sinC ++++=34.在△ABC 中,cos C2=55,BC =1,AC =5,则AB = 。
【答案】4 2【解析】因为cos C =2cos 2C2-1=2×⎝ ⎛⎭⎪⎫552-1=-35,所以c 2=a 2+b 2-2ab cos C =1+25-2×1×5×⎝ ⎛⎭⎪⎫-35=32,∴c =AB =42。
5.在△ABC 中,BC =2,AB =4,cos C =-14,则AC 的值为( ) 【答案】3【解析】△ABC 中,a =BC =2,c =AB =4,cos C =-14,∴c 2=a 2+b 2-2ab cos C ,即16=4+b 2-4b ×⎝ ⎛⎭⎪⎫-14,化简得b 2+b -12=0,解得b =3或b =-4(不合题意,舍去),∴b =AC =3.考法二:边角互换1.在△ABC 中,若a =2bsinA ,则角B 等于 。
正余弦定理知识点经典题有答案

正余弦定理1.定理内容:(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即2sin sin sin a b cR A B C=== (2)余弦定理:三角形中任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的两倍。
即:2222cos a b c bc A =+- 2222cos b a c ac B =+- 2222cos c a b ab C =+-(3)面积定理:111sin sin sin 222ABC S ab C bc A ac B ∆=== 2.利用正余弦定理解三角形: (1)已知一边和两角:(2)已知两边和其中一边的对角: (3)已知两边和它们所夹的角: (4)已知三边:正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .2 6 2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6 3.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定 解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6. 5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .26.在△ABC 中,若cos A cos B =ba,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形 7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或328.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .29.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________.10.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.11.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________. 12.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.13.在△ABC 中,A =60°,a =63,b =12,S △ABC =183,则a +b +csin A +sin B +sin C =________,c =________.14.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.15.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________.16.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少?18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .2 6C .3 6D .4 6 2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( )D .2 3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( )A .60°B .45°C .120°D .150°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( )或5π6 或2π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( )A .2B .-2C .4D .-4 8.在△ABC 中,b =3,c =3,B =30°,则a 为( )B .2 3 或2 3 D .29.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________. 10.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数.11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________. 12.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.14.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.15.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________.16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -π4)的值.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.正弦定理1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( )D .2 6解析:选A.应用正弦定理得:a sin A =b sin B ,求得b =a sin Bsin A= 6.2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6解析:选=45°,由正弦定理得b =a sin Bsin A=4 6.3.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( )A .45°或135°B .135°C .45°D .以上答案都不对解析:选C.由正弦定理a sin A =b sin B 得:sin B =b sin A a =22,又∵a >b ,∴B <60°,∴B =45°.4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( )A .1∶5∶6B .6∶5∶1C .6∶1∶5D .不确定解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6. 5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( )A .1 C .2解析:选=180°-105°-45°=30°,由b sin B =c sin C 得c =2×sin 30°sin45°=1.6.在△ABC 中,若cos A cos B =ba,则△ABC 是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰三角形或直角三角形解析:选D.∵b a =sin B sin A ,∴cos A cos B =sin Bsin A,sin A cos A =sin B cos B ,∴sin2A =sin2B即2A =2B 或2A +2B =π,即A =B ,或A +B =π2.7.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积为( )或 3 或32解析:选=AC sin B ,求出sin C =32,∵AB >AC ,∴∠C 有两解,即∠C =60°或120°,∴∠A =90°或30°.再由S △ABC =12AB ·AC sin A 可求面积.8.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若c =2,b =6,B =120°,则a 等于( )B .2解析:选D.由正弦定理得6sin120°=2sin C,∴sin C =12.又∵C 为锐角,则C =30°,∴A =30°, △ABC 为等腰三角形,a =c = 2.9.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________.解析:由正弦定理得:a sin A =csin C,所以sin A =a ·sin C c =12.又∵a <c ,∴A <C =π3,∴A =π6.答案:π610.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________.解析:由正弦定理得a sin A =bsin B⇒sin B =b sin A a =4×12433=32.答案:3211.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________.解析:C =180°-120°-30°=30°,∴a =c ,由a sin A =b sin B 得,a =12×sin30°sin120°=43, ∴a +c =8 3. 答案:8 312.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.解析:由正弦定理,得a =2R ·sin A ,b =2R ·sin B , 代入式子a =2b cos C ,得 2R sin A =2·2R ·sin B ·cos C , 所以sin A =2sin B ·cos C , 即sin B ·cos C +cos B ·sin C =2sin B ·cos C , 化简,整理,得sin(B -C )=0. ∵0°<B <180°,0°<C <180°, ∴-180°<B -C <180°, ∴B -C =0°,B =C . 答案:等腰三角形13.在△ABC 中,A =60°,a =63,b =12,C=30°则a +b +csin A +sin B +sin C=________,c =________.解析:由正弦定理得a +b +c sin A +sin B +sin C =a sin A =63sin60°=12,又S △ABC =12bc sin A ,∴12×12×sin60°×c =183,∴c =6.答案:12 614.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________.解析:由∠A ∶∠B ∶∠C =1∶2∶3得,∠A =30°,∠B =60°,∠C =90°,∴2R =a sin A =1sin30°=2,又∵a =2R sin A ,b =2R sin B ,c =2R sin C ,∴a -2b +c sin A -2sin B +sin C =2R sin A -2sin B +sin Csin A -2sin B +sin C =2R =2. 答案:215.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________.解析:依题意,sin C =223,S △ABC =12ab sin C =43,解得b =2 3. 答案:2 316.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.解析:∵b sin C =43×12=23且c =2,∴c <b sin C ,∴此三角形无解. 答案:0 17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少?解:在△ABC 中,BC =40×12=20,∠ABC =140°-110°=30°, ∠ACB =(180°-140°)+65°=105°, 所以∠A =180°-(30°+105°)=45°, 由正弦定理得AC =BC ·sin ∠ABC sin A=20sin30°sin45°=102(km). 即货轮到达C 点时,与灯塔A 的距离是10 2 km.18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c .解:由sin C 2cos C 2=14,得sin C =12,又C ∈(0,π),所以C =π6或C =5π6.由sin B sin C =cos 2A2,得sin B sin C =12[1-cos(B +C )],即2sin B sin C =1-cos(B +C ),即2sin B sin C +cos(B +C )=1,变形得 cos B cos C +sin B sin C =1,即cos(B -C )=1,所以B =C =π6,B =C =5π6(舍去),A =π-(B +C )=2π3.由正弦定理a sin A =b sin B =csin C,得b =c =a sin Bsin A =23×1232=2.故A =2π3,B =π6,b =c =2.19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b 、c ,且cos 2A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值. 解:(1)∵A 、B 为锐角,sin B =1010,∴cos B =1-sin 2B =31010.又cos 2A =1-2sin 2A =35,∴sin A =55,cos A =255,∴cos(A +B )=cos A cos B -sin A sin B =255×31010-55×1010=22.又0<A +B <π,∴A +B =π4.(2)由(1)知,C =3π4,∴sin C =22.由正弦定理:a sin A =b sin B =csin C得5a =10b =2c ,即a =2b ,c =5b .∵a -b =2-1,∴2b -b =2-1,∴b =1. ∴a =2,c = 5.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.解:由S =12ab sin C 得,153=12×603×sin C ,∴sin C =12,∴∠C =30°或150°.又sin B =sin C ,故∠B =∠C . 当∠C =30°时,∠B =30°,∠A =120°.又∵ab =603,a sin A =bsin B,∴b =215.当∠C =150°时,∠B =150°(舍去). 故边b 的长为215.余弦定理1.在△ABC 中,如果BC =6,AB =4,cos B =13,那么AC 等于( )A .6B .2 6C .3 6D .4 6 解析:选A.由余弦定理,得 AC =AB 2+BC 2-2AB ·BC cos B= 42+62-2×4×6×13=6.2.在△ABC 中,a =2,b =3-1,C =30°,则c 等于( ) D .2解析:选B.由余弦定理,得c 2=a 2+b 2-2ab cos C =22+(3-1)2-2×2×(3-1)cos30° =2, ∴c = 2.3.在△ABC 中,a 2=b 2+c 2+3bc ,则∠A 等于( ) A .60° B .45° C .120° D .150°解析:选∠A =b 2+c 2-a 22bc =-3bc 2bc =-32,∵0°<∠A <180°,∴∠A =150°. 4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( ) 或5π6 或2π3解析:选D.由(a 2+c 2-b 2)tan B =3ac ,联想到余弦定理,代入得cos B =a 2+c 2-b 22ac =32·1tan B =32·cos B sin B .显然∠B ≠π2,∴sin B =32.∴∠B =π3或2π3.5.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( ) A .a B .b C .c D .以上均不对解析:选·a 2+c 2-b 22ac +b ·b 2+c 2-a 22bc =2c 22c=c .6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .由增加的长度决定 解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2. 设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m +2m 2>c 2+2cm +m 2=(c +m )2, ∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1,△ABC 的面积为3,则AB →·AC →的值为( ) A .2 B .-2 C .4 D .-4解析:选△ABC =3=12|AB →|·|AC →|·sin A=12×4×1×sin A , ∴sin A =32,又∵△ABC 为锐角三角形,∴cos A =12,∴AB →·AC →=4×1×12=2.8.在△ABC 中,b =3,c =3,B =30°,则a 为( ) B .2 3 或2 3 D .2解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-33a , ∴a 2-33a +6=0,解得a =3或2 3. 9.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B =π3.在△ABD 中,AD =AB 2+BD 2-2AB ·BD cos B= 1+4-2×1×2×12= 3.答案: 310.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数. 解:∵sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10, ∴a ∶b ∶c =(3-1)∶(3+1)∶10.设a =(3-1)k ,b =(3+1)k ,c =10k (k >0), ∴c 边最长,即角C 最大.由余弦定理,得cos C =a 2+b 2-c 22ab =-12,又C ∈(0°,180°),∴C =120°. 11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =53,则边c 的值为________.解析:S =12ab sin C ,sin C =32,∴C =60°或120°.∴cos C =±12,又∵c 2=a 2+b 2-2ab cos C ,∴c 2=21或61,∴c =21或61. 答案:21或6112.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________. 解析:由正弦定理a ∶b ∶c =sin A ∶sin B ∶sin C =2∶3∶4, 设a =2k (k >0),则b =3k ,c =4k ,cos B =a 2+c 2-b 22ac =2k 2+4k 2-3k 22×2k ×4k =1116,同理可得:cos A =78,cos C =-14,∴cos A ∶cos B ∶cos C =14∶11∶(-4). 答案:14∶11∶(-4)13.在△ABC 中,a =32,cos C =13,S △ABC =43,则b =________.解析:∵cos C =13,∴sin C =223.又S △ABC =12ab sin C =43, 即12·b ·32·223=43, ∴b =2 3.答案:2 314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则AB →·BC →的值为________.解析:在△ABC 中,cos B =AB 2+BC 2-AC 22AB ·BC=49+25-362×7×5=1935, ∴AB →·BC →=|AB →|·|BC →|·cos(π-B )=7×5×(-1935) =-19.答案:-1915.已知△ABC 的三边长分别是a 、b 、c ,且面积S =a 2+b 2-c 24,则角C =________. 解析:12ab sin C =S =a 2+b 2-c 24=a 2+b 2-c 22ab ·ab 2=12ab cos C ,∴sin C =cos C ,∴tan C =1,∴C =45°. 答案:45°16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________. 解析:设三边长为k -1,k ,k +1(k ≥2,k ∈N ),则⎩⎪⎨⎪⎧k 2+k -12-k +12<0k +k -1>k +1⇒2<k <4, ∴k =3,故三边长分别为2,3,4,∴最小角的余弦值为32+42-222×3×4=78. 答案:7817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-23x +2=0的两根,且2cos(A +B )=1,求AB 的长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=12,即cos C =-12. 又∵a ,b 是方程x 2-23x +2=0的两根,∴a +b =23,ab =2.∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-12) =a 2+b 2+ab =(a +b )2-ab=(23)2-2=10,∴AB =10.18.已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边AB 的长;(2)若△ABC 的面积为16sin C ,求角C 的度数.解:(1)由题意及正弦定理得AB +BC +AC =2+1,BC +AC =2AB ,两式相减,得AB =1.(2)由△ABC 的面积12BC ·AC ·sin C =16sin C ,得BC ·AC =13, 由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC =AC +BC 2-2AC ·BC -AB 22AC ·BC =12, 所以C =60°.19.在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -π4)的值. 解:(1)在△ABC 中,由正弦定理AB sin C =BC sin A, 得AB =sin C sin ABC =2BC =2 5. (2)在△ABC 中,根据余弦定理,得 cos A =AB 2+AC 2-BC 22AB ·AC =255, 于是sin A =1-cos 2A =55. 从而sin 2A =2sin A cos A =45, cos 2A =cos 2 A -sin 2 A =35. 所以sin(2A -π4)=sin 2A cos π4-cos 2A sin π4=210.20.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.解:由正弦定理,得sin C sin B =c b. 由2cos A sin B =sin C ,有cos A =sin C 2sin B =c 2b. 又根据余弦定理,得cos A =b 2+c 2-a 22bc ,所以c 2b =b 2+c 2-a 22bc, 即c 2=b 2+c 2-a 2,所以a =b .又因为(a +b +c )(a +b -c )=3ab ,所以(a +b )2-c 2=3ab ,所以4b 2-c 2=3b 2,所以b =c ,所以a =b =c ,因此△ABC 为等边三角形.。
正弦定理与余弦定理【参考答案】

正弦定理、余弦定理《参考答案》【1】 a = b = c = 2Rsinsin C sin A B【2】 2 2 - 2bc cos Ab + c【3】 b 2 + c 2 - a 22bc【4】 sin C 【5】 -cos C 【6】 - tan C【7】 cosC2【8】 sinC2【9】 60︒ 【10】 tan A ⋅ tan B ⋅ tan C 【11】c【12】 1ab sin C2 【13】 1xv - yu2【14】一解 【15】正弦定理 【16】一解 【17】余弦定理 【18】讨论 【19】正、余弦定理 【20】一解或无解 【21】余弦定理 【22】无解 【23】无解 【24】一解 【25】无解 【26】无解 【27】一解 【28】两解 【29】一解 【30】无解 【31】一解 【32】一解 【33】相等 【34】相反数 【35】边角互换 【第 1 题】【答案】D【解析】5∵tanA =-12<0,A 是△ABC 的内角,π∴2<A <π.∴cosA <0.∵sin A =tanA =- 5 ,cos A12 且 sin 2A +cos 2A =1,12∴cosA =-13. 【第 2 题】【答案】B【解析】∵C >90°,∴A +B <90°, ∴tan (A +B )>0,tanA +tanB >0, ∴1-tanAtanB >0,即 tanA ·tanB <1. 【第 3 题】【答案】B【解析】∵a 、b 、c 成等比数列,∴b 2=ac . 又 c =2a , ∴b 2=2a 2.a 2+c 2-b2∴cosB =2aca 2+4a 2-2a2=4a23=4.【第 4 题】【答案】C【解析】若 a 为最大边,则 b 2+c 2-a 2>0,即a 2<5, ∴a < 5,若 c 为最大边,则 a 2+b 2-c 2>0,即 a 2>3, ∴a > 3,故3<a < 5.另法:【第 5 题】【答案】C 【解析】由正弦定理得a =b ,sin B sin 30° 3∴sinB = 2 , 又∵B 为锐角, ∴B =60°, ∴C =90°,即 C >B > A .【第 6 题】【答案】C 【解析】由 sinB ·sinC =cos 2A2,得2sinB ·sinC =2cos 2A2=1+cosA ,即 2sinB ·sinC =1-cos (B +C )=1-cosBcosC +sinBsinC ,∴sinB ·sinC +cosBcosC =1,即 cos (B -C )=1,又-π<B -C <π. ∴B -C =0,即 B =C .∴△ABC 为等腰三角形.【第 7 题】【答案】A【解析】正弦定理sin A sin 750sin(3045 )sin 30 0cos 45 0cos 30 0sin 451 2 3 2 2 2 2 226 .4由a c ,得C A 75 0 .∴ B30 0 , sin B1 .2又a 6 2 ,由正弦定理得basin Bsin A6212 .26 24故选 A .另法:余弦定理另法:射影定理b a cos Cc cos A .另法:作高,简单【第 8 题】π【答案】3【解析】由已知得(b +c )2-a 2=3bc ,∴b 2+c 2-a 2=bc . b 2+c 2-a 2 1∴2bc=2,1 ∴cosA =2, π∴A =3.【第 9 题】【答案】5 2【解析】1S △ABC =2ac ·sinB1·c ·sin 45°= 2 c , =2 4又因为 S △ABC =2,所以 c =4 2,由余弦定理得b 2=a 2+c 2-2accosB2=1+32-2×1×4 2× 2=25,∴b =5,b所以△ABC 外接圆的直径 2R =sin B=5 2.【第 10 题】【答案】1【解析】由 A C 2B 及 A B C 180 ,得 B 60 .由正弦定理,得13 sin A ,即sin 60sin A1 .2由a b ,得 A B ,∴ A30 , C180 A B180 306090 ,sin Csin 901.【第 11 题】【答案】2【解析】解:(余弦定理) 由b 2 a 2 c 22ac cos B ,得6 a 22 2 2a cos120 , a 22a4 0 .12 2 1 2∴a 2 .另法:(正弦定理)b c, sin Bsin C sin Cc sin Bb2 sin1206 12∵c b ,∴C B , ∴C 是锐角, C 30 , A 30a c2 .【第 12 题】【答案】 2113【解析】 ∵ cos A = 4 ,cos C = 5,且 A , C 为三角形内角,5 13 ∴ sin A = 3 , sin C = 12, 5 13∴ sin B = sin ( A + C )= sin A cos C + cos A sin C= 6563,由正弦定理得, sin b B = sin aA解得 b 21.13【第 13 题】【答案】【解析】证:a 2b 2c 2 a ∵cos C , cos C ,2b2aba 2b 2c 2 a∴.2ab 2b化简后得b 2 2.c∴b c .∴△ABC 是等腰三角形.另证:∵a2b cos C,由正弦定理,得2R sin A22R sin B cos C∴ 2 sin B cos C sin Asin B Csin B cos C cos B sin C.∴ sin B cos C cos B sin C 0 ,即sin B C 0 ,∴ B C k k Z.∵ B,C 是三角形的内角,∴ B C ,即三角形为等腰三角形. 另证:根据射影定理,有a b cos C c cos B ,又∵a 2b cos C,∴ 2b cos C b cos C c cos B ,∴b cos C c cos B ,即b cos B .c cos C又∵b sin B,c sin C∴sin B cos B ,即sin C cos Ctan B tan C,∴ B C k k Z .∵ B,C 是三角形的内角,∴ B C ,即三角形为等腰三角形.欲证△ABC 为等腰三角形,可证明其中有两角相等,因而在已知条件中化去边元素,使只含角的三角函数.【第 14 题】【答案】【解析】解:∵ cos A3,50 A 180 ,∴ sin A4.5∵ sin B5 4sin A ,13 5A, B 为三角形的内角,∴ B A ,∴ B 为锐角,∴ cos B12.13∴ cos A Bcos A cos B sin A sin B3 124 55 13 5 131665.又 cos C cos 180 A B∴cos C cos A B16.65点评:此题要求在利用同角的正、余弦平方关系时,应根据已知的三角函数值确定角的范围,以便对正负进行取舍.【第 15 题】【答案】【解析】解:(1)∵cos C cos 180 A B∴ cos C cos A B 1 . 2∴C 120 .(2)由题设,得a b 2 3 ab 2∴c 2 a 2 b 2 2ab cos 120a 2b 2 ab(a2ab b )(222 3)10 ,即AB 10 .(3)S1ab sin C ABC 221ab sin 1201 322 23.2【第 16 题】【答案】【解析】解:(1)由题设及 A+B+C=π得sin B= 8 sin 2B2= 8 ⋅1 - cos B= 4(1 - cos B) .2上式两边平方,得16(1 - cos B )2 2B= sin2 2B =1 ,又 sin B +cos∴16(1 - cos B )2 2B =1 ,+ cos∴(17 cos B- 15)(cos B- 1) = 0 ,∴cos B= 15 ,或 cos B=1(舍去). 17(2)由(1)可知sin B=8.17∵S△ABC=2,∴1 ac sin B =2,2∴1 ac ⋅ 8 = 2,2 17∴ac =17,2∵cos B=15 ,17∴a 2+ c 2- b2 = 15,2 ac 17∴a 2+ c 2- b2=15,∴( a+c ) 2- 2 ac-b2=15 ,又a + c =6,∴36 - 17 -b2=15 ,∴b =2.。
08正弦定理与余弦定理(含经典例题+答案)

正弦定理与余弦定理(1)S =12a ·h a (h a 表示边a 上的高);(2)S =12ab sin C =12ac sin B =12bc sin A ;(3)S =12r (a +b+c )(r 为内切圆半径).例1:在ABC ∆中,下列等式总能成立的是 ( )A ()C sin sin ab C bcB = ()D sin sin aC c A =B = ( )例4.在ABC △中,设,,a b c 满足条件 b c bc a +-=,求A ∠。
.解: αβcos cos A b =sin cos sin cos A A B B ⇒=;11sin 2sin 2;222+2=18022A B A B A B ∴==︒或故△ABC 为等腰或者直角三角形。
例7.已知△ABC 中,a =4,b =34,∠A =30°,则∠B 等于解:4433sin sin sin sin30sin 2a b B A B B =⇒=⇒=︒,根据三角形大边对大角,B 可以为锐角或者钝角,故∠B=60°或120°ABC ∆A.0020,45,80b A C === B.030,28,60a c B === C.014,16,45a b A === D. 012,15,120a c A === 解:A 选项的已知条件是ASA ,故只有一解;B 选项的已知条件是SAS ,故只有一解;C 选项是SSA ,无全等的三角形定理,且大边b 对的角为未知角,42sin 7B =故有两解;D 选项是SSA ,无全等的三角形定理,且大边b 对的角为未知角,小角0120A =但与大边对大角矛盾,故无解。
在△ABC 中,若a =18,b =24,A =45°,则此三角形有 ( ) A .无解 B .两解 C .一解 D .解的个数不确定解:因a sin A =b sin B ,∴sin B =b a sin A =2418sin 45°,∴sin B =223.又∵a <b ,∴B 有两个.例10在△ABC 中,若A b a sin 23=,则B ∠为( )A .3π B.6π C.3π或32π D.6π或65π解:32sin 3232sin 3sin 2sin sin sin 22233a b A a b A A B A B B R R ππ=⇒=⇒=⇒=⇒=或。
正弦定理与余弦定理练习题共3套(附答案)

正弦定理与余弦定理练习第一套正弦定理(一)●作业导航掌握正弦定理,会利用正弦定理求已知两角和任意一边或两边和一边对角的三角形问题.一、选择题(本大题共5小题,每小题3分,共15分)1.已知△ABC 中,a =4,b =43,∠A =30°,则∠B 等于()A .30°B .30°或150°C .60°D .60°或120°2.已知△ABC 中,AB =6,∠A =30°,∠B =120°,则△ABC 的面积为()A .9B .18C .93D .1833.已知△ABC 中,a ∶b ∶c =1∶3∶2,则A ∶B ∶C 等于()A .1∶2∶3B .2∶3∶1C .1∶3∶2D .3∶1∶24.已知△ABC 中,sin A ∶sin B ∶sin C =k ∶(k +1)∶2k (k≠0),则k 的取值范围为()A .(2,+∞)B .(-∞,0)C .(-21,0)D .(21,+∞) 5.在△ABC 中,sin A >sin B 是A >B 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件二、填空题(本大题共5小题,每小题3分,共15分)1.在△ABC 中,若∠B =30°,AB =23,AC =2,则△ABC 的面积是________.2.在△ABC 中,若b =2c sin B ,则∠C =________.3.设△ABC 的外接圆半径为R ,且已知AB =4,∠C =45°,则R =________.4.已知△ABC 的面积为23,且b =2,c =3,则∠A =________.5.在△ABC 中,∠B =45°,∠C =60°,a =2(3+1),那么△ABC 的面积为________.三、解答题(本大题共5小题,每小题6分,共30分)1.在△ABC 中,∠C =60°,BC =a ,AC =b ,a +b =16.(1)试写出△ABC 的面积S 与边长a 的函数关系式.(2)当a 等于多少时,S 有最大值?并求出这个最大值.2.在△ABC 中,已知a 2-a =2(b +c ),a +2b =2c -3,若sin C ∶sin A =4∶13,求a ,b ,c .3.在△ABC 中,求证2tan 2tanBA BA b a b a +-=+-.4.△ABC 中,A 、B 、C 成等差数列,b =1,求证:1<a +c ≤2.5.在一个三角形中,若有一个内角不小于120°,求证:最长边与最短边之比不小于3.参考答案一、选择题(本大题共5小题,每小题3分,共15分)1.D 分析:由正弦定理得,B bA a sin sin =,∴sin B =23sin =aA b ,∴∠B =60°或∠B =120°.2.C 分析:∵∠A =30°,∠B =120°,∴∠C =30°,∴BA =BC =6,∴S △ABC =21×BA ×BC ×sin B =21×6×6×23=93.3.A 分析:由正弦定理得,C cB b A a sin sin sin ==,∴sin A ∶sin B ∶sin C =1∶3∶2=21∶23∶1,∴A ∶B ∶C =30°∶60°∶90°=1∶2∶3.4.D 分析:利用正弦定理及三角形两边之和大于第三边.5.C 分析:A >B ⇔a >b ⇔2Rsin A >2Rsin B ⇔sin A >sin B .二、填空题(本大题共5小题,每小题3分,共15分)1.23或3分析:sin C =23230sin 32=︒,于是,∠C =60°或120°,故∠A =90°或30°,由S △ABC =21×AB ×AC ×sin A ,可得S △ABC =23或S △ABC =3.2.30°或150°分析:由b =2c sin B 及正弦定理C cB B c Cc B b sin sin sin 2sin sin ==得,∴sin C =21,∴∠C =30°或150°.3.22分析:∵c =2R sin C ,∴R =22sin 2=C c.4.60°或120°分析:∵S △ABC =21bc sin A ,∴23=21×2×3sin A ,∴sin A=23,∴∠A =60°或120°.5.6+23分析:∵B bA a sin sin =,∴︒=︒-︒-︒+45sin )6045180sin()13(2b,∴b =4.∴S △ABC =21ab sin C =6+23.三、解答题(本大题共5小题,每小题6分,共30分)1.解:(1)∵a +b =16,∴b =16-aS =21ab sin C =21a (16-a )sin60°=43(16a -a 2)=-43(a -8)2+163(0<a <16)(2)由(1)知,当a =8时,S 有最大值163.2.解:∵sin C ∶sin A =4∶13∴c ∶a =4∶13设c =4k ,a =13k ,则⎪⎩⎪⎨⎧-=++=-38213)4(213132k b k k b kk∵k =133时b <0,故舍去.∴k =1,此时a =13,b =2135-,c =4.3.证明:由正弦定理,知a =2R sin A ,b =2R sin B2tan2tan2cos 2sin 22cos 2sin 2)22sin(22sin()22sin()22sin(sin sin sin sin sin 2sin 2sin 2sin 2B A B A B A B A B A B A B A B A B A B A B A B A B A B A BA BA B R A R B R A R b a b a +-=-++-=--++-++--+--++=+-=+-=+-∴4.证明:∵A 、B 、C 成等差数列,∴2B =A +C ,又A +B +C =π,∴B =3π,A +C =32π.∵b =1,设△ABC 的外接圆半径为R ,∴b =2R sin 3π∴1=2R ·23,∴3R =1.∴a +c =2R sin A +2R sin C =2R (sin A +sin C )=2R [sin(32π-C )+sin C ]=2R (23cos C +23sin C )=23R (21cos C +23sin C )=23R sin(C +6π)=2sin(C +6π)∵A +C =32π,∴0<C <32π∴6π<C +6π<65π∴21<sin(C +6π)≤1∴1<2sin(C +6π)≤2 ∴1<a +c ≤2.5.证明:在△ABC 中,设C ≥120°,则c 最长,令最短边为a ,由正弦定理得A B A A C a c sin )sin(sin sin +==∵A ≤B∴2A ≤A +B ≤180°-C ≤60°∵正弦函数在(0,3π)上是增函数,∴sin(A +B )≥sin2A >0∴A B A a c sin )sin(+=≥A A A A A sin cos sin 2sin 2sin ==2cos A ∴a c≥2cos A ∵2A ≤60° ∴0°<A ≤30°∴cos A ≥cos30°=23∴a c ≥2·23∴a c≥3∴最长边与最短边之比不小于第二套正弦定理练习(二)1.在ABC ∆中,已知角04345,2,,3B c b ===则角A 的值是()A.15°B.75°C.105°D.75°或15°2.ABC ∆中,bsinA<a<b,则此三角形有()A.一解B.两解C.无解D.不确定3.若sin cos cos ,A B CABC a b c==∆则是()A.等边三角形B.有一内角是30°C.等腰直角三角形D.有一内角是30°的等腰三角形4.在ABC ∆中,已知0060,45,8,B C BC AD BC ===⊥于D,则AD 长为()A.4(31)- B.4(3+1)3+3)D.4(33)5.在ABC ∆中,A>B 是sinA>sinB 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在ABC ∆中,060,6,14B b a ===,则A=7.在ABC ∆ABC ∆中,已知cos 2cos 21sin 2sin cos ,cos sin B C A B C C B +=+==求证:b=c 且A=900。
正弦定理余弦定理习题及答案

正 余 弦 定 理1.在ABC ∆中,A B >是sin sin A B >的 ( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件 2、已知关于x 的方程22cos cos 2sin02Cx x A B -⋅+=的两根之和等于两根之积的一半,则ABC ∆一定是 ( ) (A )直角三角形(B )钝角三角形(C )等腰三角形(D )等边三角形.3、 已知a,b,c 分别是△ABC 的三个内角A,B,C 所对的边,若a=1,b=3, A+C=2B,则sinC= .4、如图,在△ABC 中,若b = 1,c =3,23C π∠=,则a= 。
5、在ABC ∆中,角,,A B C 所对的边分别为a ,b ,c ,若2a =,2b =,sin cos 2B B +=,则角A 的大小为 .6、在∆ABC 中,,,a b c 分别为角,,A B C 的对边,且274sin cos 222B C A +-= (1)求A ∠的度数(2)若3a =,3b c +=,求b 和c 的值7、 在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.8、如图,在△ABC 中,已知3=a ,2=b ,B=45︒ 求A 、C 及c .1、解:在ABC A B ∆>中,2sin 2sin sin sin a b R A R B A B ⇔>⇔>⇔>,因此,选C .2、【答案】由题意可知:211cos cos cos 2sin 222C CA B -=⋅⋅=,从而2cos cos 1cos()1cos cos sin sin A B A B A B A B =++=+-AB323πcos cos sin sin 1A B A B +=,cos()1A B -=又因为A B ππ-<-<所以0A B -=,所以ABC ∆一定是等腰三角形选C3、【命题立意】本题考察正弦定理在解三角形中的应用.【思路点拨】由已知条件求出B 、A 的大小,求出C ,从而求出sin .C【规范解答】由A+C=2B 及180A B C ++=得60B =,由正弦定理得1sin 60A =得1sin 2A =,由a b <知60A B <=,所以30A =,180C A B =-- 90=,所以sin sin 90 1.C ==4、【命题立意】本题考查解三角形中的余弦定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴由余弦定理可得:cosC= = = .
故答案为: .
14.(2016•抚顺一模)已知△ABC的周长为 +1,且sinA+sinB= sinC,则边AB的长为1.
【解答】解:由题意及正弦定理,得:AB+BC+AC= +1.
BC+AC= AB,
两式相减,可得AB=1.
故答案为:1.
15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于1.
(1)求角A的值;
(2)若a= ,则求b+c的取值范围.
【解答】解:(1)在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2 =a﹣2a• ,
利用正弦定理可得(sinB﹣2sinC)cosA=sinA(﹣cosB),
即sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,
【解答】解:(1)∵ .
∴由正弦定理,得 ,化简得cosA= ,
∴A= ;
(2)∵∠B= ,∴C=π﹣A﹣B= ,
可知△ABC为等腰三角形,
在△AMC中,由余弦定理,得AM2=AC2+MC2﹣2AC•MCcos120°,即7= ,
解得b=2,
∴△ABC的面积S= b2sinC= = .
19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2aco模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是( )
A.等腰三角形B.直角三角形
C.等腰或直角三角形D.等腰直角三角形
【解答】解:根据正弦定理可知∵bcosB=acosA,
∴sinBcosB=sinAcosA
∴sin(B+C)=sinA,又sinA≠0,
∴cosB=﹣ ,而B∈(0,π),
∴B= .
故选:C.
9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则 等于( )
A. B. C. D.
【解答】解:∵A+B+C=π,A=2B,
∴ = = = .
再结合正弦定理得: .
【解答】解:B=π﹣A﹣C= ,△ABC中,由正弦定理可得 ,∴b=2,
故答案为:2.
三.解答题(共4小题)
17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知 =
(1)求角C的大小,
(2)若c=2,求使△ABC面积最大时a,b的值.
【解答】解:(1)∵A+C=π﹣B,即cos(A+C)=﹣cosB,
故选:D.
二.填空题(共7小题)
10.(2016•上海二模)△ABC中, ,BC=3, ,则∠C= .
【解答】解:由 ,a=BC=3,c= ,
根据正弦定理 = 得:
sinC= = ,
又C为三角形的内角,且c<a,
∴0<∠C< ,
则∠C= .
故答案为:
11.(2016•丰台区一模)在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,若b=2asinB,则角A等于30°.
A.2 B.2 C. D.
【解答】解:∵△ABC中,asinAsinB+bcos2A= a,
∴根据正弦定理,得sin2AsinB+sinBcos2A= sinA,
可得sinB(sin2A+cos2A)= sinA,
∵sin2A+cos2A=1,
∴sinB= sinA,得b= ,可得 = .
故选:C.
16.(2016•湖南校级模拟)设△ABC的内角A,B,C的对边分别为a,b,c.若 , ,则b=.
三.解答题(共4小题)
17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知 =
(1)求角C的大小,
(2)若c=2,求使△ABC面积最大时a,b的值.
18.(2016•安徽校级一模)在△ABC中,角A,B,C的对边分别为a,b,c,且 .
即sinC=2sinCcosA,∴cosA= ,∴A= .
(2)若a= ,则由正弦定理可得 = =2,
∴b+c=2(sinB+sinC)=2[sinB+sin( ﹣B)]=3sinB+ cosB=2 sin(B+ ).
由于 ,求得 <B< ,∴ <B+ < .
∴sin(B+ )∈( ,1],∴b+c∈(3,2 ].
∴ bcsinA= bc = ,
∴bc=3,①
又a=2,A是锐角,
∴cosA= = ,
∴由余弦定理得:a2=b2+c2﹣2bccosA,
即(b+c)2=a2+2bc(1+cosA)=4+6(1+ )=12,
∴b+c=2 ②
由①②得: ,
解得b=c= .
故选A.
2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的( )
(Ⅰ)求B;
(Ⅱ)若△ABC的面积为 ,求b的取值范围.
正余弦定理高中数学组卷
参考答案与试题解析
一.选择题(共9小题)
1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若 ,a=2, ,则b的值为( )
A. B. C. D.
【解答】解:∵在锐角△ABC中,sinA= ,S△ABC= ,
A.2 B.2 C. D.
8.(2016•新余二模)在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.角B的值为( )
A. B. C. D.
9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则 等于( )
A. B. C. D.
A.等腰三角形B.直角三角形
C.等腰或直角三角形D.等腰直角三角形
5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且 ,则∠B=( )
A. B. C. D.
6.(2016•宝鸡一模)在△ABC,a= ,b= ,B= ,则A等于( )
A. B. C. D. 或
7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A= a,则 =( )
∴sin2A=sin2B
∴A=B,或2A+2B=180°即A+B=90°,
即有△ABC为等腰或直角三角形.
故选C.
5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且 ,则∠B=( )
A. B. C. D.
【解答】解:已知等式利用正弦定理化简得: = ,即c2﹣b2=ac﹣a2,
故选A.
3.(2016•岳阳校级模拟)在△ABC中,A:B:C=1:2:3,则a:b:c等于( )
A.1:2:3B.3:2:1C.1: :2D.2: :1
【解答】解:在△ABC中,若∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=π
所以∠A= ,∠B= ,∠C= .
由正弦定理可知:a:b:c=sin∠A:sin∠B:sin∠C=sin :sin :sin =1: :2.
正余弦定理高中数学组卷
一.选择题(共9小题)
1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若 ,a=2, ,则b的值为( )
A. B. C. D.
2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的( )
A.充分不必要条件B.必要不充分条件
∴a2+c2﹣b2=ac,
∴cosB= = ,
∵B为三角形的内角,
∴B= .
故选:C.
6.(2016•宝鸡一模)在△ABC,a= ,b= ,B= ,则A等于( )
A. B. C. D. 或
【解答】解:由正弦定理可得:sinA= = =
∵a= <b=
∴
∴∠A= ,
故选:B.
7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A= a,则 =( )
∴由正弦定理化简已知等式得: = ,
整理得:2sinAcosC+sinBcosC=﹣sinCcosB,即﹣2sinAcosC=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,
∴cosC=﹣ ,
∵C为三角形内角,
∴C= ;
(Ⅱ)∵c=2,cosC=﹣ ,
∴由余弦定理得:c2=a2+b2﹣2abcosC,即4=a2+b2+ab≥2ab+ab=3ab,
∴由正弦定理 ,
得:b= = =4 .
故答案为:4
13.(2016•潍坊一模)已知△ABC中,a,b,c分别为内角A,B,C的对边,且a•cosB+b•cosA=3c•cosC,则cosC= .
【解答】解:∵a•cosB+b•cosA=3c•cosC,
∴利用余弦定理可得:a× +b× =3c× ,整理可得:a2+b2﹣c2= ,
【解答】解:利用正弦定理化简b=2asinB得:sinB=2sinAsinB,
∵sinB≠0,∴sinA= ,
