第七章习题解答
普通化学第七章课后习题解答

第七章沉淀反应参考答案P 142【综合性思考题】:给定体系0.02mol/LMnCl 2溶液(含杂质Fe 3+),经下列实验操作解答问题。
(已知K θSPMn(OH)2=2.0×10-13,K θSPMnS =2.5×10-13,K θbNH3=1.8×10-5,K θaHAc =1.8×10-5①与0.20mol/L 的NH 3.H 2O 等体积混合,是否产生Mn(OH)2沉淀?解:等体积混合后浓度减半,[Mn 2+]=0.01mol/L ,c b =[NH 3.H 2O]=0.10mol/L∵是一元弱碱体系,且c b /K b θ>500∴10.0108.1][5⨯⨯=⋅=--b b c K OH θ又∵ 622108.101.0][][--+⨯⨯=⋅=OH Mn Q c=1.8×10-8> K θSPMn(OH)2=2.0×10-13∴ 产生Mn(OH)2沉淀。
②与含0.20mol/L 的NH 3.H 2O 和0.2mol/LNH 4Cl 的溶液等体积混合,是否产生Mn(OH)2沉淀? 解:混合后属于NH 3.H 2O~NH 4Cl 的碱型缓冲液体系此时浓度减半:c b =[NH 3.H 2O]=0.2V/2V=0.1(mol.L -1)c S= [NH 4+]=0.2V/2V=0.1(mol.L -1)[Mn 2+]=0.02V/2V=0.01(mol.L -1)A 、求[OH -] 用碱型缓冲液计算式求算:s b b c c K OH ⋅=-θ][ 55108.11.01.0108.1--⨯=⨯⨯= B 、求Qc 22][][-+⋅=OH Mn Q c=0.01×[1.8×10-5]2=3.24×10-12C 、比较θ2)(,OH Mn SP K ∵13)(,100.22-⨯=>θOH Mn SP C K Q故有Mn(OH)2沉淀产生。
第七章 习题答案
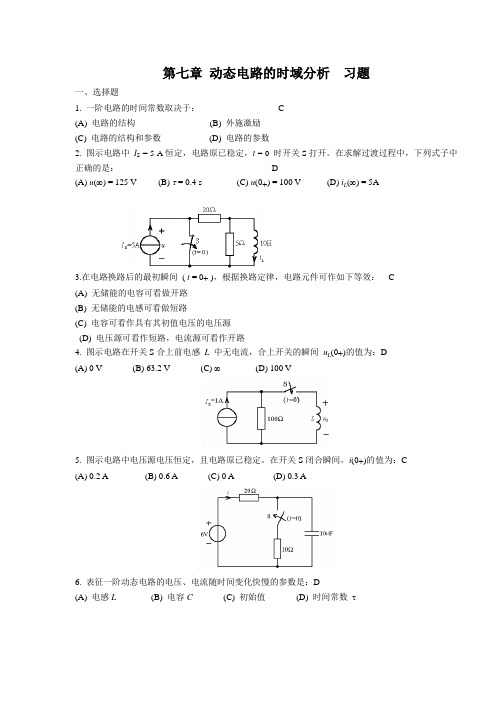
第七章动态电路的时域分析习题一、选择题1. 一阶电路的时间常数取决于: C(A) 电路的结构(B) 外施激励(C) 电路的结构和参数(D) 电路的参数2. 图示电路中I S = 5 A恒定,电路原已稳定,t = 0时开关S打开。
在求解过渡过程中,下列式子中正确的是: D(A) u(∞) = 125 V (B) τ = 0.4 s (C) u(0+) = 100 V (D) i(∞) = 5AL3.在电路换路后的最初瞬间( t = 0+ ),根据换路定律,电路元件可作如下等效: C(A) 无储能的电容可看做开路(B) 无储能的电感可看做短路(C) 电容可看作具有其初值电压的电压源(D) 电压源可看作短路,电流源可看作开路(0+)的值为:D4. 图示电路在开关S合上前电感L中无电流,合上开关的瞬间uL(A) 0 V (B) 63.2 V (C) ∞(D) 100 V5. 图示电路中电压源电压恒定,且电路原已稳定。
在开关S闭合瞬间,i(0+)的值为:C(A) 0.2 A (B) 0.6 A (C) 0 A (D) 0.3 A6. 表征一阶动态电路的电压、电流随时间变化快慢的参数是:D(A) 电感L(B) 电容C(C) 初始值(D) 时间常数τ7. 图示正弦脉冲信号的数学表达式为:B (A) sin ω t ⋅ ε (t ) + sin ω ( t - T ) ⋅ ε ( t - T ) (B) sin ω t ⋅ ε (t ) - sin ω t ⋅ ε ( t - T ) (C) sin ω t ⋅ ε (t ) - sin ω ( t - T ) ⋅ ε ( t - T ) (D) sin ω t ⋅ ε (t ) + sin ω t ⋅ ε ( t - T )8. 图示电路中,原已达稳态, t = 0开关 S 打开,电路的时间常数为:D (A)s 41 (B) s 61(C) s 4 (D)s 69. 示电路中,t = 0 时开关打开,则 u (0+)为:C(A) 0V (B) 3.75V (C) – 6V (D) 6V10.图示电路中,开关打开已久,在 t = 0 时开关闭合,i (0+) 为:D(A) 0A (B) 0.8A(C) 2A (D)1A11.R 、C 串联电路,已知全响应()()10C 83V,0t u t e t -=-≥,其零状态响应为:(A )(A) 1088V te-- (B) 1083V t e -- (C) 103V t e -- (D) 105V t e -12. .一阶电路的全响应()()10C 106V,0tu t et -=-≥若初始状态不变而输入增加一倍,则全响应u C (t)为 ( D ) (A) 20-12e -10t ; (B) 20-6e -10t ; (C) 10-12e -10t ; (D) 20-16 e -10t 。
最新(完美版)第七章习题答案_数值分析

第七章习题解答2、试确定系数a ,b 的值使220[()cos ]ax b x dx p+-ò达到最小解:设220(,)[()cos ]I a b ax b x dx p=+-ò确定a ,b 使(,)I a b 达到最小,必须满足0,0I Ia b ¶¶==¶¶即3222222000022222000012[cos ]0cos 248212[cos ]0cos 82a b ax b x xdx a x dx b xdx xxdx a b ax b x dx a xdx b dx xdx p p p p p p p pp p p p p ììì+=-+-=+=ïïïïïïÞÞíííïïï+=+-=+=ïïïîîîòòòòòòòò解得:0.6644389, 1.1584689a b »-»5、试用Legendre 多项式构造()f x x =在[-1, 3]上的二次最佳平方逼近多项式 解:作变量代换,将区间[-1, 3]变为[-1, 1],令21x t =+,即12x t -=则()()(21)21(11)F t f x f t t t ==+=+-££对()F t 利用Legendre 多项式求其在}{21,,span t t上的最佳平方逼近多项式20()()j j j S t C P t ==å,其中11(,)21()()(0,1,2)(,)2j j j j j P f j C F t P t dt j P P -+===ò20121()=1,()=t,()=(31)2P t P t P t t - 则有:1121012112111212212121215[(21)(21)]24311[(21)(21)]285(31)(31)45[(21)(21)]22264C t dt t dt C t tdt t tdt t t C t dt t dt ---------=--++==--++=--=--++=òòòòòò 01251145()()()()4864S t P t P t P t \=++则()f x 在[-1, 3]上的最佳二次逼近多项式*01222151111451()()()()()()2428264251114511=()((3()1))4826422135+82243512x x x x S t S t S P P P x x x x ----===++--++-+=7、确定一条经过原点的二次曲线,使之拟合下列数据ix123iy0.2 0.5 1.0 1.2并求平方误差2d解:设2012()1,(),()x x x x x j j j ===由题,拟合函数须过原点 则令001122()()()()f x C x C x C x j j j =++,其中00C =,即212()f x C x C x =+ 12000.2110.5,,24 1.039 1.2Y f f æöæöæöç÷ç÷ç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷ç÷ç÷èøèøèø 11122122(,)(,)1436(,)(,)3698G f f f f f f f f æöæö==ç÷ç÷èøèø 12(,) 6.1(,)15.3Y F Y f f æöæö==ç÷ç÷èøèø得法方程GC F = 121436 6.1369815.3C C æöæöæö=ç÷ç÷ç÷èøèøèø解方程得:120.61840.0711C C »»-2()0.61840.0711f x x x \=-误差222121(,) 2.730.6184(,)0.0711(,)0.04559j j j YC Y Y Y df f f ==-=-´+´=å8、已知一组数据ix1 2 3iy3 2 1.5试用拟合函数21()S x a bx =+拟合所给数据解:令2()f x a bx =+ 201()1,()x x x j j ==01()()()f x a x b x j j =+则123113111114,219213y A F y y æöæö÷ç÷çæöç÷ç÷ç÷ç÷===ç÷ç÷ç÷ç÷èøç÷ç÷ç÷ç÷èøèøT T a A A A F b æö\=ç÷èø,即331422514983a b æöç÷æöæö=ç÷ç÷ç÷ç÷èøèøç÷èø解方程组得0.3095,0.0408a b == 即210.30950.0408()x f x y=+=从而有21()0.30950.0408S x x =+补充题:用插值极小化法求()sin f x x =在[0, 1]上的二次插值多项式2()P x ,并估计误差 解:作变量替换1(1)2x t =+,将[0, 1]变换[-1, 1]取插值点11(21)cos 0,1,2222(1)K K x K n p+=+=+ 0120.933001270.50.0669873x x x ===利用这些点做插值商表i xi y一阶插商 二阶插商0.9330127 0.80341740.5 0.479425 0.74863250.0669873 0.0659372 0.9549092 -0.23818779则:20.9330127()0.80)0.2341740.743818779(0.9330127)(0.5)86325(x P x x x ---=+-同时误差213322()()()22(1)!3!24n n M M M R x f x P x n --+=-£==+其中(3)3max ()M f x = 由于1(1)2x t =+,即21t x =- 则(3)(3)3max (21)max sin (21)8max cos(21)8[0,1]M f x x x x =-=-=-=Î281()243R x \£=。
大学物理习题答案解答第七章直流电路

第七章 直流电路二、填空题1、0S j dS ⋅=⎰⎰或0j ∇⋅=2、非静电力3、充电,放电4、串联时,两导线的电流强度相等,即12I I =,因截面积12:3:1S S =,所以电流密度大小121212::1:3I I j j S S ==,再由欧姆定律的微分形式j E σ=(其中σ是导体的电导率,通常仅与导体材料和温度有关,此处12σσ=),可得两导线的电场之比为121212::1:3j j E E σσ==;若将二导线并联,接上同一电池,则12εε=,因导线长度12l l =,注意到导线电动势与电场满足关系El ε=,所以两导线的电场之比为121212::1:1E E l l εε== 因导线的电阻满足l R S ρ=(其中1ρσ=是导体的电阻率,此处12ρρρ==)。
所以两导线的电阻之比为 12121212::1:3l l R R S S ρρ== 不妨记01R R =,则203R R =,当两导线串联时,总电阻1204R R R R =+=,电源输出功率为221=4P I R R εεε==串 当两导线并联时,由11112R R R ---=+,可得总电阻034R R =,电源输出功率为 2204=3P R R εε=并所以,电池供给的总电功率之比为220014:=:=3:1643P P R R εε串串5、零6、升高,降低。
三、选择题1、选A2、选C3、选B4、质量为m ,电量为q 的油滴静止时,设其所在位置的电场强度大小为E ,则有qE mg =当电荷量减小时,为维持该油滴仍处于静止状态,需要增大其所在位置处的电场强度。
因平行板电容器内电场是匀强场,由课本平行板电容器的电容一节可知两极板电势差为0AB Qd V Ed Sε== 由此可得电容内部电场强度0Q E Sε= 因所给选项均无法改变电场强度大小,故不选。
5、选D 。
四、计算题1、解:记四个灯泡的通电电阻为12340 6.0R R R R R =====Ω,电源电动势和内阻分别为ε和r 。
第七章习题答案解析

第七章 不完全竞争的市场1、根据图中线性需求曲线d 和相应的边际收益曲线MR ,试求:(1)A 点所对应的MR 值;(2)B 点所对应的MR 值。
解答:(1)根据需求的价格点弹性的几何意义,可得A 点的需求的价格弹性为:25)515(=-=d e 或者 2)23(2=-=d e 再根据公式)11(d e P MR -=,则A 点的MR 值为:MR=2×(2×1/2)=1 (2)与(1)类似,根据需求的价格点弹性的几何意义,可得B 点的需求的价格弹性为:21101015=-=d e 或者 21131=-=d e 再根据公式d e MR 11-=,则B 点的MR 值为:1)2111(1-=-⨯=MR 2、图7-19是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC 曲线和SMC 曲线;(3)长期均衡时的利润量。
解答:本题的作图结果下图所示:(1)长期均衡点为E 点,因为,在E 点有MR=LMC 。
由E 点出发,均衡价格为P 0,均衡数量为Q 0。
(2)长期均衡时代表最优生产规模的SAC 曲线和SMC 曲线如图所示。
在Q 0 的产量上,SAC 曲线和LAC 曲线相切;SMC 曲线和LMC 曲线相交,且同时与MR 曲线相交。
(3)长期均衡时的利润量有图中阴影部分的面积表示,即л=(AR(Q 0)-SAC(Q 0)Q 03、已知某垄断厂商的短期成本函数为30001461.023++-=Q Q Q STC ,反需求函数为P=150-3.25Q求:该垄断厂商的短期均衡产量与均衡价格。
解答:因为140123.02+-==Q Q dQ dSTC SMC且由225.3150)25.3150()(Q Q Q Q Q Q P TR -=-==得出MR=150-6.5Q根据利润最大化的原则MR=SMCQ Q Q 5.6150140123.02-=+-解得Q=20(负值舍去)以Q=20代人反需求函数,得P=150-3.25Q=85所以均衡产量为20 均衡价格为854、已知某垄断厂商的成本函数为236.02++=Q Q TC ,反需求函数为P=8-0.4Q 。
第7章习题详细解答

第7章习题解答7—1判断题(对的打√,不对的打×)1。
数字电路分为门电路和时序逻辑电路两大类。
(× )2。
边沿触发器和基本RS触发器相比,解决了空翻的问题.(×)3. 边沿触发器的状态变化发生在CP上升沿或下降沿到来时刻,其他时间触发器状态均不变。
(√)4. 基本RS 触发器的输入端就是直接置0端和直接置1端。
(√)23 的计数器。
(×)5。
3位二进制计数器可以构成模为16。
十进制计数器最高位输出的周期是输入CP脉冲周期的10倍。
(√)7. 构成一个7进制计数器需要7个触发器。
(×)8.当时序电路存在无效循环时该电路不能自启动.( √)9。
寄存器要存放n位二进制数码时,需要n2个触发器。
(×)10.同步计数器的计数速度比异步计数器快。
(√)11。
在计数器电路中,同步置零与异步置零的区别在于置零信号有效时,同步置零还需要等到时钟信号到达时才能将触发器置零,而异步置零不受时钟的控制。
(√)12。
计数器的异步清零端或异步置数端在计数器正常计数时应置为无效状态。
(√)13。
自启动功能是任何一个时序电路都具有的。
(× )14。
无论是用置零法还是用置数法来构成任意N进制计数器时,只要置零或置数控制端是异步的,则在状态循环过程中一定包含一个过渡状态;只要是同步的,则不需要过渡状态。
(√)15。
用置零法或置位法可以设计任意进制的计数器.(×)7—2 由或非门组成的基本RS触发器如图7—38所示,已知R、S的电压波形,试画出与之对应的Q和Q的波形。
图7—38 题7-2图解:由或非门组成的基本RS触发器的特性表,可得该题的输出端波形如下图所示:或非门RS 触发器特性表 题7—2 波形图7—3由与非门组成的基本RS 触发器如图7-39所示,已知R 、S 的电压波形,试画出与之对应的Q 和Q 的波形。
图7-39 题7-3图解:由与非门组成的基本RS 触发器的特性表,可得该题的输出端波形如下图所示:与非门RS 触发器特性表 题7—3波形图7-4已知如图7-40所示的各触发器的初始状态均为0,试对应画出在时钟信号CP 的连续作用下各触发器输出端Q 的波形。
(完整版)大学物理学(课后答案)第7章

第七章课后习题解答一、选择题7-1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[ ](A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强 (C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析:理想气体分子的平均平动动能32k kT ε=,仅与温度有关,因此当氦气和氮气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式p nkT =,当两者分子数密度相同时,它们压强也相同。
故选(C )。
7-2 理想气体处于平衡状态,设温度为T ,气体分子的自由度为i ,则每个气体分子所具有的[ ](A) 动能为2i kT (B) 动能为2iRT(C) 平均动能为2i kT (D) 平均平动动能为2iRT分析:由理想气体分子的的平均平动动能32k kT ε=和理想气体分子的的平均动能2ikT ε=,故选择(C )。
7-3 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()1/21/21/222::2A B Cv v v =1:2:4,则其压强之比为A B C p :p :p[ ](A) 1:2:4 (B) 1:4:8 (C) 1:4:16 (D) 4:2:1=,又由物态方程p nkT =,所以当三容器中得分子数密度相同时,得123123::::1:4:16p p p T T T ==。
故选择(C )。
7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果()2p O v 和()2p H v 分别表示氧气和氢气的最概然速率,则[ ](A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析:在温度相同的情况下,由最概然速率公式p ν=质量22H O M M <,可知氢气的最概然速率大于氧气的最概然速率,故曲线a 对应于氧分子的速率分布曲线。
(完整版)高等代数(北大版)第7章习题参考答案

第七章 线性变换1. 判别下面所定义的变换那些是线性的,那些不是:判别下面所定义的变换那些是线性的,那些不是:1) 在线性空间V 中,A αξξ+=,其中∈αV 是一固定的向量;是一固定的向量; 2) 在线性空间V 中,A αξ=其中∈αV 是一固定的向量;是一固定的向量;3) 在P 3中,A),,(),,(233221321x x x x x x x +=; 4) 在P 3中,A ),,2(),,(13221321x x x x x x x x +-=; 5) 在P[x ]中,A )1()(+=x f x f ;6) 在P[x ]中,A ),()(0x f x f =其中0x ∈P 是一固定的数;是一固定的数;7) 把复数域上看作复数域上的线性空间,把复数域上看作复数域上的线性空间,A ξξ=。
8) 在P nn ⨯中,A X=BXC 其中B,C∈P nn ⨯是两个固定的矩阵. 解 1)当0=α时,是;当0≠α时,不是。
不是。
2)当0=α时,是;当0≠α时,不是。
不是。
3)不是.例如当)0,0,1(=α,2=k 时,k A )0,0,2()(=α, A )0,0,4()(=αk ,A ≠)(αkk A()α。
4)是.因取),,(),,,(321321y y y x x x ==βα,有A )(βα+= A ),,(332211y x y x y x +++=),,22(1133222211y x y x y x y x y x ++++--+ =),,2(),,2(1322113221y y y y y x x x x x +-++- = A α+ A β, A =)(αk A ),,(321kx kx kx),,2(),,2(1322113221kx kx kx kx kx kx kx kx kx kx +-=+-==k A )(α, 故A 是P 3上的线性变换。
上的线性变换。
5) 是因任取][)(],[)(x P x g x P x f ∈∈,并令并令 )()()(x g x f x u +=则A ))()((x g x f += A )(x u =)1(+x u =)1()1(+++x g x f =A )(x f + A ))((x g , 再令)()(x kf x v =则A =))((x kf A k x kf x v x v =+=+=)1()1())((A ))((x f , 故A 为][x P 上的线性变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X
X EX
X
4.解
由于
EXi
,i
1, 2, 3,故得
E
1
E
2
E
3
,而
E
4
6 7
,
所以 1, 2 , 3 为 的无偏估计,而 4 为 的有偏估计,故舍去 4 .
又由于 X1, X 2 , X3 相互独立,且 DX i 2 , i 1, 2, 3 ,故计算得
D
1
7 18
2,
D
2
1 3
i 1
i 1
由 d ln L
d
2n
n i 1
xi
0 ,得 的最大似然估计量为 ˆ
2 X
.
3.解 由 E( X kS 2 ) E X kES 2 EX kDX np knp(1 p) np2 ,得 k 1 .
4.解
n
n
E(
X
2 i
)
E( X i 2) nE( X
i 1
1 2
1 6
4
n i 1
zi2
2
0 ,解得
1 3n
n
Zi2 .
i 1
⑶由于
2
E( )
1 3n
n i 1
E (Zi2
)
1 3
E(Z 2)
1 [DZ 3
( EZ)2
]
1 (3 2 3
02 )
2 ,所
^
以 2 为 2 的无偏估计量.
10.证 由于 E X EY ) ,故
Eˆ1
1 2
(E
X
EY
由于U 0.05
1 n
10.235 10
0.235 ,且U0.05
1.645 ,故
1 0.235 1 , n 1.645 7
解得 n 49 ,所以(B)正确.
由 于 U0 . 0 25 1 . 9 6, 故 的 置 信 度 为 95% 的 置 信 区 间 为 (x U0.025
1 ) n
的置信区间为
(
(n 1)
2
(n
1)
s,
(n 2
1
1) (n
1)
s)
(
9 35.22 , 16.919
9 35.22) (25.69,57.94) . 3.325
2
2
14. 解 设 机 器 A 生 产 的 钢 管 内 径 为 X , 机 器 B 生 产 钢 管 的 内 径 为 Y , 则
X
~
)
1 2
(
)
,
Eˆ2
1 3
(E
X
2EY
)
1 3
(
2)
,
所以 ˆ1, ˆ2 均为 的无偏估计.
又由于 D X 1 , DY 1 ,且 X 与Y 相互独立,故
n
2n
Dˆ1
1 4
(DX
DY )
1 4
(1 n
1) 2n
3 8n
,
Dˆ2
1 9
(DX
4DY )
1 9
(1 n
4
1) 2n
1 3n
.
因为 Dˆ1 Dˆ2 ,所以 ˆ2 比 ˆ1 更有效.
f (z, 2)
1
e
z2 6 2
,
z
(,
)
.
6
n
⑵似然函数为 L 2 (
1
zi2 e ) (6 ) ( ) e 6 2
n 2
,则 2
n 2
1 6 2
n i1
zi2
i1 6
ln
L
2
n 2
ln(6
)
n 2
ln(
2
)
1 6
2
n i 1
zi2
,
令
d
ln L 2 d ( 2 )
n 2
2,
D
4
9 25
2
,
其中 D 2 最小,故选(B).
5.解
E
X
2 1
DX1
EX1 2
2
02
2
,所以
X12
为
2
的无偏估计.
E[( X1 X 2 )2 ] D( X1 X 2 ) [E( X1 X 2 )]2 2 2 2 ,所以 ( X1 X 2 )2 为 2 的
有偏估计,舍去.
E 1 n
n i 1
X
2 i
1 n
n i 1
E
X
2 i
1 n
n
2
i 1
2 ,所以 1 n
n i 1
X
2 i
为 2 的无偏估计.
ES 2 2 ,所以 S 2 为 2 的无偏估计.
由 于 X12 ~ 2 , 所 以 D X12 2 , 得
2
2
D 1
n
n i 1
X
2 i
1 n2
n
D
X
2 i
i 1
n;
L( ) 为
的单增函数,而
的取值范围为
min
1in
xi
,故当
min
1in
xi
时,
L( ) 取最
大值,所以
最大似然估计量
min
1in
Xi
,选(A).
2.解 因为 Eaˆ b aEˆ b a b ,而 Eˆ2 Dˆ Eˆ2 Dˆ 2 2 , 所以 aˆ b 是 a b 的无偏估计,ˆ2 是 2 的有偏估计,选(B).
2
s n
,
x
t
2
(n
1)
s) n
(457.5 2.2622 35.22 , 457.5 2.2622 35.22) (432.3047, 482.6953) .
10
10
⑵
由于
未知,且 n 10, 1
0.90
,得
2 0.05
(9)
16.919,
2 0.95
(9)
3.325
,
的
置信水平为
0.90
3.解 因为 E X EX 1 ,所以 X 是 1 的无偏估计.
由于 X 为连续型随机变量,故对于任意的常数 a ,P{X a} 0 ,所以不存在常数 a ,
使得 P{ X a 1 } 1或 P{ 1 a X } 1 ,利用柯西-许瓦兹不等式得 E X E 1
X
X
X
[E( X 1 )]2 E12 1,得 E 1 1 ,所以 1 是 的有偏估计,选(C).
6.解
由于 2
1,所以 的置信度为1 的置信区间为 (x
n
U
2
,
x
n
U
2
)
,
将 x 40, 1 , n 16, 0.05, U U0.025 1.96 代入其中,即得 的置信度为 0.95
2
的置信区间是 (39.51, 40.49) .
7.解
由于
未知,且 n
10, 1
N (1,12 ) ,Y
~
N
(2
,
2 2
)
,而两总体方差未知但相等,故 1
2 的置信度为1
的置信区间为
((x y) t (n1 n2 2)s
2
11
n1
, n2
(x y) t (n1 n2 2)s
2
1 1 ), n1 n2
其中 s
(n1
1)
s
2 X
(n2
1) sY2
p
p
p 的矩估计量为
pM
1 X
.
⑵ 似然函数为 L(x1, x2 ,
n
, xn; p)
n
p(1
p)xi 1
pn (1
xi n p) i1
,故
i 1
n
ln L n ln p ( xi n) ln(1 p) , i 1
令
d ln L dp
n p
n
(
i 1
xi
n) 1 1 p
0
,解得
n
42 n
4
因此 4X 2 不是 2 的无偏估计量.
6.解
此为 k
2
的情形.由
X 1
m
1 m
m i 1
Xi
EX
m
( X i X )2 DX
i 1
np, np(1
p)
解得 n
和
p
的矩估计
量为 n
X
1 m
2
X
m
(Xi
i 1
X )2
,
p 1
1 X
1 m
m
(Xi
i 1
X )2 .
7.解 由于
2 2
(1
a
)
2
1 ( n1
2 1
1 n2
2 2
)a
2
2 n2
2 2
a
1 n2
2 2
,
故当 a
2 n2
2 2
2(
1 n1
2 1
2
n212
n1
2 2
,b
1 a
n2
2 1
n2
2 1
n1
2 2
时, DZ
最小.
12. 证
由切比雪夫不等式及概率的性质得
1 P{
} P{ E
}
1
4 n
, x U
0
.
0
2
5
4 n
)
,所以得
l 2U0.025
