运筹学典型考试试题及答案
《运筹学》试题及答案大全

《运筹学》试题及参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为可行解。
2、在线性规划问题中,图解法适合用于处理变量为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点,化为供求平衡的标准形式。
4、在图论中,称无圈的连通图为树。
5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题:1)max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ,解:此题在“《运筹学》复习参考资料.doc ”中已有,不再重复。
2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:可行解域为abcda ,最优解为b 点。
⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =(11,0)T∴min z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:AB C 甲94370乙46101203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解。
(10分)解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z 是产品售后的总利润,则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ,2)用单纯形法求最优解:加入松弛变量x 3,x 4,x 5,得到等效的标准模型:max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下:四、(10分)用大M 法或对偶单纯形法求解如下线性规划模型:min z =5x 1+2x 2+4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解:用大M 法,先化为等效的标准模型:max z /=-5x 1-2x 2-4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7,得到:max z /=-5x 1-2x 2-4x 3-M x 6-M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下:五、(15分)给定下列运输问题:(表中数据为产地A i 到销地B j 的单位运费)B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181)用最小费用法求初始运输方案,并写出相应的总运费;(5分)2)用1)得到的基本可行解,继续迭代求该问题的最优解。
运筹学试题与答案
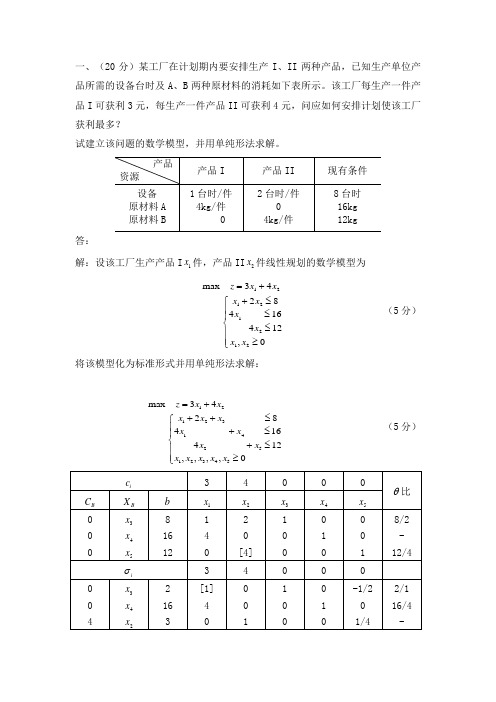
一、(20分)某工厂在计划期内要安排生产I 、II 两种产品,已知生产单位产品所需的设备台时及A 、B 两种原材料的消耗如下表所示。
该工厂每生产一件产品I 可获利3元,每生产一件产品II 可获利4元,问应如何安排计划使该工厂获利最多?试建立该问题的数学模型,并用单纯形法求解。
答:解:设该工厂生产产品I 1x 件,产品II 2x 件线性规划的数学模型为12121212max3428416412,0z x x x x x x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩ (5分) 将该模型化为标准形式并用单纯形法求解:12123142512345max3428416412,,,,0z x x x x x x x x x x x x x x =+++≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ (5分)i σ30 0 0 -1 3 0 4 1x 4x 2x2 83 1 0 0 0 0 1 1 -4 0 0 1 0 -1/2 [2] 1/4 - 8/2 3*4 i σ0 0 -3 0 1/2 3 0 41x 4x 2x4 4 21 0 0 0 0 1 0 -2 1/2 1/4 1/2 -1/8 0 1 0 i σ-2-1/4(8分)因此,最优解()*4,2,0,0,4TX =,最优值*20z =,即生产产品I4件,产品I2件,获得总利润最大为20元。
(2分)二、(20分)已知某运输问题的运价表如下:甲 乙 丙 丁 产量 A B C 6 4 2 7 5 9 5 10 7 8 8 3 8 9 7 销量8655求此运输问题的最优调运方案。
答:解:用伏格尔法给出初始调运方案如下(10分)计算空格的检验数如下甲 乙 丙 丁 产量 A ③ ⑤ 8 B ⑥ ③ 9 C ② ⑤ 7 销量8655甲乙丙丁产量销地产 地(7分)所有检验数都非负,因此,该初始方案即为最优方案,总运费104。
(3分)三、(20分)某工厂用一条生产线生产两种产品A 和B ,每周生产线运行时间为60小时,生产一台A 产品需要4小时,生产一台B 产品需要6小时。
数学:运筹学试题及答案

数学:运筹学试题及答案1、判断题求最小值问题的目标函数值是各分支函数值的下界。
正确答案:对2、填空题动态规划大体上可以分为()、()、()、()四大类。
正确答案:离散确定型;离散随机型;连续确定型;连续随机(江南博哥)型3、多选系统模型按照抽象模型形式可以分为()A.数学模型B.图象模型C.模糊性模型D.逻辑模型E.仿真模型正确答案:A, B, D, E4、单选线性规划一般模型中,自由变量可以代换为两个非负变量的()A.和B.差C.积D.商正确答案:B5、填空题运筹学的目的在于针所研究的系统求得一个合理应用人才,物力和财力的最佳方案。
发挥和提高系统的(),最终达到系统的()。
正确答案:效能及效益;最优目标6、填空题采用人工变量法时,若基变量中出现了()的人工变量,表示在原问题有解。
正确答案:非零7、填空题满足()的基本解称为基本可行解。
正确答案:非负条件8、填空题在箭线式网络图中从始点出发,由各个关键活动连续相接,直到终点的费时最长的线路称为()。
正确答案:关键线路9、单选在求解运输问题的过程中可运用到下列哪些方法()。
A.西北角法B.位势法C.闭回路法D.以上都是正确答案:D10、问答题请简要回答一般系统模型的三个特征。
正确答案:①它是现实世界一部分的抽象和模仿;②它由那些与分析的问题有关的要素所构成;③它表明了系统有关要素间的逻辑关系或定量关系。
11、名词解释初始基本可行解正确答案:多个基本可行解中一个,一般情况下在求最大时取最小的基本可行解,求最小时取最大的基本可行解。
12、名词解释不确定条件下的决策正确答案:指在需要决策的问题中,只估测到可能出现的状态,但状态发生的概率,由于缺乏资源和经验而全部未知。
它属于不确定情况下的决策.13、名词解释时间优化正确答案:时间优化是在人力材料设备资金等资源基本上有保证的条件下寻求最短的工程周期14、填空题企业在采购时,供应方根据批发量的大小定出不同的优惠价格,这种价格上的优惠称为()正确答案:数量折扣15、填空题常用的两种时差是工作总时差和工作()正确答案:自由时差16、多选根据对偶理论,在求解线性规划的原问题时,可以得到以下结论()A.对偶问题的解B.市场上的稀缺情况C.影子价格D.资源的购销决策E.资源的市场价格正确答案:A, C, D17、问答题运用单纯形法求解线性规划问题的步骤是什么?正确答案:(1)确定初始基可行解(2)检验初始基可行解是否最优(3)无解检验(4)进行基变换(5)进行旋转运算,之后回到步骤2,循环直到完成整个问题的求解18、单选设一个线性规划问题(P)的对偶问题为(D),则关于它们之间的关系的陈述不正确的是()。
运筹学试题及详细答案

运筹学试题及详细答案
一、选择题
1、Nash均衡的定义是:
A、每位参与者的行为均达到最佳利益的状态
B、每位参与者的行为均达到得到最大胜利的状态
C、每位参与者的行为均达到合作的最佳状态
D、每位参与者的行为均达到合作的最大胜利的状态
答案:A
2、决策就是参与者用来实现选择的:
A、计划
B、机构
C、程序
D、工具
答案:D
3、运筹学可以分为:
A、组合数学
B、运动学
C、博弈论
D、概率论
答案:A、B、C、D
4、非线性规划有:
A、分支定界法
B、梯度下降法
C、基于格法的解法
D、对偶法
答案:A、B、C、D
5、关于迭代法,下列表述正确的有:
A、可以求解非凸优化问题
B、单次迭代过程简单
C、收敛性较好
D、用于非线性规划
答案:A、B、C
二、填空题:
1、博弈论是研究__参与者之间的__的科学。
答案:多,竞争。
历年运筹学考研试题及答案

历年运筹学考研试题及答案试题:一、单项选择题(每题2分,共10分)1. 线性规划问题的标准形式是:A. 所有变量非负B. 目标函数为最小化C. 约束条件为等式D. 所有变量非负,约束条件为等式和不等式2. 在单纯形法中,如果某个非基变量的检验数为负,则:A. 该变量不能进入基B. 该变量可以进入基C. 该变量必须进入基D. 以上都不对3. 对于运输问题,当供应量等于需求量时,我们称其为:A. 平衡运输问题B. 不平衡运输问题C. 线性运输问题D. 非线性运输问题4. 在动态规划中,最优子结构性质意味着:A. 问题的最优解包含子问题的最优解B. 问题的所有解都包含子问题的最优解C. 问题的一个解包含子问题的最优解D. 以上都不对5. 网络最大流问题中,Ford-Fulkerson算法的核心思想是:A. 寻找增广路径B. 寻找最短路径C. 寻找最长路径D. 寻找最小割二、简答题(每题10分,共20分)1. 简述线性规划的几何意义及其在实际问题中的应用。
2. 解释什么是灵敏度分析,并说明其在解决线性规划问题中的作用。
三、计算题(每题15分,共30分)1. 假设有以下线性规划问题:Max Z = 3x + 4ySubject to:2x + y ≤ 6x + 2y ≤ 7x, y ≥ 0请用图解法找到该问题的最优解。
2. 给定一个网络流问题,网络中有三个节点A, B, C,以及三条边(A,B), (B, C), (A, C),每条边的容量分别为10, 5, 8。
要求从节点A到节点C的最大流量。
使用Ford-Fulkerson算法求解。
四、论述题(每题20分,共20分)1. 论述动态规划与分治法在解决组合优化问题时的异同,并给出一个适合使用动态规划法解决的实际问题例子。
答案:一、单项选择题1. D2. C3. A4. A5. A二、简答题1. 线性规划的几何意义是在n维空间中寻找一个多边形的顶点,这个多边形由约束条件定义,而目标函数则定义了一个目标方向。
运筹学试卷及参考答案

运筹学试卷及参考答案运筹学试卷一、选择题(每小题2分,共20分)1、下列哪个不是线性规划的标准形式?() A. min z = 3x1 + 2x2B. max z = -4x1 - 3x2C. s.t. 2x1 - x2 <= 1D. s.t. x1 + x2 >= 0答案:C2、以下哪个是最小生成树的Prim算法?() A. 按照权值从小到大的顺序选择顶点 B. 按照权值从大到小的顺序选择顶点 C. 按照距离从小到大的顺序选择顶点 D. 按照距离从大到小的顺序选择顶点答案:B3、下列哪个不是网络流模型的典型应用?() A. 道路交通流量优化 B. 人员部署 C. 最短路径问题 D. 生产计划答案:C4、下列哪个是最小化问题中常用的动态规划解法?() A. 自顶向下的递推求解 B. 自底向上的递推求解 C. 分治算法 D. 回溯法答案:A5、下列哪个是最大流问题的 Ford-Fulkerson 算法?() A. 增广路径的寻找采用深度优先搜索 B. 增广路径的寻找采用广度优先搜索 C. 初始流采用最大边的二分法求解 D. 初始流采用最小边的二分法求解答案:B二、简答题(每小题10分,共40分)1、请简述运筹学在现实生活中的应用。
答案:运筹学在现实生活中的应用非常广泛。
例如,线性规划可以用于生产计划、货物运输和资源配置等问题;网络流模型可以用于解决道路交通流量优化、人员部署和生产计划等问题;动态规划可以用于解决最短路径、货物存储和序列安排等问题;图论模型可以用于解决最大流、最短路径和最小生成树等问题。
此外,运筹学还可以用于医疗资源管理、金融风险管理、军事战略规划等领域。
总之,运筹学的理论和方法可以帮助人们更好地解决实际生活中的问题,提高决策的效率和准确性。
2、请简述单纯形法求解线性规划的过程。
答案:单纯形法是一种求解线性规划问题的常用方法。
它通过不断迭代和修改可行解,最终找到最优解。
具体步骤如下: (1) 将线性规划问题转化为标准形式; (2) 根据标准形式构造初始可行基,通常选取一个非基变量,使其取值为零,其余非基变量的取值均为零; (3) 根据目标函数的系数,计算出目标函数值; (4) 通过比较目标函数值和已选取的非基变量的取值,选取最优的非基变量进行迭代; (5) 在迭代过程中,不断修正基变量和非基变量的取值,直到找到最优解或确定无解为止。
运筹学试题及答案

一、填空题:(每空格2分,共16分)1、线性规划的解有唯一最优解、无穷多最优解、 无界解 和无可行解四种。
2、在求运费最少的调度运输问题中,如果某一非基变量的检验数为4,则说明 如果在该空格中增加一个运量运费将增加4 。
3、“如果线性规划的原问题存在可行解,则其对偶问题一定存在可行解”,这句话对还是错? 错4、如果某一整数规划: MaxZ=X 1+X 2 X 1+9/14X 2≤51/14 -2X 1+X 2≤1/3 X 1,X 2≥0且均为整数所对应的线性规划(松弛问题)的最优解为X 1=3/2,X 2=10/3,MaxZ=6/29,我们现在要对X 1进行分枝,应该分为 X1≤1 和 X1≥2 。
5、在用逆向解法求动态规划时,f k (s k )的含义是: 从第k 个阶段到第n 个阶段的最优解 。
6. 假设某线性规划的可行解的集合为D ,而其所对应的整数规划的可行解集合为B ,那么D 和B 的关系为 D 包含 B7. 已知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约问:(1)写出B -1=⎪⎪⎪⎭⎫ ⎝⎛---1003/20.3/1312(2)对偶问题的最优解: Y =(5,0,23,0,0)T8. 线性规划问题如果有无穷多最优解,则单纯形计算表的终表中必然有___某一个非基变量的检验数为0______;9. 极大化的线性规划问题为无界解时,则对偶问题_无解_________; 10. 若整数规划的松驰问题的最优解不符合整数要求,假设X i =b i 不符合整数要求,INT (b i )是不超过b i 的最大整数,则构造两个约束条件:Xi ≥INT (b i )+1 和 Xi ≤INT (b i ) ,分别将其并入上述松驰问题中,形成两个分支,即两个后继问题。
11. 知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束问:(1)对偶问题的最优解: Y =(4,0,9,0,0,0)T (2)写出B -1=⎪⎪⎪⎭⎫ ⎝⎛611401102二、计算题(60分)1、 已知线性规划(20分) MaxZ=3X 1+4X 2 X 1+X 2≤5 2X 1+4X 2≤12 3X 1+2X 2≤8 X 1,X 2≥02) 若C 2从4变成5,最优解是否会发生改变,为什么?3) 若b 2的量从12上升到15,最优解是否会发生变化,为什么?4) 如果增加一种产品X 6,其P 6=(2,3,1)T ,C 6=4该产品是否应该投产?为什么? 解:1)对偶问题为Minw=5y1+12y2+8y3y1+2y2+3y3≥3 y1+4y2+2y3≥4 y1,y2≥02)当C 2从4变成5时, σ4=-9/8 σ5=-1/4由于非基变量的检验数仍然都是小于0的,所以最优解不变。
《运筹学》课程考试试卷试题(含答案)

《运筹学》课程考试试卷试题(含答案)一、选择题(每题5分,共25分)1. 运筹学的核心思想是()A. 最优化B. 系统分析C. 预测D. 决策答案:A2. 在线性规划中,约束条件可以用()表示。
A. 等式B. 不等式C. 方程组D. 矩阵答案:B3. 以下哪个不是运筹学的基本模型?()A. 线性规划B. 整数规划C. 非线性规划D. 随机规划答案:D4. 在目标规划中,以下哪个术语描述的是决策变量的偏离程度?()A. 目标函数B. 约束条件C. 偏差变量D. 权重系数答案:C5. 在动态规划中,以下哪个概念描述的是在决策过程中,某一阶段的最优决策对后续阶段的影响?()A. 最优子结构B. 无后效性C. 最优性原理D. 阶段性答案:B二、填空题(每题5分,共25分)1. 运筹学是一门研究在复杂系统中的______、______和______的科学。
答案:决策、优化、实施2. 在线性规划中,若目标函数为最大化,则其标准形式为______。
答案:max z = c^T x3. 在非线性规划中,若目标函数和约束条件均为凸函数,则该规划问题为______。
答案:凸规划4. 在目标规划中,若决策变量x_i的权重系数为w_i,则目标函数可以表示为______。
答案:min Σ(w_i d_i^+ + w_i d_i^-)5. 在动态规划中,若状态变量为s_n,决策变量为u_n,则状态转移方程可以表示为______。
答案:s_{n+1} = f(s_n, u_n)三、判断题(每题5分,共25分)1. 线性规划问题的最优解一定在可行域的顶点处取得。
()答案:正确2. 在整数规划中,若决策变量为整数,则目标函数和约束条件也必须为整数。
()答案:错误3. 目标规划中的偏差变量可以是负数。
()答案:正确4. 在动态规划中,最优策略具有最优子结构。
()答案:正确5. 在非线性规划中,若目标函数为凸函数,则约束条件也必须为凸函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、计算题(60分)
1、已知线性规划(20分)
MaxZ=3X1+4X2
X1+X2≤5
2X1+4X2≤12
3X1+2X2≤8
X1,X2≥0
2)若C2从4变成5,最优解是否会发生改变,为什么?
3)若b2的量从12上升到15,最优解是否会发生变化,为什么?
4)如果增加一种产品X6,其P6=(2,3,1)T,C6=4该产品是否应该投产?为什么?解:
1)对偶问题为
Minw=5y1+12y2+8y3
y1+2y2+3y3≥3
y1+4y2+2y3≥4
y1,y2≥0
2)当C2从4变成5时,
σ4=-9/8
σ5=-1/4
由于非基变量的检验数仍然都是小于0的,所以最优解不变。
3)当若b2的量从12上升到15
X=9/8
29/8
1/4
由于基变量的值仍然都是大于0的,所以最优解的基变量不会发生变化。
4)如果增加一种新的产品,则
P6’=(11/8,7/8,-1/4)T
σ6=3/8>0
所以对最优解有影响,该种产品应该生产
解:初始解为
计算检验数
由于存在非基变量的检验数小于0,所以不是最优解,需调整 调整为:
重新计算检验数
所有的检验数都大于等于0,所以得到最优解
3、某公司要把4个有关能源工程项目承包给4个互不相关的外商投标者,规定每个承包商只能且必须承包一个项目,试在总费用最小的条件下确定各个项目的承包者,总费用为多少?各承包商对工程的报价如表2所示: (15分)
答最优解为:
X= 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 总费用为50
4. 考虑如下线性规划问题(24分)
Max z=-5x1+5x2+13x3
2012x1+4x2+10x3≤90
≥0
3
2)求对偶问题的最优解
3)当b1由20变为45,最优解是否发生变化。
4)求新解增加一个变量x6,c6=10,a16=3,a26=5,对最优解是否有影响
5)c2有5变为6,是否影响最优解。
答:最优解为
最优解为X1=185/33, X3=35/11
2)对偶问题最优解为
Y=(1/22,1/11,68/33,0,0)T
3)
当b1=45时
X= 45/11
-11/90
由于X2的值小于0,所以最优解将发生变化
4)P6’=(3/11,-3/4)T
σ6=217/20>0
所以对最优解有影响。
5)当C2=6
σ1=-137/33
σ4=4/11
σ5=-17/22
由于σ4大于0所以对最优解有影响
5.求如图所示的网络的最大流和最小截集(割集),每弧旁的数字是(c ij , f ij)。
(15分)
V1
(5,0) (3,3)
(3,3)
V S (4,1)V2
(4,0)
(9,3) (8,4)
V3Vt
(6,0)
最大流为:14
V3 (6,6)
6. 考虑如下线性规划问题(20分)
Max z=3x1+x2+4x3
s.t. 6x1+3x2+5x3≤9
3x1+4x2+5x3≤8
x1,x2,x3≥0
回答以下问题:1)求最优解;2)直接写出上述问题的对偶问题及其最优解;
3)若问题中x2列的系数变为(3,2)T,问最优解是否有变化;
4)c2由1变为2,是否影响最优解,如有影响,将新的解求出。
最优解为X1=1/3,X3=7/5,Z=33/5
2)对偶问题为
Minw=9y1+8y2
6y1+3y2≥3
3y1+4y2≥1
5y1+5y2≥4
y1,y2≥0
对偶问题最优解为y1=1/5,y2=3/5
3)若问题中x2列的系数变为(3,2)T 则P2’=(1/3,1/5)T σ2=-4/5<0 所以。
对最优解没有影响
4)c2由1变为2 σ2=-1<0
所以。
对最优解没有影响
7. 求如图所示的网络的最大流和最小截集(割集),每弧旁的数字是(c ij , f ij )。
(10分)
V 1
(4,4 ) V 3
(9,5) (6,3)
V S (3,1) (3,0) (4,1) Vt
(5,3) (7,5)
V 2 (5,4) V 4
解:
最大流=11
8. 某厂Ⅰ、Ⅱ、Ⅲ三种产品分别经过A 、B 、C 三种设备加工。
已知生产单位各种产品所需的设备台时,设备的现有加工能力及每件产品的预期利润见表:
1)建立线性规划模型,求获利最大的产品生产计划。
(15分)
2)产品Ⅲ每件的利润到多大时才值得安排生产?如产品Ⅲ每件利润增加到50/6元,求最优计划的变化。
(4分) 3)产品Ⅰ的利润在多大范围内变化时,原最优计划保持不变。
(2分) 4)设备A 的能力在什么范围内变化时,最优基变量不变。
(3分)
5)如有一种新产品,加工一件需设备A 、B 、C 的台时各为1、4、3h ,预期每件为8元,是否值得生产。
(3分) 6)如合同规定该厂至少生产10件产品Ⅲ,试确定最优计划的变化。
(3分) 解:1)建立线性规划模型为: MaxZ=10x1+6x2+4x3 x1+x2+x 3≤100 10x1+4x2+5x 3≤600 2x1+2x2+6x 3≤300 x j ≥0,j=1,2,3
获利最大的产品生产计划为:X*=(x1,x2,x3,x4,x5,x6)’=(100/3,200/3,0,0,0,100)’ Z*=2200/3
2)产品Ⅲ每件利润到20/3才值得生产。
如果产品Ⅲ每件利润增加到50/6元,最优计划的变化为:X*=(x1,x2,x3,x4,x5,x6)’=(175/6,275/6,25,0,0,0)’ Z*=775 3)产品Ⅰ的利润在[6,15]变化时,原最优计划保持不变。
4)设备A 的能力在[60,150]变化时,最优基变量不变。
5)新产品值得生产。
6)最优计划的变化为:X*=(x1,x2,x3,x4,x5,x6)’=(190/6,350/6,10,0,0,60 )’ Z*=706.7 9. 给出成性规划问题:(15分) Min z=2x 1+3x 2+6x 3
x 1+2x 2+x 3≥2 -2x 1+x 2+3x 3≤-3 x j ≥0 j=1,…,4 要求:
(1)写出其对偶问题。
(5分) (2)利用图解法求解对偶问题。
(5分) (3)利用(2)的结果,根据对偶问题性质写出原问题最优解。
(5分) 解:1)该问题的LD 为: MaxW=2y1-3y2 y1-2y 2≤2 2y1+y 2≤3 y1+3y 2≤6 y1≥0,y 2≤0
2)用图解法求得LD 的最优解为:Y*=(y1,y2)’=(8/5,-1/5)’ W*=19/5 3)由互补松弛定理:
原问题的最优解为:X*=(x1,x2,x3)’=(8/5,1/5,0)’
10. 某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点(销地)出售,各工厂的生产量,各销售点的销售量(单位.t)以及各工厂到各销售点的单位运价(元/t)示于下表中,要求研究产品如何调运才能使总运量最小?(10分)
B 1 B 2 B 3 B 4 产量 A 1 4 12 4 11 32 A 2 2 10 3 9 20 A 3
8
5 11
6 44 销量 16
28
28
24
96╲96
解:最优调运方案为: A1-B3和B4 28t 和4t A2-B1和B4 16t 和4t A3-B2和B4 28t 和16t 最小总运费为:460元
11. 求解下列0-1规划问题 maxz=3x 1+2x 2-5x 3-2x 4+3x 5
x 1+x 2+x 3+2x 4+x 5≤4 7x 1+3x 3-4x 4+3x 5≤8 11x 1-6x 2+3x 4-3x 5≥3
x j =0或1 (j=1, (5)
解:最优解为:x1=x2=1,其他为0 ,最优目标函数值为5
算题(本大题共5小题,每小题8分,共40分)
销
产
利用对偶理论证明其目标函数值无界。
由于①不成立,所以对偶问题无可行解,由此可知原问题无最优解。
又容易知x=[0,1,0]是原问题的可行解,所以原问题具有无界解,即目标值无界。
25.试用大M法解下列线性规划问题。
25.解:加入人工变量,化原问题为标准形
最优单纯形表如下:
26.福安商场是个中型的百货商场,它对售货人员的需求经过统计分析如下表所示,为了保证售货人员充分休息,售货人员每周工作五天,休息两天,并要求休息的两天是连续的,问该如何安排售货人员的休息,既满足了工作需要,又使配备的售货人员的人数最少,请列出此问题的数学模型。
时间所需售货人员数时间所需售货人员数
星期一 28 星期五 19
星期二 15 星期六 3l
星期三 24 星期日 28
星期四 25
27.某公司拟定扩大再生产的三种方案,给出四种自然状态和益损矩阵(单位:万元)。
试根据以下决策准则选择方案。
①悲观准则;②等概率准则;⑨后悔值准则
③后悔值矩阵
28.A、B两人分别有10分(1角)、5分、1分的硬币各一枚,双方都不知道的情况下各出一枚,规定和为偶数,A 赢得B所出硬币,和为奇数,B赢得A所出硬币,试据此列出二人零和对策模型,并说明此游戏对双方是否公平。
11/ 11。
