多项式的插值实验报告
插值法实验报告

实验二插值法1、实验目的:1、掌握直接利用拉格郎日插值多项式计算函数在已知点的函数值;观察拉格郎日插值的龙格现象。
2、了解Hermite插值法、三次样条插值法原理,结合计算公式,确定函数值。
2、实验要求:1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2)编写上机实验程序,作好上机前的准备工作;3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4)分析和解释计算结果;5)按照要求书写实验报告;3、实验内容:1) 用拉格郎日插值公式确定函数值;对函数f(x)进行拉格郎日插值,并对f(x)与插值多项式的曲线作比较。
已知函数表:(0.56160,0.82741)、(0.56280,0.82659)、(0.56401,0.82577)、(0.56521,0.82495)用三次拉格朗日插值多项式求x=0.5635时函数近似值。
2) 求满足插值条件的插值多项式及余项1)4、题目:插值法5、原理:拉格郎日插值原理:n次拉格朗日插值多项式为:Ln (x)=yl(x)+y1l1(x)+y2l2(x)+…+ynln(x)n=1时,称为线性插值,L 1(x)=y(x-x1)/(x-x1)+y1(x-x)/(x1-x)=y+(y1-x)(x-x)/(x1-x)n=2时,称为二次插值或抛物线插值,L 2(x)=y(x-x1)(x-x2)/(x-x1)/(x-x2)+y1(x-x)(x-x2)/(x1-x)/(x1-x2)+y2(x-x0)(x-x1)/(x2-x)/(x2-x1)n=i时,Li= (X-X0)……(X-X i-1)(x-x i+1) ……(x-x n)(X-X0)……(X-X i-1)(x-x i+1) ……(x-x n)6、设计思想:拉格朗日插值法是根据n + 1个点x0, x1, ... x n(x0 < x1 < ... x n)的函数值f (x0), f (x1) , ... , f (x n)推出n次多項式p(x),然后n次多項式p (x)求出任意的点x对应的函数值f (x)的算法。
数值分析 插值多项式实验报告

三、实验内容及要求:
1.已知数据如下:
xi
f ( xi )
0 0+学号
0.2 0.04+学号
0.4 0.16+学号
0.6 0.36+学号
0.8 0.64+学号
1.0 1+学号
注学号取后面两位数,如 122320101,学号=1。 (1)用 MATLAB 等语言编写按 Lagrange 插值法和 Newton 插值法计算插值的程序,对以上数据进行插值; (2)利用 MATLAB 在第一个图中画出离散数据及插值函数曲线。 2.给定函数 f ( x) =
6
end end b=1; for k=1:9 if k~=i b=b*(x0(i)-x0(k)); end end A(i)=expand(a/b); end L=0; for p=1:9 L=L+y0(p)*A(p); end L L=-745631513600000000/6545742033698309*x^8+3419841600000000000/65457420 33698309*x^7-6621592639456000000/6545742033698309*x^6+701929935000000 0000/6545742033698309*x^5-4393156359065510000/6545742033698309*x^4+16 03771386328125000/6545742033698309*x^3-22515465371294825/503518617976 793*x^2+7750485791015625/13091484067396618*x+1 x1=0:0.0001:1; y1=1./(1+25.*x1.^2); y2=-745631513600000000/6545742033698309.*x1.^8+3419841600000000000/65 45742033698309.*x1.^7-6621592639456000000/6545742033698309.*x1.^6+701 9299350000000000/6545742033698309.*x1.^5-4393156359065510000/65457420 33698309.*x1.^4+1603771386328125000/6545742033698309.*x1.^3-225154653 71294825/503518617976793.*x1.^2+7750485791015625/13091484067396618.*x 1+1; plot(x1,y1,'--r') hold on plot(x1,y2,'k') (4)取十一个节点 clear clc x0=0:0.1:1; y0=1./(1+25.*x0.^2); syms x for i=1:11 a=1; for j=1:11 if j~=i a=expand(a*(x-x0(j))); end end b=1; for k=1:11
多项式插值实验报告

实验报告一题目:多项式插值摘要:熟悉插值多项式构造,通过计算机解决实验问题;龙格现象的发生、防止,通过拉格朗日插值、分段线性插值以及三次样条插值进展插值效果的比拟通过分析、推导,掌握数据插值的思想方法;通过对插值方法的进一步讨论,了解插值的“龙格〞现象;熟悉常用的分段线性插值和样条插值的使用方法;掌握上机编程与调试能力。
由于高次多项式插值不收敛,会产生Runge 现象,本实验在给出具体的实例后,采用分段线性插值和三次样条插值的方法有效的克制了这一现象,而且还取的很好的插值效果。
前言:〔目的和意义〕1. 掌握拉格朗日插值法,分段线性插值法,三次样条插值法。
2. 深刻认识多项式插值的缺点。
3. 明确插值的不收敛性怎样克制。
4. 明确精度与节点和插值方法的关系。
数学原理:在给定n+1个节点和相应的函数值以后构造n 次的Lagrange 插值多项式,实验结果说明〔见后面的图〕这种多项式并不是随着次数的升高对函数的逼近越来越好,这种现象就是Rung 现象。
解决Rung 现象的方法通常有分段线性插值、三次样条插值等方法。
分段线性插值:设在区间[a, b ]上,给定n+1个插值节点a=x 0<x 1<…<x n =b和相应的函数值y 0,y 1,…,y n ,,求作一个插值函数)(x φ,具有如下性质:1) j j y x =)(φ,j=0,1,…,n 。
2) )(x φ在每个区间[x i , x j ]上是线性连续函数。
那么插值函数)(x φ称为区间[a, b ]上对应n 个数据点的分段线性插值函数。
三次样条插值:给定区间[a, b ]一个分划⊿:a=x 0<x 1<…<x N =b假设函数S(x)满足以下条件:1)S(x)在每个区间[x i, x j]上是不高于3次的多项式。
2)S(x)及其2阶导数在[a, b]上连续。
那么称S(x)使关于分划⊿的三次样条函数。
程序设计:本实验采用Matlab的M文件编写。
插值多项式实验报告

2010年——2011年第一学期合肥学院数理系实验报告课程名称:数值分析实验项目:插值多项式实验类别:验证性专业班级: 08数学与应用数学(2)班姓名:卢王菲学号:0807022048 实验地点: 7#604实验时间:指导教师:孙梅兰成绩:一.实验目的:熟悉插值多项式构造,通过计算机解决实验问题;龙格现象的发生、防止,通过拉格朗日插值、分段线性插值以及三次样条插值进行插值效果的比较通过分析、推导,掌握数据插值的思想方法;通过对插值方法的进一步讨论,了解插值的“龙格”现象;熟悉常用的分段线性插值和样条插值的使用方法;掌握上机编程与调试能力。
二.实验内容:1、拉格朗日插值2、分段线性插值3、三次样条插值三. 实验步骤或程序:第一题:L的函数近似值用四次拉格朗日多项式求)5.0(4function yy=Lagrange(x,y,xi)m=length(x);n=length(y);if m~=n,error('向量x与y的长度必须一致');ends=0;for i=1:nz=ones(1,length(xi));for j=1:nif j~=iz=z.*(xi-x(j))/(x(i)-x(j));endends=s+z*y(i);endyy=s;在命令窗口调用Lagrange函数如下>> x=[0.4,0.5,0.80,0.9,1];>> y=[0.41075,0.57815,0.88811,1.02652,1.17520];>> xi=[0.5];>> yi=Lagrange(x,y,xi)第二题:已知sin(0.32)= 0.314567,sin(0.34)=0.333487用Lagrangeq求sin(0.33)的近似值x=[0.32,0.34];y=[0.314567,0.333487];xi=[0.33];yi=Lagrange(x,y,xi)yi = 0.3240>> plot(x,y,'o',xi,yi,'g)用拉格朗日多项式求x=21.4的函数近似值x=[20,21,22,23,24];y=[1.30130,1.32222,1.34242,1.36173,1.38021]; xi=[21.4];yi=Lagrange(x,y,xi)yi =1.3304>> plot(x,y,'o',xi,yi,'g^')四.实验总结:通过本次试验,我初步了解并掌握了用拉格朗日插值、分段线性插值以及三次样条插值解决多项式求解问题,认识到数值分析的重要作用,其在生活实际中有不可忽视的作用,我需要刻苦努力脚踏实地的认真学习。
插值运算实验报告

#### 一、实验目的1. 理解插值运算的基本概念和原理。
2. 掌握几种常见的插值方法,如拉格朗日插值、牛顿插值等。
3. 通过实验,验证插值方法在数值计算中的应用效果。
4. 培养动手能力和分析问题的能力。
#### 二、实验原理插值运算是指根据已知数据点,构造一个近似函数来描述这些数据点之间的变化规律。
常见的插值方法有拉格朗日插值、牛顿插值、分段线性插值等。
#### 三、实验内容1. 数据准备准备一组数据点,例如:```x: [1, 2, 3, 4, 5]y: [2, 4, 6, 8, 10]```2. 拉格朗日插值根据给定的数据点,构造拉格朗日插值多项式。
以三次拉格朗日插值为例,其公式如下:```L(x) = y0 ((x - x1) (x - x2) (x - x3)) / ((x0 - x1) (x0 - x2) (x0 - x3))+ y1 ((x - x0) (x - x2) (x - x3)) / ((x1 - x0) (x1 - x2) (x1 - x3))+ y2 ((x - x0) (x - x1) (x - x3)) / ((x2 - x0) (x2 - x1) (x2 - x3))+ y3 ((x - x0) (x - x1) (x - x2)) / ((x3 - x0) (x3 - x1)(x3 - x2))```将数据点代入上述公式,得到拉格朗日插值多项式。
3. 牛顿插值根据给定的数据点,构造牛顿插值多项式。
以三次牛顿插值为例,其公式如下:```N(x) = y0 + (x - x0) (y1 - y0) / (x1 - x0) + (x - x0) (x - x1) (y2 - y1) / ((x1 - x0) (x2 - x1)) + (x - x0) (x - x1) (x - x2) (y3 - y2) / ((x1 - x0) (x2 - x1) (x3 - x2))```将数据点代入上述公式,得到牛顿插值多项式。
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
插值数值实验报告(3篇)

第1篇一、实验目的1. 理解并掌握插值法的基本原理和常用方法。
2. 学习使用拉格朗日插值法、牛顿插值法等数值插值方法进行函数逼近。
3. 分析不同插值方法的优缺点,并比较其精度和效率。
4. 通过实验加深对数值分析理论的理解和应用。
二、实验原理插值法是一种通过已知数据点来构造近似函数的方法。
它广泛应用于科学计算、工程设计和数据分析等领域。
常用的插值方法包括拉格朗日插值法、牛顿插值法、样条插值法等。
1. 拉格朗日插值法拉格朗日插值法是一种基于多项式的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等。
2. 牛顿插值法牛顿插值法是一种基于插值多项式的差商的插值方法。
其基本思想是:给定一组数据点,构造一个次数不超过n的多项式,使得该多项式在这些数据点上的函数值与已知数据点的函数值相等,并且满足一定的差商条件。
三、实验内容1. 拉格朗日插值法(1)给定一组数据点,如:$$\begin{align}x_0 &= 0, & y_0 &= 1, \\x_1 &= 1, & y_1 &= 4, \\x_2 &= 2, & y_2 &= 9, \\x_3 &= 3, & y_3 &= 16.\end{align}$$(2)根据拉格朗日插值公式,构造插值多项式:$$P(x) = \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}y_3.$$(3)计算插值多项式在不同点的函数值,并与实际值进行比较。
拉格朗日插值实验报告

拉格朗日插值实验报告一、实验目的本实验旨在通过实际实验,深入理解拉格朗日插值法的原理和应用,掌握其计算过程和相关技巧。
二、实验原理Pn(x) = ∑ [yi * li(x)]其中,li(x)称为拉格朗日基函数,具体的计算公式如下:li(x) = ∏ [(x-xj)/(xi-xj)] (i≠j)利用拉格朗日插值法可以对数据进行插值计算,从而得到原函数未知的点的函数值。
三、实验步骤1.根据实验要求,选择一组离散的数据点,确保它们在横坐标轴上不共线。
2. 使用拉格朗日插值法计算插值多项式的各个基函数li(x)。
3.对插值多项式进行求和,得到最终的插值多项式Pn(x)。
4.在给定的范围内选择一些未知数据点,利用插值多项式Pn(x)计算其函数值。
5.将实际计算的函数值与原函数值进行对比,评估插值方法的准确性和精确度。
四、实验结果以实验要求给定的数据点为例,具体数据如下:x:1,2,3,4,5,6y:5,19,43,79,127,187根据拉格朗日插值法的计算公式,可以得到以下结果:l0(x)=(x-2)(x-3)(x-4)(x-5)(x-6)/(-120)l1(x)=(x-1)(x-3)(x-4)(x-5)(x-6)/120l2(x)=(x-1)(x-2)(x-4)(x-5)(x-6)/(-48)l3(x)=(x-1)(x-2)(x-3)(x-5)(x-6)/48l4(x)=(x-1)(x-2)(x-3)(x-4)(x-6)/(-20)l5(x)=(x-1)(x-2)(x-3)(x-4)(x-5)/20插值多项式Pn(x)=5*l0(x)+19*l1(x)+43*l2(x)+79*l3(x)+127*l4(x)+187*l5(x)综合以上计算结果,可以对给定范围内的未知数据点进行插值计算,从而得到相应的函数值。
五、实验分析与结论在实际实验中,我们可以利用拉格朗日插值法对任意给定的函数进行逼近计算,从而得到函数在离散数据点之间的近似值。
数值计算方法实验之Lagrange多项式插值(Python代码)

数值计算⽅法实验之Lagrange多项式插值(Python代码)⼀、实验⽬的在已知f(x),x∈[a,b]的表达式,但函数值不便计算,或不知f(x),x∈[a,b]⽽⼜需要给出其在[a,b]上的值时,按插值原则f(x i)= y i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x i,处成⽴P(x i)=y i(i=0,1,……,n),⽽在[a,b]上的其它点处成⽴f(x)≈P(x).⼆、实验原理三、实验内容求之f(x)=x4在[0,2]上按5个等距节点确定的Lagrange插值多项式.四、实验程序1import matplotlib.pyplot as plt2from pylab import mpl34#计算插值多项式的系数。
5 x = [0, 0.5, 1, 1.5, 2]6 y = [0, 0.0625, 1, 5.0625, 16]78def ParametersOfLagrangeInterpolation(data_x,data_y,size):9 parameters=[]1011 i=0;#i⽤来控制参数的个数12while i < size:13 j = 0;#j⽤来控制循环的变量做累乘14 temp = 1;15while j < size:16if(i != j):17 temp*=data_x[i]-data_x[j]18 j+=1;19 parameters.append(data_y[i]/temp)20 i += 1;21return parameters2223#计算拉格朗⽇插值公式的值。
2425def CalculateTheValueOfLarangeInterpolation(data_x,parameters,x):26 returnValue=027 i = 0;28while i < len(parameters):29 temp = 130 j = 0;31while j< len(parameters):32if(i!=j):33 temp *=x-data_x[j]34 j+=135 returnValue += temp * parameters[i]36 i += 137return returnValue3839#将函数绘制成图像40def Draw(data_x,data_y,new_data_x,new_data_y):41 plt.plot(new_data_x, new_data_y, label="拟合曲线", color="red")42 plt.scatter(data_x,data_y, label="离散数据",color="yellow")43 plt.scatter(1.75, 9.37890625, label="真实数据", color="orange")44 plt.scatter(1.25, 2.44140625, color="green")45 mpl.rcParams['font.sans-serif'] = ['SimHei']46 mpl.rcParams['axes.unicode_minus'] = False47 plt.title("Lagrange插值拟合数据")48 plt.legend(loc="upper left")49 plt.show()5051 parameters=ParametersOfLagrangeInterpolation(x,y,5)52 datax=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2]53 datay=[]54for temp in datax:55 datay.append(CalculateTheValueOfLarangeInterpolation(x,parameters,temp))56 x.append(1.75)57 y.append(CalculateTheValueOfLarangeInterpolation(x,parameters,1.75))58 Draw(x,y,datax,datay)59print("得到的四次Lagrange插值多项式为:L(x) = %f(x-0)(x-1)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1)(x-2) + %f(x-0)(x-0.5)(x-1)(x-1.5)"%(parameters[1],parameters[2],parameters[3],parameters[4]))五、运算结果(1)图像得到的四次Lagrange插值多项式为:L(x) = -0.166667(x-0)(x-1)(x-1.5)(x-2) + 4.000000(x-0)(x-0.5)(x-1.5)(x-2) + -13.500000(x-0)(x-0.5)(x-1)(x-2) + 10.666667(x-0)(x-0.5)(x-1)(x-1.5)。
数值分析实验报告-插值、三次样条

实验报告:牛顿差值多项式&三次样条问题:在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及()f x 的图形。
实验目的:通过编程实现牛顿插值方法和三次样条方法,加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求:1. 认真分析问题,深刻理解相关理论知识并能熟练应用; 2. 编写相关程序并进行实验; 3. 调试程序,得到最终结果; 4. 分析解释实验结果; 5. 按照要求完成实验报告。
实验原理:详见《数值分析 第5版》第二章相关内容。
实验内容:(1)牛顿插值多项式1.1 当n=10时:在Matlab 下编写代码完成计算和画图。
结果如下:代码:clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式,其结果为:P10(x)=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36* x^4+2.0202e-14*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.1)。
第6章 实验五插值多项式的误差

第6章 实验五插值多项式的误差实验目的:明确插值多项式逼近函数是有误差的,了解误差的分布,哪些地方误差大些,哪些地方误差小些。
我们应该如何控制这些误差。
6.1 插值误差余项多项式举例说明多项式插值误差情况,用ππ≤≤-x 上的5个等距点对函数)cos(x y =进行插值估计,插值多项式是通过以下给定的数据点的四次多项式:⎥⎦⎤⎢⎣⎡--=ππππ,2,0,2,x[])sin(),2/sin(),0sin(),2/sin(),sin(ππππ--=y误差定义为:)()cos()(4x L x x e -=),())(cos(!5))(2/)(0)(2/)(()5(ππξξππππ-∈---++=x x x x x其中)(x e 是插值余项,)(4x L 是5个数据点的拉格朗日插值多项式。
图6.1是函数和误差的图形,可以观察到误差曲线是震荡的,它的值在接近端点的区间上最大,这种误差特性在等距多项式插值中十分典型,误差分布形状上的变化还取决于被插函数的性质及插值区间的大小a b -。
-0.8-0.6-0.4-0.20.20.40.60.8xc o s (x ) e (x )图6.1 函数和误差曲线的图形清单6.1 (是作图6.1的程序)clear clcx=[-pi,-pi/2,0,pi/2,pi]; % 插值节点横坐标 y=[cos(-pi),cos(pi/2),cos(0),cos(pi/2),cos(pi)]; % 插值节点纵坐标 x1=-pi:0.001:pi; % 绘图点的横坐标 y1=Lagran_(x,y,x1); % 绘图点的纵坐标 e=cos(x1)-y1; % 插值误差 y2=e;plot(x,cos(x),'.',x1,cos(x1),'b',x1,y2,'r') % 绘出两个函数曲线图形 xlabel('x');ylabel('cos(x) e(x)') text(1.2,0.6,'cos(x)','fontsize',18) text(-1.1,-0.1,'e(x)=cos(x)-y','fontsize',18)一般分析插值的误差:),()()!1()())(()(11)1(121+++∈+---=n n n x x f n x x x x x x x R ξξ)(m a x )!1()())(()()1(),(12111ξξ+∈+++---≤n x x n f n x x x x x x x R n 如果当被插值)(x f 是一个n 阶或更低阶多项式,则)(x R =0,即误差为零。
分段线性插值多项式上机实验报告
中国矿业大学(北京)理学院数值分析实验报告实验名称 分段线性插值多项式 实验时间 4.17组长签名龙纯鹏 班级信息与计算科学(1)班学号11107200110 成绩组员签名111072001011110720010211107200103 1110720011911107200120一、实验目的 二、实验内容 三、代码 四、数值结果 五、计算结果的分析 六、计算中出现的问题,解决方法及体会一、实验目的 实验目的:1. 了解分段线性插值多项式的基本原理和方法;2. 掌握分段线性插值多项式的用法,适用范围及精确度;3. 学习掌握MATLAB 软件有关的命令。
二、实验内容: 已知245)(xx f +=,求在55≤≤-x 上取n=10,分别用 (1)用高次Lagrange 插值,(2)按等距节点求分段线性插值函数S(x),计算各节点间中点处的近似值, 并与准确值f(x)比较精度并估计误差,把f(x)和插值多项式的曲线画在同一张图中进行比较。
实验背景:在数值分析领域中, 龙格现象是用高阶多项式进行多项式插值时所出现的问题。
它是 Carle David Tolm é Runge 在研究使用多项式插值逼近特定函数的误差过程中发现的。
问题:考虑以下函数:龙格发现如果使用阶多项式在−1 与 1 之间按照这样的等距点x i进行插值,那么在接近端点−1 与 1 的地方插值结果就会出现震荡。
可以证明,在多项式的阶数增高时插值误差甚至会趋向无限大:三、代码(Matlab)f.m function y=f(x)y=5./(4+x.^2)主程序x=[-5,-4,-3,-2,-1,0,1,2,3,4,5];y=f(x);k=1;i=1;for a=-4.5:1:4.5while x(k+1)<ak=k+1;endresult_y(i)=(a-x(k+1))*f(x(k))/(x(k)-x(k+1))+(a-x(k))*f(x(k+1))/(x(k+1)-x(k)); i=i+1;enda=-4.5:1:4.5result_y结果a =Columns 1 through 8-4.5000 -3.5000 -2.5000 -1.5000 -0.5000 0.5000 1.5000 2.5000Columns 9 through 103.50004.5000result_y =Columns 1 through 80.2112 0.3173 0.5048 0.8125 1.1250 1.1250 0.8125 0.5048Columns 9 through 100.31730.2112>> plot(a,result_y)>> hold on>> plot(x,f(x))四、数值结果:x -4.5 -3.5 -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 4.5resul t_y 0.21120.31730.50480.81251.1251.1250.81250.50480.31730.2112f(x) 0.2062 0.30770.48780.8001.17651.17650.8000.48780.30770.2062误差0.0050 0.00960.0170.0125-0.0515-0.05150.01250.0170.00960.005曲线图:五、计算结果的分析数值计算结果各节点间中点处的近似值如上表格所示,与准确值f(x)比较精度并估计误差,并把f(x)和插值多项式的曲线画在同一张图中进行比较如上图所示:六、计算中出现的问题,解决方法及体会在整个的试验过程当中,首先理解与学习阶段是最难的,只有在学习当中理解了、领悟了,在实践的过程中才能够明白问题的出现所在,我们的开始的最大问题在于对于此方法没能理解清楚,以至于开始时候手足无措,在看书理解后,弄清楚差值函数的构造后,问题才慢慢解决。
《数值计算方法》---多项式插值实验报告

1
2
3
4
5
6
y
0
0.6931
1.0986
1.3863
1.6094
1.7918
2根据下面的数据点,分别求牛顿前插多项式和牛顿后插多项式,并计算x=1.55时y的值。
x
1
2
3
4
5
6
y
0
0.6931
1.0986
1.3863
1.6094
1.79ቤተ መጻሕፍቲ ባይዱ8
3根据下面的数据点,求埃尔米特插值多项式,并计算x=1.44时y的值。
《数值计算方法》---多项式插值实验报告
实验名称:多项式插值
实验目的:
1、熟悉Matlab的编程。
2、学会求解拉格朗日插值、牛顿插值及埃尔米特插值多项式并估计函数在某点处的值。
实验设备与环境:计算机,Windows系统,Matlab等。
实验内容:
1.根据下面的数据点,分别求拉格朗日插值多项式和牛顿插值多项式,并计算x=1.5时y的值。
x
1
1.2
1.4
1.6
1.8
y
1
1.0954
1.1832
1.2649
1.3416
y’
0.5000
0.4564
0.4226
0.3953
0.3727
f =
10850.7*(t - 1.0)^2*(t - 1.4)^2*(t - 1.6)^2*(t - 1.8)^2*(9.58473*t - 10.4063) - 10850.7*(t - 1.0)^2*(t - 1.2)^2*(t - 1.4)^2*(t - 1.8)^2*(10.1455*t - 17.4978) + 24414.1*(t - 1.0)^2*(t - 1.2)^2*(t - 1.6)^2*(t - 1.8)^2*(0.4226*t + 0.59156) - 678.168*(27.5773*t - 50.9807)*(t - 1.0)^2*(t - 1.2)^2*(t - 1.4)^2*(t - 1.6)^2 + 678.168*(t - 1.2)^2*(t - 1.4)^2*(t - 1.6)^2*(t - 1.8)^2*(21.3333*t - 20.3333)
数值计算插值法实验报告

数值计算插值法实验报告
一、实验目标
本实验的目标是学习和掌握插值法的基本原理,通过实际操作,验证插值法的有效性,并利用插值法解决实际问题。
二、实验原理
插值法是一种数学方法,用于通过已知的离散数据点,构造一个连续的函数来近似地表示未知的函数值。
常用的插值法包括线性插值、多项式插值、样条插值等。
其中,多项式插值是一种常用的方法,其基本思想是选择一个多项式来逼近已知的数据点,从而得到未知点的近似值。
三、实验步骤
1.准备数据:收集一组已知的数据点,并将其整理成表格形式。
2.选择插值方法:根据实际情况选择适当的插值方法,如线性插值、多项式插值或样条插值等。
3.计算插值函数:根据选择的插值方法,利用已知的数据点计算插值函数的系数。
4.验证插值函数:利用已知的数据点对插值函数进行验证,检查其精度和误差。
5.应用插值函数:利用插值函数计算未知点的近似值,并将结果与实际值进行比较。
四、实验结果及分析
下面是本次实验的结果及分析:
1.已知数据点:。
数值分析——多项式插值的振荡现象

数值分析实验报告多项式插值的振荡现象姓名:班级:学号:数值分析实验报告从图中可以看出,插值函数过两端和原点,并且也是奇函数;n 增大的现象;b)当节点为偶数个时,即n=3:4:11时,可以得到:N 取得很大的时候,插值函数和被插值函数几乎重合x节点为均匀节点时:n i nix i ,,2,1,0,105 =+-=当节点为奇数时,即n=2:4:10,可以得到如下图像从图中可以看出,插值函数过两端和原点,并且也是奇函数;n越大拟合度越好,没有出现误差增大的现象;b)当节点为偶数个时,即n=3:4:11时,可以得到:N取得很大的时候,插值函数和被插值函数几乎重合综合分析上面的图像和数据可以发现:节点数目的奇偶对实验没有什么影响,而且节点不是越多拟合越好,可能会发生发散现象,对称的节点选取,得到的插值函数的对称性与被插值函数相同节数值分析上机实验原始记录实验名称:多项式插值的振荡现象实验时间: 2013年 10月23日姓名:学号:班级:实验一的关键程序:事先估计程序m=150; x=-1:2/(m-1):1; y=1./(1+25*x.^2); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=1/(1+25*x^2)'),pausen=3; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y1=lagr1(x0,y0,x);hold on,plot(x,y1,'g'),gtext('n=2'),pause,hold offn=4; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y2=lagr1(x0,y0,x);hold on,plot(x,y2,'b:'),gtext('n=3'),pause,hold offn=5; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y3=lagr1(x0,y0,x);hold on,plot(x,y3,'r'),gtext('n=4'),pause,hold offn=11; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y4=lagr1(x0,y0,x);hold on,plot(x,y4,'r:'),gtext('n=10'),pause,hold offn=51; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y5=lagr1(x0,y0,x);hold on,plot(x,y5,'m'),gtext('n=50'),pause,hold offn=81; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y6=lagr1(x0,y0,x);hold on,plot(x,y6,'m'),gtext('n=80'),pause,hold off%%1.1.a y=1./(1+25*x.^2) 的程序——均匀节点m=150; x=-1:2/(m-1):1; y=1./(1+25*x.^2); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=1/(1+25*x^2)'),pausen=2; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y1=lagr1(x0,y0,x);hold on,plot(x,y1,'g'),gtext('n=1'),pause,hold offn=4; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y2=lagr1(x0,y0,x);hold on,plot(x,y2,'b:'),gtext('n=3'),pause,hold offn=6; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y3=lagr1(x0,y0,x);hold on,plot(x,y3,'r'),gtext('n=5'),pause,hold offn=8; x0=-1:2/(n-1):1; y0=1./(1+25*x0.^2); y4=lagr1(x0,y0,x);hold on,plot(x,y4,'r:'),gtext('n=7'),pause,hold off%%1.1b ——切比雪夫节点m=150; x=-1:2/(m-1):1; y=1./(1+25*x.^2); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=1/(1+25*x^2)'),pausex=q(2); y=1./(1+25*x.^2);n=2; x0=-1:2/(n-1):1;y1=lagr1(x,y,x0);hold on,plot(x0,y1,'g'),gtext('n=1'),pause,hold offx=q(4); y=1./(1+25*x.^2);n=4; x0=-1:2/(n-1):1; y2=lagr1(x,y,x0);hold on,plot(x0,y2,'b:'),gtext('n=3'),pause,hold offx=q(6); y=1./(1+25*x.^2); n=6;x0=-1:2/(n-1):1;y3=lagr1(x,y,x0);hold on,plot(x0,y3,'r'),gtext('n=5'),pause,hold offx=q(8); y=1./(1+25*x.^2);n=8;x0=-1:2/(n-1):1;y4=lagr1(x,y,x0);hold on, plot(x0,y4,'r:'),gtext('n=7'),pause,hold off%%2.1 a y=x./(1+x.^4)的程序——均匀节点m=150; x=-5:10/(m-1):5; y=x./(1+x.^4); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=x/(1+x^4)'),pausen=2; x0=-5:10/(n-1):5; y0=x0./(1+x0.^4); y1=lagr1(x0,y0,x);hold on,plot(x,y1,'g'),gtext('n=1'),pause,hold offn=6;x0=-5:10/(n-1):5; y0=x0./(1+x0.^4); y3=lagr1(x0,y0,x);hold on,plot(x,y3,'r'),gtext('n=5'),pause,hold offn=10; x0=-5:10/(n-1):5; y0=x0./(1+x0.^4); y4=lagr1(x0,y0,x);hold on,plot(x,y4,'r:'),gtext('n=9'),pause,hold off%%2.1 b ——切比雪夫节点m=150; x=-5:10/(m-1):5; y=x./(1+x.^4); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=x/(1+x^4)'),pausex=q(2); y=x./(1+x.^4);n=3; x0=-5:10/(n-1):5;y1=lagr1(x,y,x0);hold on,plot(x0,y1,'g'),gtext('n=1'),pause,hold offx=q(6); y=x./(1+x.^4);n=5; x0=-5:10/(n-1):5; y2=lagr1(x,y,x0);hold on,plot(x0,y2,'b:'),gtext('n=5'),pause,hold offx=q(10); y=x./(1+x.^4); n=10;x0=-5:10/(n-1):5;y3=lagr1(x,y,x0);hold on,plot(x0,y3,'r'),gtext('n=9'),pause,hold off%%3.1 a y=atan(x) 的程序——均匀节点m=150; x=-5:10/(m-1):5; y=atan(x); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=atan x'),pausen=2; x0=-5:10/(n-1):5; y0=atan(x0); y1=lagr1(x0,y0,x);hold on,plot(x,y1,'g'),gtext('n=1'),pause,hold offn=6;x0=-5:10/(n-1):5; y0=atan(x0); y3=lagr1(x0,y0,x);hold on,plot(x,y3,'r'),gtext('n=5'),pause,hold offn=10; x0=-5:10/(n-1):5; y0=atan(x0); y4=lagr1(x0,y0,x);hold on,plot(x,y4,'y:'),gtext('n=9'),pause,hold off%%3.1 b ——切比雪夫节点m=150;x=-5:10/(m-1):5; y=atan(x); z=0*x;plot(x,z,'r',x,y,'k-'),gtext('y=1/(1+25*x^2)'),pausex=q(1); y=atan(x);;n=2; x0=-5:10/(n-1):5;y1=lagr1(x,y,x0);hold on,plot(x0,y1,'g'),gtext('n=1'),pause,hold offx=q(5); y=atan(x); n=6;x0=-5:10/(n-1):5;y3=lagr1(x,y,x0);hold on,plot(x0,y3,'r'),gtext('n=5'),pause,hold offx=q(9); y=atan(x);n=10;x0=-5:10/(n-1):5;y4=lagr1(x,y,x0);hold on,plot(x0,y4,'r:'),gtext('n=9'),pause,hold off实验二的关键程序问题一的程序x0=linspace(-1,1,11);y0=1./(1+9*x0.^2);x=-1:0.02:1;y=lagr1(x0,y0,x);yi=spline(x0,y0,x)%%求三次样条插值z=1./(1+9*x.^2);Ri=abs((z-yi)./z);%%三次样条插值相对误差R=abs((z-y)./z);%%lagrange插值相对误差x,y,z,yi,R,Ri=[x',y',z',yi',R',Ri']n=size(x0)plot(x,z,'o',x,y,'-',x,yi,'r*')legend('原始图像','lagrange插值','三次样条插值')问题二的程序m=101;x=-1:2/(m-1):1;y=1./(1+25*x.^2);plot(x,y)xi=0:10;yi=[0.0,0.79,1.53,2.19,2.71,3.03,3.27,2.89,3.06,3.19,3.29];pp=csape(x,y,'complete',[0.8,0.2]);xj=0:0.1:10;yj=ppval(pp,xi);plot(x,y,'*');plot(xi,yi)思考题程序%%以下为三种不同的方式——1x0=[100 200 300 400];y0=[100200300400];z0=[636 697 624 478698 712 630 478680 674 598 412662 626 552 334];pp=csape({x0,y0},z0') ;xi=100:1:400;yi=100:1:400 ;cz1=fnval(pp,{xi,yi}) ;cz2=interp2(x0,y0,z0,xi,yi','Linear') ;[i,j]=find(cz1==max(max(cz1))) ;x=xi(i),y=yi(j),zmax=cz1(i,j)——2x0=[100 200 300 400];y0=[100200300400];z0=[636 697 624 478698 712 630 478680 674 598 412662 626 552 334];pp=csape({x0,y0},z0') ;xi=100:1:400;yi=100:1:400 ;cz1=fnval(pp,{xi,yi}) ;cz2=interp2(x0,y0,z0,xi,yi','cubic') ;[i,j]=find(cz1==max(max(cz1))) ;x=xi(i),y=yi(j),zmax=cz1(i,j)——3x0=[100 200 300 400];y0=[100200300400];z0=[636 697 624 478698 712 630 478680 674 598 412662 626 552 334];pp=csape({x0,y0},z0') ;xi=100:1:400;yi=100:1:400 ;cz1=fnval(pp,{xi,yi}) ;cz2=interp2(x0,y0,z0,xi,yi','spline') ;[i,j]=find(cz1==max(max(cz1))) ;x=xi(i),y=yi(j),zmax=cz1(i,j)指导教师:年月日。
数值分析实验报告插值与拟合
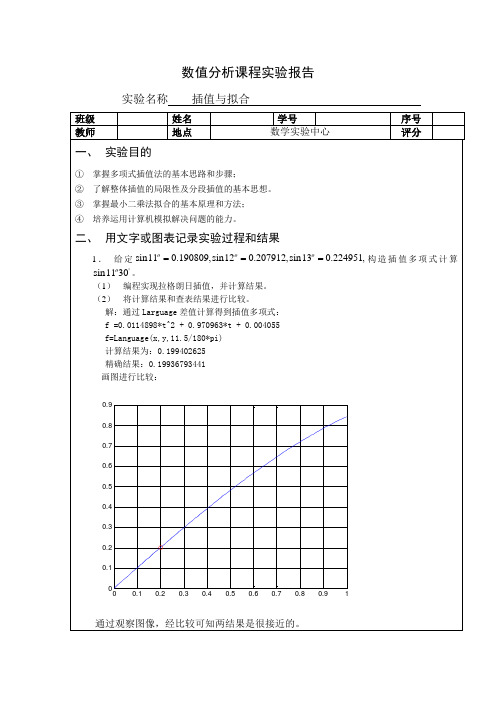
结果分析:高次插值稳定性差,而低次插值对于较大区间逼近精度又不够,而且,随着节点的加密,采用高次插值,插值函数两端会发生激烈震荡。解决这一矛盾的有效方法就是采用分段低次代数插值。
(2)
通过采用分段线性插值得到以下结果:
结果分析:通过采用分段线性插值,发现随着插值节点增多,插值计算结果的误差越来越小,而且分段线性插值的优点是计算简单,曲线连续和一致收敛,但是不具有光滑性。
拟合是指通过观察或测量得到一组离散数据序列 ,i=1,2,…,m,构造插值函数 逼近客观存在的函数 ,使得向量 与 的误差或距离最小。
可知当基函数的选择不同时,拟合函数的误差也会不同,所以在对数据进行拟合时应选择适合的基函数。
三、练习思考
整体插值有何局限性?如何避免?
答:整体插值的过程中,若有无效数据则整体插值后插值曲线的平方误差会比较大,即在该数据附近插值曲线的震动幅度较大。在插值处理前,应对原始数据进行一定的筛选,剔除无效数据。
②相同点:通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律目的
四、本次实验的重点难点分析
答:加强了对插值和拟合的认识,了解了其算法思想,并使用matlab将其实现。学会了观察插值拟合后的图形,并分析其问题。
画图进行比较:
通过观察图像,经比较可知两结果是很接近的。
2.区间 作等距划分: ,以 ( )为节点对函数 进行插值逼近。(分别取 )
(1)用多项式插值对 进行逼近,并在同一坐标系下作出函数的图形,进行比较。写出插值函数对 的逼近程度与节点个数的关系,并分析原因。
(2)试用分段插值(任意选取)对 进行逼近,在同一坐标下画出图形,观察分段插值函数对 的逼近程度与节点个数的关系。
多项式的插值实验报告

0.3
0.4
0.5
0.6
0.7
f(x)
0.2985
0.39646
0.49311
0.58813
0.68122
2.已知f(x)=e^(-x)的部分函数值列表如下:
x
0.10
0.15
0.25
0.30
e^(-x)
0.904837
0.860708
0.778801
0.740818
试用牛顿插值求出在x=0.2的近似函数值.
printf("\n f(x)在x1的近似值为:%lf",fun(x1));
}
运行结果:
第一种编程:
#include"stdio.h"
#defineN 4
voidmain()
{inti,j,n;
doublex[N]={0.10,0.15,0.25,0.30};
doubley[N]={0.904837,0.860708,0.778801,0.740818};
doubles,t,p,x1,y1=y[0];
printf("请输入插值点x1的值:");
scanf("%lf",&x1);
for(n=2;n<=N;n++)
{s=0.0;p=1.0;
for(i=0;i<n;i++)
{t=1.0;
for(j=0;j<n;j++)
{if(i!=j) t=t*(x[i]-x[j]);}
s=s+y[i]/t;
if(i<n-1) p=p*(x1-x[i]);
数值分析拟合实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析方法对一组已知数据点进行拟合,掌握线性插值、多项式插值、样条插值等方法的基本原理和实现过程,并学会使用MATLAB进行数值拟合。
二、实验内容1. 线性插值线性插值是一种简单的插值方法,适用于数据点分布较为均匀的情况。
其基本原理是通过两个相邻的数据点,利用线性关系拟合出一条直线,然后通过该直线来估算未知的值。
2. 多项式插值多项式插值是一种较为精确的插值方法,通过构造一个多项式函数来逼近已知数据点。
其基本原理是利用最小二乘法求解多项式的系数,使得多项式在已知数据点上的误差最小。
3. 样条插值样条插值是一种更灵活的插值方法,通过构造一系列样条曲线来逼近已知数据点。
其基本原理是利用最小二乘法求解样条曲线的系数,使得样条曲线在已知数据点上的误差最小。
三、实验步骤1. 线性插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`linspace`生成插值点:xi = linspace(1, 5, 100);(3)使用MATLAB内置函数`interp1`进行线性插值:yi = interp1(x, y, xi, 'linear');(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');2. 多项式插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`polyfit`求解多项式系数:p = polyfit(x, y, 3);(3)使用MATLAB内置函数`polyval`进行多项式插值:yi = polyval(p, xi);(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');3. 样条插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`spline`进行样条插值:yi = spline(x, y, xi);(3)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');四、实验结果与分析1. 线性插值线性插值方法简单易行,但精度较低,适用于数据点分布较为均匀的情况。
数值计算方法实验报告--newton插值多项式

数值计算方法实验报告实验报告题目:newton插值多项式实验要求用mat1ab解析Newton插值多项式的程序二、实验分析(包括数学原理,小组分析讨论后确定实验方案和实现思路)根据经过n+1个不同的差值点x1,x2,…,x(n+1),构造牛顿插值公式∕V(x)=y[x1,x2](x-Λ1)+∕[x1,x2,x3](x-Jc1)(x-x2)+∙∙∙+∕[x1,Λ2∕∙∙xn+1](x-x1)(x-x 2)∙∙∙(x-xn)三、实脸步骤(过程)(包括程序及上机的实现的结果)function[p2,z]=newton(x,y,t)n=1ength(x);chaS(1)=y(1);for i=2:nx1=x;y1=y;x1(i+1:n)=[];y1(i+1:n)=[];n1=1ength(x1);s1=0;for j=1:n1t1=1;for k=1:n1if k==j continue;e1set1=t1*(x1(j)-x1(k));ehdehds1=s1+y1(j)∕t1;end chaS(i)=s1;ehd b(1,:)=[zeros(1,n-1)chaS(1)];c1=ce11(1,n-1);for i=2:nυ1=1;for j=1:i-1u1=conv(u1,[1-x(j)]);c1{i-1}=u1;end c1{i-1}chaS(i)*c1{i-1);b(i,:)=[zeros(1,n-i)z c1{i-1}];end四、总结(包括实脸过程遇到的情况等,组长总结组员在整个过程的参与情况)实验过程中大家都积极参与,搞明白了牛顿插值多项式的程序。
有不明白的地方,也通过询问同班学霸,或是网页查询得到了解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
运行结果:
第一种编程:
#include"stdio.h"
#dinti,j,n;
doublex[N]={0.10,0.15,0.25,0.30};
doubley[N]={0.904837,0.860708,0.778801,0.740818};
doubles,t,p,x1,y1=y[0];
printf("请输入插值点x1的值:");
scanf("%lf",&x1);
for(n=2;n<=N;n++)
{s=0.0;p=1.0;
for(i=0;i<n;i++)
{t=1.0;
for(j=0;j<n;j++)
{if(i!=j) t=t*(x[i]-x[j]);}
doubley[N]={0.904837,0.860708,0.778801,0.740818};
doublex1,c=1.0,y1=y[0],t[100];
inti,j,k;
printf("请输入插值点x1的值:");
scanf("%lf",&x1);
for(i=1;i<N;i++)
{
for(j=i;j<N;j++)
X
0.3
0.4
0.5
0.6
0.7
f(x)
0.2985
0.39646
0.49311
0.58813
0.68122
2.已知f(x)=e^(-x)的部分函数值列表如下:
x
0.10
0.15
0.25
0.30
e^(-x)
0.904837
0.860708
0.778801
0.740818
试用牛顿插值求出在x=0.2的近似函数值.
t[j]=(y[j]-y[j-1])/(x[j]-x[j-i]);
c=c*(x1-x[i-1]);
y1=y1+c*t[i];
for(k=i;k<N;k++)
y[k]=t[k];
}
printf("\n f(x)=e^(-x)在x1的近似值为:%lf",y1);
}
运行结果:
实验3插值多项式的实验报告
数学与应用数学教育班
劳期叙0818020089
一、实验名称:插值多项式
实验日期:2010年6月3日星期四
二、实验目的
掌握用构造Lagrange插值多项式和牛顿插值多项式的方法。
三、实验内容
1.已知f(x)部分函数值列表如下,构造Lagrange插值多项式计算f(x)在x=0.462处的近似函数值。
s=s+y[i]/t;
if(i<n-1) p=p*(x1-x[i]);
}
y1=y1+p*s;
}
printf("\n f(x)=e^(-x)在x1的近似值为:%lf",y1);
}
运行结果:
2.牛顿插值法的程序代码:
第二种编程:
#include"stdio.h"
#defineN 4
voidmain()
{doublex[N]={0.10,0.15,0.25,0.30};
四、源程序代码及其运算结果
grange插值法的程序代码:
#include"stdio.h"
doublefun(doublex1)
{
inti,j;
doublet,s=0.0;
doublex[5]={0.3,0.4,0.5,0.6,0.7},y[5]={0.2985,0.39646,0.49311,0.58813,0.68122};
for(i=0;i<5;i++)
{
t=1.0;
{
for(j=0;j<5;j++)
if(i!=j)
t=t*(x1-x[j])/(x[i]-x[j]);
}
s=s+t*y[i];
}
return(s);
}
voidmain()
{doublex1;
printf("请输入插值点x1的值:");
scanf("%lf",&x1);
