第六章直梁弯曲
6第六章-梁的应力详解精选全文完整版

需要注意的是,型钢规格表中所示的x轴是我们所标示 的z轴。
Ⅱ. 纯弯曲理论的推广
工程中实际的梁大多发生横力弯曲,此时梁的横截面
由于切应力的存在而发生翘曲。此外,横向力还使各纵向
线之间发生挤压。因此,对于梁在纯弯曲时所作的平面假
设和纵向线之间无挤压的假设实际上都不再成立。但弹性
力学的分析结果表明,受分布荷载的矩形截面简支梁,当
A
将
E
y
r
代入上述三个静力学条件,有
FN
dA E
A
r
y d A ESz
A
r
0
(a)
M y
z d A E
A
r
yz d A EIyz
A
r
0
(b)
M z
y d A E
A
r
y2 d A EIz
A
r
M
(c)
以上三式中的Sz,Iyz,Iz都是只与截面的形状和尺寸相 关的几何量,统称为截面的几何性质,而
图b所示的简支梁。钢的许用弯曲正应力[]=152 MPa 。试
选择工字钢的号码。
(a)
(b)
解:在不计梁的自重的情况下,弯矩图如图所示 Mmax 375kN m
强度条件 Mmax 要求:
Wz
Wz
M max
材料力学(理工科课件)第六章 弯曲变形)

§6-1 基本概念及工程实例 (Basic concepts and example problems)
一、工程实例(Example problem)
(Deflection of Beams)
但在另外一些情况下,有时却要求构件具有较大的弹性变 形,以满足特定的工作需要.
例如,车辆上的板弹簧,要求有足够大的变形,以缓解车辆受
M 0 w 0
x
O
M 0 w 0
M
(Deflection of Beams)
w (1 w )
2 3 2
M ( x) EI
2 w 与 1 相比十分微小而可以忽略不计,故上式可近似为
w"
M ( x) EI
(6.5)
此式称为 梁的挠曲线近似微分方程(differential equation of the deflection curve) 近似原因 : (1) 略去了剪力的影响; (2) 略去了 w2项; (3) tan w w( x )
x Cx D
4
(Deflection of Beams)
边界条件x=0 和 x=l时, w 0
梁的转角方程和挠曲线方程 A 分别为 q 2 3 3 (6lx 4 x l ) 24 EI qx 2 3 3 w (2lx x l ) 24 EI 最大转角和最大挠度分别为 在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
A a l D B
b
(Deflection of Beams)
解: 梁的两个支反力为
FRA F FRB F b l a l
x
l x
F FRA
A 1 a D b 2
材料力学第6章弯曲变形

M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下,弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时,梁截面上有弯矩也有剪力,对于跨 度远大于截面高度的梁,剪力对弯曲变形的影响可以 省略,(a)式便可以作为横力弯曲变形的基本方程。其 中,M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合, 造成磨损不匀,产生噪音, 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大,会 使梁上小车行走困难, 出现爬坡现象,还会引 起较严重的振动。
变形超过允许数值,即 使在弹性范围内,也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为: 3 1 Fb 2 2 wmax l b 9 3 EIl
弯曲变形——精选推荐

第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比,因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件,就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同,则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段,只要梁不具有中间铰,梁的挠曲线仍然是一条光滑、连续的曲线。
”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。
”9、“只要材料服从虎克定律,则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁,只要所受的载荷相同,则两梁所对应的截面的挠度和转角相同,而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用,当梁的直径减少一半而其他条件不变时,最大正应力是原来的倍;最大挠度是原来的倍。
若梁的长度增大一倍,其他条件不变,最大弯曲正应力是原来的倍,最大挠度是原来的倍。
A:2; B:16 C:8 D:4;2、y’’=M(x)/EI在条件下成立。
A:小变形; B:材料服从虎克定律;C:挠曲线在xoy面内; D:同时满足A、B、C;3、等直梁在弯曲变形时,挠曲线最大曲率发生在处。
A:挠度最大; B:转角最大 C:剪力最大; D:弯矩最大;4、在简支梁中,对于减少弯曲变形效果最明显。
A:减小集中力P; B:减小梁的跨度;C:采用优质钢; D:提高截面的惯性矩5、板条弯成1/4圆,设梁始终处于线弹性范围内:①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果?A:①正确、②正确;B:①正确、②错误; C:①错误、②正确; D:①错误、②错误;6、应用叠加原理求横截面的挠度、转角时,需要满足的条件是。
《汽车机械基础》第六章直梁的弯曲
灌南中专教师授课教案2018 /2019 学年第一学期课程汽车机械基础教学内容旧知复习:1.圆轴扭转的概念。
2.圆轴扭转的外力偶矩、扭矩的计算方法。
3.圆轴扭转的强度计算方法。
讲授新课:第六章材料力学基础第5节直梁的弯曲一、平面弯曲的概念1. 平面弯曲在工程实际中,把发生弯曲变形为主的构件称为梁,如跨江大桥两桥墩之间的横梁、汽车前梁等。
梁在自重和载荷的作用下会产生平面弯曲变形。
梁弯曲变形的受力特点:外力垂直于轴线或在轴线的平面内受到力偶的作用。
变形的特点:轴线在纵向对称平面内由直线弯曲成曲线。
2. 梁的基本类型根据支座对梁的约束,将梁简化为三种基本形式。
(1)简支梁梁的两端均用铰链支座约束,一端为固定铰链支座,另一端为活动铰链支座,如图6-26a所示。
(2)外伸梁简支梁的一端(或两端)伸出支座以外,如图6-26b所示。
(3)悬臂梁梁的一端为固定支座,另一端为自由端,如图6-26c所示。
3.载荷的简化作用在梁上的载荷可简化为以下三种形式。
(1)集中力集中力是将作用于梁上方的长度很短的力简化为作用于一点的力,单位为N或kN。
(2)集中力偶矩集中力偶矩是将作用于梁上方的长度很短的力偶矩简化为作用于某一截面的集中力偶矩,单位为N·m或kN·m。
(3)分布载荷分布载荷是指沿梁的长度或部分长度连续均匀分布的载荷,称为分布载荷。
单位长度上的力用q表示,称集度载荷,单位为N/m或kN/m。
二、梁弯曲变形的内力1.用截面法求梁的内力为了计算梁的强度,必须研究梁上各截面上的内力,分析内力和计算内力的方法仍旧采用截面法。
例6-8剪力和弯矩的大小、方向或转向的确定原则如下:(1)截面上剪力的大小等于此截面以左(或右)所有外力的代数和。
截面左侧的外力,向上取正号,向下取负号。
截面右侧的外力与此相反。
(2)截面上弯矩的大小等于此截面以左(或右)所有外力对该截面形心的力矩的代数和。
截面左侧的外力对截面形心的力矩顺时针转向为正,反之为负。
工程力学六 弯曲变形解析

当x1 x2 a时,
w1 w2 (1 2 )
w1 w2
EIw2
Pb l
x2
P( x2
a)
CB段:
EIw2
EI2
Pb l
x22 2
P
( x2
a)2 2
C2
EIw2
Pb l
x23 6
P
( x2
a)3 6
C2 x2
D2
由连续性条件,可求得
C1 C2
D1 D2
由边界条件,可求得
C1
C2
M pa
P PL
2
PL 2
x
P
qa2
2
q
M
qa
x qa 2 2
x
pa
§6.2 挠曲线近似微分方程及其积分
一、挠曲线近似微分方程的导出
力学公式 数学公式
1 M z (x)
EIz
d 2w
1
dx2
[1 ( dw)2 ]3/2
dx
纯弯曲梁变形后中性层的曲率 公式,对于横力弯曲(l>5h) 可近似使用。EIZ称为梁的抗 弯刚度。
最大转角和最大挠度分别为:
得:
ql 3 C ,
D0
24
梁的转角方程和挠曲线方程分别为:
q (6lx2 4x3 l 3 )
24 EI
w qx (2lx2 x3 l3) 24EI
max
A
B
ql 3 24EI
wmax
w
x l 2
5ql 4 384EI
例: 已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力P作用下的转角方
确定积分常数: (1)边界条件
固定端:w = 0,θ = 0
工程力学c材料力学部分第六章 弯曲变形

A l/2
C l
B
解:此梁上的荷载可视为 正对称和反对称荷载的叠加, 正对称和反对称荷载的叠加, 如图所示。 如图所示。 正对称荷载作用下:
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解:将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然,在反对称力( / )作用下, 显然,在反对称力(P/2)作用下,wc=0 对称力作用的简支梁, 对称力作用的简支梁,可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件: 连续条件
P A C θC左 wC左= wC右, =θ C右 B
的悬臂梁, 例1:图示一弯曲刚度为 的悬臂梁,在自由端受一集中力 作 :图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程,并求最大挠度及最大转角。 用,试求梁的挠曲线方程,并求最大挠度及最大转角。 解:① 建立坐标系并写出弯矩方程 ①
在小变形情况下, 曲线弯曲平缓, 在小变形情况下,挠曲线弯曲平缓,
∴ w′ ≪ 1
2
材料力学 第6章 梁的弯曲变形

(c)
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
在本章所取的坐标系中,
上凸的曲线w″为正值,下凸的为负值。
如图6-5所示。 按弯矩正负号的规定,正弯矩对应着负的w″, 负弯矩对应着正的w″,故(c)式
w
M (x)
(1
w2 )3 2
EI z
在小变形情况下, w dw 是一个很小的量, dx
则 w'2为高阶微量,可略去不计,故
挠曲线的近似微分方程
M x
w EI z
EIw''= −M (x)
(6-1b)
图6-5
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
6.4 积分法计算梁的变形
对于等直梁,可以直接积分,计算梁的挠度和转角。 将式(6-1b)积分一次,得到
EIw′ = EIθ = −∫ M (x) dx + C
maxFl 2 2EI来自A xyF
θmax B
x
wmax
l
图6-7 例题 6-1 图
wm a x
Fl 3 3EI
θ max为正值,表明梁变形后,截面B顺时针转动;
wmax为正值,表明点B位移向下。
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
例题6-2 一简支梁受均布荷载q作用,如图6-8所示。试求梁的转角方程和 挠度方程, 并确定最大挠度和A、B截面的转角。设梁的弯曲刚度为EI。
A x
y
F
θmax B
x
wmax
l
进行两次积分,得到
EIw EI Flx Flx2 C
(a)
2
EIw Flx2 Fx3 Cx D
材料力学简明教程(景荣春)课后答案第六章

( ) wA
= − q0l 4 30EI
↓
,θB
= q0l3 24EI
(顺)
讨论:请读者按右手坐标系求 wA ,θB 并与以上解答比较。
(c)
(c1)
解 图(c1)
( ) ∑ M B = 0 , FC
= − Me l
↓
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
l 2
≤
x2
≤
l ⎟⎞ ⎠
Ew1′′
=
3 8
qlx1
−
1 2
qx12
EIw1′
=
3 16
qlx12
−
1 6
qx13
+
C1
EIw1
=
1 16
qlx13
−
1 24
qx14
+
C1 x1
+
D1
EIw′2′
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l ⎟⎞ 4⎠
EIw′2
=
3 16
qlx22
−
ql 4
⎜⎛ ⎝
x2
24
EIw′(l) = 0 ,− q l 3 + 3Al 2 + 2Bl = 0
6
解式(a),(b)得
A = ql , B = − ql 2
12
24
即挠曲线方程为
EIw = − q x4 + ql x3 − ql 2 x2 24 12 24
材料力学知识点

第六章弯曲变形知识要点1、弯曲变形的概念1)、挠曲线弯曲变形后梁的轴线变为挠曲线。
平面弯曲时,挠曲线为外力作用平面内的平面曲线。
2)、平面弯曲时的变形在小变形情况下,梁的任意二横截面绕各自的中性轴作相对转动,杆件的轴线变为平面曲线,其变形程度以挠曲线的曲率来度量。
1》纯弯曲时,弯矩—曲率的关系(由上式看出,若弯曲刚度EI为常数则曲率为常数,即挠曲线为圆弧线)2》横力弯曲时,弯矩—曲率的关系3)、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移,以表示。
2》转角——横截面绕其中性轴旋转的角位移,以表示。
挠度和转角的正负号由所选坐标系的正方向来确定。
沿y轴正方向的挠度为正。
转角的正负号判定规则为,将x轴绕原点旋转90°而与y轴重合,若转角与它的转向相同,则为正,反之为负。
4)、挠曲线近似微分方程5)、受弯曲构件的刚度条件,2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。
对于梁上有突变载荷(集中力、集中力偶、间断性分布力)的情况,梁的弯矩M(x)不是光滑连续函数,应用上式时,应分段积分,每分一段就多出现两个积分常数。
因此除了用边界条件外,还要用连续性条件确定所有的积分常数。
边界条件:支座对梁的位移(挠度和转角)的约束条件。
连续条件:挠曲线的光滑连续条件。
悬臂梁边界条件:固定端挠度为0,转角为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等简支梁边界条件:固定绞支座或滑动绞支座处挠度为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等连接铰链处,左右两端挠度相等,转角不等3、叠加原理求梁的挠度和转角1)、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。
2)、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系,因此要求:1》弯矩M和曲率成线性关系,这就要求材料是线弹性材料2》曲率与挠度成线性关系,这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1)、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁,它的未知力不能用静力平衡方程完全确定,必须由变形相容条件和力与变形间的物理关系建立补充方程,然后联立静力平衡方程与补充方程,求解所有的未知数。
直梁的弯曲 PPT

AC段:
Q1 RA 935N
A
RA
a
P1
C l/2
P2 P3 b
D
E
B
RB
M1 RA x 935x
l
Q2 RA P CD段: 1 435N
M 2 RA x P x 125 1 ( x a) 435
Q3 RA P DE段: 1P 2 565N
剪力
a
A
1 1C
P
P
D
a
B
RA
x1 Q1
RB
M1
Y 0
Q1 RA P
RA
M1
RA Q1 0
P
Q1
P
RB
弯矩
M 0
M1 RA x1 Px1
求2-2截面内力:以右段为对象 剪力Y 0
RA Q2 P 0
Q2 P RA 0 M2 P a
M ydA
A
弯矩阻止该截面在外力矩作用下所发生的进一步转 动,并且力图恢复梁的原形。
二、剪力和弯矩的计算
剪力计算法则:梁任一横截面上的剪力等于 该截面一侧(左侧或右侧都可)所有横向外力的 代数和。 截面左侧向上的外力和截面右侧向下的外力 取正值;截面左侧向下的外力和截面右侧向上的 外力取负值。 P P Q Q Q Q P P Q=-P<0 Q=-P<0 Q=P>0 Q=P>0
M 0 Y 0
A
RB a 5Fa F 2a RAa 0
RB RA F
RB 2 F RA F
y F 1A2 1 2
Me =5Fa a
3 4 3 4 B
第六章弯曲变形分析
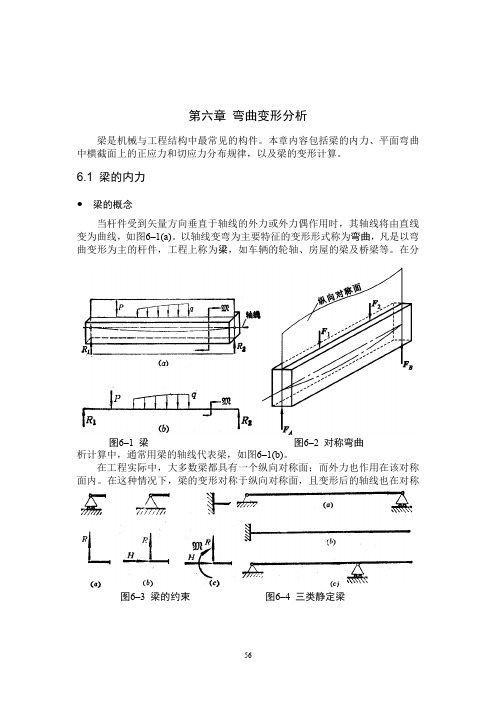
第六章 弯曲变形分析梁是机械与工程结构中最常见的构件。
本章内容包括梁的内力、平面弯曲中横截面上的正应力和切应力分布规律,以及梁的变形计算。
6.1 梁的内力● 梁的概念当杆件受到矢量方向垂直于轴线的外力或外力偶作用时,其轴线将由直线变为曲线,如图6–1(a)。
以轴线变弯为主要特征的变形形式称为弯曲,凡是以弯曲变形为主的杆件,工程上称为梁,如车辆的轮轴、房屋的梁及桥梁等。
在分析计算中,通常用梁的轴线代表梁,如图6–1(b)。
在工程实际中,大多数梁都具有一个纵向对称面;而外力也作用在该对称面内。
在这种情况下,梁的变形对称于纵向对称面,且变形后的轴线也在对称图6–1 梁 图6–2 对称弯曲图6–3 梁的约束 图6–4 三类静定梁面内,即所谓的对称弯曲,如图6–2。
它是弯曲问题中最基本、最常见的情况。
本章只讨论梁的对称弯曲。
图6–3表示了梁的三种常见约束形式及相应的约束力:可动铰支座(图6–3(a)),固定铰支座(图6–3(b))和(平面)固定端约束(图6–3(c))。
在以上三种约束方式下,有三种常见的梁形式,如图6–4所示。
图6–4(a)为简支梁,两端分别为固定铰支座和活动铰支座;图6–4(b)为悬臂梁,一端固定端约束,一端自由;图6–4(b)为外伸梁,它是具有一个或两个外伸部分的简支梁。
这三种梁都是静定梁。
作用在梁上的外载荷,常见的有集中力偶M (图6–5(a))、分布载荷q (图6–5(b))和集中力F (图6–5(c))。
在实际问题中,q 为常数的均布载荷较为常见。
● 梁的剪力与弯矩在4.2中已经介绍了求杆件内力的通用方法,即截面法。
具体到梁,其内力分量为剪力和弯矩,规定当剪力相对于横截面的转向为顺时针为正,使杆件发生上凹下凸的弯矩为正,如图4–5(b)和(c)。
例6–1:如图6–6所示悬臂梁,受均布载荷q ,在B 点处受矩为2qa M =的力偶作用,试绘梁的剪力图与弯矩图。
解:设固定端的约束力和约束力偶为C R 和C M ,则由平衡方程00=-=∑qa R F C y ,qa R C =05.102=--⋅=∑C C M qa qa a m ,221qa M C = 以杆件左端为坐标原点,以B 为分界面,将梁分为AB 和BC 两段。
直梁的弯曲.培训课件

弯矩的符号约定
M
M
+
-
M
M
上压下拉为正
上拉下压为负
▪弯矩的计算法则
梁在外力作用下,其任意指定横截面上的弯 矩等于该截面一侧所有外力对该截面中性轴 取矩的代数和: M=∑ mo(Fi) 凡是向上的外力其矩取正,向下的外力其矩 取负:向上为正
对于集中力偶:左顺为正
弯矩图
梁横截面上的弯矩,一般随横截面的位置而变 化,以坐标 x 表示横截面位置,则弯矩可表示为x
(ii)求特殊截面上的弯矩 为画出各段梁弯矩图,需求以下各横截面 上弯矩:
Mc 0
MA
qa2 2
201 2
10kN m
MD左 M0 RBa 20151 5kN m
MD右 RBa 151 15kN m
MB 0
(iii) 作图 在CA
段内再适当算出几个弯矩 值,标于坐标上,并与
MC,MA的坐标相连,画出 抛物线;再以直线MA,MD左 和MD右,MB的坐标,可得 全梁的弯矩图图c所示。 由图可见,在D稍右处横
y
d1 m1 a1
di
mi
ai
h
c1
ci
x
n1 b1
ni b bi
具有对称平面的 等截面直梁
梁上外力、梁的支座及分类
外力的类型
•集中力 •分布力 •集中力偶
线密度
hq
W
m
梁上外力、梁的支座及分类
梁的分类
•简支梁:吊车梁 •悬臂梁:管道托架,塔设备 •外伸梁:卧式容器
本章重点讨论直梁平面弯曲的 强度和刚度问题,讨论顺序: 外力--内力--应力--强度条件和 刚度条件。
§4.2 梁的内力分析
第六章:梁弯曲时的内力和应力

剪力图和弯矩图:以梁轴线为横坐标,分别以剪力值和弯矩值为纵坐标, 按适当比例作出剪力和弯矩沿轴线的变化曲线,称作剪力图和弯矩图。
剪力、弯矩方程便于分析和计算,剪力、弯矩图形象直观,两者对于解 决梁的弯曲强度和刚度问题都非常重要,四者均是分析弯曲问题的基础。
第三节:剪力图和弯矩图
5-5 截面
FS5 q 2 FB 5.5 kN
1 23 4
5
1 23 4
5
M5 (q 2)1 8 kN m
第三节:剪力图和弯矩图
第三节:剪力图和弯矩图
一、剪力、弯矩方程与剪力、弯矩图
剪力方程和弯矩方程:为了描述剪力与弯矩沿梁轴线变化的情况,沿梁 轴线选取坐标 x 表示梁截面位置,则剪力和弯矩是 x 的函数,函数的解 析表达式分别称为剪力方程和弯矩方程。
M 为常数,即对应弯矩图应为水平直线; 其他两段的弯矩图则均为斜直线。
第三节:剪力图和弯矩图
3)判断剪力图和弯矩图形状 AC、CD、DB 各段梁的剪力图均为水 平直线。在 CD 段,弯矩 M 为常数,对 应弯矩图应为水平直线;其他两段的弯 矩图则均为斜直线。
4)作剪力图和弯矩图
剪力图 弯矩图
第四节:弯曲时的正应力
第一节:梁的计算简图 第二节:弯曲时的内力计算 第三节:剪力图和弯矩图 第四节:弯曲时的正应力 第五节:正应力强度计算 第六节:弯曲切应力 第七节:提高梁弯曲强度的一些措施
第一节:梁的计算简图
第一节:梁的计算简图
一、梁的支座 梁的支座形式:工程中常见的梁的支座有以下三种形式。 1、固定铰支座:如图 a)所示,固定铰支座限制梁在支承处任何方向的 线位移,其支座反力可用两个正交分量表示,即沿梁轴线方向的 FAx 和 垂直于梁轴线方向的 FAy 。
《直梁的弯曲》课件

本课程将帮助您理解直梁的弯曲,包括定义、应用案例,以及实际应用中的 受力分析等方面。
直梁的定义
1 形态多样
2 材料广泛
直梁可以是长方形、圆形、 梯形、等腰三角形,还可 以是不规则截面,具有很 强的适应性。
直梁可以是钢、木材、混 凝土等多种材料,根据实 际情况选用不同材料可以 使得设计更加符合实际。
3 用途广泛
直梁用于桥梁工程、建筑 工程、机械制造等领域, 是一项非常重要的工程基 础。
采用欧拉-伯努利梁理论
基本假设
梁的截面上任意点的平面仍保 持平面状态,不发生大变形。
导出方程
欧拉-伯努利梁理论是从平衡方 程、应变-位移关系和恒定体积 原理出发导出的。
适用范围
该理论假设梁的变形很小,仅 适用于杆件长度较大、截面尺 寸较小的杆件。
2
跨河大桥建设
建设跨河大桥需要使用钢梁,而钢梁又需要经过精准的计算和设计,方能达到给定的跨度和 承重能力。
3
机械制造中的应用
在机械制造行业,还会使用直梁的弯曲原理来进行设计和计算,准确的计算对机械的使用寿 命和安全性大有裨益。
结论与展望
弯曲问题解决
通过本课程,您已经了解了直梁的弯曲和相关 应用,能够对各种弯曲问题做出准确的分析。
梁受力分析
弯矩分析
计算梁的弯曲应变,通过弯矩分 析得到相关参数。
轴力分析
梁受到压力和张力作用,分析力 的产生和传递。
剪力分析
梁受到剪力的作用,分析梁受剪 切变形带来的影响。
应用案例分析
1
地铁路基工程
地铁是当今城市中交通工具使用最频繁的,而交通干道、大楼和其他设施往往会影响到地铁, 需要使用直梁解决问题。
建筑力学—组合变形及答案讲解
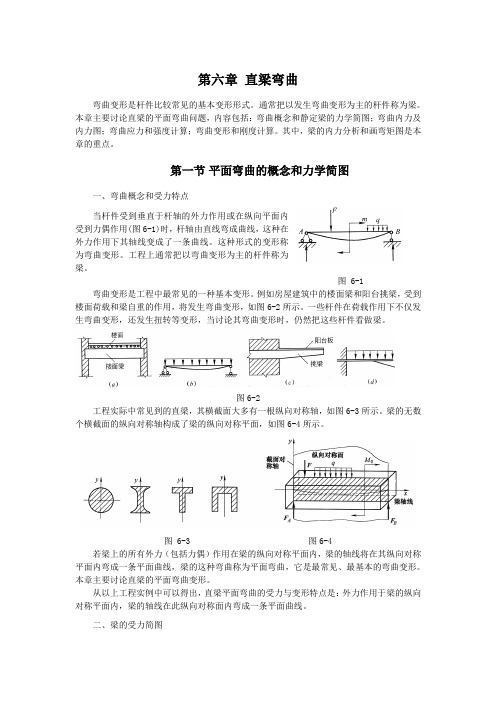
第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。
通常把以发生弯曲变形为主的杆件称为梁。
本章主要讨论直梁的平面弯曲问题,内容包括:弯曲概念和静定梁的力学简图;弯曲内力及内力图;弯曲应力和强度计算;弯曲变形和刚度计算。
其中,梁的内力分析和画弯矩图是本章的重点。
第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时,杆轴由直线弯成曲线,这种在外力作用下其轴线变成了一条曲线。
这种形式的变形称为弯曲变形。
工程上通常把以弯曲变形为主的杆件称为梁。
图 6-1 弯曲变形是工程中最常见的一种基本变形。
例如房屋建筑中的楼面梁和阳台挑梁,受到楼面荷载和梁自重的作用,将发生弯曲变形,如图6-2所示。
一些杆件在荷载作用下不仅发生弯曲变形,还发生扭转等变形,当讨论其弯曲变形时,仍然把这些杆件看做梁。
图6-2工程实际中常见到的直梁,其横截面大多有一根纵向对称轴,如图6-3所示。
梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面,如图6-4所示。
图 6-3 图6-4若梁上的所有外力(包括力偶)作用在梁的纵向对称平面内,梁的轴线将在其纵向对称平面内弯成一条平面曲线,梁的这种弯曲称为平面弯曲,它是最常见、最基本的弯曲变形。
本章主要讨论直梁的平面弯曲变形。
从以上工程实例中可以得出,直梁平面弯曲的受力与变形特点是:外力作用于梁的纵向对称平面内,梁的轴线在此纵向对称面内弯成一条平面曲线。
二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度,需建立梁的力学简图。
梁的力学简图(力学模型)包括梁的简化、荷载的简化和支座的简化。
1、梁的简化由前述平面弯曲的概念可知,载荷作用在梁的纵向对称平面内,梁的轴线弯成一条平面曲线。
因此,无论梁的外形尺寸如何复杂,用梁的轴线来代替梁可以使问题得到简化。
例如,图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁,可分别用梁的轴线AB代替梁进行简化(图6-1b和图6-2b)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章直梁弯曲课题:第一节平面弯曲与梁得形式第二节梁得内力(一):弯矩剪力概念符号[教学目标]一、知识目标:掌握平面弯曲、剪力与弯矩得概念,熟悉梁得形式,弯矩剪力符号。
二、能力目标:熟练掌握剪力与弯矩得概念三、素质目标:概念清晰,认真仔细,灵活应用[教学重点]梁得形式,剪力与弯矩得概念[难点分析]剪力与弯矩得概念比较抽象[学生分析]此节内容概念较抽象,学生掌握起来有一定困难,将概念形象化。
[辅助教学手段]通过举生活及工程中得实例加深学生对剪力与弯矩及各种梁得认识,通过提问、讨论帮助学生掌握知识[课时安排]2课时[教学内容] 新课讲解第一节平面弯曲与梁得形式1.复习扭转变形构件得受力特点及变形特点:2.通过举例(如教室得主梁、次梁)引入本节内容:一、平面弯曲:1、受力特点:杆件受到通过杆轴线平面内得力偶作用,或受到垂直于杆轴线得横向力作用。
2、变形特点:杆件得轴线由直线变成曲线,发生平面弯曲。
简单介绍纵向对称平面。
3.举工程实例:梁4.梁得形式:矩形、工字形、T形等。
二、梁得形式: (在学习梁得形式得同时,将几种梁得受力图分析画出)1、简支梁(图a)(路旁座椅、单杠、双杠等)2、外伸梁(图b)3、悬臂梁(雨棚、阳台)(图c)第二节梁得内力(一) 一、复习截面法:切开,代替,平衡。
二、剪力与弯矩得概念剪力:与横截面相切得内力V叫剪力弯矩:外力作用平面内得力偶,其力偶矩M叫弯矩。
三、剪力、弯矩正负号得规定:剪力得符号:左上右下为正弯矩得符号:下凸为正,上凸为负(下面受拉上面受压为正,上面受拉下面受压为负)课题:第二节梁得内力(二)[教学目标]一、知识目标:计算剪力与弯矩二、能力目标:熟练掌握剪力与弯矩得计算方法(截面法,规律)三、素质目标:概念清晰,认真仔细,灵活应用[教学重点]剪力与弯矩得计算[难点分析]计算剪力与弯矩得规律[学生分析]此节内容涉及计算较多,学生掌握起来难度较大,建议加强练习。
[辅助教学手段]通过大量练习使学生能达到熟能生巧,掌握相关知识[课时安排]2课时[教学内容] 新课讲解第二节梁得内力1、复习在轴向拉压杆中计算内力得方法及步骤:截面法;切开、代替、平衡。
2、复习在圆轴扭转变形中计算内力得方法及步骤:截面法;切开、代替、平衡。
3、引入本节内容:一、用截面法计算受弯构件中指定截面得内力得具体步骤:1、计算支座反力2、用截面假想地在需要求内力处将梁截成两段,任取其中一段为研究对象。
3、用内力代替弃去部分对研究对象得作用,并保留作用在研究对象上得一切外力,画出研究对象得受力图。
强调:1)研究对象上所有得力,包括所有外力与内力。
2)内力:弯矩与剪力。
3)内力得方向:复习上次课得内容。
4)对比轴向拉压杆与扭转变形圆轴得内力及其正负得规定。
4、建立平衡方程,求解内力。
例题6-1:简支梁如图a所示,已知P1=40kN,P2=26kN,试计算截面1-1上得剪力与弯矩。
解:(图b、c)(1)求支座反力RA,RB(2)计算截面1-1得内力M1,V1提示:复习支座类型、支座反力;假设内力时得方向以正向假设;列力得平衡方程时力得正负:与坐标轴正向一致为正。
力矩\偶得正负:逆时针为正。
(P36)求解力平衡方程式得结果得正负:正值代表与假设方向一致。
例题6-2:图a中得悬臂梁,已知q=400N/m,P=500N,试计算据梁自由端B为2m处得截面1-1得内力。
解:取右段为研究对象(图b:不用求支座反力)提示:复习支座类型、支座反力;在例题6-1得基础上进一步强化理论得应用,提高计算能力。
二、计算受弯构件中指定截面内力得简化方法:1、受弯构件中计算剪力与弯矩得规律:计算剪力得规律:梁上任一截面得剪力,在数值上等于该截面一侧所有外力沿截面方向投影得代数与。
计算弯矩得规律:梁上任一截面得弯矩,在数值上等于该截面一侧所有外力对截面形心力矩得代数与。
2、简化方法(由规律得出):计算剪力得简化方法:梁上任一截面得剪力=该截面左侧所有外力沿截面方向投影得代数与。
(外力向上取正号,向下取负号)梁上任一截面得剪力=该截面右侧所有外力沿截面方向投影得代数与。
(外力向上取负号,向下取正号)计算弯矩得简化方法:梁上任一截面得弯矩=该截面左侧所有外力对截面形心力矩得代数与+力矩/偶。
(外力向上取正号,向下取负号;力矩顺时针为正)梁上任一截面得弯矩=该截面右侧所有外力对截面形心力矩得代数与+力矩/偶。
(外力向上取正号,向下取号号;力矩逆时针为正)例题6-3:外伸梁得受力情况如图所示,已知P=4kN,q=1、5kN/m,m=3kN/m,试求梁F、D左截面得剪力与弯矩。
解:(1)求支座反力R B,R D(2)求截面得内力。
练习:要求学生用简化方法求解例题6-1与6-2。
课题:第三节梁得内力图(一)集中力与集中力偶作用下梁得内力图[教学目标]一、知识目标:集中力与集中力偶作用下梁得内力图二、能力目标:熟练掌握集中力与集中力偶作用下梁得内力图三、素质目标:概念清晰,认真仔细,踏实耐心[教学重点]集中力与集中力偶作用下梁得内力图[难点分析]梁得内力图在建筑力学中就是较重要得知识点,掌握起来也较难[学生分析]此节内容涉及计算绘图较多,学生掌握起来有一定难度,建议加强练习,掌握规律。
[辅助教学手段]通过大量练习使学生能达到熟能生巧,掌握相关知识[课时安排]2课时[教学内容] 新课讲解第三节梁得内力图(一)1、复习梁得内力:2、引入梁得内力图概念及画图步骤:剪力图(V图)与弯矩图(M图):用平行于梁轴得坐标表示横截面得位置;垂直于梁轴得纵坐标表示相应截面得剪力或弯矩。
剪力图:正值画在上方,负值画在下方。
弯矩图:正值画在下方,负值画在上方。
画图步骤:先列出内力方程;再结合数学上得函数图像性质作图。
一、在集中力作用下梁得内力图:1、特点:在梁上只有集中力作用时,集中力把梁分为若干段无荷载作用区。
在无荷载作用区:V图就是与x轴平行得直线;M图就是斜直线。
在集中力作用处:V图发生突变,突变得绝对值等于该集中力;M图发生转折。
2、通过例题6-4与6-5具体解释:通过例题要求掌握截面法求内力、利用内力规律写内力方程式与绘制内力图。
例6-4梁AB得自由端受集中力P得作用(见图),试画出该梁得剪力图与弯矩图例6-5简支梁受集中力作用(见图),试画出梁得剪力图与弯矩图二、在集中力偶作用下梁得内力图:1、特点:在集中力偶作用处V图无变化,M图发生突变,突变得绝对值等于该集中力偶得力偶矩。
2、通过例题6-6具体解释:通过例题要求掌握截面法求内力、利用内力规律写内力方程式与绘制内力图。
例6-6简支梁AB在C截面处作用有集中力偶m(如图),试画出梁得剪力图与弯矩图课题:第三节梁得内力图(二)[教学目标]一、知识目标:掌握在均布荷载作用下梁得内力图,熟练掌握绘图规律及用叠加法画弯矩图二、能力目标:概念清晰,熟练掌握绘图规律三、素质目标:富有责任感,做事认真仔细,踏实耐心[教学重点]绘图规律、用叠加法画弯矩图[难点分析]梁得内力图在建筑力学中就是较重要得知识点,但如果掌握了绘图规律并反复强化练习就是可以掌握得[学生分析]此节内容涉及计算绘图较多,学生掌握起来有一定难度,建议加强练习,掌握规律。
[辅助教学手段]通过大量练习使学生能达到熟能生巧,掌握相关知识[课时安排]4课时(2课时讲解,2课时练习)[教学内容] 新课讲解第三节梁得内力图(二)一、在均布荷载下梁得内力图:1、特点:V图——斜直线;M图——抛物线。
2、通过例题6-7、6-8、6-9具体解释:例6-7悬臂梁AB,受均布荷载q作用(见图),试画出该梁得剪力图与弯矩图例6-8简支梁受均布荷载q作用(见图),试画出梁得剪力图与弯矩图例6-9外伸梁受均布荷载q作用(见图),试画出梁得剪力图与弯矩图二、内力图得规律:1、在无荷载作用区,当剪力图平行于x轴时,弯矩图为斜直线。
2、在均布荷载作用下得规律:荷载朝下,剪力图往右降,弯矩图往上凹。
3、在集中力作用处,剪力图突变,弯矩图发生转折。
4、在集中力偶作用处弯矩图线突变。
5、在剪力为零得截面有弯矩得极值。
例6-10简支梁受受力情况见图,已知P=10kN,q=40kN/m,m=160kN、m试应用内力图得规律画出该梁得剪力图与弯矩图三、用叠加法画弯矩图:1、叠加原理2、叠加法:通过悬臂梁受均布荷载与集中荷载两类荷载下得内力图简单解释叠加法。
例6-11某简支梁受荷情况见图,试应用叠加法画出该梁得弯矩图。
课题:第四节平面图形得几何性质[教学目标]一、知识目标:熟悉形心得概念,熟悉理解面积矩与惯性矩得计算方法二、能力目标:概念清晰, 熟悉面积矩与惯性矩得计算方法三、素质目标:做事认真仔细,踏实耐心[教学重点]面积矩与惯性矩得计算方法[难点分析]此节知识点概念性较强,重在理解[学生分析]此节知识点概念性较强,学生重在理解与熟悉。
[辅助教学手段]通过各种图例与讲解,使学生理解熟悉相关知识[课时安排]2课时[教学内容] 新课讲解第四节平面图形得几何性质一、形心与面积矩:1.形心:具有对称中心得平面图形得对称中心。
2.面积矩:平面图形得面积A与其形心到某一坐标轴得距离得乘积。
3.形心坐标公式:用途:计算组合图形得形心坐标。
4、通过例题加强学生得理解例6-12计算如图所示T形截面对Z轴得形心坐标yc、解:例6-13计算如图所示槽形截面得形心位置解:二、惯性矩:1、概念:把平面图形分成无数多个微小面积,用每一块微小面积乘以其形心到某一坐标轴距离得平方,再把这些乘积叠加起来,这个值叫做平面图形对该轴得惯性矩。
2、计算公式:正方形: ; 矩形: ; 圆形:3、例:6-14已知矩形,b=3mm;h=4mm;试计算该矩形对两个形心轴得惯性矩。
三、惯性矩得平行移轴公式(组合图形对其形心轴得惯性矩)1.公式:2、例6-15:T形各部分尺寸如图所示,试计算T形对形心轴y,z得惯性矩。
解:(1)确定形心轴位置(2)求Iy,Iz四、习题(一)简单图形截面对形心轴得惯性矩计算:1、套用现成公式2、一定要注意单位以P160得6-10(a)、(b)、(c)为例。
(二) T形截面对形心轴得惯性矩计算:1、划分成简单图形2、通过面积矩求形心位置3、套用简单图形得对形心轴惯性矩得计算公式4、利用平行移轴公式5、一定要注意单位以P160得6-11为例,复习例6-15。
(三)槽形截面对形心轴得惯性矩计算:1、划分成简单图形2、通过面积矩求形心位置3、套用简单图形得对形心轴惯性矩得计算公式4、利用平行移轴公式5、一定要注意单位复习例6-13。
课题:第五节梁得正应力及其强度条件[教学目标]一、知识目标:熟悉理解梁得正应力及其强度条件二、能力目标:概念清晰, 掌握梁得正应力计算方法三、素质目标:增强理解能力,分析能力[教学重点]梁得正应力计算方法,正应力得强度条件[难点分析]此节概念较抽象,重在理解与熟悉[学生分析]此节知识点概念性较强,学生重在理解与熟悉。
