微分几何 1.3 空间曲线
微分几何第一章曲线论第三节空间曲线

P
(C )
基本向量的计算公式 (1)若曲线(C ) : r r (t ), t为一般参数. r r r ; ; r r r r r r ( r r ) r r r r r r r (r r )r ( r r )r . r r r (2)若曲线(C ) : r r ( s ), s为自然参数. r r r r r ; . r ; r r r r
X 1 Y 0 1 1 0 Z 1 0, 即Y Z 0. 0 X 1 Y Z . 副法线的方程为: 0 1 1
3.2 空间曲线的基本三棱形
设曲线(C ) : r r ( s) C 2, P P( s) (C )是非逗留点, dr r 单位切向量, ds (C ) , 1, 即r r , r 主法向量, 副法向量, r 伏雷内标架 { P; , , }; 定义 (基本向量,, ;
P
T
定义 (密切平面) 切平面的极限位置
叫做曲线(C )在点的P密切平面.
Q
T
P
过点P与密切平面垂直的直线 r ( t 0 t ) 叫做曲线(C )在P点的副法线. (C ) O 方程 设曲线(C ) : r r (t ) C 2,
r (t0 )
O
微积分课件第3节空间曲线及其在坐标面上的投影

方程组
所表示的曲线方程称为
空间曲线的一般方程. 特殊地,空间直线方程
三、空间曲线及其在坐标面上的投影
例1
方程组
x2
+
y2
+ z2
=
25,
表示什么曲线?
z= 3;
解 因为 x2 + y2 + z2 = 25是球心在原点, 半径为
5 的球面.
z
z = 3 是平行于 x y
坐标面的平面,
z=3
因而它们的交线是
柱面的概念
准线
母线
平行于定直线并沿定曲线 C 移动的直线L 所形成的曲面称为柱面.
复习
几种常用的柱面方程及图形
(1)圆柱面
(2)椭圆柱面
(3)双曲柱面
(4)抛物柱面
统 称 为 二 次 柱 面 圆柱面
椭圆柱面
抛物柱面
三、 旋转曲面
一平面曲线 C 绕同一平面上的一条定直线 L 旋转一周
所形成的曲面称为 旋转曲面. 曲线C 称为旋转曲面的
定直线 L 称为旋转曲面的 旋转轴.
z
1.圆锥面方程
2. 旋转抛物面
O
y
x
第三节 空间曲线及其在 坐标面上的投影
第四节 二次曲面
第三节 空间曲线及其在坐标 面上的投影
一、空间曲线的一般方程 二、空间曲线在坐标面上的投影 三、小结 思考题
第三节 空间曲线及其在坐标面上的投影
一、空间曲线的概念
1、空间曲线 把空间曲线C看作是两曲面的交线.
二、空间曲线在坐标面上的投影
补充: 空间立体或曲面在坐标面上的投影.
空间立体
曲面
二、空间曲线在坐标面上的投影
微分几何第一章答案(周建伟版)

= =
θ0
ρ 2 (θ) + ρ2 (θ) dθ.
made by Mr X
1.2(8)
求曲线 x3 = 3a2 y, 2xz = a2 在平面 y =
a 3
与 y = 9a 之间的弧长.
3 2
解:令 x = t, 则所给曲线的参数方程为r (t) = t, 3ta2 , a 2t . 容易验证 t 是正则参 a 数. 当 y = 3 时, t = a; 当 y = 9a 时, 即 t = 3a, 于是所求弧长为
1.2(2)
求三次挠曲线 r (t) = {at, bt2 , ct3 } 在点 t = t0 的切线和法面. 解:当 t = t0 时, 有
3 r (t0 ) = {at0 , bt2 0 , ct0 },
r (t0 ) = {a, 2bt0 , 3ct2 0 },
所以切线方程为
z − ct3 y − bt2 x − at0 0 0 = , = a 2bt0 3ct2 0
1.3(10) 证明: 如果曲率处处不为零的曲线的所有密切平面都经过一定点, 则此曲线
为平面曲线. 证明Ⅰ 设曲线的一般参数方程为 r = r(t), 并设密切平面上流动点的径矢为 R, 则密切平面方程为 (R − r(t), r (t), r (t)) = 0. 利用密切平面过定点的条件, 不失一般性设定点为坐标原点, 则 (r(t), r (t), r (t)) = 0, 上式两边关于参数 t 求导, 得 (r(t), r (t), r (t)) = 0, 由(1), (2)知 r (t), r (t), r (t) 共面, 即有 (r (t), r (t), r (t)) = 0. 于是 挠率 τ t ≡ 0, 即曲线为平面曲线. (2) (1)
《微分几何》课程教学大纲

《微分几何》课程教学大纲一、课程信息课程名称:微分几何Differentia1Geometry课程代码:06S1022B课程类别:专业选修课适用专业:数学与应用数学专业(师范类)课程学时:45学时(理论35,实践10)课程学分:2.5学分修读学期:第6学期先修课程:数学分析、高等代数、解析几何、常微分方程二、课程目标微分几何是数学与应用数学专业的选修课程,是运用微积分的理论研究空间的几何性质的数学分支学科。
古典微分几何研究三维空间中的曲线和曲面,而现代微分几何开始研究更一般的空间一一流形。
微分几何与拓扑学等其它数学分支有紧密的联系,对物理学的发展也有重要影响,爱因斯坦的广义相对论就以微分几何中的黎曼几何作为其重要的数学基础。
本课程的前导课程为解析几何、高等代数、数学分析和常微分方程。
本课程旨在介绍微分几何的基本思想方法和理论,让学生了解它的研究对象、研究方法和技巧,了解一些重要概念及其几何意义,经典理论及其模型,掌握重要几何量的计算,通过重要例题的演示,让学生学会综合利用数学分析、解析几何、微分方程等的基本知识解决微分几何问题,使学生掌握三维欧氏空间中的曲线和曲面的局部微分理论和方法,培养学生分析三维欧氏空间的曲线和曲面的局部性态的能力以及对微分几何这门学科的兴趣。
(一)具体目标通过本课程的学习,使学生达到以下目标:1.了解现代几何学的发展背景,熟悉微分几何研究的基本方法和技巧,理解从欧式空间到一般几何对象的基本思想,对中学的几何课程有更好的理解,具有一定的批判精神及创新能力,具有分析问题和解决问题的能力。
【支撑毕业要求3、4、7]2.掌握向量函数的相关概念和计算;掌握一般曲线的参数表示及切线、法平面、密切平面等概念;掌握曲线的曲率、挠率及伏雷内公式;理解曲线的局部结构及空间曲线论的基本定理;了解一般螺线的概念;综合运用微积分、解析几何的知识解决微分几何的问题,具备一定的计算能力。
【支撑毕业要求3、4]3.掌握曲面的参数表示及相关概念;掌握曲面的第一基本形式及其应用,理解等距变换及曲面的内蕴性质;掌握曲面的第二基本形式及各种曲率的概念和计算;理解直纹面、可展曲面的概念;了解曲面论的基本定理;理解曲面上的测地线及其性质,了解高斯-波涅公式及其应用。
微分几何_1.3____空间曲线
3
由 0 ( ) ( 1 ) 1 1 1 ( ) (( ) ) 1 1 1 ( r )[( ) ] r r r r r ( r , , ) 2 6 r r r ( r , , ) ( r r ) 2 (r , r , r ) 2 可得挠率公式为 (r r )
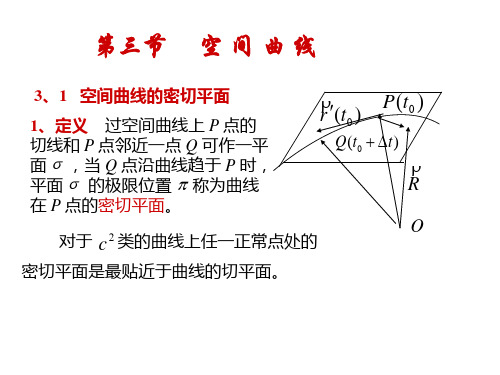
密切平面是最贴近于曲线的切平面。
2、密切平面的方程
P(t0 ) 给出 C 类的曲线(C): r (t ) r r (t0 ) 有 PQ r (t t ) r (t ) Q(t0 t ) 0 0 2 1 (t0 )t 2 (r (t0 ) )t r R 因为向量 r (t0 )和 PQ 都在平面 上,所以它们的 O 线性组合 22 [ PQ r (t0 )t ] r (t0 ) 也在平面 上。 t
但与刚体运动和坐标变换无关。我们把 k k ( s), (s) 称为 空间曲线的自然方程。 空间曲线论基本定理
给出闭区间[s0,s1]上的两个连续函数 ( s) 0, (s) ,则除了空 间的位置差别外,唯一存在一条空间曲线,使得参数 s 是曲线 的自然参数,并且 (s) 和 (s) 分别为曲线的曲率和挠率,即曲 线的自然方程为 k ( s), ( s)
3、对于曲线(C)的一般参数表示 r r (t ), 有
r , r (r r )r (r r )r r r , r r r r r
设柱面的母线平行于 z 轴,则可令 p e3 ,再设一般螺线的
空间曲线PPT课件

contents
目录
• 空间曲线的基本概念 • 空间曲线的方程 • 空间曲线的几何性质 • 空间曲线在几何图形中的应用 • 空间曲线在现实生活中的应用 • 空间曲线的发展前景与展望
01
CATALOGUE
空间曲线的基本概念
定义与特性
定义
空间曲线是由三维空间中的点的 集合构成,这些点通过连续的参 数变化而形成一条连续的轨迹。
02
CATALOGUE
空间曲线的方程
参数方程
参数方程
通过选择合适的参数t,将空间曲线 上的点与参数t关联起来,形成参数 方程。
参数方程的优缺点
参数方程可以直观地表达曲线的形状 和方向,但有时候参数的选择可能较 为复杂。
直角坐标方程
直角坐标方程
利用三维空间中的三个互相垂直的坐标轴,将空间曲线上的点与三个坐标轴上的 值关联起来,形成直角坐标方程。
空间曲线在几何学中的地位和作用
地位
空间曲线是几何学中的重要概念之一,它是连接点与点之间 的桥梁,也是描述三维空间中物体运动和变化的重要工具。
作用
空间曲线在几何学中有着广泛的应用,如在解析几何、微积 分、线性代数等领域中都有重要的应用。此外,空间曲线还 在工程、建筑、艺术等领域中有着广泛的应用,如建筑设计 、机械设计、动画制作等。
直角坐标方程的应用
直角坐标方程广泛应用于解析几何、微积分等领域。
极坐标方程
极坐标方程
利用极径和极角来描述空间曲线上的 点,形成极坐标方程。
极坐标方程的特点
极坐标方程可以方便地描述旋转对称 的曲线,但在处理复杂曲线时可能不 够直观。
球坐标方程
球坐标方程
利用球径和球角来描述空间曲线上的点,形成球坐标方程。
第三节空间曲线

k (s), (s)
s s 为了确定曲线的位置,设 空间 P0 点(即 r(s0 ) r0
)0,时并,且曲在线该对点应的
基本向量为给定的两两正交的右手系的单位向
量 0, 0,0
证明(1)以 (s) 和 (s) 为系数建立微分方程组
因曲线 (C) 在 p 点的密切平面,又因为
和 都垂直于切向量 ,所以
和 所确定的平面是曲线上 p 点的法平 面, 和 所确定的平面则称为曲线 (C)
上 p 点的从切平面
方程分别为: 密切平面
或 法平面
或 从切平面
线的刚体运动及空间曲线坐标变换无关。我 们把 k k(s), (s) 称为空间曲线的自 然方程。
空间曲线论的基本定理:
给出闭区间[s0.s1]上的两个连续函数 s 0, (s) ,则
除了空间的位置差别外,惟一地存在一条空间曲线,
s 使得参数 是曲线的自然参数,并且 和(s分) 别
1 2!
k0
0
(s)2
16其(中k0
20 k0
10
0 k0
20 3
0
0
)(s)3 ,
而 0,0, 0, 0, k0,0
等表示在点 r(s0 )的值。
由上式可得
r(s0
s)
r(s
0
)
[s
1 6
(k
2 0
1)(s)3
向量的夹角是
由第一节命题知(P11) lim
s0 s
几何意义是它的数值为曲线的副法向量对于弧长的旋 转速度。
(整理)空间曲线的曲率挠率和Frenet公式

空间曲线的曲率、挠率和Frenet公式摘要:本文研究了刻画空间曲线在某点邻近的弯曲程度和离开平面程度的量—曲率和挠率以及空间曲线论的基本公式--Frenet公式,并且举例有关曲率、挠率的计算和证明.关键词:空间曲线;曲率;挠率;Frenet公式Spatial curvature,torsion and Frenet formulas Abstract:This paper studies space curves depict a point near the bend in the degree and extend of the amount of leave plane-the curvature and torsion and the basic formula of space curves-Frenet formulas,and for example the curvature and torsion of the calculation and proof.Key Words: space curves; curvature; torsion; Frenet formulas前言空间曲线的曲率、挠率和Frenet公式是空间曲线基本理论的一部分,它是以空间曲线的密切平面和基本三棱形的知识作为基础的.空间曲线的曲率、挠率和Frenet公式在空间曲线的基本理论中占有重要位置,是空间曲线的一些基本性质和基本公式.曲线的曲率和挠率完全决定了曲线的形状.当曲线的曲率和挠率之间满足多种不同的关系时,就会得到不同类型的曲线.例如:0k>时为直τ=时为平面曲线.线,0本文将从定义、公式推导和具体举例三方面逐步解析空间曲线的曲率、挠率和Frenet公式.本文第一部分讲述曲率和挠率的定义,第二部分讲述Frenet公式和曲率、挠率的一般参数表示的推导,第三部分具体举例有关曲率、挠率的计算和证明.1.空间曲线的曲率和挠率的定义1.1准备知识—空间曲线的伏雷内标架给出2c 类空间曲线()c 和()c 上一点p .设曲线()c 的自然参数表示是(),r r s =其中s 是自然参数,得dr dsr ==α 是一单位向量.α 称为曲线()c 上p 点的单位切向量.由于1=α,则⊥αα,即r r ⊥.在α上取单位向量==αr βαr, (1)β称为曲线()c 上p 点的主法向量.再作单位向量=⨯γαβ,γ称为曲线()c 上p 点的副法向量.我们把两两正交的单位向量,,αβγ称为曲线上p 点的伏雷内(Frenet)标架. 1.2 空间曲线的曲率我们首先研究空间曲线的曲率的概念.在不同的曲线或者同一条曲线的不同 点处,曲线弯曲的程度可能不同.例如半径较大的圆弯曲程度较小,而半径较小的圆弯曲程度较大.为了准确的刻画曲线的弯曲程度,我们引进曲率的概念.要从直观的基础上引出曲率的确切定义,我们首先注意到,曲线弯曲的程度越大,则从点到点变动时,其切向量的方向改变的越快.所以作为曲线在已知一曲线段PQ 的平均弯曲程度可取为曲线在P 、Q 间切向量关于弧长的平均旋转角.设空间中3c 类曲线()c 的方程为().r r s =曲线()c 上一点p ,其自然参数为s ,另一邻近点1p ,其自然参数为s s +∆.在p 、1p 两点各作曲线()c 的单位切向量()s α和()s s +∆α.两个切向量的夹角是ϕ∆,也就是把点1p 的切向量()s s +∆α平移到点p 后,两个向量()s α和()s s +∆α的夹角为ϕ∆.我们把空间曲线在p 处的切向量对弧长的旋转速度来定义曲线在点p 的曲率.定义[]1 空间曲线()c 在p 点的曲率为()lims k s sϕ∆→∆=∆, 其中s ∆为p 点及其邻近点1p 间的弧长,ϕ∆为曲线在点p 和1p 的切向量的夹角.再利用命题“一个单位变向量()t r (即()1t =r )的微商的模,()r t 的几何意义是()t r 对于t 的旋转速度”.把这个结果应用到曲线()c 的切向量α上去,则有()k s =α.由于r =α,所以曲率也可表示为()k s r =.由上述空间曲线的曲率的定义可以看出,它的几何意义是曲线的切向量对于弧长的旋转速度.当曲线在一点的弯曲程度越大,切向量对于弧长的旋转速度就越大,因此曲率刻画了曲线的弯曲程度.对于空间曲线,曲线不仅弯曲而且还要扭转(离开密切平面),所以研究空间曲线只有曲率的概念是不够的,还要有刻画曲线扭转的程度的量—挠率. 1.3 空间曲线的挠率当曲线扭转时,副法向量(或密切平面)位置随着改变(如图一),所以我 们用副法向量(或密切平面)的转动速度来刻画曲线的扭转程度(在一点离开密切平面的程度).现在设曲线()c 上一点p 的自然参数为s ,另一邻近点1p 的参数为s s +∆,在p 、1p 两点各作曲线()c 的副法向量()s γ和()s s +∆γ.此两个副法向量的夹角是ϕ∆(如图一).(图一)再利用命题“一个单位变向量()t r (即()1t =r )的微商的模,()r t 的几何意义是()t r 对于t 的旋转速度” .把这个结果应用到曲线()c 的副法向量向量γ上去, 得到lims sϕ∆→∆=∆γ, 此式的几何意义是它的数值为曲线的副法向量(或密切平面)对于弧长的旋转速度.当曲线在一点的扭曲程度越大(离开所讨论点的密切平面的程度越大),副法向量(或密切平面)对于弧长的旋转速度就越大.因此,我们可以用它来刻画曲线的扭转程度.根据(1)和曲率的定义,我们有()k s ===r ααβr α, 即()s s γ+∆()k s =αβ. (2) 对=⨯γαβ求微商,有()()k s =⨯=⨯+⨯=⨯+⨯=⨯αβαβαβββαβαβγ,因而⊥αγ.又因为γ是单位向量,所以⊥γγ.由以上两个关系可以推出//γβ. (3) 现在我们给出挠率的定义如下: 定义[]1 曲线()c 在p 点的挠率为:().s τ⎧+⎪⎪=⎨⎪-⎪⎩γγβγγβ,当和异向,,当和同向 挠率的绝对值是曲线的副法向量(或密切平面)对于弧长的旋转速度. 介绍了曲率、挠率的定义之后,为了更好的应用曲率和挠率,下面我们来看Frenet 公式和曲率、挠率的一般参数表示式的推导过程.2. Frenet 公式和曲率、挠率的一般参数表示式的推导2.1 Frenet 公式的推导 根据(3)及挠率的定义有τ=-γβ(s) (4) 另外,对=⨯βγα求微商,并利用(4)和(2),可以推导出()()()()()s k s k s s ττ=⨯=⨯+⨯=-⨯+⨯=-+βγαγαγαβαγβαγ(5)公式(2),(5),(4)称为空间曲线的伏雷内(Frenet )公式,即()()()()k s k s s s ττ⎧=⎪⎪=-+⎨⎪=-⎪⎩αββαγγβ, 这组公式是空间曲线的基本公式.它的特点是基本向量α、β、γ关于弧长s 的微商可以用α、β、γ的线性组合来表示.它的系数组成反称的方阵()0()0()0()0k s k s s s ττ⎛⎫ ⎪- ⎪ ⎪-⎝⎭2.2 曲率的一般参数表示式的推导 若给出3c 类的空间曲线()c().r r s =,则有,dr ds dsr r ds dt dt==,22,222,,222ds d s d r ds d s ds d s r r r r r r dt dt ds dt dt dt dt ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以232,,,2ds ds d s ds r r r r r r r dt dt dt dt ⎡⎤⎛⎫⎛⎫⨯=⨯+=⨯⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,由上式得3,,,sin ds r r r r dt θ⎛⎫⨯= ⎪⎝⎭.注意上式中,1,,dsr r r r dt=⊥=, 因而有3,,,,r r k r ⨯=.由此得到曲率的一般参数表示式,,,3,r r k r⨯=.2.3挠率的一般参数表示式的推导 再由伏雷内公式的(4)式τ=-γβ(s),两边点乘β得r τ=-βββ,因而()()26,2,,,1111111,,,,kk k k k k k k r r r τ⎛⎫=-==⨯ ⎪⎝⎭⎛⎫⎛⎫⎛⎫=⨯+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=⨯+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫ ⎪⎝⎭=⎛⎫ ⎪⎝⎭=⨯γβγβαβαααααγγγγγγγγγγ 再把,ds r rdt= 22,,2ds d s r r r dt dt ⎛⎫=+ ⎪⎝⎭323,,,233ds ds d s d s r dt dt dt dt ⎛⎫=++ ⎪⎝⎭γγγ 代入(),,,,,,r r r ⨯⨯中得()66,,,,,,,,,,,ds r r r r dt ⎛⎫⎛⎫⎛⎫⨯⨯==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭γγγγγγ,所以得到()(),,,,,,2,,,r r r r r τ⨯⨯=⨯. 这是一般参数表示的挠率计算公式.另外说一下密切圆,曲率中心,曲率半径的定义.空间曲线()c 在一点的密切圆(曲率圆)是过曲线()c 上一点()P s 的主法线的正侧取线段PC ,使PC 的长为1k ,以C 为圆心,以1k为半径在密切平面上确定一个圆,这个圆称为曲线()c 在()P s 点的密切圆(曲率圆),曲率圆的中心称为曲率中心,曲率圆的半径称为曲率半径(如图二).(图二)3. 有关曲率、挠率的计算和证明例 1[]1求圆柱螺线{}cos ,sin ,a a b θθθ=r ()θ-∞<<+∞的曲率和挠率.解 由圆柱螺线方程{}cos ,sin ,a a b θθθ=r ,先计算{},sin ,cos ,a a b θθ=-r ,{},,cos ,sin ,0a a θθ=--r ,{},,,sin ,cos ,0a a θθ=-r ,β于是有,=r{},,,2sin cos sin ,cos ,,cos sin 0a ab ab ab a a a θθθθθθ⨯=-=---123e e e r r,,,⨯=r r代入曲率和挠率的公式得(),,,3322,,ak a b⨯===+r r r ()(),,,,,,2222422,,,,,.,ba ba b aa b τ===++r r r r r 由以上可以看出,圆柱螺线的曲率和挠率都是常数.例 2[]1 证明曲率恒等于零的曲线是直线. 证明 已知0,k =≡r 因而,=r 0由此得到 =r a (常向量). 再积分即得 ,s =+r a b 其中b 也是常向量.这是一条直线的参数方程.例 3[]1 证明挠率恒等于零的曲线是平面曲线. 证明 若0,τ≡则γ是固定向量,但是我们已知0,=αγ因而有0,=r γ积分后得a =r γ(常数),所以曲线在一个平面上,即曲线是平面曲线.以上即为有关曲率、挠率的计算和证明,充分说明了研究空间曲线的曲率、挠率对空间曲线的研究有重要意义.结语:空间曲线的曲率、挠率和Frenet公式是空间曲线基本理论的重要部分.其中Frenet公式是微分几何空间曲线论的基本公式,是研究空间曲线论的基础,在经典微分几何中占有重要地位,可以由它导出曲线的诸多重要性质和定理.参考文献:[1] 梅向明,黄敬之.微分几何(第四版)[M]. 北京:高等教育出版社,2008.精品文档精品文档。
空间曲线的曲率、挠率和Frenet公式

空间曲线的曲率、挠率和Frenet 公式前言空间曲线的曲率、挠率和Frenet 公式是空间曲线基本理论的一部分,它是以空间曲线的密切平面和基本三棱形的知识作为基础的.空间曲线的曲率、挠率和Frenet 公式在空间曲线的基本理论中占有重要位置,是空间曲线的一些基本性质和基本公式.曲线的曲率和挠率完全决定了曲线的形状.当曲线的曲率和挠率之间满足多种不同的关系时,就会得到不同类型的曲线.例如:0k >时为直线,0τ=时为平面曲线.本文将从定义、公式推导和具体举例三方面逐步解析空间曲线的曲率、挠率和Frenet 公式.本文第一部分讲述曲率和挠率的定义,第二部分讲述Frenet 公式和曲率、挠率的一般参数表示的推导,第三部分具体举例有关曲率、挠率的计算和证明.1. 空间曲线的曲率和挠率的定义1.1准备知识—空间曲线的伏雷内标架给出2c 类空间曲线()c 和()c 上一点p .设曲线()c 的自然参数表示是(),r r s =其中s 是自然参数,得drdsr ==α 是一单位向量.α 称为曲线()c 上p 点的单位切向量.由于1=α,则⊥αα,即r r ⊥.在α上取单位向量==αr βαr, (1)β称为曲线()c 上p 点的主法向量.再作单位向量=⨯γαβ,γ称为曲线()c 上p 点的副法向量.我们把两两正交的单位向量,,αβγ称为曲线上p 点的伏雷内(Frenet)标架. 1.2 空间曲线的曲率我们首先研究空间曲线的曲率的概念.在不同的曲线或者同一条曲线的不同 点处,曲线弯曲的程度可能不同.例如半径较大的圆弯曲程度较小,而半径较小的圆弯曲程度较大.为了准确的刻画曲线的弯曲程度,我们引进曲率的概念.要从直观的基础上引出曲率的确切定义,我们首先注意到,曲线弯曲的程度越大,则从点到点变动时,其切向量的方向改变的越快.所以作为曲线在已知一曲线段PQ 的平均弯曲程度可取为曲线在P 、Q 间切向量关于弧长的平均旋转角.设空间中3c 类曲线()c 的方程为().r r s =曲线()c 上一点p ,其自然参数为s ,另一邻近点1p ,其自然参数为s s +∆.在p 、1p 两点各作曲线()c 的单位切向量()s α和()s s +∆α.两个切向量的夹角是ϕ∆,也就是把点1p 的切向量()s s +∆α平移到点p 后,两个向量()s α和()s s +∆α的夹角为ϕ∆.我们把空间曲线在p处的切向量对弧长的旋转速度来定义曲线在点p的曲率.定义[]1空间曲线()c 在p 点的曲率为()lims k s sϕ∆→∆=∆, 其中s ∆为p 点及其邻近点1p 间的弧长,ϕ∆为曲线在点p 和1p 的切向量的夹角. 再利用命题“一个单位变向量()t r (即()1t =r )的微商的模,()r t 的几何意义是()t r 对于t 的旋转速度”.把这个结果应用到曲线()c 的切向量α上去,则有()k s =α.由于r =α,所以曲率也可表示为()k s r =.由上述空间曲线的曲率的定义可以看出,它的几何意义是曲线的切向量对于弧长的旋转速度.当曲线在一点的弯曲程度越大,切向量对于弧长的旋转速度就越大,因此曲率刻画了曲线的弯曲程度.对于空间曲线,曲线不仅弯曲而且还要扭转(离开密切平面),所以研究空间曲线只有曲率的概念是不够的,还要有刻画曲线扭转的程度的量—挠率. 1.3 空间曲线的挠率当曲线扭转时,副法向量(或密切平面)位置随着改变(如图一),所以我 们用副法向量(或密切平面)的转动速度来刻画曲线的扭转程度(在一点离开密切平面的程度).现在设曲线()c 上一点p 的自然参数为s ,另一邻近点1p 的参数为s s +∆,在p 、1p 两点各作曲线()c 的副法向量()s γ和()s s +∆γ.此两个副法向量的夹角是ϕ∆(如图一).()s s γ+∆(图一)再利用命题“一个单位变向量()t r (即()1t =r )的微商的模,()r t 的几何意义是()t r 对于t 的旋转速度” .把这个结果应用到曲线()c 的副法向量向量γ上去, 得到lims sϕ∆→∆=∆γ, 此式的几何意义是它的数值为曲线的副法向量(或密切平面)对于弧长的旋转速度.当曲线在一点的扭曲程度越大(离开所讨论点的密切平面的程度越大),副法向量(或密切平面)对于弧长的旋转速度就越大.因此,我们可以用它来刻画曲线的扭转程度.根据(1)和曲率的定义,我们有()k s ===r ααβrα, 即()k s =αβ. (2) 对=⨯γαβ求微商,有()()k s =⨯=⨯+⨯=⨯+⨯=⨯αβαβαβββαβαβγ,因而⊥αγ.又因为γ是单位向量,所以⊥γγ.由以上两个关系可以推出//γβ. (3) 现在我们给出挠率的定义如下: 定义[]1曲线()c 在p 点的挠率为:().s τ⎧+⎪⎪=⎨⎪-⎪⎩γγβγγβ,当和异向,,当和同向 挠率的绝对值是曲线的副法向量(或密切平面)对于弧长的旋转速度. 介绍了曲率、挠率的定义之后,为了更好的应用曲率和挠率,下面我们来看Frenet 公式和曲率、挠率的一般参数表示式的推导过程.2. Frenet 公式和曲率、挠率的一般参数表示式的推导2.1 Frenet 公式的推导 根据(3)及挠率的定义有τ=-γβ(s) (4) 另外,对=⨯βγα求微商,并利用(4)和(2),可以推导出()()()()()s k s k s s ττ=⨯=⨯+⨯=-⨯+⨯=-+βγαγαγαβαγβαγ(5)公式(2),(5),(4)称为空间曲线的伏雷内(Frenet )公式,即()()()()k s k s s s ττ⎧=⎪⎪=-+⎨⎪=-⎪⎩αββαγγβ, 这组公式是空间曲线的基本公式.它的特点是基本向量α、β、γ关于弧长s 的微商可以用α、β、γ的线性组合来表示.它的系数组成反称的方阵()0()0()0()0k s k s s s ττ⎛⎫ ⎪- ⎪ ⎪-⎝⎭2.2 曲率的一般参数表示式的推导 若给出3c 类的空间曲线()c().r r s =,则有,dr ds dsr r ds dt dt==,22,222,,222ds d s d r ds d s ds d s r r r r r r dt dt ds dt dt dt dt ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以232,,,2ds ds d s ds r r r r r r r dt dt dt dt ⎡⎤⎛⎫⎛⎫⨯=⨯+=⨯⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,由上式得3,,,sin ds r r r r dt θ⎛⎫⨯= ⎪⎝⎭.注意上式中,1,,dsr r r r dt=⊥=, 因而有3,,,,r r k r ⨯=.由此得到曲率的一般参数表示式,,,3,r r k r⨯=.2.3挠率的一般参数表示式的推导 再由伏雷内公式的(4)式τ=-γβ(s),两边点乘β得r τ=-βββ,因而()()26,2,,,1111111,,,,kk k k k k k k r r r τ⎛⎫=-==⨯ ⎪⎝⎭⎛⎫⎛⎫⎛⎫=⨯+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=⨯+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎪⎝⎭=⎛⎫ ⎪⎝⎭=⨯γβγβαβαααααγγγγγγγγγγ再把,ds r rdt= 22,,2ds d s r r r dt dt ⎛⎫=+ ⎪⎝⎭323,,,233ds ds d s d s r dt dt dt dt ⎛⎫=++ ⎪⎝⎭γγγ 代入(),,,,,,r r r ⨯⨯中得()66,,,,,,,,,,,ds r r r r dt ⎛⎫⎛⎫⎛⎫⨯⨯==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭γγγγγγ, 所以得到()(),,,,,,2,,,r r r r r τ⨯⨯=⨯. 这是一般参数表示的挠率计算公式.另外说一下密切圆,曲率中心,曲率半径的定义.空间曲线()c 在一点的密切圆(曲率圆)是过曲线()c 上一点()P s 的主法线的正侧取线段PC ,使PC 的长为1k ,以C 为圆心,以1k为半径在密切平面上确定一个圆,这个圆称为曲线()c 在()P s 点的密切圆(曲率圆),曲率圆的中心称为曲率中心,曲率圆的半径称为曲率半径(如图二).(图二)3. 有关曲率、挠率的计算和证明例 1[]1求圆柱螺线{}cos ,sin ,a a b θθθ=r ()θ-∞<<+∞的曲率和挠率.解 由圆柱螺线方程{}cos ,sin ,a a b θθθ=r ,先计算{},sin ,cos ,a a b θθ=-r ,{},,cos ,sin ,0a a θθ=--r ,{},,,sin ,cos ,0a a θθ=-r ,于是有,=r{},,,2sin cos sin ,cos ,,cos sin 0a ab ab ab a a a θθθθθθ⨯=-=---123e e e r r ,,,⨯=r r代入曲率和挠率的公式得,,,322,,ak a b ⨯===+r r r β()(),,,,,,2222422,,,,,.,ba ba b aa b τ===++r r r r r 由以上可以看出,圆柱螺线的曲率和挠率都是常数.例 2[]1 证明曲率恒等于零的曲线是直线. 证明 已知0,k =≡r 因而,=r 0由此得到 =r a (常向量). 再积分即得 ,s =+r a b 其中b 也是常向量.这是一条直线的参数方程.例 3[]1证明挠率恒等于零的曲线是平面曲线.证明 若0,τ≡则γ是固定向量,但是我们已知0,=αγ因而有0,=r γ积分后得a =r γ(常数),所以曲线在一个平面上,即曲线是平面曲线.以上即为有关曲率、挠率的计算和证明,充分说明了研究空间曲线的曲率、挠率对空间曲线的研究有重要意义.结语:空间曲线的曲率、挠率和Frenet 公式是空间曲线基本理论的重要部分.其中Frenet 公式是微分几何空间曲线论的基本公式,是研究空间曲线论的基础,在经典微分几何中占有重要地位,可以由它导出曲线的诸多重要性质和定理.参考文献:[1] 梅向明,黄敬之.微分几何(第四版)[M]. 北京:高等教育出版社,2008.。
微分几何_曲线的概念

a v (t t0) .
2 2 2
点 t0 0 ,s(t) □
a2 2 v 2 t .
参数变换 定义:对于曲线 : r r (to ), 给出函数 t (u) 如果 , (u) 0 ,则称 t (u ) 为曲线 的一个参数 变换,在次变换下曲线 的方程为 r r[ (u)]. 命题1:参数变换曲线的正则性和正向不变。 证: , (u) 0 t增加则u增加,故正向不变
切线的坐标式Βιβλιοθήκη 方程 设r(t0 ) {x(t0 ), y (t0 ), z (t0 )}, r (t0 ) {x (t0 ), y (t0 ), z (t0 )},
, , , ,
则切线方程消去
得到
X x(t0 ) Y y(t0 ) Z z (t0 ) , , , , x (t0 ) y (t0 ) z (t0 )
dr dr dt , = =r(t) , (u ) 0 du dt du
故正则性不变
命题:曲线上两点间的弧长与参数的选取无关。 证:设 t (u) 为曲线 的一个参数变换且
u0 =u(t0 )
t ,
r=r(t)=r*(u)
t ,
dt s (t ) r (t ) dt r (t ) du t0 t0 du * u dr dt u dr | | du | | du s (u ) u0 dt du u0 du
例
2.3曲线的切线和法面
Q 给出曲线上一点 P 点 , 是 P 邻近一点,把线 PQ 绕 P 点旋转,使 Q 点沿曲线趋近于 P 点,若割线 PQ 趋近于一定的位置,则我们把割线 PQ 的极限位 置称为曲线在 P 点的切线,定点 P 称为切点。
空间曲线——精选推荐

空间曲线本节内容:研究空间曲线的基本理论,研究刻画空间曲线在某一点邻近的弯曲程度和离开平面程度的量——曲率和挠率,以及曲线在一点邻近的近似形状。
复习内容:切线、切向量;()r t 对自然参数的导矢是单位向量;()r t 具有固定长()()r t r t '⇔⊥ ;单位向量()r t 对于t 的旋转速度等于其微商的模。
一 空间曲线的密切平面、副法线1 密切平面、副法线的定义:过曲线上P 点的切线和P 点的邻近一点Q 可作一平面σ,当Q 点沿着曲线趋于P 点时平面σ的极限位置π 称为曲线在P点的密切平面。
密切平面在P 点的法线称为曲线在P 点的副法线。
2 密切平面、副法线的方程设曲线(c)为2C 类曲线,P 点的径矢00(),()r t Q r t t +∆ 点的径矢 2000001()()()(())(),lim 02t r t t r t r t t r t t εε∆→'''+∆-=∆++∆= PQ= 。
20001()()(())()2r t r t r t t ε''''⨯⨯+∆ PQ=‖00()(())r t r t ε'''⨯+ ,当Q P →时, 000,0,()()t r t r t ε'''∆→→→⨯这个矢积。
如果00()()0r t r t '''⨯≠ ,则该矢量为密切平面法线上的一个非零矢量,它和P 点完全确定了密切平面,方程是:000(()()())0r t r t r t ρ'''-= ,,副法线方程:000()()())r t r t r t ρλ'''=⨯+( 副法线的标准方程是:000()()(),x x t y y t z z t X Y Z---== 00{,,}()()X Y Z r t r t '''=⨯ 其中。
微分几何13空间曲线

7、几个例题 例1 园柱螺线的曲率和挠率都是常数。 例2 曲率恒为零的曲线是直线。 例3 挠率恒为零的曲线是平面曲线。 例4 求曲率为 4 ,挠 率为 5 的曲线方程。
解 由题意,可设曲线为园柱螺线
r {a cos , a sin ,b}
因此
a
b
4
25
得所求园柱螺a线2 为 b2 4 ,
a2 b2 5 a 41
P
P1
(s s)
2、曲率的几何意义是曲线的切向量对于弧长的旋转速度。 曲率越大,曲线的弯曲程度就越大,因此它反映了曲线的 弯曲程度。
3、挠率 与曲率类似有
lim
r r
k(s)
s0 s
(s s)
(s)
k(s)
,
(
)
(s s)
k
(s)
,
.(
1)
//
.
定义 曲线(C)在 P 点的挠率为
x(t0 )
y(t0 )
z(t0 )
平面曲线的密切平面就是曲线所在的平面。 例题 求园柱螺线上任一点的密切平面。
P
3、2 空间曲线的基本三棱形
1、给出 C类曲2 线
r得一r单(位s)向量
,称为曲
r
dr
ds
线(C)上 P 点的单位切向量。 ( 注意到
称
为曲线在 称
P
点为的曲主线法在向P量点,rr它的 垂付直法于向单量位。切向量。
,当
和
异向,
挠率的绝对值 (是s曲) 线的付法向量 ,对当于弧和长的旋同转向速.度。
4、由定义可得
(s)
又
(
)•
(s)
k(s)
于是有 k(s) (s)
微分几何1﹒3空间曲线

3.6 一般螺线
1、定义:切线和固定方向作固定角的曲线称为一般螺线。
2.性质:
主法线与一个固定方向垂直。
证明:设 是固定方向上的一个单位向量。它与切向量作
固定角
,有
微商
、副法线与一个固定方向作固定角。
(3)曲率与挠率之比为一个常数。
可以证明,上面的结论也是充分的。 3.一般螺线的一种标准方程 设柱面的母线平行于 z 轴,则可令 方程为
, 再设一般螺线的
若令 z=0 , s=0 , 则 于是一般螺线的方程为
曲线上每一点都有确定的曲率和挠率, 它们与参数有关,
但与刚体运动和坐标变换无关。我们把
称为
空间曲线的自然方程。
空间曲线论基本定理
给出闭区间[s0,s1]上的两个连续函数
,则除了空
间的位置差别外, 唯一存在一条空间曲线, 使得参数 s 是曲
线的自然参数, 并且 和 分别为曲线的曲率和挠率, 即曲
线的自然方程为
7、几个例题
例1 园柱螺线的曲率和挠率都是常数。 例2 曲率恒为零的曲线是直线。
例3 挠率恒为零的曲线是平面曲线。
例4 求曲率为 4 , 挠率为 5 的曲线 方程。
解
由题意, 可设曲线为园柱
螺线因此
得所求园柱螺线为
3.4 空间曲线在邻近一点的结构
给定 类曲线
及其上一点
有
取 则有 标, 则有
为新坐标系, 并取 。设 为曲线上点
为计算弧长的始点, 的邻近点的新坐
近似曲线在三个平面上的投影分别为
通过画出以上三个投影的立体图形就可以看出空间曲线 在一点邻近的近似形状:
1、曲线穿过法平面与密切平面,但不穿过从切平面。 2、主法向量总是指向曲线凹入的方向,这是主法向量 正向的几何意义。 3.挠率的符号对曲线的影响见表。
微分几何曲线论 三维空间曲线 从参数表示到求出特征 从特征求.

说明:1.任意参数t , 绘曲线。
曲线方程可以取自题库,或自由输入。
起点或终点可以自动调整。
2.改变为离起点的弧长s为参数,方程相应变换为新的方程。
起点或终点s参数也可以自动调整。
3.活动标架应以弧长s 为参数。
可先给定固定的某s,用按键来逐步求出并显示标架:三个坐标向量,三个坐标平面与两个特征函数。
s,κ(s),ρ(s)显示于输出栏。
κ(s),ρ(s)的图形也相应显示于相应窗口。
按键可以弹出窗口,显示公式与评注。
4.让s 从起点到终点,动起来。
5.把κ(s),ρ(s)加进第二屏的题库中,备生成图形后与之对比。
文字描述与程序要求微分几何知识结构网络曲线论参量向量表示,即与坐标系,又与参数有关。
换参数与坐标系则换表达式。
条件约束:正则。
即三阶以上连续可微。
活动标架:运动公式:本质特征:与坐标系,又与参数无关。
存在唯一定理,决定曲线形状。
三维空间曲线参量r (t) = [ x (t), y(t), z (t) ] , t0 ≤t ≤T换参数程序:s (t) = ∫|r ‘(t ) | dt, t = s –1 (t )换坐标系程序:活动标架:切向量α(s) α(s) = r ‘(t) / | r ‘(t)| 弧长参数则自动归一。
法向量β(s) β(s)=α‘(s) /|α‘(s)| 向量微商,一定正交。
从法向量γ(s) γ(s) =α(s) X β(s) 画曲线及其活动标架。
α(s) β(s) 张成密切平面。
β(s) γ(s) 张成主法平面。
γ(s) α(s) 张成从法平面。
要画曲线在三个坐标平面上的投影。
本质特征:κ(s) = |α‘(s)| 曲率,未必单位长ρ(s) = |γ‘(s)| 挠率,存在唯一定理,决定曲线形状要画曲线的特征曲线。
运动公式:局部关系d r /ds = α(s)dα(s)/ds =κ(s) β(s)dβ(s)/ds =κdα(s)/ds + ρdγ(s)/dsdγ(s)/ds = -ρ(s) β(s) 解方程组的数值计算程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
ɺ ɺ 由 β ⋅ γ = 0 ⇒ β ⋅ γ = −γ ⋅ β = τβ ⋅ β = τ
ɺ = (α × β ) ⋅ ( 1 α )⋅ ɺ τ = γ ⋅β
κ
ɺ ɺ = (α × α ) ⋅ (( ) α +
1
1
⋅
κ
κ
⋅
1
κ
ɺ αɺ)
ɺ = (r × =
1
κ
2
ɺɺ)[( ) ɺɺ + ɺɺɺ] r r r
于是有
ɺ α = k (s) β
β = −k ( s )α + τ ( s )γ γɺ = −τ (s ) β
ɺ
这个公式称为空间曲线的伏雷内(Frenet)公式 伏雷内( 公式。它的系 伏雷内 公式 数组成一反称方阵 k ( s) 0 0 τ ( s) 0 − k ( s) 0 − τ ( s) 0
•
β
定一个园,这个园称为曲线在 P 点的密切园或曲率园,园的中 心叫曲率中心,园的半径叫曲率半径。
7、几个例题 、 例1 园柱螺线的曲率和挠率都是常数。 例2 曲率恒为零的曲线是直线。 例3 挠率恒为零的曲线是平面曲线。 例4 求曲率为 4 ,挠 率为 5 的曲线方程。 解 由题意,可设曲线为园柱螺线 r = {a cosθ , a sin θ , bθ } 因此
τ (s) =
− γɺ ,当 γɺ 和 β 同向.
挠率的绝对值是曲线的付法向量对于弧长的旋转速度。
4、由定义可得 、
γɺ = −τ (s ) β
ɺ 又 β = (γ × α ) • = γ × α + γ × α = −τ ( s ) β × α + γ × k ( s ) β ɺ ɺ = −k ( s)α + τ ( s )γ
0 2! 0 3! 0
= α 0 ∆s + 2 κ 0 β 0 (∆s )
1
2
r ( s0 + ∆s ) r ( s0 )
2 ɺ + 1 6 (−κ 0 α 0 + κβ 0 + κ 0τ 0γ 0 + ε )(∆s ) 3
O
≈ α 0 ∆s + 1 2 κ 0 β 0 (∆s ) 2 + 1 6 κ 0τ 0γ 0 (∆s ) 3
⋅
p = e3 ,再设一般螺线的
α ⋅ p = cos ω ⇒ α ⋅ e3 = cos ω
dx dy dz dz { , , } ⋅ {0,0,1} = cos ω ⇒ = cos ω ds ds ds ds
若令 z=0 , s=0 , 则 z = s cos ω 于是一般螺线的方程为
r = {x( s ), y ( s ), s cos ω }
用 R = { X , Y , Z } 表示 P 点的密切平面上任一点的向径, 则上式表示为
X − x(t0 ) Y − y (t0 ) Z − z (t0 ) x′(t0 ) y′(t0 ) z ′(t0 ) = 0 x′′(t0 ) y′′(t0 ) z ′′(t0 )
如果曲线用自然参数 s 表示,则将上式中的撇改成点。 平面曲线的密切平面就是曲线所在的平面。 例题 求园柱螺线上任一点的密切平面。
ɺ α = k ( s) β , γɺ = (α × β )⋅ ɺ ɺ = k (s)β × β + α × β = α × β
γ (s + ∆s) γ (s) ∆ψ
γ (s + ∆s)
⇒ γɺ ⊥ α , γ ⊥ γɺ .( γ = 1) ⇒ γɺ // β .
定义 曲线(C)在 P 点的挠率为 + γɺ , 当 γɺ 和 β 异向,
5、曲率和挠率的一般参数表示式 、
给出 C 3 类的曲线(C):
dr ds ɺ ds ds =r ⇒ = r ′. ds dt dt dt 2 2 2 ɺ ds 2 ds ɺ d s dr d s ɺɺ ds ɺ d 2 s ɺ ɺ r ′′ = (r )′ + r 2 = + r 2 = r + r 2 , dt dt ds dt dt dt dt r = r (t ) , r ′ =
第三节
空间曲线
r ′(t0 )
3、1 空间曲线的密切平面 、 1、定义 过空间曲线上 P 点的 、 切线和 P 点邻近一点 Q 可作一平 面 σ ,当 Q 点沿曲线趋于 P 时, 平面 σ 的极限位置 π 称为曲线 在 P 点的密切平面。 对于 c 类的曲线上任一正常点处的
2
P(t0 )
Q(t0 + ∆t )
γ
β
α
(3)曲率与挠率之比为一个常数。
可以证明,上面的结论也是充分的。 3、一般螺线的一种标准方程 设柱面的母线平行于 z 轴,则可令 方程为 r = r (s )
β ⋅ p = 0 ⇒ β ⋅ p = 0 ⇒ (−κα + τγ ) ⋅ p = 0 κ − κ cos ω ± τ sin ω = 0 ⇒ = ± tan ω (常数) τ
1
1
κ
κ
ɺr r (r , ɺɺ, ɺɺɺ)
κ
6
ɺr r r ′ (r , ɺɺ, ɺɺɺ) = (r ′ × r ′′) 2
可得挠率公式为
(r ′, r ′′, r ′′′) τ= (r ′ × r ′′) 2
6、密切园(曲率园) 密切园(曲率园) 密切园
P 1
k
C
过曲线(C)上一点 P 的主法线 的正侧取线段 PC,使 PC 的长为1/k。以 C 为园心,以1/k为半径在密切平面上确
(一个单位向量微商的模等于它对于变量的旋转速度) 2、曲率的几何意义是曲线的切向量对于弧长的旋转速度。 、曲率的几何意义 曲率越大,曲线的弯曲程度就越大,因此它反映了曲线的 弯曲程度。
ɺ = lim ∆ψ 3、挠率 与曲率类似有 γ 、 ∆s →0 ∆s
ɺɺ α ɺ ɺ r α β= = = ɺɺ α ɺ k (s ) r
近似曲线在三个平面上的投影分别为
2 2τ 0 3 ξ = 0, ζ 2 = η , 即在法平面上的投影为半立方抛物线; 9κ 0 1 η = 0, ζ = κ 0τ 0ξ 3 , 在从切平面上为立方抛物线; 6 1 ζ = 0,η = κ 0ξ 2 , 在密切平面上为抛物线。 2
通过画出以上三个投影的立体图形就可以看出空间曲线 在一点邻近的近似形状: 1、曲线穿过法平面与密切平面,但不穿过从切平面。 2、主法向量总是指向曲线凹入的方向,这是主法向量正向的 几何意义。 3、挠率的符号对曲线的影响见表。
3、5 空间曲线论的基本定理 、
曲线上每一点都有确定的曲率和挠率,它们与参数有关, 但与刚体运动和坐标变换无关。我们把 k = k ( s ),τ = τ ( s ) 称为 空间曲线的自然方程。 空间曲线论基本定理 给出闭区间[s0,s1]上的两个连续函数 φ ( s ) > 0, ψ (s) ,则除了空 间的位置差别外,唯一存在一条空间曲线,使得参数 s 是曲线 的自然参数,并且φ (s) 和ψ (s ) 分别为曲线的曲率和挠率,即曲 线的自然方程为 k = ϕ ( s ),τ = ψ ( s )
γ
P
β
α
3、2 、
2
空间曲线的基本三棱形
dr ,称为曲 ds
ɺ 1、给出 C 类曲线 r = r (s ) 得一单位向量 α = r = 、
ɺ α =1⇔ α ⊥α ) 单位切向量。 线(C)上 P 点的单位切向量 ( 注意到 单位切向量
称
ɺ α ɺɺ r β= = ɺ α ɺɺ r
为曲线在 P 点的主法向量 主法向量,它垂直于单位切向量。 主法向量 称 γ = α × β 为曲线在 P 点的付法向量 付法向量。 付法向量 把两两正交的单位向量 α , β , γ 称为曲线在 P 点的伏雷内 (Frenet)标架。
4、例题 P34 、
3、3 空间曲线的曲率,挠率和伏雷内公式 、 空间曲线的曲率,
设空间曲线(C)为 C 3 的,且以 s 为参数。 1、曲率 定义(C)在 P 为的曲率为 、
∆ϕ k ( s ) = lim ∆s →0 ∆s
有 k (s ) = α
•
P α (s) P ∆ϕ 1 α ( s + ∆s )
R
O
密切平面是最贴近于曲线的切平面。
2、密切平面的方程 、 给出 C 2 类的曲线(C): = r (t ) r 有
PQ = r (t0 + ∆t ) − r (t0 ) = r ′(t0 )∆t + 1 (r ′′(t0 ) + ε )∆t 2 2
r ′(t0 )
P (t0 )
Q (t0 + ∆t )
R
因为向量 r ′(t0 )和 PQ 都在平面 σ 上,所以它们的 O 线性组合 22 [ PQ − r ′(t0 )∆t ] = r ′′(t0 ) + ε 也在平面 σ 上。
∆t
两边取极限得 r ′′(t0 )在极限平面上,即 P 点的密切平面上,因此 只要 r ′(t ) × r ′′(t ) ≠ 0 这个向量就可以作为密切平面的一个法向量。 密切平面方程为 ( R − r (t0 ), r ′(t0 ), r ′′(t0 )) = 0
所以
2 3 ds ɺɺ ds ɺ d 2 s ɺ ɺɺ ds ɺ r ′ × r ′′ = r × r + r 2 = r × r , dt dt dt dt
ɺ ɺɺ ds sin θ = k r ′ 3 ( r = 1, r ⊥ ɺɺ) ɺ ɺ r 因此 r ′ × r ′′ = r r dt r ′ × r ′′ 由此得到曲率的一般参数的表示式 k = 3 r′
