14网络分析-A矩阵及其他
网 络 分 析

最小生成树的算法——克罗斯克法
• 1)先把图G中各边按权数从小到大重新排列,并取权数最 小的一条边为T中的边;
• 2)在剩下的边中,按顺序取下权数最小一条边,若该边与 T中已有的边构成回路,则舍去,否则选进T中;
• 3)重复2操作,直到有m-1条边被选进T中,这m-1条边就 是G的最小生成树。
地理信息系统原理及应用
1
网络由一组线状要素(一系列联结的 弧段)相互联结组成的,是物质、信 息流通的通道,非计算机网络。
2
网络模型是对现实世界网络的抽象。 在模型中,网络由链(Link)、结点(Node)、 站点(Stop)、中心(Center)和转向点 (Turn)组成。
建立一个好的网络模型的关键是清楚 地认识现实网络的各种特性与以网络模型 的要素(Link, Node, Stop, Center, Turn)表示的特性之间的关系。
8
e2
v3 e3 v4
v2
e8
e5 v6
e4
e1
e6 v7 e7 v8
v5
v1
e9
v9
9
• 3.连通性:
无向图
连通 不连通
有向图
连通 不连通
强连 通性
10
e4 v5
v1
e3 v4
e1 v3
v2 e2 (1)
v2 v4
v3 v5
e1 e2 e3
v4
v1
v2
v2
v3
e3 e1 e2
v1
v1
v5 v3
的点
4
5
一、网络图论基础
• 1.网络图:由一些点及点之间的线段所组成的图形。这些 图形与地图,与各种函数图形有较大的区别。
Z矩阵、Y矩阵、A矩阵、S矩阵、T矩阵定义、推导及转换公式

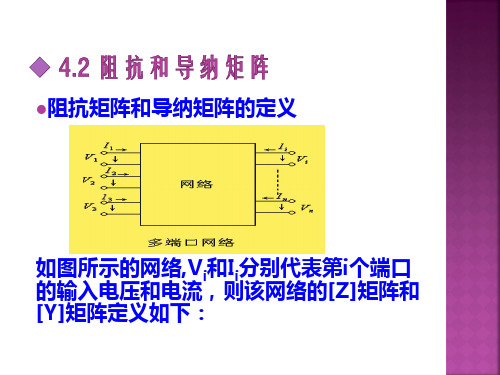
一、 微波网络各种参量矩阵定义图 1所示为二端口微波网络,1端口电压为U 1,电流为I 1;二端口电压为U 2,电流为I 2。
图 1 二端口微波网络1.1 Z 矩阵阻抗矩阵如下:11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (1.1-1) 111121221222U Z Z I U Z Z I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦[][][]U Z I = (1.1-2) 其中,211101I U Z I ==,111202I U Z I ==,222101I U Z I ==,122202I UZ I == (1.1-3)➢ 对于互易网络:1221Z Z = (1.1-4) ➢ 对于对称网络:1122Z Z = (1.1-5) ➢ 对于无耗网络:ij ij Z jX = (i,j=1, 2) (1.1-6)1.2 Y 矩阵导纳矩阵如下:11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.2-1)111121221222I Y Y U I Y Y U ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦[][][]I Y U = (1.2-2) 其中,211101U I Y U ==,111202U I Y U ==,222101U I Y U ==,122202U IY U == (1.2-3)➢ 对于互易网络:1221Y Y = (1.2-4)➢ 对于对称网络:1122Y Y = (1.2-5) ➢ 对于无耗网络:ij ij Y jB = (i, j=1,2) (1.2-6)1.3 A 矩阵端口2的电流取向外,应为-I 2。
图 2 二端口微波网络(A 矩阵)转移矩阵如下:11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.3-1) []11112221212222U A A U U A I A A I I ⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦(1.3-2) 其中,21110I U A U ==,21120U U A I ==-,11210U IA U ==,21220U IA I ==- (1.3-3)1122122111221221➢ 对于对称网络:1122A A = (1.3-8) ➢ 对于无耗网络:A 11,A 22为实数;A 12,A 21为虚数 (1.3-9)二、 微波网络各种参量矩阵转换2.1 Z 矩阵<=>Y 矩阵以归一化矩阵为例,根据归一化阻抗矩阵和归一化导纳矩阵,有1111122221122211111222211222u z i z i u z i z i i y u y u i y u y u =+⎧⎨=+⎩=+⎧⎨=+⎩ (2.1-1)则122112011221221,u i z y z z z z z u z====- (2.1-2)1112120u i y u z===-(2.1-3) 2221210u i y u z===-(2.1-4)至此,[][]111122212212221111y y z z y z y y z z z --⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦(2.1-6)同理,有[][]111122212212221111z z y y z y z z y y y --⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦(2.1-7) 即[][]1z y =,与归一化导纳矩阵中结论一致。
以IEEE14、30、39节点为例应用计算机形成关联矩阵教材

2、IEEE30节点
1
2
5
7
8
3
4
6
13
11 9
12
14
16 15
17 10
28
29 27
18 15
21
22
19
20
24
IEEE30节点系统图
30 25 26
30个节点,41条支路
2、IEEE30节点系统各线路数据
将各线路数据输入到excel表格中, 便于程序的调用
高等电力网络分析
题目
以IEEE14、30、39节点为例应用计算机形成关联 矩阵,用matlab编程,结果存到excel中
电力系统中IEEE节点:是为了验证某一个计算方法行不行 而设立的节点
1、IEEE14节点
14个节点,20条支路
IEEE14节点系统图
1、IEEE14节点程序设 计
对于含有变压器的支路, 节点电流的正负规则不变, 以支路首端为参考,则末 端为负的变比。
设计思路:将IEEE14节点系统的数据存入到data中,定义14*20的零矩阵,以 支路号为循环变量并作为A的列元素,取出data中该支路号对应的首端节点数 并作为A的行元素,令节点数并作为A的行元素,令A矩阵对应的位置为-1。遵循节点电流流出 为正,流入为负的规则。
含有变压器的支路中变压器的变比
2、IEEE30节点程序设计
编程思路与IEEE14节点系统类似。 区别之处在于:调用的excel数据库不同;定义的关联矩阵A 维数不同。
2、IEEE30节点A矩阵结果
剩下的结果略
3、IEEE39节点系统图
未查到相关数据,思路与前面的一样
网络分析与综合-1.2 关联矩阵及其特性

1, 支路 j与节点 i关联且支路方向离开节 点 a ij 1, 支路 j与节点 i关联且支路方向指向节 点 0,支路 j与节点 i不关联
i 1, 2,, n; j 1, 2,, b
关联矩阵A
1 2 3 4 5 6
1 (1) 4 (4) 6 2 3 (2) 5 (3)
ut u 若 u l
则 B f u Bt
ut 1l Bt ut ul 0 ul
所以 ul Bt ut ——KVL方程的另一种矩阵形式
(2)
Qf i 0 用Qf 表示的KCL方程的矩阵形式为:
(1)
1 2 4 (4)
5 (3) 3 6
§1-2 关联矩阵A、Bf、Qf 及其特性
北京邮电大学
电子工程学院 俎云霄
如果两件事之间发生了关系,则称这两件事有关联。
描述节点、回路、割集与支路之间关系的矩阵称为关联矩阵。
关联矩阵A
描述图的支路与节点的关联性质,又称为节点支路关联矩阵。 如果一条支路连接于某个节点,则称此支路与该节点关联。 对一联性质可用nb阶矩阵Aa表示。其中的元素aij定义如下:
i 1, 2,, n 1; j 1, 2,, b
n-1为独立割集数,b为支路数,所以Q为(n-) b阶矩阵。 描述图的基本割集与支路的关联性质的矩阵称为基本割集矩 阵Qf。
基本割集矩阵Qf
树支
1 2 3 4
连支
5 6
(1)
1
C1
(2) 5 2
C2
(3) 3
1 1 0 0 1 | 0 1 | 1 1 Qf 2 0 1 0 1 | 3 0 0 1 0 1 1 Ql 1t
13网络分析-散射矩阵

该不变,因此必有
sij s ji
sii s jj
由此可知
对称网络必定是互易网络
无耗网络 无耗网络散射参量的性质可由网络的功率特性 导出 网络无耗,有
由归一电压和电流与归一入射电压和电流的关
系,有
v v v U sv i v v U sv
0 e j 2 0
0 0 j n e
j n
由此得到参考面2上入射和反射波电压和电流
的关系
即
v' e se v'
j j
e j1 0 s' 0
0 e j 2 0
0 e j1 0 0 s j n e 0
v v z0 1 i i
i i
i i
vi v v ii ii i v vi
i i
i i
S矩阵的定义
一个网络的散射参量定义为该网络归一 反射波与归一入射波的线性关系,即
v s v s v s v v s v s v s v vn sn1v1 sn 2 v2 snn vn
归一入射波与归一反射波
如图所示的网络,各端口定义归一入射电压和电流、归
一反射电压和电流
vi Vi
Z0
ii I i Z 0
且有
v i Pi 2
i
* i
V I 2 2
v
2 0
0
* 0
归一入射电压、电流和归一反射电压、电流与归 一端口电压、电流的关系
矩阵的基本概念与运算

矩阵的基本概念与运算矩阵是线性代数中的重要概念,广泛应用于数学、物理、计算机科学等领域。
本文将介绍矩阵的基本概念、运算规则以及常见的应用。
一、矩阵的基本概念矩阵是由数个数排列成的矩形阵列。
矩阵可以用方括号表示,例如:A = [a11, a12, a13;a21, a22, a23;a31, a32, a33]其中a11、a12等为矩阵元素,按行排列。
矩阵的行数为m,列数为n,则该矩阵称为m×n矩阵。
矩阵可以是实数矩阵,也可以是复数矩阵。
实数矩阵的元素全为实数,复数矩阵的元素可以是复数。
例如:B = [3+2i, -4-7i, 5+6i;-2+3i, 1-5i, -2i]二、矩阵的运算1. 矩阵的加法和减法若A、B为同型矩阵(行数和列数相同),则有:A +B = [a11+b11, a12+b12, a13+b13;a21+b21, a22+b22, a23+b23;a31+b31, a32+b32, a33+b33]A -B = [a11-b11, a12-b12, a13-b13;a21-b21, a22-b22, a23-b23;a31-b31, a32-b32, a33-b33]2. 矩阵的数乘若A为m×n矩阵,k为标量,则有:kA = [ka11, ka12, ka13;ka21, ka22, ka23;ka31, ka32, ka33]3. 矩阵的乘法若A为m×n矩阵,B为n×p矩阵,则它们的乘积AB为m×p矩阵,满足:AB = [c11, c12, c13;c21, c22, c23;c31, c32, c33]其中:c11 = a11b11 + a12b21 + a13b31c12 = a11b12 + a12b22 + a13b32c13 = a11b13 + a12b23 + a13b33...c33 = a31b13 + a32b23 + a33b334. 矩阵的转置若A为m×n矩阵,则其转置记作A^T,为n×m矩阵,满足:A^T = [a11, a21, a31;a12, a22, a32;a13, a23, a33]三、矩阵的应用1. 网络图论矩阵可以用于表示和分析网络图论中的关系和连接。
Siglent SSM5000A 系列开关矩阵数据手册说明书

SSM5000A 系列开关矩阵数据手册CN02A目录一、产品综述 (2)二、指标特色 (2)三、原理框图 (3)四、应用场景 (5)五、条件定义 (6)六、指标参数 (7)七、远程控制 (9)八、切换时间 (9)九、一般技术规格 (10)十、订购信息 (11)十一、联系我们 (11)一、产品综述SSM5000A系列开关矩阵,可对网络分析仪,信号源,频谱仪等设备的测试端口数进行扩展。
该系列命名为SSM5XYZ A,其中X代表工作频率,Y代表合路端口数目,Z代表分路端口数目(除以6)。
X为1时,工作频率范围涵盖9 kHz-9 GHz,X为3时,工作频率范围涵盖100 kHz - 26.5 GHz。
输入端口最多4个,输出端口最多24个,支持USB、LAN、Direct Control通信方式,其中通过开关矩阵上的Direct Control接口可进一步扩展测试端口的数量,支持简化的多端口校准算法,可大大提高校准的效率,除支持Siglent仪器仪表外,也支持其它主流的仪器仪表产品,适配19英寸标准机箱,可广泛应用在天线,5G器件模块等多端口测试环境上。
二、指标特色阻抗:50 Ω最高频率:9 GHz(或者26.5GHz)最大输入端口数:4最大输出端口数:24射频连接器:3.5mm/ Female最大输入功率:20dBm最大输入直流电压:35V接口:LAN,USB Device,Direct Control (in),Direct Control (out)屏幕尺寸:2.4英寸三、原理框图开关矩阵包含8个开关子模块,其中4个1-4开关子模块和4个2-6子模块,通过选择不同的模块搭配和模块数量来得到不同的扩展端口数。
SSM5321A(2端口输入,6端口输出)PortA PortBSSM5122A(2端口输入,12端口输出)SSM5124A (2端口输入,24端口输出)PortAPortBPortCPortDSSM5142A 、SSM5342A (4端口输入,12端口输出)SSM5144A (4端口输入,24端口输出)四、应用场景应用场景一:使用开关矩阵对网络分析仪的测试端口进行扩展,对多个器件的S参数进行测量,依据具体的测试需求可以将矩阵开关扩展成24个单端口,12个全2端口,8个全3端口,6个全4端口,4个全6端口,3个全8端口,2个全12端口,1个全24端口等,下图显示的是扩展成4个全6端口的情况,此时只需要对矩阵开关的1-2-3-4-5-6,7-8-9-10-11-12,13-14-15-16-17-18,19-20-21-22-23-24这4组端口分别进行全6端口校准即可,通过软件即可实现对DUT1,DUT2,DUT3,DUT4 四个器件进行测试,大大提高测试效率。
矩阵知识点总结加法

矩阵知识点总结加法矩阵的基本概念矩阵由 m 行 n 列的元素组成,通常表示为一个大写字母加括号:A = [a[i,j]]其中 a[i,j] 表示矩阵 A 的第 i 行第 j 列的元素。
矩阵也可以用矩阵元素构成的表格来表示:A = | a[1,1] a[1,2] ... a[1,n] || a[2,1] a[2,2] ... a[2,n] || ... ... ... ... || a[m,1] a[m,2] ... a[m,n] |矩阵的大小通常用 m×n 来表示,其中 m 表示矩阵的行数,n 表示矩阵的列数。
若 m = n,则称该矩阵为方阵。
若m ≠ n,则称该矩阵为非方阵。
矩阵中的元素可以是实数、复数或者其他类型的数值。
矩阵的性质1. 矩阵的相等:两个矩阵 A 和 B 相等,当且仅当它们的大小相等,且对应元素相等,即a[i,j] = b[i,j]。
2. 零矩阵:所有元素均为零的矩阵,记作 0。
3. 单位矩阵:主对角线上的元素均为 1,其他元素均为 0 的方阵,记作 I 或者 E。
4. 对角矩阵:除了主对角线上的元素外,其他元素均为零的矩阵。
5. 转置矩阵:矩阵的列变成行,行变成列,记作 A^T。
6. 矩阵的加法:对应元素相加得到的新矩阵。
7. 矩阵的数乘:矩阵中的每个元素乘以一个数得到的新矩阵。
8. 矩阵的乘法:矩阵 A 的列数等于矩阵 B 的行数时,可以进行矩阵乘法运算。
9. 矩阵的逆:满足 AB=BA=I 的矩阵 B 称为矩阵 A 的逆矩阵。
矩阵的运算1. 矩阵的加法:矩阵 A 和矩阵 B 相加得到矩阵 C,表示为 C = A + B。
矩阵的加法满足交换律和结合律。
2. 矩阵的数乘:矩阵 A 乘以数 k 得到矩阵 B,表示为 B = kA。
数乘满足分配律。
3. 矩阵的乘法:矩阵 A 乘以矩阵 B 得到矩阵 C,表示为 C = AB。
矩阵的乘法不满足交换律,但满足结合律。
4. 矩阵的转置:矩阵 A 的转置记作 A^T,即将矩阵 A 的行变成列,列变成行。
12网络分析-阻抗矩阵
阻抗矩阵
写成矩阵形式有
导纳矩阵
写成矩阵形式有
阻抗矩阵和导纳矩阵分别可简写为:
V Z I
阻抗矩阵和导纳矩阵的关系
I Y V
Z Y
1
或
Z Y U
[Z]矩阵和[Y]矩阵参数的意义
Z矩阵
Zii是除第i个端口外,其余端口都开路 时,i端口的自阻抗
由此可以导出,互易网络的Z和Y矩阵参数 的关系
Zij Z ji Yij Yji
如果网络是对称的,则有
Zij Z ji
Zii Z jj Yij Yji Yii Yjj
n 1 Re Vi I i* 0 2 i 1
展开,由阻抗和导纳矩阵的定义,有
可以证明
Zij是除第j个端口外,其余端口都开路时,端口i和 端口j之间的转移阻抗,又称为互阻抗。
由上面的定义可计算出网络的Z矩阵参数 以T型网络为例
计算∏型网络的阻抗矩阵
导纳矩阵
Yii是除第i个端口外,其余端口都短路时,i
端口的自导纳
Yij是除第i个端口外,其余端口都短路时, 端口j和端口i之间的转移导纳(互导纳)。 同样由上面的定义可计算出网络的Y参数
定义
设网络的两个端口分别为a和b,如果它们之间满
足如下关系,则这个网络的端口a和b是互易的。
V1a I1b V1b I1a V2a I 2b V2b I 2a 0(4.34)
如果网络所有端口之间都满足上面的关系,则这
个网络称为互易网络。其中下标a和b表示网络中 某处的两个独立源产生的等效电压和电流。
由此可以导出互易网络的z和y矩阵参数的关系如果网络是对称的则有422无耗网络网络只有功率的交换没有功率的损耗展开由阻抗和导纳矩阵的定义有可以证明由于端口电压是任意的由此得到必有rez0同样的过程有rey0
网络分析

aij表示连接顶点vi与vj的边的数目。
v2
例:
v1
e1 e7 e5 e6
e2 v3 e3Leabharlann v5e4v4
该图的邻接矩阵为:
0 1 A(G ) 1 0 1
1 1 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 1 0
(二)有关测度指标
对于任何一个网络图,都存在着三种共同的基础指标: ① 连线(边或弧)数目m; ② 结点(顶点)数目n; ③ 网络中亚图的数目p。
(17)支撑树。 设G=(V,E)是一个无向图,如果T=(V1,E1)是G 的支撑子图,并且T是树,则称T是G的一个支撑树。
(18)树的重量。
一个树的所有边的权值之和称为该树的重量。 (19)最小支撑树。
在一个图的所有支撑树中,重量最小的那个叫做该图
的最小支撑树。
二、地理网络的测度
许多现实的地理问题,只要经过一定的简化和抽象,就可以将 它们描述为图论意义下的地理网络,点和线的排布格局,并可以进
(二)图的一些相关概念
(1)无向图与有向图 无向图——图的每条边都没有给定方向, 即(u,v)=(v,u); 有向图——图的每条边都给定了方向, 即(u,v)≠(v,u)。
有向图
一般将有向图的边集记为A,无向图的边集记为E。这样,G= (V,A)就表示有向图,而G=(V,E)则表示无向图。
(2)赋权图。 如果图G=(V,E)中的每一条边(vi,vj)都相应地赋有 一个数值wij,则称G为赋权图,其中wij称为边(vi,vj)的权值。 除了可以给图的边赋权外,也可以给图的顶点赋权。这就 是说,对于图G中的每一顶点vj,也可以赋予一个载荷a(vj)。 (3)关联边。 若e=(u,v),则称u和v是边e的端点,e是u和v的关联边。 (4)环。 若e的两个端点相同,即u=v,则称为环。 (5)多重边。
心理学上的矩阵-解释说明

心理学上的矩阵-概述说明以及解释1.引言1.1 概述概述:矩阵在心理学中扮演着重要的角色,在各个领域都有广泛的应用。
矩阵是一个由行和列组成的二维数组,其中每个元素都可以表示心理学中的一个潜变量、观测变量或指标。
心理学中的矩阵包含了大量的数据,可以帮助研究者更好地理解和解释心理学现象,并进行定量分析。
本文将介绍矩阵的定义、在心理学中的应用以及矩阵对心理学研究的意义。
此外,也会探讨矩阵在心理学领域未来发展的可能性。
在心理学研究中,矩阵可以用于描述各种心理现象和变量之间的关系。
通过构建合适的矩阵模型,研究者可以从多个维度去衡量和分析心理学数据。
例如,在人格心理学研究中,可以使用矩阵来描述不同人格特征之间的相关性。
通过分析这些相关性,我们可以更好地了解人格特征在心理学中的作用以及与其他变量之间的相互关系。
此外,矩阵还可用于分析和预测心理学实验中的数据。
例如,在认知心理学研究中,可以使用矩阵来描述参与者在各个认知任务中的表现。
通过分析矩阵中的模式和趋势,我们可以揭示认知过程中的规律,并将其应用于实际认知训练和干预中。
矩阵的应用不仅局限于描述变量之间的关系,还可以用于分析大规模数据集和网络结构。
在社会网络分析中,矩阵可以用来表示人与人之间的连接和关系,从而揭示社会系统的结构和动态。
通过分析这些矩阵,我们可以推断人际关系的强度、网络的层次性以及信息的传播与扩散方式。
这对于理解社交行为和群体心理学具有重要意义。
总之,矩阵在心理学研究中起着重要作用,可以提供系统性的观察和分析方法。
研究者可以通过利用矩阵模型来研究不同心理现象之间的联系,揭示规律和趋势,进一步深化我们对心理学的理解。
未来,随着数据分析技术的不断进步和心理学研究领域的发展,矩阵在心理学中的应用也将变得更加多样化和深入。
因此,我们对矩阵在心理学中的作用有着广阔的展望。
1.2文章结构文章结构部分的内容应该对整篇文章的框架进行概述和解释。
在这一部分,你可以介绍每个章节的主要内容和目标,以及它们在整体结构中的作用。
社会网络分析-凝聚子群

子图Gs,点集Ns{1,2,3,4}
Ns在N中的补集 N-Ns {5,6,7,8,9,10,11,12} Ns的一个真子集Ss{1}
Ss在Ns的补集 Ns-Ss{2,3,4} 请大家用同样的方法判断集合{5,6,7,8}是否 为一个LS集合?
凝聚子群的 类型
建立在“子群内外关系”基础上的凝聚子群
块 :一个图分为一些相对独立的子图,则称各个子图为 块。把一个网络中的各个行动者按照一定标准分成几个离 散的子集,称这些子集为“位置”,也可称之为“聚类”、 “块”
K应该是多少?
凝聚子群的类型
➢ 建立在“子群内外关系”基础上的凝聚子群
• 成分 :如果一个图可以分为几个部分,每个部分内部成员之间 存在关联,而各个部分之间没有任何关联,在这种情况下,我 们把这些部分称为成分
• 切点:在一个图中,如果拿走其中的某点,那么整个图的结构 就分为两个互不关联的成分
该社群图包 含几个成分?
n-派系的局限性
对于n>2的情况下,很难给它社会学的解释
n-派系作为子图,其直径有可能大于n,因此n-派系的成员 可能被本身不是派系的成员的那些行动者连在一起
○ 这些局限性表明, n-派系往往并不像我们期待的那样是一个具有较高 凝聚性的凝聚子群
凝聚子群的类型
建立在可达性基础上的凝聚子群
n-宗派 :n-宗派比n-派系的概念更严格些, 其指的是子图中任何两点的距离不超过n, n-宗派是n-派系,反之不成立。
第二部分
PART ONE
目前虚拟咨询企业(如威客网、猪八戒网)从萌生到发展到现在势头良 好,吸引了大批用户,但是也可以发现在相应网站上也有咨询者发布任 务后始终无人应标,这种现象不利于企业进一步拓展服务内容,分析原 因为用户提出的任务难,仅靠个人无法完成,但又没有专业的团队,针 对上述问题,应该如何解决呢?
银行间市场系统性风险传染研究--基于矩阵网络分析法

北京化工大学学报(社会科学版)Journal of Beijing University of Chemical Technology(Social Sciences Edition)2021年第1期总第114期No. 1. 2021Total No. 114银行间市场系统性风险传染研究——基于矩阵网络分析法(1.福建工程学院管理学院,福建福州350108;2,福州大学经济与管理学院,福建福州350116)[摘 要]基于完全连接网络,利用中国上市银行同业数据,运用最大爛方法估计银行间资产负债关系, 建立上市银行间同业市场网络。
在内部冲击与内外联合冲击的影响下探究影响上市银行间市场系统性风险 的因素,模拟分析我国单个银行破产引发的破产风险传染条件和传染路径。
同时,运用矩阵网络分析法和阈值分析法对上市银行间市场系统性风险大小进行比较,测度破产风险传染所需的外部冲击阈值,分析变化趋 势。
[关键词]最大爛;系统性风险;完全连接网络;内外联合冲击[中图分类号]F832.3[文献标识码]A [文章编号]1671-6639(2021)01-0030-07一、引言经济全球化格局下,全球金融机构的联系变得 越加紧密复杂,不同地域间的金融机构业务活动与 交易行为变得更加频繁,各国金融体系遭受系统性 风险冲击的可能性大大增加。
系统性风险是指整个金融体系内某个机构倒闭或是市场崩溃这种类型的尾端事件从一家机构传染至多家机构,从一个市场内延伸至多个市场中,导致损失在整个金融体系内 不断扩散、对国家实体经济造成冲击的风险,这一个 过程也常常体现出多米诺骨牌效应。
银行业作为金融体系的主要组成部分,其稳定性理应得到重视。
近年来,我国银行同业拆借规模不断扩大,2008到2014年银行同业资产规模明显上升,同比平均增速 为21.68%,截至2015年,16家上市银行同业资产规模达到175445亿元①。
虽然银行同业业务的扩大可 以降低银行的破产风险,但是,Mistrulli 的研究表明银行同业拆借市场也会成为危机传染发生的源头⑴。
IEEE14节点电力网络分析

IEEE14节点电力网络分析《高等电力网络分析》—— IEEE14节点电力网络分析专业班级: 电力工程1403班姓名:学号: Z14050394同组成员:导师: 刘润华二〇一四年十二月第1章 IEEE14简介 ..................................................1 第2章汇报内容总结 (3)2.1 用支路追加法建立节点阻抗矩阵 (3)2.2 补偿法求网络方程的修正解(前补偿、中补偿、后补偿) (9)2.3 统一的网络分块解法 (14)第3章调节变比使中枢点电压控制在给定值 (21)第4章连续潮流法在静态电压稳定性分析和计算中的应用 (23)4.1连续潮流算法 (23)4.2连续潮流计算方法在静态电压稳定性的分析和计算中的应用 (24)4.3正确认识连续潮流及其对静态稳定分析的作用 (26)第5章课程总结....................................................27第1章 IEEE简介第1章 IEEE14简介本文选用14节点系统作为分析对象,绘制IEEE14节点标准试验系统图如图1.1所示:1651224111371038914图1.1 IEEE14系统图母线系统数据如下表格:表1.1 母线数据表节点号节点类型有功功率无功功率电压幅值电压相角并联电容 1 3 0 0 1.0600 0 0 2 2 21.7000 12.7000 1.0450 -4.9800 0 3 2 94.2000 19.00001.0100 -12.7200 0 4 1 47.8000 -3.9000 1.0190 -10.3300 0 5 1 7.60001.6000 1.0200 -8.7800 0 6 2 11.2000 7.5000 1.0700 -14.2200 0 7 1 0 01.0620 -13.3700 0 8 2 0 0 1.0900 -13.3600 0 9 1 29.5000 16.6000 1.0560 -14.9400 0.19 10 1 9 5.8000 1.0510 -15.1000 0 11 1 3.5000 1.8000 1.0570 -14.7900 0 12 1 6.1000 1.6000 1.0550 -15.0700 0 13 1 13.5000 5.80001.0500 -15.1600 0 14 1 14.9000 5 1.0360 -16.0400 01第1章 IEEE简介表1.2 支路数据表支路号发点收点电阻电抗电纳变比 1 1 2 0.01938 0.05917 0.0264 0 2 1 5 0.05403 0.22304 0.0246 0 3 2 3 0.04699 0.19797 0.0219 0 4 2 40.05811 0.17632 0.0187 0 5 2 5 0.05695 0.17388 0.0170 0 6 3 4 0.06701 0.17103 0.0173 0 7 4 5 0.01335 0.04211 0.0064 0 8 4 7 0 0.20912 0 0.97809 4 9 0 0.55618 0 0.9690 10 5 6 0 0.25202 0 0.9320 11 6 11 0.094980.19890 0 0 12 6 12 0.12291 0.25581 0 0 13 6 13 0.06615 0.13027 0 0 14 7 8 0 0.17615 0 0 15 7 9 0 0.11001 0 0 16 9 10 0.03181 0.08450 0 0 17 9 14 0.12711 0.27038 0 0 18 10 11 0.08205 0.19207 0 0 19 12 13 0.220920.19988 0 0 20 13 14 0.17093 0.34802 0 02第2章汇报内容总结第2章汇报内容总结2.1 用支路追加法建立节点阻抗矩阵1、部分网络部分网络是指所要分析的电网的一个连通子网络。
图与网络分析-(共34张PPT)

弧上的箭头,所得到的无向图。记之为G(D)。
第九页,共34页。
6、链:设(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的
一个点弧交错序列,如果这个序列在基础图G(D)中
所对应的点边序列是一条链,则称这个点弧交错序列
v(f) fij–fji= 0
–v(f)
i=s is,t
i=t
且使v(f)达到最大。
第二十三页,共34页。
3、增广链 给定可行流f={fij},使fij=cij的弧称为饱和弧,使
fij<cij的弧称为非饱和弧,把fij=0的弧称为零流弧, fij>0
的弧称为非零流弧。
若是网络中连接发点vs和收点vt的一条链,定义链
22
21
44
(0,Vvs)1
89
62
31
32 63
45
24
47
(44,V1) v4
37 27
(78,V3)
v6
32
v3 (31, V1) 34
第十九页,共34页。
v5 (62,V1)
第三节 最大流问题
如下是一运输网络,弧上的数字表示每条弧上 的容量,问:该网络的最大流量是多少?
4 vs
3
v1
3
1 2
2
v2
v3 3
2
vt
4 v4
第二十页,共34页。
一、基本概念和基本定理
1、网络与流
定义1:给定一个有向图D=(V,A),在V中有一个发点 vs和一收点vt,其余的点为中间点。对于每一条弧 (vi,vj),对应有一个c(vi,vj)0,(cij)称为弧的容量。这 样的有向图称为网络。记为D=(V,A,C)。
社交网络分析的矩阵数据模型

社交网络分析的矩阵数据模型社交网络分析(Social Network Analysis,SNA)是一种基于图论和统计学的研究方法,用于揭示人际关系及其动态变化的规律和特征。
而在社交网络分析中,矩阵数据模型是一种重要的工具,用于描述和处理社交网络中的人际关系。
一、社交网络分析概述社交网络分析是一门研究人际关系和社会结构的学科,它通过确定个体之间的联系,揭示人际关系网络中的关键结点和核心群体,进而研究和预测在这些关系网中信息和影响的传播路径和速度。
二、社交网络中的矩阵数据模型在社交网络中,我们可以通过矩阵数据模型来表示人际关系。
由于社交网络的复杂性,我们常常需要使用不同的矩阵来表示网络中的不同属性和关系。
1. 邻接矩阵邻接矩阵是社交网络中最常用的矩阵之一。
它用于表示每个个体之间是否存在联系。
邻接矩阵可以是对称的,也可以是非对称的。
对称的邻接矩阵适用于无向网络,而非对称的邻接矩阵适用于有向网络。
2. 相似度矩阵相似度矩阵用于度量个体之间的相似性。
它通过计算个体之间共同邻居的数量或其他相似性指标,来反映个体之间的近似程度。
相似度矩阵在社交网络分析中常常用于寻找关联度高的个体、发现共同兴趣群体等方面。
3. 距离矩阵距离矩阵用于度量个体之间的距离或差异。
在社交网络分析中,我们可以使用不同的度量方法,如欧氏距离、哈曼顿距离等来计算个体之间的差异。
距离矩阵通常用于聚类分析、社区检测等方面。
三、矩阵数据模型的应用矩阵数据模型在社交网络分析中有着广泛的应用。
以下是一些主要的应用领域:1. 社交关系分析通过邻接矩阵和相似度矩阵,我们可以分析个体之间的关系强度和类型,如友好关系、合作关系等。
这些分析可以帮助我们了解社交网络中不同个体之间的相互作用和连接。
2. 影响传播预测通过矩阵数据模型,我们可以分析社交网络中信息和影响的传播路径和速度。
例如,通过距离矩阵和邻接矩阵,可以预测某一信息在社交网络中的传播范围和媒介个体等。
社会网络分析法

2、指数分析 是通过社会网络分析指数分析个人在群体中的地位,比较同一群体内不同情景下每个人的社会地位,且对不同群体的特征进行比较。 几种常用的指数有:a.社会地位指数,表明个人在群体中受重视的程度;b.受选地位指数,表明个人在群体中受支持的程度;c.受拒地位指数,表明个人在群体中受拒斥的程度;d.吸引率,表明群体中吸引作用发生的程度;e.拒斥率,表明群体中拒斥作用发生的程度;f.凝聚指数,表明群体凝聚的程度;g.相对声望指数,表明一个群体受外群体成员支持的程度。
工作标准:强调个人在群体中完成群体任务,达到群体目标的过程中所扮演的角色。比如,“你愿意和谁在一块做实验?”“你宁愿和谁一同学习?”
正面标准与反面标准
“标准”的确定
在设计问卷时要确定以什么为“标准”来测量所要了解的人们之间的关系。“标准”通常是一个问题,如“你最愿意与谁谈心?” 标准的选择关键:首先是要准确反映出所要测量的关系;其次是具体而切实,易于为被调查者了解和回答。 标准可选择积极的问题,标准也可以是消极的问题。
人际选择的标准是什么?
所谓的标准,指的就是被调查者作出选择的依据,通常也是一个问题,比如,“你宁愿谁坐在你的旁边?”一般而言,标准的选择是根据群体的性质或者施测的目的来确定的。
三、社会关系网络分析方法与技巧
标准的类型:休闲标准和工作标准
休闲标准:强调人际间的亲昵的需要、亲疏关系。比如,“你最愿意和谁座在一条板凳上?”“你最愿意和谁一块看电影?”
1.社会网络分析矩陣
將每個人的選擇數量做簡單的計算而成一個表,如下:
0
-5
0
0
0
師大人
-1
1
呂嗅憐
-1
1
肚正剩
-1
网络分析与综合-1.3 关联矩阵之间的关系

Bt阶数为(b-n+1) (n-1)。
Ql阶数为(n-1) (b-n+1) 。
A、Bf、Qf表示的KCL、KVL的矩阵形式
KCL KVL | | ————————————————— T u A un Ai 0 | A — | ————————————————— T | i B | Bf u 0 f il — B f | 或 i BT 或 ul Bt ut f il | —————————————————— T | Qf i 0 | u Q f ut Q T u Q | 或 it Ql il 或 l l ut |
6
C3
4
1 1 0 0 | 1 0 1 | 1 1 1 Qf 2 0 1 0 | 3 0 0 1 0 1 1 Ql 1t
Bt QlT Ql BtT
T i t Bt i l KCL的矩阵形式 T i B f il T ul Ql ut KVL的矩阵形式 T u Q f ut
1l
(2) 1 (1) 4 (4) 6 2 3 5 (3)
B f Bt
则
Bt AlT ( At1 )T
矩阵Bf与Qf之间的关系
定理1-3:如果同一连通图的Bf 和Qf 的列具有相同的支路排 列次序,则:
Q f BT f 0
或
B f QT f 0
推论1-1:如果同一连通图的Bf 和Qf 的列具有相同的支路排 列次序,则:
Bt QlT
或
Ql BtT
矩阵Bf与Qf之间的关系
1 2 3 4 5 6 4 1 1 0 Bf 5 0 1 1 6 1 1 1 Bt 1 2 3
网络分析

在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不 大于从源点v到U中任何顶点的最短路径长度
主要特点:以起始点为中心向外层层扩展,直到扩展到终点为止
基本过程
(1)初始时,S只包含源点,即S=源点,v的距离为0。U包含除v外的 其他顶点,U中顶点u距离为边上的权 (2)从U中选取一个距离v最小的顶点k,把k加入S中(该选定的距离 就是v到k的最短路径长度) (3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶
B. 其对应数据结构中的无向图
3.4.1 网络分析功能
追踪分析 路径分析 资源分配 服务范围
(1)网络跟踪(Trace)
概念:网络中用于研究网络中资源和信息的
流向就是网络跟踪的过程
在点污染研究中,可以跟踪污染物从污染源
开始,沿河流向下游扩散的过程。在电网应
用中,可以根据不同开关的开、关状态,确
网络中运移资源的种类、运移的方向,弧段中的特殊
情况等
网络组成要素与属性
转弯的阻强描述了从一条链弧经结点到另一条链弧的阻 力大小,它随着两相连链弧的条件状况而变化
运用阻强概念的目的在于模拟真实网络中各路线及转弯
的变化条件。对不构成通道的弧段或转弯往往赋以负的 阻强。这样,在分析应用中如选取最佳路线时可自动跳 过这些弧段或转弯
网络分析的主要用途是:选择最佳路 径、设施以及进行网络流分析 最佳路径是指从始点到终点的最短距 离或花费最少的路线,如图所示
最佳布局中心位置是指各中心所覆盖
范围内任一点到中心的距离最近或花 费最小
网络流量是指网络上从起点到终点的
某个函数,如运输价格,运输时间等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V1 A V2 B V1 I2
I1 V2
I 2 0
V2 0
端口2开路时的端口1到端口2的电压转 移系数 端口2短路时端口1与端口2的转移阻抗 端口2开路时的端口1与端口2的转移导 纳 端口2短路时的端口1到端口2的电流转 移系数
C
V2 0
I1 D I2
V2 0
由网络1和网络2、网络2和网络3的关系,有
abcd S11 a b c d abcd S 22 abcd 2 S12 abcd 2( a d b c) S 21 abcd
S 参量的物理量是归一化入波 a 和归一化出波 b, 并以微波网络为参考方向。A 参量的物理量是总电 压波和总电流波,并以波源到负载的方向为参考方 向。 S 参量是归一化量,其值与输入、输出传输线的特 征阻抗有关。A 参量既可以是归一化量也可以是非 归一化量,当其为归一化量时与输入、输出传输线 的特征阻抗有关;当其为非归一化量时与输入、输 出传输线的特征阻抗无关。
对称网络
1பைடு நூலகம்
AD BC 1
AD
无耗网络 A、D:实数 B、C: 虚数
(1 S11 )(1 S 22 ) 1 } a 2 {S12 S 21 b 1 {S (1 S11 )(1 S 22 ) } 12 2 S 21 (1 S11 )(1 S 22 ) 1 c {S12 } 2 S 21 (1 S11 )(1 S 22 ) 1 } d {S12 2 S 21
a b Z01 a c d 0
0 A B Z02 Z 01 0 C D
1 Z02
展开后有
Z 02 A a b Z 01 a c d C Z Z 01 02
V3 V1 V2 V2 I A1 I I A2 I 1 2 2 3
由此得到
V3 V3 V1 V2 I A1 I A1 A2 I ATT I 1 2 3 3 即级联网络的传输矩阵为各网络传输矩阵的乘 积。
B Z 01Z 02 Z 01 D Z 02
与阻抗矩阵的关系
A Z11 Z 21 (4.67a) Z11Z 22 Z12 Z 21 B (4.67b) Z 21 C 1 Z 21 (4.67c) D Z 22 Z 21 (4.67d )
传输矩阵的性质 互易网络 AD BC
ABCD矩阵(又称为A矩阵)反映了双端口网络的
输出和输入的关系,因此当需要处理网络的级联
问题时,采用ABCD矩阵比较方面
传输矩阵的定义
V1 AV2 BI2 I1 CV2 DI2
写成矩阵形式,有
V1 A B V2 I C D I (4.63) 2 1
Att A1 A2 An
设
有
于是
v1 Z 01 i 1 0
1
0 A B Z 02 C D Z 01 0
1
0 Z 02
0
v2 1 i2
由此
