12网络分析-阻抗矩阵
电网潮流组成分析方法比较研究(一)--概述

电网潮流组成分析方法比较研究(一)1——概述荆朝霞华南理工大学电力学院,广州(510640)email: emsunny@摘要:电力市场环境下,电网潮流组成分析,也就是确定电网的潮流分别是由哪些市场参与者造成的,贡献分别有多大是许多问题,包括输电定价,阻塞管理和网损分摊等的基础。
但是由于电网的一些特殊性质,到目前为止还没有被广泛认同的方法。
目前关于潮流组成分析方面的研究主要集中在对现有的方法进行一些改进或试图提出一些新的方法,但更加有意义的工作应该是对这些不同方法的比较。
本文对目前常见的潮流组成分析的方法进行了系统地总结和深入地探讨,分别用理论分析和算例比较的方法分析了各种方法的本质特点、优缺点、适用条件等,得到了一些有用的结论,期望可以对正确理解各种潮流组成分析方法以及实际应用等有所帮助。
本论文总共分四个部分,第一部分,即本文对各种潮流组成分析方法进行了总体的概述。
关键词:电力市场;潮流组成分析;输电定价;潮流跟踪1引言自20世纪80年代以来,以打破发电环节的垄断、引入竞争和输电系统开放为主要特征的电力工业市场化改革的浪潮波及了世界上许多的国家和地区。
市场化改革在提高电力工业运营效率的同时,也带来了许多新的问题和挑战。
电力工业市场化以后,发电环节和网络环节分离,形成多个发电公司和一个电网公司。
在一些自由化程度较高的电力市场,发电公司可以参与电力现货市场的竞价发电,也可以直接和大用户或配电公司签订双向合同;电网公司为发电公司和用户提供输电服务,发电公司和用户承担输电服务费用。
输电服务的定价方法是电力市场规则的重要内容之一,也是影响电力市场运行效率的一个关键因素。
输电定价问题引起了广大电力工作者、相关科研机构的重视,也已经提出了很多输电定价的方案,但由于电网的复杂性和一些特殊的属性,如电力不易储存、电在网络中的流动难以控制和跟踪等,至今为止还没有被广泛认同的方法,在输电定价的许多问题上还存在分歧[1-5]。
节点阻抗矩阵

节点阻抗矩阵
节点阻抗矩阵方程是电力系统故障分析计算以及继电保护整定计算中应用较广泛的一种数学模型。
支路追加法是形成节点阻抗矩阵的常用方法,它要求支路追加顺序必须满足一定的条件,而此顺序可由人工预先通过对支路编号来制定,或者由计算程序自动查找。
节点导纳矩阵是以网络中某一点为参考点,Yjj为j节点的自导纳,Yij为i,j两节点间的共导纳的相反数。
节点导纳矩阵( node admittance matrix jiedian daona juzhen)以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线...节点导纳矩阵的对角元素Yij(i=j)为节点自导纳,等于与该节点相连接的各支路导纳之和式中yi0为节点i对地支路的导纳。
节点导纳矩阵是一个对称的方阵,...2.2节点导纳矩阵的计算(1)节点导纳矩阵的阶数n等于电力网络的节点数。
(2)节点导纳矩阵的非对角元素Yij(i≠j)为节点。
阻抗分析仪和网络分析仪的区别

阻抗分析仪和网络分析仪的区别背景介绍在电子工程领域中,阻抗和网络分析是两个非常重要的概念。
阻抗是指电路中电流与电压之比的绝对值,它的单位为欧姆,是衡量电路的电阻程度的指标。
网络分析则是指对电路中各个元件进行分析,掌握各个元件之间的相互关系和特性,以便优化电路性能的过程。
阻抗分析仪和网络分析仪是电子工程领域中经常使用的两种测试仪器,它们在强调不同方面的测试能力的同时,也存在一些不同之处。
本文将从测试分析的对象、测试方法、测试范围和测试精度四个方面来探讨阻抗分析仪和网络分析仪的区别。
测试分析的对象阻抗分析仪主要用于测试电路中的阻抗,包括电感、电容和电阻等等。
它的主要作用是确认电路各元件的参数,以便更深入更详细地了解整个电路的特性。
阻抗分析仪一般可以根据测试对象的不同,选择不同的测试方式和测试参数,以便更准确地测试。
网络分析仪则更偏重于测试整个电路的性能,包括电路中各种元件之间的相互关系、反应和耦合等。
网络分析仪可以测试电路的高频特性,如S参数、功率、噪声系数等等。
它的主要作用是通过测试电路的性能,找到其优化方案,以提高其性能和效率。
测试方法阻抗分析仪主要依靠恒流源和交流电路源进行测试。
在测试电路中的阻抗时,阻抗分析仪将恒定电流通入电路中,然后测量产生的电压大小和相位,最后根据交流电路源的频率在所选的频率范围内进行测试。
阻抗分析仪的测试方法简单直接,但要求测试电路中无电源。
网络分析仪则主要依靠扫频信号源和测试端口进行测试。
网络分析仪通过扫描频率,将输出信号注入到待测试的电路中,然后通过测试端口将测试结果反馈给网络分析仪。
网络分析仪的测试方法复杂,但可以测试各种电路,包括有电源和电源噪声的电路。
测试范围阻抗分析仪一般只适用于测试单个电路中的元件,例如测试一个电容或者电感的参数,测试特定电阻的阻值,等等。
阻抗分析仪的测试范围相对较小,只能测试某些特定电路中的阻抗。
而网络分析仪则可以测试电路的整体性能,包括测试整个电路的反应和耦合。
Z矩阵、Y矩阵、A矩阵、S矩阵、T矩阵定义、推导及转换公式

一、 微波网络各种参量矩阵定义图 1所示为二端口微波网络,1端口电压为U 1,电流为I 1;二端口电压为U 2,电流为I 2。
图 1 二端口微波网络1.1 Z 矩阵阻抗矩阵如下:11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (1.1-1) 111121221222U Z Z I U Z Z I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦[][][]U Z I = (1.1-2) 其中,211101I U Z I ==,111202I U Z I ==,222101I U Z I ==,122202I UZ I == (1.1-3)➢ 对于互易网络:1221Z Z = (1.1-4) ➢ 对于对称网络:1122Z Z = (1.1-5) ➢ 对于无耗网络:ij ij Z jX = (i,j=1, 2) (1.1-6)1.2 Y 矩阵导纳矩阵如下:11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.2-1)111121221222I Y Y U I Y Y U ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦[][][]I Y U = (1.2-2) 其中,211101U I Y U ==,111202U I Y U ==,222101U I Y U ==,122202U IY U == (1.2-3)➢ 对于互易网络:1221Y Y = (1.2-4)➢ 对于对称网络:1122Y Y = (1.2-5) ➢ 对于无耗网络:ij ij Y jB = (i, j=1,2) (1.2-6)1.3 A 矩阵端口2的电流取向外,应为-I 2。
图 2 二端口微波网络(A 矩阵)转移矩阵如下:11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.3-1) []11112221212222U A A U U A I A A I I ⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦(1.3-2) 其中,21110I U A U ==,21120U U A I ==-,11210U IA U ==,21220U IA I ==- (1.3-3)1122122111221221➢ 对于对称网络:1122A A = (1.3-8) ➢ 对于无耗网络:A 11,A 22为实数;A 12,A 21为虚数 (1.3-9)二、 微波网络各种参量矩阵转换2.1 Z 矩阵<=>Y 矩阵以归一化矩阵为例,根据归一化阻抗矩阵和归一化导纳矩阵,有1111122221122211111222211222u z i z i u z i z i i y u y u i y u y u =+⎧⎨=+⎩=+⎧⎨=+⎩ (2.1-1)则122112011221221,u i z y z z z z z u z====- (2.1-2)1112120u i y u z===-(2.1-3) 2221210u i y u z===-(2.1-4)至此,[][]111122212212221111y y z z y z y y z z z --⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦(2.1-6)同理,有[][]111122212212221111z z y y z y z z y y y --⎡⎤⎡⎤===⎢⎥⎢⎥-⎣⎦⎣⎦(2.1-7) 即[][]1z y =,与归一化导纳矩阵中结论一致。
天线隔离度的分析与计算讲稿演示文稿

电磁兼容中的天线耦合问题 天线隔离度与空间隔离度
重新考虑天线隔离度的定义。天线隔离度是指发射天 线发射的功率与接收天线接收到的功率之比,当两天 线都在对方远场时,所谓的发射功率指的实际是天线 的辐射功率,以为只有辐射场才能影响接收天线。而 当两天线在对方的近区场时,由于接收天线受到的不 仅仅是近区场中微不足道的辐射场的影响,更多的是 受到束缚场或者感应场的影响,因此这时发射天线的 发射功率指的应该是天线的输出功率。
标系中接收点指向角, 是接收天线坐标系中发射点的指
向角。
( r ,r )
早期电磁兼容预测采用这一算法,但实际上远场条件场不 满足,计算得到的隔离度就有较大的误差,为此需要寻求 更加精确的方法。
第二十三页,共104页。
电磁兼容中的天线耦合问题 天线隔离度与空间隔离度
如果接收天线不在发射天线的远区中,或者发射天线不在接收天线 的远区中时,两天线之间的相互干扰主要不是通过辐射场进行的, 而是近区束缚场或者近区感应场。这种情况经常出现在计算线天线 阵中天线间隔离度的问题中。我们知道,天线功率增益的概念是在 远场建立的,因此上页中的计算式是不能用于近场天线隔离度分析 的。即使把功率增益的概念延拓到近区场,也仍然是描述辐射场功 率增益的,而这时天线间干扰的主要因素并不是辐射场,因此,由 上式算得的天线隔离度将远小于近区场中天线间的真实隔离度。
第十五页,共104页。
电磁兼容中的天线耦合问题 天线隔离度与空间隔离度
天线隔离度与空间隔离度的概念与物理意义
在一个系统中,为保证每个天线正常工作,天线的隔离 度必须满足一定的要求,否则天线间的干扰会压制住有 用信号,从而使系统无法正常工作。一般将发射天线的 发射功率与另一天线所接受功率的比值定义为天线的隔 离度。在具体问题中,对于不同的情况,接收天线可能 通过不同的方式对发射天线施加干扰。所谓的不同的情 况,主要指的就是远区场与近区场。
二端口阻抗参数矩阵

二端口阻抗参数矩阵二端口阻抗参数矩阵是电路分析中常用的一种工具,用于描述二端口网络的特性。
它是一个4×4的矩阵,其中包含了电路的阻抗参数信息。
本文将介绍二端口阻抗参数矩阵的定义、性质以及在电路分析中的应用。
首先,我们来看一下二端口阻抗参数矩阵的定义。
对于一个二端口网络,我们可以将其表示为一个四端口网络,其中两个端口为输入端口,另外两个端口为输出端口。
假设输入端口的电压为V1和V2,输出端口的电流为I1和I2,那么二端口阻抗参数矩阵可以表示为:[Z] = [V1, V2] / [I1, I2]其中,[Z]为二端口阻抗参数矩阵,V1和V2为输入端口的电压向量,I1和I2为输出端口的电流向量。
矩阵的每个元素表示了输入端口的电压与输出端口的电流之间的关系。
接下来,我们来看一下二端口阻抗参数矩阵的性质。
首先,二端口阻抗参数矩阵是一个4×4的方阵。
其次,矩阵的对角线元素表示了输入端口的电压与输出端口的电流之间的直接关系,非对角线元素表示了输入端口的电压与输出端口的电流之间的互感关系。
最后,二端口阻抗参数矩阵是一个复数矩阵,其实部表示了电路的电阻特性,虚部表示了电路的电感或电容特性。
最后,我们来看一下二端口阻抗参数矩阵在电路分析中的应用。
二端口阻抗参数矩阵可以用于求解电路的输入输出关系,从而得到电路的传输特性。
通过对矩阵进行运算,我们可以得到电路的输入阻抗、输出阻抗、传输函数等重要参数。
此外,二端口阻抗参数矩阵还可以用于分析电路的稳定性和频率响应。
通过对矩阵进行特征值分解,我们可以得到电路的特征频率和特征阻抗,从而判断电路的稳定性和频率响应。
总之,二端口阻抗参数矩阵是电路分析中一种重要的工具,用于描述二端口网络的特性。
它可以帮助我们求解电路的输入输出关系,分析电路的稳定性和频率响应。
在实际应用中,我们可以通过计算和仿真来得到二端口阻抗参数矩阵,从而更好地理解和设计电路。
希望本文对读者理解二端口阻抗参数矩阵有所帮助。
13网络分析-散射矩阵

该不变,因此必有
sij s ji
sii s jj
由此可知
对称网络必定是互易网络
无耗网络 无耗网络散射参量的性质可由网络的功率特性 导出 网络无耗,有
由归一电压和电流与归一入射电压和电流的关
系,有
v v v U sv i v v U sv
0 e j 2 0
0 0 j n e
j n
由此得到参考面2上入射和反射波电压和电流
的关系
即
v' e se v'
j j
e j1 0 s' 0
0 e j 2 0
0 e j1 0 0 s j n e 0
v v z0 1 i i
i i
i i
vi v v ii ii i v vi
i i
i i
S矩阵的定义
一个网络的散射参量定义为该网络归一 反射波与归一入射波的线性关系,即
v s v s v s v v s v s v s v vn sn1v1 sn 2 v2 snn vn
归一入射波与归一反射波
如图所示的网络,各端口定义归一入射电压和电流、归
一反射电压和电流
vi Vi
Z0
ii I i Z 0
且有
v i Pi 2
i
* i
V I 2 2
v
2 0
0
* 0
归一入射电压、电流和归一反射电压、电流与归 一端口电压、电流的关系
电力系统分析第4章 电力网络的数学模型

Vn
I2(1)
•
•
Y (1) n2
V2
Y (1) nn
Vn
I2(1)
式中
Y (1) ij
Yij
Yi1Yj1 Y11
; Ii(1)
I
Yi1 Y11
I1
第四章电力网络的数学模型
4.2 网络方程的解法
➢ 对方程式再作一次消元,其系数矩阵便演变为
Y11
Y (2)
Y12 Y13 Y1n
Y (1) 22
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢一般地,对于有n个独立节点地网络,可以列写n个 节点方程
•
•
•
Y11 V1 Y12 V2 Y1n Vn
•
I1
•
•
•
Y21 V1 Y22 V2 Y2n Vn
•
I2
•
•
• •
Yn1 V1 Yn2 V2 Ynn Vn In
(4-3)
4.1 节点导纳矩阵
➢上述方程经过整理可以写成
•
•
Y11 V1 Y12 V2
0
•
•
•
•
Y21 V1 Y22 V2 Y23 V3 Y24 V4 0
•
•
•
Y32 V2 Y33 V3 Y34 V4 0
•
•
•
Y42 V2 Y43 V3 Y44 V4
•
I
4
(4-2)
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢将电势源和阻抗的串联变 换成电流源和导纳的并联,得 到的等值网络如图所示,其中:
•
•
I 1 y10 E1
微波网络的阻抗和导纳矩阵

05
微波网络中的阻抗和导 纳矩阵
微波网络中的阻抗矩阵
阻抗矩阵定义
阻抗矩阵是一个描述微波网络中各个端口之间电压和电流关系的 复数矩阵。
阻抗矩阵的元素
阻抗矩阵的元素由网络中各个元件的阻抗值和连接方式决定,反 映了网络中各个端口之间的相互作用关系。
阻抗矩阵的特点
阻抗矩阵是一个对称矩阵,其对角线元素表示各个端口在无外部 激励下的自阻抗。
阻抗矩阵的性质
对称性
阻抗矩矩阵的元素可以表示为电导G_{ij}和电纳B_{ij}的线性组合,即 Z_{ij}=G_{ij}+jB_{ij}。
奇异值分解
阻抗矩阵可以进行奇异值分解,将其分解为三个部分,即左奇异向量 矩阵、奇异值矩阵和右奇异向量矩阵。
微波网络的阻抗和导 纳矩阵
目 录
• 引言 • 阻抗矩阵 • 导纳矩阵 • 阻抗和导纳矩阵的关系 • 微波网络中的阻抗和导纳矩阵
01
引言
背景介绍
01
微波网络在通信、雷达、导航等 领域具有广泛应用,其性能受到 阻抗和导纳矩阵的影响。
02
阻抗和导纳矩阵是描述微波网络 特性的重要参数,对网络性能的 优化和设计具有重要意义。
阻抗和导纳矩阵的相似性
阻抗矩阵和导纳矩阵在某些情况下具 有相似的特性。例如,当网络的元件 都是纯电阻或纯电导时,阻抗矩阵和 导纳矩阵将具有相同的对角线元素和 非对角线元素。
VS
这种相似性意味着阻抗和导纳矩阵在 描述网络特性时可能提供相同的信息, 尽管它们的表达形式不同。因此,在 某些情况下,选择使用阻抗矩阵或导 纳矩阵可能仅仅是一个个人偏好问题。
阻抗和导纳矩阵的转换关系
阻抗矩阵和导纳矩阵可以通过简单的数学转换相互转换。具 体来说,一个网络的导纳矩阵可以通过将阻抗矩阵的每个元 素都除以对应的频率平方根得到,反之亦然。
节点导纳矩阵和节点阻抗矩阵的关系

节点导纳矩阵和节点阻抗矩阵的关系1.节点导纳矩阵是描述电力系统网络中各个节点之间电气连接关系的矩阵。
The node admittance matrix is a matrix that describes the electrical connection between nodes in a power system network.2.节点导纳矩阵中的元素代表了网络中各个节点之间的导纳值。
The elements in the node admittance matrix represent the admittance values between nodes in the network.3.节点导纳矩阵可以用来分析电力系统中各个节点的电压、电流等电气参数。
The node admittance matrix can be used to analyzeelectrical parameters such as voltage and current at various nodes in a power system.4.节点导纳矩阵的计算可以通过对电力系统的拓扑结构进行建模和分析得出。
The node admittance matrix can be calculated by modeling and analyzing the topological structure of a power system.5.节点导纳矩阵在电力系统的潮流计算、短路分析、稳态分析等方面具有重要的应用价值。
The node admittance matrix has important applications in power system load flow calculations, short-circuit analysis, and steady-state analysis.6.节点导纳矩阵与节点阻抗矩阵之间存在数学上的对偶关系。
阻抗矩阵和导纳矩阵的定义

阻抗矩阵和导纳矩阵的定义阻抗矩阵和导纳矩阵是电路分析中常用的工具,用于描述电路中各个元件之间的关系。
阻抗矩阵描述了电路中各个节点之间的阻抗关系,而导纳矩阵则描述了电路中各个节点之间的导纳关系。
本文将分别介绍阻抗矩阵和导纳矩阵的定义和应用。
一、阻抗矩阵的定义阻抗矩阵是描述电路中各个节点之间的阻抗关系的一种矩阵表示方法。
在电路分析中,将电路中的每个元件看作一个节点,节点之间的连接线看作一个支路。
根据欧姆定律和基尔霍夫定律,可以得到各个节点之间的电流和电压之间的关系。
通过整理这些关系,可以得到一个由节点电压和节点电流表示的方程组。
将这个方程组整理成矩阵形式,就得到了阻抗矩阵。
阻抗矩阵的元素由电路中各个元件的阻抗决定。
对于电路中的每个节点,阻抗矩阵的对角元素表示该节点的自阻抗,非对角元素表示节点之间的互阻抗。
阻抗矩阵是一个对称矩阵,因为互阻抗是相互关联的。
阻抗矩阵的应用非常广泛。
在电路分析中,可以通过求解阻抗矩阵来得到电路中各个节点的电压和电流。
此外,阻抗矩阵还可以用于电路的拓扑分析、电路的稳定性分析等方面。
二、导纳矩阵的定义导纳矩阵是描述电路中各个节点之间的导纳关系的一种矩阵表示方法。
导纳矩阵是阻抗矩阵的逆矩阵,用于描述电路中各个节点之间的导纳关系。
导纳矩阵的元素由电路中各个元件的导纳决定。
导纳矩阵的元素由电路中各个元件的导纳决定。
对于电路中的每个节点,导纳矩阵的对角元素表示该节点的自导纳,非对角元素表示节点之间的互导纳。
导纳矩阵是一个对称矩阵,因为互导纳是相互关联的。
导纳矩阵的应用也非常广泛。
在电路分析中,可以通过求解导纳矩阵来得到电路中各个节点的电压和电流。
此外,导纳矩阵还可以用于电路的拓扑分析、电路的稳定性分析等方面。
三、阻抗矩阵和导纳矩阵的关系阻抗矩阵和导纳矩阵是电路分析中常用的工具,它们之间存在着密切的关系。
阻抗矩阵是导纳矩阵的逆矩阵。
也就是说,如果我们已知一个电路的阻抗矩阵,那么我们可以通过求逆来得到该电路的导纳矩阵。
12网络分析-阻抗矩阵
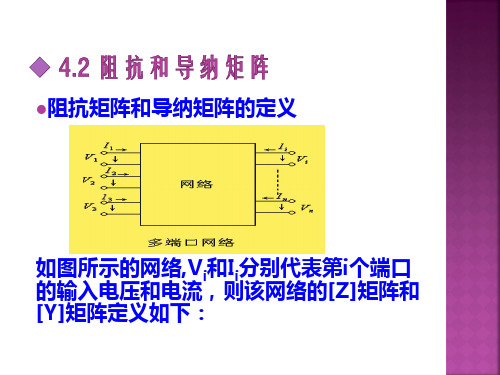
阻抗矩阵
写成矩阵形式有
导纳矩阵
写成矩阵形式有
阻抗矩阵和导纳矩阵分别可简写为:
V Z I
阻抗矩阵和导纳矩阵的关系
I Y V
Z Y
1
或
Z Y U
[Z]矩阵和[Y]矩阵参数的意义
Z矩阵
Zii是除第i个端口外,其余端口都开路 时,i端口的自阻抗
由此可以导出,互易网络的Z和Y矩阵参数 的关系
Zij Z ji Yij Yji
如果网络是对称的,则有
Zij Z ji
Zii Z jj Yij Yji Yii Yjj
n 1 Re Vi I i* 0 2 i 1
展开,由阻抗和导纳矩阵的定义,有
可以证明
Zij是除第j个端口外,其余端口都开路时,端口i和 端口j之间的转移阻抗,又称为互阻抗。
由上面的定义可计算出网络的Z矩阵参数 以T型网络为例
计算∏型网络的阻抗矩阵
导纳矩阵
Yii是除第i个端口外,其余端口都短路时,i
端口的自导纳
Yij是除第i个端口外,其余端口都短路时, 端口j和端口i之间的转移导纳(互导纳)。 同样由上面的定义可计算出网络的Y参数
定义
设网络的两个端口分别为a和b,如果它们之间满
足如下关系,则这个网络的端口a和b是互易的。
V1a I1b V1b I1a V2a I 2b V2b I 2a 0(4.34)
如果网络所有端口之间都满足上面的关系,则这
个网络称为互易网络。其中下标a和b表示网络中 某处的两个独立源产生的等效电压和电流。
由此可以导出互易网络的z和y矩阵参数的关系如果网络是对称的则有422无耗网络网络只有功率的交换没有功率的损耗展开由阻抗和导纳矩阵的定义有可以证明由于端口电压是任意的由此得到必有rez0同样的过程有rey0
电网络分析与综合学习报告 (1)

基本回路的方向规定为所含连支的方向。
2.2独立的基尔霍夫定律方程
割集:
割集:
割集:
注意:1、2、3为树枝
推广为一般情况:基本割集的基尔霍夫电流定律方程是一组独立方程,方程的数目等于树支数,基本割集是一组独立割集。
电网络理论读书报告
电网络理论主要包括:网络分析、网络综合、模拟电路故障诊断。其中网络分析主要是一致网络结构、网络参数和输入求输出,网络综合主要是已知网络输入和输出去确定网络的结构与参数,模拟电路故障分析是已知网络的输入和输出确定网络结构参数与故障分析。
第一章网络原件和网络的基本性质
1.1实际电路与电路模型
理想变压器:
阻抗匹配:
1.6网络的基本性质
线性和非线性
线性特性指均匀性,叠加性。
均匀性(齐次性):
叠加性:
时变与时不变
一个网络在零初始条件下,其输出响应与输入信号施加于网络的时间起点无关,称为非时变网络,否则称为时变网络。
因果与非因果
因果网络当且仅当输入信号激励时,才会出现输出(响应)。也就是说,因果网络的(响应)不会出现在输入信号激励的以前时刻。也叫做非超前网络。
割集:是一组支路集合。并且满足:
(1)如果移去包含在此集合中的全部支路,则此图变成两个分离的部分;
(2)如果留下该集合中的任一支路,则剩下的图仍是连通的。
基本割集(fundamental cut-set):由数的一条树支与相应的一组连支所构成的割集,称为基本割集。
基本割集的方向规定为所含树支的方向。
电网络理论是建立在电路模型基础上的一门科学,它所研究的直接对象不是实际电路,而是实际电路的模型。实际电路:为了某种目的,把电器件按照一定方式连接起来构成的整体。电路模型:实际电路的科学抽象,由理想化的网络原件连接而成的整体。器件:客观存在的物理实体,是实际电路的组成单元。元件:理想化的模型,其端子上的物理量服从一定的数学规律,是网络的基本构造单元。
国家电网考试-25电力网络分析

电力网络分析讲义第一、二章第一部分:本组选用IEEE30节点作为分析对象,首先,根据标准数据,画出电力网络图,如图1所示。
然后根据网路图,本单元计算了网络的关联矩阵、节点导纳和节点阻抗矩阵以及添加和移去一条支路的处理。
图1 IEEE30节点电力网络图一、计算关联矩阵:为了计算关联矩阵,首先对网络进行节点和支路进行编号和标注方向,尤其是道-支关联矩阵,要求支路必须有方向。
选取树枝和连枝,重新编号,如图2所示。
图2 有向图利用Matlab 编程,可直接求出节-支关联矩阵A:然后根据关联矩阵之间的关系,可分别求出回-支关联矩阵、割-支关联矩阵和道-支关联矩阵。
1. 回-支关联矩阵B:和A 的关系:2.割-支关联矩阵Q :和A 的关系:3.道-支关联矩阵T :和A 的关系:具体程序如下:function IEEE30[x,y]=xlsread('C:\Documents and Settings\Administrator\work\30节点数据.xls','sheet3','A2:C51');A=zeros(30,50);A1=zeros(31,50);for s=1:50start=x(s,2);tail=x(s,3);zong=x(s,1);A1(start,zong)=1;A1(tail,zong)=-1;end%去掉参考节点的最后一行,降阶for s=1:30for j=1:50A(s,j)=A1(s,j);endendfprintf(‘节-支关联矩阵A=%8.5f\n')Afor s=1:30for j=1:30 [ ]T L A A A =[ ]T B B I =0, 0T T N L L N AB BA ⨯⨯==1()T T T L T B A A -=-[ ]L Q I Q =11(())T T T L T T L Q A A A A --==[ ]T L T T T =TI AT =AT(s,j)=A(s,j); %树支endendfor s=1:30for j=31:50AL(s,j-30)=A(s,j); %连支endendBL=eye(20);QT=eye(30); BT=-1*(AL')*inv(AT');B=[BT,BL];fprintf('回-支关联矩阵B=%8.5f\n')BQL=-BT';Q=[QT,QL];fprintf('割-支关联矩阵=%8.5f\n')QTT=(inv(AT))';TL=zeros(30,20);T=[TT,TL];fprintf('道-支关联矩阵T=%8.5f\n')T运行结果如下:A=B=Q=T=二、计算节点导纳(阻抗)矩阵在本节中,本组采用了两种方法对网络进行求解节点导纳矩阵Y,法一,先求解网络的不定导纳矩阵,然后去掉参考节点或者地,形成定导纳矩阵;法二,根据导纳矩阵的定义,利用网络直接求出Y。
电力系统稳态分析部分习题答案

电力系统稳态分析部分习题答案之答禄夫天创作第一章电力系统的基本概念12 电力系统的部分接线示与图 12,各电压级的额定电压及功率输送方向已标明在图中。
题图 12 系统接线图试求:(1)发电机及各变压器高、低压绕组的额定电压;(2)各变压器的额定变比;(3)当变压器T1工作于+5%抽头,T2、T4工作于主轴头,T3工作于—2.5%轴头时,各变压器的实际比?解(1)发电机及各变压器高、低压绕组的额定电压。
发电机:VGN=10.5KV,比同电压级网络的额定电压高5%。
对于变压器的各侧绕组,将依其电压级别从高到低赋以标号1、2和3。
变压器T1为升压变压器:VN2=10.5KV,等于发电机额定电压;VN1=242KV,比同电压级网络的额定电压高10%。
变压器T2为将压变压器:VN2=121KV和VN3=38.5KV,分别比同电压级网络的额定电压高10%。
同理,变压器T3:VN1=35KV和VN2=11KV。
变压器T4:VN1=220KV和VN2=121KV(2)各变压器的额定变比。
以比较高的电压作为分子。
(3)各变压器的实际比。
各变压器的实际变比为两侧运行时实际整定的抽头额定电压之比。
T4:kT3 =220/110=213电力系统的部分接线如题图13所示,网络的额定电压已在图中标明。
试求:(1)发电机,电动机及变压器高、中、低压绕组的额定电压;(2)当变压器T1高压侧工作于+2.5%抽头,中压侧工作于+5%抽头;T2工作于额定抽头;T3工作于—2.5%抽头时,各变压器的V GN实际变比;题图 13 系统接线图解(1)发电机、电动机及变压器高、中、低压绕组额定电压。
(a)发电机:网络无此电压等级,此电压为发电机专用额定电压,故VGN=13.8KV。
(b)变压器T1:一次侧与发电机直接连接,故其额定电压等于发电机额定电压;二次侧额定电压高于网络额定电压10%,故T1的额定电压为121/38.5/13.8KV。
节点导纳矩阵和阻抗矩阵的互感支路组整体追加方法

节点导纳矩阵和阻抗矩阵的互感支路组整体追加方法陈明;李银红;石东源;柳焕章;王若曦;段献忠【摘要】在以支路追加法形成节点导纳矩阵和节点阻抗矩阵的过程中,互感支路的追加远比非互感支路复杂,因此提出以支路组为单位的节点导纳矩阵及节点阻抗矩阵支路组追加法。
该方法将相互之间有互感耦合的支路分为一组,应用所推导的追加公式以整组互感支路为单位直接追加到节点导纳矩阵和节点阻抗矩阵中,使得计算方法简单统一,可显著减少计算量,提高计算效率。
最后通过算例验证和比较了所提方法的实用性和有效性。
%In the process of building node-admittance matrix and node-impedance matrix by traditional adding branches method, the addition of mutual inductance line is more complex than non-mutual inductance line. A novel algorithm of building node-admittance matrix and node-impedance matrix based on branch groups is proposed in this paper. The method makes mutual coupling branches into a group. We can add the entire branches as a group into the network according to the derived adding equations. The algorithm has the characteristic of simple and unified computing method, reducing the amount of computation and improving the computational efficiency. The Practicality and Effectiveness of this proposed method is proved by calculation and comparison.【期刊名称】《电工技术学报》【年(卷),期】2016(031)021【总页数】8页(P94-101)【关键词】互感线路;支路组;节点导纳矩阵;节点阻抗矩阵【作者】陈明;李银红;石东源;柳焕章;王若曦;段献忠【作者单位】强电磁工程与新技术国家重点实验室华中科技大学武汉 430074;强电磁工程与新技术国家重点实验室华中科技大学武汉 430074;强电磁工程与新技术国家重点实验室华中科技大学武汉 430074;华中电网有限公司武汉 430077;强电磁工程与新技术国家重点实验室华中科技大学武汉 430074;强电磁工程与新技术国家重点实验室华中科技大学武汉 430074【正文语种】中文【中图分类】TM744电力网络的数学模型是现代电力系统分析的基础,通常使用节点导纳矩阵和节点阻抗矩阵描述[1,2]。
2012级研究生考试《电网络分析》试卷
g
2
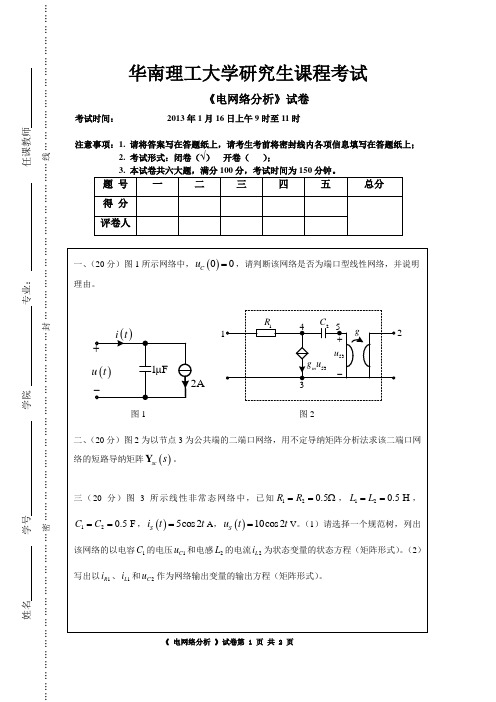
图2
二、 (20 分)图 2 为以节点 3 为公共端的二端口网络,用不定导纳矩阵分析法求该二端口网 络的短路导纳矩阵 Ysc s 。
三 ( 20 分)图 3 所示线 性非常 态网络 中,已知 R1 R2 0.5 , L1 L2 0.5 H ,
学号
C1 C2 0.5 F , iS t 5cos 2t A, uS t 10cos 2t V。 (1)请选择一个规范树,列出
该网络的以电容 C1 的电压 uC1 和电感 L2 的电流 iL 2 为状态变量的状态方程(矩阵形式) 。 (2) 写出以 iR1 、 iL1 和 uC 2 作为网络输出变量的输出方程(矩阵形式) 。
姓名
《 电网络分析 》试卷第 1 页 共 2 页
iL 2
iL1
L2
L1
C1
iR1
R1
R2
iS t
uC 2
C2
uC1
uS t
图3 四、 (20 分) 已知某二端口网络的开路阻抗矩阵 Z oc , 用信号流图分析法求该网络的出传输参数矩阵 T 。 其中:
U1 z11 z12 I1 I1 U z z I Z 0 c I 2 21 22 2 2
………………………………………密………………………………………………封………………………………………线…………………………………… ………………………………
华南理工大学研究生课程考试
《电网络分析》试卷
考试时间: 2013 年 1 月 16 日上午 9 时至 11 时
任课教师
注意事项:1. 请将答案写在答题纸上,请考生考前将密封线内各项信息填写在答题纸上; 2. 考试形式:闭卷(√) 开卷( ) ; 3. 本试卷共六大题,满分 100 分,考试时间为 150 分钟。
二端口阻抗参数矩阵

二端口阻抗参数矩阵1. 什么是二端口阻抗参数矩阵?二端口阻抗参数矩阵(Two-port impedance parameter matrix),也被称为Z参数矩阵,是描述二端口网络的一种常用的参数表示方法。
二端口网络是指由两个输入端口和两个输出端口组成的电路或系统。
在电路分析和设计中,我们经常需要对二端口网络进行建模和分析。
二端口阻抗参数矩阵提供了一种简洁而有效的方式来描述二端口网络的性质和行为。
2. 二端口阻抗参数矩阵的形式二端口阻抗参数矩阵通常用一个4x4的矩阵表示,其中包含了四个参数:Z11、Z12、Z21和Z22。
这些参数分别表示了输入端口和输出端口之间的关系。
输入端口1 输入端口2输出端口1 Z11 Z12输出端口2 Z21 Z22其中,Z11表示输入端口1的阻抗对于输出端口1的影响;Z12表示输入端口2的阻抗对于输出端口1的影响;Z21表示输入端口1的阻抗对于输出端口2的影响;Z22表示输入端口2的阻抗对于输出端口2的影响。
3. 二端口阻抗参数矩阵的意义二端口阻抗参数矩阵可以帮助我们了解二端口网络的特性和性能。
通过分析和计算矩阵中的参数,我们可以得到以下信息:3.1 输入阻抗和输出阻抗通过二端口阻抗参数矩阵,我们可以计算输入端口的阻抗和输出端口的阻抗。
输入阻抗是指当信号从外部输入到网络时,网络对信号的阻抗响应。
输出阻抗是指当信号从网络输出到外部时,网络对信号的阻抗响应。
3.2 传输参数二端口阻抗参数矩阵还可以用于计算传输参数。
传输参数是指输入端口和输出端口之间的信号传输特性。
通过计算矩阵中的参数,我们可以得到传输函数,从而了解信号在网络中的传输情况。
3.3 端口耦合二端口阻抗参数矩阵中的参数还可以用于描述端口之间的耦合效应。
耦合效应是指当信号从一个端口传输到另一个端口时,两个端口之间的相互影响。
通过计算矩阵中的参数,我们可以了解端口之间的耦合程度。
4. 如何计算二端口阻抗参数矩阵?要计算二端口阻抗参数矩阵,我们需要通过实验或者模拟来获取网络的输入输出数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图所示的网络,Vi和Ii分别代表第i个端口 的输入电压和电流,则该网络的[Z]矩阵和 [Y]矩阵定义如下:
阻抗矩阵
写成矩阵形式有
导纳矩阵
写成矩阵形式有
阻抗矩阵和导纳矩阵分别可简写为:
V Z I
阻抗矩阵和导纳矩阵的关系
I Z ji
Zii Z jj Yij Yji Yii Yjj
n 1 Re Vi I i* 0 2 i 1
展开,由阻抗和导纳矩阵的定义,有
可以证明
由于端口电压是任意的,由此得到,必有 Re[Z]=0 同样的过程,有Re[Y]=0
Z Y
1
或
Z Y U
[Z]矩阵和[Y]矩阵参数的意义
Z矩阵
Zii是除第i个端口外,其余端口都开路 时,i端口的自阻抗
Zij是除第j个端口外,其余端口都开路时,端口i和 端口j之间的转移阻抗,又称为互阻抗。
由上面的定义可计算出网络的Z矩阵参数 以T型网络为例
计算∏型网络的阻抗矩阵
导纳矩阵
Yii是除第i个端口外,其余端口都短路时,i
端口的自导纳
Yij是除第i个端口外,其余端口都短路时, 端口j和端口i之间的转移导纳(互导纳)。 同样由上面的定义可计算出网络的Y参数
定义
设网络的两个端口分别为a和b,如果它们之间满
足如下关系,则这个网络的端口a和b是互易的。
V1a I1b V1b I1a V2a I 2b V2b I 2a 0(4.34)
如果网络所有端口之间都满足上面的关系,则这
个网络称为互易网络。其中下标a和b表示网络中 某处的两个独立源产生的等效电压和电流。
由此可以导出,互易网络的Z和Y矩阵参数 的关系
Zij Z ji Yij Yji
