递推最小二乘法与广义最小二乘法matlab源程序
递推最小二乘法参数估计matlab程序
递推增广最小二乘法Matlab 程序与仿真设被控对象差分方程形式为:y (k )−1.5y (k −1)+0.7y (k −2)=u (k −3)+0.5u (k −4)+ξ(k )−ξ(k −1)+0.2ξ(k −2)式中,为方差为1的白噪声。
取初值6ˆ(0)10(0)0P I θ==、。
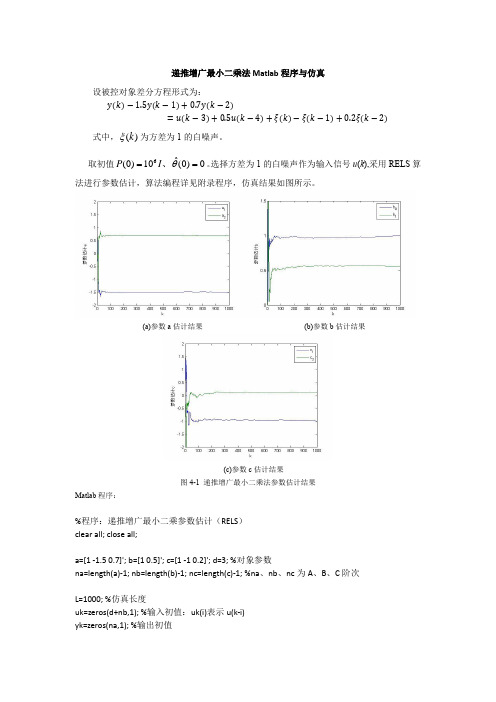
选择方差为1的白噪声作为输入信号u (k ),采用RELS 算法进行参数估计,算法编程详见附录程序,仿真结果如图所示。
(a)参数a 估计结果 (b)参数b 估计结果(c)参数c 估计结果图4-1 递推增广最小二乘法参数估计结果Matlab 程序:%程序:递推增广最小二乘参数估计(RELS )clear all; close all;a=[1 -1.5 0.7]'; b=[1 0.5]'; c=[1 -1 0.2]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %na 、nb 、nc 为A 、B 、C 阶次L=1000; %仿真长度uk=zeros(d+nb,1); %输入初值:uk(i)表示u(k-i)yk=zeros(na,1); %输出初值()kξxik=zeros(nc,1); %噪声初值xiek=zeros(nc,1); %噪声估计初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b;c(2:nc+1)]; %对象参数thetae_1=zeros(na+nb+1+nc,1); %na+nb+1+nc为辨识参数个数P=10^6*eye(na+nb+1+nc);for k=1:Lphi=[-yk;uk(d:d+nb);xik];y(k)=phi'*theta+xi(k); %采集输出数据phie=[-yk;uk(d:d+nb);xiek]; %组建phie%递推增广最小二乘法K=P*phie/(1+phie'*P*phie);thetae(:,k)=thetae_1+K*(y(k)-phie'*thetae_1);P=(eye(na+nb+1+nc)-K*phie')*P;xie=y(k)-phie'*thetae(:,k); %白噪声的估计值%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);for i=nc:-1:2xik(i)=xik(i-1);xiek(i)=xiek(i-1);endxik(1)=xi(k);xiek(1)=xie;endfigure(1)plot([1:L],thetae(1:na,:));xlabel('k'); ylabel('参数估计a');legend('a_1','a_2'); axis([0 L -2 2]);figure(2)plot([1:L],thetae(na+1:na+nb+1,:)); xlabel('k'); ylabel('参数估计b');legend('b_0','b_1'); axis([0 L 0 1.5]); figure(3)plot([1:L],thetae(na+nb+2:na+nb+nc+1,:)); xlabel('k'); ylabel('参数估计c');legend('c_1','c_2'); axis([0 L -2 2]);。
matlab练习程序(递推最小二乘)

matlab练习程序(递推最⼩⼆乘)⼀般的最⼩⼆乘通常是⼀次拿到全部的数据,对所有数据进⾏统⼀优化计算得到模型系数。
递推最⼩⼆乘是以⼀种递推的⽅式计算最⼩⼆乘,每次使⽤最新的测量值,来不断更新模型系数。
递推公式如下:公式中A和B为测量值,X为模型系数。
matlab代码如下:clear all;close all;clc;a=2;b=2;c=-3;d=1;e=2;f=30; %原始系数[x,y]=meshgrid(0:0.1:30);z=a*x.^2+b*y.^2+c*x.*y+d*x+e*y +f; %模型mesh(x,y,z)hold on;%%准备数据X=x(:);Y=y(:);Z=z(:);p = randperm(90000,100); %90000个点中随机选100个X=X(p);Y=Y(p);Z=Z(p);plot3(X,Y,Z,'ro')%%正常最⼩⼆乘A=[X.^2 Y.^2 X.*Y X Y ones(length(X),1)];B=Z;C=inv(A'*A)*A'*B;%%递推最⼩⼆乘figure;plot3(X,Y,Z,'ro')hold on;P = eye(6)*1000;X = zeros(6,1);for i=1:length(A)A1 = A(i,:);% P = inv(inv(P)+A1'*A1);P = P - P*A1'*A1*P/(1+A1*P*A1');X = X + P*A1'*(B(i) - A1*X);end%%画出RLS计算出的结果a=X(1);b=X(2);c=X(3);d=X(4);e=X(5);f=X(6); %拟合系数[x,y]=meshgrid(0:0.1:30);z=a*x.^2+b*y.^2+c*x.*y+d*x+e*y +f; %模型mesh(x,y,z)拟合结果:从结果上看,递推最⼩⼆乘结果不如常规最⼩⼆乘精确。
广义最小二乘

递推的最小二乘辨识程序matlab 2007-07-11 14:21:39 阅读116 评论0字号:大中小%递推的最小二乘辨识程序clear allL=15;u=wgn(1,L,1);v=wgn(1,15,1);z(2)=0;z(1)=0;%取z的前两个初始值为零for k=3:15;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2);%给出理想的辨识输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005;%相对误差E=0.000000005c=[c0,zeros(4,14)];%被辨识参数矩阵的初始值及大小e=zeros(4,15);%相对误差的初始值及大小for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]'; x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1;%求被辨识参数ce1=c1-c0;%求参数当前值与上一次的值的差值e2=e1./c0;%求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1;%新获得的参数作为下一次递推的旧参数c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1];%求出p(k)的值p0=p1;%给下次用if e2<=E break;%若参数收敛满足要求,终止计算end%小循环结束end%大循环结束a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(1);%第2个图形i=1:15;%横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1,a2,b1,b2的各次辨识结果figure(2); %第3个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1,a2,b1,b2的各次辨识结果的收敛情况广义最小二乘辨识的matlab实现(2007-07-05 01:35:37)转载最近在做系统辨识的工作,经典的方法林林种种,最小二乘诸法最是好用。
各种最小二乘法汇总(算例及MATLAB程序)

u(400)
⎟ ⎠
Matlab程序见附录 1。
1.2. 递推最小二乘算法
递推最小二乘算法公式:
^
^
^
θ (k) = θ (k −1) + K (k)[z(k) − h' (k)θ (k −1)]
K (k) = P(k −1)h(k)[h' (k)P(k −1)h(k) + 1 ]−1
(1.2)
Λ(k)
b2 a1 50 100 150 200 250 300 350 400 450
图 1 一般最小二乘参数过渡过程
4
盛晓婷 最小二乘算法总结报告
估计方差变化过程
100
90
80
70
60
50
40
30
20
10
0
0
50 100 150 200 250 300 350 400 450
图 2 一般最小二乘方差变化过程
1.1. 一次计算最小二乘算法
⎛ ⎜
^
a1
⎞ ⎟
⎛ -1.4916 ⎞
^
θ
LS
=
⎜^ ⎜ a2 ⎜^ ⎜ b1
⎟ ⎟ ⎟ ⎟
=
(
H
T L
H
L
)−1
H
T L
Z
L
=
⎜ ⎜
0.7005
⎟ ⎟
⎜1.0364 ⎟
⎜
⎟
(1.1)
⎜⎜⎝
^
b2
⎟⎟⎠
⎝ 0.4268 ⎠
⎛ Z (3) ⎞
⎛ hT (3) ⎞ ⎛ −Z (2) −Z (1)
图 1 一般最小二乘参数过渡过程 .....................................................4 图 2 一般最小二乘方差变化过程 ....................................................5 图 3 遗忘因子法参数过渡过程 ........................................................7 图 4 遗忘因子法方差变化过程 ........................................................8 图 5 限定记忆法参数过渡过程 ......................................................10 图 6 限定记忆法方差变化过程 ......................................................10 图 7 偏差补偿最小二乘参数过渡过程 ..........................................12 图 8 偏差补偿最小二乘方差变化过程 ..........................................12 图 9 增广最小二乘辨识模型 ..........................................................13 图 10 增广最小二乘参数过渡过程 ................................................14 图 11 广义最小二乘参数过渡过程 ................................................16 图 12 广义最小二乘方差变化过程 ................................................16 图 13 辅助变量法参数过渡过程 ....................................................18 图 14 辅助变量法方差变化过程 ....................................................18 图 15 二步法参数过渡过程 ............................................................20 图 16 二步法方差变化过程 ............................................................20
广义最小二乘法和递推最小二乘法

广义最小二乘法和递推最小二乘法
广义最小二乘法和递推最小二乘法是最小二乘法算法的改进版本。
最小二乘法
是一种常见的统计学技术,它有效地估计未知参数集,也可以用于回归分析。
本文旨在详细介绍广义最小二乘法和递推最小二乘法。
首先让我们了解最小二乘法。
最小二乘法(Least Squares)是一种最常用的
方法,其中未知参数的估计量是穷举法的最优估计,这是一种很有效的技术。
最小二乘法的求解过程中,以平方的残差来最小化两个估计量的差异,以求得最优参数。
然而,最小二乘法有时也会出现缺陷,其中一个原因是可能会把噪声干扰包含
在结果中,另一个原因是它依赖被观测值的方差,而方差受因素影响。
因此,有了广义最小二乘法。
广义最小二乘法是在最小二乘法的基础上改进的算法。
在广义最小二乘法中,
我们通过加入惩罚参数来最小化残差,以对噪声进行抑制。
惩罚参数的加入,使得预测变更的安全降低,同时噪声的影响也可以得以抑制。
因此,广义最小二乘法在回归分析中也有广泛的应用。
此外,基于最小二乘法的另一种增强方法是“递推最小二乘法”。
递推最小二
乘法是将最小二乘法算法进行改良,从而改善对噪声的抑制能力。
和广义最小二乘法一样,递推最小二乘法也需要惩罚参数的加入。
递推最小二乘法也通过持续更新未知参数,来达到最小化残差的目的,从而能有效地抑制噪声。
以上就是本文要陈述的关于广义最小二乘法和递推最小二乘法的改进方法以及
它们的比较。
从技术上讲,广义最小二乘法和递推最小二乘法都比最小二乘法更能抑制噪声和拟合回归曲线,因此,它们在回归分析中都有广泛的应用。
最小二乘法、最佳均方逼近、随机拟合及其MATLAB程序

2曲线拟合的线性最小二乘法及其MATLAB?序例2给出一组数据点(X i, y i)列入表2中,试用线性最小二乘法求拟合曲线, 估计其误差,作出拟合曲线•解 (1)在MATLAB工作窗口输入程序>> x=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6];y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.126.50 68.04];plot(x,y , 'r*'),lege nd( '实验数据(xi,yi)' )xlabel( 'x' ), ylabel( 'y'),title( '数据点(xi,yi) 的散点图’)运行后屏幕显示数据的散点图(略)(3)编写下列MATLAB程序计算f(x)在(X j,yj处的函数值,即输入程序>> syms al a2 a3 a4x=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6];fi=a1.*x.A3+ a2.*x.A2+ a3.*x+ a4运行后屏幕显示关于a1,a2, a3和a4的线性方程组fi =[ -125/8*a1+25/4*a2-5/2*a3+a4,-4913/1000*a1+289/100*a2-17/10*a3+a4,-1331/1000*a1+121/100*a2-11/10*a3+a4, -64/125*a1+16/25*a2-4/5*a3+a4,a4, 1/1000*a1+1/100*a2+1/10*a3+a4,27/8*a1+9/4*a2+3/2*a3+a4,19683/1000*a1+729/100*a2+27/10*a3+a4, 5832/125*a1+324/25*a2+18/5*a3+a4]编写构造误差平方和的MATLAB程序>> y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.12 6.50 68.04];fi=[-125/8*a1+25/4*a2-5/2*a3+a4, -4913/1000*a1+289/100*a2-17/10*a3+a4, -1331/1000*a1+121/100*a2-11/10*a3+a4,-64/125*a1+16/25*a2-4/5*a3+a4, a4,1/1000*a1+1/100*a2+1/10*a3+a4,27/8*a1+9/4*a2+3/2*a3+a4,19683/1000*a1+729/100*a2+27/10*a3+a4,5832/125*a1+324/25*a2+18/5*a3+a4];fy=fi-y; fy2=fy.A2; J=sum(fy.A2)运行后屏幕显示误差平方和如下J=(-125/8*a1+25/4*a2-5/2*a3+a4+1929/10)A2+(-4913/1000*a1+289/100*a2-17/10*a3+a4+171/2)A2+(-1331/1000*a1+121/100*a2-11/10*a3+a4+723/20F2+(-64/125*a1+16/25*a2-4/5*a3+a4+663/25F2+(a4+91/10F2+(1/1000*a1+1/100*a2+1/10*a3+a4+843/100)A2+(27/8*a1+9/4*a2+3/2*a3+a4+328/25)A2+(19683/1000 *a1+729/100*a2+27/10*a3+a4-13/2F2+(5832/125*a1+324/25*a2 +18/5*a3+a4-1701/25F2为求31,32,33,34使J达到最小,只需利用极值的必要条件-丄 0 a k (k 1,2,3,4),得到关于31,32,33,34的线性方程组,这可以由下面的MATLAB程序完成,即输入程序>> syms a1 a2 a3 a4 J=(-125/8*a1+25/4*32-5/2*a3+34+1929/10)A2+(-4913/1000*a1+289/100*32-17/10*33+34...+171/2)A2+(-1331/1000*a1+1 21/100*a2-11/10*a3+34+723/20)A2+(-64/125*31+16/25*32-4/5*a3+34+663/25)A2+(34+91/10)A2+(1/1000*31+1/100*32+1/10*a3+a4+843/100)A2+(27/8*31+9/4*32+3/2*a3+34+328/25)A2+(19683/ 1000*a1+729/100*32+27/10*a3+34-13/2)A2+(5832/125*31+324/2 5*a2+18/5*a3+a4-1701/25)A2;Ja1=diff(J,a1); Ja2=diff(J,a2); Ja3=diff(J,a3);Ja4=diff(J,a4);Ja11=simple(Ja1), Ja21=simple(Ja2), Ja31=simple(Ja3),Ja41=simple(Ja4),运行后屏幕显示J分别对31, 32 ,33 ,34的偏导数如下Ja1仁56918107/10000*31+32097579/25000*32+1377283/2500*33+23667/250*34-8442429/625J321 =32097579/25000*31+1377283/2500*32+23667/250*33 +67*34+767319/625 J331 = 1377283/2500*31+23667/250*32+67*33+18/5*34-232638/125J341 = 23667/250*31+67*32+18/5*33+18*34+14859/25解线性方程组J311 =0,J321 =0,J331 =0,J341 =0,输入下列程序>>A=[56918107/10000, 32097579/25000, 1377283/2500,23667/250; 32097579/25000, 1377283/2500, 23667/250, 67; 1377283/2500, 23667/250, 67, 18/5; 23667/250, 67, 18/5, 18];B=[8442429/625, -767319/625, 232638/125, -14859/25];C=B/A, f=poly2sym(C)运行后屏幕显示拟合函数f及其系数C如下C = 5.0911 -14.1905 6.4102 -8.2574f=716503695845759/140737488355328*xA3-7988544102557579/562949953421312*xA2+1804307491277693/281474976710656*x -4648521160813215/562949953421312 故所求的拟合曲线为f (x) 5.0911 x314.1905 x2 6.4102 x 8.2574 .(4)编写下面的MATLAB 程序估计其误差,并作出拟合曲线和数据的图形.输入程序>> xi=[-2.5 -1.7 -1.1 -0.8 0 0.1 1.5 2.7 3.6]; y=[-192.9 -85.50 -36.15 -26.52 -9.10 -8.43 -13.12 6.50 68.04]; n=length(xi);f=5.0911.*xi.A3-14.1905.*xi.A2+6.4102.*xi -8.2574;x=-2.5:0.01: 3.6;F=5.0911.*x.A3-14.1905.*x.A2+6.4102.*x -8.2574;fy=abs(f-y); fy2=fy.A2; Ew=max(fy),E1=sum(fy)/n, E2=sqrt((sum(fy2))/n) plot(xi,y,'r*'), hold on, plot(x,F, 'b-'),hold off legend('数据点(xi,yi)','拟合曲线y=f(x)'),xlabel('x'), ylabel('y'),title(例2的数据点(xi,yi)和拟合曲线y=f(x)的图形')运行后屏幕显示数据(X i,yj与拟合函数f的最大误差平均误差E i和均方根误差E2及其数据点(X j,yj和拟合曲线y=f(x)的图形(略).Ew = E1 = E2 =3.105 4 0.903 4 1.240 96函数逼近及其MATLAB?序最佳均方逼近的MATLAB^程序function [yy1,a,WE]=zjjfbj(f,X,Y,xx) m=size(f);n=length(X);m=m(1);b=zeros(m,m); c=zeros(m,1);if n~=length(Y) error( 'X和丫的维数应该相同') end for j=1:m for k=1:mb(j,k)=0;for i=1:nb(j,k)=b(j,k)+feval(f(j,:),X(i))*feval(f(k,:),X(i));endendc(j)=0;for i=1:nc(j)=c(j)+feval(f(j,:),X(i))*Y(i);endenda=b\c;WE=0;for i=1:nff=0;for j=1:m ff=ff+a(j)*feval(f(j,:),X(i)); endWE=WE+(Y(i)-ff)*(Y(i)-ff);endif nargin==3return ;endyy=[];for i=1:ml=[];for j=1:length(xx) l=[l,feval(f(i,:),xx(j))]; end yy=[yy l'];endyy=yy*a; yy1=yy'; a=a';WE;例6. 1对数据X和Y,用函数y 1,y x, y x2进行逼近,用所得到的逼近函数计算在x 6.5处的函数值,并估计误差.其中X=(1 3 4 5 6 7 8 9); Y=(-11 -13 -11 -7 -1 7 17 29). 解在MATLA工作窗口输入程序>> X=[ 1 3 4 5 6 7 8 9]; Y=[-11 -13 -11 -7 -17 17 29];f=['fun0';'fun1';'fun2'];[yy,a,WE]=zjjfbj(f,X,Y,6.5) 运行后屏幕显示如下yy =2.75000000000003a =-7.00000000000010 -4.999999999999951.00000000000000WE =7.172323350269439e-027例 6.2 对数据X 和丫,用函数 y 1, y x, y x2,y cosx,y e x,y sinx进行逼近,其中X=(0 0.50 1.00 1.50 2.00 2.50 3.00 ),丫=(0 0.47940.8415 0.9815 0.9126 0.5985 0.1645 ) .解在MATLA工作窗口输入程序>> X=[ 0 0.50 1.00 1.50 2.00 2.50 3.00];丫=[0 0.4794 0.8415 0.9815 0.9126 0.1645];f=['fun0';'fun1';'fun2';'fun3';'fun4';'fun5'];xx=0:0.2:3;[yy,a,WE]=zjjfbj(f,X,Y,plot(X,Y,'ro',xx,yy,'b-')运行后屏幕显示如下(图略)yy = Columns 1 through 7-0.0005 0.2037 0.3939 0.5656 0.8348 0.9236Columns 8 through 140.9771 0.9926 0.9691 0.9069 0.6766 0.5191Columns 15 through 160.3444 0.1642 0.5985xx), 0.7141 0.8080a = 0.3828 0.4070 -0.3901 0.0765 -0.4598 0.5653 WE = 1.5769e-004 即,最佳逼近函数为y=0.3828+0.4070*x-0.3901*xA2+0.0765*exp(x) +0.5653*sin(x) .8随机数据点上的二元拟合及其MATLA 程序例 8 设节点 ( X,Y,Z ) 中的 X 和 Y 分别是在区间 [ 3,3] 和 [ 2.5,3.5]上的 5022个 随 机 数 , Z 是 函 数 Z=7-3 x 3e -x2 -y2 在 (X,Y ) 的 值 , 拟 合 点 ( X I ,Y I ) 中的 X I =-3:0.2:3, Y I =-2.5:0.2:3.5. 分别用二元拟合方法中最近邻内插法、三 角基线性内插法、三角基三次内插法和 MATLAB4 网格化坐标方法计算在 ( X I ,Y I ) 处的值,作出它们的图形,并与被拟和曲面进行比较 .解 (1 )最近邻内插法 .输入程序>> x=rand(50,1); y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x , y .X=-3+(3-(-3))*x; %利用x 生成的随机变量.title( ' 用最近邻内插法拟合函数 z =7-3 xA3 exp(-xA2 - yA2) 的曲面和节点的图形 ' )%legend( ' 拟合曲面 ',' 节点 (xi,yi,zi)' )hold on%在当前图形上添加新图形面及其插值乙(略).(2)三角基线性内插法 输入程序>> x=rand(50,1); y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x; %利用x 生成 上的随机变量.Y=-2.5+(3.5-(-2.5))*y;%利用 y 生成 上的随机变量 .Z=7-3* X.A3 .* exp(-X.A2 - Y.A2);%在每个随机点( X,Y )处计算Z 的值.-0.4598*cos(x)Y=-2.5+(3.5-(-2.5))*y;Z=7-3* X.A3 .* exp(-X.A2 - Y.A2);处计算Z 的值.X1=-3:0.2:3; Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); ZI=griddata(X,Y,Z,XI,YI, (XI,YI )处的插值 ZI.mesh(XI,YI, ZI)xlabel( 'x' ), ylabel( 'y'%利用 y 生成的随机变量 .%在每个随机点( X,Y )%将坐标( XI,YI )网格化 .'nearest' ) %计算在每个插值点 %作二元拟合图形 . ), zlabel( 'z' ),plot3(X,Y,Z, 'bo' ) (X,Y,Z). hold of 运行后屏幕显示用最近邻内插法拟合函数%用兰色小圆圈画出每个节点 %结束在当前图形上添加新图形 .22Z=7-3 x 3e-x2 -y2在两组不同节点处的曲X1=-3:0.2:3;title('用三角基线性内插法拟合函数z =7-3 x A3 exp(-x A2 -y A2)的曲面和节点的图形’) %legend( ' 拟合曲面',' hold on plot3(X,Y,Z, 'bo' ) (X,Y,Z). hold of22运行后屏幕显示用三角基线性内插法拟合函数Z=7-3 x 3e-x -y在两组不同节点处的曲面和节点的图形及其插值 乙(略).(3)三角基三次内插法 . 输入程序>> x=rand(50,1); y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .title( ' 用三角基三次内插法拟合函数 z =7-3 xA3 exp(-xA2 -22运行后屏幕显示用三角基三次内插法拟合函数 Z=7-3 x 3e -x -y 在两组不同节点处的曲面和节点的图形及其插值 Z I (略).( 4 ) MATLAB 4网格化坐标方法 . 输入程序>> x=rand(50,1); y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x;%利用x 生成 上的随机变量.Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); ZI=griddata(X,Y,Z,XI,YI,XI,YI )处的插值 ZI.mesh(XI,YI, ZI)xlabel( 'x' ), ylabel( 'y%将坐标( XI,YI )网格化 .'linear' ) %计算在每个插值点 %作二元拟合图形 . ), zlabel( 'z' ),节点 (xi,yi,zi)' )%在当前图形上添加新图形 .%用兰色小圆圈画出每个节点 %结束在当前图形上添加新图形 . X=-3+(3-(-3))*x; %利用x 生成上的随机变量.Y=-2.5+(3.5-(-2.5))*y;Z=7-3* X.A3 .* exp(-X.A2 - Y.A2);处计算Z 的值.X1=-3:0.2:3; Y1=-2.5:0.2:3.5;[XI,YI] = meshgrid(X1,Y1); ZI=griddata(X,Y,Z,XI,YI,( XI,YI )处的插值 ZI.mesh(XI,YI, ZI) xlabel( 'x' ), ylabel( 'y'%利用y 生成上的随机变量•%在每个随机点( X,Y )%将坐标( XI,YI )网格化 .'cubic' ) %计算在每个插值点 %作二元拟合图形 . ), zlabel( 'z' ),yA2) 的曲面和节点的图形 ' )%legend( ' 拟合曲面','hold on 节点 (xi,yi,zi)' )%在当前图形上添加新图形plot3(X,Y,Z,'bo' ) (X,Y,Z).hold of%用兰色小圆圈画出每个节点%结束在当前图形上添加新图形 .22运行后屏幕显示用MATLAB 网格化坐标方法拟合函数Z=7-3 x 3e -x-y 在两组不同 节点处的曲面和节点的图形及其插值 ZI (略).22(5) 作被拟合曲面Z=7-3x 3e -x-y 和节点的图形. 输入程序>> x=ra nd(50,1); y=rand(50,1); %生成50个一元均匀分布随机数x 和y , x ,y .X=-3+(3-(-3))*x; %利用x 生成随机变量.Y=-2.5+(3.5-(-2.5))*y;%利用y 生成随机变量.Z=7-3* X.A3 .* exp(-X.A2 - Y.A2);%在每个随机点( X,Y )处计算Z 的值.X1=-3.:0.1:3.;Y1=-2.5:0.1:3.5;[XI,YI] = meshgrid(X1,Y1);%将坐标( XI,YI )网格化 .ZI=7-3* XI.A3 .* exp(-XI.A2 - YI.A2); mesh(XI,YI, ZI) %作二元拟合图形 .xlabel( 'x'), ylabel('y' ), zlabel( 'z' ),title( ' 被拟合函数 z =7-3 xA3 exp(-xA2 - yA2) 的曲面和节点的图形 ' )%legend('被拟合函数曲面','节点(xi,yi,zi)' )hold on%在当前图形上添加新图形 .plot3(X,Y,Z, 'bo' )%用兰色小圆圈画出每个节点 (X,Y,Z).hold of%结束在当前图形上添加新图形 .22运行后屏幕显示被拟合函数 Z=7-3 x 3e -x-y 的曲面和节点的图形及其函数值 ZI(略) .Y=-2.5+(3.5-(-2.5))*y;Z=7-3* X.A3 .* exp(-X.A2 - Y.A2);处计算Z 的值.X1=-3:0.2:3; Y1=-2.5:0.2:3.5; [XI,YI] = meshgrid(X1,Y1); ZI=griddata(X,Y,Z,XI,YI, (XI,YI )处的插值 ZI.mesh(XI,YI, ZI) xlabel( 'x' ), ylabel( 'y' %利用y 生成上的随机变量.%在每个随机点( X,Y )'v4'%将坐标( XI,YI )网格化 . ) %计算在每个插值点%作二元拟合图形 . ), zlabel( 'z' ),' 用 MATLAB 4 网格化坐标方法 拟合函数 z =7-3 xA3 的曲面和节点的图形 ' )%legend( ' 拟合曲面 ',' 节点 (xi,yi,zi)' ) hold on %在当前图形上添加新图形 . plot3(X,Y,Z, 'bo' ) %用兰色小圆圈画出每个节点(X,Y,Z).hold oftitle(exp(-x A2 - y A2)'bo' ) %结束在当前图形上添加新图形 .。
递推最小二乘法算法

---------------------------------------------------------------最新资料推荐------------------------------------------------------递推最小二乘法算法题目:(递推最小二乘法)考虑如下系统:) ( ) 4 ( 5 . 0 ) 3 ( ) 2 ( 7 . 0 ) 1 ( 5 . 1 ) ( k k uk u k y k y k y + + = + 式中,) (k 为方差为 0.1 的白噪声。
取初值 I P610 ) 0 ( = 、 0 0 =)(。
选择方差为 1 的白噪声作为输入信号 ) (k u ,采用 PLS 法进行参数估计。
Matlab代码如下:clear all close all L=400; % 仿真长度 uk=zeros(4,1); %输入初值:uk(i) 表示u(k-i) yk=zeros(2,1); % 输出初值u=randn(L,1); % 输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); % 方差为0.1 的白噪声序列theta=[-1.5;0.7;1.0;0.5]; % 对象参数真值thetae_1=zeros(4,1); % ()初值 P=10 *eye(4); % 题目要求的初值 for k=1:L phi=[-yk;uk(3:4)]; %4004 矩阵 phi 第k 行对应的y(k-1),y(k-2),u(k-3), u(k-4) y(k)=phi’*theta+xi(k); % 采集输出数据 % 递推最小二乘法的递推公式K=P*phi/(1+phi’*P*phi);1/ 3thetae(:,k)=thetae_1+K*(y(k)-phi’*thetae_1);P=(eye(4)-K*phi’)*P; % 更新数据thetae_1=thetae(:,k); for i=4:-1:2 uk(i)=uk(i-1); end uk(1)=u(k); fori=2:-1:2 yk(i)=yk(i-1); end plotxlablege%ax结分系统由C可以我们end yk(1)=y(kt([1:L],thetabel(‘k’); ylabend(‘a_1’,’a_xis([0 L -2 2果析如下统方程为 ( yCAR模型:( y以得到:们可以知道k); ae); %line([bel(‘参数估_2’,’b_0’,’b_2]); ( 5 . 1 ) ( k y k ( 5 . 1 ) ( k y k =道纯迟延为31,L],[theta,计 a、b’);1’); ( 7 . 0 ) 1 y k + 7 .0 ) 1 y k 1 )(= z A(1 z BT,na=2,theta]); ( ) 2 ( k u k = ( )2 ( k u k + 15 . 1 1+ = z0 1 ( )3 + = znb=1,d=35 . 0 ) 3 u k+ 5 . 0 ) 3 u k + 27 . 0 z ) 5 . 01 z 3, ( ) 4 (k u + ( )4 (k u + ) (k ) (k phi(y(k)列向这是一开初始所以经过的y于是不同 pphi 递推相比(k,:)=[-yk;u)=phi*theta向量不需要是循环的主开始我们赋始输入 u(0)以过白噪声的y(1)给到下一是我让程序同:phi = -1.9333 -3.3952 -0.4448 -0.4710 推最小二乘比于第一次uk(3:4)]’; 40a+xi(k);输出要用phi(k,:)形主体,接下来赋给初值给输=u(-1)=u(-21 ) 1 ( = y更新代码后一组y(2)的计) 2 ( =---------------------------------------------------------------最新资料推荐------------------------------------------------------y序中显示phi乘法phi截图如次作业的批处04矩阵ph出等于矩阵p形式来输入以及输2)=u(-3)=0;7 . 0 ) 0 ( 5 . 1 y后,以及输入计算中区去. 0 ) 1 ( 5 . 1 y以便只观的如下:处理最小二hi第k行对应phi与真值矩输出;初始输出- ( ) 1 - ( 7 +u y入输出值得去:- ( ) 0 ( 7 +u y的表现递推最二乘法的phi应的y(k-1),y矩阵相乘加出 y(0)=y(-1)3 - ( 5 . 0 ) 2 - + u得更新后我们2 - ( 5 .0 ) 1 + u最小二乘法:y(k-2),u(k-3加上白噪声。
5.递推最小二乘法程序

5. 最小二乘参数的递推算法根据递推公式用循环实现递增。
如果满足所要求的精度,则跳出循环。
递推公式如下:)ˆ)1((ˆˆT 11θw K θθ⨯-++=++NN N N N z 1T 1))(1()(-++=N N N N N N w P w w P K))(1/()()()()1(T T N N N N N N N N N w P w P w w P P P +-=+源程序为:“ls.dsw ” 。
输入信号M 序列存在数据文件“data1.txt ”中 ,均值为0,方差为0.1的高斯白噪声存在数据文件“data2.txt ”中 。
估计结果存在数据文件“data3.txt ”中。
源程序:math.h"#include "stdio.h"#include "brmul.c"#include "brinv.c"int main(){FILE *fp1,*fp2,*fp;int u[600]; double v[600];int i, j, k, count;double y1[4][1],y[510],y2[1][1];double t1[4][1],t2[1][4],t3[1][1],t5[4][4],t6[4][4];double o[4][1], o1[500][4], w[4][1], w1[1][4];double p[4][4], km[4][1], er[4][1];double maxe;t3[0][0] = 0.0;y2[0][0] = 0.0;fp1 = fopen("data1.txt","r");fp2 = fopen("data2.txt","r");for( i = 0; i < 600; i++ ){fscanf(fp1,"%d",&u[i]);//输入信号M 序列fscanf(fp2,"%lf",&v[i]);//均值为0,方差为0.1的白噪声}fclose(fp1);fclose(fp2);y[0] = v[0];y[1] = v[1]; for( i = 2; i < 510; i++ )y[i] = 1.5*y[i-1]-0.7*y[i-2]+u[i-1]+0.5*u[i-2]+v[i];y1[0][0] = -1.5;y1[1][0] = 0.7;y1[2][0] = 1.0;y1[3][0] = 0.5;for( i = 0; i < 4; i++ ) o[i][0] = 0;for( i = 0; i < 4; i++ )for( j = 0; j < 4;j++ ){if( i == j ) p[i][j] = 1000000;else p[i][j] = 0;}for( k = 0; k < 500; k++ ){for( i = 0; i < 2; i++ ) w[i][0] = w1[0][i] = -y[1-i+k];for( i = 2; i < 4; i++ ) w[i][0] = w1[0][i] = u[3-i+k];brmul(p,w,4,4,1,t1);brmul(w1,p,1,4,4,t2);brmul(t2,w,1,4,1,t3);for( i = 0; i < 4; i++ ) km[i][0] = t1[i][0]/(1+t3[0][0]);brmul(w1,o,1,4,1,y2);for( i = 0; i < 4; i++ ) o[i][0] = o[i][0] + km[i][0]*(y[k+2] - y2[0][0]);brmul(t1,w1,4,1,4,t5);brmul(t5,p,4,4,4,t6);for( i = 0; i < 4; i++ )for( j = 0; j < 4; j++ ) p[i][j] = p[i][j] - t6[i][j]/(1+t3[0][0]);for ( i = 0; i < 4; i++ ) o1[k][i] = o[i][0];maxe = 0;for( i = 0; i < 4; i++ ){er[i][0] = fabs((o[i][0] - y1[i][0])/y1[i][0]);maxe = max( er[i][0], maxe );}count = k;if( maxe < 0.01 ) break;}fp = fopen("Data3.txt","w");fprintf(fp,"a0\t\ta1\t\tb0\t\tb1\n");for( i = 0; i < count+1; i++ ){fprintf(fp,"%f\t%f\t%f\t%f\n",o1[i][0],o1[i][1],o1[i][2],o1[i][3]);}fclose(fp);return 0; }。
最小二乘法matlab

(1)matlab中的lsqcurvefit使用2013-04-04 12:28manaijin|分类:工程技术科学|浏览9318次求讲解[a,Jm]=lsqcurvefit(fun,a0,x,y)(最好举例)各个符号的意思我有更好的答案分享到:按默认排序|按时间排序1条回答2013-04-04 20:39 白肚河蟹不让说|十级非线性曲线拟合是已知输入向量xdata和输出向量ydata,并且知道输入与输出的函数关系为ydata=F(x, xdata),但不知道系数向量x。
今进行曲线拟合,求x使得输出的如下最小二乘表达式成立:min Σ(F(x,xdatai)-ydatai)^2函数lsqcurvefit格式x = lsqcurvefit(fun,x0,xdata,ydata)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)[x,resnorm] = lsqcurvefit(…)[x,resnorm,residual] = lsqcurvefit(…)[x,resnorm,residual,exitflag] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda,jacobian] =lsqcurvefit(…) 参数说明:x0为初始解向量;xdata,ydata为满足关系ydata=F(x, xdata)的数据;lb、ub为解向量的下界和上界lb≤x≤ub,若没有指定界,则lb=[ ],ub=[ ];options为指定的优化参数;fun为待拟合函数,计算x处拟合函数值,其定义为function F = myfun(x,xdata)resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和;residual=fun(x,xdata)-ydata,即在x处的残差;exitflag为终止迭代的条件;output为输出的优化信息;lambda为解x处的Lagrange乘子;jacobian为解x处拟合函数fun的jacobian矩阵。
matlab递推最小二乘法函数

一、介绍在数学和工程领域中,最小二乘法是一种常见的参数估计方法,用于寻找一组参数使得观测数据和模型预测值之间的误差最小。
而在matlab中,递推最小二乘法函数是指使用递推方式来实现最小二乘法计算的函数。
本文将介绍matlab中如何编写递推最小二乘法函数,并对其原理和应用进行详细讲解。
二、递推最小二乘法的原理递推最小二乘法是一种迭代方法,通过不断更新参数来逼近最优解。
其原理可以简单描述为以下几个步骤:1. 初始化参数:首先需要初始化参数向量,通常可以使用随机数或者某些先验知识来确定初始参数值。
2. 迭代更新:接下来进入迭代更新阶段,根据当前参数值和观测数据,更新参数向量以降低误差。
3. 判断停止条件:迭代更新的过程中需要设立停止条件,当满足某个条件时停止迭代,可以是达到一定的迭代次数或者参数变化小于某个阈值等。
三、matlab编写递推最小二乘法函数在matlab中,编写递推最小二乘法函数可以通过以下步骤实现:1. 编写初始化函数:首先需要编写一个初始化函数来初始化参数向量,该函数可以接受观测数据和模型的输入,并返回初始参数向量。
2. 编写更新函数:接下来需要编写一个更新函数来进行参数的迭代更新,该函数也可以接受观测数据和当前参数向量的输入,并返回更新后的参数向量。
3. 编写停止条件函数:最后需要编写一个停止条件函数来判断迭代是否应该停止,该函数可以接受当前参数向量和更新前的参数向量的输入,并返回是否停止的逻辑值。
四、matlab递推最小二乘法函数的应用递推最小二乘法函数在matlab中的应用非常广泛,特别是在参数估计、信号处理、系统识别等领域。
通过使用递推最小二乘法函数,可以快速准确地估计出模型参数,从而提高算法的精度和效率。
由于递推最小二乘法具有较好的收敛性和稳定性,因此在实际工程中也得到了广泛的应用。
五、总结通过本文的介绍,读者可以了解到matlab中递推最小二乘法函数的编写和应用。
递推最小二乘法作为一种迭代方法,能够快速准确地估计出模型参数,并在各种工程领域中得到了广泛的应用。
matlab计算最小二乘法

matlab计算最小二乘法最小二乘法是一种常用的最优化方法,用于拟合数据点到拟合函数的最小误差平方和。
在MATLAB中,可以使用lsqcurvefit()函数来进行最小二乘拟合。
首先,需要定义拟合函数的形式。
假设我们要拟合一个线性函数:y = ax + b,其中a和b是待拟合的参数。
然后,准备数据。
将要拟合的数据的自变量x和因变量y以向量的形式准备好。
接下来,使用lsqcurvefit()函数进行拟合。
该函数的输入包括拟合函数的句柄、初始参数的猜测值、自变量和因变量等。
最后,利用拟合结果,可以得到最优化的参数值以及其他统计信息。
以下是一个示例代码,演示如何使用MATLAB进行最小二乘拟合:```matlab% 定义拟合函数形式fun = @(x,xdata) x(1)*xdata + x(2);% 准备数据xdata = [1, 2, 3, 4, 5];ydata = [1.3, 3.5, 4.2, 4.8, 6.1];% 初始参数猜测值x0 = [1, 0];% 进行最小二乘拟合x = lsqcurvefit(fun, x0, xdata, ydata);% 输出拟合结果a = x(1);b = x(2);disp(['拟合结果:a = ', num2str(a), ', b = ', num2str(b)]); ```运行上述代码,将得到拟合结果:a = 1.225, b = 1.045。
这表示拟合函数的形式为 y = 1.225x + 1.045,最小化了数据点到拟合函数的误差平方和。
希望以上内容对您有帮助!。
最小二乘法MATLAB程序及结果

最小二乘递推算法的MATLAB仿真针对辨识模型,有z(k)-+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k)模型结构,对其进行最小二乘递推算法的MATLAB仿真,对比真值与估计值。
更改a1、a2、b1、b2参数,观察结果。
仿真对象:z(k)-1.5*z(k-1)+0.7*z(k-2)=u(k-1)+0.5*u(k-2)+v(k)程序如下:L=15;y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的初始值for i=1:L; %移位循环x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4; %取出作为输出信号,即M序列if y(i)>0.5,u(i)=-0.03; %输入信号else u(i)=0.03;endy1=x1;y2=x2;y3=x3;y4=x4;endfigure(1);stem(u),grid onz(2)=0;z(1)=0;for k=3:15;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endc0=[0.001 0.001 0.001 0.001]'; %直接给出被识别参数的初始值p0=10^6*eye(4,4); %直接给出初始状态P0E=0.000000005;c=[c0,zeros(4,14)];e=zeros(4,15);for k=3:15; %开始求kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x);k1=p0*h1*x1; %开始求k的值d1=z(k)-h1'*c0;c1=c0+k1*d1;e1=c1-c0;e2=e1./c0; %求参数的相对变化e(:,k)=e2;c0=c1;c(:,k)=c1;p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出P(k)的值p0=p1;if e2<=E break;endendc,e %显示被辨识参数及其误差情况a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(2);i=1:15;plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':')title('Parameter Identification with Recursive Least Squares Method')figure(3);i=1:15;plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:')title('Identification Precision')程序运行结果:p0 =1000000 0 0 00 1000000 0 00 0 1000000 00 0 0 1000000c =Columns 1 through 90.0010 0 0.0010 -0.4984 -1.2325 -1.4951 -1.4962 -1.4991 -1.49980.0001 0 0.0001 0.0001 -0.2358 0.6912 0.6941 0.6990 0.69980.0010 0 0.2509 1.2497 1.0665 1.0017 1.0020 1.0002 0.99990.0010 0 -0.2489 0.7500 0.5668 0.5020 0.5016 0.5008 0.5002Columns 10 through 15-1.4999 -1.5000 -1.5000 -1.5000 -1.4999 -1.49990.6999 0.7000 0.7000 0.7000 0.7000 0.70000.9998 0.9999 0.9999 0.9999 0.9999 0.99990.5002 0.5000 0.5000 0.5000 0.5000 0.5000e =1.0e+003 *Columns 1 through 90 0 0 -0.4994 0.0015 0.0002 0.0000 0.0000 0.00000 0 0 0 -2.3592 -0.0039 0.0000 0.0000 0.00000 0 0.2499 0.0040 -0.0001 -0.0001 0.0000 -0.0000 -0.00000 0 -0.2499 -0.0040 -0.0002 -0.0001 -0.0000 -0.0000 -0.0000Columns 10 through 150.0000 0.0000 0.0000 -0.0000 -0.0000 0.00000.0000 0.0000 -0.0000 0.0000 0.0000 0.0000-0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000-0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000程序运行曲线:图1.输入信号图2.a1,a2,b1,b2辨识仿真结果图3. a1,a2,b1,b2各次辨识结果收敛情况分析:由运行结果可看出,输出观测值没有任何噪声成分时,辨识结果最大相对误差达到3位数。
用Matlab作最小二乘及微分方程

用Matlab作最小二乘及微分方程用Matlab 作最小二乘曲线拟合已知?m m y y y y x x x x ......1010::,要用一个函数)(x f 来近似代表y ,此函数中含有几个待定参数n a a a ,...,,21,现在的任务是:确定参数的值,使得在节点处的总误差∑=-m i i i y x f 02))((达到最小。
用Matlab 计算:先按照)(x f 建立一个函数文件,文件第一句格式为:function f=文件名(参数组, 节点数组)再用下面命令格式:参数组=lsqcurvefit (‘函数文件名’,参数组初值,节点数组,函数值数组)例:对函数C=C(t)测量得下面一组数据:t : 1 2 3 4 5 6 7 8 9C :4.54, 4.99, 5.35, 5.65, 5.90, 6.10, 6.26, 6.39, 6.50用函数x a e a a y 321-+=作拟合,并画图显示拟合效果,给出节点处总误差。
先建立并保存函数文件:文件名syp78hswj 内容为:function f=syp78hswj(a,x0)f=a(1)+a(2)*exp(-a(3)*x0);再下面主程序:clearhold onx0=1:9;y0=[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50];for i=1:9plot(x0(i),y0(i),'+')endcscz=[1,1,1];a=lsqcurvefit('syp78hswj',cscz,x0,y0)x=0:0.2:10;f=syp78hswj(a,x);plot(x,f)f=syp78hswj(a,x0);wc=sqrt(sum((f-y0).^2))hold off执行得:)2031.0,9911.2,9805.6(),,(321-=a a a 节点处总误差wc=0.0076 题1: bn an t +=2求 a=? b=?t 0 20 40 60 80 100 120 140 160 183.5n 0 1153 2045 2800 3466 4068 4621 5135 5619 6152答案:,1051.26-?=a .1044.12-?=b题2: ct be a C -+= 求 a=? b=? c=? 节点处总误差=?t : 1 2 3 4 5 6 7 8 9 10C :4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59 .答案:a=6.9811, b= -2.9918, c=0.2031 节点处总误差=0.0077 微分方程数值解 ??=≤≤-=.1)0(,10,2y x y x y dx dy 现以步长h=0.1求数值解:先建立“函数M —文件”:function f=eqs1(x,y)f=y-2*x/y;将此函数文件,以文件名eqs2保存.再命令:格式为: [自变量,因变量]=ode45(‘函数文件名’,节点数组,初始值) 命令为: [x,y]=ode45('eqs1',0:0.1:1,1)==+-='≤≤-+='.3.0)0(,2.0)0(,2sin ,10,2cos 21212211y y y y x y x y y x y 只须向量化,即可用前面方法:function f=eqs2(x,y)f=[cos(x)+2*y(1)-y(2);sin(x)-y(1)+2*y(2)];将此函数文件以文件名eqs2保存后,再下命令:[x,y]=ode45('eqs2',0:0.1:1,[0.2;0.3]) (注:输出的y 是矩阵,第i 列为函数i y 的数值解)要画图,就命令plot(x,y(:,1)), 及命令plot(x,y(:,2))22))10(9())20(16()20(161)(-+---?='X Y Y t X 22))10(9())20(16()10(91)(-+--?='X Y X t Y 22))()(())()(()()()(t y t Y t x t X t x t X w t x -+--?='22))()(())()(()()()(t y t Y t x t X t y t Y w t y -+--?='X (0)=30 , Y (0)=20 . x (0)=0 , y (0)=0 .当w =20时,function f=eqseqs20(t,y)w=20;aa=-16*(y(2)-20);bb=9*(y(1)-10);fm=sqrt(aa^2+bb^2);cc=y(1)-y(3);dd=y(2)-y(4);fm2= sqrt(cc^2+dd^2);f=[aa/fm;bb/fm;w*cc/fm2;w*dd/fm2];将此函数文件,以文件名eqseqs20保存后,再下命令:[t,y]=ode45('eqseqs20',0:0.1:1,[30;20;0;0])(注:输出y 是矩阵,第1、2、3、4列分别为函数X(t)、Y(t)、x(t)、y(t) 的数值解)要画图,继续命令:hold on,plot(y(:,1),y(:,2)),grid,plot(y(:,3),y(:,4)),hold off结果:当人速=1 狗速=20 时 t=1.9秒追击到。
各种最小二乘法汇总(算例及MATLAB程序)

1
盛晓婷 最小二乘算法总结报告
附录 8、广义最小二乘递推算法 ...........................................................34 附录 9、辅助变量法 ...............................................................................36 附录 10、二步法......................................................................................38 附录 11、多级最小二乘法......................................................................39 附录 12、Yule-Walker辨识算法 .............................................................42
各种最小二乘乘算法总结报告
目录
1. 一般最小二乘法 ...............................................................................3 1.1. 一次计算最小二乘算法 .............................................................3 1.2. 递推最小二乘算法 .....................................................................3
最小二乘法原理及其MATLAB实现

最小二乘法原理及其MATLAB实现一、本文概述最小二乘法是一种广泛应用于数学、统计学、工程学、物理学等众多领域的数学优化技术。
其核心原理在于通过最小化误差的平方和来寻找最佳函数匹配,从而实现对数据的最佳逼近。
本文将对最小二乘法的原理进行详细阐述,并通过MATLAB编程实现,帮助读者深入理解并掌握这一强大的数据分析工具。
文章将首先介绍最小二乘法的基本原理,包括其历史背景、基本概念以及数学模型的构建。
然后,通过实例分析,展示如何应用最小二乘法进行线性回归模型的拟合,以及如何处理过拟合和欠拟合等问题。
接着,文章将详细介绍如何在MATLAB中实现最小二乘法,包括数据准备、模型构建、参数估计以及结果可视化等步骤。
文章还将对最小二乘法的优缺点进行讨论,并探讨其在不同领域的应用前景。
通过本文的学习,读者将能够全面理解最小二乘法的原理和应用,掌握其在MATLAB中的实现方法,为实际工作中的数据处理和分析提供有力支持。
二、最小二乘法原理最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
这种方法起源于19世纪的统计学,由数学家阿德里安-马里·勒让德(Adrien-Marie Legendre)和卡尔·弗里德里希·高斯(Carl Friedrich Gauss)分别独立发展。
建立模型:我们需要建立一个描述数据关系的数学模型。
这通常是一个线性方程,如 y = ax + b,其中 a和b是待求解的参数。
误差计算:对于给定的数据集,我们可以将每个数据点代入模型中进行计算,得到预测值。
预测值与真实值之间的差异就是误差。
平方误差和:为了衡量模型的拟合程度,我们需要计算所有误差的平方和。
这是因为平方误差和能够更好地反映误差的大小,尤其是在误差较大时。
最小化平方误差和:最小二乘法的核心思想是找到一组参数,使得平方误差和达到最小。
这通常通过求导和令导数等于零来实现,从而找到使平方误差和最小的参数值。
最小二乘法拟合圆公式推导及matlab实现

2009-01-17 | 最小二乘法拟合圆公式推导及matlab实现最小二乘法(least squares analysis)是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配。
最小二乘法是用最简的方法求得一些绝对不可知的真值,而令误差平方之和为最小。
最小二乘法通常用于曲线拟合(least squares fitting) 。
这里有拟合圆曲线的公式推导过程和vc实现。
matlab 实现:function[R,A,B]=irc(x,y,N)%x,y是平面点的坐标,N是点个数%R是拟合半径,A,B是圆心的平面坐标x1=0;x2=0;x3=0;y1=0;y2=0;y3=0;x1y1=0;x1y2=0;x2y1=0;for i=1:Nx1=x1+x(i);x2=x2+x(i)*x(i);x3=x3+x(i)*x(i)*x(i);y1=y1+y(i);y2=y2+y(i)*y(i);y3=y3+y(i)*y(i)*y(i);x1y1=x1y1+x(i)*y(i);x1y2=x1y2+x(i)*y(i)*y(i);x2y1=x2y1+x(i)*x(i)*y(i);endC=N*x2-x1*x1;D=N*x1y1-x1*y1;E=N*x3+N*x1y2-(x2+y2)*x1;G=N*y2-y1*y1;H=N*x2y1+N*y3-(x2+y2)*y1;a=(H*D-E*G)/(C*G-D*D);b=(H*C-E*D)/(D*D-G*C);c=-(a*x1+b*y1+x2+y2)/N;A=a/(-2);B=b/(-2);R=sqrt(a*a+b*b-4*c)/2;VCvoid CViewActionImageTool::LeastSquaresFitting() {if (m_nNum<3){ return; }int i=0;double X1=0;double Y1=0;double X2=0;double Y2=0;double X3=0;double Y3=0;double X1Y1=0;double X1Y2=0;double X2Y1=0;for (i=0;i<m_nNum;i++){X1 = X1 + m_points[i].x;Y1 = Y1 + m_points[i].y;X2 = X2 + m_points[i].x*m_points[i].x;Y2 = Y2 + m_points[i].y*m_points[i].y;X3 = X3 + m_points[i].x*m_points[i].x*m_points[i].x;Y3 = Y3 + m_points[i].y*m_points[i].y*m_points[i].y;X1Y1 = X1Y1 + m_points[i].x*m_points[i].y;X1Y2 = X1Y2 + m_points[i].x*m_points[i].y*m_points[i].y;X2Y1 = X2Y1 + m_points[i].x*m_points[i].x*m_points[i].y; }double C,D,E,G,H,N;double a,b,c;N = m_nNum;C = N*X2 - X1*X1;D = N*X1Y1 - X1*Y1;E = N*X3 + N*X1Y2 - (X2+Y2)*X1;G = N*Y2 - Y1*Y1;H = N*X2Y1 + N*Y3 - (X2+Y2)*Y1;a = (H*D-E*G)/(C*G-D*D);b = (H*C-E*D)/(D*D-G*C);c = -(a*X1 + b*Y1 + X2 + Y2)/N;double A,B,R;A = a/(-2);B = b/(-2);R = sqrt(a*a+b*b-4*c)/2;m_fCenterX = A;m_fCenterY = B;m_fRadius = R; return;}。
最小二乘法及matlab程序

最小二乘法及matlab 程序最小二乘法简介:最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法的矩阵形式:Ax b = 若未知量的个数大于方程的个数,则方程无解,但在数值计算领域,我们通常是计算min ||||Ax b - ,解出其中的x 。
比较直观的做法是求解T T A Ax A b = ,但通常比较低效。
其中一种常见的解法是对 A 进行QR 分解(A=QR ),其中Q 是n k ⨯正交矩阵(Orthonormal Matrix ),R 是n k ⨯上三角矩阵(Upper Triangular Matrix ),则有:1min min min Ax b QRx b Rx Q b --=-=-。
Matlab 命令:一次函数线性拟合使用polyfit (x,y,1);多项式函数线性拟合使用 polyfit (x,y,n ),n 为次数;例如:x=[0.5,1.0,1.5,2.0,2.5,3.0]; y=[1.75,2.45,3.81,4.80,7.00,8.60]; p=polyfit(x,y,2) x1=0.5:0.5:3.0; y1=polyval(p,x1); plot(x,y,'*r',x1,y1,'-b') 计算结果为:p =0.5614 0.8287 1.1560即所得多项式为y=0.5614x^2+0.8287x+1.15560然后可以使用polyval在t处预测:y_hat=polyval(p,t)非线性函数使用:lsqcurvefit、nlinfit格式:lsqcurvefit(f,a,x,y)、nlinfit(x,y,f,a)f:符号函数句柄,如果是以m文件的形式调用的时候,别忘记加@.这里需要注意,f函数的返回值是和y匹对的,即拟合参数的标准是(f-y)^2取最小值,具体看下面的例子a:最开始预估的值(预拟合的未知参数的估计值)。
MATLAB最小二乘拟合源程序

for N = 1:length(t) Alp3 = t(N)*((t(N)-Alpha2)*(t(N)-Alpha1)-Beta1*P0_x)^2; Alpha3_1 = Alpha3_1 + Alp3; Alp4 = ((t(N)-Alpha2)*(t(N)-Alpha1)-Beta1*P0_x)^2; Alpha3_2 = Alpha3_2 + Alp4; end Alpha3 = sym((Alpha3_1)/(Alpha3_2)); % 计算得到Alpha1 fprintf('系数Alpha3为:Alpha3 = %f\n',eval(Alpha3)) % 计算系数Beta2. Beta2_1 = 0; Beta2_2 = 0; for N = 1:length(t) Bt3 = ((t(N)-Alpha2)*(t(N)-Alpha1)*P0_x-Beta1*P0_x)^2; Beta2_1 = Beta2_1 + Bt3; Bt4 = ((t(N)-Alpha1)*P0_x)^2; Beta2_2 = Beta2_2 + Bt4; end Beta2 = sym(Beta2_1/Beta2_2); % 计算得到Beta2 fprintf('系数Beta2为:Beta2 = %f\n',eval(Beta2)); % 计算正交多项式P3_x. syms x P3_x = collect((x-Alpha3)*P2_x-Beta2*P1_x); % 得到3次正交多项式. % 计算系数a0_*,a1_*,a2_*,a3_*. a0_1 = 0; a0_2 = 0; a1_1 = 0; a1_2 = 0; a2_1 = 0; a2_2 = 0; a3_1 = 0; a3_2 = 0; for ii = 1:length(t) a1 = y(ii)*P0_x; a0_1 = a0_1 + a1; a2 = P0_x^2; a0_2 = a0_2 + a2; a3 = y(ii)*(t(ii)-Alpha1)*P0_x; a1_1 = a1_1 + a3; a4 = (t(ii)-Alpha1)^2; a1_2 = a1_2 + a4; a5 = y(ii)*((t(ii)-Alpha2)*(t(ii)-Alpha1)-Beta1*P0_x);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
00000,-1.23318000000000,1.57300000000000,1.15200000000000;-1.09394000000000,0.584038000000000,0.626000000000000,1.57300000000000;0.583966000000000,-1.09394000000000,0.433000000000000,0.626000000000000;]
for i=3:30;
uk(i)=uk(i)+f(1)*uk(i-1)+f(2)*uk(i-2);
end
uk(2)=uk(2)+f(1)*uk(1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for j=1:30
for i=1:29;
yk=yk';
uk=[1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.626 0.433 -0.958 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.450 1.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 1.144 1.177 -0.390];
%pn_1=A-A*faik(1,:)'/(faik(1,:)*A*faik(1,:)'+1)*faik(1,:)*A
siit=[0.001,0.001,0.001,0.001]';
%siit=A*B'*[0.479840000000000,-1.02448000000000,0.443946000000000,-0.962888000000000,1.23318000000000,-0.584038000000000,1.09394000000000,-0.583966000000000,0.564678000000000;]'+A*faik(10,:)'/(faik(10,:)*A*faik(10,:)'+1)*(yk(12)-faik(10,:)*A*B'*[0.479840000000000,-1.02448000000000,0.443946000000000,-0.962888000000000,1.23318000000000,-0.584038000000000,1.09394000000000,-0.583966000000000,0.564678000000000;]')
%faik(1,:)'*faik(1,:)*faik(1,:)'*[yk(3)]+faik(1,:)'*faik(1,:)*faik(2,:)'/(faik(2,:)*faik(1,:)'*faik(1,:)*faik(2,:)'+1)*(yk(4)-faik(2,:)*faik(1,:)'*faik(1,:)*faik(1,:)'*[yk(3)])
clear;
clc;
nn = normrnd(0,sqrt(0.5),1,31)';
uk=[1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.626 0.433 -0.958 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.450 1.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 1.144 1.177 -0.390];
A(i,:)=[-yk(i+1) -yk(i) uk(i+1) uk(i)];
end
siit=inv(A'*A)*A'*yk(3:31)';
e(1)=yk(1);
e(2)=yk(2)+siit(1)*(yk(1))-siit(3)*uk(1);
for i=3:31;
B=A;
A=A'*A;
A*faik(10,:)'
A*B'
faik(10,:)*A
A=6*10000000*eye(4);
faik(10,:)*A*faik(10,:)'
kn_1=A*faik(10,:)'/(faik(10,:)*A*faik(10,:)'+1)
for i=1:28;
pn_1=A-A*faik(1+i,:)'/(faik(1+i,:)*A*faik(1+i,:)'+1)*faik(1+i,:)*A;
siit=siit+A*faik(1+i,:)'/(faik(1+i,:)*A*faik(1+i,:)'+1)*(yk(3+i)-faik(1+i,:)*siit)
end
uk(2)=uk(2)+f(1)*uk(1);
end
siit';
if(siit(1)>0&&siit(2)>0&&siit(3)>0&&siit(4)>0)
display('方差为0.0001时,利用广义最小二乘法获得参数结果:')
for i=1:29;
faik(i,:)=[-yk(i+1) -yk(i) uk(i+1) uk(i)];
end
%faik(3,:)'*faik(3,:)
%faik(1,:)'*faik(1,:)-faik(1,:)'*faik(1,:)*faik(2,:)'/(faik(2,:)*faik(1,:)'*faik(1,:)*faik(2,:)'+1)*faik(2,:)*faik(1,:)'*faik(1,:)
siit'
end
clear;
yk=[0
0
0.47984
-1.02448
0.443946
-0.962888
1.23318
-0.584038
1.09394
-0.583966
0.564678
-0.731735
0.778365
-0.488544
0.599589
end
for i=1:29;
fai(i,:)=[-e(i+1) -e(i)];
end
f=inv(fai'*fai)*fai'*e(3:31)';
for i=3:31;
yk(i)=yk(i)+f(1)*yk(i-1)+f(2)*yk(i-2);
end
yk(2)=yk(2)+f(1)*yk(1);
end
siit=inv(A'*A)*A'*(yk(3:31)+nn(2:30)')';
e(1)=yk(1);
e(2)=yk(2)+siit(1)*yk(1)-siit(3)*uk(1);
for i=3:31;
e(i)=yk(i)+siit(1)*yk(i-1)+siit(2)*yk(i-2)-siit(3)*uk(i-1)-siit(4)*uk(i-2);
e(i)=yk(i)+siit(1)*(yk(i-1))+siit(2)*(yk(i-2))-siit(3)*uk(i-1)-siit(4)*uk(i-2);
end
for i=1:29;
fai(i,:)=[-e(i+1) -e(i)];
end
f=inv(fai'*fai)*fai'*e(3:31)';
yk(1)=0;
yk(2)=0;
for i=1:29;
yk(i+2)=-1.642*yk(i+1)-0.715*yk(i)+0.39*uk(i+1)+0.35*uk(i)+nn(i+2)+1.642*nn(i+1)+0.715*nn(i);
end;
for i=1:29;
A(i,:)=[-yk(i+1) -yk(i) uk(i+1) uk(i)];
-0.878625
0.217687
-0.0144152
-0.590687
1.16106
-0.527737
0.628383
0.152147
-0.1108
0.605338
0.214697
-0.320849
0.601426
-0.000474461
0.430189
-0.446182];
