2013学年奉贤区初三数学二模试题(含答案)
2013年奉贤二模卷

第6题2013年奉贤区调研测试九年级数学 2014041.下列各数中,属于无理数的是( )A . 0)2(π; B .33; C .4; D . 38-;2.下列根式中,属于最简二次根式的是( )A .28; B .22b a +; C .ba ; D .4.0;3.不等式062>+x 的解集在数轴上表示正确的是( )4. 右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是( ) A.16、10.5; B.8、9; C.16、8.5; D.8、8.5;5.在数学活动课上,老师要同学们判断一个四边形门框是否为矩形, 下面是某学习小组的4位同学拟定的方案,其中正确的是( ) A .测量对角线是否相互平分; B .测量两组对边是否分别相等; C .测量一组对角是否都为直角; D .测量其中三个角是否都为直角; 6.如图,直线1l ∥2l ,3l ⊥4l .下列命题中真命题是( )A .︒=∠+∠9031;B .︒=∠+∠9032;C .42∠=∠;D .31∠=∠; 7.计算:52)(m - = ; 8.分解因式:282-a = ;9.二次函数32+=x y 图象的顶点坐标是 ; 10.已知函数2)(-=x x f ,若3)(=x f ,那么x = ; 11.随着中国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2013年海外学习汉语的学生人数已达1500000000人,将1500000000用科学记数法表示为 人;12.若点A (1,y 1)和点B (2,y 2)都在正比例函数kx y =()0>k 图像上,则y 1 y 2(选择“>”、“<”、“=”填空); 13.从-1,-2,3这三个数中任取两个不同的数作为点的坐标,该点在第三象限的概率是 ;14.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图。
()奉贤区中考数学二模试题(含答案),文档

上海市奉贤区2021届九年级数学4月调研测试题〔二模〕〔考试时间100分钟,总分值150分〕一、选择题:〔本大题共6题,每题4分,总分值24分〕1、2的倒数是〔〕A、2B、-22D、-2 C、2 22、以下算式的运算为m2的是〔〕A、m4m2B、m6m3C、(m1)2D、m4m23、直线y=〔3-π〕x经过的象限是〔〕A、一、二象限B、一、三象限C、二、三象限D、二、四象限4、李老师用软件记录了某个月〔30天〕每天走路的步数〔单位:万步〕它将记录的结果绘制成了如图一所示的统计图,在李老师每天走路的步数这组数据中,众数与中位数分别为〔〕A、与B、与C、与D、与5、小明用如图2所示的方法画出了△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以E为圆心,CA长为半径画弧,两弧相交于点F;③联结FD、FE;这样△DEF就是所要画的三角形,小明这样画的依据是全等三角形判定方法中的〔〕A、边角边B、角边角C、角角边D、边边边6、两圆相交,它们的圆心距为3,一个圆的半径是 2,那么另一个圆的半径长可以是〔〕A、1B、3C、5D、7二、填空题:〔本大题共12题,每题4分,总分值48〕7、计算:〔-1〕2021+20-4=;8、函数y=x+2的定义域是;9、方程x=-x的解是;110、如果抛物线y=a x 2 -3的顶点是它的最低点,那么 a 的取值范围是;11、如果抛物线yax 23的顶点是它的最低点,那么a 的取值范围是;12、如果点P 〔m-3,1〕在反比例函数y1的图像上,那么m 的值是;x13、学校组织“中华经典诗词大赛 〞,共设有20个试题,其中有关“诗句理解〞的试题 10个,有关“诗句作者〞的试题6个,有关“试卷默写〞的试题 4个.小杰从中任选一个试题作答, 他选中有关“诗句作者〞的试题的概率是;14、为了解某区3600名九年级学生的体育训练情况,随机抽取了区内 200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级: A 级:优秀;B 级:良好;C 级:及格;D 级:不及格,并将测试结果绘制成了如下列图的统计图 .由此估计全区九年级体育测试成绩可以到达优秀的人数约为;15、在梯形ABCD中,AD //BC ,AD=1 ABa ,DCb ,那么BC 等于BC ,设2〔结果用a 、b 的线性组合表示〕;16、如果正n 边形的内角是它的中心角的2倍,那么边数 n 的值是;17、在等腰ABC 中,当顶角A 的大小确定时,它的对边〔即底边BC 〕与邻边〔即腰AB 或AC 〕的对边〔底边〕T 〔A 〕,即TAABC.例:T 〔60 的比值也确定了,我们把这个比值记作的邻边〔腰〕〕AAB〕=;=1,那么T 〔12018、如图,矩形ABCD ,点E 是边AD 上一点,过点E 作EF BC ,垂足为点F ,将BEF 绕着点E 逆时针旋转,使点B 落在边BC上的点N 处,点 F 落在边DC 上的点M 处,如果点M 恰好是边DC 的中点,那么AD的值是。
【解析版】上海市奉贤区2013届高三二模数学理试题

2013年上海市奉贤区高考数学二模试卷(理科)参考答案与试题解析一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1.(4分)(2013•奉贤区二模)函数f(x)=2sin2x的最小正周期是π.=2.(4分)(2013•奉贤区二模)在的二项展开式中,常数项是70.解:在=703.(4分)(2013•奉贤区二模)已知正数x,y满足x+y=xy,则x+y的最小值是4.4.(4分)(2013•奉贤区二模)执行如图所示的程序框图,输出的S值为30.5.(4分)(2013•奉贤区二模)已知直线y=t与函数f(x)=3x及函数g(x)=4•3x的图象分别相交于A、B两点,则A、B两点之间的距离为log34.,=log6.(4分)(2013•奉贤区二模)用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在的平面所成角为45°,容器的高为10cm,制作该容器需要100cm2的铁皮.,rl=故答案为:7.(4分)(2013•奉贤区二模)若实数t满足f(t)=﹣t,则称t是函数f(x)的一个次不动点.设函数f(x)=lnx与反函数的所有次不动点之和为m,则m=0.8.(4分)(2013•奉贤区二模)关于x的方程x2+mx+2=0(m∈R)的一个根是1+ni(n∈R+),在复平面上的一点Z对应的复数z满足|z|=1,则|z﹣m﹣ni|的取值范围是[,].=,故﹣+1[[,9.(4分)(2013•奉贤区二模)在极坐标系中,直线的位置关系是相离.解:直线﹣,即=10.(4分)(2013•奉贤区二模)已知函数f(x)=lg(a x﹣b x)(a>1>b>0),且a2=b2+1,则不等式f(x)>0的解集是(2,+∞).11.(4分)(2013•奉贤区二模)设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1),,则函数f(x)在(1,2)上的解析式是y=.=12.(4分)(2013•奉贤区二模)设正项数列{a n}的前n项和是S n,若{a n}和{}都是等差数列,且公差相等,则a1+d=.}与,},两边平方得:②得:.时,代入③故答案为13.(4分)(2013•奉贤区二模)椭圆上的任意一点M(除短轴端点除外)与短轴两个端点B1,B2的连线交x轴于点N和K,则|ON|+|OK|的最小值是2a.==|ON|=|=|ON|=|=2a14.(4分)(2013•奉贤区二模)如图放置的等腰直角三角形ABC薄片(∠ACB=90°,AC=2)沿x轴滚动,设顶点A(x,y)的轨迹方程是y=f(x),当x∈[0,]时y=f(x)=.,轨迹方程为(点的最大横坐标为)为圆心,以(..二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.[,[,]16.(5分)(2013•奉贤区二模)设事件A,B,已知P(A)=,P(B)=,P(A∪B)=,=,=17.(5分)(2013•淄博一模)数列{a n}前n项和为S n,已知,且对任意正整数m,n,B,同理令所以此数列是首项为公比,以==∴18.(5分)(2013•奉贤区二模)直线x=2与双曲线的渐近线交于A,B两点,设P为双曲线C上的任意一点,若(a,b∈R,O为坐标原点),则下列的坐标,根据,确定坐标之间的关系,可得,利用基,则∵∴∴∴三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.(12分)(2013•奉贤区二模)长方体ABCD﹣A1B1C1D1中,底面ABCD是正方形,AA1=2,AB=1,E是DD1上的一点.(1)求异面直线AC与B1D所成的角;(2)若B1D⊥平面ACE,求三棱锥A﹣CDE的体积.∴,∴所成的角为,则∴,.20.(14分)(2013•奉贤区二模)位于A处的雷达观测站,发现其北偏东45°,与A相距20海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(0°<θ<45°)的C处,.在离观测站A的正南方某处E,cos∠EAC=﹣(1)求cosθ;(2)求该船的行驶速度v(海里/小时).)∵,∴∴,∴21.(14分)(2013•奉贤区二模)三阶行列式,元素b(b∈R)的代数余子式为H(x),P={x|H(x)≤0},(1)求集合P;(2)函数的定义域为Q,若P∩Q≠∅,求实数a的取值范围.,元素)∴,则说明在值,使成立,,则只需时,,22.(16分)(2013•奉贤区二模)已知数列{a n}中,a2=1,前n项和为S n,且.(1)求a1,a3;(2)求证:数列{a n}为等差数列,并写出其通项公式;(3)设,试问是否存在正整数p,q(其中1<p<q),使b1,b p,b q成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.)在)由,即,得②=,则,即①②.时,{<23.(18分)(2013•奉贤区二模)动圆C过定点F,且与直线相切,其中p>0.设圆心C的轨迹Γ的程为F(x,y)=0(1)求F(x,y)=0;(2)曲线Γ上的一定点P(x0,y0)(y0≠0),方向向量的直线l(不过P 点)与曲线Γ交与A、B两点,设直线PA、PB斜率分别为k PA,k PB,计算k PA+k PB;(3)曲线Γ上的两个定点P0(x0,y0)、,分别过点P0,Q0作倾斜角互补的两条直线P0M,Q0N分别与曲线Γ交于M,N两点,求证直线MN的斜率为定值.的方程为作直线与定直线为焦点,为准线,方程为得=,,∴,得∴,)计算得.是定值,命题得证。
上海市奉贤区2013届九年级4月调研测试(二模)数学试题

2013上海市奉贤区中考数学二模试卷一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸的相应题号的选项上用2B铅笔填涂]1.(4分)(2013•奉贤区二模)与无理数最接近的整数是()A.1B.2C.3D.4考点:估算无理数的大小.分析:由于1<3<4,且3更接近4,则1<<2,于是可判断与最接近的整数为2.解答:解:∵1<3<4,∴1<<2,∴与无理数最接近的整数为2.故选B.点评:本题考查了估算无理数的大小:利用完全平方数和算术平方根对无理数的大小进行估算.2.(4分)(2013•奉贤区二模)下列二次根式中最简二次根式是()A.B.C.D.考点:最简二次根式.分析:利用最简二次根式的定义判断即可得到正确的选项.解答:解:A、为最简二次根式,故本选项正确;B、可化为,不是最简二次根式,故本选项错误;C、可化为|a|,不是最简二次根式,故本选项错误;D、可化为3,不是最简二次根式,故本选项错误;故选A.点评:此题考查了最简二次根式,以及二次根式的化简,熟练掌握最简二次根式的判断方法是解答本题的关键.3.(4分)(2011•江津区)直线y=x﹣1的图象经过的象限是()A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限考点:一次函数的性质.专题:计算题.分析:由y=x﹣1可知直线与y轴交于(0,﹣1)点,且y随x的增大而增大,可判断直线所经过的象限.解答:解:直线y=x﹣1与y轴交于(0,﹣1)点,且k=1>0,y随x的增大而增大,∴直线y=x﹣1的图象经过第一、三、四象限.故选D.点评:本题考查了一次函数的性质.关键是根据图象与y轴的交点位置,函数的增减性判断图象经过的象限.4.(4分)(2012•杭州)一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件B.摸到白球是不可能事件C.摸到红球比摸到白球的可能性相等D.摸到红球比摸到白球的可能性大考点:可能性的大小;随机事件.分析:利用随机事件的概念,以及个数最多的就得到可能性最大分别分析即可.解答:解:A.摸到红球是随机事件,故此选项错误;B.摸到白球是随机事件,故此选项错误;C.摸到红球比摸到白球的可能性相等,根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项错误;D.根据不透明的盒子中装有2个红球和1个白球,得出摸到红球比摸到白球的可能性大,故此选项正确;故选:D.点评:此题主要考查了随机事件以及可能性大小,利用可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等得出是解题关键.5.(4分)(2013•奉贤区二模)对角线相等的四边形是()A.矩形B.等腰梯形C.正方形D.不能确定考点:多边形.分析:根据多边形中特殊多边形矩形,等腰梯形,正方形的对角线都相等,即可得出答案无法确定.解答:解:根据特殊四边形的性质可知:矩形,等腰梯形,正方形的对角线都相等,所以无法确定,故选D.点评:此题主要考查了特殊四边形的性质,题目把几种四边形综合起来考查,有效的考查了同学们对多边形性质的掌握情况.6.(4分)(2009•滨州)已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是()A.0<d<1 B.d>5 C.0<d<1或d>5 D.0≤d<1或d>5考点:圆与圆的位置关系.专题:压轴题.分析:若两圆没有公共点,则可能外离或内含,据此考虑圆心距的取值范围.解答:解:若两圆没有公共点,则可能外离或内含,外离时的数量关系应满足d>5;内含时的数量关系应满足0≤d<1.故选D.点评:考查了两圆的位置关系和数量关系之间的等价关系.二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)(2013•奉贤区二模)计算x6÷x2=x4.考点:同底数幂的除法.分析:根据同底数幂相除,底数不变指数相减解答.解答:解:x6÷x2=x6﹣2=x4.点评:本题考查了同底数幂的除法运算,熟练掌握运算性质是解题的关键.8.(4分)(2013•奉贤区二模)分解因式:x2﹣8x+16=(x﹣4)2.考点:因式分解-运用公式法.分析:直接利用完全平方公式分解因式即可.解答:解:x2﹣8x+16,=x2﹣2×4×x+42,=(x﹣4)2.故答案为:(x﹣4)2.点评:本题考查了运用公式法分解因式,熟练掌握完全平方公式的结构特点是解本题的关键.9.(4分)(2013•奉贤区二模)函数的定义域是x≥﹣3.考点:函数自变量的取值范围.专题:函数思想.分析:根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.解答:解:根据题意得:x+3≥0,解得:x≥﹣3.故答案为:x≥﹣3.点评:考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.10.(4分)(2013•南平)分式方程的解是x=9.考点:解分式方程.专题:计算题;压轴题.分析:观察可得最简公分母是x(x﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.解答:解:方程的两边同乘x(x﹣3),得3x﹣9=2x,解得x=9.检验:把x=9代入x(x﹣3)=54≠0.∴原方程的解为:x=9.点评:本题考查了解分式方程,注:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.11.(4分)(2009•贺州)已知关于x的一元二次方程x2﹣x﹣m=0有两个不相等的实数根,则实数m的取值范围是m>.考点:根的判别式.分析:若一元二次方程有两不等根,则根的判别式△=b2﹣4ac>0,建立关于m的不等式,求出m的取值范围.解答:解:∵方程有两个不相等的实数根,a=1,b=﹣1,c=﹣m∴△=b2﹣4ac=(﹣1)2﹣4×1×(﹣m)>0,解得m>﹣,点评:总结:一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.12.(4分)(2013•奉贤区二模)如果点A、B在同一个反比例函数的图象上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是2.考点:反比例函数图象上点的坐标特征.专题:推理填空题.分析:根据同一反比例函数图象上的点的横纵坐标的积相等来解答.解答:解:点B的纵坐标为m,则3m=2×3,解得m=2.故答案为2.点评:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.13.(4分)(2013•奉贤区二模)正多边形的中心角为72度,那么这个正多边形的内角和等于540度.考点:多边形内角与外角.分析:先根据周角等于360°求出边数,再根据多边形的内角和公式(n﹣2)•180°列式计算即可得解.解答:解:∵正多边形的中心角为72度,∴边数为:360°÷72°=5,∴这个正多边形的内角和=(5﹣2)•180°=540°.故答案为:540.点评:本题考查了多边形的内角和公式,熟记正多边形中心角的定义求出边数的是解题的关键.14.(4分)(2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是38度.考点:对顶角、邻补角;余角和补角.分析:首先根据邻补角的定义可得∠COA的度数,再根据垂直可得∠AOE=90°,再根据互余两角的关系可计算出答案.解答:解:∵∠AOD=128°,∴∠COA=180°﹣128°=52°,∵OE⊥AB,∴∠AOE=90°,∴∠COE=90°﹣52°=38°,故答案为:38.点评:此题主要考查了邻补角和垂直定义,关键是掌握邻补角的定义.15.(4分)(2013•奉贤区二模)如图,已知∠E=∠C,如果再增加一个条件就可以得到,那么这个条件可以是∠B=∠D (或∠BAD=∠CAE等)(只要写出一个即可).考点:相似三角形的判定与性质.专题:开放型.分析:根据两组角对应相等的两个三角形相似,可找出除∠E=∠C之外的任意一组对应角即可.解答:解:∠B=∠D或∠BAC=∠DAE;∵∠E=∠C,∠B=∠D,∴△ABC∽△ADE,∴=;∵∠E=∠C,∠BAC=∠DAE,∴△ABC∽△ADE,∴=;故答案是:∠B=∠D或∠BAC=∠DAE(答案不唯一).点评:本题考查了相似三角形的判定与性质.解题的关键是找出另一组相等的对应角.16.(4分)(2013•奉贤区二模)梯形ABCD中,AB∥DC,E、F分别是AD、BC中点,DC=1,AB=3,设,如果用表示向量,那么=.考点:*平面向量.分析:先表示出,然后判断出EF是梯形ABCD的中位线,继而根据中位线的性质可得出答案.解答:解:如图所示:∵AB∥DC,EDC=1,AB=3,∴==,∵E、F分别是AD、BC中点,∴EF是梯形ABCD的中位线,∴EF=(CD+AB),∴=(+)=.故答案为:.点评:本题考查了平面向量及梯形的知识,注意掌握梯形的中位线的性质,属于基础题.17.(4分)(2013•奉贤区二模)我们把梯形下底与上底的差叫做梯形的底差,梯形的高与中位线的比值叫做梯形的纵横比,如果某一等腰梯形腰长为5,底差等于6,面积为24,则该等腰梯形的纵横比等于.考点:等腰梯形的性质;梯形中位线定理.分析:利用勾股定理求出高,根据面积求出中位线的长度,然后按照题目所给信息即可求出纵横比.解答:解:根据题意做出图形,过A作BC边的高AE,由题意得:BC﹣AD=6,则BE=3,∵AB=5,∴AE==4,又∵面积为24,∴(AD+BC)•AE=24,代入AE可得:=6,故等腰梯形的中位线长度为6,则该等腰梯形的纵横比==.故答案为:.点评:本题考查了等腰梯形的性质,难度适中,认真读题求出高及中位线的长度是关键.18.(4分)(2013•奉贤区二模)如图,在△ABC中,∠C=90°,AB=10,tanB=,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是.考点:旋转的性质.分析:连接PM,根据∠B的正切值设AC=3k,BC=4k,利用勾股定理列式求出k值,得到AC、BC的长,根据直角三角形斜边上的中线等于斜边的一半可得AM=DM=EM,再根据等边对等角的性质可得∠EAM=∠E,然后求出∠EAM=∠B,根据等腰三角形三线合一的性质可得PM⊥AB,然后求出△ABC和△PMB相似,根据相似三角形对应边成比例列式求出PB的长,再根据CP=BC﹣PB代入数据进行计算即可得解.解答:解:连接PM,∵tanB=,∴设AC=3k,BC=4k,则(3k)2+(4k)2=102,解得k=2,∴AC=3×2=6,BC=4×2=8,∵点M是AB边的中点,△DEA是△ABC绕点M旋转得到,∴AM=MB=DM=EM=5,∴∠EAM=∠E,又∵∠B=∠E,∴∠EAM=∠B,∴△APB是等腰三角形,∵点M是AB的中点,∴PM⊥AB,∴△ABC∽△PMB,∴=,即=,解得PB=,∴CP=BC﹣PB=8﹣=.故答案为:.点评:本题考查了旋转的性质,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,也是本题的难点.三、解答题:(本大题共7题,满分78分)19.(10分)(2013•奉贤区二模)计算:.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:本题涉及零指数幂、负整数指数幂、二次根式化简、特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=2﹣+1+3+3×=6.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值、特殊角的三角函数值等考点的运算.20.(10分)(2013•奉贤区二模)解不等式组,并将它的解集在数轴上表示出来.考点:解一元一次不等式组;在数轴上表示不等式的解集.分析:先分别求出各不等式的解集,再求其公共解集即可.解答:解:,由①得:x>2.5由②得:x≤4,∴不等式组的解集为:2.5<x≤4,点评:此题主要考查了一元一次不等式组的解法,求不等式组的解集应遵循“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.21.(10分)(2013•奉贤区二模)已知△ABC中,AB=AC,BD是AC边上的中线,若AB=13,BC=10,试求tan∠DBC的值.考点:三角形中位线定理;等腰三角形的性质;勾股定理;锐角三角函数的定义.分析:(1)作等腰三角形底边上的高AH并根据勾股定理求出,与BD交点为E,则E是三角形的重心,再根据三角形重心的性质求出EH,∠DBC的正切值即可求出.(2)作出底边上的高,在过D作DF⊥BC,先根据勾股定理求出AH的长,再根据三角形中位线定理求出DF的长,BF的长就等于BC的,∠DBC的正切值即可求出.解答:解:方法一:过点A作AH⊥BC,垂足为点H,交BD于点E(1分)∵AB=AC=13,BC=10∴BH=5(1分)在Rt△ABH中,AH=12(2分)∵BD是AC边上的中线所以点E是△ABC的重心∴EH==4(2分)∴在Rt△EBH中,.(2分)方法二:过点A、D分别作AH⊥BC、DF⊥BC,垂足分别为点H、F(1分)∵BC=10,AH⊥BC,AB=AC,∴BH=5(1分)∵AB=13,∴AH==12,在Rt△ABH中,AH=12(2分)∵AH∥DF∴DF=BF==(2分)∴在Rt△DBF中,.(2分)点评:本题利用等腰三角形三线合一的性质和勾股定理,第一种方法还运用三角形的重心把中线分成2:1的两段,第二种方法还运用三角形中位线定理都需要熟练掌握.22.(10分)(2013•奉贤区二模)我区开展了“关爱老人从我做起”的主题活动.在活动中随机调查了本区部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表:老人与子女同住情况 同住 不同住 (子女在本区) 不同住 (子女在区外)其他 百分比a 50%b 4% 老人与子女同住人数条形图:据统计图表中提供的信息,回答下列问题:(1)本次共抽样调查了 50 老人,老人与子女同住情况百分比统计表中的a= 32% ;(2)将条形统计图补充完整;(画在答题纸相对应的图上)(3)根据本次抽样调查,试估计我区约15万老人中与子女“不同住”的老人总数是 96000 人.考点: 条形统计图;用样本估计总体;统计表.专题: 计算题.分析: (1)由条形统计图中不同住子女在本区的人数除以所占的百分比,求出调查的总人数,进而求出不同住(子女在区外)所占的百分比,即可求出a 的值;(2)求出其他的人数,即可求出同住的人数,补充条形统计图即可;(3)由不同住的人数为25+7=32人,利用比例即可求出我区约15万老人中与子女“不同住”的老人总数.解答: 解:(1)25÷50%=50,不同住(子女在区外)的所占的比例是×100%=14%,则a=1﹣50%﹣14%﹣4%=32%;(2)如图所示;(3)根据题意得:150000×=96000. 故答案为:(1)50;32%;(3)96000点评:此题考查了条形统计图,弄清题意是解本题的关键.23.(12分)(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.(1)求证:△AEB≌△ADC;(2)如果BC=CD,判断四边形BCGE的形状,并说明理由.考点:菱形的判定;全等三角形的判定与性质;等边三角形的性质.分析:(1)根据等边三角形性质得出AB=AC,AE=AD,∠CAB=∠EAD=60°,求出∠BAE=∠CAD,根据SAS推出即可;(2)根据全等得出BE=CD,∠ABE=∠ACD=120°,求出∠CBE=60°,推出BE∥AG,得出平行四边形,根据BE=CD=BC即可得出菱形.解答:证明:(1)∵等边△ABC和等边△ADE,∴AB=AC,AE=AD,∠CAB=∠EAD=60°,∵∠BAE+∠EAC=60°,∠DAC+∠EAC=60°,∴∠BAE=∠CAD,在△AEB和△ADC中∴△AEB≌△ADC(SAS);(2)解:四边形BCGE的形状是菱形,理由是:∵△AEB≌△ADC∴∠ABE=∠ACD,BE=CD,∵∠ABC=∠ACB=60°,∴∠ABE=∠ACD=∠BCG=120°,∴∠DBE=60°,∴∠BCG+∠DBE=180°,∴BE∥CG,∵BC∥EG,∴四边形BCGE是平行四边形,∵BC=CD,∴BE=BC,∴四边形平行四边形BCGE是菱形.点评:本题考查了全等三角形的性质和判定,等边三角形的性质,菱形的判定,平行四边形的判定等知识点的应用,主要考查学生的推理能力.24.(12分)(2013•奉贤区二模)如图,已知二次函数y=﹣x2+2mx的图象经过点B(1,2),与x轴的另一个交点为A,点B关于抛物线对称轴的对称点为C,过点B作直线BM⊥x轴垂足为点M.(1)求二次函数的解析式;(2)在直线BM上有点P(1,),联结CP和CA,判断直线CP与直线CA的位置关系,并说明理由;(3)在(2)的条件下,在坐标轴上是否存在点E,使得以A、C、P、E为顶点的四边形为直角梯形?若存在,求出所有满足条件的点E的坐标;若不存在,请说明理由.考点:二次函数综合题.分析:(1)将点B(1,2),代入二次函数y=﹣x2+2mx,得到关于m的方程,求得m的值,从而得到二次函数的解析式;(2)根据题意可知点A(3,0),C(2,2),P(1,),根据两点间的距离公式可得PA,PC,AC的长,再根据勾股定理的逆定理即可判断直线CP与直线CA的位置关系;(3)分①当点E在x轴上,PE∥CA,②当点E在y轴上,PC∥AE,两种情况讨论即可得到使得以A、C、P、E为顶点的四边形为直角梯形的点E的坐标.解答:解:(1)∵点B(1,2)在二次函数y=﹣x2+2mx的图象上,∴﹣12+2m=2解得m=.故二次函数的解析式为y=﹣x2+3x;(2)直线CP与直线CA的位置关系是垂直.∵二次函数的解析式为y=﹣x2+3x,∴点A(3,0),C(2,2),∵P(1,),∴PA2=,PC2=,AC2=5,∴PA2=PC2+AC2,∴∠PCA=90°,即CP⊥CA;(3)假设在坐标轴上存在点E,使得以A、C、P、E为顶点的四边形为直角梯形,∵∠PCA=90°,则①当点E在x轴上,PE∥CA,∴△CBP∽△PME,∴=,∴ME=,∴E1(,0);②当点E在y轴上,PC∥AE,∴△CBP∽△AOE,∴=,∴OE=,∴E2(0,﹣).即点Q的坐标E1(,0)、E2(0,﹣)时,以A、C、P、E为顶点的四边形为直角梯形.点评:考查了二次函数综合题,涉及到:直角梯形的性质、二次函数解析式的确定、两点间的距离公式、勾股定理的逆定理、相似三角形的判定和性质等重要知识点.(3)题中,注意要分类讨论,以免漏解.25.(14分)(2013•奉贤区二模)如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,联结OD,过点B作OD 的平行线交⊙O于点E、交射线CD于点F.(1)若,求∠F的度数;(2)设CO=x,EF=y写出y与x之间的函数解析式,并写出定义域;(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.考点:圆的综合题.分析:(1)首先连接OE,由,OD∥BF,易得∠OBE=∠OEB=∠BOE=60°,又由CF⊥AB,即可求得∠F的度数;(2)作OH⊥BE,垂足为H,易得△HBO≌△COD,即可得CO=BH=x,求得BE=2x,易得△COD∽△CBF,然后由相似三角形的对应边成比例,可得,则可求得y与x之间的函数解析式;(3)由∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,可得∠COD=∠DOE,即可得C关于直线OD的对称点为P在线段OE上,然后分别从PB=PE,EB=EP,BE=BP 去分析求解即可求得答案.解答:解:(1)连接OE,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵=,∴∠BOE=∠EOD﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵OD∥BF,∴∠DOE=∠BEO,∵OB=OE,∴∠OBE=∠OEB,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∴∠OBE=∠OEB=∠BOE=60°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵CF⊥AB,∴∠FCB=90°,∴∠F=30°;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)(2)作OH⊥BE,垂足为H,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵在△HBO和△COD中,,∴△HBO≌△COD(AAS),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∴CO=BH=x,∴BE=2x,∵OD∥BF,∴△COD∽△CBF,∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∴,∴y=(0<x<4);﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,∴∠COD=∠DOE,∴C关于直线OD的对称点为P在线段OE上,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)若△PBE为等腰三角形,设CO=x,∴OP=OC=x,则PE=OE﹣OP=4﹣x,由(2)得:BE=2x,①当PB=PE,不合题意舍去;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)②当EB=EP,2x=4﹣x,解得:x=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)③当BE=BP,作BM⊥OE,垂足为M,∴EM=PE=,∴∠OEB=∠COD,∠BME=∠DCO=90°,∴△BEM∽△DOC,∴,∴,整理得:x2+x﹣4=0,解得:x=(负数舍去).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)综上所述:当OC的长为或时,△PBE为等腰三角形.点评:此题考查了圆的性质、等边三角形的判定与性质、等腰三角形的性质、全等三角形的判定与性质以及相似三角形的判定与性质等性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想、分类讨论思想与方程思想的应用.。
2013年上海中考数学二模嘉定卷及答案

2012学年嘉定九年级第二次质量调研数学试卷(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】一、选择题:(本大题共6题,每题4分,满分24分) 1.下列说法中,正确的是(▲)(A )23是分数; (B )0是正整数; (C )722是有理数;(D )16是无理数.2.抛物线2(1)4y x =-+与y 轴的交点坐标是(▲)(A )(0,4); (B )(1,4); (C )(0,5); (D )(4,0). 3.下列说法正确的是(▲)(A )一组数据的平均数和中位数一定相等; (B )一组数据的平均数和众数一定相等; (C )一组数据的方差一定是正数;(D )一组数据的众数一定等于该组数据中的某个数据.4.今年春节期间,小明把2000元压岁钱存入中国邮政储蓄银行,存期三年,年利率是%.254,小明在存款到期后可以拿到的本利和为(▲)(A )20003%)25.41(+元; (B )20002+0003254⨯⨯%.元; (C )20003254⨯⨯%.元; (D )20003%)25.41(⨯+元. 5.如图1,已知向量a、b、c,那么下列结论正确的是(▲)(A )b c a =+; (B )b c a =-; (C )c b a -=+; (D )c b a=+.6.已知⊙1O 的半径长为cm 2,⊙2O 的半径长为cm 4.将⊙1O 、⊙2O 放置在直线l 上(如图2),如果⊙1O 在直线l 上任意滚动,那么圆心距21O O 的长不可能是(▲) (A )cm 1; (B )cm 2; (C )cm 6; (D )cm 8.l图21O2Oabc图1二、填空题(本大题共12题,每题4分,满分48分) 7.化简:21-= ▲ .8. 计算:=23)(a ▲ .9. 计算:=÷3166 ▲ (结果表示为幂的形式). 10.不等式组⎩⎨⎧>+≤-04201x ,x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球和8个红球,它们除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到红球的概率是 ▲ .(将计算结果化成最简分数) 12.如果关于x 的方程1)1(2+=-a x a 无解,那么实数a = ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 100=.如果近似眼镜镜片的焦距250.x =米,那么近视眼镜的度数y 为 ▲ . 14.方程x x -=+6的根是 ▲ .15.手机已经普及,家庭座机还有多少?为此,某校中学生从某街道5000户家庭中随机抽取50户家庭进行统计,列表如下: 拥有座机数(部) 0 1 2 3 4 相应户数10141871该街道拥有多部电话(指1部以上,不含1部)的家庭大约有 ▲ 户.16.如果梯形两底的长分别为3和7,那么联结该梯形两条对角线的中点所得的线段长为 ▲ .17.在平面直角坐标系中,对于平面内任意一点(x ,y ),若规定以下两种变换:①),(y x f =(2+x ,y ).如)1,1(f =)1,3(;②),(y x g =),(y x --,如)2,2(g =)2,2(--. 按照以上变换有:))1,1((f g =)1,3(g =)1,3(--,那么))4,3((-g f 等于 ▲ .18.如图3,在梯形ABCD 中,已知AB ∥CD ,︒=∠90A ,cm AB 5=,cm BC 13=.以点B 为旋转中心,将BC 逆时针旋转︒90至BE ,BE 交CD 于F 点.如果点E 恰好落在射线AD 上,那么DF 的长为 ▲ cm .ACB D E图3FABCD E FMN图6三、简答题(本大题共7题,满分78分) 19.(本题满分10分)计算:︒+︒︒-︒+-60sin 45tan 30sin 30cos 42730)(.20.(本题满分10分)解方程:12221=++-x x .21.(本题满分10分,第(1)小题4分,第(2)小题6分)如图4,在ABC ΔRt 中,90A C B ∠=︒,点D 在AC 边上,且CA CD BC ⋅=2.(1)求证:CBD A ∠=∠;(2)当α=∠A ,2=BC 时,求AD 的长(用含α的锐角三角比表示).22.(本题满分10分,每个小题各5分)某游泳池内现存水)(m 18903,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水——清洗——灌水”的过程,其中游泳池 内剩余的水量y (3m )与换水时间....t (h )之间的 函数关系如图5所示.根据图像解答下列问题:(1)根据图中提供的信息,求排水的速度及清洗该游泳池所用的时间;(2)求灌水过程中的y (3m )与换水时间....t (h )之间的函数关系式,写出函数的定义域.23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图6,点E 是正方形ABCD 边BC 上的一点(不与B 、C 重合),点F 在CD 边的延长线上,且满足BE DF =.联结EF ,点M 、N 分别是EF 与AC 、AD 的交点. (1)求AFE ∠的度数; (2)求证:FCAC CMCE =.ACBD图4(h)tO1890521 图5)(m 3y24.(本题满分12分,每小题满分4分) 已知平面直角坐标系xOy (如图7),抛物线c bx xy ++=221经过点)0,3(-A 、)23,0(-C .(1)求该抛物线顶点P 的坐标; (2)求CAP ∠tan 的值;(3)设Q 是(1)中所求出的抛物线的一个动点,点Q 的横坐标为t ,当点Q 在第四象限时,用含t 的代数式表示△QAC 的面积.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知AP 是半圆O 的直径,点C 是半圆O 上的一个动点(不与点A 、P 重合),联结AC ,以直线AC 为对称轴翻折AO ,将点O 的对称点记为1O ,射线1AO 交半圆O 于点B ,联结OC .(1)如图8,求证:AB ∥OC ;(2)如图9,当点B 与点1O 重合时,求证:CB AB =;(3)过点C 作射线1AO 的垂线,垂足为E ,联结OE 交AC 于F .当5=AO ,11=B O 时,求AFCF 的值.AC(O 1)BO 图9P AO 备用图PA B CO 1O 图8P 图7 O xy1- 1-11参考答案一、选择题:(本大题共6题,每题4分,满分24分) 1.C ;2.C ;3.D ;4.B ;5.C ;6.A.二、填空题(本大题共12题,每题4分,满分48分)7.12-;8.6a ;9.326;10.12≤<-x ;11.54;12.1=a ;13.400=y ;14.2-=x ;15.2600;16.2;17.(5,4-);18.1235(或写成12112).三、简答题(本大题共7题,满分78分)19.解:原式=23121234331+-⨯+- ……………………6分=32132331+-+- …………1分=13231-=+--. …………2+1分20.解:方程两边同时乘以)x )x 2(2+-(,得 4)2(222-=-++x x x …1+1+1+1分整理,得 0232=--x x . ……2分解这个整式方程,得 21731+=x ,21732-=x . ……2+1分(若记错了求根公式,但出现了17,即根的判别式计算正确,可得1分)经检验知,21731+=x ,21732-=x 都是原方程的根. ……1分所以,原方程的根是 21731+=x ,21732-=x .21.解:(1)∵CA CD BC⋅=2,∴BCCA CDBC =. ……1分∵90A C B ∠=︒,点D 在AC 边上,∴BCD ACB ∠=∠. ……1分 ∴△ACB ∽△BCD . ∴CBD A ∠=∠. ……1+1分 说明:若没有写出“∵90A C B ∠=︒,点D 在AC 边上,∴BCD ACB ∠=∠”,但只要写出了BCD ACB ∠=∠,可得1分.(2)∵CBD A ∠=∠,α=∠A ,∴α=∠CBD .……………………………1分 在Rt △ACB 中,90A C B ∠=︒,2=BC ,α=∠A . ∵BCAC A =∠cot ,∴ααcot 2cot =⋅=BC AC . …………………………………………2分 在Rt △BCD 中,︒=∠90BCD ,α=∠CBD ,2=BC , ∵BCCD CBD =∠tan ,∴ααtan 2tan =⋅=BC CD . …………………………………………2分 ∴ ααtan 2cot 2-=-=CD AC AD . ……………………………1分 本题解题方法较多,请参照评分.如写成 ααtan 2tan 2-=AD ;4cos4tan 22--=ααAD ;4cos44sin422---=ααAD ;ααtan 24sin42--=AD 等等,均正确.22.解(1)由图像可知,该游泳池5个小时排水)(m 18903, ……1分所以该游泳池排水的速度是37851890=÷(/h m 3). ……1分由题意得该游泳池灌水的速度是18921378=⨯(/h m 3),……1分由此得灌水)(m 18903需要的时间是101891890=÷(h ) ……1分 所以清洗该游泳池所用的时间是610521=--(h ) ……1分(2)设灌水过程中的y (3m )与换水时间t (h )之间的函数关系式是b kt y +=(0≠k ).将(11,0),(21,1890)代入b kt y ++=,得⎩⎨⎧=+=+.b k ,b k 189021011 解得⎩⎨⎧-==.b ,k 2079189 ……1+2分所以灌水过程中的y (3m )与时间t (h )之间的函数关系式是2079189-=t y (2111≤<t ). ……1+1分备注:学生若将定义域写成2111≤≤t ,亦视为正确,此处不是问题的本质. 23.解:(1)在正方形ABCD 中, ︒=∠=∠=∠90BAD ADC B ,AD AB =.……1分 ∵BE DF =,︒=∠=∠90ADF B ,AD AB =,∴△ABE ≌△ADF .……1分 ∴AF AE =,DAF BAE ∠=∠. ……………1+1分 ∴︒=∠=∠+∠=∠+∠=∠90BAD BAE EAD DAF EAD EAF . ……1分 ∵AF AE =,∴AEF AFE ∠=∠. ∴︒=︒⨯=∠=∠459021AEF AFE . ……………1分(2) 方法1:∵四边形ABCD 是正方形,∴︒=∠45ACD . ……………1分∵︒=∠45AEF ,∴ACF AEF ∠=∠. ……………1分 又∵FMC AME ∠=∠, ……………1分 ∴△ABE ∽△ADF , ……………2分 ∴FCAC CMCE =. ……………1分方法2:∵四边形ABCD 是正方形,∴︒=∠=∠45ACD ACB . …………1分 ∵△ABE ≌△ADF ,∴AFD AEB ∠=∠. ……………1分∵CAE CAE ACB AEB ∠+︒=∠+∠=∠45, C F M C F M A F E A F D ∠+︒=∠+∠=∠45,∴CFM CAE ∠=∠. ……………2分又∵ACD ACB ∠=∠,△ACE ∽△FCM . ……………1分∴FCAC CMCE =. ……………1分其他方法,请参照评分. 24.解:(1)将)0,3(-A 、)23,0(-C 代入c bx xy ++=221,得⎪⎪⎩⎪⎪⎨⎧-==+--.23,032)3(2c c b 解得⎪⎩⎪⎨⎧-==.c ,b 231 ………………2分 所以抛物线的表达式为23212-+=x xy . ………………1分其顶点P 的坐标为(1-,2-). ………………1分 (2)方法1:延长AP 交y 轴于G ,过 C 作AG CH ⊥,垂足是H . 设直线AP 的表达式为b kx y +=, 将),(A 03-、),(P 21--代入,得⎩⎨⎧-=+-=+-203b k b k ,解得⎩⎨⎧-=-=31b k . ∴3--=x y . 进而可得G (30-,). ………1分 ∴OA OG =,︒=∠=∠45OAG G . 在Rt △CHG 中,42345sin =︒⋅==CG CH HG . ………1分在Rt △AOG 中,2345cos =︒=OG AG,∴429=-=HG AG AH .∴31tan ==∠AHCH CAP .……1+1分方法2:设a CH =,易得a CG 2=,a OG 22=,a AG 4=,a AH 3=, 31tan ==∠AHCH CAP .方法3:联结OP ,利用两种不同的方式分别表示四边形APCO 的面积:49+=+=∆∆∆APC AOC APC APCOS S S S 四边形; 415433=+=+=∆∆POC APO APCOS S S 四边形;∴23=∆APC S ,然后求523=AC 、22=AP ,利用面积求AC 边上的高552=h ,求1010sin =∠CAP ,进而求31tan =∠CAP.(3)设)2321,(2-+t tt Q , …………1分由Q 在第四象限,得t t =,2321232122+--=-+t tt t.联结OQ ,易得 AOQ QOC AOC QAC S S S S ∆∆∆∆-+=. ∵4923321=-⨯-⨯=∆AOC S ,t t S QOC 432321=⨯-⨯=∆, ………1分492343232132122+--=-+⨯-⨯=∆t tt tS QOA …………1分∴t tt tt S QAC 4943)492343(434922+=+---+=∆. …………1分25.解:(1)∵点1O 与点O 关于直线AC 对称,∴AC O OAC 1∠=∠. ………1分 在⊙O 中,∵OC OA =,∴C OAC ∠=∠. …………1分 ∴C AC O ∠=∠1. ∴1AO ∥OC ,即AB ∥OC . …………1+1分 (2)方法1:联结OB . ………1分 ∵点1O 与点O 关于直线AC 对称,AC 1OO ⊥, ………1分 由点1O 与点B 重合,易得AC OB ⊥. ………1分 ∵点O 是圆心,AC OB ⊥,∴CB AB = ………2分方法2:∵点1O 与点O 关于直线AC 对称,∴1AO AO =,1CO CO = ………1+1分由点1O 与点B 重合,易得 AB AO =,CO CB = …………1分 ∵OC OA =,∴CB AB =. ∴ CB AB = ………1+1分 方法3:证平行四边形1AOCO是菱形.(3) 过点O 作AB OH ⊥,垂足为H .∵AB OH ⊥,AB CE ⊥,∴OH ∥CE ,又∵AB ∥OC ,∴5==OC HE .……1分当点1O 在线段AB 上(如图),6111=+=+=B O AO B O AO AB ,又∵ AB OH ⊥,∴321==AB AH .∴835=+=+=AH EH AE ……1分 ∵AB ∥OC , ∴85==AEOC AFCF ……1分当点1O 在线段AB 的延长线上,类似可求75==AEOC AFCF . …2分。
2023年上海市奉贤区中考数学二模试卷(含答案)

2023年上海市奉贤区中考数学二模试卷(完卷时间100分钟,满分150分) (202305)考生注意: 1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分)1.下列实数中,有理数是( )(A )8; (B )9; (C )10; (D )12. 2.下列运算正确的是( )(A )325a a a +=; (B) 32a a a −=; (C) 326a a a ⋅=; (D) 32a a a ÷=. 3.下列函数图像中,可能是反比例函数xy 6=的图像的是( ) (A ) (B ) (C ) (D )4.在一次学校的演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分这两组数据相比,一定不变的是( )(A )中位数; (B )众数; (C )平均数; (D )方差. 5.正方形具有而菱形不一定具有的性质是( )(A )对角线相等; (B )对角线互相垂直; (C )对角线平分一组对角; (D )对角线互相平分.6.如图1,矩形ABCD 中,AB =1,∠ABD=60°,点O 在对角线BD 上,圆O 经过点C .如果矩形ABCD 有2个顶点在圆O 内,那么圆O 的半径长r 的取值范围是( ) (A )0<r ≤1; (B )1<r ≤3; (C )1<r ≤2; (D )3<r ≤2.图1A BCD图5ACBD 二、填空题(本大题共12题,每题4分,满分48分)7.计算:()23ab = .8.化简分式bab b+的结果为 . 9.如果关于x 的方程022=+−m x x 有两个相等的实数根,那么m 的值是 . 10.如果一个二次函数的图像顶点是原点,且它经过平移后能与221yx x =−+−的图像重合,那么这个二次函数的解析式是 .11.如果正比例函数kx y =(k 是常数,k ≠0)的图像经过点(4,-1),那么y 的值随x的增大而 .(填“增大”或“减小”)12.布袋里有4个小球,分别标注了数字﹣1、0、2、3,这些小球除了标注数字不同外,其它都相同.从布袋里任意摸出一个球,这个球上标注数字恰好是正数的概率是 . 13.图2是某商场2022年四个季度的营业额绘制成的扇形统计图,其中二季度的营业额为100万元,那么该商场全年的营业额为 万元.14.如图3,在平行四边形ABCD 中,BD 为对角线,E 是边DC 的中点,联结BE .如果设a AD =,b BD =,那么BE = ▲ (含a 、b 的式子表示). 15.在△ABC 中,AB=AC ,如果BC =10,135cos =B ,那么△ABC 的重心到底边的距离为 .16.如果四边形有一组邻边相等,且一条对角线平分这组邻边的夹角,我们把这样的四边形称为“准菱形”.有一个四边形是“准菱形”,它相等的邻边长为2,这两条边的夹角是90°,那么这个“准菱形”的另外一组邻边的中点间的距离是 .17.如图4,某电信公司提供了A 、B 两种方案的移动通讯费用y (元)与通话时间x (元)之间的关系.如果通讯费用为60元,那么A 方案与B 方案的通话时间相差 分钟.18.如图5,在正方形ABCD 中,点E 、F 分别在边AD 、AB 上,EF ⊥CE .将△CDE 沿直线CE 翻折,如果点D 的对应点恰好落在线段CF 上,那么∠EFC 的正切值是 .E图3 ACBD图47050 30120 170 200 250x (分)(元)A 方案B 方案y 图2三、解答题(本大题共7题,满分78分)19.(本题满分10分)计算:2202321113231−⎛⎫−+−−−− ⎪−⎝⎭().20.(本题满分10分)解不等式组⎪⎪⎩⎪⎪⎨⎧−<−−≤−;,52157353131x x x x 将其解集在数轴上表示出来,并写出这个不等式组的整数解.21.(本题满分10分,每小题满分5分)如图6,在平面直角坐标系xOy 中,直线l 上有一点A (3,2),将点A 先向左平移3个单位,再向下平移4个单位得到点B ,点B 恰好在直线l 上. (1)写出点B 的坐标,并求出直线l 的表达式;(2)如果点C 在y 轴上,且∠ABC=∠ACB ,求点C 的坐标.-2 1 2 34-1 0 xOxy11 图6A (3,2)图7-1是某地下商业街的入口的玻璃顶,它是由立柱、斜杆、支撑杆组成的支架撑起的,图7-2是它的示意图.经过测量,支架的立柱AB 与地面垂直(∠BAC=90°),AB =2.7米,点A 、C 、M 在同一水平线上,斜杆BC 与水平线AC 的夹角∠ACB=33°,支撑杆DE ⊥BC ,垂足为E ,该支架的边BD 与BC 的夹角∠DBE=66°,又测得CE =2.2米.(1)求该支架的边BD 的长;(2)求支架的边BD 的顶端D 到地面AM 的距离.(结果精确到0.1米)(参考数据:sin33054.︒≈,sin66091.︒≈,cos33084.︒≈,cos66040.︒≈,tan33065.︒≈,tan66225.︒≈)23.(本题满分12分,每小题满分6分)已知:如图8,在菱形ABCD 中,AE ⊥BC ,AF ⊥CD ,垂足分别为E 、F ,射线EF 交AD 的延长线于点G . (1)求证:CE =CF ;(2)如果DG AG FG ⋅=2,求证:BEAFAE AG =.图7-2ABC DEM 图7-1立柱支撑杆斜杆图8FE CABO图9xy 如图9,在平面直角坐标系中,抛物线32++−=bx x y 与x 轴交于点A (1,0)和点B ,与y 轴交于点C .(1)求该抛物线的表达式和对称轴;(2)联结AC 、BC ,D 为x 轴上方抛物线上一点(与点C 不重合),如果△ABD 的面积与△ABC 的面积相等,求点D 的坐标; (3)设点P (m ,4)(m >0),点E 在抛物线的对称轴上(点E 在顶点上方),当∠APE =90°, 且45=AP EP 时,求点E 的坐标.25.(本题满分14分,第(1)小题满分4分,第(2)(3)小题满分5分)在梯形ABCD 中,AD //BC ,AD =4,∠ABC =90°,BD =BC ,过点C 作对角线BD 的垂线,垂足为E ,交射线BA 于点F .(1)如图10,当点F 在边AB 上时,求证:△ABD ≌△ECB ; (2)如图11,如果F 是AB 的中点,求FE :EC 的值; (3)联结DF ,如果△BFD 是等腰三角形,求BC 的长.xOy E图10 ABCDFE图11ABCDF参考答案一、选择题(本大题共6题,每题4分,满分24分)1. B2. D3. C4. A5. A6. B二、填空题(本大题共12题,每题4分,满分48分)7. 9. 1 10. y=-2x 11. 减小 12.13. 50014. 15. 4 16.17. 30 18. 2三、解答题(本大题共7题,满分78分)19. -720. 解不等式(1)得2x ≤.解不等式(2)得12x >−. 解集在数轴上正确表示.所以,不等式组的解集是:122x −<≤. 它的整数解是0,1,221. (1)由题意得点B 的坐标为(0,-2) 直线的表达式是(2)点C 的坐标为(0,6)22. (1)该支架的边BD 的长7米(2)支架的边BD 的顶端D 到地面AM 的距离为6.5米23. (1)∵四边形ABCD 是菱形,∴AB=AD ,∠B =∠ADF .∵AE ⊥BC ,AF ⊥CD ,垂足分别为E 、F ,∴90AEB AFD ∠=∠=︒. ∴ABE ADF ∆≅∆. ∴BE=DF .∵四边形ABCD 是菱形,∴BC=DC . ∴BC -BE=DC-DF ,即CE=CF .(2)∵DG AG FG ⋅=2,∴FG DGAG FG.∵∠G=∠G ,∴△GDF ∽△GFA .∴∠GFD =∠GAF .∵AD //BC ,∴DF DGCF CE.∵CE=CF ,∴DF =DG . ∴∠GFD =∠G . ∴∠G=∠GAF .∵ABE ADF ∆≅∆,∴∠BAE =∠GAF . ∴∠BAE=∠G .∵AD //BC ,∴∠AEB =∠GAE . ∴△AEG ∽△EBA .∴AG AE AEBE. ∵AE =AF ,∴BEAFAE AG =. 24. (1)抛物线的表达式是; 该抛物线的对称轴是直线x=-1(2)点D 的坐标(-2,3)(3)点E25. (1)∵CF ⊥BD ,∴∠CEB =90°.∵AD//BC ,∠ABC =90°,∴∠A =90°,∠ADB =∠CBE . ∴∠CEB =∠A .∵BD=BC ,∴△ABD ≌△ECB .(2(3)如果△BFD 是等腰三角形,BC=8。
2024年4月 上海市中考数学二模题型 分类汇编3--- 实际应用含综合与实践(22题)

4 从这两个统计图中能准确求出样本的平均数.
上述结论中错误的是
(填序号).
(3)估计本次六年级参赛学生中荣获优秀的共有 m 人.学校“环保社团”决定:这 m
名学生都光荣的成为学校的小小环保“宣传员”,从中选派 x 人帮助本年级参赛得分 60 分以
下的学生普及环保知识.经计算,x 与(m-x)的积恰好等于样本容量的 15 倍. 你认为 x
越适宜.我们可通过计算一组 GDP 所有实际值偏离图像上对应点纵坐标值的程度,即偏离 方差,来进行模型分析,一般偏离方差越小越适宜.)
例如,分析直线 AB 即 f (x) x 9 上的点:可知 f (1) 10 , f (2) 11 , f (3) 12 , f (4) 13 ,
求得偏离方差
有几种租车方案?
载客量(人/辆) 租金(元/辆)
45
1500
33
1200
第 22 题表
(3)在(2)的条件下,选择哪种租车方案最省钱?此时租车的总费用是多少元?
【2024.4 月 松江区二模】
22.(本题满分 10 分,第(1)小题 2 分,第(2)小题 4 分,第(3)小题 4 分) 一个凸四边形的四条边及两条对角线共 6 条线段中,如果只有两种大小不同的长度,那
和∠θ,通过计算就可以得到大厦的高度.
测量并通过计算得:CD=60 米,cotα=10.667,cotβ=10.161,cotγ=10.159,cotθ=10.254.
(1)教学楼(AB)的高度为
米;
(2)请你在两种方案中选.取.一.种.方.案.,计算出上海中心大厦(SH)的高度(精确到 1 米).
(第 22 题图 2)(第 22 题图 1)
(1) 估计六年级参赛学生中成绩为良好的学生有
上海奉贤区中考数学质量抽查试卷(二模)

2012学年奉贤区调研测试九年级数学试卷 2012. 03(完卷时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题,答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)14 )A .2;B .2±;C .2-;D .2.2.下列计算正确的是( )A .2a a a +=;B .()3326a a =;C .()2211a a -=-; D .32a a a ÷=.3.已知:在Rt △ABC 中,90C ∠=,A ∠、B ∠、C ∠所对的边分别是a 、b 、c .且3a =,4b =, 那么B ∠的正弦值等于( )A .35;B .45;C .43;D .34.4.小亮从家步行到公交车站台,等公交车去学校。
图中的折线表示小亮的行程()s km 与所花时间()min t 之间的函数关系,下列说法错误的是( )A .他离家8km 共用了30min ;B .他等公交车时间为6min ;C .他步行的速度是100/m min ;D .公交车的速度是350/m min ;5.解方程2212x x x x-+=-时,如果设2y x x =-,那么原方程可变形为关于y 的整式方程是( ) A .2210y y --=; B .2210y y +-=;C .2210y y ++=;D .2210y y -+=.6.已知长方体ABCD EFGH -如图所示,那么下列直线中与直线AB 不平行也不垂直的直线是( ) A .EA ; B .GH ; C .GC ; D .EF .二、填空题:(本大题共12题,每题4分,满分48分)7.函数21x y x +=-中,自变量x 的取值范围是 .8.2010年11月,我国进行了第六次全国人口普查,据统计全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学计数法可以表示为 .91=的解是 .10.分解因式:221x x --= .11.已知关于x 的方程240x x a -+=有两个相同的实数根,则a 的值是 .12.如果反比例函数3m y x-=的图像在0x <的范围内,y 随x 的增大而减小,那么m 取值范是 .13.为响应“红歌唱响中国”活动,某镇举行了一场“红歌”歌咏比赛,组委会规定:任何一名参赛选手的成绩x 满足:60100x ≤<n = .14.小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等。
奉贤区2013届初三(九年级)上学期数学期中试题及答案_题型归纳

奉贤区2013届初三(九年级)上学期数学期中试题及答案_题型归纳
数学网讯:期中考试要到了,初三的同学们,你的数学复习的如何?数学要想得高分,需要多练习,下面的奉贤区2013届初三(九年级)上学期数学期中试题及答案,供大家练习!
奉贤区2013届初三(九年级)上学期数学期中试题
(答题时间100分钟,满分150分)
奉贤区2013届初三(九年级)上学期数学期中试题集答案
以上“奉贤区2013届初三(九年级)上学期数学期中试题及答案”的全部内容是由数学网整理的,更多的数学期中试题请查看数学网。
2013年上海中考数学奉贤卷及答案

上海奉贤区2013年中考数学二模试卷(满分150分,考试时间100分钟)一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸的相应题号的选项上用2 B铅笔填涂]1.与无理数最接近的整数是()A.1;B.2 ;C.3;D.4;2.下列二次根式中最简二次根式是()3.函数y=x-1的图像经过的象限是()A.第一、二、三象限;B.第一、二、四象限;C.第一、三、四象限;D.第二、三、四象限;4.一个不透明的盒子中装有5个红球和3个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是()A.摸到红球是必然事件;B.摸到白球是不可能事件;C.摸到红球和摸到白球的可能性相等;D.摸到红球比摸到白球的可能性大;5.对角线相等的四边形是()A.菱形;B.矩形;C.等腰梯形;D.不能确定;6.已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是()A.0<d<1;B.d>5;C.0<d<1或d>5;D.或d>5;二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】围是;12.如果点A、B在同一个反比例函数的图像上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是;13.正多边形的中心角为72度,那么这个正多边形的内角和等于度;三、解答题:(本大题共7题,满分78分)19.(本题满分10分)上海奉贤区2013年中考数学二模试卷及答案一、选择题:(本大题共8题,满分24分)1.B ;2.A;3.C;4.D ;5.D;6.D;二、填空题:(本大题共12题,满分48分)三、。
2024上海初三二模数学试卷分类《25题解答压轴题》
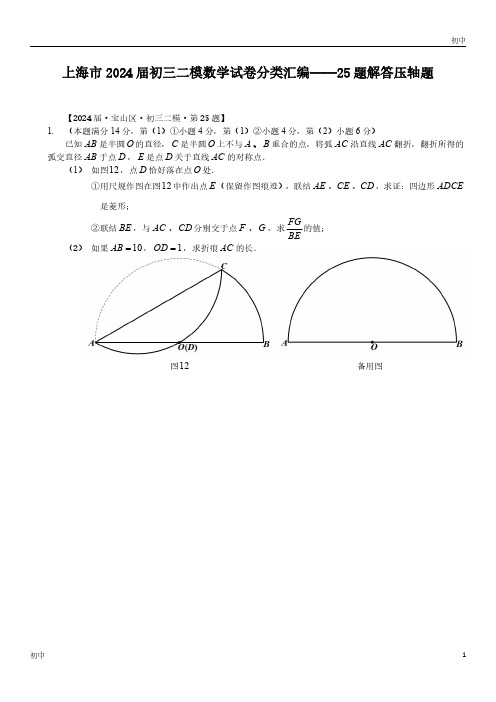
图12备用图上海市2024届初三二模数学试卷分类汇编——25题解答压轴题【2024届·宝山区·初三二模·第25题】1.(本题满分14分,第(1)①小题4分,第(1)②小题4分,第(2)小题6分)已知AB 是半圆O 的直径,C 是半圆O 上不与A 、B 重合的点,将弧AC 沿直线AC 翻折,翻折所得的弧交直径AB 于点D ,E 是点D 关于直线AC 的对称点.(1)如图12,点D 恰好落在点O 处.①用尺规作图在图12中作出点E (保留作图痕迹),联结AE 、CE 、CD ,求证:四边形ADCE 是菱形;②联结BE ,与AC 、CD 分别交于点F 、G ,求FGBE的值;(2)如果10AB =,1OD =,求折痕AC 的长.备用图2【2024届·崇明区·初三二模·第25题】2.(本题满分14分,第(1)①小题4分,第(1)②小题5分,第(2)小题5分)如图,已知Rt ABC ∆中,90ACB ∠=︒,6AC =,3sin 5B =,点D 是射线BA 上一动点(不与A 、B 重合),过点D 作//DE AC ,交射线BC 于点E ,点Q 为DE 中点,联结AQ 并延长,交射线BC 于点P .(1)如图1,当点D 在线段AB 上时.①若2AD =,求PC 的长;②当ADQ ∆与ABP ∆相似时,求AD 的长;(2)当ADQ ∆是以AD 为腰的等腰三角形时,试判断以点A 为圆心、AD 为半径的⊙A 与以点C 为圆心、CE 为半径的⊙C 的位置关系,并说明理由.第25题图1备用图1图10备用图【2024届·奉贤区·初三二模·第25题】3.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图10,已知半圆O 的直径为MN ,点A 在半径OM 上,B 为 MN 的中点,点C 在 BN 上,以AB 、BC为邻边作矩形ABCD ,边CD 交MN 于点E .(1)如果6MN =,2AM =,求边BC 的长;(2)联结CN ,当CEN ∆是以CN 为腰的等腰三角形时,求BAN ∠的度数;(3)联结DO 并延长,交AB 于点P ,如果2BP AP =,求BCAB的值.【2024届·虹口区·初三二模·第25题】4.(本题满分14分,第(1)小题4分,第(2)①小题5分,第(2)②小题5分)在梯形ABCD 中,//AD BC ,点E 在射线DA 上,点F 在射线AB 上,联结CE 、DF 相交于点P ,EPF ABC ∠=∠.(1)如图10①,如果AB CD =,点E 、F 分别在边AD 、AB 上.求证:AF DFDE CE=;(2)如图10②,如果AD CD ⊥,5AB =,10BC =,3cos 5ABC ∠=.在射线DA 的下方,以DE 为直径作半圆O ,半圆O 与CE 的另一个交点为点G .设DF 与弧EG 的交点为Q .①当6DE =时,求EG 和AF 的长;②当点Q 为弧EG 的中点时,求AF 的长.图10①图10②图10②备用图图10备用图【2024届·黄浦区·初三二模·第25题】5.(本题满分14分)已知:如图10,ABC ∆是圆O 的内接三角形,AB AC =,弧 AB 、AC 的中点分别为M 、N ,MN 与AB 、OA 、AC 分别交于点P 、T 、Q .(1)求证:OA MN ⊥;(2)当ABC ∆是等边三角形时,求ATOT的值;(3)如果圆心O 到弦BC 、MN 的距离分别为7和15,求线段PQ 的长.图9图10备用图在菱形ABCD 中,60DAB ∠=︒,点E 在射线AB 上,联结CE 、BD .(1)如图9,当点E 是边AB 的中点,求ECD ∠的正切值;(2)如图10,当点E 在线段AB 的延长线上,联结DE 与边BC 交于点F ,如果6AD =,EFC ∆的面积等于33EF 的长;(3)当点E 在边AB 上,CE 与BD 交于点H ,联结DE 并延长DE 与CB 的延长线交于点G ,如果6AD =,BCH ∆与以点E 、G 、B 所组成的三角形相似,求AE 的长.第25题图1第25题图2如图,已知:等腰梯形ABCD 中,//AD BC ,AB DC =,以A 为圆心,AB 为半径的圆与BC 相交于点E ,与CD 相交于点F ,联结AE 、AC 、BF ,设AE 、AC 分别与BF 相交于点G 、H ,其中H 是AC 的中点.(1)求证:四边形AECD 为平行四边形;(2)如图1,如果AE BF ⊥,求ABBC的值;(3)如图2,如果BG GH =,求ABC ∠的余弦值.=第25题图1第25题图2如图1,ABC ∆中,已知6AB =,9BC =,B ∠为锐角,1cos 3ABC ∠=.(1)求sin C 的值;(2)如图2,点P 在边AB 上,点Q 是边BC 的中点,⊙P 经过点A ,⊙P 与⊙Q 外切,且⊙Q 的直径不大于BC ,设⊙P 的半径为x ,⊙Q 的半径为y ,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题条件下,联结PQ ,如果BPQ ∆是等腰三角形,求AP 的长.第25题图1第25题图2备用图【2024届·闵行区·初三二模·第25题】9.(本题满分14分,第(1)①小题4分,第(1)②小题5分,第(2)小题5分)如图,OB 是⊙O 的半径,弦AB 垂直于弦BC ,点M 是弦BC 的中点,过点M 作OB 的平行线,交⊙O 于点E 和点F .(1)如图1,当AB BC =时.①求ABO ∠的度数;②联结OE ,求证:30OEF ∠=︒;(2)如图2,联结OE ,当AB BC ≤时,tan OEF x ∠=,ABy BC=,求y 关于x 的函数关系式并直接写出定义域.第25题图1第25题图2第25题图3【2024届·浦东新区·初三二模·第25题】10.(本题满分14分,第(1)小题5分,第(2)小题4分,第(3)小题5分)已知:⊙1O 和⊙2O 相交于A 、B 两点,线段12O O 的延长线交⊙2O 于点C ,CA 、CB 的延长线分别交⊙1O 于点D 、E .(1)联结AB 、DE ,AB 、DE 分别与连心线12O O 相交于点H 、点G .如图1,求证://AB DE ;(2)如果125O O .①如图2,当点G 与1O 重合,⊙1O 的半径为4时,求⊙2O 的半径;②联结2AO 、BD ,BD 与连心线12O O 相交于点F ,如图3,当2//BD AO ,且⊙2O 的半径为2时,求1O G 的长.11.(本题满分14分)如图9,在梯形ABCD 中,//AD BC (AD BC <),90A ∠=︒,6BC CD ==.将梯形ABCD 绕点C 按顺时针方向旋转,使点B 与点D 重合,此时点A 、D 的对应点分别是点E 、F .(1)当点F 正好落在AD 的延长线上时,求BCD ∠的度数;(2)联结AE ,设AD x =,AE y =.①求y 关于x 的函数解析式;②定义:同中心同边数的两个正多边形称为双同正多边形.设BCF ∠是一个正多边形的中心角,联结BD ,请说明以线段BD 、AE 为边的正多边形是双同正多边形的理由.当这两个正多边形的面积比是4:5时,求双同正多边形的边数.图9第25题(1)图第25题(2)图12.(本题满分14分,第(1)①小题4分,第(1)②小题5分,第(2)小题5分)在ABC ∆中,2AB AC ==,以C 为圆心、CB 为半径的弧分别与射线BA 、射线CA 相交于点D 、E ,直线ED 与射线CB 相交于点F .(1)如图,当点D 在线段AB 上时.①设ABC α∠=,求BDF ∠;(用含α的式子表示)②当1BF =时,求cos ABC ∠的值;(2)如图,当点D 在BA 的延长线上时,点M 、N 分别为BC 、DF 的中点,联结MN ,如果//MN CE ,求CB 的长.图9备用图13.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图9,已知矩形ABCD 中,1AB =,2BC =,点P 是边AD 上一动点,过点P 作PE AC ⊥,垂足为点E ,联结BE ,过点E 作EF BE ⊥,交边AD 于点F (点F 与点A 不重合).(1)当F 是AP 的中点时,求证:BA BE =;(2)当AP 的长度取不同值时,在PEF ∆中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由;(3)延长PE 交边BC 于点G ,联结FG ,EFG ∆与AEF ∆能否相似?若能相似,求出此时AP 的长;若不能相似,请说明理由.第25题图14.(本题满分14分,第(1)①小题2分,第(1)②小题3分,第(2)①小题5分,第(2)②小题4分)如图,在扇形OAB 中,62OA OB ==90AOB ∠=︒,点C 、D 是弧AB 上的动点(点C 在点D 的上方,点C 不与点A 重合,点D 不与点B 重合),且45COD ∠=︒.(1)①请直接写出弧AC 、弧CD 和弧BD 之间的数量关系;②分别联结AC 、CD 和BD ,试比较AC BD +和CD 的大小关系,并证明你的结论;(2)联结AB 分别交OC 、OD 于点M 、N .①当点C 在弧AB 上运动过程中,AN BM ⋅的值是否变化?若变化,请说明理由;若不变,请求AN BM ⋅的值;②当5MN =时,求圆心角DOB ∠的正切值.第25题图1备用图15.(本题满分14分,第(1)小题4分,第(2)小题10分)已知以AB 为直径的半圆O 上有一点C ,CD OA ⊥,垂足为点D ,点E 是半径OC 上一点(不与点O 、C 重合),作EF OC ⊥交弧BC 于点F ,联结OF .(1)如图1,当FE 的延长线经过点A 时,求CD AF的值;(2)如图2,作FG AB ⊥,垂足为点G ,联结EG .①试判断EG 与CD 的大小关系,并证明你的结论;②当EFG ∆是等腰三角形,且4sin 5COD ∠=,求OE OD 的值.第25题图1备用图备用图16.(本题满分14分,第(1)小题4分,第(2)①小题5分,第(2)②小题5分)已知在ABC ∆中,CA CB =,6AB =,3cos 5CAB ∠=,点O 为边AB 上一点,以点O 为圆心,OA 为半径作⊙O ,交边AC 于点D (点D 不与点A 、C 重合).(1)当4AD =时,判断点B 与⊙O 的位置关系,并说明理由;(2)过点C 作CE OD ⊥,交OD 延长线于点E .以点E 为圆心,EC 为半径作⊙E ,延长CE ,交⊙E 于点'C .①如图1,如果⊙O 与⊙E 的公共弦恰好经过线段EO 的中点,求CD 的长;②联结'AC 、OC ,如果'AC 与BOC ∆的一条边平行,求⊙E 的半径长.。
奉贤区中考数学二模试卷及答案

2015学年奉贤区调研测试九年级数学(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.如果两个实数a,b满足0a,那么a,b一定是(▲)+b=A.都等于0; B.一正一负; C.互为相反数; D.互为倒数.2.若x =2,y = -1,那么代数式222y+的值是(▲)x+xyA.0;;;.3.函数3y的图像不经过(▲)2-+=xA.第一象限; B.第二象限; C.第三象限; D.第四象限.4.一组数据3,3,2,5,8,8的中位数是(▲)A .3; ; ; .5.下列说法中,正确的是(▲)A.关于某条直线对称的两个三角形一定全等;B.两个全等三角形一定关于某条直线对称;C.面积相等的两个三角形一定关于某条直线之间对称;D.周长相等的两个三角形一定关于某条直线之间对称.6.已知⊙O 1与⊙O 2外离,⊙O 1的半径是5,圆心距721=O O ,那么⊙O 2的半径可以是(▲)A .4; ; ; . 二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.化简:a 16= ▲ ;8.因式分解:a a -2= ▲ ;9.函数11-=x y 的定义域是 ▲ ;10.一个不透明的袋子中装有若干个除颜色外形状大小完全相同的小球,如果其中有2个白球,n 个黄球,从中随机摸出白球的概率是32,那么n = ▲ ;11.不等式组1228x x ->⎧⎨-<⎩的解集是 ▲ ; 12.已知反比例函数xy 3=,在其图像所在的每个象限内,y 的值随x 的值增大而 ▲ ;(填“增大”或“减小”)13.直线)(0≠+=k b kx y 平行于直线x y 21=且经过点(0,2),那么这条直线的解析式是 ▲ ;14.小明在高为18米的楼上看到停在地面上的一辆汽车的俯角为60o ,那么这辆汽车到楼底的距离是 ▲ 米;(结果保留根号)15.如图,在△ABC 中,点D 在边BC 上,且DC =2BD ,点E 是边AC 的中点,设=,=b ,那么= ▲ ;(用、b 的线性组合表示)16.四边形ABCD 中,AD BF CF311-0-28-2-2016+)()(c bx x y ++-=2(1)求该抛物线解析式;(2)联结BC ,当P 点坐标为((3)当点D 落在抛物线的对称轴上时,求点P 的坐标.25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)已知:如图,在边长为5的菱形ABCD 中,cos A =35,点P 为边AB 上一点,以A 为圆心、AP 为半径的⊙A 与边AD 交于点E ,射线CE 与⊙A 另一个交点为点F .(1)当点E 与点D 重合时,求EF 的长;(2)设AP =x ,CE =y ,求y 关于x 的函数关系式及定义域;(3)是否存在一点P ,使得2EF PE =⋅,若存在,求AP 的长,若不存在,请说明理由.2015学年奉贤区调研测试九年级数学答案一、选择题:(本大题共6题,每题4分,满分24分)1. C ; 2. B ; 3.C ; 4.B ; 5. A ; 6.D . 二、填空题:(本大题共12题,每题4分,满分48分)7.a 4; 8.)a (a 1-; 9.1≠x ; 10.1; 11.x > 3;12.减小; 13.221+=x y ; 14.36; 15.2132-;16.AD=BC 等; 17.23; 18.13+;三、解答题:(本大题共7题,满分78分)19.(本题满分10分)解:原式=22-22-22-1+ (2)=2-1……………………………………………………………………………2分20. (本题满分10分)解:方程两边同乘以)4(2-x ……………………………………………………………1分得:16)2()2(2=--+x x …………………………………………………………3分整理,得:01032=-+x x …………………………………………………………2分 解得:21=x ,52-=x ……………………………………………………………2分 经检验:21=x 是增根,52-=x 是原方程的根 …………………………………1分所以原方程的根是5-=x ……………………………………………………………1分21.(本题满分10分,每小题满分各5分)解:(1)∵ AB =4,41=AB BE∴BE=1……………………………………………………1分 ∵ DE ⊥AD ,∠ACB =90o ∴∠CAD +∠ADC =∠BDE+∠ADC. ∴∠CAD =∠BDE∵ AD 是∠BAC 的角平分线,∴∠CAD =∠BAD ∴∠BAD =∠BDE …………2分∵∠B=∠ B ∴ △BDE ∽△BAD ………………………………………………1分∴AB BD BD BE = ∴BD=2…………………………………………………………1分(2)解法一:∵△BDE ∽△BAD ∴21==AD DE BD BE ……………………………………1分 ∴ 在Rt △ADE 中,∠ADE =90o ,tan ∠AED =2=DEAD ……………………2分 ∵ ∠CAD =∠BAD ,∠ADE =90o ,∠ACB =90o ∴ ∠AED =∠ADC …………1分∴ tan ∠ADC =2,即:∠ADC 的正切值为2……………………………………1分解法二:过点D 作DH ⊥AB 于点H …………………………………………………………1分∴∠AHD =90o ∵ AD 是∠BAC 的角平分线,∠ACB =90o ∴ CD=DH ………1分∵ ∠AHD =∠ACB =90o ,∠B =∠B ,△BDH ∽△BAC ………………………………1分∴ 2142===AB BD AC DH ,∴21=AC CD ………………………………………………1分∴在Rt △ACD 中,∠ACD =90o ,tan ∠ADC =2=CD AC即:∠ADC 的正切值为2……1分22.(本题满分10分,第(1)小题4分,第(2)小题6分)(1)50,60;…………………………………………………………………………每空各2分(2)设参与敬老院服务的六、七年级学生分别有x 人、y 人 …………………………1分根据题意,得:⎩⎨⎧=+++=+9060%140%160y x y x )()( ………………………………3分 解得⎩⎨⎧==3030y x ……………………………………………………………2分 答:参与敬老院服务的六、七年级学生各有30人.23.(本题满分12分,每小题满分各6分)证明:(1)∵ DC ∥AB , AD=BC=DC∴ ∠DCB =∠ADC ,∠DCB =∠CBE ∴∠ADC=∠CBE …………………1分∵ ∠BCE =∠ACD, BC=DC ∴△ADC ≌△EBC ……………………………2分∴ AD=BE ∴DC=BE ……………………………………………………2分 ∵ DC ∥AB ∴ 四边形DBEC 是平行四边形……………………………………1分(2)∵ 四边形DBEC 是平行四边形 ∴ BD=CE∵ DC ∥AB , AD=BC=DC ∴ AC=BD ∴ AC=BD …………………………1分∵ ∠DCA =∠CAB ∠BCE =∠ACD ∴ ∠BCE =∠CAB ∵∠E=∠ E ∴ △ECB ∽△EAC ……………………………………………………3分∴AE EC EC BE = ∴AE BE CE ⋅=2 即2AC AD AE =⋅ (2)分 24.(本题满分12分,每小题满分各4分)(1)∵抛物线c bx x y ++-=2交x 轴交于点A )0,1(-和点C )0,3(∴⎩⎨⎧=++-=+--03901c b c b 解得:⎩⎨⎧==32c b………………………………………………3分 ∴该抛物线的解析式:322++-=x x y …………………………………………1分(2)由322++-=x x y 得点B (0,3)……………………………………………………1分∵AD ⊥CD ∴∠DBP+∠BPD=90° ∵∠POA=90° ∴∠OAP+∠APO=90°∵∠BPD =∠APO ∴∠DBP =∠OAP ∵∠AOP=∠BOE=90° ∴△AOP ∽△BOE …1分∴OE PO BO AO = ∵OA =1,PO =32,BO =3 ∴OE3231= ∴OE =2……………1分∵OC =3 ∴EC =1 ∴233121=⨯⨯=∆EBC S………………………………………1分 (3)设点P ),0(y ,则OP=y ,BP=y -3,AP=21y + ∵点D 在抛物线的对称轴上,过点D 作DH ⊥x 轴,垂足为点H ∴AH=2 ∴AO=OH ∴PD =AP=21y +∵∠BPD =∠APO ∠AOP=∠BDP=90° ∴△AOP ∽△BDP …………………1分∴PD PO BP AP = ∴22131y y y y +=-+ 解得:21,121==y y .………………1分 经检验:21,121==y y 都是原方程的根 ∴)1,0(1P ,)21,0(2P ………………2分 25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)(1)解:当点E 与点D 重合时,AE =5,EF//AB ∴∠ADF =∠DAB ……………………1分过点A 作AH ⊥EF 于点H ……………………………………………………………1分∴在⊙A 中,EF =2EH ,∠AHE =90o …………………………………………………1分 ∴cos ∠ADF=cos ∠DAB =AE EH =35∴EH=3 EF =6………………………………2分(2) 解:过点C 作CM ⊥AD 交AD 延长线于点M ………………………………………1分在Rt △CMD 中,∠CMD =90o ,cos ∠MDC=cosA =35,CD=5∴MD =3,∴CM =4………………………………………………………………………1分在Rt △CME 中,∠CME =90o ,∴222ME CM CE +=∵CM =4,MD =3,DE =5-x ,CE =y ∴222534)x (y -++=……………………1分∴ 80162+-=x x y (0<x ≤5)………………………………………………………2分(3)解:假设存在一点P ,使得2EF PE =⋅过圆心A 作AH ⊥EF 于点H ,交⊙A 为点N …………………………………………1分∴2EF EN =⋅,∵2EF PE =⋅,∴PE EN = ∴∠NAE =∠PAE ………………1分∵AH ⊥EF , ∴∠NAE+∠HEA=90°. ∵∠CME=90°,∴∠CEM+∠ECM=90°.∵∠HEA =∠CEM , ∴∠NAE =∠ECM =∠PAE=∠MDC . ∴tan ∠ECM=tan ∠MDC=34 ∴ 在Rt △CME 中,∠CME =90o ,CM =4,ME =MD +DE =3+5-x tan∠ECM=3448=-=x MC ME , 解得 x=38…………………………………………2分即:存在点P ,使得2EF PE =⋅,此时AP 长为38.。
2013学年奉贤区初三数学期终调研试卷

4321第5题图O ACDB2013 学年奉贤区调研测试九年级数学试卷(满分∶150分,考试时间∶100分钟)命题人:张忠华 夏红波 钟菊红考生注意∶1. 本试卷含三个大题,共25题。
答题时,考生务必按答题要求在试卷答题纸规定的制定位置上作答,在草稿纸、本试卷上答题一律无效。
2. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题∶(本大题共6题,每题4分,满分24分)1.把抛物线2y x =向下平移2个单位,再向右平移4个单位后得到的抛物线是( )A .2(4)2y x =++;B .2(4)2y x =-+;C .2(4)2y x =+-;D .2(4)2y x =--.2.下列二次函数的图像经过原点的是( )A .22y x =+;B .2y x x =+;C .2(1)y x =-;D .221y x x =+-.3.已知在Rt △ABC 中,90C ∠=,1BC =,2AC =,则tanA 的值为( )A .2;B .12; C .55; D .255. 4.已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,若43AD BD =,则DEBC为( ) A .34; B .43; C .73; D .74.5.如图,四边形ABCD 的对角线AC 、BD 相交于点O ,且将这个三角形分成①、②、③、④四个三角形,若OA ∶OC =OB ∶OD ,则下列结论中一定正确的是( )A .①和②相似;B .①和③相似;C .①和④相似;D .②和④相似.6.关于半径是5的圆,下列说法正确的是( )A .若有一点到圆心的距离是3,则该点在圆外;B .若有一点在圆外,则该点到圆心的距离不小于5;C .圆上任意两点之间的线段长度不大于10;D .圆上任意两点间的部分可以大于10π.二、填空题∶(本大题共12题,每题4分,满分48分) 7.如果23x y =,那么x yy-= . 8.抛物线231y x =-的顶点坐标为 .9.二次函数22(2)y x =--的图像在对称轴左侧部分是 (填“上升”或“下降”). 10.写出一个对称轴为直线1x =-的抛物线解析式是 .第11题图CB F E DA 第16题图CBA21第17题图A CB第20题图HGF E AD BC 11.如图,已知AD ∥EF ∥BC ,如果AE ∶EB =2∶3,6FC =,那么DC = .12.如果两个相似三角形的周长之比是2∶3,其中小三角形一角的角平分线长是6cm ,那么大三角形对应角的角平分线长是 cm . 13.在Rt △ABC 中,90C ∠=,6AB =,23cosB =,则BC = . 14.计算:3(2)5(23)a b a b →→→→-+-= .15.如果在平面直角坐标系xOy 中,点P 的坐标(2,1),射线OP 与x 轴的正半轴所夹的角为α,那么α的余弦值等于 .16.如图所示,河堤横断面迎水坡AB 的坡比是1∶3,堤高5BC =米,则坡面AB 的长度是 米.17.如图,若12∠=∠,那么AB 与BC 相等(填“一定”、“一定不”、“不一定”).18.我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂三角形.已知等腰三角形的腰长为5,底边长为6,则该三角形的垂三角形的周长是 .三、解答题∶(本大题共7题,满分78分) 19.(本题满分10分)计算: 260304545cos cot tan sin ++.20.(本题满分10分,每一题5分)如图,已知平行四边形ABCD 中,点E 、F 分别是DC 、AB 的中点,AE 、CF 与对角线BD 分别交于点G 、H . (1)求GHBD的值; (2)若设AB a =,AD b =,试用a 、b 的线性组合表示向量GH .第22题图DA B C FE 第23题图CB AE D xy第24题图P B A CDO 21.(本题满分10分)如图是已建设封顶的16层楼房和它的塔吊示意图,吊臂AG 与地面EH 平行,测得A 点到楼顶D 点的距离是5米,每层楼高3.5米,在吊臂上有一点B ,16AB =米,在C 点测得A 点的俯角(MCA ∠)为20°,B 点的俯角(MCB ∠)为40°,AE 、CH 都垂直于地面,求塔吊的高CH 的长(结果精确到0.1米).参考数据:200.34sin ≈,200.94cos ≈,200.36tan ≈,400.64sin ≈,400.77cos ≈,400.84tan ≈. 22.(本题满分10分,每小题5分)如图,已知在直角梯形ABCD 中,ADC ∠=90°,AD ∥BC ,8AD =,6DC =,点E 在BC 上,点F 在AC 上,且DFC AEB ∠=∠,4AF =. (1)求线段CE 的长; (2)若34sinB =,求线段BE 的长. 23.(本题满分12分,每小题各6分)如图,已知在等腰△ABC 中,AB AC =,点E 、D 是底边所在直线上的两点,联结AE 、AD ,若2AD DC DE =⋅,求证: (1)△ADC ∽△EDA ;(2)22AE EB AD CD =.24.(本题满分12分,每小题各4分)如图,已知抛物线223y x bx c =++与x 轴交于点A 、B 两点,点B 的坐标为(3,0),它的对称轴为直线2x =.(1)求二次函数的解析式;(2)若抛物线的顶点为D 点,联结BD 并延长交于y 轴于点P ,联结PA ,求APC ∠的余切值; (3)在(2)的条件下,若在抛物线上存在点E ,使得DPE ACB ∠=∠,求点E 的坐标.25.本题满分14分,其中第(1)小题4分,第(2)小题5,第三小题5分 如图(1),在半径为5的扇形AOB 中,90AOB ∠=,点C 、D 分别在半径OA 与弧AB 上,且2AC =,CD ∥OB ,点P 是CD 上一动点,过点P 作OP 的垂线交弧AB 于点E 、F ,联结DE 、DF .(1)求DEPDFPS S ∆∆的值;第25题图2EFDCAOBP第25题图1EFDCAOBP(2)如图(2),联结EO 、FO ,若60EOF ∠=,求CP 的长;(3)设CP x =,△DEF 的面积为y ,求y 关于x 的函数关系式,并写出它的定义域.2013~14学年上海市奉贤区初三第一学期期末考试数学试卷参考答案一、选择题∶ 1.D . 2.B .3.B . 4.D . 5.B . 6.C . 7.12. 8.()0,1-. 9.上升.10.()21y x =+等. 11.10. 12.9. 13.4. 14.1618a b -.15.255. 16.10. 17.一定.18.19225.19.解:原式()2123212=++1322=++242=-. 20. 解:(1)四边形ABCD 为平行四边形,∴DC ∥AB ,=DC BC .∵点E 、F 分别是DC 、AB 的中点,∴12DE DG AB BG ==,12BF BH CD DH ==. ∴13DG BD =,13BH BD =. ∴13GH BD =. (2)∵AB a =,AD b =,∴BD b a =-.∵13GH BD =, ∴()11113333GH BD b a a b =-=--=-.21.解:根据题意得, 3.51656DE =⨯=米,16AB EF ==米.∵20ACB CBG CAB ∠=∠-∠=, ∴ACB CAB ∠=∠. ∴16CB AB ==米.在Rt △GBC 中,40160.6410.24CG BC sin =⋅=⨯=米,∴10.2456571.2471.2CH CG HG CG DE AD =+=++=++=≈米. ∴塔吊的高CH 的长约为71.2米. 22、 解:(1)∵AD ∥BC ,∴DAF ECA ∠=∠. ∵DFC AEB ∠=∠, ∴AFD CEA ∠=∠. ∴△ADF ∽△CAE .∴AD AFAC CE=. ∵8AD =,6DC =,ADC ∠=90°, ∴10AC =. ∵4AF =, ∴8410CE =. ∴5CE =.(2)过点A 作AH BC ⊥,垂足为点H .则6AH DC ==.在Rt △ABH 中,3sin 4AHB AB==,∴8AB =,27BH =.∴827BC BH HC =+=+. ∴327BE BC CE =-=+.23.证明:(1)∵2AD DC DE =⋅,∴AD DEDC AD=. ∵D D ∠=∠, ∴△ADC ∽△EDA . (2)∵△ADC ∽△EDA ,∴DAC E ∠=∠. ∵AB AC =, ∴ABC ACB ∠=∠.∴△ABE ∽△DCA .∴222ABE DCAS AE AE SAD AD ⎛⎫== ⎪⎝⎭. 过点A 作AH BC ⊥,垂足为点H .∴1212ABE DCABE AH SBE SDC DC AH ⋅⋅==⋅⋅. ∴22AE EB CD AD=. 24、(1)()22303y x bx c B ,x=2=++抛物线过点,对称轴为直线293083322223b c b bc ⎧⨯++=⎪⎧=-⎪⎪∴⎨⎨-=⎪⎪=⎩⨯⎪⎩解得: 228233y x x ∴=-+二次函数解析式为 (2)()222,1,0,233D A BD y=x ⎛⎫-- ⎪⎝⎭由题意得顶点直线:()0,2P ∴- c o t 2POPOA APC AO∠==在直角三角形中, (3),BC BP AC AP ==,BCO BPO ACO APO ∴∠=∠∠=∠ B A C B PA ∴∠=∠ PA E E EH x ∴⊥延长交抛物线于点,过点作轴∴△AOP ∽△AHE 2PO EHAO AH∴== (),2,1,2AH=x EH x E x x =+设则点()()228211233x x x ∴=+-++ 120,5x x ==解得: ()()121,0,6,10E E ∴25、(1),DM EF M ⊥作垂足为O P E F P E =P F⊥∴ 12112DEP DFPPE DM S SPF DM ⋅⋅∴==⋅⋅(2)6030EOF EOP ∠=︒∴∠=︒552OE AO EP ==∴=532OP EFOP ⊥∴=CD ∥,903OB AOB OC ∠=︒∴=227539942CP OP OC ∴=-=-=(3),,5,44OD CDO OC=3OD=CD=DP=x ∴-联结在直角三角形中,EH CD H ⊥作垂足为23,9OC=CP=x OP x ∴=+ 2,16EPO EP=x ∴-在直角三角形中30COP=EPH=∠∠︒ ∴△OCP ∽△PHE 2222169169CP EHx EH x x =EH PO EPx xx -∴∴=∴=+-+()()22222416116224299DEFDPEx x x x x y SSDP EH x x x ---===⨯⨯⨯=-⋅=++ ()()222416649x x x y x x --∴=≤<+。
中考二模数学卷上海

2013年中考二模数学卷(上海)金山区2012学年第二学期初三模拟考试数学试卷2013.5一.选择题1.下列各数中,与是同类二次根式的是A.B.()C.D.2.满足不等式的最小整数解是A.-3B.-2C.-1D.03.在平面直角坐标系中国,一次函数的图像不经过A.第一象限B.第二象限C.第三象限D.第四象限4.一位射箭选手在训练中,五次射箭的成绩分别是10,7,8,10,10(单位:环)。
这组数据的平均数和众数分别是A.8,7B.8,10C.9,8D.9,105.下列命题中,逆命题是真命题的是A.对顶角相等B.两直线平行,同位角相等C.全等三角形的对应角相等D.正方形的四个内角都相等6.在Rt△ABC中,∠C=90°,AC=3,BC=4,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是A.点P,M均在圆A内B.点P、M均在圆A外C.点P在圆A内,点M在圆A外D.点P在圆A外,点M 在圆A内二.填空题7.计算:=____________8.因式分解:=___________9.方程的根是______________10.方程的根是_____________11.如果关于x的一元二次方程:(为常数)有两个实数根,那么的取值范围是___________________12.已知正比例函数(≠0)的图像经过点(1,-2),那么正比例函数的解析式为___________13.在六张大小质地相同的卡片分别写上2010,2011,2013,2013,2013,2014,随机抽取一张,抽取的卡片上的数字是偶数的概率是_____________14.为了解各年龄段观众对某电视节目的收视率,小明调查了部分观众的收视情况,并分成A、B、C、D、E、F六组进行调查,其频率分布直方图如图所示,各长方形上方的数据表示该组的频率,若E组的频数为48,那么被调查的观众总人数为_______15.如图,已知,AB=AC,CE平分∠BCD,∠A=120°,那么∠ACE=_________16.如图,已知点D、E分别是边AC和AB的中点,设,,那么=__________(用来表示)17.如图,已知在△ABC中,BC∥DE,,AB=a,那么BD=_____________(用a的代数式来表示)18.已知正方形ABCD的边长为,点E在DC上,且∠DAE=30°,若将△ADE绕着点A顺时针旋转60°,点D 至D’处,点E至E’处,那么△AD’E’与四边形ABCE 重叠部分的面积是____________三.解答题19.,其中.20.解方程组:21.如图,已知在△ABC中,DE是AC的垂直平分线,交AC于点D,AB于点E,若BC=8,△BCE的周长为21,cos∠B=.求:(1)AB的长(2)AC的长22.某工厂计划生产甲、乙两种型号的机器200台,生产机器一定要有A、B两种材料,现厂里有A种材料10000吨,B种材料6000吨,已知生产一台甲机器和一台乙机器所需A、B两种材料的数量和售后利润如下表所示:机器型号A种材料B种材料售后利润甲55吨20吨5万元乙40吨36吨6万元设生产甲种型号的机器台,售后的总利润为万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013学年奉贤区调研测试九年级数学 201404(满分150分,考试时间100分钟)一、选择题:(本大题共6题,每题4分,满分24分) 1.下列各数中,属于无理数的是( )A . 0)2(π;B . 33 ; C .4; D . 38-;2.下列根式中,属于最简二次根式的是( ) A .28; B .22b a +; C.ba; D.4.0; 3.不等式062>+x 的解集在数轴上表示正确的是( )4. 右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是( ) A .16、10.5; B .8、9; C .16、8.5; D .8、8.5;5.在数学活动课上,老师要同学们判断一个四边形门框是否为矩形, 下面是某学习小组的4位同学拟定的方案,其中正确的是( )A .测量对角线是否相互平分;B .测量两组对边是否分别相等;C .测量一组对角是否都为直角;D .测量其中三个角是否都为直角; 6.如图,直线1l ∥2l ,3l ⊥4l .下列命题中真命题是( ) A .︒=∠+∠9031; B .︒=∠+∠9032; C .42∠=∠; D .31∠=∠;二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:52)(m - = ; 8.分解因式:282-a = ;A .B .C .D .(小时)(第5题图)第4题第6题10.已知函数2)(-=x x f ,若3)(=x f ,那么 x = ;11.随着中国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2013年海外学习汉语的学生人数已达00人,将00用科学记数法表示为 人;12.若点A (1,y 1)和点B (2,y 2)都在正比例函数kx y =()0>k 图像上,则y 1 y 2(选择“>”、“<”、“=”填空);13.从-1,-2,3这三个数中任取两个不同的数作为点的坐标,该点在第三象限的概率是 ; 14.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图。
若该校有1000名学生,则赞成该方案的学生约有 人; 15.如图,在ABC △中,D 是边BC 上的点,21=DC BD ,设向量=,=,如果用向量a ,b 的线性组合来表示向量,那么= ;16.如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF =2,BC =5,CD =3, 则tan C= ;17.在⊙O 中,弦AB 的长为6,它所对应的弦心距为4,那么半径OA = ; 18.如图,在Rt △ABC 中,∠C =90°,BC =9,AC =12,点D 在边AC 上,且CD =31AC ,过点D 作DE ∥AB ,交边BC 于点E ,将△DCE 绕点E 旋转,使得点D 落在AB 边上的D ’处,则Sin ∠DED ’= ;三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)化简求值:xx x x 1)1111(2-∙+--,其中x =12-.ADC第15题第16D第1820.(本题满分10分,每小题5分)解方程组:⎩⎨⎧=-+-=+0125222y xy x y x .21.(本题满分10分,第(1)小题4分,第(2)小题6分) 已知:如图,在Rt ∆ACB 中,∠A =300,∠B =450, AC =8,点P 在 线段AB 上,联结CP ,且43cot =∠APC , (1)求CP 的长;(2)求∠BCP 的正弦值;22.(本题满分10分,每小题5分)在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y (米)与施工时间x (时)之间关系的部分图象.请解答下列问题:(1)求乙队在2≤x ≤6的时段内,y 与x 之间的函数关系式; (2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到 完工所铺设的彩色道砖的长度为多少米?时)第22题CABP第21题23.(本题满分12分,每小题满分各6分)已知:如图,点E 是四边形ABCD 的对角线BD 上一点,且∠BAC =∠BDC =∠DAE .⑴求证:△ABE ∽△ACD ;⑵求证:AC DE AD BC ⋅=⋅;24.(本题满分12分,每小题6分)已知:如图,在平面直角坐标系xoy 中,抛物线y =交x 轴于A (4,0)、B (1,0)-两点,交y 轴于点C . (1)求抛物线的表达式和它的对称轴;(2)若点P 是线段OA 上一点(点P 不与点O 和点A重合),点Q 是射线AC 上一点,且PQ PA =, 在x 轴上是否存在一点D ,使得ACD ∆与APQ ∆ 相似,如果存在,请求出点D 请说明理由. 第24题E第23题DCBA25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)已知:如图1,在梯形ABCD中,∠A=90°,AD∥BC, AD=2,AB=3, tan C=12,点P是AD延长线上一点,F为DC的中点,联结BP,交线段DF于点G.(1)若以AB为半径的⊙B与以PD为半径的⊙P外切,求PD的长;(2)如图2,过点F作BC的平行线交BP于点E,①若设DP=x,EF=y,求y与x的函数关系式并写出自变量x的取值范围;②联结DE和PF,若DE=PF,求PD的长.第25题图1第25题图2备用图奉贤区初三调研考数学卷参考答案 201404一 、选择题:(本大题共8题,满分24分)1.B ; 2.B ; 3.C ; 4.B ; 5.D ; 6.A ; 二、填空题:(本大题共12题,满分48分)7.10m -; 8.)12)(12(2-+a a ; 9.(0,3); 10.11;11.9105.1⨯; 12.<; 13.31; 14.700; 15.3132+; 16.34; 17.5; 18.2524;三.(本大题共7题,满分78分) 19. (本题满分10分)解:x x x x 1)1111(2-∙+--=xx x x x x 11111122-∙+--∙-………………………2分 =xx x x x 211=--+ ……………………………………………………………4分 当12-=x 时2221222+=-=x…………………………………………4分20. (本题满分10分)解:⎩⎨⎧=-+-=+)2(012)1(5222y xy x y x由(2)得:1=-y x 或1-=-y x …………………………………………………2分原方程组可化为⎩⎨⎧=-=+152y x y x 和⎩⎨⎧-=-=+152y x y x …………………………………2分解这两个方程组得原方程组得解:⎪⎩⎪⎨⎧==343711y x ,⎩⎨⎧==2112y x …………………………6分21. (本题满分10分)(1)解:过点C 作CH ⊥AB 于点H ,………………………………………………1分 ∵∠A =300, AC =8,∴CH =4………………………………………………………1分 ∵在直角三角形CHP 中,3cot =∠APC ∴PH=3………………………………1分∴CP=5 ………………………………………………………………………………1分 (2)∵在直角三角形CHB 中,∠B =450 ,CH =4 ∴BH =4…………………1分 ∴PB =1,……………………………………………………………………………1分 过点P 作PG ⊥BC 于点G ,……………………………………………………………1分 ∵在直角三角形PGB 中,∠B =450 ,PB =1 ∴PG =22…………………………1分∴在直角三角形PGC 中BCP ∠sin =102=CP PG ………………………………………2分 22.(本题满分10分)(1)设乙队在2≤x ≤6的时段内y 与x 之间的函数关系式为y =kx +b ,……1分由图可知,函数图象过点(2,30)、(6,50),∴⎩⎨⎧=+=+506302b k b k 解得⎩⎨⎧==205b k ……………………………………………3分∴y =5x +20. ……………………………………………………………………1分 (2)由图可知,甲队速度是:60÷6=10(米/时). ……………………………1分设甲队从开始到完工所铺设彩色道砖的长度为z 米,依题意,得……………1分6050.1012z z --= ……………………………………………………2分解得 z =110.………………………………………………………1分答:甲队从开始到完工所铺设彩色道砖的长度为110米.23.(本题满分12分,每小题满分各6分)证明:(1)∵∠BAC =∠DAE ∴∠BAE =∠DAC …………………………2分∵ ∠BAC =∠BDC ,∠BOA =∠DOC∴∠ABE =∠ACD …………………………………………………2分 ∴△ABE ∽△ACD ………………………………………………2分 (2) ∵△ABE ∽△ACD ∴ADAEAC AB =……………………………2分 ∵∠BAC =∠DAE ∴△ABC ∽△AED ………………………1分 ∴ADACDE BC =……………………………………………………2分 ∴AC DE AD BC ⋅=⋅…………………………………………1分24.(本题满分12分,每小题6分) (1)∵抛物线c bx x y ++-=23交x 轴于A (4,0)、B (1,0)-两点 E 第23题DBAO∴⎪⎪⎩⎪⎪⎨⎧=+--=++⨯-043041643c b c b 解得:⎪⎩⎪⎨⎧==349c b ……………………………………3分∴抛物线的表达式:349432++-=x x y …………………………………………1分 它的对称轴是:直线23=x …………………………………………………………2分(2)假设在x 轴上是否存在一点D ,使得ACD ∆与APQ ∆相似∵∠A =∠A 则①△APQ ∽△ACD ∴CDACPQ AP = ∵PQ PA = ∴AC =CD∵A (4,0) ∴)0,4(1-D ………………………………………………………3分 ②△APQ ∽△ADC ∴CDADPQ AP = ∵C (0,3) ,PQ PA =∴AD=CD ∴)0,87(2D …………………………………………………………3分 ∴点D 的坐标)0,87(),0,4(21D D -时,△ACD 与△APQ 相似。
