疲劳裂纹扩展与强度理论
复合材料的疲劳裂纹扩展与评估

复合材料的疲劳裂纹扩展与评估在现代工程领域,复合材料凭借其优异的性能,如高强度、高刚度、良好的耐腐蚀性等,得到了广泛的应用。
然而,就像任何材料一样,复合材料在长期的使用过程中也会面临疲劳损伤的问题,其中疲劳裂纹的扩展是导致其性能下降甚至失效的重要原因之一。
因此,深入研究复合材料的疲劳裂纹扩展机制,并建立有效的评估方法,对于确保复合材料结构的可靠性和安全性具有至关重要的意义。
要理解复合材料的疲劳裂纹扩展,首先需要了解复合材料的基本组成和结构。
复合材料通常由两种或两种以上具有不同物理和化学性质的材料组成,其中一种作为基体,另一种或几种作为增强相。
常见的复合材料有纤维增强复合材料,如碳纤维增强复合材料和玻璃纤维增强复合材料,以及颗粒增强复合材料等。
在疲劳载荷作用下,复合材料中的裂纹起始和扩展过程与传统的单一材料有很大的不同。
对于单一材料,裂纹通常在材料的表面或内部缺陷处起始,并沿着特定的晶体学方向扩展。
而对于复合材料,由于其复杂的微观结构,裂纹的起始位置可能在基体、增强相或者基体与增强相的界面处。
而且,裂纹在扩展过程中会遇到不同的相和界面,其扩展路径也会变得更加复杂。
影响复合材料疲劳裂纹扩展的因素众多。
首先是材料的组分和微观结构。
增强相的类型、含量、分布以及与基体的结合强度都会对疲劳性能产生影响。
例如,碳纤维具有较高的强度和刚度,能够显著提高复合材料的疲劳性能;而增强相的分布不均匀可能导致局部应力集中,从而加速裂纹的起始和扩展。
其次,加载条件也是一个重要因素。
加载频率、应力比、加载波形等都会影响疲劳裂纹的扩展速率。
此外,环境因素如温度、湿度等也可能对复合材料的疲劳性能产生不利影响。
为了研究复合材料的疲劳裂纹扩展行为,科学家们采用了多种实验方法。
其中,最常用的是疲劳试验。
通过对试样施加循环载荷,监测裂纹的长度随循环次数的变化,从而得到疲劳裂纹扩展曲线。
在实验中,通常采用光学显微镜、扫描电子显微镜等设备来观察裂纹的形态和扩展路径。
疲劳裂纹扩展速率 模型

疲劳裂纹扩展速率模型简介疲劳裂纹扩展速率是材料力学领域一个重要的研究课题。
疲劳裂纹扩展是指在材料受到疲劳载荷作用下,裂纹会以一定速率扩展,最终导致材料的疲劳失效。
了解疲劳裂纹扩展速率模型,对材料的疲劳寿命预测和结构设计具有重要意义。
本文将深入探讨疲劳裂纹扩展速率模型及其应用。
疲劳裂纹扩展速率模型的基本原理疲劳裂纹扩展速率模型是基于疲劳裂纹扩展的基本机理和实验数据建立的。
疲劳裂纹扩展通常表现为裂纹的逐渐扩展和材料的逐渐疲劳破坏。
疲劳裂纹扩展速率模型的基本原理可以归纳如下:1.裂纹尖端应力分布:裂纹尖端是裂纹扩展的起点,其应力集中在该处。
裂纹尖端的应力分布对裂纹扩展速率有重要影响。
2.应力强度因子:应力强度因子是表征裂纹尖端应力分布的一个重要参数。
它可以通过应力分析或实验测量得到。
3.断裂力学:根据线弹性断裂力学理论,裂纹尖端的应力强度因子与裂纹扩展速率之间存在一定的关系。
4.实验数据拟合:通过对大量实验数据进行分析和处理,建立裂纹扩展速率模型。
常用的实验数据包括裂纹扩展速率与应力强度因子、载荷频率、温度等因素的关系。
疲劳裂纹扩展速率模型的应用疲劳裂纹扩展速率模型在工程实践中具有广泛应用,主要包括以下几个方面:1. 疲劳寿命预测疲劳寿命是指材料在特定工况下能够承受多少次疲劳载荷循环而不发生裂纹扩展和失效。
基于疲劳裂纹扩展速率模型,可以通过计算裂纹扩展速率和已有裂纹长度,预测材料的疲劳寿命。
2. 结构设计在工程结构设计中,了解材料的疲劳裂纹扩展速率模型对于提高结构的耐久性和安全性非常重要。
根据疲劳裂纹扩展速率模型,可以针对不同材料和结构形式,选择合适的材料和结构设计方案,以延长结构的使用寿命。
3. 材料评估和筛选通过疲劳裂纹扩展速率模型,可以评估和筛选材料的疲劳性能。
根据不同材料的裂纹扩展速率特性,可以选择适用于不同工况和要求的材料。
4. 裂纹控制和修复了解疲劳裂纹扩展速率模型,可以对已发生裂纹的结构进行控制和修复。
断裂力学 疲劳裂纹的扩展

5.2 疲劳裂纹的扩展速率
a
疲劳裂纹扩展的定量表示用 N
或 da
dN
, N 是交变应力循环
次数增量, a 是相应的裂纹长度的增量。
疲劳裂纹扩展速率:
a N
(或
da dN
),表示交变应力每循环
一次裂纹长度的平均增量(mm/次),它是裂纹长度a、应
KK1m axK1m in
其中 K1max、K1min 分别是交变应力最大值和最小值所计算的应 力强度因子。
Paris公式为最基本的公式,许多学者提出了对其的修正方案。主 要有Donahue、Priddle、Walker等。
Paris应力强度因子理论与实验结果符合较好的一种 理论.
第 I 阶段 KI Kth 门槛值
(疲劳裂纹扩展寿命)
其中 Kf(a)为应力强度因子幅度,f ( a ) 是裂纹长
度的函数,c、m为常数。
三. 影响疲劳裂纹扩展速率的因素
虽然Paris公式中只有几个参数,但实际还有其它的影响因素:
1)平均应力 m 的影响:平均应力升高,da/dN升高, 故常在表面做喷丸处理,产生压应力,减小 m 。 2)超载的影响:大载荷时能产生塑性区,然后相当 于卸载,但塑性变形不能恢复,而弹性必须要恢复, 产生压应力,相当于减小 m ,故降低 da/ dN。 3)加载频率的影响。 4)其他因素的影响
dN
式中: 为裂纹尖端张开位移幅度。
2.J积分表达式
da C(J )r dN
C与r是材料常数,J积分写成: J2Y2 de
其中Y为裂纹的几何形状因子。
扩展速率为 1 0 3 mm/每循环.
4)断裂阶段 扩展到 a c 时,失稳导致快速断裂。
材料疲劳裂纹扩展研究综述

材料疲劳裂纹扩展研究综述摘要:疲劳裂纹扩展行为是现代材料研究中重要的内容之一。
论述了组织结构、环境温度、腐蚀条件以及载荷应力比、频率变化对材料疲劳裂纹扩展行为的影响。
总结出疲劳裂纹扩展研究的常用方法和理论模型,并讨论了“塑性钝化模型”和“裂纹闭合效应”与实际观察结果存在的矛盾温度、载荷频率和应力比是影响材料疲劳裂纹扩展行为的主要因素。
发展相关理论和方法,正确认识影响机理,科学预测疲劳裂纹扩展行为一直是人们追求的目标。
指出了常用理论的不足,对新的研究方法进行了论述。
关键词: 温度; 载荷频率; 应力比; 理论; 方法; 疲劳裂纹扩展1 前言19世纪40年代随着断裂力学的兴起,人们对于材料疲劳寿命的研究重点逐渐由不考虑裂纹的传统疲劳转向了主要考察裂纹扩展的断裂疲劳。
尽量准确地估算构件的剩余疲劳寿命是人们研究材料疲劳扩展行为的一个重要目的。
然而,材料的疲劳裂纹扩展研究涉及了力学、材料、机械设计与加工工艺等诸多学科,材料、载荷条件、使用环境等诸多因素都对疲劳破坏有着显著的影响,这给研究工作带来了极大困难。
正因为此,虽然对于疲劳的研究取得了大量有意义的研究成果,但仍有很多问题存在着争议,很多学者还在不断的研究和探讨,力求得到更加准确的解决疲劳裂纹扩展问题的方法和理论。
经过几十年的发展,人们已经认识到断裂力学是研究结构和构件疲劳裂纹扩展有力而现实的工具。
现代断裂力学理论的成就和工程实际的迫切需要,促进了疲劳断裂研究的迅速发展。
如Rice的疲劳裂纹扩展力学分析(1967年) ,Elber的裂纹闭合理论(1971年) ,Wheeler 等的超载迟滞模型(1970年) ,Hudak等关于裂纹扩展速率标准的测试方法,Sadananda和Vasudevan ( 1998年)的两参数理论等都取得了一定成果。
本文将对其研究中存在问题、常用方法和理论模型、以及温度、载荷频率和应力比对疲劳裂纹扩展影响的研究成果和新近发展起来的相关理论进行介绍。
疲劳强度理论分析

1. 名义应立法:计算全寿命,主要用于高周疲劳; 2. 局部应力—应变法:计算裂纹形成寿命; 3. 断裂力学法:计算裂纹扩展寿命。
(四):疲劳试验 材料试验,实物结构试验,高周疲劳试验,低周疲劳试验,裂纹扩展寿命试验
(五):常规疲劳强度设计:
),可
4.P-S-N 曲线 不同可靠度下的应力——寿命曲线
(1) S-N曲线中S,N的概率密度函数
大量实验表明:疲劳强度符合正态分布
(同寿命下的应力分布)。疲劳寿命符合对数
正态或威布尔分布(同应力水平下的寿命)
正态分布
——均值,也叫数学期望。
——标准差,数学上叫均方根值。
对数正态分布,将随机变量的对数函数进行分析。威布尔分布(寿命)
随机载荷下疲劳寿命研究实测载荷谱当量成对称循环下的载荷谱ii根据材料的sn曲线实物试验值和实测载荷谱代入计算模型638可计算不同可靠度下的疲劳寿命图612表621表622这里进行了两种构件侧架和摇枕的疲劳寿命计算iii与实际统计数据比较讲实际统计数据进行整理表627采用常规定时截尾试验发最后论证摇枕的实际平均寿命为328年计算值为3537年两值接近说明计算公式可以
疲劳试验在疲劳试验机上进行,有弯曲疲劳试验机和拉—压疲劳 试验机等。
2 疲劳分析的有关参数
应力幅
平均应力 最大应力 最小应力 应力范围
应力比
对称循环, 脉动循环 静应力
3 材料的S—N曲线 根据不同应力水平分组进行疲劳试验,
根据实验数据进行拟合,一般采用最小二乘 法。 曲线为指数曲线,即: 对上式两边去对数 :
也就是许用应力法: 存在问题:
a. 设计的机械零件特别笨重(为了安全,只有加大整个截面尺寸); b. 尽管笨重,但仍有疲劳裂纹产生。 原因: a. 疲劳裂纹发生在构件的危险点的局部区域,通过裂纹不断扩展,
疲劳裂纹扩展速率 模型

疲劳裂纹扩展速率模型
疲劳裂纹扩展速率模型是指在材料受到反复载荷作用时,疲劳裂纹在材料中出现并逐
渐扩展的速率模型。
该模型是通过实验测试来确定的,可以帮助工程师预测材料在长时间
使用中的性能表现。
疲劳裂纹扩展速率模型通常由三个部分组成:金属的循环应力应变曲线、应力强度因
子和应力对裂纹扩展速率的敏感度。
其中,金属的循环应力应变曲线描述了材料在受到循
环载荷作用下的应力应变行为。
应力强度因子是描述疲劳裂纹扩展速率的指标,它与应力、裂纹尺寸和材料性质有关。
应力对裂纹扩展速率的敏感度是指应力变化对裂纹扩展速率的
影响程度。
根据实验结果,疲劳裂纹扩展速率通常是与应力强度因子成幂函数关系的,即:
dv/dN = C(ΔK)m
其中,dv/dN表示单位时间裂纹扩展速率,C和m为材料常数,ΔK为应力强度因子的变化量。
通过实验得到材料的C和m值,便可应用上述公式,计算出材料在不同应力强度
因子下的疲劳裂纹扩展速率。
此外,疲劳裂纹扩展速率模型还可进一步拓展为考虑裂纹形态、预先应力等因素的模型,以更准确地预测材料的疲劳性能。
总之,疲劳裂纹扩展速率模型是研究材料疲劳性能的重要手段,通过实验验证和分析,可以帮助工程师预测材料在使用过程中的裂纹扩展情况,为工程设计提供依据。
最新09--裂纹扩展与疲劳裂纹扩展

KP f (a)
f(a)C C(a(a))PC daMf(a)Pda
裂纹扩展稳定性分析
• 即得:
• 通常 Ca ,0 因此:
K aT
f(a) C(a)Pf(a)P C(a)CM
K a
K a
关于裂纹扩展的分析
•
考虑一个尺寸为a 0 的裂纹,随着外加载
荷P(或位移u)的逐渐增加,应力强度因
K
子K 逐渐增大,当K 达到K C 时(B点),裂纹 开始启裂。
• 在对应的加载条件L下,随着裂纹尺寸
的变化,K
a 随之变化,如果
K a
L
则Ka该R
裂纹在扩展一个微小的尺寸后即停止扩
Kc
C B
a
o
b
➢对于这样的材料,裂纹 K 一 旦达到K I C 就很容易发生失稳
扩展,除非K a 随着裂纹的长
大,逐渐减小。对于很脆的材 料(如玻璃)以及在平面应变 条件下的高强低韧金属,作为 一次近似,通常可以采用上图 所示的这种关系。
K
➢对于大多数材料,在裂纹尖端都存在 着多种不同的细观损伤机制,如细观尺
裂纹扩展,必须满足:
• 即一个裂K纹扩K展R,a其应力强
dK R da
Байду номын сангаас
K a
L
dK R da
dK R da
稳定性扩展 随遇扩展 失稳扩展
度因子必须达到当前状态下 的临界应力强度因子。
具体的加载条件,可以是载荷控 制的加载,也可以是位移控制的
加载,或是介于上述两者之间的
某一加载条件。
• 在位移控制加载条件下,K a 曲线的斜率总是负值, 因此,按照裂纹扩展的稳定性条件,裂纹的扩展 总是稳定的。
机械工程中的裂纹扩展与疲劳分析研究

机械工程中的裂纹扩展与疲劳分析研究在现代机械工程中,疲劳是一种十分常见的现象,它是金属材料在连续受到交变载荷作用后所出现的渐进性损伤过程。
疲劳问题一旦发生,往往会对机械系统的安全性和可靠性产生严重影响,因此,对疲劳问题的研究与分析成为机械工程领域中的一个重要课题。
裂纹扩展作为疲劳破坏的一种主要形式,是引起机械元件失效的关键因素之一。
因此,对裂纹扩展行为的研究具有重要意义。
一般而言,裂纹扩展行为可通过数学模型来预测和分析。
在研究机械工程中的裂纹扩展时,最常用的方法之一就是有限元法。
有限元法是一种通过将复杂结构分割为无限小的有限元素,以近似求解连续介质力学问题的数值方法。
通过有限元法对裂纹扩展行为进行建模和仿真,可以揭示裂纹扩展的机制和规律,为裂纹扩展的控制和预测提供依据。
此外,还可以通过实验手段对模型进行验证,从而提高数值模拟的准确性。
在裂纹扩展的机理研究中,马尔文等人提出了著名的“裂纹扩展力学”理论,即线弹性力学中的弹性应力场理论与线弹塑性力学中的应变能释放率理论相结合。
根据这一理论,裂纹扩展的驱动力主要来自应变能释放率,即裂纹前端的弹性应力能转化为其扩展所需的变形能。
根据裂纹形态的不同,裂纹扩展的方式也有所不同,常见的扩展方式包括沿单一平面、沿不同平面和远离应力场。
在疲劳分析研究中,我们也需要考虑到应力幅和寿命之间的关系。
疲劳寿命是指材料在一定应力幅范围内经历的循环次数,其与应力幅呈相反的指数关系。
通过疲劳试验,我们可以获得不同应力幅下的疲劳寿命数据,并通过拟合得到应力寿命曲线。
通过应力寿命曲线,我们可以预测在特定应力幅下的疲劳寿命,从而为机械元件的设计和优化提供指导。
除了裂纹扩展与疲劳分析的基础研究外,工程实践中还需要考虑到实际工况下的各种复杂因素。
例如,在航空航天领域,飞机机身结构处于动态载荷的作用下,高空环境下氧化腐蚀等因素也可能引起裂纹扩展和疲劳失效。
因此,我们需要进行更加全面和深入的研究,以便更好地应对复杂工况下的疲劳问题。
ISO 12108-2002 金属材料 疲劳试验疲劳裂纹扩展方法

ISO 12108-2002 金属材料疲劳试验疲劳裂纹扩展方法
(一) ISO 12108-2002
标准英文名称:Metallic materials –Fatigue testing –Fatigue crack growth method 标准中文名称
金属材料疲劳试验疲劳裂纹扩展方法
适用范围
适用于金属材料疲劳裂纹扩展速率和疲劳裂纹扩展门槛值的测定。
应用于材料检验,失效分析,质量控制,选材及新金属材料研发等方面。
试验原理
对预疲劳裂纹缺口试样施加力循环,测量裂纹扩展增量Δa,得到da/dN ΔK 数据点,测定4 / 6疲劳裂纹扩展速率和门槛值。
测定性能参数
疲劳裂纹扩展速率da/dN
疲劳裂纹扩展门槛值ΔKth
试验程序
1)测量试样尺寸;
2)试样预制疲劳裂纹;
3)采用恒力幅增K 试验方法测定疲劳裂纹扩展速率大于10-5mm/cycle 材料的疲劳裂纹长度a 和力循环数N。
采用降K 方法测定疲劳裂纹扩展速率小于10-5mm/cycle 材料的疲劳裂纹长度a 和力循环数N;
4)采用割线方法,或者,对于增K 试验,采用拟合递增多项式a-N 曲线求导方法确定扩展速率。
采用线形回归方法确定扩展速率相应为10-8mm/cycle 时的应力强度因子范围为疲劳裂纹扩展门槛值。
结果及试验报告
国际标准编号;
材料名称、试样标识、取样方向部位;
试样形状和尺寸;
试样力学性能;
力变量(包括力范围,力比值,加力波形和频率);试验环境参数(包括温度,介质,湿度);
数据处理方法;
测定的性能结果。
试验设备:。
第5讲 疲劳裂纹扩展速率、影响因素、疲劳机理、工程塑料的疲劳、影响疲劳强度的主要因素
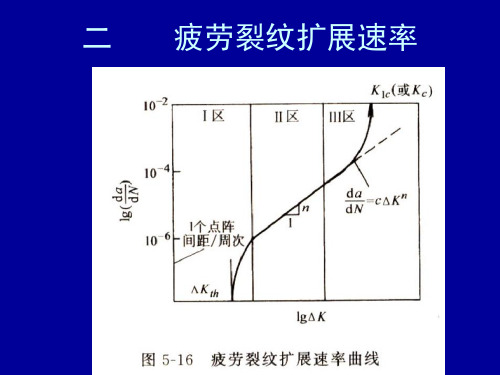
K th
lg(K)
C、m和Kth, 是描述疲劳裂
纹扩展性能的 基本参数。
常用材料的Paris关系可以查阅有关资料(如下表所示)
三 影响疲劳裂纹扩展速率的因素
1.应力比或平均应力的影响
S
Sm
O r=-1
r=-1/3
r=0 N
Sa
r增大
Sm>0
Sm<0 Sm=0
N
另外,考虑材料和环境的共同作用,有些资料 中的修正公式为
• 长期受交变应力或脉动应力作用,在应力集中区产 生。
• 从零件上划伤、刻槽、内凹拐角处及表面缺陷处。 • 红色光滑线条。
焊接缺陷
5. 温度的影响
Effect of Temperature on Fatigue
• Low-Temperature Fatigue • High-Temperature Fatigue
第七节、影响疲劳强度的主要因素
第五节 疲劳过程及机理
一.疲劳裂纹萌生过程及机理(裂纹形成 阶段,Ⅰ阶段)
对于宏观均匀的材料,零件上的疲劳裂纹 发展都是由表面裂纹的形核、微(短)裂纹的 扩展和长裂纹的扩展三个阶段所组成的
(一)滑移带开裂产生裂纹
(二) 相界面开裂产生裂纹
举 例
(三) 晶界开裂产生裂纹
在循环应力的作用下,位错在多晶 体晶界处塞积,当塞积位错和应力集中 得不到释放、应力峰值超过晶界强度时 就会在晶界处形成裂纹,造成晶界开裂 产生裂纹
回火温度越低、门 槛值越小,材料变 脆越容易产生裂纹
试验观察表明,疲劳裂纹扩展的三个区域对 应着三个不同的断裂机制。Ⅰ区的疲劳断口类似 解理断裂,由许多小断裂平面组成;Ⅱ区的疲劳 断口则对应着出现疲劳条纹;在高△K的Ⅲ区, 断口形貌则转向微孔的形成与聚合。
强度理论疲劳裂纹扩展

故控制参量 K定义为:
K=Kmax-Kmin R>0
K=Kmax
R<0
应力比 R=Kmin/Kmax= min/ max;
与 K相比,R的影响是第二位的。
5
三.疲劳裂纹扩展速率FCGR a (mm) Ds R=0
Fatigue Crack Growth Rate ai
da
实验
a0
dN
N
a =a0 R=0 =con
-1
-
1 ] 0.5m-1 aC
1
ln(aC )
C( fDs p )m a0
m2 m=2
11
2. Paris公式的应用
基本 方程
断裂判据: Kmax = f s max p aC KC
裂纹扩展方程:Nc=(f, Ds,R, a0, ac)
抗疲劳断裂设计计算
1)已知载荷条件DS,R,初始裂纹尺寸a0, 估算临界裂纹尺寸ac , 剩余寿命Nc.
pa ]m
积分有:D
sm
N
=
2)已知载荷条件 S,R, 给定寿命Nc, 确定 ac及可允许的初始裂纹尺寸a0。
3)已知 a0, ac, 给定寿命Nc, 估算在使用工 况(R)下所允许使用的最大应力Smax。
12
例1:边裂纹板a0=0.5mm, 载荷为 smax=200Mpa。 R=0, 材料参数sys=630MPa, su=670MPa, DKth=5.5MPa, Kc=104MPa, 裂纹扩展速率为 da/dN=6.9×10-12(DK)3, 试估算其寿命。
中心裂纹宽板 f=1;
应力强度因子:K=f s p a 单边裂纹宽板 f=1.12
临界裂纹尺寸aC:有线弹性断裂判据:
第十四讲--疲劳裂纹扩展

第十四讲疲劳裂纹扩展上节回顾Dugdale模型(带状屈服模型)裂纹尖端张开位移(COD)无限大板的COD,有限宽板的CODCOD准则J积分,J积分的守恒性,J积分准则平面应力断裂的R阻力曲线1.疲劳裂纹扩展速率疲劳裂纹扩展的定量表示用da/dN,称为裂纹扩展速率,表示每个循环裂纹长度的平均增量。
da/dN-ΔK曲线与S-N、ε-N曲线类似,描述疲劳裂纹扩展规律的曲线为da/dN-ΔK曲线只有在拉伸应力作用下裂纹才能扩展,则疲劳裂纹应力强度因子幅度定义为ΔK = K max-K min R > 0ΔK = K max R < 0基本da/dN-ΔK曲线:R = 0的da/dN-ΔK曲线双对数坐标下da/dN-ΔK曲线的形状疲劳裂纹扩展的三个区域Array一般情况下,da/dN-ΔK曲线在双对数坐标上可分为三个区域1区:低速率区,该区内ΔK的微小降低,da/dN急剧下降。
存在ΔK的一个下限值ΔK th,该值处裂纹扩展速率近似为零,ΔK th称为门槛值。
ΔK th受R的影响较大。
2区:中速裂纹扩展区,裂纹扩展速率一般在10-9~10-5m/C范围内。
中速裂纹扩展区的da/dN-ΔK在双对数坐标上近似为线性关系。
3区:高速扩展区,即K max K C时,裂纹快速扩展,其寿命通常不考虑。
其上限值以铅垂渐近线表示2.裂纹扩展速率公式1)低速率区一般是进行裂纹不扩展设计ΔK < ΔK th2)中速裂纹扩展区,Paris公式Paris 对具有中心穿透裂纹平板拉伸实验数据归纳, 对中速裂纹扩展区(2区)提出的经验关系式m K C dNda)(∆= C ,m :材料常数m 不随构件的形状和荷载性质(拉伸或弯曲)改变,C 与材料性能相关。
由于存在门槛值ΔKth ,Donahue 等(Donahue ,1972)建议如下修正公式m th K K C dNda)(∆-∆= 3)高速扩展区可由下式估计裂纹扩展速率从2区向3区转变的应力强度因子 ys T E K σ00637.0max =K maxT :R = 0时的最大循环应力作用下的应力强度因子3.da /dN 的理论公式 塑性钝化模型C. Laird (1967)的观测结果裂纹尖端载循环荷载下出现反复钝化和 重新尖锐化的交替过程。
疲劳裂纹扩展相关概念要点

疲劳裂纹不扩展或扩 展速率极其缓慢
da 10-7 mm/ 循环 dN 在室温及R=0.1条件下A533钢 的疲劳裂纹扩展曲线
图4-4
二、疲劳裂纹扩展速率 图4-4
第二阶段 :中速率裂纹扩展区
疲劳裂纹扩展遵循幂函数规律,也就是疲劳裂纹扩展率可以用
应力强度幅值 K 的幂函数表示,这就是目前采用的Paris公式。
——尺寸影响系数
——表面强化处理影响系数
K ——外形影响系数
n ——安全因数
4、构件的疲劳设计
“安全寿命”设计: 需要建立疲劳载荷谱,测定S-N曲线(S为交变应
力,N为应力循环周数),并用累积损伤理论估算 “安全寿命”。
综上,以上两种方法所依据的S-N曲线,是用无裂 纹光滑试样测得的,不能充分保证构件的可靠性和经 济性。
4、构件的疲劳设计
研究疲劳扩展的意义
最早的“无限寿命”设计,要求在无限长的试用期 内,不发生疲劳破坏。 以最大应力为纵坐标,循环 max
r min max
次数(寿命)为横坐标,将疲 劳试验结果描绘成的曲线,
max 1 max 2
S-N曲线
称为应力—寿命曲线或S—N
曲线。
K Kmax Kmin
C、m是材料常数,对于同一材料,m不随构件的形状和载荷性质而改变,
常数C与材料的力学性质(如 s 及硬化指数等)、试验条件有关。
对数形式
lg da lg C m lg K dN
对应图4-3
二、疲劳裂纹扩展速率
第一阶段低速率区
也称做疲劳裂纹扩展 缓慢区,存在着一个 疲劳裂纹扩展的门槛
常温试验结果表明:
N1 N2
疲劳裂纹;扩展速率;门槛值;剩余寿命;测试系统精讲

研究内容及方法
⑵监测系统软件 表面疲劳裂纹监测系 统软件全部由C语言编程。系统特点如 下: ①通过人机对话方式对采样参数进行 设定,操作简便; ②数据采集采用实时时钟中断方式进 行,采集过程中可对采样数据进行实 时处理、实时显示采样数据、波形和 图形,不影响数据采集的连续性;
研究内容及方法
③采样监视阶段,可对采样数据的漂移 做进一步的调零处理,使采样精度大大 提高; ④实现了对采样时间的累加与再现,为 疲劳寿命预测提供了依据; ⑤根据设定报警限实时报警,以测得的 裂纹值作为初始裂纹,按照损伤容限设 计理论实时预测疲劳裂纹剩余寿命;
论文总结
(2)对影响疲劳裂纹扩展速率的因素进行分 析,提出表面疲劳裂纹监测系统框图,说 明在工程中应用的意义及特点。
论文总结
(3) 因为疲劳裂纹扩展而使机械零 件和工程构件出现疲劳失效,因为没 有即时的预防而造成的损失是非常大 的,为了预防其破坏设备和构件的正 常运行,就要对构件进行适时监控, 用最有效的方法解决问题,所以对疲 劳裂纹扩展规律研究是十分必要的。
, m J 1.84。列出拟合后得到的结果以及
da 1.40 (J )1.84 dN
研究内容及方法 用最小二乘法拟合 得到的压力容器业 常用材料16 MnR的 J 积分疲劳裂纹扩 展公式为:
da 1.40 (J )1.84 dN
16MnR的 ln( da / dN ) ln( J ) 拟和曲线
研究内容及方法
若理论门槛值 K thT与实用门槛值 K thO 相差很小,用后者替代前者当然可行。但 有试验发现,当 K K thO 时,仍能观测到 K thT 裂纹的明显扩展。对于有的材料, 与 K thO 之间的差别是明显的。在这样的场合,将 材料的实用门槛值代替理论门槛值用于结 构的损伤容限设计,无疑将冒风险。因此, 找到一种较为可靠的确定理论门槛值的方 法就显得很有意义。
第5章 疲劳断裂 第3节 疲劳裂纹扩展

16
疲劳寿命的估算
采用稳定扩展阶段 寿命估算总寿命
17
环境对第2扩展阶段的影响
1968年发现的现象:在潮湿空气中铝合金 能够形成清晰的疲劳条纹,但在真空中却 不能形成疲劳条纹。 1983年发现在真空中铝合金疲劳裂纹扩展 速率低于潮湿空气条件 在2024Al,7075Al,TC4中也有类似现象。 上述材料共同的特点是在潮湿空气中能够 形成氧化膜。
23
新形成的裂纹面附近金属发生弹性恢复
可以解释应力比、瞬时过载对疲劳裂纹扩展的 24 影响
3.2.2 氧化物诱发的裂纹闭合
潮湿气氛在新形成的表面形成氧化物,氧化物诱发裂纹闭合
25
3.2.3 裂纹面粗糙诱发裂纹闭合
应力场强度因子低,裂纹张开角度小; 粗晶粒引起裂纹面呈现锯齿形状; 晶界,第二相,载荷突然变化引起裂纹偏折。
18
19
3.1.3 疲劳裂纹第3阶段扩展
断裂时裂纹长度取决于材料的断裂韧性 此时裂纹长度已经较大,因此δK较大,此时裂纹 扩展速率很快,试验环境对扩展速率影响不大。 断口上有疲劳条纹,还可能有韧窝或结理断裂刻 面,而韧窝或解理断裂对组织敏感,因此这一阶 段扩展速率对材料组织十分敏感。 从机制上有交变应力作用下的塑性锐化机制,也 有单调加载条件下的微孔聚集机制
9
材料的组织
欠时效态: 位错能够剪切GP区, 位错容易运动,滑 移容易进行;容易 形成单滑移;在遇 到晶界后滑移改变 方向;使得裂纹运 动方向改变。 过时效态: 位错只能绕过析出 相,形变时往往形 成双滑移,裂纹扩 展平直。
10
11
欠时效时材料强度较低,但门槛值大。 但材料的强度低,其疲劳强度(σ-1)小。 门槛值适用于疲劳裂纹扩展,尤其是低应力强度因子范围的疲 劳裂纹扩展。 疲劳强度主要适用于疲劳裂纹萌生。
预测疲劳裂纹扩展的多种理论模型研究_石凯凯_蔡力勋_包陈

1
I 型裂纹尖端循环应力应变场
基于材料低周疲劳行为预测 I 型疲劳裂纹扩展 的预测模型是由裂纹尖端循环载荷下的应力应变 场,继而结合裂纹尖端失效准则分析疲劳裂纹扩展 规律。现有的预测模型采用的循环应力应变场是基 于小范围屈服条件下的静应力应变场结合 RICE 的 塑性叠加法衍生得到的。 1.1 静态拉伸下的裂纹尖端应力应变场 目前可用于描述平面应力条件下裂尖区的应 力应变场主要有两类。 [18] [19] 一类是 KUJAWSKI 等 将 RICE 对 III 型裂 纹尖端的应力应变场,扩展应用至 I 型裂纹尖端小 范围屈服应力应变场
n /(1 n ) 2 K y 2 (1 n) π y r n /(1 n ) 1/(1 n ) 2 K K2 y y 2 2 (1 ) π n r y (1 n) π y r
在往复载荷作用下,构件均会发生疲劳破坏 。线 弹性断裂力学认为,疲劳失效分析中裂纹尖端附近 的应力场是由应力强度因子 K 控制的,所以裂纹在 疲劳载荷下的扩展行为可利用应力强度因子进行定 性和定量的描述。 基于材料低周疲劳行为预测 I 型疲劳裂纹扩展 行为,国外已经提出了多种模型,其模型从研究对 象的角度分为材料微观参量描述的裂纹扩展模 [4-5] 型 和材料宏观参量表征的裂纹扩展模型,如 [6-7] GLINKA 等 基于裂尖扩展区内常应变假定, [8-12] SKELTON KUJAWSKI 等 在裂尖引入钝化假定,
(1) 式中 σ, ε ——裂纹尖端应力和应变; σy, εy ——屈服强度和屈服应变; n——材料应变硬化指数; r ——离裂纹尖端的距离。
52
机
械 50 卷第 18 期期
桥梁负载激励下疲劳裂纹扩展研究

桥梁负载激励下疲劳裂纹扩展研究一、桥梁负载激励下疲劳裂纹扩展概述桥梁作为重要的交通基础设施,其结构的稳定性和安全性至关重要。
在实际使用过程中,桥梁会受到各种荷载的作用,包括静荷载、动荷载以及环境因素等。
这些荷载的长期作用会导致桥梁结构产生疲劳裂纹,进而影响桥梁的使用寿命和安全性能。
因此,研究桥梁在负载激励下的疲劳裂纹扩展机制,对于保障桥梁的安全运营具有重要意义。
1.1 桥梁疲劳裂纹扩展的基本概念桥梁疲劳裂纹扩展是指在循环荷载作用下,桥梁结构中微小裂纹逐渐扩展直至结构失效的过程。
这一过程涉及到材料的微观结构变化、裂纹尖端的应力场分布以及裂纹扩展路径等多个方面。
疲劳裂纹扩展的研究,旨在通过理论分析和实验验证,揭示裂纹扩展的规律,预测裂纹扩展的速度和寿命,为桥梁的维护和加固提供科学依据。
1.2 桥梁疲劳裂纹扩展的影响因素桥梁疲劳裂纹扩展的影响因素众多,主要包括以下几个方面:- 材料特性:桥梁结构的材料特性,如屈服强度、疲劳极限、断裂韧性等,对裂纹扩展速率和路径有着直接影响。
- 荷载特性:荷载的大小、频率、循环次数等特性,决定了裂纹扩展的动力条件。
- 环境因素:温度、湿度、腐蚀介质等环境因素,会加速材料的疲劳损伤,影响裂纹扩展速率。
- 结构细节:桥梁结构的设计细节,如焊缝、连接件、应力集中区域等,也是影响裂纹扩展的重要因素。
二、桥梁负载激励下疲劳裂纹扩展的理论研究2.1 疲劳裂纹扩展的理论模型疲劳裂纹扩展的理论模型是研究裂纹扩展规律的基础。
目前,国内外学者提出了多种疲劳裂纹扩展模型,如Paris 法则、Forman法则等。
这些模型通过描述裂纹长度与循环次数之间的关系,预测裂纹扩展速率。
然而,由于实际桥梁结构的复杂性,单一的理论模型往往难以准确预测裂纹扩展行为,因此,需要结合桥梁的具体工况,对理论模型进行修正和完善。
2.2 疲劳裂纹扩展的数值模拟随着计算机技术的发展,数值模拟已成为研究桥梁疲劳裂纹扩展的重要手段。
机械结构的疲劳裂纹扩展特性分析与优化

机械结构的疲劳裂纹扩展特性分析与优化概述:机械结构的疲劳裂纹扩展特性是工程设计和使用过程中必须要考虑的重要问题之一。
疲劳裂纹扩展会导致结构强度下降,甚至引起严重事故。
因此,对机械结构的疲劳裂纹扩展特性进行深入分析和优化是至关重要的。
疲劳裂纹扩展的基本理论:疲劳裂纹扩展是指材料内部或表面的裂纹在受到交变载荷作用时逐渐扩展,在终止于结构破裂之前的过程。
裂纹扩展主要受到应力水平、载荷频率、环境条件以及材料的力学性能等因素的影响。
根据线弹性断裂力学理论,裂纹扩展速率可以用裂纹尖端位移增量和应力强度因子之间的关系来描述。
疲劳裂纹扩展的影响因素:1. 应力水平:应力水平是疲劳裂纹扩展的重要因素之一。
较高的应力水平会加速裂纹扩展过程,而较低的应力水平则会减缓裂纹扩展。
2. 载荷频率:载荷频率是指材料在受到交变载荷作用时的频率。
高频率下的载荷会加速裂纹扩展速度,而低频率下的载荷则会减缓裂纹扩展。
3. 环境条件:环境条件包括温度、湿度、腐蚀介质等因素。
某些环境条件下,如高温、高湿等,会导致材料的腐蚀和渗透,从而加速裂纹扩展。
4. 材料的力学性能:材料的强度、韧性和断裂韧性等力学性能会影响疲劳裂纹扩展的速率和路径。
疲劳裂纹扩展分析方法:1. 线性弹性断裂力学法:该方法假设材料具有线弹性行为,在结构的局部区域进行裂纹尖端位移和应力强度因子的计算。
2. 塑性力学法:该方法考虑材料的塑性行为,将材料的强度和塑性变形考虑在内,从而可以更准确地计算裂纹尖端位移和应力强度因子。
3. 数值模拟方法:数值模拟方法通过建立有限元分析模型,利用计算机进行裂纹扩展过程的模拟,得到裂纹尖端位移和应力强度因子。
疲劳裂纹扩展优化方法:1. 结构优化:通过改变结构的几何形状和尺寸,减少应力集中和应力激励,从而减缓裂纹扩展速率。
2. 材料优化:选择具有较高强度、韧性和断裂韧性的材料,可以增加结构的抵抗裂纹扩展的能力。
3. 加工和热处理优化:通过合理的加工和热处理工艺,降低材料中的缺陷和应力,减少裂纹扩展的可能性。
轧辊材料疲劳裂纹扩展理论计算与分析

轧辊材料疲劳裂纹扩展理论计算与分析温宏权;李彦龙;瞿海霞;吴琼;孙大乐【摘要】Surface spalling is one of main forms of the roll failure .The crack propagation process d a/dN-ΔK was calculated for the roll material with the fatigue crack propagation theory . The effects of various parameters on the roll crack growth were analyzed , as well as the crack propagation characteristics of different rolls .The results showed that elastic modulus , stress ratio, residual stress , crystal size , fracture plastic , work stress and tensile strength had less and less effects on the crack propagation rate , elastic modulus was the most remarkable factor and tensile strength was the lest .Higher elastic modulus , lower residual stress , rougher crystal , and higher fracture plastic of the roll material could efficiently restrain fatigue crack propagation of rolls .Work layer had higher crack propagation resistance than centre of the roll , so as to the backup roll than the work roll and the forged roll than the cast roll .It was helpful to make clear the failure mechanism and take effective precautions against the roller ’ s spalling .%辊面剥落是轧辊失效的主要形式之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.沃勒为常规疲劳强度设计奠定了基础,他发现在试验中平 均应力对疲劳寿命有影响.
对称循环 非对称循环 为了考虑平均应力的影响,就出现了疲劳极限图,这里贡献最大 的就是W.格伯和J.Goodman,通过疲劳极限图可将有平均应力下的 疲劳问题转化为对称循环下的疲劳寿命曲线。
二战期间,飞机疲劳失事频繁出现,一些动力机械也出现疲劳事 故,使得循环应力作用下的疲劳事故成为实际问题。出现了疲劳累积 损伤理论,人们开始研究有限寿命设计。疲劳累积损伤贡献最大的要 算Palmgren和Miner,Palmgren于1924年提出了线性累积损伤理论他 在估算滚动轴承的寿命时假设累积损伤与转动次数成线性关系。1945 年,美国人Miner对线行累积损伤进行了理论推导,形成广泛应用的 Miner-Palmgren线性累积损伤法则。 断裂力学的出现,使人们注意研究裂纹扩展寿命,最为著名就是 美国人P.C.Paris于1957年提出的Paris公式,它是计算裂纹扩展寿命 的基本公式。 裂纹形成寿命的研究可追溯到二十世纪五十年代Manson和Coffin 进行了开拓性的研究,提出了著名的Manson-Coffin应变—寿命曲线。 Neuber利用结构切口根部材料可用光滑式样来模拟实验的原理提出了 局部应力—应变法,从而形成了裂纹形成寿命计算方法。
即从第3级加载开始到构件破坏的剩余寿命为885次。 4 疲劳强度的影响因素 若寿命计算采用材料的S-N曲线,则必须考虑影响疲劳寿命的几个因 素。 (1)应力集中系数
——光滑试样的疲劳极限 ——缺口试样(结构)的疲劳极限 一般查表可得,也有各种计算公式。郑州机械研究所建议采用下式计 算:
迟滞回线所包围的面积代表材料塑性变形时外力所做的功或所消耗的能 量,也表示材料抗循环塑性变形的能力,该面积可以通过积分来计算。 (2)材料的记忆特性
(a) 应力-时间历程 (b)应力-应变响应 记忆特性:由34时,先由3点,再由4点,不是沿3的延长线(虚 线),而是沿着12的延长线,即材料记忆原来路径。 记忆特性用来评价材料的循环应变历史对应力—应变的影响。 (3)载荷顺序效应 载荷顺序对疲劳寿命的影响已经被试验所证实。
(三):疲劳寿命计算:名义应力法,局部应力—应变法,断裂力学法。 1. 名义应立法:计算全寿命,主要用于高周疲劳; 2. 局部应力—应变法:计算裂纹形成寿命; 3. 断裂力学法:计算裂纹扩展寿命。 (四):疲劳试验 材料试验,实物结构试验,高周疲劳试验,低周疲劳试验,裂纹扩展寿命试验
(五):常规疲劳强度设计:
由于第i级载荷 单独作用下一直到构件破坏 的循环次数为 (由S-N曲线可知),故: w 1: w = n i : N I 即:
代入上式可得:
即: ——Miner定律 Miner定律的不足之处: (1)没有考虑载荷的加载顺序 事实上,载荷顺序对于疲劳累积损伤是有影响的,若采用二级 加载实验,若进行低—高应力实验,则 >1。若进行高—低应 力试验,则 <1。 低周:在低应力下材料产生低载“锻炼”效应,使裂纹形成时间 推迟。先进行高应力作用则易形成裂纹,后续低应力能使裂纹扩展。 对于随机载荷下的疲劳试验结果表明,由于“加速”和“迟滞” 效应相互综合。最终结果与加载顺序差异不大。 (2) 累积损伤D= ,试验数据大多数介于0.3~3.0之间,但统计结 果表明D的平均值 =1.0。若将D看作为随机变量。则D服从对数 正态分布。(P86~P87) 2 Miner法则的应用方法
(4)循环硬化与软化
(a)循环硬化(产生同样的应变需要更大的应力) (b)循环软化(产生同样的应变需要更小的应力) 迟滞回线的变化:
材料产生循环硬化还是循环软化取决于材料的屈强比 一般情况下 : 产生循环硬化
产生循环软化 要根据实际材料决定,退火材料产生硬化, 冷硬材料产生软化 (5) 循环应力—应变曲线的测试 一般通过多级加载试验测定
(a).第一大载荷以压载荷结束,应力集中处产生拉力残余应力; (b).第一大载荷以拉载荷结束,应力集中处产生压力残余应力。 压力残余应力有利于提高疲劳强度 载荷的迟滞效应: 大载荷后跟小载荷,大载荷结束后在裂纹尖端会形成一个大的 塑性区,小载荷在很长时间内才使裂纹穿过塑性区,也就是说这种 加载顺序会延缓裂纹扩展。
令 则 即: 已知 : 和 P-S-N曲线: 已知 : 则: 即: P-S-N曲线:
——存活率为p(可靠度为p)时的疲劳寿命 ——应力均值 ——与存活率有关的材料常数,查表
p<50%
P=50%
P>50%
5 疲劳极限线图 在规定的破坏循环寿命下,根据不同的应力比r记录的疲劳极限,画出 图线: 格伯 (1)格伯图线 Goodman 取曲线方程为抛物线
2) 动强度设计方法,即疲劳设计: 根据结构受力载荷,确定疲劳危险部位,保证结构危险部位满足疲劳 强度要求。 疲劳设计分为:有限疲劳设计,无限疲劳设计(早期)
设计要求 参考相关结构,进行受力分析, 包括:动力学彷真,有限元计算,疲劳强度计算
确定结构尺寸
结构疲劳实验 修改结构 是否满足要求
结束
疲劳设计包括:力学,材料学,测试试验技术工程设计 (2) 疲劳强度发展史 疲劳强度起源于十九世纪处,当时由于铁路运输的发展,不断出 现机车车轴的疲劳破坏。德国人 艾伯特 1829年;法国人 彭塞则 1839年;苏格兰人 兰金 1843年先后进行研究。 真正的车轴疲劳研究是德国人 A.沃勒 他设计了一台旋转弯曲疲 劳实验机,对车轴在不同应力下进行了疲劳实验,得到了第一条S-N 曲线,他发现在应力低于弹性极限时也会发生疲劳破坏,但存在一个 应力幅极限值,当应力小于该值时就不会发生疲劳破坏。
(3)疲劳的分类 疲劳主要分为高周疲劳与低周疲劳,高周用应力-寿命曲线进行 计算,名义应力法(应力疲劳);低周用应变-寿命曲线进行计算, 局部应力—应变法,(应变疲劳);高周疲劳与低周疲劳的分界一 般是104次。
( 4)疲劳破坏的三个阶段: 裂纹形成—裂纹扩展—疲劳断裂。 在交变载荷作用下,在结构有缺陷部位或有应力集中部位, 结构形成塑性变形晶粒在晶界面之间滑移形成微裂纹裂纹扩展 就形成宏观裂纹裂纹继续扩展到一定时候截面强度削弱到截面 应力达到强度极限瞬断。 (5)疲劳断口 瞬间断裂区 疲劳断口由三部分组成:疲劳源区; 疲劳扩展区;瞬断区。 断裂位置一般都在应力集中部位, 疲劳扩展区 如拐弯,轴臂的过度处。 2:金属的循环应力—应变 疲劳源区 (1)循环加载的迟滞回线
索德倍尔
或 (2)Goodman图线 极限图为直线:
或
(3)索德倍尔
二 疲劳累积损伤理论
疲劳过程既可以看成是损伤趋于一个临界损伤值的累计过程,也 可以看成是材料固有寿命的消耗过程。 1 Miner线性法则 Miner根据功能原理推导出了累积损伤计算公式。 设构件在m级载荷( , ,… )作用。各级载荷循环次数分别 为 , ,… 。即构件经过次循环后发生破坏。 设构件破坏时吸收的净功为W,各级载荷下各构件吸收的净功分 别为 , … ,则
——均值,也叫数学期望。
——标准差,数学上叫均方根值。
对数正态分布,将随机变量的对数函数进行分析。威布尔分布(寿命)
N ——试样寿命 ——最小寿命参数 ——特征寿命参数 b——形状参数 威布尔曲线为一种偏态分布 可靠度的概念:可靠度R也叫做成活率 例如研究疲劳强度, 为概率分布密度,则有: 设材料的工作载荷xp,则材料的强度x< xp ,材 料将发生破坏,故破坏概率就是图中的阴影部 分。剩下部分就是不发生破坏的概率。称为存 活率或可靠度。故:
应力比
对称循环,
脉动循环
静应力
3 材料的S—N曲线 根据不同应力水平分组进行疲劳试验, 根据实验数据进行拟合,一般采用最小二乘 法。 曲线为指数曲线,即: 对上式两边去对数 :
疲劳试验经常不是对称循环下进行的, 即 所以有平均应力 存在, (拉应力) 疲劳寿命降低, (压应力) 疲劳寿命增高。
疲劳试验的应力比如何确定?一般根据实际受力情况来确定,当 实际载荷的应力比变化时,要根据Goodman疲劳极限图将实际载荷 转化为试验载荷,再用试验S—N曲线进行疲劳寿命评估。 一般资料给出的材料S—N曲线一般都是对称循环( ),可 以把疲劳极限记为 4.P-S-N 曲线 不同可靠度下的应力——寿命曲线 (1) S-N曲线中S,N的概率密度函数 大量实验表明:疲劳强度符合正态分布 (同寿命下的应力分布)。疲劳寿命符合对数 正态或威布尔分布(同应力水平下的寿命) 正态分布
结构疲劳寿命 令
:
——第i级载荷次数与总次数之比。 已知载荷谱的总次数和分次数与总次数之比,
3 其它损伤理论 有非线性疲劳累积损伤模型,还有双线性疲劳累积损伤模型,都 比较复杂。预测精度改进不明显。应用较多的就是科尔顿—多兰累积 损伤模型,推导过程略。最后计算公式为
d也是材料常数,计算时一般取d≈0.8m 例:作三级应力下的疲劳试验 =2000Mpa, =827 Map, =1380 Map。已知 =200次, =4000次,求 作用下的剩余寿命。 解:由S-N曲线可知
教学参考书
(1)徐灏: 《疲劳强度》; (2)吕彭民:《大型复杂结构抗疲劳设计》; (3)张祖民:《机械结构抗疲劳设计》; (4)J.Fatigue (5)《机械强度》杂志 (6)J.Fracture&Fatigue
一 疲劳强度基本概念
1 概论: (1)疲劳强度在工业中的地位 机械零件失效的三种形式:a:磨损;b:腐蚀;c:断裂。其中前两 种过程慢,可以更换或者修复;而断裂则是灾难性的。受动载荷作用的机 械零件和工程结构80%是由金属疲劳断裂引起的。疲劳强度校核是新产品 和已有产品强度校核的主要内容。 机械设计有两种方法: 1)静强度设计方法:工程机械设计目前主要采用这种方法(国外40年代)。 也就是许用应力法: 存在问题: a. 设计的机械零件特别笨重(为了安全,只有加大整个截面尺寸); b. 尽管笨重,但仍有疲劳裂纹产生。 原因: a. 疲劳裂纹发生在构件的危险点的局部区域,通过裂纹不断扩展, 最终导致断裂。 b. 疲劳危险部位往往与静强度危险部位不一致。
