中考数学压轴题分类练习圆与动点专题无答案

合集下载

2019-2020学年中考数学压轴题分类练习圆与动点专题.doc

2019-2020学年中考数学压轴题分类练习圆与动点专题1.在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 上存在一点Q ，使得P Q 、两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当O 的半径为2时，①在点123115,0,,,0222P P P ⎛⎛⎫⎛⎫⎪ ⎪ ⎝⎭⎝⎭⎝中，O 的关联点是_______________． ②点P 在直线y x =-上，若P 为O 的关联点，求点P 的横坐标的取值范围．（2）C 的圆心在x 轴上，半径为2，直线1y x =-+与x 轴、y 轴交于点A B 、．若线段AB 上的所有点都是C 的关联点，直接写出圆心C 的横坐标的取值范围．2.如图，AB 是O 的直径，,2AC BC AB ==，连接AC ．（1）求证：045CAB ∠=；（2）若直线l 为O 的切线，C 是切点，在直线l 上取一点D ，使,BD AB BD =所在的直线与AC 所在的直线相交于点E ，连接AD ．①试探究AE 与AD 之间的数量关系，并证明你的结论； ②EBCD是否为定值？若是，请求出这个定值；若不是，请说明理由．3. 如图，动点M 在以O 为圆心，AB 为直径的半圆弧上运动（点M 不与点A B 、及AB 的中点F 重合），连接OM .过点M 作ME AB ⊥于点E ，以BE 为边在半圆同侧作正方形BCDE ，过M 点作O 的切线交射线DC 于点N ，连接BM 、BN .（1）探究：如左图，当M 动点在AF 上运动时； ①判断OEMMDN ∆∆是否成立？请说明理由；②设ME NCkMN+=，k是否为定值？若是，求出该定值，若不是，请说明理由；③设MBNα∠=，α是否为定值？若是，求出该定值，若不是，请说明理由；（2）拓展：如右图，当动点M在FB上运动时；分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由）4.已知二次函数y=﹣x2+bx+c+1，①当b=1时，求这个二次函数的对称轴的方程；②若c=14b2﹣2b，问：b为何值时，二次函数的图象与x轴相切？③若二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜x2，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足13DEEF=，求二次函数的表达式．5．已知：AB 是O ⊙的弦，点C 是AB 的中点，连接OB 、OC ，OC 交AB 于点D . (1)如图1，求证：AD BD =；(2)如图2，过点B 作O ⊙的切线交OC 的延长线于点M ，点P 是AC 上一点，连接AP 、BP ，求证：90APB OMB -=∠∠°.(3)如图3，在(2)的条件下，连接DP 、MP ，延长MP 交O ⊙于点Q ，若6MQ DP =，3sin 5ABO =∠，求MP MQ 的值.6.如图，⊙M 的圆心M （﹣1，2），⊙M 经过坐标原点O ，与y 轴交于点A ，经过点A 的一条直线l 解析式为：y=﹣x+4与x 轴交于点B ，以M 为顶点的抛物线经过x 轴上点D （2，0）和点C （﹣4，0）．（1）求抛物线的解析式；（2）求证：直线l 是⊙M 的切线；（3）点P 为抛物线上一动点，且PE 与直线l 垂直，垂足为E ，PF ∥y 轴，交直线l 于点F ，是否存在这样的点P ，使△PEF 的面积最小？若存在，请求出此时点P 的坐标及△PEF 面积的最小值；若不存在，请说明理由．7.如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE．（1）求证：AC2=AE•AB；（2）过点B作⊙O的切线交EC的延长线于点P，试判断PB与PE是否相等，并说明理由；（3）设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．8.如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC 的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，（1）点点同学通过画图和测量得到以下近似数据：猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．9. 如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．（1）当∠APB=28°时，求∠B和CM的度数；（2）求证：AC=AB。

河北省中考数学总复习动点问题专题(无答案)

河北中考复习之动点问题1、如图6所示，一艘轮船以20里/时的速度由西向东航行，途中接到台风警报，台风中心正以40里/时的速度由南向北移动，距台风中心2010里的圆形区域（包括边界）都属台风区．当轮船到A 处时，测得台风中心移到位于点A 正南方向B 处，且AB = 100里．（1）若这艘轮船自A 处按原速度继续航行，在途中会不会遇到台风？若会，试求轮船最初遇到台风的时间；若不会，请说明理由；（2）现轮船自A 处立即提高船速，向位于东偏北300方向，相距60里的D 港驶去．为使台风到来之前，到达D 港，问船速至少应提高多少（提高的船速取整数，1336≈.）？2、如图10，在菱形ABCD 中，AB ＝10，∠BAD ＝60°．点M 从点A 以每秒1个单位长的速度沿着AD 边向点D 移动；设点移动的时间为t 秒(100≤≤t ).(1) N 点为BC 边上任意一点.在点M 移动过程中，线段MN 是否一定可以将菱形分割成面积相等的两部分，并说明理由；(2) N 点从点B (与点M 出发的时刻相同)以每秒2个单位长的速度沿着BC 边向点C 移动，在什么时刻，梯形ABNM 的面积最大?并求出面积的最大值；(3) 点N 从点B (与点M 出发的时刻相同)以每秒)2(≥a a 个单位长的速度沿着射线BC 方向（可以超越C 点）移动，过点M 作MP ∥AB ，交BC 于点P .当MPN ∆≌ABC ∆时，设分的面积为S ，求出用t 表示S 的关系式，并求当0=S 时a 的值．3、如图12，在矩形ABCD 中，AB =12厘米，BC =6厘米．点P 沿AB 边从点A 开始向点B 以2厘米/秒的速度移动；点Q 沿DA 边从点D 开始向点A 以1厘米/秒的速度移动．如果P 、Q 同时出发，用t (秒)表示移动的时间(0≤t ≤6),那么：（1）当t 为何值时，QAP ∆为等腰直角三角形？（2）求四边形QAPC 的面积；提出一个与计算结果有关的结论；（3）当t 为何值时，以点Q 、A 、P 为顶点的三角形与ABC ∆相似？图10图124、如图12，已知A 为∠POQ 的边OQ 上一点，以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点，且∠MAN ＝∠POQ ＝α（α为锐角）．当∠MAN 以点A 为旋转中心，AM 边从与AO 重合的位置开始，按逆时针方向旋转（∠MAN 保持不变）时， M 、N 两点在射线OP 上同时以不同的速度向右平行移动．设OM ＝x ，ON ＝y （y ＞x ≥0），△AOM 的面积为S ．若cos α、OA 是方程2z 2－5 z ＋2＝0的两个根．（1）当∠MAN 旋转30°（即∠OAM ＝30°）时，求点N 移动的距离；（2）求证：MN ON AN ⋅=2；（3）求y 与x 之间的函数关系式及自变量x 的取值范围；（4）试写出S 随x 变化的函数关系式，并确定S 的取值范围．5、已知：如图12，等边三角形ABC 的边长为6，点D ，E 分别在边AB ，AC 上，且AD =AE =2．若点F 从点B 开始以每秒1个单位长的速度沿射线BC 方向运动，设点F 运动的时间为t 秒．当t ＞0时，直线FD 与过点A 且平行于BC 的直线相交于点G ，GE 的延长线与BC 的延长线相交于点H ，AB 与GH 相交于点O ．（1）设△EGA 的面积为S ，写出S 与t 的函数关系式；（2）当t 为何值时，AB ⊥GH ；（3）请你证明△GFH 的面积为定值；（4）当t 为何值时，点F 和点C 是线段BH 的三等分点．6、如图12，在直角梯形ABCD 中，AD ∥BC ，∠C =90°，BC =16，DC =12，AD =21．动点P 从点D 出发，沿射线DA 的方向以每秒2个单位长的速度运动，动点Q 从点C 出发，在线段CB 上以每秒1个单位长的速度向点B 运动，点P ，Q 分别从点D ，C 同时出发，当点Q 运动到点B 时，点P 随之停止运动．设运动时间为t （秒）．（1）设△BPQ 的面积为S ，求S 与t 之间的函数关系式；（2）当t 为何值时，以B ，P ，Q 三点为顶点的三角形是等腰三角形？（3）当线段PQ 与线段AB 相交于点O ，且2AO =OB 时，求∠BQP 的正切值；（4）是否存在时刻t ，使得PQ ⊥BD ？若存在，求出t 的值；若不存在，请说明理由．P ON M A 图12Q 图12 A B CD P Q 图127、如图10所示，一段街道的两边缘所在直线分别为AB，PQ，并且AB∥PQ．建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N．小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等候小亮．（1）请你在图10中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置（用点C标出）；（2）已知：MN=20 m，MD=8 m，PN=24 m，求（1）中的点C到胜利街口的距离CM．P图108、如图13，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒）．（1）设四边形PCQD的面积为y，求y与t的函数关系式；（2）t为何值时，四边形PQBA是梯形？（3）是否存在时刻t，使得PD∥AB？若存在，求出t的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t，使得PD⊥AB？若存在，请估计t的值在括号中的哪个时间段内（0≤t≤1；1＜t≤2；2＜t≤3；3＜t≤4）；若不存在，请简要说明理由．图139、如图16，在等腰梯形ABCD中，AD∥BC，AB=DC=50，AD=75，BC=135．点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动，过点Q向上作射线QK⊥BC，交折线段CD-DA-AB于点E．点P、Q同时开始运动，当点P与点C重合时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当点P到达终点C时，求t的值，并指出此时BQ的长；（2）当点P运动到AD上时，t为何值能使PQ∥DC ？（3）设射线QK扫过梯形ABCD的面积为S，分别求出点E运动到CD、DA上时，S与t的函数关系式；（不必写出t的取值范围）（4）△PQE能否成为直角三角形？若能，写出t的取值范围；若不能，请说明理由．图10、如图15，在Rt △ABC 中，∠C =90°，AB =50，AC =30，D ，E ，F 分别是AC ，AB ，BC 的中点．点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动；点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动，过点Q 作射线QK ⊥AB ，交折线BC -CA 于点G ．点P ，Q 同时出发，当点P 绕行一周回到点D 时停止运动，点Q 也随之停止．设点P ，Q 运动的时间是t 秒（t ＞0）．（1）D ，F 两点间的距离是；（2）射线QK 能否把四边形CDEF 分成面积相等的两部分？若能，求出t 的值．若不能，说明理由；（3）当点P 运动到折线EF -FC 上，且点P 又恰好落在射线QK 上时，求t 的值；（4）连结PG ，当PG ∥AB 时，请直接．．写出t 的值．12、如图16，在Rt △ABC 中，∠C =90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，到达点A 后立刻以原来的速度沿AC 返回；点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动．伴随着P 、Q 的运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交折线QB -BC -CP 于点E ．点P 、Q 同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当t = 2时，AP = ，点Q 到AC 的距离是；（2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围）（3）在点E 从B 向C 运动的过程中，四边形QBED 能否成为直角梯形？若能，求t 的值．若不能，请说明理由；（4）当DE 经过点C 时，请直接．．写出t 的值． 13、如图，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，AD=6，BC=8，AB ＝33，点M 是BC 的中点．点P 从点M 出发沿MB 以每秒1个单位长的速度向点B 匀速运动，到达点B 后立刻以原速度沿BM 返回；点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动．在点P ，Q 的运动过程中，以PQ 为边作等边三角形EPQ ，使它与梯形ABCD 在射线BC 的同侧．点P ，Q 同时出发，当点P 返回到点M 时停止运动，点Q 也随之停止．设点P ，Q 运动的时间是t 秒（t ＞0）．（1）设PQ 的长为y ，在点P 从点M 向点B 运动的过程中，写出y 与t 之间的函数关系式（不必写t 的取值范围）；（2）当BP=1时，求△EPQ 与梯形ABCD 重叠部分的面积；（3）随着时间t 的变化，线段AD 会有一部分被△EPQ 覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t 的取值范围；若不能，请说明理由．B DE K P Q CA 图15 F GACB PQED图1614、如图，梯形ABCD 中，AB ∥DC ，DE ⊥AB ，CF ⊥AB ，且AE=EF=FB=5，DE=12动点P 从点A 出发，沿折线AD-DC-CB 以每秒1个单位长的速度运动到点B 停止．设运动时间为t 秒，y=S △EPF ，则y 与t 的函数图象大致是（）15、如图151-和图152-，在ABC △中，51314cos .13AB BC ABC ===，，∠ 探究在如图151-，AH BC ⊥于点H ，则AH =_______，AC =_______， ABC △的面积ABC S △=___________．拓展如图152-，点D 在AC 上（可与点A C ，重合），分别过点A C ，作直线BD 的垂线，垂足为E F ，.设.BD x AE m CF n ===，，（当点D 与点A 重合时，我们认为ABC S △=0.（1）用含x m ，或n 的代数式表示ABD S △及CBD S △；（2）求()m n +与x 的函数关系式，并求()m n +的最大值和最小值．（3）对给定的一个x 值，有时只能确定唯一的点D ，指出这样的x 的取值范围. 发现请你确定一条直线，使得A B C ，，三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.A ．B ．C ．D ．16、一透明的敞口正方体容器ABCD-A ′B ′C ′D ′装有一些液体，棱AB 始终在水平桌面上，容器底部的倾斜角为α（∠CBE=α，如图1所示）．探究如图1，液面刚好过棱CD ，并与棱BB ′交于点Q ，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．解决问题：（1）CQ 与BE 的位置关系是，BQ 的长是 dm ；（2）求液体的体积；（参考算法：直棱柱体积V 液=底面积S △BCQ ×高AB ）（3）求α的度数．（注：sin49°=cos41°=43，tan37°=34）拓展：在图1的基础上，以棱AB 为轴将容器向左或向右旋转，但不能使液体溢出，图3或图4是其正面示意图．若液面与棱C ′C 或CB 交于点P ，设PC=x ，BQ=y ．分别就图3和图4求y 与x 的函数关系式，并写出相应的α的范围．延伸：在图4的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图5，隔板高NM=1dm ，BM=CM ，NM ⊥BC ．继续向右缓慢旋转，当α=60°时，通过计算，判断溢出容器的液体能否达到4dm 3．17、某景区内的环形路是边长为800米的正方形ABCD，如图1和图2．现有1号、2号两游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为200米/分．探究：设行驶吋间为t分．（1）当0≤t≤8时，分别写出1号车、2号车在左半环线离出口A的路程y1，y2（米）与t（分）的函数关系式，并求出当两车相距的路程是400米时t的值；（2）t为何值时，1号车第三次恰好经过景点C？并直接写出这一段时间内它与2号车相遇过的次数．发现：如图2，游客甲在BC上的一点K（不与点B，C重合）处候车，准备乘车到出口A，设CK=x米．情况一：若他刚好错过2号车，便搭乘即将到来的1号车；情况二：若他刚好错过1号车，便搭乘即将到来的2号车．比较哪种情况用时较多？（含候车时间）决策：己知游客乙在DA上从D向出口A走去．步行的速度是50米/分．当行进到DA上一点P （不与点D，A 重合）时，刚好与2号车迎面相遇．（1）他发现，乘1号车会比乘2号车到出口A用时少，请你简要说明理由：（2）设PA=s（0＜s＜800）米．若他想尽快到达出口A，根据s的大小，在等候乘1号车还是步行这两种方式中．他该如何选择？。

中考数学压轴题之圆的综合(中考题型整理,突破提升)及答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．在⊙O 中，点C是AB上的一个动点(不与点A，B重合)，∠ACB=120°，点I是∠ABC的内心，CI的延长线交⊙O于点D，连结AD,BD．（1）求证：AD=BD．（2）猜想线段AB与DI的数量关系，并说明理由．（3）若⊙O的半径为2，点E，F是AB的三等分点，当点C从点E运动到点F时，求点I 随之运动形成的路径长．23【答案】（1）证明见解析；（2）AB=DI，理由见解析（3【解析】分析：（1）根据内心的定义可得CI平分∠ACB，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I 随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE是直径∴DE=4，∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，∴∠ADB=60°∴弧AB的度数为120°，∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.2．如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，交BC的延长线于点E，使得∠DAC=∠B．（1）求证：DA是⊙O切线；（2）求证：△CED∽△ACD；（3）若OA=1，sinD=13，求AE的长．【答案】（1）证明见解析；（22【解析】分析：（1）由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线；（2）由∠DAC=∠DCE，∠D=∠D可知△DEC∽△DCA；（3）由题意可知AO=1，OD=3，DC=2，由勾股定理可知AD=2，故此可得到DC2=DE•AD，故此可求得DE的长，于是可求得AE的长．详解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°．∵∠DAC=∠B，∴∠CAB+∠DAC=90°，∴AD⊥AB．∵OA是⊙O半径，∴DA为⊙O的切线；（2）∵OB=OC，∴∠OCB=∠B．∵∠DCE=∠OCB，∴∠DCE=∠B．∵∠DAC=∠B，∴∠DAC=∠DCE．∵∠D=∠D，∴△CED∽△ACD；（3）在Rt△AOD中，OA=1，sin D=13，∴OD=OAsinD=3，∴CD=OD﹣OC=2．∵AD=22OD OA-=22．又∵△CED∽△ACD，∴AD CDCD DE=，∴DE=2CDAD=2，∴AE=AD﹣DE=22﹣2=2．点睛：本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定，证得△DEC∽△DCA是解题的关键．3．如图，已知AB为⊙O直径，D是BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．（1）求证：直线DE与⊙O相切；（2）已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．【答案】（1）证明见解析；（2）2．【解析】试题分析：（1）连接BC、OD，由D是弧BC的中点，可知：OD⊥BC；由OB为⊙O的直径，可得：BC⊥AC，根据DE⊥AC，可证OD⊥DE，从而可证DE是⊙O的切线；（2）直接利用勾股定理得出GO的长，再利用锐角三角函数关系得出tan∠F的值．试题解析：解：（1）证明：连接OD，BC，∵D是弧BC的中点，∴OD垂直平分BC，∵AB 为⊙O的直径，∴AC⊥BC，∴OD∥AE．∵DE⊥AC，∴OD⊥DE，∵OD为⊙O的半径，∴DE 是⊙O的切线；（2）解：∵D是弧BC的中点，∴DC DB=，∴∠EAD=∠BAD，∵DE⊥AC，DG⊥AB且DE=4，∴DE=DG=4，∵DO=5，∴GO=3，∴AG=8，∴tan∠ADG=84=2，∵BF是⊙O的切线，∴∠ABF=90°，∴DG∥BF，∴tan∠F=tan∠ADG=2．点睛：此题主要考查了切线的判定与性质以及勾股定理等知识，正确得出AG，DG的长是解题关键．4．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA 的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．（1）求证：BF=EF：（2）求证：PA是⊙O的切线；（3）若FG=BF，且⊙O的半径长为32，求BD的长度.【答案】(1)证明见解析；(2) 证明见解析；（3）2【解析】分析：（1）利用平行线截三角形得相似三角形，得△BFC∽△DGC且△FEC∽△GAC，得到对应线段成比例，再结合已知条件可得BF=EF；（2）利用直角三角形斜边上的中线的性质和等边对等角，得到∠FAO=∠EBO，结合BE是圆的切线，得到PA⊥OA，从而得到PA是圆O的切线；（3）点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性质即可以求出BD 的长度．详解：证明：(1)∵BC是圆O的直径，BE是圆O的切线，∴EB⊥BC.又∵AD⊥BC，∴AD∥BE.∴△BFC∽△DGC，△FEC∽△GAC，∴BFDG=CFCG，EFAG=CFCG，∴BFDG=EFAG，∵G是AD的中点，∴BF=EF；(2)连接AO，AB.∵BC是圆O的直径，∴∠BAC=90°，由(1)得：在Rt△BAE中，F是斜边BE的中点，∴AF=FB=EF，可得∠FBA=∠FAB，又∵OA=OB，∴∠ABO=∠BAO，∵BE是圆O的切线，∴∠EBO=90°，∴∠FBA+∠ABO=90°，∴∠FAB+∠BAO=90°，即∠FAO=90°，∴PA⊥OA，∴PA是圆O的切线；（3）过点F作FH⊥AD于点H，∵BD⊥AD，FH⊥AD，∴FH∥BC，由(2)，知∠FBA=∠BAF，∴BF=AF.∵BF=FG，∴AF=FG，∴△AFG是等腰三角形.∵FH⊥AD，∴AH=GH，∴DG =2HG . 即12HG DG =， ∵FH ∥BD ，BF ∥AD ，∠FBD =90°，∴四边形BDHF 是矩形，∴BD =FH ，∵FH ∥BC∴△HFG ∽△DCG ，∴12FH HG CD DG ==，即12BD CD =， ∴23 2.153≈， ∵O 的半径长为32，∴BC =62，∴BD =13BC ＝22. 点睛：本题考查了切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质.结合已知条件准确对图形进行分析并应用相应的图形性质是解题的关键.5．如图，正三角形ABC 内接于⊙O ，P 是BC 上的一点，且PB ＜PC ，PA 交BC 于E ，点F 是PC 延长线上的点，CF=PB ，AB=13，PA=4．（1）求证：△ABP ≌△ACF ；（2）求证：AC 2=PA•AE ；（3）求PB 和PC 的长．【答案】（1）证明见解析；（2）证明见解析；（3）PB=1，PC=3．【解析】试题分析：（1）先根据等边三角形的性质得到AB=AC ，再利用圆的内接四边形的性质得∠ACF=∠ABP ，于是可根据“SAS”判断△ABP ≌△ACF ；（2）先根据等边三角形的性质得到∠ABC=∠ACB=60°，再根据圆周角定理得∠APC=∠ABB=60°，加上∠CAE=∠PAC ，于是可判断△ACE ∽△APC ，然后利用相似比即可得到结论；（3）先利用AC 2=PA •AE 计算出AE=134 ，则PE=AP-AE=34，再证△APF 为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP ∽△CEP ，得到PB•PC=PE•A=3，然后根据根与系数的关系，可把PB 和PC 看作方程x 2-4x+3=0的两实数解，再解此方程即可得到PB 和PC 的长．试题解析：（1）∵∠ACP+∠ABP=180°，又∠ACP+∠ACF=180°，∴∠ABP=∠ACF在ABP ∆和ACF ∆中，∵AB=AC ，∠ABP=∠ACF ， CF PB =∴ABP ∆≌ACF ∆．(2)在AEC ∆和ACP ∆中，∵∠APC=∠ABC ，而ABC ∆是等边三角形，故∠ACB=∠ABC=60º，∴∠ACE =∠APC .又∠CAE =∠PAC ，∴AEC ∆∽ACP ∆ ∴AC AE AP AC=,即2AC PA AE =⋅. 由（1）知ABP ∆≌ACF ∆，∴∠BAP=∠CAF ， CF PB =∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°，又∠APC ＝∠ABC ＝60°.∴APF ∆是等边三角形∴AP=PF∴4PB PC PC CF PF PA +=+===在PAB ∆与CEP ∆中，∵∠BAP=∠ECP ，又∠APB=∠EPC=60°，∴PAB ∆∽CEP ∆ ∴PB PA PE PC=,即PB PC PA PE ⋅=⋅ 由（2）2AC PA AE =⋅， ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+= ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴22222243PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解．解这个方程，得11x =， 23x =．∵PB<PB ，∴PB=11x =，PC=23x =，∴PB 和PC 的长分别是1和3。

备战中考数学与圆的综合有关的压轴题含答案解析

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，A、B两点的坐标分别为（0，6），（0，3），点P为x轴正半轴上一动点，过点A作AP的垂线，过点B作BP的垂线，两垂线交于点Q，连接PQ，M为线段PQ的中点．（1）求证：A、B、P、Q四点在以M为圆心的同一个圆上；（2）当⊙M与x轴相切时，求点Q的坐标；（3）当点P从点（2，0）运动到点（3，0）时，请直接写出线段QM扫过图形的面积．【答案】(1)见解析;(2) Q的坐标为（32，9）;(3)63 8.【解析】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= 12 PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。

（2）解：作MG⊥y轴于G，MC⊥x轴于C，∵AM＝BM∴G是AB的中点，由A（0，6），B（0，3）可得MC＝OG＝4.5∴在点P运动的过程中，点M到x轴的距离始终为4.5则点Q到x轴的距离始终为9，即点Q的纵坐标始终为9，当⊙M与x轴相切时则PQ⊥x轴，作QH⊥y轴于H，HB＝9－3＝6，设OP＝HQ＝x由△BOP∽△QHB，得x2＝3×6＝8，x＝2∴点Q的坐标为（2，9）（3）解：由相似可得：当点P在P1（2，0）时，Q1（4，9）则M1（3，4.5）当点P在P2（3，0）时，Q2（6，9），则M2（4.5，4.5）∴M1M2＝92－3＝32， Q1Q2＝6－4＝2线段QM扫过的图形为梯形M1M2Q2Q1其面积为：12×(32＋2)×4.5＝638.【解析】【分析】根据已知可得出三角形APQ和三角形BPQ都是直角三角形，再根据这个条件结合题意直接解答此题.【详解】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。

【数学】备战中考数学圆的综合解答题压轴题提高专题练习含详细答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．已知O 的半径为5，弦AB 的长度为m ，点C 是弦AB 所对优弧上的一动点． ()1如图①，若m 5=，则C ∠的度数为______；()2如图②，若m 6=．①求C ∠的正切值；②若ABC 为等腰三角形，求ABC 面积．【答案】()130；()2C ∠①的正切值为34；ABC S 27=②或43225. 【解析】【分析】 ()1连接OA ，OB ，判断出AOB 是等边三角形，即可得出结论；()2①先求出10AD =，再用勾股定理求出8BD =，进而求出tan ADB ∠，即可得出结论；②分三种情况，利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论．【详解】()1如图1，连接OB ，OA ，OB OC 5∴==，AB m 5==，OB OC AB ∴==，AOB ∴是等边三角形，AOB 60∠∴=，1ACB AOB 302∠∠∴==，故答案为30；()2①如图2，连接AO 并延长交O 于D ，连接BD ，AD 为O 的直径，AD 10∴=，ABD 90∠=，在Rt ABD 中，AB m 6==，根据勾股定理得，BD 8=， AB 3tan ADB BD 4∠∴==， C ADB ∠∠=，C ∠∴的正切值为34； ②Ⅰ、当AC BC =时，如图3，连接CO 并延长交AB 于E ，AC BC =，AO BO =，CE ∴为AB 的垂直平分线，AE BE 3∴==，在Rt AEO 中，OA 5=，根据勾股定理得，OE 4=，CE OE OC 9∴=+=，ABC 11S AB CE 692722∴=⨯=⨯⨯=； Ⅱ、当AC AB 6==时，如图4，连接OA 交BC 于F ，AC AB =，OC OB =，AO ∴是BC 的垂直平分线，过点O 作OG AB ⊥于G ， 1AOG AOB 2∠∠∴=，1AG AB 32==， AOB 2ACB ∠∠=，ACF AOG ∠∠∴=，在Rt AOG 中，AG 3sin AOG AC 5∠==， 3sin ACF 5∠∴=，在Rt ACF 中，3sin ACF 5∠=， 318AF AC 55∴==， 24CF 5∴=， ABC 111824432S AF BC 225525∴=⨯=⨯⨯=； Ⅲ、当BA BC 6==时，如图5，由对称性知，ABC 432S 25=．【点睛】圆的综合题，主要圆的性质，圆周角定理，垂径定理，等腰三角形的性质，三角形的面积公式，用分类讨论的思想解决问题是解本题的关键．2．如图，AB 为O 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O 的切线，理由见解析；（2）证明见解析.【解析】【分析】（1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE ∽即可解决问题.【详解】()1解：结论：DE 是O 的切线．理由：连接OD ．CDB ADE ∠=∠，ADC EDB ∴∠=∠，//CD AB ，CDA DAB ∴∠=∠，OA OD =，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠， AB 是直径，90ADB ∴∠=，90ADB ODE ∴∠=∠=，DE OD ∴⊥，DE ∴是O 的切线．()2//CD AB ，ADC DAB ∴∠=∠，CDB DBE ∠=∠，AC BD∴=，∴=，AC BD∠=∠，EDB DABDCB DAB∠=∠，∴∠=∠，EDB DCB∴∽DBE，CDBCD DB∴=，BD BE2∴=⋅，BD CD BE2∴=⋅．AC CD BE【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.3．如图，在以点O为圆心的两个同心圆中，小圆直径AE的延长线与大圆交于点B，点D 在大圆上，BD与小圆相切于点F，AF的延长线与大圆相交于点C，且CE⊥BD．找出图中相等的线段并证明．【答案】见解析【解析】试题分析：由AE是小⊙O的直径，可得OA=OE，连接OF，根据切线的性质，可得OF⊥BD，然后由垂径定理，可证得DF=BF，易证得OF∥CE，根据平行线分线段成比例定理，可证得AF=CF，继而可得四边形ABCD是平行四边形，则可得AD=BC，AB=CD．然后连接OD、OC，可证得△AOD≌△EOC，则可得BC=AD=CE=AE．试题解析：图中相等的线段有：OA=OE，DF=BF，AF=CF，AB=CD，BC=AD=CE=AE．证明如下：∵AE是小⊙O的直径，∴OA=OE．连接OF，∵BD与小⊙O相切于点F，∴OF⊥BD．∵BD是大圆O的弦，∴DF=BF．∵CE⊥BD，∴CE∥OF，∴AF=CF．∴四边形ABCD是平行四边形．∴AD=BC，AB=CD．∵CE：AE=OF：AO，OF=AO，∴AE=EC．连接OD、OC，∵OD=OC，∴∠ODC=∠OCD．∵∠AOD=∠ODC，∠EOC=∠OEC，∴∠AOC=∠EOC，∴△AOD≌△EOC，∴AD=CE．∴BC=AD=CE=AE．【点睛】考查了切线的性质，垂径定理，平行线分线段成比例定理，平行四边形的判定与性质以及全等三角形的判定与性质等知识．此题综合性很强解题的关键是注意数形结合思想的应用，注意辅助线的作法，小心不要漏解．4．已知：如图1，∠ACG=90°，AC=2，点B为CG边上的一个动点，连接AB，将△ACB沿AB边所在的直线翻折得到△ADB，过点D作DF⊥CG于点F．（1）当23时，判断直线FD与以AB为直径的⊙O的位置关系，并加以证明；（2）如图2，点B在CG上向点C运动，直线FD与以AB为直径的⊙O交于D、H两点，连接AH，当∠CAB=∠BAD=∠DAH时，求BC的长．【答案】（1）直线FD与以AB为直径的⊙O相切，理由见解析；（2）222.【解析】试题分析：（1）根据已知及切线的判定证明得，直线FD与以AB为直径的⊙O相切；（2）根据圆内接四边形的性质及直角三角形的性质进行分析，从而求得BC的长．试题解析：（1）判断：直线FD与以AB为直径的⊙O相切．证明：如图，作以AB为直径的⊙O；∵△ADB是将△ACB沿AB边所在的直线翻折得到的，∴△ADB≌△ACB，∴∠ADB=∠ACB=90°．∵O为AB的中点，连接DO，∴OD=OB=AB，∴点D在⊙O上．在Rt△ACB中，BC=，AC=2；∴tan∠CAB==，∴∠CAB=∠BAD=30°，∴∠ABC=∠ABD=60°，∴△BOD是等边三角形．∴∠BOD=60°．∴∠ABC=∠BOD，∴FC∥DO．∵DF⊥CG，∴∠ODF=∠BFD=90°，∴OD⊥FD，∴FD为⊙O的切线．（2）延长AD交CG于点E，同（1）中的方法，可证点C在⊙O上；∴四边形ADBC是圆内接四边形．∴∠FBD=∠1+∠2．同理∠FDB=∠2+∠3．∵∠1=∠2=∠3，∴∠FBD=∠FDB，又∠DFB=90°．∴EC=AC=2．设BC=x，则BD=BC=x，∵∠EDB=90°，∴EB=x ．∵EB+BC=EC，∴x+x=2，解得x=2﹣2，∴BC=2﹣2．5．如图，已知在△ABC中，∠A=90°，（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．（2）若∠B=60°，AB=3，求⊙P的面积．【答案】（1）作图见解析；（2）3π【解析】【分析】（1）与AB、BC两边都相切．根据角平分线的性质可知要作∠ABC的角平分线，角平分线与AC的交点就是点P的位置．（2）根据角平分线的性质和30°角的直角三角形的性质可求半径，然后求圆的面积．【详解】解：（1）如图所示，则⊙P为所求作的圆．（2）∵∠ABC=60°，BP平分∠ABC，∴∠ABP=30°，∵∠A=90°，∴BP=2APRt△ABP中,AB=3，由勾股定理可得：AP=3，∴S⊙P=3π6．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A ＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C ＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB＝90°,∴点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,除去点（2,2）,∴当PM⊥x轴时,点P纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆．7．如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E 是AB延长线上一点，CE交⊙O于点F，连接OC、AC．（1）求证：AC平分∠DAO．（2）若∠DAO=105°，∠E=30°①求∠OCE的度数；②若⊙O的半径为2EF的长．【答案】（1）证明见解析；（2）①∠OCE=45°；②EF =23-2.【解析】【试题分析】（1）根据直线与⊙O相切的性质，得OC⊥CD.又因为AD⊥CD，根据同一平面内，垂直于同一条直线的两条直线也平行，得：AD//OC. ∠DAC=∠OCA.又因为OC=OA，根据等边对等角，得∠OAC=∠OCA.等量代换得：∠DAC=∠OAC.根据角平分线的定义得：AC平分∠DAO.（2）①因为 AD//OC，∠DAO=105°，根据两直线平行，同位角相等得，中，∠E=30°，利用内角和定理，得：∠OCE=45°.∠EOC=∠DAO=105°，在OCE②作OG⊥CE于点G，根据垂径定理可得FG=CG，因为OC=22，∠OCE=45°.等腰直角三角形的斜边是腰长的2倍，得CG=OG=2. FG=2.在Rt△OGE中，∠E=30°，得GE=23，则EF=GE-FG=23-2.【试题解析】（1）∵直线与⊙O相切，∴OC⊥CD.又∵AD⊥CD，∴AD//OC.∴∠DAC=∠OCA.又∵OC=OA，∴∠OAC=∠OCA.∴∠DAC=∠OAC.∴AC平分∠DAO.（2）解：①∵AD//OC，∠DAO=105°，∴∠EOC=∠DAO=105°∵∠E=30°，∴∠OCE=45°.②作OG⊥CE于点G，可得FG=CG∵OC=22，∠OCE=45°.∴CG=OG=2.∴FG=2.∵在Rt△OGE中，∠E=30°，∴GE=23.∴EF=GE-FG=23-2.【方法点睛】本题目是一道圆的综合题目，涉及到圆的切线的性质，平行线的性质及判定，三角形内角和，垂径定理，难度为中等.8．如图，在ABC △中，10AC BC ==，3cos 5C =,点P 是BC 边上一动点（不与点,A C 重合），以PA 长为半径的P 与边AB 的另一个交点为D ，过点D 作DE CB ⊥于点E .()1当P 与边BC 相切时，求P 的半径；()2联结BP 交DE 于点F ，设AP 的长为x ，PF 的长为y ，求y 关于x 的函数解析式，并直接写出x 的取值范围；()3在()2的条件下，当以PE 长为直径的Q 与P 相交于AC 边上的点G 时，求相交所得的公共弦的长.【答案】（1）409；（2）)25880010320x x y x x -+=<<+；（3）105-【解析】【分析】（1）设⊙P 与边BC 相切的切点为H ，圆的半径为R ，连接HP ，则HP ⊥BC ，cosC=35，则sinC=45，sinC=HP CP =R 10R -=45，即可求解；（2）PD ∥BE ，则EB PD ＝BFPF，即：2248805x x x y xy--+=，即可求解；（3）证明四边形PDBE 为平行四边形，则AG=GP=BD ，即：5求解．【详解】（1）设⊙P 与边BC 相切的切点为H ，圆的半径为R ，连接HP ，则HP ⊥BC ，cosC=35，则sinC=35， sinC=HP CP =R 10R -=45，解得：R=409；（2）在△ABC 中，AC=BC=10，cosC=35，设AP=PD=x ，∠A=∠ABC=β，过点B 作BH ⊥AC ，则BH=ACsinC=8，同理可得：CH=6，HA=4，AB=45，则：tan ∠CAB=2BP=()2284x +-=2880x x -+， DA=25x ，则BD=45-25x ，如下图所示，PA=PD ，∴∠PAD=∠CAB=∠CBA=β，tanβ=2，则cosβ=5，sinβ=5，EB=BDcosβ=（45-25x）×5=4-25x，∴PD∥BE，∴EBPD＝BFPF，即：2248805x x x yx y--+-=，整理得：y=()25x x8x800x10-+<<；（3）以EP为直径作圆Q如下图所示，两个圆交于点G，则PG=PQ，即两个圆的半径相等，则两圆另外一个交点为D，GD为相交所得的公共弦，∵点Q时弧GD的中点，∴DG⊥EP，∵AG是圆P的直径，∴∠GDA=90°，∴EP∥BD，由（2）知，PD∥BC，∴四边形PDBE为平行四边形，∴AG=EP=BD，∴5设圆的半径为r，在△ADG中，55AG=2r，5551+，则：55相交所得的公共弦的长为5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．9．对于平面内的⊙C 和⊙C 外一点Q ，给出如下定义：若过点Q 的直线与⊙C 存在公共点，记为点A ，B ，设AQ BQk CQ+=，则称点A （或点B ）是⊙C 的“K 相关依附点”，特别地，当点A 和点B 重合时，规定AQ=BQ ，2AQ k CQ =（或2BQCQ）．已知在平面直角坐标系xoy 中，Q(-1,0)，C(1,0)，⊙C 的半径为r ．（1）如图1，当2r =时，①若A 1(0,1)是⊙C 的“k 相关依附点”，求k 的值． ②A 2(1+2，0)是否为⊙C 的“2相关依附点”．（2）若⊙C 上存在“k 相关依附点”点M ， ①当r=1，直线QM 与⊙C 相切时，求k 的值． ②当3k =时，求r 的取值范围．（3）若存在r 的值使得直线3y x b =-+与⊙C 有公共点，且公共点时⊙C 的“3相关依附点”，直接写出b 的取值范围．【答案】（1）2．②是；（2）①3k =②r 的取值范围是12r <≤；（3）333b -<．【解析】【分析】（1）①如图1中，连接AC 、1QA ．首先证明1QA 是切线，根据2AQk CQ=计算即可解决问题；②根据定义求出k 的值即可判断；（2）①如图，当1r =时，不妨设直线QM 与C 相切的切点M 在x 轴上方（切点M 在x 轴下方时同理），连接CM ，则QM CM ⊥，根据定义计算即可；②如图3中，若直线QM 与C 不相切，设直线QM 与C 的另一个交点为N （不妨设QN QM <，点N ，M 在x 轴下方时同理），作CD QM ⊥于点D ，则MD ND =，可得()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=，2CQ ，推出2MQ NQ DQk DQ CQ CQ+===，可得当3k =时，3DQ =，此时221CD CQ DQ =-=，假设C 经过点Q ，此时2r ，因为点Q 早C 外，推出r 的取值范围是12r <；（3）如图4中，由（2）可知：当3k =时，12r <．当2r 时，C 经过点(1,0)Q -或(3,0)E ，当直线3y x b =-+经过点Q 时，3b =-，当直线3y x b=-+经过点E 时，33b =，即可推出满足条件的b 的取值范围为333b -<<．【详解】（1）①如图1中，连接AC 、1QA ．由题意：1OC OQ OA ==，∴△1QA C 是直角三角形，190CA Q ∴∠=︒，即11CA QA ⊥，1QA ∴是C 的切线，12222QA k QC ∴=== ②2(12,0)A +在C 上，2212122k +∴==，2A ∴是C 的“2相关依附点”．2（2）①如图2，当1r =时，不妨设直线QM 与C 相切的切点M 在x 轴上方（切点M在x 轴下方时同理），连接CM ，则QM CM ⊥．(1,0)Q -，(1,0)C ，1r =，2CQ ∴=，1CM =，∴3MQ =，此时23MQk CQ=②如图3中，若直线QM 与C 不相切，设直线QM 与C 的另一个交点为N （不妨设QN QM <，点N ，M 在x 轴下方时同理），作CD QM ⊥于点D ，则MD ND =，()222MQ NQ MN NQ NQ ND NQ DQ ∴+=++=+=，2CQ =，∴2MQ NQ DQk DQ CQ CQ+===，∴当3k =3DQ =221CD CQ DQ =-，假设C 经过点Q ，此时2r ，点Q 早C 外，r ∴的取值范围是12r <．（3）如图4中，由（2）可知：当3k =时，12r <．当2r时，C 经过点(1,0)Q -或(3,0)E ，当直线3y x b =-+经过点Q 时，3b =-，当直线3y x b =-+经过点E 时，33b =，∴满足条件的b 的取值范围为333b -<<．【点睛】本题考查了一次函数综合题、圆的有关知识、勾股定理、切线的判定和性质、点A （或点)B 是C 的“k 相关依附点”的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会考虑特殊位置解决问题，属于中考压轴题．10．如图，已知AB 是⊙O 的直径，点C 、D 在⊙O 上，∠D ＝60°且AB ＝6，过O 点作OE ⊥AC ，垂足为E ．（1）求OE 的长；（2）若OE 的延长线交⊙O 于点F ，求弦AF 、AC 和弧CF 围成的图形（阴影部分）的面积．（结果保留π）【答案】（1）OE的长为32；（2）阴影部分的面积为3 2π【解析】（1）OE=32（2）S=32π。

中考数学与圆的综合有关的压轴题及答案解析

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过BD上一点E作EG∥AC 交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．（1）求证：∠G=∠CEF；（2）求证：EG是⊙O的切线；（3）延长AB交GE的延长线于点M，若tanG =34，AH=33，求EM的值．【答案】（1）证明见解析；（2）证明见解析；（3）253.【解析】试题分析：（1）由AC∥EG，推出∠G=∠ACG，由AB⊥CD推出AD AC=，推出∠CEF=∠ACD，推出∠G=∠CEF，由此即可证明；（2）欲证明EG是⊙O的切线只要证明EG⊥OE即可；（3）连接OC．设⊙O的半径为r．在Rt△OCH中，利用勾股定理求出r，证明△AHC∽△MEO，可得AH HCEM OE=，由此即可解决问题；试题解析：（1）证明：如图1．∵AC∥EG，∴∠G=∠ACG，∵AB⊥CD，∴AD AC=，∴∠CEF=∠ACD，∴∠G=∠CEF，∵∠ECF=∠ECG，∴△ECF∽△GCE．（2）证明：如图2中，连接OE．∵GF=GE，∴∠GFE=∠GEF=∠AFH，∵OA=OE，∴∠OAE=∠OEA，∵∠AFH+∠FAH=90°，∴∠GEF+∠AEO=90°，∴∠GEO=90°，∴GE⊥OE，∴EG是⊙O的切线．（3）解：如图3中，连接OC．设⊙O的半径为r．在Rt△AHC中，tan∠ACH=tan∠G=AHHC=34，∵AH=33∴HC=3Rt△HOC中，∵OC=r，OH=r﹣33HC=43∴222(33)(43)r r-+=，∴r=2536，∵GM∥AC，∴∠CAH=∠M，∵∠OEM=∠AHC，∴△AHC∽△MEO，∴AH HCEM OE=，∴33432536=，∴EM253．点睛：本题考查圆综合题、垂径定理、相似三角形的判定和性质、锐角三角函数、勾股定理等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，正确寻找相似三角形，构建方程解决问题吗，属于中考压轴题．2．图 1 和图 2 中，优弧AB纸片所在⊙O 的半径为 2，AB＝3，点P为优弧AB上一点（点P 不与A，B 重合），将图形沿BP 折叠，得到点A 的对称点A′．发现：（1）点O 到弦AB 的距离是，当BP 经过点O 时，∠ABA′＝；（2）当BA′与⊙O 相切时，如图 2，求折痕的长．拓展：把上图中的优弧纸片沿直径MN 剪裁，得到半圆形纸片，点P（不与点M， N 重合）为半圆上一点，将圆形沿NP 折叠，分别得到点M，O 的对称点A′， O′，设∠MNP＝α．（1）当α＝15°时，过点A′作A′C∥MN，如图 3，判断A′C 与半圆O 的位置关系，并说明理由；（2）如图 4，当α＝ °时，NA′与半圆O 相切，当α＝ °时，点O′落在NP上．（3）当线段NO′与半圆O 只有一个公共点N 时，直接写出β的取值范围．【答案】发现：（1）1，60°；（2）3；拓展：（1）相切，理由详见解析；（2）45°；30°；（3）0°＜α＜30°或45°≤α＜90°．【解析】【分析】发现：（1）利用垂径定理和勾股定理即可求出点O到AB的距离；利用锐角三角函数的定义及轴对称性就可求出∠ABA′．（2）根据切线的性质得到∠OBA′=90°，从而得到∠ABA′=120°，就可求出∠ABP，进而求出∠OBP=30°．过点O作OG⊥BP，垂足为G，容易求出OG、BG的长，根据垂径定理就可求出折痕的长．拓展：（1）过A'、O作A'H⊥MN于点H，OD⊥A'C于点D．用含30°角的直角三角形的性质可得OD=A'H=12A'N=12MN=2可判定A′C与半圆相切；（2）当NA′与半圆相切时，可知ON⊥A′N，则可知α=45°，当O′在PB时，连接MO′，则可知NO′=12MN，可求得∠MN O′=60°，可求得α=30°；（3）根据点A′的位置不同得到线段NO′与半圆O只有一个公共点N时α的取值范围是0°＜α＜30°或45°≤α＜90°．【详解】发现：（1）过点O作OH⊥AB，垂足为H，如图1所示,∵⊙O的半径为2，AB=23，∴OH=22OB HB-=222(3)1-=在△BOH中，OH=1，BO=2∴∠ABO=30°∵图形沿BP折叠，得到点A的对称点A′．∴∠OBA′=∠ABO=30°∴∠ABA′=60°（2）过点O作OG⊥BP，垂足为G，如图2所示．∵BA′与⊙O相切，∴OB⊥A′B．∴∠OBA′=90°．∵∠OBH=30°，∴∠ABA′=120°．∴∠A′BP=∠ABP=60°．∴∠OBP=30°．∴OG=12OB=1．∴3．∵OG⊥BP，∴3．∴3．∴折痕的长为3拓展：（1）相切．分别过A'、O作A'H⊥MN于点H，OD⊥A'C于点D．如图3所示，∵A'C∥MN∴四边形A'HOD是矩形∴A'H=O∵α=15°∴∠A'NH=30∴OD=A'H=12A'N=12MN=2∴A'C与半圆（2）当NA′与半圆O相切时，则ON⊥NA′，∴∠ONA′=2α=90°，∴α=45当O′在PB上时，连接MO′，则可知NO′=12 MN，∴∠O′MN=0°∴∠MNO′=60°，∴α=30°，故答案为：45°；30°．（3）∵点P，M不重合，∴α＞0，由（2）可知当α增大到30°时，点O′在半圆上，∴当0°＜α＜30°时点O′在半圆内，线段NO′与半圆只有一个公共点B；当α增大到45°时NA′与半圆相切，即线段NO′与半圆只有一个公共点B．当α继续增大时，点P逐渐靠近点N，但是点P，N不重合，∴α＜90°，∴当45°≤α＜90°线段BO′与半圆只有一个公共点B．综上所述0°＜α＜30°或45°≤α＜90°．【点睛】本题考查了切线的性质、垂径定理、勾股定理、三角函数的定义、30°角所对的直角边等于斜边的一半、翻折问题等知识，正确的作出辅助线是解题的关键．3．如图1，以边长为4的正方形纸片ABCD的边AB为直径作⊙O，交对角线AC于点E．（1）图1中，线段AE=；（2）如图2，在图1的基础上，以点A为端点作∠DAM=30°，交CD于点M，沿AM将四边形ABCM剪掉，使Rt△ADM绕点A逆时针旋转（如图3），设旋转角为α（0°＜α＜150°），在旋转过程中AD与⊙O交于点F．①当α=30°时，请求出线段AF的长；②当α=60°时，求出线段AF的长；判断此时DM与⊙O的位置关系，并说明理由；③当α=°时，DM与⊙O相切．【答案】（1）2（2）①2②2，相离③当α=90°时，DM与⊙O相切【解析】（1）连接BE，∵AC是正方形ABCD的对角线，∴∠BAC=45°，∴△AEB是等腰直角三角形，又∵AB=8，∴AE=4；（2）①连接OA、OF，由题意得，∠NAD=30°，∠DAM=30°，故可得∠OAM=30°，∠DAM=30°，则∠OAF=60°，又∵OA=OF，∴△OAF是等边三角形，∵OA=4，∴AF=OA=4；②连接B'F，此时∠NAD=60°，∵AB'=8，∠DAM=30°，∴AF=AB'cos∠DAM=8×=4；此时DM与⊙O的位置关系是相离；③∵AD=8，直径的长度相等，∴当DM与⊙O相切时，点D在⊙O上，故此时可得α=∠NAD=90°．点睛：此题属于圆的综合题，主要是仔细观察每一次旋转后的图形，根据含30°角的直角三角形进行计算，另外在解答最后一问时，关键是判断出点D的位置，有一定难度．4．如图，已知AB是⊙O的直径，点C，D在⊙O上，BC=6cm,AC=8cm,∠BAD=45°．点E在⊙O外，做直线AE，且∠EAC=∠D．（1）求证：直线AE是⊙O的切线．（2）求图中阴影部分的面积.【答案】(1)见解析;(2) 25-504.【解析】分析：（1）根据圆周角定理及推论证得∠BAE=90°，即可得到AE是⊙O的切线；（2）连接OD，用扇形ODA的面积减去△AOD的面积即可.详解：证明：（1）∵AB是⊙O的直径，∴∠ACB=90°，即∠BAC+∠ABC=90°，∵∠EAC=∠ADC，∠ADC=∠ABC，∴∠EAC=∠ABC∴∠BAC+∠EAC =90°，即∠BAE= 90°∴直线AE 是⊙O 的切线；（2）连接OD∵ BC=6 AC=8∴ 226810AB =+=∴ OA = 5又∵ OD = OA∴∠ADO =∠BAD = 45°∴∠AOD = 90°∴AOD ODA S S S ∆-阴影扇形＝=90155553602π⨯⨯-⨯⨯ 25504π-= （2cm ）点睛：此题主要考查了圆周角定理和圆的切线的判定与性质，关键是利用圆周角定理和切线的判定与性质，结合勾股定理的和弓形的面积的求法求解，注意数形结合思想的应用.5．已知：AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ，BD=CD,连接AD 、AC ．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ，交AB 于点K,求证AK=2OF ；(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析12105【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ，可得GF =2a ，AF =4a ．由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠= ，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°．∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ．（2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ．∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ．∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°．∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α．∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°．∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM =12AG ．在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α．设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6． ∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK =22(2)m m +=6，解得：m =655，∴AH =2m =1255．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD =45°，∴HL=AH ，AL =2AH = 1210．6．已知A （2,0），B （6,0），CB ⊥x 轴于点B ，连接AC画图操作：（1）在y正半轴上求作点P，使得∠APB=∠ACB（尺规作图，保留作图痕迹）理解应用：（2）在（1）的条件下，①若tan∠APB12=，求点P的坐标②当点P的坐标为时，∠APB最大拓展延伸：（3）若在直线y43=x+4上存在点P，使得∠APB最大，求点P的坐标【答案】（1）图形见解析（2）（0，2），（0，4）（0，33）（953 5-，1255）【解析】试题分析：（1）以AC为直径画圆交y轴于P，连接PA、PB，∠PAB即为所求；（2）①由题意AC的中点K（4，4），以K为圆心AK为半径画圆，交y轴于P和P′，易知P（0，2），P′（0，6）；②当⊙K与y轴相切时，∠APB的值最大，（3）如图3中，当经过AB的园与直线相切时，∠APB最大．想办法求出点P坐标即可解决问题；试题解析：解：（1）∠APB如图所示；（2）①如图2中，∵∠APB=∠ACB，∴tan∠ACB=tan∠APB=12=ABBC．∵A（2，0），B（6，0），∴AB=4，BC=8，∴C（6，8），∴AC的中点K（4，4），以K为圆心AK为半径画圆，交y轴于P和P′，易知P（0，2），P′（0，6）．②当⊙K与y轴相切时，∠APB的值最大，此时AK=PK=4，AC=8，∴BC=22AC AB=43，∴C（6，43），∴K（4，22），∴P（0，23）．故答案为：（0，23）．（3）如图3中，当经过AB的园与直线相切时，∠APB最大．∵直线y=43x+4交x轴于M（﹣3，0），交y轴于N（0，4）．∵MP是切线，∴MP2=MA•MB，∴MP=35，作PK⊥OA于K．∵ON∥PK，∴ONPK=OMMK=NMMP，∴4PK=3MK=35，∴PK=125，MK=95，∴OK=95﹣3，∴P（95﹣3，125）．点睛：本题考查了一次函数综合题、直线与圆的位置关系、平行线的性质、切线的判定和性质、勾股定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线解决问题，学会构造辅助圆解决最大角问题，属于中考压轴题．7．如图1，延长⊙O的直径AB至点C，使得BC=12AB，点P是⊙O上半部分的一个动点（点P不与A、B重合），连结OP，CP．（1）∠C的最大度数为；（2）当⊙O的半径为3时，△OPC的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；（3）如图2，延长PO交⊙O于点D，连结DB，当CP=DB时，求证：CP是⊙O的切线．【答案】（1）30°；（2）有最大值为9，理由见解析；（3）证明见解析.【解析】试题分析：（1）当PC与⊙O相切时，∠OCP的度数最大，根据切线的性质即可求得；（2）由△OPC的边OC是定值，得到当OC边上的高为最大值时，△OPC的面积最大，当PO⊥OC时，取得最大值，即此时OC边上的高最大，于是得到结论；（3）根据全等三角形的性质得到AP=DB，根据等腰三角形的性质得到∠A=∠C，得到CO=OB+OB=AB，推出△APB≌△CPO，根据全等三角形的性质得到∠CPO=∠APB，根据圆周角定理得到∠APB=90°，即可得到结论．试题解析：（1）当PC与⊙O相切时，∠OCP最大．如图1，所示：∵sin∠OCP=OPOC =24=12，∴∠OCP=30°∴∠OCP的最大度数为30°，故答案为：30°；（2）有最大值，理由：∵△OPC的边OC是定值，∴当OC边上的高为最大值时，△OPC的面积最大，而点P在⊙O上半圆上运动，当PO⊥OC时，取得最大值，即此时OC边上的高最大，也就是高为半径长，∴最大值S△OPC=12OC•OP=12×6×3=9；（3）连结AP，BP，如图2，在△OAP与△OBD中，OA ODAOP BODOP OB=⎧⎪∠=∠⎨⎪=⎩，∴△OAP≌△OBD，∴AP=DB，∵PC=DB，∴AP=PC，∵PA=PC，∴∠A=∠C，∵BC=12AB=OB，∴CO=OB+OB=AB，在△APB和△CPO中，AP CPA CAB CO=⎧⎪∠=∠⎨⎪=⎩，∴△APB≌△CPO，∴∠CPO=∠APB，∵AB为直径，∴∠APB=90°，∴∠CPO=90°，∴PC切⊙O于点P，即CP是⊙O的切线．8．四边形ABCD内接于⊙O，点E为AD上一点，连接AC，CB，∠B=∠AEC．（1）如图1，求证：CE=CD；（2）如图2，若∠B+∠CAE=120°，∠ACD=2∠BAC，求∠BAD的度数；（3）如图3，在（2）的条件下，延长CE交⊙O于点G，若tan∠BAC= 53，EG=2，求AE的长．【答案】（1）见解析；（2）60°；（3）7.【解析】试题分析：(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α，由（1）CE=CD，用α表示∠CAE，∠BAC，而∠BAD=∠BAC+∠CAE.（3）连接AG，作GN⊥AC，AM⊥EG，先证明∠CAG=∠BAC，设NG=53m，可得AN=11m，利用直角AGM,AEM，勾股定理可以算出m的值并求出AE长.试题解析：（1）解：证明：∵四边形ABCD内接于⊙O.∴∠B+∠D=180°，∵∠B=∠AEC，∴∠AEC+∠D=180°，∵∠AEC+∠CED=180°，∴∠D=∠CED，∴CE=CD．（2）解：作CH⊥DE于H．设∠ECH=α，由（1）CE=CD，∴∠ECD=2α，∵∠B=∠AEC，∠B+∠CAE=120°，∴∠CAE+∠AEC=120°，∴∠ACE=180°﹣∠AEC﹣∠ACE=60°，∴∠CAE=90°﹣∠ACH=90°﹣（60°+α）=30°﹣α，∠ACD=∠ACH+∠HCD=60°+2α，∵∠ACD=2∠BAC，∴∠BAC=30°+α，∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°．（3）解：连接AG，作GN⊥AC，AM⊥EG，∵∠CED=∠AEG，∠CDE=∠AGE，∠CED=∠CDE，∴∠AEG =∠AGE ， ∴AE =AG ， ∴EM=MG =12EG =1， ∴∠EAG =∠ECD =2α，∴∠CAG =∠CAD +∠DAG =30°﹣α+2α=∠BAC ， ∵tan ∠BAC =53， ∴设NG=53m ，可得AN =11m ，AG =22AG AM -=14m ，∵∠ACG =60°，∴CN=5m ，AM =83m ，MG =22AG AM -=2m =1，∴m =12， ∴CE=CD =CG ﹣EG =10m ﹣2=3， ∴AE =22AM EM +=221+43（）=7．9．如图，△ABC 中，AC ＝BC ＝10，cosC ＝35，点P 是AC 边上一动点（不与点A 、C 重合），以PA 长为半径的⊙P 与边AB 的另一个交点为D ，过点D 作DE ⊥CB 于点E ．（1）当⊙P 与边BC 相切时，求⊙P 的半径．（2）连接BP 交DE 于点F ，设AP 的长为x ，PF 的长为y ，求y 关于x 的函数解析式，并直接写出x 的取值范围．（3）在（2）的条件下，当以PE 长为直径的⊙Q 与⊙P 相交于AC 边上的点G 时，求相交所得的公共弦的长.【答案】（1）409R =;（2）25880320xy x x x =-++（3）505- 【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝ACsinC＝8，同理可得：CH＝6，HA＝4，AB＝5tan∠CAB＝2，BP228+(4)x-2880x x-+DA ＝255x ，则BD ＝45﹣255x ，如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ＝5，sinβ＝5， EB ＝BDcosβ＝（45﹣25x ）×5＝4﹣25x ，∴PD ∥BE ，∴EB BFPD PF=，即：2024588x y x xx y-+--=，整理得：y ＝25xx 8x 803x 20-++；（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦， ∵点Q 是弧GD 的中点， ∴DG ⊥EP ， ∵AG 是圆P 的直径， ∴∠GDA ＝90°， ∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形， ∴AG ＝EP ＝BD ，∴AB＝DB+AD＝AG+AD＝45，设圆的半径为r，在△ADG中，AD＝2rcosβ＝5，DG＝5，AG＝2r，5+2r＝45，解得：2r＝51+，则：DG＝5＝50﹣105，相交所得的公共弦的长为50﹣105．【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．10．如图，在△ABC中，AB＝AC，以AC为直径作⊙O交BC于点D，过点D作FE⊥AB于点E，交AC的延长线于点F．（1）求证：EF与⊙O相切；（2）若AE＝6，sin∠CFD＝35，求EB的长．【答案】(1)见解析（2）3 2【解析】【分析】()1如图，欲证明EF与O相切，只需证得OD EF⊥．()2通过解直角AEF可以求得AF10.=设O的半径为r，由已知可得△FOD∽△FAE，继而得到OF ODAF AE=，即10r r106-=，则易求15AB AC2r2===，所以153EB AB AE622 =-=-=．【详解】（1）如图，连接OD，OC OD =，OCD ODC ∠∠∴=． AB AC =， ACB B ∠∠∴=， ODC B ∠∠∴=， OD //AB ∴，ODF AEF ∠∠∴=， EF AB ⊥，ODF AEF 90∠∠∴==，OD EF ∴⊥，OD 是O 的半径，EF ∴与O 相切；()2由()1知，OD//AB ，OD EF ⊥．在Rt AEF 中，AE 3sin CFD AF 5∠==，AE 6=，则AF 10=，OD //AB ，∴△FOD ∽△FAE ，OF ODAF AE∴=，设O 的半径为r ， 10r r106-∴=，解得，15r 4=， 15AB AC 2r 2∴===， 153EB AB AE 622∴=-=-=．【点睛】本题考查了切线的判定、相似三角形的判定与性质、解直角三角形的应用等，正确添加辅助线、灵活应用相关知识是解题的关键.。

2020年中考数学压轴题之动点产生的定值和最值专题Word版无答案

2020年中考数学压轴题之动点产生的定值和最值专题Word版无答案中考数学压轴题专题动点产生的定值与最值问题中考数学压轴题——动点产生的定值与最值问题目录第1 讲角为定值的常规解法第2 讲角为定值的高级解法第3 讲边为定值的动点问题第4 讲线段的和或差为定值的动点问题第5 讲比值为定值的动点问题第6 讲乘积为定值的动点问题第7 讲面积为定值的动点问题第8 讲动点产生的几何最值问题【几何法证明角为定值】（1）三角形内角和定理（2）三角形外角定理第 1 讲角为定值的常规解法（3）等腰三角形底角相等（4）直角三角形两锐角互余（5）平行线的同位角相等、内错角相等、同旁内角互补（6）平行四边形的对角相等、邻角互补（7）等腰梯形底角相等（8）圆所涉及的角的关系：圆心角、圆周角、弦切角定理等【例】如图,平面内两条互相垂直的直线相交于点 O,∠MON=90°，点 A 、B 分别在射线 OM 、 ON 上移动，AC 是△BAO 的角平分线，BD 为∠ABN 的角平分线，AC 与 BD 的反向延长线交于点 P.试问：随着点 A 、B 位置的变化，∠APB 的大小是否会变化?若保持不变，请求出∠APB 的度数；若发生变化，求出变化范围。

、【例】如图所示,O 的直径 AB=4,点 P 是 AB 延长线上的一点,过 P 点作 O 的切线,切点为 C ，连接 AC.(1)若∠CPA=30°，求 PC 的长；(2)若点 P 在 AB 的延长线上运动，∠CPA 的平分线交 AC 于点 M ，你认为∠CMP 的大小是否发生变化?若变化，请说明理由；若不变化，求出∠CMP 的大小。

【代数法求角为定值】一般在直角坐标系中，可以用坐标的方法表示出边或角，从而求解具体角为定值的问题。

【例】如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t秒(t>0),抛物线y = ax2 + bx + c 经过点O和点P,已知矩形ABCD的三个顶点为A(1,0),B(1,−5),D(4,0).(1)求c,b (用含t的代数式表示):(2)当4<t<5时，设抛物线分别与线段AB，CD交于点M，N.①在点P的运动过程中，你认为∠AMP的大小是否会变化?若变化，说明理由；若不变，求出∠AMP 的值；②求△MPN的面积S与t的函数关系式,并求t为何值时,S=218；(3)在矩形ABCD的内部(不含边界)，把横、纵坐标都是整数的点称为“好点”。

中考数学压轴题复习-胡不归和阿氏圆模型 (无答案)

P中考模拟压轴题（2）集合 3.胡不归模型姓名学习评价1. 如图，在等腰△ABC 中，AB=AC=10，∠BAC=30°，AD ⊥BC ，点 P 在线段 AD 上，则PA+PB+PC 的最小值为.AABDC（第 1 题图）（第 2 题图）C（第 3 题图）2. 如图，在△ABC 中，AB=AC=10，tan A=2，BE ⊥AC 于点 E ，D 是线段 BE 上的一个动点，则CD +BD 的最小值为．513. 如图，在△ABC 中，AB=4，AC=6，∠A=30°，点 D 为 AC 边上一动点，则最小值为．4. 如图，四边形 ABCD 是菱形，AB=6，且∠ABC=60°，点 M 是对角线 BD 上任意一点，则2AM + BM 的最小值为．AD + DB 的2（第 4 题图）5 DB5.如图，一条笔直的公路l 穿过草原，公路边有一消防站A，距离公路5 千米的地方有一居民点B，A、B 的直线距离是13 千米.一天，居民点B 着火，消防员受命欲前往救火，若消防车在公路上的最快速度是80 千米/小时，而在草地上的最快速度是40 千米/小时，则消防车在出发后最快经过小时可到达居民点B. (消防车可从公路的任意位置进入草地行驶)6.如图，已知海岛A 到海岸公路BC 的距离AB=50 km，B、C 间的距离为100 km，从A 到C 必须先坐船到BC 上的某一点D，航速为25 km/h，再乘汽车到C，车速为50 km/h，由A 到C 所用的时间t 最少h.（第5 题图）（第6 题图）7.如图，AB 为半圆O 的直径，AB=4，点P 为半圆O 圆弧上的一动点，点Q 为线段AB 上一点，且∠PQA=60°，则PQ+AQ 的最大值为．（第7 题图）（第8 题图）8.如图，在△ACE 中，CA=CE，∠CAE=30°，⊙O 经过点C，且⊙O 的直径AB 在线段AE 上，1设点D 是线段AC 上任意一点（不含端点），连接OD，当⊙O 的直径AB 为．CD OD 的最小值为6 时，则23 9. 如图，二次函数 y = 415 x 2- 815x - 4 的图象与 x 轴交于 A 、B 两点（点 A 在点 B 的左边），3与 y 轴交于点 C ，其对称轴与 x 轴交于点 D ，若 P 为 y 轴上的一个动点，连接 PD ，则 5的最小值为．10. 如图，P 为正方形 ABCD 对角线 BD 上一动点，若 AB=4，则 AP+BP+CP 的最小值为．（第 10 题图）PC+PD11. 如图，在平面直角坐标系中，二次函数 y = ax 2 + bx + c 的图象经过点 A(−1,0)，B(0, - )，C(2,0)，其对称轴与 x 轴交于点 D（1）求二次函数的表达式及其顶点坐标；1（2）若 P 为 y 轴上的一个动点，连接 PD ，求 2PB+PD 的最小值为.yx集合 4.阿氏圆模型姓名学习评价1. 如图，在 Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点 D 是△ABC 内一动点，满足 CD=2，2则AD + BD 的最小值为.3BDCA（第 1 题图）（第 2 题图）2. 如图，菱形 ABCD 的边长为 2，∠ABC 的度数为 60°，⊙A 与 BC 相切于点 E ，在⊙A 上任取一点 P ，则PB+PD 的最小值为 .23. 在平面直角坐标系中，A （2，0），B （0，2），C （4，0），D （3，2），P 是△AOB 外部的第一象限内一动点，且∠BPA=135°，则 2PD+PC 的最小值是.（第 3 题图）3PBCC P ODGPC4. 如图，在正方形 ABCD 中，G 是正方形内一点，AD=4，P 是 BC 中点，且 BG=BP ，则 DG +的最小值为.1 CG2ADADB（第 4 题图）（第 5 题图）5. 如图，已知菱形 ABCD 的边长为 4，∠B=60°，⊙B 的半径为 2，点 P 为⊙B 上的一动点，则1PD + PC 的最小值为.216. 如图，已知正方形 ABCD 的边长为 4，⊙B 的半径为 2，点 P 为⊙B 上的一动点，则 PD + PC21的最小值为； P D - PC 的最大值为. 2DC（第 6 题图）AB（第 7 题图）APB7. 如图，点 A 、B 在⊙O 上，OA=OB=12，且 OA ⊥OB .点 C 是 OA 的中点，点 D 在 OB 上，且1OD=10.动点 P 在⊙O 上，则PC+ PD 的最小值为.2⌒8. 如图，已知⊙O 的半径是 1，AC 、BD 为切线，AC=1，BD=2，P 为AB上一动点，则PC + PD2的最小值为.DA O（第 8 题图）B（第 9 题图）9. 如图，在△ABC 中，∠B=90°，AB=CB=2，以点 B 为圆心作⊙B 于 AC 相切，P 为⊙B 上任意一点，则PA +PC 的最小值为 .210. 如图，已知扇形 COD ，∠COD=90°，OC=6， ⌒OA=3，OB=5，点 P 是CD 上任意一点，则2PA + PB 的最小值为.（第 10 题图）2 2 CP11. 如图1，抛物线y =ax2 + (a + 3)x + 3 (a≠0)与x 轴交于点A(4,0)，与y 轴交于点B，在x 轴上有一动点E(m,0)(0<m<4)，过点E 作x 轴的垂线交直线AB 于点N，交抛物线于点P，过点P 作PM⊥AB 于点M.（1）求a 的值和直线AB 的函数表达式；（2）设△PMN 的周长为C1，△AEN 的周长为C2，若C1 =6，求m 的值；C25（3）如图2，在（2）条件下，将线段OE 绕点O 逆时针旋转得到OE′，旋转角为α(0°<α<90°)，2连接E′A、E′B，求E′A+3E′B 的最小值.。

2024数学中考压轴题-圆(九大题型和解题方法)

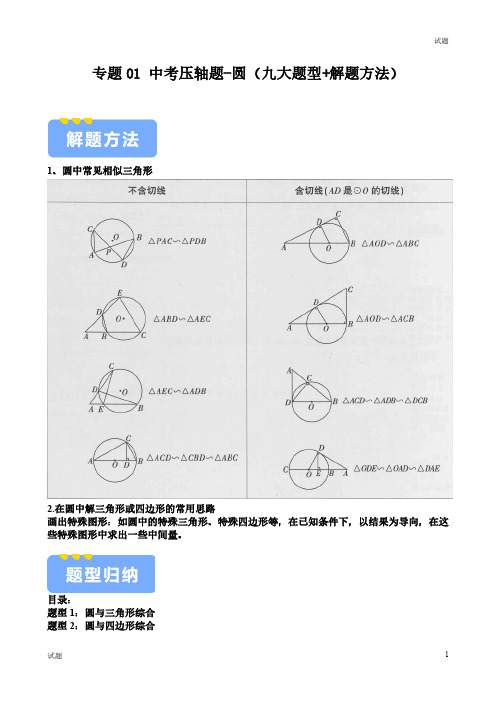
专题01 中考压轴题-圆（九大题型+解题方法）1、圆中常见相似三角形2.在圆中解三角形或四边形的常用思路画出特殊图形：如圆中的特殊三角形、特殊四边形等，在已知条件下，以结果为导向，在这些特殊图形中求出一些中间量。

目录：题型1：圆与三角形综合题型2：圆与四边形综合题型3：圆有关的动态问题题型4：圆与坐标系或函数题型5：以实际问题为背景，求圆与三角形、四边形综合问题题型6：最值问题题型7：在解三角形、四边形中作辅助圆题型8：定值问题题型9：在圆综合中求解三角函数值题型1：圆与三角形综合1．（2024·黑龙江哈尔滨·一模）已知，AD 、BC 为O 两条弦，AD BC ⊥于点E ，连接OE ，AE CE =．(1)如图1，连接OE ，求AEO ∠的度数；(2)如图2，连接AC ，延长EO 交AC 于点N ，点F 为AC 上一点，连接EF ，在EF 上方作等腰直角三角形EFG ，且90EGF ∠=︒，连接NG ，求证：NG BC ∥；(3)在（2）的条件下，连接AB ，CD ，当点G 落在线段AB 上时，过点O 做OL OE ⊥，交CD 于点L ，交CE于点T ，若2OE EG CL ==，求O 半径的长．2．（2024·黑龙江哈尔滨·一模）已知：AB 为O 的直径，点C 为 AB 上一点，连接AC ，点D 为 BC上一点，连接AD ，过点D 作AB 的垂线，垂足为点F ，交O 于点E ，连接CE ，分别交AD 和AB 于点H 和点K ，且90AHE =︒∠．(1)如图1，求证：CAD BAD ∠=∠；(2)如图2，连接HF ，过点H 作HF 的垂线交AB 于点T ，求证：2AB FT =；(3)如图3，在（2）的条件下，连接BC 交AD 于点G ，延长CD 交AB 的延长线于点M ，若CM AG =，5FT =，求CG 的长．3．（2024·黑龙江哈尔滨·一模）如图1，在O 中，直径AB 垂直弦CD 于点G ，连接AD ，过点C 作CF AD ⊥于F ，交AB 于点H ，交O 于点E ，连接DE ．(1)如图1，求证：2E C ∠=∠；(2)如图2，求证：DE CH =；(3)如图3，连接BE ，分别交AD CD 、于点M N 、，当2OH OG =，HF =EN 的长．4．（2024·浙江·模拟预测）如图1，ABC 内接于O ，作AD BC ⊥于点D ．(1)连结AO ，BO ．求证：2180AOB DAC ∠+∠=︒；(2)如图2，若点E 为弧AC 上一点，连结BE 交AD 于点F ，若2BAD CAD ∠∠＝，490DBF CAD ∠+∠=︒，连结OF ，求证：OF 平分AFB ∠；(3)在（2）的条件下，如图3，点G 为BC 上一点，连结EG ，2BGE C ∠=∠．若AD =3BD EG +=，求DF 的长．题型2：圆与四边形综合5．（2024·浙江杭州·模拟预测）如图，四边形ABCD 内接于O ，AC 为O 的直径，DE AC ⊥于点F 交BC 于点E ．(1)设DBC α∠=，试用含α的代数式表示ADE ∠；(2)如图2，若3BE CE =，求BDDE的值；(3)在（2）的条件下，若,AC BD 交于点G ，设FGx CF=，cos BDE y ∠=．①求y 关于x 的函数表达式．②若BC BD =，求y 的值．6．（2024·广东珠海·一模）如图1，F 为正方形ABCD 边BC 上一点，连接AF ，在AF 上取一点O ，以OA 为半径作圆，恰好使得O 经过点B 且与CD 相切于点E ．(1)若正方形的边长为4时，求O 的半径；(2)如图2，将AF 绕点A 逆时针旋转45︒后，其所在直线与O 交于点G ，与边CD 交于点H ，连接DG BG ，．①求ADG ∠的度数；②求证：··²AB BF AG FG BG +=．题型3：圆有关的动态问题7．（2024·广东·一模）综合探究：如图，已知10AB =，以AB 为直径作半圆O ，半径OA 绕点O 顺时针旋转得到OC ，点A 的对应点为C ，当点C 与点B 重合时停止．连接BC 并延长到点D ，使得CD BC =，过点D 作DE AB ⊥于点E ，连接AD ，AC ．(1)如图1，当点E 与点O 重合时，判断ABD △的形状，并说明理由；(2)如图2，当1OE =时，求BC 的长；(3)如图3，若点P 是线段AD 上一点，连接PC ，当PC 与半圆O 相切时，判断直线PC 与AD 的位置关系，并说明理由．8．（2024·浙江湖州·一模）如图，在ABCD Y 中，∠B 是锐角，AB =10BC =，在射线BA 上取一点P ，过P 作PE BC ⊥于点E ，过P ，E ，C 三点作O ．(1)当3cos 5B =时，①如图1，若AB 与O 相切于点P ，连结CP ，求CP 的长；②如图2，若O 经过点D ，求O 的半径长．(2)如图3，已知O 与射线BA 交于另一点F ，将BEF △沿EF 所在的直线翻折，点B 的对应点记为B '，且B '恰好同时落在O 和边AD 上，求此时PA 的长．9．（2024·云南昭通·模拟预测）如图，在O 中，AB 是O 的直径，点M 是直径AB 上的一个动点，过点M 的弦CD AB ⊥，交O 于点C 、D ，连接BC ，点F 为BC 的中点，连接DF 并延长，交AB 于点E ，交O 于点G ．图1 图2 备用图(1)如图1，连接CG ，过点G 的直线交DC 的延长线于点P ．当点M 与圆心O 重合时，若PGC MDE ∠=∠，求证：PG 是O 的切线；(2)在点M 运动的过程中，DE kDF =（k 为常数），求k 的值；(3)如图2，连接BG OF MF 、、，当MOF △是等腰三角形时，求BGD ∠的正切值．题型4：圆与坐标系或函数10．（2024·福建龙岩·一模）如图，抛物线234y x x =-++与x 轴分别交于A 、B 两点(点A 在点B 的左侧)与y 轴交于点C ．(1)直接写出A 、B 、C 三点的坐标；(2)如图(1)，P 是抛物线上异于A ，B 的一点，将点B 绕点P 顺时针旋转45︒得到点Q ，若点Q 恰好在直线AP 上，求点P 的坐标；(3)如图(2)，MN 是抛物线上异于B ，C 的两个动点，直线BN 与直线CM 交于点T ，若直线MN 经过定点()1,3，求证：点T 的运动轨迹是一条定直线．11．（2024·江苏常州·模拟预测）定义：在平面直角坐标系xOy 中，P 、Q 为平面内不重合的两个点，其中1122(,),(,)P x y Q x y ．若：1122x y x y +=+，则称点Q 为点P 的“等和点”．(1)如图1，已知点()21P ，，求点P 在直线1y x =+上“等和点”的坐标；(2)如图2，A 的半径为1，圆心A 坐标为()20，．若点()0P m ，在A 上有且只有一个“等和点”，求m 的值；(3)若函数()22y x x m =-+≤的图像记为1W ，将其沿直线x m =翻折后的图像记为2W ．当1W ，2W 两部分组成的图像上恰有点()0P m ，的两个“等和点”，请直接写出m 的取值范围．12．（2024·江苏宿迁·一模）如图1，在平面直角坐标系xOy 中，抛物线23y ax bx =++与x 轴分别相交于A 、B 两点，与y 轴相交于点C ，已知点A 的坐标为(10)-，，点B 的坐标为(30)，．(1)求出这条抛物线的函数表达式；(2)如图2，点D 是第一象限内该抛物线上一动点，过点D 作直线l y 轴，直线l 与ABD △的外接圆相交于点E ．①仅用无刻度直尺找出图2中ABD △外接圆的圆心P ．②连接BC 、CE ，BC 与直线DE 的交点记为Q ，如图3，设CQE △的面积为S ，在点D 运动的过程中，S是否存在最大值？如果存在，请求出S 的最大值；如果不存在，请说明理由．13．（2024·江苏宿迁·二模）中国象棋棋盘上双方的分界处称为“楚河汉界”，以“楚河汉界”比喻双方对垒的分界线．在平面直角坐标系中，为了对两个图形进行分界，对“楚河汉界线”给出如下定义：点()11,P x y 是图形1G 上的任意一点，点()22,Q x y 是图形2G 上的任意一点，若存在直线()0l y kx b k =+≠∶满足11y kx b ≤+且22y kx b ≥+，则直线(0)y k b k =+≠就是图形1G 与2G 的“楚河汉界线”．例如：如图1，直线4l y x =--∶是函数6(0)y x x=<的图像与正方形OABC 的一条“楚河汉界线”．(1)在直线①2y x =-，②41y x =-，③23y x =-+，④31y x =--中，是图1函数6(0)y x x=<的图像与正方形OABC 的“楚河汉界线”的有______；（填序号）(2)如图2，第一象限的等腰直角EDF 的两腰分别与坐标轴平行，直角顶点D 的坐标是()2,1，EDF 与O 的“楚河汉界线”有且只有一条，求出此“楚河汉界线”的表达式；(3)正方形1111D C B A 的一边在y 轴上，其他三边都在y 轴的右侧，点(2,)M t 是此正方形的中心，若存在直线2y x b =-+是函数2)304(2y x x x =-++≤≤的图像与正方形1111D C B A 的“楚河汉界线”，求t 的取值范围．题型5：以实际问题为背景，求圆与三角形、四边形综合问题14．（2024·陕西西安·一模）【问题提出】（1）如图1，已知在边长为5的等边ABC 中，点D 在边BC 上，3BD =，连接AD ，则ACD 的面积为；【问题探究】（2）如图2，已知在边长为6的正方形ABCD 中，点E 在边BC 上，点F 在边CD 上，且45EAF ∠=︒，若5EF =，求AEF △的面积；【问题解决】（3）如图3是某座城市廷康大道的一部分，因自来水抢修在4AB =米，AD =ABCD 区域内开挖一个AEF △的工作面，其中B 、F 分别在BC CD 、边上（不与B 、C 、D 重合），且60EAF ∠=︒，为了减少对该路段的拥堵影响，要求AEF △面积最小，那么是否存在一个面积最小的AEF △？若存在，请求出AEF △面积的最小值；若不存在，请说明理由．15．（2024·陕西西安·一模）【问题提出】（1）如图1，点D 为ABC 的边BC 上一点，连接2,,3BD AD BDA BAC AB ∠=∠=，若ABD △的面积为4，则ACD 的面积为______；【问题探究】（2）如图2，在矩形ABCD 中，6,5AB BC ==，在射线BC 和射线CD 上分别取点E F 、，使得65BE CF =，连接AE BF 、相交于点P ，连接CP ，求CP 的最小值；【问题解决】（3）如图3，菱形ABCD 是某社区的一块空地，经测量，120AB =米，60ABC ∠=︒．社区管委会计划对该空地进行重新规划利用，在射线AD 上取一点E ，沿BE CE 、修两条小路，并在小路BE 上取点H ，将CH 段铺设成某种具有较高观赏价值的休闲通道（通道宽度忽略不计），根据设计要求，BHC BCE ∠=∠，为了节省铺设成本，要求休闲通道CH 的长度尽可能小，问CH 的长度是否存在最小值？若存在，求出CH 长度的最小值；若不存在，请说明理由．题型6：最值问题16．（2024·湖南长沙·三模）如图1，,,A B C 为O 上不重合的三点，GC 为O 的切线，1902G A ∠+∠=︒．(1)求证：GB 为O 的切线；(2)若ABC 为等腰三角形，345,tan 4BAC BAC ∠<︒∠=，求BC AG的值；(3)如图2，若AB 为直径，M 为线段AC 上一点且GM GB ⊥，2223880AM OB GB GB +-+-=，02GB <<，求MGBA S 四边形的最大值．17．（2024·重庆·模拟预测）如图，在直角ABC 中，90BAC ∠=︒．点D 为ABC 内一点，且60ADB ∠=︒，E 为线段BD 的中点，连接AE ．(1)如图1，若AB AC ==，2AD =，求BE 的长；(2)如图2，连接CD ，若AB AC =，BAE ACD ∠=∠，过点E 作EF AD ⊥交于F ，求证：AE =；(3)如图3，过点D 作DM AC ⊥于点M ，DN BC ⊥于点N ，连接MN ，若AB =4AC =，求MN 的最小值．题型7：在解三角形、四边形中作辅助圆18．（2024·福建泉州·一模）如图1，在ABCD Y 中，BE 平分ABC ∠交AD 于点E ，F 是CD 上一点，且DF DE =．(1)求证：BE EF ⊥；(2)如图2，若120A ∠=︒，FG BC ⊥于点G ，H 是BF 的中点，连接DG ，EH ，EG ，且EG 与BF 相交于点K ．①求证：DG EH =；②若2CF DF =，求KFGK的值．题型8：定值问题19．（2024·浙江·模拟预测）如图1，E 点为x 轴正半轴上一点，E 交x 轴于A 、B 两点，P 点为劣弧 BC上一个动点，且(1,0)A -、(1,0)E ．(1) BC的度数为 °；(2)如图2，连结PC ，取PC 中点G ，则OG 的最大值为；(3)如图3，连接AC 、AP 、CP 、CB ．若CQ 平分PCD ∠交PA 于Q 点，求AQ 的长；(4)如图4，连接PA 、PD ，当P 点运动时（不与B 、C 两点重合），求证：PC PDPA+为定值，并求出这个定值．题型9：在圆综合中求解三角函数值20．（2024·湖南长沙·一模）如图1，在Rt ABC △中，90ABC ∠=︒，30C ∠=︒，B C =，D 是BC 的中点．经过A ，B ，D 三点的O 交AC 于点E ，连接BE ．(1)求AE 和BE 的长；(2)如图2，两动点P 、Q 分别同时从点A 和点C 出发匀速运动，当点P 运动到点E 时，点Q 恰好运动到点B ，P 、Q 停止运动，连接PQ ．①记AP x =，当PQC △的面积最大时，求x 的值；②如图3，连接BP 并延长交O 于点F ，连接AF 、FE ．当BE 平分FBC ∠时，求sin ABF ∠的值．21．（2024·上海杨浦·一模）已知以AB 为直径的半圆O 上有一点C ，CD OA ⊥，垂足为点D ，点E 是半径OC 上一点（不与点O 、C 重合），作EF OC ⊥交弧BC 于点F ，连接OF ．(1)如图1，当FE 的延长线经过点A 时，求CDAF的值；(2)如图2，作FG AB ⊥，垂足为点G ，连接EG ．①试判断EG 与CD 的大小关系，并证明你的结论；②当EFG 是等腰三角形，且4sin 5COD ∠=，求OE OD的值．专题01 中考压轴题-圆（九大题型+解题方法）1、圆中常见相似三角形2.在圆中解三角形或四边形的常用思路画出特殊图形：如圆中的特殊三角形、特殊四边形等，在已知条件下，以结果为导向，在这些特殊图形中求出一些中间量。

中考数学圆的综合提高练习题压轴题训练含详细答案

中考数学18道圆相关的压轴题，不想丢分速看！

中考数学18道圆相关的压轴题，不想丢分速看！GUIDE导读不少同学留言说几何部分的圆很难。

一般来讲，对于圆的大题，第1~2问基本是证明，也就相当于给你提供了一个解题思路，同学们顺着这个思路去进行求证就好。

这次，王老师精选了18道圆相关的压轴题，全都是各省份的中考真题，有需要的同学快领走练习~我们先来说说圆的基本性质。

圆的基本性质一. 性质圆既是轴对称图形，又是中心对称图形，任何一条直径所在的直线都是它的对称轴，圆心是它的对称中心二. 垂径定理及其推论1. 定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧2. 推论：•平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧•弦的垂直平分线经过圆心，并且平分弦所对的两条弧•平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧•在同圆或者等圆中，圆的两条平行弦所夹的弧相等3. 垂径定理与推论的延伸：三. 弦、弧、圆心角的关系1. 定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等2. 推论：•在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量都分别相等•弧的度数等于它所对圆心角的度数四. 圆周角定理及其推论1. 定理：一条弧所对的圆周角等于它所对的圆心角的一半2. 推论•同弧或等弧所对的圆周角相等•半圆（或直径）所对的圆周角是直角，９０°的圆周角所对的弦是直径五. 圆与多边形1. 圆内接多边形2. 正多边形和圆六. 三角形的外接圆与圆有关的位置关系一. 点与圆的位置关系（设圆的半径为ｒ，平面内任一点到圆心的距离为ｄ）点在圆外ｄ＞ｒ，如右图中点Ａ点在圆上ｄ＝ｒ，如右图中点Ｂ点在圆内ｄ＜ｒ，如右图中点Ｃ二. 直线与圆的位置关系（设圆的半径为ｒ，圆心到直线的距离为ｄ）三. 切线的性质数量关系：圆心到切线的距离等于半径位置关系：切线垂直于过切点的半径四. 切线的判定直线与圆有公共点，连半径，证垂直直线与圆无公共点，作垂线，证半径五. 切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角如图，过⊙Ｏ外一点Ｐ可引两条切线ＰＡ、ＰＢ，则ＰＡ＝ＰＢ，ＰＯ平分∠ＡＰＢ六. 三角形的内切圆18道与圆相关的压轴题。

2024年中考数学压轴题型-专题03 与圆有关问题的压轴题之五大题型(解析版)

专题03与圆有关问题的压轴题之五大题型目录【题型一与圆中三角形全等的有关问题】 (1)【题型二与圆中三角形相似问题的有关问题】 (5)【题型三与圆中证明直线是切线的有关问题】 (29)【题型四与圆中求弧长、扇形面积的有关问题】 (40)【题型五与圆中求函数表达式的有关问题】 (50)【题型一与圆中三角形全等的有关问题】【变式训练】(1)求证：CD BF =．(2)若14BE BF ==，，求GE 的长．(3)连结GO OF ，，如图2，求证：122+EOG AOF ∠∠=【答案】(1)见解析(2)的长为3，由（1）得： CFBD =，FBC BCD ∴∠=∠，BG CG ∴=，AB 为O 的直径，CD 12DE CE CD ∴===，，AF AF =，12AOF OBF ∴∠=∠，在OCG 和OBG △中，OC OB =⎧⎪【题型二与圆中三角形相似问题的有关问题】例题：（2023·浙江宁波·校考一模）如图，已知BC 是O 的直径，点D 为BC 延长线上的一点，点A 为圆上一点，且AB AD =，AC CD =．(1)求证：ACD BAD ∽ ；(2)求证：AD 是O 的切线．【答案】(1)见解析(2)见解析【分析】（1）根据等腰三角形的性质得到CAD B ∠=∠，由于D D ∠=∠，于是得到ACD BAD ∽ ；（2）连接OA ，根据等腰三角形的性质得到B OAB ∠=∠，得到OAB CAD ∠=∠，由BC 是O 的直径，得到90BAC ∠=︒，即可得到结论．【详解】（1）证明：（1）∵AB AD =，∴B D ∠=∠，∵AC CD =，∴CAD D ∠=∠，∴CAD B ∠=∠，∵D D ∠=∠，∴ACD BAD ∽ ；（2）连接OA ，∵OA OB =，∴B OAB ∠=∠，∴OAB CAD ∠=∠，∵BC 是O 的直径，∴90BAC ∠=︒，∴OA ⊥AD ，∴AD 是O 的切线．【点睛】本题考查了相似三角形的判定和性质，切线的判定，等腰三角形的性质，圆周角定理，正确的作出辅助线是解题的关键．【变式训练】(1)求证：BDE DCE △∽△．(2)若2,DE C =为BE 中点，求【答案】(1)见解析(2)3AC =【分析】（1）根据CD 平分∠BDE DCE △∽△；（2）由BDE DCE △∽△得BE DE 在由Rt DCE V 中，cos ACD ∠【详解】（1）∵CD 平分ACE ∠∴ACD DCE∠=∠∵AB DE ∥，（2）∵BDE DCE △∽△，∴BE DE DE CE=，∵点C 为BE 中点，设BC =则2a DE DE a=，∴22D E a ==，即1a =∵90ABC ∠=︒，∴90E ADC ∠=∠=︒在Rt DCE V 中，1CE CD =，∴cos cos ACD DCE ∠=∠=∴3AC =．【点睛】此题主要考查了相似三角形的判定和性质，三角形的外接圆等，解答此题的关键是熟练掌握相似三角形的判定方法，理解相似三角形的对应边成比例，难点是正确的作出辅助线．2．（2023·浙江杭州·杭州市公益中学校考三模）如图，AC ，BD 交于点E ，P 为DB(1)求证：ABE DBA∽；的切线；(2)求证：PA是O(3)若E为BD的中点，求tan 【答案】(1)见解析(2)见解析(3)2(1)求B D ∠-∠的值．(2)当75B ∠=︒时，求(3)若BC CE =，DOE 【答案】(1)45︒∵AB是O的直径，半径∴OAD ODA∠=∠=∵ AC AC=，∴ABC ADC∠=∠，（3）解：如图所示，连接∵ BDBD =，∴12BCD BOD =∠∠∵BC CE =，∴B CEB ∠=∠67.5=(1)求BGC ∠的度数．(2)①求证：AF BC =．②若AG DF =，求tan GBC ∠的值，(3)如图2，当点O 恰好在BG 上且1OG =时，求AC 的长．【答案】(1)90︒(2)①证明见解析；②15tan 5GBC ∠=；(3)3172+∵OB OC =，∴CBE OBC OCB ∠=∠=∠，∴OC BE ∥，∵BD CD =，BDE CDN ∠=∠∴EBD NCD ≌，∴BE CN =，DB DG = ，DBG DGB ∠=∠∴．又,DBG CAG BGD ∠=∠∠=∠ CAG AGM ∴∠=∠，MA MG ∴=．OB OC = ，OBC OCB ∴∠=∠，(1)求ACB ∠的大小（用α，β表示）；(2)连接CF ，交AB 于H （如图2）．若45β=︒，且BC EF AE CF ⨯=⨯．求证：(3)在（2）的条件下，取CH 中点M ，连接OM 、GM （如图3），若OGM ∠①求证：GM BC ∥，12GM BC =；②OM∵AF AG =，∴AFG AGF ∠∠==∴ACF AGF ∠∠==∵FAB ∠β=，∴ACB ACF ∠=∠+∠∵AF AG =，45β=︒，∴AFG G ACH ∠=∠=∠∵EAF FAC ∠=∠，∴EAF FAC ∽，∴EF AE CF FA=，∴AE CF EF FA ⨯=⨯，∵BC EF AE CF ⨯=⨯，∴BC EF EF AF ⨯=⨯，∴BC AF =，∴ AF BC=，∴45BAC AGF ∠=∠=︒，∴180454590AHC ∠=︒-︒-︒=︒，∴2AHC BAC ∠=∠；（3）①证明：如图3中，连接CG ，延长GM 交AB 于点I ．∵245OGM α∠=-︒，45AGF ∠=︒，∴2AGM α∠=，∵45AFG G ACH ∠=∠=∠=︒，∴90FAG ∠=︒，∴FG 是直径，∴90FCG ∠=︒，∵90AHC ∠=︒，∴180AHC GCH ∠+∠=︒，∴AB CG ∥，∴MHI MCG ∠=∠，∵MH MC =，HMI CMG ∠∠=，∴ASA MHI MCG ≌（），∴MI MG =，HI CG =，MGC HIM ∠=∠，∵90FAG ∠=︒，∴90FAG BAF BAG BAG α∠=∠+∠=+∠=︒，在AIG V 中，180AGM BAG HIM ∠+∠+∠=︒，∴2180BAG HIM α+∠+∠=︒即()22BAG HIM BAG αα+∠+∠=+∠，∴HIM BAG ∠=∠，又45BAC ∠=︒，【点睛】本题属于圆综合题，考查了圆周角定理，相似三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是正确寻找相似三角形或全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．6．（2023·浙江·统考中考真题）如图，在径CE 交AB 于点F ，连结(1)求证：AD HC ∥；(2)若2OG GC=，求tan FAG ∠的值；(3)连结BC 交AD 于点N ，若O ①若52OF =，求BC 的长；②若10AH =，求ANB 的周长；∠=∠．∴BAD CAD∴52CF =．∴54CG FG ==，∴154OG =，∴22574AG OA OG =-=．∵CE AD ⊥，∴5272AD AG ==．∵ ==AC CDDB ，∴ AD CB=，∵,AD HC FG GC =∥，∴AH AF =．∵90HCF ∠=︒，∴10AC AH AF ===．设CG x =，则,5FG x OG ==-由勾股定理得222AG AO OG =-2225(5)10x x --=-，设CG x =，则,5FG x OG x ==-由勾股定理得222AG AO OG =-2222210AF AG FG x x x =+=-+∵,AD HC FG GC =∥，∴12AH AF HF ==，∴12AG HC =．(1)设E ∠为α，请用α表示BAC ∠的度数．(2)如图1，当BE AD ⊥时，①求证：DE BG =．②当3tan ,54ABE BG ∠==时，求半径的长．(3)如图2，当BE 过圆心O 时，若tan ABE k ∠=90 ABC ADC∴∠=∠=又AB AD=，AC=∴ABC ADC△≌△．∴12 BAC CAD∠=∠=∠E BADα∠=∠=，3tan 4ABE ∠=，BG =∴3tan 4FDE ∠=，DE 3EF FG ∴==，FD =8BF BG GF ∴=+=．AB AD = ，BAC ∠AC BD ∴⊥，【题型三与圆中证明直线是切线的有关问题】(1)求证：DE 为圆O 的切线；(2)连接OC 交DE 于点F ，若cos ABC ∠O为AB中点，D为BC中点，OD AC∴∥．DE AC⊥，DE OD∴⊥，且点D在O上，DE∴是O的切线；OD AC∥，∴OF OD FC EC=．AB为O的直径，90ADB ADC∴∠=∠=︒．又D为BC的中点，【变式训练】1．（2023·浙江台州·台州市书生中学统考一模）如图，直线AB 经过O 上的点M ，并且,OA OB MA MB ==，OA 交O 于点N ．(1)求证：直线AB 是O 的切线；(2)当ON AN =时，求AOB ∠的度数．【答案】(1)见解析(2)120AOB ∠=︒【分析】（1）连接OM ，根据等腰三角形的性质与判定推出OM AB ⊥，即可证明结论；（2）连接MN ，根据直角三角形的性质和圆的基本性质得出OMN 是等边三角形，从而得到60MON ∠=︒，即可求解．【详解】（1）连接OM ，∵OA OB =，∴OAB 是等腰三角形，∵MA MB =，∴OM AB ⊥，又点M 在O 上，∴直线AB 是O 的切线；（2）连接MN ，∵,OM AB ON AN ⊥=，∴MN AN ON ==，又OM ON =，∴OMN 是等边三角形，∴60MON ∠=︒，∴906030A B ==︒-︒=︒∠∠，∴120AOB ∠=︒．【点睛】本题考查了圆的性质，圆的切线证明，等腰三角形的性质与判定，等边三角形的性质与判定，直角三角形的性质等知识点，熟练掌握相关知识点是解题的关键．2．（2023·浙江金华·校联考模拟预测）如图，BC 是O 的直径，PB 是O 的切线，切点为B ，连接PO ，过点C 作AC PO 交O 于点A ，连接PA ．(1)求证：AP是O的切线；(2)若4cos5APO∠=，O的半径为∵OA OC=，∴OAC OCA∠=∠．∵O 的半径为3，∴3,6OA BC ==．∵POB POA △≌△，(1)求证：DG 是O 的切线．(2)已知3DG =，1EG =，求【答案】(1)见解析(2)O 的半径为5【分析】（1）连接OD ，根据（2）解：∵OD DG ⊥∴四边形ODGF 为矩形，∴3OF DG ==，OD 设O 的半径为r ，即∵1EG =，(1)求证：DC 为O 的切线；(2)若ACB ∠的角平分线CE 交线段AB 于点F ，交O 于点E ，连接BE ，求CF CE ⋅．OA OC，=∴∠=∠，OAC OCA ，DCB OAC ∠=∠∴∠=∠，OCA DCB 是直径，AB(1)求证：直线AB 是O 的切线；(2)若2BC OC =，①求tan ADB ∠的值；②作CAD ∠的平分线AP 交O 于点P 的代数式表示）．∴90OAC OAD ∠+∠=︒，又∵OA OD =，∴OAD ODA ∠=∠，∵BAC ADB ∠=∠，∴OAD BAC ∠=∠，∴90BAC OAC ∠+∠=°，即90BAO ∠=∴AB OA ⊥，又∵OA 为半径，∴直线AB 是O 的切线；（2）解：①解：∵BAC ADB ∠=∠，∴BCA BAD △∽△，∴AC BC AD BA=，2②在Rt CAD △中，22AC AD =，2AC +∴()()222222AC AC CD r +==解得233AC r =，263AD r =，∵AP 平分CAD ∠，∴CAP EAD ∠=∠，又∵APC ADE ∠=∠，∴CAP EAD △∽△，∴AC AP AE AD=，∴2423AE AP AC AD r ⋅=⋅=，∵22AB r k ==，∴24r k =，∴224212386AE AP k k ⋅=⋅=．【点睛】本题考查圆周角定理、切线的判定、等腰三角形的性质、相似三角形的判定与性质、勾股定理、角平分线的定义等知识，熟练掌握相关知识的联系与运用，会利用相似三角形的性质求解是解答的关键．【题型四与圆中求弧长、扇形面积的有关问题】(1)求证：BC BD =．(2)若,2OB OA AE ==．①求半圆O 的半径．②求图中阴影部分的面积．【变式训练】1．（2023·浙江绍兴·校联考三模）如图，已知，在ABC 中，4AB =，以AB 为直径作O ，交边BC 的中点D ．DE AC ⊥于点E ，连结AD ．(1)求证：DE 是O 的切线．(2)请你给ABC 添加一个条件，并求弧【答案】(1)证明过程见详解(2)添加条件为：60DAB ∠=︒（添加条件不唯一）【分析】（1）如图所示，连接OD 由此即可求证；（2）根据圆周角的性质，可求出∵点D 是BC 的中点，点O 是∴12BD BO BC BA ==，∴OD AC ∥，∴ADO DAE ∠=∠，∵DE AC ⊥，∴90ADE DAE ∠+∠=︒，∴90ADE ADO ∠+∠=︒，∴OD DE ⊥，点D 在O 上，∥；(1)求证：OD ACAB=，求阴影部分的面积．(2)若6【答案】(1)见解析393∵OA OC =，60A ∠=︒，∴AOC 是等边三角形，过点C 作CF AO ⊥，(1)证明： BDCE =；(2)若60A ∠=︒，2BC =，求阴影部分面积．【答案】(1)证明见解析∵AB AC =，∴A ABC CB =∠∠，∵BC 为O 的直径，∵AB AC =，60BAC ∠=︒，OB ∴ABC 为等边三角形，AO ∴60ABC ACB ∠=∠=︒，OB(1)求证:DE AB ⊥．(2)若3DE =，30C ∠=︒，求阴影部分面积．【答案】(1)见解析(2)332π23-∵AC 为直径，∴AD BC ⊥，∵AB AC =，(1)求证：ACD E∠=∠；(2)若3AC=，1AD=，求弧【答案】(1)见解析(2)π3∵直线AC与O相切于点C ∴OC CA⊥，∴190ACD︒∠+∠=，∵ED为直径，【题型五与圆中求函数表达式的有关问题】(1)求CD 的长；(2)如图2，当90PQD ∠=︒时，求PEC 的正切值；(3)如图1，设PE x DF y ==，．①求y 关于x 的函数解析式；②若20PF DQ ⨯=，求y 的值．【答案】(1)8(2)322x 73。

中考数学---与圆有关的动点几何压轴题1

中考数学---与圆有关的动点几何压轴题1定圆结合直角三角形：1、已知：如图，在Rt △ABC 中， 90=∠C ，4=BC ，21tan =∠CAB ，点O 在边AC 上，以点O 为圆心的圆过A 、B 两点，点P 为AB 上一动点.（1）求⊙O 的半径；（2）联结AP 并延长，交边CB 延长线于点D ，设x P A =，y D B =，求y 关于x 的函数解析式，并写出x 的取值范围；（3）联结P B ，当点P 是AB 的中点时，求△ABP 的面积与△ABD 的面积比ABDABPS S ∆∆的值．2、如图，在Rt △ABC 中，∠ACB=90°．半径为1的圆A 与边AB 相交于点D ，与边AC 相交于点E ，连接DE 并延长，与线段BC 的延长线交于点P ．（1）当∠B=30°时，连接AP ，若△AEP 与△BDP 相似，求CE 的长；（2）若CE=2，BD=BC ，求∠BPD 的正切值；（3）若tan ∠BPD=，设CE=x ，△ABC 的周长为y ，求y 关于x 的函数关系式．PD第1题图备用图B3、如图，在半径为5的⊙O 中，点A 、B 在⊙O 上，∠AOB=90°，点C 是弧AB 上的一个动点，AC 与OB 的延长线相交于点D ，设AC=x ，BD=y ．（1）求y 关于x 的函数解析式，并写出它的定义域；（2）如果⊙O 1与⊙O 相交于点A 、C ，且⊙O 1与⊙O 的圆心距为2，当BD=OB 时，求⊙O 1的半径；（3）是否存在点C ，使得△DCB ∽△DOC ？如果存在，请证明；如果不存在，请简要说明理由．定圆中结合平行线：2、在半径为4的⊙O 中，点C 是以AB 为直径的半圆的中点，OD ⊥AC ，垂足为D ，点E 是射线AB 上的任意一点，DF //AB ，DF 与CE 相交于点F ，设EF =x ，DF =y ．（1）如图1，当点E 在射线OB 上时，求y 关于x 的函数解析式，并写出函数定义域；（2）如图2，当点F 在⊙O 上时，求线段DF 的长；（3）如果以点E 为圆心、EF 为半径的圆与⊙O 相切，求线段DF 的长．ABEFCDOABF C D O动圆结合直角梯形：5、如图，已知在梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AB=4，AD=3，sin ∠DCB=，P 是边CD 上一点（点P 与点C 、D 不重合），以PC 为半径的⊙P 与边BC 相交于点C 和点Q ．（1）如果BP ⊥CD ，求CP 的长；（2）如果PA=PB ，试判断以AB 为直径的⊙O 与⊙P 的位置关系；（3）联结PQ ，如果△ADP 和△BQP 相似，求CP 的长．动圆结合内切直角三角形：6、在△ABC 中，∠ABC ＝90°，AB ＝4，BC ＝3，O 是边AC 上的一个动点，以点O 为圆心作半圆，与边AB 相切于点D ，交线段OC 于点E ，作EP ⊥ED ，交射线AB 于点P ，交射线CB 于点F 。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

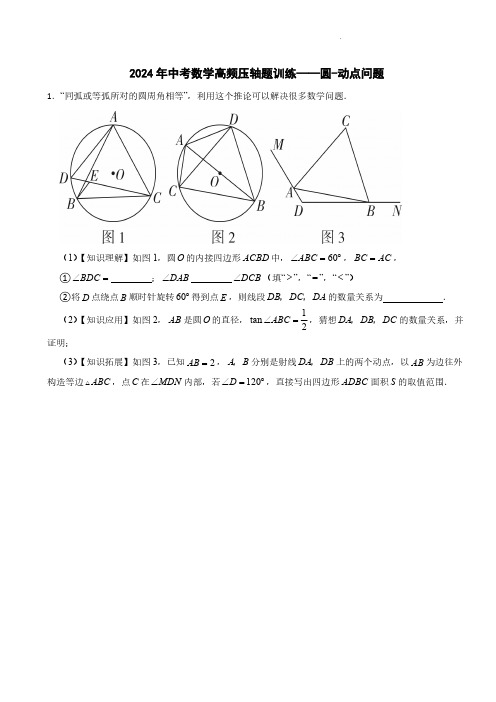
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

2018年中考数学压轴题专题练习---动点问题专题训练

2018年中考数学压轴题专题练习---动点问题专题训练1、如图6所示，一艘轮船以20里/时的速度由西向东航行，途中接到台风警报，台风中心正以40里/时的速度由南向北移动，距台风中心20里的圆形区域（包括边界）都属台风区．当轮船到A 处时，测得台风中心移10到位于点A 正南方向B 处，且AB = 100里．（1）若这艘轮船自A 处按原速度继续航行，在途中会不会遇到台风？若会，试求轮船最初遇到台风的时间；若不会，请说明理由；（2）现轮船自A 处立即提高船速，向位于东偏北300方向，相距60里的D 港驶去．为使台风到来之前，到达D 港，问船速至少应提高多少（提高的船速取整数，）？ 1336≈.2、如图10，在菱形中，＝10，∠＝60°．点从点以每秒1个单位长的速度沿着边ABCD AB BAD M A AD 向点移动；设点移动的时间为秒().D t 100≤≤t (1) 为边上任意一点.在点移动过程中，线段是否一定可以将菱形分割成面积相等的两N 点BC M MN 部分，并说明理由；(2) 从点(与点M 出发的时刻相同)以每秒2个单位长的速度沿着边向点移动，在什么时N 点B BC C 刻，梯形的面积最大?并求出面积的最大值；ABNM (3) 点从点(与点出发的时刻相同)以每秒个单位长的速度沿着射线方向（可以超越N B M )2(≥a a BC C 点）移动，过点作∥，交于点.当≌时，设M MP AB BC P MPN ∆ABC∆∆分的面积为，求出用表示的关系式，并求当时的值．S t S 0=S a 3、如图12，在矩形ABCD 中，AB =12厘米，BC =6厘米．点P 沿AB 边从点A 开始向点B 以2厘米/秒的速度移动；点Q 沿DA 边从点D 开始向点A 以1厘米/秒的速度移动．如果P 、Q 同时出发，用t (秒)表示移动的时间(0≤t ≤6),那么：（1）当t 为何值时，为等腰直角三角形？QAP ∆（2）求四边形的面积；提出一个与计算结果有关的结论；QAPC （3）当t 为何值时，以点Q 、A 、P 为顶点的三角形与相似？ABC ∆图10图124、如图12，已知A 为∠POQ 的边OQ 上一点，以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点，且∠MAN ＝∠POQ ＝（为锐角）．当∠MAN 以点A 为旋转中心，AM 边从与AO 重合的位置开始，按逆时针方向旋转αα（∠MAN 保持不变）时， M 、N 两点在射线OP 上同时以不同的速度向右平行移动．设OM ＝x ，ON ＝y （y ＞x ≥0），△AOM 的面积为S ．若cos 、OA 是方程2z 2－5 z ＋2＝0的两个根．α（1）当∠MAN 旋转30°（即∠OAM ＝30°）时，求点N 移动的距离；（2）求证：；MN ON AN ⋅=2（3）求y 与x 之间的函数关系式及自变量x 的取值范围；（4）试写出S 随x 变化的函数关系式，并确定S 的取值范围．5、已知：如图12，等边三角形的边长为6，点D ，E 分别在边AB ，AC 上，且AD =AE =2．若点F 从点B 开ABC 始以每秒1个单位长的速度沿射线BC 方向运动，设点F 运动的时间为t 秒．当t ＞0时，直线FD 与过点A 且平行于BC 的直线相交于点G ，GE 的延长线与BC 的延长线相交于点H ，AB 与GH 相交于点O ．（1）设△EGA 的面积为S ，写出S 与t 的函数关系式；（2）当t 为何值时，AB ⊥GH ；（3）请你证明△GFH 的面积为定值；（4）当t 为何值时，点F 和点C 是线段BH 的三等分点．6、如图12，在直角梯形ABCD 中，AD ∥BC ，∠C =90°，BC =16，DC =12，AD =21．动点P 从点D 出发，沿射线DA 的方向以每秒2个单位长的速度运动，动点Q 从点C 出发，在线段CB 上以每秒1个单位长的速度向点B 运动，点P ，Q 分别从点D ，C 同时出发，当点Q 运动到点B 时，点P 随之停止运动．设运动时间为t （秒）．（1）设△BPQ 的面积为S ，求S 与t 之间的函数关系式；（2）当t 为何值时，以B ，P ，Q 三点为顶点的三角形是等腰三角形？（3）当线段PQ 与线段AB 相交于点O ，且2AO =OB 时，求∠BQP 的正切值；（4）是否存在时刻t ，使得PQ ⊥BD ？若存在，求出t 的值；若不存在，请说明理由．PO N MA 图12Q 图12A BCDP Q 图127、如图10所示，一段街道的两边缘所在直线分别为AB ，PQ ，并且AB ∥PQ ．建筑物的一端DE 所在的直线MN ⊥AB 于点M ，交PQ 于点N ．小亮从胜利街的A 处，沿着AB 方向前进，小明一直站在点P 的位置等候小亮．（1）请你在图10中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置（用点C 标出）；（2）已知：MN =20 m ，MD =8 m ，PN =24 m ，求（1）中的点C 到胜利街口的距离CM ．8、如图13，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝16，动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动，动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动．P ，Q 分别从点A ，C 同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ 关于直线PQ 对称的图形是△PDQ ．设运动时间为t （秒）．（1）设四边形PCQD 的面积为y ，求y 与t 的函数关系式；（2）t 为何值时，四边形PQBA 是梯形？（3）是否存在时刻t ，使得PD ∥AB ？若存在，求出t 的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t ，使得PD ⊥AB ？若存在，请估计t 的值在括号中的哪个时间段内（0≤t ≤1；1＜t ≤2；2＜t ≤3；3＜t ≤4）；若不存在，请简要说明理由．9、如图16，在等腰梯形ABCD 中，AD ∥BC ，AB =DC =50，AD =75，BC =135．点P 从点B 出发沿折线段BA -AD -DC 以每秒5个单位长的速度向点C 匀速运动；点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动，过点Q 向上作射线QK ⊥BC ，交折线段CD -DA -AB 于点E ．点P 、Q 同时开始运动，当点P 与点C 重合时停止运动，点Q 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当点P 到达终点C 时，求t 的值，并指出此时BQ 的长；（2）当点P 运动到AD 上时，t 为何值能使PQ ∥DC ？（3）设射线QK 扫过梯形ABCD 的面积为S ，分别求出点E 运动到CD 、DA 上时，S 与t 的函数关系式；（不必写出t 的取值范围）（4）△PQE 能否成为直角三角形？若能，写出t 的取值范围；若不能，请说明理由．图13APC图16P 图1010、如图15，在Rt △ABC 中，∠C =90°，AB =50，AC =30，D ，E ，F 分别是AC ，AB ，BC 的中点．点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动；点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动，过点Q 作射线QK ⊥AB ，交折线BC -CA 于点G ．点P ，Q 同时出发，当点P 绕行一周回到点D 时停止运动，点Q 也随之停止．设点P ，Q 运动的时间是t 秒（t ＞0）．（1）D ，F 两点间的距离是；（2）射线QK 能否把四边形CDEF 分成面积相等的两部分？若能，求出t 的值．若不能，说明理由；（3）当点P 运动到折线EF -FC 上，且点P 又恰好落在射线QK 上时，求t 的值；（4）连结PG ，当PG ∥AB 时，请直接写出t 的值．12、如图16，在Rt△ABC 中，∠C =90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，到达点A 后立刻以原来的速度沿AC 返回；点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动．伴随着P 、Q 的运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交折线QB -BC -CP 于点E ．点P 、Q 同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当t = 2时，AP = ，点Q 到AC 的距离是；（2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围）（3）在点E 从B 向C 运动的过程中，四边形QBED 能否成为直角梯形？若能，求t 的值．若不能，请说明理由；（4）当DE 经过点C 时，请直接写出t 的值．图15A 图1614、如图，梯形ABCD 中，AB ∥DC ，DE ⊥AB ，CF ⊥AB ，且AE=EF=FB=5，DE=12动点P 从点A 出发，沿折线AD-DC-CB 以每秒1个单位长的速度运动到点B 停止．设运动时间为t 秒，y=S △EPF ，则y 与t 的函数图象大致是（）15、如图和图，在中，151-152-ABC △51314cos .13AB BC ABC ===，，∠探究在如图，于点，则_______，_______，的面积151-AH BC ⊥H AH =AC =ABC △ABCS △=___________．拓展如图，点在上（可与点重合），分别过点作直线的垂线，垂足为.设152-D AC A C ，A C ，BD E F ，（当点与点重合时，我们认为=0..BD x AE m CF n ===，，D A ABC S △（1）用含或的代数式表示及；x m ，n ABD S △CBD S △（2）求与的函数关系式，并求的最大值和最小值．()m n +x ()m n +（3）对给定的一个值，有时只能确定唯一的点，指出这样的的取值范围.x D x 发现请你确定一条直线，使得三点到这条直线的距离之和最小（不必写出过程），并写出这个最小A B C ，，值.A ．B ．C ．D．17、某景区内的环形路是边长为800米的正方形ABCD，如图1和图2．现有1号、2号两游览车分别从出口A 和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为200米/分．探究：设行驶吋间为t分．（1）当0≤t≤8时，分别写出1号车、2号车在左半环线离出口A的路程y1，y2（米）与t（分）的函数关系式，并求出当两车相距的路程是400米时t的值；（2）t为何值时，1号车第三次恰好经过景点C？并直接写出这一段时间内它与2号车相遇过的次数．发现：如图2，游客甲在BC上的一点K（不与点B，C重合）处候车，准备乘车到出口A，设CK=x米．情况一：若他刚好错过2号车，便搭乘即将到来的1号车；情况二：若他刚好错过1号车，便搭乘即将到来的2号车．比较哪种情况用时较多？（含候车时间）决策：己知游客乙在DA上从D向出口A走去．步行的速度是50米/分．当行进到DA上一点P （不与点D，A 重合）时，刚好与2号车迎面相遇．（1）他发现，乘1号车会比乘2号车到出口A用时少，请你简要说明理由：（2）设PA=s（0＜s＜800）米．若他想尽快到达出口A，根据s的大小，在等候乘1号车还是步行这两种方式中．他该如何选择？。

中考数学动点问题专题练习(含答案)

动点专题一、应用勾股定理建立函数解析式例1(2000年·上海)如图1，在半径为6，圆心角为90°的扇形OAB 的弧ＡB 上,有一个动点P,ＰH ⊥O Ａ,垂足为H,△OPH 的重心为G ．（1)当点Ｐ在弧AB 上运动时，线段ＧO 、GP 、GH 中,有无长度保持不变的线段？如果有，请指出这样的线段，并求出相应的长度．(２)设P Ｈx =,GP y =，求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围)．(3）如果△PG Ｈ是等腰三角形,试求出线段PH 的长．二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ＡBC 中,ＡＢ=AC ＝1,点D,Ｅ在直线B Ｃ上运动.设BD=,x ＣＥ=y . (1)如果∠B ＡC=3０°,∠DA Ｅ=105°,试确定y 与x 之间的函数解析式;(２)如果∠B ＡＣ的度数为α,∠DAE 的度数为β,当α，β满足怎样的关系式时,（1)中y 与x 之间的函数解析式还成立?试说明理由.AEDCB 图2H M NG PO A B 图1 x yC三、应用求图形面积的方法建立函数关系式例4(２0０4年·上海）如图,在△A ＢＣ中,∠BAC ＝９0°,AB=AC ＝22,⊙A 的半径为1.若点Ｏ在BC 边上运动(与点B 、C 不重合)，设ＢO=x ,△AOC 的面积为y .（1）求y 关于x 的函数解析式，并写出函数的定义域．(2)以点O 为圆心,BO 长为半径作圆Ｏ，求当⊙O 与⊙Ａ相切时， △AO Ｃ的面积．一、以动态几何为主线的压轴题（一）点动问题．１.(09年徐汇区)如图，ABC ∆中，10==AC AB ,12=BC ，点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ，交射线CA 于点F . (1)当6=AE 时，求AF 的长；（２)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; （3）当以边AC 为直径的⊙O 与线段DE 相切时,求BE的长．AB C O 图8HAB CDEOlA ′(二）线动问题2,在矩形A ＢＣD 中,AB ＝3,点O 在对角线A Ｃ上，直线ｌ过点O ，且与AC 垂直交ＡＤ于点E ．（1)若直线l 过点B,把△ABE 沿直线l 翻折,点A 与矩形A ＢＣＤ的对称中心A ＇重合，求BC 的长; （2)若直线l 与AB 相交于点F,且ＡＯ=41AC,设AD 的长为x ,五边形ＢＣDEF 的面积为S.①求S 关于x 的函数关系式，并指出x 的取值范围;②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在，请求出x 的值;若不存在,请说明理由．(三)面动问题３.如图，在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点（D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG .(１）试求ABC ∆的面积；(２)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =，ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4）当BDG ∆是等腰三角形时,请直接写出AD 的长.解决动态几何问题的常见方法有:C一、特殊探路,一般推证例２:（２00４年广州市中考题第11题)如图,⊙O １和⊙Ｏ2内切于A,⊙O1的半径为３，⊙O2的半径为2，点Ｐ为⊙O1上的任一点（与点A 不重合)，直线ＰA 交⊙O2于点Ｃ,PB 切⊙O2于点B ，则PCBP的值为(A)2 (Ｂ）3 （C)23（Ｄ)26二、动手实践,操作确认例４(２003年广州市中考试题）在⊙Ｏ中，C 为弧AB 的中点,D 为弧A Ｃ上任一点(与A 、C 不重合）,则(A)A Ｃ+CB=AD+ＤB (B) A Ｃ＋C Ｂ<AD+DB（Ｃ） AC+CB ＞A Ｄ＋D Ｂ（D) ＡＣ+C Ｂ与AD+ＤB 的大小关系不确定例５:如图，过两同心圆的小圆上任一点C 分别作小圆的直径CA 和非直径的弦CD ，延长CA 和C Ｄ与大圆分别交于点B 、Ｅ，则下列结论中正确的是( ＊ ) （A)AB DE = (B ）AB DE >(Ｃ）AB DE <(D ）AB DE ,的大小不确定三、建立联系，计算说明例6:如图,正方形ABCD 的边长为4,点Ｍ在边DC 上,且ＤM=１,Ｎ为对角线A Ｃ上任意一点,则ＤN ＋ＭN 的最小值为 .BMND CBA以圆为载体的动点问题中,AC＝５，ＢC=12，∠ＡCＢ＝90°,P是ＡB边上的动点（与点A、B不重例1．在Rt ABC合）,Q是BC边上的动点（与点B、C不重合),当PQ与ＡＣ不平行时，△CPＱ可能为直角三角形吗?若有可能，请求出线段CＱ的长的取值范围；若不可能,请说明理由。

2020中考数学复习压轴题《动点问题》专题提升练习%28六大动点必考相关问题%29(无答案)

2020中考数学复习压轴题《动点问题》专题提升练习(六大动点必考相关问题)题型一动点与函数图像关系1. 如图，菱形ABCD 的边长是4厘米，∠B=60°，动点P 以1厘米秒的速度自A 点出发沿AB 方向运动至B 点停止，动点Q 以2厘米/秒的速度自B 点出发沿折线BCD 运动至D 点停止．若点P 、Q 同时出发运动了t 秒，记△BPQ 的面积为S 厘米2，下面图象中能表示S 与t 之间的函数关系的是（）A ．B ．C ．D ．2. 如图，已知边长为4的正方形ABCD ，P 是BC 边上一动点（与B 、C 不重合），连结AP ，作PE⊥AP 交∠BCD 的外角平分线于E ．设BP=x ，△PCE 面积为y ，则y 与x 的函数关系式是（）A ．y=2x+1B ．21y x 2x 2=-C ．21y 2x x 2=-D ．y=2x3. 如图，已知A 、B 是反比例函数y ＝k x (k ＞0，x ＞0)图象上的两点，BC∥x 轴，交y 轴于点C ．动点P 从坐标原点O 出发，沿O →A →B →C 匀速运动，终点为C．过点P作PM⊥x轴，PN⊥y轴，垂足分别为M、N．设四边形OMPN的面积为S，点P运动的时间为t，则S关于t的函数图象大致为（）.题型二动点与图形面积问题1. 如图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，沿AC 方向匀速运动到终点C,动点Q从点C出发，沿CB方向匀速运动到终点B.已知P，Q两点同时出发，并同时到达终点.连结MP，MQ，PQ.在整个运动过程中，△MPQ的面积大小变化情况是( )A.一直增大B.一直减小C.先减小后增大D.先增大后减小2. 如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则当x=7时，点E应运动到( )A．点C处 B．点D处 C．点B处 D．点A处3. 已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O 顺时针旋转60°，如题图1，连接BC.（1）填空：∠OBC=_______°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？题型三动点与等腰三角形问题1. 如图1，在△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm．如果点P由点B 出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连结PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：（1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？（2）如图2，连结PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；（3）当t为何值时，△APQ是等腰三角形？图1 图22. 如图，已知抛物线与轴交于、两点，与轴交于点，且，设抛物线的顶点为．(1)求抛物线的解析式(2)在抛物线对称轴的右侧的抛物线上是否存在点，使得是等腰三角形？若存在，求出符合条件的点的坐标；若不存在，请说明理由；3.已知：如图，抛物线经过、、三点．求抛物线的函数关系式；若过点的直线与抛物线相交于点，请求出的面积的值；写出二次函数值大于一次函数值的的取值范围；在抛物线上是否存在点使得为等腰三角形？若存在，请指出一共有几个满足条件的点，并求出其中一个点的坐标；若不存在这样的点，请说明理由．题型四动点与线段最值问题1.点P为抛物线上直线AM下方一动点，E为线段AM上一动点，且PE//Y轴，当点P的坐标为多少时，线段PE的长度有最大值？2. 如图1,矩形ABCD中,AB=4, AD=3, M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.(1) 当AN平分∠MAB时,求DM的长;(2) 连结BN,当DM=1时,求△ABN的面积;(3) 当射线BN交线段CD于点F时,求DF的最大值.图1 备用图3. 如图,顶点为A(, 1)的抛物线经过坐标原点O,与x轴交于点B.(1) 求抛物线对应的二次函数的表达式;(2) 过B作OA的平行线交y轴于点C,交抛物线于点D,求证: △OCD≌△OAB;(3) 在x轴上找一点P,使得△PCD的周长最小,求出点P的坐标.题型五动点与切线问题1. 如图1,抛物线y=-x2+mx+n的图象经过点A(2, 3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、 B位于点P的同侧.(1) 求抛物线的解析式;(2) 若PA∶PB=3∶1,求一次函数的解析式;(3) 在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得☉C同时与x轴和直线AP相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.2. 如图1,在Rt△ABC中,∠ACB=90°, cosB=, BC=3, P是射线AB上的一个动点,以P为圆心、PA为半径的☉P与射线AC的另一个交点为D,直线PD交直线BC于点E.(1) 当PA=1时,求CE的长;(2) 如果点P在边AB上,当☉P与以C为圆心、CE为半径的☉C内切时,求☉P 的半径;(3) 设线段BE的中点为Q,射线PQ与☉P相交于点F,点P在运动过程中,当PE ∥CF时,求AP的长.题型六动点与辅助圆问题1. 如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB＝30°，则满足条件的点P的个数是（）A．1个 B．2个 C．3个 D．无数个2. 如图，矩形CDEF是由矩形ABCG（AB＜BC）绕点C顺时针旋转90°而得，∠APE的顶点在线段BD上移动，则能够使∠APE为直角的点P的个数是_______．3. 如图，已知足球球门宽AB约为52米，一球员从距B点52的C点（点A、B、C均在球场底线上），沿与AC成45°角的CD方向带球．试问，该球员能否在射线CD上找到一点P，使得点P为最佳射门点（即∠APB 最大）？若能找到，求出这时点P与点C的距离；若找不到，请说明理由．。

中考圆有关的动点几何压轴题

北辰教育学科老师辅导讲义定圆结合直角三角形，考察三角形相似，线段及三角形周长的函数关系2（2010•上海）如图，在△中，∠90°．半径为1的圆A及边相交于点D，及边相交于点E，连接并延长，及线段的延长线交于点P．（1）当∠30°时，连接，若△及△相似，求的长；（2）若2，，求∠的正切值；（3）若∠，设，△的周长为y，求y关于x的函数关系式．定圆结合直角三角形，考察两线段函数关系，圆心距，存在性问题3．如图，在半径为5的⊙O中，点A、B在⊙O上，∠90°，点C是弧上的一个动点，及的延长线相交于点D，设，．（1）求y关于x的函数解析式，并写出它的定义域；（2）如果⊙O1及⊙O相交于点A、C，且⊙O1及⊙O的圆心距为2，当时，求⊙O1的半径；（3）是否存在点C，使得△∽△？如果存在，请证明；如果不存在，请简要说明理由．动圆结合直角梯形，考察圆相切和相似5（14分）（2014•金山区二模）如图，已知在梯形中，∥，⊥，4，3，∠，P是边上一点（点P及点C、D不重合），以为半径的⊙P及边相交于点C和点Q．（1）如果⊥，求的长；（2）如果，试判断以为直径的⊙O及⊙P的位置关系；（3）联结，如果△和△相似，求的长．1时，求2过点P、在直线AP上（如图AP x=，的函数关系式，并写出函数的定义域；2）的条件下，当（3）是否存在⊙M，使得、恰好是一个正五边形的两条边？若存在，试求的长度和⊙M 的半径长；若不存在，试说明理由．动圆结合三角形，考察相似，线段比，圆位置关系9.2006中考25.（本题满分14分，第（1）小题满分4分，第（2）小题满分7分，第（3）小题满分3分）已知点P在线段上，点O在线段的延长线上。

以点O为圆心，为半径作圆，点C是圆O上的一点。

（1）如图，如果2，。

求证：△∽△；（2）如果（m是常数，且m>1），1，是、的比例中项。

当点C在圆O上运动时，求：的值（结果用含m的式子表示）；（3）在（2）的条件下，讨论以为半径的圆B和以为半径的圆C的位置关系，并写出相应m的取值范围。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆与动点专题
1.在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 上存在一点Q ，使得P Q 、两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当
O 的半径为2时，
①在点1231135,0,,,,02222P P P ⎛⎫⎛⎫⎛⎫
⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
⎝中，O 的关联点是_______________． ②点P 在直线y x =-上，若P 为O 的关联点，求点P 的横坐标的取值范围．
（2）
C 的圆心在x 轴上，半径为2，直线1y x =-+与x 轴、y 轴交于点A B 、．若线段AB 上的所有点都是
C 的关联点，直接写出圆心C 的横坐标的取值范围．
2.如图，AB 是
O 的直径，,2AC BC AB ==，连接AC ．
（1）求证：045CAB ∠=；（2）若直线l 为
O 的切线，C 是切点，在直线l 上取一点D ，使,BD AB BD =所在的直线与AC 所在的直线
相交于点E ，连接AD ．
①试探究AE 与AD 之间的数量关系，并证明你的结论； ②EB
CD
是否为定值？若是，请求出这个定值；若不是，请说明理由．
3.如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A B
、及AB的中点F重合连接OM.过点M作ME AB
⊥于点E，以BE为边在半圆同侧作正方形BCDE，过M点作O的切线交射线DC 于点N，连接BM、BN.
（1）探究：如左图，当M动点在AF上运动时；
①判断OEM MDN
∆∆是否成立？请说明理由；
②设ME NC
k
MN
+
=，k是否为定值？若是，求出该定值，若不是，请说明理由；
③设MBNα
∠=，α是否为定值？若是，求出该定值，若不是，请说明理由；
（2）拓展：如右图，当动点M在FB上运动时；
分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由）
4.已知二次函数y=﹣x2bxc1，
①当b=1时，求这个二次函数的对称轴的方程； ②若c=
14
b 2
﹣2b ，问：b 为何值时，二次函数的图象与x 轴相切？ ③若二次函数的图象与x 轴交于点A （x 1，0B （x 2，0且x 1＜x 2，与y 轴的正半轴交于点M ，以AB 为直径的半圆恰好过点M ，二次函数的对称轴l 与x 轴、直线BM 、直线AM 分别交于点D 、E 、F ，且满足1
3
DE EF ，求二次函数的表达式．
5．已知：AB 是O ⊙的弦，点C 是AB 的中点，连接OB 、OC ，OC 交AB 于点D . (1)如图1，求证：AD
BD ；
(2)如图2，过点B 作O ⊙的切线交OC 的延长线于点M ，点P 是AC 上一点，连接AP 、BP ，求证：90APB OMB ∠∠°.
(3)如图3，在(2)的条件下，连接DP 、MP ，延长MP 交O ⊙于点Q ，若6MQ DP ，3
sin 5
ABO ∠，求MP MQ 的
值.
6.如图，⊙M 的圆心M （﹣1，2⊙M 经过坐标原点O ，与y 轴交于点A ，经过点A 的一条直线l 解析式为：y=﹣x4与x 轴交于点B ，以M 为顶点的抛物线经过x 轴上点D （2，0）和点C （﹣4，0）．（1）求抛物线的解析式；（2）求证：直线l 是⊙M 的切线；
（3）点P 为抛物线上一动点，且PE 与直线l 垂直，垂足为E ，PF ∥y 轴，交直线l 于点F ，是否存在这样的点
P，使△PEF的面积最小？若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．
7.如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE．
（1）求证：AC2=AE•AB；
（2）过点B作⊙O的切线交EC的延长线于点P，试判断PB与PE是否相等，并说明理由；
（3）设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．
8.如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG∠EBA=γ，
（1）点点同学通过画图和测量得到以下近似数据：
ɑ30°40°50°60°
β120°130°140°150°
γ150°140°130°120°
猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：
（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．
9. 如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上连结AC，DE．
（1）当∠APB=28°时，求∠B和CM的度数；
（2）求证：AC=AB。

（3）在点P的运动过程中
①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；
②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．
M。