强混合鞅差序列部分和乘积的几乎处处中心极限定理
强混合随机变量序列的一个几乎处处中心极限定理

强混合随机变量序列的一个几乎处处中心极限定理
冯凤香
【期刊名称】《桂林理工大学学报》
【年(卷),期】2014(000)004
【摘要】研究了强混合随机变量序列的几乎处处中心极限定理。
利用子序列等方法,获得了强混合随机变量序列几乎处处中心极限定理的一个较优结果。
【总页数】3页(P782-784)
【作者】冯凤香
【作者单位】桂林理工大学理学院,广西桂林 541004
【正文语种】中文
【中图分类】O211.4
【相关文献】
1.强混合序列加权和及部分和之和乘积的几乎处处中心极限定理的推广 [J], 郝晓春;吴群英
2.ρ--混合序列部分和乘积的几乎处处中心极限定理的推广ρ--混合序列部分和乘积的几乎处处中心极限定理的推广 [J], 张明达;谭希丽;张莹
3.强混合序列部分和乘积的几乎处处中心极限定理 [J], 金敬森
4.强混合鞅差序列部分和乘积的几乎处处中心极限定理 [J], 钱和平;宋家乐
5.α混合随机变量序列部分和乘积的几乎处处中心极限定理 [J], 冯凤香;吴群英因版权原因,仅展示原文概要,查看原文内容请购买。
中心极限定理的三个结论和证明

中心极限定理的三个结论和证明中心极限定理,你听说过吗?哦,这可真是概率论里的一颗璀璨明珠。
就像是打麻将的时候,别人摸到的牌看着随意,可最后那手牌却总能拿到胜利!在数学里,中心极限定理也是这种“逆天”的存在,它告诉我们一个超级重要的事:不管你原本的数据分布是什么样的,经过足够多的实验和计算,最终的结果都可以像一个钟摆一样,稳定地聚集在一个中心点附近。
听起来有点抽象?别急,咱们慢慢聊。
中心极限定理有三个最关键的结论。
如果你对概率稍微有点儿了解,肯定会觉得这玩意儿特别酷。
第一个结论呢,就是无论我们原始的数据分布长什么样,经过多次独立抽样,算出样本均值(也就是所有数据的平均数),这些均值会随着样本量的增加,逐渐形成一个钟形的分布——也就是你经常看到的正态分布。
简单来说,像是在掷骰子,虽然每次你掷出来的点数都是不同的,但当你掷够了很多次,点数的平均值就会聚集在某个地方,这个地方通常就是3.5,差不多是骰子的中心。
虽然掷骰子的过程看似是乱七八糟的,但结果却总能偏向一个稳定的数值,这就是中心极限定理的神奇之处。
第二个结论,也许你会觉得更有意思,那就是不管原本的数据分布是怎样的,不管它有多么奇怪或者偏斜(比如那种左右不对称、像个山脊一样的分布),经过足够多次的抽样,它的样本均值也会趋向于正态分布。
这就像是即使你吃的东西特别奇葩,最后吃进肚里的也就是一些基本的营养成分。
所以,不要看数据分布初始时的样子奇奇怪怪,一旦样本量大了,它们就会自动“修正”成正常的模样。
至于第三个结论嘛,听着就有点让人拍案叫绝。
它告诉我们,即使我们抽样的方式有点复杂,或者数据本身有点“曲线”——比如不完全独立、或者样本之间有点相互影响,中心极限定理依然能够成立。
也就是说,即使你的样本数据看似“稀奇古怪”,只要满足了一些基本的条件,最终它们的样本均值还是会收敛到正态分布。
这是怎么做到的呢?这个过程就像是大自然的规律,虽然有时候乱七八糟,但最后总能回归平衡。
部分和乘积的几乎处处中心极限定理

部分和乘积的几乎处处中心极限定理这里有文采较好的400字文章,介绍部分和乘积的几乎处处中心极限定理:
部分和乘积的几乎处处中心极限定理是现代统计学中一个重要的定理,以俄国数学家高斯贝尔第一次提出该定理命名。
它指出,对于两个不同的随机变量X和Y 的任意分布的总体,一组无穷多的独立随机变量X 1 、X 2 、
X 3 、… 和 Y 1 、Y 2 、Y 3 、… 。
在遍历分布考虑之下,我们得到了它们的某种组合Z,其中:
Z = X_1Y_1+X_2Y_2+X_3Y_3+...
此外,在某种方面,它还进一步规定了平均值和标准差,期望和方差,变量与它们比率也可以计算出来。
换句话说,一组服从某种分布的随机变量的线性组合的偏度和峰度将接近于它们局部分量的偏度和峰度的和,在一定的条件下,当变量的个数趋近于无穷,这一限制将逐渐趋于绝对的。
这样一来,几乎处处中心极限定理可以提供统计分析的经典理论,为统计学应用以及估计和测量统计模型中变量之间关系提供了来源。
它也有助于研究者们开展更复杂的变量分析,从而改进统计数据推断过程。
总之,部分和乘积的几乎处处中心极限定理在现代统计学中起着重要的作用,其理论上的有效性为数据分析提供了基础,同时也有助于改进统计数据的推断。
第14讲(大数定律、中心极限定理)资料

设X i
1, 0,
第i 第i
次试 验 次试 验
A发生, A不发生,
i
1,2,,n.
n
则 X Xi,
i 1
X
n
1 n
n i 1
Xi
是n次试验中 A发生的频率.
于是, 有下面定理. 定理3 (贝努里大数定律) 设 X是n 重贝努里试验中事件A发生的次数, p是 A 在一次试验中发生的概率,
则对 0,有
2
证明:当X 是离散时,
分布律为P{X xk } Pk , k 1,2,. 0, 有
P| X E(X ) | P{X xk } |xk E ( X )|
|xk E ( X )|
(xk
E( X )) 2
2
Pk
k
(xk
E( X )) 2
2
Pk
1
2
k
(xk E( X )) 2 Pk
定义2 设 X1, X2, …相互独立且有共同的 分布,则称X1, X2, ….是独立同分布的随机变 量列.
定义3 设 X1, X2, …是一随机变量序列,
若有随机变量X, 对 0, 有
lim P
n
Xn X
0 或 lim P n
Xn X
1.
p
称{X n}依概率收敛于随机变量X,记X n X
或 lim n
Xn
X (P).
几个常见的大数定律
定理2 (切比雪夫大数定律) 设 X1, X2, … 相互独立,且有期望与方差, D(Xi) <M(i=1, 2, ….,M为某常数),
则对 0,有
1 n
lim P n
n
i 1
截断和乘积几乎处处中心极限定理的注记

截断和乘积几乎处处中心极限定理的注记赵珈玉;高瑞梅【摘要】设{X n ,n≥1}为连续独立同中尾分布的正平方可积随机变量序列。
对于固定的常数a >0,T n (a)=S n -S n (a)为截断和。
利用截断和的极限性质及大数定律,在一般的权重条件下,证明了截断和乘积的几乎处处中心极限定理。
%Let {Xn,n ≥ 1 }be a sequence of i.i.d.positive square integrable random variables with continuous and independent medium tail distribution function. For a fixed constant a > 0, Tn (a)=Sn -Sn (a)denoted the trimmed sum,we proved the almost sure central limit theorem for the product of trimmed sums under the general weight by using the limit properties of the trimmed sums and the law of large numbers.【期刊名称】《吉林大学学报(理学版)》【年(卷),期】2016(054)005【总页数】3页(P1036-1038)【关键词】截断和;几乎处处中心极限定理;中尾分布;对数平均【作者】赵珈玉;高瑞梅【作者单位】长春理工大学光电信息学院,长春 130012;长春理工大学理学院,长春 130022【正文语种】中文【中图分类】O211.4研究简报设{Xn, n≥1}为正值独立同分布的随机变量序列, 具有连续的中尾分布[1], 其部分和及最大值分别记为Xi和 Xi. 定义截断和为其中a>0为固定的常数, XiI{Mn-a<Xi≤Mn}为所有渐近最大值的和, Kn(a)=#{i, Xi∈(Mn-a, Mn]}为渐近最大值的数目. 目前, 关于随机变量序列截断和的研究已有许多结果[2-11]. 文献[10]讨论了对数平均下截断和乘积的几乎处处中心极限定理, 本文把权重推广到一般的情形, 得到如下结果.定理1 设{Xn, n≥1}是独立同分布的正平方可积随机变量序列, 且有连续的中尾分布, μ=EX1>0, σ2=Var X1<∞, 变异系数为固定的正常数, Tn(a)如式(1)所定义. 令其中则其中F1(·)为随机变量的分布函数, N为标准正态分布.注1 如果式(2)对于dk成立, 则对于满足0≤ak≤dk和的序列{ak}, 式(2)也成立. 从而式(2)对也成立.注2 当α=0, 即权重为对数平均时, 文献[10]中的定理1是本文的一个特例. 设C 表示正常数, 不同之处可表示不同的值.引理1[12] 设{ζn, n≥1}为一致有界的随机变量序列, {dk},{Dn}定义如定理1. 如果存在C>0, δ>0, 使得则引理2 在定理1的条件下, 有其中Φ(·)为标准正态随机变量的分布函数.证明: 由于因此, 由引理1类似文献[13]中的定理4可知又由文献[9]中引理2的证明知 A2=0. 于是, 对几乎所有的样本点ω和任意小的ε>0, 存在正整数N=N(ω,ε,x), 使得当k>N时, 有联立式(4)可知结论成立.下面证明定理1. 要证明式(2)成立只需证明下式成立即可:由定义易知Sj(a)≤Kj(a)Mj, 再由文献[10]中的引理1可知, 对有从而对充分大的j, 有由Marcinkiewicz强大数定律可得又由于log(1+x)=x+O(x2), 因此有从而对几乎所有的样本点ω和任意小的ε>0, 存在正整数N1=N1(ω,ε,x), 使得当k>N1时, 有再由引理2可知定理1成立.【相关文献】[1] Pakes A G, Steutel F W. On the Number of Records Near the Maximum [J]. Austral J Statist, 1997, 39(2): 179-192.[2] Pakes A G, LI Yun. Limit Laws for the Number of Near Maxima via the Poission Approximation [J]. Statist Probab Lett, 1998, 40(4): 395-401.[3] HU Zhishui, SU Chun. Limit Theorems for the Number and Sum of Near-Maxima for Medium Tails [J]. Statist Probab Lett, 2003, 63(3): 229-237.[4] 邹海连, 张立新. 一类截断部分和乘积的渐近正态性 [J]. 浙江大学学报(理学版), 2007, 34(2): 128-131. (ZOU Hailian, ZHANG Lixin. Asymptotic Distribution of Product of Trimmed Sums [J]. Journal of Zhejiang University (Science Edition), 2007, 34(2): 128-131.)[5] 臧庆佩, 林正炎. 截断和随机乘积的渐近性质 [J]. 系统科学与数学, 2009, 29(2): 145-152. (ZANG Qingpei, LIN Zhengyan. The Asymptotic Distribution of the Random Product of Trimmed Sums [J]. J Systems Sci Math Sci, 2009, 29(2): 145-152.)[6] FU Ke’ang, ZHANG Lixin. A General LIL for Trimmed Sums of Random Fie lds in Banach Spaces [J]. Acta Math Hungar, 2009, 122(1/2): 91-103.[7] FU Ke’ang. An Almost Sure Invariance Principle for Trimmed Sums of Random Vectors [J]. Proc Indian Acad Sci Math Sci, 2010, 120(5): 611-618.[8] 周蕊, 杨金英. 截断和乘积的不变原理 [J]. 吉林大学学报(理学版), 2012, 50(5): 912-916. (ZHOU Rui, YANG Jinying. Invariance Principle for the Product of Trimmed Sums [J]. Journal of Jilin University (Science Edition), 2012, 50(5): 912-916.)[9] WANG Wensheng. A LIL and Limit Distributions for Trimmed Sums of Random Vectors Attracted to Operator Semi-stable Laws [J]. Acta Math Sin (Engl Ser), 2014, 30(9): 1555-1565.[10] 邹广玉. 截断和乘积的几乎处处中心极限定理 [J]. 西南师范大学学报(自然科学版), 2015,40(11): 1-4. (ZOU Guangyu. On Almost Sure Central Limit Theorem for Product of Trimmed Sums [J]. Journal of Southwest China Normal University (Natural Science Edition), 2015, 40(11): 1-4.)[11] FU Ke’ang, QIU Yuyang, TONG Yeling. Limit Law of the Iterated Logarithm for B-Valued Trimmed Sums [J]. Proc Indian Acad Sci Math Sci, 2015, 125(2): 221-225.[12] 叶大相, 吴群英. 随机元序列几乎处处中心极限定理的推广 [J]. 吉林大学学报(理学版), 2011, 49(2): 251-254. (YE Daxiang, WU Qunying. Popularization of Almost Sure Central Limit Theorem for Sequences of Random Elements [J]. Journal of Jilin University (Science Edition), 2011, 49(2): 251-254.)[13] 冯凤香. 独立随机变量序列部分和乘积的几乎处处中心极限定理 [J]. 吉林大学学报(理学版), 2012, 50(2): 270-274. (FENG Fengxiang. Almost Sure Central Limit Theorem for the Product of Partial Sums of i.i.d Positive Variables [J]. Journal of Jilin University (Science Edition), 2012, 50(2): 270-274.)。
φ-混合序列的随机中心极限定理

φ-混合序列的随机中心极限定理邢峰;邹广玉【摘要】设{Xn,n≥1}为严平稳的φ-混合序列,{Nn,n≥1}为一列非负整值随机变量序列,且与{Xn,n≥1}独立,随机部分和为(SNn=Nn∑i-1Xi),在适当的假设条件下,利用φ混合序列的极限性质,证明了严平稳φ混合序列的随机中心极限定理,得到了(Tn=SNn-ES Nn/√Var(SNn))依分布收敛于T(Z1,Z2),其中T(Z1,Z2)为Z1和Z2的线性函数,Z1~N(0,1),Z2为{Nn,n≥1}正则化后的极限分布.【期刊名称】《浙江大学学报(理学版)》【年(卷),期】2018(045)004【总页数】3页(P413-415)【关键词】φ-混合序列;随机和;随机中心极限定理【作者】邢峰;邹广玉【作者单位】长春工程学院理学院,吉林长春130012;长春工程学院理学院,吉林长春130012【正文语种】中文【中图分类】O211.41 引言及主要结果定义1 若n→,其中则称随机序列{Xn,n≥1}是φ-混合的. 这是混合条件中常见的一种,具体应用和例子可参见文献[1].定义2 若Cov(f(X1,X2,…,Xn),g(X1,X2,…,Xn))≥0,其中f和g是任何2个使上式协方差存在且对每个变元均单调非降的函数,则称随机序列{Xk,1≤k≤n}是相伴(associated)的. 如果对任何n≥2,{X1,X2,…,Xn} 都是相伴的,则随机序列{Xn,n≥1}是相伴的.定义3 定义随机变量X与Y之间的Kolmogorov距离为IBRAGIMOV[2]给出了下列严平稳φ-混合序列的中心极限定理:定理A 设{Xn,n≥1}为严平稳的φ-混合序列,满足,, 那么,(1)其中,为部分和,Z1~N(0,1), Φ(·)为Z1的分布函数.随机序列部分和的相关研究一直是概率极限理论研究的热点之一,它与很多实际问题密切相关,比如,保险公司在一定时间内的索赔可表示为随机部分和的形式,此外,金融数学、更新过程、证券、风险投资等领域中的问题也属于随机部分和问题. 因此,研究随机部分和的极限性质不仅具有理论意义, 更具有现实意义. 对此,很多学者已做了深入的研究[3-7].最近,PRAKASA等[8]在相伴情形下研究了随机中心极限定理,给出了与已有研究不同的结论.首先给出一些假设条件和记号.下文中总记{Xn,n≥1}为严平稳序列,且满足, .{Nn,n≥1}为一列非负整数随机序列,且与{Xn,n≥1} 独立,假设, n→,(2),(3)其中Z2为连续型随机变量. 记定理 B[8] 设{Xn,n≥1}为严平稳的相伴序列,且{Xn,n≥1}, {Nn,n≥1}满足上述假设条件, 那么dK(Tn,T(Z1,Z2))→0, n→.目前对混合序列下的随机中心极限定理的研究还较少,本文研究φ-混合序列,得到定理 1 设{Xn,n≥1}为严平稳的φ-混合序列,满足,且{Xn,n≥1}, {Nn,n≥1}满足上述假设条件, 那么dK(Tn,T(Z1,Z2))→0, n→.(4)注 1 定理1说明在Kolmogorov距离下,适当正则化之后,随机部分和SNn依分布收敛于T(Z1,Z2),其中 T(Z1,Z2)为2个独立随机变量 Z1~N(0,1)和Z2的线性函数. 特别地,当Z2~N(0,1)时,T(Z1,Z2)~N(0,1).注 2 假设{Yk,k≥1}为一列独立同分布的取非负整值的随机序列,满足EY1=ν, Var(Y1)=τ2>0,并且与{Xn,n≥1}独立,令那么,式(3)中的极限分布Z2~N(0,1), 从而有T(Z1,Z2)~N(0,1).注 3 由定义可知,相伴序列和φ-混合序列互不包含,因此本文推广了已有的结果.2 定理的证明为了证明定理1, 需要以下几个引理.引理1 记P(Nn=k)=pn,k, cj=Cov(X1,X1+j),在定理的假设条件下,有Var(SNn)=E(Nn)σ2+Var(Nn)μ2-(5)(6)证明类似文献[8]中引理2.1的证明,可知式(5)成立,进一步,由以及式(2),可知式(6)成立.引理2[8] 设{Un,U}为一随机变量序列,满足U的分布函数是α-Lipschitz连续的(α>0),V与{Un,U}独立的随机变量满足E|V|<. g为直线上的连续函数.那么对于任意的常数c,δ>0以及任意的z∈R,有|P(Un+Vg(Un)≤z)-P(Un+cV≤z)|≤P(|g(Un)-c|>δ)+2αδE|V|.引理3[9] 如果Fn⟹F,F在闭集A上处处连续,那么,.定理1的证明首先证明dK(Tn,Tn(Z1))→0, n→.(7)记P(Nn=k)=pn,k,那么,由全概率公式以及{Xn}与{Nn} 的独立性,可知P(Z1≤x(n,k))|+P(|Nn-nν|>nν/2)=∶I1+I2,由定理A和引理3,注意到标准正态分布函数的连续性,可知I1→0,由Markov 不等式以及式(2),可知I2→0,从而得式(7)成立.其次证明dK(Tn(Z1),Tn(Z1))→0, n→.(8)由Chebyshev不等式以及式(2)和式(6),易推得(9)由式(2)和引理1,可得,(10)由式(10)以及Slutsky定理,知,(11)注意到{Nn,Z2}与Z1独立,在引理2中取由式(9)、(11)、引理3及δd的任意性,可推得式(8)成立.接下来证明dK(Tn(Z1),T(Z1,Z2))→0, n→.(12)注意到Z1与Z2独立,从而有dK(Tn(Z1),T(Z1,Z2))=P(T(u,Z2)≤x)|dΦ(u)=其中,再由式(3)、引理3以及Z2为连续性随机变量,可知式(12)成立.最后联立式(7)、(8)、(12)以及三角不等式:dK(Tn,T(Z1,Z2))≤dK(Tn,Tn(Z1))+dK(Tn(Z1),Tn(Z1))+dK(Tn(Z1),T(Z1,Z2)).可知定理1成立.参考文献(References):【相关文献】[1] LIN Z Y, LU C R. Limit Theory for Mixing Dependent Random Variables[M]. Beijing: Science Press / Kluwer Academic Publishers, 1997.[2] IBRAGIMOV I A. Some limit theorems for stationary processes [J]. Akademija Nauk SSSR Teorija Verojatnoste1iee Primenenija, 1962(7): 361-392.[3] PRAKASA RAO B L S. Remark on the rate of convergence in the random central limit theorem for mixing sequences [J]. Z Wahrscheinlichkeitstheorie Und Verw Gebiete, 1975, 31(2): 157-160.[4] LEE S. Random central limit theorem for the linear process generated by a strong mixing process [J].Statistics & Probability Letters, 1997,35(2): 189-196.[5] 谭希丽, 杨晓云. B值m相依随机元序列的随机指标中心极限定理 [J].吉林大学学报(理学版), 2003, 41(4): 419-430.TAN X L, YANG X Y. The central limit theorem for the sum of a random number of m-dependent B-valued random variables [J]. Journal of Jilin University (Science Edition), 2003, 41(4): 419-430.[6] 谭希丽, 杨晓云. B值m相依随机元列移动平均过程的随机指标中心极限定理 [J]. 吉林大学学报(理学版), 2007, 45(2): 159-164.TAN X L, YANG X Y. The central limit theorem for the sum of a random number of moving average processes of m-dependent B-valued elements [J]. Journal of Jilin University (Science Edition), 2007, 45(2): 159-164.[7] HWANG E, SHIN D W. Random central limit theorems for linear processes with weakly dependent innovations [J]. Journal of the Korean Statistical Society, 2012, 41(3): 313-322.[8] PRAKASA RAO B L S, SREENHARI M. Random central limit theorem for associated random variables and the order of approximation [J]. Statistics & Probability Letters, 2016, 111: 1-7.[9] BILLINGSLEY P. Convergence of Probability Measures[M]. New York: Wiley, 1968.。
中心极限定理的名词解释

中心极限定理的名词解释1. 嘿,中心极限定理啊,就像是一把神奇的钥匙!它说的是如果从一个总体中多次抽取样本,那这些样本的均值就会趋近于总体均值。
就好比你扔骰子,扔很多很多次,那平均点数就会很接近理论上的 3.5 呢!2. 中心极限定理呀,简直是统计世界里的大明星!它意味着无论原来的总体分布是啥样,只要样本够多,样本均值的分布就会接近正态分布。
这就好像不管一群人原来多么五花八门,最后聚在一起的某些特征就会变得有规律啦!比如一堆不同身高的人,多次测量他们的平均身高就会呈现一定规律呢。
3. 哇塞,中心极限定理啊,那可是超厉害的!它表明随着样本数量增加,样本均值会稳定下来。
就像你不断地搅拌一杯混合液体,到最后它会变得很均匀一样。
比如调查一个城市的收入水平,抽取足够多的样本,就能得到比较可靠的平均收入呢。
4. 嘿呀,中心极限定理呢,就像是一个魔法法则!它让我们知道就算总体很复杂,通过大量样本也能找到规律。
好比在一堆乱麻中,抽丝剥茧找到头绪。
就像统计很多学生的考试成绩,就能知道大致的平均成绩范围啦。
5. 中心极限定理哦,这可是个宝贝呀!它告诉我们即使原始数据乱七八糟,可样本多了就会有秩序出现。
就好像一场混乱的聚会,到最后总会形成一些小团体一样。
比如研究各种动物的体重,大量样本下就能看出一些体重的集中趋势呢。
6. 哇哦,中心极限定理啊,那可是统计学的得力助手!它保证了在足够多样本下,我们能对总体有个大概了解。
就跟你从远处看一幅画能看出个大概轮廓一样。
比如统计一个地区每天的用电量,大量样本就能知道个大概的用电情况呢。
7. 中心极限定理呀,真的是太重要啦!它让我们能从复杂的数据中找到线索。
就像在黑暗中找到一束光。
比如研究不同年龄段的消费习惯,通过大量样本就能总结出一些特点呢。
8. 嘿,中心极限定理呢,绝对是个神奇的存在!它可以让杂乱无章的数据变得有规律可循。
就像给迷路的人指了一条明路。
比如统计很多产品的质量数据,就能知道整体的质量水平啦。
φ-混合序列的随机中心极限定理

第45卷第4期2018年7月浙㊀江㊀大㊀学㊀学㊀报(理学版)J o u r n a l o fZ h e j i a n g U n i v e r s i t y(S c i e n c eE d i t i o n )h t t p ://w w w .z j u jo u r n a l s .c o m /s c i V o l .45N o .4J u l .2018收稿日期:2017G06G07.基金项目:国家自然科学基金资助项目(11401090);吉林省教育厅 十二五 科学技术研究项目(吉教科合字[2012]第399号).作者简介:邢峰(1970 ),O R C I D :h t t p ://o r c i d .o r g/0000G0002G7566G5483,男,硕士,副教授,主要从事概率统计㊁应用数学研究,E Gm a i l :x i n g f e n g19700508@s o h u .c o m.D O I :10.3785/j.i s s n .1008G9497.2018.04.006φG混合序列的随机中心极限定理邢峰,邹广玉(长春工程学院理学院,吉林长春130012)摘㊀要:设{X n ,n ȡ1}为严平稳的φG混合序列,{N n ,n ȡ1}为一列非负整值随机变量序列,且与{X n ,n ȡ1}独立,随机部分和为S N n =ðN ni =1X i,在适当的假设条件下,利用φ混合序列的极限性质,证明了严平稳φ混合序列的随机中心极限定理,得到了T n =S N n -E S N nV a r (S N n)依分布收敛于T (Z 1,Z 2),其中T (Z 1,Z 2)为Z 1和Z 2的线性函数,Z 1~N (0,1),Z 2为{N n ,n ȡ1}正则化后的极限分布.关㊀键㊀词:φG混合序列;随机和;随机中心极限定理中图分类号:O211.4㊀㊀㊀㊀文献标志码:A㊀㊀㊀㊀文章编号:1008G9497(2018)04G413G03X I N GF e n g ,Z O U G u a n g y u (S c h o o l o f S c i e n c e ,C h a n g c h u n I n s t i t u t e o f T e c h n o l o g y ,C h a n g c h u n 130012,C h i n a )T h e r a n d o mc e n t r a l l i m i t t h e o r e mf o r φGm i x i n g s e qu e n c e .J o u r n a l o f Z h e j i a n g U n i v e r s i t y (S c i e n c eE d i t i o n ),2018,45(4):413G415A b s t r a c t :L e t {X n ,n ȡ1}b eas t r i c t l y s t a t i o n a r y φGm i x i n g s e q u e n c e ,{N n ,n ȡ1}b eas e q u e n c eo fn o n n e ga t i v e i n t e g e r v a l u e d r a n d o mv a r i ab l e .N o t e S N n =ðN ni =1X i b e t h er a n d o m p a r t i a l s u m s ,w e p r o v e t h er a n d o mc e n t r a l l i m i t t h e o r e mf o r s t r i c t l y s t a t i o n a r y φGm i x i n g s e q u e n c e u s i n g t h e l i m i t p r o p e r t i e s o f φGm i x i n g s e q u e n c e u n d e r s o m e s u i t a b l e c o n d i t i o n s ,a n do b t a i n t h a t T n =S N n -E S N nV a r (S N n)c o n v e r g e s t o T (Z 1,Z 2),w h e r e T (Z 1,Z 2)i s t h e l i n e a r f u n c t i o no f Z 1a n d Z 2,Z 1~N (0,1),Z 2i s t h e l i m i t d i s t r ib u t i o na f t e r n o r m a l i z a t i o no f N n ,n ȡ1{}.K e y W o r d s :φGm i x i n g s e q u e n c e ;r a n d o m p a r t i a l s u m s ;r a n d o mc e n t r a l l i m i t t h e o r e m 1㊀引言及主要结果定义1㊀若φ(n )=s u p k ȡ1s u pA ɪF k 1,B ɪF ¥k +n ,P (A )>0|P (B |A )-P (B )|ң0,n ң¥,其中F ba =σ(X i ,a ɤi ɤb ),则称随机序列{X n ,n ȡ1}是φG混合的.这是混合条件中常见的一种,具体应用和例子可参见文献[1].定义2㊀若C o v (f (X 1,X 2, ,X n ),g (X 1,X 2, ,X n ))ȡ0,其中f 和g 是任何2个使上式协方差存在且对每个变元均单调非降的函数,则称随机序列{X k ,1ɤk ɤn }是相伴(a s s o c i a t e d )的.如果对任何n ȡ2,{X 1,X 2,,X n }都是相伴的,则随机序列{X n ,n ȡ1}是相伴的.定义3㊀定义随机变量X 与Y 之间的K o l m o g o r o v 距离为d K (X ,Y )=s u px ɪR|P (X ɤx )-P (Y ɤx )|.I B R A G I MO V [2]给出了下列严平稳φG混合序列的中心极限定理:定理A ㊀设{X n ,n ȡ1}为严平稳的φG混合序列,满足E X 1=μ,0<σ2=V a r (X 1)+2ð¥j =2C o v (X 1,X j )<¥,ð¥n =1φ1/2(n )<¥,那么S n -n μσndңZ 1,㊀n ң¥,(1)其中,S n =ðni =1X i 为部分和,Z 1~N (0,1),Φ( )为Z 1的分布函数.随机序列部分和的相关研究一直是概率极限理论研究的热点之一,它与很多实际问题密切相关,比如,保险公司在一定时间内的索赔可表示为随机部分和的形式,此外,金融数学㊁更新过程㊁证券㊁风险投资等领域中的问题也属于随机部分和问题.因此,研究随机部分和的极限性质不仅具有理论意义,更具有现实意义.对此,很多学者已做了深入的研究[3G7].最近,P R A K A S A 等[8]在相伴情形下研究了随机中心极限定理,给出了与已有研究不同的结论.首先给出一些假设条件和记号.下文中总记{X n ,n ȡ1}为严平稳序列,且满足E X 1=μ,ð¥j=1j |C o v (X 1,X 1+j )|<¥,0<σ2=V a r (X 1)+2ð¥j=2Co v (X 1,X j )<¥.{N n ,n ȡ1}为一列非负整数随机序列,且与{X n ,n ȡ1}独立,假设E N n n ңν>0,V a r (N n )nңτ2<¥,n ң¥,(2)N n -E N n V a r (N n )dңZ 2,㊀n ң¥,(3)其中Z 2为连续型随机变量.记S N n =ðN ni =1X i,T n =S N n -E S N nV a r (S N n)=S N n -μN nV a r (S N n)+(N n -E N n )μV a r (S N n ),T n (Z 1)=N n V a r (S N n )σZ 1+(N n -E N n )μV a r (S N n),T n (Z 1)=ννσ2+μ2τ2σZ 1+(N n -E N n )μV a r (S N n),T (Z 1,Z 2)=μτνσ2+μ2τ2σνμτZ 1+Z 2éëêêùûúú.定理B [8]㊀设{X n ,n ȡ1}为严平稳的相伴序列,且{X n ,n ȡ1},{N n ,n ȡ1}满足上述假设条件,那么d K (T n ,T (Z 1,Z 2))ң0,㊀n ң¥.目前对混合序列下的随机中心极限定理的研究还较少,本文研究φG混合序列,得到定理1㊀设{X n ,n ȡ1}为严平稳的φG混合序列,满足ð¥n =1φ1/2(n )<¥,且{X n ,n ȡ1},{N n ,n ȡ1}满足上述假设条件,那么d K (T n ,T (Z 1,Z 2))ң0,㊀n ң¥.(4)注1㊀定理1说明在K o l m o go r o v 距离下,适当正则化之后,随机部分和S N n依分布收敛于T (Z 1,Z 2),其中T (Z 1,Z 2)为2个独立随机变量Z 1~N (0,1)和Z 2的线性函数.特别地,当Z 2~N (0,1)时,T (Z 1,Z 2)~N (0,1).注2㊀假设{Y k ,k ȡ1}为一列独立同分布的取非负整值的随机序列,满足E Y 1=ν,V a r (Y 1)=τ2>0,并且与{X n ,n ȡ1}独立,令N n =ðnk =1Y k ,那么,式(3)中的极限分布Z 2~N (0,1),从而有T (Z 1,Z 2)~N (0,1).注3㊀由定义可知,相伴序列和φG混合序列互不包含,因此本文推广了已有的结果.2㊀定理的证明为了证明定理1,需要以下几个引理.引理1㊀记P (N n =k )=p n ,k ,c j =Co v (X 1,X 1+j ),在定理的假设条件下,有V a r (S N n )=E (N n )σ2+V a r (N n )μ2-2ð¥j =1j c j P (N n >j )-2ð¥j =1c j ðjk =0k p n ,k (),(5)l i mn ң¥V a r (S N n )n=νσ2+μ2τ2.(6)证明㊀类似文献[8]中引理2.1的证明,可知式(5)成立,进一步,由ð¥j =1j |c j |<¥以及式(2),可知式(6)成立.引理2[8]㊀设{U n ,U }为一随机变量序列,满足U 的分布函数是αGL i p s c h i t z 连续的(α>0),V 与{U n ,U }独立的随机变量满足E |V |<¥.g 为直线上的连续函数.那么对于任意的常数c ,δ>0以及任意的z ɪR ,有|P (U n +V g (U n )ɤz )-P (U n +c V ɤz )|ɤ2s u px ɪR|P (U n ɤx )-P (U ɤx )|+P (|g (U n )-c |>δ)+2αδE |V |.引理3[9]㊀如果F n ⇒F ,F 在闭集A 上处处连续,那么,s u p x ɪA|F n (x )-F (x )|ң0,㊀n ң¥.定理1的证明㊀首先证明d K (T n ,T n (Z 1))ң0,㊀n ң¥.(7)记P (N n =k )=p n ,k ,x (n ,k )=xV a r (S N n )-μ(k -E N n )σk,414浙江大学学报(理学版)㊀第45卷㊀那么,由全概率公式以及X n {}与N n {}的独立性,可知s u p x ɪR|P (T n ɤx )-P (T n (Z 1)ɤx )|ɤðn ν/2ɤk ɤ3n ν/2p n ,k s u p x ɪR P S k -μk σk ɤx (n ,k )æèçöø÷-P (Z 1ɤx (n ,k ))+P (|N n -n ν|>n ν/2)=ʒI 1+I 2,由定理A 和引理3,注意到标准正态分布函数的连续性,可知I 1ң0,由M a r k o v 不等式以及式(2),可知I 2ң0,从而得式(7)成立.其次证明d K (T n (Z 1),T n (Z 1))ң0,㊀n ң¥.(8)由C h e b ys h e v 不等式以及式(2)和式(6),易推得N n V a r (S N n )P ңννσ2+μ2τ2,(9)由式(2)和引理1,可得V a r (N n )V a r (S N n )ңτ2νσ2+μ2τ2,㊀n ң¥,(10)由式(10)以及S l u t s k y 定理,知N n -E N n V a r (S N n )d ңτνσ2+μ2τ2Z 2,㊀n ң¥,(11)注意到{N n ,Z 2}与Z 1独立,在引理2中取U n =(N n -E N n )μV a r (S N n ),U =τμZ 21νσ2+μ2τ2,V =Z 1,g (U n )=σN n V a r (S N n ),c =σννσ2+μ2τ2,由式(9)㊁(11)㊁引理3及δd 的任意性,可推得式(8)成立.接下来证明d K (T n (Z 1),T (Z 1,Z 2))ң0,㊀n ң¥.(12)注意到Z 1与Z 2独立,从而有d K (T n (Z 1),T (Z 1,Z 2))=ʏs u px ɪR|P (T n (u )ɤx )-P (T (u ,Z 2)ɤx )|d Φ(u )=ʏs u p x ɪR P (N n -E N n )μV a r (S N n )ɤy (x ,u )æèçöø÷-P τμZ 21νσ2+μ2τ2ɤy (x ,u )æèçöø÷d Φ(u )ɤs u p Z ɪR P N n -E N n V a r (S N n )ɤz æèçöø÷-P τZ 21νσ2+μ2τ2ɤz æèçöø÷,其中,y (x ,u )=x -u σννσ2+μ2τ2.再由式(3)㊁引理3以及Z 2为连续性随机变量,可知式(12)成立.最后联立式(7)㊁(8)㊁(12)以及三角不等式:d K (T n ,T (Z 1,Z 2))ɤd K (T n ,T n (Z 1))+d K (T n (Z 1),T n (Z 1))+d K (T n (Z 1),T (Z 1,Z 2)).可知定理1成立.参考文献(R e f e r e n c e s):[1]㊀L I NZY ,L UCR.L i m i t T h e o r y f o rM i x i n g D e pe n d e n t R a n d o m V a r i a b l e s [M ].B e i j i n g :S c i e n c e P r e s s /K l u w e rA c a d e m i cP u b l i s h e r s ,1997.[2]㊀I B R A G I MO VIA.S o m e l i m i t t h e o r e m s f o r s t a t i o n a r yp r o c e s s e s [J ].A k a d e m i j a N a u k S S S R T e o r i ja V e r o j a t n o s t e 1i e eP r i m e n e n i ja ,1962(7):361G392.[3]㊀P R A K A S A R A O B L S .R e m a r k o n t h e r a t e o fc o n v e r g e n c e i nt h er a nd o m ce n t r a l l i m i tt h e o r e mf o r m i x i ng s e qu e n c e s [J ].Z W a h r s c h e i n l i c h k e i t s t h e o r i e U n dV e r wG e b i e t e ,1975,31(2):157G160.[4]㊀L E ES .R a n d o m c e n t r a l l i m i tt h e o r e m f o rt h el i n e a rp r o c e s s g e n e r a t e d b y as t r o n g m i x i n g pr o c e s s [J ].S t a t i s t i c s&P r o b a b i l i t y L e t t e r s ,1997,35(2):189G196.[5]㊀谭希丽,杨晓云.B 值m 相依随机元序列的随机指标中心极限定理[J ].吉林大学学报(理学版),2003,41(4):419G430.T A N XL ,Y A N G XY.T h e c e n t r a l l i m i t t h e o r e mf o rt h e s u mo f a r a n d o mn u m b e r o f m Gd e p e n d e n t B Gv a l u e d r a n d o m v a r i a b l e s [J ].J o u r n a l o f J i l i n U n i v e r s i t y(S c i e n c eE d i t i o n ),2003,41(4):419G430.[6]㊀谭希丽,杨晓云.B 值m 相依随机元列移动平均过程的随机指标中心极限定理[J ].吉林大学学报(理学版),2007,45(2):159G164.T A N XL ,Y A N G XY.T h e c e n t r a l l i m i t t h e o r e mf o rt h e s u m o f a r a n d o m n u m b e r o f m o v i n g a v e r a g e p r o c e s s e s o f m Gd e pe n d e n t B Gv a l u e d e l e m e n t s [J ].J o u r n a l of J i l i nU n i v e r s i t y (S c i e n c eE d i t i o n ),2007,45(2):159G164.[7]㊀HWA N G E ,S H I N D W.R a n d o m c e n t r a ll i m i tt h e o r e m s f o rl i n e a r p r o c e s s e s w i t h w e a k l y d e pe n d e n t i n n o v a t i o n s [J ].J o u r n a l of t h e K o r e a n S t a t i s t i c a l S o c i e t y,2012,41(3):313G322.[8]㊀P R A K A S A R A O B L S ,S R E E N HA R I M.R a n d o mc e n t r a l l i m i tt h e o r e m f o ra s s o c i a t e dr a nd o m v a r i a b le sa n d t h e o r d e r o f a p p r o x i m a t i o n [J ].S t a t i s t i c s &P r ob a b i l i t y L e t t e r s ,2016,111:1G7.[9]㊀B I L L I N G S L E YP .C o n v e rg e n c e o f P r o b a b i l i t y Me a s u r e s [M ].N e w Y o r k :W i l e y ,1968.514㊀第4期邢峰,等:φG混合序列的随机中心极限定理。
【国家自然科学基金】_几乎处处收敛性_基金支持热词逐年推荐_【万方软件创新助手】_20140731
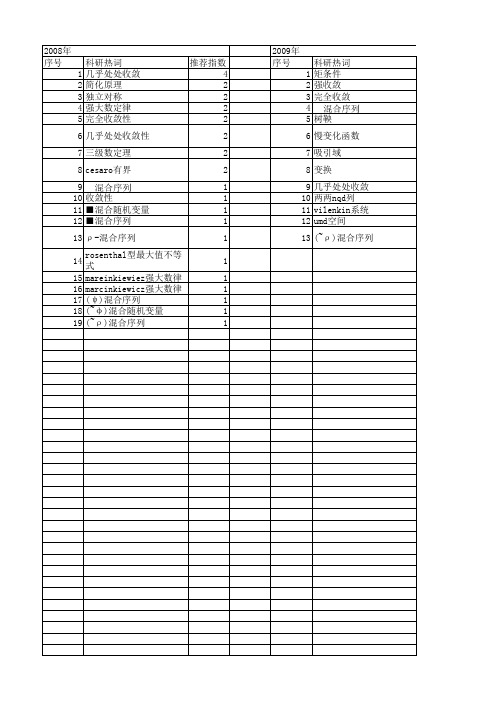
科研热词 推荐指数 完全收敛性 3 加权和 3 几乎处处收敛性 3 混合随机变量 1 推广的三级数定理 1 强大数定理 1 ■混合随机变量 1 ■-mixing random variables 1 weighted sums 1 kolmogorov型不等式 1 complete convergence 1 aqsi序列 1 almost sure convergence 1 (~φ )混合随机变量 1
2009年 序号
科研热词 1 矩条件 2 强收敛 3 完全收敛 4 5 树鞅 6 慢变化函数 7 吸引域 8 变换 9 几乎处处收敛 10 两两nqd列 11 vilenkin系统 12 umd空间 13 (~ρ )混合序列
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1
2014年 科研热词 谱序列 算术平均和 权重 平稳高斯序列 古典傅里叶级数 几乎处处收敛 推荐指数 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 推荐指数 几乎处处收敛 2 鞅差序列 1 集值模糊测度 1 随机变量 1 部分和 1 概率不等式 1 最大适应值 1 收敛速度 1 强混合随机序列 1 几乎处处收敛性 1 几乎处处中心极限定理 1 以概率收敛 1 下鞅 1 ega 1 (伪)几乎处处 1 (伪)依集值模糊测度收敛 1 (伪)依集值模糊测度基本 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 几乎处处收敛 完全收敛性 加权和 鞅差序列 随机环境 迁入分枝过程 几乎处处收敛性 下鞅 na随机变量 l^2收敛 (φ )混合随机变量序列
推荐指数 3 2 2 1 1 1 1 1 1 1 1
混合随机序列部分和乘积的中心极限定理

中心极限定理
中心极限定理(CLT)是一个重要的概率理论,它描述了一个混合随机序列的乘积的分布。
它的定义是:任意一组独立同分布的随机变量的和在大量实验中,其分布收敛于正态分布。
中心极限定理的历史
中心极限定理最初是由俄国数学家列夫·马努夫斯基在19世纪末提出的。
在他的论文中,他首先提出了一个概念,即混合随机序列的乘积的分布收敛于正态分布。
然而,他的论文
没有得到当时科学界的重视,直到20世纪初,德国数学家卡尔·施密特重新发现了这一
定理,并将它命名为中心极限定理。
中心极限定理的应用
中心极限定理在统计学中有着广泛的应用,它可以用来估计一组数据的参数,并且可以用
来推测一组数据的分布情况。
例如,在一组调查数据中,我们可以使用中心极限定理来估
计每个受访者的平均收入,从而推测出收入的分布情况。
此外,中心极限定理也可以用来
估计一组数据的方差,这对于研究一组数据的分布情况非常有用。
中心极限定理的实例
下面我们来看一个具体的例子,来说明中心极限定理的应用。
假设我们有一组数据,其中
包含1000个样本,每个样本的值都是独立同分布的。
我们可以使用中心极限定理来推测
这1000个样本的分布情况,即这1000个样本的和将收敛于正态分布。
结论
从上面的讨论可以看出,中心极限定理是一个重要的概率理论,它描述了一个混合随机序
列的乘积的分布。
它可以用来估计一组数据的参数,并且可以用来推测一组数据的分布情况。
此外,它还可以用来估计一组数据的方差,从而更好地理解数据的分布情况。
一类统计量的乘积的渐近性质和几乎处处中心极限定理

=
E Xi , =V a r X1 >0 . 记变异系数 , y = / , =∑ X i . 设 = ( Xx , …, ) 是一
=
1
统计 量 ( 或 随机 函数) , 可 被表示 为
=a n +R , ( 1 . 1 )
其中 a > 0为 常数 序列 , R 称 为 余项 .熟知 许 多统 计量 ( 或随 机 函数) 可 被表 示成 ( 1 . 1 ) 式,例如 u统计量, V o n — Mi s e s 统计量,线性模型的误差方差估计量,线性过程 ( 和移动平
收稿 日 期: 2 0 1 1 — 1 1 — 1 9 ; 修订 日 期: 2 0 1 3 — 0 2 — 2 8
E— ma i l : q i u j i n 一 7 1 @h o t ma i l . C O l l l
基金项 目:浙 江省 自 然科学基金 ( Y 6 1 1 0 6 1 5 ) 和教育部人文社会科学研究规划基金 ( 1 2 Y J A 9 1 0 0 0 3 ) 资助
2 主要结论
对 于形 如 ( 1 . 1 ) 式的统 计量 , 若 余项 R 满足条 件
R =0 ( 0
)a . S . ,
( 2 . 1 )
我们证 明 下列 几乎 处处 中心极 限定理 ,且给 出它 的渐近分 布和 弱不变 原理 定理 2 . 1 在条 件 ( 2 . 1 ) 下 ,对任 给的 实数 X , 有
MR( 2 0 0 0 )主题分类: 6 0 F 0 5 ; 6 2 G 2 0 中图分类号:O 2 1 1 . 4 文献标识码: 1 3 ) 0 3 — 4 7 5 — 0 8
1 引言
随机变量部分和乘积的渐近分布又称为 “ 算术平均的几何平均 ”中心极限定理,最先由 A r n o l d和 V i l l a s e i f o r ( 1 9 9 8 ) 在讨论记录值的和的极限性质时引入,之后便引起了许多学者的 研 究兴 趣. A r n o l d和 Vi l l a s e i f o r的结果 是针 对独 立 同分 布 的指数 分布 随机变 量 , R e mp a [ a 和 We s o t o w s k i ( 2 0 0 2 ) 将其推广到一般的独立同分布平方可积正值随机变量, 并进一步推广至 u统计量. G o n c h i g d a n z a n和 R e mp a t a ( 2 0 0 6 ) 讨 论 了独 立 同分 布 随机变 量 部分 和乘 积 的几 乎处 处 中心极 限 定理 , Go n c h i g d a n z a n ( 2 0 0 5 ) 给 出 了 u 统 计量的几 乎处处 中心极限 定理 . 个 很 自然的 问题产 生了 : 对 于较 一般 的统 计量 的乘积 ,其渐 近分布是 怎 样的 ?几乎处 处 中心极 限定 理是 否成 立 ?设 f , 一。 。< n< 。 。 }为 独立 同分布 平方 可积 正值 随机变 量 ,
ρ--混合序列自正则部分和乘积的几乎处处中心极限定理

ρ--混合序列自正则部分和乘积的几乎处处中心极限定理曹阳;吴群英【摘要】设{X,Xn}n∈N是一严平稳的ρ--混合随机变量序列.在一定的条件下,证明了自正则部分和乘积(Πki=1(Si/(μi)))μ/(βvi)的几乎处处中心极限定理,其中,Sn=∑ni=1Xi,V2n=∑ni=1X2i.%Let {X,Xn } n∈N be a strictly stationary sequence ofρ--mixing random variables.The result about the kalmost sure central limit theorem for self-normalized products of partial sums (-Π (Si/(μi)))μ/(βV,)is gotten,i=1n nwhereSn =ΣXi,V/2n =ΣX~i=1 i=1.【期刊名称】《桂林理工大学学报》【年(卷),期】2017(037)001【总页数】9页(P208-216)【关键词】ρ--混合序列;自正则部分和乘积;几乎处处中心极限定理【作者】曹阳;吴群英【作者单位】桂林理工大学理学院,广西桂林541004;桂林理工大学理学院,广西桂林541004【正文语种】中文【中图分类】O211.4定义1[1] 记S和T为自然数集N中两个不相交的子集, f和g为连续函数。
如果下列条件成立:其中则称随机变量序列{Xk, k≥1}为ρ- -混合序列。
1999年, Zhang和Wang[1]首次提出了ρ- -混合序列的概念, 它是比NA序列及ρ*-混合序列更为宽泛的一种混合序列。
因此在科研领域应用十分广泛, 并取得了许多成果。
2005年, Zhou[2]证明了ρ- -混合序列的几乎处处中心极限定理;2012年, Tan[3]等人获得了ρ- -混合序列部分和乘积的几乎处处中心极限定理。
由于在许多统计推断中需要用到经典的极限定理, 但是鉴于经典的极限定理中部分和Sn/σn常常含有未知参数σ, 通常先用统计量对这些未知参数进行估计, 然后把这些统计量代入经典的极限定理中。
相依序列加权和的几乎处处中心极限定理

相依序列加权和的几乎处处中心极限定理
相依序列加权和的几乎处处中心极限定理,也被称为“顺序加权均值极限定理”,是海森堡统计的重要理论之一。
这个定理说明,一个由相同分布的独立随机变量组成的顺序加权均值序列收敛到一个固定的常数值,并且不受初值影响。
该理论可以解释因变量协变分布随着时间变化而不断改变的现象,这种现象也被称作“蒙式”效应。
在这个理论中,一个相依序列加权和的顺序可以通过相关函数的分析而求得。
当这个序列的收敛值与当下某一时刻的信息不同时,将会产生“蒙式”效应。
换句话说,就是某一时刻之前的信息影响着结果,但不受初始条件的限制。
此外,该理论还表明,如果随机变量具有某种流行特征,那么对应的加权和将会趋近于一个定值。
通过推断或拟合模型,我们可以预测出该收敛值,从而得出一般定理所表达的结果。
因此,相依序列加权和的几乎处处中心极限定理的应用非常广泛,可以帮助我们理解变量如何在不同的时间段随时效果而发生改变,它也可以用来预测或对有特征趋势的变量进行建模。
虽然有很多的限制存在,但这个定理仍然是统计领域的一个重要理论。
aqsi序列部分和与乘积和的强大数定律

aqsi序列部分和与乘积和的强大数定律在数学界,Aqsi序列(也被称为Aqsi项)是一种著名的序列,其定义如下:B_n= 2^n+1, (n = 1, 2, 3, 4, ...)其中,B_n代表第n项的值,n可以是任意大于1的正整数。
Aqsi序列的部分和指的是在Aqsi序列中,任意两个正整数m和n(m<n)之间,从B_m到B_n的和。
例如当m=1,n=4时,求得Aqsi序列的部分和为:B_1+B_2+B_3+B_4 = 2+2^2+2^3+2^4 = 15可以看出,Aqsi序列部分和是一种可以用来衡量Aqsi数列某一段序列中数值之和的方法。
在Aqsi序列的部分和与乘积和的强大数学定律中,乘积和指的是第m到第n项的乘积的和,即:B_m * B_(m+1) * ... * B_(n-1) * B_n可以看出,该定律也是衡量Aqsi序列某一段序列总乘积的方法。
Weyl(1919-1998)在20世纪30至40年代首先提出了Aqsi序列部分和与乘积和的强大数学定理,具体表述如下:对于任何正整数m和n(其中m < n),部分和和乘积和的结果必须相等:B_m+B_(m+1)+...+B_n=B_m*B_(m+1)...*B_n经过多年的数学研究,这一数学定理得到了强有力的证明,已经被公认为数学界中的一个重要数定律。
直观上而言,可以把Aqsi序列的部分和与乘积和的强大数学定理看作是用加法和乘法公式进行计算的一种技巧,而且它可以有效求出符合要求的最大值或最小值。
从而为解决工程中可能遇到的多变量优化问题提供了有效的解决方案。
比如,在电子设计中,有时会遇到需要给每个电路的驱动电流设置合适的最大值或最小值的问题,这时候就可以利用定律找到合适的解决方案,而不用担心可能出现的复杂问题。
除此之外,Aqsi序列部分和与乘积和的强大数学定律也有另一个优点就是它可以有效解决某些复杂的组合问题,例如:有时候在电子设计中我们需要从几个不同的元件中选择一种,可以利用这个定理来得出最优的答案。
中心极限定理

中心极限定理中心极限定理(central limit theorem)是概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。
这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量积累分布函数逐点收敛到正态分布的积累分布函数的条件。
它是概率论中最重要的一类定理,有广泛的实际应用背景。
在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。
中心极限定理就是从数学上证明了这一现象。
最早的中心极限定理是讨论n 重伯努利试验中,事件A出现的次数渐近于正态分布的问题。
1716年前后,A.棣莫弗对n重伯努利试验中每次试验事件A出现的概率为1/2的情况进行了讨论,随后,P.-S.拉普拉斯和A.M.李亚普诺夫等进行了推广和改进。
自P.莱维在1919~1925年系统地建立了特征函数理论起,中心极限定理的研究得到了很快的发展,先后产生了普遍极限定理和局部极限定理等。
极限定理是概率论的重要内容,也是数理统计学的基石之一,其理论成果也比较完美。
长期以来,对于极限定理的研究所形成的概率论分析方法,影响着概率论的发展。
同时新的极限理论问题也在实际中不断产生。
简介中心极限定理是研究独立随机变量和的极限分布为正态分布的问题。
规范和的定义设随机变量序列X1,X2,、、、Xn,、、、相互独立,均具有相同的数学期望与方差,且E(Xi)= Ui,D(Xi)=Ri^2>0,i=1,2,、、、,令:Yn=X1+X2+、、、+XnZn=〔Yn-E(Yn)〕/√D(Yn)=∑(Xi-Ui)/√∑Ri^2 (i=1,2、、、、n)则称随机变量Zn为随机变量序列X1,X2,、、、,Xn的规范和。
中心极限定理:设从均值为μ、方差为σ^2;(有限)的任意一个总体中抽取样本量为n的样本,当n 充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ^2/n 的正态分布。
