昆明理工大学材料力学1-14计算答案
昆明理工大学2006~2007学年第二学期《材料力学》期末考试试卷(A卷)及答案【用心整理精品资料】

昆明理工大学2006~2007学年第二学期《材料力学》期末考试试卷(A 卷)答案一、 是非判断题(每题2分,共20分)1、对;2、错;3、错;4、错;5、对;6、对;7、错;8、对;9、错;10、对;二、选择题(每题3分,共12分)1、D ;2、A ;3、C 、D 、B;4、D 、A;三、填空题 (本题共13分)1、(本题3分)大柔度杆的临界应力用 欧拉 公式计算,中柔度杆的临界应力用 经验公式计算,短粗杆的临界应力用 强度 公式计算。
2、(本题4分)某构件内一点处的交变应力随时间变化的曲线如图所示,则该交变应力的循环特征是 -0.5 (注:本空1分) , 最大应力是 100MPa (注:本空1分) ,最小应力是 —50MPa (注:本空1分) ,平均应力是 25MPa (注:本空1分) 。
3、(本题4分)试根据下图所示载荷及支座情况,写出由积分法求解时,积分常数的数目及确定积分常数的条件.积分常数 6 (注:本空1分) 个;支承条件0;0;0;A A B ωθω===.(注:每个条件0.5分)连续条件是;;C C B B B Bωωωωθθ-+-+-+===。
(注:每个条件0.5分,或是写成4支承条件,2连续条件也可以)4、(本题2分)图示各梁的材料和尺寸相同,但支承不同,受相同的冲击载荷,则梁内最大冲击应力最大的是 a (注:本空1分) 、最小的是 b(注:本空1分)。
四、计算题yx1、 (本题10分)已知应力状态如下图所示,试用解析法求: (1)主应力大小,主平面位置;(2)在单元体上绘出主平面位置及主应力方向; (3)最大切应力.解:因为图示应力状态有:100MPa x σ=30MPa y σ=-(1分)40MPa x y ττ=-=-(1)12x yσσσ+=+ (公式1分,结果0。
5分)32x yσσσ+=(公式1分,结果0。
5分) 20σ= (1分)0280tan 20.61538130x x y τασσ-===- (1分)()02111arctan arctan 0.6153831.615.8222x x yτασσ⎛⎫-===⨯=⎪⎪-⎝⎭(1分) (2(方向0。
昆明理工大学工程力学习题册答案

昆明理工大学工程力学习题册答案一、选择题1. 在平面力系中,力对点的矩的常用单位是(A)A. N·mB. N/mC. N·sD. N·m^2答案:A2. 平面汇交力系的平衡方程是(C)A. Fx=0, Fy=0, M=0B. Fx=0, Fy=0C. Fx=0, Fy=0, M=0(其中M为力矩)D. Fx=0, Fy=0, M≠0答案:C3. 在空间力系中,力的投影与原力的关系是(B)A. 投影等于原力B. 投影小于等于原力C. 投影大于原力D. 投影与原力无关答案:B二、填空题1. 力对物体的作用效果包括______和______。
答案:使物体发生形变,使物体产生运动2. 平面力系中的合力可以用______和______来确定。
答案:力的大小,力的方向3. 在平面力系中,力矩的计算公式为______。
答案:M=F×d(其中F为力,d为力臂)三、计算题1. 已知:力F=10N,作用点距离A点4cm,求力F 对A点的力矩。
解:力矩的计算公式为M=F×d,其中d为力臂,即作用点到力作用点的距离。
本题中,d=4cm=0.04m。
所以,M=10N×0.04m=0.4N·m。
答案:0.4N·m2. 平面汇交力系中,已知F1=20N,F2=30N,F3=40N,求该力系的合力。
解:首先,将F1和F2合成,得到合力F12。
F12的大小为F12=√(F1^2+F2^2+2F1F2cosθ),其中θ为F1和F2之间的夹角。
假设F1和F2之间的夹角为60°,则F12=√(20^2+30^2+2×20×30×cos60°)=√(400+900+ 1200×0.5)=√(2000)=44.72N。
然后,将F12与F3合成,得到合力F123。
F123的大小为F123=√(F12^2+F3^2+2F12F3cosθ),其中θ为F12和F3之间的夹角。
昆明理工大学 材料力学A 80学时 练习册1-13章答案

杆
螺
FN杆 A杆
FN螺 A螺
p ( D 2 d12 ) D 2 d12 p 杆 4 d12 4 d12
p ( D 2 d12 ) D 2 d12 p 螺 24 d 2 4 6d 2
18.1MPa D 2 d12 6 螺 d 2 p 6.5 MPa D 2 d12
2 2
11
材料力学 练习册 80 学时
昆明理工大学
此答案由李鹏程师傅提供,qiangguo 编辑整理。鹏程师傅祝大家学习进步身体健康 !
2.6 F m F 解:1)为使杆件承受最大拉力,应使胶 合面上的 σ 和 τ 同时达到它们的许用应 力,即:
cos
2
α
2 cos2 2 sin 2
FB
a a a a
M1 1 2 P F a N1 a 1 a B P 2 FS1 2 FB P a a
2 a 2 a 2 P a a a a a P a P a P 2 2 2 P
a C P
P
2a
F
2-2 截面:
C P P P P P
X
1
0
, FN 2 FB 2 2F
P P
n
2
sin 2
cos 0 ctg 2 26.57 sin
2)求许可载荷:
F cos2 A A 100106 4 104 F 50kN 取 F 50kN cos2 (cos 26.570 )2 由: cos2
);1.13 ( ×
二、填空题 1.1 杆件 变形 , 应力,应变 。 1.2 外力的合力作用线通过杆轴线 , 沿杆轴线伸长或缩短 。 1.3 受一对等值,反向,作沿剪切面发生相对错动 , 沿剪切面发生相对错动 。 1.4 外力偶作用面垂直杆轴线 。 任意二横截面发生绕杆轴线的相对转动 。 1.5 外力作用线垂直杆轴线,外力偶作用面通过杆轴线 , 梁轴线由直线变为曲线 。 1.6 包含两种或两种以上基本变形的组合 。 1.7 1.8 1.9 1.10 1.11 1.12 强度 , 刚度 , 稳定性 。
考研_2014年云南昆明理工大学材料力学考研真题A卷

hd P 2021年云南昆明理工大学材料力学考研真题A 卷一、概念题〔包含单项选择选择题和填空题,每题4分,15小题,共60分〕1. 以下结论中哪些是正确的?答: 。
〔1〕为保证构件能正常工作,应尽量提高构件的强度; 〔2〕为保证构件能正常工作,应尽量提高构件的刚度; 〔3〕为保证构件能正常工作,应尽量提高构件的稳定性;〔4〕为保证构件能正常工作,应尽量提高构件的强度、刚度和稳定性。
(A)〔1〕、〔2〕、〔3〕; (B)〔3〕、〔4〕; (C) 全对; (D) 全错。
2. 变截面杆如图示,设F 1、F 2、F 3分别表示杆件中截面1-1,2-2,3-3上的内力,那么以下结论中正确的选项是 。
(A) F 1≠F 2,F 2≠F 3 ; (B) F 1=F 2,F 2>F 3 ; (C) F 1=F 2,F 2<F 3 ; (D) F 1=F 2, F 2=F 3 。
3. 实心圆轴受扭转力偶作用,横截面上的扭矩为T ,横截面上沿径向的切应力分布图有如下四种,其中正确的选项是 。
插销穿过水平放置的平板上的圆孔,在其下端作用拉力P 。
该插销的剪切面面积和挤压面积分别等于。
(A) πdh ,πD 2/4;(B) πdh ,π(D 2-d 2)/4;(C) πDh ,πD 2/4;(D) πDh ,π(D 2-d 2)/4。
5. 梁在集中力偶作用截面处 。
(A) 弯矩图无变化,剪力图有突变; (B) 弯矩图无变化,剪力图有折角; (C) 弯矩图有突变,剪力无变化; (D) 弯矩图有突变,剪力图有折角。
6. 矩形截面梁剪切弯曲时,在横截面的中性轴处 。
(A) 正应力最大,切应力为零; (B) 正应力为零,切应力最大; (C) 正应力和切应力均最大; (D) 正应力和切应力均为零。
P3 3 2 2 1 1 (A) (B) (C) (D) T T T T7. 用积分法求图示简支梁挠曲线方程时,确定积分常数的条件有以下几组, 其中哪组是错误的? 。
昆明理工大学材力A测验(一)解答09级

昆 明 理 工 大 学 力 学 测 验 试 卷09级材料力学(一) 日期: 2011 年 月 日专业: 学号: 姓名:一、选择题(3×6=18分)1、关于确定截面内力的截面法的适用范围,有下列四种说法:(A )适用于等截面直杆;(B )适用于直杆承受基本变形;(C )适用于不论基本变形还是组合变形,但限于直杆的横截面;(D )适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
正确答案是: 。
2、关于下列结论的正确性:① 同一截面上正应力σ与切应力τ必相互垂直。
② 同一截面上各点的正应力σ必定大小相等,方向相同。
③ 同一截面上各点的切应力必相互平行。
现有四种答案:(A )①对;(B )①、②对;(C )①、③对;(D )②、③对。
正确答案是: 。
3、低碳钢拉伸经过冷作硬化后,以下四种指标中哪种得到提高:(A )强度极限;(B )比例极限;(C )断面收缩率;(D )伸长率(延伸率)。
正确答案是: 。
4、公式 的应用条件:(A )应力在比例极限内; (B )外力合力作用线必须沿着杆的轴线; (C )杆件必须为矩形截面杆; (D )小变形。
正确答案是: 。
AF bs=σF N5、在相同轴力作用下的二拉杆,有__________________。
(A )粗杆强度一定大于细杆; (B ) 材料好的杆件强度、刚度都大;(C )短杆刚度一定大于长杆; (D ) 相同材料下,粗杆强度、刚度都大于细杆。
正确答案是: 。
6、对于等截面梁,以下结论____是错误的。
A. 最大正应力︱σ︱max 必须在弯矩值︱M ︱为最大的截面上;B. 最大切应力︱τ︱max 必须出现在剪力值︱F S ︱为最大的截面上;C. 最大切应力︱τ︱max 的方向必与最大剪力︱F S ︱max 的方向一致;D. 最大拉应力与最大压应力在数值上必定相等。
正确答案是: D 。
二、填空题(2×11=22分)1、构件的承载能力包括 强度 , 刚度 和 稳定性 。
昆明理工大学材料力学习题册概念答案

材料力学练习册 80 学时昆明理工大学专业学号姓名日期评分第一章绪论一、是非判断题1.1材料力学的研究方法与理论力学的研究方法完全相同。
(×) 1.2内力只作用在杆件截面的形心处。
(×) 1.3杆件某截面上的内力是该截面上应力的代数和。
(×) 1.4确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
(∨) 1.5根据各向同性假设,可认为材料的弹性常数在各方向都相同。
(∨) 1.6根据均匀性假设,可认为构件的弹性常数在各点处都相同。
(∨) 1.7同一截面上正应力σ与切应力τ必相互垂直。
(∨) 1.8同一截面上各点的正应力σ必定大小相等,方向相同。
(×) 1.9同一截面上各点的切应力τ必相互平行。
(×)1.10应变分为正应变ε和切应变γ。
(∨)1.11应变为无量纲量。
(∨) 1.12若物体各部分均无变形,则物体内各点的应变均为零。
(∨) 1.13若物体内各点的应变均为零,则物体无位移。
(×) 1.14平衡状态弹性体的任意部分的内力都与外力保持平衡。
(∨) 1.15题 1.15 图所示结构中, AD 杆发生的变形为弯曲与压缩的组合变形。
(∨) 1.16题 1.16 图所示结构中, AB 杆将发生弯曲与压缩的组合变形。
(×)FFA A CBBCD D题 1.15 图题 1.16 图二、填空题1.1材料力学主要研究杆件受力后发生的变形,以及由此产生的应力,应变。
1.2拉伸或压缩的受力特征是外力的合力作用线通过杆轴线,变形特征专业学号姓名日期评分是沿杆轴线伸长或缩短。
1.3剪切的受力特征是受一对等值,反向,作用线距离很近的力的作用,变形特征是沿剪切面发生相对错动。
1.4扭转的受力特征是外力偶作用面垂直杆轴线,变形特征是任意二横截面发生绕杆轴线的相对转动。
外力作用线垂直杆轴线,外力偶作用面通过杆轴线1.5 弯曲的受力特征是,变形特征是梁轴线由直线变为曲线。
昆明理工大学工程力学习题册答案
昆明理⼯⼤学⼯程⼒学习题册答案只限⾃⼰使⽤,请不要传播 —— 李鹏程第⼀章静⼒学基础⼆、填空题2.1 –F 1 sin α1; F 1 cos α1; F 2 cos α2; F 2 sin α2 ; 0 ;F 3 ; F 4 sin α4; F 4 cos α4。
2.2 1200 , 0 。
2.3 外内。
2.4 约束;相反;主动主动。
2.5 3 ,2.6 ⼒偶矩代数值相等(⼒偶矩的⼤⼩相等,转向相同)。
三、选择题3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.14.2五、受⼒图5.1B(e)(d) (a) mm KN F M ?-=18030)(mm KN F M ?=-=3.2815325)(20mm KN F M ?-=25210.)(01=)(F M x m N F M y ?-=501)(01=)(F M z m N F M x ?-=2252)(m N F M y ?-=2252)(m N F M z ?=2252)(mN F M x ?=2253)(mN F M y ?-=2253)(mN F M z ?=2253)(5.25.3(b)(c)P 2(d)(1) ⼩球 (2) ⼤球(3) 两个球合在⼀起ACB(1) AB 杆 (2) CD 杆 (3)整体只限⾃⼰使⽤,请不要传播 —— 李鹏程(1) AC 杆(2) CB 杆 (3)整体(1) AC 段梁 (2) CD 段梁(3)整体(1) CD 杆 (2) AB 杆 (3) OA 杆C(1) 滑轮D (2) AB 杆 (3) CD 杆只限⾃⼰使⽤,请不要传播——李鹏程第⼆章⼒系的简化⼀、是⾮判断题1.1( ×) 1.2( ∨) 1.2( ×)⼆、填空题2.1 平衡。
2.2 分布载荷图形的⾯积,合⼒矩定理,分布载荷图形的形⼼。
2.3平⾏⼒系合⼒的作⽤点;物体合重⼒的作⽤点;物体的⼏何中⼼。
昆明理工大学大二机械专业材料力学试卷及答案(1)
诚信应考,考试作弊将带来严重后果!昆明理工大学期末考试《材料力学》测验20XX-51. 考前请将密封线内填写清楚; 所有答案请直接答在试卷上; .考试形式:闭卷;4. 本试卷共 六 大题,满分100分, 考试时间120分钟。
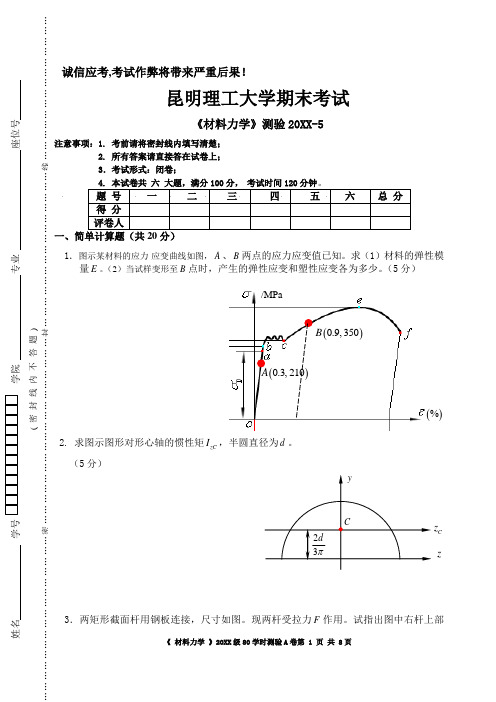
题 号 一 二 三 四 五 六 总 分 得 分 评卷人一、简单计算题(共20分).图示某材料的应力-应变曲线如图,A 、B 两点的应力应变值已知。
求(1)材料的弹性模量E 。
(2)当试样变形至B 点时,产生的弹性应变和塑性应变各为多少。
(5分)求图示图形对形心轴的惯性矩zC I ,半圆直径为d 。
(5分).两矩形截面杆用钢板连接,尺寸如图。
现两杆受拉力F 作用。
试指出图中右杆上部()0.9,350B ()%/MPa()0.3,21023d πz Cz Cy的剪切面和挤压面(图上示出),并求剪切应力和挤压应力。
(5分)4.木质悬臂梁横截面是高为200mm,宽为60mm的矩形。
端部作用2kNF=,在A点木材纤维语水平线夹角为45。
求通过A点沿纤维方向得截面上的正应力何切应力。
(5分)FA45x45σ-45στA二、作图示梁的剪力图与弯矩图。
(15分)三、不计剪力的影响,已知各杆的EI 相同,试用单位荷载法求A 、B 两点的相对位移。
(151kN5kN2kN/m–1kN m⋅1kN m⋅ 1.25kN m⋅分)四、圆轴直径60mmd=,长2ml=,左端固定,右端有一直径400mmD=的鼓轮。
轮上绕以钢绳,绳的端点B悬挂重物W,轴发生扭转变形。
绳长110ml=,横截面面积2100mmA=,弹性模量200GPaE=。
重量1kNW=。
轴的切变模量。
求轴内最大扭转切应力和重物下降的距离。
(15分)五、如图No20a工字钢悬臂梁受均布载荷q和集中力2F qa=的作用,F在平面内,30ϕ=。
工字钢的截面参数为6323710m W -=⨯,4235.510m A -=⨯。
已知10kN /m q =,1m a =。
昆明理工大学材料力学1-14计算答案
FS
m
m
解:假想沿 n-n 面切开,取右半部分为 研究对象并作左视图。由对称性可知, 每个螺栓所受的切力相等,设为 Fs。
o
∑M
截面 n-n
0
=0
FS ×
D0 ×4−m = 0 2
n
∴τ =
Fs = 15 .92 MPa ≤ [τ ] = 60 MPa A
2.13*
图示正方形截面的混凝土柱,其横截面边长为 200mm,浇注在混凝土基础上。基础 分两层,每层厚为 t,上层基础为边长 a=300mm 的正方形混凝土板。下层基础为边长 b=800mm 的正方形混凝土板。柱承受轴向压力 F=200kN,假定地基对混凝土板的反力 均匀分布,混凝土的许用剪应力 [τ] = 1.5MPa ,试计算为使基础不被剪坏所需的厚度
a a 2a
F
解:取 ABC 杆为研究对象:
A
2 2
F’B
B x1 1-1 截面:
∑M
A
=0
⇒ FB = 2 2F
FN2
a a 2a
F
y x
a 2a
∑X =0 ∑Y = 0 ∑M = 0
C1
⇒ FN 1 = 2 F
⇒ Fs1 = − F ⇒ M1 = −aF
A 45
0
C B
F
2-2 截面:
解:设木材承受的轴力为 FNw,每个等边角钢承受的轴力为 FNs
3
F
F
∑Y = 0
FNw + 4FNs − F = 0
(a )
为 1 次超静定问题
由 Δl w = Δl s
⇒
FNwl F l = Ns Ew Aw Es As
昆明理工大学工程力学习题册答案资料

工程力学习题集只限自己使用,请不要传播昆明理工大学李鹏程第一章静力学基础二、填空题2.1 -F i sin a ; F i cos a ; F 2 cos 02 ; F 2 sin a ; ___ 0 ___ ; _F 3_ ; F 4 sin 0; F 4 cos a 4。
2.2 _____ 120° _____ , __________ 0 __________ 。
2.3 —外 __________________ 内 ___________ 。
2.4 —约束 —; __________ 相反 _______ ; ________ 主动 _______________ 主动2.5 ___ 3—,2.6___ 偶矩代数值相等(力偶矩的大小相等,转向相同) —。
三、选择题3.1 _(c)_。
3.2 _A_。
3.3 D 。
3.4 _D_。
3.5 _A_。
3.6 _B_。
3.7 _C ____________________3.8M 0(F 3) = -180KN mm4.2M x (FJ = 0M x (F 2尸-25 2N m M x (F )= 25.2N m(a) 四、计算题 (b) (c)(d)4.1M 0(F 1) - -2.5 2 KN mmM °(F 2) =25-3-15 =28.3 KN mm五、受力图 M y (FJ - -50N m M y (F 2) = -25. 2N m M y (F 3) = -25 2N mM z (F 1) = 0 M z (F 2) =25 2N m Mzkp25 2N m5.2 (c)P 25.3 (1) 小球(2) 大球(3) 两个球合在一起PAEC口(1) AB 杆 ⑵CD 杆 ⑶整体只限自己使用,请不要传播李鹏程T AP IBCP2T A T BCB(c)(1) AC 杆(2) CB 杆Y B (3)整体S HII X A^.B YB (d)(1) AC段梁(2) CD段梁⑶整体vY D(1) CD 杆⑵AB杆⑶0A杆Y D(1) 滑轮D(2) AB 杆⑶CD杆只限自己使用,请不要传播李鹏程Y AX 。
昆明理工大学工程力学习题集册答案解析

第一章静力学基础二、填空题2、1 –F1 sinα1; F1 cosα1; F2 cosα2; F2 sinα2; 0;F3; F4 sinα4; F4 cosα4。
2、2 1200, 0。
2、3 外内。
2、4约束; 相反; 主动主动。
2、53,2、6力偶矩代数值相等(力偶矩得大小相等,转向相同)。
三、选择题3、1(c)。
3、2A。
3、3 D。
3、4D。
3、5 A。
3、6B。
3、7C。
3、8四、计算题4、1(d)(a) (b) (c)4、2五 、受力图 5、15、2(a)(c)ACC AB B(b)A5、3q(c)P 2(1)小球(2)大球(1) AC 杆 (2) CB 杆 (3)整体 (1) (2) (3)整体(d)(1) CD 杆 (2) AB 杆 (3) OA 杆C(i)(1) 滑轮D (2) AB 杆 (3) CD 杆(1) AB 杆 (2) CD 杆 (3)整体B BA B1、1、2 ( × )二、填空题2、1 平衡 。
2、2 分布载荷图形得面积 , 合力矩定理 , 分布载荷图形得形心 。
2、3 平行力系合力得作用点 ; 物体合重力得作用点 ; 物体得几何中心 。
三、计算题3、13、2:解:由(2、10)式:由(2、14)式:BB第三章力系得平衡方程及其应用一、就是非判断题1、1( ∨) ;1、2 ( ×);1、3 ( ∨) ;1、4( ×);1、5 ( ×);1、6 ( ∨)二、填空题2、1力偶矩得代数值相等; 。
2、2力多边形自行封闭; 。
2、3, A、B得连线不垂直x轴。
2、4, A、B、C三点不共线。
2、5(a)、(b)、(c)、(d)。
三、计算题解:取锻锤为研究对象∵力偶只能用力偶平衡,∴F A = F B方向如图。
3、23、33、4(c)CF(d)(b)DF 1q解:取CD 为研究对象3、5取ABC 为研究对象D EP 1解:取EBCD 为研究对象∴杆AC 受压3、6360˚解:取整体为研究对象,设滑轮E 得半径为r 。
材料力学1-(答案)
资料力学请在以下五组题目中任选一组作答,满分100 分。
第一组:计算题(每题25 分,共 100 分)1.梁的受力状况以以下图,资料的 a。
若截面为圆柱形,试设计此圆截面直径。
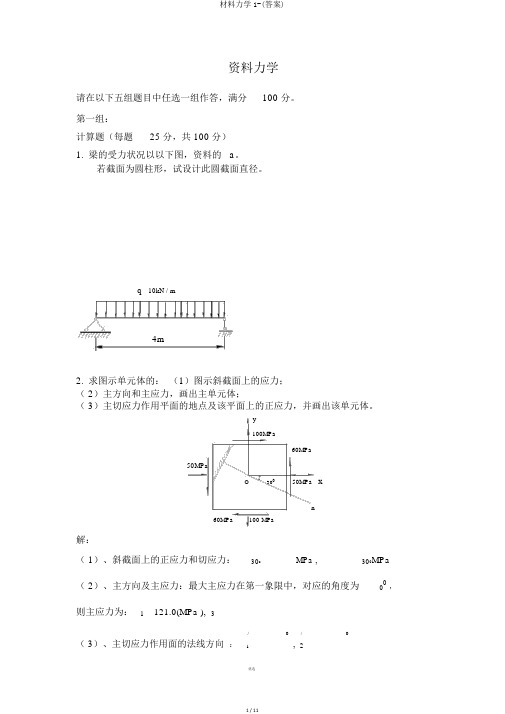
q10kN / m4m2.求图示单元体的:(1)图示斜截面上的应力;( 2)主方向和主应力,画出主单元体;( 3)主切应力作用平面的地点及该平面上的正应力,并画出该单元体。
y100MPa60MPa50MPaO 300 50MPa xn60MPa 100 MPa解:( 1)、斜截面上的正应力和切应力:30o MPa , 300M Pa ( 2)、主方向及主应力:最大主应力在第一象限中,对应的角度为00,则主应力为:1 121.0(MPa ), 3( 3)、主切应力作用面的法线方向:/ 0,/ 02主切应力为:/ /1 225.0( MPa ) ,主单元体如图3-2所示。
此两截面上的正应力为:/ /1 2y1xO03图 3-125.67 0O图 3-23.图中所示传动轴的转速 n=400rpm,主动轮 2 输入功率 P2=60kW,从动轮 1,3,4和 5 的输出功率分别为 P1=18kW,P3=12kW,P4=22kW,P5=8kW。
试绘制该轴的扭矩图。
4.用积分法求图所示梁的挠曲线方程和转角方程,并求最大挠度和转角。
各梁EI 均为常数。
第二组:计算题(每题25 分,共 100 分)1. 简支梁受力以下图。
采纳一般热轧工字型钢,且已知 = 160MPa。
试确立工字型钢型号,并按最大切应力准则对梁的强度作全面校核。
(已知选工字钢: W = 692.2 cm3, Iz = 11075.5 cm4)解:1.F RA = F RB = 180kN (↑)kN·mkN·mkN3m由题设条件知:W = 692.2 cm 2, Iz = 11075.5 cm 4cmE截面:MPaMPa2. A +、 B-截面:MPaMPa3.C-、 D+截面:MPaMPa∴选 No.32a 工字钢安全。
昆明理工大学工程力学习题集册答案解析

第一章 静力学基础二、填空题2.1 –F 1 sin α1; F 1 cos α1; F 2 cos α2; F 2 sin α2 ; 0 ;F 3 ; F 4 sin α4; F 4 cos α4。
2.2 1200, 0 。
2.3 外 内 。
2.4 约束 ; 相反 ; 主动 主动 。
2.5 3 ,2.6 力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题 3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.1(d)(a) (b) (c)mmKN F M ⋅-=18030)(mmKN F M ⋅=-=3.2815325)(20mmKN F M ⋅-=25210.)(4.2五 、受力图5.15.2(a)(c)ACCAB B(b)1=)(F M x mN F M y ⋅-=501)(01=)(F M z m N F M x ⋅-=2252)(m N F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M x ⋅=2253)(mN F M y ⋅-=2253)(mN F M z ⋅=2253)(qAM BA(c)P 2(d)5.3(1) 小球 (2) 大球(3) 两个球合在一起P 2P 1ACB(a)(1) AB 杆 (2) CD 杆 (3)整体(1) AC杆(2) CB杆(3)整体(1) AC段梁(2) CD段梁(3)整体第二章 力系的简化一、是非判断题1.1 ( × ) 1.2 ( ∨ ) 1.2 ( × ) 二、填空题2.1 平衡 。
2.2 分布载荷图形的面积 , 合力矩定理 , 分布载荷图形的形心 。
2.3 平行力系合力的作用点 ; 物体合重力的作用点 ; 物体的几何中心 。
三、计算题 3.1F 3F 1ykNX 98340.=⋅⋅⋅=∑kNY 13587.=⋅⋅⋅=∑解:由(2.10)式:kNY X F R 9667822.)()('=+=∑∑(1) CD 杆 (2) AB 杆 (3) OA 杆C(i)(1) 滑轮D (2) AB 杆 (3) CD 杆(j)DDF PPABKIBCF AY AX IY IX KY CID,DF ,BCF 'IX 'I Y DCE,EFFCF ABE.EF AY AX BY BX CAO,CF,A Y ,AXY 0X3.2第三章 力系的平衡方程及其应用一、是非判断题1.1 ( ∨ ) ;1.2 ( × );1.3 ( ∨ ) ;1.4 ( × );1.5 ( × );1.6 ( ∨ )(a)(b)5020.cos '==∑R F Xα8650.cos '==∑R F Y βcmkN FM M i ⋅=⋅⋅⋅==∑58460000.)(kNF F R R 96678.'==cm F M d R7860.'==M=c mmc 086.=mm125.mm1210.由(2.14)式:二、填空题2.1 力偶矩的代数值相等 ; 。
昆明理工大学材料力学习题册1-14概念答案

专业 学号 姓名 日期 评分第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × )1.2 内力只作用在杆件截面的形心处。
( × )1.3 杆件某截面上的内力是该截面上应力的代数和。
( × )1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ )1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ )1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ )1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ )1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × )1.9 同一截面上各点的切应力τ必相互平行。
( × )1.10 应变分为正应变ε和切应变γ。
( ∨ )1.11 应变为无量纲量。
( ∨ )1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ )1.13 若物体内各点的应变均为零,则物体无位移。
( × )1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题 1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ,变形特征B 题1.15图题1.16图 外力的合力作用线通过杆轴线 杆件专业 学号 姓名 日期 评分是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:设木材承受的轴力为 FNw,每个等边角钢承受的轴力为 FNs
3
F
F
∑Y = 0
FNw + 4FNs − F = 0
(a )
为 1 次超静定问题
由 Δl w = Δl s
⇒
FNwl F l = Ns Ew Aw Es As
⇒
FNs Es As = FNw Ew Aw
查附录ⅡP393,每个等边角钢的横截面积 As =3.086cm2 。
、
NB = 60 kW ,从动轮 A
和 C 输出的功率为 NA = NC = 30 kW。已知[τ]=40MPa,[ φ ]=0.5o/m,G=80GPa。试按强 度和刚度条件选择轴的直径 d。
MA A 2m
MB
MC C
1) 按强度条件:
τ max =
Tmax 16TAB = ≤ [τ ] Wt πd 3
FS 1 (1 − 0 .2 2 a 2 ) F = τ = ≤ [τ ] 0 .2 t × 4 A (1 − 0 .2 2 a 2 ) F ⇒t≥ = 0 .0926 m = 92 .6 mm 0 .2 × 4 × [τ ]
取 t = 96mm
第三章
四、计算题
扭转
3.2
图示一阶梯形传动轴,上面装有三个皮带轮。主动轮Ⅰ输出的功率为 动轮Ⅱ传递的功率为
2m
解:设各杆均受拉;先取销钉 B 为研究对象;
C 2 A 1 4m
FN4
C
θ
D
4
5m
3 B
FN3 FN2 FN1
B P
3m
FN3
y
∑Y = 0 ∑X = 0
P
⇒ FN 3 = 5P 3 ⇒ FN1 = − 4P 3 ⇒ FN 4 = 4P 3 ⇒ FN 2 = − P
取销钉 C 为研究对象;
x
∑X = 0 ∑Y = 0
∴(FNw )max = FN1 = − 4P 3
(FNs )max = FN3 = 5P 3
σ w max = σ s max
( FNw ) max ≤ [σ ]木 Aw
⇒ P ≤ 60kN ⇒ P ≤ 57.6kN
∴ [P ] = 57 . 6 kN
(F ) = Ns max ≤ [σ ]钢 As
D0
FS
m
m
解:假想沿 n-n 面切开,取右半部分为 研究对象并作左视图。由对称性可知, 每个螺栓所受的切力相等,设为 Fs。
o
∑M
截面 n-n
0
=0
FS ×
D0 ×4−m = 0 2
n
∴τ =
Fs = 15 .92 MPa ≤ [τ ] = 60 MPa A
2.13*
图示正方形截面的混凝土柱,其横截面边长为 200mm,浇注在混凝土基础上。基础 分两层,每层厚为 t,上层基础为边长 a=300mm 的正方形混凝土板。下层基础为边长 b=800mm 的正方形混凝土板。柱承受轴向压力 F=200kN,假定地基对混凝土板的反力 均匀分布,混凝土的许用剪应力 [τ] = 1.5MPa ,试计算为使基础不被剪坏所需的厚度
⇒ d ≥ 45.01mm
2) 按刚度条件:
B
2m
, ϕ max =
716.2 Nm
( +)
T max 180 × ≤ [ϕ '] π GI p
A
B
(—) C
⇒ d ≥ 56.9mm
716.2 Nm
∴ 取 d = 57 mm
3.4 图示一实心圆轴,直径 d = 10 cm ,自由端所受外扭矩 Me = 14 kN·m , (1)试计算
∴σ1 = FN1 A1 = −6MPa
1
F2 F2
1
F2
σ 2 = FN 2 A2 = −10MPa
σ 3 = FN 3 A3 = −9MPa
杆内横截面上的最大正应力(压应力)为:
2
F2
2
3
3
σ c max = σ 2 = 10MPa
作用在中段(2-2)横截面上。
2
2.5 在图示简易吊车中,BC 为钢杆,AB 为木杆。木杆 AB 横截面积 A1=100 cm2,许用应力 钢杆 BC 的横截面积 A2=6 cm2, 许用拉应力[σ]2=160MPa。 试求许可吊重 F。 [σ]1=7MPa;
解:
用在各自截面的形心(如图)且△ls=△li A
∑Y = 0
F Ns + F Ni − F P = 0
(a )
为 1 次超静定问题;
由 Δl s = Δli ⇒
y
F Ns l F l = Ni EsA Ei A
⇒ F Ns = 2 F Ni
FNs FNi
代入(a)式得: FNs = 2 FP 3
FNi = FP 3
FBC
C
解:取整体为研究对象;
钢
FAB
A
木
30 y
o
B x F
∑Y = 0 ∑X = 0
⇒ F BC = 2 F
⇒ FAB = 3FBC 2 = 3F
σ AB =
FNAB ≤ [σ ]1 A1
⇒ F ≤ 40.4kN
σ BC
F = NBC ≤ [σ ]2 A2
∴ [F ] = 40 . 4 kN
⇒ F ≤= 48kN
F F
τ =
Fs F = = 0.952 MPa A hb
F
F
σ bs =
Fbs F = = 7.407MPa Abs cb
ቤተ መጻሕፍቲ ባይዱ
5
2.12 图示凸缘联轴节传递的力偶矩为 m =200N·m,凸缘之间由四只螺栓联接,螺栓内径 d =10mm,对称地分布在 D0 = 80mm 的圆周上。如螺栓的剪切许用应力[τ]= 60 MPa,试校核螺 栓的剪切强度。 n m
2.6 图示拉杆沿斜面 m-n 由两部分胶合而成。设在胶合面上许用拉应力[σ]=100 MPa,许用 剪应力[τ]=50 MPa。并设胶合面的强度控制杆件的拉力。试问:为使杆件承受最大拉力 0 F,α角的值应为多少?若杆件横截面积为 4cm2,并规定α≤60 ,试确定许可载荷 F。 m F F
α θ n
ϕ AC = 2.708 ×10−2 rad = 1.5510
8
3.5 阶梯形圆轴,受力如图所示,外扭矩 MA= 18 kN·m ,MB= 32kN·m ,MC= 14kN·m 。 AE 段为空心圆截面,外径 D = 140 mm ,内径 d = 100 mm ;BC 段为实心圆截面,直
径 d = 100 mm 。已知 [τ] = 80MPa, [φ’] = 1.2°∕m ,G = 0.8×10 MPa
∑M
A
=0
⇒x=
5 b 6
2.10 试校核图示连接销钉的剪切强度。已知 F =100kN,销钉直径 d =30 mm,材料的许用剪 应力[τ]= 60 MPa。若强度不够,应改用多大直径的销钉?
d ≥ 0 .0326 m = 32 .6 mm
FF
F F F
2.11 木榫接头如图所示。a = b =12 cm,h =35 cm,c =4.5 cm。F = 40 kN。试求接头的剪切、 挤压应力。
∴最大油压 pmax = 6.5MPa
2.4 一阶梯形立柱受力如图示, F1=120kN, F2=60kN。柱的上、中、下三段的横截面面积 分别是 A1 = 2 × 10 mm , A2 = 2.4 × 10 mm , A3 = 4 × 10 mm ,试求:(1)各段横截
4 2 4 2
4
2
面上的正应力; (2)杆内横截面上的最大正应力,并指明其作用位置。 F1
C1
⇒ FN 1 = 2 F
⇒ Fs1 = − F ⇒ M1 = −aF
A 45
0
C B
F
2-2 截面:
M1 FN1 FS1
FB
1 1
C B
∑X
1
=0
FB
, ⇒ FN 2 = − FB = −2 2 F
第二章
拉伸、压缩与剪切
四、计算题 2.2 图示等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成。 直杆各部分的直径均为 d=36mm, 受力如图示。若不考虑杆的自重,试求 AC 段和 AD 段杆的轴向变形量 Δl AC 和 Δl AD 。
t 值。 F
y
F
四个可能的剪切面如图中红线所示 对下层基础如图:
⇒ q = F b2
t t q F t a q
a b
∑Y
=0
qa2 + FS − F = 0
2
a2 ⇒ FS = F − qa = (1− 2 )F b
由(2.23)式:
FS (1 − a 2 b 2 ) F τ = = ≤ [τ ] A 4 at
4
2.9 * 图示组合柱由钢和铸铁制成,组合柱横截面是边长为 2b 的正方形,钢和铸铁各占横截 面的一半( b × 2b ) 。载荷 FP 通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹 性模量分别为 Es=196GPa,Ei=98.OGPa。今欲使刚性板保持水平位置,试求加力点的位 置 x 应为多少。 欲使刚性板保持水平位置,FNs 和 FNi 应分别作
Fs
(1 − a 2 b 2 ) F ⇒t≥ = 0 .0955 m = 95 .5 mm 4 a [τ ]
6
对上层基础如图:
F t 200mm q1
⇒ q1 = F a2
∑Y
Fs1
=0
0.22 q1 + FS1 − F = 0 0.22 )F a2
⇒ FS1 = F − 0.22 q1 = (1 −
