乘法器和除法器
电路中的除法器设计

电路中的除法器设计在电路设计中,除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算,将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用,因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算,要实现除法器的设计,首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后,除法器将被除数和除数进行比较,并开始迭代过程。
在每一次迭代中,被除数的位数向左移动,直到其高位与除数相等或超过除数。
然后,除法器进行减法操作,将除数减去被除数,结果作为商的一位。
此后,商持续左移,被减数保持不变,重复上述过程,直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中,有几种常见的策略可以考虑。
1. 组合逻辑除法器:这种类型的除法器使用组合逻辑电路实现,通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快,但缺点是占用较多的电路资源。
2. 串行逻辑除法器:与组合逻辑除法器相反,串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号,逐位地进行计算,因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源,因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器:这种除法器通过多个并行的子除法器实现,并行计算多个位的商。
重复系列除法器具有较高的性能,但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率,可以采用一些优化方法。
1. 位级并行思路:通过将除法器分解为多位的子除法器,并行计算多个子除法器,可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧:利用乘法器计算除法运算,可以加速除法器的运算速度。
通过将除数进行逆运算,转化为乘法操作,可以利用乘法器的高速性能,提升除法器的效率。
3. 进制转换思想:将数字进行二进制到十进制的转换,然后进行简单的除法运算,可以减少运算的复杂程度,提高除法器的运算速度。
乘法器除法器

x
1010
10100多工器0110選1 致擇能
0101
加法器 cout
cin
Add’Sub
27
第112章. 硬乘體法乘器法與除器法器 範例:無號數乘法 1010b ×1011b
Step 3
位移
y 101
1 1 1 1 0 位移
z(2)
x
1010
10100多工器0110選1 致擇能
1010
0101
加法器 0
mfhi
$t2
mflo
$t3
位元乘積 # $t2 = Hi
#$t3 = 32
(Lo)
slt sll sra
$t1, $t3, $zero $t1, $t1, 31 $t1, $t1, 31
加法器 0
cout
cin
0 Add’Sub
1010
37
第112章. 硬乘體法乘器法與除器法器 範例:無號數乘法 1010b ×1011b
位移 Step 2
y
0 1 0 1 0 1位0移1
x
1010
0多工器1
致能 選擇
0101
加法器 cout
cin
Add’Sub
38
第112章. 硬乘體法乘器法與除器法器 範例:無號數乘法 1010b ×1011b
Step 3
y
1 1 1 1 0 1位0移1
x
1010
0多工器1
致能 選擇
1010
0101
加法器 0
cout
cin
0 Add’Sub
1111
39
第112章. 硬乘體法乘器法與除器法器 範例:無號數乘法 1010b ×1011b
乘法器的工作原理

乘法器的工作原理
乘法器是一种用于实现数字乘法运算的电路或器件。
它将两个输入的数字进行相乘,并得到其乘积作为输出。
乘法器的工作原理基于逻辑门电路的组合与串联。
乘法器通常是由多个部分组成的,其中包括乘法器的位数、运算规则以及乘法器内部的逻辑门电路。
这些部分协同工作以实现精确且高效的乘法运算。
在一个典型的乘法器中,输入信号将首先被分为不同的位数。
每一位数将被独立处理,并最终合并以得到最终的乘积结果。
每个位数的处理过程包括了多个逻辑运算,例如与门、或门和异或门。
为了完成乘法运算,乘法器将两个输入位进行逐位相乘。
这里的位可以是二进制位,也可以是十进制位。
逐位相乘的方法可以通过一系列的逻辑门电路来实现。
这些逻辑门电路可以对输入位进行操作,并生成相乘位的输出。
在乘法器中,最低有效位(LSB)的运算最先进行。
在相邻的
位运算完成后,它们的结果会被以并行的方式传递给下一位的运算。
这样一直进行到最高有效位(MSB)的运算完成。
最后,所有位的乘法结果会被整合在一起,形成最终的乘积。
乘法器的性能取决于其位数和逻辑门电路的设计。
更高的位数会产生更精确的乘法结果,但也会增加乘法器的复杂性和功耗。
因此,在设计乘法器时需要权衡精确性和性能之间的关系。
总之,乘法器是一种通过组合逻辑门电路来实现数字乘法运算的电路或器件。
它将输入信号分解为不同的位数,并使用逻辑门电路逐位相乘。
最后,将每个位的乘法结果合并在一起,得到总体的乘积输出。
计算机组成 Quiz答案(全)

• 19. 下列哪项不属于系统总线?
○ 地址总线 ○ 数据总线 ○ 逻辑总线
分区 MOOC的quiz 的第 4 页
○ 运算总线 ○ 控制总线 • 20.对于按字节编址的存储器来说,控制器有10条地址线,对应的存储空间有多大? ○ 10KB ○ 10MB ○ 1MB ○ 1KB • 21. 在指令的取指阶段,CPU中的MAR的内容会来自哪里? ○ R0 ○ MDR ○ ALI ○ PC ○ IR
intel 80386于1985年推出
3. x86体系结构中,寄存器EAX长度为多少位?
8位 16位 32位 64位
4. IA-32寄存器模型中包括以下哪些寄存器?(多选题)
段寄存器 标志寄存器 页面寄存器 通用寄存器 指令指针寄存器
5. 8086系统中标志位CF的含义是?
符号标志 零标志 溢出标志 进位标志
中,会访问几次存储器?
○ 0次
○ 1次(√)
○ 2次
○ 3次
○ 4次
计入从存储器内取出PC对应指令的过程
• 8.哪位人物被称为“现代电子计算机之父”?
○ 安迪•格鲁夫
○ 史蒂夫•乔布斯
○ 阿兰•麦席森•图灵
○ 比尔•盖茨
○ 戈登•摩尔
○ 冯•诺依曼
• 9.下列关于EDVAC的描述正确的是
○ 全称为“离散变量自动电子计算机”
14. 很多x86指令的功能比较复杂,往往一条x86指令可以完成的功能,需要多条MIPS指令才能实现。 请问下列x86指令中,哪些确定能够只用一条MIPS指令完成对应的功能?(注:只需考虑这条指令本 身,不用考虑对后续指令的影响) REP MOVSB MOV EDX, [EBX+11H] JZ LOOP_1(不能) ADD EAX, [13H] ADD ECX, 15H MOV EAX, 28H ADD [EBX+ESI*4+200H], EAX ADD EDX, EBX
乘法器原理

乘法器原理
乘法器是一种用于执行乘法运算的数字电路。
它通常由多个逻辑门、寄存器和时钟信号组成。
乘法器的主要原理是将两个输入数(被乘数和乘数)进行相乘,然后输出它们的乘积。
乘法器的输入是一系列位(比特),每个位代表一个二进制数。
这些输入位通过逻辑门来实现不同位上的相乘。
一般来说,较高位的输入乘数与较低位的被乘数相乘后,得到的乘积需要左移若干位。
这个左移操作可以通过使用寄存器和时钟信号来完成。
乘法器可以分为多种类型,其中最常见的是布斯乘法器和Wallace树乘法器。
布斯乘法器通过将被乘数和乘数进行分割,并使用部分积和约化乘法器来实现乘法运算。
Wallace树乘法
器是一种高效的乘法器类型,它通过将乘法操作转化为加法操作来提高运算速度。
这种乘法器通常使用布斯乘法器和连锁加法器来实现。
乘法器的输出是乘法的结果,通常也是一系列位(比特)。
输出可以进一步用于其他计算或者存储在寄存器中。
同时,乘法器也可以进一步扩展为多位乘法器,用于执行更大位数的乘法操作。
综上所述,乘法器是一种将两个输入数进行相乘的数字电路。
它的原理是利用逻辑门、寄存器和时钟信号来实现乘法运算。
乘法器可以分为不同类型,其中最常见的是布斯乘法器和
Wallace树乘法器。
乘法器的输出是乘法的结果,通常用于其他计算或者存储在寄存器中。
cpu中用来对数据进行各种算术运算和逻辑运算的部件

cpu中用来对数据进行各种算术运算和逻辑运算的部件CPU是计算机的核心部件,它负责执行各种算术运算和逻辑运算,以处理和执行计算机程序中的指令。
CPU中的运算部件是实现这些功能的关键部分。
一、算术运算部件CPU中的算术运算部件主要负责执行加、减、乘、除等算术运算。
这些运算在计算机程序中非常常见,例如在处理数值数据、进行数学计算或执行科学计算时。
1. 加法器:加法器是CPU中最基本的算术运算部件,用于执行加法运算。
它接收两个操作数,并将它们相加,生成结果。
加法器在CPU中通常是多位的,可以处理不同长度的数据。
2. 减法器:减法器与加法器类似,用于执行减法运算。
它接收两个操作数,并将它们相减,生成结果。
3. 乘法器:乘法器用于执行乘法运算。
它接收两个操作数,并将它们相乘,生成结果。
乘法器在CPU中通常是多位的,可以处理不同长度的数据。
4. 除法器:除法器用于执行除法运算。
它接收两个操作数,其中一个作为被除数,另一个作为除数,生成商和余数。
除法器在CPU中通常是多位的,可以处理不同长度的数据。
二、逻辑运算部件CPU中的逻辑运算部件主要负责执行逻辑运算,如与、或、非等。
这些运算在计算机程序中也非常常见,例如在处理布尔逻辑、条件判断或控制流程时。
1. 逻辑与门:逻辑与门用于执行逻辑与运算。
它接收两个操作数,只有当两个操作数都为真时,结果才为真。
2. 逻辑或门:逻辑或门用于执行逻辑或运算。
它接收两个操作数,只要其中一个操作数为真,结果就为真。
3. 逻辑非门:逻辑非门用于执行逻辑非运算。
它接收一个操作数,并对其取反。
如果操作数为真,结果为假;如果操作数为假,结果为真。
除了以上介绍的算术运算和逻辑运算部件外,CPU中还可能包含其他类型的运算部件,如移位器、比较器等,以满足不同的计算需求。
三、总结CPU中的运算部件是实现计算机程序中各种算术和逻辑运算的关键部分。
这些部件通过精心的设计和优化,使得CPU能够高效地完成各种复杂的计算任务。
除法器实验报告

计算机组成原理实验报告题目:运算器部件实验:除法器学院数学与信息学院学科门类工学专业12软件工程学号2012436138姓名王赛赛指导教师王兵一、实验目的1.掌握乘法器以及booth 乘法器的原理二、实验原理除法是乘法的倒数。
首先我们看一下十进制数的除法。
为了方便起见,我们假定十进制数的各位要么为1要么为0,例如(1001010)10 ÷(1000): 1 0 0 1 商1000)1 0 0 1 0 1 0 被除数 -1 0 0 01 01 0 11 0 1 0- 1 0 0 01 010 余数被除数、除数、商、和余数的关系如下式所示:被除数=商×除数+余数式中,余数必须比除数小。
除法中求商的基本方法是利用被除数减去除数,看结果是正还是负,来决定商的这位是1还是0。
假定被除数和除数都是正的,因此商和余数都是非负的。
操作数和结果都是32位的,忽略符号。
比较善于节省空间的人们发现,商寄存器浪费的空间正好和余数寄存器浪费的空间一样,因此,将商寄存器和余数寄存器结合起来。
下图为除法器的算法流程。
除数从寄存器左移一位 从余数寄存器左半部分减去除数寄存器,结果存在余数寄存器的左半部分 测试余数 余数寄存器左移一位,第0位置1 余数≥0 加除数到余数寄存器的左半部分已恢复原来的被除数值。
商寄存器左移,第0位置0余数<0 开始No<32三、实验步骤1.打开Quartus->tools->programmer,将booth_divider.sof下载到FPGA中。
注意进行programmer 时,应在program/configure下的方框中打勾,然后下载。
2.在实验台上通过模式开关选择FPGA独立调试模式010。
3.将短路子DZ3短接且短路子DZ4断开,使FPGA-CPU所需要的时钟使用正单脉冲时钟。
四、实验现象本实验实现4位数的除法(无符号除法),输入输出规则对应如下:1、输入的4位被除数(dividend)md3~md0对应开关SD11~SD8。
模拟电子技术基础-第七章信号的运算和处理

在模拟电子技术中,信号的乘法运算是一种重要的运算方式。通过将一个信号 与另一个信号对应时间点的值相乘,可以得到一个新的信号。这种运算在信号 处理中常用于调制和解调、放大和衰减等操作。
除法运算
总结词
信号的除法运算是指将一个信号除以另一个信号,得到一个新的信号。
详细描述
在模拟电子技术中,信号的除法运算也是一种重要的运算方式。通过将一个信号除以另一个信号,可以得到一个 新的信号。这种运算在信号处理中常用于滤波器设计、频谱分析和控制系统等领域。需要注意的是,除法运算可 能会引入噪声和失真,因此在实际应用中需要谨慎使用。
减法运算
总结词
信号的减法运算是指将一个信号从另一个信号中减去,得到一个新的信号。
详细描述
信号的减法运算在模拟电子技术中也是常用的一种运算方式。通过将一个信号从 另一个信号中减去,可以得到一个新的信号。这种运算在信号处理中常用于消除 噪声、提取特定频率成分或者对信号进行滤波等操作。
乘法运算
总结词
信号的乘法运算是指将一个信号与另一个信号对应时间点的值相乘,得到大是指通过电子电路将输入的微弱信号放大到所需 的幅度和功率,以满足后续电路或设备的需要。
放大器的分类
根据工作频带的不同,放大器可以分为直流放大器和交流 放大器;根据用途的不同,放大器可以分为功率放大器、 电压放大器和电流放大器。
放大器的应用
在通信、音频、视频等领域,放大器是必不可少的电子器 件,例如在音响系统中,我们需要使用功率放大器来驱动 扬声器。
信号调制
信号调制的概念
信号调制是指将低频信息信号加载到 高频载波信号上,以便于传输和发送。
调制方式的分类
调制技术的应用
在无线通信中,调制技术是必不可少 的环节,通过调制可以将信息信号转 换为适合传输的载波信号,从而实现 信息的传输。
乘法器原理

乘法器原理乘法器是一种用来进行乘法运算的电子元件,它在数字电路中起着非常重要的作用。
乘法器的原理是怎样的呢?让我们一起来探讨一下。
首先,我们需要了解乘法器的基本结构。
乘法器通常由多个逻辑门和触发器组成,其中包括与门、或门、非门等。
这些逻辑门和触发器相互连接,形成了一个复杂的电路结构,用来实现乘法运算。
乘法器的原理可以简单地用一个例子来说明。
假设我们要计算8乘以3的结果。
首先,我们将8和3转换为二进制数,分别为1000和0011。
然后,我们使用乘法器进行计算。
乘法器通过逐位相乘的方式,将每一位上的乘积相加,最终得到最终的乘法结果。
在乘法器的工作过程中,每一个逻辑门都承担着重要的作用。
与门用来进行位与运算,或门用来进行位或运算,非门用来进行位取反运算。
这些逻辑门相互组合,形成了一个高效的乘法器电路。
除了基本的逻辑门,乘法器还包括了触发器。
触发器在乘法器中的作用是非常重要的,它用来存储中间结果,并在计算过程中进行数据传递和控制。
乘法器的原理不仅仅局限于二进制乘法,它还可以应用到其他进制的乘法运算中。
无论是二进制、八进制还是十进制,乘法器都能够高效地进行乘法运算,这正是乘法器在数字电路中被广泛应用的原因之一。
总的来说,乘法器是一种非常重要的数字电路元件,它通过逻辑门和触发器的组合,实现了高效的乘法运算。
乘法器的原理是基于逐位相乘和相加的方式,通过逻辑门的运算和触发器的存储,最终得到乘法的结果。
乘法器不仅可以应用于二进制乘法,还可以适用于其他进制的乘法运算,具有非常广泛的应用价值。
希望通过本文的介绍,读者能对乘法器的原理有一个更加深入的了解。
布斯算法乘法器和算术运算器
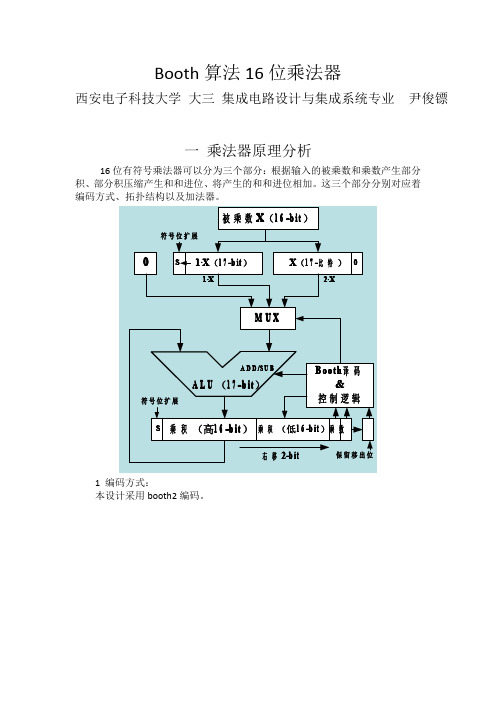
Booth算法16位乘法器西安电子科技大学大三集成电路设计与集成系统专业尹俊镖一乘法器原理分析16位有符号乘法器可以分为三个部分:根据输入的被乘数和乘数产生部分积、部分积压缩产生和和进位、将产生的和和进位相加。
这三个部分分别对应着编码方式、拓扑结构以及加法器。
1编码方式:本设计采用booth2编码。
部分积是负数时S=1,部分积是正数时S=0;当部分积是+0时,E=1,部分积是-0时,E=0,其余情况E=S取反。
2拓扑结构:本设计采用二进制树的拓扑结构。
二进制树拓扑结构排列的较为规整,且部分积压缩的速度也非常快。
部分积压缩的目的是为了减小进位传播的延时,采用进位保留加法器,根据当前位信息产生下一位的进位,仅仅产生而没有进位行波传播,这样就可以把当前的多位压缩到较少的位数。
经过几次压后,把部分积压缩成和以及进位。
部分积主要是通过counter和compressor进行压缩,通常使用(3:2)counter 和(4:2)compressor。
(3:2)counter其实质就是一个全加器,进位输入为ci,进位输出为c;(4:2)compressor可以由两个全加器组成,ci为进位输入,Coin为内部进位,输入到下一位的进位输入Ci,Coex为输出进位。
上图为二进制树的拓扑结构图,每4个部分积输入到一个(4:2)compressor 中,产生两个输出,则8个部分积使用3次(4:2)compressor就可以得到和和进位。
部分积的压缩方式可以见下图。
如图中所示,加上最后一个部分积的进位,共有9个部分积,本设计把最后的进位位移到第一个部分积上,使用5个全加器,把进位融合到第一个部分积,这样就转变成8个部分积了,再使用两级二进制树压缩,所以总共使用了三级压缩,最终得到部分积的和和进位。
为了免去不必要的硬件开销,对于部分积边上的位采用counter压缩。
上文提到的符号位扩展的改进方法,其目的也就是减少硬件开销,所以在不影响性能的情况下,单独出来部分积的边缘位是十分有必要的。
第2章(3) 乘法器除法器

这种乘法器要实现n位×n位时,需要n(n-1)个全加器和n2个 “与”门。该乘法器的总的乘法时间可以估算如下: 令Ta为“与门”的传输延迟时间,Tf为全加器(FA)的进位传输延 迟时间,假定用2级“与非”逻辑来实现FA的进位链功能,那么我们就 有: Ta = Tf = 2T 从演示中可知,最坏情况下延迟途径,即是沿着矩阵P4垂直线和 最下面的一行。因而得 n位×n位不带符号的阵列乘法器总的乘法时间为: tm=Ta+(n-1)×6T+(n-1)×Tf =2T+(n-1)×6T+(n-1)×2T=(8n-6)T
笔算乘法改进
A • B = A • 0.1011 = 0.1A + 0.00A + 0.001A +0.0001A = 0.1A + 0.00A + 0.001( A +0.1A) = 0.1A + 0.01[0 • A + 0. 1( A +0.1A)]
右移一位
= 0.1{A +0.1[ 0 • A+0.1(A + 0.1A)]} = 2-1{A +2-1[ 0 • A+2-1(A + 2-1(A+0))]}
9
3.带符号的阵列乘法器
(1) 对2求补器电路 我们先来看看算术运算部件设计中经常用到的求补电路。具 有使能控制的二进制对2求补器电路图,其逻辑表达式如下: C-1=0, Ci=ai+Ci-1 ai*=ai⊕ECi-1, 0≤i≤n
在对2求补时,要采用按位扫描技术来执行所需要的求补操作。 令A=an…a1a0是给定的(n+1)为带符号的数,要求确定它的补码形 式。 进行求补的方法就是从数的最右端a0开始,,由右向左,直到找出 第一个“1”,例如ai=1, 0≤i≤n。这样,ai以左的每一个输入位都求 反,即1变0,0变1。 最右端的起始链式输入C-1必须永远置成“0”。当控制信号线 E为“1”时,启动对2求补的操作。当控制信号线E为“0”时,输出将和 输入相等。显然,我们可以利用符号位来作为控制信号。
乘法器原理

乘法器原理在现代科技中,乘法器是非常重要的一种电子元件,它可以实现数字信号的乘法运算,广泛应用于各种计算机、通信、控制等领域。
本文将介绍乘法器的工作原理、分类以及应用。
一、乘法器的工作原理乘法器是一种数字电路,它的主要作用是实现数字信号的乘法运算。
在乘法器中,输入信号经过一系列的逻辑门电路处理后,输出结果为两个输入信号的乘积。
乘法器的基本原理可以用以下公式表示: A × B = C其中,A和B为输入信号,C为输出结果。
乘法器的工作原理可以分为两种类型:串行和并行。
串行乘法器是将两个输入信号分别进行位移和加法运算,最终得到输出结果。
而并行乘法器则是将两个输入信号分别进行分解和加法运算,最终得到输出结果。
两种类型的乘法器均采用逻辑门电路实现,具体实现方式有多种。
二、乘法器的分类根据乘法器的不同实现方式,可以将其分为以下几种类型:1. 串行乘法器串行乘法器是一种最简单的乘法器,它采用逐位相乘的方式实现。
串行乘法器的输入信号经过位移和加法运算后,得到输出结果。
串行乘法器的优点是结构简单,适合于低速应用。
但是,由于其逐位相乘的方式,其速度较慢,不适合于高速应用。
2. 并行乘法器并行乘法器是一种较为复杂的乘法器,它采用分解和加法运算的方式实现。
并行乘法器的输入信号分别进行分解,然后进行加法运算,得到输出结果。
并行乘法器的优点是速度快,适合于高速应用。
但是,由于其结构较为复杂,相对于串行乘法器来说,成本较高。
3. Booth乘法器Booth乘法器是一种改进的串行乘法器,它采用位移和加减运算的方式实现。
Booth乘法器的输入信号经过位移和加减运算后,得到输出结果。
Booth乘法器的优点是速度快,适合于高速应用。
但是,由于其结构较为复杂,相对于串行乘法器来说,成本较高。
4. Wallace树乘法器Wallace树乘法器是一种改进的并行乘法器,它采用分解和加法运算的方式实现。
Wallace树乘法器的输入信号分别进行分解,然后进行加法运算,得到输出结果。
算术逻辑运算部件构造

算术逻辑运算部件构造算术逻辑运算部件是指在计算机硬件中用于实现算术和逻辑运算的部件。
这些部件可以执行各种算术运算(如加法、减法、乘法、除法)和逻辑运算(如与、或、非)。
在计算机中,算术逻辑运算部件是非常重要的,它们负责执行各种数学运算和逻辑判断,是计算机运行的基础。
这些部件通常由逻辑门电路组成,可以实现各种复杂的数学运算和逻辑判断。
算术逻辑运算部件通常包括加法器、减法器、乘法器、除法器、逻辑门电路等。
这些部件可以单独使用,也可以组合在一起实现更复杂的功能。
下面来详细介绍一下几种常见的算术逻辑运算部件。
1. 加法器加法器是计算机中常用的算术逻辑运算部件之一,用于实现两个数的加法运算。
加法器一般由半加器和全加器组成。
半加器用于实现单位数的二进制加法,而全加器可以实现多位数的二进制加法。
加法器的输入是两个二进制数和一个进位位,输出是一个二进制数和一个进位位。
2. 减法器减法器也是计算机中常用的算术逻辑运算部件之一,用于实现两个数的减法运算。
减法器一般由半减器和全减器组成。
半减器用于实现单位数的二进制减法,而全减器可以实现多位数的二进制减法。
减法器的输入是两个二进制数和一个借位位,输出是一个二进制数和一个借位位。
3. 乘法器乘法器是计算机中用于实现两个数的乘法运算的部件。
乘法器可以实现各种乘法操作,如加法器和减法器一样,乘法器也可以由多个乘法位相加器组成。
乘法器的输入是两个二进制数,输出是一个二进制数。
4. 除法器除法器是计算机中用于实现两个数的除法运算的部件。
除法器需要实现除法的所有步骤,包括除法法则、被除数和除数的对齐、试商、加减、取商和取余等操作。
除法器的输入是一个二进制被除数和一个二进制除数,输出是一个二进制商和一个二进制余数。
5. 逻辑门电路逻辑门电路是计算机中用于实现逻辑运算的部件,包括与门、或门、非门等。
与门实现逻辑与运算,或门实现逻辑或运算,非门实现逻辑非运算。
逻辑门电路一般由晶体管、集成电路等元器件组成,可以实现各种逻辑运算。
第2章 乘法器除法器.

用移位的次数判断乘法是否结束
逻辑移位
(3) 原码一位乘的硬件配置
乘数原 码
部分乘 积原码
0
A
n
加法器
0
Q
n
右移
移位和加控制
被乘数 原码
控制门
0
X
n 计数器 C
S
GM
A、X、Q 均 n+1 位 移位和加受末位乘数控制
逐位相 乘次数
乘积的 符号
2.3.3 原码阵列乘法器
在定点计算机中,两个原码表示的数相乘的运算规则是:乘积的
部分积
0.0000 +0.1101
0.1101 0.0110 +0.1101 1.0011 0.1001 +0.0000 0.1001 0.0100 + 0.1101
1.0001 0.1000
乘数 1 0 1 1=
1 1 0 1= 1 1 1 1 0= 11 1 1 1 1=
111 1111
说明
初态,部分积 = 0 乘数为 1,加被乘数
右移一位 = 0.1{A +0.1[ 0 • A+0.1(A + 0.1A)]}
= 2-1{A +2-1[ 0 • A+2-1(A + 2-1(A+0))]}
第一步 被乘数A + 0
①
第二步 右移 一 位,得新的部分积
②
第三步 部分积 + 被乘数
③
…
第八步 右移 一 位,得结果
⑧
3. 改进后的笔算乘法过程(竖式)
¾ 被乘数只与部分积的高位相加
硬件
3 个寄存器,具有移位功能 1 个全加器
4. 原码乘法
(1) 原码一位乘运算规则 以小数为例
verilog 乘法 除法

verilog 乘法除法
在Verilog中,乘法和除法可以通过多种方式实现,下面是一些常见的方法:
- 使用移位运算符:可以将乘法转换为移位相加的方式,将除法转换为移位相减的方式。
- 使用乘法器和除法器IP核:在Verilog中,可以使用FPGA提供的乘法器和除法器IP核来实现乘法和除法运算。
- 使用算术运算符:在Verilog中,可以使用算术运算符(如`*`和`/`)直接进行乘法和除法运算。
请注意,具体的实现方式取决于设计需求和硬件资源的限制。
在实际应用中,需要根据具体情况选择合适的实现方式。
NEC乘法器除法器

用户手册 U17336CA5V0UD
455
第十七章 乘法器/除法器(仅 PD78F0514,78F0515 和 78F0515D)
在执行操作时 MDA0 的功能如下。 表 17-2. 操作执行期间 MDA0 的功能
DMUSEL0 0 1 除法模式 乘法模式 操作模式 被除数 高 16 位: 0 低 16 位: 乘数 A 设置 操作结果 除法结果 ( 商) 乘法结果 ( 乘积)
460
用户手册 U17336CA5V0UD
第十七章 乘法器/除法器(仅 PD78F0514 ,78F0515 和 78F0515D)
图 17-7. 除法操作 (DCBA2586H 0018H) 的 时序图
内部时钟
工作时钟
计数器
用户手册 U17336CA5V0UD
461
乘法器/ 除法器的框图如图 17-1 所示。
用户手册 U17336CA5V0UD
453
454
图 17-1. 乘法器/ 除法器框图 内部总线 乘法器/ 除法器控制 寄存器 0(DMUC0)
余数寄存器 0 (SDR0(SDR0 H+SDR0L)) 乘 /除数寄存器 A0(MDA0H(MDA0HH+M DA0 HL) +MDA0L(MDA 0LH+MDA0LL)) 启动 清零
DMUE
注
启动/ 停止操作 停止操作 启动操作 操作模式(乘法/ 除法)的选择 除法模式 乘法模式
注
当 DMUE =1 时,启动操作。操作结束后 DMUE 被自动清零。
注意事项 1. 如果操作期间(当 DMUE = 1)DMUE 被清零,则操作结果不确定。如果设置了中断标志,在执行清零 指令时操作完成,操作结果可以得到保证。 2. 在操作期间(当 DMUE = 1)时,不要修改 DMUSEL0 的值。如果修改了,则存放在乘/除数寄存器 A0 (MDA0)和余数寄存器 0 (SDR0) 中的操作结果不确定。 3. 如果在操作期间(当 DMUE = 1)将 DMUE 清零,则停止操作。若要再次执行操作,应对乘/ 除数寄存 器 A0 (MDA0) 、乘/除数寄存器 B0 (MDB0)和乘法器/ 除法器控制寄存器 0 (DMUC0) 进行设置,然后 启动操作(通过设置 DMUE = 1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
手工进行乘法运算
×
2 3 4 5 9 8 7 6 11 4 20 27 30
手工进行乘法运算
手工进行乘法运算
×
? ? ? ? ? ? ? ? ? 2 3 4 5 9 8 7 6 114 20 27 30 ? ? ? ? ? ? ? ? ? ? ? ? ??
较为简单的数字
× 1 0 0 0 1 0 0 1 1 0 0 0
Shift right
8-bit Adder
Multiplier
0 1 0 0
4-bit
Write
0 0 0 0 1 0 0 0
8-bit
Product
Control test
乘法器的工作过程(2)
0 0 0 1 0 0 0 0
8-bit Multiplicand
Shift left
第2轮
1 0 0 0 two × 1 0 0 1two
0 0 0
乘积 Product
十进制和二进制运算的选择
采用十进制的ENIAC 采用二进制的EDVAC
十进制和二进制运算的选择
电子管是一种“全或无”设备( allor-none ),适合表示只有两个数值 的系统,即二进制。 二进制可以大幅度地简化乘法和除法 的运算过程。尤其是对于乘法,不再 需要十进制乘法表,也不再需要两轮 的加法。 关于EDVAC的 报告草案 1945 必须要记住,十进制才是适合人使用 约翰· 冯· 诺依曼 的。因此,输入输出设备需要承担二 John Von Neumann 进制和十进制之间的转换工作。 1903~1957
简化后的运算过程
× 0 0 0 1 0 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
被乘数 Multiplicand
乘数 Multiplier
如果当前参与运算的乘数位为1, 则直接将被乘数放置在对应位置上 如果当前参与运算的乘数位为0, 则直接将“0”放置在对应位置上
0 0 0
乘积 Product
简化后的运算过程 ×
0 0 0 1 0 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
被乘数 Multiplicand
乘数 Multiplier
如果当前参与运算的乘数位为1, 则直接将被乘数放置在对应位置上
0 0 0
乘积 Product
被乘数 Multiplicand 乘数 Multiplier
0 0 0
乘积 Product
运算过程的进一步调整
× 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
被乘数 Multiplicand
乘数 Multiplier
0 0 0 1 0 0 1 0 0
运算开始时,乘积记为“0”
乘积 Product
0 0 0
运算过程的进一步调整
× 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
被乘数 Multiplicand
乘数 Multiplier
0 0 0 1 0 0 0 0 0
运算开始时,乘积记为“0”
乘积 Product
0 0 0
运算过程的进一步调整 ×
手工进行乘法运算
手工进行乘法运算
×
2 3 4 5 9 8 7 6
手工进行乘法运算
手工进行乘法运算
×
2 3 4 5 9 8 7 6 30
手工进行乘法运算
手工进行乘法运算
×
2 3 4 5 9 8 7 6 27 30
手工进行乘法运算
手工进行乘法运算
×
2 3 4 5 9 8 7 6 20 27 30
手工进行乘法运算
8-bit
Shift right
Multiplicand
Shift left
1 0 0 0 two × 1 0 0 1two
8-bit Adder
Multiplier
1 0 0 1
4-bit
Write
0 0 0 0 0 0 0 0
8-bit
Product
Control test
乘法器的工作过程(1)
Shift right
8-bit Adder
Multiplier
0 0 1 0
4-bit
Write
0 0 0 0 trol test
4th repetition?
No!
乘法器的工作过程(1)
0 0 1 0 0 0 0 0
8-bit Multiplicand
0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
被乘数 Multiplicand
乘数 Multiplier
每个中间结果产生后 直接与当前的乘积累加
0 0 0
乘积 Product
运算过程的进一步调整 ×
0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
Shift right
8-bit Adder
Multiplier
0 1 0 0
4-bit
Write
0 0 0 0 1 0 0 0
8-bit
Product
Control test
乘法器的工作过程(4)
0 0 1 0 0 0 0 0
8-bit Multiplicand
Shift left
第2轮
1 0 0 0 two × 1 0 0 1two
8-bit
Product
Control test
乘法器的工作过程(3)
0 0 0 1 0 0 0 0
8-bit
Shift right
Multiplicand
Shift left
1 0 0 0 two × 1 0 0 1two
8-bit Adder
Multiplier
1 0 0 1
4-bit
Write
乘数 Multiplier
每个中间结果产生后 直接与当前的乘积累加 每产生一个中间结果 被乘数向左移动一位
乘积 Product
运算过程的进一步调整
1 0 0 0 1 × 1 0 0 0 0 0 1 0 0 0 1 0 0 1
被乘数 Multiplicand
0 0 1 0 0 0 0 0 0 0 0 0
Product
Control test
乘法器的工作过程(2)
0 0 0 0 1 0 0 0
8-bit
Shift right
Multiplicand
Shift left
1 0 0 0 two × 1 0 0 1two
8-bit Adder
Multiplier
1 0 0 1
4-bit
Write
0 0 0 0 1 0 0 0 0
被乘数 Multiplicand
乘数 Multiplier
每个中间结果产生后 直接与当前的乘积累加 每产生一个中间结果 被乘数向左移动一位
乘积 Product
运算过程的进一步调整
1 0 0 0 1 × 1 0 0 0 0 0 1 0 0 0 0 0 0 1
被乘数 Multiplicand
0 0 1 0 0 0 0 0 0 0 0 0
乘数 Multiplier
每个中间结果产生后 直接与当前的乘积累加 每产生一个中间结果 被乘数向左移动一位
乘积 Product
运算过程的进一步调整
1 0 0 0 1 0 0 1 ×
被乘数 Multiplicand
乘数 Multiplier
适合硬件实现的运算过程!
1 0 0 1 0 0 0
乘积 Product
被乘数 Multiplicand
乘数 Multiplier
每个中间结果产生后 直接与当前的乘积累加 每产生一个中间结果 被乘数向左移动一位
0 0 0
乘积 Product
运算过程的进一步调整
1 0 0 1 × 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0
Shift right
8-bit Adder
Multiplier
0 1 0 0
4-bit
Write
0 0 0 0 1 0 0 0
8-bit
Product
Control test
乘法器的工作过程(3)
0 0 1 0 0 0 0 0
8-bit Multiplicand
Shift left
第2轮
1 0 0 0 two × 1 0 0 1two
0 1 0 0
4-bit
Write
0 0 0 0 1 0 0 0 0
8-bit
Product
Control test
4th repetition?
No!
乘法器的工作过程(1)
0 0 0 1 0 0 0 0
8-bit Multiplicand
Shift left
第2轮
1 0 0 0 two × 1 0 0 1two
Shift left
第3轮
1 0 0 0 two × 1 0 0 1two
Shift right
8-bit Adder
Multiplier
0 0 1 0
4-bit
Write
0 0 0 0 1 0 0 0
8-bit
Product
Control test
乘法器的工作过程(1)
0 1 0 0 0 0 0 0
