数值分析试验幂法与反幂法matlab
幂法和反幂法求矩阵特征值课程

index = 0
k= 1001
修改 M0=0 m= 2.6820
u=
0.8577 0.6937 0.5624 1.0000
index = 1
k=
7
总结以上,幂法如下:
U [1 1 1 1] [1 2 3 4] [3 5 6 7]
m0 0.0001 0.001
大型稀疏矩阵。反幂法是计算海森伯格阵或三角阵的对应一个给定近似特
征值的特征向量的有效方ຫໍສະໝຸດ 之一。二.算法设计及流程图
1、幂法算法
(1)取初始向量 u (0) (例如取 u (0) =(1,1,…1) T ),置精度要求 ,置 k=1.
(2)计算
v (k ) =Au (k 1) ,m =max(v (k ) ), u (k ) = v (k ) / m
index 1 0 1 1 1 1 1 0 1
k 49 1001 10 9 7 9 7 1001 7
反幂法结果显示:在 m0 为 0 时
M0=0.001 U=[1 1 1 1]
M0=0.1 u=[1 1 1 1]
M0=0 u=[1 3 5 7]
M0=0.1 u=[1 3 5 7]
M0=0.5 u=[1 3 5 7]
的第一式改为求解线性方程组
A v (k ) = u (k 1)
(3)
但由于在反幂法中,每一步迭代都需求解线性方程组(3)式,迭代做了大量的
重复计算,为了节省工作量,可事先把矩阵 A 作 LU 分解,即 A=LU
所以线性方程组(3)改为
Ly (k ) =u (k 1) ,Uv (k ) =y (k)
四、算法程序设计代码
数值分析幂法和反幂法

数值分析幂法和反幂法数值分析中的幂法和反幂法是求解矩阵最大特征值和最小特征值的常用方法。
这两种方法在许多数值计算问题中都有着广泛的应用,包括图像压缩、数据降维、谱聚类等。
幂法(Power Method)是一种迭代算法,通过不断迭代矩阵与一个向量的乘积,来逼近原矩阵的最大特征值和对应的特征向量。
其基本思想是,对于一个矩阵A和一维向量x,可以通过不断迭代计算Ax,Ax,Ax...,来使得向量x逼近最大特征值对应的特征向量。
具体的迭代过程如下:1.初始化一个向量x0(可以是单位向量或任意非零向量)2.令x1=Ax0,对向量进行归一化(即除以向量的范数)得到x13.重复步骤2,即令x2=Ax1,x3=Ax2...,直到收敛(即相邻迭代向量的差的范数小于一些阈值)为止4. 最终得到的向量xn就是A的最大特征值对应的特征向量在实际求解时,我们可以将迭代过程中的向量进行归一化,以防止数值溢出或下溢。
此外,为了提高迭代速度,我们可以选择使得xn与xn-1的内积大于0的方向作为迭代方向,这样可以使得特征值的模快速收敛到最大特征值。
幂法的收敛性是保证的,但收敛速度可能较慢,尤其是当最大特征值与其他特征值非常接近时。
此时可能需要使用一些改进的方法来加速收敛,例如Rayleigh商或位移策略。
相反,反幂法(Inverse Power Method)是求解矩阵的最小特征值和对应的特征向量的方法。
它的基本思想和幂法类似,但在每次迭代中,需要计算A和依其逆矩阵A-1的乘积。
迭代过程如下:1.初始化一个向量x0(可以是单位向量或任意非零向量)2.令x1=A-1x0,对向量进行归一化(即除以向量的范数)得到x13.重复步骤2,即令x2=A-1x1,x3=A-1x2...4. 最终得到的向量xn就是A的最小特征值对应的特征向量反幂法和幂法的区别在于迭代过程中乘以了A的逆矩阵,从而可以利用矩阵的特殊结构或性质来提高迭代速度。
同时,在实际求解时,可能需要将矩阵进行一些变换,以确保A-1存在或数值稳定性。
数值分析-MATLAB相关算法

数值分析-MATLAB算法刘亚1、四阶龙格库塔法:function yout=xin(bianliang)%定义输入输出clear allx0=0;xn=1;y0=1;h=0.1;%设置初始值、区间和步长[y,x]=lgkt4j(x0,xn,y0,h);%四阶龙格库塔法n=length(x);fprintf(' i x(i) y(i)\n');%输出格式for i=1:nfprintf('%2d %3.3f %4.4f\n',i,x(i),y(i)); endfunction [y,x]=lgkt4j(x0,xn,y0,h)x=x0:h:xn;%设置区间n=length(x);y1=x;y1(1)=y0;for i=1:nK1=f(x(i),y1(i));K2=f(x(i)+h/2,y1(i)+h/2*K1);K3=f(x(i)+h/2,y1(i)+h/2*K2);K4=f(x(i)+h,y1(i)+h*K3);y1(i+1)=y1(i)+h/6*(K1+2*K2+2*K3+K4);endy=y1;function Dy=f(x,y)Dy=y-2*x/y;C语言程序#include<math.h>main(){float x=0,y0=1,h=0.2,y1,k1,k2,k3,k4;k1=y0-2*x/y0;k2=y0+h/2*k1-(2*x+h)/(y0+h/2*k1);k3=y0+h/2*k2-(2*x+h)/(y0+h/2*k2);k4=y0+h*k3-(2*x+2*h)/(y0+h*k3);y1=y0+h/6*(k1+2*k2+2*k3+k4);do{printf("%5.4f\n",y1);x=x+h;y0=y1;k1=y0-2*x/y0;k2=y0+h/2*k1-(2*x+h)/(y0+h/2*k1);k3=y0+h/2*k2-(2*x+h)/(y0+h/2*k2);k4=y0+h*k3-(2*x+2*h)/(y0+h*k3);y1=y0+h/6*(k1+2*k2+2*k3+k4);}while(x<1);}2、幂法求特征值function [m x biaozhi]=mifa(A,jingdu,cishu)%幂法求矩阵最大特征值,其中%m为绝对值最大的特征值,x为对应最大特征值的特征向量%biaozhi表明迭代是否成功if nargin<3cishu=100;endif nargin<2jingdu=1e-5;endn=length(A);x=ones(n,1);biaozhi='迭代失败!';k=0;m1=0;while k<=cishuv=A*x;[vmax,k]=max(abs(v));m=v(k);x=v/m;if abs(m-m1)<jingdubiaozhi='迭代成功!';break;endm1=m;k=k+1;end3、拉格朗日插值function [c,l]=lglr(x,y)%x为n个节点的横坐标组成的向量,y为纵坐标组成的向量%c为插值函数的系数组成的向量%输出为差值多项式的系数w=length(x);n=w-1;l=zeros(w,w);for k=1:n+1v=1;for j=1:n+1if k~=jv=conv(v,poly(x(j)))/(x(k)-x(j));endendl(k,:)=v;endc=y*l;举例4、改进欧拉法function yout=gaijinoula(f,x0,y0,xn,n)%定义输入输出x=zeros(1,n+1);y=zeros(1,n+1);x(1)=x0;y(1)=y0;h=(xn-x0)/n;for i=1:nx(i+1)=x(i)+h;z0=y(i)+h*feval(f,x(i),y(i));y(i+1)=y(i)+(feval(f,x(i),y(i))+feval(f,x(i+1),z0))*h/2; endshuchu=[x',y']fprintf(' x(i) y(i)')function Dy=f(x,y)Dy=x+y;5、最小二乘M文件:function c=zxrc(x,y,m)%x 是数据点横坐标,y 数据点纵坐标%m 要构造的多项式的系数,c 是多项式由高到低的系数所组成的向量 n=length(x);b=zeros(1:m+1);f=zeros(n,m+1);for k=1:m+1f(:,k)=x'.^(k-1);enda=f'*f;b=f'*y';c=a\b;c=flipud(c);-2-1.5-1-0.500.51 1.52---6、矩阵相关的算法(1).求矩阵的行列式function d=hanglieshi(a)%求任意输入矩阵的行列式clear all;a=input('输入矩阵a=');d=1;n=size(a); %方阵的行(或者列)数for k=1:n-1e=a(k,k); %设矩阵的主元for i=k:n %求出矩阵的全主元for j=k:nif abs(a(i,j))>ee=a(i,j);p=i;q=j;else c=0;endendendfor j=k:n %行交换t=a(k,j);a(k,j)=a(p,j);a(p,j)=t;endif p~=k %判断行列式是否换号d=d*(-1);else d=d;endfor i=k:n %列交换t=a(i,k);a(i,k)=a(i,q);a(i,q)=t;endif q~=k %判断行列式是否换号d=d*(-1);else d=d;endif a(k,k)~=0for i=k+1:n %消元r=a(i,k)/a(k,k);for j=k+1:na(i,j)=a(i,j)-r*a(k,j);endendelse d=d;endendfor i=1:n%求行列式d=d*a(i,i);enddisp('矩阵a的行列式为:')d(2)矩阵的换行function c=huanhang(a)%实现矩阵换行clear all;a=input('输入矩阵a=');[m,n]=size(a);for j=1:nt=a(1,j);a(1,j)=a(2,j);a(2,j)=t;endc=a;disp('换行后矩阵a变为:')c(3)列主元消元法解方程function d=jiefang(a)%列主元消元法解方程clear all;a=input('输入矩阵a=');[row,column]=size(a);for i=1:column%每一列的列标m(i)=i;s(i)=0;x(i)=0;endfor k=1:row-1%最后一行不用比较e=a(k,k);p=k;q=k;for i=k:rowfor j=k:column-1if abs(a(i,j))>abs(e)e=a(i,j);p=i;q=j;else c=0;endendendt=m(k); %换列标记m(k)=m(q);m(q)=t;for i=1:row %列交换t=a(i,k);a(i,k)=a(i,q);a(i,q)=t;endfor j=k:column %行变换t=a(k,j);a(k,j)=a(p,j);a(p,j)=t;endif a(k,k)==0 %消元disp('非唯一解')else for i=k+1:rowr=a(i,k)/a(k,k);for j=k:columna(i,j)=a(i,j)-r*a(k,j);endendendendif a(row,row)==0disp('非唯一解')elses(row)=a(row,column)/a(row,row);s(row)q=m(row);x(q)=s(row);for i=row-1:1for j=i+1:rows(i)=s(i)+a(i,j)*x(i);ends(i)=[a(i,column)-s(i)]/a(i,i);q=m(i);x(q)=s(i);endendfor i=1:rowx(i)endend(4)两矩阵相乘function d=chengfa(A,B)% 实现两个矩阵相乘clear all;A=input('输入矩阵A=');B=input('输入矩阵B=')[m n]=size(A);[nb p]=size(B);C=zeros(m,p);if n~=nbdisp('不满足矩阵相乘条件') else for i=1:mfor j=1:pd=0;for k=1:nd=d+A(i,k)*B(k,j);endC(i,j)=d;endenddisp('矩阵AB结果为:')CEnd(5)矩阵元素最大值及下标function d=xunzhuyuan(a)%求一个矩阵的最大元素及其下标clear all;a=input('输入矩阵a=');e=a(1,1); %设e=a(1,1)为最大元素p=1;q=1;[m,n]=size(a);for i=1:mfor j=1:nif abs(a(i,j))>ee=a(i,j);p=i;q=j;else c=0;endendenddisp('最大元素为:')d=a(p,q)disp('最大元素所在的行为:')pdisp('最大元素所在的列为:')qend(6)矩阵元素最大值及下标function d=zuidazhi(A)%求矩阵的最大元素及其下标clear all;A=input('输入矩阵A=');B=A'; %转置[a,r]=max(A); %求出矩阵A每一列的最大值和每列最大值所在的行数[maxV,column]=max(a); %最大元素及其所在的列[b,c]=max(B);[maxV1,row]=max(b);%最大元素及其所在的行disp('矩阵A的最大元素为:')maxVdisp('矩阵A最大元素所在的列为:')columndisp('矩阵A最大元素所在的行为:')row。
数值分析试验幂法与反幂法matlab

一、问题的描述及算法设计(一)问题的描述我所要做的课题是:对称矩阵的条件数的求解设计1、求矩阵A 的二条件数问题 A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----210121012 2、设计内容:1)采用幂法求出A 的 错误!未找到引用源。
.2)采用反幂法求出A 的错误!未找到引用源。
.3)计算A 的条件数 ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=错误!未找到引用源。
/错误!未找到引用源。
.(精度要求为10-6)3、设计要求1)求出ⅡA Ⅱ2。
2)并进行一定的理论分析。
(二)算法设计1、幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1.(2)计算v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k(3)若| m k = m 1-k |<ε,则停止计算(m k 作为绝对值最大特征值1λ,u )(k 作为相应的特征向量)否则置k=k+1,转(2)2、反幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1.(2)对A 作LU 分解,即A=LU(3)解线性方程组 Ly )(k =u )1(-k ,Uv )(k =y )(k(4)计算m k =max(v )(k ), u )(k = v )(k / m k(5)若|m k =m 1-k |<ε,则停止计算(1/m k 作为绝对值最小特征值n λ,u )(k 作为相应的特征向量);否则置k=k+1,转(3).二、算法的流程图(一)幂法算法的流程图为 v )(k = A 1-u )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k (2)2、对于反幂法的定理按式(2)计算出的m k 和u )(k 满足:∞>-k lim m k =nλ1, ∞>-k lim u )(k =)max (n n x x 在式(2)中,需要用到A 1-,这给计算带来很大的不方便,因此,把(2)式的第一式改为求解线性方程组A v )(k = u )1(-k (3) 但由于在反幂法中,每一步迭代都需求解线性方程组(3)式,迭代做了大量的重复计算,为了节省工作量,可事先把矩阵A 作LU 分解,即 A=LU所以线性方程组(3)改为Ly )(k =u )1(-k ,Uv )(k =y )(k 四、相关的数值结果(一)幂法程序的运行结果m = 3.4142 u = -0.7071 index = 11.0000-0.7071(二)反幂法程序的运行结果m 0 = 0.5858 u = 0.7071 index = 11.00000.7071(三)矩阵A 的二条件数的结果ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=m/ m 0=3.4142/0.5858=5.828269五、数值计算结果的分析求n阶方阵A的特征值和特征向量,是实际计算中常常碰到的问题。
数值分析之幂法及反幂法C语言程序实例

数值分析之幂法及反幂法C 语言程序实例1、算法设计方案:①求1λ、501λ和s λ的值:s λ:s λ表示矩阵的按模最小特征值,为求得s λ直接对待求矩阵A 应用反幂法即可。
1λ、501λ:已知矩阵A 的特征值满足关系 1n λλ<<,要求1λ、及501λ时,可按如下方法求解: a . 对矩阵A 用幂法,求得按模最大的特征值1m λ。
b . 按平移量1m λ对矩阵A 进行原点平移得矩阵1m BA I λ=+,对矩阵B 用反幂法求得B 的按模最小特征值2m λ。
c . 321m m m λλλ=-则:113min(,)m m λλλ=,13max(,)n m m λλλ=即为所求。
②求和A 的与数5011140k k λλμλ-=+最接近的特征值ik λ(k=0,1,…39):求矩阵A 的特征值中与k μ最接近的特征值的大小,采用原点平移的方法:先求矩阵 B=A-k μI 对应的按模最小特征值k β,则k β+k μ即为矩阵A 与k μ最接近的特征值。
重复以上过程39次即可求得ik λ(k=0,1,…39)的值。
③求A 的(谱范数)条件数2cond()A 和行列式det A :在(1)中用反幂法求矩阵A 的按模最小特征值时,要用到Doolittle 分解方法,在Doolittle 分解完成后得到的两个矩阵分别为L 和U ,则A 的行列式可由U 阵求出,即:det(A)=det(U)。
求得det(A)不为0,因此A 为非奇异的实对称矩阵,则: max 2()scond A λλ=,max λ和s λ分别为模最大特征值与模最小特征值。
2、程序源代码:#include<stdio.h>#include<stdio.h>#include<math.h>#define N 501 //列#define M 5 //行#define R 2 //下带宽#define S 2 //上带宽#define K 39#define e 1.0e-12 //误差限float A[M][N]; //初始矩阵float u[N]; //初始向量float y[N],yy[N];float maximum,value1,value2,value_1,value_N,value_s,value_abs_max;const float b=0.16f,c=-0.064f;int max_sign,max_position;void Init_matrix_A() //初始化矩阵A{int i;for(i=2;i<N;i++){A[0][i]= c;}for(i=1;i<N;i++){A[1][i]= b;}for(i=0;i<N;i++){A[2][i]= (1.64-0.024*(i+1))*sin(0.2*(i+1))-0.64*exp(0.1/(i+1));}for(i=0;i<N-1;i++){A[3][i]= b;}for(i=0;i<N-2;i++){A[4][i]= c;}}void Init_u() //初始化迭代向量{int i;for(i=0;i<N;i++)u[i]=1.0;}void Get_max() //获得绝对值最大的数值的模{int i;max_position=0;maximum=fabs(u[0]);for(i=1;i<N;i++){if(maximum<fabs(u[i])){max_position=i;maximum=fabs(u[i]);}}if(u[max_position]<0)max_sign=-1;else max_sign=1;}void Get_y() //单位化迭代向量{int i;for(i=0;i<N;i++)y[i]=u[i]/maximum;}void Get_u() //获得新迭代向量{int i;u[0]=A[2][0]*y[0]+A[1][1]*y[1]+A[0][2]*y[2];u[1]=A[3][0]*y[0]+A[2][1]*y[1]+A[1][2]*y[2]+A[0][3]*y[3];u[N-2]=A[4][N-4]*y[N-4]+A[3][N-3]*y[N-3]+A[2][N-2]*y[N-2]+A[1][N-1]*y[N-1];u[N-1]=A[4][N-3]*y[N-3]+A[3][N-2]*y[N-2]+A[2][N-1]*y[N-1];for(i=2;i<N-2;i++)u[i]=A[4][i-2]*y[i-2]+A[3][i-1]*y[i-1]+A[2][i]*y[i]+A[1][i+1]*y[i+1]+A[0][i+2]*y[i+2]; }void Get_value() //获得迭代后特征值{value2=value1;value1=max_sign*u[max_position];}void Check_value() //幂法第二迭代格迭代{Init_u();Get_max();Get_y();Get_u();Get_value();while(1){Get_max();Get_y();Get_u();Get_value();if(fabs((value2-value1)/value1)<e)break;}}void The_value() //获取绝对值最大的特征值λ_501 {Check_value();value_abs_max=value1;}void The_Other_value() //获取特征值λ_1{int i;float value_temp=value1;for(i=0;i<N;i++){A[2][i]-=value_temp;}Check_value();value1+=value_temp;if(value1<value_temp){value_1=value1;value_N=value_temp;}else{value_N=value1;value_1=value_temp;}}int min(int a,int b) //两值中取最小{if(a<b)return a;elsereturn b;}int max(int a,int b) //两值中取最大{if(a<b)return b;elsereturn a;}void Resolve_LU(){int k,i,j,t;float temp;for(k=1;k<=N;k++){for(j=k;j<=min(k+S,N);j++){temp=0;for(t=max(max(1,k-R),j-S);t<=k-1;t++)temp+=A[k-t+S][t-1]*A[t-j+S][j-1];A[k-j+S][j-1]=A[k-j+S][j-1]-temp;}for(i=k+1;i<=min(k+R,N);i++){temp=0;for(t=max(max(1,i-R),k-S);t<=k-1;t++)temp+=A[i-t+S][t-1]*A[t-k+S][k-1];A[i-k+S][k-1]=(A[i-k+S][k-1]-temp)/A[S][k-1];}}}void Back_substitution()//方程组回代过程{int i,t;float temp=0;for(i=2;i<N+1;i++){for(t=max(1,i-R);t<i;t++)y[i-1]-=A[i-t+S][t-1]*y[t-1];}u[N-1]=y[N-1]/A[S][N-1];for(i=N-1;i>0;i--){temp=0;for(t=i+1;t<=min(i+S,N);t++)temp+=A[i-t+S][t-1]*u[t-1];u[i-1]=(y[i-1]-temp)/A[S][i-1];}}double Det_matrix() //求矩阵行列式值{int i;double det=1;Init_matrix_A();Resolve_LU();for(i=0;i<N;i++)det=det*A[2][i];return det;}float Get_norm() //获得迭代向量模{int i;float normal=0;for(i=0;i<N;i++)normal+=u[i]*u[i];normal=sqrt(normal);return normal;}void Get_yy(float normal) //迭代向量单位化{int i;for(i=0;i<N;i++){y[i]=u[i]/normal;yy[i]=y[i];}}void Get_value_s() //获得绝对值最小的特征值{int i;value2=value1;value1=0;for(i=0;i<N;i++)value1+=yy[i]*u[i];value1=1/value1;}void Value_min() //反幂法求绝对值最小的特征值{float norm=0;int count=0;value1=0,value2=0;Init_u();norm=Get_norm();Get_yy(norm);Back_substitution();Get_value_s();while(count<10000){count++;norm=Get_norm();Get_yy(norm);Back_substitution();Get_value_s();if(fabs((value2-value1)/value1)<e)break;}value_s=value1;}float Get_cond_A() //求矩阵条件数{float cond1;cond1=fabs(value_abs_max/value_s);return cond1;}void Value_translation_min() //偏移条件下反幂法求特征值{int i,k;float tr;for(k=1;k<K+1;k++){tr=value_1+k*(value_N-value_1)/40;Init_matrix_A();for(i=0;i<N;i++)A[2][i]-=tr;Resolve_LU();Value_min();value_s+=tr;printf("k=%d =>>>λi%d=%.13e\n",k,k,value_s);}}void main(){float cond;double value_det;printf("Contactme:****************\n");Init_matrix_A(); //初始化矩阵AThe_value(); //获取绝对值最大的特征值λ_501 The_Other_value(); //获取特征值λ_1printf("λ1=%.13e\n",value_1);printf("λ501=%.13e\n",value_N);value_det=Det_matrix(); //求矩阵行列式值Value_min(); //反幂法求绝对值最小的特征值printf("λs=%.13e\n",value_s);cond=Get_cond_A(); //求矩阵条件数Value_translation_min();//偏移条件下反幂法求特征值printf("cond_A=%.13e\n",cond);printf("value_det=%.13e\n",value_det);}3、程序运行结果:4、迭代初始向量的选取对计算结果的影响:本次计算实习求矩阵A的具有某些特征的特征值,主要用到的方法是幂法和反幂法,这两种方法从原理上看都是迭代法,因此迭代初始向量的选择对计算结果会产生一定影响,主要表现在收敛速度上。
北航数值分析大作业第一题幂法与反幂法

《数值分析》计算实习题目第一题:1. 算法设计方案(1)1λ,501λ和s λ的值。
1)首先通过幂法求出按模最大的特征值λt1,然后根据λt1进行原点平移求出另一特征值λt2,比较两值大小,数值小的为所求最小特征值λ1,数值大的为是所求最大特征值λ501。
2)使用反幂法求λs ,其中需要解线性方程组。
因为A 为带状线性方程组,此处采用LU 分解法解带状方程组。
(2)与140k λλμλ-5011=+k 最接近的特征值λik 。
通过带有原点平移的反幂法求出与数k μ最接近的特征值 λik 。
(3)2cond(A)和det A 。
1)1=nλλ2cond(A),其中1λ和n λ分别是按模最大和最小特征值。
2)利用步骤(1)中分解矩阵A 得出的LU 矩阵,L 为单位下三角阵,U 为上三角阵,其中U 矩阵的主对角线元素之积即为det A 。
由于A 的元素零元素较多,为节省储存量,将A 的元素存为6×501的数组中,程序中采用get_an_element()函数来从小数组中取出A 中的元素。
2.全部源程序#include <stdio.h>#include <math.h>void init_a();//初始化Adouble get_an_element(int,int);//取A 中的元素函数double powermethod(double);//原点平移的幂法double inversepowermethod(double);//原点平移的反幂法int presolve(double);//三角LU 分解int solve(double [],double []);//解方程组int max(int,int);int min(int,int);double (*u)[502]=new double[502][502];//上三角U 数组double (*l)[502]=new double[502][502];//单位下三角L 数组double a[6][502];//矩阵Aint main(){int i,k;double lambdat1,lambdat2,lambda1,lambda501,lambdas,mu[40],det;init_a();//初始化Alambdat1=powermethod(0);lambdat2=powermethod(lambdat1);lambda1=lambdat1<lambdat2?lambdat1:lambdat2;lambda501=lambdat1>lambdat2?lambdat1:lambdat2;presolve(0);lambdas=inversepowermethod(0);det=1;for(i=1;i<=501;i++)det=det*u[i][i];for (k=1;k<=39;k++){mu[k]=lambda1+k*(lambda501-lambda1)/40;presolve(mu[k]);lambda[k]=inversepowermethod(mu[k]);}printf("------------所有特征值如下------------\n");printf("λ=%1.11e λ=%1.11e\n",lambda1,lambda501);printf("λs=%1.11e\n",lambdas);printf("cond(A)=%1.11e\n",fabs(lambdat1/lambdas));printf("detA=%1.11e \n",det);for (k=1;k<=39;k++){printf("λi%d=%1.11e ",k,lambda[k]);if(k % 3==0) printf("\n");} delete []u;delete []l;//释放堆内存return 0;}void init_a()//初始化A{int i;for (i=3;i<=501;i++) a[1][i]=a[5][502-i]=-0.064;for (i=2;i<=501;i++) a[2][i]=a[4][502-i]=0.16;for (i=1;i<=501;i++) a[3][i]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i); }double get_an_element(int i,int j)//从A中节省存储量的提取元素方法{if (fabs(i-j)<=2) return a[i-j+3][j];else return 0;}double powermethod(double offset)//幂法{int i,x1;double beta=0,prebeta=-1000,yita=0;for (i=1;i<=501;i++)u[i]=1,y[i]=0;//设置初始向量u[]for (int k=1;k<=10000;k++){yita=0;for (i=1;i<=501;i++) yita=sqrt(yita*yita+u[i]*u[i]);for (i=1;i<=501;i++) y[i]=u[i]/yita;for (x1=1;x1<=501;x1++){u[x1]=0;for (int x2=1;x2<=501;x2++)u[x1]=u[x1]+((x1==x2)?(get_an_element(x1,x2)-offset):get_an_element(x1,x2))*y[x2];} prebeta=beta;beta=0;for (i=1;i<=501;i++) beta=beta+ y[i]*u[i];if (fabs((prebeta-beta)/beta)<=1e-12) {printf("offset=%f lambda=%f err=%e k=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};//输出中间过程,包括偏移量,误差,迭代次数}return (beta+offset);}double inversepowermethod(double offset)//反幂法{int i;double u[502],y[502];double beta=0,prebeta=0,yita=0;for (i=1;i<=501;i++)u[i]=1,y[i]=0; //设置初始向量u[]for (int k=1;k<=10000;k++){yita=0;for (i=1;i<=501;i++) yita=sqrt(yita*yita+u[i]*u[i]);for (i=1;i<=501;i++) y[i]=u[i]/yita;solve(u,y);prebeta=beta;beta=0;for (i=1;i<=501;i++) beta=beta+ y[i]*u[i];beta=1/beta;if (fabs((prebeta-beta)/beta)<=1e-12) {printf("offset=%f lambda=%f err=%e k=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};//输出中间过程,包括偏移量,误差,迭代次数}return (beta+offset);}int presolve(double offset)//三角LU分解{int i,k,j,t;double sum;for (k=1;k<=501;k++)for (j=1;j<=501;j++){u[k][j]=l[k][j]=0;if (k==j) l[k][j]=1;} //初始化LU矩阵for (k=1;k<=501;k++){for (j=k;j<=min(k+2,501);j++){sum=0;for (t=max(1,max(k-2,j-2)) ; t<=(k-1) ; t++)sum=sum+l[k][t]*u[t][j];u[k][j]=((k==j)?(get_an_element(k,j)-offset):get_an_element(k,j))-sum;}if (k==501) continue;for (i=k+1;i<=min(k+2,501);i++){sum=0;for (t=max(1,max(i-2,k-2));t<=(k-1);t++)sum=sum+l[i][t]*u[t][k];l[i][k]=(((i==k)?(get_an_element(i,k)-offset):get_an_element(i,k))-sum)/u[k][k];}}return 0;}int solve(double x[],double b[])//解方程组{int i,t;double y[502];double sum;y[1]=b[1];for (i=2;i<=501;i++){sum=0;for (t=max(1,i-2);t<=i-1;t++)sum=sum+l[i][t]*y[t];y[i]=b[i]-sum;}x[501]=y[501]/u[501][501];for (i=500;i>=1;i--){sum=0;for (t=i+1;t<=min(i+2,501);t++)sum=sum+u[i][t]*x[t];x[i]=(y[i]-sum)/u[i][i];}return 0;}int max(int x,int y){return (x>y?x:y);}int min(int x,int y){return (x<y?x:y);}3.计算结果结果如下图所示:部分中间结果:给出了偏移量(offset),误差(err),迭代次数(k)4.讨论迭代初始向量的选取对计算结果的影响,并说明原因使用u[i]=1(i=1,2,...,501)作为初始向量进行迭代,可得出以上结果。
数值分析 -第7讲_幂法和反幂法

则存在酉矩阵U使 定理9( Schur定理) 设A ∈ R n×n, r11 r12 L r1n r22 L r2n ∆ = R, U T AU = O rnn 其中rii (i = 1,2,L, n)为A的特征值.
定理10(实Schur分解) 设A ∈ R n×n, 则存在正交矩阵Q使 R11 R12 L R1m R22 L R2m , QT AQ = O Rmm 其中当Rii (i = 1,2,L, m)为一阶时Rii是A的实特征值,当Rii为 二阶时Rii的两个特征值是A的两个共轭复特征值.
xn xn
α1 x1 α1 x1
数值分析
不同范数选取下的特征值的计算
1. 取范数为2-范数时 取范数为2
T T yk −1uk = yk −1 Ayk −1 ⇒
α1 x1T α1 x1 A = λ1 α1 x1 2 α1 x1 2
对应的迭代公式
∀ u0 ∈ R n T η k −1 = uk −1uk −1 yk −1 = uk −1 η k −1 uk = Ayk −1 T β k = yk −1uk ( k = 1, 2,...)
数值分析
实际使用的迭代公式为: 实际使用的迭代公式为:
uk −1 yk −1 = u k −1 u = Ay k −1 k
于是可得
Auk −1 A2uk −2 A k u0 uk = = = L = k −1 uk −1 Auk −2 A u0
uk Ak u0 yk = = k uk A u0
数值分析
定义3 定义3 设A = (aij ) n×n , 令 n ( )i = ∑ | aij | (2) Di = {z | | z − aii |≤ ri , z ∈ C }, (i = 1,L, n) 1 r , j≠i 称Di为复平面上以aii为圆心以ri为半径的Gerschgorin圆盘.
matlab 幂次方

MATLAB 幂次方引言幂次方是数学中常见的运算方式之一,它表示一个数的指数次方。
在MATLAB中,我们可以使用内置函数或运算符来进行幂次方的计算。
本文将详细介绍MATLAB中幂次方的使用方法和相关注意事项。
幂次方的基本概念幂次方是指一个数的指数次方,即将一个数自乘多次。
例如,2的3次方可以表示为2^3,结果为8。
幂次方运算可以应用于整数、小数和复数等不同类型的数值。
MATLAB中的幂次方运算符在MATLAB中,我们可以使用运算符“^”来进行幂次方运算。
例如,计算2的3次方可以使用以下代码:result = 2^3;disp(result);运行结果为:8MATLAB中的幂次方函数除了使用幂次方运算符外,MATLAB还提供了内置函数来进行幂次方计算。
其中最常用的函数是power和^。
这两个函数的使用方法相同,都可以用于计算幂次方。
例如,计算2的3次方可以使用以下代码:result = power(2, 3);disp(result);运行结果为:8幂次方的应用幂次方在数学和工程领域中有着广泛的应用。
下面介绍几个常见的应用场景:1. 概率计算在概率统计中,幂次方可以用于计算事件发生的概率。
例如,假设一个硬币正面朝上的概率为0.5,那么连续抛掷10次硬币正面朝上的概率可以通过计算0.5的10次方来得到。
2. 信号处理在信号处理中,幂次方可以用于对信号进行幅度调整或增强。
例如,可以将音频信号的幂次方提高来增加音量。
3. 图像处理在图像处理中,幂次方可以用于对图像进行灰度变换。
通过将图像的像素值进行幂次方运算,可以改变图像的对比度和亮度。
4. 控制系统在控制系统中,幂次方可以用于模拟非线性系统。
通过引入幂次方运算,可以增加系统的非线性特性,提高系统的控制性能。
幂次方的注意事项在使用幂次方运算时,需要注意以下几点:1. 整数幂次方和小数幂次方在MATLAB中,整数幂次方和小数幂次方的计算方式是不同的。
对于整数幂次方,可以直接使用运算符“^”进行计算;对于小数幂次方,应使用幂次方函数power 进行计算。
幂法和反幂法的matlab实现

幂法和反幂法的matlab实现幂法求矩阵主特征值及对应特征向量摘要矩阵特征值的数值算法,在科学和工程技术中很多问题在数学上都归结为矩阵的特征值问题,所以说研究利用数学软件解决求特征值的问题是非常必要的。
实际问题中,有时需要的并不是所有的特征根,而是最大最小的实特征根。
称模最大的特征根为主特征值。
幂法是一种计算矩阵主特征值(矩阵按模最大的特征值)及对应特征向量的迭代方法,它最大的优点是方法简单,特别适用于大型稀疏矩阵,但有时收敛速度很慢。
用java来编写算法。
这个程序主要分成了四个大部分:第一部分为将矩阵转化为线性方程组;第二部分为求特征向量的极大值;第三部分为求幂法函数块;第四部分为页面设计及事件处理。
其基本流程为幂法函数块通过调用将矩阵转化为线性方程组的方法,再经过一系列的验证和迭代得到结果。
关键字:主特征值;特征向量;线性方程组;幂法函数块POWER METHOD FOR FINDING THE EIGENVALUES AND CORRESPONDING EIGENVECTORS OF THEMATRIXABSTRACTNumerical algorithm for the eigenvalue of matrix, in science and engineering technology, alot of problems in mathematics are attributed matrix characteristic value problem, so that studies using mathematical software to solve the eigenvalue problem is very necessary. In practical problems, sometimes need not all eigenvalues, but the maximum and minimum eigenvalue of real. The characteristic value of the largest eigenvalue of the modulus maximum.Power method is a calculation of main features of the matrix values (matrix according to the characteristics of the largest value) and the corresponding eigenvector of iterative method. It is the biggest advantage is simple method, especially for large sparse matrix, but sometimes the convergence speed is very slow.Using java to write algorithms. This program is divided into three parts: the first part is the matrix is transformed into linear equations; the second part for the sake of feature vector of the maximum; the third part isthe exponentiation function block. The fourth part is the page design and eventprocessing .The basic process is a power law function block by calling the matrix is transformed into linear equations method, after a series of validation and iteration results.Power method for finding the eigenvalues and corresponding eigenvectors of the matrixKey words: Main eigenvalue; characteristic vector; linear equations; power function block、目录1幂法......................................................... . (1)1.1幂法的基本理论和推导 (1)1.2幂法算法的迭代向量规范化 (2)2概要设计........................................................ (3)2.1设计背景 (3)2.2运行流程........................................... . (3)2.3运行环境........................................... (3)3程序详细设计 (4)3.1矩阵转化为线性方程组……..………………………………………. .43.2特征向量的极大值 (4)3.3求幂法函数块............….....…………...…......…………………………3.4界面设计与事件处理..........................................................................4运行过程及结果................................................ (6)4.1 运行过程....................................... ..................………………………………………. .64.2 运行结果................................................ .. (6)4.3 结果分析.......................................... (6)5结论 (7)参考文献 (8)附录 (56)1 幂法设实矩阵nn ij a A ⨯=)(有一个完备的特征向量组,其特征值为nλλλ ,,21,相应的特征向量为nx x x ,,21。
幂法及其MATLAB程序

5.2 幂法及其MATLAB 程序5.2.2 幂法的MATLAB 程序用幂法计算矩阵A 的主特征值和对应的特征向量的MATLAB 主程序function [k,lambda,Vk,Wc]=mifa(A,V0,jd,max1)lambda=0;k=1;Wc =1; ,jd=jd*0.1;state=1; V=V0;while ((k<=max1)&(state==1))Vk=A*V; [m j]=max(abs(Vk)); mk=m;tzw=abs(lambda-mk); Vk=(1/mk)*Vk;Txw=norm(V-Vk); Wc=max(Txw,tzw); V=Vk;lambda=mk;state=0;if (Wc>jd)state=1;endk=k+1;Wc=Wc;endif (Wc<=jd)disp('请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:')elsedisp('请注意:迭代次数k 已经达到最大迭代次数max1,主特征值的迭代值lambda,主特征向量的迭代向量Vk,相邻两次迭代的误差Wc 如下:') endVk=V;k=k-1;Wc;例 5.2.2 用幂法计算下列矩阵的主特征值和对应的特征向量的近似向量,精度510-=ε.并把(1)和(2)输出的结果与例5.1.1中的结果进行比较.(1)⎪⎪⎭⎫ ⎝⎛-=4211A ; (2)⎪⎪⎪⎭⎫ ⎝⎛=633312321B ;(3)⎪⎪⎪⎭⎫ ⎝⎛--=1124111221C ;(4)⎪⎪⎪⎭⎫ ⎝⎛---=20101350144D . 解 (1)输入MATLAB 程序>>A=[1 -1;2 4]; V0=[1,1]';[k,lambda,Vk,Wc]=mifa(A,V0,0.00001,100),[V,D] = eig (A), Dzd=max(diag(D)), wuD= abs(Dzd- lambda), wuV=V(:,2)./Vk,运行后屏幕显示结果请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc =33 3.00000173836804 8.691862856124999e-007Vk = V = wuV =-0.49999942054432 -0.70710678118655 0.44721359549996 -0.894428227562941.00000000000000 0.70710678118655 -0.89442719099992 -0.89442719099992Dzd = wuD =3 1.738368038406435e-006由输出结果可看出,迭代33次,相邻两次迭代的误差W c ≈8.69 19e-007,矩阵A 的主特征值的近似值lambda ≈3.000 00和对应的特征向量的近似向量V k ≈(-0.500 00,1.00000T ), lambda 与例5.1.1中A 的最大特征值32=λ近似相等,绝对误差约为1.738 37e-006,V k 与特征向量X =T22k T )1,21(- )0(2≠k 的第1个分量的绝对误差约等于0,第2个分量的绝对值相同.由wuV 可以看出,2λ的特征向量V (:,2) 与V k 的对应分量的比值近似相等.因此,用程序mifa.m 计算的结果达到预先给定的精度510-=ε.(2) 输入MATLAB 程序>>B=[1 2 3;2 1 3;3 3 6]; V0=[1,1,1]';[k,lambda,Vk,Wc]=mifa(B,V0,0.00001,100), [V,D] = eig (B), Dzd=max(diag(D)), wuD= abs(Dzd- lambda), wuV=V(:,3)./Vk,运行后屏幕显示结果请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc = Dzd = wuD =3 9 0 9 0Vk = wuV =0.50000000000000 0.816496580927730.50000000000000 0.816496580927731.00000000000000 0.81649658092773V =0.70710678118655 0.57735026918963 0.40824829046386-0.70710678118655 0.57735026918963 0.408248290463860 -0.57735026918963 0.81649658092773(3) 输入MATLAB 程序>> C=[1 2 2;1 -1 1;4 -12 1];V0=[1,1,1]';[k,lambda,Vk,Wc]=mifa(C,V0,0.00001,100), [V,D] = eig (C), Dzd=max(diag(D)), wuD=abs(Dzd-lambda),Vzd=V(:,1),wuV=V(:,1)./Vk,运行后屏幕显示请注意:迭代次数k 已经达到最大迭代次数max1,主特征值的迭代值lambda,主特征向量的迭代向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc =100 0.09090909090910 2.37758124193119Dzd = wuD =1.00000000000001 0.90909090909091Vk= Vzd = wuV =0.99999999999993 0.90453403373329 0.904534033733350.99999999999995 0.30151134457776 0.301511344577781.00000000000000 -0.30151134457776 -0.30151134457776由输出结果可见,迭代次数k 已经达到最大迭代次数max 1=100,并且lambda 的相邻两次迭代的误差Wc ≈2.377 58>2,由wuV 可以看出,lambda 的特征向量V k 与真值Dzd 的特征向量V zd 对应分量的比值相差较大,所以迭代序列发散.实际上,实数矩阵C 的特征值的近似值为i ,i ,010*********.000321=-==λλλ ,并且对应的特征向量的近似向量分别为X T1=1k (0.90453403373329,0.30151134457776,-0.30151134457776)T ,X =T 22k (-0.72547625011001,-0.21764287503300-0.07254762501100i, 0.58038100008801-0.29019050004400i )T ,X =T33k ( -0.72547625011001, -0.21764287503300 + 0.07254762501100i,0.58038100008801 + 0.29019050004400i)T0,0(21≠≠k k , 03≠k 是常数).(4)输入MATLAB 程序>> D=[-4 14 0;-5 13 0;-1 0 2]; V0=[1,1,1]';[k,lambda,Vk,Wc]=mifa(D,V0,0.00001,100), [V,Dt] =eig (D), Dtzd=max(diag(Dt)), wuDt=abs(Dtzd-lambda),Vzd=V(:,2),wuV=V(:,2)./Vk,运行后屏幕显示结果请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc如下:k = lambda = Wc =19 6.00000653949528 6.539523793591684e-006Dtzd = wuDt =6.00000000000000 6.539495284840768e-006Vk = Vzd = wuV =0.79740048053564 0.79740048053564 0.797400480535640.71428594783886 0.56957177181117 0.79740021980618-0.24999918247180 -0.19935012013391 0.797403088133705.3 反幂法和位移反幂法及其MATLAB程序5.3.3 原点位移反幂法的MATLAB程序(一)原点位移反幂法的MATLAB主程序1用原点位移反幂法计算矩阵A的特征值和对应的特征向量的MATLAB主程序1 function [k,lambdan,Vk,Wc]=ydwyfmf(A,V0,jlamb,jd,max1)[n,n]=size(A); A1=A-jlamb*eye(n); jd= jd*0.1;RA1=det(A1);if RA1==0disp('请注意:因为A-aE的n阶行列式hl等于零,所以A-aE不能进行LU分解.')returnendlambda=0;if RA1~=0for p=1:nh(p)=det(A1(1:p, 1:p));endhl=h(1:n);for i=1:nif h(1,i)==0disp('请注意:因为A-aE的r阶主子式等于零,所以A-aE不能进行LU分解.')returnendendif h(1,i)~=0disp('请注意:因为A-aE的各阶主子式都不等于零,所以A-aE 能进行LU分解.')k=1;Wc =1;state=1; Vk=V0;while((k<=max1)&(state==1))[L U]=lu(A1); Yk=L\Vk;Vk=U\Yk; [mj]=max(abs(Vk));mk=m;Vk1=Vk/mk; Yk1=L\Vk1;Vk1=U\Yk1;[m j]=max(abs(Vk1));mk1=m;Vk2=(1/mk1)*Vk1;tzw1=abs((mk-mk1)/mk1);tzw2=abs(mk1-mk);Txw1=norm(Vk)-norm(Vk1);Txw2=(norm(Vk)-norm(Vk1))/norm(Vk1);Txw=min(Txw1,Txw2); tzw=min(tzw1,tzw2);Vk=Vk2;mk=mk1; Wc=max(Txw,tzw);Vk=Vk2;mk=mk1;state=0;if(Wc>jd)state=1;endk=k+1;%Vk=Vk2,mk=mk1,endif (Wc<=jd)disp('A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:')elsedisp('A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k 已经达到最大迭代次数max1,按模最小特征值的迭代值lambda,特征向量的迭代向量Vk,相邻两次迭代的误差Wc 如下:')endhl,RA1endend[V,D]=eig(A,'nobalance'),Vk;k=k-1;Wc;lambdan=jlamb+1/mk1;例5.3.2 用原点位移反幂法的迭代公式(5.28),根据给定的下列矩阵的特征值n λ的初始值n λ~,计算与n λ对应的特征向量n X 的近似向量,精确到0.000 1. (1)⎪⎪⎪⎭⎫ ⎝⎛----210242011,2.0~2=λ;(2)⎪⎪⎭⎫ ⎝⎛-4211,001.2~2=λ;(3)⎪⎪⎪⎭⎫ ⎝⎛--3315358215211,8.26~3=λ.解 (1)输入MATLAB 程序>> A=[1 -1 0;-2 4 -2;0 -1 2];V0=[1,1,1]';[k,lambda,Vk,Wc]=ydwyfmf(A,V0,0.2,0.0001,10000)运行后屏幕显示结果 请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行LU 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc = hl =3 0.2384 1.0213e-007 0.8000 1.0400 0.2720Vk = V = D =1.0000 -0.2424 -1.0000 -0.5707 5.1249 0 00.7616 1.0000 -0.7616 0.3633 0 0.2384 00.4323 -0.3200 -0.4323 1.0000 0 0 1.6367(2)输入MATLAB 程序>> A=[1 -1;2 4];V0=[20,1]';[k,lambda,Vk,Wc]=ydwyfmf(A,V0,2.001,0.0001,100)运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行LU 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc = hl =2 2.0020 5.1528e-007 -1.0010 -0.0010Vk = V = D =1.0000 -1.0000 0.5000 2 0-1.0000 1.0000 -1.0000 0 3(3)输入MATLAB 程序>> A=[-11 2 15;2 58 3;15 3 -3];V0=[1,1,-1]';[k,lambdan,Vk,Wc]=ydwyfmf(A,V0,8.26, 0.0001,100)运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行LU 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambdan= Wc = hl =2 8.2640 6.9304e-008 -19.2600 -961.9924 -6.1256Vk = V = D =-0.7692 0.7928 0.6081 0.0416 -22.5249 0 00.0912 0.0030 -0.0721 0.9974 0 8.2640 0-1.0000 -0.6095 0.7906 0.0590 0 0 58.2609例 5.3.3 用原点位移反幂法的迭代公式(5.28),计算⎪⎪⎪⎭⎫ ⎝⎛-----=1026471725110A 的分别对应于特征值 1.001~11=≈λλ,.001 2~22=≈λλ, 001.4~33=≈λλ的特征向量1X ,2X ,3X 的近似向量,相邻迭代误差为0.001.将计算结果与精确特征向量比较. 解 (1)计算特征值 1.001~11=≈λλ对应的特征向量1X 的近似向量.输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]= ydwyfmf(A,V0,1.001, 0.001,100),[V,D]=eig(A);Dzd=min(diag(D)), wuD= abs(Dzd- lambda),VD=V(:,1),wuV=V(:,1)./Vk,运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行L U 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:hl =-1.00100000000000 5.98500100000000 -0.00299600100000k = lambda = RA1 =5 1.00200000000000 -0.00299600100000Vk = VD = wuV =-0.50000000000000 -0.40824829046386 0.81649658092773-0.50000000000000 -0.40824829046386 0.81649658092773-1.00000000000000 -0.81649658092773 0.81649658092773Wc = Dzd = wuD =1.378794763695562e-009 1.00000000000000 0.00200000000000 从输出的结果可见,迭代5次,特征向量1X 的近似向量1~X 的相邻两次迭代的误差Wc ≈1.379 e-009,由wuV 可以看出,1~X = Vk 与VD 的对应分量的比值相等.特征值1λ的近似值lambda ≈1.002与初始值=1~λ 1.001的绝对误差为0.001,而与 1λ的绝对误差为0.002,其中 =1X T )000000000001.000 , 000000000000.500- , 000000000000.500( -, =1~X T )000000000001.000 , 000000000000.500- , 000000000000.500(-. (2)计算特征值.001 2~22=≈λλ对应特征向量2X 的近似向量.输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]=ydwyfmf(A,V0,2.001, 0.001,100) ,[V,D]=eig(A); WD=lambda-D(2,2),VD=V(:,2),wuV=V(:,2)./Vk,运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行L U 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:hl =-2.00100000000000 -8.01299900000000 0.00200099900000k = Wc = lambda = WD =2 3.131363162302120e-007 2.00200000000016 0.00200000000016Vk = VD = wuV =-0.24999999999999 0.21821789023599 -0.87287156094401 -0.49999999999999 0.43643578047198 -0.87287156094398 -1.00000000000000 0.87287156094397 -0.87287156094397 从输出的结果可见,迭代2次,特征向量2X 的近似向量2~X 的相邻两次迭代的误差Wc ≈3.131e-007,2~X 与2X 的对应分量的比值近似相等.特征值2λ的近似值lambda ≈2.002与初始值=2~λ 2.001的绝对误差约为0.001,而lambda 与2λ的绝对误差约为0.002,其中 =2~X T )00000000000000.1,99999999999499.0,99999999999249.0(---, =2X T ) 000000000001.000- ,000000000000.500- ,99999999999-0.249( . (3)计算特征值 001.4~33=≈λλ对应特征向量3X 的近似向量.输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]=ydwyfmf(A,V0,4.001, 0.001,100)[V,D]=eig(A);WD=lambda-max(diag(D)),VD=V(:,3),wuV=V(:,3)./Vk,运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行L U 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:hl =-4.00100000000000 -30.00899900000000 -0.00600500099999 k = lambda = Wc = WD =2 4.00199999999990 1.996084182914842e-007 0.00199999999990Vk = VD = wuV =0.40000000000001 -0.32444284226153 -0.81110710565380 0.60000000000001 -0.48666426339229 -0.81110710565381 1.00000000000000 -0.81110710565381 -0.81110710565381 从输出的结果可见,迭代2次,特征向量3X 的近似向量3~X 的相邻两次迭代的误差Wc ≈1.996e-007,3~X 与3X 的对应分量的比值近似相等.特征值3λ的近似值 4.001~4.0022=≈λ与初始值lambda 的绝对误差近似为001.0,而lambda 与3λ的绝对误差约为0.002,其中 =3X (-0.400 000 000 000 00,-0.600 000 000 000 00,-1.000 000 000 000 00T ), =3~X T )000000000001.000 ,100000000000.600 ,10000000000.400(.(二)原点位移反幂法的MATLAB 主程序2用原点位移反幂法计算矩阵A 的特征值和对应的特征向量的MATLAB 主程序2function [k,lambdan,Vk,Wc]=wfmifa1(A,V0,jlamb,jd,max1)[n,n]=size(A); jd= jd*0.1;A1=A-jlamb*eye(n);nA1=inv(A1); lambda1=0;k=1;Wc =1;state=1; U=V0;while ((k<=max1)&(state==1))Vk=A1\U; [m j]=max(abs(Vk)); mk=m; Vk=(1/mk)*Vk;Vk1=A1\Vk;[m1 j]=max(abs(Vk1)); mk1=m1,Vk1=(1/mk1)*Vk1;U=Vk1,Txw=(norm(Vk1)-norm(Vk))/norm(Vk1);tzw=abs((lambda1-mk1)/mk1);Wc=max(Txw,tzw); lambda1=mk1;state=0;if (Wc>jd)state=1;endk=k+1;endif (Wc<=jd)disp('请注意迭代次数k,特征值的近似值lambda,对应的特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:')elsedisp('请注意迭代次数k 已经达到最大迭代次数max1, 特征值的近似值lambda,对应的特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:') end[V,D] =eig(A,'nobalance'),Vk=U;k=k-1;Wc;lambdan=jlamb+1/mk;例5.3.4 用原点位移反幂法的迭代公式(5.27),计算例题5.3.3,并且将这两个例题的计算结果进行比较.再用两种原点位移反幂法的MATLAB 主程序,求979999999990.999~1=λ对应的特征向量. 解 (1)计算特征值 1.001~11=≈λλ对应特征向量1X 的近似向量.输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]=wfmifa1(A,V0,1.001,0.001,100)运行后屏幕显示结果请注意迭代次数k,特征值的近似值lambda,对应的特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = lambda = Wc =5 1.00200000000138 1.376344154436924e-006Vk’ = -0.50000000000000 -0.50000000000000 -1.00000000000000同理可得,另外与两个特征值对应的特征向量.(2)再用两种原点位移反幂法的MATLAB 主程序,求979999999990.999~1=λ对应的特征向量.输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]=ydwyfmf(A,V0,0.99999999999997,0.001,100) 运行后屏幕显示结果请注意:因为A-aE 的各阶主子式都不等于零,所以A-aE 能进行LU 分解.A-aE 的秩R(A-aE)和各阶顺序主子式值hl 、迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:hl =-0.99999999999997 6.00000000000045 0.00000000000010RA1 = 1.039168751049192e-013 k = 2 lambda = 1.00000000000000输入MATLAB 程序>> A=[0 11 -5;-2 17 -7;-4 26 -10];V0=[1,1,1]';[k,lambda,Vk,Wc]=wfmifa1(A,V0, 0.99999999999997,0.001,100) 运行后屏幕显示结果请注意迭代次数k,特征值的近似值lambda,对应的特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:k = 3 lambda = 1.00000000000000 Wc =5.412337245047640e-016Vk = 0.50000000000000 0.50000000000000 1.00000000000000 Wc = 4.317692037236759e-013 Vk =0.500000000000000.500000000000001.000000000000005.4 雅可比(Jacobi)方法及其MATLAB 程序5.4.3 雅可比方法的MATLAB 程序用雅可比方法计算对称矩阵A 的特征值和对应的特征向量的MATLAB 主程序function [k,Bk,V,D,Wc]=jacobite(A,jd,max1)[n,n]=size(A);Vk=eye(n);Bk=A;state=1;k=0;P0=eye(n); Aij=abs(Bk-diag(diag(Bk)));[m1 i]=max(Aij);[m2 j]=max(m1);i=i(j);while ((k<=max1)&(state==1))k=k+1,aij=abs(Bk-diag(diag(Bk)));[m1 i]=max(abs(aij));[m2 j]=max(m1);i=i(j),j,Aij=(Bk-diag(diag(Bk)));mk=m2*sign(Aij(i,j)),Wc=m2,Dk=diag(diag(Bk));Pk=P0;c=(Bk(j,j)-Bk(i,i))/(2*Bk(i,j)),t=sign(c)/(abs(c)+sqrt(1+c^2)),pii=1/( sqrt(1+t^2)), pij=t/( sqrt(1+t^2)),Pk(i,i)=pii;Pk(i,j)=pij;Pk(j,j)=pii; Pk(j,i)=-pij;Pk,B1=Pk'*Bk;B2=B1*Pk; Vk=Vk*Pk,Bk=B2,if (Wc>jd)state=1;elsereturnendPk;Vk;Bk=B2;Wc;endif (k>max1)disp('请注意迭代次数k 已经达到最大迭代次数max1,迭代次数k,对称矩阵Bk,以特征向量为列向量的矩阵V,特征值为对角元的对角矩阵D 如下:')elsedisp('请注意迭代次数k,对称矩阵Bk,以特征向量为列向量的矩阵V,特征值为对角元的对角矩阵D 如下:')endWc;k=k; V=Vk;Bk=B2;D=diag(diag(Bk));[V1,D1]=eig(A,'nobalance')例5.4.2 用雅可比方法的MATLAB 程序计算矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=12101152302756135612A 的特征值i λ和对应的特征向量i X (4,3,2,1=i ).解 (1)保存名为jacobite.m 为M 文件;(2)输入MATLAB 程序>> A=[12 -56 3 -1;-56 7 2 0;3 2 5 1;-1 0 1 12];[k,B,V,D,Wc]=jacobite(A,0.001,100)(3)运行后屏幕显示如下:k = i = j = mk = Wc =1 2 1 -56 56c = t =-0.04464285714286 -0.95635313919972pii = pij =0.72270271801843 -0.69115901308510Pk =0.72270271801843 0.69115901308510 0 0 -0.69115901308510 0.72270271801843 0 0 0 0 1.00000000000000 00 0 0 1.00000000000000Vk =0.72270271801843 0.69115901308510 0 0 -0.69115901308510 0.72270271801843 0 00 0 1.00000000000000 00 0 0 1.00000000000000Bk =65.55577579518456 0 0.78579012788509 -0.72270271801843 -0.00000000000001 -46.55577579518456 3.51888247529217 -0.691159013085100.78579012788509 3.51888247529217 5.00000000000000 1.00000000000000 -0.72270271801843 -0.69115901308510 1.00000000000000 12.00000000000000 k =i = j = mk = Wc =2 3 2 3.51888247529217 3.51888247529217c = t =-7.32558932518824 -0.06793885568129pii = pij =0.99770011455446 -0.06778260409592Pk =1.00000000000000 0 0 00 0.99770011455446 0.06778260409592 00 -0.06778260409592 0.99770011455446 00 0 0 1.00000000000000Vk =0.72270271801843 0.68956942653035 0.04684855775127 0 -0.69115901308510 0.72104058455581 0.04898667221449 00 -0.06778260409592 0.99770011455446 00 0 0 1.00000000000000Bk =65.55577579518456 -0.05326290114092 0.78398290060672 -0.72270271801843 -0.05326290114093 -46.79484464383285 0 -0.757352030626270.78398290060672 0.00000000000000 5.23906884864829 0.95085155680318 -0.72270271801843 -0.75735203062627 0.95085155680318 12.00000000000000 k = i = j = mk = Wc =3 4 3 0.95085155680318 0.95085155680318c = t =-3.55519802380213 -0.13796227443116pii = pij =0.99061693994324 -0.13666776612460Pk =1.00000000000000 0 0 00 1.00000000000000 0 00 0 0.99061693994324 0.136667766124600 0 -0.13666776612460 0.99061693994324 Vk =0.72270271801843 0.68956942653035 0.04640897492032 0.00640268773403 -0.69115901308510 0.72104058455581 0.04852702732712 0.006694899061430 -0.06778260409592 0.98833863446096 0.136353445918420 0 -0.13666776612460 0.99061693994324 Bk =65.55577579518456 -0.05326290114092 0.87539690801061 -0.60877636330628 -0.05326290114093 -46.79484464383285 0.10350561019562 -0.750245751038800.87539690801061 0.10350561019562 5.10788720522532 -0.00000000000000 -0.60877636330628 -0.75024575103880 -0.00000000000000 12.13118164342297 k =i = j = mk = Wc =4 1 3 0.87539690801061 0.87539690801061c = t =-34.52598931799430 -0.01447880833914pii = pij =0.99989519853186 -0.01447729093877Pk =0.99989519853186 0 -0.01447729093877 00 1.00000000000000 0 00.01447729093877 0 0.99989519853186 00 0 0 1.00000000000000Vk =0.72329885394465 0.68956942653035 0.03594133368062 0.00640268773403 -0.69038403871280 0.72104058455581 0.05852805174080 0.006694899061430.01430846595712 -0.06778260409592 0.98823505512105 0.13635344591842-0.00197857901214 0 -0.13665344314206 0.99061693994324Bk =65.56845049923633 -0.05175883827808 -0.00000000000000 -0.60871256264964-0.05175883827809 -46.79484464383285 0.10426586517177 -0.75024575103880-0.00000000000000 0.10426586517177 5.09521250117356 0.00881343252823-0.60871256264964 -0.75024575103880 0.00881343252823 12.13118164342297 k = i = j = mk = Wc =5 4 2 -0.75024575103880 0.75024575103880c = t =39.27114962375084 0.01272992971264pii = pij =0.99991898429114 0.01272889838836Pk =1.00000000000000 0 0 00 0.99991898429114 0 -0.012728898388360 0 1.00000000000000 00 0.01272889838836 0 0.99991898429114Vk =0.72329885394465 0.68959505973603 0.03594133368062 -0.00237529014628-0.69038403871280 0.72106738763160 0.05852805174080 -0.002483695665250.01430846595712 -0.06604148348220 0.98823505512105 0.13720519702737-0.00197857901214 0.01260946237032 -0.13665344314206 0.99053668440964Bk =65.56845049923633 -0.05950288535679 -0.00000000000000 -0.60800441437674-0.05950288535680 -46.80439521951078 0.10436960328590 0.00000000000000-0.00000000000000 0.10436960328590 5.09521250117356 0.00748552889860-0.60800441437674 0.00000000000000 0.00748552889860 12.14073221910090 k =i = j = mk = Wc =6 4 1 -0.60800441437674 0.60800441437674c = t =-43.93694931878409 -0.01137847012503pii = pij =0.99993527149402 -0.01137773361366Pk =0.99993527149402 0 0 0.011377733613660 1.00000000000000 0 00 0 1.00000000000000 0-0.01137773361366 0 0 0.99993527149402Vk =0.72327906130899 0.68959505973603 0.03594133368062 0.00585436528595-0.69031109235777 0.72106738763160 0.05852805174080 -0.010338540582940.01274645560931 -0.06604148348220 0.98823505512105 0.13735911385404-0.01324851347145 0.01260946237032 -0.13665344314206 0.99045005670500Bk =65.57536865930122 -0.05949903382392 -0.00008516835377 -0.00000000000000-0.05949903382393 -46.80439521951078 0.10436960328590 -0.00067700797883-0.00008516835377 0.10436960328590 5.09521250117356 0.00748504437150-0.00000000000000 -0.00067700797883 0.00748504437150 12.13381405903603 k =i = j = mk = Wc =7 3 2 0.10436960328590 0.10436960328590c = t =-2.486337309269764e+002 -0.00201098208240pii = pij =0.99999797798167 -0.00201097801616Pk =1.00000000000000 0 0 00 0.99999797798167 0.00201097801616 00 -0.00201097801616 0.99999797798167 00 0 0 1.00000000000000…………………………………………………………………………请注意迭代次数k,对称矩阵Bk,以特征向量为列向量的矩阵V,特征值为对角元的对角矩阵D 如下:V1 =0.68990429476497 -0.03732423222484 0.00588594854431 -0.722913771734500.72058252860300 -0.05998661236737 -0.01028322161977 0.69069289931337-0.06802029759277 -0.98795368410472 0.13841044442471 -0.012779125692250.01288885768193 0.13768088498200 0.99030407443219 0.01325486405899D1 =-46.80463661419736 0 0 00 5.09541442877727 0 00 0 12.13382202426702 00 0 0 65.57540016115307k =10B =65.57540016045945 0.00000000000175 -0.00020481967566 0.000000148628360.00000000000175 -46.80463661419739 0.00000062739984 0.00000000000000-0.00020481967566 0.00000062739984 5.09541442947090 -0.000000000007370.00000014862836 -0.00000000000000 -0.00000000000737 12.13382202426704V =0.72291389811507 0.68990429521617 0.03732177568689 0.00588595055487-0.69069269613201 0.72058252932816 0.05998894273570 -0.010283223540620.01278247108107 -0.06802028564977 0.98795364164379 0.13841044446122-0.01325533307898 0.01288885601755 -0.13768084024946 0.99030407439520D =65.57540016045945 0 0 00 -46.80463661419739 0 00 0 5.09541442947090 00 0 0 12.13382202426704Wc =6.920584967017158e-0045.5 豪斯霍尔德(Householder)方法及其MATLAB程序5.5.1 豪斯霍尔德方法及其MATLAB程序求初等反射矩阵P,使得PX的第一个分量以外的其余的分量都为零的MATLAB主程序function [xigema,rou,miou,P,PX]=Householder(X)n=size(X);nX=norm(X,2);xigema=nX*sign(X(1));rou=xigema*(xigema+X(1));miou=[xigema,zeros(1,n-1)]'+X,E=eye(n,n); C=2*miou*(miou)';P=E-C/(norm(miou,2)^2); PX=P*X;例5.5.1设向量=X()T1,2,2,确定一个初等反射矩阵P,使得PX的后两个分量为零.解输入MATLAB程序>> X=[2 2 1]'; [xigema,rou,miou,P,PX]=Householder(X)运行后屏幕显示结果P = PX =-0.6667 -0.6667 -0.3333 -3.0000-0.6667 0.7333 -0.1333 0.0000-0.3333 -0.1333 0.9333 0.00005.5.2 矩阵约化为上豪斯霍尔德矩阵及其MATLAB程序用豪斯霍尔德变换将n阶矩阵A规约成上豪斯霍尔德矩阵的MATLAB主程序function [k,Sk,uk,ck,Pk,Uk,Ak]=Householdrer1(A)n=size(A); Ak=A;for k=1:n-2k,Sk=norm(Ak(k+1:n,k))*sign(Ak(k+1,k)),uk= Ak(k+1:n,k)+ Sk*eye(n-k,1),ck=(norm(uk,2)^2)/2,Pk= eye(n-k,n-k)-uk*uk'/ck,Uk=[eye(k,k),zeros(k,n-k);zeros(n-k, k),Pk],A1=Uk*Ak;Ak=A1,end例5.5.3 用初等反射矩阵正交相似约化实矩阵A 为上豪斯霍尔德矩阵.其中⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=34 19- 37 78- 41- 31 11 72- 98 10.2- 78- 32-94- 21 12 1 0 1- 63- 72 1 5 2 3 17- 32 02 7 56- 51- 17 12- 34 52- 12A . 解 输入MATLAB 程序>> A=[12 -52 34 -12 17 -51;-56 7 2 0 32 -17;3 2 5 1 72 -63;-1 0 1 12 21 -94;-32 -78 -10.2 98 -72 11;31 -41 -78 37 -19 34];[k,Sk,uk,ck,Pk,Uk,Ak]=Householdrer1(A)运行后屏幕显示结果k = Sk = ck =1 -71.6310 9.1423e+003uk = Pk =-127.6310 -0.7818 0.0419 -0.0140 -0.4467 0.43283.0000 0.0419 0.9990 0.0003 0.0105 -0.0102-1.0000 -0.0140 0.0003 0.9999 -0.0035 0.0034-32.0000 -0.4467 0.0105 -0.0035 0.8880 0.108531.0000 0.4328 -0.0102 0.0034 0.1085 0.8949Uk =1.0000 0 0 0 0 00 -0.7818 0.0419 -0.0140 -0.4467 0.43280 0.0419 0.9990 0.0003 0.0105 -0.01020 -0.0140 0.0003 0.9999 -0.0035 0.00340 -0.4467 0.0105 -0.0035 0.8880 0.10850 0.4328 -0.0102 0.0034 0.1085 0.8949Ak =12.0000 -52.0000 34.0000 -12.0000 17.0000 -51.000071.6310 11.7128 -30.5678 -27.8930 1.6473 21.76430.0000 1.8892 5.7655 1.6556 72.7134 -63.9112-0.0000 0.0369 0.7448 11.7815 20.7622 -93.6963-0.0000 -76.8184 -18.3655 91.0066 -79.6101 20.71910.0000 -42.1447 -70.0897 43.7749 -11.6277 24.5846k = Sk = ck =2 87.6402 7.8464e+003uk = Pk =89.5295 -0.0216 -0.0004 0.8765 0.48090.0369 -0.0004 1.0000 0.0004 0.0002-76.8184 0.8765 0.0004 0.2479 -0.4126-42.1447 0.4809 0.0002 -0.4126 0.7736Uk =1.0000 0 0 0 0 00 1.0000 0 0 0 00 0 -0.0216 -0.0004 0.8765 0.48090 0 -0.0004 1.0000 0.0004 0.00020 0 0.8765 0.0004 0.2479 -0.41260 0 0.4809 0.0002 -0.4126 0.7736Ak =12.0000 -52.0000 34.0000 -12.0000 17.0000 -51.000071.6310 11.7128 -30.5678 -27.8930 1.6473 21.7643-0.0000 -87.6402 -49.9272 100.7790 -76.9476 31.4002-0.0000 -0.0000 0.7219 11.8223 20.7005 -93.6570-0.0000 0.0000 29.4202 5.9564 48.8026 -61.06030.0000 0.0000 -43.8731 -2.8860 58.8230 -20.2818…………………………………………………………………………k = Sk = ck =4 -12.2088 195.0398uk = Pk =-15.9753 -0.3085 0.951211.6133 0.9512 0.3085Uk =1.0000 0 0 0 0 00 1.0000 0 0 0 00 0 1.0000 0 0 00 0 0 1.0000 0 00 0 0 0 -0.3085 0.95120 0 0 0 0.9512 0.3085Ak =12.0000 -52.0000 34.0000 -12.0000 17.0000 -51.000071.6310 11.7128 -30.5678 -27.8930 1.6473 21.7643-0.0000 -87.6402 -49.9272 100.7790 -76.9476 31.40020.0000 -0.0000 -52.8292 -5.8754 21.3902 18.44030.0000 0.0000 0.0000 12.2088 40.2435 -106.81340.0000 0.0000 -0.0000 0.0000 64.7555 -34.09095.5.3 实对称矩阵的三对角化及其MATLAB程序将n阶实对称矩阵A规约成三对角形式的MATLAB主程序function T=house(A)[n,n]=size(A);for k=1:n-2s=norm(A(k+1:n,k),2);if (A(k+1,k)<0)s=-s;endr=sqrt(2*s*(A(k+1,k)+s));U(1:k)=zeros(1,k);U(k+1)=(A(k+1,k)+s)/r;U(k+2:n)=A(k+2:n,k)'/r;V(1:k)=zeros(1,k);V(k+1:n)=A(k+1:n,k+1:n)*U(k+1:n)';C=U(k+1:n)*V(k+1:n)';P(1:k)=zeros(1,k);P(k+1:n)=V(k+1:n)-C*U(k+1:n);A(k+2:n,k)=zeros(n-k-1,1);A(k,k+2:n)=zeros(1,n-k-1);A(k+1,k)=-s; A(k,k+1)=-s;A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-2*U(k+1:n)'*P(k+1:n)-2*P( k+1:n)'*U(k+1:n);endT=A;例5.5.4 用初等反射矩阵正交相似约化实对称矩阵A为三对角矩阵.其中⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------------=5261215121416134237299021237312611451721253233219612371564901435612A 解 输入MATLAB 程序>> A=[12 -56 3 -14 -90 -4;-56 71 23 61 -9 -21;3 23 53 12 -72 51;-14 61 12 73 23 21;-90 -9 -72 23 -34 -61;-41 -21 51 21 -61 -52];T=house(A)运行后屏幕显示结果T =12.0000 114.5513 0 0 0 0114.5513 -43.2395 -108.2763 0 0 00 -108.2763 49.7411 -22.7766 0 00 0 -22.7766 40.2476 -89.1355 00 0 0 -89.1355 44.9606 39.30900 0 0 0 39.3090 19.29025.6 QR 方法及其MATLAB 程序5.6.5 最末元位移QR 法计算实对称矩阵特征值及其MATLAB 程序用最末元位移QR 方法求实对称矩阵A 全部特征值的MATLAB 主程序function tzg=qr4(A,t,max1)[n,n]=size(A); k=0;Ak=A;tzg=zeros(n); state=1;for i=1:n;while ((k<=max1)&(state==1)&(n>1))b1=abs(Ak(n,n-1)); b2=abs(Ak(n,n));b3=abs(Ak(n-1,n-1));b4=min(b2, b3); jd=10^(-t); jd1=jd*b4;if (b1>=jd1)sk=Ak(n,n); Bk=Ak-sk*eye(n); [Qk,Rk]=qr(Bk);At=Rk*Qk+sk*eye(n); k=k+1;tzgk=Ak(n,n);disp('请注意:下面的i 表示求第i 个特征值,k 是迭代次数,sk 是原点位移量,')disp(' Bk=Ak-sk*eye(n),Qk 和Rk 是Bk 的QR 分解,At=Rk*Qk+sk*eye(n)迭代矩阵:')i,state=1;k,sk,Bk,Qk,Rk,At,Ak=At;elsedisp('请注意:i 表示求第i 个特征值,tzgk 是矩阵A 的特征值的近似值,k 是迭代次数,')disp(' 下面的矩阵B 是m 阶矩阵At 的(m-1)阶主子矩阵,即At 降一阶.')i,tzgk=Ak(n,n),tzg(n,1)=tzgk;k=k,sk,Ak;B=Ak(1:n-1,1:n-1),Ak=B;n=n-1;state==1; i=i+1;endendendtzg(1,1)=Ak;tzg=sort(tzg(:,1));tzgk=Akdisp('请注意:n 阶实对称矩阵A 的全部真特征值lamoda 和至少含t个有效数字的近似特征值tzg 如下:')lamoda=sort(eig(A))例5.6.5 用最末元位移QR 方法求下列实对称矩阵的全部近似特征值,并将计算结果与A 全部真特征值比较.其中,2 1 1 1 1 3 1 21 1 4- 21 2 2 5)1(⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 精度为=ε510-; ,52612151214161342372990212373126114517212532332196123715641901435612)2(⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------------=A 精度为=ε410-.解 (1)首先保存用最末元位移QR 方法求实对称矩阵A 全部特征值的MATLAB 主程序为M 文件,取名为qr4.m.在MATLAB 工作窗口输入程序>> A=[5 2 2 1;2 -4 1 1;2 1 3 1;1 1 1 2]; tzg=qr4(A,5,100) 运行后屏幕显示结果请注意:下面的i 表示求第i 个特征值,k 是迭代次数,sk 是原点位移量,Bk=Ak-sk*eye(n),Qk 和Rk 是Bk 的QR 分解,At=Rk*Qk+sk*eye(n)迭代矩阵:i =1k =1sk =2Bk =3 2 2 12 -6 1 12 1 1 11 1 1 0Qk =-0.70710678118655 0.38807526285317 0.12674485010490 -0.57735026918963-0.47140452079103 -0.87963726246718 0.06337242505245 0-0.47140452079103 0.20697347352169 -0.63372425052448 0.57735026918963-0.23570226039552 0.18110178933148 0.76046910062937 0.57735026918963 Rk =-4.24264068711929 0.70710678118655 -2.59272486435067 -1.649915822768610 6.44204936336256 0.28458852609232 -0.284588526092320 0 0.44360697536713 -0.443606975367130 0 0 0.00000000000000At =6.27777777777778 -3.10388935193069 -0.10455916682125 0.00000000000000-3.10388935193069 -3.65930388219545 0.01147685957127 0.00000000000000-0.10455916682125 0.01147685957127 1.38152610441767 0.00000000000000 -0.00000000000000 0.00000000000000 0.00000000000000 2.00000000000000 请注意:i 表示求第i 个特征值,tzgk 是矩阵A 的特征值的近似值,k 是迭代次数,下面的矩阵B 是m 阶矩阵At 的(m-1)阶主子矩阵,即At 降一阶.i =1tzgk =2.00000000000000k =1sk =2B =6.27777777777778 -3.10388935193069 -0.10455916682125-3.10388935193069 -3.65930388219545 0.01147685957127-0.10455916682125 0.01147685957127 1.38152610441767请注意:下面的i 表示求第i 个特征值,k 是迭代次数,sk 是原点位移量,Bk=Ak-sk*eye(n),Qk和Rk是Bk的QR分解,At=Rk*Qk+sk*eye(n)迭代矩阵:i =2k =2sk =1.38152610441767Bk =4.89625167336011 -3.10388935193069 -0.10455916682125-3.10388935193069 -5.04082998661312 0.01147685957127-0.10455916682125 0.01147685957127 0Qk =-0.84445320114929 -0.53537837009187 0.016394874396770.53532568873289 -0.84460953959679 -0.007818734217300.01803324849744 0.00217404228940 0.99983502413586Rk =-5.79813264571247 -0.07718952005739 0.094439180886190 5.91931326753920 0.046285251232420 0 -0.00180396892170At =6.23815929000691 3.16959512520840 -0.000032531419853.16959512520840 -3.61788172311421 -0.00000392190472-0.00003253141985 -0.00000392190472 1.37972243310730请注意:i表示求第i个特征值,tzgk是矩阵A的特征值的近似值,k是迭代次数,下面的矩阵B是m阶矩阵At的(m-1)阶主子矩阵,即At降一阶.i =2tzgk =1.37972243310730k =2sk =1.38152610441767B =6.23815929000691 3.169595125208403.16959512520840 -3.61788172311421请注意:下面的i表示求第i个特征值,k是迭代次数,sk是原点位移量,Bk=Ak-sk*eye(n),Qk和Rk是Bk的QR分解,At=Rk*Qk+sk*eye(n)迭代矩阵:i =3k =3sk =-3.61788172311421Bk =9.85604101312112 3.169595125208403.16959512520840 0Qk =-0.95198403663348 -0.30614766697629-0.30614766697629 0.95198403663348Rk =-10.35315786173815 -3.017403961789690 -0.97036415284199At =7.16193047323385 0.297074721510000.29707472151000 -4.54165290634115请注意:下面的i表示求第i个特征值,k是迭代次数,sk是原点位移量,Bk=Ak-sk*eye(n),Qk和Rk是Bk的QR分解,At=Rk*Qk+sk*eye(n)迭代矩阵:i =3k =4sk =-4.54165290634115Bk =11.70358337957500 0.297074721510000.29707472151000 0。
数值分析幂法和反幂法

数值分析幂法和反幂法数值分析中,幂法(Power method)和反幂法(Inverse Power method)是求解矩阵的特征值和特征向量的两种常用方法。
它们都是通过迭代过程逼近特征值和特征向量。
1.幂法:幂法是求解矩阵的最大特征值和对应的特征向量的一种迭代方法。
幂法的原理是通过迭代过程,将一个任意选择的初始向量不断与矩阵相乘,使其逼近对应最大特征值的特征向量。
幂法的迭代公式为:$x^{(k+1)} = \frac{Ax^{(k)}}{\,Ax^{(k)}\,}$幂法的迭代过程是不断对向量进行归一化,使其逐渐逼近最大特征值对应的特征向量。
当迭代次数足够多时,可以得到非常接近最大特征值的估计。
2.反幂法:反幂法是幂法的一种变形,用于求解矩阵的最小特征值和对应的特征向量。
反幂法的原理是通过迭代过程,将一个任意选择的初始向量不断与矩阵的逆相乘,使其逼近对应最小特征值的特征向量。
反幂法的迭代公式为:$x^{(k+1)} = \frac{A^{-1}x^{(k)}}{\,A^{-1}x^{(k)}\,}$反幂法的迭代过程同样是不断对向量进行归一化,使其逐渐逼近最小特征值对应的特征向量。
当迭代次数足够多时,可以得到非常接近最小特征值的估计。
3.收敛性分析:幂法和反幂法的收敛性分析与矩阵的特征值分布有关。
对于幂法而言,如果矩阵$A$的最大特征值是唯一的,并且其他特征值的绝对值小于最大特征值的绝对值,那么幂法是收敛的,而且收敛速度是指数级的。
对于反幂法而言,如果矩阵$A$的最小特征值是唯一的,并且其他特征值的绝对值大于最小特征值的绝对值,那么反幂法是收敛的,而且同样是指数级的收敛速度。
4.实际应用:幂法和反幂法在实际中广泛应用于各个领域,例如物理、工程、计算机科学等。
比如在结构力学中,幂法可以用来求解结构的自振频率和相应的振型;在电力系统中,反幂法可以用来求解电力系统决定性特征值,例如功率稳定性的最小特征值。
数值方法课程设计幂法反幂法计算矩阵特征值和特征向量-附Matlab程序

矩阵的特征值与特征向量的计算摘要物理,力学,工程技术中的很多问题在数学上都归结于求矩阵特征值的问题,例如振动问题(桥梁的振动,机械的振动,电磁振动等)、物理学中某些临界值的确定问题以及理论物理中的一些问题。
矩阵特征值的计算在矩阵计算中是一个很重要的部分,本文使用幂法和反幂法分别求矩阵的按模最大,按模最小特征向量及对应的特征值。
幂法是一种计算矩阵主特征值的一种迭代法,它最大的优点是方法简单,对于稀疏矩阵比较合适,但有时收敛速度很慢。
其基本思想是任取一个非零的初始向量。
由所求矩阵构造一向量序列。
再通过所构造的向量序列求出特征值和特征向量。
反幂法用来计算矩阵按模最小特征向量及其特征值,及计算对应于一个给定近似特征值的特征向量。
本文中主要使用反幂法计算一个矩阵的按模最小特征向量及其对应的特征值。
计算矩阵按模最小特征向量的基本思想是将其转化为求逆矩阵的按模最大特征向量。
然后通过这个按模最大的特征向量反推出原矩阵的按模最小特征向量。
关键词:矩阵;特征值;特征向量;冥法;反冥法THE CALCULATIONS OF EIGENVALUE AND EIGENVECTOR OF MATRIXABSTRACTPhysics, mechanics, engineering technology in a lot of problems in mathematics are attributed to matrix eigenvalue problem, such as vibration (vibration of the bridge, mechanical vibration, electromagnetic vibration, etc.) in physics, some critical values determine problems and theoretical physics in some of the problems. Matrix eigenvalue calculation is a very important part in matrix computation. In this paper, we use the power method and inverse power method to calculate the maximum of the matrix, according to the minimum characteristic vector and the corresponding characteristic value.Power method is an iterative method to calculate the eigenvalues of a matrix. It has the advantage that the method is simple and suitable for sparse matrices, but sometimes the convergence rate is very slow. The basic idea is to take a non - zero initial vector. Construct a vector sequence from the matrix of the matrix. Then the eigenvalues and eigenvectors are obtained by using the constructed vector sequence.The inverse power method is used to calculate the minimum feature vectors and their eigenvalues of the matrix, and to calculate the eigenvalues of the matrix. In this paper, we use the inverse power method to calculate the minimum eigenvalue of a matrix and its corresponding eigenvalues. The basic idea of calculating the minimum characteristic vector of a matrix is to transform it to the maximumc haracteristic vector of the modulus of the inverse matrix. Then, according to the model, the minimum feature vector of the original matrix is introduced.Key words: Matrix ;Eigenvalue ;Eigenvector ;Iteration methods;目录1引言 (1)2相关定理。
北航数值分析报告第一次大作业(幂法反幂法)

一、问题分析与算法描述1. 问题的提出:〔1〕用幂法、反幂法求矩阵的按摸最大和最小特征值,并求出相应的特征向量。
其中要求:迭代精度达到。
〔2〕用带双步位移的QR法求上述的全部特征值,并求出每一个实特征值相应的特征向量。
2. 算法的描述:(1) 幂法幂法主要用于计算矩阵的按摸为最大的特征值和相应的特征向量。
其迭代格式为:终止迭代的控制选用。
幂法的使用条件为实矩阵A具有n个线性无关的特征向量,其相应的特征值满足不等式或幂法收敛速度与比值或有关,比值越小,收敛速度越快。
(2) 反幂法反幂法用于计算实矩阵A按摸最小的特征值,其迭代格式为:每迭代一次都要求解一次线性方程组。
当k足够大时,,可近似的作为矩阵A的属于的特征向量。
比值越小,收敛的越快。
反幂法要求矩阵A非奇异。
(3) 带双步位移的QR分解法QR方法适用于计算一般实矩阵的全部特征值,尤其适用于计算中小型实矩阵的全部特征值。
本算例中采用带双步位移的QR方法,可加速收敛,其迭代格式为:二、计算结果与分析1. 计算结果:(1) 幂法:初始条件:最大迭代次数L=1000;向量计算结果:第1次迭代结果:最大特征值:0.00000e+000第2次迭代结果:最大特征值:2.48910e+000 相对误差:1.00000e+000 第3次迭代结果:最大特征值:1.67719e+000 相对误差:第4次迭代结果:最大特征值:-2.10960e+000 相对误差:1.79503e+000 第5次迭代结果:最大特征值:-6.13203e-001 相对误差:2.44030e+000 ……第794次迭代结果:最大特征值:-1.97638e+000 相对误差:最大特征值:-1.97638e+000 相对误差:********************最终迭代结果***************特征值:-1.97638e+000 相对误差:迭代次数:795(2) 反幂法:初始条件:最大迭代次数L=1000;向量运行结果:第1次迭代结果:最大特征值:1.07542e+000第2次迭代结果:最大特征值:-3.66550e+000 相对误差:1.29339e+000 第3次迭代结果:最大特征值:1.22709e+001 相对误差:1.29871e+000 第4次迭代结果:最大特征值:-1.03421e+000 相对误差:1.28650e+001 第5次迭代结果:最大特征值:相对误差:……第995次迭代结果:最大特征值:相对误差:第996次迭代结果:最大特征值:相对误差:最大特征值:相对误差:第998次迭代结果:最大特征值:相对误差:第999次迭代结果:最大特征值:相对误差:第1000次迭代结果:最大特征值:相对误差:******************************超过最大设定迭代次数,迭代失败!(3) 带双步位移的QR法:初始条件:最大迭代次数L=1000;向量运行结果:全部特征值:特征向量〔经谱X数归一化〕:实特征值对应特征向量:-0.062705 -0.022368 0.304372 0.064466 0.521833 -0.157024 0.136942 -0.218108 0.250264 -0.043064 -0.228688 -0.184632 -0.072871 0.124721 0.029070 0.102566 -0.136358 0.167727 0.085747 0.546165 实特征值对应特征向量:-0.018001 0.019652 0.273447 0.070528 0.274896 -0.144015 0.048385 0.376439 -0.583051 -0.054008 -0.168682 -0.113430 -0.034709 0.009204 0.472291 0.125664 -0.190617 0.113145 0.046278 0.059871 实特征值对应特征向量:0.106861 0.087709 -0.024967 -0.020897 0.064302 0.034047 0.535143 0.046383 0.028832 0.003479-0.097276 -0.383801 0.089445 -0.039560 -0.036928 -0.021330 0.014811 0.705836 -0.108904 0.082022 实特征值对应特征向量:-0.055201 0.003399 0.242191 0.102847 0.372470 -0.372826 0.113953 0.240659 -0.310401 -0.076590 -0.244632 -0.192549 -0.077259 0.263328 0.201662 0.154166 -0.407814 0.186782 0.094649 0.173302 实特征值对应特征向量:0.427828 -0.546801 0.007822 -0.382580 0.025199 0.012788 0.033241 0.005389 -0.004065 0.043524 -0.032112 -0.044233 0.135395 -0.006564 0.001214 0.020165 0.011678 0.050001 -0.585765 0.013115 实特征值对应特征向量:0.236032 -0.139250 -0.008143 0.638527 -0.009049 -0.002911 -0.001307 0.003054 0.006515 -0.030134 0.012712 0.011368 -0.018792 -0.001753 -0.005749 -0.014290 -0.005292 -0.014591 0.717590 0.001369 实特征值对应特征向量:-0.227404 -0.048154 0.022615 0.297305 0.070372 0.039927 0.078503 0.015822 -0.012182 0.605334 -0.083616 -0.106270 -0.573963 -0.019907 0.003839 0.051362 0.036567 0.115613 0.332707 0.036954 实特征值对应特征向量:-0.027768 -0.051081 -0.159642 -0.054573 -0.084441 0.118378 0.029553 0.211088 0.203867 0.0486272. 结果分析以上三种方法中,幂法计算共进展了795次迭代才达到收敛,计算量较大,收敛性不好;反幂法计算结果未能收敛,通过进一步分析发现,这是因为反幂法迭代程序未考虑按模最小特征值为复数的情况,造成迭代失败。
幂法和反幂法的matlab实现

幂法求矩阵主特征值及对应特征向量摘要矩阵特征值的数值算法,在科学和工程技术中很多问题在数学上都归结为矩阵的特征值问题,所以说研究利用数学软件解决求特征值的问题是非常必要的。
实际问题中,有时需要的并不是所有的特征根,而是最大最小的实特征根。
称模最大的特征根为主特征值。
幂法是一种计算矩阵主特征值(矩阵按模最大的特征值)及对应特征向量的迭代方法,它最大的优点是方法简单,特别适用于大型稀疏矩阵,但有时收敛速度很慢。
用java来编写算法。
这个程序主要分成了四个大部分:第一部分为将矩阵转化为线性方程组;第二部分为求特征向量的极大值;第三部分为求幂法函数块;第四部分为页面设计及事件处理。
其基本流程为幂法函数块通过调用将矩阵转化为线性方程组的方法,再经过一系列的验证和迭代得到结果。
关键字:主特征值;特征向量;线性方程组;幂法函数块POWER METHOD FOR FINDING THE EIGENVALUES AND CORRESPONDING EIGENVECTORS OF THEMATRIXABSTRACTNumerical algorithm for the eigenvalue of matrix, in science and engineering technology, a lot of problems in mathematics are attributed matrix characteristic value problem, so that studies using mathematical software to solve the eigenvalue problem is very necessary. In practical problems, sometimes need not all eigenvalues, but the maximum and minimum eigenvalue of real. The characteristic value of the largest eigenvalue of the modulus maximum.Power method is a calculation of main features of the matrix values (matrix according to the characteristics of the largest value) and the corresponding eigenvector of iterative method. It is the biggest advantage is simple method, especially for large sparse matrix, but sometimes the convergence speed is very slow.Using java to write algorithms. This program is divided into three parts: the first part is the matrix is transformed into linear equations; the second part for the sake of feature vector of the maximum; the third part is the exponentiation function block. The fourth part is the page design and event processing .The basic process is a power law function block by calling the matrix is transformed into linear equations method, after a series of validation and iteration results.Power method for finding the eigenvalues and corresponding eigenvectors of the matrixKey words: Main eigenvalue; characteristic vector; linear equations; power function block、目录1幂法 (1)1.1幂法的基本理论和推导 (1)1.2幂法算法的迭代向量规范化 (2)2概要设计 (3)2.1设计背景 (3)2.2运行流程 (3)2.3运行环境 (3)3程序详细设计 (4)3.1矩阵转化为线性方程组 (4)3.2特征向量的极大值 (4)3.3求幂法函数块............….....…………...…......…………………………3.4界面设计与事件处理............….....…………...…......…………………………4 运行过程及结果 (6)4.1 运行过程.........................................................………………………………………. .64.2 运行结果 (6)4.3 结果分析 (6)5结论 (7)参考文献 (8)附录 (56)1 幂法设实矩阵n n ij a A ⨯=)(有一个完备的特征向量组,其特征值为n λλλ ,,21,相应的特征向量为n x x x ,,21。
matlab幂法求特征值和特征向量方法实现和函数表示

matlab幂法求特征值和特征向量方法实现和函数表示1. 引言在数值分析中,求解特征值和特征向量是一项重要而且经常出现的任务。
特征值和特征向量在矩阵和线性代数中有着广泛的应用,涉及到许多领域,如机器学习、信号处理、结构动力学等。
在matlab中,幂法是一种常用的求解特征值和特征向量的方法,同时也有对应的函数可以实现这一过程。
2. 幂法的原理幂法是一种迭代方法,它利用矩阵的特征值和特征向量的性质,通过不断地迭代计算,逼近矩阵的主特征值和对应的特征向量。
具体来说,假设A是一个n阶矩阵,它的特征值λ1>λ2≥...≥λn,并且对应着线性无关的特征向量v1,v2,...,vn。
如果选择一个任意的非零初始向量x0,并进行以下迭代计算:```x(k+1) = Ax(k) / ||Ax(k)||```其中,||.||表示向量的模长。
不断迭代计算后,x(k)将收敛到矩阵A的主特征向量v1上,并且相应的特征值即为A的主特征值λ1。
3. matlab实现幂法求解特征值和特征向量在matlab中,幂法的实现也非常简单。
可以使用自带的eig函数,该函数可以直接求解矩阵的特征值和特征向量。
使用方法如下:```[V,D] = eig(A)```其中,A为待求解的矩阵,V为特征向量矩阵,D为特征值矩阵。
利用eig函数,即可一步到位地求解矩阵的特征值和特征向量,非常简单方便。
4. 函数表示幂法求解特征值和特征向量的过程可以表示为一个matlab函数。
通过封装相关的迭代算法和收敛判据,可以方便地实现幂法的函数表示。
可以定义一个名为powerMethod的函数:```matlabfunction [lambda, v] = powerMethod(A, x0, maxIter, tol)% 初始化k = 1;x = x0;% 迭代计算while k <= maxItery = A * x;lambda = norm(y, inf);x = y / lambda;% 检查收敛性if norm(A * x - lambda * x) < tolbreak;endk = k + 1;endv = x;end```利用这个函数,就可以自己实现幂法求解特征值和特征向量的过程。
幂法和反幂法

(a)
kl im uk
x1 ; maxx1)(
(b ) k l i m kk l i m mvk a ) x1.(
且收敛速度由比值 r | 2 | 确定。 1
下面我们把改进的幂法简称为幂法。
用(改进的)幂法求矩阵A的主特征第值九和章 主特特征值征与向特量征向的量步的数骤值:求法
m
(vk1 )i (vk )i
v
为
k
相
应
的
特
征
向
量
,
即
对
这
种
情
况
幂
法
仍
然
有
效
。
( 2 ) 1 2 , 1 3 , 且 矩 阵 A 有 n 个第九线章性特无征关值与的特特征征向量向的量数值。求法
vk
k 1
[
1
x
1
(1)k 2 x2
(
3 1
)
k
3
x
3
(
n 1
)k
n
xn
]
由 上 式 可 知 , v k 是 个 摆 动 序 列 , 当 k 充 分 大 时 , 有
v1Au0(0,1,2)T,
1m a x (v1)2 , u 1v1(0 , 0 .5 ,1 )T , 1
v2A u 1(0 .5 , 2 ,2 .5 )T, 2 2.5,
u2
v2
2
(0.2,0.8,1)T,......
第九章 特征值与特征向量的数值求法
v 8 A u 7 ( 2 .7 6 5 0 9 4 8 , 2 .9 9 8 1 8 4 8 ,2 .9 9 9 0 9 2 4 ) T, 8 2 .9 9 9 0 9 2 4
数值分析课程设计+幂法与反幂法MATLAB

一、问题的描述及算法设计(一)问题的描述本次课程设计我所要做的课题是:对称矩阵的条件数的求解设计 1、求矩阵A 的二条件数问题 A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----210121012 2、设计内容: 1)采用幂法求出A 的. 2)采用反幂法求出A 的.3)计算A 的条件数 ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=/.(精度要求为10-6)3、设计要求 1)求出ⅡA Ⅱ2。
2)并进行一定的理论分析。
(二)算法设计1、幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)计算v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k(3)若| m k = m 1-k |<ε,则停止计算(m k 作为绝对值最大特征值1λ,u )(k 作为相应的特征向量)否则置k=k+1,转(2) 2、反幂法算法(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)对A 作LU 分解,即A=LU(3)解线性方程组 Ly )(k =u )1(-k ,Uv )(k =y )(k (4)计算m k =max(v )(k ), u )(k = v )(k / m k(5)若|m k =m 1-k |<ε,则停止计算(1/m k 作为绝对值最小特征值n λ,u )(k 作为相应的特征向量);否则置k=k+1,转(3).二、算法的流程图(一)幂法算法的流程图(二)反幂法算法的流程图三、算法的理论依据及其推导(一)幂法算法的理论依据及推导幂法是用来确定矩阵的主特征值的一种迭代方法,也即,绝对值最大的特征值。
稍微修改该方法,也可以用来确定其他特征值。
幂法的一个很有用的特性是它不仅可以生成特征值,而且可以生成相应的特征向量。
实际上,幂法经常用来求通过其他方法确定的特征值的特征向量。
数值分析3.1幂法和反幂法

第三章 矩阵的特征值与特征向量
3.1 幂法与反幂法 3.2 Jacobi方法
3.3 QR方法
第三章 矩阵的特征值与特征向量
3.1幂法与反幂法
一、乘幂法 二、反幂法
三、带原点位移的反幂法
四、反幂法的特点
第三章 矩阵的特征值与特征向量
3.1幂法与反幂法
一、乘幂法
1、基本思想
2、算法(迭代公式) ◆一般算法
具体算法: (1)使用范数 2
1 X 1 yk , k 1 1 X 1
(2)使用范数
uk A yk 1
令
k
er u k er y k 1
T
T
k
lim k 1
留为作业自学
具体算法: (1)使用范数 2 1 X 1 yk , k 1 1 X 1
1 2 n
第三章 矩阵的特征值与特征向量
一、乘幂法 1、基本思想 设A有n个线性无关的特征向量 X 1 , X 2 ,, X n ,
AX j j X j , j 1,2,, n
3.1幂法与反幂法
★ 设 1为实数而且是单根: 1 2 n
u0 1 X 1 2 X 2 n X n
具体算法: 按取范数的不同, 迭代公式也不同。 (1)使用范数 2
任取初始向量u0 R n T k 1 u k 1 u k 1 u k 1 yk 1 k 1 (3.4) u k A yk 1 k yk 1T uk k 1,2,
T
精确结果:
X 1 (0,0.5,1) , 1 45
T
max( uk ) 表示 u k 的绝对值最大的分量。 (3)
数值分析幂法与反幂法-matlab程序
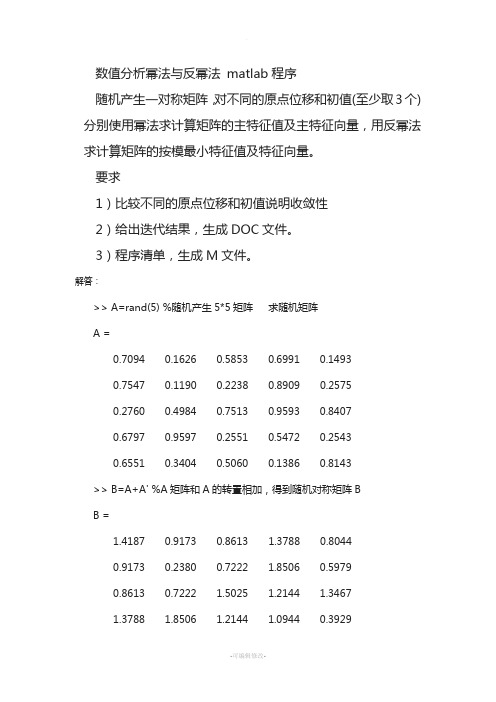
数值分析幂法与反幂法matlab程序随机产生一对称矩阵,对不同的原点位移和初值(至少取3个)分别使用幂法求计算矩阵的主特征值及主特征向量,用反幂法求计算矩阵的按模最小特征值及特征向量。
要求1)比较不同的原点位移和初值说明收敛性2)给出迭代结果,生成DOC文件。
3)程序清单,生成M文件。
解答:>> A=rand(5) %随机产生5*5矩阵求随机矩阵A =0.7094 0.1626 0.5853 0.6991 0.14930.7547 0.1190 0.2238 0.8909 0.25750.2760 0.4984 0.7513 0.9593 0.84070.6797 0.9597 0.2551 0.5472 0.25430.6551 0.3404 0.5060 0.1386 0.8143>> B=A+A' %A矩阵和A的转置相加,得到随机对称矩阵BB =1.4187 0.9173 0.8613 1.3788 0.80440.9173 0.2380 0.7222 1.8506 0.59790.8613 0.7222 1.5025 1.2144 1.34671.3788 1.8506 1.2144 1.0944 0.39290.8044 0.5979 1.3467 0.3929 1.6286B=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡6286.13929.03467.15979.08044.03929.00944.12144.18506.13788.13467.12144.15025.17222.08613.05979.08506.17222.02380.09173.08044.03788.18613.09173.04187.1编写幂法、反幂法程序:function [m,u,index,k]=pow(A,u,ep,it_max) % 求矩阵最大特征值的幂法,其中 % A 为矩阵;% ep 为精度要求,缺省为1e-5; % it_max 为最大迭代次数,缺省为100; % m 为绝对值最大的特征值; % u 为对应最大特征值的特征向量;% index ,当index=1时,迭代成功,当index=0时,迭代失败 if nargin<4 it_max=100; end if nargin<3 ep=1e-5; endn=length(A);index=0;k=0;m1=0;m0=0.01;% 修改移位参数,原点移位法加速收敛,为0时,即为幂法I=eye(n)T=A-m0*Iwhile k<=it_maxv=T*u;[vmax,i]=max(abs(v));m=v(i);u=v/m;if abs(m-m1)<ep;index=1;break;endm=m+m0;m1=m;k=k+1;endfunction[m,u,index,k]=pow_inv(A,u,ep,it_max)% 求矩阵最大特征值的反幂法,其中% A为矩阵;% ep为精度要求,缺省为1e-5;% it_max为最大迭代次数,缺省为100;% m为绝对值最大的特征值;% u为对应最大特征值的特征向量;% index,当index=1时,迭代成功,当index=0时,迭代失败if nargin<4it_max=100;endif nargin<3ep=1e-5;endn=length(A);index=0;k=0;m1=0;m0=0;% 修改移位参数,原点移位法加速收敛,为0时,即为反幂法I=eye(n);T=A-m0*I;invT=inv(T);while k<=it_maxv=invT*u;[vmax,i]=max(abs(v));m=v(i);u=v/m;if abs(m-m1)<epindex=1;break;endm1=m;k=k+1;endm=1/m;m=m+m0;修改输入的m0的值,所得结果:幂法:反幂法:THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
同济大学数值分析matlab编程

同济⼤学数值分析matlab编程MATLAB 编程题库1.下⾯的数据表近似地满⾜函数21cx bax y ++=,请适当变换成为线性最⼩⼆乘问题,编程求最好的系数c b a ,,,并在同⼀个图上画出所有数据和函数图像.625.0718.0801.0823.0802.0687.0606.0356.0995.0628.0544.0008.0213.0362.0586.0931.0ii y x ----解:>> x=[-0.931 -0.586 -0.362 -0.213 0.008 0.544 0.628 0.995]'; >> y=[0.356 0.606 0.687 0.802 0.823 0.801 0.718 0.625]'; >> A= [x ones(8,1) -x.^2.*y]; >> z=A\y;>> a=z(1); b=z(2); c=z(3); >>xh=[-1:0.1:1]';>>yh=(a.*xh+b)./(1+c.*xh.^2); >>plot(x,y,'r+',xh,yh,'b*')2.若在Matlab ⼯作⽬录下已经有如下两个函数⽂件,写⼀个割线法程序,求出这两个函数精度为1010-的近似根,并写出调⽤⽅式:>> edit gexianfa.mfunction [x iter]=gexianfa(f,x0,x1,tol) iter=0;x=x1;while(abs(feval(f,x))>tol) iter=iter+1;x=x1-feval(f,x1).*(x1-x0)./(feval(f,x1)-feval(f,x0)); x0=x1;x1=x; end>> edit f.m function v=f(x) v=x.*log(x)-1;>> edit g.m function z=g(y) z=y.^5+y-1;>> [x1 iter1]=gexianfa('f',1,3,1e-10) x1 =1.7632 iter1 = 6>> [x2 iter2]=gexianfa('g',0,1,1e-10) x2 =0.7549 iter2 = 83.使⽤GS 迭代求解下述线性代数⽅程组:123123123521242103103x x x x x x x x x ì++=--++=í???-+=??解:>> edit gsdiedai.mfunction [x iter]=gsdiedai(A,x0,b,tol) D=diag(diag(A)); L=D-tril(A); U=D-triu(A); iter=0; x=x0;>> A=[5 2 1;-1 4 2;1 -3 10]; >> b=[-12 10 3]'; >>tol=1e-4; >>x0=[0 0 0]';>> [x iter]=gsdiedai(A,x0,b,tol); >>x x =-3.0910 1.2372 0.9802 >>iter iter = 64.⽤四阶Range-kutta ⽅法求解下述常微分⽅程初值问题(取步长h=0.01),(1)2x dy y e xy dx y ì??=++?í??=??解:>> edit ksf2.mfunction v=ksf2(x,y)v=y+exp(x)+x.*y; >> a=1;b=2;h=0.01; >> n=(b-a)./h; >> x=[1:0.01:2]; >>y(1)=2;>>for i=2:(n+1)k1=h*ksf2(x(i-1),y(i-1));k2=h*ksf2(x(i-1)+0.5*h,y(i-1)+0.5*k1); k3=h*ksf2(x(i-1)+0.5*h,y(i-1)+0.5*k2); k4=h*ksf2(x(i-1)+h,y(i-1)+k3); y(i)=y(i-1)+(k1+2*k2+2*k3+k4)./6; end >>y调⽤函数⽅法>> edit Rangekutta.mfunction [x y]=Rangekutta(f,a,b,h,y0) x=[a:h:b]; n=(b-a)/h; y(1)=y0; for i=2:(n+1)k1=h*(feval(f,x(i-1),y(i-1)));k2=h*(feval(f,x(i-1)+0.5*h,y(i-1)+0.5*k1)); k3=h*(feval(f,x(i-1)+0.5*h,y(i-1)+0.5*k2)); k4=h*(feval(f,x(i-1)+h,y(i-1)+k3)); y(i)=y(i-1)+ (k1+2*k2+2*k3+k4)./6; end>> [x y]=Rangekutta('ksf2',1,2,0.01,2); >>y5.取0.2h =,请编写Matlab 程序,分别⽤欧拉⽅法、改进欧拉⽅法在12x ≤≤上求解初值问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题的描述及算法设计
(一)问题的描述
我所要做的课题是:对称矩阵的条件数的求解设计
1、求矩阵A 的二条件数
问题 A=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡----210121012 2、设计内容:
1)采用幂法求出A 的
. 2)采用反幂法求出A 的.
3)计算A 的条件数 ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=/.(精度要求为10-6) 3、设计要求
1)求出ⅡA Ⅱ2。
2)并进行一定的理论分析。
(二)算法设计
1、幂法算法
(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1.
(2)计算
v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k
(3)若| m k = m 1-k |<ε,则停止计算(m k 作为绝对值最大特征值1λ,u )(k 作为相应的特征向量)否则置k=k+1,转(2)
2、反幂法算法
(1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1.
(2)对A 作LU 分解,即A=LU
(3)解线性方程组 Ly )(k =u )1(-k ,Uv )(k =y )(k
(4)计算
m k =max(v )(k ), u )(k = v )(k / m k
(5)若|m k =m 1-k |<ε,则停止计算(1/m k 作为绝对值最小特征值n λ,u )(k 作为相应的特征向量);否则置k=k+1,转(3).
二、算法的流程图(一)幂法算法的流程图
(二)反幂法算法的流程图
三、算法的理论依据及其推导
(一)幂法算法的理论依据及推导
幂法是用来确定矩阵的主特征值的一种迭代方法,也即,绝对值最大的特征值。
稍微修改该方法,也可以用来确定其他特征值。
幂法的一个很有用的特性是它不仅可以生成特征值,而且可以生成相应的特征向量。
实际上,幂法经常用来求通过其他方法确定的特征值的特征向量。
1、幂法的迭代格式与收敛性质
设n 阶矩阵A 的特征值1λ,2λ,…,n λ是按绝对值大小编号的,x i (i=1,2,…,n)
为对应i λ的特征向量,且1λ为单根,即
|1λ|>|2λ|≥…≥|n λ|
则计算最大特征值与特征向量的迭代格式为
v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k (1)
其中max(v )(k )表示向量v )(k 绝对值的最大分量。
2、对于幂法的定理
按式(1)计算出m k 和u )(k 满足
∞>-k lim m k =1λ, ∞>-k lim u )(k =)
max(11x x (二)反幂法算法的理论依据及推导
反幂法是用来计算绝对值最小的特征值忽然相应的特征向量的方法。
是对幂法的修改,可以给出更快的收敛性。
1、反幂法的迭代格式与收敛性质
设A 是非奇异矩阵,则零不是特征值,并设特征值为
|1λ|≥|2λ|≥…≥|1-n λ|>|n λ|
则按A 1-的特征值绝对值的大小排序,有 |n λ1|>|11-n λ|≥…≥|11
λ|
对A 1-实行幂法,就可得A 1-的绝对值最大的特征值1/n λ和相应的特征向量,即A 的绝对值最小的特征值和相应的特征向量。
由于用A 1-代替A 作幂法计算,因此该方法称为反幂法,反幂法的迭代格式
为 v
)(k = A 1-u )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k (2)
2、对于反幂法的定理
按式(2)计算出的m k 和u )(k 满足:
∞>-k lim m k =n λ1, ∞>-k lim u )(k =)
max(n n x x 在式(2)中,需要用到A 1-,这给计算带来很大的不方便,因此,把(2)式的第一式改为求解线性方程组
A v )(k = u )1(-k (3) 但由于在反幂法中,每一步迭代都需求解线性方程组(3)式,迭代做了大量的重复计算,为了节省工作量,可事先把矩阵A 作LU 分解,即 A=LU
所以线性方程组(3)改为
Ly )(k =u )1(-k ,Uv )(k =y )
(k 四、相关的数值结果
(一)幂法程序的运行结果
m = 3.4142 u = -0.7071 index = 1
1.0000
-0.7071
(二)反幂法程序的运行结果
m 0 = 0.5858 u = 0.7071 index = 1
1.0000
0.7071
(三)矩阵A 的二条件数的结果
ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=m/ m 0=3.4142/0.5858=5.828269
五、数值计算结果的分析
求n阶方阵A的特征值和特征向量,是实际计算中常常碰到的问题。
对于n 阶矩阵A,若存在数λ和n维向量x满足
Ax=λx (1)
则称λ为矩阵A的特征值,x为相应的特征向量。
由线性代数知识可知,特征值是代数方程
|λI-A|=λn+a
1λ1-n+…+a
1-
n
λ+a
n
=0 (2)
的根。
从表面上看,矩阵特征值与特征向量的求解问题似乎很简单,只需求解方程(2)的根,就能得到特征值λ,再解齐次方程组
(λI-A)x=0 (3)
的解,就可得到相应的特征向量。
上述方法对于n很小时是可以的。
但当n稍大时,计算工作量将以惊人的速度增大,并且由于计算带有误差,方程(2)未必是精确的特征方程,自然就不必说求解方程(2)与(3)的困难了。
本次实验所用的幂法和反幂法分别是求解最大特征值和最小特征值,并根据它们的结果求解二条件数。
幂法和反幂法的Matlab程序很好的解决了手算时所会遇到的麻烦。
通过实验我们可以看到,幂法程序可以用来计算矩阵绝对值最大的特征值及相应的特征向量。
幂法的缺点是开始的时候并不知道矩阵是否有单一的主特征值。
也不知道如何选择x
以保证它关于矩阵特征向量的表达中包含一个与主特征值相关的非零特征向量。
反幂法程序可以用来计算矩阵绝对值最小的特征值及相应的特征向量,反幂法的收敛是线性的,它是对幂法的修改,可以给出更快的收敛性。
六、附件
(一) 幂法程序
/*幂法程序,函数名:pow.m*/
function[m,u,index]=pow(A,ep,N)
%A为矩阵;ep为精度要求;N为最大迭代次数;m为绝对值最大的特征值;u为对应最大特征值的特征向量。
N=100;
ep=1e-6;
n=length(A);u=ones(n,1);
index=0;k=0;m1=0;
while k<=N
v=A*u;[vmax,i]=max(abs(v));
m=v(i);u=v/m;
if abs(m-m1)<ep
index=1;break;
end
m1=m;k=k+1;
end
输入A=[2 -1 0;-1 2 -1;0 -1 2];
[m,u,index]=pow(A,1e-6)
(二) 反幂法程序
/*反幂法程序,函数名:pow_inv.m*/
,u,index]=pow_inv(A,ep,N)
function[m
%A为矩阵;ep为精度要求;N为最大迭代次数;m
为绝对值最小的特征值;u
为对应最小特征值的特征向量。
N=100;
ep=1e-6;
n=length(A);u=ones(n,1);
index=0;k=0;m1=0;
invA=inv(A);
while k<=N
v=invA*u;[vmax,i]=max(abs(v));
m
0=v(i);u=v/ m
;
if abs(m-m1)<ep index=1;break; end
m1 m
;k=k+1; end
m
0=1/ m
;
输入A=[2 -1 0;-1 2 -1;0 -1 2]; [m
,u,index]=pow_inv(A,1e-6)
七、参考文献:
(1)薛毅.数值分析与实验.北京工业大学出版社.2005
(2)杜廷松等. 数值分析及实验.科学出版社,2006
(3)Richard L.Burden等. 数值分析(第七版)高等教育出版社,2005
数理系课程设计评分表
教师签名:
日期:如有侵权请联系告知删除,感谢你们的配合!。
