k最近邻算法实验报告
代做算法实验报告

实验名称:基于K近邻算法的图像识别实验日期:2023年10月26日实验目的:1. 理解K近邻算法的基本原理。
2. 学习如何应用K近邻算法进行图像识别。
3. 评估K近邻算法在图像识别任务中的性能。
实验环境:- 操作系统:Windows 10- 编程语言:Python 3.8- 库:NumPy, Pandas, Matplotlib, Scikit-learn实验内容:本次实验采用K近邻算法对一组图像进行分类识别。
实验数据集为MNIST数据集,包含60000个训练样本和10000个测试样本。
实验步骤:1. 数据预处理:- 加载MNIST数据集,将图像数据转换为灰度图。
- 将图像数据归一化到[0, 1]区间。
- 将标签数据转换为独热编码形式。
2. 模型训练:- 将训练数据集分为训练集和验证集,用于训练和评估模型。
- 设置K近邻算法的参数,如K值、距离度量方法等。
- 使用训练集数据训练K近邻模型。
3. 模型评估:- 使用验证集数据评估模型的性能。
- 计算准确率、召回率、F1分数等指标。
4. 图像识别:- 使用训练好的模型对测试集数据进行图像识别。
- 统计识别结果,计算准确率。
实验结果与分析:1. 数据预处理:- 数据预处理过程顺利,图像数据已转换为灰度图并归一化。
2. 模型训练:- 设置K值为5,距离度量方法为欧氏距离。
- 模型训练时间约为2分钟。
3. 模型评估:- 使用验证集数据评估模型,准确率为97.5%。
- 召回率为97.3%,F1分数为97.4%。
4. 图像识别:- 使用训练好的模型对测试集数据进行图像识别,准确率为97.2%。
结论:本次实验成功实现了基于K近邻算法的图像识别。
实验结果表明,K近邻算法在图像识别任务中具有较高的准确率。
然而,K近邻算法的识别速度相对较慢,且对噪声数据较为敏感。
改进建议:1. 尝试不同的K值和距离度量方法,以提高模型性能。
2. 使用数据增强技术,增加训练数据集的多样性。
实验二K-近邻算法及应用

实验⼆K-近邻算法及应⽤K-近邻算法及应⽤所在班级实验要求学习⽬标理解K-近邻算法原理,能实现算法K近邻算法;学号3180701310【实验⽬的】理解K-近邻算法原理,能实现算法K近邻算法;掌握常见的距离度量⽅法;掌握K近邻树实现算法;针对特定应⽤场景及数据,能应⽤K近邻解决实际问题。
【实验内容】实现曼哈顿距离、欧⽒距离、闵式距离算法,并测试算法正确性。
实现K近邻树算法;针对iris数据集,应⽤sklearn的K近邻算法进⾏类别预测。
针对iris数据集,编制程序使⽤K近邻树进⾏类别预测。
【实验报告要求】对照实验内容,撰写实验过程、算法及测试结果;代码规范化:命名规则、注释;分析核⼼算法的复杂度;查阅⽂献,讨论K近邻的优缺点;举例说明K近邻的应⽤场景。
【实验运⾏结果】【实验代码及其注释】⼀、距离度量利⽤python代码遍历三个点中,与1点距离最近的点# 导⼊所需要的包import mathfrom itertools import combinations# 当p=1时,就是曼哈顿距离;# 当p=2时,就是欧⽒距离;# 当p=inf时,就是闵式距离。
# 函数主要⽤于距离测算def L(x, y, p=2):# x1 = [1, 1], x2 = [5,1]if len(x) == len(y) and len(x) > 1:sum = 0for i in range(len(x)):sum += math.pow(abs(x[i] - y[i]), p)return math.pow(sum, 1/p)else:return 0# 输⼊样例,该列来源于课本x1 = [1, 1]x2 = [5, 1]x3 = [4, 4]# 计算x1与x2和x3之间的距离for i in range(1, 5): # i从1到4r = { '1-{}'.format(c):L(x1, c, p=i) for c in [x2, x3]} # 创建⼀个字典print(min(zip(r.values(), r.keys()))) # 当p=i时选出x2和我x3中距离x1最近的点输出:⼆、编写K-近邻算法python实现,遍历所有数据点,找出n个距离最近的点的分类情况,少数服从多数(不使⽤直接的python中现有的K-近邻算法包) # 导包import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom collections import Counter# data 输⼊数据iris = load_iris() # 获取python中鸢尾花Iris数据集df = pd.DataFrame(iris.data, columns=iris.feature_names) # 将数据集使⽤DataFrame建表df['label'] = iris.target # 将表的最后⼀列作为⽬标列df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label'] # 定义表中每⼀列# data = np.array(df.iloc[:100, [0, 1, -1]])df # 将建好的表显⽰在屏幕上查看输出:# 绘制数据散点图plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0') # 绘制前50个数据的散点图plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1') # 绘制50-100个数据的散点图plt.xlabel('sepal length')plt.ylabel('sepal width') # 设置x,y轴坐标名plt.legend() # 绘图注释:train_test_split()是分离器函数,⽤于将数组或矩阵划分为训练集和测试集,函数样式为:X_train, X_test, y_train, y_test = train_test_split(train_data, train_target, test_size, random_state,shuffle)train_data:待划分的样本数据train_target:待划分的对应样本数据的样本标签test_size:1)浮点数,在0 ~ 1之间,表⽰样本占⽐(test_size = 0.3,则样本数据中有30%的数据作为测试数据,记⼊X_test,其余70%数据记⼊X_train,同时适⽤于样本标签);2)整数,表⽰样本数据中有多少数据记⼊X_test中,其余数据记⼊X_train)data = np.array(df.iloc[:100, [0, 1, -1]]) # iloc函数:通过⾏号来取⾏数据,读取数据前100⾏的第0,1列和最后⼀列# X为data数据集中去除最后⼀列所形成的新数据集# y为data数据集中最后⼀列数据所形成的新数据集X, y = data[:,:-1], data[:,-1]# 选取训练集,和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 建⽴⼀个类KNN,⽤于k-近邻的计算class KNN:#初始化def __init__(self, X_train, y_train, n_neighbors=3, p=2): # 初始化数据,neighbor表⽰邻近点,p为欧⽒距离self.n = n_neighborsself.p = pself.X_train = X_trainself.y_train = y_traindef predict(self, X):# X为测试集knn_list = []for i in range(self.n): # 遍历邻近点dist = np.linalg.norm(X - self.X_train[i], ord=self.p) # 计算训练集和测试集之间的距离knn_list.append((dist, self.y_train[i])) # 在列表末尾添加⼀个元素for i in range(self.n, len(self.X_train)): # 3-20max_index = knn_list.index(max(knn_list, key=lambda x: x[0])) # 找出列表中距离最⼤的点dist = np.linalg.norm(X - self.X_train[i], ord=self.p) # 计算训练集和测试集之间的距离if knn_list[max_index][0] > dist: # 若当前数据的距离⼤于之前得出的距离,就将数值替换knn_list[max_index] = (dist, self.y_train[i])# 统计knn = [k[-1] for k in knn_list]count_pairs = Counter(knn) # 统计标签的个数max_count = sorted(count_pairs, key=lambda x:x)[-1] # 将标签升序排列return max_count# 计算测试算法的正确率def score(self, X_test, y_test):right_count = 0n = 10for X, y in zip(X_test, y_test):label = self.predict(X)if label == y:right_count += 1return right_count / len(X_test)11、clf = KNN(X_train, y_train) # 调⽤KNN算法进⾏计算12、clf.score(X_test, y_test) # 计算正确率输出:test_point = [6.0, 3.0] # ⽤于算法测试的数据print('Test Point: {}'.format(clf.predict(test_point))) # 结果输出:plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0') # 将数据的前50个数据绘制散点图plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1') # 将数据的50-100个数据绘制散点图plt.plot(test_point[0], test_point[1], 'bo', label='test_point') # 将测试数据点绘制在图中plt.xlabel('sepal length')plt.ylabel('sepal width') # x,y轴命名plt.legend() # 绘图输出:三、使⽤scikitlearn中编好的包直接调⽤实现K-近邻算法sklearn.neighbors.KNeighborsClassifiern_neighbors: 临近点个数p: 距离度量algorithm: 近邻算法,可选{'auto', 'ball_tree', 'kd_tree', 'brute'}weights: 确定近邻的权重15、# 导包from sklearn.neighbors import KNeighborsClassifier# 调⽤clf_sk = KNeighborsClassifier()clf_sk.fit(X_train, y_train)输出:clf_sk.score(X_test, y_test) # 计算正确率输出:四、针对iris数据集,编制程序使⽤K近邻树进⾏类别预测建造kd树# 建造kd树# kd-tree 每个结点中主要包含的数据如下:class KdNode(object):def __init__(self, dom_elt, split, left, right):self.dom_elt = dom_elt#结点的⽗结点self.split = split#划分结点self.left = left#做结点self.right = right#右结点class KdTree(object):def __init__(self, data):k = len(data[0])#数据维度#print("创建结点")#print("开始执⾏创建结点函数")def CreateNode(split, data_set):#print(split,data_set)if not data_set:#数据集为空return None#print("进⼊函数")data_set.sort(key=lambda x:x[split])#开始找切分平⾯的维度#print("data_set:",data_set)split_pos = len(data_set)//2 #取得中位数点的坐标位置(求整)median = data_set[split_pos]split_next = (split+1) % k #(取余数)取得下⼀个节点的分离维数return KdNode(median,split,CreateNode(split_next, data_set[:split_pos]),#创建左结点CreateNode(split_next, data_set[split_pos+1:]))#创建右结点#print("结束创建结点函数")self.root = CreateNode(0, data)#创建根结点#KDTree的前序遍历def preorder(root):print(root.dom_elt)if root.left:preorder(root.left)if root.right:preorder(root.right)遍历kd树# 遍历kd树#KDTree的前序遍历def preorder(root):print(root.dom_elt)if root.left:preorder(root.left)if root.right:preorder(root.right)from math import sqrtfrom collections import namedtuple# 定义⼀个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数result = namedtuple("Result_tuple","nearest_point nearest_dist nodes_visited")#搜索开始def find_nearest(tree, point):k = len(point)#数据维度def travel(kd_node, target, max_dist):if kd_node is None:return result([0]*k, float("inf"), 0)#表⽰数据的⽆nodes_visited = 1s = kd_node.split #数据维度分隔pivot = kd_node.dom_elt #切分根节点if target[s] <= pivot[s]:nearer_node = kd_node.left #下⼀个左结点为树根结点further_node = kd_node.right #记录右节点else: #右⾯更近nearer_node = kd_node.rightfurther_node = kd_node.lefttemp1 = travel(nearer_node, target, max_dist)nearest = temp1.nearest_point# 得到叶⼦结点,此时为nearestdist = temp1.nearest_dist #update distancenodes_visited += temp1.nodes_visitedprint("nodes_visited:", nodes_visited)if dist < max_dist:max_dist = disttemp_dist = abs(pivot[s]-target[s])#计算球体与分隔超平⾯的距离if max_dist < temp_dist:return result(nearest, dist, nodes_visited)# -------#计算分隔点的欧式距离temp_dist = sqrt(sum((p1-p2)**2 for p1, p2 in zip(pivot, target)))#计算⽬标点到邻近节点的Distance if temp_dist < dist:nearest = pivot #更新最近点dist = temp_dist #更新最近距离max_dist = dist #更新超球体的半径print("输出数据:" , nearest, dist, max_dist)# 检查另⼀个⼦结点对应的区域是否有更近的点temp2 = travel(further_node, target, max_dist)nodes_visited += temp2.nodes_visitedif temp2.nearest_dist < dist: # 如果另⼀个⼦结点内存在更近距离nearest = temp2.nearest_point # 更新最近点dist = temp2.nearest_dist # 更新最近距离return result(nearest, dist, nodes_visited)return travel(tree.root, point, float("inf")) # 从根节点开始递归# 数据测试data= [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]kd=KdTree(data)preorder(kd.root)输出:# 导包from time import clockfrom random import random# 产⽣⼀个k维随机向量,每维分量值在0~1之间def random_point(k):return [random() for _ in range(k)]# 产⽣n个k维随机向量def random_points(k, n):return [random_point(k) for _ in range(n)]# 输⼊数据进⾏测试ret = find_nearest(kd, [3,4.5])print (ret)输出:N = 400000t0 = clock()kd2 = KdTree(random_points(3, N)) # 构建包含四⼗万个3维空间样本点的kd树ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四⼗万个样本点中寻找离⽬标最近的点t1 = clock()print ("time: ",t1-t0, "s")print (ret2)输出:查阅⽂献,讨论K近邻的优缺点;1.k kk近邻法是基本且简单的分类与回归⽅法。
K近邻分类算法范文

K近邻分类算法范文K近邻(K Nearest Neighbors,KNN)分类算法是一种基本的机器学习算法,用于解决分类问题。
它是一种非参数算法,可以用于处理离散和连续型特征的数据集。
本文将详细介绍KNN算法的原理、步骤和算法的优缺点。
一、KNN算法原理1.计算距离:对于新样本,需要与训练集中每个样本计算距离。
常用的距离度量方法有欧式距离、曼哈顿距离和闵可夫斯基距离等。
2.选择K个最近邻居:根据距离选择K个最近邻居。
K的选择是一个重要参数,通常通过交叉验证来确定。
4.输出分类结果:将新样本标记为投票结果的类别。
二、KNN算法步骤KNN算法的步骤如下:1.数据预处理:对训练集进行数据预处理,包括特征标准化、缺失值处理和离散特征转换等。
2.特征选择:通过统计分析、特征重要性评估等方法选择合适的特征。
3.计算距离:对于新样本,计算它与训练集中每个样本的距离。
4.选择最近邻:根据距离选择K个最近邻居。
6.进行预测:将新样本标记为投票结果的类别。
7.模型评估:使用评估指标(如准确率、召回率和F1分数等)评估模型性能。
三、KNN算法的优缺点KNN算法具有以下优点:1.简单易理解:KNN算法的原理直观简单,易于理解和实现。
2.无假设:KNN算法不需要对数据做任何假设,适用于多种类型的数据。
3.非参数模型:KNN算法是一种非参数学习算法,不对数据分布做任何假设,适用于复杂的数据集。
KNN算法也有以下缺点:1.计算复杂度高:KNN算法需要计算新样本与训练集中所有样本的距离,计算复杂度较高,尤其是在大数据集上。
2.内存开销大:KNN算法需要保存整个训练集,占用内存较大。
3.对数据特征缩放敏感:KNN算法对特征缩放敏感,如果特征尺度不同,可能会导致距离计算不准确。
四、总结KNN算法是一种简单而有效的分类算法,适用于多种类型的数据。
通过计算新样本与训练集中所有样本的距离,并选择最近的K个邻居进行投票决策,可以得到新样本的分类结果。
模式识别大作业-k近邻
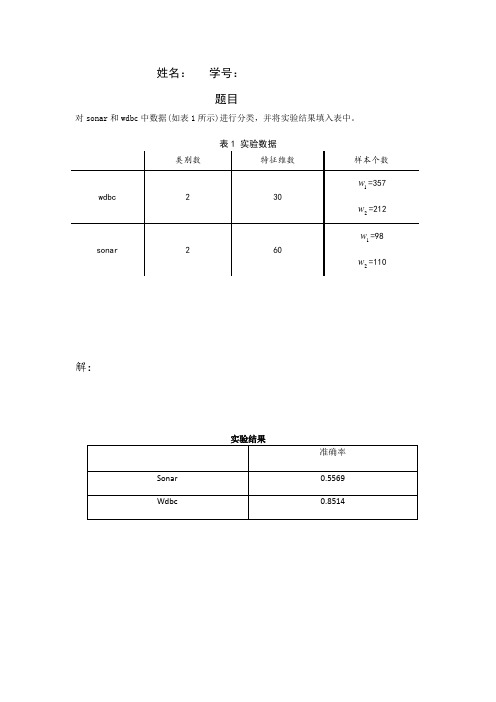
姓名:学号:题目对sonar和wdbc中数据(如表1所示)进行分类,并将实验结果填入表中。
解:实验结果K-Means聚类算法一.算法思想K-均值算法的主要思想是先在需要分类的数据中寻找K组数据作为初始聚类中心,然后计算其他数据距离这三个聚类中心的距离,将数据归入与其距离最近的聚类中心,之后再对这K个聚类的数据计算均值,作为新的聚类中心,继续以上步骤,直到新的聚类中心与上一次的聚类中心值相等时结束算法。
在本次算法实现中,选择在两类样本点中随机选择两个点作为两类数据的初始聚类中心,然后在开始迭代,计算,直至找到最优分类。
二.算法流程图三.程序运行结果1、对sonar数据进行k均值聚类表一:sonar(Kmeans)程序迭代次数:6得到第一类聚类中心是(0.0325 0.0443 0.0469 0.0585 0.0717 0.0983 0.1162 0.1306 0.1742 0.19900.2179 0.2389 0.2562 0.2737 0.2965 0.3458 0.3568 0.3937 0.4486 0.5130 0.5266 0.4825 0.4894 0.5234 0.5312 0.5745 0.5790 0.6056 0.5951 0.5803 0.5220 0.4791 0.5020 0.5387 0.5508 0.5327 0.4823 0.4541 0.4271 0.3914 0.3547 0.3225 0.2724 0.2381 0.2208 0.1799 0.1263 0.0908 0.0525 0.0223 0.0161 0.0144 0.0118 0.0118 0.0107 0.0091 0.0091 0.0089 0.0094 0.0073)得到第二类聚类中心是(0.0264 0.0336 0.0413 0.0501 0.0781 0.1097 0.1263 0.1383 0.1811 0.2159 0.2510 0.2596 0.2874 0.3155 0.3397 0.4055 0.4647 0.5007 0.5511 0.6043 0.6771 0.7411 0.7769 0.7957 0.7943 0.8032 0.8037 0.7669 0.6808 0.5814 0.4900 0.4060 0.3473 0.2916 0.2621 0.2630 0.2661 0.2453 0.2422 0.2450 0.2353 0.2418 0.2252 0.1943 0.1778 0.1447 0.1193 0.0919 0.05140.0189 0.0160 0.0126 0.0098 0.0102 0.0081 0.0075 0.0068 0.0072 0.0067 0.0058)2、对wdbc数据进行k均值聚类表二:wdbc(Kmeans)运行了几次程序,发现准确率一直保持不变,分析可能是由于两类数据比较集中而类间距离又足够大导致,随机选择的样本点对数据分类没有产生什么影响。
K-近邻算法

K-近邻算法目录一、K-近邻算法优缺点二、K.近邻算法工作原理及示例三、K-近邻算法的一般流程四、准备:使用Python导入数据通实施kNN分类算法六、示例L改进约会网站的配对结果七:示例2:手写识别系统K-近邻算法优缺点简单地说,K.近邻算法(又称KNN)采用测量不同特征值之间的距离方法进行分类。
其优缺点及适用数据范围如下:优点:精度高、对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高。
适用数据罐;数值型和标称型。
示例:手写识别系统3.测试算法:之前我们将数据处理成分类器可以识别的格式,现在我们将这些数据输入到分类器,检测分类器的执行效果。
def handwritingClassTest():hwLabels=[]trainingFileList=listdirCtrainingDigits*)#获取目录中的文件内容存储于列表中m=len(trainingFileList)trainingMat=zeros((m,1024))for i in range(m):fileNameStr二traininTFileList【ilfileStr二fileNameStr・split(?H01tftake off・txta trainingMat[i/]=i mg2vector('tra i n i ng Digits/%s,%fileNameStr)dassNumStr二int(fileStr・split(''HOI)#从文件名解析分类数字hwLabels.append(classNumStr)testFileList=listdir('testDigits')iterate through the test seterrorCount=0.0mTest=len(testFileList)for i in range(mTest):fileNameStr=testFileList[i]fileStr=fileNameStr.split('.')[O]#take off.txtclassNumStr=int(fileStr.split('_')vectorUnderTest=img2vector('testDigits/%s'%fileNameStr)classifierResult=classify Of^ectorUnderTest,trainingMat,hwLabels,3)print"the classifier came back with:%d,the real answer is:%d"%(classifierResult,classNumStr)if(classifierResult!=classNumStr):errorCount+=1.0print"\nthe total number of errors is:%d"%errorCountprint”\nthe total error rate is:%f"%(errorCount/float(mTest))示例:手写识别系统(2)上述代码所示的自包含函数handwritingClassTest。
人工智能实验-k-近邻算法

k-近邻算法一、 实验题目1. kNN 代码实现-AB 分类采用测量不同特征值之间的距离方法进行分类,用所给的函数创建具有两个特征与一个标签类型的数据作 为训练集,编写 classify0 函数对所给的数据进行 AB 分类。
2. k-近邻算法改进约会网站的配对效果k-近邻算法改进约会网站的配对效果通过收集的一些约会网站的数据信息,对匹配对象的归类:不喜欢的人、魅力一般的人、极具魅力的人。
数据中包含了 3 种特征:每年获得的飞行常客里程数、玩视频游戏所耗时间百分比、每周消费的冰淇淋公升数二、 实验代码1. kNN 代码实现-AB 分类kNN from http.client import ImproperConnectionStatefrom numpy import ∗ from collections importCounter import operator def createDataSet():group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])labels = [’A ’, ’A ’, ’B’, ’B’] return group, labelsdef classify0(inX, group, labels, k = 3):res1 = (inX − group)∗∗2 dist =res1[:,0] + res1[:,1] dic = argsort(dist) dic = dic[0:k:1] newdic = [] for i in range (k): newdic.append(labels[dic[i]]) c = Counter(newdic).most_common(1) return c[0][0] tests import kNN group, lables = kNN.createDataSet() print (’分类结果’) print (’[0,0] %c’ %(kNN.classify0([0, 0], group, lables, k = 3))) print (’[0.8,0.7] %c’ %(kNN.classify0([0.8, 0.7], group, lables, k = 3)))2.k-近邻算法改进约会网站的配对效果1 2 3 4 5 67 8 910111213141516171819 1 2 3 4 5import pandas as pdimport kNNfrom sklearn.model_selection import train_test_splitdf = pd.read_table(’datingTestSet2.txt’,sep=’\s+’, names = [’A ’, ’B’, ’C’, ’Y’])# 对特征进行归一化处理df2 = df.iloc[:, :3] df2 =(df2−df2.mean())/df2.std() lable=df.iloc[:,3:4] df2.loc[:, ’Y’] =lable# 对数据集进行测试集和训练集划分,90%作为训练集,10%作为测试集X_train, X_test, Y_train, Y_test = train_test_split(df2.iloc[:, :3], df2.Y, train_size=.90)# 将DataFrame 格式转化为numpy 格式处理 group = X_train.values label =Y_train.values length =len (X_test) X_test.iloc[0:1,:]# res 以储存测试结果res = []# 设置错误正确数count 以计算正确率Tnum = 0 Fnum = 0 for iin range (length):inX = X_test.iloc[i:i+1 , :].values res.append(kNN.classify0(inX,group, label, k = 3)) if (kNN.classify0(inX, group, label, k = 3) ==Y_test.values[i]):Tnum += 1 else :Fnum += 1res1 = pd.DataFrame(data = res, columns=[’TestResult’])Y_test.reset_index(inplace=True,drop=True)res1.loc[:, ’OriginTest’] = Y_testprint (’前20个数据测试结果和原数据比较’) print (’−−−−−−−−−−−−−−−−−−−−−——−−−−’) print (res1.head(20))print (’−−−−−−−−−−−−−−−−−−−−−——−−−−’) print (’正确率%.2f%%’ %(100∗Tnum/(Tnum+Fnum))) 三、 实验结果及分析1. kNN 代码实现-AB 分类分类结果[0, 0] B[0.8, 0.7] A2. k-近邻算法改进约会网站的配对效果1 2 3 45 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 27 28 29 3031 32 33 3435363738 1 2 3前20个数据测试结果和原数据比较−−−−−−−−−−−−−−−−−−−−−——−−−TestResult OriginTest0 2 2 1 3 3 2 1 3 3 2 2 4 2 2 5 3 3 6 3 3 7 2 2 8 1 1 9 1 1 10 1 1 11 3 3 12 2 2 13 2 2 14 1 1 15 2 2 16 1 1 17 2 2 18 1 1 19 3 3−−−−−−−−−−−−−−−−−−−−−——−−− 正确率97.00%从实验结果可以看出,通过 k-近邻算法改进后的约会网站的配对效果比较显著,多次随机划分测试集和训练集后发现正确率基本可以达到 90% 以上。
(完整版)KNN算法实验报告

KNN算法实验报告一试验原理K最近邻(k-NearestNeighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN算法中,所选择的邻居都是已经正确分类的对象。
该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。
由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
KNN算法不仅可以用于分类,还可以用于回归。
通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。
无论怎样,数量并不能影响运行结果。
可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
二试验步骤那么根据以上的描述,我把结合使用反余弦匹配和kNN结合的过程分成以下几个步骤:1.计算出样本数据和待分类数据的距离2.为待分类数据选择k个与其距离最小的样本3.统计出k个样本中大多数样本所属的分类4.这个分类就是待分类数据所属的分类数学表达:目标函数值可以是离散值(分类问题),也可以是连续值(回归问题).函数形势为f:n维空间R—〉一维空间R。
算法实验报告范文

实验题目:K近邻算法(K-Nearest Neighbors, KNN)在鸢尾花数据集上的应用一、实验目的1. 理解K近邻算法的基本原理和实现过程。
2. 掌握K近邻算法在分类问题中的应用。
3. 通过实验验证K近邻算法在鸢尾花数据集上的性能。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 库:NumPy,Matplotlib,Scikit-learn三、实验原理K近邻算法(KNN)是一种基于距离的最近邻分类算法。
其基本思想是:对于待分类的数据点,找到与它距离最近的K个数据点,这K个数据点中多数属于某个类别,则待分类数据点也属于该类别。
K近邻算法的步骤如下:1. 计算待分类数据点与训练集中每个数据点的距离。
2. 找到距离最近的K个数据点。
3. 根据这K个数据点的多数类别,对待分类数据点进行分类。
四、实验数据本次实验使用鸢尾花数据集(Iris dataset),该数据集包含150个样本,每个样本有4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度),分为3个类别(setosa,versicolor,virginica)。
五、实验步骤1. 导入所需库和数据集。
```pythonfrom sklearn import datasetsfrom sklearn.model_selection import train_test_splitfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn.metrics import accuracy_scoreimport matplotlib.pyplot as pltimport numpy as np# 加载数据集iris = datasets.load_iris()X = iris.datay = iris.target```2. 数据预处理。
```python# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)```3. 实现K近邻算法。
人工智能实验报告

⼈⼯智能实验报告⼈⼯智能课程项⽬报告姓名:班级:⼆班⼀、实验背景在新的时代背景下,⼈⼯智能这⼀重要的计算机学科分⽀,焕发出了他强⼤的⽣命⼒。
不仅仅为了完成课程设计,作为计算机专业的学⽣,了解他,学习他我认为都是很有必要的。
⼆、实验⽬的识别⼿写字体0~9三、实验原理⽤K-最近邻算法对数据进⾏分类。
逻辑回归算法(仅分类0和1)四、实验内容使⽤knn算法:1.创建⼀个1024列矩阵载⼊训练集每⼀⾏存⼀个训练集2.把测试集中的⼀个⽂件转化为⼀个1024列的矩阵。
3.使⽤knnClassify()进⾏测试4.依据k的值,得出结果使⽤逻辑回归:1.创建⼀个1024列矩阵载⼊训练集每⼀⾏存⼀个训练集2.把测试集中的⼀个⽂件转化为⼀个1024列的矩阵。
3.使⽤上式求参数。
步长0.07,迭代10次4.使⽤参数以及逻辑回归函数对测试数据处理,根据结果判断测试数据类型。
五、实验结果与分析5.1实验环境与⼯具Window7旗舰版+python2.7.10+numpy(库)+notepad++(编辑)Python这⼀语⾔的发展是⾮常迅速的,既然他⽀持在window下运⾏就不必去搞虚拟机。
5.2实验数据集与参数设置Knn算法:训练数据1934个,测试数据有946个。
数据包括数字0-9的⼿写体。
每个数字⼤约有200个样本。
每个样本保持在⼀个txt⽂件中。
⼿写体图像本⾝的⼤⼩是32x32的⼆值图,转换到txt⽂件保存后,内容也是32x32个数字,0或者1,如下图所⽰建⽴⼀个kNN.py脚本⽂件,⽂件⾥⾯包含三个函数,⼀个⽤来⽣成将每个样本的txt⽂件转换为对应的⼀个向量:img2vector(filename):,⼀个⽤来加载整个数据库loadDataSet():,最后就是实现测试。
5.3评估标准看测试数与测试结果是否相同。
相同输出结果正确,否则输出结果错误。
5.4实验结果与分析实验分析:KNN算法可以说是使⽤蛮⼒进⾏分类,每进⾏⼀个测试样本的判断,都要对所以的训练集操作⼀次,时间复杂度和空间复杂度都会随着训练集和测试集的数量⽽增加。
Parzen窗估计与KN近邻估计实验报告材料

模式识别实验报告题目:Parzen 窗估计与KN 近邻估计学 院 计算机科学与技术 专 业 xxxxxxxxxxxxxxxx 学 号 xxxxxxxxxxxx 姓 名 xxxx 指导教师 xxxx20xx 年xx 月xx 日Parzen 窗估计与KN 近邻估计一、实验目的装 订 线本实验的目的是学习Parzen窗估计和k最近邻估计方法。
在之前的模式识别研究中,我们假设概率密度函数的参数形式已知,即判别函数J(.)的参数是已知的。
本节使用非参数化的方法来处理任意形式的概率分布而不必事先考虑概率密度的参数形式。
在模式识别中有躲在令人感兴趣的非参数化方法,Parzen窗估计和k最近邻估计就是两种经典的估计法。
二、实验原理1.非参数化概率密度的估计对于未知概率密度函数的估计方法,其核心思想是:一个向量x落在区域R中的概率可表示为:其中,P是概率密度函数p(x)的平滑版本,因此可以通过计算P来估计概率密度函数p(x),假设n个样本x1,x2,…,xn,是根据概率密度函数p(x)独立同分布的抽取得到,这样,有k个样本落在区域R中的概率服从以下分布:其中k的期望值为:k的分布在均值附近有着非常显著的波峰,因此若样本个数n足够大时,使用k/n作为概率P的一个估计将非常准确。
假设p(x)是连续的,且区域R足够小,则有:如下图所示,以上公式产生一个特定值的相对概率,当n趋近于无穷大时,曲线的形状逼近一个δ函数,该函数即是真实的概率。
公式中的V是区域R所包含的体积。
综上所述,可以得到关于概率密度函数p(x)的估计为:在实际中,为了估计x处的概率密度函数,需要构造包含点x的区域R1,R2,…,Rn。
第一个区域使用1个样本,第二个区域使用2个样本,以此类推。
记Vn为Rn的体积。
kn为落在区间Rn中的样本个数,而pn (x)表示为对p(x)的第n次估计:欲满足pn(x)收敛:pn(x)→p(x),需要满足以下三个条件:有两种经常采用的获得这种区域序列的途径,如下图所示。
Parzen窗估计及KN近邻估计实验报告总结计划

Parzen窗估计及KN近邻估计实验报告总结计划装订线模式辨别实验报告题目:Parzen窗预计与KN近邻预计学院计算机科学与技术专业xxxxxxxxxxxxxxxx学号xxxxxxxxxxxx姓名xxxx指导教师xxxx20xx年xx月xx日1.Parzen窗预计与KN近邻预计一、实验目的本的目的是学Parzen窗估和k近来估方法。
在以前的模式研究中,我假概率密度函数的参数形式已知,即判函数J(.)的参数是已知的。
本使用非参数化的方法来理随意形式的概率散布而不用预先考概率密度的参数形式。
在模式中有在令人感趣的非参数化方法,Parzen窗估和k近来估就是两种典的估法。
二、实验原理非参数化概率密度的预计于未知概率密度函数的估方法,此中心思想是:一个向量x落在地区R中的概率可表示:此中,P是概率密度函数p(x)的光滑版本,所以能够通算P来估概率密度函数p(x),假n个本x1,x2,⋯,xn,是依据概率密度函数p(x)独立同散布的抽取获得,,有k个本落在地区R中的概率听从以下散布:此中k的希望:概率k的散布在均邻近有着特别著的波峰,所以若本个数P的一个估将特别正确。
假p(x)是的,且地区n足大,使用R足小,有:k/n作以下所示,以上公式生一个特定的相概率,迫近一个δ函数,函数即是真的概率。
公式中的能够获得对于概率密度函数p(x)的估:当n近于无大,曲的形状V是地区R所包括的体。
上所述,在中,了估x的概率密度函数,需要结构包括点x的地区R1,R2,⋯,Rn。
第一个地区使用1个本,第二个地区使用2个本,以此推。
VnRn的体。
kn落在区Rn中的本个数,而pn(x)表示p(x)的第n次估:欲足pn(x)收:pn(x)→p(x),需要足以下三个条件:有两种常采纳的得种地区序列的门路,以下所示。
此中“Parzen窗方法”就是根据某一个确立的体函数,比方Vn=1/√n来逐收一个定的初始区。
就要求随机量kn和kn/n能保pn(x)能收到p(x)。
基于K最近邻距离的离群点挖掘实验

数据挖掘技术学生姓名:学号:专业:计算机科学与技术班级:一、实验名称:基于K最近邻距离的离群点挖掘实验二、实验目的1、掌握基于K最近邻距离的离群点的数据挖掘算法2、通过查找数据中的离群点对数据进行异常分析三、实验数据Clementine数据质量的探究主要包括数据缺失问题、数据离群点和极端值两大方面。
离群点是指数据中,远离数值的一般水平的极端大值和极端小值,也称之为歧异值,有时也称其为野值,其对后续的数据处理有很大的影响;本文研究的目的是拟建立适当的数学模型,评判出一组数据中的离群点,并对出现的离群点进行处理。
本示例将离群点模型应用于开河数据提取,其中的目标字段为开河日期天数。
变量字Clementine段包括0221-0302三湖河口平均流量(X1),0109-0126平均流量(X2),0221-0302平均流量(X3),二月下旬平均水位(X4),最高气温转正日到0302累计最高正气温(X5),0221-0302气温和(X6)(为绝对温度),二月下旬平均气温(X7)(为绝对温度)最高气温转正天数(X8)(连续为正日期距离2月1日的天数,考虑到可能出现负数,因此+30),最大冰厚(X9)。
此示例使用名为 Stream1.str 的流,该流引用名为开河数据.xls 的数据文件。
这些文件可以任何 Clementine Client 程序打开。
此目录可通过 Windows “开始”菜单的 Clementine 程序组进行访问。
四、实验原理基于邻近度的离群点检测是指一个对象是异常的,如果它远离大部分点。
这种方法比统计学方法更一般、更容易使用,因为确定数据集的有意义的邻近性度量比确定它的统计分布更容易。
一个对象的离群点得分由到它的k-最近邻的距离给定。
离群点得分对k的取值高度敏感。
如果k太小(例如1),则少量的邻近离群点可能导致较低的离群点得分;如果K太大,则点数少于k的簇中所有的对象可能都成了离群点。
为了使该方案对于k的选取更具有鲁棒性,可以使用k个最近邻的平均距离。
k近邻算法的原理和实现过程

k近邻算法的原理和实现过程
k近邻算法是一种基本的分类和回归算法,它的原理和实现过程如下:
原理:
1. 确定一个样本的k个最近的邻居,即选取与该样本距离最近的k个样本。
2. 根据这k个最近邻居的标签进行投票或者加权,确定该样本的预测标签。
如果
是分类问题,那么选取票数最多的标签作为预测标签;如果是回归问题,那么选
取k个最近邻居的标签的平均值作为预测标签。
实现过程:
1. 准备数据集:收集已知样本和其对应的标签。
2. 确定距离度量准则:选择合适的距离度量准则来度量样本间的距离,例如欧氏
距离、曼哈顿距离等。
3. 选择合适的k值:根据问题的要求选择适当的k值。
4. 计算样本之间的距离:对于每个未知样本,计算它与已知样本之间的距离,选
择k个最近邻居。
5. 统计k个最近邻居的标签:对于分类问题,统计k个最近邻居的标签的出现次数,并选择出现次数最多的标签作为预测标签;对于回归问题,计算k个最近邻
居的标签的平均数作为预测标签。
6. 将样本进行分类或预测:根据预测标签将未知样本进行分类或预测。
需要注意的是,在实际应用中,可以采取一些优化措施来提高k近邻算法的效率,比如使用kd树来加速最近邻搜索过程。
还可以对特征进行归一化处理,以避免
某些特征的权重过大对距离计算的影响。
k-近邻算法实例 -回复

k-近邻算法实例-回复什么是k近邻算法,以及如何在实践中应用它?k近邻算法(k-Nearest Neighbors,简称kNN算法)是一种用于分类和回归问题的非参数化机器学习算法。
在分类问题中,kNN算法通过计算新样本与已知样本的距离,找到其k个最近邻居,并将新样本分配到与其最相似的类别中。
在回归问题中,kNN算法将新样本的目标值设为其k个最近邻居的平均值。
kNN算法的基本思想是新样本与已知样本的相似性取决于它们在特征空间中的距离。
在实践中,kNN算法具有许多应用场景。
以下是一个kNN算法实例,描述了如何使用该算法来解决一个分类问题。
假设我们有一组已知的鸢尾花数据集,包含了150个样本和4个特征。
每个样本都属于三个不同的类别中的一个:山鸢尾(Setosa)、变色鸢尾(Versicolor)和维吉尼亚鸢尾(Virginica)。
我们的目标是根据这些特征将新样本分类到正确的类别中。
首先,我们需要对数据集进行预处理和准备工作。
我们将数据集拆分为特征集和目标变量集。
特征集包括4个特征列,而目标变量集则包含每个样本所属的类别。
接下来,我们需要将数据集划分为训练集和测试集。
我们将通过训练集来训练模型,并使用测试集来评估模型的性能。
通常情况下,我们将数据集的80用于训练,20用于测试,可以通过使用train_test_split()函数来轻松实现。
然后,我们需要选择一个合适的k值。
k值决定了我们要考虑多少个最近邻居。
通常情况下,k的选择需要根据具体问题和数据集来确定。
较小的k值可能导致模型过于复杂和过拟合,而较大的k值可能导致欠拟合。
因此,我们需要进行交叉验证来选择一个合适的k值。
在k近邻算法中,常见的选择是使用奇数k值,以避免在多个类别中出现平局。
接下来,我们使用训练集来训练kNN模型。
训练过程实际上只是简单地将训练集存储在模型中,以便在需要时进行比较。
然后,我们使用测试集来评估模型的性能。
对于每个测试样本,我们计算它与训练集中各个样本的距离,并选择与之最接近的k个样本。
KNN算法实验报告11页

KNN算法实验报告11页KNN算法是一种非常简单但实用的机器学习算法,它非常适用于分类和回归问题。
本文主要介绍了KNN算法的原理以及在实际问题中的应用。
实验通过使用Python语言实现了KNN算法,并在多个数据集上进行了测试,证实了该算法的有效性。
1. KNN算法简介KNN算法(K-Nearest Neighbor)最初由Cover和Hart在1967年提出,是一种基于实例的分类算法,它的基本思想是通过比较不同样本之间距离的大小来实现分类或者回归。
在KNN算法中,距离的度量方式有很多种,最常见的是欧氏距离和曼哈顿距离。
在KNN算法中,K表示邻居的个数,对于一个待分类的样本,算法会找出与其距离最近的K个样本,并统计这K个样本中属于每个类别的数量,最终将待分类样本归为数量最多的那个类别。
如果K=1,则为最近邻算法。
2.1 Python代码实现本文使用Python语言实现KNN算法,实现过程如下:首先,需要定义距离度量方式。
本文采用欧氏距离:def distance(x1, x2):return np.sqrt(np.sum((x1 - x2) ** 2))然后,通过相似度计算函数对数据进行分类,代码如下:2.2 测试数据为了验证KNN算法的有效性,本文使用了三个不同的数据集,分别是Iris鸢尾花数据集、Wine酒数据集和Diabetes糖尿病数据集。
Iris鸢尾花数据集是常用的分类实验数据集,由Fisher于1936年收集整理,包含3种不同种类的鸢尾花,每种鸢尾花有4个不同的属性。
本文只考虑其中前两种鸢尾花,样本数量分别为50。
Wine酒数据集是一个常用的分类实验数据集,由UCI Machine Learning Repository 提供,包含13个不同的属性,涉及到葡萄品种、酒精、酸度等等。
本文只考虑其中前两个葡萄品种,样本数量分别为59和71。
Diabetes糖尿病数据集是美国国家糖尿病和肾脏疾病研究所提供的数据集,包括了一些糖尿病患者和非患者的生理指标数据,以及一个二元分类变量(是否患有糖尿病)。
KNN算法实验报告

KNN算法实验报告一、引言(100字)KNN(K-Nearest Neighbors)算法是一种常用的分类算法,在机器学习领域有广泛的应用。
本实验旨在通过实际案例的运用,探究KNN算法的原理及其在分类问题中的应用效果。
二、实验过程(200字)1.数据准备:从UCI机器学习库中选择合适的数据集,包括特征和目标变量,用于训练和测试KNN分类器。
2.数据预处理:对数据进行必要的处理,包括数据清洗、特征提取和特征归一化等。
3.划分数据集:将数据集分为训练集和测试集,一般采用80%训练集和20%测试集的比例。
4.特征选择:选择合适的特征子集作为输入数据,以避免维度灾难和提高算法的性能。
5.构建模型:使用KNN算法进行模型训练,根据训练集数据计算每个测试样本与训练样本之间的距离,并根据K值确定测试样本的类别。
6.模型评估:使用测试集数据对模型进行评估,包括准确率、召回率和F1值等指标。
7.参数调优:根据评估结果,调整K值和特征选择的相关参数,优化模型的性能。
三、实验结果(300字)本实验选取了UCI机器学习库中的鸢尾花数据集,该数据集包括4个特征变量和1个目标变量,用于分类三种不同种类的鸢尾花。
在数据预处理阶段,对数据进行了清洗和特征提取。
对于缺失值,采用均值填充的方式进行处理;对于离散特征,采用one-hot编码将其转化为连续特征。
同时,还对数据进行了归一化处理,使得各个特征之间的数值范围相同。
然后将数据集分为训练集和测试集,其中80%作为训练集,20%作为测试集。
经过特征选择和模型训练后,将得到的模型应用到测试集上,得到了较好的分类结果。
通过计算准确率、召回率和F1值等指标,可以评估模型的性能。
最后,通过调整K值,并使用交叉验证的方法进行参数选择,进一步优化了模型的性能。
四、实验分析(400字)通过本实验,我们可以得出以下结论:其次,数据预处理是提高模型性能的重要步骤。
对于缺失值和离散特征,需要进行适当的处理,以避免对模型的影响。
机器学习实验之K近邻

机器学习实训实验报告(六)调试过程中的关键问题及修改:1、报错:'dict' object has noattribute 'iteritems'原因:版本的问题(表达的变化)解决方法:把iteritems改为items就成了sqDiffMat = diffMat ** 2# 行数据相加,如果axis=0,则是列向量数据相加sqDistances = sqDiffMat.sum(axis=1)# 取根distances = sqDistances ** 0.5# 从小到排序,值为索引数组sortedDistIndicies = distances.argsort()classCount = {}for i in range(k):voteIlabel = labels[sortedDistIndicies[i]]# classCount.get(voteIlabel, 0)是指不存在相对应key值的value则返回0classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1#对所有可迭代的对象进行排序操作,按从大到小顺序,key为按哪个元素排序sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]if __name__ == '__main__':group,labels = createDateSet()classfiy=classify0([2,1,1,0,1,0], group, labels, 3)print("测试结果:",classfiy)运行结果:就结果而言,预测正确实验总结:本节学习了k邻近算法的算法思想、过程等等,了解欧式距离公式,也对k邻近的k值的含义有了进一步的认识。
实验报告

K-最邻近算法与算法的简单改进学院计算机科学与技术专业计算机科学与技术年级2011级姓名王云标指导教师宫秀军2014年5月3日K-最邻近算法与算法的简单改进1.基本介绍K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN算法中,所选择的邻居都是已经正确分类的对象。
该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。
由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
KNN算法不仅可以用于分类,还可以用于回归。
通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。
无论怎样,数量并不能影响运行结果。
可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
基于决策树和K最近邻算法的文本分类研究共3篇

基于决策树和K最近邻算法的文本分类研究共3篇基于决策树和K最近邻算法的文本分类研究1基于决策树和K最近邻算法的文本分类研究随着大数据时代的到来,信息量的爆炸性增长也引发了对文本分类技术的重视。
传统的文本分类方法依赖于手动构建特征词典,费时费力。
随着机器学习算法的发展,自动构建特征成为了一种主要方案,其中决策树和K最近邻算法分别被认为是成功的技术之一。
决策树是一种树形结构,在分类问题中非常有用,因为它可以快速简单地判断输入文本属于哪个类别。
决策树算法通常基于信息增益或基尼指数进行特征选择,以确定在新的文本分类问题中哪些特征有利于提高正确分类的准确性。
在这种算法中,每个节点代表了一个分类特征,每个分支表示一个在该分类特征下可能的分类结果。
决策树算法会基于文本特征递归地划分出一个特征子集,并在每个节点基于信息增益或基尼指数选择最优特征进行分裂,直到达到预定的停止标准。
决策树分类算法的优点是易于理解,容易解释,而且对于高维稀疏的数据集分类效果不错。
然而,决策树只针对训练数据中的分类特征进行分类,没有考虑输入文本之间的相似性。
这时就需要使用K最近邻算法。
K最近邻算法是一种基于样本特征之间相似性的有监督学习算法。
该算法主要基于样本之间的距离测量进行分类,即选取离样本最近的k个训练样本的类别作为当前样本的类别,其中k是用户指定的参数。
在文本分类问题中,选定的特征是文本中出现的关键词汇,而从相似性角度看,每个文本可以被表示为一个特征向量,每个特征向量的维度是关键词的数量。
通过计算欧氏距离或余弦相似度,便可以找到与当前文本最相似的文本,从而能够对当前文本进行分类。
在实际的文本分类任务中,决策树和K最近邻算法通常会结合使用。
首先,决策树算法可以基于特征的规律将输入文本归为某一类别。
然后,将分类结果转化为特征向量,使用K最近邻算法找到距离最近的训练样本,以进一步确定分类结果。
这种分类方式的优点是可以同时使用文本特征和相似性信息,更准确地对输入文本进行分类,从而提高分类器的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目k-最近邻算法实现学生学生学号专业班级指导教师2015-1-2实验二k-最近邻算法实现一、实验目的1.加强对k-最近邻算法的理解;2.锻炼分析问题、解决问题并动手实践的能力。
二、实验要求使用一种你熟悉的程序设计语言,如C++或Java,给定最近邻数k和描述每个元组的属性数n,实现k-最近邻分类算法,至少在两种不同的数据集上比较算法的性能。
三、实验环境Win7 旗舰版+ Visual Studio 2010语言:C++四、算法描述KNN(k Nearest Neighbors)算法又叫k最临近方法。
假设每一个类包含多个样本数据,而且每个数据都有一个唯一的类标记表示这些样本是属于哪一个分类,KNN就是计算每个样本数据到待分类数据的距离。
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
KNN 方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。
因此,采用这种方法可以较好地避免样本的不平衡问题。
另外,由于KNN 方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN 方法较其他方法更为适合。
该方法的不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K 个最近邻点。
目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
1、 算法思路K-最临近分类方法存放所有的训练样本,在接受待分类的新样本之前不需构造模型,并且直到新的(未标记的)样本需要分类时才建立分类。
K-最临近分类基于类比学习,其训练样本由N 维数值属性描述,每个样本代表N 维空间的一个点。
这样,所有训练样本都存放在N 维模式空间中。
给定一个未知样本,k-最临近分类法搜索模式空间,找出最接近未知样本的K 个训练样本。
这K 个训练样本是未知样本的K 个“近邻”。
“临近性”又称为相异度(Dissimilarity ),由欧几里德距离定义,其中两个点 X (x1,x2,…,xn )和Y (y1,y2,…,yn )的欧几里德距离是:2222211)()()(),(n n y x y x y x y x D -+⋯+-+-=未知样本被分配到K 个最临近者中最公共的类。
在最简单的情况下,也就是当K=1时,未知样本被指定到模式空间中与之最临近的训练样本的类。
2、算法步骤step.1---初始化距离为最大值;step.2---计算未知样本和每个训练样本的距离dist;step.3---得到目前K个最临近样本中的最大距离maxdist;step.4---如果dist小于maxdist,则将该训练样本作为K-最近邻样本;step.5---重复步骤2、3、4,直到未知样本和所有训练样本的距离都算完;step.6---统计K-最近邻样本中每个类标号出现的次数;step.7---选择出现频率最大的类标号作为未知样本的类标号。
3、算法伪代码搜索k个近邻的算法:kNN(A[n],k)输入:A[n]为N个训练样本在空间中的坐标(通过文件输入),k为近邻数输出:x所属的类别取A[1]~A[k]作为x的初始近邻,计算与测试样本x间的欧式距离d (x,A[i]),i=1,2,.....,k;按d(x,A[i])升序排序,计算最远样本与x间的距离D<-----max{d(x,a[j]) | j=1,2,.....,k};for(i=k+1;i<=n;i++)计算a[i]与x间的距离d(x,A[i]);if(d(x,A[i]))<Dthen 用A[i]代替最远样本按照d(x,A[i])升序排序,计算最远样本与x间的距离D<---max{d(x,A[j]) | j=1,...,i };计算前k个样本A[i]),i=1,2,...,k所属类别的概率,具有最大概率的类别即为样本x的类。
五、数据结构代码结构如图所示,方法描述如下:KNN:KNN类构造函数,用于读取数据集;get_all_distance:KNN类公有函数,计算要分类的点到所有点的距离;get_distance:KNN类私有函数,计算两点间的距离;get_max_freq_label:KNN类公有函数,在k个数据里,获取最近k个数据的分类最多的标签,将测试数据归位该类。
类图如上图所示,KNN类的成员变量描述如下:dataSet:tData型二维数组,用于训练的数据集;k:int型,从k个最近的元素中,找类标号对应的数目的最大值,归类;labels:tLable型一维数组,类标签;map_index_dist:map<int,double>型,记录测试点到各点的距离;map_label_freq:map<tLable,int>型,记录k个邻居类,各类的个数。
六、程序截图七、实验总结八、附件1.程序源码kNN1.cpp#include<iostream>#include<map>#include<vector>#include<algorithm>#include<fstream>using namespace std;typedef char tLabel;typedef double tData;typedef pair<int,double> PAIR;const int colLen = 2;const int rowLen = 10;ifstream fin;class KNN{private:tData dataSet[rowLen][colLen];tLabel labels[rowLen];int k;map<int,double> map_index_dis;map<tLabel,int> map_label_freq;double get_distance(tData *d1,tData *d2);public:KNN(int k);void get_all_distance(tData * testData);void get_max_freq_label();struct CmpByValue{bool operator() (const PAIR& lhs,const PAIR& rhs){return lhs.second < rhs.second;}};};KNN::KNN(int k){this->k = k;fin.open("data.txt");if(!fin){cout<<"can not open the file data.txt"<<endl;exit(1);}/* input the dataSet */for(int i=0;i<rowLen;i++){for(int j=0;j<colLen;j++){fin>>dataSet[i][j];}fin>>labels[i];}}/** calculate the distance between test data and dataSet[i] */double KNN:: get_distance(tData *d1,tData *d2)double sum = 0;for(int i=0;i<colLen;i++){sum += pow( (d1[i]-d2[i]) , 2 );}// cout<<"the sum is = "<<sum<<endl;return sqrt(sum);}/** calculate all the distance between test data and each training data */void KNN:: get_all_distance(tData * testData){double distance;int i;for(i=0;i<rowLen;i++){distance = get_distance(dataSet[i],testData);//<key,value> => <i,distance>map_index_dis[i] = distance;}//traverse the map to print the index and distancemap<int,double>::const_iterator it = map_index_dis.begin();while(it!=map_index_dis.end()){cout<<"index = "<<it->first<<" distance = "<<it->second<<endl;it++;}}/** check which label the test data belongs to to classify the test data*/void KNN:: get_max_freq_label(){//transform the map_index_dis to vec_index_disvector<PAIR>vec_index_dis( map_index_dis.begin(),map_index_dis.end() );//sort the vec_index_dis by distance from low to high to get the nearest datasort(vec_index_dis.begin(),vec_index_dis.end(),CmpByValue());for(int i=0;i<k;i++){cout<<"the index = "<<vec_index_dis[i].first<<" the distance = "<<vec_index_dis[i].second<<" the label = "<<labels[vec_index_dis[i].first]<<" the coordinate ( "<<dataSet[ vec_index_dis[i].first ][0]<<","<<dataSet[ vec_index_dis[i].first ][1]<<" )"<<endl;//calculate the count of each labelmap_label_freq[ labels[ vec_index_dis[i].first ] ]++;}map<tLabel,int>::const_iterator map_it = map_label_freq.begin();tLabel label;int max_freq = 0;//find the most frequent labelwhile( map_it != map_label_freq.end() ){if( map_it->second > max_freq ){max_freq = map_it->second;label = map_it->first;}map_it++;}cout<<"The test data belongs to the "<<label<<" label"<<endl; }int main(){tData testData[colLen];int k ;cout<<"please input the k value : "<<endl;cin>>k;KNN knn(k);cout<<"please input the test data :"<<endl;for(int i=0;i<colLen;i++)cin>>testData[i];knn.get_all_distance(testData);knn.get_max_freq_label();system("pause");return 0;}2.数据集data.txt。
