K-近邻算法
K-近邻算法(KNN)

K-近邻算法(KNN) ⽂本分类算法、简单的机器学习算法、基本要素、距离度量、类别判定、k取值、改进策略 kNN算法是著名的模式识别统计学⽅法,是最好的⽂本分类算法之⼀,在机器学习分类算法中占有相当⼤的地位,是最简单的机器学习算法之⼀。
外⽂名:k-Nearest Neighbor(简称kNN) 中⽂名:k最邻近分类算法 应⽤:⽂本分类、模式识别、图像及空间分类 典型:懒惰学习 训练时间开销:0 提出时间:1968年 作者:Cover和Hart提出 关键字:kNN算法、k近邻算法、机器学习、⽂本分类思想: 官⽅:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进⾏预测。
通俗点说:就是计算⼀个点与样本空间所有点之间的距离,取出与该点最近的k个点,然后统计这k个点⾥⾯所属分类⽐例最⼤的(“回归”⾥⾯使⽤平均法),则点A属于该分类。
k邻近法实际上利⽤训练数据集对特征向量空间进⾏划分,并作为其分类的“模型”。
三个基本要素:k值的选择、距离度量、分类决策规则图例说明:上图中,绿⾊圆要被决定赋予哪个类,是红⾊三⾓形还是蓝⾊四⽅形?如果K=3,由于红⾊三⾓形所占⽐例为2/3,绿⾊圆将被赋予红⾊三⾓形那个类,如果K=5,由于蓝⾊四⽅形⽐例为3/5,因此绿⾊圆被赋予蓝⾊四⽅形类。
算法计算步骤 1、算距离:给定测试对象,计算它与训练集中的每个对象的距离; 2、找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻; 3、做分类:根据这k个近邻归属的主要类别,来对测试对象分类;距离的计算⽅式(相似性度量): 欧式距离: 曼哈顿距离:类别的判定: 投票法:少数服从多数,近邻中哪个类别的点最多就分为该类。
加权投票法:根据距离的远近,对邻近的投票进⾏加权,距离越近则权重越⼤(权重为距离平⽅的倒数)。
优点: 1、简单,易于理解,易于实现,⽆需估计参数,⽆需训练; 2、适合对稀有事件进⾏分类; 3、特别适合于多分类问题(multi-modal,对象具有多个类别标签), kNN⽐SVM的表现要好。
KNN(k近邻)机器学习算法详解

KNN(k近邻)机器学习算法详解KNN算法详解一、算法概述1、kNN算法又称为k近邻分类(k-nearest neighbor classification)算法。
最简单平凡的分类器也许是那种死记硬背式的分类器,记住所有的训练数据,对于新的数据则直接和训练数据匹配,如果存在相同属性的训练数据,则直接用它的分类来作为新数据的分类。
这种方式有一个明显的缺点,那就是很可能无法找到完全匹配的训练记录。
kNN算法则是从训练集中找到和新数据最接近的k条记录,然后根据他们的主要分类来决定新数据的类别。
该算法涉及3个主要因素:训练集、距离或相似的衡量、k的大小。
2、代表论文Discriminant Adaptive Nearest Neighbor ClassificationTrevor Hastie and Rolbert Tibshirani3、行业应用客户流失预测、欺诈侦测等(更适合于稀有事件的分类问题)二、算法要点1、指导思想kNN算法的指导思想是“近朱者赤,近墨者黑”,由你的邻居来推断出你的类别。
计算步骤如下:1)算距离:给定测试对象,计算它与训练集中的每个对象的距离?2)找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻?3)做分类:根据这k个近邻归属的主要类别,来对测试对象分类2、距离或相似度的衡量什么是合适的距离衡量?距离越近应该意味着这两个点属于一个分类的可能性越大。
觉的距离衡量包括欧式距离、夹角余弦等。
对于文本分类来说,使用余弦(cosine)来计算相似度就比欧式(Euclidean)距离更合适。
3、类别的判定投票决定:少数服从多数,近邻中哪个类别的点最多就分为该类。
加权投票法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大(权重为距离平方的倒数)三、优缺点简单,易于理解,易于实现,无需估计参数,无需训练适合对稀有事件进行分类(例如当流失率很低时,比如低于0.5%,构造流失预测模型)特别适合于多分类问题(multi-modal,对象具有多个类别标签),例如根据基因特征来判断其功能分类,kNN比SVM的表现要好懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢可解释性较差,无法给出决策树那样的规则。
机器学习经典分类算法——k-近邻算法(附python实现代码及数据集)

机器学习经典分类算法——k-近邻算法(附python实现代码及数据集)⽬录⼯作原理存在⼀个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每⼀数据与所属分类的对应关系。
输⼊没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进⾏⽐较,然后算法提取样本集中特征最相似数据(最近邻)的分类特征。
⼀般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不⼤于20的整数。
最后选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
举个例⼦,现在我们⽤k-近邻算法来分类⼀部电影,判断它属于爱情⽚还是动作⽚。
现在已知六部电影的打⽃镜头、接吻镜头以及电影评估类型,如下图所⽰。
现在我们有⼀部电影,它有18个打⽃镜头、90个接吻镜头,想知道这部电影属于什么类型。
根据k-近邻算法,我们可以这么算。
⾸先计算未知电影与样本集中其他电影的距离(先不管这个距离如何算,后⾯会提到)。
现在我们得到了样本集中所有电影与未知电影的距离。
按照距离递增排序,可以找到k个距离最近的电影。
现在假定k=3,则三个最靠近的电影依次是He's Not Really into Dudes、Beautiful Woman、California Man。
python实现⾸先编写⼀个⽤于创建数据集和标签的函数,要注意的是该函数在实际⽤途上没有多⼤意义,仅⽤于测试代码。
def createDataSet():group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])labels = ['A','A','B','B']return group, labels然后是函数classify0(),该函数的功能是使⽤k-近邻算法将每组数据划分到某个类中,其伪代码如下:对未知类别属性的数据集中的每个点依次执⾏以下操作:(1)计算已知类别数据集中的点与当前点之间的距离;(2)按照距离递增次序排序;(3)选取与当前点距离最⼩的k个点;(4)确定前k个点所在类别的出现频率;(5)返回前k个点出现频率最⾼的类别作为当前点的预测分类。
K最近邻算法

K最近邻算法K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。
所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
kNN方法在类别决策时,只与极少量的相邻样本有关。
由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
KNN算法的机器学习基础显示相似数据点通常如何彼此靠近存在的图像大多数情况下,相似的数据点彼此接近。
KNN算法就是基于这个假设以使算法有用。
KNN利用与我们童年时可能学过的一些数学相似的想法(有时称为距离、接近度或接近度),即计算图上点之间的距离。
例如,直线距离(也称为欧氏距离)是一个流行且熟悉的选择。
KNN通过查找查询和数据中所有示例之间的距离来工作,选择最接近查询的指定数字示例( K ),然后选择最常用的标签(在分类的情况下)或平均标签(在回归的情况下)。
在分类和回归的情况下,我们看到为我们的数据选择正确的K是通过尝试几个K并选择最有效的一个来完成的。
KNN算法的步骤1.加载数据2.将K初始化为你选择的邻居数量3.对于数据中的每个示例4.3.1 根据数据计算查询示例和当前示例之间的距离。
5.3.2 将示例的距离和索引添加到有序集合中6.按距离将距离和索引的有序集合从最小到最大(按升序)排序7.从已排序的集合中挑选前K个条目8.获取所选K个条目的标签9.如果回归,返回K个标签的平均值10.如果分类,返回K个标签的模式'为K选择正确的值为了选择适合你的数据的K,我们用不同的K值运行了几次KNN算法,并选择K来减少我们遇到的错误数量,同时保持算法在给定之前从未见过的数据时准确预测的能力。
机器学习:K-近邻算法(KNN)

机器学习:K-近邻算法(KNN)机器学习:K-近邻算法(KNN)⼀、KNN算法概述KNN作为⼀种有监督分类算法,是最简单的机器学习算法之⼀,顾名思义,其算法主体思想就是根据距离相近的邻居类别,来判定⾃⼰的所属类别。
算法的前提是需要有⼀个已被标记类别的训练数据集,具体的计算步骤分为⼀下三步:1、计算测试对象与训练集中所有对象的距离,可以是欧式距离、余弦距离等,⽐较常⽤的是较为简单的欧式距离;2、找出上步计算的距离中最近的K个对象,作为测试对象的邻居;3、找出K个对象中出现频率最⾼的对象,其所属的类别就是该测试对象所属的类别。
⼆、算法优缺点1、优点思想简单,易于理解,易于实现,⽆需估计参数,⽆需训练;适合对稀有事物进⾏分类;特别适合于多分类问题。
2、缺点懒惰算法,进⾏分类时计算量⼤,要扫描全部训练样本计算距离,内存开销⼤,评分慢;当样本不平衡时,如其中⼀个类别的样本较⼤,可能会导致对新样本计算近邻时,⼤容量样本占⼤多数,影响分类效果;可解释性较差,⽆法给出决策树那样的规则。
三、注意问题1、K值的设定K值设置过⼩会降低分类精度;若设置过⼤,且测试样本属于训练集中包含数据较少的类,则会增加噪声,降低分类效果。
通常,K值的设定采⽤交叉检验的⽅式(以K=1为基准)经验规则:K⼀般低于训练样本数的平⽅根。
2、优化问题压缩训练样本;确定最终的类别时,不是简单的采⽤投票法,⽽是进⾏加权投票,距离越近权重越⾼。
四、python中scikit-learn对KNN算法的应⽤#KNN调⽤import numpy as npfrom sklearn import datasetsiris = datasets.load_iris()iris_X = iris.datairis_y = iris.targetnp.unique(iris_y)# Split iris data in train and test data# A random permutation, to split the data randomlynp.random.seed(0)# permutation随机⽣成⼀个范围内的序列indices = np.random.permutation(len(iris_X))# 通过随机序列将数据随机进⾏测试集和训练集的划分iris_X_train = iris_X[indices[:-10]]iris_y_train = iris_y[indices[:-10]]iris_X_test = iris_X[indices[-10:]]iris_y_test = iris_y[indices[-10:]]# Create and fit a nearest-neighbor classifierfrom sklearn.neighbors import KNeighborsClassifierknn = KNeighborsClassifier()knn.fit(iris_X_train, iris_y_train)KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',metric_params=None, n_jobs=1, n_neighbors=5, p=2,weights='uniform')knn.predict(iris_X_test)print iris_y_testKNeighborsClassifier⽅法中含有8个参数(以下前两个常⽤):n_neighbors : int, optional (default = 5):K的取值,默认的邻居数量是5;weights:确定近邻的权重,“uniform”权重⼀样,“distance”指权重为距离的倒数,默认情况下是权重相等。
机器学习--K近邻(KNN)算法的原理及优缺点

机器学习--K近邻(KNN)算法的原理及优缺点⼀、KNN算法原理 K近邻法(k-nearst neighbors,KNN)是⼀种很基本的机器学习⽅法。
它的基本思想是:在训练集中数据和标签已知的情况下,输⼊测试数据,将测试数据的特征与训练集中对应的特征进⾏相互⽐较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类。
由于KNN⽅法主要靠周围有限的邻近的样本,⽽不是靠判别类域的⽅法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN⽅法较其他⽅法更为适合。
KNN算法不仅可以⽤于分类,还可以⽤于回归。
通过找出⼀个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
更有⽤的⽅法是将不同距离的邻居对该样本产⽣的影响给予不同的权值(weight),如权值与距离成反⽐。
KNN算法的描述: (1)计算测试数据与各个训练数据之间的距离; (2)按照距离的递增关系进⾏排序; (3)选取距离最⼩的K个点; (4)确定前K个点所在类别的出现频率 (5)返回前K个点中出现频率最⾼的类别作为测试数据的预测分类。
算法流程: (1)准备数据,对数据进⾏预处理。
(2)选⽤合适的数据结构存储训练数据和测试元组。
(3)设定参数,如k。
(4)维护⼀个⼤⼩为k的的按距离由⼤到⼩的优先级队列,⽤于存储最近邻训练元组。
随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存⼊优先级队列。
(5)遍历训练元组集,计算当前训练元组与测试。
元组的距离,将所得距离L 与优先级队列中的最⼤距离Lmax。
(6)进⾏⽐较。
若L>=Lmax,则舍弃该元组,遍历下⼀个元组。
若L < Lmax,删除优先级队列中最⼤距离的元组,将当前训练元组存⼊优先级队列。
(7)遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
k-近邻法求解互信息的计算过程

K-近邻法是一种常用的机器学习算法,它在分类和回归问题中有着广泛的应用。
而互信息是一种用于衡量两个随机变量之间关联性的指标,它在特征选择、信息检索等领域具有重要的作用。
本文将以k-近邻法为基础,探讨如何利用k-近邻法来求解互信息的计算过程。
1. 什么是K-近邻法K-近邻法(K-nearest neighbors, KNN)是一种基本的分类与回归方法。
在K-近邻法中,对于一个未知样本,通过计算它与训练集中所有样本的距离,然后选择与它距离最近的k个样本,最后根据这k个样本的类别来对该未知样本进行分类或回归预测。
2. 什么是互信息互信息(Mutual Information, MI)是信息论中的一个重要概念,用于衡量两个随机变量之间的相关性。
互信息的定义如下:对于离散型随机变量X和Y,其联合概率分布为P(X, Y),边缘概率分布分别为P(X)和P(Y),则X和Y的互信息I(X; Y)定义为:I(X; Y) = ΣΣP(X, Y)log(P(X, Y) / (P(X)P(Y)))对于连续型随机变量X和Y,互信息的定义稍有不同,这里不做详细展开。
3. K-近邻法与互信息的关联K-近邻法的关键在于样本之间的距离度量,通常使用的距离度量有欧氏距离、曼哈顿距离、闵可夫斯基距离等。
而互信息则可以用于衡量两个随机变量之间的关联程度。
我们可以利用K-近邻法来近似计算互信息。
4. K-近邻法求解互信息的计算过程我们假设有两个随机变量X和Y,它们分别有n个样本。
现在,我们希望利用K-近邻法来计算它们之间的互信息。
步骤一:计算X和Y的联合概率分布在K-近邻法中,我们需要计算样本之间的距离。
对于X和Y的每一个样本Xi和Yi,我们可以根据它们的特征值计算它们之间的距离,得到一个距离矩阵。
假设我们选择欧氏距离作为距离度量,那么对于Xi和Yi,它们之间的距离可以表示为:d(Xi, Yi) = sqrt(Σ(Xij - Yij)^2)其中,Xij和Yij分别表示Xi和Yi的第j个特征值。
k近邻算法——精选推荐
第一部分、K近邻算法1.1、什么是K近邻算法何谓K近邻算法,即K-Nearest Neighbor algorithm,简称KNN算法,单从名字来猜想,可以简单粗暴的认为是:K个最近的邻居,当K=1时,算法便成了最近邻算法,即寻找最近的那个邻居。
为何要找邻居?打个比方来说,假设你来到一个陌生的村庄,现在你要找到与你有着相似特征的人群融入他们,所谓入伙。
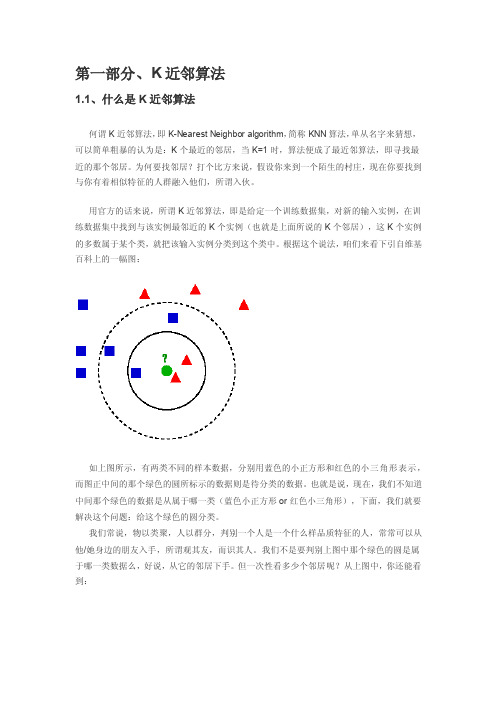
用官方的话来说,所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例(也就是上面所说的K个邻居),这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
根据这个说法,咱们来看下引自维基百科上的一幅图:如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。
也就是说,现在,我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形or红色小三角形),下面,我们就要解决这个问题:给这个绿色的圆分类。
我们常说,物以类聚,人以群分,判别一个人是一个什么样品质特征的人,常常可以从他/她身边的朋友入手,所谓观其友,而识其人。
我们不是要判别上图中那个绿色的圆是属于哪一类数据么,好说,从它的邻居下手。
但一次性看多少个邻居呢?从上图中,你还能看到:∙如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
∙如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
于此我们看到,当无法判定当前待分类点是从属于已知分类中的哪一类时,我们可以依据统计学的理论看它所处的位置特征,衡量它周围邻居的权重,而把它归为(或分配)到权重更大的那一类。
这就是K近邻算法的核心思想。
1.2、近邻的距离度量表示法上文第一节,我们看到,K近邻算法的核心在于找到实例点的邻居,这个时候,问题就接踵而至了,如何找到邻居,邻居的判定标准是什么,用什么来度量。
KNN(K近邻法)算法原理
KNN(K近邻法)算法原理⼀、K近邻概述k近邻法(k-nearest neighbor, kNN)是⼀种基本分类与回归⽅法(有监督学习的⼀种),KNN(k-nearest neighbor algorithm)算法的核⼼思想是如果⼀个样本在特征空间中的k(k⼀般不超过20)个最相邻的样本中的⼤多数属于某⼀个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
简单地说,K-近邻算法采⽤测量不同特征值之间的距离⽅法进⾏分类。
通常,在分类任务中可使⽤“投票法”,即选择这k个实例中出现最多的标记类别作为预测结果;在回归任务中可使⽤“平均法”,即将这k个实例的实值输出标记的平均值作为预测结果;还可基于距离远近进⾏加权平均或加权投票,距离越近的实例权重越⼤。
k近邻法不具有显式的学习过程,事实上,它是懒惰学习(lazy learning)的著名代表,此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进⾏处理K近邻算法的优缺点:优点:精度⾼、对异常值不敏感、⽆数据输⼊假定缺点:计算复杂度⾼、空间复杂度⾼适⽤数据范围:数值型和标称型⼆、K近邻法的三要素距离度量、k值的选择及分类决策规则是k近邻法的三个基本要素。
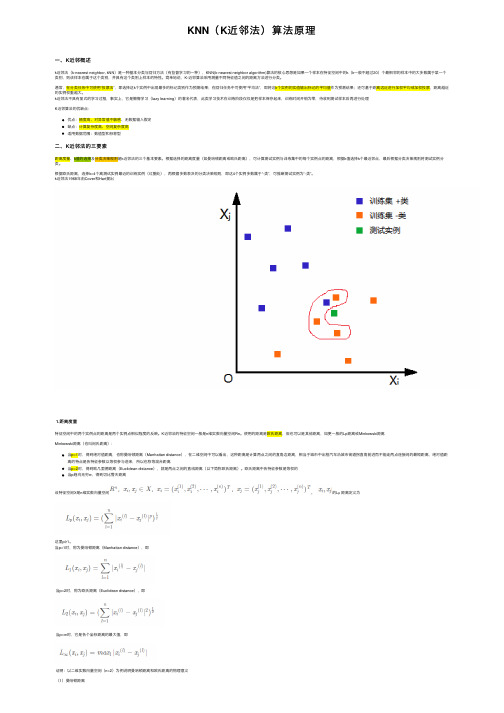
根据选择的距离度量(如曼哈顿距离或欧⽒距离),可计算测试实例与训练集中的每个实例点的距离,根据k值选择k个最近邻点,最后根据分类决策规则将测试实例分类。
根据欧⽒距离,选择k=4个离测试实例最近的训练实例(红圈处),再根据多数表决的分类决策规则,即这4个实例多数属于“-类”,可推断测试实例为“-类”。
k近邻法1968年由Cover和Hart提出1.距离度量特征空间中的两个实例点的距离是两个实例点相似程度的反映。
K近邻法的特征空间⼀般是n维实数向量空间Rn。
使⽤的距离是欧⽒距离,但也可以是其他距离,如更⼀般的Lp距离或Minkowski距离Minkowski距离(也叫闵⽒距离):当p=1时,得到绝对值距离,也称曼哈顿距离(Manhattan distance),在⼆维空间中可以看出,这种距离是计算两点之间的直⾓边距离,相当于城市中出租汽车沿城市街道拐直⾓前进⽽不能⾛两点连接间的最短距离,绝对值距离的特点是各特征参数以等权参与进来,所以也称等混合距离当p=2时,得到欧⼏⾥德距离(Euclidean distance),就是两点之间的直线距离(以下简称欧⽒距离)。
机器学习:k-NN算法(也叫k近邻算法)

机器学习:k-NN算法(也叫k近邻算法)⼀、kNN算法基础# kNN:k-Nearest Neighboors# 多⽤于解决分类问题 1)特点:1. 是机器学习中唯⼀⼀个不需要训练过程的算法,可以别认为是没有模型的算法,也可以认为训练数据集就是模型本⾝;2. 思想极度简单;3. 应⽤数学知识少(近乎为零);4. 效果少;5. 可以解释机械学习算法使⽤过程中的很多细节问题6. 更完整的刻画机械学习应⽤的流程; 2)思想:根本思想:两个样本,如果它们的特征⾜够相似,它们就有更⾼的概率属于同⼀个类别;问题:根据现有训练数据集,判断新的样本属于哪种类型;⽅法/思路:1. 求新样本点在样本空间内与所有训练样本的欧拉距离;2. 对欧拉距离排序,找出最近的k个点;3. 对k个点分类统计,看哪种类型的点数量最多,此类型即为对新样本的预测类型; 3)代码实现过程:⽰例代码:import numpy as npimport matplotlib.pyplot as pltraw_data_x = [[3.3935, 2.3312],[3.1101, 1.7815],[1.3438, 3.3684],[3.5823, 4.6792],[2.2804, 2.8670],[7.4234, 4.6965],[5.7451, 3.5340],[9.1722, 2.5111],[7.7928, 3.4241],[7.9398, 0.7916]]raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]# 训练集样本的datax_train = np.array(raw_data_x)# 训练集样本的labely_train = np.array(raw_data_y)# 1)绘制训练集样本与新样本的散点图# 根据样本类型(0、1两种类型),绘制所有样本的各特征点plt.scatter(x_train[y_train == 0, 0], x_train[y_train == 0, 1], color = 'g')plt.scatter(x_train[y_train == 1, 0], x_train[y_train == 1, 1], color = 'r')# 新样本x = np.array([8.0936, 3.3657])# 将新样本的特征点绘制在训练集的样本空间plt.scatter(x[0], x[1], color = 'b')plt.show()# 2)在特征空间中,计算训练集样本中的所有点与新样本的点的欧拉距离from math import sqrt# math模块下的sqrt函数:对数值开平⽅sqrt(number)distances = []for x_train in x_train:d = sqrt(np.sum((x - x_train) ** 2))distances.append(d)# 也可以⽤list的⽣成表达式实现:# distances = [sqrt(np.sum((x - x_train) ** 2)) for x_train in x_train]# 3)找出距离新样本最近的k个点,并得到对新样本的预测类型nearest = np.argsort(distances)k = 6# 找出距离最近的k个点的类型topK_y = [y_train[i] for i in nearest[:k]]# 根据类别对k个点的数量进⾏统计from collections import Countervotes = Counter(topK_y)# 获取所需的预测类型:predict_ypredict_y = votes.most_common(1)[0][0]封装好的Python代码:import numpy as npfrom math import sqrtfrom collections import Counterdef kNN_classify(k, X_train, y_train, x):assert 1 <= k <= X_train.shape[0],"k must be valid"assert X_train.shape[0] == y_train.shape[0], \"the size of X_train nust equal to the size of y_train"assert X-train.shape[1] == x.shape[0],\"the feature number of x must be equal to X_train"distances = [sprt(np.sum((x_train - x) ** 2)) for x_train in X_train]nearest = np.argsort(distances)topK_y = [y_train[i] for i in nearest[:k]]vates = Counter(topK_y)return votes.most_common(1)[0][0] # assert:表⽰声明;此处对4个参数进⾏限定;代码中的其它Python知识:1. math模块下的sprt()⽅法:对数开平⽅;from math import sqrtprint(sprt(9))# 32. collections模块下的Counter()⽅法:对列表中的数据进⾏分类统计,⽣产⼀个Counter对象;from collections import Countermy_list = [0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3]print(Counter(my_list))# ⼀个Counter对象:Counter({0: 2, 1: 3, 2: 4, 3: 5})3. Counter对象的most_common()⽅法:Counter.most_common(n),返回Counter对象中数量最多的n种数据,返回⼀个list,list的每个元素为⼀个tuple;from collections import Countermy_list = [0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3]votes = Counter(my_list)print(votes.most_common(2))# [(3, 5), (2, 4)]⼆、总结 1)k近邻算法的作⽤ 1、解决分类问题,⽽且天然可以解决多分类问题; 2、也可以解决回归问题,其中scikit-learn库中封装的KNeighborsRegressor,就是解决回归问题; 2)缺点缺点1:效率低下1. 原因:如果训练集有m个样本,n个特征,预测每⼀个新样本,需要计算与m个样本的距离,每计算⼀个距离,要使⽤n个时间复杂度,则计算m个样本的距离,使⽤m * n个时间复杂度;2. 算法的时间复杂度:反映了程序执⾏时间随输⼊规模增长⽽增长的量级,在很⼤程度上能很好反映出算法的优劣与否。
k近邻算法回归原理

k近邻算法回归原理
k近邻算法(k-nearest neighbor,简称kNN)是一种基本的分类与回归方法。
它的基本原理是基于样本之间的距离进行分类或回归预测。
对于分类问题,k近邻算法通过统计距离待分类样本最近的k个样本中各类别的数量来决定新样本所属的类别。
在具体操作中,先计算待分类样本与训练数据集中每个样本的距离,然后取距离最近的k个样本。
待分类样本的类别就由这k个最近邻样本中数量最多的类别决定。
对于回归问题,k近邻算法通过计算距离待预测样本最近的k个样本的平均值或加权平均值来预测新样本的输出值。
同样地,先计算待预测样本与训练数据集中每个样本的距离,然后取距离最近的k个样本。
预测样本的输出值就由这k个最近邻样本的平均值或加权平均值决定。
值得注意的是,k近邻算法没有显式的训练过程,而是在预测时根据训练数据来进行实时计算。
这种算法适用于数值型和标称型数据,且精度高、对异常值不敏感、无数据输入假定。
然而,其计算复杂度和空间复杂度较高,当数据集很大时,性能可能会受到影响。
以上内容仅供参考,如需更多信息,建议查阅机器学习相关文献或咨询相关领域的研究人员。
第二章 K近邻算法

KD树的构建
构建kd树 构造其它节点,递归: 对深度为j的节点,split策略,计算split所 对应的维度(坐标轴)x(l),以所有实例的x (l)坐标内的中位数作为切分点,将该节点对 应的超矩形区域垂直切分成两个子区域 由该节点生成深度为j+1的左右两个节点,左 子节点对应坐标x(l)小于切分点的子区域, 右子节点对应坐标x(l)大于切分点的子区域 将落在切分超平面上的实例点保存于该节点 直到两个子区域没有实例时停止,从而形成kd树的 区域划分。
Kd-树是K-dimension tree的缩写,是对数据点在k 维空间中划分的一种数据结构,主要应用于多维空 间关键数据的搜索(如:范围搜索和最近邻搜索)。 本质上说,kd-树就是一种平衡二叉树 范围查询就是给定查询点和查询距离的阈值,从 数据集中找出所有与查询点距离小于阈值的数 K近邻查询是给定查询点及正整数K,从数据集中 找到距离查询点最近的K个数据 k-d树是一种空间划分树,即把整个空间划分为特定 的几个部分,然后在特定空间的部分内进行相关搜 索操作
1 P (l ) P j
当p=2时,为欧几里得距离 当p=1时,为曼哈顿距离 当p=+∞时,为切比雪夫距离
(l ) LP xi x l 1
n
LP max xi(l ) x (jl )
l
注意:使用的距离不同,k近邻的结果也会不同的, 即“由不同的距离度量所确定的最邻近点是不同的”
y arg max
cj x i N k x
Iy
i
= cj
i 1,2,3,.., N ; j 1,2,3,..., K
Company Logo
第3章--k-近邻算法--(《统计学习方法》PPT课件)

• 一般来说,只选择样本数据集中前N个最相似的数据。K一般不大于20, 最后,选择k个中出现次数最多的分类,作为新数据的分类
K近邻算法的一般流程
• 收集数据:可以使用任何方法 • 准备数据:距离计算所需要的数值,最后是结构化的数据格式。 • 分析数据:可以使用任何方法 • 训练算法: (此步骤kNN)中不适用 • 测试算法:计算错误率 • 使用算法:首先需要输入样本数据和结构化的输出结果,然后
K-Nearest Neighbors算法特点
• 优点
• 精度高 • 对异常值不敏感 • 无数据输入假定
• 缺点
• 计算复杂度高 • 空间复杂度高
• 适用数据范围
• 数值型和标称型
K-Nearest Neighbors Algorithm
• 工作原理
• 存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据 都存在标签,即我们知道样本集中每个数据与所属分类的对应关系。
提纲
• KNN算法原理和流程 • Python程序调试
• Python文件类型 • 模块 • Idle调试环境 • 数据载入
• 算法和关键函数分析 • 算法改进和实验作业
K-Nearest Neighbors算法原理
K=7 Neighborhood
?
K=1 Neighborhood
Dependent of the data distributions. Can make mistakes at boundaries.
• import py_compile • py_pile('D:\python\machinelearninginaction\Ch02\kNN.py')
K-近邻算法

K-近邻算法⼀、概述k-近邻算法(k-Nearest Neighbour algorithm),⼜称为KNN算法,是数据挖掘技术中原理最简单的算法。
KNN 的⼯作原理:给定⼀个已知标签类别的训练数据集,输⼊没有标签的新数据后,在训练数据集中找到与新数据最邻近的k个实例,如果这k个实例的多数属于某个类别,那么新数据就属于这个类别。
可以简单理解为:由那些离X最近的k个点来投票决定X归为哪⼀类。
图1 图1中有红⾊三⾓和蓝⾊⽅块两种类别,我们现在需要判断绿⾊圆点属于哪种类别当k=3时,绿⾊圆点属于红⾊三⾓这种类别;当k=5时,绿⾊圆点属于蓝⾊⽅块这种类别。
举个简单的例⼦,可以⽤k-近邻算法分类⼀个电影是爱情⽚还是动作⽚。
(打⽃镜头和接吻镜头数量为虚构)电影名称打⽃镜头接吻镜头电影类型⽆问西东1101爱情⽚后来的我们589爱情⽚前任31297爱情⽚红海⾏动1085动作⽚唐⼈街探案1129动作⽚战狼21158动作⽚新电影2467?表1 每部电影的打⽃镜头数、接吻镜头数和电影分类表1就是我们已有的数据集合,也就是训练样本集。
这个数据集有两个特征——打⽃镜头数和接吻镜头数。
除此之外,我们也知道每部电影的所属类型,即分类标签。
粗略看来,接吻镜头多的就是爱情⽚,打⽃镜头多的就是动作⽚。
以我们多年的经验来看,这个分类还算合理。
如果现在给我⼀部新的电影,告诉我电影中的打⽃镜头和接吻镜头分别是多少,那么我可以根据你给出的信息进⾏判断,这部电影是属于爱情⽚还是动作⽚。
⽽k-近邻算法也可以像我们⼈⼀样做到这⼀点。
但是,这仅仅是两个特征,如果把特征扩⼤到N个呢?我们⼈类还能凭经验“⼀眼看出”电影的所属类别吗?想想就知道这是⼀个⾮常困难的事情,但算法可以,这就是算法的魅⼒所在。
我们已经知道k-近邻算法的⼯作原理,根据特征⽐较,然后提取样本集中特征最相似数据(最近邻)的分类标签。
那么如何进⾏⽐较呢?⽐如表1中新出的电影,我们该如何判断他所属的电影类别呢?如图2所⽰。
k- 最近邻算法

k- 最近邻算法摘要:1.K-最近邻算法的定义和原理2.K-最近邻算法的计算方法3.K-最近邻算法的应用场景4.K-最近邻算法的优缺点正文:1.K-最近邻算法的定义和原理K-最近邻(K-Nearest Neighbors,简称KNN)算法是一种基于相似度度量的聚类分析方法。
该算法的基本思想是:在数据集中,每个数据点都与距离它最近的K 个数据点属于同一类别。
这里的K 是一个超参数,可以根据实际问题和数据情况进行调整。
KNN 算法的主要步骤包括数据预处理、计算距离、确定最近邻和进行分类等。
2.K-最近邻算法的计算方法计算K-最近邻算法的过程可以分为以下几个步骤:(1)数据预处理:将原始数据转换为适用于计算距离的格式,如数值型数据。
(2)计算距离:采用欧氏距离、曼哈顿距离等方法计算数据点之间的距离。
(3)确定最近邻:对每个数据点,找到距离最近的K 个数据点。
(4)进行分类:根据最近邻的数据点所属的类别,对目标数据点进行分类。
3.K-最近邻算法的应用场景K-最近邻算法广泛应用于数据挖掘、机器学习、模式识别等领域。
常见的应用场景包括:(1)分类:将数据点划分到不同的类别中。
(2)回归:根据特征值预测目标值。
(3)降维:通过将高维数据映射到低维空间,减少计算复杂度和噪声干扰。
4.K-最近邻算法的优缺点K-最近邻算法具有以下优缺点:优点:(1)简单易懂,易于实现。
(2)对数据规模和分布没有特殊要求。
(3)对噪声不敏感,具有较好的鲁棒性。
缺点:(1)计算复杂度高,尤其是大规模数据集。
(2)对离群点和噪声敏感。
kneighborsclassifier 算法介绍

k-nearest neighbors(k-近邻)是一种简单而有效的监督式学习算法。
该算法在分类和回归问题上都有广泛的应用,并且易于理解和实现。
k-nearest neighbors算法的核心思想是基于输入样本的特征,来预测新样本的分类标签或者数值输出。
k-nearest neighbors算法的原理如下:1. 数据集准备:将训练数据集中的样本按照特征进行标记,这些特征用来决定样本的类别或者数值。
另外,还需要准备测试数据集,用于模型的验证和评估。
2. 计算距离:在预测过程中,计算测试样本与训练样本之间的距离。
通常使用的距离度量包括欧氏距离、曼哈顿距离、闵可夫斯基距离等。
3. 选择k值:选择一个合适的k值,该值表示在预测时将考虑最接近的k个训练样本。
选择合适的k值对算法的性能有着重要影响。
4. 预测:根据测试样本与训练样本的距离,选择最接近的k个训练样本,根据这k个训练样本的标签或数值进行预测。
通常采用投票法(对分类问题)或者平均法(对回归问题)来确定最终的预测结果。
k-nearest neighbors算法的优缺点如下:优点:1. 简单、直观:算法实现简单,易于理解和解释。
2. 适用于多类别问题:对于多分类问题,k-nearest neighbors算法表现良好。
3. 适用于非线性数据:对于非线性数据集,k-nearest neighbors算法也能够取得不错的预测效果。
缺点:1. 计算复杂度高:在大型数据集中,由于需要计算相互之间的距离,算法的计算开销比较大。
2. 对异常值敏感:k-nearest neighbors算法对异常值比较敏感,因此在使用该算法时需要注意异常值的处理。
3. 需要合适的k值:k值的选择对算法的性能有着重要的影响,选择不当会导致预测效果下降。
在使用k-nearest neighbors算法时,需要注意以下几点:1. 数据预处理:在应用k-nearest neighbors算法之前,需要对数据进行一定的预处理。
k近邻算法 ptt

k近邻算法K近邻算法(K-Nearest Neighbors,简称KNN)是一种基本的分类(或回归)算法,常用于模式识别和数据挖掘领域。
它的原理很简单,即通过查找与待分类样本最近的K个已知类别样本,在这K个样本中进行投票或平均来确定待分类样本的类别(或预测值)。
在使用KNN算法进行分类时,常见的步骤如下:1. 准备数据集:首先,需要准备一个已知类别的数据集,其中包含特征(属性)和类别标签。
通常将数据集划分为训练集和测试集,用于训练模型和评估性能。
2. 计算距离:针对待分类样本,需要计算其与训练集中每个已知样本之间的距离。
常见的距离度量方法包括欧氏距离、曼哈顿距离等。
3. 选择K值:选择合适的K值,即在K个最近邻中进行投票判断的邻居数量。
K值的选择会影响KNN算法的性能,通常通过交叉验证或其他评估方法来确定。
4. 确定类别:根据K个最近邻的类别(或平均值),来确定待分类样本的类别。
对于分类问题,一般选择多数投票的类别作为预测结果;对于回归问题,一般选择平均值作为预测结果。
需要注意的是,KNN算法对于特征的选择和预处理非常重要。
对于连续特征,可能需要进行归一化或标准化处理,以避免某些特征对距离计算产生过大的影响。
在PTT中,由于是一个网络社区平台,KNN算法可以应用于多个场景,如用户推荐、文本分类、情感分析等。
通过收集用户的行为数据或文本数据,构建相应的特征和类别标签,然后使用KNN算法进行分类或回归预测。
总之,KNN算法是一种简单而常用的分类算法,通过计算待分类样本与已知样本之间的距离,利用最近的K个邻居进行分类或回归预测。
在PTT等领域中,可以应用于各种数据分析和模式识别任务。
kneighborsclassifier 算法

kneighborsclassifier 算法K-最近邻算法(K-Nearest Neighbors Algorithm,简称KNN)是一种常见的分类算法之一,它可以对未知样本进行分类,它的基本原理是将未知样本与已知样本进行比较,以最近的K个样本为参考,将该未知样本归类到与最近的K个样本类别相同的类别中。
KNN算法的主要特点包括简单易用、非常适用于多类别样本分类问题,但是对于大规模数据的分类问题,计算量会变得非常大。
KNN算法的基本步骤包括:1. 选择和确定分类方式:可以是分析每个特征变量并按照最小误差或者最大分类准确率的方式进行;2. 选择要用于分类的近邻数量:这就是K的值,对于不同的问题要结合经验和理解来选择;3. 计算未知样本和已知样本之间的距离:可以使用欧式距离计算;4. 找到最近的K个样本:根据已知样本和未知样本之间的距离,找到最近的K个样本;5. 进行分类:通过统计K个样本中每个类别的数量,将未知样本归类到数量最大的类别中。
KNN算法是一个非常直观且易于理解的算法,但也存在一些缺点。
其中最明显的问题是需要大量的计算资源,特别是在样本数量非常大的时候。
算法需要存储所有的已知样本,也会占用大量的存储空间。
KNN算法的优点是对于高维数据,它不需要假设数据的任何分布类型。
这使得该算法适用于具有复杂结构和分布的数据集。
它适用于多分类问题和二分类问题。
在Python编程中,我们可以使用scikit-learn库中的KNeighborsClassifier来实现KNN算法。
下面是一个简单的代码示例:在使用KNN算法时,需要注意的一个关键问题是如何设置K值。
如果K值设置过小,那么模型会过于敏感,产生过拟合的现象;如果K值设置过大,那么模型会过于简单,容易出现欠拟合的情况。
K值的选择需要结合实际问题和模型评价指标进行综合考虑。
KNN算法是一个简单而有效的分类算法,可以用于多类别分类问题,尤其适用于非线性和高维数据。
k-近邻法综述

KNN(K-Nearest Neighbor),代表k 个最近邻分类法,通过K 个最与之相近的历史记录的组合来辨别新的记录。
KNN 是一个众所周知的统计方法,在过去的40年里在模式识别中集中地被研究[7]。
KNN 在早期的研究策略中已被应用于文本分类,是基准Reuters 主体的高操作性的方法之一。
其它方法,如LLSF、决策树和神经网络等。
K-近邻算法的。
K-近邻法的概念K-近邻算法的思想如下:首先,计算新样本与训练样本之间的距离,找到距离最近的K个邻居;然后,根据这些邻居所属的类别来判定新样本的类别,如果它们都属于同一个类别,那么新样本也属于这个类;否则,对每个后选类别进行评分,按照某种规则确定新样本的类别。
取未知样本X的K个近邻,看着K个近邻多数属于哪一类,就把X分为哪一类。
即,在X的K个样本中,找出X的K个近邻。
K-近邻算法从测试样本X 开始生长,不断的扩大区域,直到包含进K个训练样本,并且把测试样本X的类别归为着最近的K个训练样本中出现频率最大的类别。
例如,图3.1中K=6的情况,根据判定规则,测试样本X被归类为黑色类别。
..°.°.°..°..。
...。
°. . .°.°图3.1K-近邻法近邻分类是基于眼球的懒散的学习法,即它存放所有的训练样本,并且知道新的样本需要分类时才建立分类。
这与决策数和反向传播算法等形成鲜明对比,后者在接受待分类的新样本之前需要构造一个一般模型。
懒散学习法在训练时比急切学习法快,但在分类时慢,因为所有的计算都推迟到那时。
优点:简单,应用范围广;可以通过SQL语句实现;模型不需要预先构造。
缺点:需要大量的训练数据;搜索邻居样本的计算量大,占用大量的内存;距离函数的确定比较困难;分类的结果与参数有关。
K-近邻法算法研究K-近邻法的数学模型用最近邻方法进行预测的理由是基于假设:近邻的对象具有类似的预测值。
k-近邻法综述

KNN(K-Nearest Neighbor),代表k 个最近邻分类法,通过K 个最与之相近的历史记录的组合来辨别新的记录。
KNN 是一个众所周知的统计方法,在过去的40 年里在模式识别中集中地被研究[7]。
KNN 在早期的研究策略中已被应用于文本分类,是基准Reuters 主体的高操作性的方法之一。
其它方法,如LLSF、决策树和神经网络等。
K-近邻算法的。
K-近邻法的概念K-近邻算法的思想如下:首先,计算新样本与训练样本之间的距离,找到距离最近的K个邻居;然后,根据这些邻居所属的类别来判定新样本的类别,如果它们都属于同一个类别,那么新样本也属于这个类;否则,对每个后选类别进行评分,按照某种规则确定新样本的类别。
取未知样本X的K个近邻,看着K个近邻多数属于哪一类,就把X分为哪一类。
即,在X的K个样本中,找出X的K个近邻。
K-近邻算法从测试样本X开始生长,不断的扩大区域,直到包含进K个训练样本,并且把测试样本X的类别归为着最近的K个训练样本中出现频率最大的类别。
例如,图3.1中K=6的情况,根据判定规则,测试样本X被归类为黑色类别。
图3.1 K-近邻法近邻分类是基于眼球的懒散的学习法,即它存放所有的训练样本,并且知道新的样本需要分类时才建立分类。
这与决策数和反向传播算法等形成鲜明对比,后者在接受待分类的新样本之前需要构造一个一般模型。
懒散学习法在训练时比急切学习法快,但在分类时慢,因为所有的计算都推迟到那时。
优点:简单,应用范围广;可以通过SQL语句实现;模型不需要预先构造。
缺点:需要大量的训练数据;搜索邻居样本的计算量大,占用大量的内存;距离函数的确定比较困难;分类的结果与参数有关。
K-近邻法算法研究K-近邻法的数学模型用最近邻方法进行预测的理由是基于假设:近邻的对象具有类似的预测值。
最近邻算法的基本思想是在多维空间R n中找到与未知样本最近邻的k 个点,并根据这k个点的类别来判断未知样本的类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
示例:使用k-近邻算法
改进约会网站的配对结果
(2)佩琪保存的样本具有以下3个特征: 每年获得的飞行常客里程数 玩视频游戏所耗时间百分比 每周消费的冰淇淋公升数
在将上述特征数据输入到分类器之前,必须 将待处理数据的格式改变为分类器可以接受 的格式。在kNN.py文件中添加名为file2matrix 的函数,以此来处理该问题。
示例:使用k-近邻算法
改进约会网站的配对结果
Python语言可以使用索引值-1表示列表 中的最后一列元素,利用这种索引,我们可 以很方便地将列表的最后一行储存到向量 classLabel-Vector中。 值得注意的是,我们必须明确告诉解释 器列表中存储的元素是整型。 ⑤ 继续输入以下命令:
>>> reload(kNN) >>> datingDataMat,datingLabels = kNN.file2matrix('datingTestSet2.txt')
K-近邻算法工作原理
1.工作原理: 存在一个样本数据集合(1)(也称为训练样本 集),并且样本集中每个数据都存在标签(即我们 知道样本集中每一数据与所属分类的对应关系(2))。 输入没有标签的新数据后,将新数据的每个特征 与样本集中数据对应的特征进行比较,然后算法 提供样本集中特征最相似数据(最近邻)的分类标 签(3)。一般来说,我们只选择样本数据集中前k 个最相似的数据(4),这便是算法中k的出处(通常 k≤20)。最后,选择k个最相似数据中出现次数最 多的分类,作为新标签的分类。
K-近邻算法示例
2.示例 (1)问题描述: 电影的分类可以按照题材来,然而题材本身 是如何定义的?也就是说同一题材的电影具 有哪些共同特征?这些都是电影分类时必须 要考虑的因素。现在有一种简单的方法,例 如在爱情片中会出现打斗场面,动作片亦会 出现轻吻镜头,但是很明显两者的频率是不 同的,因此接下来将讲述K-近邻算法关于此 的简单应用。
实施kNN分类算法
显然输出结果为B,当然也可以输入其他值例如 [0.5,0.5],结果如下: 到目前为止,我们已经构建了一个分类器,接下 来我们将从实例出发进行讲解: (4)关于分类器 分类器并不会得到100%正确的结果,我们可以 通过错误率来进行评估。
示例:使用k-近邻算法
改进约会网站的配对结果
示例:使用k-近邻算法
改进约会网站的配对结果
① 该函数的输入为文件名字符串,输出为 训练样本矩阵和类标签向量。 ② 下划线部分为得到文件行数。 ③ 倾斜部分为创建以0填充的矩阵Numpy。 ④ 下划线+倾斜字体部分循环处理文件中的 每行数据,首先使用函数line.strip()截掉 所有回车字符,然后使用\t字符将上一步 得到的整行数据分割成一个元素列表。 接着我们选取前3个元素,将他们存储到 特征矩阵中。
准备:使用Python导入数据
在上述代码中,我们导入了两个模块: 科学计算包Numpy以及运算符模块,k-近邻算 法执行排序操作时将使用这个模块提供的参 数,后面我们将进一步介绍。 为了方便使用createDataSet()函数,它创 建数据集和标签,我们需进入Python开发环 境并输入以下命令: (1)>>> import kNN 上述命令导入kNN模块。
准备:使用Python导入数据
(2)为了确保输入相同的数据集,继续输 入以下命令: >>> group,labels = kNN.createDataSet() 该命令创建了变量group和labels。 (3)输入变量的名字以检验是否正确的定 义变量: >>> group
准备:使用Python导入数据
K-近邻算法
目录
一、K-近邻算法优缺点 二、K-近邻算法工作原理及示例 三、K-近邻算法的一般流程 四、准备:使用Python导入数据 五、实施kNN分类算法 六、示例1:改进约会网站的配对结果 七、示例2:手写识别系统 八、小结
K-近邻算法优缺点
简单地说,K-近邻算法 (又称KNN)采用测 量不同特征值之间的距离方法进行分类。 其优缺点及适用数据范围如下: 优点:精度高、对异常值不敏感、无数 据输入假定。 缺点:计算复杂度高、空间复杂度高。 适用数据范围:数值型和标称型。
K-近邻算法示例
(2)下图示例了六部电影的打斗和接吻镜头数。
K-近邻算法示例
(3)假如有一部未看过的电影,如何确定它是爱情片 还是动作片呢?接下来将展示如何使用KNN来解决 这个问题。
① 首先我们需要知道需分类电影的打斗镜头和接吻 镜头数量,下图给出了一个详细示例:
K-近邻算法示例
② 即使不知道待分类电影属于哪种类型,我 们也可以通过某种方法计算方法。下图展 示的是待分类电影与样本集中其他电影的 距离计算结果:
实施kNN分类算法
现在我们已经知道Python如何解析数据,如何加载数据,以 及kNN算法的工作原理,接下来我们将使用这些方法完成分 类任务。 (1)以下为K-近邻算法的伪代码 对未知类别属性的数据集中的每个点依次执行以下操作: ① 计算已知类别数据集中点与当前点之间的距离; ② 按照距离递增次序排序; ③ 选取与当前点距离最小的k个点; ④ 确定前k个点所在类别出现的频率; ⑤ 返回前k个点出现频率最高的类别作为当前点的预测分类。
1.问题描述:
我都朋友佩琪一直使用在线约会网站寻找适 合自己的约会对象。尽管约会网站会推荐不 同的人选,但是她并不是喜欢每一个人。经 过一番总结,她发现曾交往过三种类型的人: 不喜欢的人 魅力一般的人 极具魅力的人
示例:使用k-近邻算法佩琪依然无法将约 会网站推荐的匹配对象归入恰当的类别。她 觉得可以在周一至约会那些魅力一般的人, 而周末则更喜欢与那些极具魅力的人为伴。 佩琪希望我们的分类软件可以更好的帮助她 将匹配到的对象划分到确切的分类中。此外, 佩琪还收集了一些约会网站未曾记录的数据 信息并保存在了文本文件datingTestSet2.txt中。
实施kNN分类算法
① classify0()函数有四个参数:用于分类的输入 向量inX,输入的样本训练集为dataSet,标签 向量为labels,最后的参数k表示用于选择最近 邻居的数目,其中标签向量和矩阵dataSet的 行数相同;
② 代码中下划线部分用于距离计算,使用的是 欧式距离公式; ③ 倾斜字体部分为对距离计算完毕后的数据按 照从小到大的次序排序并确定前k个距离最小 元素所在的主要分类(k总为正整数);
K-近邻算法的一般流程
接下来主要讲解如何在实际中应用K-近邻算法, 同时涉及如何使用Python工具和相关的机器学习术语, 以下为该算法的一般流程: (1)收集数据:可以使用任何方法。 (2)准备数据:距离计算所需要的数值,最好是结构 化的数据格式。 (3)分析数据:可以使用任何方法。 (4)测试算法:计算错误率。 (5)使用算法:首先需要输入样本数据和结构化的输 出结果,然后运行k-近邻算法判定输入数据属于哪个分 类,最后应用对计算出的分类执行后续的处理。
(此处暂时不关心如何计算得到的这些距离值,稍 后会具体讲解。)
K-近邻算法示例
③ 现在我们得到了样本集中所有电影与未知电影的 距离,按照距离递增排序,可以找到k个距离最 近的电影。假定k=3,则三个最靠近的电影依次 是He’s Not Really into Dudes、Beautiful Woman和 California Man。 ④ 结果: K-近邻算法按照距离最近的三部电影的类型,决 定待分类电影的类型,而这三部电影均为爱情片, 因此我们判定待分类电影为爱情片。
实施kNN分类算法
(2)以下为kNN近邻算法代码,将其保存于kNN.py中 def classify0(inX, dataSet, labels, k): dataSetSize = dataSet.shape[0] diffMat = tile(inX, (dataSetSize,1)) - dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis = 1) distances = sqDistances**0.5 sortedDistIndicies = distances.argsort() classCount = {} for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse = True) return sortedClassCount[0][0]
from numpy import* import operator def createDataSet(): group = array([1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]) labels = ['A', 'A', 'B', 'B'] return group, labels
>>> labels 结果显示,这里有四组数据,每组数据有两个我们已 知的属性或特征值。上面的group矩阵每行包含一个不同 的数据,我们可以将其想象成某个日志文件中不同的测量 点或者入口。由于人类大脑的限制,我们通常只能可视化 处理三维以下的实务。因此为了简单地实现数据可视化, 对于每个数据点我们通常只使用两个特征。 向量labels包含了每个数据点的标签信息,labels包含 的元素个数等于group矩阵行数。这里我们将数据点(1, 1.1)定义为A类,数据点(0,0.1)定义为B类。为了方便说明, 例子中的数值是任意选择的,并没有给出轴标签。
