典型相关分析的基本理论及方法
典型相关分析、冗余分析

两组变量的个数和性质可以是不同的
典型相关的基本思想
Nk心理
设有两组观测变量,通过权重与观测变量 对应相乘、然后将各项相加,分别对每一 组先建立一个线性组合,称典型变式。 每一个典型变式的值又构成一个新的典型 变量。
二者是一个事物的两个方面 变式:关系形式;变量:关注数值
Nk心理
冗余指数
不对称:典型相关平方相同;但两个变 式对自己一方观测变量的代表比例不同
冗余指数
变式与观测变量之间的测量,既是整体 指标(总方差百分比),又是平均指标 (平均每个观测变量方差的百分比)
冗余分析
典型相关:两个多元集团两元间分析; 冗余分析:这两元之间关系的分析
Spss实例与操作
Nk心理
典型冗余分析
冗余
如果一个变量可以由另一个变量的方差来解 释或预测,那么就说这个方差部分与另一变 量方差冗余 即:变量的这个方差部分可以由另一个变量 的一部分方差所预测或解释 常用相关形容词关系(不确切),相关系数 的平方(确定系数)属于冗余分析的范畴, 因为冗余是重叠方差
Nk心理
冗余
冗余
两个变式中的冗余:典型相关系数取平方。 它不是一侧变式与另一侧观测变量的共享方 差比,而是两侧对应变式之间的共享方差比
第二组变式1对第一组变量的 平均解释比例: 交叉负载 乘方 1 X1 -0.548 0.3003 X2 0.299 0.0894 合计 0.3897 平均值 0.1949
典型相关分析的统计指标
冗余指数(manova)
Nk心理
1.典型变式序号(CAN.VAR);2、3.每个变式所代表的某分组 的方差比例和累计方差比例,DE因变量组,CO自变量组;4、 5.另一组解释的方差比例以及累计方差比例
统计学中常用的数据分析方法10典型相关分析与ROC分析

统计学中常用的数据分析方法
典型相关分析
相关分析一般分析两个变量之间的关系,而典型相关分析是分析两组变量(如3个学术能力指标与5个在校成绩表现指标)之间相关性的一种统计分析方法。
典型相关分析的基本思想和主成分分析的基本思想相似,它将一组变量与另一组变量之间单变量的多重线性相关性研究转化为对少数几对综合变量之间的简单线性相关性的研究,并且这少数几对变量所包含的线性相关性的信息几乎覆盖了原变量组所包含的全部相应信息。
R0C分析
R0C曲线是根据一系列不同的二分类方式(分界值或决定阈).以真阳性率(灵敏度)为纵坐标,假阳性率(1-特异度)为横坐标绘制的曲线
用途:
1、R0C曲线能很容易地査出任意界限值时的对疾病的识别能力用途;
2、选择最佳的诊断界限值。
R0C曲线越靠近左上角,试验的准确性就越高;
3、两种或两种以上不同诊断试验对疾病识别能力的比较,一股用R0C曲线下面积反映诊断系统的准确性。
典型相关分析

典型相关分析典型相关分析(Canonical Correlation Analysis)什么是典型相关分析典型相关分析是指利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。
它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
典型相关分析基本思想典型相关分析方法canonical correlation analysis最早源于荷泰林H,Hotelling 。
他所提出的方法于1936 年在《生物统计》期刊上发表的一篇论文《两组变式之间的关系》经过多年的应用及发展,逐渐达到完善,在70 年代臻于成熟。
由于典型相关分析涉及较大量的矩阵计算,其方法的应用在早期曾受到相当的限制。
但随着当代计算机技术及其软件的迅速发展,弥补了应用典型相关分析中的困难,因此它的应用开始走向普及化。
典型相关分析是研究两组变量之间相关关系的一种统计分析方法。
为了研究两组变量X 1 ,X 2 ,…,X p 和Y1 ,Y2 ,…,Yq 之间的相关关系,采用类似于主成分分析的方法,在两组变量中,分别选取若干有代表性的变量组成有代表性的综合指标,通过研究这两组综合指标之间的相关关系,来代替这两组变量间的相关关系,这些综合指标称为典型变量。
[编辑]典型相关分析的应用典型相关分析的用途很广。
在实际分析问题中,当我们面临两组多变量数据,并希望研究两组变量之间的关系时,就要用到典型相关分析。
例如,为了研究扩张性财政政策实施以后对宏观经济发展的影响,就需要考察有关财政政策的一系列指标如财政支出总额的增长率、财政赤字增长率、国债发行额的增长率、税率降低率等与经济发展的一系列指标如国内生产总值增长率、就业增长率、物价上涨率等两组变量之间的相关程度。
又如,为了研究宏观经济走势与股票市场走势之间的关系,就需要考察各种宏观经济指标如经济增长率、失业率、物价指数、进出口增长率等与各种反映股票市场状况的指标如股票价格指数、股票市场融资金额等两组变量之间的相关关系。
第10章 典型相关分析

X2
0.80 1.00 0.33 0.59 0.34
Y1
ቤተ መጻሕፍቲ ባይዱ
0.26 0.33 1.00 0.37 0.21
Y2
0.67 0.59 0.37 1.00 0.35
Y3
0.34 0.34 0.21 0.35 1.00
W V11ab111Y X 111ba22Y 11X 2 2 b3Y 13
(V1,W 1)?
V 1 X 1 2 X 2 p X p'X
和 W 1 Y 12 Y 2 q Y q'Y
之间有最大可能的相关,基于这个思想就产生了典型相关分析.
§10.1 总体典型相关
设 X(X1, ,Xp)'及 Y(Y1,,Yq)'为随机向量,我们用
X 和 Y 的线性组合 ' X 和 'Y 之间的相关性来研究两组随机变量
V2a12 X1a22 X2 ap2Xp W 2b1Y 21b2Y 22 bq2Yq
V2和W2与V1和W1相互独立,但V2和W2相关.如 此继续下去,直至进行到 r 步,两组变量的相关性 被提取完为止. R min(p,q),可以得到 r 组变量.
典型相关的数学描述
一般地,假设有一组变量X1,…,Xp与Y1,…,Yq ,我们要 研究这两组变量的相关关系,如何给两组变量之间的相
为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量:
XX12: :每 每年 年去 外餐 出馆 看就 电餐 影的 频率频 率 Y1:户主的年龄 Y2:家庭的年收入 Y3:户主受教育程度
分析两组变量之间的关系。
变量间的相关系数矩阵
X1
X2
Y1
Y2
Y3
典型相关分析方法研究

典型相关分析方法研究摘要:典型相关分析是研究两组变量(或两个随机向量)之间的相关关系的一种统计方法。
与仅研究二个变量间线性关系的简单相关分析相比,典型相关分析能揭示出两组变量之间的内在联系,且两组变量的数目可以改变,这确定了它的重要性。
随着计算机技术的发展,典型相关分析在各个行业试验研究中应用日渐广泛.本文主要介绍典型相关分析的基本原理与步骤并举例说明其应用.关键词:典型相关分析;基本原理;步骤;应用Abstract:Canonical correlation analysis is the study of two groups of variables (or two random vectors)a statistical method the relationship between the. Compared with only the simple correlation analysis of linear relationship between two variables and canonical correlation analysis can reveal the internal relations between two sets of variables,and the number of two groups of variables can change,this determines the importance of it. With the development of computer technology, the canonical correlation analysis system has been widely used in various industries in experimental study。
This paper mainly introduces the basic principle and procedure of canonical correlation analysis and examples of its application.Key words:Canonical correlation analysis; basic principle;step; application一、引言典型相关分析(Canonical Correlation Analysis 简称CCA)是处理两个随机矢量之间相关性的统计方法,在多元统计分析中占有非常重要的地位。
第9章-典型相关分析资料

2020/11/11
主编:费宇
13
3.样本典型相关变量
• 前面我们是从变量x与变量y的协方差阵Σ出发考虑x 与y的典型相关变量,这称为总体典型相关变量,但
(9.3)
Cov(u, v) Cov(aT x, bT y) aTCov( x, y)b aT 12b.
2020/11/11
主编:费宇
6
1.总体典型相关变量
• 两个新变量u和v之间的相关系数(即典型相关 系数)为
Corr(u, v) Corr(aT x, bT y)
aT 12b
(aT 11a) (bT 22b)
另一组变量为y=(y1, y2,…, yq )T ,且p≤q ,变量x 与变量y的协方差阵为
Var(x)
Σ
Cov(
x,ቤተ መጻሕፍቲ ባይዱ
y)
Cov(
y,
x)
Cov( Var
x, y) ( y)
11 21
12
22
(9.1)
2020/11/11
主编:费宇
5
1.总体典型相关变量
• 为研究变量x与变量y之间的线性相关关系,我们 考虑它们之间的线性组合
2 2
x2 y2
aip xp aiT x, biq yq biT y.
(i 1,2,
, p)
(9.11)
每一对变量称为一对典型变量,其中u1和v1称为第一
对典型变量,它们之间的相关系数λ1称为第一典型相 关系数.
2020/11/11
主编:费宇
11
2.典型相关变量的性质
• 我们不加证明的给出典型变量以下三个性质: • (1)每一对典型变量ui及vi (i=1,2,…,p)的标准差
多元统计分析第9章典型相关分析

0
Σ12
Σ
1 22
Σ
21a
2Σ11a
0
(9.7)
同理,由方程组(9.4)式可得
Σ21Σ111Σ12b 2Σ22b 0
(9.8)
一、典型相关分析的基本思想
用
Σ1 11
和
Σ1 22
得
ΣΣ121211ΣΣ1221ΣΣ121211ΣΣ1221ab
2a 2b
X(2)
X (2) 11
X (2) 21
样本均值向量
X
(2) n1
X (2) 12
X (2) 22
X (2) n2
X (2) 1q
Σ
Σ 1
22
21
B
Σ221Σ
Σ Σ 1
21 11 12
其中 A 为 p×p 阶矩阵, B 为 q×q 阶矩阵。
一、典型相关分析的基本思想
因为 aΣ12b Corr(U ,V ) ,求 Corr(U,V ) 最大值也就
是求 的最大值,而求 的最大值又转化为求 A 和 B 的最
大特征根。
可以证明, A 和 B 的特征根和特征向量有如下性质: 1. A 和 B 具有相同的非零特征根,且所有特征根非负。 2. A 和 B 的特征根均在 0~1 之间。 3. 设 A 和 B 的 非 零 特 征 根 为 12 22 r2 ,
X
(2) 2
a (1) P
X
(1) P
b(1) q
X
(2) q
我们称其为第一对典型变量,最大特征根的平方根 1 即为两
典型变量的相关系数,我们称其为第一典型相关系数。
一、典型相关分析的基本思想
如果第一典型变量不足以代表两组原始变量的信息,则需要求
如何在SPSS中实现典型相关分析

如何在SPSS中实现典型相关分析?SPSS 11.015.1典型相关分析15.1.1方法简介在相关分析一章中,我们主要研究的是两个变量间的相关,顶多调整其他因素的作用而已;如果要研究一个变量和一组变量间的相关,则可以使用多元线性回归,方程的复相关系数就是我们要的东西,同时偏相关系数还可以描述固定其他因素时某个自变量和应变量间的关系。
但如果要研究两组变量的相关关系时,这些统计方法就无能为力了.比如要研究居民生活环境与健康状况的关系,生活环境和健康状况都有一大堆变量,如何来做?难道说做出两两相关系数?显然并不现实,我们需要寻找到更加综合,更具有代表性的指标,典型相关(CanonicalCorrelation)分析就可以解决这个问题。
典型相关分析方法由Hotelling提出,他的基本思想和主成分分析非常相似,也是降维.即根据变量间的相关关系,寻找一个或少数几个综合变量(实际观察变量的线性组合)对来替代原变量,从而将二组变量的关系集中到少数几对综合变量的关系上,提取时要求第一对综合变量间的相关性最大,第二对次之,依此类推。
这些综合变量被称为典型变量,或典则变量,第1对典型变量间的相关系数则被称为第1典型相关系数.一般来说,只需要提取1~2对典型变量即可较为充分的概括样本信息。
可以证明,当两个变量组均只有一个变量时,典型相关系数即为简单相关系数;当一组变量只有一个变量时,典型相关系数即为复相关系数。
故可以认为典型相关系数是简单相关系数、复相关系数的推广,或者说简单相关系数、复相关系数是典型相关系数的特例。
15。
1。
2引例及语法说明在SPSS中可以有两种方法来拟合典型相关分析,第一种是采用Manova过程来拟合,第二种是采用专门提供的宏程序来拟合,第二种方法在使用上非常简单,而输出的结果又非常详细,因此这里只对它进行介绍。
该程序名为Canonical correlation。
sps,就放在SPSS的安装路径之中,调用方式如下:INCLUDE ’SPSS所在路径\Canonical correlation.sps’。
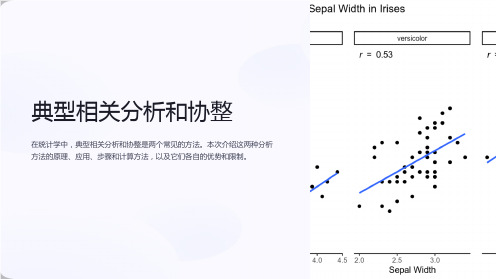
典型相关分析和协整
2 应用领域
具体应用领域也是选择方 法的一个因素,例如需要 研究市场平衡时可以使用 协整分析。
3 实际需求
根据实际问题中的需求, 选择合适的分析方法。
总结
典型相关分析和协整是两种不同的统计分析方法,各自有其适用领域和局限 性。使用这些方法可以从不同维度和角度解读变量之间的关系,有助于更好 地理解和分析数据。
原理和应用领域
适用于研究两个或两个以上时间序列之间的长期关 系,可以用于股票市场、汇率、商品价格等领域的 分析。
步骤和计算方法
选择需要分析的时间序列,进行单位根检验以判断
优势和限制
可以排除短期市场波动的影响,更容易发现市场中
典型相关分析与协整的不同之处
基础理论
典型相关分析基于主成分分析, 而协整分析基于时间序列分析。
原理和应用领域
适用于研究多个变量之间的关系,既可以揭示 变量之间的线性关系,也可以检测非线性关系。
优势和限制
可以提高变量之间的关系解释效果,但需要数 据具有一定的正态性和线性性。也会受到样本 数量的限制,在样本量较少时易受到误导。
什么是协整分析
定义
在时间序列分析中,指两个或两个以上的时间序列 彼此关联,但是它们的差分是平稳的。即可以通过 线性组合消除非平稳性。
分析对象
典型相关分析基于多个变量之 间的关系,而协整分析常用于 两个或两个以上时间序列的分 析。
数据要求
典型相关分析对数据正态分布 和线性相关性的要求较高,而 协整分析对数据平稳性的要求 较高。
如何选择方法
1 数据类型
对于数量型变量,可以考 虑使用典型相关分析;对 于时间序列数据,可以使 用协整分析。
典型相关分析ቤተ መጻሕፍቲ ባይዱ协整
多元统计分析——典型相关分析

多元统计分析——典型相关分析典型相关分析(Canonical correlation analysis)是一种多元统计分析方法,用于研究两组变量之间的关联性。
与传统的相关分析不同,典型相关分析可以同时考虑多组变量,找出最佳的线性组合,使得两组变量之间的相关性最大化。
它主要用于探索一组自变量与另一组因变量之间的线性关系,并且可以提供详细的相关性系数、特征向量和特征值等信息。
典型相关分析的基本原理是将两组变量分别投影到最佳的线性组合上,使得投影后的变量之间的相关性最大。
这种投影是通过求解特征值问题来实现的,其中特征值表示相关系数的大小,特征向量表示两组变量的线性组合。
通常情况下,我们希望保留具有最大特征值的特征向量,因为它们对应着最强的相关性。
典型相关分析的应用广泛,可以用于众多领域,如心理学、社会科学、经济学等。
例如,在心理学研究中,我们可能对人们的人格特征和行为方式进行测量,然后使用典型相关分析来探索它们之间的关系。
在经济学研究中,我们可以将宏观经济指标与企业盈利能力进行比较,以评估它们之间的相关性。
典型相关分析的步骤如下:1.收集数据:首先,我们需要收集两组变量的数据。
这些数据可以是定量数据(如收入、年龄)或定性数据(如性别、职业)。
2.建立模型:然后,我们需要建立一个数学模型,用于描述两组变量之间的关系。
这可以通过线性回归、主成分分析等方法来实现。
3.求解特征值问题:接下来,我们需要求解特征值问题,以获得相关系数和特征向量。
在实际计算中,我们可以使用统计软件来完成这一步骤。
4.解释结果:最后,我们需要解释典型相关分析的结果。
通常情况下,我们会关注最大的特征值和对应的特征向量,因为它们表示着最强的相关性。
典型相关分析的结果提供了一组线性组合,这些组合可以最大化两组变量之间的相关性。
通过分析这些组合,我们可以洞察两组变量之间的潜在关系,并提供有关如何解释和预测这种关系的指导。
总结而言,典型相关分析是一种强大的多元统计分析方法,可以用于研究两组变量之间的关联性。
典型相关分析

引言在一元统计分析中,用相关系数来衡量两个随机变量之间的线性相关关系;用复相关系数研究一个随机变量和多个随机变量的线性相关关系。
然而,这些统计方法在研究两组变量之间的相关关系时却无能为力。
比如要研究生理指标与训练指标的关系,居民生活环境与健康状况的关系,人口统计变量与消费变量(之间是否具有相关关系。
阅读能力变量(阅读速度、阅读才能)与数学运算能力变量(数学运算速度、数学运算才能)是否相关。
典型相关分析(Canonical Correlation )是研究两组变量之间相关关系的一种多元统计方法。
它能够揭示出两组变量之间的内在联系。
1936年霍特林(Hotelling )最早就“大学表现”和“入学前成绩”的关系、政府政策变量与经济目标变量的关系等问题进行了研究,提出了典型相关分析技术。
之后,Cooley 和Hohnes (1971),Tatsuoka (1971)及Mardia ,Kent 和Bibby (1979)等人对典型相关分析的应用进行了讨论,Kshirsagar (1972)则从理论上给出了最好的分析。
典型相关分析的目的是识别并量化两组变量之间的联系,将两组变量相关关系的分析,转化为一组变量的线性组合与另一组变量线性组合之间的相关关系分析。
目前,典型相关分析已被应用于心理学、市场营销等领域。
如用于研究个人性格与职业兴趣的关系,市场促销活动与消费者响应之间的关系等问题的分析研究。
第一章、典型相关的基本理论 1.1 典型相关分析的基本概念典型相关分析由Hotelling 提出,其基本思想和主成分分析非常相似。
首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此继续下去,直到两组变量之间的相关性被提取完毕为此。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
典型相关系数度量了这两组变量之间联系的强度。
典型相关分析

典型相关分析典型相关分析(canonical correlation analysis)就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。
它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量1U 和1V (分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
通常情况下,为了研究两组变量12122,,,,,,,p q x x x y y y w ⎡⎤⎡⎤⋅⋅⋅⋅⋅⋅⎣⎦⎣⎦的相关系数,可以用最原始的方法,分别计算两组变量之间的全部相关系数,一共有pq 个简单相关系数,这样既繁琐又不能抓住问题的本质。
首先分别在每组变量中找出第一对线性组合,使其具有最大相关性,即1111212111112121p pq q u x x x v y y y αααβββ=++⋅⋅⋅+⎧⎪⎨=++⋅⋅⋅+⎪⎩ 然后在每组变量中找出第二对线性组合,使其分别与本组内的第一对线性组合不相关,第二对线性组合本身具有次大的相关性,有2121222221212222p pq q u x x x v y y y αααβββ=++⋅⋅⋅+⎧⎪⎨=++⋅⋅⋅+⎪⎩ 2u 与1u ,2v 与1v 不相关,但2u 与2v 相关。
如此继续下去,直至进行到r 步,两组变量的相关性被提取完为止,可以得到r 组变量,这里min(,)r p q ≤。
步骤:假设两组随机变量1212,,,,,,,p q X x x x Y y y y ⎡⎤⎡⎤=⋅⋅⋅=⋅⋅⋅⎣⎦⎣⎦,C 为p q +维总体的n 次标准化观测数据阵,有11111121221211()pq p q n np n nq n p q a a b b a a b b C a a b b ⨯+⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 第一步,计算相关系数矩阵R ,并将R 剖分为11122122RR R R R ⎡⎤=⎢⎥⎣⎦,其中11R 和22R 分别为第一组变量和第二组变量的相关系数阵,T1221R R =为第一组与第二组变量的相关系数阵。
学术研究中的典型相关分析方法

学术研究中的典型相关分析方法一、引言典型相关分析是一种广泛应用于社会科学和生物统计学领域的统计方法,主要用于研究两个或多个变量之间的关系。
典型相关分析能够从大量数据中提取出有用的信息,帮助研究者更好地理解研究对象之间的相互作用。
本文将详细介绍典型相关分析的基本原理、步骤和应用,为学术研究提供有益的参考。
二、典型相关分析的基本原理典型相关分析是一种用于探索多个变量之间关系的方法。
它通过寻找一组代表性变量,来反映原始变量之间的相关关系。
这些代表性变量通常被称为主成分或典型变量,它们能够反映原始变量的绝大部分信息。
通过分析典型变量之间的关系,可以推断出原始变量之间的潜在关系。
典型相关分析的基本原理可以概括为以下三个步骤:1.数据的降维:通过主成分分析或类似的方法,将原始数据从多个维度降至少数几个典型变量。
2.寻找代表性变量:根据典型变量的方差贡献和相关性,选择最重要的几个典型变量。
3.解释原始变量之间的关系:通过分析典型变量之间的关系,推断出原始变量之间的潜在关系。
三、典型相关分析的步骤典型相关分析通常包括以下步骤:1.准备数据:收集并整理需要进行分析的数据,确保数据的质量和准确性。
2.降维:使用主成分分析、独立成分分析或其他降维方法,将数据从多个维度降至少数几个典型变量。
3.确定典型变量:根据方差贡献和相关性,选择最重要的几个典型变量。
4.统计分析:使用适当的统计方法,如线性回归、相关系数等,分析典型变量之间的关系,并解释其意义。
5.结果解释:将典型变量之间的关系与原始变量之间的相关性进行比较,推断出原始变量之间的潜在关系。
四、典型相关分析的应用典型相关分析在许多领域都有广泛的应用,包括但不限于社会学、心理学、生物学和医学。
以下是一些典型相关分析的应用实例:1.研究社会现象:在研究社会现象时,典型相关分析可以用于探索人口统计学特征(如年龄、性别、教育水平等)与行为、态度和价值观之间的关系。
通过分析典型变量,可以更深入地了解社会现象的内在机制。
典型相关分析

10
八、冗余分析
是典型变式对本组所有观测变量的总方差
的代表比例,共有:
⑴第一组观测变量总方差中由本组变式代表的比例 ⑵第一组观测变量总方差中由第二组变式解释的比例 ⑶第二组观测变量总方差中由本组变式代表的比例 ⑷第二组观测变量总方差中由第二组变式解释的比例
0.2721
1.6443
Y组典型变量的系数
V1 Y1(年龄) Y2(收入) 0.0491 0.8975
V2 1.0003 -0.5837
Y3(文化)
0.1900
0.2956
u1 0.7689 x1 0.2721 x2 u2 1.4787 x1 1.6443 x2
v1 0.0491 y1 0.8975 y2 0.1900 y3 v2 1.0003 y1 0.5837 y2 0.2956 y3
3
二、在SPSS中如何进行典型相关 分析
例1:生育状况与影响因素的相关分析
X1--多孩率 X2--综合节育率
X3--初中以上受教育程度的人口比例
X4--人均国民收入
X5--城镇人口比例
4
在SPSS中有一个命令文件 CANONICAL CORRELATION.SPS 1.打开数据文件T3-2.SAV 2.在FILE中选NEW --SYNTAX 3.输入命令
典型变量的结构(相关系数) U1 X1 X2 0.9866 0.8872 U2 -0.1632 0.4614
V1 Y1 Y2 0.4211 0.9822
V2 0.8464 -0.1101
第九章-典型相关分析

二、典型相关分析原理及方法
设有两组随机向量, X (1) 代表第一组的 p 个变量, X (2) 代表
第二组的 q 个变量,假设 p≤q。令
Cov( X (1) ) Σ11 , Cov( X (2) ) Σ22 , Cov( X (1) , X (2) ) Σ12 Σ21
X (1) 1
关变量之后,可以类似的求出各对之间互不相关的第二对、第三对
等典型相关变量。这些典型相关变量就反映了 X (1) , X (2) 之间的
线性相关情况。这里值得注意的是,我们可以通过检验各对典型相 关变量相关系数的显著性,来反映每一对综合变量的代表性,如果 某一对的相关程度不显著,那么这对变量就不具有代表性,不具有 代表性的变量就可以忽略。这样就可以通过对少数典型相关变量的 研究,代替原来两组变量之间的相关关系的研究,从而容易抓住问 题的本质。
X (1) 2
X ( pq)1
X (1)
X
(
2)
X
(1) p
X1(
2)
X
(2) 2
X
(2) q
Σ
Cov( X
,
X
)
(
11
p p)
Σ
21
(q p)
Σ
(
12
pq )
Σ22 ( qq )
根据典型相关分析的基本思想,要进行两组随机向量间的相
关分析,首先要计算出各组变量的线性组合——典型变量,
并使其相关系数达到最大。因此,我们设两组变量的线性组
合分别为:
U
aX (1)
a1
X (1) 1
a2
X
(1) 2
ap
X
(1) p
V
典型相关分析

当我们分析两个变量间的线性相关关系时,可以用简单相关系数;分析一个变量与多个变量间的线性相关关系时,可以用复相关系数;但是当分析多个变量与多个变量间的相关关系时,并没有一个确切的指标加以反映,虽然可以两两计算简单相关系数,形成一个相关矩阵,但是这样做有两个问题:1.计算繁琐,当变量较多时矩阵庞大,不易解释。
2.简单相关系数只是孤立的单个变量间的相关,当分析两组变量时,由于交互作用的存在,简单相关系数并不能真实反映变量间的相关性。
多个变量与多个变量间的分析,可以看成是组与组之间的相关分析,此时可以使用典型相关分析(Canonical Correlation Analysis),也是一种多元分析方法。
======================================================一、典型相关分析的基本原理我们知道在回归分析中,为了预测一个因变量Y,要寻找n个自变量,这n个自变量的最佳线性组合,就是预测Y的回归模型。
在面对两组变量时,我们也可以按照同样的做法,在每组中寻找等个数的线性组合,分析这些线性组合的相关性,并以此来反映两组变量之前的相关性。
可以看出,典型相关分析和主成分分析思路是一致的,因此也是一种降维方法。
典型相关分析首先将每组变量转换为用线性组合表示,然后两两计算每对组合之间的简单相关系数,取最大值,即在两个变量组各自的总变化中先寻求他们之间最大的一部分共变关系,这个最大值就是两组变量的第一典型相关系数,具有最大值的这两个线性组合称为第一典型变量。
接下来在余下的线性组合中计算第二典型相关系数,并要求与第一对线性组合不相关,如此反复,直至提取出两组变量的全部信息,并可以得到若干个典型相关系数和典型变量。
可以看出,当两组变量均只有一个变量时,典型相关系数就是简单相关系数;当其中一组只有一个变量时,典型相关系数就是复相关系数。
======================================================二、典型系数、典型相关系数、典型载荷系数、冗余系数典型系数:一组变量对应于线性化后特征根的典型变量的系数,称为典型系数。
典型相关分析

典型相关分析典型相关分析是一种统计学方法,用于研究两组变量之间的关系。
典型相关分析可以帮助我们了解这两组变量之间的相互关系以及它们是否能够彼此预测。
在本文中,我们将探讨典型相关分析的基本概念、应用场景、计算方法以及结果的解释和解读。
典型相关分析,又称为典型相关系数分析,是一种多变量统计技术,它可以在两组变量之间寻找最具相关性的线性组合,这个线性组合被称为典型变量。
典型相关分析的核心思想是将两组变量转化为一组最具相关性的综合变量,以便探索和解释它们之间的关系。
典型相关分析通常用于探索两组变量之间的关系,并确定是否存在一个或多个典型相关系数。
在许多实际应用中,这些变量可能代表相互关联的特征或维度,比如市场规模和销售额、学习时间和考试成绩等。
典型相关分析可以用于许多领域的研究。
例如,在市场研究中,我们可以使用典型相关分析来研究不同市场因素之间的关系,并确定市场的发展趋势。
在教育研究中,我们可以使用典型相关分析来研究学生的学习习惯和学术成绩之间的关系,以帮助教育者改进教学方法和学习环境。
接下来,我们将介绍典型相关分析的计算方法。
假设我们有两组变量X和Y,其中X包含p个变量,Y包含q个变量。
首先,我们计算X和Y的样本协方差矩阵SXX和SYY,以及它们之间的协方差矩阵SXY。
然后,我们对SXX和SYY进行特征值分解,得到它们的特征向量和特征值。
接下来,我们选择最大的r个特征值和对应的特征向量。
最后,我们计算典型相关系数以及典型变量。
结果的解释和解读是典型相关分析的最后一步。
典型相关系数的取值范围为-1到1,其中取值为1表示两组变量之间存在完全正相关的关系,取值为-1表示存在完全负相关的关系,取值为0表示两组变量之间不存在相关性。
此外,我们还可以通过检验统计量来判断典型相关系数是否显著。
总结起来,典型相关分析是一种统计学方法,用于研究两组变量之间的关系。
它可以帮助我们了解这两组变量之间的相互关系以及它们是否能够彼此预测。
数据分析中的典型相关分析方法

数据分析中的典型相关分析方法数据分析在当今社会中扮演着重要的角色,帮助企业和组织做出明智的决策。
典型相关分析是数据分析中的一种重要方法,用于探索两组变量之间的关系。
本文将介绍典型相关分析的基本概念、应用场景以及分析步骤。
典型相关分析是一种多元统计方法,用于研究两组变量之间的关系。
它可以帮助我们了解两组变量之间的相关性,并找到最相关的变量组合。
典型相关分析通常用于探索多个自变量与多个因变量之间的关系,以及在这些关系中起主导作用的变量。
典型相关分析的应用场景非常广泛。
例如,在市场营销领域,我们可以使用典型相关分析来研究产品特征与消费者购买行为之间的关系。
在医学研究中,我们可以使用典型相关分析来研究疾病和基因表达之间的关系。
在人力资源管理中,我们可以使用典型相关分析来研究员工满意度与绩效之间的关系。
进行典型相关分析的步骤如下:1. 收集数据:首先,我们需要收集两组变量的数据。
这些数据可以是连续的、离散的或分类的,但必须是数值型数据。
2. 数据预处理:在进行典型相关分析之前,我们需要对数据进行预处理。
这包括检查数据的完整性、处理缺失值和异常值,并进行数据标准化。
3. 计算相关系数:接下来,我们需要计算两组变量之间的相关系数。
典型相关分析使用的是典型相关系数,它衡量了两个变量组合之间的相关性。
4. 解释结果:一旦计算出典型相关系数,我们可以解释结果。
典型相关系数的取值范围为-1到1,其中1表示完全正相关,-1表示完全负相关,0表示无相关性。
5. 判断显著性:最后,我们需要判断典型相关系数是否显著。
通常使用假设检验来判断典型相关系数是否显著。
典型相关分析的结果可以帮助我们理解两组变量之间的关系,并找到最相关的变量组合。
例如,在市场营销领域,典型相关分析可以帮助我们确定哪些产品特征与消费者购买行为最相关,从而优化产品设计和市场推广策略。
在医学研究中,典型相关分析可以帮助我们发现哪些基因与疾病发生最相关,从而帮助疾病的早期预测和治疗。
现代统计分析方法的学与用_十一_典型相关分析

能要全部写进分析文章 也可能 摘要 写入 有时可能不被
引用 若及时把这些细节进行信息转化 无疑会扩大我们的
调研成果 提高我们的服务质量
例一
系统转换经营机制 企业活力大增
今年上半年 我县 系统通过转换经营机制 使企业活
力大增
指标实现
同比增长
经营效益明显
提高 其转换经营机制的具体措施是
例二
食品收购站 官商 作风严重 群众反映强烈 信
息内容略
例三
景区商贩追缠游人现象亟待治理 信息内容略
在上述三例中 例一取自文字资料 例二取自 口头交
流 例三取自 现场目击 不管取自何方 都是为撰写分析
而准备的 原材料 这些 原材料 被提炼成信息产品后 既
没有 埋没 有反馈价值的调研细节 又对统计分析产品起到
若将这两组变量各组成一个线性组合 即
U = L1 x1+L 2x2+ +Lrx r V=M 1y 1+M 2 y2 + + M sy s 其中 Li(i=1,2, r)和Mj(j=1,2, 为
s)是任意实数 用矩阵表示
U=L X
V=M Y
其中
( )L1
L= Lr
( )M 1
第三 利用统计软件对所搜集到的数据资料进行处理 得
到典型相关变量和典型相关系数如下表
下转第42页
40 北京统计 2000-11 总第 129 期
实务教程
的身份选进建议条款 其他素材也视与 建议 的关联程度决 定取舍 综上 全文 浓缩是对分析文章的 二次提炼 和 二 次加工 浓缩的目光一定要盯准 反馈价值 这个焦点上 核 心找准了 信息的雏形也就出来了
度应是发展旅游业的工作重点
在上两例中 是报表信息 是根据统计分析过程中数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辑框图
第2步:设计典型相关分析 典型相关分析作为一种多元分析方法,与其他的多
元分析技术有共同的基本的要求。其它方法(尤其
是多元回归、判别分析和方差分析)所讨论的测量
误差的影响、变量类型及变换也与典型相关分析有 很大关系。
样本大小的影响和每个变量需要足够的观测都是典
型相关分析经常遇到的。研究者容易使自变量组和
1. 总体典型相关和典型变量
2019/8/13
8
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
9
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
10
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
21
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论
及方法
3. 典型相关系数的显著性检验
2019/8/13
22
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
23
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
24
2019/8/13
4
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论
及方法
典型相关分析是借助于主成分分析的思想,对 每一组变量分别寻找线性组合,使生成的新的 综合变量能代表原始变量大部分的信息,同时, 与由另一组变量生成的新的综合变量的相关程 度最大,这样一组新的综合变量称为第一对典 型相关变量,同样的方法可以找到第二对,第 三对,…,使得各对典型相关变量之间互不相 关,典型相关变量之间的简单相关系数称为典 型相关系数,典型相关分析就是用典型相关系 数衡量两组变量之间的相关性。
11
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8相关分析的基本理论 及方法
2019/8/13
13
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
14
目录 上页 下页 返回 结束
2019/8/13
25
目录 上页 下页 返回 结束
§8.2 典型相关分析的步骤及逻
辑框图
第1步:确定典型相关分析的目标 典型相关分析所适用的数据是两组变量。我们假定
每组变量都能赋予一定的理论意义,通常一组可以
定义为自变量,另一组可以定义为因变量。典型相 关分析可以达到以下目标:
(1) 确定两组变量是相互独立,或者相反,确定两组 变量间存在关系的大小。
§8.1典型相关分析的基本理论 及方法
2019/8/13
15
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
16
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
17
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
多元统计分析
2019/8/13
1
第八章 典型相关分析
• §8.1典型相关分析的基本理论及方法
• §8.2 典型相关分析的步骤及逻辑框图
• §8.3 典型相关分析的上机实现
• §8.4 社会经济案例研究
2019/8/13
2
第八章 典型相关分析
• 典型相关分析(canonical correlation analysis)是 研究两组变量之间相关关系的多元分析方法。它 借用主成分析降维的思想,分别对两组变量提取 主成分,且使从两组变量提取的主成分之间的相 关程度达到最大,而从同一组内部提取的各主成 分之间互不相关,用从两组之间分别提取的主成 分的相关性来描述两组变量整体的线性相关关系。 典型相关分析的思想首先由Hotelling于1936年提 出,计算机的发展解决了典型相关分析在应用中 计算方面的困难,目前成为普遍应用的进行两组 变量之间相关性分析的技术。本章主要介绍典型 相关分析的思想,基本理论及分析方法,并介绍 利用SPSS软件进行典型相关分析的方法。
(2) 为每组变量推导出一组权重,使得每组变量的线 性组合达到最大程度相关。最大化余下的相关关系 的其他的线性函数是与前面的线性函数独立的。
(3) 解释自变量与因变量组中存在的相关关系,通常 是通过测量每个变量对典型函数的相对贡献来衡量。
2019/8/13
26
目录 上页 下页 返回 结束
§8.2 典型相关分析的步骤及逻
2019/8/13
3
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
8.1.1 典型相关分析的统计思想 典型相关分析研究两组变量之间整体的线性 相关关系,它是将每一组变量作为一个整体 来进行研究而不是分析每一组变量内部的各 个变量。所研究的两组变量可以是一组变量 是自变量,而另一组变量是因变量的情况, 两组变量也可以处于同等的地位,但典型相 关分析要求两组变量都至少是间隔尺度的。
因变量组包含很多的变量,而没有认识到样本量的
含义。小的样本不能很好的代表相关关系,这样掩
盖了有意义的相关关系。建议研究者至少保持每个 变量10个观测,以避免数据的“过度拟合”。
2019/8/13
5
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
6
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
7
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
8.1.2 典型相关分析的基本理论及方法
目录 上页 下页 返回 结束
§8.2 典型相关分析的步骤及逻
辑框图
典型相关分析的步骤有以下6 步:(1)确定典型相关分析 的目标;(2)设计典型相关 分析;(3)检验典型相关分 析的基本假设;(4)估计典 型模型,评价模型拟合情况; (5)解释典型变量;(6)验 证模型。见参考文献[5]。它实 现的逻辑框图如下:
2019/8/13
18
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
19
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 2.及样本方典法型相关和典型变量
2019/8/13
20
目录 上页 下页 返回 结束
§8.1典型相关分析的基本理论 及方法
2019/8/13
