第八章典型相关分析
第八章 相关分析与回归分析

下一页
返回本节首页
19
③在数据区域中输入B2:C11,选择“系列产 生在—列”,如下图所示,单击“下一步” 按钮。
上一页
第8章 回归分析
下一页
返回本节首页
20
④打开“图例”页面,取消图例,省略标题,如 下图所示。
上一页
第8章 回归分析
下一页
返回本节首页
21
⑤单击“完成”按钮,便得到XY散点图如下图 所示。
n 8, x 36.4, x 207.54 , y 104214 y 880, . xy 4544 6
2 2
r
n xy x y n x2 x 2 n y2 y 2 8 4544 6 36.4 880 .
第8章 回归分析
40
(二)回归分析的种类: 1、按自变量 x 的多少,分为一元回归和多 元回归; 2、按 y 与 x 关系的形式,分为线性回归和 非线性回归。
第8章 回归分析
41
二、一元线性回归分析
x y 62 86 80 110 115 132 135 160
42
(一)一元线性回归方程:
2、非线性相关:当一个变量变动时, 另一个变量也相应发生变动,但这种变 动是不均等的。
第8章 回归分析
9
㈢根据相关关系的方向 1、正相关:两个变量间的变化方向一 致,都是增长趋势或下降趋势。 2、负相关:两个变量变化趋势相反。
上一页
第8章 回归分析
下一页
返回本节首页
10
(四)根据相关关系的程度 1、完全相关:两个变量之间呈函数关系 2、不相关:两个变量彼此互不影响,其 数量的变化各自独立
第8章 相关分析-6. 最大互相关方法(MCC)

第8章 相关分析6. 最大互相关方法(MCC)除了上面介绍的各种相关分析方法,还存在一种称为最大互相关方法(MCC :Maximum Cross Correlation)的算法。
MCC 算法是非常传统的算法,在许多文献中都有提及,其特性和缺陷也在许多文献中有所讨论。
MCC 算法是一种基于互相关系数,取决于两张图片相似性的模板匹配算法,国内外研究人员在极区海冰漂移分析和海洋表面流场分析中经常使用该方法,因为前面的举例中笔者已经列举了极区海冰漂移分析结果,笔者后面列举的算例中提供MCC 算法在海表流场中的遥感分析应用。
6.1 MCC 原理MCC 计算过程可用图8-14表示。
A :源模块B :诊断窗口C :位移矢量图8-14 MCC 计算过程简略图解 假定),(1n j m i I ++,2/2/M m M <≤-、2/2/N n N <≤-表示图8-14-A 中中心位置在(i ,j )、形状大小为M ×N 的图像块每一个点的数值(如图像灰度值),对应的),(2n l j m k i I ++++表示图8-14-B 中中心位置在(i+k ,j+l )、形状大小为M ×N 的图像块每一个点的数值。
源模块和目标模块之间的相似性可以用如下公式(8-34)的互相关系数量化表示出来:∑∑∑∑∑∑--=--=--=--=--=--=++-++++⨯-++++-++++⨯-++=1221222221221222111221222211)],(),([)],(),([)],(),([)],(),([),(M M m N N n M M m N N n M M m N N n l j k i I n l j m k i Ij i I n j m i I l j k i I n l j m k i I j i I n j m i I l k r (8-34) 上式中,),(1j i I 表示图8-14-A 中中心位置在(i ,j )的选定的源模块范围的平均值,),(2l j k i I ++表示图8-14-B 中中心位置在(i+k ,j+l )的选定的目标模块范围的平均值。
第8章 相关分析

第8章 相关分析相关分析(Correlations)是研究两个变量间。
或一个变量与多个变量间,或多个变量两两变量间,或两组变量间,或多个变量组与组之间密切程度的一种常用统计学方法。
变量间的密切程度常用相关系数(Correlation Coefficients)或统计量描述。
SAS /Win(v8)系统非编程有如下5种相关量度(Correlation Measure)。
(1)Pearson product-moment correlation ,皮尔逊积矩相关分析。
(2)Spearman coefficients ,斯皮尔曼相关系数s r(3)Cronbach ’coefficient alpha ,克龙巴哈系数α(4)Kendall ’s tan –b coefficient ,肯德尔b τ系数。
(5)Hoeffding ’s D statistic ,霍夫丁D 统计量。
同时将输出变量的简单统计量(Simple Statistics),相关系数(Correlation Coefficients),相应的P 值与图形(P1ots)等。
8-1皮尔逊积矩相关分析[例8-1] 已知5-6岁儿童体检数据的指标为编号(1x ),性别(2x ),月龄(3x ),体重(4x ,kg),身高(5x ,cm),坐高(6x ,cm),胸围(7x ,cm),头围(8x ,cm),左眼视力(9x )与右眼视力(10x ),并已建立SAS 数据集SASUSER.child 。
试对体重(4x )与身高(5x )做皮尔逊(Pearson)相关分析。
(1)进入SAS /Win(V8)系统,单击So1utions->Analysis->Analyst ,进入分析家窗口。
(2)单击File->open By SAS Name->Sasuser->Child->OK ,调入SAS 数据集SASUSER.child(3)单击statistics->Descriptive->correlations ,得到图8-1所示对话框。
薛薇,《SPSS统计分析方法及应用》第八章 相关分析和线性回归分析

以控制,进行偏相关分析。
偏相关分 析输出结 果;负的 弱相关
相关分析 输出结果 ;正强相 关
8.4.1
8.4.2
回归分析概述
线性回归模型
8.4.3
8.4.4 8.4.5 8.4.6
回归方程的统计检验
基本操作
其它操作
应用举例
线性回归分析的内容
能否找到一个线性组合来说明一组自变量和因变量
可解释x对Y的影响大小,还可 以对y进行预测与控制
目的是刻画变量间的相关 程度
8.2.1 8.2.2 8.2.3 8.2.4
散点图 相关系数 基本操作 应用举例
•
相关分析通过图形和数值两种方式,有效地揭示事物
之间相关关系的强弱程度和形式。
8.2.1 散点图 它将数据以点的的形式画在直角坐标系上,通过
Distances 过程用于对各样本点之间或各个变量之间 进行相似性分析,一般不单独使用,而作为聚类分
析和因子分析等的预分析。
1) 选择菜单Analyze Correlate Bivariate,出现 窗口:
2) 把要分析的变量选到变量Variables框。
3) 在相关系数Correlation Coefficents框中选择计算哪种
一元线性回归模型的数学模型:
y 0 1 x
其中x为自变量;y为因变量; 0 为截距,即常量;
1 为回归系数,表明自变量对因变量的影响程度。
用最小二乘法求解方程中的两个参数,得到
1
( x x )( y y ) (x x)
i i 2 i
0 y bx
第八章 方差分析与相关分析
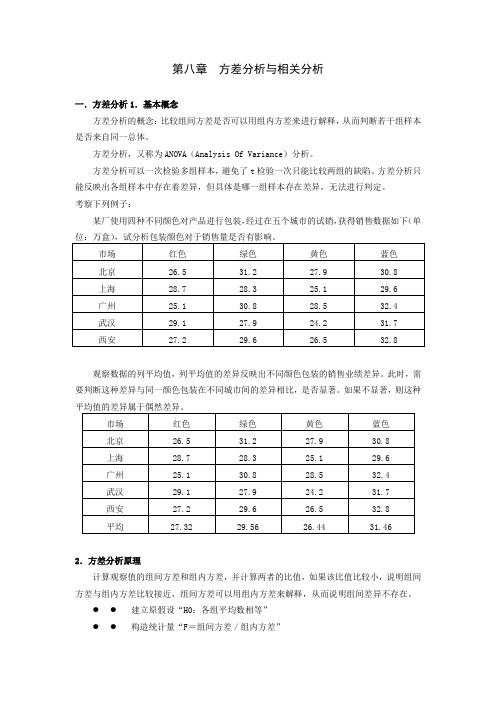
第八章方差分析与相关分析一.方差分析1.基本概念方差分析的概念:比较组间方差是否可以用组内方差来进行解释,从而判断若干组样本是否来自同一总体。
方差分析,又称为ANOVA(Analysis Of Variance)分析。
方差分析可以一次检验多组样本,避免了t检验一次只能比较两组的缺陷。
方差分析只能反映出各组样本中存在着差异,但具体是哪一组样本存在差异,无法进行判定。
考察下列例子:某厂使用四种不同颜色对产品进行包装,经过在五个城市的试销,获得销售数据如下(单观察数据的列平均值,列平均值的差异反映出不同颜色包装的销售业绩差异。
此时,需要判断这种差异与同一颜色包装在不同城市间的差异相比,是否显著。
如果不显著,则这种2.方差分析原理计算观察值的组间方差和组内方差,并计算两者的比值,如果该比值比较小,说明组间方差与组内方差比较接近,组间方差可以用组内方差来解释,从而说明组间差异不存在。
●●建立原假设“H0:各组平均数相等”●●构造统计量“F=组间方差/组内方差”●●在计算组间方差时,使用自由度为(r-1),计算组内方差时,使用自由度为(n-r)。
●●F满足第一自由度为(r-1),第二自由度为(n-r)的F分布。
●●查表,若F值大于0.05临界值,则拒绝原假设,认为各组平均数存在差异。
根据方差计算的原理,生成方差分析表如下:其中:组间离差平方和 SSA (Sum of Squares for factor A) =39.084误差项离差平方和 SSE (Sum of Squares for Error) =76.8455总离差平方和 SST (Sum of Squares for Total)=115.9295P-value值为0.000466,小于0.05,所以拒绝原假设。
3.双因素方差分析观察下列销售数据,欲了解包装方式和销售地区是否对于销售业绩有影响,涉及到双因素的方差分析。
此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。
第八章相关分析

11-16 5
6-11
-
合计 7
1
3
3
4
1
13
3
3
1
1
8
7
7
2
1 24
24
按耕作深度
分组(cm)
3
8
1
10
1
12
1
14
16
18
合计
3
双变量分组相关表
平均收获率(100kg/亩)
4
5
6
7
1
1
3
2
2
6
3
2
3
5
2
1
2
3
13 11 6
8 合计
3
6
14
1
11
2
5
1
1
4
40
25
多因素复合分组相关表 (日产吨数)
11
第一节 相关分析的一般问题
相关关系种类
相关程度 相关方向 关系表现形式 影响因素 依存关系
完不完 全完全 相全不 关相相
正 相 关
负 相 关
线 性 相
非 线 性
单复 相相 关关
关关
关相
关
因非 果因 关果 系关
系
12
第一节 相关分析的一般问题
二、相关分析与回归分析 (一)涵义
1、相关分析是对具有相关关系的变 量之间的关系密切程度进行分析研究的 统计方法。
倾斜度
煤层深度(m)
100以下
年采掘量(千吨) 100 ̄250 250 ̄400 400以上
0.7m
13
35度以下 (缓斜度)
0.7 ̄0.9 0.9 ̄1.1
典型事故案例分析

近年氯气泄漏事故: 氯气泄漏事故屡见不鲜,几乎年年都有 氯气中毒事故发生。事故惨状,刻骨铭心。 近年来,大大小小的氯气泄漏事故造成人员 伤亡的就有十几起。“避免此类事故的重现, 安全生产不容忽视”。
近年氯气泄漏事故: ●1996年2月14日上午10时左右,上海某农药厂 装卸液氯钢瓶时,从本厂码头用卡车将液氯钢瓶驳 至厂内三氯化磷存氯场地(每只钢瓶载重量1000公 斤),车子倒入地下斜坡车道后,将钢瓶滚至地面。 由于车子装货面与地面有位差,该位差用一个橡皮 垫圈作避震。当装卸工胡某和候某在装卸第四车最 后一只钢瓶时,钢瓶从卡车上滚至地面平台上时橡 皮垫圈跳了一下,钢瓶斜转滚下时,撞到边上一只 氯气钢瓶的针形阀,导致针形阀齐根开裂,大量氯 气外溢。厂消防队员迅速赶至现场抢险,跑氯得到 有效控制。在事故发生和处理过程中共有43人不同 程度氯气吸入,其中有2人属氯气轻度中毒。
2. 事故调查: 1)C1氯化釜停用前后的情况调查:根据查看相关记录,该 氯化釜最后一次投料使用时间为10月13日下午15:36,到14 日21:00转为主釜,在15日15:00氯化反应中期发现釜体穿孔 后停用。停用后,工段组织人员对通氯阀、进出水阀等进行 了关闭,并对釜内料液进行了抽空处理。 2)化验室人员对氯乙酸氯化系统相关气体及该氯化釜釜内 残液(约500㎏)等进行了化验分析,具体结果如下: a) 主釜尾气组成:HCl:64.5%;Cl2:1.75%;H2/ Cl2: 3.17%; b) 副釜尾气组成:HCl:73%;H2/ Cl2:3.15%; c) 氯化釜釜内残液:HAc 34.55%;HCl 2.10%; 另外氯化釜残液内含有大量Fe2+离子。
(2)工人未经培训,仓促上岗。 该化工厂自租赁以后,生产操作人员全部重新招用外来 劳动力,进厂做早的在95年4月中旬,最迟的一批人5月15日 下午刚刚从青海赶到工厂,仅当晚开会说说注意事项,第二 天就上岗操作。因此工人没有起码的工业生产的常识,没有 任何安全知识,不懂得安全操作规程,也不知道本企业生产 的操作要求,根本不认识化工生产的危险特点,尤其对如何 处理生产中出现的异常情况更是不懂。整个生产过程全由租 赁方总经理颜冬和生产副厂长王某具体指挥每个工人如何做, 工人自己不知道怎样做。
第八章 相关分析与回归分析习题答案

第八章 相关分析与回归分析习题参考答案一、名词解释函数关系:函数关系亦称确定性关系,是指变量(现象)之间存在的严格确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,必定有另一个且只有一个变量有确定的值与之对应。
相关关系:是指变量(现象)之间存在着非严格、不确定的依存关系。
在这种关系中,当一个或几个相互联系的变量取一定的数值时,可以有另一变量的若干数值与之相对应。
这种关系不能用完全确定的函数来表示。
相关分析:相关分析主要是研究两个或者两个以上随机变量之间相互依存关系的方向和密切程度的方法,直线相关用相关系数表示,曲线相关用相关指数表示,多元相关用复相关系数表示。
回归分析:回归分析是研究某一随机变量关于另一个(或多个)非随机变量之间数量关系变动趋势的方法。
其目的在于根据已知非随机变量来估计和预测随机变量的总体均值。
单相关:单相关是指仅涉及两个变量的相关关系。
复相关:复相关是指一个变量对两个或者两个以上其他变量的相关关系。
正相关:正相关是指两个变量的变化方向是一致的,当一个变量的值增加(或减少)时,另一变量的值也随之增加(或减少)。
负相关:负相关是指两个变量的变化方向相反,即当一个变量的值增加(或减少)时,另一个变量的值会随之减少(或增加)。
线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈一条直线,则称为线性相关。
非线性相关:如果相关的两个变量对应值在直角坐标系中的散点图近似呈现出某种曲线形式,则为非线性相关。
相关系数:相关系数是衡量变量之间线性相关密切程度及相关方向的统计分析指标。
取值在-1到1之间。
两个变量之间的简单样本相关系数的计算公式为:()()niix x y y r --∑二、单项选择1.B;2.D;3.D;4.C;5.A;6.D 。
三、判断题(正确的打“√”,错误的打“×”) 1.×; 2.×; 3.√; 4.×; 5.×; 6.×; 7.×; 8.√. 四、简答题1、什么是相关关系?相关关系与函数关系有什么区别?答:相关关系,是指变量(现象)之间存在着非严格、不确定的依存关系。
第8章 相关与回归分析

4、在相关关系中,变量之间是平等关系,不存在自变量和因变量。 、在相关关系中,变量之间是平等关系,不存在自变量和因变量。
而在回归分析中必须明确划分自变量和因变量。 而在回归分析中必须明确划分自变量和因变量。
8-9
统计学
STATISTICS
8.2 简单线性相关与回归分析
8 - 10
STATISTICS
8-5
统计学
STATISTICS
(三)从变量相关关系变化的方向看 从变量相关关系变化的方向看 变化的方向 正相关: A 正相关:变量同方向变化 , 即同增同减 (A) 同增同减 负相关:变量反方向变化, 负相关:变量反方向变化, 即一增一减 (B) B 一增一减 从变量相关的程度 相关的程度看 (四)从变量相关的程度看
完全相关 (B) 不完全相关 (A) 不相关 (C)
8-6
25 20 15 10 5 0 0 2 4 6 8 10 12
25 20 15 10 5 0 0 2 4 6 8 10 12
C
35 30 25 20 15 10 5 0 0 5 10 15
统计学
STATISTICS
三、回归分析
回归一词的由来: 回归一词的由来:
8 - 13
见第218页例题 页例题 见第 页例
统计学
STATISTICS
相关系数的特点: 相关系数的特点:
1、r 的取值范围是 − 1 ≤ r ≤ 1 。 、 2、r<0时,β<0 为负相关;r>0时, β>0 为正相关。 为负相关; 为正相关。 、 时 时 3、|r|=1,为完全相关。r =1,为完全正相关;r = -1, 、 ,为完全相关。 ,为完全正相关; , 为完全负正相关。 为完全负正相关。 4、r = 0,不存在线性相关。 、 线性相关。 ,不存在线性相关 5、|r|越趋于 表示两变量线性关系越密切;|r|越趋于 、 越趋于 表示两变量线性关系越密切; 越趋于 越趋于1表示两变量线性关系越密切 越趋于0 表示两变量线性关系越不密切。 表示两变量线性关系越不密切。 线性关系越不密切 6、r是一个随机变量。 、 是一个随机变量 是一个随机变量。
多元统计分析第八章 典型相关分析

第8章 典型相关分析典型相关分析是用来描述两组随机变量(两个随机向量)间关系的统计分析方法。
两组随机向量,各含有许多随机变量,能否用少量随机变量来描述其相关性?例如为了研究饲料与荤菜价格的关系,统计若干年玉米、大豆、稻子、麦子、鱼粉以及猪肉、牛肉、羊肉、鸡肉、鸡蛋、鸭肉、鸭蛋的价格,分析饲料与荤菜价格的关系时,发现单独一种饲料和单独一种肉蛋禽价格关系并不密切(由显著性检验可见),但饲料的某种综合价格则与肉蛋禽综合价格的关系很密切。
把饲料价格看成一组随机变量,肉蛋禽价格看成另一组随机变量,找这两组随机变量的线性组合,使之相关系数平方最大,从而分析两组随机变量间的关系,判定这两组随机变量是否有关联,这就是典型相关分析。
8.1 典型相关分析数学模型设随机向量)',...(1p x x X =与)',...(1p y y Y =的方差yy xx ∑∑,存在,协方差为xy Y X ∑=),cov(。
b a ,为常数向量。
则1/2(',')'/('')xy xx yy corr a X b Y a b a ab b =∑∑∑,为了计算确定性,限制,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy 。
定义8.1 设11,b b a a ==在条件:,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy下使co v(',')a X b Y 大,则称Y b w X a v ','1111==为第一对典型相关变量,c o v(',')a Xb Y 称为第一典型相关系数。
由定义可见,11,w v 尽可能多地反映原来p 对随机变量相关的信息。
第一对典型相关变量往往不能完全反映随机向量间的关系,必须建立其它典型相关变量,它应当最能反映随机向量间的关系,但是它应当与第一对典型相关变量不相关(不包含第一对典型相关变量的信息)。
统计学习题第8章相关分析

第八章相关分析一、单项选择⒈当自变量按必然数量转变时,因变量也相应随之而等量转变,这时两个变量之间存在着( )①直线相关关系;②曲线相关关系;③负相关关系;④正相关关系。
⒉当变量x值增加时,变量y值随之下降,那x和y两个变量之间存在着( ) ①正相关关系;②负相关关系;③曲线相关关系;④直线相关关系。
⒊假设变量x值减少,而变量y值却增加,那么变量x与变量y之间存在着( )①直线相关关系;②正相关关系;③曲线相关关系;④负相关关系。
⒋圆的面积与半径间存在着( )①相关关系;②因果关系;③函数关系;④比较关系。
⒌若是变量x和变量y之间的相关系数为-1,这说明两变量之间是( ) ①高度相关关系;②完全相关关系;③低度相关关系;④完全不相关。
⒍相关分析和回归分析相较,对变量的性质要求是不同的。
回归分析中要求( )①自变量是给定的,因变量是随机的; ②两个变量都是非随机的; ③两个变量都是随机的; ④以上三个都不对。
⒎若是变量x和变量y之间的相关系数为1,那么说明两个变量之间是( ) ①完全不相关;②高度相关关系;③完全相关关系;④低度相关关系。
⒏相关关系中,两个变量的关系是对等的,从而变量x对变量y的相关,同变量y对变量x的相关( )①完全不同;②有联系但不一样;③是同一问题;④不必然相同。
⒐已知某工厂甲产品产量和生产本钱有直接关系,在这条直线上,当产量为1000时,其生产本钱为30000元,其中不随产量转变的本钱为6000元,那么本钱总额对产量的回归方程是( )①y=6000+24x ;②y=6+;③y=24000+6x ;④y=24+6000x 。
⒑已知)(∑-x x 2是)(∑-y y 2的两倍,并已知)(∑-x x ·)(y y -是)(∑-y y 2的倍,那么相关系数r为( ) ①不能计算;②;③22.1;④22.1。
⒒在相关分析中,要求相关的两个变量( ) ①都是随机变量; ②都不是随机变量;③其中因变量是随机变量; ④其中自变量是随机变量。
统计学原理第八章相关分析与回归分析

21
例1:P354页,第1题
企业 产量 X 单位成 XY
X2
Y2
序号 (4件) 本(元)Y
1
2
52
104
4
2704
2
3
54
162
9
2916
3
4
52
208
16
2704
4
4
48
192
16
2304
5
5
48
240
25
2304
6
6
∑
24
46
276
36
2116
300
1182
106 15048
即:∑X=24,∑Y=300, ∑XY=1182,
• 2) X倚Y的直线方程的确定
• 根据最小平方法的原理:(x xc )2 最小值
• 将xc = c + dy代入上述公式中,分别对c和d 求一阶偏导数,并令偏导数等于0,就可以
得出两个正规方程:
x nc dy yx cy dy2
d
nyx y n y2 (
x
y )2
c x dy
举例:P355,第4题。
• 偏相关:在复相关中,当假定其他变量不 变时,其中两个变量间的相关关系称为偏 相关。例如,在假定人们收入水平不变的 条件下,某种商品的需求与其价格水平的 关系就是一种偏相关。
9
三、相关分析与回归分析
• (一)相关分析 • 是用一个指标(相关系数)来表明现象
之间相互依存的密切程度。 • (二)回归分析 • 是根据相关关系的具体形态,选择一个
• 曲线相关:如果现象之间的相关关系近似 地表现为某种曲线形式时,就称这种相关 关系为曲线相关。
第八章 相关与回归分析-一元线性回归

12
1、散点图
不良贷款
14
12
10
8
6
4
2
0 0
100
200
300
400
贷款余额 不良贷款与贷款余额的散点图
14
12
10
8 6
4
2
0 0
10
20
30
40
贷款项目个数
不良贷款与贷款项目个数的散点图不来自贷款不良贷款14
12
10
8
6
4
2
0 0
10
20
30
累计应收贷款
不良贷款与累计应收贷款的散点图
14
2
本章主要内容
➢ 相关分析
• 相关关系度量 • 相关关系显著性检验
➢ 一元线性回归分析
• 一元线性回归模型 • 参数的最小二乘估计 • 回归直线的拟合优度 • 显著性检验
➢ 利用回归方程进行预测
➢ 残差分析
3
第一节 直线相关分析 一、变量间的关系
函数关系
相关关系
函数关系的例子
▪ 某种商品的销售额(y)与销售量(x)之间的关系可 表示为 y = px (p 为单价)
儿子与父亲的身高关系:Y=33.73+0.516X(英寸)
24
一、概述——什么是回归分析(Regression )?
1. 从一组样本数据出发,确定变量之间的数学关系式 2. 对这些关系式的可信程度进行各种统计检验,并从
影响某一特定变量的诸多变量中找出哪些变量的影 响显著,哪些不显著 3. 利用所求的关系式,根据一个或几个变量的取值来 预测或控制另一个特定变量的取值,并给出这种预 测或控制的精确程度
统计学原理第8章相关与回归分析

此x与y间相关的程度比较高。()
27
同步练习
★ 判断题 (1) 根据结果标志对因素标志的不同反映,可以把现象间数量上的依存关系划分为
函数关系和相关关系。() (2) 正相关指的就是因素标志和结果标志的数量变动方向都是上升的。() (3) 相关系数是测定变量间相关密切程度的唯一方法。() (4) 只有当相关系数接近于1时,才能说明两变量之间存在高度相关系数。() (5) 若变量x的值减少,y的值也减少,说明变量x与y之间存在相关关系。() (6) 回归系数b和相关系数r都可以来判断现象之间相关的密切程度。() (7) 若回归直线方程为:yc=160-2.3x,则变量x与y之间存在负的相关关系。() (8) 回归分析中,对于没有明显因果关系的两个变量x与y,可以建立y依x和x依y的
D产量每增加1000件时,单位成本下降78元
E产品的产量随生产用固定资产价值的减少而减少
(4) 测定现象间有无相关关系的方法是()。
A编制相关表 B绘制相关图 C对客观现象作定性分析
D计算估计标准误系数时,()。
A相关的两个变量都是随机的
B相关的两个变量是对等的关系
C相关的两个变量一个是随机的,一个是可以控制的量
特点 在进行回归分析时,必须根据研究目的确定相关的变量中谁为自变 量,谁为因变量。 回归方程的作用在于由自变量的数值来估计因变量的值。一个回 归方程只能作一种推算或估计。 在回归分析中,因变量是随机的,自变量是可以控制的量。
第八章典型相关分析

中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
33
§8.2 典型相关分析的步骤及逻 辑框图
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
34
§8.2 典型相关分析的步骤及逻 辑框图
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
24
§8.2 典型相关分析的步骤及逻 辑框图
典型相关分析的步骤有以下6 步:(1)确定典型相关分析 的目标;(2)设计典型相关 分析;(3)检验典型相关分 析的基本假设;(4)估计典 型模型,评价模型拟合情况; (5)解释典型变量;(6)验 证模型。见参考文献[5]。它实 现的逻辑框图如下:
目录 上页 下页 返回 结束
7
8.1.2 典型相关分析的基本理论及方法
1. 总体典型相关和典型变量
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
8
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
多元统计分析
何晓群
中国人民大学出版社
2015/10/18
中国人民大学六西格玛质量管理研究中心
1
第八章 典型相关分析
• §8.1典型相关分析的基本理论及方法
• §8.2 典型相关分析的步骤及逻辑框图 • §8.3 典型相关分析的上机实现
• §8.4 社会经济案例研究
2015/10/18
中国人民大学六西格玛质量管理研究中心
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
12
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
13
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
2015/10/18
§8.2 典型相关分析的步骤及逻 辑框图
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
28
§8.2 典型相关分析的步骤及逻 辑框图
第4步:推导典型函数、评价整体拟合情况 每个典型函数都包括一对变量,通常一个代 表自变量,另一个代表因变量。可从变量组 中提取的典型变量(函数)的最大数目等于 最小数据组中的变量数目。比如,一个研究 问题包含5个自变量和3个因变量,可提取的 典型函数的最大数目是3。
2015/10/18 4
目录 上页 下页 返回 结束
中国人民大学六西格玛质量管理研究中心
§8.1典型相关分析的基本理论 及方法
典型相关分析是借助于主成分分析的思想,对 每一组变量分别寻找线性组合,使生成的新的 综合变量能代表原始变量大部分的信息,同时, 与由另一组变量生成的新的综合变量的相关程 度最大,这样一组新的综合变量称为第一对典 型相关变量,同样的方法可以找到第二对,第 三对,…,使得各对典型相关变量之间互不相 关,典型相关变量之间的简单相关系数称为典 型相关系数,典型相关分析就是用典型相关系 数衡量两组变量之间的相关性。
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
31
§8.2 典型相关分析的步骤及逻 辑框图
通常认为一个有统计显著性的相关系数可接受显著 性水平是0.05(也有0.01的水平)。统计软件所提供 的最常见的检验是基于Rao近似的F统计量。除了对 每个典型函数分别的检验以外,全部典型根的多元 检验也可以用来评价典型根的显著性。许多评价判 别函数显著性的测量,包括Wilks’Lamada、 Hotelling迹、Pillai迹和Roy’s gcr,这里也可以给出。 典型函数的实际重要性是由典型相关系数的大小代 表的。当决定解释哪些函数时,应当考虑典型相关 系数。
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 基本理论 及方法
8.1.1 典型相关分析的统计思想 典型相关分析研究两组变量之间整体的线性 相关关系,它是将每一组变量作为一个整体 来进行研究而不是分析每一组变量内部的各 个变量。所研究的两组变量可以是一组变量 是自变量,而另一组变量是因变量的情况, 两组变量也可以处于同等的地位,但典型相 关分析要求两组变量都至少是间隔尺度的。
21
§8.1典型相关分析的基本理论 及方法
3. 典型相关系数的显著性检验
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
22
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
23
§8.1典型相关分析的基本理论 及方法
目录 上页 下页 返回 结束
9
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
10
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
11
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
17
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
18
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
33
§8.2 典型相关分析的步骤及逻 辑框图
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
34
§8.2 典型相关分析的步骤及逻 辑框图
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
24
§8.2 典型相关分析的步骤及逻 辑框图
典型相关分析的步骤有以下6 步:(1)确定典型相关分析 的目标;(2)设计典型相关 分析;(3)检验典型相关分 析的基本假设;(4)估计典 型模型,评价模型拟合情况; (5)解释典型变量;(6)验 证模型。见参考文献[5]。它实 现的逻辑框图如下:
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
30
§8.2 典型相关分析的步骤及逻 辑框图
2. 典型函数的解释 一般来讲,实际提取的典型函数都是典型相 关系数在某个水平(比如0.05)上显著的函 数。对显著的典型变量的解释是基于这样的 假设,即认为相关的函数中,每组中的变量 都对共同方差有较大贡献。 Hair(1984)等人推荐三个准则结合使用来解释 典型函数。这三个准则是(1)函数的统计显 著性水平,(2)典型相关的大小,(3)两 个数据集中方差解释的冗余测量。
2015/10/18
§8.2 典型相关分析的步骤及逻 辑框图
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
26
第2步:设计典型相关分析 典型相关分析作为一种多元分析方法,与其他的多 元分析技术有共同的基本的要求。其它方法(尤其 是多元回归、判别分析和方差分析)所讨论的测量 误差的影响、变量类型及变换也与典型相关分析有 很大关系。 样本大小的影响和每个变量需要足够的观测都是典 型相关分析经常遇到的。研究者容易使自变量组和 因变量组包含很多的变量,而没有认识到样本量的 含义。小的样本不能很好的代表相关关系,这样掩 盖了有意义的相关关系。建议研究者至少保持每个 变量10个观测,以避免数据的“过度拟合”。
目录 上页 下页 返回 结束
7
8.1.2 典型相关分析的基本理论及方法
1. 总体典型相关和典型变量
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
8
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
5
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
6
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
25
第1步:确定典型相关分析的目标 典型相关分析所适用的数据是两组变量。我们假定 每组变量都能赋予一定的理论意义,通常一组可以 定义为自变量,另一组可以定义为因变量。典型相 关分析可以达到以下目标: (1) 确定两组变量是相互独立,或者相反,确定两组 变量间存在关系的大小。 (2) 为每组变量推导出一组权重,使得每组变量的线 性组合达到最大程度相关。最大化余下的相关关系 的其他的线性函数是与前面的线性函数独立的。 (3) 解释自变量与因变量组中存在的相关关系,通常 是通过测量每个变量对典型函数的相对贡献来衡量。
多元统计分析
何晓群
中国人民大学出版社
2015/10/18
中国人民大学六西格玛质量管理研究中心
1
第八章 典型相关分析
• §8.1典型相关分析的基本理论及方法
• §8.2 典型相关分析的步骤及逻辑框图 • §8.3 典型相关分析的上机实现
• §8.4 社会经济案例研究
2015/10/18
中国人民大学六西格玛质量管理研究中心
2
第八章
典型相关分析
• 典型相关分析(canonical correlation analysis)是 研究两组变量之间相关关系的多元分析方法。它 借用主成分析降维的思想,分别对两组变量提取 主成分,且使从两组变量提取的主成分之间的相 关程度达到最大,而从同一组内部提取的各主成 分之间互不相关,用从两组之间分别提取的主成 分的相关性来描述两组变量整体的线性相关关系。 典型相关分析的思想首先由 Hotelling于 1936 年提 出,计算机的发展解决了典型相关分析在应用中 计算方面的困难,目前成为普遍应用的进行两组 变量之间相关性分析的技术。本章主要介绍典型 相关分析的思想,基本理论及分析方法,并介绍 利用SPSS软件进行典型相关分析的方法。
目录 上页 下页 返回 结束
14
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
15
§8.1典型相关分析的基本理论 及方法
2015/10/18
中国人民大学六西格玛质量管理研究中心
目录 上页 下页 返回 结束
16
§8.1典型相关分析的基本理论 及方法
