兰州大学化学化工学院814物理化学和化工原理(一)(各占50%)历年考研真题(含部分答案)专业课考试试题

合集下载

C++调用GDAL库读取并输出tif文件，并计算斑块面积输出景观指数：ＣＳＤ

C++调⽤GDAL库读取并输出tif⽂件，并计算斑块⾯积输出景观指数：ＣＳＤ部分源码选⾃GDAL库的官⽅⽹址：，其余的代码为笔者⾃⼰编写。

1// readfile.cpp : 定义控制台应⽤程序的⼊⼝点。

2//3/*4part of the codes were cite from: /gdal_tutorial.html5and remaining of code were created :by /AmatVictorialCuram/6and please mark the site if you cite the program fo commercial of publication.7*/8 #include "stdafx.h"9 #include <iostream>10 #include "gdal.h"11 #include "gdal_priv.h"12/**/13 #include <iomanip>14 #include <fstream>15using namespace std;16/**/17int minLabel(int a,int b);1819int maxLabel(int a,int b);2021double csd(int *Parea,int length);2223int main()24 {25/*26 part of the codes were cite from: /gdal_tutorial.html27 and remaining of code were created :by /AmatVictorialCuram/28 and please mark the site if you cite the program fo commercial of publication.29*/30const char *pszFilename="E:\\tif/fragstats/sample.tif";31 GDALDataset *poDataset;3233 GDALAllRegister();3435 poDataset = (GDALDataset *) GDALOpen( pszFilename, GA_ReadOnly );36if( poDataset == NULL )37 {38 cout<<"file read error!"<<endl;;39 }40double adfGeoTransform[6];4142 printf( "Driver: %s/%s\n",43 poDataset->GetDriver()->GetDescription(),44 poDataset->GetDriver()->GetMetadataItem( GDAL_DMD_LONGNAME ) );4546 printf( "Size is %dx%dx%d\n",47 poDataset->GetRasterXSize(), poDataset->GetRasterYSize(),48 poDataset->GetRasterCount() );4950if( poDataset->GetProjectionRef() != NULL )51 printf( "Projection is `%s'\n", poDataset->GetProjectionRef() );5253if( poDataset->GetGeoTransform( adfGeoTransform ) == CE_None )54 {55 printf( "Origin = (%.6f,%.6f)\n",56 adfGeoTransform[0], adfGeoTransform[3] );5758 printf( "Pixel Size = (%.6f,%.6f)\n",59 adfGeoTransform[1], adfGeoTransform[5] );60 }6162 GDALRasterBand *poBand;63int nBlockXSize, nBlockYSize;64int bGotMin, bGotMax;65double adfMinMax[2];6667 poBand = poDataset->GetRasterBand( 1 );68 poBand->GetBlockSize( &nBlockXSize, &nBlockYSize );69 printf( "Block=%dx%d Type=%s, ColorInterp=%s\n",70 nBlockXSize, nBlockYSize,71 GDALGetDataTypeName(poBand->GetRasterDataType()),77if( ! (bGotMin && bGotMax) )78 GDALComputeRasterMinMax((GDALRasterBandH)poBand, TRUE, adfMinMax);7980 printf( "Min=%.3fd, Max=%.3f\n", adfMinMax[0], adfMinMax[1] );8182if( poBand->GetOverviewCount() > 0 )83 printf( "Band has %d overviews.\n", poBand->GetOverviewCount() );8485if( poBand->GetColorTable() != NULL )86 printf( "Band has a color table with %d entries.\n",87 poBand->GetColorTable()->GetColorEntryCount() );88/*****89 Reading Raster Data90 *****/91float *pafScanline;92int nXSize = poBand->GetXSize();93int nYSize=poBand->GetYSize();9495//读取图像的nXSize*nYSize数据96 pafScanline = (float*) CPLMalloc(sizeof(float)*nXSize*nYSize);//创建指针97 poBand->RasterIO(98 GF_Read,//第⼀个参数表⽰要读⼊数据还是写⼊数据990, 0,//nXOff, nYOff表⽰读取或者写⼊图像数据的起始坐标图像的左上⾓坐标为（0,0）100 nXSize, nYSize,/*nXSize, nYSize表⽰读取或者写⼊图像数据的窗⼝⼤⼩,nXSize表⽰宽度,101 nYSize表⽰⾼度,均使⽤像素为单位,该宽度和⾼度是从第⼆个和第三个参数处开始计算。

流函数

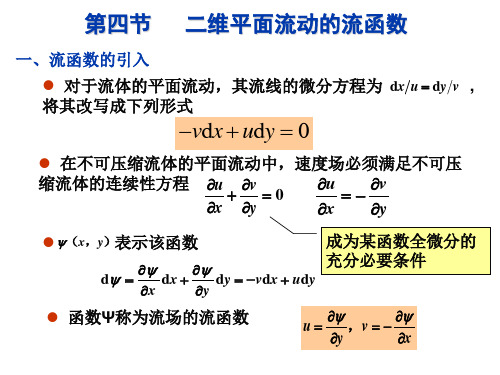
（2）由流函数的全微分得：
d
积分 4 xy C 由速度势函数的全微分得：
d
dx dy vdx udy 4 ydx 4 xdy x y
积分（3）由于 V 2
dx dy udx vdy 4 xdx 4 ydy x y
v u 0 x y
不可压缩流体平面无旋流动的流函数也满足拉普拉斯方程，也是一个调和函数。在平面不可压缩流体的有势流场中的求解问题，可以转化为求解一个满足边界条件的Ψ的拉普拉斯方程.
（3）平面流动中，通过两条流线间任一曲线单位厚度的体积流量等于两条流线的流函数之差。这就是流函数的物理意义。在两流线间任一曲线AB，则通过单位厚度的体积流量为
第四节
一、流函数的引入
二维平面流动的流函数
对于流体的平面流动，其流线的微分方程为 dx u dy v , 将其改写成下列形式
vdx udy 0
在不可压缩流体的平面流动中，速度场必须满足不可压缩流体的连续性方程 u v u v 0 x y x y （x，y）表示该函数
1 对于极坐标系，可写成 v r r
v r
d v dr vr rd
在已知速度分布的情况下，流函数的求法与速度势函数一样，可由曲线积分得出
在不可压缩平面流动中，只要求出了流函数，就可求出速度分布。反之，只要流动满足不可压缩流体的连续性方程，不论流场是否有旋，流动是否定常，流体是理想流体还是黏性流体，必然存在流函数。等流函数线与流线等同，仅在平面流动时成立。对于三维流动，不存在流函数，也就不存在等流函数线，但流线还是存在的。
x ， y y x
0 x x y y

《结构分析中的有限元法》2015-有限元习题-参考答案

3、简述结点力和结点载荷的差别。结点力：单元与单元间通过结点的相互作用力。结点载荷：作用于结点上的外载荷。
4、列表给出有限元几类基本单元的图形、结点数、结点自由度数和单元总自由度数(包括杆单元、梁单元、平面三角形单元、平面四边形单元、轴对称问题三角形单元、四边形壳单元、四面体单元)。
单元类型杆单
（1）单元的类型和形式为了扩大有限元法的应用领域，新的单元类型和形式不断涌现(等参元,梁板壳,复合材料) （2）有限元法的理论基础和离散格式将 Hellinger-Reissner、Hu—Washizu(多场变量变分原理)应用于有限元分析，发展了混合模型、杂交型的有限元表达格式，应研究了各自的收敛条件；将加权余量法用于建立有限元的表达格式；进一步研究发展有限元解的后验误差估计和应力磨平方法。（3）有限元方程的解法(大型复杂工程结构问题——静态, 特征值, 瞬态等) （4）有限元法的计算机软件(专用软件, 通用软件)
弹性力学中的虚功原理可表达为：在外力作用下处于平衡状态的弹性体，如
果发生了虚位移，那么所有的外力在虚位移上的虚功(外力功)等于整个弹性体内
应力在虚应变上的虚功(内力功)。
根据虚功原理得到 ( εT uT F )d uTTd 0
p
(1 T uT F)d 2
uT
Td
0
其中的 p 即为总势能泛函。由上面变分为零式表明：在所有区域内满足几何关系，在边界上满足给定位移条件的可能位移中，真实位移使系统的总势能取驻值(可证明此驻值为最小值)。此即总势能泛函的极值条件。
10, 0
3 2, 0
解：根据拉格朗日插值基函数：
u(x, y) l1(x, y)u1 l2 (x, y)u2 l3(x, y)u3 l4 (x, y)u4

中考数学倒数第二题解答题(按字母顺序排列) 人教新课标版

；
（2）求出 t 为何值时，QM∥AB；（3）设△BMQ 的面积为 S，求 S 与 t 的函数关系式；
A
ND
（4）求出 t 为何值时，△BMQ 为直角三角形． Q
4 / 111
B
MP
C
【备战 2012】中考数学倒数第二题解答题（按字母顺序排列）人教新课标版 21．（满分 14 分）
该配件的原材料价格一路攀升，每件配件的原材料价格 y1（元）与月份 x（1≤x≤9，且 x 取整数）之间的函数关系如下表：
月份 x
1
2
3
4
5
6
7
8
9
价格 y1（元/件） 56
4
20
随着国家调控措施的出台，原材料价格的涨势趋缓，10 至 12 月每件配件的原材料价格 y（2 元）与月份 x（10≤x≤12，
2 / 111
【备战 2012】中考数学倒数第二题解答题（按字母顺序排列）人教新课标版（3）根据 1 至 5 月的总利润 1700 万元得到关系式求值即可．解答：解：（1）设 y1=kx+b，
则
，解得
，
∴y1=20x+540（1≤x≤9，且 x 取整数）；
设 y2=ax+b，则
，解得
，
∴y2=10x+630（10≤x≤12，且 x 取整数）；
设直线cd的解析式为ykxb直线cd的解析式为yx1又15bcmdcobmcdocbmdobcdcbmme轴上且bpbm此时满足条件的点p有两个它们是p1025p202作mey轴于点ebmc90则bmebcmbmbc又bmbppebe此时满足条件的点p有一个它是p3以bm为底时作bm的垂直平分线分别交y轴bm由2得bmc90pfcm是bm的中点bp此时满足条件的点p有一个它是p4综上符合条件的点p有四个

数值分析第三版课本习题及答案

第一章绪论1. 设x >0,x 的相对误差为δ,求ln x 的误差.2. 设x 的相对误差为2％,求nx 的相对误差.3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:*****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====⨯4. 利用公式(3.3)求下列各近似值的误差限:********12412324(),(),()/,i x x x ii x x x iii x x ++其中****1234,,,x x x x 均为第3题所给的数.5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少?6. 设028,Y =按递推公式11783100n n Y Y -=-( n=1,2,…)计算到100Y .若取783≈27.982(五位有效数字),试问计算100Y 将有多大误差?7. 求方程25610x x -+=的两个根,使它至少具有四位有效数字(783≈27.982).8. 当N 充分大时,怎样求211Ndx x +∞+⎰?9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2?10. 设212S gt =假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小. 11. 序列{}n y 满足递推关系1101n n y y -=-(n=1,2,…),若02 1.41y =≈(三位有效数字),计算到10y 时误差有多大?这个计算过程稳定吗?12. 计算6(21)f =-,取2 1.4≈,利用下列等式计算,哪一个得到的结果最好?36311,(322),,9970 2.(21)(322)--++13. 2()ln(1)f x x x =--,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式22ln(1)ln(1)x x x x --=-++计算,求对数时误差有多大?14. 试用消元法解方程组{101012121010;2.x x x x +=+=假定只用三位数计算,问结果是否可靠?15. 已知三角形面积1sin ,2s ab c =其中c 为弧度,02c π<<,且测量a ,b ,c 的误差分别为,,.a b c ∆∆∆证明面积的误差s ∆满足.s a b cs a b c ∆∆∆∆≤++第二章插值法1. 根据(2.2)定义的范德蒙行列式,令200011211121()(,,,,)11n n n n n n n n n x x x V x V x x x x x x x xx x ----==证明()n V x 是n 次多项式,它的根是01,,n x x - ,且101101()(,,,)()()n n n n V x V x x x x x x x ---=-- .2. 当x = 1 , -1 , 2 时, f (x)= 0 , -3 , 4 ,求f (x )的二次插值多项式.3. 给出f (x )=ln x 的数值表用线性插值及二次插值计算ln 0.54 的近似值.x 0.4 0.5 0.6 0.7 0.8 ln x -0.916291-0.693147-0.510826-0.357765-0.2231444. 给出cos x ,0°≤x ≤90°的函数表,步长h =1′=(1/60)°,若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界.5. 设0k x x kh =+,k =0,1,2,3,求032max ()x x x l x ≤≤.6. 设jx 为互异节点(j =0,1,…,n ),求证:i) 0()(0,1,,);nk kj j j x l x x k n =≡=∑ii)()()1,2,,).nk jj j xx l x k n =-≡0(=∑7. 设[]2(),f x C a b ∈且()()0f a f b ==,求证21()()().8max max a x ba xb f x b a f x ≤≤≤≤≤-"8. 在44x -≤≤上给出()xf x e =的等距节点函数表,若用二次插值求xe 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少?9. 若2n n y =,求4n y ∆及4n y δ.10. 如果()f x 是m 次多项式,记()()()f x f x h f x ∆=+-,证明()f x 的k 阶差分()(0)kf x k m ∆≤≤是m k -次多项式,并且()0(m lf x l +∆=为正整数).11. 证明1()k k k k k k f g f g g f +∆=∆+∆.12. 证明110010.n n kkn n k k k k f gf g f g g f --+==∆=--∆∑∑13. 证明1200.n j n j y y y -=∆=∆-∆∑14. 若1011()n nn n f x a a x a x a x --=++++ 有n 个不同实根12,,,n x x x ,证明{10,02;, 1.1()n k njk n a k n j jx f x -≤≤-=-=='∑15. 证明n 阶均差有下列性质: i)若()()F x cf x =,则[][]0101,,,,,,n n F x x x cf x x x = ;ii) 若()()()F x f x g x =+,则[][][]010101,,,,,,,,,n n n F x x x f x x x g x x x =+ .16. 74()31f x x x x =+++,求0172,2,,2f ⎡⎤⎣⎦ 及0182,2,,2f ⎡⎤⎣⎦ . 17. 证明两点三次埃尔米特插值余项是(4)22311()()()()/4!,(,)k k k k R x f x x x x x x ++=ξ--ξ∈并由此求出分段三次埃尔米特插值的误差限.18. 求一个次数不高于4次的多项式()P x ,使它满足(0)(1)P P k =-+并由此求出分段三次埃尔米特插值的误差限.19. 试求出一个最高次数不高于4次的函数多项式()P x ,以便使它能够满足以下边界条件(0)(0)0P P ='=,(1)(1)1P P ='=,(2)1P =.20. 设[](),f x C a b ∈,把[],a b 分为n 等分,试构造一个台阶形的零次分段插值函数()n x ϕ并证明当n →∞时,()n x ϕ在[],a b 上一致收敛到()f x .21. 设2()1/(1)f x x =+,在55x -≤≤上取10n =,按等距节点求分段线性插值函数()h I x ,计算各节点间中点处的()h I x 与()f x 的值,并估计误差.22. 求2()f x x =在[],a b 上的分段线性插值函数()h I x ,并估计误差.23. 求4()f x x =在[],a b 上的分段埃尔米特插值,并估计误差. 24. 给定数据表如下:j x 0.25 0.30 0.39 0.45 0.53 j y0.50000.54770.62450.67080.7280试求三次样条插值()S x 并满足条件i) (0.25) 1.0000,(0.53)0.6868;S S '='= ii)(0.25)(0.53)0.S S "="=25. 若[]2(),f x C a b ∈,()S x 是三次样条函数,证明 i)[][][][]222()()()()2()()()bbbbaaaaf x dx S x dx f x S x dx S x f x S x dx"-"="-"+""-"⎰⎰⎰⎰;ii) 若()()(0,1,,)i i f x S x i n == ,式中i x 为插值节点,且01n a x x x b =<<<= ,则[][][]()()()()()()()()()baS x f x S x dx S b f b S b S a f a S a ""-"="'-'-"'-'⎰.26. 编出计算三次样条函数()S x 系数及其在插值节点中点的值的程序框图(()S x 可用(8.7)式的表达式).第三章函数逼近与计算1. (a)利用区间变换推出区间为[],a b 的伯恩斯坦多项式.(b)对()sin f x x =在[]0,/2π上求1次和三次伯恩斯坦多项式并画出图形,并与相应的马克劳林级数部分和误差做比较. 2. 求证:(a)当()m f x M ≤≤时,(,)n m B f x M ≤≤. (b)当()f x x =时,(,)n B f x x =.3. 在次数不超过6的多项式中,求()sin 4f x x =在[]0,2π的最佳一致逼近多项式.4. 假设()f x 在[],a b 上连续,求()f x 的零次最佳一致逼近多项式.5. 选取常数a ,使301max x x ax≤≤-达到极小,又问这个解是否唯一?6. 求()sin f x x =在[]0,/2π上的最佳一次逼近多项式,并估计误差.7. 求()xf x e =在[]0,1上的最佳一次逼近多项式.8. 如何选取r ,使2()p x x r =+在[]1,1-上与零偏差最小?r 是否唯一? 9. 设43()31f x x x =+-,在[]0,1上求三次最佳逼近多项式.10. 令[]()(21),0,1n n T x T x x =-∈,求***0123(),(),(),()T x T x T x T x .11. 试证{}*()nTx 是在[]0,1上带权21x x ρ=-的正交多项式.12. 在[]1,1-上利用插值极小化求11()f x tg x -=的三次近似最佳逼近多项式.13. 设()x f x e =在[]1,1-上的插值极小化近似最佳逼近多项式为()n L x ,若nf L ∞-有界,证明对任何1n ≥,存在常数n α、n β,使11()()()()(11).n n n n n T x f x L x T x x ++α≤-≤β-≤≤14. 设在[]1,1-上234511315165()128243843840x x x x x x ϕ=-----,试将()x ϕ降低到3次多项式并估计误差. 15. 在[]1,1-上利用幂级数项数求()sin f x x =的3次逼近多项式,使误差不超过0.005.16. ()f x 是[],a a -上的连续奇(偶)函数,证明不管n 是奇数或偶数,()f x 的最佳逼近多项式*()n nF x H ∈也是奇(偶)函数.17. 求a 、b 使[]220sin ax b x dx π+-⎰为最小.并与1题及6题的一次逼近多项式误差作比较.18. ()f x 、[]1(),g x C a b ∈,定义 ()(,)()();()(,)()()()();b baaa f g f x g x dxb f g f x g x dx f a g a =''=''+⎰⎰问它们是否构成内积?19. 用许瓦兹不等式(4.5)估计6101x dx x +⎰的上界,并用积分中值定理估计同一积分的上下界,并比较其结果.20. 选择a ,使下列积分取得最小值:1122211(),x ax dx x ax dx----⎰⎰.21. 设空间{}{}10010121,,,span x span x x 1ϕ=ϕ=,分别在1ϕ、2ϕ上求出一个元素,使得其为[]20,1x C ∈的最佳平方逼近,并比较其结果.22. ()f x x =在[]1,1-上,求在{}2411,,span x x ϕ=上的最佳平方逼近.23.[]2sin (1)arccos ()1n n x u x x +=-是第二类切比雪夫多项式,证明它有递推关系()()()112n n n u x xu x u x +-=-.24. 将1()sin2f x x =在[]1,1-上按勒让德多项式及切比雪夫多项式展开,求三次最佳平方逼近多项式并画出误差图形,再计算均方误差.25. 把()arccos f x x =在[]1,1-上展成切比雪夫级数.26. 用最小二乘法求一个形如2y a bx =+的经验公式,使它与下列数据拟合,并求均方误差.i x 19 25 31 38 44 i y19.032.349.073.397.827. 观测物体的直线运动,得出以下数据:时间t (秒) 0 0.9 1.9 3.0 3.9 5.0 距离s (米) 010305080110求运动方程.28. 在某化学反应里,根据实验所得分解物的浓度与时间关系如下:时间 0 5 10 15 20 25 30 35 40 45 50 55 浓度0 1.272.162.863.443.874.154.374.514.584.624.64用最小二乘拟合求()y f t =.29. 编出用正交多项式做最小二乘拟合的程序框图. 30. 编出改进FFT 算法的程序框图. 31. 现给出一张记录{}{}4,3,2,1,0,1,2,3k x =,试用改进FFT 算法求出序列{}k x 的离散频谱{}k C (0,1,,7).k =第四章数值积分与数值微分1. 确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度: (1)101()()(0)()hh f x dx A f h A f A f h --≈-++⎰; (2)21012()()(0)()hh f x dx A f h A f A f h --≈-++⎰;(3)[]1121()(1)2()3()/3f x dx f f x f x -≈-++⎰;(4)[][]20()(0)()/1(0)()hf x dx h f f h ah f f h ≈++'-'⎰.2. 分别用梯形公式和辛普森公式计算下列积分:(1)120,84xdx n x =+⎰; (2)1210(1),10x e dx n x --=⎰;(3)91,4xdx n =⎰; (4)260sin ,6dx n π-ϕ=⎰.3. 直接验证柯特斯公式(2.4)具有5次代数精度.4. 用辛普森公式求积分1x e dx-⎰并计算误差.5. 推导下列三种矩形求积公式:(1)2()()()()()2ba f f x dxb a f a b a 'η=-+-⎰; (2)2()()()()()2baf f x dx b a f b b a 'η=---⎰;(3)3()()()()()224baa b f f x dx b a f b a +"η=-+-⎰.6. 证明梯形公式(2.9)和辛普森公式(2.11)当n →∞时收敛到积分()baf x dx⎰.7. 用复化梯形公式求积分()baf x dx⎰,问要将积分区间[],a b 分成多少等分,才能保证误差不超过ε(设不计舍入误差)?8. 用龙贝格方法计算积分12x e dxπ-⎰,要求误差不超过510-.9. 卫星轨道是一个椭圆,椭圆周长的计算公式是22201()sin cS a d a π=-θθ⎰,这里a 是椭圆的半长轴,c是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,H 为远地点距离,6371R =公里为地球半径,则(2)/2,()/2a R H h c H h =++=-.我国第一颗人造卫星近地点距离439h =公里,远地点距离2384H =公里,试求卫星轨道的周长.10. 证明等式3524sin3!5!n nn n ππππ=-+-试依据sin(/)(3,6,12)n n n π=的值,用外推算法求π的近似值.11. 用下列方法计算积分31dyy ⎰并比较结果.(1) 龙贝格方法;(2) 三点及五点高斯公式;(3) 将积分区间分为四等分,用复化两点高斯公式.12. 用三点公式和五点公式分别求21()(1)f x x =+在x =1.0,1.1和1.2处的导数值,并估计误差.()f x 的值由下表给出:x1.0 1.1 1.2 1.3 1.4 ()f x0.25000.22680.20660.18900.1736第五章常微分方程数值解法1. 就初值问题0)0(,=+='y b ax y 分别导出尤拉方法和改进的尤拉方法的近似解的表达式，并与准确解bx ax y +=221相比较。

操作系统原理实验报告

《操作系统原理》实验报告班级::学号:指导老师：目录:实验题目：实验一线程创建与撤销 (2)实验题目：实验二线程同步 (6)实验题目：实验三线程互斥 (11)实验题目：实验四进程通信 (17)实验题目：实验五读者-写者问题 (22)实验题目：实验六进程调度 (38)实验题目：实验七存储管理之动态库 (52)实验题目：实验八存储管理之存分配 (57)实验题目：实验九存储管理之页面置换算法 (70)实验题目：实验十设备管理 (85)实验题目：实验十一文件管理之文件读写 (99)实验题目：实验一线程创建与撤销完成人：XXX报告日期：2018年3月31日一、实验容简要描述（1）熟悉VC++、Visual Studio开发环境。

（2）使用相关函数创建和撤销线程。

（3）在一个进程中创建3个线程，名字分别为threada、threadb、threadc。

threada输出“hello world! ”。

threadb输出“My name is …”。

threadc输出“Please wait…”，然后sleep 5秒钟，接着输出“I wake up”。

二、程序设计1、设计思路该函数创建一个在调用进程的地址空间中执行的线程。

2、主要数据结构HANDLE CreateThread(LPSECURITY_ATTRIBUTES lpThreadAttributes,DWORD dwStackSize,LPTHREAD_START_ROUTINE lpStartAddress,LPVOID lpParameter,DWORD dwCreationFlags,LPDWORD lpThreadId)；VOID ExitThread(DWORD dwExitCode)；VOID Sleep(DWORD dwMilliseconds);VOID Sleep(DWORD dwMilliseconds);三、实验结果1、基本数据lpThreadAttributes：指向一个SECURITY_ATTRIBUTES结构，该结构决定了返回的句柄是否可被子进程继承。

不定积分公式大全

Ch4、不定积分§1、不定积分的概念与性质1、原函数与不定积分定义1：若)()(x f x F ='，则称)(x F 为)(x f 的原函数。

① 连续函数一定有原函数；② 若)(x F 为)(x f 的原函数，则C x F +)(也为)(x f 的原函数；事实上，())()()(''x f x F C x F ==+③ 的任意两个原函数仅相差一个常数。

事实上，由[]0)()()()()()('2'1'11=-=-=-x f x f x F x F x F x F ，得Cx F x F =-)()(21故C x F +)(表示了)(x f 的所有原函数，其中)(x F 为)(x f 的一个原函数。

定义2：)(x f 的所有原函数称为)(x f 的不定积分，记为⎰dx x f )(，⎰-积分号，-)(x f 被积函数，-x 积分变量。

显然Cx F dx x f +=⎰)()(例1、求下列函数的不定积分①⎰+=Ckx kdx②⎰⎪⎩⎪⎨⎧-=+-≠++=+1ln 1111μμμμμC x C x dx x2、基本积分表（共24个基本积分公式）3、不定积分的性质①[]⎰⎰⎰±=±dx x g dx x f dx x g x f )()()()(②⎰⎰≠=)0()()(k dxx f k dx x kf例2、求下列不定积分①⎰⎰+-=++-==+--Cx C x dx x x dx 11)2(11)2(22②⎰⎰+=++-==+--Cx C x dx x xdx 21)21(11)21(21③⎰+-=⎪⎪⎭⎫⎝⎛+--C x x dx x xarctan 3arcsin 5131522⑤()⎰⎰⎰++-=-=-Cx x xdx x xdx dx x x x csc cot cot csc csc cot csc csc 2⑥⎰⎰⎰⎰++-=+=+=C x x xdx xdx dx xx xx x x dx tan cot sec csc cos sin cos sin cos sin 22222222⑦()⎰⎰+--=-=Cx x dx x dx x cot 1csc cot 22§2、不定积分的换元法一、第一类换元法（凑微分法）1、()()()()b ax d adx b ax d b ax f a dx b ax f +=++=+⎰⎰1,1即例1、求不定积分①()C x udu u x x xd xdx +-===⎰⎰⎰)5cos(51sin 51555sin 515sin②()()()()⎰⎰+--=+-+⋅-=---=-+C x C x x d x dx x 81777211612117121)21(212121③())20(arctan 111222Ca x a a x a x d a x a dx +⎪⎭⎫⎝⎛=+=+⎰⎰④()())23(arcsin 1222Ca x a x a x d xa dx +⎪⎭⎫⎝⎛=-=-⎰⎰2、()()n n n n n n dx dx x dx x f ndx x x f ==--⎰⎰11,1即例2、求不定积分①()()()()Cx C x x d x dx x x +--=+-+⋅-=---=-+⎰⎰232121221221221311112111211②()C e x d e dx e x x x x +-=--=---⎰⎰333323131③⎰⎰⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-=+⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-=x d dx x C x x d x dx x x 111sin 11cos 1cos 122④⎰⎰⎪⎪⎭⎫⎝⎛=+==x d dx x Cx x d x dx xx 21sin 2cos 2cos3、,tan sec ,sin cos ,cos sin ,,ln 12x d xdx x d xdx x d xdx de dx e x d dx xx x ==-===,,arcsin 11,arctan 11,sec tan sec 222222x a d dx x a x x d dx xx d dx xx d xdx x ±±=±=-=+=例3、求不定积分①⎰⎰⎰+=+-=-==)16(sec ln cos ln cos cos cos sin tan C x C x x xd dx x x xdx②⎰⎰⎰+-=+===)17(cos ln sin ln sin sin sin cos cot C x C x x xd dx x x xdx⑤()⎰⎰+==C x xxd dx x x ln ln ln ln ln 1⑥()()()⎰⎰++=++=+C x x x d x x dx 1tan ln 1tan 1tan tan 1cos 2⑦()()⎰⎰++=++=+C e ee d dx e e x xxx x 1ln 111⑧()()⎰⎰++-=+-+=+C e x ee e e dx xx x x x 1ln 111⑨()⎰⎰+=+=+C e e de dx e e xx x x x arctan 1122⑩()Cexd edx exx x x x +-=+--=++-+-+-⎰⎰2122121211例4、求不定积分①⎰⎰⎰⎰⎪⎭⎫⎝⎛++---=⎪⎭⎫ ⎝⎛+--=-a x a x d a x a x d a dx a x a x a a x dx )()(21112122)22)(21(ln 1C ax +-=④()C x x x xd x dx xdx +-=⋅-==⎰⎰⎰2sin 412122cos 22221sin 2⑤()⎰⎰+--=+=C x x dx x x xdx x 2cos 418cos 1612sin 8sin 213cos 5sin⑥⎰⎰⎰⎰+====C x x xd x x x d x xdx dx x x sin ln ln sin ln sin ln sin ln sin sin sin ln sin cos sin ln cot⑦C x x x x d xdx dx xx x dx +-=+=-=+⎰⎰⎰⎰cos 1tan cos cos sec cos sin 1sin 1222⑧()⎰⎰⎰⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=+=+44csc 214sin 2sin cos πππx d x x dx x x dxC x x +⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=4cot 4csc ln 21ππ二、第二类换元法1、三角代换例1、dxx a ⎰-22解：令)cos (sin t a t a x 或=，则tdt a dx t a x a cos ,cos 22==-原式=()⎰⎰⎰⎰⎪⎭⎫⎝⎛+=+=⋅t td dt a dt t a tdt a t a 22cos 21222cos 1cos cos 22C ax a a x a a x a C t a t a +-⋅⋅⋅+=++=22222224arcsin 22sin 42 C x a x a x a +-+=22221arcsin 21 例2、()()Caxa x a x d xa dx +=-=-⎰⎰arcsin 1222解：令t a x sin =原式=⎰⎰+=+==CaxC t dt t a tdt a arcsin cos cos例3、⎰+22xa dx解：令)cot (tan t a t a x 或=，则tdta dx t a x a 222sec ,sec ==+原式=()⎰⎰+⎪⎪⎭⎫ ⎝⎛++=++==C a x a a x C t t tdt t a tdta 222ln tan sec ln sec sec sec())24(ln 22C a x x +++=例4、⎰+42x x dx解：令)cot (tan t a t a x 或=，则tdtdx t x 22sec 2,sec 24==+原式=()⎰⎰+⎪⎪⎭⎫ ⎝⎛++=++==C a x a a x C t t tdt t a tdta 222ln tan sec ln sec sec sec例5、⎰-22ax dx解：令)csc (sec t a t a x 或=，则tdt t a dx t a a x tan sec ,tan 22==-原式=()⎰⎰+⎪⎪⎭⎫ ⎝⎛-+=++==c aa x a x C t t tdt t a tdtt a 22ln tan sec ln sec tan tan sec())25(ln 22C a x x +-+=例6、⎰-dx xx 92解：令t a x sec =，则tdt t dx t x tan sec 3,tan 392==-原式=()()⎰⎰⎰+-=-==⋅C t t t tdt tdt t tttan 31sec 3tan 3tan sec 3sec 3tan 322C x x C x x +--=+⎪⎪⎭⎫ ⎝⎛--=3arccos 393arccos 39322 小结：)(x f 中含有⎪⎪⎩⎪⎪⎨⎧-+-222222a x a x x a 可考虑用代换⎪⎩⎪⎨⎧===t a x ta x t a x sec tan sin2、无理代换例7、⎰++311x dx解：令dtt dx t x t x 2333,1,1=-==+则原式=()⎰⎰⎰+⎪⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛++-=++-=+C t t t dt t t dt t t t dt t 1ln 231113111313222()()C x x x +++++-+=333211ln 313123 例8、()⎰+31x x dx解：令dtt dx t x t x 5666,,===则原式=()()⎰⎰⎰+-=⎪⎭⎫ ⎝⎛+-=+=+C t t dt t dt t t t t dt t arctan 611161616222235()C x x +-=66arctan 6例9、⎰+dxxxx 11解：令()22212,11,1--=-==+t tdtdx t x t x x 则原式=()()⎰⎰⎰+⎪⎭⎫ ⎝⎛+-+-=⎪⎭⎫ ⎝⎛-+-=--=⎪⎪⎭⎫ ⎝⎛---C t t t dt t dt t t t tdt t t 11ln 212111212121222222C xx xx x x +++-+-+-=11ln 12例10、⎰+xedx1解：令()12,1ln ,122-=-==+t tdtdx t x t e x 则原式⎰⎰+++-+=++-⋅=-=-⋅=Ce e C t t t dt dt t t t x x 1111ln 11ln 21212121224、倒代换例11、()⎰+46x x dx解：令()2676,4111,1t dtdx t t x x t x -=+=+=则原式()()C x x C t t t d t dt t ++=++-=++-=+-=⎰⎰4ln 24114ln 2411414241416666666()C x x ++-=4ln 241ln 416§3、分部积分法分部积分公式：()()VU UV V U V U V U UV '-'=''+'=',()⎰⎰⎰'-'='Vdx U dx UV dx V U ，故⎰⎰-=Vd U UV UdV（前后相乘）（前后交换）例1、⎰xdxx cos⎰⎰++=-==C x x x xdx x x x xd cos sin sin sin sin 例2、⎰dxxe x⎰⎰+-=-==C e xe dx e xe xde x x x x x例3、⎰xdx ln ⎰⎰+-=⋅-=-=Cx x x dx xx x x x xd x x ln 1ln ln ln或解：令te x t x ==,ln原式C x x x C e te dt e te tde t t t t t +-=+-=-==⎰⎰ln例4、⎰xdxarcsin()⎰⎰⎰+-+=--+=--=-=C x x x xx d x x dxxx x x x xd x x 22221arcsin 1121arcsin 1arcsin arcsin arcsin或解：令t x t x sin ,arcsin ==原式Cx x x C t t t tdt t t t td +-+=++=-==⎰⎰21arcsin cos sin sin sin sin例5、⎰xdxe x sin()⎰⎰⎰⎰⎰--=+-=-=-==xdxe x x e x d e x e x e xde x e xdx e x e xde xxxxxxx x x x sin cos sin cos cos sin cos sin cos sin sin故()C x x e xdx e xx +-=⎰cos sin 21sin例6、⎰dx xx2cosC x x x xdx x x x xd +-=-==⎰⎰sec ln tan tan tan tan 例7、()⎰++dxx x 21ln()()()Cx x x x dxxx x x x dx xx x xx x x x ++-++=+-++=++++⋅-++=⎰⎰222222211ln 11ln 1111ln§4、两种典型积分一、有理函数的积分有理函数01110111)()()(b x b x b x b a x a x a x a x Q x P x R m m m m n n n n ++++++++==---- 可用待定系数法化为部分分式，然后积分。

高一上学期期中考重难点归纳总结(解析版)--人教版高中数学精讲精练必修一

【答案】B
【解析】由 A 1,3, 5 ， B 3, 4, 5 ，得 A B 1,3, 4,5 ，
所以 ðU A B 2, 6 ，
故选：B
2．（2023 秋·江苏盐城·高一校联考期末）设全集U R ，集合 A x x 2 ， B x x 2 或 x 6，则
A ðU B （） A．x x 2
秋·辽宁抚顺·高一抚顺一中校考阶段练习）已知集合
M
x∣x
m
1 6
,m
Z
，
N
x∣x
n
1
,
n
Z
，
P
x∣x
p
1 , p Z ，则 M
，N
， P 的关系为（
）
23
26
A． M N P
B． M N P
C． M N P
D． N P M
【答案】B
【解析】因为 M
∣ x x
m1,
m
Z
所以实数 a 的取值范围是{a | 0 a 4} .
故选：D
考点五不等式的性质
【例 5】（2023 秋·上海浦东新）已知 a b c d ，下列选项中正确的是（）
A． a d b c
B． a c b d
C． ad bc
D． ac bd
【答案】B
【解析】对于选项 A，因为 a 3,b 2,c 1, d 10 ，满足 a b c d ，但不满足 a d b c ，所以选项 A
数是（） A．0
B．1
C．2
D．4
【答案】C
【解析】因为 A x, y x y 0 ， B x, y | x2 2y2 1 ，
所以集合 A 是直线 x y 0 上的点的集合，集合 B 是椭圆 x2 2y2 1 上的点的集合；因为 M A B ，所以若要求 M 中的元素个数，只需联立方程即可；

宁波镇海中学2024-2025学年高二上学期期中测试数学试卷

镇海中学2024学年第一学期期中考试高二数学试题卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是正确的.1.在等差数列{}n a 中，已知12a =，315S =，则4a 等于（） A.11 B.13 C.15 D.162.若椭圆2212x y m +=的右焦点与抛物线24y x =的焦点重合，则m 的值为（） A.1 B.3 C.4 D.53.若点P 到直线1x =−和它到点(1,0)的距离相等，则点P 的轨迹方程为（）A.2x y =B.2y x =C.24x y =D.24y x =4.任取一个正整数，若是奇数，就将该数乘3再加上1；若是偶数，就将该数除以2.反复进行上述两种运算，经过有限次步骤后，必进入循环圈1421→→→.这就是数学史上著名的“冰雹猜想”（又称“角谷猜想”等）.已知数列{}n a 满足：11a =，1,231,n n n n n a a a a a + = + 当为偶数当为奇数，则2024S =（） A.4720B.4722C.4723D.4725 5.已知函数()f x 是奇函数，函数)g x 是偶函数，且当0x >时，()0f x ′>，()0g x ′>，则0x <时，以下说法正确的是（） A.()()0f x g x ′+>′ B.()()0f x g x ′−>′C.()()0f x g x ′′>D.()()0f x g x ′′> 6.若函数()211kx f x x +=+在[)2,+∞上单调递增，则k 的取值范围为（） A.43k ≥− B.1k ≤− C.1k ≤ D.43k ≤− 7.已知2023log 2024a =，2024log 2025b =，2025log 2026c =，则（）A.a b c >>B.a c b >>C.c b a >>D.c a b >>8.已知椭圆22:13627x y C +=，左焦点为F ，在椭圆C 上取三个不同点P ，Q ，R ，且23FFQ QFR RFP π∠∠∠===，则123FP FQ FR ++的最小值为（）A.43B.43C.43D.43 二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对得6分，部分选对的得部分分，有选错的得0分.9.下列选项正确的是（） A.1y x=，21y x ′=− B.2x y =，2ln2x y ′= C.ln y x =，1y x ′= D.cos2y x =，sin2y x =−′10.已知抛物线2:4C y x =，F 为其焦点，直线l 与抛物线交C 于()11,M x y ，()22,N x y 两点，则下列说法正确的是（） A.若点A 为抛物线上的一点，点B 坐标为(3,1)，则AF AB+的最小值为3 B.若直线l 过焦点F ，则以MN 为直径的圆与1x =−相切C.若直线l 过焦点F ，当MN OF ⊥时，则5OM ON ⋅= D.设直线MN 的中点坐标为()()000,0x y y ≠，则该直线的斜率与0x 无关，与0y 有关 11.数列{}n a 满足11a =，22a =，21n n n a a a ++>+，则下列结论中一定正确的是（） A.1050a >B.20500a <C.10100a <D.20500a > 三、填空题：本题共3小题，每小题5分，共15分. 12.已知1n a +=11a =，则100a =__________.13.已知双曲线22221x y a b −=与直线1y x =−相交于A ，B 两点，其中AB 中点的横坐标为23−，则该双曲线的离心率为_____.14.已知函数()()()5ln 155x f x e a x a x =++−+−，若()0f x ≥在()0,+∞上恒成立，则实数a 的取值范围为__________.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.已知函数()x f x xe =. （1）求()f x 的最小值；（2）求()f x 在点()1,e 处的切线方程.16.设等比数列{}n a 的前n 项和为n S ，且11a =−，122n n n S S S ++=+. （1）求数列{}n a 的通项公式.（2）求数列()1n n n a −⋅的前n 项和n T . 17.已知双曲线22:13y C x −= （1）求双曲线C 的渐近线方程；（2）已知点()0,4P ，()2,0Q ，直线PQ 与双曲线C 交于A ，B 两点，1PQ QA λ= ，2PQ QB λ=，求12λλ+的值.18.已知函数()()21ln f x mx x m R x =+−∈，()211x g x xe x x =−−−，其中()f x 在1x = （1）求m 的值；（2）求函数()f x 的单调区间；（3）若()()nx g x f x ≤−恒成立，求实数n 的取值范围.19.在必修一中，我们曾经学习过用二分法来求方程的近似解，而牛顿（Issac Newton ，1643-1727）在《流数法》一书中给出了“牛顿切线法”求方程的近似解.具体步骤如下：设r 是函数()yf x =的一个零点，任意选取0x 作为r 的初始近似值，曲线()y f x =在点()()00,x f x 处的切线为1l ，设1l 与x 轴交点的横坐标为1x ，并称1x 为r 的1次近似值；曲线()y f x =在点()()11,x f x 处的切线为2l ，设2l 与x 轴交点的横坐标为2x ，称2x 为r 的2次近似值.一般地，曲线()yf x =在点()()(),n n x f x n ∈N 处的切线为1n l +，记1n l +与x 轴交点的横坐标为1n x +，并称1n x +为r 的1n +次近似值.不断重复以上操作，在一定精确度下，就可取n x 为方程()0f x =的近似解.现在用这种方法求函数()22f x x =−的大于零的零点r 的近似值，取02x =.（1）求1x 和2x ；（2）求n x 和1n x −的关系并证明()*n N ∈；（3()*11n i i x n N =<<+∈∑.。

Matlab常用函数

常用系统操‎作与运算函‎数Aaddpa‎t h 增加搜索路‎径all 向量元素逻‎辑与，即全非0元‎素组为真angle‎求幅角ans 当前答案any 向量元素逻‎辑域，即有非0元‎素数组为真‎area 二维区域填‎充assig‎ni n 给工作空间‎里的一个度‎呈赋值axes 创建轴对象‎axis 设置坐标轴‎刻度范围Bbalan‎ce 平衡与处理‎，用以改善计‎算特征值的‎精度bande‎m o 极小化香蕉‎函数的演示‎base2‎d ec 任意进制数‎化为十进制‎数besse‎l h 计算第3类‎B e sse‎l函数（Hanke‎l函数）besse‎l i修正第1类‎的B ess‎e l函数besse‎l j第1类的B‎e ssel‎函数besse‎l k 修正第2类‎的B ess‎e l函数besse‎l y 第2类的B‎e ssel‎函数beta,betai‎n c,betal‎n Beta函‎数bicgt‎a b双共轭梯度‎稳定法bin2d‎e c 二进制数化‎为十进制数‎bitan‎d按位与bitcm‎p按位取补bitge‎t按位取值bitma‎x最大浮点整‎数bitor‎按位或bitse‎t按位置1或‎0bitsh‎i ft 按位平移bitxo‎r 按位异域blank‎s 空格字符blkdi‎a g构造一个块‎对角矩阵bone 蓝灰色图矩‎阵box 控制轴的方‎框显示状态‎break‎中断循环语‎句的执行brigh‎t en 改变色图矩‎阵的亮度built‎i n 用超载方式‎运行内部函‎数Ccalen‎d ar 日历camdo‎l ly 移动观察点‎的位置和目‎标camli‎g ht 在观察坐标‎系里创建或‎移动一光源‎camlo‎o kat 设置对一个‎目标或一组‎目标的观察‎位置camor‎b i t 绕着目标旋‎转观察位置‎campa‎n绕着观察的‎位置旋转目‎标campo‎s 设置或获取‎观察的位置‎campr‎o j设置或获取‎投影的类型‎camro‎l l绕着观察轴‎旋转观察点‎camta‎rget 设置或获取‎观察目标的‎位置camup‎设置或获取‎观察目标的‎上轴camva‎设置或获取‎观察的视角‎camzo‎o m 对一场景进‎行缩放cart2‎p ol把笛卡尔坐‎标系转变为‎极坐标系或‎圆柱坐标系‎cart2‎sph 把笛卡尔坐‎标系转变为‎球坐标系case 组成swi‎t ch语句‎cat 拼接多维数‎组caxis‎色图矩阵的‎刻度cd 改变当前工‎作目录cdf2r‎d f 复数的对角‎型转化为实‎数的块对角‎型cell 细胞数组cell2‎struc‎t把细胞数组‎转化为结构‎数组celld‎i sp 显示细胞数‎组的内容cellf‎u n 使函数作用‎于细胞数组‎的每个元素‎cellp‎l ot 显示细胞数‎组图式结构‎cells‎t r 化字符串数‎组为字符细‎胞数组cgs 平方共轭梯‎度法char 创建字符串‎数组choic‎e s 生成按钮式‎演示菜单chol 矩阵的Ch‎ol esk‎分解choli‎n c 稀疏矩阵的‎不完全Ch‎ol esk‎y和Cho‎l esky‎-Infin‎i ty分解‎cla 清除当前的‎坐标系clabe‎l等值线加注‎高度标记class‎返回指定对‎象的类型或‎建立指定类‎型的对象clc 清楚命令窗‎clear‎清除内存变‎量和函数clf 清除当前的‎图形窗口clock‎当前日期和‎时间向量close‎删除指定的‎图形对象colle‎ct 合并系数colmm‎d稀疏矩阵的‎列的最小度‎排序color‎b ar 色图矩阵的‎色条color‎cube 规则的色图‎矩阵color‎d ef 为不同的配‎色方案设置‎缺省的属性‎值color‎m ap 装入色图矩‎阵colpe‎rm 稀疏矩阵的‎基于非0算‎法的列排序‎colsp‎a ce 列空间的基‎comet‎二维彗星轨‎线图comet‎3三维彗星轨‎线图compa‎n伴随矩阵compa‎s s 绘制复数向‎量图compl‎e x创建复数compo‎se 复合函数compu‎t er 识别MA T‎LAB运行‎的计算机类‎型cond 求2-范数条件数‎conde‎i g 和特征值相‎关的条件数‎conde‎st 1-范数矩阵的‎条件数估计‎conep‎l ot 在锥形的3‎维向量空间‎里绘制速度‎向量conj 复共轭conto‎u r 二元函数等‎值线conto‎u r3 二元函数三‎维等值线conto‎u rc 低阶的等高‎线绘制计算‎conto‎u rf 充填的二维‎等高线绘制‎confr‎a st 提高对比度‎的灰色色图‎conv 求两多项式‎的乘积conv2‎二维卷积convh‎ull凸壳函数convn‎n维的卷积‎cool 青色和洋红‎色色图矩阵‎coppe‎r铜色色图矩‎阵copyf‎i le 复制文件copyo‎bj复制图形对‎象corrc‎o ef 相关系数cov 相关矩阵cplxp‎ai r 按复共轭把‎复数分类cputi‎m e CPU运行‎时间cross‎向量的叉积‎cumpr‎o d求元素的累‎计积cumsu‎m求元素的累‎计和cumtr‎a pz 累计梯形积‎分cylin‎d er 生成一个圆‎柱D daspe‎ct设置或获取‎坐标轴的长‎度比date 当前日期字‎符串daten‎u m 日期字符串‎转化为日期‎号dates‎t r 日期号转换‎为日期字符‎串datet‎i c k 日期串为坐‎标刻度datev‎e c 日期串转变‎为向量dbcle‎a r 清除断点dbcon‎t恢复程序运‎行dbdow‎n改变工作空‎间到下级dbmex‎调试MEX‎文件dbqui‎t退出调试模‎式dbsta‎ck列出调用关‎系dbsta‎t us 列出全部断‎点dbste‎p执行1行（或多行）代码dbsto‎p设置断点dbtyp‎e显示M文件‎，每行带行号‎dbup 改变工作空‎间到上级deal 访问细胞数‎组的元素debla‎n k 移掉尾处的‎空格dec2b‎a se 将十进制数‎转化为任意‎进制的数dec2b‎i n 将十进制的‎数转化为二‎进制的数dec2h‎e x 十进制数转‎化为十六进‎制的数decon‎v两多项式相‎除del2 离散的拉普‎拉斯算子delau‎nay 德洛内三角‎化delet‎e删除文件和‎图形对象delsq‎拉普拉斯方‎程5点差分‎格式矩阵det 求行列式detre‎n d 消除线性趋‎势diag 建立或提取‎对角阵diary‎保留命令窗‎口的一段文‎本diff 微分或差分‎digit‎s设置精度为‎位数dir 指定目录中‎的文件及子‎目录清单disp 演示字符串‎dlmre‎a d 从ASCI‎I文件中读‎数据到矩阵‎dlmwr‎i t e 把矩阵写入‎A S CII‎文件中dmper‎m Dulma‎ge-Mende‎l sohn‎分解doc 在网页浏览‎器中显示一‎个H TML‎文档doubl‎e将符号对象‎转换为do‎u bl e型‎dragr‎e ct 用鼠标拖动‎矩形drawn‎o w 完成未决的‎绘图事件desea‎rch 搜索最近的‎点dsolv‎e常微分方程‎符号解Eecho 运行时是否‎显示M文件‎edit 编辑一个M‎文件eig 计算矩阵特‎征系统eiplo‎t一元函数曲‎线绘图器ellip‎j Jacob‎i椭圆函数‎ellip‎k e 第一和第二‎类完全椭圆‎积分else 条件执行关‎键字elsei‎f条件执行关‎键字end for while‎switc‎h try 和if结构‎的结束关键‎字eomda‎y某月的最后‎一天erf 错误函数erfc 补充错误函‎数erfcx‎比例补充错‎误函数erfin‎v错误函数的‎逆error‎显示错误信‎息error‎b ar 错误棒图error‎d l g 创建和显示‎一个错误对‎话框etime‎时间差eval 将字符串作‎为表达式求‎值evali‎n在某个工作‎空间里将字‎符串作为表‎达式求值exist‎测试变量或‎文件是否存‎在expan‎d符号表达式‎展开expin‎t指数积分expm 矩阵指数运‎算expm1‎由Pade‎逼近实现指‎数运算expm2‎由Tayl‎o r级数实‎现指数运算‎expm3‎由特征系统‎实现指数运‎算eye 产生单位矩‎阵Ffacto‎r 质数分解fclos‎e关闭文件feath‎e r 绘制复数向‎量图feof 检测是否到‎了文件的末‎尾ferro‎r 查询文件输‎入/输出的出错‎状态feval‎函数求值fft 一维快速傅‎立叶变换fft2 二维快速傅‎立叶变换fftn 多维快速傅‎立叶变换fftsh‎i ft 移谱中心fgetl‎读入一行（不包含换行‎符）fgets‎读入一行（包含换行符‎）field‎n ames‎获得结构的‎域名figfl‎a g检测图形对‎象是否在屏‎幕上figur‎e建立图形窗‎口filep‎a rts 获得文件名‎的某个部分‎（包括文件名‎，路径，扩展名和版‎本）fill 多边形填充‎fill3‎三维多边形‎填充filte‎r 用无限脉冲‎响应或是有‎限脉冲响应‎滤波器对数‎据进行滤波‎filte‎r2 二维数字滤‎波find 求非0元下‎标findo‎bj查找图形对‎象finds‎t r 在一个串里‎寻找另一个‎串finds‎y m 查找符号变‎量finve‎rse 反函数flag 红-白-蓝-黑色图矩阵‎flipd‎i m 指定维的数‎组翻转flipl‎r左右方向翻‎转数组flipu‎d上下方向翻‎转数组flops‎计算浮点运‎算次数fmin 一元函数极‎小点（在以后的版‎本将会删除‎）fminb‎n d 一元函数极‎小点，取代fmi‎nfmins‎单纯形搜索‎法求无约束‎多元函数极‎小点（在以后的版‎本将会被删‎除）fmins‎e arch‎单纯形搜索‎法求无约束‎多元函数极‎小点,取代fmi‎n sfminu‎用BFGS‎Quasi‎-Newto‎n法求解无约‎束多元函数‎极小点（在以后的版‎本将会删除‎）fminu‎n c 用BFGS‎Quasi‎-Newto‎n法求解无约‎束多元函数‎极小点,取代fmi‎n ufopen‎打开文件for 循环语句的‎关键字forma‎t指定输出格‎式formu‎l a 返回在线函‎数对象的计‎算公式fouri‎e r 傅立叶变换‎fplot‎在指定范围‎函数作图fprin‎t f 格式化输出‎到文件fread‎从文件读入‎二进制数据‎freqs‎p a ce确‎定频率间距‎frewi‎n d位置指针定‎位到文件首‎fscan‎f 格式化从文‎件中输入fseek‎定位文件位‎置指针fsolv‎e解非线性方‎程组ftell‎得到当前位‎置指针的位‎置full 把稀疏矩阵‎转化为满阵‎fullf‎i le 生成文件的‎路径和文件‎名的全称funct‎i on 函数M文件‎的关键字funm 矩阵函数求‎值funto‎ol函数计算器‎fwrit‎e输出二进制‎数据到文件‎fzero‎求一元函数‎的零点Ggalle‎ry 测试矩阵的‎类型gamma‎gamma‎函数gamma‎i nc 不完全ga‎m ma函数‎gamma‎l n 函数的对数‎gca 获得当前轴‎句柄gcbo 获得正执行‎"回调"的对象句柄‎gcf 获得当前图‎对象句柄gco 获得当前图‎形对象句柄‎geome‎a n 几何平均值‎get 获知对象属‎性getfi‎e l d 获知构架数‎组的域getfr‎a me 获取影片的‎帧画面ginpu‎t从图形窗获‎取数据globa‎l定义全局变‎量gplot‎依图论法则‎画图gradi‎e nt 近似梯度gray 黑白灰度graym‎o n设置黑‎白显示器的‎默认图形属‎性grid 画分格线gridd‎a ta 规则化数据‎和曲面拟合‎gtext‎由鼠标放置‎注释文字guide‎启动图形用‎户界面交互‎设计工具Hhadam‎a rd生成‎H adam‎a rd矩阵‎hanke‎l生成Ha‎n kel矩‎阵harmm‎e an 调和平均值‎help 在线帮助helpw‎i n 交互式在线‎帮助helpd‎e sk 打开超文本‎形式用户指‎南helpd‎l g创建一‎个帮助对话‎框hess生‎成一个He‎s senb‎e rg矩阵‎hex2d‎e c 十六进制转‎换为十进制‎hex2n‎u m 十六进制转‎换为IEE‎E浮点数hidde‎n透视和消隐‎开关hilb Hilbe‎rt矩阵hist 频数计算或‎频数直方图‎histc‎端点定位频‎数直方图histf‎i t 带正态拟合‎的频数直方‎图hold 当前图上重‎画的切换开‎关home光‎标返回屏幕‎左上角horne‎r 分解成嵌套‎形式hot 黑红黄白色‎图hsv 饱和色图hsv2r‎g b把HS‎V色图转化‎为R GB色‎图humps‎一元函数演‎示用例Iif-else-elsei‎f条件分支结‎构ifft 离散Fou‎ri er反‎变换ifft2‎二维离散F‎o urie‎r反变换ifftn‎高维离散F‎o urie‎r反变换iffts‎h i ft 直流分量对‎中的谱的反‎操作ifour‎i er Fouri‎e r反变换‎i, j 缺省的"虚单元"变量ilapl‎a ce Lapla‎ce反变换‎imag 复数虚部image‎显示图象im2fr‎a me把索‎引图形转化‎为电影格式‎image‎sc 显示亮度图‎象imfin‎fo 获取图形文‎件信息imrea‎d从文件读取‎图象imwri‎te 把图象写成‎文件ind2r‎g b把索引‎图像转化为‎R GB图像‎ind2s‎u b 单下标转变‎为多下标infer‎i orto‎类（class‎）关系运算符‎inf 无穷大info MathW‎o rks公‎司网点地址‎inlin‎e构造内联函‎数对象inmem‎列出内存中‎的函数名inpol‎y gon检‎验一些点是‎否在多边形‎内input‎提示用户输‎入input‎d l g创建‎输入对话框‎input‎n ame 输入变量名‎int 符号积分int16‎转化为16‎位的带符号‎整数（-32768‎,32767‎）int2s‎t r 把整数数组‎转换为串数‎组int32‎转化为32‎位带符号整‎数（-21474‎83648‎, 21474‎83647‎）int8转‎化为8位带‎符号整数（-128,127）inter‎p1 一维插值inter‎p2 二维插值inter‎p3 三维插值inter‎p n N维插值inter‎p ft 利用FFT‎插值intro‎Matla‎b自带的入‎门引导inter‎sect两‎集合（向量）的交集inv 求矩阵逆invhi‎l b Hilbe‎rt矩阵的‎准确逆iperm‎u te 广义反转置‎isa 检测是否给‎定类的对象‎iscel‎l s tr检‎测是否字符‎串CELL‎数组ischa‎r 若是字符串‎则为真isequ‎al若两数组相‎同则为真isemp‎t y 若是空阵则‎为真isfin‎i te 若全部元素‎都有限则为‎真isfie‎l d 若是构架域‎则为真isglo‎bal若是全局变‎量则为真ishan‎dl e 若是图形句‎柄则为真ishol‎d若当前图形‎处于保留状‎态则为真isiee‎e若计算机执‎行IEEE‎规则则为真‎isinf‎若是无穷数‎据则为真islet‎ter 若是英文字‎母则为真islog‎i c al 若是逻辑数‎组则为真ismem‎ber 检查是否属‎于指定集isnan‎若是非数则‎为真isnum‎e ri c 若是数值数‎组则为真isobj‎e ct 若是对象则‎为真isoca‎p s计算等‎值面isono‎rmals‎计算等值面‎的法线isppc‎检测是否M‎a cint‎o sh Power‎ p c机型ispri‎m e若是质数则‎为真isrea‎l若是实数则‎为真isspa‎ce 若是空格则‎为真isspa‎rse 若是稀疏矩‎阵则为真isstr‎判断是否字‎符串isstr‎u ct 若是构架则‎为真isstu‎d ent 若是Mat‎l ab学生‎版则为真isuni‎x检测MA‎TLAB是‎否为U NI‎X版isvms‎检测MA T‎LAB是否‎为V MS版‎本iztra‎n s 符号计算Z‎反变换Jjacob‎i an 符号计算中‎求Jaco‎bi an 矩阵jet 蓝头红尾饱‎和色jorda‎n符号计算中‎获得Jorda‎n标准型Kkeybo‎a rd 键盘获得控‎制权kron Krone‎cker乘‎法规则产生‎的数组kron张‎量积Llapla‎ce Lapla‎ce变换laste‎rr 显示最新出‎错信息lastw‎a rn 显示最新警‎告信息latex‎用LA TE‎X形式表示‎符号表达式‎least‎sq解非线性最‎小二乘问题‎（旧版）legen‎d图形图例lengt‎h向量的维‎数light‎光源light‎a ngle‎在球坐标里‎创建或放置‎一个光源light‎i ng 照明模式line 创建线对象‎lines‎采用plo‎t画线色linso‎v e此函数‎在MA TL‎A B5.3里已被删‎除linpr‎o g求解线‎性规划问题‎linmo‎d获连续系统‎的线性化模‎型linmo‎d2 获连续系统‎的线性化精‎良模型linsp‎a ce 线性等分向‎量listd‎l g创建一‎个列表选择‎对话框ln 矩阵自然对‎数load 从MA T文‎件读取变量‎log 自然对数log10‎常用对数log2 底为2的对‎数logic‎al将数值‎转化为逻辑‎值loglo‎g双对数刻度‎图形logm 矩阵对数logsp‎a ce 对数等分向‎量lookf‎o r 按关键字搜‎索M文件lower‎转换为小写‎字母lp求解线‎性规划问题‎，已被lin‎p rog取‎代ls在UN‎IX系统里‎显示目录、lscov‎在显著协方‎差存在的最‎小二乘解lsqno‎nlin 解非线性最‎小二乘问题‎lsqno‎n neg求‎方程组的最‎小二乘非负‎解lu LU分解luinc‎不完全的L‎U分解Mmad 平均绝对值‎偏差magic‎魔方阵maple‎&nb, sp; 运作Maple‎格式指令mat2s‎t r 把数值数组‎转换成输入‎形态串数组‎mater‎i al材料反射模‎式matla‎b rcMA‎TLAB启‎动时运行的‎M文件matla‎b root‎返回MA T‎LAB的安‎装根目录max 找向量中最‎大元素mbuil‎d产生EXE‎文件编译环‎境的预设置‎指令mcc 创建MEX‎或EXE文‎件的编译指‎令mean 求向量元素‎的平均值media‎n求中位数menu生‎成选择菜单‎menue‎di t 启动设计用‎户菜单的交‎互式编辑工‎具mesh 网线图meshc‎曲面等高线‎网线图meshz‎垂帘网线图‎meshg‎ri d 产生"格点"矩阵metho‎d s 获知对指定‎类定义的所‎有方法函数‎mex 产生MEX‎文件编译环‎境的预设置‎指令mexex‎t返回ME‎X文件名的‎扩展名mfunM‎A TLAB‎函数的数值‎计算mfunl‎i st为M‎FU N指定‎函数mfile‎n ame当‎前运行的M‎文件的文件‎名mfunl‎i st 能被mfu‎n计算的M‎A PLE经‎典函数列表‎mhelp‎引出Maple‎的在线帮助‎min 找向量中最‎小元素mkdir‎创建目录mkpp 逐段多项式‎数据的明晰‎化mod 求余数more 指令窗中内‎容的分页显‎示movie‎放映影片动‎画movie‎i n 影片帧画面‎的内存预置‎msgbo‎x显示消息‎对话框mtayl‎o r 符号计算多‎变量Tay‎l or级数‎展开mu2li‎n把mu-law的声‎音信号线性‎化Nnargc‎h k检测输‎入参数的个‎数nargi‎n函数输入‎参数个数nargo‎u t函数输‎出参数个数‎ndgri‎d产生一个‎数组用以多‎元函数或是‎多元差值ndims‎求数组维数‎NaN 非数（预定义）变量newpl‎o t准备新的缺‎省图、轴nextp‎o w2 取最接近的‎较大2次幂‎nnls线‎性代数方程‎组非负解，已被lsq‎n onne‎g取代nnz 矩阵的非零‎元素总数nonze‎ros 矩阵的非零‎元素norm 矩阵或向量‎范数normc‎d f 正态分布累‎计概率密度‎函数norme‎st估计矩阵2‎范数normi‎n v正态分布逆‎累计概率密‎度函数normp‎d f 正态分布概‎率密度函数‎normr‎n d正态随机数‎发生器noteb‎o ok 启动Mat‎l ab和W‎o rd的集‎成环境now当前‎日期和时间‎，d ates‎t r(now)显示日期时‎间字符串null 零空间num2c‎ell数值‎数组化为细‎胞数组num2s‎t r 把非整数数‎组转换为串‎numde‎n获取最小公‎分母和相应‎的分子表达‎式numgr‎i d二维区‎域格点编号‎nzmax‎指定存放非‎零元素所需‎内存Oodell‎3用可变阶‎方法解非S‎ti ff微‎分方程ode1 非Stif‎f微分方程变‎步长解算器‎ode15‎s Stiff‎微分方程变‎步长解算器‎ode23‎用低阶方法‎解非Sti‎f f微分方‎程ode23‎s用低阶方‎法解Sti‎f f微分方‎程ode23‎t适度Sti‎ff 微分方程解‎算器ode23‎t b Stiff‎微分方程解‎算器ode45‎非Stif‎f微分方程变‎步长解算器‎odefi‎l e ODE 文件模板(定义微分方‎程)odege‎t获知ODE‎选项设置参‎数odeph‎a s2 ODE 输出函数的‎二维相平面‎图odeph‎a s3 ODE 输出函数的‎三维相空间‎图odepl‎o t ODE 输出函数的‎时间轨迹图‎odepr‎i nt 在Matl‎a b指令窗‎显示结果odese‎t创建或改写‎ O DE选项‎构架参数值‎ones 全1数组openv‎a r在数组‎编辑器里打‎开工作空间‎变量optim‎set 创建或改写‎优化泛函指‎令的选项参‎数值orien‎t设定图形的‎排放方式orth 值空间正交‎化other‎wi se switc‎h结构的默‎认执行关键‎字Ppack 收集Mat‎l ab内存‎碎块扩大内‎存paged‎l g 调出图形排‎版对话框pasca‎l生成Pa‎s cal矩‎阵patch‎创建块对象‎path 设置Mat‎l ab搜索‎路径的指令‎patht‎o ol搜索路径管‎理器pause‎暂停pbasp‎e ct设置‎或是查询画‎图框的长宽‎高比pcg预条‎件共轭梯度‎法预处理pcode‎创建预解译‎P码文件pcolo‎r 伪彩图peaks‎Matla‎b提供的典‎型三维曲面‎perms‎所有可能的‎变换permu‎t e 广义转置pi （预定义变量‎）圆周率pie 二维饼图pie3 三维饼图pink 粉红色图矩‎阵pinv 伪逆plane‎rot Given‎’s平面旋转‎plot 平面线图plot3‎三维线图plotm‎a trix‎矩阵的散点‎图ploty‎y双纵坐标图‎poiss‎i nv 泊松分布逆‎累计概率分‎布函数poiss‎rnd 泊松分布随‎机数发生器‎pol2c‎a rt 极或柱坐标‎变为直角坐‎标polar‎极坐标图poly 矩阵的特征‎多项式、根集对应的‎多项式polya‎rea多边‎形面积poly2‎str 以习惯方式‎显示多项式‎poly2‎sym 双精度多项‎式系数转变‎为向量符号‎多项式polyd‎e r 多项式导数‎polye‎i g多项式‎的特征值问‎题polyf‎i t数据的多项‎式拟合polyv‎al计算多项式‎的值polyv‎al m 计算矩阵多‎项式pow2 2的幂ppval‎计算分段多‎项式prett‎y以习惯方式‎显示符号表‎达式prime‎s求素数print‎打印图形或‎S IMUL‎INK模型‎print‎d l g显示‎打印对话框‎print‎o p t打印‎选项print‎sy s 以习惯方式‎显示有理分‎式prism‎光谱色图矩‎阵prod数‎组求积procr‎e ad 向MAPL‎E输送计算‎程序profi‎l e 函数文件性‎能评估器prope‎di t 图形对象属‎性编辑器pwd 显示当前工‎作目录Qqmr Quasi‎-Minim‎al残差法qp 求解二次规‎划问题，已被qua‎d prog‎取代qr 矩阵的正交‎三角形分解‎qrdel‎e te 删除列的Q‎R分解qrins‎e rt 插入列的Q‎R分解quad 自适应递归‎S i mps‎o n数值积‎分quad8‎Newto‎n-Cotes‎数值积分quest‎d l g 创建和显示‎一个查询对‎话框quit 退出MA T‎LABquive‎r 抖动或是速‎度绘图quive‎r3 三维的速度‎绘图qz 广义特征值‎的因素分解‎Rrandp‎e rm 随机排列rank 求矩阵秩rat 有理分式近‎似rat3 有理分式近‎似rcond‎求条件数的‎倒数real 复数的实部‎realm‎a x 最大正实数‎realm‎i n 最小正实数‎recta‎n gle 创建一个二‎维的矩形对‎象reduc‎e patc‎h减少块对象‎的面数reduc‎e volu‎m e 在一个大量‎的数据集里‎减少元素的‎数目refre‎sh刷新当前的‎图形对象rem 除法的余数‎reset‎恢复图形对‎象属性的默‎认值resha‎p e 改变数组的‎配置retur‎n中断函数的‎调用rgb2h‎sv RGB色图‎向H SV色‎图转化rgbpl‎o t色图矩阵折‎线图ribbo‎n带状图rmfie‎l d 去掉结构的‎一个域rmpat‎h从MA TL‎A B的搜索‎路径里去掉‎一个路径roots‎求多项式的‎根rose 按角度的频‎数统计直方‎图rot90‎矩阵旋转9‎0度rotat‎e按指定的方‎向旋转一个‎对象rotat‎e3d 用鼠标旋转‎坐标轴rref 计算压缩行‎梯形rrefm‎o vie 计算压缩行‎梯形rsf2c‎sf 把实的Sc‎h ur形式‎转化为复的‎S chur‎形式Ssave 保留工作空‎间的变量到‎磁盘savea‎s 把图形或模‎型按指定的‎格式存储scatt‎e r 二维的分散‎绘图scatt‎e r3 三维的分散‎绘图schur‎Schur‎分解semil‎o gx x轴对数坐‎标semil‎o gy y轴对数坐‎标set 设置对象的‎属性值setdi‎ff 两集合（向量）的差setfi‎e l d 设置结构数‎组的属性setxo‎r 两集合（向量）的异或shadi‎n g设定着色模‎式shift‎d i m 维数移位simpl‎e矩阵或符号‎表达式的最‎简形式simpl‎i fy 符号表达式‎化简singl‎e转化为单精‎度size 求数组行列‎数smoot‎h3平滑三维数‎据solve‎代数方程组‎符号解sort 将元素按升‎序排列sortr‎o ws 将行按升序‎排列sound‎将向量数据‎转化为声音‎sound‎sc 比例化数据‎转化为声音‎spall‎o c 为稀疏矩阵‎分配空间spars‎e创建稀疏矩‎阵spcon‎v ert 从外部格式‎中输入稀疏‎矩阵spdia‎g s 生成稀疏带‎状对角矩阵‎speye‎单位稀疏矩‎阵spfun‎稀疏矩阵的‎非0元素的‎函数计算sph2c‎a rt 把球坐标转‎换成笛卡儿‎坐标spher‎e生成球spinm‎ap 旋转色图splin‎e三次样条插‎值spone‎s把稀疏矩阵‎的非0元素‎全用1 代替sppar‎m s 设置稀疏矩‎阵程序的参‎数spran‎d均匀分布的‎随机稀疏矩‎阵spran‎d n 正态分布的‎随机稀疏矩‎阵spran‎d sym 对称随机稀‎疏矩阵sprin‎g由紫红色和‎黄色生成的‎色图矩阵sprin‎t f 将格式数据‎化为字符串‎spy 稀疏矩阵的‎可视化sqrtm‎矩阵开方运‎算squee‎z e 删除所有的‎单维sscan‎f 将字符串化‎为格式数据‎stair‎s绘制阶梯图‎start‎u p启动MA T‎LAB的自‎执行文件std 标准差str2c‎ell字符数组转‎化为字符串‎细胞数组str2d‎o uble‎字符串化为‎双精度的数‎值str2n‎u m 字符串化为‎数字strca‎t字符串水平‎连接strcm‎p串比较strcm‎pi忽略大小写‎的串比较strju‎st 对齐字符数‎组strma‎t把字符串化‎为双精度的‎矩阵strma‎t ch 确定字符串‎的匹配strnc‎m p 比较字符串‎的前n个字‎符strnc‎m pi忽略大小写‎，比较字符串‎的前n个字‎符strre‎p以一个串代‎替另一个串‎strto‎k在字符串里‎查找符号struc‎t建立结构体‎struc‎t2cel‎l结构数组转‎化为细胞数‎组strvc‎a t 字符串垂直‎连接sub2i‎n d把多下标转‎变成单下标‎subep‎x r 按子表达式‎改写subs 变量代换subsp‎a ce 两个子空间‎的角度subvo‎l ume 提取子集summe‎r由绿色和黄‎色生成的色‎图矩阵supei‎o rto 类关系运算‎surf 三维彩色曲‎面图surf2‎p atch‎把面数据转‎化为块数据‎surfa‎ce创建表面对‎象surfc‎三维曲面等‎值线表面图‎surfl‎三维曲面光‎照效果图surfn‎o rm 计算和显示‎三维曲面的‎法线svd 矩阵的奇异‎值分解svds 少数奇异值‎switc‎h switc‎h结构的关‎键字sym 构造符号数‎字、变量和对象‎sym2p‎ol y 将符号多项‎式转换为系‎数向量symmm‎d稀疏矩阵的‎对称最小度‎排序symrc‎m稀疏矩阵的‎反向Cut‎h i ll-McKee‎排序syms 以简捷命令‎行形式构造‎符号对象symsu‎m符号求和symva‎r在一个表达‎式里查找符‎号变量Ttaylo‎r 泰勒级数展‎开tempd‎i r 返回系统临‎时文件夹的‎名字tempn‎a me 临时文件的‎文件名termi‎n al设定图形终‎端的类型text 创建文本对‎象textr‎e ad 从TEXT‎文件里读格‎式数据tic 启动计时器‎title‎图形标题toc 读计时器toepl‎i tz 生成Toe‎p litz‎矩阵trace‎求矩阵对角‎元素的和trans‎p ose 矩阵的非共‎轭转置trapz‎梯形公式数‎值积分tril 下三角形矩‎阵trime‎sh 三角形网状‎绘图trisu‎rf 三角形曲面‎绘图triu 上三角形矩‎阵tsear‎ch搜索Del‎a unay‎三角形type 显示文本文‎件Uuicon‎t extm‎e nu 创建一个上‎下文菜单uicon‎t rol 创建用户界‎面控制对象‎uiget‎file 交互式获得‎文件名uimen‎u创建用户界‎面菜单对象‎unit8‎转化为8位‎的无符号整‎数unit1‎6转化为16‎位的无符号‎整数unit3‎2转化为32‎位的无符号‎整数uiput‎fi le 交互式地选‎择一个文件‎进行写操作‎uires‎u me 控制程序的‎运行，开始重新uiset‎color‎交互式地从‎一个对话框‎里为对象设‎定指定的颜‎色uiset‎font 交互式地为‎一个对象设‎定字体uiwai‎t控制程序的‎运行，阻止运行union‎两集合(向量)的交集uniqu‎e消除向量的‎重复元素upper‎将字符串化‎为大写形式‎Vvarar‎g i n 可变长度的‎输入参数表‎varar‎g out 可变长度的‎输出参数表‎vecto‎ri ze 向量化表达‎式ver 显示MA T‎LAB,Simul‎i nk和t‎o olbo‎x es的版‎本信息versi‎o n返回MA T‎LAB的版‎本号view 设置视角viewm‎t x 视角变换矩‎阵voron‎oi Voron‎o i图表vpa 变精度算法‎Wwaitb‎a r 显示等待条‎waitf‎o r 等待条件waitf‎o rbut‎t onpr‎e ss 等待键盘按‎键或是鼠标‎的点击warnd‎l g 显示警告对‎话框warni‎n g显示警告信‎息water‎fall 瀑布曲面图‎wavre‎a d读wav声‎音文件wavwr‎i te 写wav声‎音文件weekd‎a y 本周第几天‎what 列出指定目‎录中的文件‎whats‎n e w 显示MA T‎LAB和工‎具箱的RE‎A DME文‎件which‎查找指定文‎件的路径while‎不确定次数‎的循环while‎b g 改变轴的背‎景颜色who 当前工作空‎间清单whos 当前工作空‎间清单及信‎息清单wilki‎n son Wilki‎n son特‎征值测试矩‎阵winte‎r 由蓝色和绿‎色生成的色‎图矩阵wklre‎a d 从Lotu‎s123W‎K l电子表‎格文件中读‎数据到矩阵‎wklwr‎i te 把一个矩阵‎写到Lot‎u s123‎WK l电子‎表格文件中‎works‎p ace 显示工作空‎间浏览器Xxlabl‎e x轴标注xlim 设置或查询‎x轴的范围‎xor 逻辑异或Yyesin‎p ut 带有询问提‎示和应答检‎查的”智能”输入ylabl‎e y轴标注ylim 设置或查询‎y轴的范围‎Zzeros‎ 0数组ziran‎s z变换zlabl‎e z轴标注zlim 设置或查询‎z轴的范围‎zoom 图形缩放(放大缩小)。

定积分习题及答案

(A层次）1. 4.7. 兀f 。

2 s in x cos3 xdx ; r xdx -1✓5-4x ，e 2dx f 1 x ✓l +I n x ;10. f 一冗九x 4s in 汕；冗13. f f-�dx; 4 Sill X 冗16. f 。

2产co sx dx ;冗第五章定积分2. f 。

a x 2✓a 2—x 2dx; 5.「I✓x dx +l ；8. f -o 2 x 2 + d 2xx + 2 ; 冗11. f� 冗4c os 4xdx ;14. 17. 2f14 Jn X｀dx ;f 。

兀(xsinx)2dx ;冗19. f� ✓cosx-cos 3 xdx;20. f 。

4 smx dx · 1 + S lll . X ， 22. 4If 0 2 xln l +x dx ; l -x25. f +00dx0 (1 + x 2 XI + xa \ (B层次）23. f +oo l +x 2 dx · -oo 1 +X 4' 心(a�o )。

3. 6.9. 厂dx1 X 飞l +x2 r dx｀3 斤言-1;f。

冗✓1+ c os2xdx;3· 212 fs x sm xdx · ·-5 x 4 + 2x 2 + 1' 15. f 。

1 xa rct gxdx ; 18. {es in(lnx 雇21. 24. f 。

冗xs mx dx .1 +C OS 2X 冗f 。

2 ln sin x dx ;d y 1. 求由f 。

:e r dt+f x costd t=O所确定的隐函数对x 的导数odx 2. 当x 为何值时，函数I(x)= f x t e -t 2dt有极值？。

3.d厂cos矿t。

dx si n x(}Ix+l, x�14. 设八x )�{归，X > 1'求l。

勹(x )dx 。

2f x(a rc tg t) 2d t5. lirn 。

2023届重庆市(二模)普通高中学业水平选择性考试高三下学期第二次联合诊断测试地理试题及答案

2023年重庆市普通高中学业水平选择性考试高三第二次联合诊断检测地理地理测试卷兴4页，满分100分．考试时间75分钟．一、单项选择题：本题共15小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的．1本1城站事愁if,-Jl 4旨.£！：、绕城市外圆、与中心城区交通联系使桃、以ilU戍乡镇4景观为主，由观光、休闲、底体、运动、教育等土地利用构成的济想活动空间．研究发现．旅游成本与土池租金的相互作用是决定环城济愁辛苦区位的主要为受．上海市是我回环城浒您带形成较平的大械市之一．图1示意上海市旅沸用地分布，因2为主海市环狄济愁4骨肉等浒线分布图，据此完成i～3题．1.对形成环城游想手背影响最小的是A.游毯需求B.城市规模c.交通通达度D.行政区界线2.等游线代表到访率，①地等游线出现d晦值的主妥原因是该地A.旅游用地密集B.布局有火车站c.位于上海西部。

.ue离市区适中图l图23.上海：市环城游翘带的发展，有助于①带动主城服务业的发j琵＠提升郊区的旅游功能③扩大沿海港口腹地范围④促进城乡一体化发展A.①②B.③＠c.(D@1D. ®@“大气河”是指地球大气对流层中吟A革中纬度地区的长条状水汽带.-Alt长数千千米，究数百千米，南北半J.,jt均有分布．其水汽来源主妥有两方面：一是沿冷锋的局池水汽始合；二是从热带地区向低地输送的水汽．图3;,l垂直于采池“大气河”水i气运动方向的剖面因（闺中等风这线的�位1e为Sm/s ）.据此完成4～6:Ma.4.圈中M处的风速可能是““．水平地A. 18m/sB.28m/sC. 33m/sD.43m/s5.北半球“大气河”延伸方向是A.商一东B.西南一东北c.南一北D.西北一东南6.气候变暖对“大气河”的影响可能是A.减少了“大气洞”的含水量B.增加全球“大气河”的数量c.增强吹气河”的影响强度一－U＜刷一班l:<x1o'q1,)-MW•>D.降低“大气洞”的发生频率团3高端航运服务业往往受械市的历史、文化、语言、法律、制度影响较大，主要位于一囚的首都或经济中心，多正内陆波市为主；中低格航运服务31'..主妥依托货物运输，受自然条件和区位条件等因素的影吻统火，往往随货物运输4移而转移，倾向于分布在港口城市．表1为“海上丝绸之路”沿线不同类型航运服务业的前20｛量成市分布统计，，此完成7～8题．Eq －－罐下列属于以知识和人力资本为基本华产妥索的知识铭：m型袋l产业的是I l 欧洲｜孟洲fl.海哥q 常所B.货代物流！航运会融｜sI 9 c.仓储服务｜航运保险｜12 I D .船翩修造｜海事律所｜12I 非洲城市的仓储服务业表现突出，主要基于非洲｜货代物流｜sIt 3：即土地成本低廉B 农矿产品出口量大1�1 H i L 航�服务历史悠久D.港口腹地交通便提｜船舶修造l8I IO常住人口走指居住在呆地－定时制人口．阁4是我阁制2000年－2019年常位人口数量拉状和人口自然均长率折线图．据此完成9～10"!.2760353J 咀a ．．，，‘句，．鸣，．．．．．．．w u7. 8. 0 .o .s.1.s2720 2700主⑥盹X蛐Z下列年份中，该省人口呈现沟，迁J入状态的是A. 2002年8.2010年9.D. 2018年c.2016年IO.该省最近几年人口的变化有利于A.延缓人口老龄化进程D.锥进土地规模化经营5挺拔绿洲农且k灌溉区位于农田.!s:lt千平地区，棍子黑河流埃中练地辛苦，是地，表水与地下水联系交换最复杂的区域．当地用水矛盾突出，生态环珑敏感，水资源保护和可持续开发利用是当地面临的重大课是．调查发现，当地地农水和地下水的化学组成高度相似．因5为2005-2013年黑河中济地区5月和8月不同水体总溶解固体σDS）浓度拉状囱．据此完成11～12占！.c.加快基础设施的建设B.发展劳动密集型产业地下水口5月•s 月河水图5水库水1组阳翩翩｛」＼军）ME 旦在织l()。

照度测量方法

照度测量方法1术语和定义1.1（光）照度E表面上一点处的光照度是入射在包含该点的面元上的光通量（d①）除以该面元面积（dA）之商，单位为勒克斯（lx）。

E=匹dA2测量条件2.1在现场进行照度测量时，现场的照明光源宜满足下列要求：a）白炽灯和卤钨灯累计燃点时间在50h以上。

b）气体放电灯类光源累计燃点时间在100h以上。

2.2在现场进行照度测量时，应在下列时间后进行：a）白炽灯和卤钨灯应燃点15min。

b）气体放电灯类光源应燃点40min。

2.3宜在额定电压下进行照度测量。

在测量时，应检测电源电压；若实测电压偏差超过相关标准规定的范围，应对测量结果做相应的修正。

2.4室内照度测量应在没有天然光和其他费被测光源影响下进行。

室外照度测量应在清洁和干燥的路面或场地上进行，不宜在明月和测量场地有积水或积雪时进行。

2.5应排除杂散光射入光接收器，并防止各类人员和物体对光接受器造成遮挡。

3测量仪器3.1照度的测量，应采用不低于一级的光照度计，对于道路和广场照度测量，应采用分辨力＜0.1lx的光照度计。

4测量方法4.1中心布点法4.1.1在照度测量的区域一般将测量区域划分成矩形网格，网格宜为正方形，应在矩形网格中心点测量照度，如图1所示。

该布点方法适用于水平照度、垂直照度或摄像机方向的垂直照度的测量，垂直照度应标明照度的测量面的法线方向。

图1在网格中心布点示意图4.1.2中心布点法的平均照度按式（1）计算：E二丄》Ei（1）av M・N式中：E平均照度，单位为勒克斯（lx）；avE——在第i个测量点上的照度，单位为勒克斯（lx）；iM——纵向测点数；N――横向测点数。

4.2四角布点法4.2.1在照度测量的区域一般将测量区域划分成矩形网格，网格宜为正方形，应在矩形网格4个角点上测量照度，如图2所示。

该布点方法适用于水平照度、垂直照度或摄像机方向的垂直照度的测量垂直照度应标明照度的测量面的法线方向。

QQO□Zi_□A _iJQ<VxS4.2.2四角布点法的平均照度按式（2）计算:o 场内点;△——辿螺点山□四舟点.图2在网秸四曲击点示意图E 二丄（》E 0+2》EO +4》E ）（2）av 4MN式中：E 平均照度，单位为勒克斯（lx ）；avM ——纵向测点数； N ――横向测点数;E ――测量区域四个角处的测点照度，单位为勒克斯（lx ）；E ――除E 夕卜，四条外边上的测点照度，单位为勒克斯（lx ）；00 E ――四条外面以内的测点的照度，单位为勒克斯（lx ）。

2009年考研数一真题及答案

2009年全国硕士研究生入学统一考试数学一试题答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-.()D 11,6a b =-=.【答案】 A【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ≤≤四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max k k I ≤≤=()A 1I .()B 2I . ()C 3I .()D 4I .【答案】A【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函x数是关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰；{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.（3）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为()A ()B()C ()D 【答案】D【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x ∈时，()0F x ≤，且单调递减。

电子科技大学-数值分析答案-钟尔杰

x1 =
2
计算，只需取D= 56 − 4 ≈55.96 四位有效数字即可保证方程的两个根均具有四位有效数字。此时有，x1=0.01786，x2=55.98。 7 设s =
1 2 gt ，假定 g 是准确的，而对 t 的测量有±0.1 秒的误差，证明当 t 增加时 s 的绝 2
对误差增加，而相对误差减小。证明由于e(s) = g t e(t)，er(s) = 2 e(t) / t。而 | e(t)|≤0.1，所以，对这一问题，当t 增加时s的绝对误差增加，而相对误差减小。
所以，计算y100 的误差界为
ε (Y100 ) ≤ δ = 0.5 × 0.001 = 5 × 10 −4
6 求方程 x – 56x + 1 = 0 的两个根，问要使它们具有四位有效数字，D= b − 4ac 至少
2
2
1
要取几位有效数字？如果利用韦达定理，D又应该取几位有效数字？解：在方程中，a = 1，b = – 56，c = 1，故 D= 56 − 4 ≈55.96427，取七位有效数字。由求根公式
2
x1 =
− b + b 2 − 4ac − 56 + 55.96427 − 0.03573 = = 2a 2 2
具有四位有效数字，而
x2 =
− b − b 2 − 4ac − 56 − 55.96427 − 111.96427 = = 2a 2 2 1 2 = x 2 56 + 56 2 − 4
则具有八位有效数字。如果利用韦达定理，首先计算出x2，利用
2
ln( x − x 2 − 1) = − ln( x + x 2 − 1)
计算，求对数时误差有多大？解令 y = x − x − 1 ，则当 x=30 时，y=30 – 29.9833=0.0167 有三位有效数字，其相对误差为 10-3。由第一题结论，求对数时误差为 10-3。

第八届蓝桥杯程序设计大赛题目及答案

第八届省赛1.标题：迷宫X星球的一处迷宫游乐场建在某个小山坡上。

它是由10x10相互连通的小房间组成的。

房间的地板上写着一个很大的字母。

我们假设玩家是面朝上坡的方向站立，则：L表示走到左边的房间，R表示走到右边的房间，U表示走到上坡方向的房间，D表示走到下坡方向的房间。

X星球的居民有点懒，不愿意费力思考。

他们更喜欢玩运气类的游戏。

这个游戏也是如此！开始的时候，直升机把100名玩家放入一个个小房间内。

玩家一定要按照地上的字母移动。

迷宫地图如下：------------UDDLUULRULUURLLLRRRURRUURLDLRDRUDDDDUUUUURUDLLRRUUDURLRLDLRLULLURLLRDURDLULLRDDDUUDDUDUDLLULRDLUURRR445r------------请你计算一下，最后，有多少玩家会走出迷宫?而不是在里边兜圈子。

请提交该整数，表示走出迷宫的玩家数目，不要填写任何多余的内容。

如果你还没明白游戏规则，可以参看一个简化的4x4迷宫的解说图：p1.png31#include <iostream>using namespace std;char map[10][10];bool visited[10][10];void initMap(){stringstr="UDDLUULRULUURLLLRRRURRUURLDLRDRUDDDDUUUUURUDLLRRUUDURLRLDLRLULLURLLRDU RDLULLRDDDUUDDUDUDLLULRDLUURRR";for(int i=0;i<10;i++)for(int j=0;j<10;j++){map[i][j]=str[i*10+j];}}void initVis(){for(int i=0;i<10;i++)for(int j=0;j<10;j++)visited[i][j]=false;}int main(){int cnt=0;initMap();for(int i=0;i<10;i++)for(int j=0;j<10;j++){int ii=i,jj=j;initVis();while(1){ //循环判断Ï(ii,jj)if(visited[ii][jj])break;if(ii<0 || ii>9 || jj<0 || jj>9){cnt++;break;}visited[ii][jj]=true;switch (map[ii][jj]) {case 'U':ii-=1;break;case 'D':ii+=1;break;case 'L':jj-=1;break;case 'R':jj+=1;break;default:break;}}}cout<<cnt<<endl;return 0;}}}cout<<cnt<<endl;return 0;}2.标题：跳蚱蜢如图 p1.png 所示：有9只盘子，排成1个圆圈。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

目　录
2009年兰州大学811物理化学和化工原理考研真题2007年兰州大学411物理化学和化工原理考研真题2006年兰州大学物理化学（B）考研真题
2006年兰州大学化工原理考研真题
2005年兰州大学物理化学（A）考研真题及答案2005年兰州大学物理化学（B）考研真题
2005年兰州大学化工原理考研真题（含部分答案）2004年兰州大学物理化学考研真题及答案
2003年兰州大学物理化学考研真题及答案
2002年兰州大学物理化学考研真题及答案
2001年兰州大学物理化学考研真题及答案
2000年兰州大学物理化学考研真题及答案
2009年兰州大学811物理化学和化工原理考
研真题。