蚁群算法设计与分析
人工智能系统中的群体智能算法优化

人工智能系统中的群体智能算法优化群体智能算法(Collective Intelligence Algorithms)是一种基于群体行为和智能协作的人工智能算法,通过模拟自然界中的群体行为和社会行为,实现了人工智能系统中的优化问题。
群体智能算法在解决复杂问题、优化搜索和决策等方面展现出了巨大的潜力。
本文将对人工智能系统中的群体智能算法进行深入研究,探讨其优化方法、应用领域以及未来发展方向。
一、群体智能算法概述在自然界中,很多生物都通过集体行为来解决复杂问题。
例如,蚂蚁通过信息素沟通来找到最短路径;鸟群通过集体协作来捕食;蜜蜂通过集中决策来选择巢穴等。
这些生物集合起来形成了一个具有自组织、自适应和鲁棒性特征的群体系统。
基于这些生物现象,研究者们提出了一系列模拟生物行为的算法,并将其应用到人工智能领域。
1.1 蚁群优化算法蚁群优化(Ant Colony Optimization, ACO)算法是一种模拟蚂蚁寻找食物路径的算法。
蚂蚁在寻找食物的过程中,会释放一种称为信息素的化学物质,其他蚂蚁会根据信息素浓度选择路径。
通过模拟这一过程,ACO算法能够在解决优化问题中找到最优解。
ACO算法已经在旅行商问题、图着色问题等领域取得了显著的成果。
1.2 粒子群优化算法粒子群优化(Particle Swarm Optimization, PSO)算法是一种模拟鸟群觅食行为的算法。
PSO算法通过模拟鸟群中个体之间的信息交流和协作来寻找最优解。
每个个体根据自身经验和邻居经验来更新自己的位置和速度,从而逐步靠近最优解。
PSO算法已被广泛应用于函数优化、神经网络训练等领域。
1.3 其他群体智能算法除了ACO和PSO之外,还有许多其他类型的群体智能算法被提出和应用于人工智能领域。
例如,鱼群搜索(Fish Swarm Optimization, FSO)模拟能够在多个目标优化问题中找到最优解;蜜蜂算法(Artificial Bee Colony, ABC)模拟了蜜蜂寻找花朵的行为,用于解决连续优化问题;人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)模拟了鱼群觅食行为,用于解决连续优化问题等等。
第五章蚁群算法

8
10/11/201
1.1 组合优化问题 ₪ 例1 0-1背包问题(0-1 knapsack problem)
b :背包容积 ai : 第i件物品单位体积,i 1,, n. ci : 第i件物品单位价值,i 1,, n. 问题:如何以最大价值装包?
15
10/11/201
1.2 计算复杂性的概念
城市 24 25 26 27 28 数
计算 1 24 10 4.3 4.9 时间 sec sec min hour day
29 30 31
136.5 10.8 325 day year year
随城市增多,计算时间增加很快。 到31个城市时,要计算325年。
蚁群算法
Yuehui Chen School of Inform. Sci. and Eng. University of Jinan, 2009
10/11/2019
1
内容
一、启发式方法概述 二、蚁群优化算法
2
10/11/201
背景
₪ 传统实际问题的特点 连续性问题——主要以微积分为基础,且问题规模较小
9
10/11/201
1.1 组合优化问题
数学模型:
n
max ci xi i 1
(1.1)总价值
n
s.t. ai xi b, i 1
xi 0,1, i 1,, n.
(1.2)包容量限制 (1.3)决策变量
其中xi
1,装第i物品 0,不装第i物品
D 0,1n.
求和运算次数为:(n 1)!n n!;
枚举所有路径进行(n 1)!次比较可得最优路径,基本计算总次数为
蚁群算法
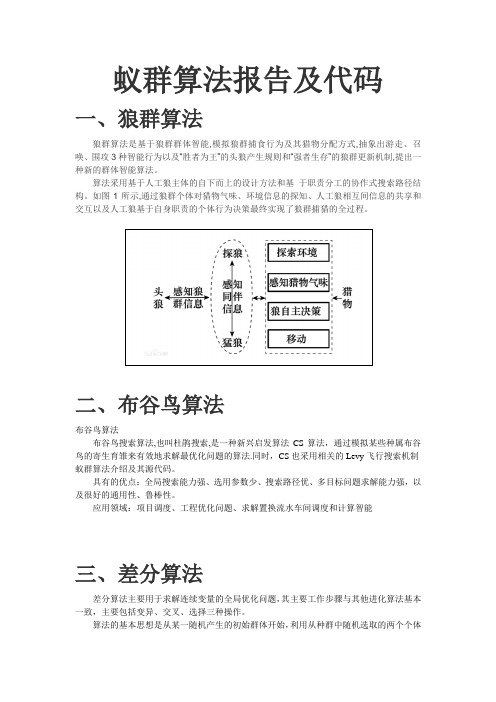
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
蚁群优化算法的研究及其应用的开题报告

蚁群优化算法的研究及其应用的开题报告一、研究背景及意义蚁群优化算法(Ant Colony Optimization,简称ACO)是一种基于自然界蚂蚁的行为特性而发展起来的群智能优化算法。
它通过模拟蚂蚁在寻找食物时的集体行为,通过正反馈和信息素等机制进行迭代搜索,最终达到问题最优解的全局优化方法,被广泛运用于组合优化、机器学习、数据挖掘、图像处理、网络计算等领域。
ACO算法在应用过程中存在的核心问题是参数的选择:如何确定信息素的启发式因子、挥发系数、蚁群大小、局部搜索参数等,以及如何在不同的问题中选择合适的参数组合。
因此,对ACO算法的研究不仅可以提高ACO算法在不同领域应用的效率和性能,还可以对其他基于自然界智慧的算法进行改进和优化。
对此,本研究将重点研究ACO算法的自适应参数优化算法及其在不同应用领域的性能评估和优化探究。
二、研究内容和方向1. ACO算法的原理、模型和迭代搜索过程研究;2. 研究ACO算法的参数选择算法,并结合实际问题进行验证和优化;3. 在不同应用领域(如组合优化、机器学习、数据挖掘等)中,探究ACO算法的性能表现及其在问题求解中的优化效果;4. 侧重于自适应参数优化的ACO算法,探究其在各种应用中的适用性、性能表现和求解效果;5. 探究ACO算法在较大规模问题优化中的可行性和效率,并对其进行实际应用。
三、研究方法和技术路线1. 查阅相关文献,深入理解ACO算法的原理、模型和参数选择等关键技术;2. 基于现有研究,设计ACO算法的自适应参数优化算法,并根据不同问题调整和优化参数组合;3. 选择不同领域问题,研究ACO算法的性能表现及其优化效果,并与其他优化算法进行对比分析;4. 将自适应参数优化的ACO算法应用于实际问题中,对ACO算法的可行性和效率进行实验验证,并与其他优化算法进行比较;5. 探究ACO算法在大规模应用中的效率及其应用瓶颈,根据实际问题调整算法优化方案。
四、预期成果及创新之处本研究旨在设计、优化ACO算法的自适应参数选择方案,并将其应用于不同领域中的优化问题,探究ACO算法在不同应用领域中的性能和优化效果。
第 6 章 蚁群算法

则,输出目前的最优解。
Hale Waihona Puke 3 目标值控制规则,给定优化问题(目标最小化)的一个下界和一个 误差值,当算法得到的目标值同下界之差小于给定的误差值时,算法 终止。
TSP应用举例
TSP应用举例
Introduction of Artificial Intelligence
Introduction of Artificial Intelligence
7
(2)鸟群行为
人们观察鸟群的群体行为发现: 当一群鸟在随机搜寻食物时,发现某个区域内有一块食物, 鸟会先后飞向食物,以及在食物最近的鸟的周围区域继续 搜寻食物。 数目庞大的鸟群在飞行中可以有形的改变方向,散开,或 者队形的重组。 科学家认为,上述行为是基于鸟类的社会行为中的两个要 素:个体经验和社会学习。 由此,创造了粒子群优化算法 (Particle Swarm optimization ,PSO)
蚁群算法的提出
人工蚁群算法
基于以上蚁群寻找食物时的最优路径选择问题,可以构造人 工蚁群,来解决最优化问题,如TSP问题。 人工蚁群中把具有简单功能的工作单元看作蚂蚁。二者的相 似之处在于都是优先选择信息素浓度大的路径。较短路径的信 息素浓度高,所以能够最终被所有蚂蚁选择,也就是最终的优 化结果。 两者的区别在于人工蚁群有一定的记忆能力,能够记忆已经 访问过的节点。同时,人工蚁群在选择下一条路径的时候是按 一定算法规律有意识地寻找最短路径,而不是盲目的。例如在 TSP问题中,可以预先知道当前城市到下一个目的地的距离。 人工蚁群 VS 自然蚁群
prey food
an obstacle is laid in the path
choosing path
the shortest path
蚁群聚类算法分析

聚类 分 析是 数据 挖 掘领 域 中的一 个 重要 分支 ,是 人们 认 识 和探 索 事物之 间 内在联 系 的有效 手 段 ,它既 可 以用 作独 立 的数据 挖 掘工 具 ,来发现 数据 库 中数据 分 布 的一些深 入 信息 ,也可 以作 为 其他 数据 挖掘 算法 的预 处理 步骤 。所 谓聚 类 (l se ig cu trn )就 是 将数 据对 象 分组成 为 多个类 或簇 ( ls e ) cu tr ,在 同一个 簇 中的
计算机光盘软件与应用
21 年第 1 期 01 3
C m u e DS f w r n p l c to s o p trC o t a ea dA p ia i n 软件设计开发
蚁群聚类算法分析
金 微
( 苏技 术 师 范学 院计 算机 工程 学 院 ,江苏 常州 230 ) 江 100
似 。 不同簇 中的对象彼 此相异 。将一 组物 理或抽 象对象分 组为类 这 种 正反馈 机制 ,蚂 蚁最 终可 以发现 最 短路 径 。 而 基 于上 述蚂 蚁 觅食 原理和 求解 TP问题 的基本 蚁群 算法 ,介 S 似对象 组成 的多个 簇 的过程被称 为聚类 。 它根据数 据的 内在特 性将 数据对 象划分 到不 同组 ( 或簇 )中 。距离 是经常采 用的度量 方式 。 绍 一种 蚁群 聚类 算法 ,用 于解 决聚类 问题 其 分述 如下 。
蚂蚁 在 寻找 食物源 时 ,能在 其走 过 的路 上释放 一种 特 殊 的分
对象 之间具 有较 高 的相 似度 ,而 不 同簇 中的对象 差别 较大 。传 统 泌 物信 息素 ,随 着时 间的 推移 该物质 会逐 渐 挥发 ,蚂 蚁选 择 该路 的聚类 算法 主 要分 为 四类 : 分方 法 ,层 次方法 基于 密度 方法 径 的概 率与 当时 这条 路径 上信 息素 的强度 成 正 比当一 条路 径 上通 划
蚁群算法理论、应用及其与其它算法的混合

基本内容
蚁群算法是一种基于自然界中蚂蚁觅食行为的启发式优化算法,被广泛应用 于解决各种优化问题。该算法具有鲁棒性、并行性和自适应性等优点,但同时也 存在一些局限性,如易陷入局部最优解等问题。本次演示将详细介绍蚁群算法的 基本理论、应用场景以及与其它算法的混合使用。
蚁群算法的实现包括两个关键步骤:构造解和更新信息素。在构造解的过程 中,每只蚂蚁根据自己的概率选择下一个节点,这个概率与当前节点和候选节点 的信息素以及距离有关。在更新信息素的过程中,蚂蚁会在构造解的过程中更新 路径上的信息素,以便后续的蚂蚁能够更好地找到最优解。
蚁群算法在许多领域都得到了广泛的应用。在机器学习领域,蚁群算法被用 来提高模型的性能和效果。例如,在推荐系统中,蚁群算法被用来优化用户和物 品之间的匹配,从而提高推荐准确率;在图像处理中,蚁群算法被用来进行特征 选择和图像分割,从而提高图像处理的效果。此外,蚁群算法在数据挖掘、运筹 学等领域也有着广泛的应用。
结论本次演示介绍了蚁群优化算法的理论研究及其应用。通过分析蚁群优化 算法的组成、行为和优化原理,以及其在不同领域的应用案例,本次演示展示了 蚁群优化算法在求解组合优化、路径规划、社会优化和生物信息学等领域问题的 优势和潜力。本次演示展望了蚁群优化算法未来的发展方向和可能挑战,强调了 其理论研究和应用价值。
总之,蚁群算法是一种具有广泛应用价值的优化算法,它通过模拟蚂蚁的觅 食行为来实现问题的优化。未来可以通过进一步研究蚁群算法的原理和应用,以 及克服其不足之处,来提高蚁群算法的性能和扩展其应用领域。
基本内容
理论基础蚁群优化算法由蚁群系统、行为和优化原理三个核心要素组成。蚁 群系统指的是一群相互协作的蚂蚁共同构成的社会组织;行为则是指蚂蚁在寻找 食物过程中表现出的行为模式;优化原理主要是指蚂蚁通过信息素引导和其他蚂 蚁的协同作用,以最短路径找到食物来源。
《基于蚁群算法的工作流任务分配机制的设计与实现》范文

《基于蚁群算法的工作流任务分配机制的设计与实现》篇一一、引言随着信息化社会的快速发展,工作流任务分配问题在各类复杂系统中扮演着重要的角色。
面对大量的任务和有限的资源,如何有效地进行任务分配成为了提升系统效率和整体性能的关键。
近年来,蚁群算法作为一种模拟自然界中蚂蚁觅食行为的智能优化算法,已经在诸多领域取得了显著的成果。
本文将详细阐述基于蚁群算法的工作流任务分配机制的设计与实现过程。
二、问题描述工作流任务分配是一个典型的组合优化问题。
在复杂的系统中,任务数量庞大,且每个任务具有不同的特性和需求。
同时,系统中的资源有限,如何将任务合理地分配给资源,使得整个系统的效率达到最优,是一个亟待解决的问题。
蚁群算法作为一种模拟自然界中蚂蚁觅食行为的智能优化算法,具有较好的寻优能力和鲁棒性,因此适用于解决工作流任务分配问题。
三、蚁群算法设计1. 算法原理蚁群算法是一种模拟蚂蚁觅食过程中信息素传递和更新的寻优算法。
在任务分配问题中,每个任务可以看作是一个食物源,而资源则可以看作是蚂蚁。
算法通过模拟蚂蚁在寻找食物过程中释放信息素的过程,实现了任务的自动分配和优化。
2. 算法实现(1)初始化阶段:设置算法的参数,如信息素初始值、挥发率、迭代次数等。
同时,将待分配的任务和资源进行初始化。
(2)信息素释放阶段:根据任务的特性和需求,以及资源的可用性,计算每个任务对资源的吸引力,并释放相应量的信息素。
(3)信息素传递阶段:模拟蚂蚁根据信息素的指引进行任务分配的过程。
每个资源根据当前的信息素分布和自身的状态,选择合适的任务进行执行。
(4)信息素更新阶段:根据任务的执行情况和系统的反馈信息,更新信息素的分布。
同时,考虑信息素的挥发和衰减,以保证算法的鲁棒性。
(5)迭代优化阶段:重复上述过程,直到达到预设的迭代次数或满足某种终止条件。
通过多次迭代,算法可以找到较为优化的任务分配方案。
四、工作流任务分配机制设计基于蚁群算法的工作流任务分配机制主要包括以下几个部分:1. 任务建模:将待分配的任务进行建模,包括任务的特性和需求等信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
34
2.1.3 蚁群优化算法研究背景 1/3
群智能理论研究领域有两种主要的算法:蚁 群算法(Ant Colony Optimization, ACO)和微粒 群算法(Particle Swarm Optimization, PSO)。 前者是对蚂蚁群落食物采集过程的模拟,已成 功应用于许多离散优化问题。微粒群算法也是 起源于对简单社会系统的模拟,最初是模拟鸟 群觅食的过程,但后来发现它是一种很好的优 化工具。
33
2.1.2 蚁群优化算法应用领域
这种方法能够被用于解决大多数优化问题或 者能够转化为优化求解的问题。现在其应用领 域已扩展到多目标优化、数据分类、数据聚类、 模式识别、电信QoS管理、生物系统建模、流程 规划、信号处理、机器人控制、决策支持以及 仿真和系统辩识等方面,群智能理论和方法为 解决这类应用问题提供了新的途径。
35
2.1.3 蚁群优化算法研究背景 2/3
与大多数基于梯度的应用优化算法不同,群智能依靠的是 概率搜索算法。虽然概率搜索算法通常要采用较多的评价 函数,但是与梯度方法及传统的演化算法相比,其优点还 是显著的 ,主要表现在以下几个方面: 1 无集中控制约束,不会因个别个体的故障影响整个问题 的求解,确保了系统具备更强的鲁棒性 2 以非直接的信息交流方式确保了系统的扩展性 3 并行分布式算法模型,可充分利用多处理器 4 对问题定义的连续性无特殊要求 5 算法实现简单
36
2.1.3 蚁群优化算法研究背景 3/3
群智能方法易于实现,算法中仅涉及各种基本的数学 操作,其数据处理过程对CPU和内存的要求也不高。而 且,这种方法只需目标函数的输出值,而无需其梯度 信息。已完成的群智能理论和应用方法研究证明群智 能方法是一种能够有效解决大多数全局优化问题的新 方法。更为重要是,群智能潜在的并行性和分布式特 点为处理大量的以数据库形式存在的数据提供了技术 保证。无论是从理论研究还是应用研究的角度分析, 群智能理论及其应用研究都是具有重要学术意义和现 实价值的。
38
2.1.4蚁群优化算法研究现状 2/7
最初提出的AS有三种版本:Ant-density、Ant-quantity和Ant-cycle。 在Ant-density和Ant-quantity中蚂蚁在两个位置节点间每移动一次后即 更新信息素,而在Ant-cycle中当所有的蚂蚁都完成了自己的行程后才对 信息素进行更新,而且每个蚂蚁所释放的信息素被表达为反映相应行程 质量的函数。通过与其它各种通用的启发式算法相比,在不大于75城市 的TSP中,这三种基本算法的求解能力还是比较理想的,但是当问题规 模扩展时,AS的解题能力大幅度下降。 因此,其后的ACO研究工作主要都集中于AS性能的改进方面。较早 的一种改进方法是精英策略(Elitist Strategy),其思想是在算法开始后即 对所有已发现的最好路径给予额外的增强,并将随后与之对应的行程记 为Tgb(全局最优行程),当进行信息素更新时,对这些行程予以加权, 同时将经过这些行程的蚂蚁记为“精英”,从而增大较好行程的选择机 会。这种改进型算法能够以更快的速度获得更好的解。但是若选择的精 英过多则算法会由于较早的收敛于局部次优解而导致搜索的过早停滞。
2 蚁群优化算法
1.
2.
3.
蚁群优化算法 概述 蚁群优化算法 概念 算法模型和收 敛性分析
4.
5. 6.
算法实现的技术问 题 应用 参考资料
31
2.1 蚁群优化算法概述
2.1.1 2.1.2 2.1.3 2.1.4 2.1.5
起源 应用领域 研究背景 研究现状 应用现状
32
2.1.1 蚁群优化算法起源
20世纪50年代中期创立了仿生学,人们从生物进化的机理中 受到启发。提出了许多用以解决复杂优化问题的新方法,如进 化规划、进化策略、遗传算法等,这些算法成功地解决了一些 实际问题。 20世纪90年代意大利学者M.Dorigo,V.Maniezzo, A.Colorni等从生物进化的机制中受到启发,通过模拟自然界 蚂蚁搜索路径的行为,提出来一种新型的模拟进化算法—— 蚁 群算法,是群智能理论研究领域的一种主要算法。用该方法求 解TSP问题、分配问题、job-shop调度问题,取得了较好的试验 结果.虽然研究时间不长,但是现在的研究显示出,蚁群算法 在求解复杂优化问题(特别是离散优化问题)方面有一定优势, 表明它是一种有发展前景的算法.
40
2.1.4蚁群优化算法研究现状 4/7
再次,还引入了负反馈机制,每当一只蚂蚁由一 个节点移动到另一个节点时,该路径上的信息素 都按照如下公式被相应的消除一部分,从而实现 一种信息素的局部调整,以减小已选择过的路径 再次被选择的概率。
41
2.1.4蚁群优化算法研究现状 5/7
37
2.1.4 蚁群优化算法研究现状 1/7
90年代Dorigo最早提出了蚁群优化算法---蚂蚁系统 (Ant System, AS)并将其应用于解决计算机算法学 中经典的旅行商问题(TSP)。从蚂蚁系统开始,基本 的蚁群算法得到了不断的发展和完善,并在TSP以及许 多实际优化问题求解中进一步得到了验证。这些AS改 进版本的一个共同点就是增强了蚂蚁搜索过程中对最 优解的探索能力,它们之间的差异仅在于搜索控制策 略方面。而且,取得了最佳结果的ACO是通过引入局 部搜索算法实现的,这实际上是一些结合了标准局域 搜索算法的混合型概率搜索算法,有利于提高蚁群各 级系统在优化问题中的求解质量。
392.1.4蚁群优化算法来自究现状 3/7为了进一步克服AS中暴露出的问题,提出了蚁群系统(Ant Colony System, ACS)。该系统的提出是以Ant-Q算法为基础的。 Ant-Q将蚂蚁算法和一种增强型学习算法Q-learning有机的结合 了起来。ACS与AS之间存在三方面的主要差异:首先,ACS采 用了更为大胆的行为选择规则;其次,只增强属于全局最优解 的路径上的信息素。其中,0<ρ<1是信息素挥发参数, 是 从寻路开始到当前为止全局最优的路径长度。
