九年级数学上册错题集.doc

合集下载

九年级数学上册错题集

12.请写出符合以下三个条件的一个函数的解析式2129y x =-+（答案不唯一）．①过点(31)，；②当0x >时，y 随x 的增大而减小； ③当自变量的值为2时，函数值小于2．13．二次函数322--=x x y 的图象关于原点O （0, 0）对称的图象的解析式是223y x x =--+。

如图所示,已知F 是以O 为圆心,BC 为直径的半圆上任一点,A 是BF 的中点,AD ⊥BC 于点D.求证:AD=1BF. 如图,⊙O 的直径AB 的两侧有定点C 和动点P.已知BC=4,CA=3,点P 在AB 上运动,过点C 作CP 的垂线,与PB 的延长线交于点Q.(1)当点P 运动到与点C 关于AB 对称时 ,求C Q 的长. (2)当点P 运动到弧AB 的中点时,求C Q 的长.(3)当点P 运动到什么位置时,CQ 取到最大值,并求此时CQ 的长.解：（1）当点P与点C关于AB对称时，CP⊥AB，设垂足为D，∵AB为⊙O的直径，∴∠ACB=90°，∴BC=4，AC=3，∵AC•BC=AB•CD，∴CD=12 5∴PC=24 5．在Rt△ACB和Rt△PCQ中，∠ACB=∠PCQ=90°，∠CAB=∠CPQ，∴△ACB∽△PCQ，∴AC BC PC CQ=∴CQ=4 3PC=32 5（2）当点P运动到AB的中点时，过点B作BE⊥PC于点E．∵点P是AB的中点，∴∠PCB=45°，BE=CE=222 2BC=在Rt△EPB中，tan∠EPB=43 BE PE=∴PE=332 42 BE=∴PC=PE+CE=722．∴CQ=4142 33 BE=（3）点P在AB上运动时，恒有CQ=43 PC所以PC最大时，CQ取到最大值，当PC过圆心O，即PC取最大值5时，CQ最大值为20 323.如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax2+bx+c经过O、A、C三点．（1）求该抛物线的函数解析式；（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．解：（1）∵抛物线y=ax2+bx+c经过点O、A、C，可得c=0，∴，解得a=，b=，∴抛物线解析式为y=x2+x．（2）设点P的横坐标为t，∵PN∥CD，∴△OPN∽△OCD，可得PN=∴P（t，），∵点M在抛物线上，∴M（t，t2+t）．如解答图1，过M点作MG⊥AB于G，过P点作PH⊥AB于H，AG=y A﹣y M=2﹣（t2+t）=t2﹣t+2，BH=PN=．当AG=BH时，四边形ABPM为等腰梯形，∴t2﹣t+2=，化简得3t2﹣8t+4=0，解得t1=2（不合题意，舍去），t2=，∴点P的坐标为（，）∴存在点P（，），使得四边形ABPM为等腰梯形．（3）如解答图2，△AOB沿AC方向平移至△A′O′B′，A′B′交x轴于T，交OC于Q，A′O′交x轴于K，交OC于R．求得过A、C的直线为y AC=﹣x+3，可设点A′的横坐标为a，则点A′（a，﹣a+3），易知△OQT∽△OCD，可得QT=，∴点Q的坐标为（a，）．解法一：设AB与OC相交于点J，∵△ARQ∽△AOJ，相似三角形对应高的比等于相似比，∴=∴HT===2﹣a，KT=A′T=（3﹣a），A′Q=yA′﹣yQ=（﹣a+3）﹣=3﹣a．S四边形RKTQ=S△A′KT﹣S△A′RQ=KT•A′T﹣A′Q•HT=••（3﹣a）﹣•（3﹣a）•（﹣a+2）=a2+a﹣=（a﹣）2+由于＜0，∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．解法二：过点R作RH⊥x轴于H，则由△ORH∽△OCD，得①由△RKH∽△A′O′B′，得②由①，②得KH=OH，OK=OH，KT=OT﹣OK=a﹣OH③由△A′KT∽△A′O′B′，得，则KT=④由③，④得=a﹣OH，即OH=2a﹣2，RH=a﹣1，所以点R的坐标为R（2a﹣2，a﹣1）S四边形RKTQ=S△QOT﹣S△ROK=•OT•QT﹣•OK•RH=a•a﹣（1+a﹣）•（a﹣1）=a2+a﹣=（a﹣）2+由于＜0，∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．解法三：∵AB=2，OB=1，∴tan∠O′A′B′=tan∠OAB=，∴KT=A′T•tan∠O′A′B′=（﹣a+3）•=a+，∴OK=OT﹣KT=a﹣（a+）=a﹣，过点R作RH⊥x轴于H，∵tan∠OAB=tan∠RKH==2，∴RH=2KH又∵tan∠OAB=tan∠ROH===，∴2RH=OK+KH=a﹣+RH，∴RH=a﹣1，OH=2（a﹣1），∴点R坐标R（2a﹣2，a﹣1）S四边形RKTQ=S△A′KT﹣S△A′RQ=•KT•A′T﹣A′Q•（xQ﹣xR）=••（3﹣a）﹣•（3﹣a）•（﹣a+2）=a2+a﹣=（a﹣）2+由于＜0，∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．。

九年级上册数学错题集70道

九年级上册数学错题集70道一、一元二次方程部分（1 10题）1. 若关于公式的一元二次方程公式的常数项为公式，求公式的值。

解析：因为方程是一元二次方程，所以二次项系数不为公式，即公式，解得公式。

又因为常数项公式，分解因式得公式，解得公式或公式。

综合前面公式的条件，所以公式。

2. 用配方法解方程公式。

解析：在方程两边加上一次项系数一半的平方，即公式。

变形为公式，移项得到公式。

然后开平方得公式，解得公式。

3. 解方程公式。

解析：对于方程公式，分解因式得公式。

则公式或者公式，解得公式或者公式。

4. 关于公式的方程公式的根的情况是（）A. 有两个不相等的同号实数根B. 有两个不相等的异号实数根C. 有两个相等的实数根D. 没有实数根解析：对于一元二次方程公式，判别式公式，在方程公式中，公式，公式，公式。

则公式。

因为公式，所以公式，方程有两个不相等的实数根。

设方程的两根为公式，公式，根据韦达定理公式，两根异号，所以方程有两个不相等的异号实数根，答案为B。

5. 若公式是方程公式的一个根，则公式____。

解析：把公式代入方程公式，得到公式，即公式。

6. 已知一元二次方程公式的两根是公式，公式，则公式____。

解析：由韦达定理可知，在方程公式中，公式，公式。

公式。

把公式，公式代入得公式。

7. 解方程公式。

解析：移项得公式。

提取公因式公式得公式，即公式。

解得公式或公式。

8. 已知关于公式的方程公式有两个不相等的实数根。

(1)求实数公式的取值范围；解析：对于一元二次方程公式，判别式公式，在方程公式中，公式，公式，公式。

公式展开得公式合并同类项得公式。

因为方程有两个不相等的实数根，所以公式，即公式，解得公式。

(2)设方程的两个实数根分别为公式，公式，是否存在这样的实数公式，使得公式？若存在，求出这样的公式值；若不存在，请说明理由。

解析：由韦达定理得公式，公式，所以公式，公式同号。

当公式，公式时，公式。

公式。

把公式，公式代入得公式。

九年级上册数学期末精选试卷易错题(Word版含答案)

九年级上册数学期末精选试卷易错题（Word 版含答案）一、初三数学一元二次方程易错题压轴题（难）1．如图，在平面直角坐标系中，()4,0A -，()0,4B ，四边形ABCO 为平行四边形，4,03D ⎛⎫- ⎪⎝⎭在x 轴上一定点，P 为x 轴上一动点，且点P 从原点O 出发，沿着x 轴正半轴方向以每秒43个单位长度运动，已知P 点运动时间为t ． (1)点C 坐标为________，P 点坐标为________；(直接写出结果，可用t 表示) (2)当t 为何值时，BDP ∆为等腰三角形；(3)P 点在运动过程中，是否存在t ，使得ABD OBP ∠=∠，若存在，请求出t 的值，若不存在，请说明理由！【答案】（1）（4，4），（43t ，0）；（2）1101-，4；（3）存在，3109t【解析】【分析】（1）利用平行四边形的性质和根据P 点的运动速度，利用路程公式求解即可；（2）分三种情况：①当BD BP 时，②当BD DP =时，③当BP DP =时，分别讨论求解，即可得出结果；（3）过D 点作DF BP 交BP 于点F ，设OP x =，则可得224BPx ，43DPx ，453DF,利用1122BDPS DP BO BP DF ，即可求出OP 的长，利用路程公式可求得t 的值。

【详解】解：（1）∵()4,0-A ，()0,4B ，四边形ABCO 为平行四边形， ∴点C 坐标为（4，4），又∵P 为x 轴上一动点，点P 从原点O 出发，沿着x 轴正半轴方向以每秒43个单位长度运动，P 点运动时间为t ，∴P 点坐标为（43t ，0），（2）∵B ，D 的坐标分别为：()0,4B ，4,03D ⎛⎫- ⎪⎝⎭， ∴4OB =,43OD =, 由勾股定理有：22224441033DB OBOD, 当BDP ∆为等腰三角形时， ①如图所示，当BDBP 时，OD OP =,∴P 点坐标为（43，0）, ∴1t =②如图所示，当BD DP =时，∵4103DB ，OP DP OD∴44410101333OP ,∴101t③如图所示，当BP DP =时，设P 点坐标为：（x ，0）则有：2224BP x，2243DPx， ∴222443xx，解之得：163x = ∴P 点坐标为（163，0）, ∴4t =综上所述，当t 为1，101-，4时，BDP ∆为等腰三角形；（3）答：存在t ，使得ABD OBP ∠=∠。

人教版九年级上册数学期中试卷易错题(Word版含答案)

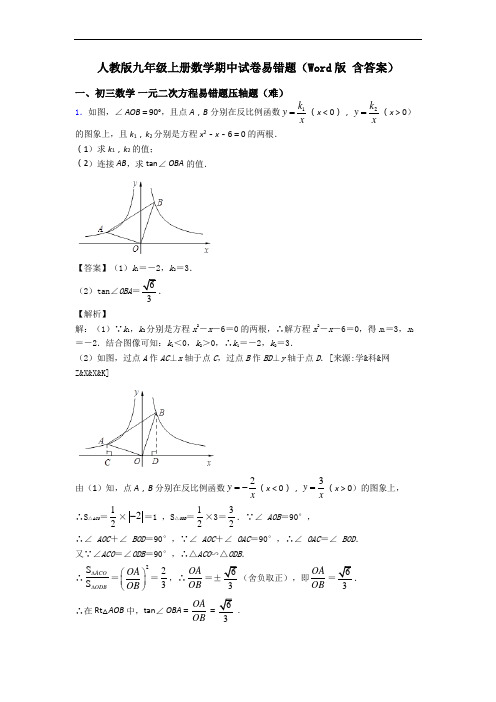
人教版九年级上册数学期中试卷易错题（Word 版含答案）一、初三数学一元二次方程易错题压轴题（难） 1．如图，∠ AOB ＝90°，且点A ，B 分别在反比例函数1k y x =（x ＜0），2k y x=（x ＞0）的图象上，且k 1，k 2分别是方程x 2－x －6＝0的两根．（1）求k 1，k 2的值；（2）连接AB ，求tan ∠ OBA 的值．【答案】（1）k 1＝－2，k 2＝3．（2）tan∠OBA ＝6．【解析】解：（1）∵k 1，k 2分别是方程x 2－x －6＝0的两根，∴解方程x 2－x －6＝0，得x 1＝3，x 2＝－2．结合图像可知：k 1＜0，k 2＞0，∴k 1＝－2，k 2＝3．（2）如图，过点A 作AC ⊥x 轴于点C ，过点B 作BD ⊥y 轴于点D ．[来源:学&科&网Z&X&X&K]由（1）知，点A ，B 分别在反比例函数2y x =-（x ＜0），3y x =（x ＞0）的图象上， ∴S △ACO ＝12×2-＝1 ，S △ODB ＝12×3＝32．∵∠ AOB ＝90°， ∴∠ AOC ＋∠ BOD ＝90°，∵∠ AOC ＋∠ OAC ＝90°，∴∠ OAC ＝∠ BOD ．又∵∠ACO ＝∠ODB ＝90°，∴△ACO ∽△ODB ．∴S S ACO ODB ∆∆＝2OA OB ⎛⎫ ⎪⎝⎭＝23，∴OA OB ＝±63（舍负取正），即OA OB ＝63． ∴在Rt △AOB 中，tan ∠ OBA ＝OA OB 6．2．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.3．计算题（1）先化简，再求值：21xx-÷（1+211x-），其中x=2017．（2）已知方程x2﹣2x+m﹣3=0有两个相等的实数根，求m的值．【答案】（1）2018；（2）m=4【解析】分析：（1）根据分式的运算法则和运算顺序，先算括号里面的，再算除法，注意因式分解的作用；（2）根据一元二次方程的根的判别式求解即可.详解：（1）21xx-÷（1+211x-）=2221111x x x x -+÷-- =()()22111x x x x x+-⋅- =x+1，当x=2017时，原式=2017+1=2018（2）解：∵方程x 2﹣2x+m ﹣3=0有两个相等的实数根，∴△=（﹣2）2﹣4×1×（m ﹣3）=0，解得，m=4点睛：此题主要考查了分式的混合运算和一元二次方程的根的判别式，关键是熟记分式方程的运算顺序和法则，注意通分约分的作用.4．如图，平面直角坐标系中，直线l 分别交x 轴、y 轴于A 、B 两点（OA ＜OB ）且OA 、OB 的长分别是一元二次方程()2x 31x 30-++=的两个根，点C 在x 轴负半轴上，且AB ：AC=1：2（1）求A 、C 两点的坐标；（2）若点M 从C 点出发，以每秒1个单位的速度沿射线CB 运动，连接AM ，设△ABM 的面积为S ，点M 的运动时间为t ，写出S 关于t 的函数关系式，并写出自变量的取值范围；（3）点P 是y 轴上的点，在坐标平面内是否存在点Q ，使以 A 、B 、P 、Q 为顶点的四边形是菱形？若存在，请直接写出Q 点的坐标；若不存在，请说明理由．【答案】解：（1）解)2x 31x 30-+=得（x 3x ﹣1）=0，解得x 13，x 2=1。

九年级数学上册一元二次方程易错题(Word版含答案)

九年级数学上册一元二次方程易错题（Word 版含答案）一、初三数学一元二次方程易错题压轴题（难）1．如图，在矩形ABCD 中，6AB cm =，8AD cm =，点P 从点A 出发沿AD 向点D 匀速运动，速度是1/cm s ，过点P 作PE AC ∥交DC 于点E ，同时，点Q 从点C 出发沿CB 方向，在射线CB 上匀速运动，速度是2/cm s ，连接PQ 、QE ，PQ 与AC 交与点F ，设运动时间为()(08)<<t s t ．（1）当t 为何值时，四边形PFCE 是平行四边形；（2）设PQE 的面积为2()s cm ，求s 与t 的函数关系式；（3）是否存在某一时刻t ，使得PQE 的面积为矩形ABCD 面积的932；（4）是否存在某一时刻t ，使得点E 在线段PQ 的垂直平分线上．【答案】（1）83t =；（2）S =299(08)8t t t -+<<；（3）当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932；（4）当573256=t 时，点E 在线段PQ 的垂直平分线上【解析】【分析】（1）由四边形PFCE 是平行四边形，可得,PF CE ∥由PD QC 得四边形CDPQ 为平行四边形，即PD CQ =，列式82t t -=，计算可解. （2）由PE AC ∥，得=DP DE DA DC ，代入时间t ，得886-=t DE 解得364=-DE t ，34CE t =再通过S S =梯形CDPQ PDE CEQ S S --△△构建联系，可列函数式299(08)8S t t t =-+<<.（3）由PQE 的面积为矩形ABCD 面积的932得299986832S t t =-+=⨯⨯，可解当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932．（4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ，得22=EQ PE ，由Rt CEQ 与△Rt PDE 可得，222+=CE CQ EQ ，222PD DE PE +=，即2222+=+CE CQ PD DE ，代入364=-DE t ，34CE t =，2CQ t =，8PD t =-可得222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t ，计算验证可解.【详解】（1）当四边形PFCE 是平行四边形时，∥PF CE ，又∵PD QC ，∴四边形CDPQ 为平行四边形， ∴PD CQ =，即82t t -=， ∴83t =（2）∵PE AC ∥，∴=DP DEDA DC ，即886-=t DE， ∴364=-DE t ， ∴336644=-+=CE t t ，∴21133(8)66242248⎛⎫=⋅=--=-+ ⎪⎝⎭△PDE S PD DE t t t t ， 2113322244=⋅=⨯⨯=△CEQ S CE CQ t t t ，S 梯形11()(28)632422=+⋅=+-⋅=+CDPQ QC PD CD t t t ，∴S S =梯形299(08)8--=-+<<△△CDPQ PDE CEQ S S t t t（3）由题意，299986832-+=⨯⨯t t 解得12t =，26t =所以当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932．（4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ， ∴22=EQ PE ，在Rt CEQ 中，222+=CE CQ EQ ，在△Rt PDE 中，222PD DE PE +=， ∴2222+=+CE CQ PD DE ，即222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t 解得1573256-=t ，2573256+=-t （舍）所以当57325-=t 时，点E 在线段PQ 的垂直平分线上．【点睛】本题考查的是一次函数与几何图形的实际应用，勾股定理，平行线的性质，解一元二次方程，需要注意的是在解一元二次方程的实际应用中经常会涉及到解的验证，不可忽略.2．如图，在长方形ABCD 中，边AB 、BC 的长（AB ＜BC ）是方程x 2-7x +12=0的两个根．点P 从点A 出发，以每秒1个单位的速度沿△ABC 边 A →B →C →A 的方向运动，运动时间为t （秒）．（1）求AB 与BC 的长；（2）当点P 运动到边BC 上时，试求出使AP 长为10时运动时间t 的值；（3）当点P 运动到边AC 上时，是否存在点P ，使△CDP 是等腰三角形？若存在，请求出运动时间t 的值；若不存在，请说明理由．【答案】(1) AB ＝3，BC ＝4;(2) t ＝4;(3) t 为10秒或9.5秒或535秒时，△CDP 是等腰三角形. 【解析】试题分析：（1）解一元二次方程即可求得边长；（2）结合图形，利用勾股定理求解即可；（3）根据题意，分为：PC ＝PD ，PD ＝PC ，PD ＝CD ，三种情况分别可求解. 试题解析：(1)∵x 2－7x ＋12＝(x －3)(x －4)＝0 ∴1x ＝3或2x ＝4 . 则AB ＝3，BC ＝4(2)由题意得()223t-310?+=（） ∴14t =，22t =(舍去) 则t ＝4时，AP ＝10.(3)存在点P ，使△CDP 是等腰三角形. ①当PC ＝PD ＝3时， t ＝3431++ ＝10(秒). ②当PD ＝PC(即P 为对角线AC 中点)时，AB ＝3，BC ＝4. ∴AC＝2234+ ＝5，CP 1＝ 12AC ＝2.5 ∴t＝34 2.51++ ＝9.5(秒) ③当PD ＝CD ＝3时，作DQ⊥AC 于Q. 1341221552DQ ⨯⨯==⨯，22129355PQ ⎛⎫=-= ⎪⎝⎭ ∴PC＝2PQ ＝185∴183453515t ++==(秒) 可知当t 为10秒或9.5秒或535秒时，△CDP 是等腰三角形.3．已知:在平面直角坐标系xoy 中,直线k y x b =+分别交x 、y 轴于点A 、B 两点,OA=5,∠OAB=60°.(1)如图1,求直线AB 的解析式；(2)如图2,点P 为直线AB 上一点，连接OP ,点D 在OA 延长线上，分别过点P 、D 作OA 、OP 的平行线,两平行线交于点C ，连接AC,设AD=m,△ABC 的面积为S,求S 与m 的函数关系式; (3)如图3,在(2)的条件下,在PA 上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE 的周长等于22，求S 的值.【答案】(1)直线解析式为353y x =-+53253+；(3)203S =.【解析】【分析】(1)先求出点B 坐标，设AB 解析式为y kx b =+，把点A(5，0)，B(0，分别代入，利用待定系数法进行求解即可；(2)由题意可得四边形ODCP 是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中利用勾股定理可求得)5m +，再由S=12AB •CH 代入相关数据进行整理即可得； (3) 先求得∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，证明△ADK 是等边三角形，继而证明△PEC ≌△DKO ，通过推导可得到OP=OK=CE=CD ，再证明△CDE 是等边三角形，可得CE=CD=DE ，连接OE ，证明△OPE ≌△EDA ，继而可得△OAE 是等边三角形，得到OA=AE=5 ，根据四边形ADCE 的周长等于22，可得ED=172m -，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=，可得关于m 的方程，解方程求得m 的值后即可求得答案.【详解】(1)在Rt △ABO 中OA=5，∠OAB=60°， ∴∠OBA=30°，AB=10 ，由勾股定理可得OB=， ∴B(0，，设AB 解析式为y kx b =+，把点A(5，0)，B(0，)分别代入，得05k bb=+⎧⎪⎨=⎪⎩，∴k b ⎧=⎪⎨=⎪⎩，∴直线解析式为y =+ (2)∵CP//OD ，OP//CD ，∴四边形ODCP 是平行四边形，∠OAB=∠APC=60°， ∴PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中 PH=52m +，由勾股定理得)5m +， ∴S=12AB •CH=110(5)2222m m ⨯⨯+=+；(3) ∵∠ECD=∠OAB=60°，∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°， ∴∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ， ∵∠DAK=60°， ∴△ADK 是等边三角形， ∴AD=DK=PE ，∠ODK=∠APC ， ∵PC=OD ， ∴△PEC ≌△DKO ，∴OK=CE ，∠OKD=∠PEC=∠OPC=60°+α， ∠AKD= ∠APC=60° ， ∴∠OPK= ∠OKB ， ∴OP=OK=CE=CD ，又∵∠ECD=60°， ∴△CDE 是等边三角形， ∴CE=CD=DE ，连接OE ，∵ ∠ADE=∠APO ，DE=CD=OP ， ∴△OPE ≌△EDA ， ∴AE=OE ， ∠OAE=60°， ∴△OAE 是等边三角形， ∴OA=AE=5 ，∵四边形ADCE 的周长等于22， ∴AD+2DE=17， ∴ED=172m-，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=，即22253517()()()222m m -++=，解得13m =，221m =-(舍去)， ∴S=15325322+=203.【点睛】本题考查的四边形综合题，涉及了待定系数法，平行四边形的判定与性质，勾股定理，全等三角形的判定与性质，等边三角形的判定与性质，解一元二次方程等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.4．如图，在平面直角坐标系中，O 为原点，点A （0，8），点B （m ，0），且m ＞0.把△AOB 绕点A 逆时针旋转90°，得△ACD ，点O ，B 旋转后的对应点为C ，D ，（1）点C 的坐标为；（2）①设△BCD 的面积为S ，用含m 的式子表示S ，并写出m 的取值范围； ②当S=6时，求点B 的坐标（直接写出结果即可）.【答案】（1）C （8，8）；（2）①S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②点B 的坐标为（7，0）或（2，0）或（6，0）. 【解析】【分析】（1）由旋转的性质得出AC ＝AO ＝8，∠OAC ＝90°，得出C （8，8）即可；（2）①由旋转的性质得出DC ＝OB ＝m ，∠ACD ＝∠AOB ＝90°，∠OAC ＝90°，得出∠ACE ＝90°，证出四边形OACE 是矩形，得出DE ⊥x 轴，OE ＝AC ＝8，分三种情况：a、当点B在线段OE的延长线上时，得出BE＝OB−OE＝m−8，由三角形的面积公式得出S ＝0.5m2−4m（m＞8）即可；b、当点B在线段OE上（点B不与O，E重合）时，BE＝OE−OB＝8−m，由三角形的面积公式得出S＝−0.5m2＋4m（0＜m＜8）即可；c、当点B与E重合时，即m＝8，△BCD不存在；②当S＝6，m＞8时，得出0.5m2−4m＝6，解方程求出m即可；当S＝6，0＜m＜8时，得出−0.5m2＋4m＝6，解方程求出m即可．【详解】（1）∵点A（0，8），∴AO=8，∵△AOB绕点A逆时针旋转90°得△ACD，∴AC=AO=8，∠OAC=90°，∴C（8，8），故答案为（8，8）；（2）①延长DC交x轴于点E，∵点B（m，0），∴OB=m，∵△AOB绕点A逆时针旋转90°得△ACD，∴DC=OB=m，∠ACD=∠AOB=90°，∠OAC=90°，∴∠ACE=90°，∴四边形OACE是矩形，∴DE⊥x轴，OE=AC=8，分三种情况：a、当点B在线段OE的延长线上时，如图1所示：则BE=OB﹣OE=m﹣8，∴S=0.5DC•BE=0.5m（m﹣8），即S=0.5m2﹣4m（m＞8）；b、当点B在线段OE上（点B不与O，E重合）时，如图2所示：则BE=OE﹣OB=8﹣m，∴S=0.5DC•BE=0.5m（8﹣m），即S=﹣0.5m2+4m（0＜m＜8）；c、当点B与E重合时，即m=8，△BCD不存在；综上所述，S=0.5m2﹣4m（m＞8），或S=﹣0.5m2+4m（0＜m＜8）；②当S=6，m＞8时，0.5m2﹣4m=6，解得：m=4±27（负值舍去），∴m=4+27；当S=6，0＜m＜8时，﹣0.5m2+4m=6，解得：m=2或m=6，∴点B的坐标为（4+27，0）或（2，0）或（6，0）.【点睛】本题是三角形综合题目，考查了坐标与图形性质、旋转的性质、矩形的判定与性质、三角形面积公式、一元二次方程的解法等知识；本题综合性强，有一定难度．5．已知二次函数y＝9x2﹣6ax+a2﹣b，当b＝﹣3时，二次函数的图象经过点（﹣1，4）①求a的值；②求当a ≤x ≤b 时，一次函数y ＝ax +b 的最大值及最小值；【答案】①a 的值是﹣2或﹣4；②最大值＝13，最小值＝9 【解析】【分析】①根据题意解一元二次方程即可得到a 的值；②根据a ≤x ≤b ，b ＝﹣3求得a=-4，由此得到一次函数为y ＝﹣4x ﹣3，根据函数的性质当x ＝﹣4时，函数取得最大值，x ＝﹣3时，函数取得最小值，分别计算即可.【详解】解：①∵y ＝9x 2﹣6ax +a 2﹣b ，当b ＝﹣3时，二次函数的图象经过点（﹣1，4） ∴4＝9×（﹣1）2﹣6a ×（﹣1）+a 2+3，解得，a 1＝﹣2，a 2＝﹣4， ∴a 的值是﹣2或﹣4； ②∵a ≤x ≤b ，b ＝﹣3 ∴a ＝﹣2舍去， ∴a ＝﹣4， ∴﹣4≤x ≤﹣3， ∴一次函数y ＝﹣4x ﹣3，∵一次函数y ＝﹣4x ﹣3为单调递减函数，∴当x ＝﹣4时，函数取得最大值，y ＝﹣4×（﹣4）﹣3＝13 x ＝﹣3时，函数取得最小值，y ＝﹣4×（﹣3）﹣3＝9. 【点睛】此题考查解一元二次方程，一次函数的性质，（2）是难点，正确理解a 、b 的关系得到函数解析式是解题的关键.6．某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其他两位成员交流的情况．小张：“该商品的进价为 24元/件．”成员甲：“当定价为 40元/件时，每天可售出 480件．”成员乙：“若单价每涨 1元，则每天少售出 20件；若单价每降 1元，则每天多售出 40件．” 根据他们的对话，请你求出要使该商品每天获利 7680元，应该怎样合理定价？【答案】要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件【解析】【分析】设每件商品定价为x 元，则在每件40元的基础上涨价时每天的销售量是[]48020(40)x --件，每件商品的利润是(24)x -元，在每件40元的基础上降价时每天的销量是[]48040(40)x +-件，每件的利润是(24)x -元，从而可以得到答案．【详解】解：设每件商品定价为x 元．①当40x ≥时，[](24)48020(40)7680x x ---= ，解得：1240,48;x x ==②当40x <时，[](24)48040(40)7680x x -+-=，解得：1236,40x x ==（舍去），.答：要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件．【点睛】本题考查的是一元二次方程中的升降价对销售量产生影响方面的应用，用含有未知数的代数式表示销售量是这一类题的关键．7．阅读下列材料计算：（1﹣﹣）×（+）﹣（1﹣﹣）（+），令+＝t ，则：原式＝（1﹣t ）（t +）﹣（1﹣t ﹣）t ＝t +﹣t 2﹣+t 2＝在上面的问题中，用一个字母代表式子中的某一部分，能达到简化计算的目的，这种思想方法叫做“换元法”，请用“换元法”解决下列问题：（1）计算：（1﹣﹣）×（+）﹣（1﹣﹣）×（+）（2）因式分解：（a 2﹣5a +3）（a 2﹣5a +7）+4 （3）解方程：（x 2+4x +1）（x 2+4x +3）＝3 【答案】（1）；（2）（a 2﹣5a +5）2；（3）x 1＝0，x 2＝﹣4，x 3＝x 4＝﹣2【解析】【分析】（1）仿照材料内容，令+＝t 代入原式计算．（2）观察式子找相同部分进行换元，令a 2﹣5a ＝t 代入原式进行因式分解，最后要记得把t 换为a ．（3）观察式子找相同部分进行换元，令x 2+4x ＝t 代入原方程，即得到关于t 的一元二次方程，得到t 的两个解后要代回去求出4个x 的解．【详解】（1）令+＝t ，则：原式＝（1﹣t ）（t +）﹣（1﹣t ﹣）t ＝t +﹣t 2﹣﹣t +t 2+＝（2）令a 2﹣5a ＝t ，则：原式＝（t +3）（t +7）+4＝t 2+7t +3t +21+4＝t 2+10t +25＝（t +5）2＝（a 2﹣5a +5）2 （3）令x 2+4x ＝t ，则原方程转化为：（t +1）（t +3）＝3t 2+4t +3＝3t （t +4）＝0∴t 1＝0，t 2＝﹣4 当x 2+4x ＝0时，x （x +4）＝0解得：x 1＝0，x 2＝﹣4当x 2+4x ＝﹣4时，x 2+4x +4＝0（x +2）2＝0解得：x 3＝x 4＝﹣2【点睛】本题考查用换元法进行整式的运算，因式分解，解一元二次方程．利用换元法一般可达到降次效果，从而简便运算．8．如图，已知AB 是⊙O 的弦，半径OA=2，OA 和AB 的长度是关于x 的一元二次方程x 2﹣4x+a=0的两个实数根．（1）求弦AB 的长度；（2）计算S △AOB ；（3）⊙O 上一动点P 从A 点出发，沿逆时针方向运动一周，当S △POA =S △AOB 时，求P 点所经过的弧长（不考虑点P 与点B 重合的情形）．【答案】（1）AB=2；（2）S △AOB 33）当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π．【解析】试题分析：（1）OA 和AB 的长度是一元二次方程的根，所以利用一元二次方程的根与系数的关系即可求出AB 的长度；（2）作出△AOB 的高OC ，然后求出OC 的长度即可求出面积；（3）由题意知：两三角形有公共的底边，要面积相等，即高要相等．试题解析：（1）由题意知：OA 和AB 的长度是x 2﹣4x+a=0的两个实数根，∴OA+AB=﹣41-=4，∵OA=2，∴AB=2；（2）过点C作OC⊥AB于点C，∵OA=AB=OB=2，∴△AOB是等边三角形，∴AC=12AB=1，在Rt△ACO中，由勾股定理可得：OC=3，∴S△AOB=12AB﹒OC=12×2×3=3；（3）延长AO交⊙O于点D，由于△AOB与△POA有公共边OA，当S△POA=S△AOB时，∴△AOB与△POA高相等，由（2）可知：等边△AOB的高为3，∴点P到直线OA的距离为3，这样点共有3个①过点B作BP1∥OA交⊙O于点P1，∴∠BOP1=60°，∴此时点P经过的弧长为：1202180π⨯=43π，②作点P2，使得P1与P2关于直线OA对称，∴∠P2OD=60°，∴此时点P经过的弧长为：2402180π⨯=83π，③作点P3，使得B与P3关于直线OA对称，∴∠P3OP2=60°，∴此时P经过的弧长为：3002180π⨯=103π，综上所述：当S△POA=S△AOB时，P点所经过的弧长分别是43π、83π、103π．【点睛】本题主要考查了一元二次方程与圆的综合知识．涉及等边三角形性质，圆的对称性等知识，能综合运用所学知识，选择恰当的方法进行解题是关键．9．在等腰三角形△ABC中，三边分别为a、b、c，其中ɑ＝4，若b、c是关于x的方程x2﹣（2k+1）x+4（k﹣12）＝0的两个实数根，求△ABC的周长．【答案】△ABC的周长为10．【解析】【分析】分a为腰长及底边长两种情况考虑：当a=4为腰长时，将x=4代入原方程可求出k值，将k值代入原方程可求出底边长，再利用三角形的周长公式可求出△ABC的周长；当a=4为底边长时，由根的判别式△=0可求出k值，将其代入原方程利用根与系数的关系可求出b+c的值，由b+c=a 可得出此种情况不存在．综上即可得出结论．【详解】当a ＝4为腰长时，将x ＝4代入原方程，得：()214421402k k ⎛⎫-++-= ⎪⎝⎭解得：52k =当52k =时，原方程为x 2﹣6x +8＝0，解得：x 1＝2，x 2＝4，∴此时△ABC 的周长为4+4+2＝10；当a ＝4为底长时，△＝[﹣（2k +1）]2﹣4×1×4（k ﹣12）＝（2k ﹣3）2＝0，解得：k ＝32， ∴b +c ＝2k +1＝4．∵b +c ＝4＝a ，∴此时，边长为a ，b ，c 的三条线段不能围成三角形．∴△ABC 的周长为10．【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系，分a 为腰长及底边长两种情况考虑是解题的关键．10．如图，某农家拟用已有的长为8m 的墙或墙的一部分为一边，其它三边用篱笆围成一个面积为12m 2的矩形园子．设园子中平行于墙面的篱笆长为ym （其中y ≥4），另两边的篱笆长分别为xm ．（1）求y 关于x 的函数表达式，并求x 的取值范围．（2）若仅用现有的11m 长的篱笆，且恰好用完，请你帮助设计围制方案．【答案】（1）y ＝；1.5≤x ≤3；（2）长为8m ，宽为1.5m ．【解析】【分析】（1）由矩形的面积公式可得出y 关于x 的函数表达式，结合4≤y ≤8可求出x 的取值范围；（2）由篱笆的长可得出y ＝（11﹣2x ）m ，利用矩形的面积公式结合矩形园子的面积，即可得出关于x 的一元二次方程，解之取其较小值即可得出结论．【详解】（1）∵矩形的面积为12m2，∴y＝．∵4≤y≤8，∴1.5≤x≤3．（2）∵篱笆长11m，∴y＝（11﹣2x）m．依题意，得：xy＝12，即x（11﹣2x）＝12，解得：x1＝1.5，x2＝4（舍去），∴y＝11﹣2x＝8．答：矩形园子的长为8m，宽为1.5m．【点睛】本题考查了一元二次方程的应用以及反比例函数的应用，解题的关键是：（1）利用矩形的面积公式，找出y关于x的函数表达式；（2）找准等量关系，正确列出一元二次方程．。

九年级数学上册期末复习(易错题精选、一元二次方程)2套含答案

人教版九年级数学上册期末复习01—易错题精选一、选择题（每小题3分，共24分）1.关于x 的方程22210m x x --+=（）有实数解，那么m 的取值范围是（）A .2m ≠B .3m ≤C .3m ≥D .32m m ≤且≠2.某校九年级一班共有学生50人，现在对他们的生日（可以不同年）进行统计，则正确的说法是（）A .至少有两名学生生日相同B .不可能有两名学生生日相同C .可能有两名学生生日相同，但可能性不大D .可能有两名学生生日相同，且可能性很大3.如图①是33⨯正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形ABCD 的中心旋转能重合的图案都视为同一种图案，例如图②中的四幅图就视为同一种图案，则得到的不同图案共有（）A .4种B .5种C .6种D .7种4.如图，在正方体的表面展开图中，要将a -、b -、c -填入剩下的三个空白处（彼此不同），则正方体三组相对的两个面中数字和均为零的概率为（）A .12B .13C .14D .165.有两个一元二次方程：2:0M ax bx c ++=，2:0N cx bx a ++=，其中0a c +=，下列四个结论中，错误的是（）A .如果方程M 有两个不相等的实数根，那么方程N 也有两个不相等的实数根B .如果方程M 的两根符号相同，那么方程N 的两根符号也相同C .如果5是方程M 的一个根，那么15是方程N 的一个根D .如果方程M 和方程N 有一个相同的根，那么这个根必是1x =6.如图，在ABC △中，AB AC =，D 是边BC 的中点，一个圆过点A ，交边AB 于点E ，且与BC 相切于点D ，则该圆的圆心是（）A .线段AE 的中垂线与线段AC 的中垂线的交点B .线段AB 的中垂线与线段AC 的中垂线的交点C .线段AE 的中垂线与线段BC 的中垂线的交点D .线段AB 的中垂线与线段BC 的中垂线的交点7.已知二次函数2y x bx c =++的图象过点1A m （，），3B m （，），若点12M y -（，），21N y -（，），38K y （，）也在二次函数2y x bx c =++的图象上，则下列结论正确的是（）A .123y y y ＜＜B .213y y y ＜＜C .312y y y ＜＜D .132y y y ＜＜8.已知抛物线20y ax bx c a =++（＞）过20-（，），23（，）两点，那么抛物线的对称轴（）A .只能是1x =-B .可能是y 轴C .在y 轴右侧D .在y 轴左侧二、填空题（每小题4分，共32分）1.请写出一个符合下列全部条件的函数解析式________；（1）图象不经过第三象限；（2）当1x -＜时，y 随x 的增大而减小；（3）图象经过点11-（，）.2.若抛物线2y ax c =+与x 轴交于点0A m （，），0B n （，），与y 轴交于点0C c （，），则ABC △称为“抛物三角形”.特别地，当0mnc ＜时，称ABC △为“倒抛物三角形”，此时a ，c 应分别满足条件________.3.已知圆的两条平行弦分别长6dm 和8dm ，若这圆的半径是5dm ，则两条平行弦之间的距离为________.4.如图，AB 是O 的弦，6AB =，点C 是O 上的一个动点，且°45ACB ∠=.若点M ，N 分别是AB ，BC 的中点，则MN 长的最大值是________.5.有四张正面分别标有数字3-，0，1，5的不透明卡片，它们除数字不同外其余全部相同.现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a ，则使关于x 的分式方程11222ax x x-+=--有正整数解的概率为________.6.如图，边长为6的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针旋转°60得到FC ，连接DF .则在点E 运动过程中，DF 的最小值是________.7.如图，已知二次函数20y ax bx c a =++（≠）的图象经过点（1，2），且与x 轴交点的横坐标分别为1x ，2x ，其中110x -＜＜，212x ＜＜，下列结论：①0abc ＜；②2a b a -＜＜；③284b a ac +＜；④10a -＜＜，其中正确结论的序号是________.8.如图，已知直线334y x =-+分别交x 轴、y 轴于点A ，B ，P 是抛物线21252y x x =-++上的一个动点，其横坐标为a ，过点P 且平行于y 轴的直线交直线334y x =-+于点Q ，则当PQ BQ =时，a 的值是________.三、解答题（共64分）1.（6分）用四块如图①所示的瓷砖拼铺一个成正方形的地板，使拼铺的图案成轴对称图形或中心对称图形，请你在图②和③中各画出一种拼法.（要求两种拼法各不相同）2.（8分）张彬和王华两位同学为得到一张观看足球比赛的入场券，商量后计划通过转盘游戏来决定，并各自设计了一种方案：张彬：将一个可以自由转动并标有阴影区域面积的转盘（如图①），随意转动，当指针指向阴影区域时，张彬得到入场券；否则，王华得到入场券；王华：将分成4等分且分别标有数字1，2，3，4的转盘，随意转动两次，当指针所指两个数字之和为偶数，王华得到入场券；否则，张彬得到入场券.（1）使用张彬设计的方案，随机转动转盘一次，指针指向阴影区域的概率是多少？（2）请你运用所学的概率知识，帮助张彬和王华选出公平的游戏方案.3.（11分）如图①所示，AB 是O 的直径，AC 是弦，直线EF 和O 相切于点C ，AD EF ⊥，垂足为D .（1）求证：DAC BAC ∠=∠；（2）若把直线EF 向上平行移动，如图②所示，EF 交O 于G ，C 两点，若题中的其他条件不变，试探究与DAC ∠相等的角是哪一个？说明理由.4.（12分）等腰ABC △的直角边10cm AB BC ==，点P ，Q 分别从A ，C 两点同时出发，均以1cm /秒的相同速度作直线运动，已知P 沿射线AB 运动，Q 沿边BC 的延长线运动，PQ 与直线AC 相交于点D .设P 点运动时间为t ，PCQ △的面积为S .（1）求出S 关于t 的函数关系式；（2）当点P 运动几秒时，PCQ ABC S S =△△？（3）作PE AC ⊥于点E ，当点P ，Q 运动时，线段DE 的长度是否改变？证明你的结论.5.（13分）已知Rt ABO △中，边1AB OB ==，°90ABO ∠=.【问题探究】（1）以AB 为边，在Rt ABO △的右边作正方形ABCD ，如图①，则点O 与点D 的距离为________.（2）以AB 为边，在Rt ABO △的右边作等边三角形ABC ，如图②，求点O 与点C 的距离.【问题解决】（3）若线段1DE =，线段DE 的两个端点D ，E 分别在射线OA ，OB 上滑动，以DE 为边向外作等边三角形DEF ，如图③，则点O 与点F 的距离有没有最大值？如果有，求出最大值；如果没有，说明理由.6.（14分）如图，抛物线2:L y x bx c =++经过A （0，3），B （1，0）4两点，点M 为顶点.（1）求b ，c 的值；（2）将OAB △绕点B 顺时针旋转：①当旋转°90时，点A 落在点C 的位置，将抛物线L 通过向上或向下平移后经过点C .求平移后所得抛物线1L 的表达式；②记OAB △绕点B 顺时针旋转过程中点A 的对应点为A '，点O 的对应点为O '，在抛物线1L 上是否存在A '，使得以点O ，A ，O '，A '为顶点的四边形是平行四边形？若存在，求出点A '的坐标；若不存在，请说明理由.期末复习—易错题精选参考答案一、1.【答案】B 2.【答案】C 3.【答案】C 4.【答案】D 5.【答案】D 6.【答案】C 7.【答案】B 8.【答案】D .二、1.【答案】211y x =--（）（答案不唯一）2.【答案】0a ＜，0c ＞3.【答案】1dm 7dm 或4.【答案】5.【答案】146.【答案】1.57.【答案】①②8.【答案】4144-+-或或三、1.【答案】答案不唯一.2.【答案】解：（1）根据转盘中阴影部分扇形的圆心角度数和°°°10070170+=则P （指针指向阴影区域）°°1701736036==.（2）由（1）得张彬设计的方案中，张彬得到入场券的概率为1736P =，王华得到入场券的概率为171913636P =-=，则张彬的方案不公平.利用王华的方案画树状图如下：由树状图得，共有16种等可能的结果，两次数字之和为偶数的有8种，则王华得到入场券的概率为81162P ==，张彬得到入场券的概率为12P =，∴王华的设计方案公平.3.【答案】（1）证明：如图①，连接OC .EF 与O 相切于点C ，OC EF ∴⊥...AD EF AD OC OCA DAC ∴∴∠=∠ ⊥，∥.OA OC OCA BAC DAC BAC =∴∠=∠∴∠=∠ ，，（2）解：BAG ∠与DAC ∠相等.理由如下：如图②，连接BC ，则B AGD ∠=∠.AB 是直径，AD EF ⊥，°90BCA GDA ∴∠=∠=，°90B BAC ∴∠+∠=，°90AGD DAG ∠+∠=.BAC DAG ∴∠=∠，BAC CAG DAG CAG ∴∠-∠=∠-∠.即BAG DAC ∠=∠.4.【答案】解：（1）当10t ＜秒时，P 在线段AB 上，此时CQ t =，10PB t =-.211101022S t t t t ∴=⨯⨯-=-（）（）.当10t ＞秒时，P 在线段AB 的延长线上，此时CQ t =，10PB t =-.211101022S t t t t ∴=⨯⨯-=-（）（）.（2）1502ABC S AB BC == △，211010502PCQ t S t t ∴=-=△当＜秒时，（）.整理，得2101000t t -+=，无解.当10t ＞秒时，2110502PCQ S t t =-=△（）.整理，得2101000t t --=，解得5t =±（舍去负值）.∴当点P 运动5±（秒时，PCQ ABC S S =△△.（3）当点P ，Q 运动时，线段DE 的长度不会改变.证明：过Q 作QM AC ⊥，交直线AC 于点M .易证APE QCM △≌△，22AE PE CM QM ∴====.∴四边形PEQM 是平行四边形，且DE 是对角线EM 的一半.又EM AC == ，DE ∴=.∴当点P ，Q 运动时，线段DE 的长度不会改变.同理，当点P 在点B 右侧时，DE =.综上所述，当点P ，Q 运动时，线段DE 的长度不会改变.5.【答案】（1.（2）过点C 作CD OB ⊥，垂足为点D .连接OC ，则°30CBD ∠=.1AB BC == ，∴在Rt CBD △中，12CD =，2BD =，1OD ∴=.∴在Rt CDO △中，OC ===.（3）点O 与点F 的距离有最大值.作ODE △的外接圆M ，连接MD ，ME ，MF ，MO ，OF ，则OF MO MF +≤.设MF 与DE 交于点N .°°4590AOB DME ∠=∴∠= ，.1DE = ，∴可得M 的半径为MD ME MO ===MD ME = ，DF EF =，MF ∴垂直平分DE .1122MN DE ∴==，3322NF EF ==.1222OF OM MF ∴+=++≤.12OF +∴=最大值.6.【答案】解：（1）已知抛物线L 经过点A （0，3），B （1，0），将其代入2y x bx c =++，得310c b c =⎧⎨++=⎩，，解得43.b c =-⎧⎨=⎩，即b ，c 的值分别为4-和3.（2）①根据点A ，B 坐标，可知3OA =，1OB =，如图，将OAB △绕点B 顺时针旋转°90后，可得点C 坐标为（4，1）.当4x =时，由243y x x =-+得3y =，可知抛物线L 经过点（4，3），∴将原抛物线沿y 轴向下平移2个单位后过点C .∴平移后的抛物线1L 的表达式为241y x x =-+.②存在.如图，OAB △绕点B 旋转过程中，当点A '，B ，A 三点在同一直线上时满足以点O ，A ，O '，A '为顶点的四边形是平行四边形.AB A B '= ，OB O B '=，∴四边形OAO A ''为平行四边形.根据图形的旋转性质，可知3O A OA ''==，1OB O B '==，且°90AOB A O B ''∠=∠=，∴点A '的坐标为23-（，）.又抛物线1L 的表达式为241y x x =-+，∴抛物线1L 的顶点坐标为23-（，）.∴点A '坐标与抛物线1L 的顶点坐标重合.∴抛物线1L 上存在一点23A '-（，），使得以点O ，A ，O '，A '为顶点的四边形是平行四边形.人教版九年级数学上册期末专项复习02—一元二次方程考点1巧用一元二次方程的定义及相关概念求值题型1利用一元二次方程的定义确定字母的取值1.已知231m x -+=（）是关于x 的一元二次方程，则m 的取值范围是（）A .3m ≠B .3m ≥C .2m -≥D .23m m -≥且≠2.已知关于x 的方程211210m xm m x +++--=（）（）.（1）m 取何值时，它是一元二次方程？并写出这个方程；（2）m 取何值时，它是一元一次方程？题型2利用一元二次方程的项的概念求字母的取值1.若一元二次方程2243680a x a x a -+++-=（）（）没有常数项，则a 的值为________.2.已知关于x 的一元二次方程221510m x x m -++-=（）的常数项为0，求m 的值.题型3利用一元二次方程的根的概念求字母或代数式的值1.已知关于x 的方程20x bx a ++=的一个根是0a a -（≠），则a b -的值为（）A .1-B .0C .1D .22.已知关于x 的一元二次方程2243160k x x k +++-=（）的一个根为0，求k 的值.3.已知实数a 是一元二次方程2201610x x -+=的根，求代数式22120152016a a a +--的值.题型4利用一元二次方程根的概念解决探究性问题1.已知m ，n 是方程2210x x --=的两个根，是否存在实数a 使22714367m m a n n -+--（）（）的值等于8？若存在，求出a 的值；若不存在，请说明理由.考点2一元二次方程的解法归类类型1限定方法解一元二次方程方法1形如20x m n n +=（）（≥）的一元二次方程用直接开平方法求解1.方程24250x -=的解为（）A .25x =B .52x =C .52x =±D .25x =±2.用直接开平方法解下列一元二次方程，其中无解的方程为（）A .255x -=B .230x -=C .240x +=D .210x +=（）方法2当二次项系数为1，且一次项系数为偶数时，用配方法求解1.用配方法解方程234x x +=，配方后的方程变为（）A .227x -=（）B .221x +=（）C .221x -=（）D .222x +=（）2.解方程：2420x x +-=.3.已知221016890x x y y -+-+=，求x y的值.方法3能化成形如0x a x b ++=（）（）的一元二次方程用因式分解法求解1.一元二次方程22x x x -=-（）的根是（）A .1-B .0C .1和2D .1-和22．解下列一元二次方程：（1）220x x -=；（2）21690x -=；（3）2441x x =-.方法4如果一个一元二次方程易于化为它的一般式，则用公式法求解1.用公式法解一元二次方程2124x x =-，方程的解应是（）A .22x -=B .22x =C .12x =D .12x =2.用公式法解下列方程.（1）23170x x +-=（）；（2）24352x x x --=-.类型2选择合适的方法解一元二次方程1.方程24490x -=的解为（）A .27x =B .72x =C .172x =，272x =-D .127x =，227x =-2.一元二次方程293x x -=-的根是（）A .3B .4-C .3和4-D .3和43.方程135x x +-=（）（）的解是（）A .11x =，23x =-B .14x =，22x =-C .11x =-，23x =D .14x =-，22x =4.解下列方程.（1）23360y y --=；（2）22310x x -+=.类型3用特殊方法解一元二次方程方法1构造法1.解方程：2619100x x ++=.2.若m ，n ，p 满足8m n -=，2160mn p ++=，求m n p ++的值.方法2换元法a .整体换元1.若280a b a b +++-=（）（），则a b +的值为（）A .4-或2B .3或32-C .2-或4D .3或2-2.已知22260x xy y x y -++--=，则x y -的值是（）A .2-或3B .2或3-C .1-或6D .1或6-3.解方程：223220x x ---+=（）（）.4.解方程：123448x x x x ----=（）（）（）（）.b .降次换元1.解方程：432635623560x x x x -+-+=.c .倒数换元1.解方程：2322x x x x --=-.方法3特殊值法1.解方程：2013201420152016x x --=⨯（）（）.考点3根的判别式的四种常见应用题型1利用根的判别式判断一元二次方程根的情况1.已知关于x 的方程2110kx k x +--=（），下列说法正确的是（）A .当0k =时，方程无解B .当1k =时，方程有一个实数解C .当1k =-时，方程有两个相等的实数解D .当0k ≠时，方程总有两个不相等的实数解2.已知方程220x x m --=没有实数根，其中m 是实数，试判断方程2210x mx m m +++=（）有无实数根.题型2利用根的判别式求字母的值或取值范围1.已知关于x 的一元二次方程22240x x k ++-=有两个不相等的实数根.（1）求k 的取值范围；（2）若k 为正整数，且该方程的根都是整数，求k 的值.2．已知关于x 的一元二次方程2220mx m x -++=（），（1）证明：不论m 为何值，方程总有实数根；（2）m 为何整数时，方程有两个不相等的正整数根.题型3利用根的判别式求代数式的值1.已知关于x 的方程22140x m x +-+=（）有两个相等的实数根，求21212m m m--+（）的值.2.已知关于x 的一元二次方程2200mx nx m +-=（≠）有两个相等的实数根，求222416mn m n ++-（）的值.题型4利用根的判别式确定三角形的形状1.已知a ，b ，c 是三角形的三边长，且关于x 的一元二次方程220b c x a b x b a -+-+-=（）（）有两个相等的实数根，试判断此三角形的形状.2.已知a ，b ，c 是三角形的三边长，且关于x 的一元二次方程204a c a c x bx -+++=（）有两个相等的实数根，试判断此三角形的形状.考点4一元二次方程与三角形的综合题型1一元二次方程与三角形三边关系的综合1.三角形的两边长分别为4和6，第三边长是方程27120x x -+=的解，则第三边的长为（）A .3B .4C .3或4D .无法确定2.根据一元二次方程根的定义，解答下列问题.一个三角形两边长分别为3cm 和7cm ，第三边长为cm a ，且整数a 满足210210a a -+=，求三角形的周长.题型2一元二次方程与直角三角形的结合1.已知一个直角三角形的两条直角边的长恰好是方程217600x x -+=的两个根，则这个直角三角形的斜边长为________.2.已知a ，b ，c 分别是ABC △的三边，当0m ＞时，关于x 的一元二次方程220c x m b x m ++--=（）（）有两个相等的实数根，试判断ABC △的形状，并说明理由.3.已知ABC △的三边a ，b ，c 中，1a b =-，1c b =+，又已知关于x 的方程2420120x x b -++=的根恰为b 的值，求ABC △的面积.题型3一元二次方程与等腰三角形的综合1.等腰三角形一条边的长为3，另两条边的长是关于x 的一元二次方程2120x x k -+=的两个根，则k 的值是（）A .27B .36C .27或36D .182.已知关于x 的一元二次方程220a c x bx a c +++-=（）（），其中a ，b ，c 分别为ABC △的三边的长.（1）如果1x =-是方程的根，试判断ABC △的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断ABC △的形状，并说明理由；（3）如果ABC △是等边三角形，试求这个一元二次方程的根.考点5根与系数的关系的四种应用类型题型1利用根与系数的关系求代数式的值1.设方程24730x x --=的两根为1x ，2x ，不解方程求下列各式的值.（1）1233x x --（）（）；（2）211211x x x x +++；（3）12x x -.题型2利用根与系数的关系构造一元二次方程1.构造一个一元二次方程，使它的两根分别是方程25230x x +-=各根的负倒数.题型3利用根与系数的关系求字母的值或取值范围1.已知关于x 的一元二次方程22210x mx m --+=的两根的平方和是294，求m 的值.2.已知关于x 的方程2220x x a ++-=.（1）若该方程有两个不相等的实数根，求实数a 的取值范围；（2）若该方程的一个根为1，求a 的值及该方程的另一根.题型4巧用根与系数的关系确定字母系数的存在性4.已知1x ，2x 是一元二次方程24410kx kx k -++=的两个实数根，是否存在实数k ，使12123222x x x x --=-（）（）成立？若存在，求出k 的值；若不存在，请说明理由.考点6：可化为一元二次方程的分式方程的应用题型1营销问题1.某玩具店采购人员第一次用100元去采购“企鹅牌”玩具，很快售完，第二次去采购时发现批发价每件上涨了0.5元，用去了150元，所购玩具数量比第一次多了10件，两批玩具的售价均为2.8元，问：第二次采购玩具多少件？（说明：根据销售常识，批发价应该低于销售价）题型2行程问题3.从甲站到乙站有150千米，一列快车和一列慢车同时从甲站开出，1小时后快车在慢车前12千米，快车到达乙站比慢车早25分钟，快车和慢车每小时各行驶多少千米？应用3工程问题4.某镇道路改造工程，由甲、乙两工程队合作20天可完成．甲工程队单独施工比乙工程队单独施工多用30天才能完成此项工程.（1）求甲、乙两工程队单独完成此项工程各需要多少天；（2）若甲工程队单独施工a 天后，再由甲、乙两工程队合作________天（用含a 的代数式表示）可完成此项工程；（3）如果甲工程队施工每天需收取施工费1万元，乙工程队施工每天需收取施工费2.5万元，那么甲工程队至少要单独施工多少天后，再由甲、乙两工程队合作施工完成剩下的工程，才能使施工费不超过64万元？考点7几种常见的热门考点题型1一元二次方程的根1.若一元二次方程220150ax bx --=有一根为1x =-，则a b +=________.2.若关于x 的一元二次方程20ax bx c ++=有一根为1-，且2a =+-，求20162015a b c +（）的值.题型2一元二次方程的解法1.用配方法解方程2210x x --=时，配方后所得的方程为（）A .210x +=（）B .210x -=（）C .212x +=（）D .212x -=（）2.一元二次方程2230x x --=的解是（）A .11x =-，23x =B .11x =，23x =-C .11x =-，23x =-D .11x =，23x =3.选择适当的方法解下列方程：（1）21210x x x -+-=（）（）；（2）221327x x x -=+-（）（）.题型3一元二次方程根的判别式1.若关于x 的方程220x x a ++=不存在实数根，则a 的取值范围是（）A .1a ＜B .1a ＞C .1a ≤D .1a ≥2.已知关于x 的一元二次方程210x m +-=（）有两个实数根，则m 的取值范围是（）A .34m -≥B .0m ≥C .1m ≥D .2m ≥3.在等腰三角形ABC 中，三边长分别为a ，b ，c .其中5a =，若关于x 的方程2260x b x b +++-=（）（）有两个相等的实数根，求ABC △的周长.题型4一元二次方程根与系数的关系1.已知α，β是关于x 的一元二次方程22230x m x m +++=（）的两个不相等的实数根，且满足111αβ+=-，则m 的值是（）A .3B .1C .3或1-D .3-或12.关于x 的方程231210ax a x a -+++=（）（）有两个不相等的实数根1x ，2x ，且有12121x x x x a +-=-，求a 的值.3.设1x ，2x 是关于x 的一元二次方程222420x ax a a +++-=的两个实数根，当a 为何值时，2212x x +有最小值？最小值是多少？题型5一元二次方程的应用1.某商品现在的售价为每件60元，每星期可卖出300件.市场调查反映：每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，在顾客得实惠的前提下，商家还想获得6080元的利润，应将销售单价定为多少元？2.某校为培养青少年科技创新能力，举办了动漫制作活动，小明设计了点做圆周运动的一个图形，如图所示，甲、乙两点分别从直径的两端点A ，B 出发，以顺时针、逆时针的方向同时沿圆周运动.甲运动的路程1cm （）与时间t s （）满足关系：2131022t t t =+（≥），乙以4cm/s 的速度匀速运动，半圆的长度为21cm .（1）甲运动4s 后的路程是多少？（2）甲、乙从开始运动到第一次相遇时，它们运动了多长时间？（3）甲、乙从开始运动到第二次相遇时，它们运动了多长时间？题型6新定义问题1.若1x ，2x 是关于x 的方程20x bx c ++=的两个实数根，且122x x k +=（k 是整数），则称方程20x bx c ++=为“偶系二次方程”．如方程26270x x --=，2280x x --=，227304x x +-=，26270x x +-=，2440x x ++=都是“偶系二次方程”.判断方程2120x x +-=是否是“偶系二次方程”，并说明理由.期末专项复习—一元二次方程答案解析考点1题型11.【答案】D【解析】由题意，得3020m m -⎧⎨+⎩≠，≥，解得2m -≥且3m ≠.2.【答案】解：（1）当21210m m ⎧+=⎨+⎩，≠时，它是一元二次方程，解得1m =.当1m =时，原方程可化为2210x x --=.（2）当22010m m ⎧-⎨+=⎩≠，或者当120m m ++-（）≠且211m +=时，它是一无一次方程.解得1m =-或0m =.故当1m =-或0m =时，它是一元一次方程.题型21.【答案】8【解析】由题意得80240.a a -=⎧⎨-⎩，≠解得8a =.2.【答案】由题意，得21010m m ⎧-=⎨-⎩，≠，解得1m =-.题型31.【答案】A【解析】∵关于x 的方程20x bx a ++=的一个根是0a a -（≠），20a ab a ∴-+=.10a a b ∴-+=（）.0a ≠，1.a b ∴-=-2.【答案】解：把0x =代入2243160k x x k +++-=（），得2160k -=，解得14k =，24k =-.40k + ≠，4k ∴-≠，4k ∴=.3.【答案】解：∵实数a 是一元二次方程2201610x x -+=的根，2201610a a ∴-+=.221201620161a a a a ∴+=-=-，.22222120162015201520152016120162016a a a a a a a a a a a +∴--=--=--=-=-题型41.【答案】解：由题意可知22210210m m n n --=--=，，22227143677232773747m m a n n m m a n n a a ⎡⎤⎡⎤∴-+--=-+--=+-=-+⎣⎦⎣⎦（）（）（）（）（）（）（），由478a -+=（）得9a =-，故存在满足要求的实数a ，且a 的值等于9-.考点2类型1方法11.【答案】C2.【答案】C方法21.【答案】C2.【答案】解：22242042262x x x x x x +-=+=+=+=，，（），1222x x =-+=--3.【答案】解：2222221016890102516640580x x y y x x y y x y -+-+=-++-+=-+-=，（）（），（）（），558.8x x y y ∴==∴=，，方法31.【答案】D2.【答案】解：（1）21220200 2.x x x x x x -=-===，（），，（2）21233169043430.44x x x x x -=+-==-=，（）（），（3）2221214414410210.2x x x x x x x =--+=-===，，（），方法41.【答案】B2.【答案】解：（1）2231703730x x x x +-=-+=（），，224743313b ac ∴-=--⨯⨯=（），12777723666x x x -∴==∴==⨯（2）2243524430x x x x x --=---=，，224444436424b ac x ∴-=--⨯⨯-=∴=⨯（）（），1231.22x x ∴==-类型21.【答案】C2.【答案】C3.【答案】B4.【答案】解：（1）22221919133360200442422y y y y y y y y --=--=-+-=-=-=±，，，（122 1.y y ∴==-，（2）22231231043421122x x b ac x ±-+=-=--⨯⨯=∴=⨯，（），即1211.2x x ∴==，类型3方法11.【答案】解：将原方程两边同乘6，得26196600x x +⨯+=（）（）.解得615x =-或64x =-.1252.23x x ∴=-=-，2.【答案】解：因为8m n -=，所以8m n =+.将8m n =+代入2160mn p ++=中，得28160n n p +++=（），所以228160n n p +++=，即2240n p ++=（）.又因为240n +（）≥，20p ≥，所以400n p +=⎧⎨=⎩，，解得40.n p =-⎧⎨=⎩，所以84m n =+=，所以4400m n p ++=+-+=（）方法2a1.【答案】A2.【答案】B3.【答案】223220.x x ---+=（）（）设2x y -=，原方程化为2320y y -+=，解得121 2.y y ==，当1y =时，213x x -==，，当2y =时，22 4.x x -==，原方程的解为1234x x ==，.4.【答案】解：原方程即[][]142348x x x x ----=（）（）（）（），即22545648x x x x -+-+=（）（）.设255y x x =-+，则原方程变为1148y y -+=（）（）.解得1277y y ==-，.当2557x x -+=时，解得125522x x +==；当2557x x -+=-时，254112230∆=--⨯⨯=-（）＜，方程无实数根．∴原方程的根为125522x x ==，.b 1.【答案】解：经验证0x =不是方程的根，原方程两边同除以2x ，得22356635620x x x x-+-+=，即2211635620x x x x+-++=（（.设1y x x =+，则22212x y x +=-，原方程可变为26235620y y --+=（）.解得152y =，2103y =.当152x x +=时，解得12x =，212x =；当1103x x +=时，解得33x =，413x =.经检验，均符合题意.∴原方程的解为12x =，212x =，33x =，413x =.c1.【答案】解：设2x y x-=，则原方程化为32y y -=，整理得2230y y --=，∴13y =，21y =-.当3y =时，23x x -=，∴1x =-.当1y =-时，21x x-=-，∴1x =.经检验，1x =±都是原方程的根，∴原方程的根为11x =，21x =-.方法31.【答案】解：方程组2013201620142015x x -=⎧⎨-=⎩，的解一定是原方程的解，解得4029x =.方程组2013201520142016x x -=-⎧⎨-=-⎩，的解也一定是原方程的解，解得2x =-.∵原方程最多有两个实数解，∴原方程的解为14029x =，22x =-.【解析】解本题也可采用换元法．设2014x t -=，则20131x t -=+，原方程可化为120152016t t +=⨯（），先求出t ，进而求出x .考点3题型11.【答案】C【解析】当0k =时，方程为一元一次方程，解为1x =；当0k ≠时，因为222141211k k k k k ∆=--⋅-=++=+（）（）（）≥0，所以当1k =时，4∆=，方程有两个不相等的实数解；当1k =-时，0∆=，方程有两个相等的实数解；当0k ≠时，0∆≥，方程总有两个实数解.故选C .2.【答案】解：220x x m --= 没有实数根，2124440m m ∴∆=--⋅-=+（）（）＜，即1m -＜.对于方程2210x mx m m +++=（），2224144m m m m ∆=-⋅+=-（）（）＞，∴方程2210x mx m m +++=（）有两个不相等的实数根.题型21.【答案】解：（1）根据题意得2444242080b ac k k -=--=-（）＞，解得25k ＜.（2）由k 为正整数，可得1k =或2k =.利用求根公式可求出方程的根为1x =-±，∵方程的根为整数，∴52k -为完全平方数，∴k 的值为2.2.【答案】（1）证明：[]22228442m m m m m ∆=-+-=-+=-（）（）.∵不论m 为何值，220m -（）≥，即0△≥.∴不论m 为何值，方程总有实数根.（2）解：解关于x 的一元二次方程2220mx m x -++=（），得22222m m m x m m ++±-==（）.∴12x m=，21x =.∵方程的两个根都是正整数，∴2m 是正整数，∴1m =或2m =.又∵方程的两个根不相等，∴2m ≠，∴1m =.题型31.【答案】解：∵关于x 的方程22140x m x +-+=（）两个相等的实数根，∴2214140m ∆=--⨯⨯=（），即214m -=±.∴52m =或32m =-.当52m =时，25111221216514m m m --==-++（）；当32m =-时，231152********m m m ---==--+-（）.2.【答案】解：由题意可知，22480b ac n m -=+=，∴28m n =-，∴222222222222222416816168mn mn mn mn mn m n m m n m m n m n n m ====++-+++-++-+（）.∵0m ≠，2228mn n m m∴==-.题型41.【答案】解：∵一元二次方程220b c x a b x b a -+-+-=（）（）有两个相等的实数根，∴[]2240a b b c b a ---⋅-=（）（）（），∴40a b a c --=（）（），∴a b =或a c =，∴此三角形是等腰三角形.2.【答案】解：∵方程204a ca c x bx -+++=（）有两个相等的实数根，∴2222404a cb ac b a c -∆=-+⋅=--=（）（），即222b c a +=，∴此三角形是直角三角形.考点4题型11.【答案】C2.【答案】解：由已知可得410a ＜＜，则a 可取5，6，7，8，9.（第一步）当5a =时，代入2210215105210a a -+=-⨯+≠，故5a =不是方程的根.同理可知6a =，8a =，9a =都不是方程的根，7a =是方程的根．（第二步）∴ABC △的周长是37717cm ++=（）.题型21.【答案】132.【答案】解：ABC △是直角三角形．理由如下：原方程可化为20b c x cm bm +-+-=（），2222444ma m c b c b m a b c ∆--++-=（）（）=（）.∵0m ＞，且原方程有两个相等的实数根，∴2220a b c +-=，即222a b c +=∴ABC △是直角三角形.3.【答案】解：将x b =代入原方程，整理得2419120b b -+=，解得14b =，234b =.当14b =时，3a =，5c =，∵222345+=，即222a b c +=，∴ABC △为直角三角形，且°90C ∠=.∴1134622ABC S ab ==⨯⨯=△；当234b =时，3104a =-＜，不合题意，舍去.因此，ABC △的面积为6.题型31.【答案】B2.【答案】解：（1）ABC △是等腰三角形.理由如下：把1x =-入原方程，得20a c b a c +-+-=，所以a b =，故ABC △是等腰三角形.（2）ABC △是直角三角形.理由如下：方程有两个相等的实数根，则2240b a c a c ∆=-+-=（）（）（），所以2220b a c -+=，所以222a b c =+，故ABC △是直角三角形.（3）如果ABC △是等边三角形，则a b c ==，所以方程可化为2220ax ax +=，所以210ax x +=（），所以方程的解为10x =，21x =-.考点5题型11.【答案】解：根据一元二次方程根与系数的关系，有1274x x +=，1234x x =-.（1）12121237333939344x x x x x x --=-++=--⨯+=（）（）（）.（2）2222122111212121212122112121212112====111111x x x x x x x x x x x x x x x x x x x x x x x x x x x x +++++++-+++++++++++++（）（）（）（）（）（）（）27372101444=3732144-⨯-+-++（）（）.（3）222121212127397=4=4=4416x x x x x x x x -+--⨯-∴-==（）（）（）（，.题型21.【答案】解：设方程25230x x +-=的两根为1x ，2x ，则1225x x +=-，1235x x =-.设所求方程为20y py q ++=，其两根为1y ，2y ，令111y x =-，221y x =-.∴121212*********==3x x p y y x x x x x x +=-+=--=+（）（，12121211153q y y x x x x ==--==-（）（.∴所求的方程为225+033y y -=，即23250y y +-=.题型31.【答案】解：设方程两根为1x ，2x ，由已知得1212=221=.2m x x m x x ⎧+⎪⎪⎨-+⎪⎪⎩∵222121212292=4x x x x x x +=+-（），即221292224m m -+-⨯=（，∴28330m m +-=.解得111m =-，23m =.当111m =-时，方程为2211230x x ++=，21142230∆=-⨯⨯＜，方程无实数根，∴11m =-不合题意，舍去；当3m =时，方程为22235034250x x --=∆=--⨯⨯-，（）（）＞，方程有两个不相等的实数根，符合题意.∴m 的值为3.2.【答案】解：（1）∵224121240a a -⨯⨯-=-（）＞，解得3a ＜.∴a 的取值范围是3a ＜.（2）设方程的另一根为1x ，由根与系数的关系得111212x x a +=-⎧⎨⋅=-⎩，，解得113.a x =-⎧⎨=-⎩，题型44.【答案】解：不存在.理由如下：∵一元二次方程24410kx kx k -++=有两个实数根，∴0k ≠，且24441160k k k k ∆=--⨯+=-（）（）≥，∴0k ＜.∵1x ，2x 是方程24410kx kx k -++=的两个实数根，∴121x x +=，1214k x x k+=.∴212121212922294k x x x x x x x x k+--=+-=-（）（）（）.又∵12123222x x x x --=-（）（），∴939425k k k +-=-∴=.又∵0k ＜，∴不存在实数k ，使12123222x x x x --=-（）（）成立.考点61.【答案】解：方法一：设第二次采购玩具x 件，则第一次采购玩具10x -（）件，由题意得1001500.510x x+=-.整理得211030000x x -+=，解得150x =，260x =，经检验150x =，260x =都是原方程的解.当50x =时，第二次采购时每件玩具的批发价为150503÷=（元），高于玩具的售价，不合题意，舍去；当60x =时，第二次采购时每件玩具的批发价为15060 2.5÷=（元），低于玩具的售价，符合题意，因此第二次采购玩具60件.方法二：设第一次采购玩具x 件，则第二次采购玩具10x +（）件，由题意得1001500.510x x +=+，整理得29020000x x -+=，解得140x =，250x =，经检验，140x =，250x =都是原方程的解.第一次采购40件时，第二次采购401050+=（件），批发价为150503÷=（元），不合题意，舍去；第一次采购50件时，第二次采购401060+=（件），批发价为15060 2.5÷=（元），符合题意.因此第二次采购玩具60件.题型23.【答案】解：设慢车每小时行驶x 千米，则快车每小时行驶12x +（）千米，依题意得150150251260x x -=+.解得172x =-（不合题意，舍去），260x =.所以1272x +=.∴快车每小时行驶72千米，慢车每小时行驶60千米.应用34.【答案】解：（1）设乙工程队单独施工x 天完成此项工程，则甲工程队单独施工30x +（）天完成此项工程，由题意得1120130x x +=+（），整理，得2106000x x --=，解得130x =，220x =-.经检验130x =，220x =-都是分式方程的解，但220x =-不符合题意，应舍去，故30x =，3060x +=.故甲、乙两工程队单独完成此项工程分别需要60天，30天.（2）203a -（）（3）由题意得11 2.520643a a +++-（）（）≤，解得36a ≥.故甲工程队至少要单独施工36天后，再由甲、乙两工程队合作施工完成剩下的工程，才能使施工费不超过64万元.考点7题型11.【答案】2015【解析】把1x =-代入方程中得到20150a b +-=，即2015a b +=.2.【答案】解：∵2a =+-，∴40c -≥且40c -≥，即4c =，则2a =-.又∵1-是一元二次方程20ax bx c ++=的根，∴0a b c -+=，∴242b a c =+=-+=.∴原式201622020154-+==⨯（）.题型21.【答案】D 2.【答案】A3.【答案】解：（1）21210x x x -+-=（）（），1120x x x --+=（）（），1310x x --=（）（），12113x x ==，.（2）221327x x x -=+-（）（），22441327x x x x -+=+-，2680x x -+=，1224x x ==，.题型31.【答案】B 2.【答案】B3.【答案】解：∵关于x 的方程2260x b x b +++-=（）（）有两个相等的实数根，∴22460b b ∆=+--=（）（），∴12b =，210b =-（舍去）.当a 为腰时，ABC △周长为55212=++.当b 为腰时，225+＜，不能构成三角形．∴ABC △的周长为12.题型41.【答案】A2.【答案】解：由题意，得1231a x x a ++=，1221a x x a +=（），∴31211a a a a a++-=-（），∴210a -=，即1a =±.又∵方程有两个不相等的实数根，∴[]2314210a a a ∆=-+-⋅+（）（）＞，即210a -（）＞，∴1a ≠，∴1a =-.3.【答案】解：∵方程有两个实数根，∴2224420a a a ∆=-+-（）（）≥，∴12a ≤.又∵122x x a +=-，21242x x a a =+-，∴22221212122224x x x x x x a +=+-=--（）（）.∵12a ≤，且2220a -（）≥，∴当12a =时，2212x x +的值最小．此时222121122422x x +=--=（），即最小值为12.【解析】本题中考虑0△≥从而确定a 的取值范围这一过程易被忽略.题型51.【答案】解：设每件商品降价x 元，则售价为每件60x -（）元，每星期的销量为30020x +（）件.根据题意，得6040300206080x x --+=（）（）.解得11x =，24x =.又要顾客得实惠，故取4x =，即销售单价为56元.答：应将销售单价定为56元.2.【答案】解：（1）当4t =时，221313144142222t t =+=⨯+⨯=.答：甲运动4s 后的路程是14cm .（2）设它们运动了s m ，根据题意，得21342122m m m ++=.解得：13m =，214m =-（不合题意，舍去）.答：甲、乙从开始运动到第一次相遇时，它们运动了3s .（3）设它们运动了s n 后第二次相遇，根据题意，得213421322n n n ++=⨯（）.解得17n =，218n =-（不合题意，舍去）.答：甲、乙从开始运动到第二次相遇时，它们运动了7s .题型61.【答案】解：不是.理由如下：解方程2120x x +-=，得14x =-，23x =.12432 3.5x x +=+=⨯.∵3.5不是整数，∴方程2120x x +-=不是“偶系二次方程”.。

人教版九年级数学上册旋转几何综合易错题(Word版含答案)

人教版九年级数学上册旋转几何综合易错题（Word 版含答案）一、初三数学旋转易错题压轴题（难）1．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是，位置关系是；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．【答案】（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492．【解析】【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =，点P ，M 是CD ，DE 的中点，//PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大．方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．2．已知：如图①，在矩形ABCD 中，3,4,AB AD AE BD ==⊥，垂足是E .点F 是点E 关于AB 的对称点，连接AF 、BF ．（1）求AF 和BE 的长；（2）若将ABF 沿着射线BD 方向平移，设平移的距离为m (平移距离指点B 沿BD 方向所经过的线段长度)．当点F 分别平移到线段AB AD 、上时，直接写出相应的m 的值．（3）如图②，将ABF 绕点B 顺时针旋转一个角1(080)a a ︒<<︒，记旋转中ABF 为''A BF ，在旋转过程中，设''A F 所在的直线与直线AD 交于点P ，与直线BD 交于点Q ．是否存在这样的P Q 、两点，使DPQ 为等腰三角形？若存在，求出此时DQ 的长；若不存在，请说明理由．【答案】（1）129,55AF BF ==；（2）95m =或165m =；（3）存在4组符合条件的点P 、点Q ，使DPQ 为等腰三角形； DQ 的长度分别为2或25891055或35105【解析】【分析】（1）利用矩形性质、勾股定理及三角形面积公式求解；（2）依题意画出图形，如图①-1所示．利用平移性质，确定图形中的等腰三角形，分别求出m 的值；（3）在旋转过程中，等腰△DPQ 有4种情形，分别画出图形，对于各种情形分别进行计算即可．【详解】（1）∵四边形ABCD 是矩形，∴∠BAD=90°，在Rt △ABD 中，AB=3，AD=4，由勾股定理得：2222345AB AD +=+=， ∵S △ABD 12=BD•AE=12AB•AD ， ∴AE=AB AD 3412BD 55⋅⨯==， ∵点F 是点E 关于AB 的对称点， ∴AF=AE 125=，BF=BE ， ∵AE ⊥BD ，在Rt△ABE中，AB=3，AE125 =，由勾股定理得：BE2222129355 AB AE⎛⎫=-=-=⎪⎝⎭；（2）设平移中的三角形为△A′B′F′，如图①-1所示：由对称点性质可知，∠1=∠2．BF=BE95 =，由平移性质可知，AB∥A′B′，∠4=∠1，BF=B′F′95 =，①当点F′落在AB上时，∵AB∥A′B′，∴∠3=∠4，根据平移的性质知：∠1=∠4，∴∠3=∠2，∴BB′=B′F′95=，即95m=；②当点F′落在AD上时，∵AB∥A′B′，AB⊥AD，∴∠6=∠2，A′B′⊥AD，∵∠1=∠2，∠5=∠1，∴∠5=∠6，又知A′B′⊥AD，∴△B′F′D为等腰三角形，∴B′D=B′F′95 =，∴BB′=BD-B′D=5-91655=，即m165=；（3）存在．理由如下：∵四边形ABCD是矩形，∵AE⊥BD，∴∠AEB=90°，∠2+∠ABD=90°，∠BAE+∠ABD=90°，∴∠2=∠BAE，∵点F是点E关于AB的对称点，∴∠1=∠BAE，∴∠1=∠2，在旋转过程中，等腰△DPQ依次有以下4种情形：①如图③-1所示，点Q落在BD延长线上，且PD=DQ，则∠Q=∠DPQ，∴∠2=∠Q+∠DPQ=2∠Q，∵∠1=∠3+∠Q，∠1=∠2，∴∠3=∠Q，∴A′Q=A′B=3，∴F′Q=F′A′+A′Q=1227355+=，在Rt△BF′Q中，由勾股定理得：2222927910 BF F Q555⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭''，∴9105；②如图③-2所示，点Q落在BD上，且PQ=DQ，则∠2=∠P，∵∠1=∠2，∴∠1=∠P，∴BA′∥PD，则此时点A′落在BC边上．∵∠3=∠2，∴∠3=∠1，∴BQ=A′Q，∴F′Q=F′A′-A′Q=125-BQ，在Rt△BQF′中，由勾股定理得：BF′2+F′Q2=BQ2，即：222 91255BQ BQ⎛⎫⎛⎫+-=⎪ ⎪⎝⎭⎝⎭，解得：158 BQ=，∴DQ= BD-BQ=5-1525 88=；③如图③-3所示，点Q落在BD上，且PD=DQ，则∠3=∠4．∵∠2+∠3+∠4=180°，∠3=∠4，∴∠4=90°-12∠2．∵∠1=∠2，∴∠4=90°-12∠1，∴∠A′QB=∠4=90°-12∠1， ∴∠A′QB=∠A′BQ ，∴A′Q=A′B=3，∴F′Q=A′Q -A′F′=3-12355=，在Rt △BF′Q 中，由勾股定理得：BQ=222293310BF F Q 555⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭''， ∴DQ=BQ-BD=31055-； ④如图④-4所示，点Q 落在BD 上，且PQ=PD ，则∠2=∠3．∵∠1=∠2，∠3=∠4，∠2=∠3，∴∠1=∠4，∴BQ=BA′=3，∴DQ=BD-BQ=5-3=2．综上所述，存在4组符合条件的点P 、点Q ，使△DPQ 为等腰三角形，DQ 的长度分别为：2或25891055或35105 【点睛】本题是四边形综合题目，主要考查了矩形的性质、轴对称的性质、平移的性质、旋转的性质、勾股定理、等腰三角形的性质等知识点；第（3）问难度很大，解题关键是画出各种旋转图形，依题意进行分类讨论．3．已知如图1，在ABC 中，90ABC ∠=︒，BC AB =，点D 在AC 上，DF AC ⊥交BC 于F ，点E 是AF 的中点．（1）写出线段ED 与线段EB 的关系并证明；（2）如图2，将CDF 绕点C 逆时针旋转()090a α︒<<︒，其它条件不变，线段ED 与线段EB 的关系是否变化，写出你的结论并证明；（3）将CDF 绕点C 逆时针旋转一周，如果6BC =，32CF =，直接写出线段CE 的范围．【答案】（1）ED EB =，DE BE ⊥，证明见解析；（2）结论不变，理由见解析；（3）最大值22=最小值322=．【解析】【分析】（1）在Rt △ADF 中，可得DE=AE=EF ，在Rt △ABF 中，可得BE=EF=EA ，得证ED=EB ；然后利用等腰三角形的性质以及四边形ADFB 的内角和为180°，可推导得出∠DEB=90°；（2）如下图，先证四边形MFBA 是平行四边形，再证△DCB ≌△DFM ，从而推导出△DMB 是等腰直角三角形，最后得出结论；（3）如下图，当点F 在AC 上时，CE 有最大值；当点F 在AC 延长线上时，CE 有最小值．【详解】（1）∵DF ⊥AC ，点E 是AF 的中点∴DE=AE=EF ，∠EDF=∠DFE∵∠ABC=90°，点E 是AF 的中点∴BE=AE=EF ，∠EFB=∠EBF∴DE=EB∵AB=BC ，∴∠DAB=45°∴在四边形ABFD 中，∠DFB=360°－90°－45°－90°=135°∠DEB=∠DEF+∠FEB=180°－2∠EFD+180°－2∠EFB=360°－2(∠EFD+∠EFB)=360°－2×135°=90°∴DE ⊥EB（2）如下图，延长BE 至点M 处，使得ME=EB ，连接MA 、ME 、MF 、MD 、FB 、DB ，延长MF 交CB 于点H∵ME=EB，点E是AF的中点∴四边形MFBA是平行四边形∴MF∥AB，MF=AB∴∠MHB=180°－∠ABC=90°∵∠DCA=∠FCB=a∴∠DCB=45°+a，∠CFH=90°－a∵∠DCF=45°，∠CDF=90°∴∠DFC=45°，△DCF是等腰直角三角形∴∠DFM=180°－∠DFC－∠CFH=45°+a∴∠DCB=∠DFM∵△ABC和△CDF都是等腰直角三角形∴DC=DF，BC=AB=MF∴△DCB≌△DFM(SAS)∴∠MDF=∠BDC，DB=DM∴∠MDF+∠FDB=∠BDC+∠FDB=90°∴△DMB是等腰直角三角形∵点E是MB的中点∴DE=EB，DE⊥EB（3）当点F在AC上时，CF有最大值，图形如下：∵BC=6，∴在等腰直角△ABC中，AC=62∵CF=32，∴AF=32∴CE=CF+FE=CF+12AF922=当点F在AC延长线上时，CE有最小值，图形如下：同理，CE=EF－CF322 =【点睛】本题考查三角形的旋转变换，用到了等腰直角三角形的性质和平行四边形的性质，解题关键是构造并证明△BDM是等腰直角三角形．4．如图一，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，若161A EEC=-，求nm的值．（3）如图二，在（2）的条件下，直线AB上有一点P，BP=2，点E是直线DC上一动点，在BE左侧作矩形BEFG且始终保持BE nBG m=，设AB=33，试探究点E移动过程中，PF 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．【答案】（1）5π；（2）3；（3）存在，63+【解析】【分析】（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．解直角三角形，求出∠ABA1，得到旋转角即可解决问题；（2）由△BCE∽△BA2D2，推出222A DCE nCB A B m==，可得CE=2nm，由161A EEC=-推出16A CEC=，推出A1C=26nm•，推出BH=A1C=26nm•，然后由勾股定理建立方程，解方程即可解决问题；（3）当A、P、F，D，四点共圆，作PF⊥DF，PF与CD相交于点M，作MN⊥AB，此时PF 的长度为最小值；先证明△FDG∽△FME，得到33FGFFM FED==，再结合已知条件和解直角三角形求出PM和FM的长度，即可得到PF的最小值.【详解】解：（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．∴AD=HA1=n=1，在Rt △A 1HB 中，∵BA 1=BA=m=2， ∴BA 1=2HA 1， ∴∠ABA 1=30°， ∴旋转角为30°， ∵BD=22125+=， ∴D 到点D 1所经过路径的长度=3055ππ⋅⋅=；（2）∵△BCE ∽△BA 2D 2，∴222A D CE nCB A B m==， ∴2n CE m =，∵161EAEC =-， ∴16A CEC =， ∴A 1C=26n m⋅，∴BH=A 1C=2226n m n m-=⋅，∴42226n m n m-=⋅，∴m 4﹣m 2n 2=6n 4，∴242416n n m m-=•，∴3n m =（负根已舍去）．（3）当A 、P 、F ，D ，四点共圆，作PF ⊥DF ，PF 与CD 相交于点M ，作MN ⊥AB ，此时PF 的长度为最小值；由（2）可知，3BE n BG m ==， ∵四边形BEFG 是矩形，∴FG FE =∵∠DFG+∠GFM=∠GFM+∠MFE=90°， ∴∠DFG=∠MFE ， ∵DF ⊥PF ，即∠DFM=90°，∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°， ∴∠FDG=∠FME ， ∴△FDG ∽△FME ，∴FG F FM FE D ==，∵∠DFM=90°，tan 3FD FMD FM ∠==， ∴∠FDM=60°，∠FMD=30°，∴FM DM =；在矩形ABCD 中，有AD AB ==3AD =， ∵MN ⊥AB ，∴四边形ANMD 是矩形， ∴MN=AD=3，∵∠NPM=∠DMF=30°， ∴PM=2MN=6，∴NP=AB =， ∴DM=AN=BP=2，∴2FM DM ===∴6PF PM MF =+=+ 【点睛】本题考查点的运动轨迹，旋转变换、解直角三角形、弧长公式、矩形的性质、相似三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于压轴题，中考常考题型．正确作出辅助线，正确确定动点的位置，注意利用数形结合的思想进行解题.5．我们定义：如图1，在△ABC看，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△A'B'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．特例感知：（1）在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD= BC；②如图3，当∠BAC=90°，BC=8时，则AD长为．猜想论证：（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．拓展应用（3）如图4，在四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=23，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．【答案】（1）①12；②4；（2）AD=12BC，证明见解析；（3）存在，证明见解析，39．【解析】【分析】（1）①首先证明△ADB′是含有30°是直角三角形，可得AD=12AB′即可解决问题；②首先证明△BAC≌△B′AC′，根据直角三角形斜边中线定理即可解决问题；（2）结论：AD=12BC．如图1中，延长AD到M，使得AD=DM，连接E′M，C′M，首先证明四边形AC′MB′是平行四边形，再证明△BAC≌△AB′M，即可解决问题；（3）存在．如图4中，延长AD交BC的延长线于M，作BE⊥AD于E，作线段BC的垂直平分线交BE于P，交BC于F，连接PA、PD、PC，作△PCD的中线PN．连接DF交PC于O．想办法证明PA=PD，PB=PC，再证明∠APD+∠BPC=180°，即可；【详解】解：（1）①如图2中，∵△ABC是等边三角形，∴AB=BC=AB=AB′=AC′，∵DB′=DC′，∴AD⊥B′C′，∵∠BAC=60°，∠BAC+∠B′AC′=180°，∴∠B′AC′=120°，∴∠B′=∠C′=30°，∴AD=12AB′=12BC，故答案为12．②如图3中，∵∠BAC=90°，∠BAC+∠B′AC′=180°，∴∠B′AC′=∠BAC=90°，∵AB=AB′，AC=AC′，∴△BAC≌△B′AC′，∴BC=B′C′，∵B′D=DC′，∴AD=12B′C′=12BC=4，故答案为4．（2）结论：AD=12 BC．理由：如图1中，延长AD到M，使得AD=DM，连接E′M，C′M∵B′D=DC′，AD=DM，∴四边形AC′MB′是平行四边形，∴AC′=B′M=AC，∵∠BAC+∠B′AC′=180°，∠B′AC′+∠AB′M=180°，∴∠BAC=∠MB′A，∵AB=AB′，∴△BAC≌△AB′M，∴BC=AM，∴AD=1BC．2（3）存在．理由：如图4中，延长AD交BC的延长线于M，作BE⊥AD于E，作线段BC的垂直平分线交BE于P，交BC于F，连接PA、PD、PC，作△PCD的中线PN．连接DF交PC于O．∵∠ADC=150°，∴∠MDC=30°，在Rt△DCM中，∵3，∠DCM=90°，∠MDC=30°，∴CM=2，DM=4，∠M=60°，在Rt△BEM中，∵∠BEM=90°，BM=14，∠MBE=30°，∴EM=1BM=7，2∴DE=EM﹣DM=3，∵AD=6，∴AE=DE，∵BE⊥AD，∴PA=PD，PB=PC，在Rt△CDF中，∵3CF=6，∴tan∠3∴∠CDF=60°=∠CPF，易证△FCP≌△CFD，∴CD=PF，∵CD∥PF，∴四边形CDPF是矩形，∴∠CDP=90°，∴∠ADP=∠ADC﹣∠CDP=60°，∴△ADP是等边三角形，∴∠ADP=60°，∵∠BPF=∠CPF=60°，∴∠BPC=120°，∴∠APD+∠BPC=180°，∴△PDC是△PAB的“旋补三角形”，在Rt△PDN中，∵∠PDN=90°，PD=AD=6，DN=3，∴PN=2222++=39．DN PD=(3)6【点睛】本题考查四边形综合题．6．在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．（1）如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，证明：①AC′=BD′；②AC′⊥BD′；（2）如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．【答案】（1）证明见解析；（2）成立，理由见解析【解析】试题分析：（1）①由旋转的性质得出OC=OC′，OD=OD′，∠AOC′=∠BOD′，证出OC′=OD′，由SAS证明△AOC′≌△BOD′，得出对应边相等即可；②由全等三角形的性质得出∠OAC′=∠OBD′，又由对顶角相等和三角形内角和定理得出∠BEA=90°，即可得出结论；（2）由旋转的性质得出OC=OC′，OD=OD′，∠AOC′=∠BOD′，由平行线得出比例式，得出，证明△AOC′∽△BOD′，得出∠OAC′=∠OBD′再由对顶角相等和三角形内角和定理即可得出∠AEB=θ．试题解析：（1）证明：①∵△OCD旋转到△OC′D′，∴OC=OC′，OD=OD′，∠AOC′=∠BOD′，∵OA=OB，C、D为OA、OB的中点，∴OC=OD，∴OC′=OD′，在△AOC′和△BOD′中，，∴△AOC′≌△BOD′（SAS），∴AC′=BD′；②延长AC′交BD′于E，交BO于F，如图1所示：∵△AOC′≌△BOD′，∴∠OAC′=∠OBD′，又∠AFO=∠BFE，∠OAC′+∠AFO=90°，∴∠OBD′+∠BFE=90°，∴∠BEA=90°，∴AC′⊥BD′；（2）解：∠AEB=θ成立，理由如下：如图2所示：∵△OCD旋转到△OC′D′，∴OC=OC′，OD=OD′，∠AOC′=∠BOD′，∵CD∥AB，∴，∴，∴，又∠AOC′=∠BOD′，∴△AOC′∽△BOD′，∴∠OAC′=∠OBD′，又∠AFO=∠BFE，∴∠AEB=∠AOB=θ．考点：相似三角形的判定与性质；全等三角形的判定与性质；旋转的性质．7．边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1)，现将正方形ABCD绕D点顺时针旋转，当A点第一次落在DF上时停止旋转，旋转过程中， AB边交DF于点M，BC边交DG于点N.（1）求边DA在旋转过程中所扫过的面积；（2）旋转过程中，当MN和AC平行时(如图2)，求正方形ABCD旋转的度数；（3）如图3，设△MBN的周长为p，在旋转正方形ABCD的过程中，p值是否有变化？请证明你的结论.【答案】（1）；（2）；（3）不变化，证明见解析.【解析】试题分析：（1）将正方形ABCD绕D点顺时针旋转，当A点第一次落在DF上时停止旋转，旋转过程中，DA旋转了，从而根据扇形面积公式可求DA在旋转过程中所扫过的面积.（2）旋转过程中，当MN和AC平行时，根据平行的性质和全等三角形的判定和性质可求正方形ABCD旋转的度数为.（3）延长BA交DE轴于H点，通过证明和可得结论.（1）∵A点第一次落在DF上时停止旋转，∴DA旋转了.∴DA在旋转过程中所扫过的面积为.（2）∵MN∥AC，∴,.∴.∴.又∵，∴.又∵,∴.∴.∴.∴旋转过程中，当MN和AC平行时，正方形ABCD旋转的度数为.(3)不变化，证明如下：如图，延长BA交DE轴于H点，则，，∴.又∵.∴．∴．又∵, ,∴．∴.∴.∴.∴在旋转正方形ABCD的过程中，值无变化.考点：1.面动旋转问题；2．正方形的性质；3.扇形面积的计算；4.全等三角形的判定和性质.8．阅读材料：小胖同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组旋转全等的三角形．小胖把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小胖发现若∠BAC＝∠DAE，AB＝AC，AD＝AE，则BD＝CE,(1)在图1中证明小胖的发现；借助小胖同学总结规律，构造“手拉手”图形来解答下面的问题：(2)如图2，AB＝BC，∠ABC＝∠BDC＝60°，求证：AD+CD＝BD；(3)如图3，在△ABC中，AB＝AC，∠BAC＝m°，点E为△ABC外一点，点D为BC中点，∠EBC＝∠ACF，ED⊥FD，求∠EAF的度数（用含有m的式子表示）．【答案】（1）证明见解析；（2）证明见解析；（3）∠EAF =12 m°.【解析】分析：（1）如图1中，欲证明BD=EC，只要证明△DAB≌△EAC即可；（2）如图2中，延长DC到E，使得DB=DE．首先证明△BDE是等边三角形，再证明△ABD≌△CBE即可解决问题；（3）如图3中，将AE绕点E逆时针旋转m°得到AG，连接CG、EG、EF、FG，延长ED到M，使得DM=DE，连接FM、CM．想办法证明△AFE≌△AFG，可得∠EAF=∠FAG=12m°.详（1）证明：如图1中，∵∠BAC=∠DAE，∴∠DAB=∠EAC，在△DAB和△EAC中，AD AEDAB EACAB AC⎧⎪∠∠⎨⎪⎩＝＝＝，∴△DAB≌△EAC，∴BD=EC．（2）证明：如图2中，延长DC到E，使得DB=DE．∵DB=DE，∠BDC=60°，∴△BDE是等边三角形，∴∠BD=BE，∠DBE=∠ABC=60°，∴∠ABD=∠CBE，∵AB=BC，∴△ABD≌△CBE，∴AD=EC，∴BD=DE=DC+CE=DC+AD．∴AD+CD=BD．（3）如图3中，将AE绕点E逆时针旋转m°得到AG，连接CG、EG、EF、FG，延长ED到M，使得DM=DE，连接FM、CM．由（1）可知△EAB≌△GAC，∴∠1=∠2，BE=CG，∵BD=DC，∠BDE=∠CDM，DE=DM，∴△EDB≌△MDC，∴EM=CM=CG，∠EBC=∠MCD，∵∠EBC=∠ACF，∴∠MCD=∠ACF，∴∠FCM=∠ACB=∠ABC，∴∠1=3=∠2，∴∠FCG=∠ACB=∠MCF，∵CF=CF，CG=CM，∴△CFG≌△CFM，∴FG=FM，∵ED=DM，DF⊥EM，∴FE=FM=FG，∵AE=AG，AF=AF，∴△AFE≌△AFG，∴∠EAF=∠FAG=12 m°．点睛：本题考查几何变换综合题、旋转变换、等腰三角形的性质、全等三角形的判定和性质等知识，解题的关键是学会利用“手拉手”图形中的全等三角形解决问题，学会构造“手拉手”模型，解决实际问题，属于中考压轴题．9．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．（1）如图①，当点D落在BC边上时，求点D的坐标；（2）如图②，当点D落在线段BE上时，AD与BC交于点H．①求证△ADB≌△AOB；②求点H的坐标．（3）记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．【答案】（1）D（1，3）；（2）①详见解析；②H（175，3）；（3）30334-≤S≤30334+．【解析】【分析】（1）如图①，在Rt△ACD中求出CD即可解决问题；（2）①根据HL证明即可；②，设AH=BH=m，则HC=BC-BH=5-m，在Rt△AHC中，根据AH2=HC2+AC2，构建方程求出m即可解决问题；（3）如图③中，当点D在线段BK上时，△DEK的面积最小，当点D在BA的延长线上时，△D′E′K的面积最大，求出面积的最小值以及最大值即可解决问题；【详解】（1）如图①中，∵A（5，0），B（0，3），∴OA=5，OB=3，∵四边形AOBC是矩形，∴AC=OB=3，OA=BC=5，∠OBC=∠C=90°，∵矩形ADEF是由矩形AOBC旋转得到，∴AD=AO=5，在Rt△ADC中，CD22AD AC-，∴BD=BC-CD=1，∴D（1，3）．（2）①如图②中，由四边形ADEF是矩形，得到∠ADE=90°，∵点D在线段BE上，∴∠ADB=90°，由（1）可知，AD=AO，又AB=AB，∠AOB=90°，∴Rt△ADB≌Rt△AOB（HL）．②如图②中，由△ADB≌△AOB，得到∠BAD=∠BAO，又在矩形AOBC中，OA∥BC，∴∠CBA=∠OAB，∴∠BAD=∠CBA，∴BH=AH，设AH=BH=m，则HC=BC-BH=5-m，在Rt△AHC中，∵AH2=HC2+AC2，∴m2=32+（5-m）2，∴m=175，∴BH=175，∴H（175，3）．（3）如图③中，当点D在线段BK上时，△DEK的面积最小，最小值=12•DE•DK=12×3×（5-342）=303344，当点D在BA的延长线上时，△D′E′K的面积最大，最大面积=12×D′E′×KD′=12×3×（5+342）=303344+．综上所述，30334-≤S≤30334+．【点睛】本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用参数构建方程解决问题．10．操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．（1）连接AE，求证：△AEF是等腰三角形；猜想与发现：（2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是；结论2：DM、MN的位置关系是；拓展与探究：（3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明参见解析；（2）相等，垂直；（3）成立，理由参见解析.【解析】试题分析：（1）根据正方形的性质以及等腰直角三角形的知识证明出CE=CF，继而证明出△ABE≌△ADF，得到AE=AF，从而证明出△AEF是等腰三角形；（2）DM、MN的数量关系是相等，利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直，利用三角形外角性质和等腰三角形两个底角相等性质，及全等三角形对应角相等即可得出结论；（3）成立，连接AE，交MD于点G，标记出各个角，首先证明出MN∥AE，MN=12AE，利用三角形全等证出AE=AF，而DM=12AF，从而得到DM，MN数量相等的结论，再利用三角形外角性质和三角形全等，等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°．从而得到DM、MN的位置关系是垂直.试题解析：（1）∵四边形ABCD是正方形，∴AB=AD=BC=CD，∠B=∠ADF=90°，∵△CEF 是等腰直角三角形，∠C=90°，∴CE=CF，∴BC﹣CE=CD﹣CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，∴△AEF是等腰三角形；（2）DM、MN的数量关系是相等，DM、MN的位置关系是垂直；∵在Rt△ADF中DM是斜边AF的中线，∴AF=2DM，∵MN 是△AEF的中位线，∴AE=2MN，∵AE=AF，∴DM=MN；∵∠DMF=∠DAF+∠ADM，AM=MD，∵∠FMN=∠FAE，∠DAF=∠BAE，∴∠ADM=∠DAF=∠BAE，∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°，∴DM⊥MN；（3）（2）中的两个结论还成立，连接AE，交MD于点G，∵点M为AF的中点，点N为EF的中点，∴MN∥AE，MN=12AE，由已知得，AB=AD=BC=CD，∠B=∠ADF，CE=CF，又∵BC+CE=CD+CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，在Rt△ADF中，∵点M为AF的中点，∴DM=12AF，∴DM=MN，∵△ABE≌△ADF，∴∠1=∠2，∵AB∥DF，∴∠1=∠3，同理可证：∠2=∠4，∴∠3=∠4，∵DM=AM，∴∠MAD=∠5，∴∠DGE=∠5+∠4=∠MAD+∠3=90°，∵MN∥AE，∴∠DMN=∠DGE=90°，∴DM⊥MN．所以（2）中的两个结论还成立.考点：1.正方形的性质；2.全等三角形的判定与性质；3.三角形中位线定理；4.旋转的性质．。

九年级上错题集文档

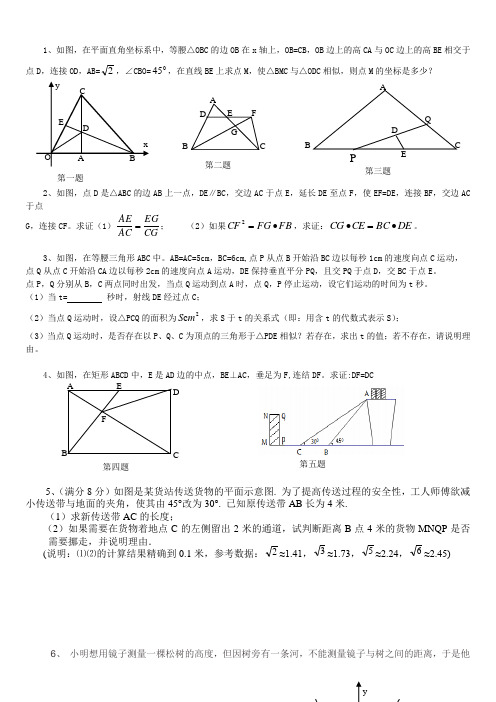
1、如图，在平面直角坐标系中，等腰△OBC 的边OB 在x 轴上，OB=CB ，OB 边上的高CA 与OC 边上的高BE 相交于点D ，连接OD ，AB=2，∠CBO=045，在直线BE 上求点M ，使△BMC 与△ODC 相似，则点M 的坐标是多少？2、如图，点D 是△ABC 的边AB 上一点，DE ∥BC ，交边AC 于点E ，延长DE 至点F ，使EF=DE ，连接BF ，交边AC 于点G ，连接CF 。

求证（1）CGEG AC AE =；（2）如果FB FG CF ∙=2，求证：DE BC CE CG ∙=∙。

3、如图，在等腰三角形ABC 中。

AB=AC=5cm ，BC=6cm,点P 从点B 开始沿BC 边以每秒1cm 的速度向点C 运动，点Q 从点C 开始沿CA 边以每秒2cm 的速度向点A 运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交BC 于点E 。

点P ，Q 分别从B ，C 两点同时出发，当点Q 运动到点A 时，点Q ，P 停止运动，设它们运动的时间为t 秒。

（1）当t= 秒时，射线DE 经过点C ；（2）当点Q 运动时，设△PCQ 的面积为2c m S ，求S 于t 的关系式（即：用含t 的代数式表示S ）；（3）当点Q 运动时，是否存在以P 、Q 、C 为顶点的三角形于△PDE 相似？若存在，求出t 的值；若不存在，请说明理由。

4、如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为F,连结DF 。

求证:DF=DC5、（满分8分）如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB 长为4米.（1）求新传送带AC 的长度；（2）如果需要在货物着地点C 的左侧留出2米的通道，试判断距离B 点4米的货物MNQP 是否需要挪走，并说明理由．(说明：⑴⑵的计算结果精确到0.1米，参考数据：2≈1.41，3≈1.73，5≈2.24，6≈2.45)6、小明想用镜子测量一棵松树的高度，但因树旁有一条河，不能测量镜子与树之间的距离，于是他第一题 Q EC B AD P 第三题 B FE DC A 第四题 CD G F BE A 第二题第五题两次利用镜子，如图所示，第一次他把镜子放在C 点，人在F 点时正好在镜子中看到树尖A ；第二次把镜子放在D 点，人在G 点正好看到树尖A．已知小明的眼睛距离地面1.70m ，量得CD=12m ，CF=1.8m ，DH=3.8m ．请你求出松树的高．7如图，二次函数 x x y 31322-=的图像经过△AOB 的三个顶点，其中A(-1，m)，B(n ，n) （1）求点A 、B 的坐标；（2）在坐标平面上找点C 使点A 、O 、B 、C 为顶点的四边形使平行四边形。

九年级上册数学一元二次方程易错题(Word版含答案)

程，
，P 不返回，Q 返回，表示好 PB，CQ 的长，用面积公式列方程，
，两点都返回，表示好 PB，CQ 的长，用面积公式列方程即可得到答案．
【详解】
解：（1）
，
.
根据三角形的面积公式，得
，
即
，
整理，得
，
解得
，
.
故当为 5 或 7 时，
的面积等于 35 .
（2）根据勾股定理，得
，
整理，得
，
解得
，
平方，把方程②分解因式，建立方程求 n，要注意 n 的值要使方程②的根是整数.
【详解】
若存在 n 满足题意.
设 x1，x2 是方程①的两个根，则 x1+x2=2n，x1x2= 3n 2 ，所以(x1-x2)2=4n2+3n+2， 4
由方程②得，(x+n-1)[x-2(n+1)]=0，
①若 4n2+3n+2=-n+1，解得 n=- 1 ，但 1-n= 3 不是整数，舍.
九年级上册数学一元二次方程易错题（Word 版含答案）
一、初三数学一元二次方程易错题压轴题（难）
1．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P 从点 A 开始沿 AB 边向点 B 以 1 cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2 cm/s 的速度移动．如果 P、 Q 分别从 A、B 同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．
①当 x≥40 时， (x 24)480 20(x 40) 7680 ，
解得： x1 40, x2 48;
②当 x 40 时， (x 24)480 40(40 x) 7680，

九年级上册二次函数易错题(Word版含答案)

九年级上册二次函数易错题（Word版含答案）一、初三数学二次函数易错题压轴题（难）1．如图，抛物线y＝﹣x2+bx+c与x轴交于A，B两点，其中A（3，0），B（﹣1，0），与y轴交于点C，抛物线的对称轴交x轴于点D，直线y＝kx+b1经过点A，C，连接CD．（1）求抛物线和直线AC的解析式：（2）若抛物线上存在一点P，使△ACP的面积是△ACD面积的2倍，求点P的坐标；（3）在抛物线的对称轴上是否存在一点Q，使线段AQ绕Q点顺时针旋转90°得到线段QA1，且A1好落在抛物线上？若存在，求出点Q的坐标；若不存在，请说明理由．【答案】（1）2y x2x3=-++；3y x=-+；（2）（﹣1，0）或（4，﹣5）；（3）存在；（1，2）和（1，﹣3）【解析】【分析】（1）将点A，B坐标代入抛物线解析式中，求出b，c得出抛物线的解析式，进而求出点C 的坐标，再将点A，C坐标代入直线AC的解析式中，即可得出结论；（2）利用抛物线的对称性得出BD＝AD，进而判断出△ABC的面积和△ACP的面积相等，即可得出结论；（3）分点Q在x轴上方和在x轴下方，构造全等三角形即可得出结论．【详解】解：（1）把A（3，0），B（﹣1，0）代入y＝﹣x2+bc+c中，得93010b cb c-++=⎧⎨--+=⎩，∴23bc=⎧⎨=⎩，∴抛物线的解析式为y＝﹣x2+2x+3，当x＝0时，y＝3，∴点C的坐标是（0，3），把A（3，0）和C（0，3）代入y＝kx+b1中，得11303k bb+=⎧⎨=⎩，∴113kb=-⎧⎨=⎩∴直线AC的解析式为y＝﹣x+3；（2）如图，连接BC，∵点D是抛物线与x轴的交点，∴AD＝BD，∴S△ABC＝2S△ACD，∵S△ACP＝2S△ACD，∴S△ACP＝S△ABC，此时，点P与点B重合，即：P（﹣1，0），过B点作PB∥AC交抛物线于点P，则直线BP的解析式为y＝﹣x﹣1①，∵抛物线的解析式为y＝﹣x2+2x+3②，联立①②解得，1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩，∴P（4，﹣5），∴即点P的坐标为（﹣1，0）或（4，﹣5）；（3）如图，①当点Q在x轴上方时，设AC与对称轴交点为Q'，由（1）知，直线AC的解析式为y＝﹣x+3，当x＝1时，y＝2，∴Q'坐标为（1，2），∵Q'D＝AD＝BD＝2，∴∠Q'AB＝∠Q'BA＝45°，∴∠AQ'B＝90°，∴点Q'为所求，②当点Q在x轴下方时，设点Q（1，m），过点A1'作A1'E⊥DQ于E，∴∠A1'EQ＝∠QDA＝90°，∴∠DAQ+∠AQD＝90°，由旋转知，AQ＝A1'Q，∠AQA1'＝90°，∴∠AQD+∠A1'QE＝90°，∴∠DAQ＝∠A1'QE，∴△ADQ≌△QEA1'（AAS），∴AD＝QE＝2，DQ＝A1'E＝﹣m，∴点A1'的坐标为（﹣m+1，m﹣2），代入y＝﹣x2+2x+3中，解得，m＝﹣3或m＝2（舍），∴Q的坐标为（1，﹣3），∴点Q的坐标为（1，2）和（1，﹣3）．【点睛】本题考查的是二次函数的综合题，涉及解析式的求解，与三角形面积有关的问题，三角形“k”字型全等，解题的关键是利用数形结合的思想，设点坐标并结合几何图形的性质列式求解．2．如图1，抛物线y＝mx2﹣3mx+n（m≠0）与x轴交于点C（﹣1，0）与y轴交于点B （0，3），在线段OA上有一动点E（不与O、A重合），过点E作x轴的垂线交直线AB 于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）分别求出抛物线和直线AB的函数表达式；（2）设△PMN的面积为S1，△AEN的面积为S2，当1236 25SS时，求点P的坐标；（3）如图2，在（2）的条件下，将线段OE绕点O逆时针旋转的到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E'A+23E'B的最小值．【答案】（1）抛物线y ＝﹣34 x 2+94 x +3，直线AB 解析式为y ＝﹣34x +3；（2）P （2，32）；（3【解析】【分析】（1）由题意令y ＝0，求出抛物线与x 轴交点，列出方程即可求出a ，根据待定系数法可以确定直线AB 解析式；（2）根据题意由△PNM ∽△ANE ，推出65PN AN =，以此列出方程求解即可解决问题；（3）根据题意在y 轴上取一点M 使得OM′＝43，构造相似三角形，可以证明AM′就是E′A+23E′B 的最小值．【详解】解：（1）∵抛物线y ＝mx 2﹣3mx+n （m≠0）与x 轴交于点C （﹣1，0）与y 轴交于点B （0，3），则有330n m m n ⎧⎨⎩++＝＝，解得433m n ⎧⎪⎨⎪-⎩＝＝， ∴抛物线239344y x x =-++，令y ＝0，得到239344x x -++＝0，解得：x ＝4或﹣1， ∴A （4，0），B （0，3），设直线AB 解析式为y ＝kx+b ，则340b k b +⎧⎨⎩＝＝，解得334k b ⎧-⎪⎨⎪⎩＝＝， ∴直线AB 解析式为y ＝34-x+3．（2）如图1中，设P （m ，239344m m -++），则E （m ，0），∵PM ⊥AB ，PE ⊥OA ， ∴∠PMN ＝∠AEN ， ∵∠PNM ＝∠ANE ， ∴△PNM ∽△ANE ，∵△PMN 的面积为S 1，△AEN 的面积为S 2，123625S S ＝， ∴65PN AN =， ∵NE ∥OB ， ∴AN AEAB OA=， ∴AN ＝54545454（4﹣m ），∵抛物线解析式为y ＝239344x x -++， ∴PN ＝239344m m -++﹣（34-m+3）＝34-m 2+3m ， ∴2336455(4)4m mm -+=-，解得m ＝2或4（舍弃）， ∴m ＝2， ∴P （2，32）．（3）如图2中，在y 轴上取一点M′使得OM′＝43，连接AM′，在AM′上取一点E′使得OE′＝OE ．∵OE′＝2，OM′•OB ＝43×3＝4， ∴OE′2＝OM′•OB ， ∴OE OBOM OE '=''， ∵∠BOE′＝∠M′OE′， ∴△M′OE′∽△E′OB ，∴M E OE BE OB '''='＝23， ∴M′E′＝23BE′，∴AE′+23BE′＝AE′+E′M′＝AM′，此时AE′+23BE′最小（两点间线段最短，A 、M′、E′共线时），最小值＝AM′2244()3+410．【点睛】本题属于二次函数综合题，考查相似三角形的判定和性质、待定系数法、最小值问题等知识，解题的关键是构造相似三角形，找到线段AM ′就是AE′+23BE′的最小值，属于中考压轴题．3．如图，直线y ＝12x ﹣2与x 轴交于点B ，与y 轴交于点A ，抛物线y ＝ax 2﹣32x+c 经过A ，B 两点，与x 轴的另一交点为C ．（1）求抛物线的解析式；（2）M 为抛物线上一点，直线AM 与x 轴交于点N ，当32MN AN =时，求点M 的坐标；（3）P 为抛物线上的动点，连接AP ，当∠PAB 与△AOB 的一个内角相等时，直接写出点P 的坐标．【答案】（1）y＝12x2﹣32x﹣2；（2）点M的坐标为：（5，3）或（﹣2，3）或（2，﹣3）或（1，﹣3）；（3）点P的坐标为：（﹣1，0）或（32，﹣258）或（173，509）或（3，﹣2）．【解析】【分析】（1）根据题意直线y＝12x﹣2与x轴交于点B，与y轴交于点A，则点A、B的坐标分别为：（0，-2）、（4，0），即可求解；（2）由题意直线MA的表达式为：y＝（12m﹣32）x﹣2，则点N（43m-，0），当MNAN＝32时，则NHON＝32，即4343mmm---＝32，进行分析即可求解；（3）根据题意分∠PAB=∠AOB=90°、∠PAB=∠OAB、∠PAB=∠OBA三种情况，分别求解即可．【详解】解：（1）直线y＝12x﹣2与x轴交于点B，与y轴交于点A，则点A、B的坐标分别为：（0，﹣2）、（4，0），则c＝﹣2，将点B的坐标代入抛物线表达式并解得：a＝12，故抛物线的表达式为：y＝12x2﹣32x﹣2①；（2）设点M（m，12m2﹣32m﹣2）、点A（0，﹣2），将点M、A的坐标代入一次函数表达式：y＝kx+b并解得：直线MA的表达式为：y＝（12m﹣32）x﹣2，则点N（43m-，0），当MNAN＝32时，则NHON＝32，即：4343mmm---＝32，解得：m＝5或﹣2或2或1，故点M的坐标为：（5，3）或（﹣2，3）或（2，﹣3）或（1，﹣3）；（3）①∠PAB＝∠AOB＝90°时，则直线AP的表达式为：y＝﹣2x﹣2②，联立①②并解得：x＝﹣1或0（舍去0），故点P（﹣1，0）；②当∠PAB＝∠OAB时，当点P在AB上方时，无解；当点P在AB下方时，将△OAB沿AB折叠得到△O′AB，直线OA交x轴于点H、交抛物线为点P，点P为所求，则BO＝OB＝4，OA＝OA＝2，设OH＝x，则sin∠H＝BO OAHB HA'=，即：2444x x=++，解得：x＝83，则点H（﹣83，0），．则直线AH的表达式为：y＝﹣34x﹣2③，联立①③并解得：x＝32，故点P（32，﹣258）；③当∠PAB＝∠OBA时，当点P在AB上方时，则AH＝BH，设OH＝a，则AH＝BH＝4﹣a，AO＝2，故（4﹣a）2＝a2+4，解得：a＝32，故点H（32，0），则直线AH的表达式为：y＝43x﹣2④，联立①④并解得：x＝0或173（舍去0），故点P（173，509）；当点P在AB下方时，同理可得：点P（3，﹣2）；综上，点P的坐标为：（﹣1，0）或（32，﹣258）或（173，509）或（3，﹣2）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、解直角三角形、勾股定理的运用等，要注意分类讨论，解题全面．4．如图，抛物线y=﹣x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．【答案】(1)抛物线的解析式为：y=﹣x2+x+2(2)存在，P1（，4），P2（，），P3（，﹣）(3)当点E运动到（2，1）时，四边形CDBF的面积最大，S四边形CDBF的面积最大=．【解析】试题分析：（1）将点A、C的坐标分别代入可得二元一次方程组，解方程组即可得出m、n的值；（2）根据二次函数的解析式可得对称轴方程，由勾股定理求出CD的值，以点C为圆心，CD为半径作弧交对称轴于P1；以点D为圆心CD为半径作圆交对称轴于点P2，P3；作CH 垂直于对称轴与点H，由等腰三角形的性质及勾股定理就可以求出结论；（3）由二次函数的解析式可求出B点的坐标，从而可求出BC的解析式，从而可设设E点的坐标，进而可表示出F的坐标，由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式，由二次函数的性质就可以求出结论．试题解析：（1）∵抛物线y=﹣x2+mx+n经过A（﹣1，0），C（0，2）．解得：，∴抛物线的解析式为：y=﹣x2+x+2；（2）∵y=﹣x2+x+2，∴y=﹣（x﹣）2+，∴抛物线的对称轴是x=．∴OD=．∵C（0，2），∴OC=2．在Rt△OCD中，由勾股定理，得CD=．∵△CDP是以CD为腰的等腰三角形，∴CP1=CP2=CP3=CD．作CH⊥x轴于H，∴HP1=HD=2，∴DP1=4．∴P1（，4），P2（，），P3（，﹣）；（3）当y=0时，0=﹣x2+x+2∴x1=﹣1，x2=4，∴B（4，0）．设直线BC的解析式为y=kx+b，由图象，得，解得：，∴直线BC 的解析式为：y=﹣x+2．如图2，过点C 作CM ⊥EF 于M ，设E （a ，﹣a+2），F （a ，﹣a 2+a+2）， ∴EF=﹣a 2+a+2﹣（﹣a+2）=﹣a 2+2a （0≤x≤4）． ∵S 四边形CDBF =S △BCD +S △CEF +S △BEF =BD•OC+EF•CM+EF•BN ， =+a （﹣a 2+2a ）+（4﹣a ）（﹣a 2+2a ）， =﹣a 2+4a+（0≤x≤4）．=﹣（a ﹣2）2+∴a=2时，S 四边形CDBF 的面积最大=， ∴E （2，1）．考点：1、勾股定理；2、等腰三角形的性质；3、四边形的面积；4、二次函数的最值5．定义：对于已知的两个函数，任取自变量x 的一个值，当0x ≥时，它们对应的函数值相等；当0x <时，它们对应的函数值互为相反数，我们称这样的两个函数互为相关函数.例如：正比例函数y x =，它的相关函数为(0)(0)x x y x x ≥⎧=⎨-<⎩. （1）已知点()5,10A -在一次函数5y ax =-的相关函数的图像上，求a 的值；（2）已知二次函数2142y x x =-+-. ①当点3,2B m ⎛⎫ ⎪⎝⎭在这个函数的相关函数的图像上时，求m 的值；②当33x -≤≤时，求函数2142y x x =-+-的相关函数的最大值和最小值. （3）在平面直角坐标系中，点M 、N 的坐标分别为1,12⎛⎫-⎪⎝⎭、9,12⎛⎫ ⎪⎝⎭，连结MN .直接写出线段MN 与二次函数24y x x n =-++的相关函数的图像有两个公共点时n 的取值范围.【答案】（1）1；（2）①22- ；②max 432y =，min 12y =-；（3）31n -<≤-，514n <≤【解析】【分析】（1）先求出5y ax =-的相关函数，然后代入求解，即可得到答案；（2）先求出二次函数的相关函数，①分为m ＜0和m ≥0两种情况将点B 的坐标代入对应的关系式求解即可；②当-3≤x ＜0时，y=x 2-4x+12，然后可此时的最大值和最小值，当0≤x≤3时，函数y=-x 2+4x-12，求得此时的最大值和最小值，从而可得到当-3≤x≤3时的最大值和最小值；（3）首先确定出二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值，然后结合函数图象可确定出n 的取值范围．【详解】解：（1）根据题意，一次函数5y ax =-的相关函数为5,(0)5,(0)ax x y ax x -≥⎧=⎨-+<⎩， ∴把点()5,10A -代入5y ax =-+，则(5)510a -⨯-+=，∴1a =；（2）根据题意，二次函数2142y x x =-+-的相关函数为2214,(0)214,(0)2x x x y x x x ⎧-+-≥⎪⎪=⎨⎪-+<⎪⎩， ①当m ＜0时，将B （m ，32）代入y=x 2-4x+12得m 2-4m+1322=，解得：m=2当m≥0时，将B （m ，32）代入y=-x 2+4x-12得：-m 2+4m-12=32，解得：或m=2．综上所述：m=25-或m=22+或m=22-．②当-3≤x ＜0时，y=x 2-4x+12，抛物线的对称轴为x=2，此时y 随x 的增大而减小， ∴当3x =-时，有最大值，即2143(3)4(3)22y =--⨯-+=， ∴此时y 的最大值为432．当0≤x≤3时，函数y=-x 2+4x 12-，抛物线的对称轴为x=2，当x=0有最小值，最小值为12-，当x=2时，有最大值，最大值y=72．综上所述，当-3≤x≤3时，函数y=-x 2+4x 12-的相关函数的最大值为432，最小值为12-；（3）如图1所示：线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有1个公共点．∴当x=2时，y=1，即-4+8+n=1，解得n=-3．如图2所示：线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有3个公共点．∵抛物线y=x 2-4x-n 与y 轴交点纵坐标为1，∴-n=1，解得：n=-1．∴当-3＜n≤-1时，线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点．如图3所示：线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有3个公共点．∵抛物线y=-x2+4x+n经过点（0，1），∴n=1．如图4所示：线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点．∵抛物线y=x2-4x-n经过点M（12，1），∴14+2-n=1，解得：n=54．∴1＜n≤54时，线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点．综上所述，n的取值范围是-3＜n≤-1或1＜n≤54．【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系，求得二次函数y=-x2+4x+n的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n的值是解题的关键．6．如图，抛物线y=ax2+bx+2经过点A(−1，0)，B(4，0)，交y轴于点C；（1）求抛物线的解析式(用一般式表示)；（2）点D为y轴右侧抛物线上一点，是否存在点D使S△ABC=23S△ABD?若存在，请求出点D坐标；若不存在，请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长.【答案】（1）213222y x x =-++（2）存在，D （1，3）或（2，3）或（5，3-）（3）10【解析】【分析】（1）由A 、B 的坐标，利用待定系数法可求得抛物线解析式；（2）由条件可求得点D 到x 轴的距离，即可求得D 点的纵坐标，代入抛物线解析式可求得D 点坐标；（3）由条件可证得BC ⊥AC ，设直线AC 和BE 交于点F ，过F 作FM ⊥x 轴于点M ，则可得BF=BC ，利用平行线分线段成比例可求得F 点的坐标，利用待定系数法可求得直线BE 解析式，联立直线BE 和抛物线解析式可求得E 点坐标，则可求得BE 的长．【详解】解：（1）∵抛物线y=ax 2+bx+2经过点A （-1，0），B （4，0），∴2016420a b a b -+=⎧⎨++=⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线解析式为：213222y x x =-++；（2）由题意可知C （0，2），A （-1，0），B （4，0），∴AB=5，OC=2，∴S △ABC =12AB•OC=12×5×2=5， ∵S △ABC =23S △ABD ， ∴S △ABD =315522⨯=，设D （x ，y ）， ∴11155222AB y y •=⨯•=，解得：3y =；当3y =时，2132322y x x =-++=，解得：1x =或2x =，∴点D 的坐标为：（1，3）或（2，3）；当3y =-时，2132322y x x =-++=-，解得：5x =或2x =-（舍去），∴点D 的坐标为：（5，-3）；综合上述，点D 的坐标为：（1，3）或（2，3）或（5，-3）；（3）∵AO=1，OC=2，OB=4，AB=5，∴22125AC =+=,222425BC =+=，∴222AC BC AB +=，∴△ABC 为直角三角形，即BC ⊥AC ，如图，设直线AC 与直线BE 交于点F ，过F 作FM ⊥x 轴于点M ，由题意可知∠FBC=45°，∴∠CFB=45°，∴25CF BC ==∴AO AC OM CF =，即1525OM = 解得：2OM =， ∴OC AC FM AF =，即2535FM = 解得：6FM =，∴点F 为（2，6），且B 为（4，0），设直线BE 解析式为y=kx+m ，则2640k m k m +=⎧⎨+=⎩，解得312k m =-⎧⎨=⎩，∴直线BE解析式为：312y x =-+；联立直线BE 和抛物线解析式可得：231213222y x y x x =-+⎧⎪⎨=-++⎪⎩，解得：40x y =⎧⎨=⎩或53x y =⎧⎨=-⎩， ∴点E 坐标为：(5,3)-， ∴22(54)(3)10BE =-+-=.【点睛】本题为二次函数的综合应用，涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）中求得D 点的纵坐标是解题的关键，在（3）中由条件求得直线BE 的解析式是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，有一定的难度．7．如图①抛物线y ＝ax 2+bx +4（a ≠0）与x 轴，y 轴分别交于点A （﹣1，0），B （4，0），点C 三点．（1）试求抛物线的解析式；（2）点D （3，m ）在第一象限的抛物线上，连接BC ，BD ．试问，在对称轴左侧的抛物线上是否存在一点P ，满足∠PBC ＝∠DBC ？如果存在，请求出点P 点的坐标；如果不存在，请说明理由；（3）点N 在抛物线的对称轴上，点M 在抛物线上，当以M 、N 、B 、C 为顶点的四边形是平行四边形时，请直接写出点M 的坐标．【答案】（1）y ＝﹣x 2+3x +4；（2）存在．P （﹣34，1916）．（3）1539(,)24M -- 21139(,)24M - 3521(,)24M 【解析】【分析】（1）将A,B,C 三点代入y ＝ax 2+bx+4求出a,b,c 值，即可确定表达式；（2）在y轴上取点G，使CG＝CD＝3，构建△DCB≌△GCB，求直线BG的解析式，再求直线BG与抛物线交点坐标即为P点，（3）根据平行四边形的对边平行且相等，利用平移的性质列出方程求解，分情况讨论.【详解】解：如图：（1）∵抛物线y＝ax2+bx+4（a≠0）与x轴，y轴分别交于点A（﹣1，0），B（4，0），点C三点．∴4016440a ba b-+=⎧⎨++=⎩解得13ab=-⎧⎨=⎩∴抛物线的解析式为y＝﹣x2+3x+4．（2）存在．理由如下：y＝﹣x2+3x+4＝﹣（x﹣32）2+254．∵点D（3，m）在第一象限的抛物线上，∴m＝4，∴D（3，4），∵C（0，4）∵OC＝OB，∴∠OBC＝∠OCB＝45°．连接CD，∴CD∥x轴，∴∠DCB＝∠OBC＝45°，∴∠DCB＝∠OCB，在y轴上取点G，使CG＝CD＝3，再延长BG交抛物线于点P，在△DCB和△GCB中，CB＝CB，∠DCB＝∠OCB，CG＝CD，∴△DCB≌△GCB（SAS）∴∠DBC＝∠GBC．设直线BP解析式为y BP＝kx+b（k≠0），把G（0，1），B（4，0）代入，得k＝﹣14，b＝1，∴BP解析式为y BP＝﹣14x+1．y BP＝﹣14x+1，y＝﹣x2+3x+4当y＝y BP时，﹣14x+1＝﹣x2+3x+4，解得x1＝﹣34，x2＝4（舍去），∴y＝1916，∴P（﹣34，1916）．（3）1539 (,)24M--21139 (,) 24M-3521 (,) 24M理由如下，如图B(4，0),C(0，4) ，抛物线对称轴为直线32x=，设N(32，n)，M(m, ﹣m2+3m+4)第一种情况：当MN与BC为对边关系时，MN∥BC,MN=BC,∴4-32=0-m，∴m=52-∴﹣m2+3m+4=39 4 -,∴1539 (,)24M--；或∴0-32=4-m，∴m=11 2∴﹣m2+3m+4=39 4 -,∴21139 (,) 24M-；第二种情况：当MN与BC为对角线关系，MN与BC交点为K,则K(2,2)，∴322 2m∴m=5 2∴﹣m2+3m+4=21 4∴3521 (,) 24M综上所述，当以M、N、B、C为顶点的四边形是平行四边形时，点M的坐标为1539 (,)24M--21139 (,) 24M-3521 (,) 24M.【点睛】本题考查二次函数与图形的综合应用，涉及待定系数法，函数图象交点坐标问题，平行四边形的性质，方程思想及分类讨论思想是解答此题的关键.8．如图，在平面直角坐标系中，二次函数y＝﹣x2+6x﹣5的图象与x轴交于A、B两点，与y轴交于点C，其顶点为P，连接PA、AC、CP，过点C作y轴的垂线l．（1）P的坐标，C的坐标；（2）直线1上是否存在点Q，使△PBQ的面积等于△PAC面积的2倍？若存在，求出点Q 的坐标；若不存在，请说明理由．【答案】（1）（3，4），（0，﹣5）；（2）存在，点Q的坐标为：（92，﹣5）或（212，﹣5）【解析】【分析】（1）利用配方法求出顶点坐标，令x=0，可得y=-5，推出C（0，-5）；（2）直线PC的解析式为y=3x-5，设直线交x轴于D，则D（53，0），设直线PQ交x轴于E，当BE=2AD时，△PBQ的面积等于△PAC的面积的2倍，分两种情形分别求解即可解决问题．【详解】解：（1）∵y＝﹣x2+6x﹣5＝﹣（x﹣3）2+4，∴顶点P（3，4），令x＝0得到y＝﹣5，∴C（0，﹣5）．故答案为：（3，4），（0，﹣5）；（2）令y＝0，x2﹣6x+5＝0，解得：x＝1或x＝5，∴A（1，0），B（5，0），设直线PC的解析式为y＝kx+b，则有534 bk b=-⎧⎨+=⎩，解得：35 kb=⎧⎨=-⎩，∴直线PC的解析式为：y＝3x﹣5，设直线交x轴于D，则D（53，0），设直线PQ交x轴于E，当BE＝2AD时，△PBQ的面积等于△PAC的面积的2倍，∵AD＝23，∴BE＝43，∴E（113，0）或E′（193，0），则直线PE的解析式为：y＝﹣6x+22，∴Q（92，﹣5），直线PE ′的解析式为y ＝﹣65x +385， ∴Q ′（212，﹣5），综上所述，满足条件的点Q 的坐标为：（92，﹣5）或（212，﹣5）；【点睛】本题考查抛物线与x 轴的交点、二次函数的性质等知识，解题的关键是熟练掌握待定系数法，学会用转化的思想思考问题，属于中考常考题型．9．如图，已知二次函数1L ：()22311y mx mx m m =+-+≥和二次函数2L ：()2341y m x m =--+-()1m ≥图象的顶点分别为M 、N ，与x 轴分别相交于A 、B 两点（点A 在点B 的左边）和C 、D 两点（点C 在点D 的左边），（1）函数()22311y mx mx m m =+-+≥的顶点坐标为______；当二次函数1L ，2L 的y 值同时随着x 的增大而增大时，则x 的取值范围是_______；（2）判断四边形AMDN 的形状（直接写出，不必证明）；（3）抛物线1L ，2L 均会分别经过某些定点；①求所有定点的坐标；②若抛物线1L 位置固定不变，通过平移抛物线2L 的位置使这些定点组成的图形为菱形，则抛物线2L 应平移的距离是多少？【答案】（1）()1,41m --+，13x ；（2）四边形AMDN 是矩形；（3）①所有定点的坐标，1L 经过定点()3,1-或()1,1，2L 经过定点()5,1-或()1,1-；②抛物线2L 应平移的距离是423+423-．【解析】【分析】（1）将已知抛物线解析式转化为顶点式，直接得到点M 的坐标；结合函数图象填空；（2）利用抛物线解析式与一元二次方程的关系求得点A 、D 、M 、N 的横坐标，可得AD 的中点为（1，0），MN 的中点为（1，0），则AD 与MN 互相平分，可证四边形AMDN 是矩形；（3）①分别将二次函数的表达式变形为1:(3)(1)1L y m x x =+-+和2:(1)(5)1L y m x x =----，通过表达式即可得出所过定点；②根据菱形的性质可得EH 1=EF=4即可，设平移的距离为x ，根据平移后图形为菱形，由勾股定理可得方程即可求解．【详解】解：（1）12b x a=-=-，顶点坐标M 为(1,41)m --+，由图象得：当13x 时，二次函数1L ，2L 的y 值同时随着x 的增大而增大．故答案为：(1,41)m --+；13x ；（2）结论：四边形AMDN 是矩形．由二次函数21:231(1)L y mx mx m m =+-+和二次函数22:(3)41(1)L y m x m m =--+-解析式可得：A 点坐标为41(1m m ---，0)，D 点坐标为41(3m m -+，0)，顶点M 坐标为(1,41)m --+，顶点N 坐标为(3,41)m -，AD ∴的中点为(1,0)，MN 的中点为(1,0)，AD ∴与MN 互相平分，∴四边形AMDN 是平行四边形，又AD MN =，∴□AMDN 是矩形；（3）①二次函数21:231(3)(1)1L y mx mx m m x x =+-+=+-+，故当3x =-或1x =时1y =，即二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点，二次函数22:(3)41(1)(5)1L y m x m m x x =--+-=----，故当1x =或5x =时1y =-，即二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点，②二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点，二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点，如图：四个定点分别为(3,1)E -、(1,1)F ，(1,1)H -、(5,1)G -，则组成四边形EFGH 为平行四边形， ∴FH ⊥HG ，FH=2，HM=4-x ，设平移的距离为x ，根据平移后图形为菱形，则EH 1=EF=H 1M=4，由勾股定理可得：FH 2+HM 2=FM 2，即22242(4)x =+-，解得：423x =±，抛物线1L 位置固定不变，通过左右平移抛物线2L 的位置使这些定点组成的图形为菱形，则抛物线2L 应平移的距离是423+或423-．【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．10．在平面直角坐标系中，二次函数y ＝ax 2+bx +2的图象与x 轴交于A （﹣3，0），B （1，0）两点，与y 轴交于点C ．（1）求这个二次函数的关系解析式；（2）点P 是直线AC 上方的抛物线上一动点，是否存在点P ，使△ACP 的面积最大？若存在，求出点P 的坐标；若不存在，说明理由；（3）在平面直角坐标系中，是否存在点Q ，使△BCQ 是以BC 为腰的等腰直角三角形？若存在，直接写出点Q 的坐标；若不存在，说明理由；【答案】（1）224233y x x =--+；（2）存在，点P 35,22⎛⎫- ⎪⎝⎭，使△PAC 的面积最大；（3）存在点Q ，使△BCQ 是以BC 为腰的等腰直角三角形．Q 点坐标为：Q 1（2，3），Q 2（3，1），Q 3（﹣1，﹣1），Q 4（﹣2，1）．【解析】【分析】（1）直接把点A （﹣3，0），B （1，0）代入二次函数y ＝ax 2+bx+2求出a 、b 的值即可得出抛物线的解析式；（2）设点P 坐标为（m ，n ），则n ＝﹣23m 2﹣43m+2，连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N ．根据三角形的面积公式得出△PAC 的表达式，再根据二次函数求最大值的方法得出其顶点坐标即可；（3）以BC 为边，在线段BC 两侧分别作正方形，正方形的其他四个顶点均可以使得“△BCQ 是以BC 为腰的等腰直角三角形”，因此有四个点符合题意要求，再过Q 1点作Q 1D ⊥y 轴于点D ，过点Q 2作Q 2E ⊥x 轴于点E ，根据全等三角形的判定定理得出△Q 1CD ≌△CBO ，△CBO ≌△BQ 2E ，故可得出各点坐标．【详解】（1）∵抛物线y ＝ax 2+bx+2过点A （﹣3，0），B （1，0），∴093202a b a b =-+⎧⎨=++⎩ 2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩解得 ∴二次函数的关系解析式为y ＝﹣23x 2﹣43x+2；（2）存在．∵如图1所示，设点P 坐标为（m ，n ），则n ＝﹣23m 2﹣43m+2．连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N ．则PM＝﹣23m2﹣43m+2．，PN＝﹣m，AO＝3．∵当x＝0时，y＝﹣23×0﹣43×0+2＝2，∴OC＝2，∴S△PAC＝S△PAO+S△PCO﹣S△ACO＝12AO•PM+12CO•PN﹣12AO•CO＝12×3×（﹣23m2﹣43m+2）+12×2×（﹣m）﹣12×3×2＝﹣m2﹣3m∵a＝﹣1＜0∴函数S△PAC＝﹣m2﹣3m有最大值∴当m＝﹣2ba＝﹣32时，S△PAC有最大值．∴n＝﹣23m2﹣43m+2＝﹣23×（﹣32）2﹣43×（﹣32）+2＝52，∴存在点P（﹣32，52），使△PAC的面积最大．（3）如图2所示，以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3，则点Q1，Q2，Q3，Q4为符合题意要求的点．过Q1点作Q1D⊥y轴于点D，过点Q2作Q2E⊥x轴于点E，∵∠1+∠2＝90°，∠2+∠3＝90°，∠3+∠4＝90°，∴∠1＝∠3，∠2＝∠4，在△Q1CD与△CBO中，∵11324Q C BC∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△Q1CD≌△CBO，∴Q1D＝OC＝2，CD＝OB＝1，∴OD＝OC+CD＝3，∴Q1（2，3）；同理可得Q4（﹣2，1）；同理可证△CBO≌△BQ2E，∴BE＝OC＝2，Q2E＝OB＝1，∴OE＝OB+BE＝1+2＝3，∴Q2（3，1），同理，Q3（﹣1，﹣1），∴存在点Q，使△BCQ是以BC为腰的等腰直角三角形．Q点坐标为：Q1（2，3），Q2（3，1），Q3（﹣1，﹣1），Q4（﹣2，1）．【点睛】本题考查的是二次函数综合题，涉及到用待定系数法求二次函数解析式，二次函数极值、全等三角形的判定与性质，正方形及等腰直角三角形的性质等知识，涉及面较广，难度较大．。

完整word版-初三上学期数学错题集(一二)及答案

初三上学期数学错题集（一元二次方程）（一） 2012.09.09已打印1、若方程（m-2）x㎡-2+mx2=7是关于x的一元二次方程，则m的值为。

2、根据题意，列出方程：（不必求解，写出一般形式）学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册，求这两年的平均增长率。

3、方程x2=0的实数根有（）A．0个B．1个C．2个D．1个或2个4、下列二次三项式中，是完全平方式的是（填序号）。

①9x2-12xy+4y2；②4y2-4y-1；③x2-25x+5；④2x2-4x+1；5、写出一个一元二次方程，使它的两根：一根是正数，另一根在-2与-1之间。

6、方程（x-2）(x+3)=6的解是（）A．x1=-4,x2=3 B．x1=2,x2=3C．x1=2,x2=-3 D．x1=4,x2=-37、用因式分解法解方程5（x+3)-2x（x+3)=0，可把它化为两个一元一次方程、求解。

初三上学期数学错题集（一元二次方程）（二）2012.09.15已打印1、解方程：（1）3y(y-1)2=2-2y （2）7 x2=21x （3）（x2+1）2-3(x2+1)-28=02、若△ABC的边长都是方程x2-10x+21=0的根，求△ABC的周长。

3、若△ABC 的边长都是方程x 2-7x+12=0的根，求△ABC 的周长。

4、已知P=157m-1,Q= m 2-158m(m 为任意实数)，则P 、Q 的大小关系为（） A ．P<Q B. P=Q C. P>Q D.不能确定 5、关于x 的方程（k+1）x 2+2(k+1) x+k=0无实数根，则k 的取值范围是。

6、已知a 是整数，满足⎩⎨⎧>->+023013a a 试解关于x 的一元二次方程x 2-4=x(ax-3).7、k 为何值时，关于x 的方程（k-1）x 2-(2k+1) x+k+1 = 0（1）有一解？（2）有两个不相等的实数根？8、已知△ABC 的两边AB 、AC 的长是关于x 的一元二次方程x 2-(2k+1) x+k(k+1) = 0的两个实数根，第三边BC 的长为5.（1）k 为何值时，△ABC 是以BC 为斜边的直角三角形？（2）k 为何值时，△ABC 是等腰三角形？并求△ABC 的边长。

初三九年级数学上册数学压轴题易错题(Word版含答案)

初三九年级数学上册数学压轴题易错题（Word 版含答案）一、压轴题1．如图①，A （﹣5，0），OA ＝OC ，点B 、C 关于原点对称，点B （a ，a +1）（a ＞0）．（1）求B 、C 坐标；（2）求证：BA ⊥AC ；（3）如图②，将点C 绕原点O 顺时针旋转α度（0°＜α＜180°），得到点D ，连接DC ，问：∠BDC 的角平分线DE ，是否过一定点？若是，请求出该点的坐标；若不是，请说明理由．2．已知在ABC 中，AB AC =．在边AC 上取一点D ，以D 为顶点、DB 为一条边作BDF A ∠=∠，点E 在AC 的延长线上，ECF ACB ∠=∠．（1）如图（1），当点D 在边AC 上时，请说明①FDC ABD ∠=∠；②DB DF =成立的理由．（2）如图（2），当点D 在AC 的延长线上时，试判断DB 与DF 是否相等？3．如图1，Rt △ABC 两直角边的边长为AC ＝3，BC ＝4．（1）如图2，⊙O 与Rt △ABC 的边AB 相切于点X ，与边BC 相切于点Y ．请你在图2中作出并标明⊙O 的圆心（用尺规作图，保留作图痕迹，不写作法和证明）（2）P 是这个Rt △ABC 上和其内部的动点，以P 为圆心的⊙P 与Rt △ABC 的两条边相切．设⊙P 的面积为S ，你认为能否确定S 的最大值？若能，请你求出S 的最大值；若不能，请你说明不能确定S 的最大值的理由．4．已知：如图1，在O 中，弦2AB =，1CD =，AD BD ⊥．直线,AD BC 相交于点E ．（1）求E ∠的度数；（2）如果点,C D 在O 上运动，且保持弦CD 的长度不变，那么，直线,AD BC 相交所成锐角的大小是否改变？试就以下三种情况进行探究，并说明理由（图形未画完整，请你根据需要补全）．①如图2，弦AB 与弦CD 交于点F ；②如图3，弦AB 与弦CD 不相交：③如图4，点B 与点C 重合．5．在长方形ABCD 中，AB ＝5cm ，BC ＝6cm ，点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动，与此同时，点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动．如果P 、Q 分别从A 、B 同时出发，当点Q 运动到点C 时，两点停止运动．设运动时间为t 秒．（1）填空：______＝______，______＝______（用含t 的代数式表示）；（2）当t 为何值时，PQ 的长度等于5cm ？（3）是否存在t 的值，使得五边形APQCD 的面积等于226cm ？若存在，请求出此时t 的值；若不存在，请说明理由．6．如图，已知矩形ABCD 中，BC =2cm ，AB 3cm ，点E 在边AB 上，点F 在边AD 上，点E 由A 向B 运动，连结EC 、EF ，在运动的过程中，始终保持EC ⊥EF ，△EFG 为等边三角形．（1）求证△AEF ∽△BCE ；（2）设BE 的长为xcm ，AF 的长为ycm ，求y 与x 的函数关系式，并写出线段AF 长的范围；（3）若点H 是EG 的中点，试说明A 、E 、H 、F 四点在同一个圆上，并求在点E 由A 到B 运动过程中，点H 移动的距离．7．如图，Rt ABC ∆中，90C ∠=︒，4AC =，3BC =.点P 从点A 出发，沿着A C B →→运动，速度为1个单位/s ，在点P 运动的过程中，以P 为圆心的圆始终与斜边AB 相切,设⊙P 的面积为S ，点P 的运动时间为t （s ）（07t <<）.（1）当47t <<时，BP = ；（用含t 的式子表示）（2）求S 与t 的函数表达式；（3）在⊙P 运动过程中，当⊙P 与三角形ABC 的另一边也相切时，直接写出t 的值.8．如图，Rt △ABC ，CA ⊥BC ，AC ＝4，在AB 边上取一点D ，使AD ＝BC ，作AD 的垂直平分线，交AC 边于点F ，交以AB 为直径的⊙O 于G ，H ，设BC ＝x ．（1）求证：四边形AGDH 为菱形；（2）若EF ＝y ，求y 关于x 的函数关系式；（3）连结OF ，CG ．①若△AOF 为等腰三角形，求⊙O 的面积；②若BC ＝3，则30CG+9＝______．（直接写出答案）．9．如图，在▱ABCD 中，AB ＝4，BC ＝8，∠ABC ＝60°．点P 是边BC 上一动点，作△PAB 的外接圆⊙O 交BD 于E ．（1）如图1，当PB＝3时，求PA的长以及⊙O的半径；（2）如图2，当∠APB＝2∠PBE时，求证：AE平分∠PAD；（3）当AE与△ABD的某一条边垂直时，求所有满足条件的⊙O的半径．10．已知抛物线y＝﹣14x2+bx+c经过点A（4，3），顶点为B，对称轴是直线x＝2．（1）求抛物线的函数表达式和顶点B的坐标；（2）如图1，抛物线与y轴交于点C，连接AC，过A作AD⊥x轴于点D，E是线段AC上的动点（点E不与A，C两点重合）；（i）若直线BE将四边形ACOD分成面积比为1：3的两部分，求点E的坐标；（ii）如图2，连接DE，作矩形DEFG，在点E的运动过程中，是否存在点G落在y轴上的同时点F恰好落在抛物线上？若存在，求出此时AE的长；若不存在，请说明理由．11．如图，一次函数122y x=-+的图象交y轴于点A，交x轴于点B点，抛物线2y x bx c=-++过A、B两点．（1）求A，B两点的坐标；并求这个抛物线的解析式；（2）作垂直x轴的直线x＝t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．12．在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形．例如，下图中的矩形A1B1C1D1，A2B2C2D2，AB3C3D3都是点A，B，C的覆盖矩形，其中矩形AB3C3D3是点A，B，C的最优覆盖矩形．（1）已知A（﹣2，3），B（5，0），C（t，﹣2）．①当t＝2时，点A，B，C的最优覆盖矩形的面积为；②若点A，B，C的最优覆盖矩形的面积为40，求直线AC的表达式；（2）已知点D（1，1）．E（m，n）是函数y＝4x（x＞0）的图象上一点，⊙P是点O，D，E的一个面积最小的最优覆盖矩形的外接圆，求出⊙P的半径r的取值范围．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）点B（3，4），点C（﹣3，﹣4）；（2）证明见解析；（3）定点（4，3）；理由见解析．【解析】【分析】（1）由中心对称的性质可得OB＝OC＝5，点C（﹣a，﹣a﹣1），由两点距离公式可求a的值，即可求解；（2）由两点距离公式可求AB ，AC ，BC 的长，利用勾股定理的逆定理可求解；（3）由旋转的性质可得DO ＝BO ＝CO ，可得△BCD 是直角三角形，以BC 为直径，作⊙O ，连接OH ，DE 与⊙O 交于点H ，由圆周角定理和角平分线的性质可得∠HBC ＝∠CDE ＝45°＝∠BDE ＝∠BCH ，可证CH ＝BH ，∠BHC ＝90°，由两点距离公式可求解．【详解】解：（1）∵A （﹣5，0），OA ＝OC ，∴OA ＝OC ＝5，∵点B 、C 关于原点对称，点B （a ，a +1）（a ＞0），∴OB ＝OC ＝5，点C （﹣a ，﹣a ﹣1），∴5＝()()220+10a a -+-，∴a ＝3，∴点B （3，4），∴点C （﹣3，﹣4）；（2）∵点B （3，4），点C （﹣3，﹣4），点A （﹣5，0），∴BC ＝10，AB ＝45 ，AC ＝25，∵BC 2＝100，AB 2+AC 2＝80+20＝100，∴BC 2＝AB 2+AC 2，∴∠BAC ＝90°，∴AB ⊥AC ；（3）过定点，理由如下：∵将点C 绕原点O 顺时针旋转α度（0°＜α＜180°），得到点D ，∴CO ＝DO ，又∵CO ＝BO ，∴DO ＝BO ＝CO ，∴△BCD 是直角三角形，∴∠BDC ＝90°，如图②，以BC 为直径，作⊙O ，连接OH ，DE 与⊙O 交于点H ，∵DE 平分∠BDC ，∴∠BDE ＝∠CDE ＝45°，∴∠HBC ＝∠CDE ＝45°＝∠BDE ＝∠BCH ，∴CH ＝BH ，∠BHC ＝90°，∵BC ＝10，∴BH ＝CH ＝52，OH ＝OB ＝OC ＝5，设点H （x ，y ），∵点H 在第四象限，∴x ＜0，y ＞0，∴x 2+y 2＝25，（x ﹣3）2+（y ﹣4）2＝50，∴x ＝4，y ＝3，∴点H （4，﹣3），∴∠BDC 的角平分线DE 过定点H （4，3）．【点睛】本题是几何变换综合题，考查了中心对称的性质，直角三角形的性质，角平分线的性质，圆的有关知识，勾股定理的逆定理，两点距离公式等知识，灵活运用这些性质解决问题是本题的关键．2．（1）见解析；（2）DB DF =【解析】【分析】（1）①直接利用三角形的外角性质，即可得到；②过D 作DG BC 交AB 于点G ，由等腰三角形的性质，平行线的性质和等边对等角，得到BG DC =，DGB FCD ∠=∠，然后证明三角形全等，即可得到结论成立；（2）连接BF ，根据题意，可证得BCF BDF A ∠=∠=∠，则B 、C 、D 、F 四点共圆，即可证明结论成立.【详解】解：（1）①∵BDC A ABD ∠=∠+∠，即BDF FDC A ABD ∠+∠=∠+∠，∵BDF A ∠=∠，∴FDC ADB ∠=∠；②过D 作DG BC 交AB 于点G ，∴ADG ACB ∠=∠，AGD ABC ∠=∠，又AB AC =，∴A ABC CB =∠∠，∴AGD ADG∠=∠，∴AD AG=，∴AB AG AC AD-=-，∴BG DC=，又ECF ACB AGD∠=∠=∠，∴DGB FCD∠=∠，在GDB△与CFD△中，,,DGB FCDGB CDGBD FDC∠=∠⎧⎪=⎨⎪∠=∠⎩∴()GDB CFD ASA△≌△∴DB DF=；（2）证明：如图：连接BF，由（1）可知，AABC CB=∠∠，∵ECF ACB∠=∠，∴ABC ECF∠=∠，∵BCA CA BCF E F=∠+∠∠+∠，∴A BCF∠=∠，∴BDF A BCF∠=∠=∠，∴B、C、D、F四点共圆，∴180DCB DFB∠+∠=︒，DBF ECF∠=∠，∴ACB DFB∠=∠，∵BC EC ACA F B=∠=∠∠，∴DBF DFB∠=∠，∴DB DF=.【点睛】本题考查了四点共圆的知识，等腰三角形的性质，全等三角形的判定和性质，平行线的性质，以及三角形外角性质，解题的关键是熟练掌握所学的知识，正确作出辅助线，从而得到角的关系，再进行证明.3．(1)作图见解析；（2）49π.【解析】试题分析：（1）作出∠B的角平分线BD，再过X作OX⊥AB，交BD于点O，则O点即为⊙O的圆心；（2）由于⊙P与△ABC哪两条边相切不能确定，故应分⊙P与Rt△ABC的边AB和BC相切；⊙P与Rt△ABC的边AB和AC相切时；⊙P与Rt△ABC的边BC和AC相切时三种情况进行讨论．试题解析：（1）如图所示：①以B为圆心，以任意长为半径画圆，分别交BC、AB于点G、H；②分别以G、H为圆心，以大于23GH为半径画圆，两圆相交于D，连接BD；③过X作OX⊥AB，交直线BD于点O，则点O即为⊙O的圆心．（2）①当⊙P与Rt△ABC的边AB和BC相切时，由角平分线的性质可知，动点P是∠ABC的平分线BM上的点，如图1，在∠ABC的平分线BM上任意确定点P1（不为∠ABC 的顶点）∵OX=BOsin∠ABM，P1Z=BPsin∠ABM，当BP1＞BO时，P1Z＞OX即P与B的距离越大，⊙P 的面积越大，这时，BM与AC的交点P是符合题意的、BP长度最大的点；如图2，∵∠BPA＞90°，过点P作PE⊥AB，垂足为E，则E在边AB上，∴以P为圆心、PC为半径作圆，则⊙P与CB相切于C，与边AB相切于E，即这时⊙P是符合题意的圆，时⊙P的面积就是S的最大值，∵AC=1，BC=2，∴5设PC=x，则PA=AC-PC=1-x在直角△APE中，PA2=PE2+AE2，∴（1-x）2=x2+5）2，∴5；②如图3，同理可得：当⊙P 与Rt △ABC 的边AB 和AC 相切时，设PC=y ，则（2-y ）2=y 2+（5-1）2，∴y=512-； ③如图4，同理可得，当⊙P 与Rt △ABC 的边BC 和AC 相切时，设PF=z ，∵△APF ∽△PBE ，∴PF ：BE=AF ：PE ，∴， ∴z=49．由①、②、③可知，49＞512-＞∴z ＞y ＞x ， ∴⊙P 的面积S 的最大值为π．考点:1. 切线的性质；2.角平分线的性质；3.勾股定理；4.作图—复杂作图．4．（1）60E ∠=︒（2）①结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．②结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．③结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．【解析】【分析】（1）根据AD BD ⊥得到AB 是直径，连接OC 、OD ，发现等边三角形，再根据圆周角定理求得30EBD ∠=︒，再进一步求得E ∠的度数；（2）分别画出三种图形，图2中，根据圆周角定理和圆内接四边形的性质可以求得；图3中，根据三角形的外角的性质和圆周角定理可以求得；图4中，根据切线的性质发现直角三角形，根据直角三角形的两个锐角互余求得．【详解】解：（1）连接OC 、OD ，如图：∵AD BD ⊥∴AB 是直径∴1OC OD CD ===∴OCD 是等边三角形∴60COD ∠=︒∴30DBE ∠=︒∴60E ∠=︒（2）①结论：直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒证明：连接OD 、OC 、AC ，如图：∵1OD OC CD ===∴OCD 为等边三角形∴60COD ∠=︒∴30DAC ∠=︒∴30EBD ∠=︒∵90ADB ∠=︒∴903060E ∠=︒-︒=︒②结论：直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒证明：连接OC 、OD ，如图：∵AD BD ⊥∴AB 是直径∴1OC OD CD === ∴OCD 是等边三角形∴60COD ∠=︒∴30DBE ∠=︒∴903060BED ∠=︒-︒=︒③结论：直线AD 、BC 相交所成锐角的大小不发生改变依然是60︒ 证明：如图：∵当点B 与点C 重合时，则直线BE 与O 只有一个公共点 ∴EB 恰为O 的切线∴90ABE ∠=︒∵90ADB ∠=︒，1CD =，2AD =∴30A ∠=︒∴60E ∠=︒．故答案是：（1）60E ∠=︒（2）①结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．②结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．③结论：直线AD 、BC 相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．【点睛】本题考查了圆周角定理、等边三角形的判定、圆内接四边形的性质．此题主要是能够根据圆周角定理的推论发现AB 是直径，进一步发现等边COD △，从而根据圆周角定理以及圆内接四边形的性质求解．5．（1）BQ ,2tcm ,PB ,()5t cm -；（2）当t ＝0秒或2秒时，PQ 的长度等于5cm ；（3）存在t ＝1秒，能够使得五边形APQCD 的面积等于226cm ．理由见解析.【解析】【分析】（1）根据点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动，与此同时，点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动，可以求得BQ ,PB .（2）用含t 的代数式分别表示PB 和BQ 的值，运用勾股定理求得PQ 为22(5)(2)t t -+＝25据此求出t 值.（3）根据题干信息使得五边形APQCD 的面积等于226cm 的t 值存在，利用长方形ABCD 的面积减去PBQ △的面积即可，有PBQ △的面积为4，由此求得t 值.【详解】解：（1）点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动，故BQ 为2tcm ,点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动，AB ＝5cm ，故PB 为()5t cm -.（2）由题意得：22(5)(2)t t -+＝25，解得：1t ＝0，2t ＝2；当t ＝0秒或2秒时，PQ 的长度等于5cm ；（3）存在t ＝1秒，能够使得五边形APQCD 的面积等于226cm ．理由如下：长方形ABCD 的面积是：56⨯＝()230cm ，使得五边形APQCD 的面积等于226cm ，则PBQ △的面积为3026-＝()24cm ，()15242t t -⨯⨯=，解得：1t ＝4（不合题意舍去），2t ＝1．即当t ＝1秒时，使得五边形APQCD 的面积等于226cm ．【点睛】本题结合长方形考查动点问题，其本质运用代数式求值，利用含t 的代数式表示各自线段的直接，根据题干数量关系即可确立等量关系式，从而求出t 值.6．（1）详见解析；（2）21y 2x =-,302AF ≤≤；(3)3. 【解析】【分析】（1）由∠A =∠B =90°，∠AFE =∠BEC ，得△AEF ∽△BCE ；（2）由（1）△AEF ∽BCE 得AF AEBE BC =，2y x x =，即212y x =-+，然后求函数最值；（3）连接FH ，取EF 的中点M ，证MA =ME =MF =MH ，则A 、E 、H 、F 在同一圆上；连接AH ，证∠EFH =30°由A 、E 、H 、F 在同一圆上，得∠EAH =∠EFH =30°，线段AH 即为H 移动的路径，在直角三角2AB 【详解】解：（1）在矩形ABCD 中，∠A =∠B =90°，∴∠AEF +∠AFE =90°，∵EF ⊥CE ，∴∠AEF +∠BEC =90°，∴∠AFE =∠BEC ，∴△AEF ∽△BCE ；（2）由（1）△AEF ∽BEC 得AF AE BE BC =，232y x x -=， ∴2132y x x =-+， ∵2132y x x =-+=213(3)22x --+，当3x =时，y 有最大值为32， ∴302AF ≤≤；（3）如图1，连接FH ，取EF 的中点M ，在等边三角形EFG 中，∵点H 是EG 的中点，∴∠EHF =90°，∴ME =MF =MH ，在直角三角形AEF 中，MA =ME =MF ，∴MA =ME =MF =MH ，则A 、E 、H 、F 在同一圆上；如图2，连接AH ，∵△EFG 为等边三角形，H 为EG 中点，∴∠EFH =30°∵A 、E 、H 、F 在同一圆上∴∠EAH =∠EFH =30°，如图2所示的线段AH 即为H 移动的路径，2AB ∵AB=∴AH =3，所以点H 移动的距离为3．【点睛】此题主要考查圆的综合问题，会证明三角形相似，会分析四点共圆，会运用二次函数分析最值，会分析最短轨迹并解直角三角形是得分的关键．7．（1）7-t （2）()()()22904;25{1674725t t S t t ππ<≤=-<<（3）516,23t t == 【解析】【分析】（1）先判断出点P 在BC 上，即可得出结论；（2）分点P 在边AC 和BC 上两种情况：利用相似三角形的性质得出比例式建立方程求解即可得出结论；（3）分点P 在边AC 和BC 上两种情况：借助（2）求出的圆P 的半径等于PC ，建立方程求解即可得出结论．【详解】（1）∵AC =4，BC =3，∴AC +BC =7．∵4＜t ＜7，∴点P 在边BC 上，∴BP =7﹣t ．故答案为：7﹣t ；（2）在Rt △ABC 中，AC =4，BC =3，根据勾股定理得：AB =5，由运动知，AP =t ，分两种情况讨论：①当点P 在边AC 上时，即：0＜t ≤4，如图1，记⊙P 与边AB 的切点为H ，连接PH ，∴∠AHP =90°=∠ACB ．∵∠A =∠A ，∴△APH ∽△ACB ，∴PH AP BC AB =，∴35PH t =，∴PH 35=t ，∴S 925=πt 2； ②当点P 在边BC 上时，即：4＜t ＜7，如图，记⊙P 与边AB 的切点为G ，连接PG ，∴∠BGP =90°=∠C ．∵∠B =∠B ，∴△BGP ∽△BCA ，∴PG BP AC AB =，∴745PG t -=，∴PG 45=（7﹣t ），∴S 1625=π（7﹣t ）2．综上所述：S 22904251674725t t t t ππ⎧≤⎪⎪=⎨⎪-⎪⎩（＜）（）（＜＜）；（3）分两种情况讨论：①当点P在边AC上时，即：0＜t≤4，由（2）知，⊙P的半径PH35=t．∵⊙P与△ABC的另一边相切，即：⊙P和边BC相切，∴PC=PH．∵PC=4﹣t，∴4﹣t35=t，∴t52=秒；②当点P在边BC上时，即：4＜t＜7，由（2）知，⊙P的半径PG45=（7﹣t）．∵⊙P与△ABC的另一边相切，即：⊙P和边AC相切，∴PC=PG．∵PC=t﹣4，∴t﹣445=（7﹣t），∴t163=秒．综上所述：在⊙P运动过程中，当⊙P与三角形ABC的另一边也相切时，t的值为52秒或163秒．【点睛】本题是圆的综合题，主要考查了切线的性质，勾股定理，相似三角形的判定和性质，用分类讨论的思想解决问题是解答本题的关键．8．（1）证明见解析；（2）y＝18x2（x＞0）；（3）①163π或8π或（17）π；②21【解析】【分析】（1）根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可；（2）只要证明△AEF∽△ACB，可得AE EFAC BC=解决问题；（3）①分三种情形分别求解即可解决问题；②只要证明△CFG∽△HFA，可得GFAF=CGAH，求出相应的线段即可解决问题；【详解】（1）证明：∵GH垂直平分线段AD，∴HA＝HD，GA＝GD，∵AB是直径，AB⊥GH，∴EG＝EH，∴DG＝DH，∴AG＝DG＝DH＝AH，∴四边形AGDH是菱形．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE⊥EF，∴∠AEF＝∠ACB＝90°，∵∠EAF＝∠CAB，∴△AEF∽△ACB，∴AE EF AC BC=，∴124x yx=，∴y＝18x2（x＞0）．（3）①解：如图1中，连接DF．∵GH垂直平分线段AD，∴FA＝FD，∴当点D与O重合时，△AOF是等腰三角形，此时AB＝2BC，∠CAB＝30°，∴AB83，∴⊙O的面积为163π．如图2中，当AF＝AO时，∵AB＝22AC BC+＝216x+，∴OA＝2 16x +，∵AF＝22EF AE+＝2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭，∴216x+＝2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭，解得x＝4（负根已经舍弃），∴AB＝42，∴⊙O的面积为8π．如图2﹣1中，当点C与点F重合时，设AE＝x，则BC＝AD＝2x，AB＝2164x+，∵△ACE∽△ABC，∴AC2＝AE•AB，∴16＝2164x+解得x2＝17﹣2（负根已经舍弃），∴AB2＝16+4x2＝17+8，∴⊙O的面积＝π•14•AB2＝（17+2）π综上所述，满足条件的⊙O的面积为163π或8π或（217+2）π；②如图3中，连接CG．∵AC＝4，BC＝3，∠ACB＝90°，∴AB＝5，∴OH＝OA＝52，∴AE＝32，∴OE＝OA﹣AE＝1，∴EG＝EH2512⎛⎫-⎪⎝⎭21，∵EF＝18x2＝98，∴FG＝212﹣98，AF22AE EF+158，AH22AE EH+302，∵∠CFG＝∠AFH，∠FCG＝∠AHF，∴△CFG∽△HFA，∴GF CG AF AH=，∴219281530 8-=∴CG 270﹣33010，30＝21．故答案为21【点睛】本题考查圆综合题、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质、菱形的判定和性质、勾股定理、解直角三角形等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，学会用分类讨论的思想思考问题．9．（1）PA O 2）见解析；（3）⊙O 的半径为2或5 【解析】【分析】（1）过点A 作BP 的垂线，作直径AM ，先在Rt △ABH 中求出BH ，AH 的长，再在Rt △AHP 中用勾股定理求出AP 的长，在Rt △AMP 中通过锐角三角函数求出直径AM 的长，即求出半径的值；（2）证∠APB ＝∠PAD ＝2∠PAE ，即可推出结论；（3）分三种情况：当AE ⊥BD 时，AB 是⊙O 的直径，可直接求出半径；当AE ⊥AD 时，连接OB ，OE ，延长AE 交BC 于F ，通过证△BFE ∽△DAE ，求出BE 的长，再证△OBE 是等边三角形，即得到半径的值；当AE ⊥AB 时，过点D 作BC 的垂线，通过证△BPE ∽△BND ，求出PE ，AE 的长，再利用勾股定理求出直径BE 的长，即可得到半径的值．【详解】（1）如图1，过点A 作BP 的垂线，垂足为H ，作直径AM ，连接MP ，在Rt △ABH 中，∠ABH ＝60°，∴∠BAH ＝30°，∴BH＝12AB ＝2，AH ＝AB •sin60°＝ ∴HP ＝BP ﹣BH ＝1，∴在Rt △AHP 中，AP∵AB 是直径，∴∠APM ＝90°，在Rt △AMP 中，∠M ＝∠ABP ＝60°，∴AM ＝APsin 60︒2，∴⊙O 的半径为3，即PA ⊙O （2）当∠APB ＝2∠PBE 时，∵∠PBE ＝∠PAE ，∴∠APB＝2∠PAE，在平行四边形ABCD中，AD∥BC，∴∠APB＝∠PAD，∴∠PAD＝2∠PAE，∴∠PAE＝∠DAE，∴AE平分∠PAD；（3）①如图3﹣1，当AE⊥BD时，∠AEB＝90°，∴AB是⊙O的直径，∴r＝12AB＝2；②如图3﹣2，当AE⊥AD时，连接OB，OE，延长AE交BC于F，∵AD∥BC，∴AF⊥BC，△BFE∽△DAE，∴BFAD ＝EFAE，在Rt△ABF中，∠ABF＝60°，∴AF＝AB•sin60°＝BF＝12AB＝2，∴28，∴EF＝5，在Rt△BFE中，BE，∵∠BOE＝2∠BAE＝60°，OB＝OE，∴△OBE是等边三角形，∴r；③当AE⊥AB时，∠BAE＝90°，∴AE为⊙O的直径，∴∠BPE＝90°，如图3﹣3，过点D作BC的垂线，交BC的延长线于点N，延开PE交AD于点Q，在Rt△DCN中，∠DCN＝60°，DC＝4，∴DN＝DC•sin60°＝CN＝12CD＝2，∴PQ＝DN＝设QE＝x，则PE＝x，在Rt △AEQ 中，∠QAE ＝∠BAD ﹣BAE ＝30°， ∴AE ＝2QE ＝2x ，∵PE ∥DN ，∴△BPE ∽△BND ，∴PE DN ＝BP BN ， ∴2323x -＝BP 10， ∴BP ＝10﹣53x ，在Rt △ABE 与Rt △BPE 中，AB 2+AE 2＝BP 2+PE 2，∴16+4x 2＝（10﹣53x ）2+（23﹣x ）2，解得，x 1＝63（舍），x 2＝3，∴AE ＝23，∴BE ＝22AB AE +＝224(23)+＝27，∴r ＝7，∴⊙O 的半径为2或475或7．【点睛】此题主要考查圆与几何综合，解题的关键是熟知圆的基本性质、勾股定理及相似三角形的判定与性质.10．（1）y＝﹣14x2+x+3，顶点B的坐标为（2，4）；（2）（i）点E的坐标为（85，3）或（125，3）；（ii）存在；当点G落在y轴上的同时点F恰好落在抛物线上，此时AE的长为43．【解析】【分析】（1）由题意得出21441,43,124b cb⎧-⨯++=⎪⎪⎨-=⎪⎛⎫⨯-⎪ ⎪⎝⎭⎩，解得1,3,bc=⎧⎨=⎩，得出抛物线的函数表达式为：y＝﹣14x2+x+3＝﹣14（x﹣2）2+4，即可得出顶点B的坐标为（2，4）；（2）（i）求出C（0，3），设点E的坐标为（m，3），求出直线BE的函数表达式为：y＝12m--x+462mm--，则点M的坐标为（4m﹣6，0），由题意得出OC＝3，AC＝4，OM＝4m﹣6，CE＝m，则S矩形ACOD＝12，S梯形ECOM＝15182m-，分两种情况求出m的值即可；（ii）过点F作FN⊥AC于N，则NF∥CG，设点F的坐标为：（a，﹣14a2+a+3），则NF＝3﹣（﹣14a2+a+3）＝14a2﹣a，NC＝﹣a，证△EFN≌△DGO（ASA），得出NE＝OD＝AC＝4，则AE＝NC＝﹣a，证△ENF∽△DAE，得出NF NEAE AD=，求出a＝﹣43或0，当a＝0时，点E与点A重合，舍去，得出AE＝NC＝﹣a＝43，即可得出结论．【详解】（1）∵抛物线y＝﹣14x2+bx+c经过点A（4，3），对称轴是直线x＝2，∴21441, 43,124b cb⎧-⨯++=⎪⎪⎨-=⎪⎛⎫⨯-⎪ ⎪⎝⎭⎩解得1,3, bc=⎧⎨=⎩∴抛物线的函数表达式为：y＝﹣14x2+x+3，∵y＝﹣14x2+x+3＝﹣14（x﹣2）2+4，∴顶点B的坐标为（2，4）；（2）（i）∵y＝﹣14x2+x+3，∴x＝0时，y＝3，则C点的坐标为（0，3），∵A（4，3），∴AC∥OD，∵AD⊥x，∴四边形ACOD是矩形，设点E的坐标为（m，3），直线BE的函数表达式为：y＝kx+n，直线BE交x轴于点M，如图1所示：则24,3, k nmk n+=⎧⎨+=⎩解得：1,246,2kmmnm-⎧=⎪⎪-⎨-⎪=⎪-⎩，∴直线BE的函数表达式为：y＝12m--x+462mm--，令：y＝12m--x+462mm--＝0，则x＝4m﹣6，∴点M的坐标为（4m﹣6，0），∵直线BE将四边形ACOD分成面积比为1：3的两部分，∴点M在线段OD上，点M不与点O重合，∵C（0，3），A（4，3），M（4m﹣6，0），E（m，3），∴OC＝3，AC＝4，OM＝4m﹣6，CE＝m，∴S矩形ACOD＝OC•AC＝3×4＝12，S梯形ECOM＝12（OM+EC）•OC＝12（4m﹣6+m）×3＝15182m-，分两种情况：①S ECOMS ACOD梯形矩形＝14，即1518212m-＝14，解得：m＝85，∴点E的坐标为：（85，3）；②S ECOMS ACOD梯形矩形＝34，即1518212m-＝34，解得：m＝125，∴点E的坐标为：（125，3）；综上所述，点E的坐标为：（85，3）或（125，3）；（ii）存在点G落在y轴上的同时点F恰好落在抛物线上；理由如下：由题意得：满足条件的矩形DEFG在直线AC的下方，过点F作FN⊥AC于N，则NF∥CG，如图2所示：设点F的坐标为：（a，﹣14a2+a+3），则NF＝3﹣（﹣14a2+a+3）＝14a2﹣a，NC＝﹣a，∵四边形DEFG与四边形ACOD都是矩形，∴∠DAE＝∠DEF＝∠N＝90°，EF＝DG，EF∥DG，AC∥OD，∴∠NEF＝∠ODG，∠EMC＝∠DGO，∵NF∥CG，∴∠EMC＝∠EFN，∴∠EFN＝∠DGO，在△EFN和△DGO中，∠NEF=∠ODG，EF=DG,∠EFN=∠DGO，∴△EFN≌△DGO（ASA），∴NE＝OD＝AC＝4，∴AC﹣CE＝NE﹣CE，即AE＝NC＝﹣a，∵∠DAE＝∠DEF＝∠N＝90°，∴∠NEF+∠EFN＝90°，∠NEF+∠DEA＝90°，∴∠EFN＝∠DEA，∴△ENF∽△DAE，∴NE NFAD AE=，即43＝214a aa--，整理得：34a2+a＝0，解得：a＝﹣43或0，当a＝0时，点E与点A重合，∴a＝0舍去，∴AE＝NC＝﹣a＝43，∴当点G落在y轴上的同时点F恰好落在抛物线上，此时AE的长为43．【点睛】本题是二次函数综合题目，考查了二次函数解析式的求法、二次函数的性质、一次函数解析式的求法、坐标与图形性质、矩形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、梯形面积公式等知识；本题综合性强，属于中考压轴题型． 11．(1) A （0，2），B(4，0)，2722y x x =-++；(2)当t=2时，MN 有最大值4；(3) D 点坐标为（0，6），（0，-2）或（4，4）．【解析】【分析】 (1)首先求得A 、B 的坐标，然后利用待定系数法求抛物线的解析式；(2)本问要点是求得线段MN 的表达式，这个表达式是关于t 的二次函数，利用二次函数的极值求线段MN 的最大值；(3)本问要点是明确D 点的可能位置有三种情况，如答图2所示，其中D 1、D 2在y 轴上，利用线段数量关系容易求得坐标；D 3点在第一象限是直线D 1N 和D 2M 的交点，利用直线解析式求得交点坐标即可．【详解】解：(1)∵122y x =-+的图象交y 轴于点A ，交x 轴于点B 点， ∴A 、B 点的坐标为：A （0，2），B(4，0)，将x=0，y=2代入2y x bx c =-++得c=2，将x=4，y=0,代入2y x bx c =-++得b=72， ∴抛物线解析式为：2722y x x =-++； (2)如答图1所示，设MN 交x 轴于点E ，则E(t ，0)，则M(t ，122t -)，又N 点在抛物线上，且x N =t ，∴2722N y t t =-++， ∴()22271224=2422N M MN y y t t t t t t ⎛⎫=-=-++--=-+--+ ⎪⎝⎭， ∴当t=2时，MN 有最大值4．(3)由(2)可知A （0，2）、M(2，1)、N(2，5)，以A 、M 、N 、D 为顶点做平行四边形，D 点的可能位置有三种情况，如答图2所示，当D在y轴上时，设D的坐标为（0，a），由AD=MN，得|a-2|=4，解得a1=6，a2=-2，从而D点坐标为（0，6）或D（0，-2），当D不在y轴上时，由图可知D3为D1N与D2M的交点，分别求出D1N的解析式为：162y x=-+，D2M的解析式为：322y x=-，联立两个方程得：D3（4，4），故所求的D点坐标为（0，6），（0，-2）或（4，4）．【点睛】本题主要考查的是二次函数综合，经常作为压轴题出现，正确的掌握二次函数的性质是解题的关键．12．（1）35，5784y x=+；（2172r≤.【解析】【分析】（1）①由矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形，得出最优覆盖矩形的长为：2+5=7，宽为3+2=5，即可得出结果；②由定义可知，t=-3或6，即点C坐标为（-3，-2）或（6，-2），设AC表达式为y=kx+b，代入即可求出结果；（2）OD所在的直线交双曲线于点E，矩形OFEG是点O，D，E的一个面积最小的最优覆盖矩形，OD所在的直线表达式为y=x，得出点E的坐标为（2，2），⊙P的半径最小2，当点E的纵坐标为1时，⊙P的半径最大17，即可得出结果．【详解】（1）①∵A（﹣2，3），B（5，0），C（2，﹣2），矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形，∴最优覆盖矩形的长为：2+5＝7，宽为3+2＝5，∴最优覆盖矩形的面积为：7×5＝35；②∵点A，B，C的最优覆盖矩形的面积为40，∴由定义可知，t＝﹣3或6，即点C坐标为（﹣3，﹣2）或（6，﹣2），设AC表达式为y＝kx+b，∴3223k bk b=-+⎧⎨-=-+⎩或3226k bk b=-+⎧⎨-=+⎩∴513kb=⎧⎨=⎩或5874kb⎧=-⎪⎪⎨⎪=⎪⎩∴y＝5x+13或5784y x=-+；（2）①OD所在的直线交双曲线于点E，矩形OFEG是点O，D，E的一个面积最小的最优覆盖矩形，如图1所示：∵点D（1，1），∴OD所在的直线表达式为y＝x，∴点E的坐标为（2，2），∴OE＝222+2=22，∴⊙P的半径最小r＝2，②当DE∥x轴时，即：点E的纵坐标为1，如图2所示：∵点D（1，1）．E（m，n）是函数y＝4x（x＞0）的图象上一点∴1＝4x ，解得x ＝4，∴OE ═，∴⊙P 的半径最大r ＝2，r ≤．【点睛】本题是圆的综合题目，考查了矩形的性质、勾股定理、待定系数法求直线的解析式、坐标与图形性质、反比例函数等知识；本题综合性强，有一定难度．。

人教版九年级上册数学一元二次方程易错题(Word版含答案)

人教版九年级上册数学一元二次方程易错题（Word版含答案）一、初三数学一元二次方程易错题压轴题（难）1．Rt△ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若△PBC与△PAD的面积和是△ABC的面积的79，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与△ABC重叠部分的面积为8，求t的值．【答案】（1）t1＝2，t2＝4；（2）t 47758．【解析】【分析】（1）先求出△ABC的面积，然后根据题意可得AP＝t，CP＝6﹣t，然后再△PBC与△PAD的面积和是△ABC的面积的79，列出方程、解方程即可解答；（2）根据不同时间段分三种情况进行解答即可.【详解】（1）∵Rt△ABC中，∠ACB＝90°，AC＝BC＝6，∴S△ABC＝12×6×6＝18，∵AP＝t，CP＝6﹣t，∴△PBC与△PAD的面积和＝12t2+12×6×（6﹣t），∵△PBC与△PAD的面积和是△ABC的面积的79，∴12t2+12×6×（6﹣t）＝18×79，解之，得t1＝2，t2＝4；（2）∵AP＝t，PQ＝2AP，∴PQ＝2t，①如图1，当0≤t≤2时，S＝（2t）2﹣12t2＝72t2＝8，解得：t1＝477，t2＝﹣477（不合题意，舍去），②如图2，当2≤t≤3时，S＝12×6×6﹣12t2﹣12（6﹣2t）2＝12t﹣25t2＝8，解得：t1＝4（不合题意，舍去），t2＝45（不合题意，舍去），③如图3，当3≤t≤6时，S＝126×6﹣12t2＝8，解得：t1＝25，t2＝﹣25（不合题意，舍去），综上，t的值为477或25时，重叠面积为8．【点睛】本题考查了三角形和矩形上的动点问题，根据题意列出方程和分情况讨论是解答本题的关键.2．阅读与应用：阅读1：a，b为实数，且a＞0，b＞0，因为()2≥0，所以a﹣2+b≥0，从而a+b≥2(当a＝b时取等号)．阅读2：若函数y＝x+(m＞0，x＞0，m为常数)，由阅读1结论可知：x+≥2，所以当x＝，即x＝时，函数y＝x+的最小值为2．阅读理解上述内容，解答下列问题：问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为2(x+)，求当x＝时，周长的最小值为；问题2：汽车的经济时速是汽车最省油的行驶速度，某种汽车在每小时70～110公里之间行驶时(含70公里和110公里)，每公里耗油()L ．若该汽车以每小时x 公里的速度匀速行驶，1h 的耗油量为yL ．(1)求y 关于x 的函数关系式(写出自变量x 的取值范围)； (2)求该汽车的经济时速及经济时速的百公里耗油量．【答案】问题1：2，8；问题2：(1)y=；(2)10.【解析】【分析】（1）利用题中的不等式得到x+=4，从而得到x=2时，周长的最小值为8；（2）根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可，经济时速就是耗油量最小的形式速度．【详解】 (1)∵x +≥2＝4，∴当x ＝时，2(x +)有最小值8．即x ＝2时，周长的最小值为8；故答案是：2；8；问题2：，当且仅当，即x ＝90时，“＝”成立，所以，当x ＝90时，函数取得最小值9，此时，百公里耗油量为，所以，该汽车的经济时速为每小时90公里，经济时速的百公里耗油量为10L ．【点睛】本题考查了配方法及反比例函数的应用，最值问题，解题的关键是读懂题目提供的材料，易错点是了解“耗油总量=每公里的耗油量×行驶的速度”，难度中等偏上．3．问题提出：（1）如图1，在四边形ABCD 中，已知：AD BC ∥，90D ∠=︒，4BC =，ABC 的面积为8，求BC 边上的高．问题探究（2）如图2在（1）的条件下，点E 是CD 边上一点，且2CE =，EAB CBA =∠∠，连接BE ，求ABE △的面积问题解决（3）如图3，在（1）的条件下，点E 是CD 边上任意一点，连接AE 、BE ，若EAB CBA =∠∠，ABE △的面积是否存在最小值；若存在，求出最小值；若不存在；请说明理由．【答案】（1）4；（2）203；（3）存在，最小值为16216- 【解析】【分析】（1）作BC 边上的高AM ，利用三角形面积公式即可求解；（2）延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，易得四边形BCDF 为矩形，在（1）的条件下BC=CD=4，则BCDF 为正方形，由EAB CBA =∠∠，结合∠FAB=∠CBA 可得∠FAB=∠EAB ，从而推出BF=BH=4，易证Rt △BCE ≌Rt △BHE ，所以EH=CE=2，设AD ＝a ，则AF=AH=4-a ，在Rt △ADE 中利用勾股定理建立方程可求出a ，最后根据S △ABE =1AE BH 2即可求解；（3）辅助线同（2），设AD=a ，CE=m ，则DE=4-m ，同（2）可得出m 与a 的关系式，设△ABE 的面积为y ，由y=1AE BH 2得到m 与y 的关系式，再求y 的最小值即可．【详解】（1）如图所示，作BC 边上的高AM ，∵S △ABC =1BC AM=82∴82AM==44⨯ 即BC 边上的高为4；（2）如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，∵AD BC ∥，90D ∠=︒ ∴∠BCD=∠D=90°=∠F ∴四边形BCDF 为矩形，又∵BC=CD=4∴四边形BCDF 为正方形， ∴DF=BF=BC=4，又∵AD ∥BC ∴∠FAB=∠CBA 又∵∠EAB=∠CBA ∴∠FAB=∠EAB ∵BF ⊥AF ，BH ⊥AE ∴BH=BF=4，在Rt △BCE 和Rt △BHE 中， ∵BE=BE ，BH=BC=4 ∴Rt △BCE ≌Rt △BHE （HL ） ∴EH=CE=2同理可证Rt △BAF ≌Rt △BAH （HL ） ∴AF=AH设AD=a ，则AF=AH=4-a在Rt △ADE 中，AD=a ，DE=2，AE=AH+EH=4-a+2=6-a 由勾股定理得AD 2+DE 2=AE 2，即()22226+=-a a解得8=3a∴AE=6-a=103S △ABE =111020AE BH=4=2233⨯⨯ （3）存在，如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，同（2）可得CE=EH ，AF=AH ，设AD=a ，CE=EH=m ，则DE=4-m ，AF=AH=4-a在Rt △ADE 中，AD 2+DE 2=AE 2，即()()22244+-=-+a m a m 整理得8=4+ma m ∴AE=AH+HE=2816444+-+=++m m m m m设△ABE 的面积为y ，则y=()222161116AE BH=42244++=++m m m m ∴()()24216+=+y m m整理得：223240++-=m ym y ∵方程必有实数根∴()2=423240∆-⨯⨯-≥y y整理得2322560+-≥y y∴()()16216162160⎡⎤⎡⎤-----≥⎣⎦⎣⎦y y （注：利用求根公式进行因式分解）又∵面积y ≥0 ∴16216≥-y即△ABE 的面积最小值为16216-．【点睛】本题考查四边形综合问题，正确作出辅助线，得出AB 平分∠FAC ，利用角平分线的性质定理得到BF=BH ，结合勾股定理求出AE 是解决（2）题的关键，（3）题中利用一元二次方程的判别式求最值是解题的关键．4．阅读下列材料计算：（1﹣﹣）×（+）﹣（1﹣﹣）（+），令+＝t ，则：原式＝（1﹣t）（t+）﹣（1﹣t﹣）t＝t+﹣t2﹣+t2＝在上面的问题中，用一个字母代表式子中的某一部分，能达到简化计算的目的，这种思想方法叫做“换元法”，请用“换元法”解决下列问题：（1）计算：（1﹣﹣）×（+）﹣（1﹣﹣）×（+）（2）因式分解：（a2﹣5a+3）（a2﹣5a+7）+4（3）解方程：（x2+4x+1）（x2+4x+3）＝3【答案】（1）；（2）（a2﹣5a+5）2；（3）x1＝0，x2＝﹣4，x3＝x4＝﹣2【解析】【分析】（1）仿照材料内容，令+＝t代入原式计算．（2）观察式子找相同部分进行换元，令a2﹣5a＝t代入原式进行因式分解，最后要记得把t换为a．（3）观察式子找相同部分进行换元，令x2+4x＝t代入原方程，即得到关于t的一元二次方程，得到t的两个解后要代回去求出4个x的解．【详解】（1）令+＝t，则：原式＝（1﹣t）（t+）﹣（1﹣t﹣）t＝t+﹣t2﹣﹣t+t2+＝（2）令a2﹣5a＝t，则：原式＝（t+3）（t+7）+4＝t2+7t+3t+21+4＝t2+10t+25＝（t+5）2＝（a2﹣5a+5）2（3）令x2+4x＝t，则原方程转化为：（t+1）（t+3）＝3t2+4t+3＝3t（t+4）＝0∴t1＝0，t2＝﹣4当x2+4x＝0时，x（x+4）＝0解得：x1＝0，x2＝﹣4当x2+4x＝﹣4时，x2+4x+4＝0（x+2）2＝0解得：x3＝x4＝﹣2【点睛】本题考查用换元法进行整式的运算，因式分解，解一元二次方程．利用换元法一般可达到降次效果，从而简便运算．5．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.6．如图，已知AB是⊙O的弦，半径OA=2，OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根．（1）求弦AB的长度；（2）计算S△AOB；（3）⊙O上一动点P从A点出发，沿逆时针方向运动一周，当S△POA=S△AOB时，求P点所经过的弧长（不考虑点P与点B重合的情形）．【答案】（1）AB=2；（2）S △AOB 33）当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π．【解析】试题分析：（1）OA 和AB 的长度是一元二次方程的根，所以利用一元二次方程的根与系数的关系即可求出AB 的长度；（2）作出△AOB 的高OC ，然后求出OC 的长度即可求出面积；（3）由题意知：两三角形有公共的底边，要面积相等，即高要相等．试题解析：（1）由题意知：OA 和AB 的长度是x 2﹣4x+a=0的两个实数根， ∴OA+AB=﹣41-=4， ∵OA=2， ∴AB=2；（2）过点C 作OC⊥AB 于点C ，∵OA=AB=OB=2，∴△AOB 是等边三角形，∴AC=12AB=1，在Rt△ACO 中，由勾股定理可得：3△AOB =12AB ﹒OC=1233；（3）延长AO 交⊙O 于点D ，由于△AOB 与△POA 有公共边OA ，当S △POA =S △AOB 时，∴△AOB 与△POA 高相等，由（2）可知：等边△AOB 3P 到直线OA 3，这样点共有3个 ①过点B 作BP 1∥OA 交⊙O 于点P 1，∴∠BOP 1=60°， ∴此时点P 经过的弧长为：1202180π⨯=43π， ②作点P 2，使得P 1与P 2关于直线OA 对称，∴∠P 2OD=60°， ∴此时点P 经过的弧长为：2402180π⨯=83π， ③作点P 3，使得B 与P 3关于直线OA 对称，∴∠P 3OP 2=60°， ∴此时P 经过的弧长为：3002180π⨯ =103π，综上所述：当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π．【点睛】本题主要考查了一元二次方程与圆的综合知识．涉及等边三角形性质，圆的对称性等知识，能综合运用所学知识，选择恰当的方法进行解题是关键．7．图1是李晨在一次课外活动中所做的问题研究：他用硬纸片做了两个三角形，分别为△ABC和△DEF，其中∠B=90°，∠A=45°，BC=，∠F=90°，∠EDF=30°， EF=2．将△DEF 的斜边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上(移动开始时点D与点A重合)．（1）请回答李晨的问题：若CD=10，则AD= ；（2）如图2，李晨同学连接FC，编制了如下问题，请你回答：①∠FCD的最大度数为；②当FC∥AB时，AD= ；③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边时，AD= ;④△FCD的面积s的取值范围是 .【答案】（1）2；（2）① 60°；②；③；④.【解析】试题分析：（1）根据等腰直角三角形的性质，求出AC的长，即可得到AD的长.（2）①当点E与点C重合时，∠FCD的角度最大，据此求解即可.②过点F作FH⊥AC于点H，应用等腰直角三角形的判定和性质，含30度角直角三角形的性质求解即可.③过点F作FH⊥AC于点H，AD=x，应用含30度角直角三角形的性质把FC用x来表示，根据勾股定理列式求解.④设AD=x，把△FCD的面积s表示为x的函数，根据x的取值范围来确定s的取值范围.试题解析：（1）∵∠B=90°，∠A=45°，BC=，∴AC=12.∵CD=10，∴AD=2.（2）①∵∠F=90°，∠EDF=30°，∴∠DEF=60°.∵当点E与点C重合时，∠FCD的角度最大，∴∠FCD的最大度数=∠DEF="60°."② 如图，过点F作FH⊥AC于点H，∵∠EDF=30°， EF=2，∴DF=. ∴DH=3，FH=.∵FC∥AB，∠A=45°，∴∠FCH="45°." ∴HC=. ∴DC=DH+HC=.∵AC=12，∴AD=.③如图，过点F作FH⊥AC于点H，设AD=x，由②知DH=3，FH=，则HC=.在Rt△CFH中，根据勾股定理，得.∵以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边，∴，即，解得.④设AD=x，易知，即.而，当时，；当时，.∴△FCD的面积s的取值范围是.考点：1.面动平移问题；2.等腰直角三角形的判定和性质；3.平行的性质；4.含30度角直角三角形的性质；5.勾股定理；6.由实际问题列函数关系式；7.求函数值.8．如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH 是正方形ABCD的外接正方形．探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．因为正方形ABCD的面积为1，则正方形EFGH的面积为2，所以EF＝FG＝GH＝HE2EB＝x，则BF2﹣x，∵Rt△AEB≌Rt△BFC∴BF＝AE2﹣x在Rt△AEB中，由勾股定理，得x2+2﹣x）2＝12解得，x1＝x2＝2 2∴BE＝BF，即点B是EF的中点．同理，点C，D，A分别是FG，GH，HE的中点．所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）探究三：已知边长为1的正方形ABCD，一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）【答案】不存在，详见解析【解析】【分析】探究二，根据探究一的解答过程、运用一元二次方程计算即可；探究三，根据探究一的解答过程、运用一元二次方程根的判别式解答；探究四，根据探究一的解答过程、运用一元二次方程根的判别式解答．【详解】探究二：因为正方形ABCD的面积为1，则正方形EFGH的面积为3，所以EF=FG=GH=HE3，设EB=x，则BF3x，∵Rt△AEB≌Rt△BFC，∴BF=AE3﹣x，在Rt△AEB中，由勾股定理，得，x 2+x ）2=12，整理得x 2x +1=0，b 2﹣4ac =3﹣4＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的3倍；探究三：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为4，所以EF =FG =GH =HE =2，设EB =x ，则BF =2﹣x ，∵Rt △AEB ≌Rt △BFC ，∴BF =AE =2﹣x ，在Rt △AEB 中，由勾股定理，得，x 2+（2﹣x ）2=12，整理得2x 2﹣4x +3=0，b 2﹣4ac =16﹣24＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的3倍，故答案为不存在；探究四：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为n ，所以EF =FG =GH =HE ，设EB =x ，则BF ﹣x ，∵Rt △AEB ≌Rt △BFC ，∴BF =AE ﹣x ，在Rt △AEB 中，由勾股定理，得，x 2+﹣x ）2=12，整理得2x 2﹣+n ﹣1=0，b 2﹣4ac =8﹣4n ＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的n 倍．【点睛】本题考查了正方形的性质、全等三角形的判定和性质、一元二次方程的解法等知识.读懂探究一的解答过程、正确运用一元二次方程根的判别式是解题的关键．9．已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3，且关于x 的方程2(1)320k x x a -+-=②有实数根，又k 为正整数，求代数式2216k k k -+-的值．【答案】0.【解析】【分析】由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3，利用根与系数的关系可以得到关于a 的方程求出a ，又由于关于x 的方程（k -1）x 2+3x -2a =0有实数根，分两种情况讨论，该方程可能是一次方程、有可能是一元二次方程，又k 为正整数，利用判别式可以求出k ，最后代入所求代数式计算即可求解．【详解】解：设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩＝＝＝，由条件，知12121211x x x x x x ++==3，即33a -=，且94a ≤，故a ＝－1，则方程②为(k -1)x 2+3x +2=0，Ⅰ.当k -1=0时，k =1,x =23-，则22106k k k -=+-. Ⅱ.当k -1≠0时，∆=9-8（k -1）=17-6-8k ≥0，则178k ≤，又k 是正整数，且k ≠1，则k =2，但使2216k k k -+-无意义. 综上，代数式2216k k k -+-的值为0 【点睛】本题综合考查了根的判别式和根与系数的关系，在解方程时一定要注意所求k 的值与方程判别式的关系．要注意该方程可能是一次方程、有可能是一元二次方程，10．如图1，已知△ABC 中，AB=10cm,AC=8cm,BC=6 cm ,如果点P 由B 出发沿BA 方向向点A 匀速运动，同时点Q 由A 出发沿AC 方向向点C 匀速运动，它们的速度均为2cm /s ，连接PQ ，设运动的时间为t （单位：s ）（0≤t≤4）.解答下列问题：（1）当t 为何值时，PQ∥BC．（2）是否存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分？若存在求出此时t 的值；若不存在，请说明理由.（3）如图2，把△APQ 沿AP 翻折，得到四边形AQPQ′.那么是否存在某时刻t 使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由.【答案】（1）当BF PC⊥s时，PQ∥BC．（2）不存在某时刻t，使线段PQ恰好把△ABC 的面积平分．（3）存在时刻t，使四边形AQPQ′为菱形，此时菱形的面积为137-cm2．【解析】（1）证△APQ∽△ABC，推出APAB=AQAC，代入得出10210t-=28t，求出方程的解即可；（2）假设存在某时刻t，使线段PQ恰好把△ABC的面积平分，得出方程-5 6t2+6t=12×12×8×6，求出此方程无解，即可得出答案.（3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ、OD、和PD的长度；然后在Rt△PQD中，根据勾股定理列出方程（8-185t）2-（6-65t）2=（2t）2，求得时间t的值；最后根据菱形的面积等于△AQP的面积的2倍，进行计算即可.解：（1）BP=2t，则AP=10﹣2t．∵PQ∥BC，∴△APQ∽△ABC，∴APAB=AQAC，即10210t-=28t，解得：t=20 9,∴当t=209时，PQ∥BC.（2）如答图1所示，过P点作PD⊥AC于点D．∴PD∥BC，∴F ，即B ，解得6PD 6-5t =． 216625S PD AQ t t =⨯=-，假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，则有S △AQP = C S △ABC ，而S △ABC =12AC•BC=24，∴此时S △AQP =12．而S △AQP 2665t t =-， ∴266125t t -=，化简得：t 2﹣5t+10=0， ∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解，∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）假设存在时刻t ，使四边形AQPQ′为菱形，则有AQ=PQ=BP=2t ．如答图2所示，过P 点作PD⊥AC 于点D ，则有PD∥BC，∴D ，即COD ∆，解得：OC ，h ，∴QD=AD﹣AQ=t ．在Rt△PQD 中，由勾股定理得：QD 2+PD 2=PQ 2，即h ，化简得：13t 2﹣90t+125=0，解得：t 1=5，t 2=t ，∵t=5s 时，AQ=10cm ＞AC ，不符合题意，舍去，∴t=52．由（2）可知，S △AQP =54∴S 菱形AQPQ′=2S △AQP =2×258=3372+cm 2．所以存在时刻t ，使四边形137-cm 2． “点睛”本题考查了三角形的面积，勾股定理的逆定理，相似三角形的性质和判定的应用，主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形，根据相似三角形的对应边成比例以及勾股定理进行列式求解.。

九上数学错题集

九上数学错题集1. 将分数1/2、3/4、5/6和7/8按从小到大的顺序排列。

解析：要比较这些分数的大小，一种方法是找到它们的相同分母，然后比较分子的大小。

另一种方法是将它们转化为小数形式进行比较。

首先，我们将这四个分数转化为相同分母：1/2 = 4/83/4 = 6/85/6 = 10/127/8 = 7/8现在我们可以直接比较分子的大小：4/8 < 6/8 < 10/12 < 7/8所以，按照从小到大的顺序排列，正确答案是1/2, 3/4, 5/6, 7/8。

2. 某购物网站在一次促销活动中，将某商品的原价从200元降价到160元。

促销期间，该商品的销售量增加了40%。

请计算促销期间该商品的销售收入是多少？解析：首先，我们计算降价后的售价：原价 - 降价金额 = 售价200元 - (200元 - 160元) = 160元然后，我们计算促销期间的销售量增加后的销售量：原销售量 + 原销售量 ×销售量增长率 = 新销售量100% + 40% = 140%100 × 1.4 = 140最后，我们计算促销期间的销售收入：售价 ×新销售量 = 销售收入160元 × 140 = 22400元所以，促销期间该商品的销售收入是22400元。

3. 若a:b = 3:4，b:c = 2:5，求a:b:c的值。

解析：已知a:b = 3:4，可以表示为a = 3k，b = 4k，其中k为比例系数。

同样，已知b:c = 2:5，可以表示为b = 2m，c = 5m，其中m为比例系数。

将上述等式代入a:b:c，得：a:b:c = 3k:4k:5m为了使a:b:c的比例系数相同，我们可以选择k和m的最小公倍数，即12，作为比例系数。

代入得：a:b:c = 3 × 12:4 × 12:5 × 12= 36:48:60所以，a:b:c的值为36:48:60。

数学九年级上册一元二次方程易错题(Word版含答案)

数学九年级上册一元二次方程易错题（Word 版含答案）一、初三数学一元二次方程易错题压轴题（难）1．已知:在平面直角坐标系xoy 中,直线k y x b =+分别交x 、y 轴于点A 、B 两点,OA=5,∠OAB=60°.(1)如图1,求直线AB 的解析式；(2)如图2,点P 为直线AB 上一点，连接OP ,点D 在OA 延长线上，分别过点P 、D 作OA 、OP 的平行线,两平行线交于点C ，连接AC,设AD=m,△ABC 的面积为S,求S 与m 的函数关系式; (3)如图3,在(2)的条件下,在PA 上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE 的周长等于22，求S 的值.【答案】(1)直线解析式为353y x =-+(2)S=5325322m +；(3)203S =. 【解析】【分析】(1)先求出点B 坐标，设AB 解析式为y kx b =+，把点A(5，0)，B(0，3分别代入，利用待定系数法进行求解即可；(2)由题意可得四边形ODCP 是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中利用勾股定理可求得CH=)352m +，再由S=12AB •CH 代入相关数据进行整理即可得； (3) 先求得∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，证明△ADK 是等边三角形，继而证明△PEC ≌△DKO ，通过推导可得到OP=OK=CE=CD ，再证明△CDE 是等边三角形，可得CE=CD=DE ，连接OE ，证明△OPE ≌△EDA ，继而可得△OAE 是等边三角形，得到OA=AE=5 ，根据四边形ADCE 的周长等于22，可得ED=172m -，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=，可得关于m 的方程，解方程求得m 的值后即可求得答案.【详解】(1)在Rt △ABO 中OA=5，∠OAB=60°， ∴∠OBA=30°，AB=10 ，由勾股定理可得OB=53，∴B(0，53)，设AB解析式为y kx b=+，把点A(5，0)，B(0，53)分别代入，得0553k bb=+⎧⎪⎨=⎪⎩，∴353kb⎧=-⎪⎨=⎪⎩，∴直线解析式为353y x=-+；(2)∵CP//OD，OP//CD，∴四边形ODCP是平行四边形，∠OAB=∠APC=60°，∴PC=OD=5+m，∠PCH=30°，过点C作CH⊥AB，在Rt△PCH中 PH=52m+，由勾股定理得CH=()35m+，∴S=12AB•CH=135325310(5)2m m⨯⨯+=+；(3) ∵∠ECD=∠OAB=60°，∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°，∴∠PEC=∠ADC，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA延长线上截取AK=AD，连接OK，DK，DE，∵∠DAK=60°，∴△ADK是等边三角形，∴AD=DK=PE，∠ODK=∠APC，∵PC=OD，∴△PEC≌△DKO，∴OK=CE，∠OKD=∠PEC=∠OPC=60°+α，∠AKD= ∠APC=60°，∴∠OPK= ∠OKB，∴OP=OK=CE=CD，又∵∠ECD=60°，∴△CDE是等边三角形，∴CE=CD=DE ，连接OE ，∵ ∠ADE=∠APO ，DE=CD=OP ， ∴△OPE ≌△EDA ， ∴AE=OE ， ∠OAE=60°， ∴△OAE 是等边三角形， ∴OA=AE=5 ，∵四边形ADCE 的周长等于22， ∴AD+2DE=17， ∴ED=172m-，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=，即22253517()()()22m m -++=，解得13m =，221m =-(舍去)， ∴S=153253+=203.【点睛】本题考查的四边形综合题，涉及了待定系数法，平行四边形的判定与性质，勾股定理，全等三角形的判定与性质，等边三角形的判定与性质，解一元二次方程等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.2．已知关于x 的方程x 2﹣（2k +1）x +k 2+1＝0．（1）若方程有两个不相等的实数根，求k 的取值范围；（2）若方程的两根恰好是一个矩形两邻边的长，且k ＝2，求该矩形的对角线L 的长．【答案】（1）k ＞34；（215【解析】【分析】（1）根据关于x 的方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根，得出△＞0，再解不等式即可；（2）当k=2时，原方程x 2-5x+5=0，设方程的两根是m 、n ，则矩形两邻边的长是m 、n ，利用根与系数的关系得出m+n=5，mn=5，，利用完全平方公式进行变形即可求得答案. 【详解】解：（1）∵方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根， ∴Δ＝[－(2k ＋1)]2－4×1×(k 2＋1)＝4k －3＞0， ∴k ＞34； (2)当k ＝2时，原方程为x 2－5x ＋5＝0，设方程的两个根为m ，n ， ∴m ＋n ＝5，mn ＝5，==.【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等，一元二次方程根的情况与判别式△的关系：（1）△＞0时，方程有两个不相等的实数根；（2）△=0时，方程有两个相等的实数根；（3）△＜0时，方程没有实数根．3．我市茶叶专卖店销售某品牌茶叶，其进价为每千克 240 元，按每千克 400 元出售，平均每周可售出 200 千克，后来经过市场调查发现，单价每降低 10 元，则平均每周的销售量可增加 40 千克，若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元，请回答：（1）每千克茶叶应降价多少元？（2）在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？【答案】（1）每千克茶叶应降价30元或80元；（2）该店应按原售价的8折出售．【解析】【分析】（1）设每千克茶叶应降价x 元，利用销售量×每件利润=41600元列出方程求解即可；（2）为了让利于顾客因此应下降价80元，求出此时的销售单价即可确定几折．【详解】（1）设每千克茶叶应降价x 元．根据题意，得：（400﹣x ﹣240）（200+10x×40）=41600．化简，得：x 2﹣10x +240=0．解得：x1=30，x2=80．答：每千克茶叶应降价30元或80元．（2）由（1）可知每千克茶叶可降价30元或80元．因为要尽可能让利于顾客，所以每千克茶叶某应降价80元．此时，售价为：400﹣80=320（元），320100%80% 400⨯=．答：该店应按原售价的8折出售．【点睛】本题考查了一元二次方程的应用，解题的关键是根据题目中的等量关系列出方程．4．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P从点 A 开始沿 AB 边向点 B 以1 cm/s的速度移动，点 Q从点 B开始沿 BC 边向点 C以 2 cm/s的速度移动．如果 P、 Q分别从 A、B同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．（1）当 t 为何值时，△PBQ的面积等于 35cm2？（2）当 t 为何值时，PQ的长度等82cm？（3）若点 P，Q的速度保持不变，点 P在到达点 B后返回点 A，点 Q在到达点 C后返回点B，一个点停止，另一个点也随之停止．问：当 t为何值时，△PCQ的面积等于 32cm2？【答案】（1）t为5或7；（2）t为45或4；（3）t为4或16【解析】【分析】（1）分别用含t的代数式表示PB，BQ的长，利用面积公式列方程求解即可．（2）分别用含t的代数式表示PB，BQ的长，利用勾股定理列方程求解即可．（3）分段要清楚，，P，Q都没有返回，表示好PB，CQ的长，用面积公式列方程，，P不返回，Q返回，表示好PB，CQ的长，用面积公式列方程，，两点都返回，表示好PB，CQ的长，用面积公式列方程即可得到答案．【详解】解：（1），.根据三角形的面积公式，得，即，整理，得，解得，.故当为5或7时，的面积等于35.（2）根据勾股定理，得，整理，得，解得，.故当为或4时，的长度等于.（3）①当时，，，由题意，得，解得：，（舍去）.②当时，，，由题意，得，次方程无解.③当时，，，由题意，得，解得：（舍去），.综上所述，当为4或16时，的面积等于. 【点睛】本题考查的是在运动过程中应用一元二次方程解决实际问题，建立正确情境下的几何模型是解决问题的关键，特别是最后一问，关键是弄懂分段的时间界点，才能正确的表示PB ，CQ 的长．5．已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，请求出这样的n 值；若不存在，请说明理由？【答案】存在，n=0. 【解析】【分析】在方程①中，由一元二次方程的根与系数的关系，用含n 的式子表示出两个实数根的差的平方，把方程②分解因式，建立方程求n ，要注意n 的值要使方程②的根是整数. 【详解】若存在n满足题意.设x1，x2是方程①的两个根，则x1+x2=2n，x1x2=324n+-，所以(x1-x2)2=4n2+3n+2，由方程②得，(x+n-1)[x-2(n+1)]=0，①若4n2+3n+2=-n+1，解得n=-12，但1-n=32不是整数，舍.②若4n2+3n+2=2(n+2)，解得n=0或n=-14 (舍)，综上所述，n=0.6．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.7．（本题满分10分）如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程－18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．（1）求点A，C的坐标；（2）若反比例函数y=的图象经过点E，求k的值；（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．【答案】(1)、A（12，0），C（﹣6，0）；(2)、k=36；(3)、6个；Q1（10，﹣12），Q2（﹣3，6﹣3）.【解析】试题分析：(1)、首先求出方程的解，根据OA＞OC求出两点的坐标；(2)、根据∠ABO的正切值求出OB的长度，根据Rt△AOB得出AB的长度，作EM⊥x轴，根据三角形相似得出点E的坐标，然后求出k的值；(3)、分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q.试题解析：（1）由题意，解方程得：x1=6，x2=12．∵OA＞OC，∴OA=12，OC=6．∴A（12，0），C（﹣6，0）；（2）∵tan∠ABO=，∠AOB=90°∴∴OB=16．在Rt△AOB中，由勾股定理，得AB=20∵BE=5，∴AE=15．如图1，作EM⊥x轴于点M，∴EM∥OB．∴△AEM∽△ABO，∴，即：∴EM=12，AM=9，∴OM=12﹣9=3．∴E（3，12）．∴k=36；（3）满足条件的点Q的个数是6，x轴的下方的Q1（10，﹣12），Q2（﹣3，6﹣3）；方法：如下图①分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；（有三种）②以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q；（有三种）如图①∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴EG2=CG•G P，∴GP=16，∵△CPE与△PCQ是中心对称，∴CH=GP=16，QH=FG=12，∵OC=6，∴OH=10，∴Q（10，﹣12），如图②作MN∥x轴，交EG于点N，EH⊥y轴于点H ∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴CE=15，∵MN=CG=，可以求得PH=3﹣6，同时可得PH=QR ，HE=CR ∴Q （﹣3，6﹣3），考点：三角形相似的应用、三角函数、一元二次方程.8．某建材销售公司在2019年第一季度销售,A B 两种品牌的建材共126件，A 种品牌的建材售价为每件6000元，B 种品牌的建材售价为每件9000元.（1）若该销售公司在第一季度售完两种建材后总销售额不低于96.6万元，求至多销售A 种品牌的建材多少件？（2）该销售公司决定在2019年第二季度调整价格，将A 种品牌的建材在上一个季度的基础上下调%a ，B 种品牌的建材在上一个季度的基础上上涨%a ；同时，与（1）问中最低销售额的销售量相比，A 种品牌的建材的销售量增加了1%2a ，B 种品牌的建材的销售量减少了2%5a ，结果2019年第二季度的销售额比（1）问中最低销售额增加2%23a ，求a 的值.【答案】（1）至多销售A 品牌的建材56件;(2)a 的值是30. 【解析】【分析】（1）设销售A 品牌的建材x 件，根据售完两种建材后总销售额不低于96.6万元，列不等式求解；（2）根据题意列出方程求解即可. 【详解】（1）设销售A 品牌的建材x 件.根据题意，得()60009000126966000x x +-≥，解这个不等式，得56x ≤，答：至多销售A 品牌的建材56件.（2）在（1）中销售额最低时，B 品牌的建材70件，根据题意，得()()()12260001%561%90001%701%6000569000701%2523a a a a a ⎛⎫⎛⎫⎛⎫-⨯+++⨯-=⨯+⨯+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令%a y =，整理这个方程，得21030y y -=，解这个方程，得1230,10y y ==， ∴10a =（舍去），230a =，即a 的值是30. 【点睛】本题考查了一元二次方程和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系和不等关系，列方程组和不等式求解．9．如图，某农家拟用已有的长为8m的墙或墙的一部分为一边，其它三边用篱笆围成一个面积为12m2的矩形园子．设园子中平行于墙面的篱笆长为ym（其中y≥4），另两边的篱笆长分别为xm．（1）求y关于x的函数表达式，并求x的取值范围．（2）若仅用现有的11m长的篱笆，且恰好用完，请你帮助设计围制方案．【答案】（1）y＝；1.5≤x≤3；（2）长为8m，宽为1.5m．【解析】【分析】（1）由矩形的面积公式可得出y关于x的函数表达式，结合4≤y≤8可求出x的取值范围；（2）由篱笆的长可得出y＝（11﹣2x）m，利用矩形的面积公式结合矩形园子的面积，即可得出关于x的一元二次方程，解之取其较小值即可得出结论．【详解】（1）∵矩形的面积为12m2，∴y＝．∵4≤y≤8，∴1.5≤x≤3．（2）∵篱笆长11m，∴y＝（11﹣2x）m．依题意，得：xy＝12，即x（11﹣2x）＝12，解得：x1＝1.5，x2＝4（舍去），∴y＝11﹣2x＝8．答：矩形园子的长为8m，宽为1.5m．【点睛】本题考查了一元二次方程的应用以及反比例函数的应用，解题的关键是：（1）利用矩形的面积公式，找出y关于x的函数表达式；（2）找准等量关系，正确列出一元二次方程．10．如图1，已知△ABC中，AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm /s，连接PQ，设运动的时间为t（单位：s）（0≤t≤4）.解答下列问题：（1）当t为何值时，PQ∥BC．（2）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在求出此时t的值；若不存在，请说明理由.（3）如图2，把△APQ沿AP翻折，得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由.【答案】（1）当BF PC ⊥s 时，PQ∥BC．（2）不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）存在时刻t ，使四边形AQPQ′为菱形，此时菱形的面积为1372-cm 2．【解析】（1）证△APQ∽△ABC，推出AP AB =AQ AC ，代入得出10210t -=28t ，求出方程的解即可；（2）假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，得出方程-56t 2+6t=12×12×8×6，求出此方程无解，即可得出答案. （3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ 、OD 、和PD 的长度；然后在Rt△PQD 中，根据勾股定理列出方程（8-185t ）2-（6-65t ）2=（2t ）2，求得时间t 的值；最后根据菱形的面积等于△AQP 的面积的2倍，进行计算即可.解：（1）BP=2t ，则AP=10﹣2t ． ∵PQ∥BC，∴△APQ∽△ABC， ∴AP AB =AQ AC ，即10210t -=28t ，解得：t=209, ∴当t=209时，PQ∥BC. （2）如答图1所示，过P 点作PD⊥AC 于点D ．∴PD∥BC，∴F ，即B ，解得6PD 6-5t =． 216625S PD AQ t t =⨯=-，假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，则有S △AQP = C S △ABC ，而S △ABC =12AC•BC=24，∴此时S △AQP =12．而S △AQP 2665t t =-， ∴266125t t -=，化简得：t 2﹣5t+10=0， ∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解，∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）假设存在时刻t ，使四边形AQPQ′为菱形，则有AQ=PQ=BP=2t ．如答图2所示，过P 点作PD⊥AC 于点D ，则有PD∥BC，∴D ，即COD ∆，解得：OC ，h ，∴QD=AD﹣AQ=t ．在Rt△PQD 中，由勾股定理得：QD 2+PD 2=PQ 2，即h ，化简得：13t 2﹣90t+125=0，解得：t 1=5，t 2=t ，∵t=5s 时，AQ=10cm ＞AC ，不符合题意，舍去，∴t=52．由（2）可知，S △AQP =54∴S 菱形AQPQ′=2S △AQP =2×258=32+cm 2．所以存在时刻t ，使四边形cm 2． “点睛”本题考查了三角形的面积，勾股定理的逆定理，相似三角形的性质和判定的应用，主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形，根据相似三角形的对应边成比例以及勾股定理进行列式求解.。

九年级上册数学圆几何综合易错题(Word版含答案)

九年级上册数学圆几何综合易错题（Word版含答案）一、初三数学圆易错题压轴题（难）1．如图，抛物线的对称轴为轴，且经过(0，0)，()两点，点P在抛物线上运动，以P为圆心的⊙P经过定点A(0，2)，(1)求的值；(2)求证：点P在运动过程中，⊙P始终与轴相交；(3)设⊙P与轴相交于M，N(＜)两点，当△AMN为等腰三角形时，求圆心P的纵坐标．【答案】（1）a=，b=c=0；（2）证明见解析；（3）P的纵坐标为0或4+2或4﹣2．【解析】试题分析：（1）根据题意得出二次函数一般形式进而将已知点代入求出a，b，c的值即可；（2）设P（x，y），表示出⊙P的半径r，进而与x2比较得出答案即可；（3）分别表示出AM，AN的长，进而分别利用当AM=AN时，当AM=MN时，当AN=MN 时，求出a的值，进而得出圆心P的纵坐标即可．试题解析：（1）∵抛物线y=ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，∴抛物线的一般式为：y=ax2，∴=a（）2，解得：a=±，∵图象开口向上，∴a=，∴抛物线解析式为：y=x2，故a=，b=c=0；（2）设P（x，y），⊙P的半径r=，又∵y=x2，则r=，化简得：r=＞x2，∴点P在运动过程中，⊙P始终与x轴相交；（3）设P（a，a2），∵PA=，作PH⊥MN于H，则PM=PN=，又∵PH=a2，则MH=NH==2，故MN=4，∴M（a﹣2，0），N（a+2，0），又∵A（0，2），∴AM=，AN=，当AM=AN时，=，解得：a=0，当AM=MN时，=4，解得：a=2±2（负数舍去），则a2=4+2；当AN=MN时，=4，解得：a=﹣2±2（负数舍去），则a2=4﹣2；综上所述，P的纵坐标为0或4+2或4﹣2．考点：二次函数综合题．2．在直角坐标系中，A（0，4），B（4，0）．点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动，同时点D从点A出发沿AO方向以每秒1个单位的速度向点O 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点C、D运动的时间是t秒(t>0)．过点C作CE⊥BO于点E，连结CD、DE．⑴当t为何值时，线段CD的长为4；⑵当线段DE与以点O为圆心，半径为的⊙O有两个公共交点时，求t的取值范围；⑶当t为何值时，以C为圆心、CB为半径的⊙C与⑵中的⊙O相切？【答案】(1); (2) 4-＜t≤; (3)或．【解析】试题分析：（1）过点C作CF⊥AD于点F，则CF，DF即可利用t表示出来，在Rt△CFD中利用勾股定理即可得到一个关于t的方程，从而求得t的值；（2）易证四边形ADEC是平行四边形，过点O作OG⊥DE于点G，当线段DE与⊙O相切时，则OG=，在直角△OEG中，OE可以利用t表示，则OG也可以利用t表示出来，当OG＜时，直线与圆相交，据此即可求得t的范围；（3）分两圆外切与内切两种情况进行讨论，当外切时，圆心距等于两半径的和，当内切时，圆心距等于圆C的半径减去圆O的半径，列出方程即可求得t的值．（1）过点C作CF⊥AD于点F，在Rt△AOB中，OA=4，OB=4，∴∠ABO=30°，由题意得：BC=2t，AD=t，∵CE⊥BO，∴在Rt△CEB中，CE=t，EB=t，∵CF⊥AD，AO⊥BO，∴四边形CFOE是矩形，∴OF=CE=t，OE=CF=4-t，在Rt△CFD中，DF2+CF2=CD2，∴（4-t-t）2+（4-t）2=42，即7t2-40t+48=0，解得：t=，t=4，∵0＜t＜4，∴当t=时，线段CD的长是4；（2）过点O作OG⊥DE于点G（如图2），∵AD∥CE，AD=CE=t∴四边形ADEC是平行四边形，∴DE∥AB∴∠GEO=30°，∴OG=OE=（4-t）当线段DE与⊙O相切时，则OG=，∴当（4-t ）＜，且t≤4-时，线段DE 与⊙O 有两个公共交点．∴当 4-＜t≤时，线段DE 与⊙O 有两个公共交点；（3）当⊙C 与⊙O 外切时，t=；当⊙C 与⊙O 内切时，t=；∴当t=或秒时，两圆相切．考点：圆的综合题．3．如图，以A （0，3）为圆心的圆与x 轴相切于坐标原点O ，与y 轴相交于点B ，弦BD 的延长线交x 轴的负半轴于点E ，且∠BEO ＝60°，AD 的延长线交x 轴于点C ．（1）分别求点E 、C 的坐标；（2）求经过A 、C 两点，且以过E 而平行于y 轴的直线为对称轴的抛物线的函数解析式；（3）设抛物线的对称轴与AC 的交点为M ，试判断以M 点为圆心，ME 为半径的圆与⊙A 的位置关系，并说明理由．【答案】（1）点C 的坐标为（－3，0）（2）2343333y x x =++3）⊙M 与⊙A 外切【解析】试题分析：（1）已知了A 点的坐标，即可得出圆的半径和直径，可在直角三角形BOE 中，根据∠BEO 和OB 的长求出OE 的长进而可求出E 点的坐标，同理可在直角三角形OAC 中求出C 点的坐标；（2）已知了对称轴的解析式，可据此求出C 点关于对称轴对称的点的坐标，然后根据此点坐标以及C ，A 的坐标用待定系数法即可求出抛物线的解析式；（3）两圆应该外切，由于直线DE ∥OB ，因此∠MED=∠ABD ，由于AB=AD ，那么∠ADB=∠ABD ，将相等的角进行置换后可得出∠MED=∠MDE ，即ME=MD ，因此两圆的圆心距AM=ME+AD ，即两圆的半径和，因此两圆外切.试题解析：（1）在Rt△EOB 中，3cot602323EO OB =⋅︒==，∴点E 的坐标为（－2，0）．在Rt△COA 中，tan tan60333OC OA CAO OA =⋅∠=⋅︒=⨯=， ∴点C 的坐标为（－3，0）．（2）∵点C 关于对称轴2x =-对称的点的坐标为F （－1，0），点C 与点F （－1，0）都在抛物线上．设()()13y a x x =++，用()03A ，代入得()()30103a =++，∴3a =． ∴()()3133y x x =++，即 234333y x x =++．（3）⊙M 与⊙A 外切，证明如下： ∵ME ∥y 轴，∴MED B ∠=∠．∵B BDA MDE ∠=∠=∠， ∴MED MDE ∠=∠． ∴ME MD =．∵MA MD AD ME AD =+=+， ∴⊙M 与⊙A 外切．4．如图，∠ABC=45°，△ADE 是等腰直角三角形，AE=AD ，顶点A 、D 分别在∠ABC 的两边BA 、BC 上滑动（不与点B 重合），△ADE 的外接圆交BC 于点F ，点D 在点F 的右侧，O 为圆心．（1）求证：△ABD ≌△AFE（2）若AB=42，82＜BE ≤413，求⊙O 的面积S 的取值范围．【答案】（1）证明见解析（2）16π＜S ≤40π【解析】试题分析：（1）利用同弧所对的圆周角相等得出两组相等的角，再利用已知AE=AD ，得出三角形全等；（2）利用△ABD ≌△AFE ，和已知条件得出BF 的长，利用勾股定理和82＜BE ≤413，求出EF,DF 的取值范围， 24S DE π=，所以利用二次函数的性质求出最值. 试题解析：（1）连接EF ，∵△ADE 是等腰直角三角形，AE=AD ， ∴∠EAD=90°，∠AED=∠ADE=45°， ∵AE AE = ， ∴∠ADE=∠AFE=45°， ∵∠ABD=45°， ∴∠ABD=∠AFE ， ∵AF AF =， ∴∠AEF=∠ADB ， ∵AE=AD ， ∴△ABD ≌△AFE ；（2）∵△ABD ≌△AFE ， ∴BD=EF ，∠EAF=∠BAD ， ∴∠BAF=∠EAD=90°， ∵42AB = ， ∴BF=42cos cos45AB ABF =∠=8，设BD=x ，则EF=x ，DF=x ﹣8，∵BE 2=EF 2+BF 2， 82＜BE ≤413 ，∴128＜EF 2+82≤208， ∴8＜EF ≤12，即8＜x ≤12，则()222844S DE x x ππ⎡⎤==+-⎣⎦=()2482x ππ-+，∵2π＞0， ∴抛物线的开口向上，又∵对称轴为直线x=4，∴当8＜x ≤12时，S 随x 的增大而增大， ∴16π＜S ≤40π．点睛：本题的第一问解题关键是找到同弧所对的圆周角，第二问的解题关键是根据第一问的结论计算得出有关线段的长度，由于出现线段的取值范围，所以在这个问题中要考虑勾股定理的问题，还要考虑圆的面积问题，得出二次函数，利用二次函数的性质求出最值.5．如图，在平面直角坐标系中，O为坐标原点，△ABC的边BC在y轴的正半轴上，点A在x轴的正半轴上，点C的坐标为（0，8），将△ABC沿直线AB折叠，点C落在x轴的负半轴D（−4，0）处．（1）求直线AB的解析式；（2）点P从点A出发以每秒45个单位长度的速度沿射线AB方向运动，过点P作PQ⊥AB，交x轴于点Q，PR∥AC交x轴于点R，设点P运动时间为t（秒），线段QR长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，点N是射线AB上一点，以点N为圆心，同时经过R、Q两点作⊙N，⊙N交y轴于点E，F．是否存在t，使得EF=RQ？若存在，求出t的值，并求出圆心N的坐标；若不存在，说明理由．【答案】（1）132y x=-+（2）d=5t （3）故当 t=85，或815，时，QR=EF，N（-6，6）或（2，2）．【解析】试题分析：（1）由C（0，8），D（-4，0），可求得OC，OD的长，然后设OB=a，则BC=8-a，在Rt△BOD中，由勾股定理可得方程：（8-a）2=a2+42,解此方程即可求得B的坐标，然后由三角函数的求得点A的坐标，再利用待定系数法求得直线AB的解析式；（2）在Rt△AOB中，由勾股定理可求得AB的长，继而求得∠BAO的正切与余弦，由PR//AC 与折叠的性质，易证得RQ=AR，则可求得d与t的函数关系式；（3）首先过点分别作NT⊥RQ于T，NS⊥EF于S，易证得四边形NTOS是正方形，然后分别从点N在第二象限与点N在第一象限去分析求解即可求解;试题解析：（1）∵C（0，8），D（-4，0），∴OC=8，OD=4，设OB=a，则BC=8-a，由折叠的性质可得：BD=BC=8-a，在Rt△BOD中，∠BOD=90°，DB2=OB2+OD2，则（8-a）2=a2+42，解得：a=3，则OB=3，则B（0，3），tan∠ODB=34OBOD=，在Rt△AOC中，∠AOC=90°，tan∠ACB=34OAOC=，则OA=6，则A（6，0），设直线AB的解析式为：y=kx+b，则60{3k bb+==，解得：1{23kb=-=，故直线AB的解析式为：y=-12x+3；（2）如图所示：在Rt△AOB中，∠AOB=90°，OB=3，OA=6，则22135,tan2OBOB OA BAOOA+=∠==，255OAcos BAOAB∠==，在Rt△PQA中，905APQ AP t∠=︒=，则AQ=10cosAPtBAO=∠,∵PR∥AC，∴∠APR=∠CAB，由折叠的性质得：∠BAO=∠CAB，∴∠BAO=∠APR，∴PR=AR，∵∠RAP+∠PQA=∠APR+∠QPR=90°，∴∠PQA=∠QPR，∴RP=RQ，∴RQ=AR，∴QR=12 AQ=5t, 即d=5t;（3）过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ， ∵EF=QR ， ∴NS=NT ，∴四边形NTOS 是正方形，则TQ=TR=1522QR t = ， ∴1115151022224NT AT AQ TQ t t t ==-=-=（）（），分两种情况，若点N 在第二象限，则设N （n ，-n ），点N 在直线132y x =-+ 上，则132n n -=-+ ，解得：n=-6，故N （-6，6），NT=6，即1564t = ，解得：85t = ;若点N 在第一象限，设N （N ，N ），可得：132n n =-+ , 解得：n=2，故N （2，2），NT=2，即1524t =, 解得：t=815∴当 t=85，或815，时，QR=EF，N（-6，6）或（2，2）。

九年级上册数学一元二次方程易错题(Word版含答案)

九年级上册数学一元二次方程易错题（Word 版含答案）一、初三数学一元二次方程易错题压轴题（难）1．为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？【答案】（1）这两年藏书的年均增长率是20%；（2）到2018年底中外古典名著的册数占藏书总量的10%．【解析】【分析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几.【详解】解：（1）设这两年藏书的年均增长率是x ，()2517.2x +=，解得，10.2x =，2 2.2x =-（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有()7.2520%0.44-⨯=（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：5 5.6%0.44100%10%7.2⨯+⨯=，答：到2018年底中外古典名著的册数占藏书总量的10%．【点睛】本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题.2．已知关于x 的方程x 2﹣（2k +1）x +k 2+1＝0．（1）若方程有两个不相等的实数根，求k 的取值范围；（2）若方程的两根恰好是一个矩形两邻边的长，且k ＝2，求该矩形的对角线L 的长．【答案】（1）k ＞34；（2 【解析】【分析】（1）根据关于x 的方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根，得出△＞0，再解不等式即可；（2）当k=2时，原方程x 2-5x+5=0，设方程的两根是m 、n ，则矩形两邻边的长是m 、n ，利用根与系数的关系得出m+n=5，mn=5，则矩形的对角线长为22m n +，利用完全平方公式进行变形即可求得答案.【详解】解：（1）∵方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根，∴Δ＝[－(2k ＋1)]2－4×1×(k 2＋1)＝4k －3＞0，∴k ＞34； (2)当k ＝2时，原方程为x 2－5x ＋5＝0，设方程的两个根为m ，n ，∴m ＋n ＝5，mn ＝5，∴矩形的对角线长为：()222215m n m n mn +=+-=. 【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等，一元二次方程根的情况与判别式△的关系：（1）△＞0时，方程有两个不相等的实数根；（2）△=0时，方程有两个相等的实数根；（3）△＜0时，方程没有实数根．3．如图，在平面直角坐标系中，O 为原点，点A （0，8），点B （m ，0），且m ＞0.把△AOB 绕点A 逆时针旋转90°，得△ACD ，点O ，B 旋转后的对应点为C ，D ，（1）点C 的坐标为；（2）①设△BCD 的面积为S ，用含m 的式子表示S ，并写出m 的取值范围；②当S=6时，求点B 的坐标（直接写出结果即可）.【答案】（1）C （8，8）；（2）①S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②点B 的坐标为（7，0）或（2，0）或（6，0）.【解析】【分析】（1）由旋转的性质得出AC ＝AO ＝8，∠OAC ＝90°，得出C （8，8）即可；（2）①由旋转的性质得出DC ＝OB ＝m ，∠ACD ＝∠AOB ＝90°，∠OAC ＝90°，得出∠ACE ＝90°，证出四边形OACE 是矩形，得出DE ⊥x 轴，OE ＝AC ＝8，分三种情况：a 、当点B 在线段OE 的延长线上时，得出BE ＝OB−OE ＝m−8，由三角形的面积公式得出S ＝0.5m 2−4m （m ＞8）即可；b 、当点B 在线段OE 上（点B 不与O ，E 重合）时，BE ＝OE−OB ＝8−m ，由三角形的面积公式得出S ＝−0.5m 2＋4m （0＜m ＜8）即可；c 、当点B 与E 重合时，即m ＝8，△BCD 不存在；②当S ＝6，m ＞8时，得出0.5m 2−4m ＝6，解方程求出m 即可；当S ＝6，0＜m ＜8时，得出−0.5m 2＋4m ＝6，解方程求出m 即可．【详解】（1）∵点A （0，8），∴AO=8，∵△AOB 绕点A 逆时针旋转90°得△ACD ，∴AC=AO=8，∠OAC=90°，∴C （8，8），故答案为（8，8）；（2）①延长DC 交x 轴于点E ，∵点B （m ，0），∴OB=m ，∵△AOB 绕点A 逆时针旋转90°得△ACD ，∴DC=OB=m ，∠ACD=∠AOB=90°，∠OAC=90°，∴∠ACE=90°，∴四边形OACE 是矩形，∴DE ⊥x 轴，OE=AC=8，分三种情况：a 、当点B 在线段OE 的延长线上时，如图1所示：则BE=OB ﹣OE=m ﹣8，∴S=0.5DC•BE=0.5m （m ﹣8），即S=0.5m 2﹣4m （m ＞8）； b 、当点B 在线段OE 上（点B 不与O ，E 重合）时，如图2所示：则BE=OE ﹣OB=8﹣m ，∴S=0.5DC•BE=0.5m （8﹣m ），即S=﹣0.5m 2+4m （0＜m ＜8）； c 、当点B 与E 重合时，即m=8，△BCD 不存在；综上所述，S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②当S=6，m ＞8时，0.5m 2﹣4m=6，解得：m=4±27（负值舍去），∴m=4+27；当S=6，0＜m ＜8时，﹣0.5m 2+4m=6，解得：m=2或m=6，∴点B 的坐标为（4+27，0）或（2，0）或（6，0）.【点睛】本题是三角形综合题目，考查了坐标与图形性质、旋转的性质、矩形的判定与性质、三角形面积公式、一元二次方程的解法等知识；本题综合性强，有一定难度．4．已知关于x 的一元二次方程()221210m x m x +-+=有两个不相等的实数根．（1）求实数m 的取值范围；（2）若原方程的两个实数根分别为1x ，2x ，且满足1212215x x x x +=-，求m 的值．【答案】（1）14m <且0m ≠；（2）15m =- 【解析】【分析】（1）根据一元二次方程的定义和判别式的意义得到：()22140m m ∴∆=-->且20m ≠，然后求出两个不等式解集的公共部分即可.（2）利用根与系数的关系得到12221m x x m -+=， 1221x x m=，加上14m <且0m ≠，则可判断10x <，20x <，所以1212215x x x x --=-，2221215m m m--=-，然后解方程求出m 即可得到满足条件的m 的值.【详解】（1）因为方程()221210m x m x +-+=有两个不相等的实数根， ()221240m m ∴∆=-->，解得14m <；又因为是一元二次方程，所以20m ≠，0m ∴≠．m ∴的取值范围是14m <且0m ≠．（2）1x ，2x 为原方程的两个实数根，12221m x x m -∴+=，1221x x m = 14m <且0m ≠，122210m x x m -∴+=<，12210x x m =>，10x ∴<，20x <． 1212215x x x x +=-，1212215x x x x --=-，2221215m m m -∴-=-，215210m m ∴--=，解得113m =，215m =-， 14m <且0m ≠，113m ∴=不合题意，舍去，15m ∴=-．【点睛】此题主要考查一元一次方程的定义和判别式的意义，正确理解概念和熟练运用根的判别式是解题的关键.5．问题提出：（1）如图1，在四边形ABCD 中，已知：AD BC ∥，90D ∠=︒，4BC =，ABC 的面积为8，求BC 边上的高．问题探究（2）如图2在（1）的条件下，点E 是CD 边上一点，且2CE =，EAB CBA =∠∠，连接BE ，求ABE △的面积问题解决（3）如图3，在（1）的条件下，点E 是CD 边上任意一点，连接AE 、BE ，若EAB CBA =∠∠，ABE △的面积是否存在最小值；若存在，求出最小值；若不存在；请说明理由．【答案】（1）4；（2）203；（3）存在，最小值为16216- 【解析】【分析】（1）作BC 边上的高AM ，利用三角形面积公式即可求解；（2）延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，易得四边形BCDF 为矩形，在（1）的条件下BC=CD=4，则BCDF 为正方形，由EAB CBA =∠∠，结合∠FAB=∠CBA 可得∠FAB=∠EAB ，从而推出BF=BH=4，易证Rt △BCE ≌Rt △BHE ，所以EH=CE=2，设AD ＝a ，则AF=AH=4-a ，在Rt △ADE 中利用勾股定理建立方程可求出a ，最后根据S △ABE =1AE BH 2即可求解；（3）辅助线同（2），设AD=a ，CE=m ，则DE=4-m ，同（2）可得出m 与a 的关系式，设△ABE 的面积为y ，由y=1AE BH 2得到m 与y 的关系式，再求y 的最小值即可．【详解】（1）如图所示，作BC 边上的高AM ，∵S △ABC =1BC AM=82∴82AM==44⨯ 即BC 边上的高为4；（2）如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，∵AD BC ∥，90D ∠=︒∴∠BCD=∠D=90°=∠F∴四边形BCDF 为矩形，又∵BC=CD=4∴四边形BCDF 为正方形，∴DF=BF=BC=4，又∵AD ∥BC∴∠FAB=∠CBA又∵∠EAB=∠CBA∴∠FAB=∠EAB∵BF ⊥AF ，BH ⊥AE∴BH=BF=4，在Rt △BCE 和Rt △BHE 中，∵BE=BE ，BH=BC=4∴Rt △BCE ≌Rt △BHE （HL ）∴EH=CE=2同理可证Rt △BAF ≌Rt △BAH （HL ）∴AF=AH设AD=a ，则AF=AH=4-a在Rt △ADE 中，AD=a ，DE=2，AE=AH+EH=4-a+2=6-a由勾股定理得AD 2+DE 2=AE 2，即()22226+=-a a 解得8=3a ∴AE=6-a=103 S △ABE =111020AE BH=4=2233⨯⨯ （3）存在，如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，同（2）可得CE=EH ，AF=AH ，设AD=a ，CE=EH=m ，则DE=4-m ，AF=AH=4-a在Rt △ADE 中，AD 2+DE 2=AE 2，即()()22244+-=-+a m a m整理得8=4+m a m ∴AE=AH+HE=2816444+-+=++m m m m m 设△ABE 的面积为y ，则y=()222161116AE BH=42244++=++m m m m ∴()()24216+=+y m m 整理得：223240++-=m ym y∵方程必有实数根∴()2=423240∆-⨯⨯-≥y y 整理得2322560+-≥y y∴()()16216162160⎡⎤⎡⎤---≥⎣⎦⎣⎦y y （注：利用求根公式进行因式分解）又∵面积y ≥0∴216≥y即△ABE 的面积最小值为16216．【点睛】本题考查四边形综合问题，正确作出辅助线，得出AB 平分∠FAC ，利用角平分线的性质定理得到BF=BH ，结合勾股定理求出AE 是解决（2）题的关键，（3）题中利用一元二次方程的判别式求最值是解题的关键．6．已知关于x 的一元二次方程x 2﹣x +a ﹣1=0．（1）当a=﹣11时，解这个方程；（2）若这个方程有两个实数根x 1，x 2，求a 的取值范围；（3）若方程两个实数根x 1，x 2满足[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，求a 的值．【答案】（1）123,4x x =-=（2）54a ≤（3）-4 【解析】【分析】（1）根据一元二次方程的解法即可求出答案；（2）根据判别式即可求出a 的范围；（3）根据根与系数的关系即可求出答案．【详解】（1）把a =﹣11代入方程，得x 2﹣x ﹣12=0，（x +3）（x ﹣4）=0，x +3=0或x ﹣4=0，∴x 1=﹣3，x 2=4；（2）∵方程有两个实数根12x x ，，∴△≥0，即（﹣1）2﹣4×1×（a ﹣1）≥0，解得54a ≤：；（3）∵12x x ，是方程的两个实数根，222211221122101011x x a x x a x x a x x a -+-=-+-=∴-=--=-，，，． ∵[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，∴221122229x x x x ⎡⎤⎡⎤+-+-=⎣⎦⎣⎦，把22112211x x a x x a -=--=-，代入，得：[2+a ﹣1][2+a ﹣1]=9，即（1+a ）2=9，解得：a =﹣4，a =2（舍去），所以a 的值为﹣4．点睛：本题考查了一元二次方程，解题的关键是熟练运用判别式以及根与系数的关系．7．近几年，全社会对空气污染问题越来越重视，空气净化器的销量也在逐年增加．某商场从厂家购进了A ，B 两种型号的空气净化器，两种净化器的销售相关信息见下表：（1）每台A 型空气净化器和B 型空气净化器的销售利润分别是多少？（2）该公司计划一次购进两种型号的空气净化器共100台，其中B 型空气净化器的进货量不少于A 型空气净化器的2倍，为使该公司销售完这100台空气净化器后的总利润最大，请你设计相应的进货方案；（3）已知A型空气净化器的净化能力为300 m3/小时，B型空气净化器的净化能力为200 m3/小时．某长方体室内活动场地的总面积为200 m２，室内墙高3 m．该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新，如不考虑空气对流等因素，至少要购买A型空气净化器多少台？【答案】（1）每台A型空气净化器的利润为200元，每台B型空气净化器的利润为100元；（2）为使该公司销售完这100台空气净化器后的总利润最大，应购进A型空气净化器33台，购进B型空气净化器67台；（3）至少要购买A型空气净化器2台.【解析】解：（1）设每台A型空气净化器的利润为x元，每台B型空气净化器的利润为y元，根据题意得：5102000,200, {{ 1052500.100. x y xx y y+==+==解得答：每台A型空气净化器的利润为200元，每台B型空气净化器的利润为100元. （2）设购买A型空气净化器m台，则购买B型空气净化器（100﹣m）台，∵B型空气净化器的进货量不少于A型空气净化器的2倍，∴100-m≥2m，解得：m≤100. 3设销售完这100台空气净化器后的总利润为W元.根据题意，得W=200m+100（100﹣m）=100m+10000.∵要使W最大，m需最大，∴当m=33时，总利润最大，最大利润为W：100×33+10000=13300（元）.此时100﹣m=67.答：为使该公司销售完这100台空气净化器后的总利润最大，应购进A型空气净化器33台，购进B型空气净化器67台.（3）设应购买A型空气净化器a台，则购买B型空气净化器（5﹣a）台，根据题意得：12[300a+200(5-a)]≥200×3.解得：a≥2.∴至少要购买A型空气净化器2台.8．如图，A、B、C、D为矩形的4个顶点，AB＝16cm，BC＝6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．(1)若点P从点A移动到点B停止，点P、Q分别从点A、C同时出发，问经过2s时P、Q 两点之间的距离是多少cm？(2)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P、Q分别从点A、C 同时出发，问经过多长时间P、Q两点之间的距离是10cm？(3)若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间△PBQ的面积为12cm2？【答案】（1）PQ=62cm；（2）85s或245s；（3）经过4秒或6秒△PBQ的面积为12cm2．【解析】试题分析：（1）作PE⊥CD于E，表示出PQ的长度，利用PE2+EQ2=PQ2列出方程求解即可；（2）设x秒后，点P和点Q的距离是10cm．在Rt△PEQ中，根据勾股定理列出关于x的方程（16-5x）2=64，通过解方程即可求得x的值；（3）分类讨论：①当点P在AB上时；②当点P在BC边上；③当点P在CD边上时．试题解析：（1）过点P作PE⊥CD于E．则根据题意，得EQ=16-2×3-2×2=6（cm），PE=AD=6cm；在Rt△PEQ中，根据勾股定理，得PE2+EQ2=PQ2，即36+36=PQ2，∴2cm；∴经过2s时P、Q两点之间的距离是2；（2）设x秒后，点P和点Q的距离是10cm．（16-2x-3x）2+62=102，即（16-5x）2=64，∴16-5x=±8，∴x1=85，x2=245；∴经过85s或245sP、Q两点之间的距离是10cm；（3）连接BQ．设经过ys后△PBQ的面积为12cm2．①当0≤y≤163时，则PB=16-3y，∴12PB•BC=12，即12×（16-3y）×6=12，解得y=4；②当163＜x≤223时，BP=3y-AB=3y-16，QC=2y，则1 2BP•CQ=12（3y-16）×2y=12，解得y1=6，y2=-23（舍去）；③223＜x≤8时，QP=CQ-PQ=22-y，则1 2QP•CB=12（22-y）×6=12，解得y=18（舍去）．综上所述，经过4秒或6秒△PBQ的面积为 12cm2．考点：一元二次方程的应用．9．如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH 是正方形ABCD的外接正方形．探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．因为正方形ABCD的面积为1，则正方形EFGH的面积为2，所以EF＝FG＝GH＝HE2EB＝x，则BF2﹣x，∵Rt△AEB≌Rt△BFC∴BF＝AE2﹣x在Rt△AEB中，由勾股定理，得x2+2﹣x）2＝12解得，x1＝x2＝2∴BE＝BF，即点B是EF的中点．同理，点C，D，A分别是FG，GH，HE的中点．所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）探究三：已知边长为1的正方形ABCD，一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）【答案】不存在，详见解析【解析】【分析】探究二，根据探究一的解答过程、运用一元二次方程计算即可；探究三，根据探究一的解答过程、运用一元二次方程根的判别式解答；探究四，根据探究一的解答过程、运用一元二次方程根的判别式解答．【详解】探究二：因为正方形ABCD的面积为1，则正方形EFGH的面积为3，所以EF=FG=GH=HE，设EB=x，则BF x，∵Rt△AEB≌Rt△BFC，∴BF=AE﹣x，在Rt△AEB中，由勾股定理，得，x2+x）2=12，整理得x2x+1=0，b2﹣4ac=3﹣4＜0，此方程无解，不存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍；探究三：因为正方形ABCD的面积为1，则正方形EFGH的面积为4，所以EF=FG=GH=HE=2，设EB=x，则BF=2﹣x，∵Rt△AEB≌Rt△BFC，∴BF=AE=2﹣x，在Rt△AEB中，由勾股定理，得，x2+（2﹣x）2=12，整理得2x2﹣4x+3=0，b2﹣4ac=16﹣24＜0，此方程无解，不存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍，故答案为不存在；探究四：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为n ，所以EF =FG =GH =HE =n ，设EB =x ，则BF =n ﹣x ，∵Rt △AEB ≌Rt △BFC ，∴BF =AE =n ﹣x ，在Rt △AEB 中，由勾股定理，得，x 2+（n ﹣x ）2=12，整理得2x 2﹣2n x +n ﹣1=0，b 2﹣4ac =8﹣4n ＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的n 倍．【点睛】本题考查了正方形的性质、全等三角形的判定和性质、一元二次方程的解法等知识.读懂探究一的解答过程、正确运用一元二次方程根的判别式是解题的关键．10．如图，在矩形ABCD 中，6AB = ，10BC = ，将矩形沿直线EF 折叠．使得点A 恰好落在BC 边上的点G 处，且点E 、F 分别在边AB 、AD 上（含端点），连接CF .（1）当32BG = 时，求AE 的长；（2）当AF 取得最小值时，求折痕EF 的长；（3）连接CF ，当△FCG 是以CG 为底的等腰三角形时，直接写出BG 的长.【答案】（1）92AE =；（2）62EF =3）185BG =. 【解析】【分析】（1）根据折叠得出AE=EG ，据此设AE=EG=x ，则有BE=6-x ，由勾股定理求解可得；（2）由FG ⊥BC 时FG 的值最小，即此时AF 能取得最小值，显然四边形AEGF 是正方形，从而根据勾股定理可得答案；（3）由△CFG 是以FG 为一腰的等腰三角形，可知应分两种情况讨论：①FG=FC ；②FG=GC ；分别求解可得．【详解】（1）由折叠易知，AE EG =，设AE EG x ==，则有6BE x =-，由勾股定理，得()(222632x x =-+，解得92x =，即92AE = （2）由折叠易知，AF FG =，而当FG BC ⊥时，FG 的值最小，即此时AF 能取得最小值，当FG BC⊥时，FG的值最小，即此时AF能取得最小值，当FG BC⊥时，点E与点B重合，此时四边形AEGF是正方形，∴折痕226662EF=+=.（3）由△CFG是以FG为一腰的等腰三角形，可知应分两种情况讨论：①当FG=FC时，如图2，过F作FH⊥CG于H，则有：AF=FG=FC，CH=DF=GH设AF=FG=FC=x，则DF=10-x=CH=GH在Rt△CFH中∵CF2=CH2+FH2∴x2=62+（10-x）2解得：x=345，∴DF=CH=GH=10-165，即BG=10-165×2=185，②当FG=GC时，则有：AF=FG=GC=x，CH=DF=10-x；∴GH=x-（10-x）=2x-10，在Rt△FGH中，由勾股定理易得：x2=62+（2x-10）2，化简得：3x2-40x+136=0，∵△=（-40）2-4×3×136=-32＜0，∴此方程没有实数根．综上可知：BG=185．【点睛】本题主要考查四边形的综合问题，解题的关键是掌握矩形和翻折变换的性质、正方形的判定与性质、勾股定理、一元二次方程根与系数的关系等知识点，也考查了分类讨论的数学思想．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

12.请写出符合以下三个条件的一个函数的解析式2129
y x =-
+（答案不唯一）． ①过点(31)，；
②当0x >时，y 随x 的增大而减小；
③当自变量的值为2时，函数值小于2． 13．二次函数322
--=x x y 的图象关于原点O （0, 0）对称的图象的解析式是223y x x =--+。

如图所示,已知F 是以O 为圆心,BC 为直径的半圆上任一点,A 是BF 的中点,AD ⊥BC 于点D.求证:AD=1
BF. 如图,⊙O 的直径AB 的两侧有定点C 和动点P.已知BC=4,CA=3,点P 在AB 上运动,过点C 作
CP 的垂线,与PB 的延长线交于点Q.
(1)当点P 运动到与点C 关于AB 对称时 ,求C Q 的长.
(2)当点P 运动到弧AB 的中点时,求C Q 的长.
(3)当点P 运动到什么位置时,CQ 取到最大值,并求此时CQ 的长.
解：（1）当点P与点C关于AB对称时，CP⊥AB，设垂足为D，∵AB为⊙O的直径，
∴∠ACB=90°，
∴BC=4，AC=3，
∵AC•BC=AB•CD，
∴CD=12 5
∴PC=24 5
．
在Rt△ACB和Rt△PCQ中，
∠ACB=∠PCQ=90°，∠CAB=∠CPQ，∴△ACB∽△PCQ，
∴AC BC PC CQ
=
∴CQ=4 3
PC=32 5
（2）当点P运动到»AB
的中点时，过点B作BE⊥PC于点E．
∵点P是»AB
的中点，
∴∠PCB=45°，
BE=CE=
2
22 2
BC=
在Rt△EPB中，tan∠EPB=
4
3 BE PE
=
∴PE=332 42 BE=
∴PC=PE+CE=72
2
．
∴CQ=4142 33 BE=
（3）点P在»AB
上运动时，恒有CQ=
4
3
PC
所以PC最大时，CQ取到最大值，
当PC过圆心O，即PC取最大值5时，CQ最大值为
3
23.如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax2+bx+c经过O、A、C三点．
（1）求该抛物线的函数解析式；
（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．
解：（1）∵抛物线y=ax2+bx+c经过点O、A、C，
可得c=0，∴，
解得a=，b=，
∴抛物线解析式为y=x2+x．
（2）设点P的横坐标为t，∵PN∥CD，∴△OPN∽△OCD，可得PN=
∴P（t，），∵点M在抛物线上，∴M（t，t2+t）．
如解答图1，过M点作MG⊥AB于G，过P点作PH⊥AB于H，
AG=y A﹣y M=2﹣（t2+t）=t2﹣t+2，BH=PN=．
当AG=BH时，四边形ABPM为等腰梯形，
∴t2﹣t+2=，
化简得3t2﹣8t+4=0，解得t1=2（不合题意，舍去），t2=，
∴点P的坐标为（，）
∴存在点P（，），使得四边形ABPM为等腰梯形．
（3）如解答图2，△AOB沿AC方向平移至△A′O′B′，A′B′交x轴于T，交OC于Q，A′O′交x轴于K，交OC于R．
求得过A、C的直线为y AC=﹣x+3，可设点A′的横坐标为a，则点A′（a，﹣a+3），
易知△OQT∽△OCD，可得QT=，
∴点Q的坐标为（a，）．
解法一：
设AB与OC相交于点J，
∵△ARQ∽△AOJ，相似三角形对应高的比等于相似比，∴=
∴HT===2﹣a，
KT=A′T=（3﹣a），A′Q=yA′﹣yQ=（﹣a+3）﹣=3﹣a．
S四边形RKTQ=S△A′KT﹣S△A′RQ=KT•A′T﹣A′Q•HT
=••（3﹣a）﹣•（3﹣a）•（﹣a+2）
=a2+a﹣=（a﹣）2+
由于＜0，
∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．
解法二：
过点R作RH⊥x轴于H，则由△ORH∽△OCD，得①
由△RKH∽△A′O′B′，得②
由①，②得KH=OH，
OK=OH，KT=OT﹣OK=a﹣OH③
由△A′KT∽△A′O′B′，得，
则KT=④
由③，④得=a﹣OH，即OH=2a﹣2，RH=a﹣1，所以点R的坐标为R（2a﹣2，a﹣1）S四边形RKTQ=S△QOT﹣S△ROK=•OT•QT﹣•OK•RH
=a•a﹣（1+a﹣）•（a﹣1）
=a2+a﹣=（a﹣）2+
由于＜0，
∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．
解法三：
∵AB=2，OB=1，∴tan∠O′A′B′=tan∠OAB=，
∴KT=A′T•tan∠O′A′B′=（﹣a+3）•=a+，
∴OK=OT﹣KT=a﹣（a+）=a﹣，
过点R作RH⊥x轴于H，∵tan∠OAB=tan∠RKH==2，∴RH=2KH
又∵tan∠OAB=tan∠ROH===，
∴2RH=OK+KH=a﹣+RH，∴RH=a﹣1，OH=2（a﹣1），
∴点R坐标R（2a﹣2，a﹣1）
S四边形RKTQ=S△A′KT﹣S△A′RQ=•KT•A′T﹣A′Q•（xQ﹣xR）
=••（3﹣a）﹣•（3﹣a）•（﹣a+2）
=a2+a﹣=（a﹣）2+
由于＜0，
∴在线段AC上存在点A′（，），能使重叠部分面积S取到最大值，最大值为．。

九年级数学上册错题集.doc