第二章 数制与编码分析
合集下载
《数制与编码》课件

WAV
波形音频文件格式,未进 行压缩,音质较高但文件 较大。
AAC
高级音频编码,支持更高 的比特率和多声道,广泛 应用于流媒体和数字广播 。
05
编码的未来发展
编码技术的创新
总结词
随着技术的不断发展,编码技术也在不断创新和进步,未来将会有更多的新技 术应用于编码领域。
详细描述
随着云计算、大数据、物联网等技术的快速发展,编码技术也在不断创新和进 步。未来可能会出现更加高效、安全的编码算法和技术,以满足更加复杂和多 样化的应用需求。
非十进制转其他数制
通过连续除基取余法进行转换。
其他数制转十进制
通过乘基取整法或加权求和法进行转换。
非十进制转十进制
通过连续乘基取整法进行转换。
02
编码的基本概念
编码的定义
编码的定义
编码是将信息转换为一种能被机器识 别的语言,也就是用某种符号代表特 定的信息。编码是信息传输和存储的 关键环节,没有编码,计算机就无法 处理信息。
数制的分类
01
有符号数制和无符号数制:有符号数制表示数值的 正负,无符号数制只表示数值的大小。
02
定点数制和浮点数制:定点数制小数点位置固定, 浮点数制小数点位置可以浮动。
03
二进制数制、八进制数制、十进制数制和十六进制 数制:根据基数不同进行分类。
数制转换的方法
十进制转其他数制
通过除基取余法或乘基取整法进行转换。
编码在人工智能中的应用
总结词
人工智能技术的快速发展为编码技术的应用提供了新的机遇和挑战,未来编码将在人工智能中发挥更加重要的作 用。
详细描述
人工智能技术的核心是数据和算法,而编码技术是其中不可或缺的一部分。未来,随着人工智能技术的不断发展 和应用,编码技术的应用场景也将更加广泛和深入。同时,编码技术也面临着如何更好地支持人工智能技术的发 展和应用,如提高算法的效率和安全性等。
计算机数制与信息编码介绍课件

计算机Байду номын сангаас制与信息编码介绍课件
演讲人
01.
02.
03.
04.
目录
计算机数制
信息编码
数据存储与传输
计算机网络与通信
计算机数制
数制基础
03
转换:不同进制之间的转换方法
02
进制:二进制、八进制、十进制、十六进制等
01
数制:计算机中表示数字的方法
04
应用:计算机硬件、软件、网络通信等领域中的数制表示
二进制、八进制、十六进制
数据安全与加密
01
数据加密技术:用于保护数据在传输和存储过程中的安全性
02
加密算法:包括对称加密算法和非对称加密算法
03
数字签名:用于验证数据的完整性和身份认证
04
安全协议:如SSL/TLS,用于保护数据在传输过程中的安全性
计算机网络与通信
网络基础
网络拓扑结构:总线型、星型、环型、树型等
网络协议:TCP/IP、UDP、IPX/SPX等
二进制:计算机内部使用的基本数制,由0和1组成,表示二进制数
八进制:由0到7的八个数字组成,表示八进制数
十六进制:由0到9和A到F的十六个数字组成,表示十六进制数
二进制、八进制、十六进制之间的转换:可以通过特定的算法进行转换,以便于计算机处理和存储数据。
数制转换
十进制转二进制:除2取余法
01
二进制转十进制:按位权展开求和
光盘:用于存储和读取数据,如CD、DVD、蓝光光盘等
02
闪存:用于存储和读取数据,如U盘、SD卡等
云存储:通过网络存储和读取数据,如Dropbox、Google Drive等
04
演讲人
01.
02.
03.
04.
目录
计算机数制
信息编码
数据存储与传输
计算机网络与通信
计算机数制
数制基础
03
转换:不同进制之间的转换方法
02
进制:二进制、八进制、十进制、十六进制等
01
数制:计算机中表示数字的方法
04
应用:计算机硬件、软件、网络通信等领域中的数制表示
二进制、八进制、十六进制
数据安全与加密
01
数据加密技术:用于保护数据在传输和存储过程中的安全性
02
加密算法:包括对称加密算法和非对称加密算法
03
数字签名:用于验证数据的完整性和身份认证
04
安全协议:如SSL/TLS,用于保护数据在传输过程中的安全性
计算机网络与通信
网络基础
网络拓扑结构:总线型、星型、环型、树型等
网络协议:TCP/IP、UDP、IPX/SPX等
二进制:计算机内部使用的基本数制,由0和1组成,表示二进制数
八进制:由0到7的八个数字组成,表示八进制数
十六进制:由0到9和A到F的十六个数字组成,表示十六进制数
二进制、八进制、十六进制之间的转换:可以通过特定的算法进行转换,以便于计算机处理和存储数据。
数制转换
十进制转二进制:除2取余法
01
二进制转十进制:按位权展开求和
光盘:用于存储和读取数据,如CD、DVD、蓝光光盘等
02
闪存:用于存储和读取数据,如U盘、SD卡等
云存储:通过网络存储和读取数据,如Dropbox、Google Drive等
04
《数制与码制 》课件

八进制数制在一些特定领域中有应用 ,例如数学和工程领域中用于简化运 算和提高运算效率。
在八进制数制中,每一位的权值是8 的幂次方,例如八位、十六位等。
02
码制的概念与分类
码制的概念
码制是指一种用于表示、传输、处理和存储数据的编码方式。
码制的主要目的是将数据转换为二进制或其他进制形式,以便计算机能够识别、处 理和存储。
码制的转换
十进制码制与二进制码制的转换
十进制转二进制
将十进制数除以2,取余数,直 到商为0,将余数从下往上排列
。
二进制转十进制
将二进制数从右往左每4位一组 ,将每组数转换为十进制数, 再将各组十进制数相加。
十进制转二进制示例
将十进制数23转换为二进制数 ,得到101011。
二进制转十进制示例
将二进制数101011转换为十进 制数,得到23。
数制与码制的发展趋势和未来展望
标准化和规范化
随着信息技术的不断发展,数制 与码制的标准化和规范化将更加 重要,以促进不同系统、平台之
间的互操作性和兼容性。
高效性和灵活性
未来数制与码制将更加注重高效性 和灵活性,以满足不同应用场景的 需求,包括物联网、云计算、大数 据等领域。
安全性与可靠性
随着信息安全威胁的不断增加,数 制与码制的未来发展将更加注重安 全性与可靠性,提高信息传输和存 储的安全防护能力。
在十进制数制中,每一位的权值 是10的幂次方,例如十位、百
位、千位等。
二进制数制
二进制数制由0和1两个数字组 成,采用逢二进一的计数原则 。
在二进制数制中,每一位的权 值是2的幂次方,例如二进制数 1011表示为十进制数11。
二进制数制在计算机科学中广 泛应用,因为计算机中的信息 都是以二进制形式存储和处理 的。
数制与编码资料PPT课件

但是,二进制的明显缺点是:数字冗长, 书写麻烦且容易出错,不便阅读,所以, 在计算机的书写中,常采用十六进制。
二、十和十六进制数
三种计数制之间的对应表示
二进制
0000 0001 0010 0011 0100
十进制
0 1 2 3 4
十六进制
0 1 2 3 4
二、十和十六进制数
二进制 0101 0110 0111 1000 1001
二进制 十六进制 方法:从小数点开始,分别向左向右出 发,四位一组,不足四位补零,四位划 一位。 例: 1011010.00101B=5A.28H
二、十和十六进制数
十六进制 二进制 方法:一位划四位。 例: 5A.28H=1011010.00101B
二、十和十六进制数
十进制 十六进制 方法一:先将十进制转换为二进制,再 将二进制转换为十六进制。 例: 97D=110 0001B=61H
二、十和十六进制数
二进制 加法规则“逢二进一” 二进制的特点: 1)简单可行,容易实现。 因为二进制只有两个数码0、1,可以用 两种不同的稳定状态来表示,如有磁和 无磁,高电位与低电位。 2) 运算规则简单。以加法为例,二进制 加法仅有四条:即0+0=0;1+0=1;
二、十和十六进制数
0+1=1;1+1=10。 3) 适合逻辑运算。二进制中的0和1正好 分别表示逻辑代数中的假值(False)和真 值(True)。二进制代表逻辑值容易实现逻 辑运算。
数制的基本概念
76.2Q=7X81+6X80+2X8-1 256.12D=2X102+5X101+6X100
+1X10-1+2X10-2 A2B.FH=10X162+2X161+11X160
二、十和十六进制数
三种计数制之间的对应表示
二进制
0000 0001 0010 0011 0100
十进制
0 1 2 3 4
十六进制
0 1 2 3 4
二、十和十六进制数
二进制 0101 0110 0111 1000 1001
二进制 十六进制 方法:从小数点开始,分别向左向右出 发,四位一组,不足四位补零,四位划 一位。 例: 1011010.00101B=5A.28H
二、十和十六进制数
十六进制 二进制 方法:一位划四位。 例: 5A.28H=1011010.00101B
二、十和十六进制数
十进制 十六进制 方法一:先将十进制转换为二进制,再 将二进制转换为十六进制。 例: 97D=110 0001B=61H
二、十和十六进制数
二进制 加法规则“逢二进一” 二进制的特点: 1)简单可行,容易实现。 因为二进制只有两个数码0、1,可以用 两种不同的稳定状态来表示,如有磁和 无磁,高电位与低电位。 2) 运算规则简单。以加法为例,二进制 加法仅有四条:即0+0=0;1+0=1;
二、十和十六进制数
0+1=1;1+1=10。 3) 适合逻辑运算。二进制中的0和1正好 分别表示逻辑代数中的假值(False)和真 值(True)。二进制代表逻辑值容易实现逻 辑运算。
数制的基本概念
76.2Q=7X81+6X80+2X8-1 256.12D=2X102+5X101+6X100
+1X10-1+2X10-2 A2B.FH=10X162+2X161+11X160
数字电子技术教案第2章 数制与编码

1-2
内
容
备注
3、2 进制数与 2n 进制数相互转换(n 为整数,n≥2) 方法:1 位 2n 进制数 -- n 位 2 进制数。 例题:(见 PPT)。 三、有符号二进制数 在上节课通过对“按位计数制”这部分内容的学习,我们知道在数 字设备中的数值采用二进制表示,但这部分内容并没有说明在数字设备 中如何区分数的符号。 (一) 有符号二进制数的表示法 提问:有符号的十进制数是如何表示的?回答:符号+绝对值。(举 例,板书) 引导学生思考: 前面提到,数字设备的信号通常只有两种——高电平和低电平,分 别用 1 和 0 表示,还句话说,数字设备只能识别 1 和 0,所有的信息都必 须表示成 1 和 0 的形式,数字设备才能处理。 通过对“按位计数制”这部分内容的学习,已经知道如何用二进制 数表示十进制数的绝对值部分,又如何在数字设备中表示正负号? 有符号二进制数的表示法:符号(1bit,最高位)+绝对值。 (1)讲解如何表示正负号。最高位为 0 代表正,最高位为 1 代表负。 (2)有符号数的绝对值部分有多种表示方法,常见的有原码表示法、 反码表示法和补码表示法。 (3)原码、反码和补码本身的概念中是不考虑符号的。但是,有符 号数绝对值部分的原码、反码和补码与该数的符号有关。 (4)负数的数值部分的原码就是其绝对值的二进制数,反码就是将 原码逐位取反,补码就是将反码的末位加 1;正数的数值部分的原码、反 码和补码相同,就是其绝对值的二进制数。 例 1、例 2(见 PPT)。注意正数和负数的区别。 (二) n 位有符号二进制数所能表示的数值范围
一样。
举例说明 n 位自然二进制编码与它的 n 位二进制数在概念上的区别。
2、典型循环码(Gray Code)
典型循环码有三个特点:相邻性、循环性、反射性。举例说明这三
第数制与编码课件
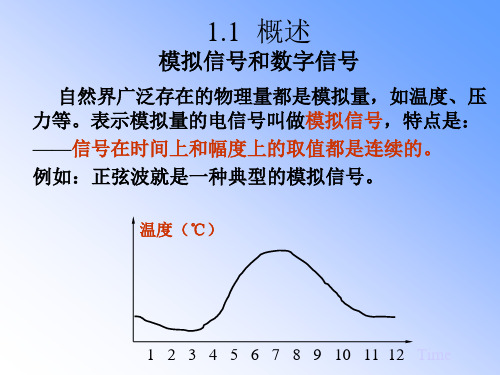
=(135.0625)10
十六进制数的权展开式: 如:(D8.A)2= 13×161 +8×160+10 ×16-1
=(216.625)10
4、十进制数转换为二进制数
采用的方法 — 基数连除、连乘法 原理:将整数部分和小数部分分别进行转换。
整数部分采用基数连除法,小数部分 采用基数连乘法。转换后再合并。
=(135.0625)10
各数位的权是8的幂
4、十六进制
数码为:0~9、A~F;基数是16。 运算规律:逢十六进一,即:F+1=10。 十六进制数的权展开式: 如:(D8.A)16= 13×161 +8×160+10 ×16-1
=(216.625)10
各数位的权是16的幂
结论
①一般地,N进制需要用到N个数码,基数是N;运算规 律为逢N进一。
典型的模拟电子系统
DAC
典型的模拟和数字混合系统
对模拟信号进行传输、处理的电子线路 称为模拟电路。
对数字信号进行传输、处理的电子线路 称为数字电路。
每个数字信号只有0、1两种取值,如何表 示模拟信号各种不同的幅度呢?
——用组合数字信号来描述这个幅度。
模拟量和数字量的相互转换
数字电路、逻辑电路
②从低位向高位的进位规则
一般地,N进制需要用到N个数码,基数 是N;运算规律为逢N进一。
十进制,二进制,八进制,十六
进制
逢二进一
逢八进一
逢十进一
逢十六进一
十进制数
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
几种进制数之间的对应关系
二进制数
八进制数 十六进制数
0000
运算 加法规则:0+0=0, 0+1=1, 1+0=1, 1+1=10 规则 乘法规则:0 × 0=0, 0 × 1=0 ,1 × 0=0,1 × 1=1
十六进制数的权展开式: 如:(D8.A)2= 13×161 +8×160+10 ×16-1
=(216.625)10
4、十进制数转换为二进制数
采用的方法 — 基数连除、连乘法 原理:将整数部分和小数部分分别进行转换。
整数部分采用基数连除法,小数部分 采用基数连乘法。转换后再合并。
=(135.0625)10
各数位的权是8的幂
4、十六进制
数码为:0~9、A~F;基数是16。 运算规律:逢十六进一,即:F+1=10。 十六进制数的权展开式: 如:(D8.A)16= 13×161 +8×160+10 ×16-1
=(216.625)10
各数位的权是16的幂
结论
①一般地,N进制需要用到N个数码,基数是N;运算规 律为逢N进一。
典型的模拟电子系统
DAC
典型的模拟和数字混合系统
对模拟信号进行传输、处理的电子线路 称为模拟电路。
对数字信号进行传输、处理的电子线路 称为数字电路。
每个数字信号只有0、1两种取值,如何表 示模拟信号各种不同的幅度呢?
——用组合数字信号来描述这个幅度。
模拟量和数字量的相互转换
数字电路、逻辑电路
②从低位向高位的进位规则
一般地,N进制需要用到N个数码,基数 是N;运算规律为逢N进一。
十进制,二进制,八进制,十六
进制
逢二进一
逢八进一
逢十进一
逢十六进一
十进制数
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
几种进制数之间的对应关系
二进制数
八进制数 十六进制数
0000
运算 加法规则:0+0=0, 0+1=1, 1+0=1, 1+1=10 规则 乘法规则:0 × 0=0, 0 × 1=0 ,1 × 0=0,1 × 1=1
最新第二章-数制与信息编码PPT课件

权 rn
r1 r0
r-1 r-2
r-m
2.1.1 数制的本质特征
每位数字代表的值:ai * ri
▪ 不同进制的进制本中质基本特符号征的个数 523
– 基数
满r进1(r=10,2,8,16) 5 * 102 + 2 * 101 + 3 * 100
–权
=500+20+3 = 523
r进制数 an ... a1 a0 . a-1 a-2 ... a-m
0表示正,1表示负。
+- 77 机器码 10 1 0 0 1 1 0 1
符号位 真值 -1001101
2.2.1 符号位的表示
▪ 真值:带正负号的数 ▪ 机器码:用0表示正,1表示负之后形成的二进制数 ▪ 符号位数字化:由真值到机器码的生成过程 ▪ 问题: ▪ 符号位数字化后,符号位和数值位都用0和1表示,
– 十进制是以10为基数,逢十进一。 – 二进制是以2为基数,逢二进一。 – 八进制以8为基数,逢八进一。 – 十六进制以16为基数,逢十六进一。
③ 权值大小不同。例如:50和500中“5”,虽然符号相同, 但是含义却不同,前者表示5个10,后者表示5个100
2.1.1 数制的本质特征
▪权
– 例如:50和500中“5”,虽然符号相同,但是含义却不同,前者 表示5个10,后者表示5个100
Company Logo
2.1.2 数据的表示
▪ 常用的数制
数制
基数
数符
十级制(Decimal) 10
0,1,2,3,4,5,6,7,8,9
二进制
2
(Binary)
八进制
8
(Octal)
第2章 计算机中数制和编码

特 点
三、机器数转换真值
① 原码转换为真值 符号位决定正负,其余各位按权展开求和 ② 反码转换为真值 先求出反码对应的原码,再按照原码转换原则转换为真值 的方法求出真值。正数的原码就是反码本身;负数的原码 是在反码的基础上,符号位不变,数值按位取反 ③补码转换为真值 先求出补码对应的原码。正数的原码与补码相同 负数的原码是在补码的基础上再次求补。 例:[Y]反=11100101B [Y]原=10011010B Y=-26 例:[X]补 =11100101B [X]原=[[X]补]补 =10011011B X=-27
③2→16 以小数点为界向左向右四位一段,不够补0,四 位二进制数用一位十六进制数表示。 ④16→2 一位十六进制数用四位二进制数表示。
1×102+2×101+3×100 1×22+0×21+1×20 +4×10-1+5×10-2 +0×2-1+1×2-2
1101011(B)=6B(H) 11 0110 1110.1101 01 (B) 3 6 E D 4 =36E.D4(H)
其中:d 称为尾数,是二进制补码纯小数,指明数的全部 有效数字;p称为阶码,是二进制补码定点整数,指明小数点 的位置,它的符号称作阶符,表明小数点的移动方向。小数 点随着p的符号和大小而浮动,故这种数称为浮点数。尾数位 数(有效数字)表示数的精度,阶码尾数表示机器数能表示 数的范围。
此处是标题
2
YHC
此处是标题
1
YHC
2. 反码 编 码 方 法 ---正数的反码表示与原码相同;负数的反码是将 其原码除符位外各位取反得到。 [X]反= 0X1X2…Xn-1=X (X≥0) (X≤0) 1X1X2…Xn-1=(2n-1)-│X│
第2章数制与编码教案

4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
第6页,此课件共55页哦
§2.2 数制间的相互转换
非十进制数 非十进制数
十进制数
十进制数
二与八、十六进制之间的转换
第7页,此课件共55页哦
2.2.2 十进制数转换成非十进制数
1.整数部分:用除基数r取余逆排法(先余为低,后余为高)
即:把一个十进制的整数不断除以所需要的基数r,直到商为0为止,
取其余数并逆排(除r取余逆排法),就能够转换成以r为基数的
数。
例1 求(29)10=( ? 1)12101
2 29
2 14
1
27
0
23
1
21
1
0
1
说明:
在十六进制中A—10 B—11 C—12 D—13 E—14 F—15
第4页,此课件共55页哦
各(8种9)1进0, (制10的1)2数, (5如5)何8, (区D3分)16?
§2.1 数 制
1.十进制数具有的特点:
(1)基数为10。 (2)位权值为10的i次幂 10i (3)逢10进1,借1当10
§2.4 计算机中数据的表示方法
第二讲:数制与编码

数据传输单位
(bps、 Kbps、 Mbps、Gbps)
1 TB =
240B
=1024GB
计算机中信息的编码
1、数字编码
(二进制编码的十进制数 BCD码) 对应关系
8421BCD码 十进制
8421BCD码,它是用4位二进制
数表示一位十进制数
例:十进制数791的8421BCD码是多少?
对应关系
8421BCD码 十进制
二进位计数制简称二进制,具有下列特点: (1)基数为2 (2)含有两个数码: 0和1 (3)逢二进一 (4)权为2i(i=-m~n-1,m、n为自然数) (5)表示方法: (1101)2或1101B
八进制( Octal )
八进位计数制简称八进制,具有下列特点: (1)基数为8 (2)含有八个数码: 0 、 1、 2、 3、 4、 5、 6、 7 (3)逢八进一 (4)权为8i(i=-m~n-1,m、n为自然数) (5)表示方法: (537)8或537O
二进制信息
数值信息在计算机内采用二进制数来表示; 采用二进制的原因:
二进制在技术上容易实现; 运算规则简单;
可以使计算机方便地进行逻辑运算;
机器可靠性高; 通用性强。
二进制数的算术运算
加法运算
规则: 0+0=0 0+1=1 1 + 0 = 1 1 + 1 = 10
逢2进1
例:1001+101=? 1001 + 101 1110
假设有A、B两个变量,有如 下运算结果:
A
B
A∧B
A∨B
~A
0 0 1 1
0 1 0 1
0 0 0 1
0 1 1 1
第2章 数制与信息编码

转换后的结果为:(0.534)10=(0.88B43)16
大学计算机基础
2.3 进位计数制
例子2-12:将(50.25)10转换成十六进制数。 解析:对于这种既有整数又有小数部分的十进制 数,可将其整数部分和小数部分分别转换成八进 制数,然后再把两者连接起来即可。 因为(50)10=(32)16,(0.25)10=(0.40)16 所以(50.25)10=(32.40)16
大学计算机基础
2.3 进位计数制
十六进制进位计数制具有如下特点:
有16个数符,分别为0、1、2、3、4、5、6、7、8、9、A、B、C、
D、E、F;
基数为16; 逢十六进一(加法运算),借一当十六(减法运算); 按权展开式。对于任意一n位整数和m位小数的十六进制数D,均
可按权展开为:D=Hn-1×16n-1+…+H1×161+H 0×16 0+
当R=16时,表示十六进制进位计数制,可使用0、1、
2、…、9、A、B、C、D、E、F共16个基本数符。
大学计算机基础
2.3 进位计数制
按基数进位和借位是指在执行加法或减法 时,遵守“逢R进一,借一当R”的规则,如 十进制数为“逢十进一,借一当十”,二进 制数的规则为“逢二进一,借一当二”。
大学计算机基础
2.1信息技术概述
信息技术的处理对象是信息和数据。
信息是人们在从事日常生产生活(如工业、农
业、军事、商业、管理、文化教育、医学卫生、 科学研究等)活动的过程中所涉及到的数字、 符号、文字、语言、图形、图像等的总称。
数据是存储在某种媒体上并且可以加以鉴别的
符号资料。
大学计算机基础
大学计算机基础
2.3 进位计数制
《数制与编码教》PPT课件教案资料

制数的形式来传送、存储加工。
§1.2.1 数制
1、人们在生产实践和日常生活中创造
了许多种表示数的方法,这些数的表示规
则称为数制。
如:
二进制 八进制 十进制 十六进制
B
O
D
H
§1.2.1 数制
2、二进制是“逢二进一”的计数方 法,有“0”和“1”两个数码。 通常在数字后加一个字母 B 表示 二进制。
§1.2.2编码
2.计算机中常用的名词 (1)位
计算机中所有的数据都是以二进制来表示 的,一个二进制代码称为一位,记为bit。 位是计算机中最小的信息单位。
(2)字节 在对二进制数据进行存储时,以八位二进制代码 为一个单元存放在一起,称为一个字节,记为 Byte。字节是计算机中存储数据的基本单位。
A、1010011B B 、257Q C、689D D、1FFH
6、与十进制数97等值的二进制数是__ B__。
A、1011111 B、1100001 C、1101111 D、1100011
7、 在计算机内部,数据处理和传递的形式是_______。
A、AsCII码 B、BCD码 C、二进制 D、十六进制
A、微软拼音输入法 B、区位码输入法 C、智能ABC输入法 D、五笔型输入法
§1.2.2编码
§1.2.2编码
结束
A、488
B、317
C、597 D、189
§练习题
13、在下列四条叙述中,正确的一条是 A 。 A、计算机中所有的信息都是以二进制形式存放的 B、256KB等于256000字节 C、2MB等于2000000字节 D、八进制数的基数为8,因此在八进数中可以使用的数
字符号是0、1、2、3、4、5、6、7、8
§1.2.1 数制
1、人们在生产实践和日常生活中创造
了许多种表示数的方法,这些数的表示规
则称为数制。
如:
二进制 八进制 十进制 十六进制
B
O
D
H
§1.2.1 数制
2、二进制是“逢二进一”的计数方 法,有“0”和“1”两个数码。 通常在数字后加一个字母 B 表示 二进制。
§1.2.2编码
2.计算机中常用的名词 (1)位
计算机中所有的数据都是以二进制来表示 的,一个二进制代码称为一位,记为bit。 位是计算机中最小的信息单位。
(2)字节 在对二进制数据进行存储时,以八位二进制代码 为一个单元存放在一起,称为一个字节,记为 Byte。字节是计算机中存储数据的基本单位。
A、1010011B B 、257Q C、689D D、1FFH
6、与十进制数97等值的二进制数是__ B__。
A、1011111 B、1100001 C、1101111 D、1100011
7、 在计算机内部,数据处理和传递的形式是_______。
A、AsCII码 B、BCD码 C、二进制 D、十六进制
A、微软拼音输入法 B、区位码输入法 C、智能ABC输入法 D、五笔型输入法
§1.2.2编码
§1.2.2编码
结束
A、488
B、317
C、597 D、189
§练习题
13、在下列四条叙述中,正确的一条是 A 。 A、计算机中所有的信息都是以二进制形式存放的 B、256KB等于256000字节 C、2MB等于2000000字节 D、八进制数的基数为8,因此在八进数中可以使用的数
字符号是0、1、2、3、4、5、6、7、8
计算机导论课件:数制与编码

数制与编码
1. 定点表示
定点表示是指小数点位置固定不变,分为定点整数与定点小数,定点整数的小数点位置隐式地固定
在数值位之后,表示纯整数;定点小数的小数点位置隐式地固定在数值位之前,表示纯小数,如图1-1所
示。数值的位数n决定了所能表示的数值范围,如机器数采用原码,则定点整数的二进制数值范围为
±
n 1...... 1
数制与编码
例1-13 设字长为8位,从高位到低位依次是:阶符1位,阶数2位,尾符1位,尾数4位,则浮点实数 表示格式如图1-6所示,小数点位置隐式地表示在尾数位之前,所能表示数值的正数范围为2-3×24~23×(1-2-4),负数范围为-23×(1-2-4)~-2-3×2-4。(-11.01)2=(-0.1101×2+10)2的浮点实数存储可见图中。
数制与编码 2. 补码 对于加法运算,原码与真值的运算步骤较复杂。为了简化运算,引入了补码。 设字长为n位,二进制整数x的补码[x]补定义为
二进制纯小数x的补码[x]补定义为
二进制数x转换为补码[x]补的简单方法是:当x为正数时,[x]补的符号位为0,数值位不变;当x为负数 时,[x]补的符号位为1,数值位为取反加1(整数相当于加1,纯小数相当于加2-(n-1))。
,十进制数值范围为±(2n-1),定点小数的二进制数值范围为±
n 0.1...... 1
,十进制数值范围为
±(1-2-n)。
数制与编码 例1-11 以定点整数为例,设字长为8位(采用8位存储数据),从高位到低位依次是:符号1位,数值7
位,小数点位置隐式地固定在数值位之后,所能表示的二进制数值范围为±1111111,对应的十进制数 值范围为±(27-1)。
一个二进制数的记阶表示不唯一,不同的记阶表示需要的阶数位数和尾数位数不同,为了提高浮点 表示的精度,人们引入了规范化浮点数。尾数最高位为1的浮点实数称为规范化浮点数。当对非规范化浮 点数进行规范化时,尾数左移1位,阶数减1,尾数右移1位,阶数加1。
数制与编码基础ppt课件

十六进制先转成二进制,再从二进制转成八进制
(6EA)16=(110 1110 1010)2 (11 011 101 010)2 =(3352)8
十六进制先转成十进制,再从十进制转成八进制
(6EA)16=(1770)10 (1770)10=(3352)8
目录
2.1 2.2 2.3 2.4 2.5
2.3 计算机中数据的表示
2.3.1 数值型数据
(4)原码、补码和反码 例如,[X]补 =(11100001)2,但
X ≠(-1100001)2, 而是 X =(-00111111)2=(-31)10。 采用补码可以把减法转换为加法,且可证明两数和的补码等 于两数补码的和,即:[X+Y]补 =[X]补 +[Y]补
例:在字长为8位的二进制数字系统中,当 X=(64)10, Y=(10)10,求 X-Y=?
2.3 计算机中数据的表示
2.3.2 字符型数据
字符编码实际上就是为每个字符确定一个对应的整型二进制 数值编码。
由于字符与整型数值之间没有必然的联系,某个字符究竟对 应哪个整数完全可以人为规定,一旦规定好,就固定下来, 以便应用。
任一数制的数都由一串数码表示,其中每一位数码所 表示的实际值大小,除与数码本身的数值有关外,还 与它所处的位置有关,由位置决定的值就叫位权。
2.1 数制
2.1.1 常用数制 (1)十进制
十进制数制系统有十个计数符号:0,1,2,3,4,5 ,6,7,8,9。
十进制数具有以下特点:
① 基数为10; ② 位权值为10i; ③ 逢十进一,借一当十。
2.1 数制
2.1.3 计算机中的二进制运算 (2)逻辑运算
逻辑非运算
2.1 数制
(6EA)16=(110 1110 1010)2 (11 011 101 010)2 =(3352)8
十六进制先转成十进制,再从十进制转成八进制
(6EA)16=(1770)10 (1770)10=(3352)8
目录
2.1 2.2 2.3 2.4 2.5
2.3 计算机中数据的表示
2.3.1 数值型数据
(4)原码、补码和反码 例如,[X]补 =(11100001)2,但
X ≠(-1100001)2, 而是 X =(-00111111)2=(-31)10。 采用补码可以把减法转换为加法,且可证明两数和的补码等 于两数补码的和,即:[X+Y]补 =[X]补 +[Y]补
例:在字长为8位的二进制数字系统中,当 X=(64)10, Y=(10)10,求 X-Y=?
2.3 计算机中数据的表示
2.3.2 字符型数据
字符编码实际上就是为每个字符确定一个对应的整型二进制 数值编码。
由于字符与整型数值之间没有必然的联系,某个字符究竟对 应哪个整数完全可以人为规定,一旦规定好,就固定下来, 以便应用。
任一数制的数都由一串数码表示,其中每一位数码所 表示的实际值大小,除与数码本身的数值有关外,还 与它所处的位置有关,由位置决定的值就叫位权。
2.1 数制
2.1.1 常用数制 (1)十进制
十进制数制系统有十个计数符号:0,1,2,3,4,5 ,6,7,8,9。
十进制数具有以下特点:
① 基数为10; ② 位权值为10i; ③ 逢十进一,借一当十。
2.1 数制
2.1.3 计算机中的二进制运算 (2)逻辑运算
逻辑非运算
2.1 数制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EXIT
数制与码制
2.1
几种常用数制
主要要求:
掌握进位计数制
掌握十进制数和二进制数
了解八进制和十六进制。 不同进制数之间的相互转换
EXIT
数制与码制
一、数制
基数和位权
十进制数456.82的值为 -1 -2 × × × × × 4 100+5 10+6 1 +8 10 + 2 10
“基数” :进位计数制中所采用的数码的个数。 R 进制计数,进位规则是“逢R进1”,采用R个数码。R就是 进制计数的基数。“几进制,基数就是几” 处在不同数位的数码,代表不同的数值,每一个数位的数值 大小由该位数码的值乘以处于该位的一个固定值,这个固定值 就是该位的“权值”,称为“位权”。
(三) 八进制和十六进制
进制 数的表示 计数规律 基数 权 数码 八进制 (Octal) (xxx)8 或(xxx)O
十六进制(Hexadecimal)
(xxx)16 或(xxx)H
逢八进一,借一当八 逢十六进一,借一当十六 8 8i 0~7 16
16i
0 ~ 9、A、B、C、D、E、F
28 1+ 7 02 1+ 2 11 1 0 1+ 2×16-2 例如例如 (3BE.C4) = 3 × 16 + × 16 14 × 16 + 12 × 16 4 (437.25) = 4 × + 3 × 8 × 8 + × 8 5 × 8 16 8 == 768 ++ 176 +0.25 0.75+ +0.078125 0.015625 256 24 + + 14 7+ == (958.765625) (1010.11) 2
i m
i 3 1 1 2 a 2 1 2 1 2 1 2 1 2 i
n 1
(8 2 0.5 0.25)10 (10.75)10 【例1-2】将八进制(27.2)8转换成十进制数。 解: n 1 (27.2)8 ai 8i 2 81 7 80 2 81
i m 1
i n 1 n2 2 1 a R a R a R a R a R i n 1 n2 2 1 2 m
将按权展开式按照十进制规律相加,即得对应十进制数。
(1011.11)2 = 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 1×2-2 = 8 + 0 + 2 + 1 + 0.5 + 0.25 = 11.75 (1011.11)2 = (11.75)10 EXIT
数制与码制
i m i a R i n 1
EXIT
数制与码制
二、几种常见的数制
(一) 十进制 (Decimal)
(xxx)10 或 (xxx)D
例如(3176.54)10 或(3176.54)D 数码:0、1、2、3、4、5、6、7、8、9 进位规律:逢十进一,借一当十 数码所处位置不同时,所代表的数值不同 (11.51)10 10i 称十进制的权 10 称为基数 1 0 1 2 1×10 1×10 5×10 1×10 0 ~ 9 十个数码称系数 权 权 权 权 数码与权的乘积,称为加权系数 十进制数可表示为各位加权系数之和,称为按权展开式 (3176.54)10 = 3×103 + 1×102 + 7×101 + 6×100 + 5×10-1 + 4×10-2 EXIT
数制与码制
(二) 二进制 (Binary)
(xxx)2 或 (xxx)B
数码:0、1
权:2i 基数:2 系数:0、1 例如 (1011.11)2 或 (1011.11)B
进位规律:逢二进一,借一当二
例如 0 + 1 = 1 1 + 1 = 10 11 + 1 = 100 10 – 1 = 1
按权展开式表示 (1011.11)2 = 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 1×2-2
i m
(16 7 0.25)10 (23.25)10
EXIT
数制与码制
(二) 不同数制间的转换
2. 十进制数转换为R进制数 任意一个十进制数N可以由整数部分和小数部分 构成,设整数部分为N1,小数部分为N2,则 (N)10 =(N)R =(N1)10 +(N2)10
( N )10
9 1001 1 1 不同数制之间有关系吗? 10 1010 2 2
3 4 5 6 7 3 4 5 6 7 11 1011
11
12 13
9
A B
12
13 14 15
1100
1101 1110 1111
14
15 16 17
返回
C
D E F EXIT
数制与码制
(二) 不同数制间的相互转换
按权展开求和 1. 各种数制转换成十进制 【例1-1】将二进制(1010.11)2转换成十进制数。
数制与码制
第二章 数制与码制
数制
码制
本章小结
EXIT
数制与码制
本章目标
1.掌握十进制、二进制、八进制和十六进制 2.熟练掌握进位计数制规则及相互转换 3.熟练掌握各种常用码制和编码方式 4.了解原码、反码和补码
EXIT
数制与码制
为什么引入各种数制? 数字系统中,为了便于电路的实现,采用二进 制来表示各种命令或字符 二进制数的缺点:可读性太差 因此,在计算机程序设计中,采用八进制和十 六进制来表示数的大小。 二进制是计算机中所使用的计数制 八进制和十六进制是编程使用的计数制 十进制是人类习惯的计数制
( N ) R an 1an 2 ...a1a0 a1a2 ...a m an 1 R n 1 an 2 R n 2 a1 R1 a0 R 0 a1 R 1 a2 R 2 a m R m
EXIT
数制与码制
二、不同数制间的关系与转换
(二、不同数制间的关系与转换 一) 不同数制间的关系 对同一个数的不同计数方法
十进制、二进制、八进制、十六进制对照表
十 0 1 2 3 4 5 6 7 二 0000 0001 0010 0011 0100 0101 0110 0111 八 0 十六 0 十 8 二 1000 八 10 十六 8
数制与码制
2.1
几种常用数制
主要要求:
掌握进位计数制
掌握十进制数和二进制数
了解八进制和十六进制。 不同进制数之间的相互转换
EXIT
数制与码制
一、数制
基数和位权
十进制数456.82的值为 -1 -2 × × × × × 4 100+5 10+6 1 +8 10 + 2 10
“基数” :进位计数制中所采用的数码的个数。 R 进制计数,进位规则是“逢R进1”,采用R个数码。R就是 进制计数的基数。“几进制,基数就是几” 处在不同数位的数码,代表不同的数值,每一个数位的数值 大小由该位数码的值乘以处于该位的一个固定值,这个固定值 就是该位的“权值”,称为“位权”。
(三) 八进制和十六进制
进制 数的表示 计数规律 基数 权 数码 八进制 (Octal) (xxx)8 或(xxx)O
十六进制(Hexadecimal)
(xxx)16 或(xxx)H
逢八进一,借一当八 逢十六进一,借一当十六 8 8i 0~7 16
16i
0 ~ 9、A、B、C、D、E、F
28 1+ 7 02 1+ 2 11 1 0 1+ 2×16-2 例如例如 (3BE.C4) = 3 × 16 + × 16 14 × 16 + 12 × 16 4 (437.25) = 4 × + 3 × 8 × 8 + × 8 5 × 8 16 8 == 768 ++ 176 +0.25 0.75+ +0.078125 0.015625 256 24 + + 14 7+ == (958.765625) (1010.11) 2
i m
i 3 1 1 2 a 2 1 2 1 2 1 2 1 2 i
n 1
(8 2 0.5 0.25)10 (10.75)10 【例1-2】将八进制(27.2)8转换成十进制数。 解: n 1 (27.2)8 ai 8i 2 81 7 80 2 81
i m 1
i n 1 n2 2 1 a R a R a R a R a R i n 1 n2 2 1 2 m
将按权展开式按照十进制规律相加,即得对应十进制数。
(1011.11)2 = 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 1×2-2 = 8 + 0 + 2 + 1 + 0.5 + 0.25 = 11.75 (1011.11)2 = (11.75)10 EXIT
数制与码制
i m i a R i n 1
EXIT
数制与码制
二、几种常见的数制
(一) 十进制 (Decimal)
(xxx)10 或 (xxx)D
例如(3176.54)10 或(3176.54)D 数码:0、1、2、3、4、5、6、7、8、9 进位规律:逢十进一,借一当十 数码所处位置不同时,所代表的数值不同 (11.51)10 10i 称十进制的权 10 称为基数 1 0 1 2 1×10 1×10 5×10 1×10 0 ~ 9 十个数码称系数 权 权 权 权 数码与权的乘积,称为加权系数 十进制数可表示为各位加权系数之和,称为按权展开式 (3176.54)10 = 3×103 + 1×102 + 7×101 + 6×100 + 5×10-1 + 4×10-2 EXIT
数制与码制
(二) 二进制 (Binary)
(xxx)2 或 (xxx)B
数码:0、1
权:2i 基数:2 系数:0、1 例如 (1011.11)2 或 (1011.11)B
进位规律:逢二进一,借一当二
例如 0 + 1 = 1 1 + 1 = 10 11 + 1 = 100 10 – 1 = 1
按权展开式表示 (1011.11)2 = 1×23 + 0×22 + 1×21 + 1×20 + 1×2-1 + 1×2-2
i m
(16 7 0.25)10 (23.25)10
EXIT
数制与码制
(二) 不同数制间的转换
2. 十进制数转换为R进制数 任意一个十进制数N可以由整数部分和小数部分 构成,设整数部分为N1,小数部分为N2,则 (N)10 =(N)R =(N1)10 +(N2)10
( N )10
9 1001 1 1 不同数制之间有关系吗? 10 1010 2 2
3 4 5 6 7 3 4 5 6 7 11 1011
11
12 13
9
A B
12
13 14 15
1100
1101 1110 1111
14
15 16 17
返回
C
D E F EXIT
数制与码制
(二) 不同数制间的相互转换
按权展开求和 1. 各种数制转换成十进制 【例1-1】将二进制(1010.11)2转换成十进制数。
数制与码制
第二章 数制与码制
数制
码制
本章小结
EXIT
数制与码制
本章目标
1.掌握十进制、二进制、八进制和十六进制 2.熟练掌握进位计数制规则及相互转换 3.熟练掌握各种常用码制和编码方式 4.了解原码、反码和补码
EXIT
数制与码制
为什么引入各种数制? 数字系统中,为了便于电路的实现,采用二进 制来表示各种命令或字符 二进制数的缺点:可读性太差 因此,在计算机程序设计中,采用八进制和十 六进制来表示数的大小。 二进制是计算机中所使用的计数制 八进制和十六进制是编程使用的计数制 十进制是人类习惯的计数制
( N ) R an 1an 2 ...a1a0 a1a2 ...a m an 1 R n 1 an 2 R n 2 a1 R1 a0 R 0 a1 R 1 a2 R 2 a m R m
EXIT
数制与码制
二、不同数制间的关系与转换
(二、不同数制间的关系与转换 一) 不同数制间的关系 对同一个数的不同计数方法
十进制、二进制、八进制、十六进制对照表
十 0 1 2 3 4 5 6 7 二 0000 0001 0010 0011 0100 0101 0110 0111 八 0 十六 0 十 8 二 1000 八 10 十六 8
