第十二届小机灵杯智力冲浪展示活动初赛试卷详解(五年
2015第13届小机灵杯五年级初赛试题

第十三届“小机灵杯”数学竞赛初赛试题(五年级组)时间:60分钟总分:120分一、判断题(正确的打“√”,错误的打“×”。
每题1分)1.“几何学”起源于割地法或测地学。
()【答案】√几何学:简称几何,是研究空间区域关系的数学分支。
“几何学”这个词,是来自阿拉伯文,原来的意义是“测量土地技术”。
名称来源:几何这个词最早来自于阿拉伯语,指土地的测量,即测地术。
后来拉丁语化为“geometria”。
中文中的“几何”一词,最早是在明代利玛窦、徐光启合译《几何原本》时,由徐光启所创。
当时并未给出所依根据,后世多认为一方面几何可能是拉丁化的希腊语GEO 的音译,另一方面由于《几何原本》中也有利用几何方式来阐述数论的内容,也可能是magnitude(多少)的意译,所以一般认为几何是geometria的音、意并译。
2.远在公元前春秋战国时代的“九九歌”就是我们现在使用的乘法口诀。
()【答案】√九九歌(乘法口诀):九九歌是汉族民间谚语,在汉族传统文化中,九为极数,乃最大、最多、最长久的概念。
九个九即八十一更是“最大不过”之数。
古代汉族人民认为过了冬至日的九九八十一日,春天肯定经已到来。
远在公元前的春秋战国时代,九九歌就已经被人们广泛使用。
在当时的许多著作中,都有关于九九歌的记载。
最初的九九歌是从“九九八十一”到“二二如四”止,共36句。
因为是从“九九八十一”开始,所以取名九九歌。
大约在公元五至十世纪间,九九歌才扩充到“一一如一”。
大约在公元十三、十四世纪,九九歌的顺序才变成和现在所用的一样,从“一一如一”到“九九八十一”止。
九九歌就是我们现在使用的乘法口诀。
现在我国使用的乘法口诀有两种,一种是45句的,通常称为“小九九”;还有一种是81句的,通常称为“大九九”。
3.数论最初是从研究整数开始的,所以叫作整数论。
()【答案】√(此题答案不确定)数论:是纯粹数学的分支之一,主要研究整数的性质。
整数可以是方程式的解(丢番图方程)。
2013年12届小机灵决赛三年级详解(仅供参考)

三、解答题(请写出必要的解题步骤)(第 17 题 12 分,第 18 题 15 分) 17.明明妈妈在购物时发现一个有趣的现象,她每次付款时钱包内的钱数正好是所付金额的 5 倍,她结账两次后钱包内还剩 320 元,请问在一开始购物前她钱包内有多少钱? 【分析】每次付款时,钱包内的金额是所付金额的 5 倍,则付完钱后,钱包内的金额是所 付金额的 4 倍。所以第二次付了 320 4=80 元,付款前有 400 元,第一次付了 400 4=100 元,付款前有 500 元。 18.出租车公司维修站有 7 辆出租车要维修。如果用 1 名工人维修这 7 辆车的维修时间分别 为 12、17、8、18、23、30、14 分钟,每辆出租车每停开 1 分钟经济损失 2 元,现在由 3 名工作效率相同的工人各自单独工作,要使经济损失减到最小程度,最少损失为多少元? 【分析】为使损失最小,则每辆车修理及等待所用时间之和应最小。3 名工人修 7 辆车, 为使总和最小,则每人修的车应尽可能接近,所以 2 名工人各修 2 辆车,1 名工 人修 3 辆车。修 3 辆车的工人修第一辆车时,1 辆车在修理,2 辆车在等候,所以 时间被计算了 3 次,修第二辆车时,1 辆车在修理,1 辆车在等候,所以时间被计 算了 2 次,修第三辆车时,1 辆车在修理,时间被计算了 1 次;修 2 辆车的工人 修第一辆车时,1 辆车在修理,1 辆车在等候,所以时间被计算了 2 次,修第二辆 车时,1 辆车在修理,时间被计算了 1 次。所以共有 1 辆车修车时间被计算 3 次, 3 辆车时间被计算 2 次,3 辆车时间被计算 1 次。 () 12 14 17 2 18 23 30=181 分钟,最少损失 所以时间之和最小为 8 3 2 181=362 元。 Nhomakorabea)。
第十二届小机灵初赛

第十二届“小机灵杯”智力冲浪展示活动初赛试卷(四年级组)一、选择题(每题1分)1、数学的希腊文愿意是()A. 科学或知识B. 数字学C. 计算学2、从前有一位老人,临终时,他把17 匹马留给3 个儿子,他说:“老大出力最多,得总数的12 ;老二得总数的13 ;老三出力最小,就拿总数的19 。
”那么老大、老二、老三分别分到()匹马。
A. 8、6、3B. 9、6、2C. 9、5、33、韦达是第一个有意识地、系统地用符号来表达数学的人,他是16 世纪末的法国数学家,后世称他为()之父。
A. 数学B. 代数学C. 几何学4、一只青蛙掉到了20 米深的井里,每天白天它可以沿着湿滑的井壁向上爬3 米,但它休息时会掉下2 米,青蛙第()天才能爬出这口井。
A. 20B. 17C. 185、由已故的加拿大数学家提出设立,被称作是数学的“诺贝尔奖”的当今数学界的最高奖项是()A. 阿贝尔奖B. 拉马努金奖C. 菲尔兹奖二、填空题(每题8 分)6、对于两个数a 和b ,规定一种新运算,a△b= 3xa + 2xb,a▽b= 2xa + 3xb,那么3△(2▽1)=_______。
7、已知一串数列:1、3、3、3、5、3、7、3、9、3、…… ,该数列前100 项的和是______。
8、用6 个边长为1的正方形可以拼成一个边长为1的正方形,如果要拼一个边长为5 的正六边形,需要边长为1的正三角形_______个。
9、爸爸和明明做游戏,爸爸说:“你随便想一个数,并记住这个数,但不要说出来,然后用这个数加上90 ,减去27 ,再减去所想的数,再乘以11,再除以3 ,我能猜出答案,最终的答案是____。
10、饲养场的鸡与兔共有210 只。
已知鸡脚是兔脚数的2 倍,鸡有_____只。
11、一个三位数各位数字的乘积是18 ,满足条件的所有三位数的总和是_______ 。
12、右图四个圆相交把圆内分成了8 个部分,把1 8 这8 个数字填入这8 个部分,使每个圆内3 个数的和都相等,算一算,和最大是______,并填出一种填法。
(word完整版)十二届十三届十四届三年级小机灵杯初赛和决赛试题

第十二届"小机灵杯"初赛试卷(三年级组)一、选择题(每题1分)1.小明妈妈花了8元买了一条鱼,以9元价格卖掉,然后觉得不合算,又花了10元买回来,以11元卖给另一个人,那么小明妈妈赚了( )元。
A、3B、2C、12.家中电度表上的一度电表示的耗电量为( )。
A、0.1千瓦小时B、1千瓦小时C、100瓦小时3.十八世纪俄国的哥尼斯堡城,一直困扰人们的七色桥问题引起了一个著名的数学家的注意。
经过他的猜想,研究证明,得出了一笔画的几何规律。
这位数学家是( )。
A、欧拉B、高斯C、牛顿4.数学运算符号中的“+”号是由德国数学家( )创造的。
A、魏德美B、莱布尼茨C、鲁道夫5.罗马数字是由罗马人发明的,它一共由( )个数字组成。
A、5B、6C、7二、填空题(每题8分)6.对于两个数字a和b,规定一种新运算,a△b=3×a+2×b和 a∇b=2×a+3×b,那么2△(3∇4)=( )7.志愿者服务队为社区里行动不便的老人送报纸,小马负责一位住在7楼的老人,每上或下一层楼都要走14秒,那么小马上下来回一次共要( )秒。
8.移动右图中的2根小棒,使2013变为另一个数。
这个数最大是( )。
9.老师要制作1~100这100张数卡,在打印时,打印机发生了故障,将数字“1”错打成了“7”,那么有( )张数字卡被打错了。
10.商店营业员去银行兑换零钱,用100张一百元的人民币兑换了二十元与五十元的人民币共260张,其中二十元的人民币有( )张,五十元的人民币有( )张。
11.在右面算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A=______,B=______,C=______,D=______。
A B C A+ A C B AD B B A B12.大、小两只水桶中都装了一些水。
已知大桶中水的重量是小桶中水的重量的一半,如果往大桶中倒入30千克水,这时大桶中水的重量是小桶中水的重量的3倍,原来大桶中有( )千克水。
第十二届“小机灵杯”初赛详解(四年级组)

2,3, 4 12 , A 、 B 、 C 三人去图书馆的情况以 12 天为一个周期;
A B C × × × √ × × × √ × √ × √ × × × √ √ × × × × √ × √ × √ × √ × × × × × √ √ √
每 12 天中,只有 1 个人来图书馆的日子有 4 天; 从 3 月 1 日到 6 月 30 日一共有 31 30 31 30 122 天; 122 12 10 2 ; 从 3 月 1 日到 6 月 30 日只有 1 个人来图书馆的日子有 4 10 1 41 天。 【第 14 题】 一群猴子分成三组去桃园摘桃子,每组猴子数目相等,采摘完工后,将桃子合在一起后平分桃子。如果每 只猴子分 5 个,那么还剩 27 个;如果每只猴子分 7 个,那么有一只猴子分到的桃子不够 7 个(至少有 1 个) 。 这群猴子所摘桃子的总数是 ________ 个。 【分析与解】 盈亏问题。 设如果每只猴子分 7 个,还差 a 个( a ≤ 6 ) ; 猴子的个数为 27 a 7 5 27 a 2 ; 猴子的个数为整数,则 27 a 为偶数, a 为奇数; 当 a 1 时,猴子的个数为 27 1 7 5 14 ; 当 a 3 时,猴子的个数为 27 3 7 5 15 ; 当 a 5 时,猴子的个数为 27 5 7 5 16 ; 因为这群猴子能分成数目相等的三组; 所以猴子的个数为 3 的倍数; 故只能是猴子个数为 15 ; 所摘桃子的总数是 5 15 27 102 个。
第十二届“小机灵杯”智力冲浪展示活动初赛试卷 四年级组
轻墨柔扬
【第 15 题】 由三张长方形纸片(甲、丙、丁)与一张正方形纸片(乙)可以拼成一个面积为 480 平方厘米大长方形(如 图) ,已知乙、丙、丁的面积都是甲的 3 倍,图中甲、乙、丙、丁四个长方形的周长总和是 ________ 厘米。
第十二届“小机灵”杯初赛三年级详解

———————————————————————————————————————— 新舟同类型题目:
三年级超常班暑假班第五讲植树问题练习 6 小王要到大厦的 36 层去上班,一日因停电他步行上楼,他从一 层到六层用了 100 秒。如果用同样的速度走到 36 层,还需要_________秒。 ——————————————————————————————————————————— 解析:从一楼到七楼需要走 6 层,而从 1 楼走到 7 楼走了 6 层,则下楼时也走了 6 层,走每一层用的时 间 14 秒,则来回需要 2 6 14 168 秒。 ————————————————————————
三年级超常班秋季班第九讲例 5: 2 角和 5 角的硬币共 30 枚,总钱数是 102 角, 2 角硬币有( )枚, 5 角硬币有( )枚。 ———————————————————————————————————————————
解析: 我们可以用假设法来解这道题目, 如果假设 260 张都是二十元的人民币, 那么有 260 20 5200 元,而实际是 100 100 10000 元,少了 10000 5200 4800 元,说明有 50 元的,而每出现一张 50 元的,
———————————————————————————————————————— 新舟同类型题目: 三年级超常班秋季班第二讲趣味数字例 7 在 1-600 的自然数中, ( 1 )出现________次数字 4 ; ( 2 )含有数字 6 的数共有_______个。
———————————————————————————————————————————
考点:数字谜
———————————————————————————————————————— 新舟同类型题目:
第十四届“小机灵杯”数学竞赛初赛试题(五年级组)最新版

爱
【第 12 题】 有 45 个工人,若每人每小时能生产甲零件 30 个,或乙零件 25 个,或丙零件 20 个。现在用甲零件 3 个,乙 零件 5 个, 丙零件 4 个装配某种机器, 那么安排生产甲、 乙、 丙零件人数分别是 ________ 人,________ 人, ________ 人时,才能使每小时生产的零件刚好配套。
1 ,小玲第 9
________ 天读完这本书。
【分析与解】分数应用题。
1 第 6 天读了这本书的 ; 9 1 1 第 1 ~ 5 天读了这本书的 2 ; 9 18
第 1 ~ 6 天读了这本书的
1 1 1 ; 18 9 6
小玲第 8 天读完这本书。
【分析与解】比例应用题
设安排生产甲、乙、丙零件人数分别是 x 人, y 人, z 人时,才能使每小时生产的零件刚好配套; 则 30 x : 25 y : 20 z 3 : 5 : 4 ;则 x : y : z
第十四届“小机灵杯”数学竞赛初赛(五年级组)
答案仅供参考,一些以官方公布为准
(第 1 题~第 5 题,每题 6 分) 【第 1 题】 已知 128 x 75 x 57 x 6.5 ,那么 x ________ 。 【分析与解】解方程;除法性质。
128 x 75 x 57 x 6.5 128 75 57 6.5 x x x 128 75 57 6.5 x 260 6.5 x x 260 6.5 x 40
4.8 x 6.6 y 167.4 ; 由题意,得 6.2 x y 167.4
x6 解得 ; y 21
2 7 6 块,巧克力蛋糕买了 27 21 块。 27 27
数学竞赛小机灵杯五年级决赛解析

第十二届“小机灵杯”智力冲浪展示活动决赛试卷(五年级组)2014年1月19日8:30~9:50时间:80分钟总分:120分一、判断题(每题1分)【第1题】小数点在十进制中用来隔开整数部分和小数部分。
中国魏晋时代的数学家刘徽第一个将“小数”这一概念用文字表达出来。
……………………………………………………………………………………………()【分析与解】中国自古以来就使用十进位制计数法,一些实用的计量单位也采用十进制,所以很容易产生十进分数,即小数的概念。
第一个将这一概念用文字表达出来的是魏晋时代的刘徽。
他在计算圆周率的过程中,用到尺、寸、分、厘、毫、秒、忽等7个单位;对于忽以下的更小单位则不再命名,而统称为“微数”。
填“√”。
【第2题】做小数加减法时要把小数点对齐。
在小数乘法法则中,两个因数中一共有几位小数,就要从积的左边向右数几位点上小数点。
…………………………………………………………………………………………()【分析与解】在小数乘法法则中,两个因数中一共有几位小数,就要从积的右边向左数几位点上小数点。
故填“×”。
第十二届“小机灵杯”智力冲浪展示活动决赛试卷五年级组中国古代数学最重要的典籍应当是《九章算术》,魏晋数学家刘徽用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法。
……………………………………………………………………………( )【分析与解】所谓“割圆术”,是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。
“圜,一中同长也”。
意思是说:圆只有一个中心,圆周上每一点到中心的距离相等。
早在我国先秦时期,《墨经》上就已经给出了圆的这个定义,而公元前11世纪,我国西周时期数学家商高也曾与周公讨论过圆与方的关系。
认识了圆,人们也就开始了有关于圆的种种计算,特别是计算圆的面积。
我国古代数学经典《九章算术》在第一章“方田”章中写到“半周半径相乘得积步”,也就是我们现在所熟悉的公式。
十三届小机灵杯五年级决赛试题解析

2
n 20 n 25 n 40 , , , a 39.5 a 27 a 4.5 n 25 仅有 满足要求,即共排成 25 排,第一排 27 1 28 人 a 27
解得 n 只小球外观相同,其中有一只小球的重量比其他小球的重量比其他小球轻(其他小球重量相 等) 。 若用一架没有砝码的天平秤作为工具, 至少称量 5 次就可以把那个重量较轻的小球找出来。 那么 n 的最大值是__________。 【解析】假设有 3a 个球,将球分成三堆,每堆 a 个,称两堆,若哪堆轻,则球在轻的那堆中,若一 样重,则球在第三堆中 9. 5 次称出, n 的最大值为 3 243 10. 如图,在△ABC 中,已知 AB=AC,AE⊥BC,CD=CA,AD=DB,则∠DAE=_____度。
1 1 升酒精, 往瓶中加入等量的水并搅匀, 然后再倒出 升混合 3 3 1 液,在加入等量的水并搅匀,最后在倒出 升混合液,并加入等量的水。这时,瓶内液体中还 3
从一只装有 1 升酒的大瓶中倒出 有酒精__________升。
第十二届“小机灵杯”智力冲浪展示活动初赛试卷详解.doc
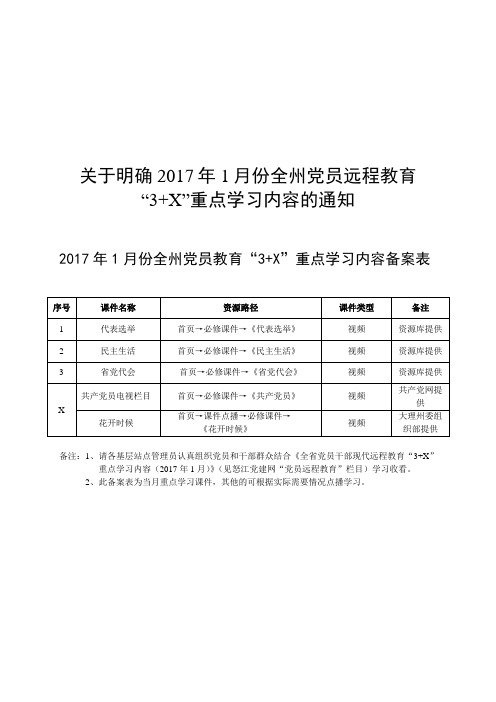
关于明确2017年1月份全州党员远程教育“3+X”重点学习内容的通知
2017年1月份全州党员教育“3+X”重点学习内容备案表
序号
课件名称
资源路径
课件类型
备注
1
代表选举
首页→必修课件→《代表选举》
视频
资源库提供
2
民主生活
首页→必修课件→《民主生活》
视频
资源库提供
3
省党代会
首页→必修课件→《省党代会》
视频
资源库提供X共来自党员电视栏目首页→必修课件→《共产党员》
视频
共产党网提供
花开时候
首页→课件点播→必修课件→
《花开时候》
视频
大理州委组织部提供
备注:1、请各基层站点管理员认真组织党员和干部群众结合《全省党员干部现代远程教育“3+X”重点学习内容(2017年1月)》(见怒江党建网“党员远程教育”栏目)学习收看。
小机灵杯五年级试卷【含答案】

小机灵杯五年级试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种动物属于哺乳动物?A. 青蛙B. 猫头鹰C. 老虎D. 鲨鱼2. 地球自转的方向是?A. 自西向东B. 自东向西C. 自南向北D. 自北向南3. 下列哪种植物可以进行光合作用?A. 蘑菇B. 草莓C. 玫瑰D. 以上都可以4. 下列哪个不是我国的传统节日?A. 春节B. 中秋节C. 愚人节D. 端午节5. 下列哪个行星离太阳最近?A. 金星B. 地球C. 水星D. 火星二、判断题(每题1分,共5分)1. 鸟类会进行迁徙。
()2. 恐龙已经全部灭绝。
()3. 光速比声速慢。
()4. 地球是太阳系中最大的行星。
()5. 鱼类可以在陆地上呼吸。
()三、填空题(每题1分,共5分)1. 我国首都是______。
2. 地球上面积最大的洲是______。
3. 人体最重要的器官是______。
4. 世界上最高的山峰是______。
5. 人类最早使用的工具是______。
四、简答题(每题2分,共10分)1. 请简述光合作用的过程。
2. 请简述我国传统节日的起源。
3. 请简述恐龙灭绝的原因。
4. 请简述鱼类的呼吸方式。
5. 请简述太阳系中的行星顺序。
五、应用题(每题2分,共10分)1. 如果一辆汽车以每小时60公里的速度行驶,那么它行驶100公里需要多长时间?2. 如果一个正方形的边长是4厘米,那么它的面积是多少平方厘米?3. 如果一个人的体重是60公斤,地球的重力加速度是9.8米/秒²,那么这个人在地球上的重力是多少牛顿?4. 如果一个水池每分钟进水5升,出水3升,那么10分钟后水池里的水是多少升?5. 如果一个班级有20个男生和30个女生,那么男生和女生的比例是多少?六、分析题(每题5分,共10分)1. 请分析为什么地球上有季节的变化。
2. 请分析为什么人类需要睡眠。
七、实践操作题(每题5分,共10分)1. 请用放大镜观察树叶的脉络,并画出你所观察到的脉络。
十二届小机灵杯决赛试题

第十二届“小机灵杯”智力冲浪展示活动决赛试卷(四年级组)2014 年1月19 日时间:80 分钟总分:120 分一、判断题(每题1分)【第1 题】中国南北朝时期的数学家、天文学家、物理学家祖冲之把圆周率数值推算到了小数点后面的第9 位,被称作π之父。
………………………………………………………………………()【第2 题】古希腊数学家阿基米德是一个将符号引入数学的人,他用元音字母表示未知量,用辅音字母表示已知量(方程的正系数)。
…………………………………………………………… ()【第3 题】把一条线段分割为两部分,使其中较长部分与全长之比等于另一段较短部分与这部分之比。
由于按此比例设计的造型十分美丽,因此这一比例被称为“美丽分割”。
【第4题】著名中国数学家陈景润1966年发表《表达偶数为一个素数及一个不超过两个素数的乘积之和》,成为哥德巴赫猜想研究史上的里程碑。
……………………………………………()【第5 题】法国数学家、物理学家、哲学家笛卡尔,他的著作生前被禁止出版或被烧毁。
《几何学》是他公开发表的唯一一部数学著作。
……………………………………………………………()二、填空题(每题8 分)【第6 题】数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…的第1000 项的值是________ 。
【第7 题】一条长为78 厘米的铁丝,每隔3 厘米涂一个红点。
将此铁丝在红点处折弯,形成一个长方形。
那么,围成的长方形的面积最大是________ 平方厘米。
【第8 题】有100 个棋子,两人轮流取棋子,每次允许取其中1 个、2 个或5 个,谁最后把棋子取完就算获胜。
如果你先取,那么第一次你取________ 个,才能保证获胜。
【第9 题】将1-6 分别填入下式的6 个方格中,积最大是________ 。
□□×□□×□□【第10 题】学校要将90 本故事书分发给三年级学生。
第十二届小机灵杯初赛(五年级)—含答案

第十二届“小机灵杯”小学数学竞赛五年级组初赛试题一、选择题(每题1分)1.世界数学最高奖是( )。
它与1932年在第九届国际数学家大会上成立,于1936年首次颁奖,是数学家的最高荣誉奖。
CA. 诺贝尔数学奖B.拉马努金奖C.菲尔兹奖2.他是古希腊最负盛名、最有影响的数学家之一。
他最著名的著作《几何原本》是欧洲数学的基础,被誉为“几何之父”。
在牛津大学自然历史博物馆还保留着他的石像,他是( )。
AA.欧几里得B.丢番图C.毕达哥拉斯3.对圆周率的研究最早发源于( )。
AA.中国B.罗马C.希腊4.“=”号是由英国人( )发明的。
BA.狄摩根B.列科尔德C.奥特雷德5.古时候的原始人捕猎,捕到一只野兽对应一根手指。
等到10根手指用完,就在绳子上打一个结,这就是运用现在的数学中的( )。
CA.出入相补原理B.等差数列求和C.十进制计数法二、填空题(每题8分)6.已知:[(11.2-1.2÷□)×4+51.2]×0.1=9.1,那么□=( )。
0.96 7.分母是两位数,分子是1,且能化成有限小数的分数有( )个。
98.五年级一班有40名学生,在数学考试中,成绩在前8名的同学平均分比全班的平均分高3分,其他同学的平均分比前8名同学的平均分低( )分。
3.75 9.将2013加上一个正整数,使和能被11和13整除,加的整数尽可能小,那么加的正整数是( )。
13210.在小于10000的正整数中,交换一个数最高位上与最低位上的数字,得到一个新数,且新数是原数的1.2倍,满足上述条件的所有数的总和是( )。
553511.从三位数100,101,102,…,699,700中任意取出n 个不同的数,使得总能找到其中三个数,他们的数字和相同。
那么n 的最小值为( )。
4712.右图是一个由数字组成的三角形,它的组成有着一定的规律,第九行从左往右第7个数是( )。
132413.李老师与小马、小陆、小周三位学生先后从学校出发走同一条路去电影院,三位同学的步行速度相等,李老师的步行速度是学生的1.5倍。
第十届小机灵杯初赛(五年级)—含答案

第十届“小机灵杯”小学数学竞赛五年级组初赛试题第一项,下列题目每题8分。
1.计算:0.1-(0.1+0.3)+(0.1+0.3+0.5)-(0.1+0.3+0.5+0.7)+…-(0.1+0.3+…+9.5)+(0.1+0.3+0.5+…+9.7)=()122.52.10211-2011的差各个数位上的数字之和是()。
18963.在7002,70002,700002,……,这样的最高位的数字是7,最低位数字为2,中间数字全为0的整数中,能被81整除的最小数是()。
7000024.粮店第一天运进50袋大米和30袋面粉,共重12400千克;第二天运进70袋大米和60袋面粉,共重18800千克。
每袋大米重()千克;每袋面粉重()千克。
200,80第二项,下列题目每题10分。
5.下图中有两只母鸡正在盘算着,要使每行、每列、每斜行中的鸡蛋不超过2个。
它们最多能在这蛋格子里下()个蛋,蛋格子里已经下了2个蛋。
106.如下图,四个圆形跑道,每个跑道的长都是1千米;A ,B ,C ,D 四名运动员同时从交点O 出发,分别沿着四个跑道跑步,他们的速度分别为每小时2千米;每小时3千米;每小时4千米;每小时5千米,那么从出发到四人相遇,四人共跑了()圈。
147.由两个2和三个4组成的不同五位数的平均数是()。
35555.28.甲、乙两人同时从A 、B 两地出发,甲每分钟行80米,乙每分钟行60米,两人在途中的C 点相遇。
如果甲晚出发7分钟,两人将在途中的D 点相遇,且A 、B 的中点距C ,D 距离相等。
A 、B 两地相距()米。
1680第三项,下列题目每题12分。
9.将一个9cm ×9cm ×9cm 的正方体切为1cm ×1cm ×1cm 的小正方体。
用这些小正方体重新粘合成一个内部为空洞但表面无空洞的大正方体,这个空心正方体要尽可能大。
那么剩下的来没有用到的小正方体有()个。
三年级小机灵杯112届初赛78届决赛真题及答案 图文

三年级小机灵杯112届初赛78届决赛真题及答案图文小机灵杯1-12届复赛真题试卷小机灵杯1-11届复赛真题答案小机灵杯7届决赛真题小机灵杯8届决赛真题第1页共41页第一届小机灵杯邀请赛1、按规律填数: 9012、在一个减法算式中,把被减数,减数,差这三个数相加,所得的和除以被减数(不等于0),商等于(3、右式中,不同的字母表示不同的数字,那么ABC表示的三位数是( ).4、如果2只白兔2天吃白菜2千克,照这样计算,那么8只白兔8天吃白菜(5、右面算式中的被除数是(6、甲,乙两人今年的年龄和是33岁,4年后,甲比乙大3岁,问甲今年(7、把边长分别为10厘米,9厘米,8厘米和7厘米的4个正方形按照从大到小的顺序排成一行(如图)排成的图形的周长是()厘米.)岁.))千克.).812723634545()()第2页共41页8、有一堆围棋子,白子的个数是黑子个数的2倍,拿走96个白子后,黑子的个数是白子个数的2倍,原来黑子有(9、有1张伍元币,4张贰元币,8张壹元币.要拿出8元钱可以有(10、亮亮和聪聪玩“石头、剪刀、布”的游戏,两人用同样多的石子做记录,输一次就给对方一颗石子,结果亮亮胜了3次,聪聪比原来多了9颗石子,他们共做了(11、任取自然数2,3,4,5,6,7中的三个数(不能重复)组成一个和,那么不相同的和共有( )个.12、新华小学的电表显示的用电量是61111,要使电表显示的用电量的五位数中有四个数码相同,学校至少再用(13、黑、白两种颜色的珠子,一层黑,一层白,排成正三角形的形状(如图),当白珠子比黑珠子多10颗时,共用了(14、公园里有一排彩旗,按3面黄旗,2面红旗,4面绿旗的顺序排列,小明看到这排彩旗的尽头是一面绿旗,已知这排彩旗不超过200面,这排旗子最多有(15、将写有数码的纸片倒过来看,0、1、8三个数字不变,6倒过来是9,9倒过来是6,而其余的数字倒过来则没有意义,某种游戏卡片是从001,002,003,004,??,998,999共有999张,那么,所有的卡片倒过来看,与原卡片数值保持不变的共有()张.)面.)颗白珠子.)度.)次游戏. )种不同的方法.)个.第3页共41页第二届小机灵杯邀请赛1. 在右面竖式的各个方框中填上适当的数字,使竖式成立.2. 推3. 按下面的规律摆五角星,第82个五角星是(第()个.)色的.在这种颜色的五角星中,它是算是24,是28,那么是()☆☆☆☆☆☆4.学校有60人要参加“金孔雀”舞蹈比赛,比赛时要求每排人数即不能少于4人,也不能多于16人,问共有()中排法.)5.根据前面三个算式的启发,括号里面应当填上(4. 5. 6. 7. 8. 9.6.一个电影院的第一排有15个座位,以后每一排都比前一排多2个座位,最后一排有73个座位,这个电影院一共有(7.下图中不含“”的三角形比含“”的三角形多()个.)个座位.第4页共41页8.把21分拆成两个自然数之和,且使这两个自然数的乘积最大,这个最大的乘积是().9.如图,在长方形ABCD中,EFGH是正方形.如果AF=11厘米,HC=14厘米,那么长方形ABCD的周长是( 5)厘米.10.将不大于12且互不相同八个自然数天使右图八个放个中,使九宫格图中的每一行,每一列以及对角线上的三个数的和都等于21.11.在一道减法算式里,被减数、减数与差的和是360,而差比减数的4倍还多20.被减数是 (12.有两个完全一样的长方形,拼成两种长方形,一种长方形的周长是100厘米,另一种长方形的周长是140厘米,原来长方形的长是(13.某商场里面花布的米数是白布的3倍,如果每天卖20米白布和45米花布.( 以后,白布全部卖完,而花布还剩下180米,原来有花布(14.____年爸爸的年龄是姐姐和妹妹年龄和的4倍,____年爸爸的年龄是姐姐和妹妹年龄和的2倍,爸爸是(15.书架上、下两层摆放着若干本书.如果从上层拿10本放到下层,则下层的本数是上层的2倍,如果从下层拿到10本放到上层,则上层的本数是下层的3倍,上层原来有图书( 下层原来有图书()本.)本,)年出生的. )米.)天)厘米,宽是( )厘米.),减数是( ),差是().第5页共41页。
第十三届小机灵杯初赛(五年级)—含答案

第十三届“小机灵杯”小学数学竞赛五年级组初赛试题一、判断题(正确的打“√”,错误的打“×”。
每题1分)1.“几何学”起源于割地法或测地学。
()√2.远在公元前春秋战国时代的“九九歌”就是我们现在使用的乘法口诀。
() √3.数论最初是从研究整数开始的,所以叫做整数论。
()√4.商高是中国古代西周初期的数学家,他被称为是“勾股定理”的最早发现者,比古希腊的毕达哥拉斯晚了好几百年。
()×5.“求解一次同余组的剩余定理”在世界数学史上被称为“中国剩余定理”。
()√二、填空题(6~10题每题5分,11~15题每题8分,16~20题每题10分)6.已知下面两个关于的方程:6(x+8)=18x和6x-2(a-x)=2a+x有相同的解,则a=()。
77.一件商品如果打对折与打七折价格相差81元,那么这件商品打八折的价格是()元。
3248.以下四个数1307674368000、1307674368500、1307674368200、1307674368010,只有一个恰为1至15这十五个整数的乘积。
这个数是()。
13076743680009.0.18×0.81+0.18+0.81=()。
139/12110.已知一个等腰三角形的最大角是最小角的4倍,那么最大角与最小角的差是()度。
90或6011.我们规定:a◎b=a×(a+1)×…×(a+b-1)。
已知x◎y◎2=420,那么y◎x=()。
120或20!12.从甲地到乙地的路只有上坡与下坡,全程21千米。
如果上坡的速度是4千米/时,下坡的速度是6千米/时,从甲地到乙地需4.25小时,那么从乙地到甲地需要()小时。
4.513.如果三位数m 同时满足如下条件:①m 的各位数字和是12;②2m 还是一个三位数,且数字和是6。
这样的三位数m 共有()个。
314.李老师去玩具店买球。
所带的钱恰好能买60个塑料球。
如果不买塑料球,恰好可以买36个玻璃球或45个木质球。
1-9届5年级小机灵杯试题

第一届 (2)第二届 (4)第三届 (9)第四届 (13)第五届 (17)第六届“聪明小机灵”小学数学邀请赛(决赛)试题 (21)第七届“聪明小机灵”小学数学邀请赛(决赛)试题没有确定是否是 (24)第七届小机灵杯复赛 (27)第八届小机灵杯五年级决赛试题(含答案) (29)第九届小机灵杯五年级复赛试题 (31)第一届第二届第三届第四届第五届第六届“聪明小机灵”小学数学邀请赛(决赛)试题1、计算:0.02+0.04+0.06+……+20.04+20.06+20.08=()。
2、已知N=95+195+1995+…+19999999995,那么,N的各位数字的和是()。
3、有9个数,每次任意抽去一个数,计算剩下8个数的平均数,得到如下9个不同的平均数:101、102、103、104、105、106、107、108、109,这9个数的平均数是()。
4、前2008个既能被2整除又能被3整除的正整数的和,除以9的余数是()。
5、一本字典共有2008页,在这本字典的页码上,数字8共出现了()次。
边长15分米的正方形分成两个高相等(AF=FD)的直角梯形与一个直角三角形,已知两个梯形面积的差是18平方分米,图中线段CG的长是()分米。
7、文具店存有一批练习本,原定每本定价是20分。
现在决定把全部练习本按同一价格降价处理,但每本价格不能低于11分(降价后的价钱是整分数)。
如果把这批练习本全部卖出后可收得39.10元。
这批练习本一共有()本,每本价钱比原定降价了()元。
8、一个棱长都是正整数的长方体表面积是210平方厘米,已知它的六个面中有两个面积大于1平方厘米的正方形,则它的体积最大是()立方厘米。
9、一次测验共有5道题,做对一题得1分,已知26人的平均分不少于4.8分,其中最低分得3分,并且至少有3人得4分,那么得5分的共有()人。
10、M÷N÷P=6,M÷N-P=30,M-N=105,M=()。
第11届小机灵五年级初赛试题(3)

第十一届小机灵杯五年级初赛试题分析1、5.5×6.6+6.6×7.7+7.7×8.8+8.8×9.92、五〔1〕班男生的平均身高是149cm,女生的平均身高是144cm,全班的平均身高是147cm。
那么,五〔1〕班的男生人数是女生人数的多少倍?3、甲、乙分别持有7 张卡片,卡片上分别写有1、2、3、4、5、6、7 七个数字。
如果两人各摸出一张卡片,那么两张卡片上数字和为8 的可能性是多少?4、有一个圆形跑道,甲用40 秒跑完一圈,乙跑的方向与甲相反,每15 秒遇到甲一次。
乙跑完一圈需要几秒?5、50 个各不相同的正整数,它们的和为2021,那么这些数里奇数最多有几个?6、把正整数排成以下数阵:1 2 5 10 …4 3 6 11 …9 8 7 12 …16 15 14 13 ………………第21 行第21 列的数是多少?8、某班有60 人,其中42 人会游泳,46 人会骑车,50 人会溜冰,55 人会打乒乓球。
可以肯定至少有多少人四项运动都会?9、把既不是平方数也不是立方数的正整数〔0 除外〕按从小到大的顺序排列,得到2,3,5,6,7,10,……,其中第1000 个数是多少?10、如下图,ABCD 是梯形,三角形ADE 的面积是1,三角形ABF 的面积是9,三角形BCF 的面积是27,那么三角形ACE 的面积是多少?11、某学生漏看了写在两个三位数之间的乘号,将它们当成了一个六位数,而该六位数恰好是原来乘积的7 倍,这两个三位数之和是多少?12、从1 到900 中选6 个正整数,使这6 个连续正整数的积的尾数恰好为4 个0,有多少种选法?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二届“小机灵杯”智力冲浪展示活动初赛试卷详解(五年级组)时间:80分钟 总分:120分一、选择题(每题1分)1、世界数学最高奖是( C )。
它于1932年在第九届国际数学家大会上设立,于1936年首次颁奖,是数学家的最高荣誉奖。
A 、诺贝尔数学奖B 、拉马努金奖C 、菲尔兹奖2、他是古希腊最负盛名、最有影响的数学家之一。
他最着名的着作《几何原本》是欧洲数学的基础,被誉为“几何之父”。
在牛津大学自然历史博物馆还保留着他的石像,他是( A )。
A 、欧几里得B 、丢番图C 、毕达哥拉斯 此题曾在ICS 五年级ICS 课件中小机灵杯智力故事中出现过3、对圆周率的研究最早发源于( A )。
A 、中国B 、罗马C 、希腊4、“=”号是由英国人( B )发明的。
A 、狄摩根B 、列科尔德C 、奥特雷德 此题曾在ICS 五年级ICS 课件中小机灵杯智力故事中出现过5、古时候的原始人捕猎,捕到一只野兽对应一根手指。
等到10根手指用完,就在绳子上打一个结,这就是运用现在数学中的( C )。
A 、出入相补原理B 、等差数列求和C 、十进制计数法二、填空题(每题8分)6、已知:[(11.2 1.2)451.2]0.19.1-÷⨯+⨯=,那么= 。
【考点】代数——解方程【解析】(11.2 1.2)451.291-÷⨯+=(11.2 1.2)439.811.2 1.29.951.2 1.251.2 1.250.96-÷⨯=-÷=÷==÷=7、分母是两位数、分子是1,且能化成有限小数的分数有个 。
【考点】数论——分数性质【解析】一个最简分数,若能化为最简分数,那么它的分母只能含有质因子2、5,而分母为两位数,分子是1的分数显然是最简分数所以这些分数的分母分解质因数后应该形如25a b ⨯1、当0b =时,a 可取4到6,共3种2、当1b =时,a 可取1到4,共4种3、当2b =时,a 可取0到1,共2种当3b ≥时,325599a b ⨯≥>综上,共3429++=个。
8、五年级一班有40名学生,在数学考试中,成绩排在前8名的同学平均分比全班的平均分高3分,其他同学的平均分比前8名同学的平均分低 分。
【考点】组合——平均数应用题【解析】法一:由于前8名同学的平均分比全班平均分高3分,可推知他们为其他同学提供了3824⨯=分,如果没有这24分,其他同学的平均分会比全班的平均分下降24(408)0.75÷-=,所以其他同学的平均分比前8名同学的平均分低分。
法二:设前8名学生平均分为x ,则全班平均分为3x -,设其他同学的平均分为y可列得方程:83240(3)x y x +=-解得:3232120 3.75x y x y -=⇒-=即其他同学的平均分比前8名同学的平均分低分。
9、将2013加上一个正整数,使和能被11和13整除,加的整数尽可能小,那么加的正整数是 。
【考点】数论——整除余数问题【解析】[11,13]143=,能被11和13整除,即能被143整除。
20131431411÷=,所以最小需要加上14311132-=。
或者,比2013大的143的倍数最小为143152145⨯=,所以最小需要加上21452013132-=。
10、在小于10000的正整数中,交换一个数最高位上与最低位上的数字,得到一个新数,且新数是原数的倍,满足上述条件的所有数的总和是 。
【考点】数论——位值原理【解析】由于新数是原数的倍,设原数为N ,则有1.2N 是整数,于是N 的个位必为0或5,而若N 的个位为0,则交换N 的最高位与最低位,得到的数一定会变小,不可能是N 的倍,所以N 的个位一定为5一、一位数中显然没有 二、两位数中,不妨设原数为5a ,由题意,有5 1.2550 1.2(105)11444a a a a a a =+=+== 所以两位数中满足条件的数为45 三、三位数中,不妨设原数为5ab ,由题意,有5 1.2550010 1.2(100105)1192494ba ab b a a b a b =++=+++=由于,a b 只能在0到9中选取,且a 不为0所以仅有一组解49a b =⎧⎨=⎩ 所以三位数中满足条件的数为495 四、四位数中,不妨设原数为5abc ,由题意,有5 1.25500010010 1.2(1000100105)11992024994bca abc b c a a b c a b c =+++=+++++=由于,,a b c 只能在0到9中选取,且a 不为0所以仅有一组解499a b c =⎧⎪=⎨⎪=⎩所以三位数中满足条件的数为4995综上,所以满足条件的数的总和为4549549955535++=11、从三位数100、101、102、……、699、700中任意取出n 个不同的数,使得总能找到其中三个数,它们的数字和相同。
那么n 的最小值是 。
【考点】组合——抽屉原理【解析】在100到700中,数字和最小的数为100,它的数字和为1,且其中数字和为1的数仅有1个;数字和最大的数为699,它的数字和为24,且其中数字和为24的数仅有1个。
剩下的数的数字和为2到23这22种数字和中的其中一个,且2到23的每种数字和至少都有2个数。
所以n 的最小值是11222147++⨯+=。
12、右图是一个由数字组成的三角形,它的组成有着一定的规律,第9行从左往右第7个数是 。
【考点】组合——找规律【解析】发现,除了第一行以外,所有奇数行的第一个数为0,以后的每个数为前一个数加上前一个数右上方的数。
所有偶数行的最后一个数为0,以后的每个数为后一个数加上后一个数左上方的数。
根据以上规律可以写出下表:27213851385132412021024800544272272256224178122616161564632161616101455542122000001111第9行从左往右的第7个数是1324。
13、李老师与小马、小陆、小周三位学生先后从学校出发走同一条路去电影院,三位同学的步行速度相等,李老师的步行速度是学生的倍。
现在李老师距学校235米,小马距学校87米,小陆距学校59米,小周距学校26米,当他们再行 米时,李老师距学校的距离刚好是三位学生距学校的距离和。
【考点】组合——列方程解应用题【解析】设学生再行x 米时,李老师距学校的距离刚好是三位学生距学校的距离和。
此时,李老师又行了1.5x 米。
列得方程:235 1.587592642x x x x x +=+++++⇒=即学生再行42米时,李老师距学校的距离刚好是三位学生距学校的距离和。
14、从23、65、35、96、18、82、70这七个数中任意取出若干个数相加,其中和是11的整数倍的取法有 种。
【考点】数论——整除余数问题【解析】一些数的和为11的整数倍,那么它们除以11的余数之和也应是11的倍数。
这7个数除以11的余数依次为1、10、2、8、7、5、4因此,本题实质为从1、2、4、5、7、8、10中取出若干个数相加,和是11的倍数有多少种取法1、取2个数,有(1、10)(4、7),共2种2、取3个数,有(1、2、8)(2、4、5)(4、8、10)(5、7、10),共4种3、取4个数,有(1、4、7、10)(2、5、7、8),共2种4、取5个数,有(1、2、4、5、10)(1、2、4、7、8),共2种5、取6个数,有(1、2、5、7、8、10),共1种6、取7个数,有0种综上,共有2422111++++=种。
15、如图,一张矩形纸片沿直线AC 折叠,顶点B 落在F 处,第二次过点F 再沿直线DE 折叠,使折痕DE∥AC,若AB =5,BC =3,则梯形ACDE 的面积为 。
【考点】几何——共边定理【解析】如下图,由于AC∥DE,所以ACF ACD ACE S S S ∆∆∆==显然,ACF ACB S S ∆∆=ACB ACD ACE S S S ∆∆∆∴== EA AB ∴=,BC CD =1244533021305322.52BDE ABD ABC ACDE BDE ABC S S S S S S ∆∆∆∆∆∴===⨯⨯⨯=∴=-=-⨯⨯=16、一个九位数所包含的数码恰好是1、2、3、4、5、6、7、8、9各一个,且这个九位数的任意两个相邻数码所组成的两位数都可以表示为两个一位数的乘积。
这个九位数是 。
【考点】组合——简易推理【解析】由于9981⨯=,所以两个一位数的乘积无法表示一个大于81的数,所以在这个九位数中,数字9后面不能再有数字,所以数字9一定在个位,而且数字8的后面一定是1由于8972⨯=,而796370⨯=<,886470⨯=<,所以数字7的后面一定是2由于17、37、47、67均为质数,57319=⨯,77711=⨯,所以17、37、47、57、67、77都无法表示为两个一位数的乘积,而2又必须在7的后面,所以27无法出现,所以在这个九位数中,7的前面不能再有数字,所以数字7一定在首位由于19、29、59、79均为质数,而39313=⨯,69323=⨯,所以19、29、39、59、69、79都无法表示为两个一位数的乘积,所以数字9的前面必须是4由于38219=⨯,58229=⨯,268217=⨯,18、48、78无法出现,所以数字8的前面必须是2所以这个九位数一定以7281开头,以49结尾还剩下的3、5、6中,5、6均可接在1后面若1后填5,则此时3不能填在5后面,所以5后面必须填6,此时6后面填3,但34217=⨯不符合要求所以1后面要填6,此时5不能填在6后面,所以6后面必须填3,此时3后面填5,整个九位数为9,经验证符合要求。
综上,所求九位数为9。
三、解答题(请写出必要的解题步骤)(第17题,12分 第18题,15分)17、商店以每个30元的批发价购进一批足球,按每个45元的零售价卖出,当卖到还剩下30个足球时,已获利1500元,请问商店购进足球多少个【考点】组合——经济问题【解析】法一:当剩下30个足球都卖出后,商店共获利150030452850+⨯=元。
每个足球获利15元,所以共购进2850(4530)190÷-=个足球。
法二:设购进足球x 个。
依题意,有45(30)301500190x x x -=+⇒=18、有若干名学生,恰好组成一个八列长方形方阵。
如果在队列中再增加120或从队列中减去120人,都能组成一个正方形方阵,那么原长方形方阵中共有多少名学生【考点】数论——平方差公式【解析】设原长方形方阵共有x 名学生,再设22120120x a x b⎧+=⎪⎨-=⎪⎩ 有22240a b -=()()240a b a b +-=而24012402120380460548640830102412201516=⨯=⨯=⨯=⨯=⨯=⨯=⨯=⨯=⨯=⨯ 由于学生能组成一个八列的长方形方阵,28812084x x a a ∴⇒+⇒⇒ 同理,4b4a b ∴+,4a b -604a b a b +=⎧∴⎨-=⎩或2012a b a b +=⎧⎨-=⎩3228904a b x =⎧⎪⇒=⎨⎪=⎩或164136a b x =⎧⎪=⎨⎪=⎩所以,原长方形方阵有904名学生或有136名学生。
