《自动控制原理》实验报告(线性系统的根轨迹)
自动控制原理实验报告
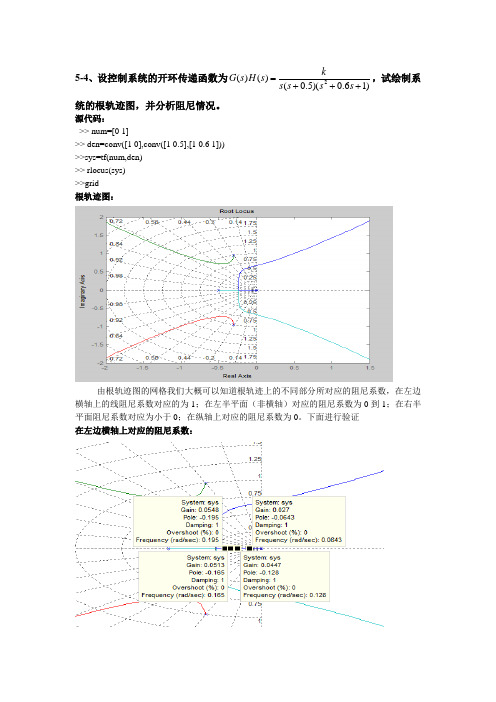
5-4、设控制系统的开环传递函数为)16.0)(5.0()()(2+++=s s s s k s H s G ,试绘制系统的根轨迹图,并分析阻尼情况。
源代码:>> num=[0 1]>> den=conv([1 0],conv([1 0.5],[1 0.6 1]))>>sys=tf(num,den)>> rlocus(sys)>>grid根轨迹图:由根轨迹图的网格我们大概可以知道根轨迹上的不同部分所对应的阻尼系数,在左边横轴上的线阻尼系数对应的为1;在左半平面(非横轴)对应的阻尼系数为0到1;在右半平面阻尼系数对应为小于0;在纵轴上对应的阻尼系数为0。
下面进行验证在左边横轴上对应的阻尼系数:在左半平面(非横轴)对应的阻尼系数:在右半平面对应的阻尼系数:经过验证可知,之前的阻尼系数分析正确5-6、已知单位反馈控制系统的开环传递函数为)3()1()(-+=s s s k s G ,试绘制系统的根轨迹图,并求出使系统稳定的k 值范围。
源代码:>> num=[1 1]>> den=conv([1 0],[1 -3])>> sys=tf(num,den)>> rlocus(sys)根轨迹图:分析稳定的k的取值范围:由上图可知:当k>3的时候,根轨迹在左半平面,此时系统稳定。
阻尼分布情况由图可以看出与上题相同:在左边横轴上的线阻尼系数对应的为1;在左半平面(非横轴)对应的阻尼系数为0到1;在右半平面阻尼系数对应为小于0;在纵轴上对应的阻尼系数为0。
另外,在右边横轴上的阻尼系数为-1。
6-4、(1))12)(12.0)(11.0()1(5)()(++++=s s s s s H s G 源代码:>> num=[5 5]>> den=conv(conv([0.1 1],[0.2 1]),[2 1])>> sys=tf(num,den)>> nyquist(sys)奈氏曲线:奈氏曲线逆时针包围(-1,j0)点0次,右半平面开环极点数为0,由奈氏判据一可知该闭环系统稳定。
第四章 线性系统的根轨迹法-4-2——【南航 自动控制原理】

根轨迹起于开环极点,终于开环零点。
由根轨迹方程,有
m
n
K (s zi )+ (s pi )=0
i 1
i 1
根轨迹起点 K =0 s pi , i 1, , n n个开环有限极点
由根轨迹方程,又有
m
n
(s zi )+(K )1 (s pi )=0
i 1
i 1
根轨迹终点 K s zi , i 1, , m m个开环有限零点
a
(2k 1)
nm
, k 0, 1,
ቤተ መጻሕፍቲ ባይዱ
a
=
(a1 n
b1 m
)
由多项式的根与系数关系
n
n
a1 pi b1 zi
i 1
i 1
n
m
pi z j
a
i 1
j 1
nm
例4.2-1 已知单位反馈系统的开环传递函数为
K G(s)
s(s 3) (s )2 2
0, 0
试分析开环极点参数变化时渐近线。
1
n
1
j1 d z j i1 d pi
分离点处相邻两条根 轨分迹离分点支处切一线共之有间多的少
夹条角根等轨于迹分支/?l
分离点处根轨迹的分离角d 为
d (2k 1) / l k 0,1,
分离点处,根轨迹进
侧的开环实有限零极点数为奇数。
系统的开环零极点分为 两类:实数零极点和复数 零极点,且复数零点或复 数极点必共轭成对。
系统开环零极点的分布为
图示,取实轴任一点 s=s1
·对复共轭开环极点
p4 j, p5 p4 j,
(s1 j)+(s1 +j)=2
自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例:开环传递函数
Gs
k1
ss
a
开环系统两个极点为:P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程: s2 as k1 0
闭环特征根:s1,2
a 2
a 2
2
k1
(闭环极点)
3
自动控制原理
在p5附近取一实验点sd, 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明:根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例:sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点,复极点提供的相角和为 3600。
2
s1=-1.172,s2=-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为:
Z 1800
其中 z p(不包括本点)
34
自动控制原理
j p5
p5
p3 p3
p2
自动控制原理-第四章 线性系统的根轨迹法(4)

暂态响应呈振荡性质,其超调量主要取决于主导极点的衰
减率
1 n
d n 1 2
1 2
并与其它极点接近原点的程度有关,调整时间主要取决于主
导极点的实部
1
。
n
(4)调节时间。调节时间主要取决于最靠近虚轴的闭环复数
极点的实部绝对值 1 n 。
(5)实数零、极点影响。闭环极点的存在会增大系统的阻尼比, 使响应速度减慢,超调量减少。闭环零点的存在减小系统阻尼, 使响应速度加快,超调量增加。
4-4 系统性能的分析
系统闭环零、极点位置与暂态响应的关系:
(1)稳定性。系统的稳定性只取决于闭环极点的位置。
(2)运行形式。如果闭环系统无零点,闭环极点均为实数 极点,则系统的暂态响应为单调的;如果闭环极点均为复 数极点,则系统的暂态响应为振荡的。
(3)超调量。如果系统具有一对闭环主导极点,则系统的
4-7 线性系统根轨迹分析的MATLAB方法
1、绘制零极点分布图 :[ p,z]=pzmap(sys);
2、绘制根轨迹图 绘制根轨迹一般步骤为: (1)先将特征方程写成 1 A P(s) 0 形式,得到等效的开 环传递函数 G A P(s) ; Q(s)
Q(s)
(2)调用rlocus命令绘制根轨迹。
Hale Waihona Puke (6)偶极子及其影响。如果系统中存在非常接近的零点和极 点,其相互距离比其本身的模值小一个数量级以上,则把这对 闭环零、极点称为偶极子。偶极子的位置距离原点非常近时, 其对暂态响应的影响一般需要考虑,但不会影响闭环主导极点 的主导作用。偶极子的位置距离原点较远时,其对暂态响应的 影响可以忽略。 (7)主导极点及高阶系统化简。在s平面上,离虚轴靠 近而附近又没有其它闭环零点的一些闭环极点 ,对系统 影响最大,称为主导极点。凡比主导极点的实部大3~6 倍以上的其他闭环零、极点,其影响均可忽略不计。对 于高阶系统,略去不十分靠近原点的偶极子,保留一个 或几个最靠近虚轴又不十分靠近闭环零点的主导极点, 将高阶系统简化为只有一、两个闭环零点和两、三个闭 环极点的二阶或三阶系统。
《自动控制原理》第4章 线性系统的根轨迹法

68
4.5 广义根轨迹
根轨迹部分是个半圆,半径是 k *
证明:根轨迹上一点S满足相角条件
s (s j2) (s j2)
代入s j
( j) ( j( 2)) ( j( 2))
arctan arctan 2 arctan 2
K* G(s)
s(s 2)(s 1)
26
法则五:根轨迹的分离点与分离角
分离点:几条根轨迹在[s]某一点相遇后又分开 的点。
说明有重根
27
实轴上的分离点(常见)
如果根轨迹位于实轴上相邻的两个开环极点之间, 其中一个可以是无限极点,则在这两个极点之间至 少存在一个分离点;
如果根轨迹位于实轴上相邻的两个开环零点之间, 其中一个可以是无限零点,则在这两个零点之间至 少存在一个分离点;
开环极点:
p1 0 p2 0 p3 2 p4 5
(2)实轴上的根轨迹 (3)根轨迹分支数
4
59
G0 ( s)
s2(s
k* 2)(s
5)
(4)渐近线
4条
渐近线与实轴的夹角
a
4
3
4
3
4
4
渐近线与实轴的交点(σa , 0)
4
pi
a
i 1
4
1.75
60
G0 ( s)
s2(s
k* 2)(s
法则二:根轨迹的分支数,对称性和 连续性
• 根轨迹的分支数与开环有限零点数m和有限 极点数n中的大者相等,它们是连续的并且 对称于实轴。
22
法则三:根轨迹的渐近线(n>m)
• 当开环有限零点数m小于有限极点数n时, 有n-m条根轨迹分支沿着与实轴交点 ,
自动控制原理-线性系统的根轨迹实验报告

线性系统的根轨迹一、 实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、 实验容1. 请绘制下面系统的根轨迹曲线。
)136)(22()(22++++=s s s s s K s G )10)(10012)(1()12()(2+++++=s s s s s K s G )11.0012.0)(10714.0()105.0()(2++++=s s s s K s G 同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的围。
2. 在系统设计工具rltool 界面中,通过添加零点和极点方法,试凑出上述系统,并观察增加极、零点对系统的影响。
三、 实验结果及分析1.(1) )136)(22()(22++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1];den=[1 8 27 38 26 0];rlocus(num,den)[r,k]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis') title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =0.0021 + 0.9627ik =28.7425r =-2.8199 + 2.1667i-2.8199 - 2.1667i-2.3313-0.0145 + 0.9873i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
由根轨迹图和运行结果知,当0<K<28.7425时,系统总是稳定的。
(2) )10)(10012)(1()12()(2+++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1 12];den=[1 23 242 1220 1000];rlocus(num,den)[k,r]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =k =1.0652e+003r=-11.4165 + 2.9641i-11.4165 - 2.9641i-0.0835 + 9.9528i-0.0835 - 9.9528i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
自动控制原理根轨迹法总结

自动控制原理根轨迹法总结
【根轨迹法概述】
-根轨迹法是分析线性时不变系统稳定性和动态性能的一个重要工具。
它通过在复平面上绘制闭环极点随系统参数变化的轨迹来实现。
【根轨迹法的基本原理】
1. 定义与目的:
-根轨迹是系统开环增益变化时,闭环极点在s平面上的轨迹。
-主要用于分析系统稳定性和设计控制器参数。
2. 绘制原则:
-根据系统开环传递函数,确定轨迹的起点和终点,分支点,穿越虚轴的点等。
-利用角度判据和幅值判据确定根轨迹。
【根轨迹法的应用】
1. 系统稳定性分析:
-根据闭环极点的位置判断系统的稳定性。
-极点在左半平面表示系统稳定,右半平面表示不稳定。
2. 控制器设计:
-调整控制器参数(如比例增益、积分时间常数、微分时间常数等),使根轨迹满足性能指标要求。
-确定合适的开环增益,使闭环系统具有期望的动态性能和稳定裕度。
【根轨迹法的优势与局限性】
-优势:直观、便于分析系统特性,特别是在控制器设计中。
-局限性:仅适用于线性时不变系统,对于非线性或时变系统不适用。
【实践中的注意事项】
-在绘制根轨迹时,应仔细考虑系统所有极点和零点的影响。
-必须结合其他方法(如奈奎斯特法、波特法等)进行综合分析。
【结语】
-根轨迹法是自动控制领域中一种非常有效的工具,对于理解和设计复杂控制系统具有重要意义。
-掌握根轨迹法,能够有效地指导实际的控制系统设计和分析。
编制人:_____________________
日期:_____________________。
控制系统的根轨迹分析实验报告

一、实验目的1. 熟悉控制系统根轨迹的基本概念和绘制方法。
2. 掌握利用MATLAB软件绘制和分析控制系统根轨迹的方法。
3. 通过根轨迹分析,了解系统参数变化对系统性能的影响。
4. 培养实验操作能力和数据处理能力。
二、实验原理根轨迹是指当系统的某一参数(如开环增益K)从0变化到无穷大时,闭环系统的特征根在s平面上的变化轨迹。
通过分析根轨迹,可以了解系统在参数变化时的稳定性、瞬态响应和稳态误差等性能。
三、实验设备1. 计算机2. MATLAB软件3. 控制系统实验箱四、实验内容1. 绘制控制系统根轨迹(1)首先,根据实验要求,搭建控制系统的数学模型。
(2)利用MATLAB中的rlocus函数绘制系统的根轨迹。
(3)观察根轨迹的变化规律,分析系统在不同参数下的稳定性。
2. 分析系统性能(1)根据根轨迹,确定系统的稳定裕度,包括增益裕度和相位裕度。
(2)分析系统在不同参数下的瞬态响应,如上升时间、调整时间、超调量等。
(3)分析系统在不同参数下的稳态误差,如稳态误差和稳态误差系数。
3. 改变系统参数,观察根轨迹变化(1)改变系统的参数,如增益、时间常数等。
(2)重新绘制根轨迹,观察根轨迹的变化规律。
(3)分析系统参数变化对系统性能的影响。
五、实验结果与分析1. 绘制控制系统根轨迹(1)根据实验要求,搭建控制系统的数学模型,得到开环传递函数。
(2)利用MATLAB中的rlocus函数绘制系统的根轨迹。
(3)观察根轨迹的变化规律,分析系统在不同参数下的稳定性。
2. 分析系统性能(1)根据根轨迹,确定系统的稳定裕度,包括增益裕度和相位裕度。
(2)分析系统在不同参数下的瞬态响应,如上升时间、调整时间、超调量等。
(3)分析系统在不同参数下的稳态误差,如稳态误差和稳态误差系数。
3. 改变系统参数,观察根轨迹变化(1)改变系统的参数,如增益、时间常数等。
(2)重新绘制根轨迹,观察根轨迹的变化规律。
(3)分析系统参数变化对系统性能的影响。
自动控制原理-线性系统的根轨迹法1

16
规则4:实轴上的根轨迹 规则 若实轴的某一个区域是一部分根轨迹,则必有:其右边 (开环实数零点数+开环实数极点数)为奇数。 这个结论可以用相角条件证明。 由相角条件
∑ ∠(s − z ) −∑ ∠(s − p ) = (2k +1)π
j =1 j i =1 i
m
n
jω
× × × ×
σ
17
规则5:根轨迹渐近线 规则 当 n>m 时,则有(n-m) 条根轨迹分支终止于无限零点。 这些根轨迹分支趋向无穷远的渐近线由与实轴的夹角和 交点来确定。 与实轴夹角
jω
K →∞
K = 2.5
2
稳态性能 开环传递函数在坐标原点有
一个极点,系统为1型系统,根轨迹上 的K值就是静态速度误差系数。如果给 定系统的稳态误差要求,则由根轨迹图 可以确定闭环极点位置的容许位置。 由开环传递函数绘制根轨迹,通常 采用根轨迹增益 根轨迹增益,根轨迹增益与开环增 根轨迹增益 益之间有一个转换关系。
o o
与实轴交点
σa =
i =1
∑ pi − ∑ z j
j =1
n
m
n−m
( 0 − 4 − 1 + j − 1 − j ) − ( − 1) = = − 1 .67 4 −1
23
24
规则6:根轨迹分离点和会合点 规则 两条或两条以上的根轨迹分支在 s 平面上相遇又立即 分开的点称为分离点(会合点)。 分离点(会合点)的坐标 d 由下列方程所决定:
K =1
1
K =0
−2
−1
0
σ
K = 0.5
−1
−2
动态性能
由K值变化所对应的闭环极 点分布来估计。
中南大学自动控制原理实验报告

中南大学自动控制原理实验报告--------------------------------------------------------------------------作者: _____________--------------------------------------------------------------------------日期: _____________信息科学与工程学院本科生实验报告实验名称自动控制原理实验预定时间实验时间姓名学号授课教师实验台号专业班级实验一 1.1典型环节的时域分析实验目的:1.熟悉并掌握 TD-ACC+(或 TD-ACS)设备的使用方法及各典型环节模拟电路的构成方法。
2.熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。
对比差异、分析原因。
3.了解参数变化对典型环节动态特性的影响。
实验设备:PC 机一台, TD-ACC+(或 TD-ACS)实验系统一套。
模拟电路图如下:实验结果:当R0=200K;R1=100K。
输出电压约为输入电压的1/2,误差范围内满足理论波形,当R0 = 200K; R1 = 200K。
积分环节模拟电路图:当R0=200K;C=1uF。
实验结果:当R0 = 200K; C = 2uF。
比例积分环节 (PI)模拟电路图:取 R0 = R1 = 200K; C = 1uF。
实验结果取 R0=R1=200K; C=2uF。
惯性环节(T)模拟电路图:取 R0=R1=200K; C=1uF。
取 R0=R1=200K; C=2uF。
比例微分环节(PD)模拟电路图:取 R0 = R2 = 100K, R3 = 10K, C = 1uF; R1 = 100K。
取 R0=R2=100K, R3=10K, C=1uF; R1=200K。
比例积分微分环节(PID)模拟电路图:取 R2 = R3 = 10K, R0 = 100K, C1 = C2 = 1uF; R1 = 100K。
自动控制原理-胡寿松-第四章-线性系统的根轨迹法.详解

系统的信号流图见图4-28,从信号流图中看出,系统中含有一个积分环节, 因此为1型系统,因此系统对阶跃输入信号的稳态误差为0。
K m 变化时系统的根轨迹, 2)为了绘制电动机传递系数(含放大器附加增益) 可将有关参数代入传递函数中,并将系统的特征方程进行整理,等价根轨迹增 益方程为:
1 K* P( s ) ( s 6.93 j 6.93)( s 6.93 j 6.93) 1 K * Q( s ) s 2 ( s 13.86)
当所有根轨迹分支都在左半平面时,系统稳定。 2) 稳态性能:
回忆:稳态性能主要取决于系统的开环增益和积分环节个数。
由根轨迹图不仅可以方便的确定开环增益和积分环节个数,而且可以根据给定系统 的稳态误差要求, 确定闭环极点位置的容许范围。
3)动态性能: 回忆:动态性能形态主要取决于系统的——闭环极点。 从根轨迹图上,可以直观地看到特征根随着参数的变化情况,从而,可以方便地 确定动态性能随着参数的变化情况。
K * lim
s
j 1 i 1 m
n
s pi s zj
lim s
s
nm
, 0 ,
nm nm
(无穷零点)
(无穷极点)
(n m 1)
(续)
且均为实数开环零、极点。
(续)
(续)
小结论: 由两个极点(实数极点或者复数极点)和一个有限零点组成的开环系 统,只要有限零点没有位于两个实数极点之间,当 K * 从零变化到无穷时, 闭环根轨迹的复数部分,是以有限零点为圆心,以有限零点到重根点的距 离为半径的一个圆,或圆的一部分。这在数学上是可以严格证明的。
例如,在上列程序之后增加语句: [k,p]=rlocfind(num,den)
自动控制原理实验报告-西南交通大学课程与资源中心

西南交通大学自动控制原理课程实验报告册
《自动控制原理》课程实验报告(一)
《自动控制原理》课程实验报告(二)
《自动控制原理》课程实验报告(三)
《自动控制原理》课程实验报告(四)
三、思考题
1. 参数在一定范围内取值才能使闭环系统稳定的系统称为条件稳定系统。
对于这类系
统可以通过根轨迹法来确定使系统稳定的参数取值范围,也可以适当调整系统参数或增加校正网络以消除条件稳定性问题。
对于下图所示条件稳定系统:
试问能否通过增加开环零极点消除系统条件稳定性问题,即对于所有根轨迹增益,根轨迹全部位于s左半平面,闭环系统稳定。
《自动控制原理》课程实验报告(五)
《自动控制原理》课程实验报告(六)
《自动控制原理》课程实验报告(七)
《自动控制原理》课程实验报告(八)
《自动控制原理》课程实验报告(九)。
自动控制原理实验02
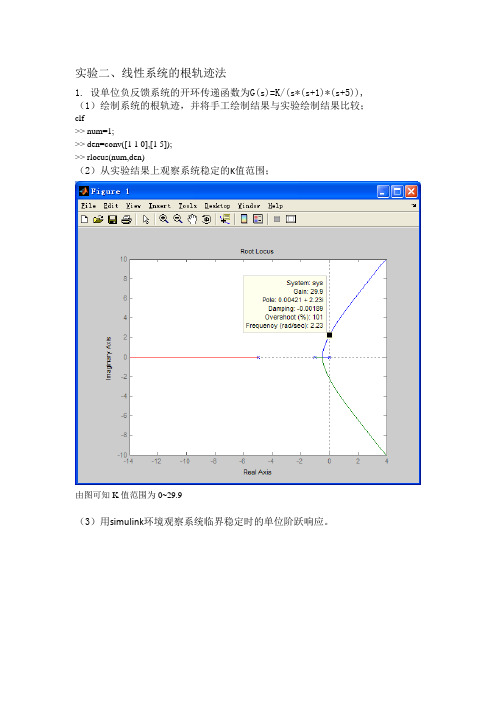
实验二、线性系统的根轨迹法1. 设单位负反馈系统的开环传递函数为G(s)=K/(s*(s+1)*(s+5)), (1)绘制系统的根轨迹,并将手工绘制结果与实验绘制结果比较;clf>> num=1;>> den=conv([1 1 0],[1 5]);>> rlocus(num,den)(2)从实验结果上观察系统稳定的K值范围;由图可知K值范围为0~29.9(3)用simulink环境观察系统临界稳定时的单位阶跃响应。
2.设单位反馈控制系统的开环传递函数为G(s)=K*(s+3)/(s*(s+1)*(s+2));(1)仿照上题绘制系统的根轨迹,并判断系统的稳定性;clf>> num=[1 3];>> den=conv([1 1 0],[1 2]);>> rlocus(num,den)由图知,该系统始终保持稳定.(2)分别取K=5 和K=50,利用simulink环境观察系统的单位阶跃响应,并比实验结果。
K=5时,该系统呈现欠阻尼状态,阻尼系数接近于1。
K=50时,该系统呈现欠阻尼状态,阻尼系数接近于0.3.完成教材第四章习题4-7,4-8,4-10(1)习题4-7,已知开环传递函数为K/(s(s+4)(s^2+4s+20));试概略画出其闭环系统根轨迹图。
clf>> num=1;>> den=conv([1 4 0],[1 4 20]);>> rlocus(num,den)该系统K值范围为0~260时系统稳定。
(2)习题4-8,已知开环传递函数为K(s+2)/((s^2+4s+9)^2);试概略画出其闭环系统根轨迹图。
clf>> num=[1 2];>> den=conv([1 4 9],[1 4 9]);>> rlocus(num,den)该系统K值范围为0~95.6时稳定。
实验3 控制系统的根轨迹作图

自动控制原理实验报告课程名称 自动控制原理 成 绩 实验项目 控制系统的根轨迹作图 指导教师 齐立省 学生姓名 赵儒桐 学号 201100805035 班级专业 11电子信息工程 实验地点 综合楼226 实验日期 年 月 日一、实验目的1.利用计算机完成控制系统的根轨迹作图2.了解控制系统根轨迹图的一般规律3.利用根轨迹进行系统分析及校正二、实验步骤1.在Windows 界面上用鼠标双击matlab 图标,即可打开MATLAB 命令平台。
2.练习相关M 函数根轨迹作图函数:rlocus(sys)rlocus(sys,k)r=rlocus(sys)[r,k]=rlocus(sys)函数功能:绘制系统根轨迹图或者计算绘图变量。
图1-1 格式1:控制系统的结构图如图1-1所示。
输入变量sys 为LTI 模型对象,k 为机器自适应产生的从0→∞的增益向量, 绘制闭环系统的根轨迹图。
格式2:k 为人工给定的增益向量。
格式3:返回变量格式,不作图。
R 为返回的闭环根向量。
格式4:返回变量r 为根向量,k 为增益向量,不作图。
更详细的命令说明,可键入“help rlocus”在线帮助查阅。
例如:系统开环传递函数为)3)(1()(++=s s s k s G g方法一:根轨迹作图程序为k=1; %零极点模型的增益值z=[]; %零点p=[0,-1,-3]; %极点sys=zpk(z,p,k); %零点/极点/增益模型rlocus(sys)作出的根轨迹图如图1-2所示。
方法二:s=tf('s'); G1=1/(s*(s+1)*(s+3));rlocus(G1); 图1-2 gridK1=12;figure;step(feedback(G1*K1,1)) % 绘制K1=12的闭环单位反馈阶跃响应曲线闭合时域仿真simulink 模型:三、实验内容给定如下各系统的开环传递函数,作出它们的根轨迹图,并完成给定要求。
自动控制原理实验根轨迹的绘制

自动控制原理实验根轨迹的绘制一、根轨迹绘制的基础知识哎呀,自动控制原理实验里的根轨迹绘制可真是个有趣又有点小麻烦的事儿呢。
根轨迹啊,简单来说就是当系统的某个参数从0变到无穷大的时候,闭环系统特征方程的根在复平面上的变化轨迹。
这就像是我们看着一个小种子慢慢长大,它的根在地下不断延伸的过程一样。
我们得先知道一些基本概念。
比如开环传递函数,这可是根轨迹绘制的基础哦。
它就像是一个神秘的魔法公式,通过它我们才能找到根轨迹的起点和终点。
开环极点和零点也很重要,极点就像是根轨迹的起始点,零点呢就像是根轨迹会被吸引过去的地方。
就像我们玩游戏的时候,角色的出生点和目标点一样。
二、绘制根轨迹的步骤1. 求开环极点和零点这个步骤就像是找宝藏的地图起点一样重要。
我们要把开环传递函数分解因式,找到那些使分母为零的点就是极点,分子为零的点就是零点。
这一步可得细心,要是找错了一个点,后面的轨迹可就全乱套啦。
2. 确定根轨迹的分支数根轨迹的分支数就等于开环极点的个数哦。
这就像数树上有多少个大树枝一样,有几个极点就有几条根轨迹分支。
3. 确定根轨迹的渐近线渐近线就像是根轨迹在无穷远处的走向。
我们要根据开环极点和零点的个数来计算渐近线的角度和交点。
这就好比我们在看远方的路,虽然还没走到那里,但是能大概知道路是朝着哪个方向去的。
4. 确定根轨迹在实轴上的分布实轴上的根轨迹分布是有规律的。
如果在实轴上某一段的右边,开环极点和零点的总数是奇数,那么这一段就是根轨迹的一部分。
这就像我们在拼图的时候,要找到那些能拼在一起的小碎片一样。
5. 求根轨迹的分离点和会合点这些点是根轨迹上比较特殊的点,就像道路上的岔路口一样。
我们可以通过解方程的方法来找到它们。
三、绘制根轨迹时的小技巧1. 利用对称性很多时候根轨迹是关于实轴对称的,我们可以利用这个特点,只画出一半,然后再对称过去,这样就能节省不少时间呢。
就像我们画一个对称的图案,只需要画一半再复制就好啦。
南邮自动控制原理实验报告

>> step(G,6)
自然频率=16.9538rad/sec
阻尼比=0.73578
实验二
2.1
(1)考察闭环系统根轨迹的一般形成规律。
(2)观察和理解引进零极点对闭环根轨迹的影响。
(3)观察、理解根轨迹与系统时域响应之间的联系。
(4)初步掌握利用产生根轨迹的基本指令和方法。
2.2
根轨迹绘制的指令法、交互界面法;复平面极点分布和系统响应的关系。
指令:rlocfind(G)
分离点:-2.0095 + 1.0186iK=0.0017
与虚轴的交点:-0.0000 + 3.6025iK=65.8411
(3)利用MATLAB的rlocfind指令,求出系统临界稳定增益,并用指令验证系统的稳定性。
系统临界稳定增益:65.8411
由于系统无右半平面的开环极点,且奈奎斯特曲线不包围(-1,j0)点,系统稳定。
1
-----------
s^2 + s + 1
>> step(G,18)
阻尼比=2:
>> G=tf([1],[1,2,1])
Transfer function:
1
-------------
s^2 + 2 s + 1
>> step(G,18)
结论:
当阻尼比取0时,其振荡频率为1,即为无阻尼振荡;当阻尼比大于0小于1时,二阶系统为欠阻尼二阶系统,其单位阶跃响应为衰减振荡;当阻尼比大于1时,二阶系统为过阻尼二阶系统,其单位阶跃响应为是非振荡的。
自动控制原理 第四章 线性系统的根轨迹方法(2011-3) (2)

பைடு நூலகம்β = 45
−ξπ 1−ξ 2
β = 60
[ s]
j
⎧45° < β < 60° ⎨ ⎩ 2 < ωn < 5
−5
−2
0
13
ξ ξ ξ ξ ξ ξ ξ
= 0.0 σ % = 100% = 0.4 σ % = 25% = 0.5 σ % = 15% = 0.6 σ % = 10% = 0.7 σ % = 5% = 0.8 σ % = 2% = 1.0 σ % = 0%
A
ξ = 0.5
Im
λ3 = −2.34 X
−2
λ1 = −0.33 + j0.58
−1
X
−0.5
60
0
X
Re
λ2 = −0.33 − j0.58
21
三、高阶系统动态性能指标估算
1、高阶系统单位阶跃响应
(1) 高阶系统的单位阶跃响应包括常数项和响应模态。 (2) 除常数项以外,高阶系统的单位阶跃响应是系统模态的组 合,组合系数即部分分式系数。 (3) 模态由闭环极点确定,而部分分式系数与闭环零点、极点 分布有关,闭环零点、极点对系统动态性能均有影响。
ξ ≥ 1− r
( α)
2
ωd ≤ r
α − r ≤ ωn ≤ α + r
α − r ≤ ξωn ≤ α + r
如果设定区域
ξωn ≥ q
则选择 r ≤ min
(α − q , α
ξ ≥ ξ min
1− ξ
2 min
)
8
[例]:如图系统,求系统具有最小阻尼时K值及相应的 动态性能和稳态误差。
自动控制原理-线性系统的根轨迹法 (2)

閉環控制系統的動態性能與閉環極點在S平面上的 分佈位置是密切相關的,分析系統的性能時,往往要求 確定系統閉環極點的位置.另一方面,在分析和設計系 統時,經常需要研究一個或幾個參量變化時,對系統的 極點和系統性能的影響。
採用分解因式的古典方法求特徵方程式的根通常不容 易,特別是當某一參量發生變化(靈敏度)時,需要反復進 行計算,這時採用上述方法就顯得十分煩瑣,難以在實際 中應用。
K=0.5 K=0
該系統對於所有的K都是穩定的 穩態性能:
-1 0
原點處有一個極點 Ⅰ型系統
根軌跡上的K值就 是靜態誤差係數
0 K 0.5 : 过阻尼系 ,階统 躍回應為非週期過程
動態 K=0.5:临界阻尼 ,階系 躍回统應為非週期過程
性能:
K
0.5:欠阻尼,階系躍统 回應為阻上尼頁振盪下過頁程
返回
根據相角條件,在同一分離點分離的各條根軌跡 分支,它們的切線將均分360度。2條根軌跡在分離 點相隔180度,4條根軌跡在分離點相隔90度。
分離點的座標為:
m
1
n
1
i1 d zi
j1 d p j
分離角:根軌跡進入分離點的切線方向與離開分離點的切 線方向之間的夾角
(2k 1)
l
l-進入並立即離開分離點的 根軌跡條數
根軌跡:當系統某一參數在規定範圍內變化時,相應的系
統閉環特徵方程根在s平面上的位置也隨之變化移動,一個
根形成一條軌跡。
系統特徵根的圖解方法!!!
廣義根軌跡:系統的任意一變化參數形成根軌跡。
狹義根軌跡(通常情況):
變化參數為開環增益K,且其變化取值範圍為0到∞。
自動控制原理
一 根軌跡的概念
根軌跡法:系統某一參數變化時,繪製特徵方程的根在 S平面的位置變化軌跡的圖解方法。 根軌跡法的優點: 1:從已知的開環零、極點的位置及某一變化參數來求 取閉環極點的分佈,即解決閉環特徵式的求根問題。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时,特征方程的根在s 平面上的变化轨迹。
这个参数一般选为开环系统的增益K 。
课本中介绍的手工绘制根轨迹的方法,只能绘制根轨迹草图。
而用MATLAB 可以方便地绘制精确的根轨迹图,并可观测参数变化对特征根位置的影响。
假设系统的对象模型可以表示为nn n n m m m m a s b s a s b s b s b s b K s KG s G ++++++++==--+-11111210)()( 系统的闭环特征方程可以写成: 0)(10=+s KG对每一个K 的取值,我们可以得到一组系统的闭环极点。
如果我们改变K 的数值,则可以得到一系列这样的极点集合。
若将这些K 的取值下得出的极点位置按照各个分支连接起来,则可以得到一些描述系统闭环位置的曲线,这些曲线又称为系统的根轨迹。
1)绘制系统的根轨迹rlocus ()MATLAB 中绘制根轨迹的函数调用格式为:rlocus(num,den) 开环增益k 的范围自动设定。
rlocus(num,den,k) 开环增益k 的范围人工设定。
rlocus(p,z) 依据开环零极点绘制根轨迹。
r=rlocus(num,den) 不作图,返回闭环根矩阵。
[r,k]=rlocus(num,den) 不作图,返回闭环根矩阵r 和对应的开环增益向量k 。
其中,num,den 分别为系统开环传递函数的分子、分母多项式系数,按s 的降幂排列。
K 为根轨迹增益,可设定增益范围。
例3-1:已知系统的开环传递函数924)1()(23++++=*s s s s K s G ,绘制系统的根轨迹的MATLAB 的调用语句如下: num=[1 1]; %定义分子多项式den=[1 4 2 9]; %定义分母多项式rlocus (num,den) %绘制系统的根轨迹 grid %画网格标度线xlabel(‘Real Axis ’),ylabel(‘Imaginary Axis ’) %给坐标轴加上说明 title(‘Root Locus ’) %给图形加上标题名则该系统的根轨迹如图3-1所示:若上例要绘制K 在(1,10)的根轨迹图,则此时的MATLAB 的调用格式如下,对应的根轨迹如图3-2所示。
num=[1 1];den=[1 4 2 9];k=1:0.5:10;rlocus (num,den,k)2)确定闭环根位置对应增益值K 的函数rlocfind ()在MATLAB 中,提供了rlocfind 函数获取与特定的复根对应的增益K 的值。
在求出的根轨迹图上,可确定选定点的增益值K 和闭环根r (向量)的值。
该函数的调用格式为:[k,r]=rlocfind(num,den)执行前,先执行绘制根轨迹命令rlocus (num,den ),作出根轨迹图。
执行rlocfind 命令时,出现提示语句“Select a point in the graphics window ”,即要求在根轨迹图上选定闭环极点。
将鼠标移至根轨迹图选定的位置,单击左键确定,根轨迹图上出现“+”标记,即得到该点的增益K 和闭环根r 的返回变量值。
图3-1 系统的完整根轨迹图形 图3-2 特定增益范围内的根轨迹图形例3-2:系统的开环传递函数为253865)(232+++++=*s s s s s K s G ,试求:(1)系统的根轨迹;(2)系统稳定的K 的范围;(3)K=1时闭环系统阶跃响应曲线。
则此时的MATLAB 的调用格式为:G=tf([1,5,6],[1,8,3,25]);rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点rG_c=feedback(G ,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线则系统的根轨迹图和闭环系统阶跃响应曲线如图3-2所示。
其中,调用rlocfind ()函数,求出系统与虚轴交点的K 值,可得与虚轴交点的K 值为0.0264,故系统稳定的K 的范围为),0264.0(∞∈K 。
二、实验内容请绘制下面系统的根轨迹曲线)136)(22()(22++++=s s s s s K s G )10)(10012)(1()12()(2+++++=s s s s s K s G )11.0012.0)(10714.0()105.0()(2++++=s s s s s K s G 同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
(a )根轨迹图形 (b )K=1时的阶跃响应曲线图3-2 系统的根轨迹和阶跃响应曲线1.1,程序代码num=[0,0,0,0,0,1]; %定义分子多项式den=[1,8,27,38,26,0]; %定义分母多项rlocus(num,den); %绘制系统的根轨迹grid %画网格标度线[k,r]=rlocfind(num,den)xlabel('Real Axis');ylabel('Imaginary Axis')title('Root Locus');1.2,截屏图k = 0.6981r =-2.9946 + 2.0027i;-2.9946 - 2.0027i; -0.9914 + 0.9696i; -0.9914 - 0.9696i; -0.0280 k =0.8946r = -2.9931 + 2.0035i;-2.9931 - 2.0035i; -0.9887 + 0.9607i;-0.9887 - 0.9607i;-0.0363 k = 31.4829r =-2.8088 + 2.1856i;-2.8088 - 2.1856i ;-2.4150 ; 0.0163 + 1.0144i; 0.0163 - 1.0144ik =40.4848r =-2.7794 + 2.2469i; -2.7794 - 2.2469i; -2.6459 ; 0.1024 + 1.0897i;0.1024 - 1.0897i1.3,分析可知k的范围是(0.6981~~~40.4848)2.1,程序代码num=[0,0,0,1,12]; %定义分子多项式den=[1,23,121,1220,1000]; %定义分母多项rlocus(num,den); grid %绘制系统的根轨迹[k,r]=rlocfind(num,den)xlabel('Real Axis');ylabel('Imaginary Axis');title('Root Locus') ;2.2,截屏图k =18.4941r = -19.8919\ -1.0151 + 7.4803i\-1.0151-7.4803i\-1.0780r =-19.9853 \ -0.5160 + 7.6445i\-0.5160 - 7.6445i\ -1.9826k =194.8401r =-20.0707 \-0.1144 + 7.8470i\-0.1144 - 7.8470i\-2.7005k =273.5006r =-20.1500 \0.2109 + 8.0566i\0.2109 - 8.0566i\-3.27172.3,分析可知:k的范围是(18.4941~~~273.5006)3.1,程序代码num=[0,0,0,0.05,1]; %定义分子多项式den=[0.0008568,0.01914,0.1714,1,0]; %定义分母多项rlocus(num,den); grid %绘制系统的根轨迹[k,r]=rlocfind(num,den)xlabel('Real Axis');ylabel('Imaginary Axis');title('Root Locus') ;3.2,截屏图r =-13.9230 \-3.9290 + 7.9404i\-3.9290 - 7.9404i\-0.5580k =3.3944r =-13.3489 \-2.0233 + 7.4794i\-2.0233 - 7.4794i\-4.9434k =7.6385r =-0.0916+8.4713i\-0.0916-8.4713i\ -11.0779 + 1.2238i-11.0779 - 1.2238i k =8.4866r = -11.3214+1.8886i\-11.3214-1.8886i\0.1519+8.6696i\0.1519-8.6696i3.3,分析可知:k的范围是(0.5225,8.4866)三,实验体会与总结:通过自动控制原理实验的学习与调试,使我学习和了解了许多知识。
首先是对关自动控制原理相关的知识点有了更深刻的理解,原本课本上不是很懂得知识点许多都得到了相应的解答;其次是对这门课有了新的认识和理解,原本不知道学习这门课有什么作用,觉得无聊,不过现在才发现,学习、掌握好这门课不仅可以使我们队信号处理的过程与原理有了根本的理解和应用,而且可以方便的利用相关知识去理解和解答相关疑难问题;更重要的事学习和掌握了许多相关matlab软件的应用方法和知识,在学习技能和方法上使得自己有了更高的进步,掌握了又多一门的学习技能和方法,为以后学习和应用打下了相关的基础知识与根基,相信在以后的学习和生后中都将受益。
不过,我也从中认识到自己在相关知识领域的认识不足和缺陷,不过通过实验的过程都有所了解和体会,在以后的学习过程中就会多方面去注意,查漏补缺。
综合而言,这门课的实验课给了我一个愉快的,丰厚的过程。
感谢这门课所带给我的巨大作用,同时感谢指导老师耐心细致的开导与指点,此致敬礼。
