实验三 线性系统的根轨迹
自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例:开环传递函数
Gs
k1
ss
a
开环系统两个极点为:P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程: s2 as k1 0
闭环特征根:s1,2
a 2
a 2
2
k1
(闭环极点)
3
自动控制原理
在p5附近取一实验点sd, 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明:根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例:sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点,复极点提供的相角和为 3600。
2
s1=-1.172,s2=-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为:
Z 1800
其中 z p(不包括本点)
34
自动控制原理
j p5
p5
p3 p3
p2
《自动控制原理》实验指导书

《自动控制原理》实验指导书梅雪罗益民袁启昌许必熙南京工业大学自动化学院目录实验一典型环节的模拟研究--------------------------1 实验二典型系统时域响应和稳定性-------------------10 实验三应用MATLAB进行控制系统根轨迹分析----------15 实验四应用MATLAB进行控制系统频域分析------------17 实验五控制系统校正装置设计与仿真-----------------19 实验六线性系统校正-------------------------------22 实验七线性系统的频率响应分析---------------------26 附录:TDN—ACP自动控制原理教学实验箱简介----------31实验一 典型环节的模拟研究一. 实验目的1.熟悉并掌握TD-ACC +设备的使用方法及各典型环节模拟电路的构成方法。
2.熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。
对比差异、分析原因。
3.了解参数变化对典型环节动态特性的影响。
二.实验内容下面列出各典型环节的方框图、传递函数、模拟电路图、阶跃响应,实验前应熟悉了解。
1.比例环节 (P)A 方框图:如图1.1-1所示。
图1.1-1B 传递函数:K S Ui S Uo =)()( C 阶跃响应:)0()(≥=t Kt U O 其中 01/R R K =D 模拟电路图:如图1.1-2所示。
图1.1-2注意:图中运算放大器的正相输入端已经对地接了100K 的电阻,实验中不需要再接。
以后的实验中用到的运放也如此。
E 理想与实际阶跃响应对照曲线:① 取R0 = 200K ;R1 = 100K 。
② 取R0 = 200K ;R1 = 200K 。
2.积分环节(I)A .方框图:如右图1.1-3所示。
图1.1-3B .传递函数:TSS Ui S Uo 1)()(=C .阶跃响应: )0(1)(≥=t t Tt Uo 其中 C R T 0=D .模拟电路图:如图1.1-4所示。
自控实验报告实验三线性系统的根轨迹

实验三 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、实验报告1.根据内容要求,写出调试好的MATLAB 语言程序,及对应的结果。
2. 记录显示的根轨迹图形,根据实验结果分析根轨迹的绘制规则。
3. 根据实验结果分析闭环系统的性能,观察根轨迹上一些特殊点对应的K 值,确定闭环系统稳定的范围。
4.写出实验的心得与体会。
三、实验内容请绘制下面系统的根轨迹曲线同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
一、 )136)(22()(22++++=s s s s s Ks G1、程序代码:G=tf([1],[1,8,27,38,26]); rlocus (G); [k,r]=rlocfind(G)G_c=feedback(G,1); step(G_c)2、实验结果:-8-6-4-22468Root LocusReal AxisI m a g i n a r y A x i sselected_point = -8.8815 + 9.4658i k =1.8560e+04 r =-10.2089 + 8.3108i -10.2089 - 8.3108i 6.2089 + 8.2888i6.2089 - 8.2888iTime (seconds)A m p l i t u d eselected_point =-9.5640 - 7.6273i k =1.3262e+04 r =-9.5400 + 7.6518i -9.5400 - 7.6518i 5.5400 + 7.6258i5.5400 - 7.6258iTime (seconds)A m p l i t u d eTime (seconds)A m p l i t u d eselected_point =-0.0095 + 2.1118i k =73.9872 r =-3.9617 + 2.4724i -3.9617 - 2.4724i -0.0383 + 2.1409i -0.0383 -2.1409iTime (seconds)A m p l i t u d e3、结果分析:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
线性系统的根轨迹-自动控制原理实验报告

自动控制原理实验报告实验题目:线性系统的根轨迹班级:学号:姓名:指导老师:实验时间:一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、实验内容同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
2.1绘制下面系统的根轨迹曲线)136)(22()(22++++=s s s s s Ks G程序:G=tf([1],[1 8 27 38 26 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-12-10-8-6-4-20246-10-8-6-4-20246810Root LocusReal AxisI m a g i n a r y A x i s0204060801001201400.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围:K>28.74252.2绘制下面系统的根轨迹曲线)10)(10012)(1()12()(2+++++=s s s s s K s G 程序:G=tf([1 12],[1 23 242 1220 1000]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-100102030-50-40-30-20-1001020304050Root LocusReal AxisI m a g i n a r y A x i s01234560.0020.0040.0060.0080.010.012Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围: K>1.1202e+032.3绘制下面系统的根轨迹曲线)11.0012.0)(10714.0()105.0()(2++++=s s s s s K s G 程序:G=tf([5 100],[0.08568 1.914 17.14 100 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-10010203040-60-40-200204060Root LocusReal AxisI m a g i n a r y A x i s012345670.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围:K> 7.8321根据实验结果分析根轨迹的绘制规则:⑴绘制根轨迹的相角条件与系统开环根轨迹增益 值的大小无关。
自动控制原理实验报告
实验课程名称 实验项目名称实验报告内容包含:实验目的、实验仪器、实验原理,实验内容、实验步骤、实验数据整理 与归纳(数据、图表、计算等)、实验结果分析、实验思考题、实验心得。
【实验目的】1、 会用PID 法设计球杆系统控制器;2、 设计并验证校正环节;【实验仪器】1、 球杆系统;2、 计算机,Matlab 平台;【实验原理】1、PID 简介PID 的控制算法有很多,不同的算法各有其针对性。
图 2.2.1,图2.2.2,图2.2.3给 出了三种不同的算法。
在模拟控制系统中,控制器最常用的控制规律是 PID 控制。
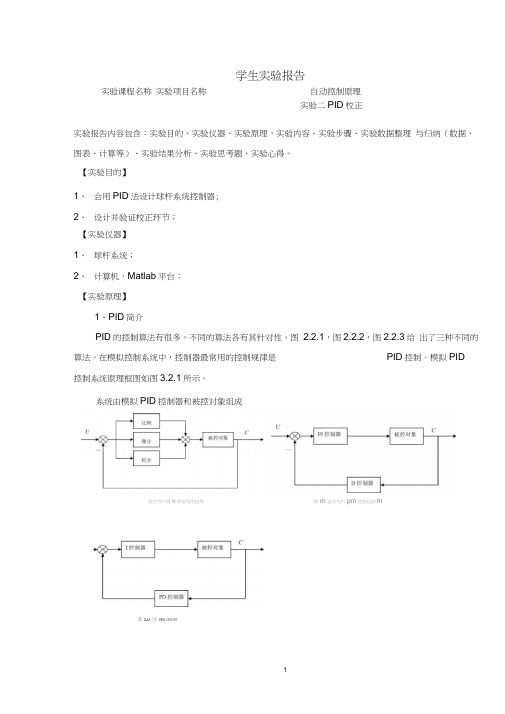
模拟PID控制系统原理框图如图3.2.1所示。
学生实验报告自动控制原理 实验二PID 校正系统由模拟PID 控制器和被控对象组成技世列口理N 慕笛甩用扭用期 m 雀莎先行pm 控制也尉mK 2JJ 蚀 HD (MUMPID 控制器是一种线性控制器,它根据给定值 rt 与实际输出值yt 构成控制偏差etet 二rt -y t ( 2.2.1)将偏差的比例P 、积分I 和微分D 通过线性组合构成控制量,对被控对象进行控制, 故称PID 控制器。
其控制规律为或写成传递函数的形式=K p 1+丄 +T D S (2.2.3)I T i S 丿式中:K p ——比例系数;T |——积分时间常数;T D ——微分时间常数 在控制系统设计和仿真中,也将传递函数写成式中:K P ——比例系数;K |——积分系数;K D ——微分系数。
上式从根轨迹角度看, 相当于给系统增加了一个位于原点的极点和两个位置可变的零点。
简单说来,PID 控制器各校正环节的作用如下:A 、 比例环节:成比例地反映控制系统的偏差信号 et ,偏差一旦产生,控制器立即产生 控制作用,以减少偏差。
B 、 积分环节:主要用于消除稳态误差,提高系统的型别。
积分作用的强弱取决于积分时间常数T |,T |越大,积分作用越弱,反之则越强。
C 、 微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差信号值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减小调节时间。
实验三 线性系统的根轨迹

实验三 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时,特征方程的根在s 平面上的变化轨迹。
这个参数一般选为开环系统的增益K 。
课本中介绍的手工绘制根轨迹的方法,只能绘制根轨迹草图。
而用MATLAB 可以方便地绘制精确的根轨迹图,并可观测参数变化对特征根位置的影响。
假设系统的对象模型可以表示为nn n n m m m m a s b s a s b s b s b s b K s KG s G ++++++++==--+-11111210)()( 系统的闭环特征方程可以写成0)(10=+s KG对每一个K 的取值,我们可以得到一组系统的闭环极点。
如果我们改变K 的数值,则可以得到一系列这样的极点集合。
若将这些K 的取值下得出的极点位置按照各个分支连接起来,则可以得到一些描述系统闭环位置的曲线,这些曲线又称为系统的根轨迹。
1)绘制系统的根轨迹rlocus ()MATLAB 中绘制根轨迹的函数调用格式为:rlocus(num,den) 开环根轨迹增益k 的范围自动设定。
rlocus(num,den,k) 开环根轨迹增益k 的范围人工设定。
rlocus(p,z) 依据开环零极点绘制根轨迹。
r=rlocus(num,den) 不作图,返回闭环根矩阵。
[r,k]=rlocus(num,den) 不作图,返回闭环根矩阵r 和对应的开环增益向量k 。
其中,num,den 分别为系统开环传递函数的分子、分母多项式系数,按s 的降幂排列。
K 为根轨迹增益,可设定增益范围。
例3-1:已知系统的开环传递函数924)1()(23++++=*s s s s K s G ,绘制系统的根轨迹的MATLAB 的调用语句如下:num=[1 1]; %定义分子多项式 den=[1 4 2 9]; %定义分母多项式 rlocus (num,den) %绘制系统的根轨迹 xlabel(‘Real Axis ’),ylabel(‘Imaginary Axis ’) %给坐标轴加上说明 title(‘Root Locus ’) %给图形加上标题名 注意:标点符号是不是中文输入法下进行输入的 则该系统的根轨迹如图3-1所示:若上例要绘制根轨迹增益K 在(1,10)的根轨迹图,则此时的MATLAB 的调用格式如下,对应的根轨迹如图3-2所示。
线性系统的根轨迹法实验报告

线性系统的根轨迹法实验报告实验二线性系统的根轨迹法一,实验目的1,掌握matlab绘制根轨迹的方法。
2,观察k值变化对系统稳定性的影响。
3,掌握系统临界稳定情况下k值得求取。
4,了解增设零点对系统稳定的影响以及改善系统稳定性的方法。
二,实验原理根轨迹的概念:所谓根轨迹就是当开环系统某一参数从零变到无穷大时,闭环系统特征方程式的根在s平面上变化的轨迹。
根轨迹与系统性能:有了根轨迹就可以分析系统的各种性能了,稳定性的判定,当开环增益从零变到无穷大时,根轨迹不会越过虚轴进入s平面的右半平面,此时K的范围为系统稳定的范围,根轨迹与虚轴的交点处的K值,为系统的临界开环增益,开根轨迹进入s平面的右半平面时所对应的K值为系统不稳定的情况。
三,实验内容A、设单位负反馈系统的开环传递函数为G(s)=K/(s*(s+1)(s+5)) (1) 绘制系统的根轨迹,并将手工绘制结果与实验绘制结果比较; (2) 从实验结果上观察系统稳定的K 值范围;(3) 用simulink 环境观察系统临界稳定时的单位阶跃响应分析:绘制根轨迹的matlab文本为clfnum=1;den=conv([1 1 0],[1 5]); rlocus(num,den) %绘制系统根轨迹1,得到如图的根轨迹图:2,用鼠标点击根轨迹与虚轴处的交点可得到临界稳定的开环增益K=30,所以系统稳定的K值范围为0―30。
3,在simulink环境下按下图连接电路:取增益为30的时候在示波器下观察单位节约响应,输出波形为:由图可以看出单位阶跃响应的输出为等幅的震荡输出,所以此时系统为临界稳定状态。
当改变开环增益为50和20时观察示波器,得到输出波形分别为:由图可知当增益K为50时输出为不稳定的震荡输出,此时系统不稳定,当增益K为20时输出的波形震荡越来越缓慢,最后趋于稳定,所以此时的系统是稳定的。
B,设单位反馈控制系统的开环传递函数为G(S)=K(s+3)/s(s+1)(s+2)(1) 仿照上题绘制系统的根轨迹,并判断系统的稳定性; 参照第一题得到matlab命令文本为:clfnum=1;den=conv([1 1 0],[1 2]); rlocus(num,den) %绘制系统根轨迹得到如图的根轨迹图:1,由图可知根轨迹没有进入s平面右半平面,所以系统在K=0到K=?都是稳定的。
实验三_线性系统的稳定性和根轨迹分析

实验三 线性系统的稳定性和根轨迹分析
一、实验目的
1、学会用MATLAB 求取系统根轨迹和暂态响应的方法。
2、掌握利用根轨迹分析系统性能的方法。
3、掌握线性定常系统暂态性能指标的测试方法。
4、研究线性定常系统的参数对其暂态性能和稳定性的影响。
二、实验内容
系统的开环传递函数为
()()(2)(10)
K G s H s s s s =++ 1、画出系统根轨迹,求出系统的临界开环增益和对应的闭环极点。
2、求出阻尼比为0.707时系统的开环增益和对应的闭环极点。
3、选取不同的K 值,观察系统在稳定、临界稳定、不稳定时的单位阶跃响应。
4、观察阻尼比为0.707时系统的单位阶跃响应,求出最大超调量和调整时间。
三、实验报告要求
1、预习报告写出各实验内容相应的程序,计算出相关的理论值。
2、实验报告记录各实验结果,并进行分析。
3、实验中存在的问题分析、讨论或建议。
《自动控制原理》课程标准

《自动控制原理》课程标准一、课程说明二、课程定位自动控制原理是电气自动化专业的一门专业核心课程,专业必修课程。
本课程与前修课程《电工基础》、《模拟电子技术》、《传感器》课程相衔接,共同树立学生自动控制的理念;与后续课程《现代控制》、《交直流调速》、《电机调速综合实训》相衔接,共同培养自动控制系统综合应用分析能力。
通过理论学习的方式,了解自动控制系统的一些工程实例、熟悉典型自动控制系统的时域分析方法和频域分析方法,培养学生逻辑思维能力、综合分析能力、再学习能力。
三、设计思路根据对应的工作岗位、工作任务、必备的能力和素质需求进行调查,根据行业、企业发展需要和完成职业岗位实际工作任务所需要的知识、能力、素质要求,选取教学内容,采用现代化教学手段,注意培养学生面向工程的思维习惯,采用多元化的考核方法,使学生掌握控制原理的精髓,并为学生可持续发展奠定良好的基础。
四、课程培养目标通过对《自动控制原理》的学习,使学生能运用现代自动控制原理的基本理论、基本知识和基本技能,了解自动控制原理的发展现状。
完成控制系统组成原理、系统调试方法,具体应从下述3个方面展开表述:1.专业能力目标:(1)掌握对常用简单系统进行性能分析、并能够提出性能改良方案。
(2)掌握自动控制的基本概念及相关知识、自动控制系统的组成和工作原理。
(3)掌握自动控制系统常用数学模型的建立方法。
(4)熟悉自动控制系统性能及根轨迹分析方法,掌握稳定性分析、时域分析和频域分析的分析方法。
2.方法能力目标:(1)学生具有资料学习和吸收能力;(2)具有独立进行分析、设计、实施、评估的能力;具有获取、分析、归纳、交流、使用信息和新技术的能力;(3)具有将知识与技术综合运用与转换的能力。
3.社会能力目标:(1)培养学生严谨、规范的工作态度;吃苦耐劳、诚实守信的优秀品质;(2)良好的职业道德和精益求精的敬业精神。
具有良好的科学文化素质和技术业务素质,能很快适应岗位要求,有发展潜力。
广东工业大学《自动控制原理》MATLAB仿真实验指导书

自动控制原理MATLAB仿真实验指导书李明编写广东工业大学自动化学院自动控制系二〇一四年九月实验项目名称:实验一线性系统的时域响应实验项目性质:MATLAB仿真实验所属课程名称:自动控制原理实验计划学时:2学时一、实验目的1.熟悉控制系统MATLAB仿真的实验环境。
2.掌握使用MATLAB进行系统时域分析的方法,研究一阶系统和二阶系统的时域响应特性。
二、实验环境装有MATLAB6.5或以上版本的PC机一台。
三、实验内容和要求1.了解和掌握MATLAB中传递函数表达式及输出时域函数表达式。
2.利用MATALB观察和分析一阶系统的阶跃响应曲线,了解一阶系统的参数:时间常数对一阶系统动态特性的影响。
3.掌握典型二阶系统模拟电路的构成方法;研究二阶系统运动规律。
研究其重要参数:阻尼比对系统动态特性的影响,分析与超调量%、过渡过程时t的关系。
间s四、实验方法1.MATLAB中建立传递函数模型的相关函数(1)有理分式降幂排列形式: tf()(2)零极点增益模型: zpk()(3)传递函数的连接方式: series(), parallel(), feedback()2.MATLAB中分析系统稳定性的相关函数(1)利用pzmap()绘制连续系统的零极点图;(2)利用roots()求分母多项式的根来确定系统的极点3.MATLAB中分析线性系统的时域响应的相关函数(1)生成特定的激励信号的函数gensig( )(2) LTI 模型任意输入的响应函数lsim( ) (3) LTI 模型的单位冲激响应函数impulse( ) (4) LTI 模型的阶跃响应函数step( )五、 实验步骤1. 线性系统的稳定性分析(1) 若线性系统的闭环传递函数为225()425G s ss,试绘制其零极点分布图,并据此判断系统的稳定性。
(2) 若线性系统的闭环传递函数为229(0.21)()( 1.29)s s G s s s s ,求出该闭环传递函 数的所有极点,并据此判断系统的稳定性。
自动控制原理实验报告-西南交通大学课程与资源中心

西南交通大学自动控制原理课程实验报告册
《自动控制原理》课程实验报告(一)
《自动控制原理》课程实验报告(二)
《自动控制原理》课程实验报告(三)
《自动控制原理》课程实验报告(四)
三、思考题
1. 参数在一定范围内取值才能使闭环系统稳定的系统称为条件稳定系统。
对于这类系
统可以通过根轨迹法来确定使系统稳定的参数取值范围,也可以适当调整系统参数或增加校正网络以消除条件稳定性问题。
对于下图所示条件稳定系统:
试问能否通过增加开环零极点消除系统条件稳定性问题,即对于所有根轨迹增益,根轨迹全部位于s左半平面,闭环系统稳定。
《自动控制原理》课程实验报告(五)
《自动控制原理》课程实验报告(六)
《自动控制原理》课程实验报告(七)
《自动控制原理》课程实验报告(八)
《自动控制原理》课程实验报告(九)。
实验六-线性系统的根轨迹分析

《自动控制理论》实验报告专业:电气工程及其自动化班号:1406111学号:1140610319姓名:赵元胜电气工程及其自动化实验中心二〇一六年十二月实验六线性系统的根轨迹分析一、实验目的1、掌握使用MATLAB 绘制控制系统根轨迹图的方法;2、掌握根据根轨迹法对控制系统进行性能分析方法;二、实验设备Pc 机一台,MA TLAB 软件。
三、实验举例已知系统开环传递函数为)2)(1()()(++=s s s K s H s G 求:绘制控制系统的根轨迹图,并分析根轨迹的一般规律。
解:1、绘制控制系统的根轨迹图MATLAB 提供rlocus()函数来绘制系统的根轨迹图,其调用格式为 rlocus(num ,den)或[k ,p]=rlocusfind(num ,den)在MATLAB 命令窗口>>提示符号下键入:(符号↵表示回车)>>k=[1]↵>>z=[]↵>>p=[0 -1 -2]↵>>[num,den]=zp2tf(z ,p ,k)↵ 零极点模型转化为多项式模型 >>rlocus(num ,den)↵ 绘制控制系统的根轨迹图>>grid ↵ 绘制坐标屏幕显示系统的根轨迹图形2.分析根轨迹的一般规律1)根轨迹3条,分别从起点(0,0)、(-1,0)和(-2,0)出发,随着k 值从0→∞变化,趋向无穷远处。
2)位于负实轴上的根轨迹(-∞,-2)和(-1,0)区段,其对应的阻尼ζ>1,超调量为0,系统处于过阻尼状态而且在远离虚轴的方向,增益k 增大,振荡频率ωn 随之提高,系统动态衰减速率相应增大。
3)在根轨迹分离点(-0.432,0)处,对应的阻尼ζ=1,超调量为0,开环增益K=0.385,系统处于临界阻尼状态。
4)根轨迹经过分离点后离开实轴,朝s 右半平面运动。
当根轨迹在分离点与虚轴这个区间时,闭环极点由实数点变为共轭复数点,对应阻尼0<ζ<1,超调量越靠近虚轴越大,系统处于欠阻尼状态,其动态响应将出现衰减震荡,而越靠近实轴,增益K 越大,阻尼越小,振荡频率ωn 越高,振荡衰减越大。
SystemView实验报告(全)

昆明理工大学(SystemView)实验报告实验名称:SystemView实验时间:20013 年 9 月 8日专业:11电信指导教师:文斯姓名:张鉴学号:2 成绩:教师签名:文斯第一章SystemView的安装与操作一实验目的1、了解和熟悉Systemview 软件的基本使用;2、初步学习Systemview软件的图符库,能够构建简单系统。
二实验内容1、熟悉软件的工作界面;2、初步了解Systemview软件的图符库,并设定系统定时窗口;3、设计一些简单系统,观察信号频谱与输出信号波形。
三实验过程及结果1.1试用频率分别为f1=200HZ、f2=2000HZ的两个正弦信号源,合成一调制信号y(t)=5sin(2πf1t)*cos(2πf2t),观察其频谱与输出信号波形。
注意根据信号的频率选择适当的系统采样数率。
画图过程:(1)设置系统定时,单击按钮,设置采样率20000Hz,采样点数512;(2)定义两个幅度分别为1V,5V,频率分别为200Hz,2000Hz的正弦和余弦信号源;(3)拖出乘法器及接收图符;(4)连线;(5)运行并分析单击按钮和。
仿真电路图:波形图如下:频谱图如下:结果分析:频率为200HZ 的信号与频率为2000HZ的信号f2相乘,相当于在频域内卷积,卷积结果为两个频率想加减,实现频谱的搬移,形成1800HZ和2200HZ的信号,因信号最高频率为2000HZ所以采用5000HZ的采样数率。
1.2将一正弦信号与高斯噪声相加后观察输出波形及其频谱。
由小到大改变高斯噪声的功率,重新观察输出波形及其频谱。
画图过程:(1)设置系统定时,单击按钮,设置采样率100Hz,采样点数128;(2)定义一个幅度为1V,频率为100Hz正弦信号源和一个高斯噪声;(3)拖出加法器及接收图符;(4)连线;(5)运行并分析单击按钮和;(6)在分析窗口下单击进入频谱分析窗口,再单击点OK分析频谱。
仿真电路图:波形图如下:频谱图如下:结果分析:原始信号的频率为1000HZ,在加入均值为0方差为1的高斯噪声后,其波形发生严重失真,输出信号的各频率分量上的功率发生不规则变化。
自动控制原理第四章根轨迹法

根轨迹法可用于仿真和实验研究,通过模拟和实验 验证系统的性能和稳定性,为实际系统的设计和优 化提供依据。
根轨迹法的历史与发展
历史
根轨迹法最早由美国科学家威纳于1940年提出,经过多年的 发展与完善,已经成为自动控制领域中一种重要的分析和设 计方法。
发展
随着计算机技术和数值分析方法的不断发展,根轨迹法的应 用范围和精度得到了进一步拓展和提高。未来,根轨迹法有 望与其他控制理论和方法相结合,形成更加完善和高效的控 制系统分析和设计体系。
根轨迹的性能分析
根轨迹的增益敏感性和鲁棒性
通过分析根轨迹在不同增益下的变化情况,可以评估系统的性能和鲁棒性。
根轨迹与性能指标的关系
通过比较根轨迹与某些性能指标(如超调量、调节时间等),可以评估系统的 性能。
04
根轨迹法与其他控制方法的比较
根轨迹法与PID制根轨迹图,直观地分析系统的稳定性、响应速度和超调量等性
特点
根轨迹法具有直观、简便、易于掌握等优点,特别适合用于分析 开环系统的稳定性和性能。
根轨迹法的应用场景
控制系统设计
根轨迹法可用于控制系统设计,通过调整系统参数 ,优化系统的性能指标,如稳定性、快速性和准确 性等。
故障诊断与排除
根轨迹法可用于故障诊断与排除,通过观察系统根 轨迹的变化,判断系统是否出现故障,以及故障的 类型和程度。
在绘制根轨迹时,需要遵循一定 的规则,如根轨迹与虚轴的交点 、根轨迹的分离点和汇合点等。
03
根轨迹分析方法
根轨迹的形状分析
根轨迹的起点和终点
根轨迹的起点是开环极点的位置,而 终点是闭环极点的位置。通过分析起 点和终点的位置,可以判断根轨迹的 形状。
根轨迹的分支数
三阶系统综合分析及设计

目录摘要1 1 设计容11.1 设计题目1 1.2 设计任务12绘制三阶系统的根轨迹22.1 常规方法绘制根轨迹2 2.2用MATLAB 绘制根轨迹4 3 不同条件下K 的取值53.1 当-8为闭环系统的一个极点时,K 的取值5 3.2 主导极点阻尼比为0.7时的k 值5 4 求系统的稳态误差64.1 位置误差系数7 4.2 速度误差系数7 4.3 加速度误差系数84.4 输入信号为25.2)(1)(t t t t r ++=时的稳态误差85 绘制单位阶跃响应曲线96 频域特性分析96.1绘制Bode 图和Nyquist 曲线10 6.2相角裕度和幅值裕度12 7 加入非线性环节判断稳定性137.1 求死区特性环节的描述函数137.2 根据负倒描述函数和Nyquist 图判断系统的稳定性14 8 设计体会15 参考文献 (17)摘要三阶系统是以三级微分方程为运动方程的控制系统。
在控制工程中,三阶系统非常普遍,其动态性能指标的确定是比较复杂。
在工程上常采用闭环主导极点的概念对三阶系统进行近似分析,或直接用MATLAB软件进行高阶系统分析。
在课程设计中,要掌握用MATLAB绘制闭环系统根轨迹和系统响应曲线,用系统的闭环主导极点来估算三系统的动态性能,以及在比较点与开环传递函数之间加一个非线性环节判断其稳定性。
1 设计容1.1 设计题目三阶系统的综合分析和设计初始条件:某单位反馈系统结构图如图1-1所示:图1-1 图1-21.2 设计任务要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、试绘制随根轨迹2、当-8为闭环系统的一个极点时,K=?3、求取主导极点阻尼比为0.7时的K 值(以下K 取这个值)4、分别求取位置误差系数、速度误差系数、加速度误差系数及输入信号为25.2)(1)(t t t t r ++=单位阶跃信号、斜坡信号及单位加速度信号时的稳态误差5、用Matlab 绘制单位阶跃相应曲线6、绘制Bode 图和Nyquist 曲线,求取幅值裕度和相角裕度7、如在比较点与开环传递函数之间加1个死区非线性环节,如图1-2所示,其中2,10==k e ,试求取非线性环节的描述函数,并根据负倒描述函数和Nyquist 图判断系统的稳定性8、认真撰写课程设计报告。
实验三 线性系统的根轨迹分析

实验三 线性系统的根轨迹分析09电信 任旭乐 20095042046一、 实验目的1.熟悉Matlab 的基本操作;2.掌握利用Matlab 函数实现系统根轨迹的绘制及设计的方法。
3.能够根据所得结果对系统进行性能分析。
二、 实验内容1、已知单位负反馈系统的开环传递函数为: (1)试画出K=0 →∞时的闭环系统根轨迹; (2)求出临界时的K 值及闭环极点; (3)求出使系统稳定的K 值的区间; (4)利用Matlab 函数将剩余的根求出。
程序: a=[1 0]; b=[0.05 1]; c=[0.05 0.2 1]; d=conv(a,b); e=conv(c,d); G=tf([1],e); figure(1); rlocus(G);[k,pole]=rlocfind(G);解:(1)根轨迹如图所示。
(2)临界时k=4.62;闭环极点p=0.336+4.34j (3)由图可知:0<k<4.62时系统稳定。
Root LocusReal AxisI m a g i n a r y A x i s-80-60-40-200204060-60-40-20204060System: G Gain: 4.62P ole: 0.336 + 4.34i Damping: -0.0772Overshoot (%): 128Frequency (rad/sec): 4.35System: G Gain: 0P ole: 0Damping: -1Overshoot (%): 0Frequency (rad/sec): 0System: GGain: 8.5P ole: -19.5Damping: 1Overshoot (%): 0Frequency (rad/sec): 19.5根轨迹2()(0.051)(0.050.21)KG s s s s s =+++2、已知单位负反馈系统的开环传递函数为:(1)试画出K=0 →∞时的闭环系统根轨迹;(2)找出ζ=0.707附近的点,绘制出其相应的单位阶跃响应曲线。
线性系统的校正 实验报告

线性系统的校正实验报告(滞后校正) (超前校正)超前校正:已知单位负反馈系统被控对象的传递函数为:()(1)(4)KG s S S S =++,使用根轨迹解析法对系统进行超前串联校正设计,使之满足: 1)阶跃响应的超调量%20%σ=2)阶跃响应的调节时间不超过4(0.02)s t s =∆=±一、基于根轨迹法的串联超前校正的校正原理:当系统的性能指标以时域形式提出时,通常用根轨迹法对系统进行校正。
基于根轨迹法校正的基本思想是:假设系统的动态性能指标可由靠近虚轴的一对共轭闭环主导极点来表征,因此,可把对系统提出的时域性能指标的要求转化为一对期望闭环主导极点。
确定这对闭环主导极点的位置后,首先根据绘制根轨迹的相角条件判断一下它们是否位于校正前系统的根轨迹上。
如果这对闭环主导极点正好落在校正前系统的根轨迹上,则无需校正,只需调整系统的根轨迹增益即可;否则,可在系统中串联一超前校正装置1()(1)1C aTsG s a Ts+=>+,通过引入新的开环零点z c =-1/aT 和新的开环极点p c =-1/T 来改变系统原根轨迹的走向,使校正后系统的根轨迹经过这对期望闭环主导极点。
二、超前校正装置及其特性:典型超前校正装置的传递函数可写为1()(0)1C aTs G s a Ts+=>+式中a 为分度系数,T 为时间常数其频率响应1()1C jaT G j jTs ωωω+=+幅频特性:()c A ω=相频特性:11122(1)()1a T tg aT tg T tg aT ωφωωωω----=-=+由于a>1,()φω始终大于0,即超前校正装置始终提供超前相角。
超前装置提供一个极点和一个零点三、校正过程1)做出校正前系统的根轨迹和阶跃响应,如下图MATLAB代码:num=[1];den=[1 5 4 0];G0=tf(num,den) figure(1);rlocus(G0);sys=feedback(G0,1);figure(2);t=0:0.01:30;step(sys,t)grid2)根据21%100%e πςςσ--=⨯,可算出0.4559ς=,考虑到非主导极点和零点对超调量的影响,取0.5ς=又因为0.02∆=时, 4.44.4s nt ςωσ==,可得 2.2, 1.1n ωσ==期望闭环极点的纵坐标为21d ωως=- 1.9053d ω= 综上可得系统的一对希望的闭环主导极点为:1,2 1.1 1.9n d s j ςωω=-±=-±3)根据求得的主导极点,计算超前校正网络在1s 处应提供的超前角:1()(atan(1.9/2.9)*180/pi+180-atan(1.9/0.1)*180/pi+180-atan(1.9/1.1)*180/pi)o G s ∠=-得1()246.3131o G s ∠=-1180()o G s φ=--∠可得:66.3131φ=把()c G s 的零点设置在期望极点的正下方,即 1.1c z =-,从期望极点向左作角60φ=的负实轴交点上,可求得 5.5c p =- 4)校正后系统的开环传递函数为( 1.1)()(1)(4)( 5.5)K s G s s s s s +=+++由根轨迹的幅值条件,求得系统工作于期望极点处的K 值为36.2。
自控原理实验指导书

实验一系统建模与转换一、实验目的1.了解MATLAB软件的基本特点和功能;2.掌握线性系统被控对象传递函数数学模型在MATLAB环境下的表示方法及转换;3.掌握多环节串联、并联、反馈连接时整体传递函数的求取方法;4.掌握在SIMULINK环境下系统结构图的形成方法及整体传递函数的求取方法;5.了解在MATLAB环境下求取系统的输出时域表达式的方法。
二、实验内容1.自确定2个传递函数,实现传递函数的录入和求取串联、并联、反馈连接时等效的整体传递函数。
要求分别采用有理多项式模型和零极点增益模型两种传递函数形式。
2.进行2例有理多项式模型和零极点增益模型间的转换。
3.在Siumlink环境下实现如下系统的传递函数的求取。
各环节传递函数自定。
三、实验报告要求1.写明实验目的和实验原理。
实验原理中简要说明求取传递函数 的途径和采用的语句或函数。
2.在实验过程和结果中,要求按项目写清楚自定的传递函数、画 出系统方框图,从屏幕上复制程序和运行结果,复制系统的 Simulink 方框图,打印报告或打印粘贴在报告上。
不方便打印 的同学,要求手动从屏幕上抄写和绘制。
3.简要写出实验心得和问题或建议。
实验二 线性系统的时域分析一、实验目的1.研究线性系统在典型输入信号作用下的暂态响应; 2.熟悉线性系统的暂态性能指标;3.研究二阶系统重要参数阻尼比ξ对系统动态性能的影响; 4.熟悉在MATLAB 下判断系统稳定性的方法; 5.熟悉在MATLAB 下求取稳态误差的方法。
二、实验内容1〃研究一阶系统对阶跃输入、脉冲输入、斜坡输入、自定义输入的响应及性能指标。
设一阶系统系统具体参数:12.01)(+=s s G 。
2〃研究二阶系统对阶跃输入、脉冲输入、斜坡输入、自定义输入的响应及性能指标。
设:单位反馈系统的:)12.0(s )(+=s Ks G 。
K 参数变化及变化方案自定。
①典型二阶系统在阶跃输入下,阻尼比或自然振荡频率改变对某1项性能指标的影响。
自动控制原理高阶系统的瞬态响应和稳定性分析

实验三高阶系统的瞬态响应和稳定性分析一、实验目的1. 通过实验,进一步理解线性系统的稳定性仅取决于系统本身的结构和参数,它与外作用及初始条件均无关的特性;2. 研究系统的开环增益K或其它参数的变化对闭环系统稳定性的影响。
二、实验设备1. THBDC-1型控制理论·计算机控制技术实验平台;2. PC机一台(含上位机软件)、USB数据采集卡、37针通信线1根、16芯数据排线、USB接口线。
三、实验内容1、观测三阶系统的开环增益K为不同数值时的阶跃响应曲线;2、观测三阶系统时间常数T(极点)不同数值时的阶跃响应曲线。
四、实验原理三阶系统及三阶以上的系统统称为高阶系统。
一个高阶系统的瞬态响应是由一阶和二阶系统的瞬态响应组成。
控制系统能投入实际应用必须首先满足稳定的要求。
线性系统稳定的充要条件是其特征方程式的根全部位于S平面的左方。
应用劳斯判断就可以判别闭环特征方程式的根在S平面上的具体分布,从而确定系统是否稳定。
本实验是研究一个三阶系统的稳定性与其参数K和T对系统性能的关系。
三阶系统的方框图如图3-1所示。
图3-1 三阶系统的方框图三阶系统模拟电路图如图3-2所示。
图3-2 三阶系统的模拟电路图图3-1的开环传递函数为)1)(1)(1(2)(321+++=S T S T S T K S G (XR K 100=) (3-1) 式中K 值可调节R X 的值来改变。
当取C 1=1μF ,C 2=1μF ,C 3=1μF ,时,三阶系统对应的闭环传递函数特征方程为:0.001S 3+0.03S 2+0.3S+1+2K=0根据劳斯稳定判据,欲使系统稳定,则K应满足:0<K<4。
即当K=4时,系统处于临界状态;K>4时,系统处于发散状态。
五、实验步骤1、根据图3-2所示的三阶系统的模拟电路图,设计并组建该系统的模拟电路(取C 1= C 2= C 3=1μF)。
当系统输入一阶跃信号时,在下列几种情况下,用上位软件观测并记录不同K 值时的实验曲线。
自动控制原理MATLAB仿真实验指导书(4个实验)

自动控制原理MATLAB仿真实验实验指导书电子信息工程教研室实验一典型环节的MA TLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MA TLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink仿真环境常规模板。
图1-1 SIMULINK仿真界面图1-2 系统方框图3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时,特征方程的根在s 平面上的变化轨迹。
这个参数一般选为开环系统的增益K 。
课本中介绍的手工绘制根轨迹的方法,只能绘制根轨迹草图。
而用MATLAB 可以方便地绘制精确的根轨迹图,并可观测参数变化对特征根位置的影响。
假设系统的对象模型可以表示为11210111()()m m m m n n n nb s b s b s b G s KG s K s a s b s a -+--++++==++++ 系统的闭环特征方程可以写成01()0KG s +=对每一个K 的取值,我们可以得到一组系统的闭环极点。
如果我们改变K 的数值,则可以得到一系列这样的极点集合。
若将这些K 的取值下得出的极点位置按照各个分支连接起来,则可以得到一些描述系统闭环位置的曲线,这些曲线又称为系统的根轨迹。
绘制系统的根轨迹rlocus ()MATLAB 中绘制根轨迹的函数调用格式为:rlocus(num,den) 开环增益k 的范围自动设定。
rlocus(num,den,k) 开环增益k 的范围人工设定。
rlocus(p,z) 依据开环零极点绘制根轨迹。
r=rlocus(num,den) 不作图,返回闭环根矩阵。
[r,k]=rlocus(num,den) 不作图,返回闭环根矩阵r 和对应的开环增益向量k 。
其中,num,den 分别为系统开环传递函数的分子、分母多项式系数,按s 的降幂排列。
K 为根轨迹增益,可设定增益范围。
例3-1:已知系统的开环传递函数32(1)()429s G s K s s s *+=+++,绘制系统的根轨迹的matlab 的调用语句如下:num=[1 1]; %定义分子多项式den=[1 4 2 9]; %定义分母多项式rlocus (num,den) %绘制系统的根轨迹grid %画网格标度线xlabel(‘Real Axis ’);ylabel(‘Imaginary Axis ’); %给坐标轴加上说明title(‘Root Locus ’) %给图形加上标题名 则该系统的根轨迹如图3-1(a )所示。
若上例要绘制K 在(1,10)的根轨迹图,则此时的matlab 的调用格式如下,对应的根轨迹如图3-1(b )所示。
num=[1 1]; den=[1 4 2 9];k=1:0.5:10;rlocus (num,den,k)1)确定闭环根位置对应增益值K 的函数rlocfind ()在MA TLAB 中,提供了rlocfind 函数获取与特定的复根对应的增益K 的值。
在求出的根轨迹图上,可确定选定点的增益值K 和闭环根r (向量)的值。
该函数的调用格式为:[k,r]=rlocfind(num,den)执行前,先执行绘制根轨迹命令rlocus (num,den ),作出根轨迹图。
执行rlocfind 命令时,出现提示语句“Select a point in the graphics window ”,即要求在根轨迹图上选定闭环极点。
将鼠标移至根轨迹图选定的位置,单击左键确定,根轨迹图上出现“+”标记,即得到了该点的增益K 和闭环根r 的返回变量值。
例3-2:系统的开环传递函数为23256()8325s s G s K s s s *++=+++,试求:(1)系统的根轨迹;(2)系统稳定的K 的范围;(3)K=1时闭环系统阶跃响应曲线。
则此时的matlab 的调用格式为:G=tf([1,5,6],[1,8,3,25]);rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点rG_c=feedback(G ,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线则系统的根轨迹图和闭环系统阶跃响应曲线如图3-2所示。
其中,调用rlocfind ()函数,求出系统与虚轴交点的K 值,可得与虚轴交点的K 值为0.0264,故系统稳定的K 的范围为(0.0264,)K ∈∞。
2)绘制阻尼比ζ和无阻尼自然频率n ω的栅格线sgrid( )当对系统的阻尼比ζ和无阻尼自然频率n ω有要求时,就希望在根轨迹图上作等ζ或等n ω线。
matlab 中实现这一要求的函数为sgrid( ),该函数的调用格式为:sgrid(ζ,n ω) 已知ζ和n ω的数值,作出等于已知参数的等值线。
sgrid(‘new ’) 作出等间隔分布的等ζ和n ω网格线。
例3-3:系统的开环传递函数为1()(1)(2)G s s s s =++,由rlocfind 函数找出能产生主导极点阻尼ζ=0.707的合适增益,如图3-3(a)所示。
G=tf(1,[conv([1,1],[1,2]),0]);(a ) 完整根轨迹图形 (b )特定增益范围内的根轨迹图形图3-1 系统的根轨迹图形zet=[0.1:0.2:1];wn=[1:10];sgrid(zet,wn);hold on;rlocus(G)[k,r]=rlocfind(G)Select a point in the graphics windowselected_point =-0.3791 + 0.3602ik =0.6233r =-2.2279-0.3861 + 0.3616i-0.3861 - 0.3616i同时我们还可以绘制出该增益下闭环系统的阶跃响应,如图3-3(b)所示。
事实上,等ζ或等n ω线在设计系补偿器中是相当实用的,这样设计出的增益K=0.6233将使得整个系统的阻尼比接近0.707。
由下面的MATLAB 语句可以求出主导极点,即r(2.3)点的阻尼比和自然频率为G_c=feedback(G ,1);step(G_c)(a )根轨迹图形 (b )K=1时的阶跃响应曲线 图3-2 系统的根轨迹和阶跃响应曲线 (a )根轨迹上点的选择 (b )闭环系统阶跃响应 图3-3 由根轨迹技术设计闭环系统dd0=poly(r(2:3,:));wn=sqrt(dd0(3));zet=dd0(2)/(2*wn);[zet,wn]ans =0.7299 0.5290我们可以由图3-3(a)中看出,主导极点的结果与实际系统的闭环响应非常接近,设计的效果是令人满意的。
3)基于根轨迹的系统设计及校正工具rltoolmatlab 中提供了一个系统根轨迹分析的图形界面,在此界面可以可视地在整个前向通路中添加零极点(亦即设计控制器),从而使得系统的性能得到改善。
实现这一要求的工具为rltool ,其调用格式为:rltool 或 rltool(G)例3-4:单位负反馈系统的开环传递函数 20.125()(5)(20)(50)s G s s s s s +=+++ 输入系统的数学模型,并对此对象进行设计。
den=[conv([1,5],conv([1,20],[1,50])),0,0];num=[1,0.125];G=tf(num,den);rltool(G)该命令将打开rltool 工具的界面,显示原开环模型的根轨迹图,如图3-4(a )所示。
单击该图形菜单命令Analysis 中的Response to Step Command 复选框,则将打开一个新的窗口,绘制系统的闭环阶跃响应曲线,如图3-4(b )所示。
可见这样直接得出的系统有很强的振荡,就需要给这个对象模型设计一个控制器来改善系统的闭环性能。
单击界面上的零点和极点添加的按钮,可以给系统添加一对共轭复极点,两个稳定零点,调整它们的位置,并调整增益的值,通过观察系统的闭环阶跃响应效果,则可以试凑地设计出一个控制器:(38.31)(10.26)()181307.29(61.30.84)(61.30.84)C s s G s s j s j ++=+++- 在此控制器下分别观察系统的根轨迹和闭环系统阶跃响应曲线。
可见,rltool 可以作为系 a )原对象模型的根轨迹 (b )闭环系统阶跃响应 图3-4 根轨迹设计工具界面及阶跃响应分析统综合的实用工具,在系统设计中发挥作用。
三、实验内容1.请绘制下面系统的根轨迹曲线 22()(22)(613)K G s s s s s s =++++ 程序:>> G=tf([1],[1 8 27 38 26 0]);>> rlocus (G)>> grid>> [k,r]=rlocfind(G)Select a point in the graphics windowselected_point =0.0071 - 0.9627ik = 28.7425r =-2.8199 + 2.1667i-2.8199 - 2.1667i-2.3313-0.0145 + 0.9873i-0.0145 - 0.9873i稳定时:K ∈(0,28.7425)2(12)()(1)(12100)(10)K s G s s s s s +=++++程序:>>G=tf([1 12],[1 23 242 230 1000]);>>rlocus (G)>>grid>>[k,r]=rlocfind(G)Select a point in the graphics windowselected_point =0.0118 + 5.8696ik = 522.9427r =-11.5988 + 8.8196i-11.5988 - 8.8196i0.0988 + 5.8529i0.0988 - 5.8529i稳定时:K ∈(522.9427)2(0.051)()(0.07141)(0.0120.11)K G s s s s s +=+++ 程序:>>G=tf([0.05 1],[0.0008568 0.01914 0.1714 1 0]); >> rlocus (G)>> grid>> [k,r]=rlocfind(G)Select a point in the graphics windowselected_point =0.0237 + 8.0745ik = 7.2730r =-0.2055 + 8.3831i-0.2055 - 8.3831i-10.9640 + 0.7119i-10.9640 - 0.7119i稳定时K ∈(0,7.2730)同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
