运算方法与运算器教案
计算机组成原理课件-4-运算方法与运算器

实验都在周六做,初步安排如下: 3月28日周六上午3-5节(3月30日上午不上课) 3月28日周六下午6-8节(3月30日晚上不上课) 4月25日周六上午3-5节(4月27日上午不上课) 4月25日周六下午6-8节(4月27日晚上不上课) 5月23日周六上午3-5节(5月18日上午不上课) 5月23日周六下午6-8节(5月18日晚上不上课) 5月30日周六上午3-5节(5月25日上午不上课) 5月30日周六下午6-8节(5月25日晚上不上课)
13
2、补码加减运算的溢出判断
对于加减运算,可能发生溢出的情况:同号(两数)相加, 或者异号(两数)相减。 确定发生溢出的情况: 正数相加,且结果符号位为1;(教材P105 例4.2 (1)) 负数相加,且结果符号位为0;(教材P105 例4.2 (2)) 负数-正数,且结果符号位为0;(教材P105 例4.2 (3)) 正数-负数,且结果符号位为1;(教材P105 例4.2 (4))
28
三、移码加减运算与判溢
[例] 已知x=1011,y=-1110,用移码运算方法计算 x+y,同时指出运算结果是否发生溢出。
[例] 已知x=1001,y=-1100,用移码运算方法计算 x-y,同时指出运算结果是否发生溢出。
例,教材P111例4.5
29
4.2
一 二 三
定点数的乘法运算及实现
2、补码加减运算的溢出判断
当运算结果超出机器数的表示范围时,称为溢出。计 算机必须具备检测运算结果是否发生溢出的能力,否 则会得到错误的结果。 【例】 设字长为8位(包括1位符号),若十进制数 x= –73,y= –83,用二进制补码求[x+y]补。 解: x=(–73)10=(–1001001)2,[x]补=10110111 y=(–83)10=(–1010011)2,[y]补=10101101 则 [x+y]补=10110111+10101101 =01100100 (溢出)
006第4章-运算方法与运算器1PPT课件

-
10
第4章 运算方法与运算器
补码加减运算举例
例:已知X=+1011,Y=-0100,用补码计算X+Y 和X-Y。
写出补码:
[X]补 =0,1011 [Y]补 =1,1100 [-Y]补 =0,0100 计算:
0,1011 + 1,1100
0,0111
[X+Y]补 = 0, 0111
0,1011 + 0,0100
-
7
第4章 运算方法与运算器
当x+y<0时, 2+(x+y)<2, 所以, (x)补+(y)补= 2+(x+y) =(x+y)补
(3)当 x<0,y>0,则x+y>0或x+y<0,该种情况和第 二种情况一样,把x和y的位置对调即得证。
(4)当x<0,y<0时,则x+y<0。
所以,(x)补=2+x,(y)补=2+y 故: (x)补+ (y)补= 2+x+ 2+y=2+(2+x+y) 因为:|x+y|<1,所以1< 2+x+y<2
4) X= –3 X补=1 1101
Y= –2 Y补=1 1110
Y= 2 Y补=0 0010
0 0001(+1补码)
1 1111(–1补码)
-
12
第4章 运算方法与运算器
例. 求(X – Y)补
1) X= 4 X补=0 0100
2) X= –4 X补=1 1100
Y= –5 Y补=1 1011Biblioteka Y= 5 Y补=0 0101
第3章运算方法与运算器

教学内容安排•第一章绪论•第二章数码系统•第三章运算方法和运算器•第四章存储系统•第五章指令系统•第六章中央处理器•第七章输入输出设备•第八章输入输出系统第三章运算方法和运算器• 3.1组成计算机硬件电路的基本逻辑部件• 3.2机器数的加减运算及其实现• 3.3定点乘法及其实现• 3.4定点除法及其实现(了解)• 3.5浮点数的算术运算(了解)• 3.6运算器的组教学重点和难点•基本逻辑运算和逻辑电路•机器数的加减运算•定点原码一位乘第三章运算方法和运算器 3.1组成计算机硬件电路的基本逻辑部件逻辑电路的基本概念•表示电路中输入信号与输出信号之间的关系的运算,为逻辑运算•赋以逻辑属性值“0”或“1”的变量,为逻辑变量。
•描述逻辑变量关系的函数(F=f(A,B)),为逻辑函数•实现逻辑函数功能的电路,为逻辑电路•逻辑电路可以做成计算机系统中常用的部件,为逻辑部件。
•逻辑部件分为:组合逻辑部件和时序逻辑电路•描述逻辑函数的值与它的逻辑变量之间关系的表格,称作真值表。
第三章运算方法和运算器 3.1组成计算机硬件电路的基本逻辑部件逻辑代数中基本逻辑运算•逻辑与(逻辑乘)•逻辑或(逻辑加)•逻辑非(逻辑求反)•逻辑异或•逻辑同或第三章运算方法和运算器 3.1组成计算机硬件电路的基本逻辑部件1.“与”逻辑------实现的电路叫与门只有决定事物结果的全部条件同时具备时,结果才会发生(有一个条件不具备,结果也不会发生)。
闭合1闭合1逻辑表达式第三章运算方法和运算器 3.1组成计算机硬件电路的基本逻辑部件2.“或”逻辑------实现的电路叫或门决定事物结果的诸条件中只要有任何一个满足时,结果就发生,这种因果关系叫做逻辑“或”,换句话说,只有所给条件均不具备,结果才不会发生。
第三章运算方法和运算器 3.1组成计算机硬件电路的基本逻辑部件3.“非”(反)逻辑-----实现的电路叫非门(或反相器)如果条件具备了,结果便不会发生;而条件不具备时结果一定发生。
计算机组成原理华科版第二章运算方法与运算器课件

4
计算机组成原理
⑵补码表示法
第二章 运算方法与运算器
• 由于补码在作二进制加、减运算时较方便,所以 在计算机中广泛采用补码表示二进制数。
• 补码运算中,可以用加法代替减法,节省元件, 降低成本。
5
计算机组成原理
第二章 运算方法与运算器
⑵补码表示法
原码求补码方法:正数不变(相同)。负数符号位不变, 数值位求反加1
第二种浮点表示的格式为
1,10001001,01111111110000000000000
17
计算机组成原理
⑶ 浮点数的表示举例
第二章 运算方法与运算器
某机用32b表示一个数,阶码部分占8b(含一位符号 位2格5式6).。5,,尾x数2=1部27分/2占56,2 4试b(写含出一x1和位x符2的号两位种)浮。点数设表x1示=-
最小负数 最大负数
最小正数
最大正数
1.0000000 1.1111111
0.0000001
0.1111111
-1
-2-7
2-7
1-2-7
11
计算机组成原理
第二章 运算方法与运算器
定点整数的表示范围:
①设字长为8b,用原码表示时,其表示范围如下:
最小负数 最大负数 最小正数 最大正数
11111111 10000001 00000001 01111111
计算机组成原理
1.真值与机器数
第二章 运算方法与运算器
采用正、负符号加上二进制的绝对值,则这种 数值称为真值。
将正负号分别用一位数码0和1来代替,一般将 这种符号位放在数的最高位。这种在机器中使 用的连同数符一起数码化的数,称为机器数。
1
计算机组成原理
第三章运算方法与运算器(定点数除法)

■ 当上述结果小于0时,商上0,恢复余数,然后左移一位,减除数比较,即:
(2Ri-Y)+Y= 2Ri 2*2Ri -Y = 4Ri –Y
■ 若当结果小于0时,商上0,不恢复余数而直接将余数左移一位,加Y:
2(2Ri-Y)+Y = 2*2Ri -2Y + Y = 4Ri –Y
第三章 3.6 定点数除法
1 00.0011
1
00.0110 0.11
+[–Y]补 11.0101
0 11.1011
0
11.0110 0.110
+[Y]补 00.1011
1 00. 0001 0.1101 1
减Y比较
余数 <0 商上零 左移一位 加Y比较 余数>0,商上1 左移一位 减Y比较 余数>0,商上1 左移一位 减Y比较 余数<0 商上零 左移一位 加Y比较
■重复上述过程直到商达到所需要的位数为止。
第三章 3.6 定点数除法
2
原码恢复余数除法
已知 X=0.1001,Y=- 0.1011,用原码一位除法求X/Y
解:[X]原= 0 .1001 [Y]原= 1.1011
[|X|]补=0.1001 [|Y|] 补=0.1011 [-|Y|]补 =1.0101
最后结果: 商Q = (X0 Y0).1101=1.1101 余数 R = 0.0001 * 2 -4
该方法存在的不足: 运算步数不确定
左移一位 减Y比较
1 余数>0,商上1,移商
第三章 3.6 定点数除法
3
原码加/减交替除法运算方法(不恢复余数法)
■ 设某次余数为Ri,将Ri左移一位减除数进行比较并上商,即:
中职计算机原理(高教版)教案:运算方法和运算器——定点运算器的组成和结构(全3课时)
江苏省XY中等专业学校2022-2023-2教案教学内容逻辑异或和逻辑非操作;移位操作主要完成逻辑左移、逻辑右移、算术左移、算术右移及其它一些移位操作。
在某些机器上ALU还要完成数值比较、变更数值符号、计算操作数在存储器中的地址等工作。
提问:ALU能够处理数据的位数与机器的字长有关码?试举例说明。
引导学生思考、回答并相互补充。
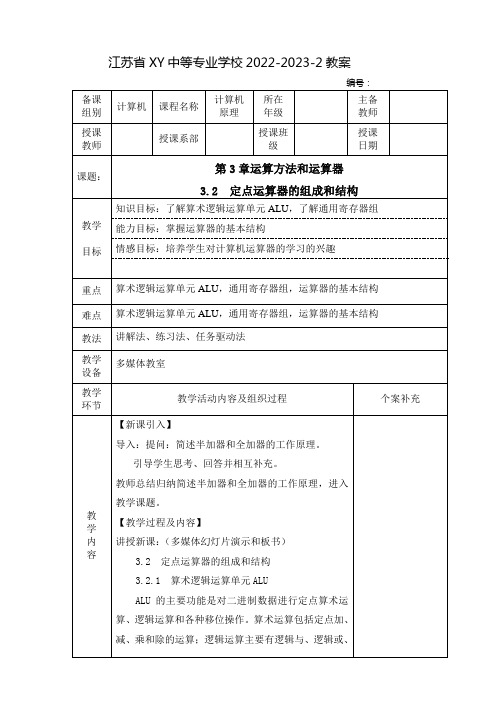
从下图可以看出,算术逻辑运算单元ALU有两个数据输入端A和B,一个数据输出端Y。
输入输出数据的宽度与ALU处理的数据宽度相同。
ALU一般具有A十B、A—B、B—A等算术运算功能,以及与、或、非、异或等逻辑运算的功能,还有左移、右移的功能。
3.2.2 通用寄存器组近代计算机的运算器中都有一组通用寄存器,它的主要用途是保存参加算的操作数和运算的结果。
寄存器是计算机中存取速度最快的存储器件,寄存器的存取周期一般是十几个毫微秒,远远快于内存储器的存取周期。
如果ALU的两个操作数都来自于寄存器,则可以极大地提高运算速度,这也就是为什么近代计算机都有一组相当数目的通用寄存器的道理。
江苏省XY中等专业学校2022-2023-2教案教学内容理解指令执行过程,也就是计算机总体运行过程。
假设这个通用寄存器组有两个输出端口RA和RB,有一个输人端口RI。
寄存器中的数据以补码表示。
并假设寄存器组中的寄存器1用R,表示,寄存器2用R.表示,寄存器3用R、表示。
运算之前,R,=0110,R2=1100,Z、N、C、V标志位全为0。
进行下面的操作后,标志位Z、N、C、V和R;的值如何?(1)第一种操作:R1加R2 ,结果送到R3中其操作过程如下:R1的内容通过端口RA输出,MUX1选择RA的内容送入ALU的输入端;R2的内容通过端口RB输出,MUX2选择RB的内容送人ALU的B输人端。
令ALU 做A+B算术加法操作,从Y输出端输出加的结果,并存人R,寄存器中。
(2)第二种操作:求与R,相补的数(取负数)其操作过程如下:R,的内容从RB输出,经过MUX2选择,送到ALU 的B输人端,在MUX1处选择常数"0"送入ALU的A 输人端,在ALU中选择A-B的算术运算功能。
第二章 计算方法和运算器(十一)

第3位的进位输出(即整个4位运算进位输出)公式为
Cn+4=Y3+X3Cn+3=Y3+Y2X3+Y1X2X3+Y0X1X2X3+X0X1X2X3Cn
设
G=Y3+Y2X3+Y1X2X3+Y0X1X2X3
P=X0X1X2X3
则
Cn+4=G+PCn
图2-15 ALU的逻辑结构原理图
控制参数S0,S1,S2,S3分别控制输入Ai和Bi,产生Xi和Yi的函数。其中Yi是受S0,S1控制的Ai和Bi的组合函数,而Xi是受S2,S3控制的Ai和Bi的组合函数,其函数关系如表2-4所示。
表2-4Xi、Yi与控制参数和输入量的关系
S0S1
Yi
S2S3
Xi
讲授法、演示法、实践操作法
教学手段
多媒体教学
教学内容:
第二章计算方法和运算器(十一)
我们曾介绍由一位全加器(FA)构成的行波进位加法器,它可实现补码数的加法运算和减法运算。但是这种加法/减法器存在两个问题:一是由于串行进位,它的运算时间很长。假如加法器由n位全加器构成,每一位的进位延迟时间为20ns,那么最坏情况下,进位信号从最低位传递到最高位而最后输出稳定,至少需要n×20ns,这在高速计算中显然是不利的。二就是行波进位加法器本身来说,它只能完成加法和减法两种操作而不能完成逻辑操作。为此,本节我们先介绍多功能算术/逻辑运算单元(ALU),它不仅具有多种算术运算和逻辑运算的功能,而且具有先行进位逻辑,从而能实现高速运算。
根据以上表达式,用TTL器件实现的成组先行进位部件74182的逻辑电路图如图2-17所示。其中G*称为成组进位发生输出,P*称为成组进位传送输出。
图2-17成组先行进位部件74182的逻辑电路图
《用计算器计算和运算律》教案

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与计算器和运算律相关的实际问题,如如何快速计算购物时的总价。
三、教学难点与重点
1.教学重点
-熟练使用计算器进行四则运算,确保计算的准确性和速度。
-掌握加法交换律、结合律,乘法交换律、结合律和分配律的基本概念及其在实际计算中的应用。
-能够运用运算律简化计算过程,提高解决问题的效率。
举例说明:
-重点讲解计算器操作步骤,确保学生能够正确进行423+527等基本运算。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《用计算器计算和运算律》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要进行快速计算的情况?”(例如购物时计算总价)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索计算器和运算律的奥秘。
还有一个值得注意的问题是,部分学生在解决实际问题时,还不能很好地将计算器和运算律结合起来。针对这个问题,我打算在下一节课中进行针对性地讲解和练习,让学生们明白计算器和运算律在解决实际问题中的重要性。
总之,今天的课程让我更加明确了今后的教学方向。我将继续关注学生的学习情况,及时调整教学方法,努力提高他们的数学素养。同时,我也会鼓励学生们多问问题同进步!
《用计算器计算和运算律》教案
一、教学内容
本节课选自《数学》五年级下册第五章《计算器和运算律》。教学内容主要包括:使用计算器进行加、减、乘、除基本运算;运用加法交换律、结合律,乘法交换律、结合律和分配律进行简便计算;通过计算器探索运算律在实际计算中的应用。具体内容包括:
第二章 计算方法和运算器(六)
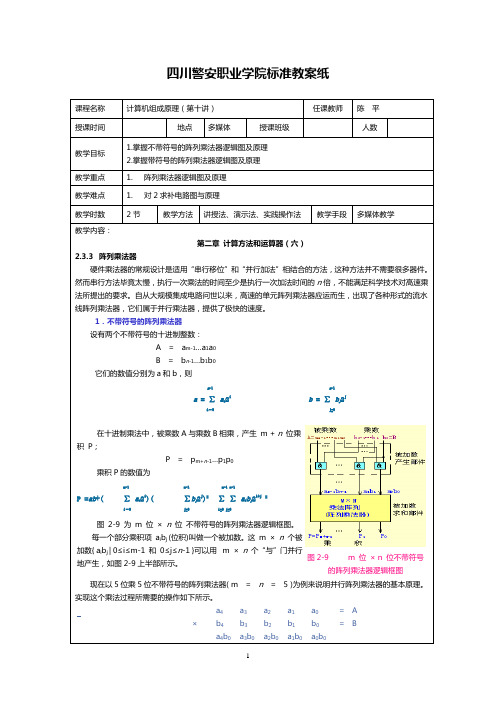
四川警安职业学院标准教案纸m+∑k=位×5位不带符号的阵列乘法器逻辑电路图图2-10为5 位×5 位不带符号的阵列乘法器的逻辑电路图,其中FA是我们前面讲过的5位×5位一位全加器,FA的斜线方向为进位输出,竖线方向为而所有被加数项的排列和前述A×B = P 乘法过程中的被加数矩阵相同。
图中阵列中最后一行构成了一位行波进位加法器,其时间延迟为(n - 1)2T。
当然,为了缩短加法时间,最下一行的行波进位加法器也可以用先行进位加法器来代替。
这种乘法器要实现n 位×n 位时,需要n ( n-1) 个全加器和n2个“与”门。
该乘法器的总的乘法时间可以估算如下:为“与门”的传输延迟时间,T f为全加器(FA)的进位传输延迟时间,假定用2级“与非”逻辑或者图2-11 对2求补器电路图。
这样,a i 以右的每一个输入位,包括a i自己,都保持不变,而i 以左的每一个输入位都求。
鉴于此,横向链式线路中的第i扫描级的输出C i为1的条件是:第级链式输入(即第i - 1级的输出C i - 1)C i - 1 = 1。
另外,最右端的起始链式输入C2-12 (n + 1)位×(n + 1)位带求补器的阵列乘法器逻辑方框图示出了(n + 1)位×(n + 1)位带求补器的阵列乘法器逻辑方框图。
通常,的乘法器又称为符号求补的阵列乘法器。
在这种逻辑结构中,共使用了三个求补器。
其中两个算前求补器的A和B在被不带符号的乘法阵列(核心部件)相乘以前,先变成正整数。
而算后求补器的作用则是:当两个输入操作数的符号不一致时,把运算结果变换成带符号的数。
a0和B = b n b n-1…b1b0均为用定点表示的(n + 1)位带符号整数。
由图A和B的码值输送给n位×n位不带符号的阵列乘法器,并由此产生A ×B = P = p2n-1…p1p0。
第2章运算方法与运算器2ppt课件

26
例1 x= -0.1101,y=-0.1011,求:[x×y]原=?
解: |x|=00.1101 (用双符号表示) |y|= 0.1011 (用单符号表示)
R0部分积 00.0000
R1乘数 yn 0.1011
说明
+ 00.1101 00.1101
yn=1,加|x| R2
P1
00.01101
0.101
INFO DEPT@ZUFE HANGZHOU.CHINA
16
(1)双符号法(变形补码法)
• 用两个相同的符号位Sf1 Sf2表示一个数的符号。 – 左边第一位为第一符号位Sf1,相邻的为第二符号位 Sf2。
• 双符号位的含义为: – 00表示正号; – 11表示负号; – 01表示产生正向溢出; – 10表示产生负向溢出。
• 其判断溢出表达式如下:V=Cn⊕Cn-1 , – 此逻辑式可用异或门实现
INFO DEPT@ZUFE HANGZHOU.CHINA
19
例如:
[x] 补= 1.0101
+ [y] 补= 1.1001
[x+y] 补= 1 0.1110
最高有效位没有进位,即Cn-1 =0,符号位有进位,即 Cn=1,故V=1⊕0=1,有溢出发生。
y)是负数,且其绝对值又小于1,那么(2+x+y)就一
定是小于2而大于1的数,进位”2”必丢失。又因(x+
y)<0, 所以
[x]补+[y]补=(2+x+y)=2+(x+y)=[x+y]补
INFO DEPT@ZUFE HANGZHOU.CHINA
7
[例]x=+0.1011, y=-0.0101,求
x+y。
yn)]=Pf.P1…P2n
2019精品第五章运算方法和运算器课件化学

1.溢出的产生
在补码加减运算中,有时会遇到这样的情况: 两个正数相加,而结果的符号位却为1(结果为负); 两个负数相加,而结果的符号位却为0(结果为正)。
例1: 设:X=1011B=11D,Y=111B=7D 则:[X]补=0,1011,[Y]补=0,0111 有: 0,1 0 1 1 + 0,0 1 1 1 1,0 0 1 0
出,须作溢出判断。一般机器溢出后,提示溢出信息, 然后停机。
原码一般不用来做加减运算,而多用来做乘除运算,
做加减运算时,多用补码。
第五章 运算方法和运算器
§5.1 定点加减运算
5.1.2补码加减法运算(重点)
引入补码后,不仅减法能变成加法,而且符号位能同 数值位一样参与加运算,这样可以大大简化运算器的结构。
当运算结果大于2n-1 或小于-2n时,就产生溢出。
设参加运算的两数为X、Y,做加法运算。
若X、Y异号,不会溢出。 若X、Y同号,运算结果为正且大于所能表示的最大正数或运算结果为 负且小于所能表示的最小负数 (绝对值最大的负数)时,产生溢出。
溢出分为2种:正溢和负溢。
第五章 运算方法和运算器
双符号位的含义如下:
Ss1Ss2=00 结果为正数,无溢出
Ss1Ss2=11 结果为负数,无溢出
[X]补 00.0101 +[Y]补 11.0111
[X+Y]补 11.1100
[X]补 00.0101 +[-Y]补 00.1001
[X-Y]补 00.1110
两符号位相同,无溢出
X+Y= - 0.0100
X-Y= + 0.1110
第五章 运算方法和运算器
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章运算方法和运算器学习重点●数据与文字的表示●定点加法、减法运算●定点运算器的组成●浮点运算的步骤2.1 数据与文字的表示方法2.1.1 数据格式计算机中使用的数据可分成两大类:数值数据:数字数据的表示(定点、浮点)符号数据:非数字符号的表示(ASCII、汉字、图形等)数值数据的表示格式有定点数、浮点数两种1.定点数的表示方法小数点的位置固定不变,通常表示成纯小数或纯整数。
用n+1位字表示定点数X,x= x n x n-1x n-2 (x1x0)纯小数时表示范围:0≤|X|≤1-2-n纯整数时表示范围:0≤|X|≤2n-12.浮点数的表示方法任意进制数N表示:N=R e·MM为尾数,数的精度;e为指数(整数),数的范围;R为基数,二进制为2,十进制为10;浮点数由阶码、尾数及其符号位组成。
规格化:若不对浮点数的表示作出明确规定,同一个浮点数的表示就不是惟一的。
例如:0.01010010×2110.001010010×21000.1010010×210IEEE754标准(规定了浮点数的表示格式,运算规则等)规则规定了32位和64位两种基本格式规则中,尾数用原码,指数用移码(便于对阶和比较),基数为2尾数域的最高有效位为1,称为浮点数的规格化表示。
32位的浮点数S数的符号位,1位,在最高位,“0”表示正数,“1”表示负数。
E是阶码,8位,采用移码表示。
移码比较大小方便。
M是尾数,23位,在低位部分,采用纯小数表示。
规格化的浮点数尾数域最左位(最高有效位)总是1,故这一位经常不予存储,而认为隐藏在小数点的左边(1.M) 。
采用这种方式时,将浮点数的指数真值e变成阶码E时,应将指数e加上一个固定的偏移值127(01111111),即E=e+127。
一个规格化的32位浮点数x的真值表示为x=(-1)S×(1.M)×2E-127设e=E-127x=(-1)S×(1.M)×2e[例1]若浮点数x的754标准存储格式为()16,求其浮点数的十进制数值。
解:将16进制数展开后,可得二制数格式为0 011 0110 0000 0000 0000 0000S 阶码(8位) 尾数(23位)指数e=阶码E-127=-01111111=00000011=(3)10包括隐藏位1的尾数M=1.011 0110 0000 0000 0000 0000=1.011011于是有x=(-1)S×1.M×2e=+(1.011011)×23=+1011.011=(11.375)10[例2]将数(20.59375)10转换成754标准的32位浮点数的二进制存储格式。
解:首先分别将整数和小数部分转换成二进制数:20.59375=10100.10011然后移动小数点,使其在第1,2位之间10100.10011=1.0×24e=4于是得到:E=e+127=4+127=131S=0, E=131=, M=0最后得到32位浮点数的二进制存储格式为:00=(41A4C000)16真值x为零表示:当阶码E为全0且尾数M也为全0时的值,结合符号位S为0或1,有正零和负零之分。
真值x为无穷大表示:当阶码E为全1且尾数M为全0时,结合符号位S为0或1,也有+∞和-∞之分。
这样在32位浮点数表示中,要除去E用全0和全1(255)表示零和无穷大的特殊情况,对于规格化浮点数,E的范围变为1到254,因为E=e+127,所以真正的指数值e则为-126到+127。
因此32位浮点数表示的绝对值的范围是10-38~1038(以10的幂表示)。
64位的浮点数中符号位1位,阶码域11位,尾数域52位,指数偏移值是1023。
因此规格化的64位浮点数x的真值为:x=(-1)S×(1.M)×2E-1023e=E-1023浮点数所表示的范围远比定点数大。
一台计算机中究竟采用定点表示还是浮点表示,要根据计算机的使用条件来确定。
一般在高档微机以上的计算机中同时采用定点、浮点表示,由使用者进行选择。
而单片机中多采用定点表示。
机器码:机器中表示的数, 要解决在计算机内部数的正、负符号和小数点运算问题。
原码、反码、补码、移码[例7]将十进制真值(-127,-1,0,+1,+127)列表表示成二进制数及原码、反码、补码、移码值。
[例8]设机器字长16位,定点表示,尾数15位,数符1位,问:(1)定点原码整数表示时,最大正数是多少?最小负数是多少?(2)定点原码小数表示时,最大正数是多少?最小负数是多少?定点原码整数表示最大正数值=(215-1)10=(+32767)10最小负数值=-(215-1)10=(-32767)10定点原码小数表示最大正数值=(1-2-15)10=(+0.111...11)2最小负数值=-(1-2-15)10=(-0.111..11)2数字编码输入的优点是无重码,且输入码与内部编码的转换比较方便,缺点是代码难以记忆。
拼音码是以汉字拼音为基础的输入方法。
使用简单方便,但汉字同音字太多,输入重码率很高,同音字选择影响了输入速度。
为了加快输入速度,在上述方法基础上,发展了词组输入、联想输入等多种快速输入方法。
更理想的输入方式是利用语音或图象识别技术“自动”将拼音或文本输入到计算机内,并将其自动转换为机内代码表示。
目前这种理想已经成为现实,如语音输入、手写输入、OCR等。
汉字内码汉字内码是用于汉字信息的存储、交换、检索等操作的机内代码,一般采用两个字节表示。
汉字机内代码中两个字节的最高位均规定为“1”。
(一级汉字3755个,二级汉字3008个)注意:有些系统中字节的最高位用于奇偶校验,此情况下用三个字节表示汉字内码。
2.1.5 校验码校验码(只介绍奇偶校验码)引入:信息传输和处理过程中受到干扰和故障,容易出错。
解决方法:是在有效信息中加入一些冗余信息(校验位)奇偶校验位定义缺点其它校验方法还有Hamming,CRC2.2定点加法、减法运算2.2.1 补码加减法补码加法公式:[x+y]补=[x]补+[y]补补码减法公式:[x-y]补=[x]补+[-y]补该公式将减法转变为加法如何求[-y]补?y=0.0111 [y]补=0.0111[-y]补=1.1001例: x=-0.1011,y=0.0111,求x+y=?解: [x]补=1.0101 [y]补=0.0111[x+y]补=[x]补+[y]补=1.0101+0.0111=1.1100x+y=-0.0100例: x=0.11011,y=-0.11111,求x-y=?解: [x]补=0.11011 [y]补=1.00001[-y]补=0.11111[x-y]补=[x]补+[-y]补=1.11010课堂练习例: x=+0.1011, y=+0.1001,求[x+y]补=?例: x=-0.1101,y=-0.1011,求[x+y ]补=?2.2.2 溢出的检测可能产生溢出的情况两正数加,变负数,上溢(大于机器所能表示的最大数)两负数加,变正数,下溢(小于机器所能表示的最小数)双符号位法(参与加减运算的数采用变形补码表示)S f1 S f20 0 正确(正数)0 1 上溢1 0 下溢1 1 正确(负数)S f1和S f2相同表示正确的符号,逻辑表达式为V=S f1⊕S f2,可以用异或门来实现单符号位法Cf C00 0 正确0 1 上溢1 0 下溢1 1 正确V=Cf⊕C0 其中Cf为符号位产生的进位,C0为最高有效位产生检验举例:x=+0.1100, y=+0.1000,求x+yx=-0.1100, y=-0.1000,求x+y结果出现了01或10的情况就为溢出基本的加法和减法器全加器半加器全加器考虑低位进位Ci和向高位的进位Ci+1半加器不考虑低位进位图2.3行波进位的补码加法/减法器2.3 定点乘法运算乘法实现方法●在现有的加法和减法器的基础上增加适当的线路及控制逻辑可以实现●用LSI和VLSI工艺实现专用的乘法器LSI (Large-scale integration大规模集成电路)●编制子程序(单片机等低端机器)2.3.1 原码并行乘法人工算法与机器算法的同异性由加法器完成乘法运算需要如下改进⏹n位乘n位积可能为2n位.⏹乘积的最后是所有部分积之和,有n个数相加,而FA只有两个输入端方法一:硬件实现方法(串行的“加法和移位”),硬件结构简单,速度太慢(已经淘汰).方法二:不带符号位的阵列乘法器要实现n位×n位时,需要n(n-1)个全加器和n2个“与”门。
图2.4 m×n位不带符号的阵列乘法器逻辑图带符号位的阵列乘法器计算机中定点数通常用补码表示,而前面介绍的不带符号阵列乘法器是用原码计算乘法的,为了能进行补码乘法,需要在计算乘法之前和之后增加求补电路。
原理:算前求补→乘法器→算后求补求补电路工作特点E=0时,输入和输出相等E=1时,则从数最右端往左边扫描,直到第一个1的时候,该位和右边各位保持不变0⊕A=A,左边各数值位按位取反1⊕A=A[例17] 设x=+15,y=-13,用带求补器的原码阵列乘法器求出乘积x·y=?[解:]设最高位为符号位,则输入数据为[x]原=01111[y]原=11101符号位单独考虑,算前求补级后|x|=1111,|y|=1101算后经求补级输出并加上乘积符号位1,则原码乘积值为1。
换算成二进制数真值是x·y=(-)2=(-195)10十进制数验证:x×y=15×(-13)=-195相等。
2.4定点运算器的组成2.4.1 多功能算术/逻辑运算单元(ALU)一位全加器(FA)的逻辑表达式为Fi=Xi⊕Yi⊕Cn+i (2.30)Cn+i+1=XiYi+YiCn+i+Cn+iXi4位ALU图2.10ALU的逻辑结构原理框图问题:片内是串行进位还是并行进位?4位之间采用先行进位公式,根据式(2.30),每一位的进位公式可递推如下:第0位向第1位的进位公式为Cn+1=Y0+X0Cn其中Cn是向第0位(末位)的进位。
第1位向第2位的进位公式为Cn+2=Y1+X1Cn+1=Y1+Y0X1+X0X1Cn第2位向第3位的进位公式为Cn+3=Y2+X2Cn+2=Y2+Y1X1+Y0X1X2+X0X1X2Cn第3位的进位输出(即整个4位运算进位输出)公式为Cn+4=Y3+X3Cn+3=Y3+Y2X3+Y1X2X3+Y0X1X2X3+X0X1X2X3Cn设G=Y3+Y2X3+Y1X2X3+Y0X1X2X3 P=X0X1X2X3则Cn+4=G+PCn这样,对一片ALU来说,可有三个进位输出。
