2020年河南中考复习专题八二次函数压轴题_课件(共37张PPT)

合集下载

中考二次函数压轴题PPT

∴ 点 F 到 AC 的距离为 9 × = ， 4
又∵ AC=
=3 ，
∴ △ ACE 的最大面积=×3 × = ，此时 E 点坐标为（ 5 ，﹣ 3 ）．
24
9
7、（2013•曲靖压轴题）如图，在平面直角坐标系 xOy 中，直线 y=x+4 与坐标轴分别交于 A、B 两点，过 A、B 两点的抛物线为 y=﹣x2+bx+c．点 D 为线段 AB 上一动点，过点 D 作 CD⊥x 轴于点 C，交抛物线于点 E．（1）求抛物线的解析式．（2）当 DE=4 时，求四边形 CAEB 的面积．（3）连接 BE，是否存在点 D，使得△ DBE 和△ DAC 相似？若存在，求此点 D 坐标；若不存在，说明理由．
解得
，
所以，直线 AC 的解析式为 y=x﹣1，
∵ y=x2﹣4x+3=（x﹣2）2﹣1，
∴ 抛物线的对称轴为直线 x=2，
当 x=2 时，y=2﹣1=1，
∴ 抛物线对称轴上存在点 D（2，1），使△ BCD 的周长最小；
8
（3）如图，设过点 E 与直线 AC 平行线的直线为 y=x+m，联立，消掉 y 得，x2﹣5x+3﹣m=0， △ =（﹣5）2﹣4×1×（3﹣m）=0，
7
解：（1）∵ 抛物线 y=ax2+bx+3 经过点 A（1，0），点 C（4，3），
∴
，解得
，
所以，抛物线的解析式为 y=x2﹣4x+3；
（2）∵ 点 A、B 关于对称轴对称， ∴ 点 D 为 AC 与对称轴的交点时△ BCD 的周长最小，设直线 AC 的解析式为 y=kx+b（k≠0），则，
S 四边形 CAEB=S△ ACE+S 梯形 OCEB﹣S△ BCO= ×2×6+ （6+4）×2﹣ ×2×4=12．

2024河南中考数学微专题复习二次函数的图象与性质课件

解得 = − ，
∴ 抛物线的表达式为 = − + + .
（2）为抛物线上任意一点，将点向上平移2个单位长度得到点 ′ ,若点
′ 关于原点的对称点恰好落在抛物线上，求此时点的坐标；
[答案] 设点的横坐标为 ,则点的坐标为 , − + + ,点 ′ 的
②当 0 ≤ ≤ 3 时，求函数值的取值范围.
[答案] 由①可知抛物线的对称轴为直线 = .
∵ 抛物线的开口向上， ≤ ≤ ,
∴ 当 = 时，取最小值，为 − .
∵ 抛物线开口向上， − > − ，∴Βιβλιοθήκη 当 = 时，取最大值，为0，
∵ − < < ， + < < + ，
∴ + < + < + ,
∴ + ≥ 或 + ≤ ，
解得 ≥

或

≤

− .

3.［原创新题］如图，抛物线 = 2 − 2 + 3 与轴交
= − ⋅ − = − − ，即 − − = − ，解得
= − （不合题意，舍去）， = ；
③当 > + ，即 < − 时，在 − ≤ ≤ + 范围内，随
的增大而减小.
∴ = +

− + − = − + ，即 − + = − ，解
得 = （不合题意，舍去）.
综上可知， = .

2020年中考数学二次函数压轴题(含答案40页)

2020年中考数学冲刺复习资料:二次函数压轴题面积类1．如图，已知抛物线经过点A（﹣1，0）、B（3，0）、C（0，3）三点．（1）求抛物线的解析式．（2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长．（3）在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．解：（1）设抛物线的解析式为：y=a（x+1）（x﹣3），则：a（0+1）（0﹣3）=3，a=﹣1；∴抛物线的解析式：y=﹣（x+1）（x﹣3）=﹣x2+2x+3．（2）设直线BC的解析式为：y=kx+b，则有：，解得；故直线BC的解析式：y=﹣x+3．已知点M的横坐标为m，MN∥y，则M（m，﹣m+3）、N（m，﹣m2+2m+3）；∴故MN=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m（0＜m＜3）．（3）如图；∵S△BNC=S△MNC+S△MNB=MN（OD+DB）=MN•OB，∴S△BNC=（﹣m2+3m）•3=﹣（m﹣）2+（0＜m＜3）；∴当m=时，△BNC的面积最大，最大值为．2．如图，抛物线的图象与x轴交于A、B两点，与y轴交于C 点，已知B点坐标为（4，0）．（1）求抛物线的解析式；（2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；（3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．解：（1）将B（4，0）代入抛物线的解析式中，得：0=16a﹣×4﹣2，即：a=；∴抛物线的解析式为：y=x2﹣x﹣2．（2）由（1）的函数解析式可求得：A（﹣1，0）、C（0，﹣2）；∴OA=1，OC=2，OB=4，即：OC2=OA•OB，又：OC⊥AB，∴△OAC∽△OCB，得：∠OCA=∠OBC；∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°，∴△ABC为直角三角形，AB为△ABC外接圆的直径；所以该外接圆的圆心为AB的中点，且坐标为：（，0）．（3）已求得：B（4，0）、C（0，﹣2），可得直线BC的解析式为：y=x﹣2；设直线l∥BC，则该直线的解析式可表示为：y=x+b，当直线l与抛物线只有一个交点时，可列方程：x+b=x2﹣x﹣2，即：x2﹣2x﹣2﹣b=0，且△=0；∴4﹣4×（﹣2﹣b）=0，即b=﹣4；∴直线l：y=x﹣4．所以点M即直线l和抛物线的唯一交点，有：，解得：即M（2，﹣3）．过M点作MN⊥x轴于N，S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×（2+3）+×2×3﹣×2×4=4．3．如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D 的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．解：（1）∵抛物线y=ax2+bx+3经过点A（1，0），点C（4，3），∴，解得，所以，抛物线的解析式为y=x2﹣4x+3；（2）∵点A、B关于对称轴对称，∴点D为AC与对称轴的交点时△BCD的周长最小，设直线AC的解析式为y=kx+b（k≠0），则，解得，所以，直线AC的解析式为y=x﹣1，∵y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线的对称轴为直线x=2，当x=2时，y=2﹣1=1，∴抛物线对称轴上存在点D（2，1），使△BCD的周长最小；（3）如图，设过点E与直线AC平行线的直线为y=x+m，联立，消掉y得，x2﹣5x+3﹣m=0，△=（﹣5）2﹣4×1×（3﹣m）=0，即m=﹣时，点E到AC的距离最大，△ACE的面积最大，此时x=，y=﹣=﹣，∴点E的坐标为（，﹣），设过点E的直线与x轴交点为F，则F（，0），∴AF=﹣1=，∵直线AC的解析式为y=x﹣1，∴∠CAB=45°，∴点F到AC的距离为×=，又∵AC==3，∴△ACE的最大面积=×3×=，此时E点坐标为（，﹣）．4.（2013•菏泽）如图，三角形ABC是以BC为底边的等腰三角形，点A、C分别是一次函数y=x+3的图象与y轴的交点，点B在二次函数的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．（1）试求b，c的值，并写出该二次函数表达式；（2）动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：①当P 运动到何处时，有PQ⊥AC？②当P运动到何处时，四边形PDCQ的面积最小？此时四边形PDCQ的面积是多少？解：（1）由y=﹣x+3，令x=0，得y=3，所以点A（0，3）；令y=0，得x=4，所以点C（4，0），∵△ABC是以BC为底边的等腰三角形，∴B点坐标为（﹣4，0），又∵四边形ABCD是平行四边形，∴D点坐标为（8，3），将点B（﹣4，0）、点D（8，3）代入二次函数y=x2+bx+c，可得，解得：，故该二次函数解析式为：y=x2﹣x﹣3．（2）①设点P运动了t秒时，PQ⊥AC，此时AP=t，CQ=t，AQ=5﹣t，∵PQ⊥AC，∴△APQ∽△CAO，∴=，即=，解得：t=．即当点P运动到距离A点个单位长度处，有PQ⊥AC．②∵S四边形PDCQ+S△APQ=S△ACD，且S△ACD=×8×3=12，∴当△APQ的面积最大时，四边形PDCQ的面积最小，当动点P运动t秒时，AP=t，CQ=t，AQ=5﹣t，设△APQ底边AP上的高为h，作QH⊥AD于点H，由△AQH∽CAO可得：=，解得：h=（5﹣t），∴S△APQ=t×（5﹣t）=（﹣t2+5t）=﹣（t﹣）2+，∴当t=时，S△APQ达到最大值，此时S四边形PDCQ=12﹣=，故当点P运动到距离点A个单位处时，四边形PDCQ面积最小，最小值为．等腰三角形类10. （2012江苏扬州12分）已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．(1)求抛物线的函数关系式；(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．【答案】解：（1）∵A(－1，0)、B(3，0)经过抛物线y＝ax2＋bx＋c，∴可设抛物线为y＝a（x＋1）（x－3）。

2020届中考数学压轴题全揭秘专题08 二次函数的图象性质与应用问题(含解析)

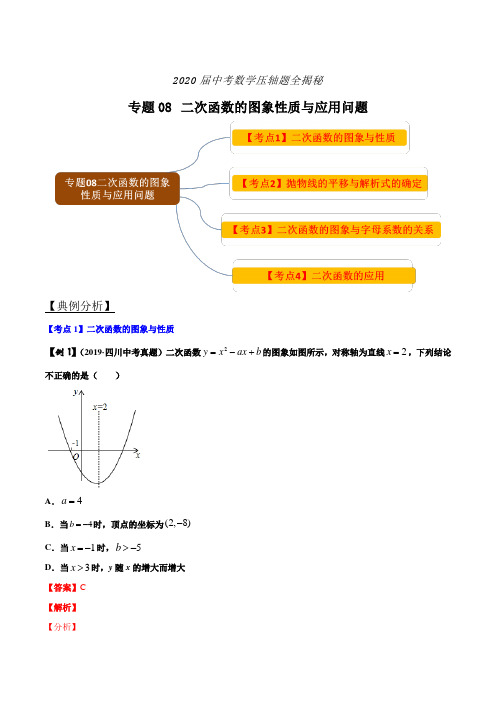
2020届中考数学压轴题全揭秘专题08 二次函数的图象性质与应用问题【典例分析】【考点1】二次函数的图象与性质【例1】（2019·四川中考真题）二次函数2y x ax b =-+的图象如图所示，对称轴为直线2x =，下列结论不正确的是（）A ．4a =B ．当4b =-时，顶点的坐标为(2,8)-C ．当1x =-时，5b >-D ．当3x >时，y 随x 的增大而增大【答案】C 【解析】【分析】根据对称轴公式2bx a=和二次函数的性质，结合选项即可得到答案. 【详解】解：∵二次函数2y x ax b =-+ ∴对称轴为直线22ax == ∴4a =，故A 选项正确；当4b =-时，2244(2)8y x x x =--=-- ∴顶点的坐标为(2,8)-，故B 选项正确；当1x =-时，由图象知此时0y < 即140b ++<∴5b <-，故C 选项不正确； ∵对称轴为直线2x =且图象开口向上∴当3x >时，y 随x 的增大而增大，故D 选项正确；故选C ．【点睛】本题考查二次函数，解题的关键是熟练掌握二次函数.【变式1-1】（2019·重庆中考真题）抛物线2362y x x =-++的对称轴是（）A ．直线2x =B ．直线2x =-C ．直线1x =D ．直线1x =-【答案】C 【解析】【分析】将抛物线的一般式配方成为顶点式，可确定顶点坐标及对称轴．【详解】解：∵223623(1)5y x x x =-++=--+， ∴抛物线顶点坐标为(1,5)，对称轴为1x =．故选：C ．本题考查了二次函数的性质．抛物线2()y a x h k =-+的顶点坐标为（h ，k ），对称轴为x ＝h ．【变式1-2】（2019·浙江中考真题）已知抛物线224y x x c =-+与x 轴有两个不同的交点.(1)求c 的取值范围；(2)若抛物线224y x x c =-+经过点()2,A m 和点()3,B n ，试比较m 与n 的大小，并说明理由. 【答案】(1) c 的取值范围是2c <； (2)m n <. 理由见解析. 【解析】【分析】（1）由二次函数与x 轴交点情况，可知△＞0；（2）求出抛物线对称轴为直线x=1，由于A （2，m ）和点B （3，n ）都在对称轴的右侧，即可求解；【详解】(1)()2244816 8b ac c c -=--=-. 由题意，得240b ac ->， ∴16 80c ->∴c 的取值范围是2c <. (2)m n <. 理由如下:∵抛物线的对称轴为直线1x =，又∵20a =>，∴当1x ≥时，y 随x 的增大而增大. ∵23<，∴m n <. 【点睛】本题考查二次函数图象及性质；熟练掌握二次函数对称轴，函数图象的增减性是解题的关键．【考点2】抛物线的平移与解析式的确定【例2-1】（2019·山东中考真题）将抛物线265y x x =-+向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（） A ．2(4)6y x =-- B ．2(1)3y x =-- C ．2(2)2y x =-- D ．2(4)2y x =--【答案】D【分析】由平移可知，抛物线的开口方向和大小不变，顶点改变，将抛物线化为顶点式，求出顶点，再由平移求出新的顶点，然后根据顶点式写出平移后的抛物线解析式．【详解】解：()226534y x x x =-+=--，即抛物线的顶点坐标为()3,4-，把点()3,4-向上平移2个单位长度，再向右平移1个单位长度得到点的坐标为()4,2-，所以平移后得到的抛物线解析式为()242y x =--．故选：D ．【点睛】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a 不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．【例2-2】（2019·山西中考真题）北中环桥是省城太原的一座跨汾河大桥(如图1)，它由五个高度不同，跨径也不同的抛物线型钢拱通过吊桥，拉锁与主梁相连，最高的钢拱如图2所示，此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内，与拱脚所在的水平面相交于A ，B 两点，拱高为78米(即最高点O 到AB 的距离为78米)，跨径为90米(即AB=90米)，以最高点O 为坐标原点，以平行于AB 的直线为x 轴建立平面直角坐标系，则此抛物线钢拱的函数表达式为( )A ．226675y x =B ．226675y x =-C ．2131350y x =D ．2131350y x =-【答案】B 【解析】【分析】设抛物线解析式为y=ax 2，由已知可得点B 坐标为(45，-78)，利用待定系数法进行求解即可. 【详解】∵拱高为78米(即最高点O 到AB 的距离为78米)，跨径为90米(即AB=90米)，以最高点O 为坐标原点，以平行于AB 的直线为x 轴建立平面直角坐标系， ∴设抛物线解析式为y=ax 2，点B(45，-78)， ∴-78=452a ，解得：a=26675-， ∴此抛物线钢拱的函数表达式为226675y x =-，故选B. 【点睛】本题考查了二次函数的应用，熟练掌握待定系数法是解本题的关键.【变式2-1】（2019·西藏中考真题）把函数212y x =-的图象，经过怎样的平移变换以后，可以得到函数()21112y x =--+的图象（）A ．向左平移1个单位，再向下平移1个单位B ．向左平移1个单位，再向上平移1个单位C ．向右平移1个单位，再向上平移1个单位D ．向右平移1个单位，再向下平移1个单位【答案】C 【解析】【分析】根据抛物线顶点的变换规律作出正确的选项．【详解】抛物线212y x =-的顶点坐标是00（，），抛物线线()21112y x =--+的顶点坐标是11（，），所以将顶点00（，）向右平移1个单位，再向上平移1个单位得到顶点11（，），即将函数212y x =-的图象向右平移1个单位，再向上平移1个单位得到函数()21112y x =--+的图象．故选：C ．【点睛】主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．【变式2-2】（2019·江苏中考真题）已知二次函数的图象经过点(2,2)P ，顶点为(0,0)O 将该图象向右平移，当它再次经过点P 时，所得抛物线的函数表达式为__．【答案】21(4)2y x =-．【解析】【分析】设原来的抛物线解析式为：2y ax =．利用待定系数法确定函数关系式；然后利用平移规律得到平移后的解析式，将点P 的坐标代入即可．【详解】设原来的抛物线解析式为：2y ax =(0)a ≠，把(2,2)P 代入，得24a =，解得12a =，故原来的抛物线解析式是：212y x =，设平移后的抛物线解析式为：21()2y x b =-，把(2,2)P 代入，得212(2)2b =-，解得0b =(舍去)或4b =，所以平移后抛物线的解析式是：21(4)2y x =-，故答案是：21(4)2y x =-．【点睛】本题考查了二次函数图象与几何变换，二次函数的性质，二次函数图象上点的坐标特征．利用待定系数法确定原来函数关系式是解题的关键．【变式2-3】（2019·浙江中考真题）在平面直角坐标系中，抛物线(5)(3)y x x =+-经过变换后得到抛物线(3)(5)y x x =+-，则这个变换可以是（） A ．向左平移2个单位 B ．向右平移2个单位 C ．向左平移8个单位D ．向右平移8个单位【答案】B 【解析】【分析】根据变换前后的两抛物线的顶点坐标找变换规律．【详解】y=（x+5）（x-3）=（x+1）2-16，顶点坐标是（-1，-16）． y=（x+3）（x-5）=（x-1）2-16，顶点坐标是（1，-16）．所以将抛物线y=（x+5）（x-3）向右平移2个单位长度得到抛物线y=（x+3）（x-5），故选B ．【点睛】此题主要考查了次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．【变式2-4】（2019·四川中考真题）将抛物线23)2y x＝(﹣﹣向左平移_______个单位后经过点(22)A ，．【答案】3 【解析】【分析】直接利用二次函数的平移规律结合二次函数图象上点的性质进而得出答案．【详解】解：∵将抛物线232y x ＝（﹣）﹣向左平移后经过点22A （，）， ∴设平移后解析式为：232y x a +＝（﹣）﹣，则22232a +＝（﹣）﹣，解得：3a ＝或1a ＝﹣（不合题意舍去），故将抛物线232y x ＝（﹣）﹣向左平移3个单位后经过点22A （，）．故答案为：3．【点睛】考查了二次函数图象与几何变换，正确记忆平移规律是解题关键．【考点3】二次函数的图象与字母系数的关系【例3】（2019·辽宁中考真题）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc >；②930a b c ++=；③248b ac a -<；④50a b c ++>．其中正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】C 【解析】【分析】根据图象可直接判断a 、c 的符号，再结合对称轴的位置可判断b 的符号，进而可判断①；抛物线的图象过点（3，0），代入抛物线的解析式可判断②；根据抛物线顶点的位置可知：顶点的纵坐标小于－2，整理后可判断③；根据图象可知顶点的横坐标大于1，整理后再结合③的结论即可判断④. 【详解】解：①由图象可知：0a >，0c <，由于对称轴02ba->，∴0b <，∴0abc >，故①正确； ②∵抛物线过(3,0)，∴3x =时，930y a b c =++=，故②正确；③顶点坐标为：24,24b ac b aa ⎛⎫-- ⎪⎝⎭.由图象可知：2424ac b a -<-，∵0a >，∴248ac b a -<-，即248b ac a ->，故③错误；④由图象可知：12ba->，0a >，∴20a b +<， ∵930a b c ++=，∴93c a b =--，∴5593422(2)0a b c a b a b a b a b ++=+--=--=-+>，故④正确；故选：C ．【点睛】本题考查了抛物线的图象与性质和抛物线的图象与其系数的关系，熟练掌握抛物线的图象与性质、灵活运用数形结合的思想方法是解题的关键.【变式3-1】（2019·浙江中考真题）小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论：①这个函数图象的顶点始终在直线y=-x+1上；②存在一个m的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；③点A(x1,y1)与点B(x2,y2)在函数图象上，若x1<x2，x1+x2>2m，则y1<y2；④当-1<x<2时，y随x的增大而增大，则m的取值范围为m≥2其中错误结论的序号是（）A．①B．②C．③D．④【答案】C【解析】【分析】把顶点坐标代入y=-x+1即可判断①；根据勾股定理即可判断②；根据在对称轴的右边y随x的增大而减小可判断③；；根据在对称轴的右边y随x的增大而增大可判断④.【详解】把（m，-m+1）代入y=-x+1，-m+1=-m+1，左=右，故①正确；当-(x-m)2-m+1=0时，x 1=, x2=,若顶点与轴的两个交点构成等腰直角三角形，则1-m+(1-m)2+1-m+(1-m)2=4(1-m)，即m2-m=0，∴m=0或1时，∴存在一个m的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；故②正确；当x1<x2，且x1、x2在对称轴右侧时，∵-1<0, ∴在对称轴右侧y随x的增大而减小，即y1>y2，故③错误；∵-1<0, ∴在对称轴左侧y随x的增大而增大，∴m≥2，故④正确.故选C.【点睛】本题考查了二次函数的图像与性质，勾股定理，二次函数与坐标轴的交点，熟练掌握二次函数的图像与性质是解答本体的关键. 对于二次函数y=a(x-h)2+k（a，b，c为常数，a≠0），当a>0时，抛物线开口向上，在对称轴的左侧y随x的增大而减小，在对称轴的右侧y随x的增大而增大；当a<0时，抛物线开口向下，在对称轴的左侧y随x的增大而增大，在对称轴的右侧y随x的增大而减小.其顶点坐标是(h，k)，对称轴为直线x=h.【变式3-2】（2019·广西中考真题）已知抛物线()20y ax bx c a =++≠的对称轴是直线1x =，其部分图象如图所示，下列说法中：①0abc <；②0a b c -+<；③30a c +=；④当13x -<<时，0y >，正确的是_____（填写序号）．【答案】①③④．【解析】【分析】首先根据二次函数图象开口方向可得0a ＜，根据图象与y 轴交点可得0c ＞，再根据二次函数的对称轴b12a x ＝﹣＝，结合a 的取值可判定出b>0，根据a,b,c 的正负即可判断出①的正误；把1x ＝﹣代入函数关系式2y ax bx c y a b c +++＝中得＝﹣，再根据对称性判断出②的正误；把2b a a b c +＝﹣代入﹣ 中即可判断出③的正误；利用图象可以直接看出④的正误．【详解】解：根据图象可得：00a c ＜，＞，对称轴：b 12ax ＝﹣＝， 2b a ∴＝﹣， 0a Q ＜， 0b ∴＞，， 0abc ∴＜，故①正确；把1x ＝﹣ 代入函数关系式2y ax bx c y ab c +++＝中得：＝﹣，由抛物线的对称轴是直线130x ＝，且过点（，），可得当10x y ＝﹣时，＝， 0a b c ∴+﹣＝，故②错误； 2b a Q ＝﹣，a--2a +c=0∴（），即：30a c +＝，故③正确；由图形可以直接看出④正确．故答案为①③④．【点睛】此题主要考查了二次函数图象与系数的关系，关键是熟练掌握①二次项系数a 决定抛物线的开口方向，当0a ＞时，抛物线向上开口；当0a ＜时，抛物线向下开口；②一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即0ab ＜），对称轴在y 轴左侧；当a 与b 异号时（即0ab ＜），对称轴在y 轴右侧．（简称：左同右异）；③常数项c 决定抛物线与y 轴交点，抛物线与y 轴交于0c （，）．【考点4】二次函数的应用【例4】（2019·辽宁中考真题）某商场销售一种商品的进价为每件30元，销售过程中发现月销售量y （件）与销售单价x （元）之间的关系如图所示．（1）根据图象直接写出y 与x 之间的函数关系式．（2）设这种商品月利润为W （元），求W 与x 之间的函数关系式．（3）这种商品的销售单价定为多少元时，月利润最大？最大月利润是多少？【答案】（1）y ＝180(4060)3300(6090)x x x x -+≤≤⎧⎨-+<≤⎩；（2）W ＝222105400(4060)33909000(6090)x x x x x x ⎧-+-≤≤⎨-+-<≤⎩;（3）这种商品的销售单价定为65元时，月利润最大，最大月利润是3675．【解析】【分析】（1）当40≤x≤60时，设y 与x 之间的函数关系式为y=kx+b ，当60＜x≤90时，设y 与x 之间的函数关系式为y=mx+n ，解方程组即可得到结论；（2）当40≤x≤60时，当60＜x≤90时，根据题意即可得到函数解析式；（3）当40≤x≤60时，W=-x2+210x-5400，得到当x=60时，W最大=-602+210×60-5400=3600，当60＜x≤90时，W=-3x2+390x-9000，得到当x=65时，W最大=-3×652+390×65-9000=3675，于是得到结论．【详解】解：（1）当40≤x≤60时，设y与x之间的函数关系式为y＝kx+b，将（40，140），（60，120）代入得40140 60120k bk b+=⎧⎨+=⎩，解得：1180 kb=-⎧⎨=⎩，∴y与x之间的函数关系式为y＝﹣x+180；当60＜x≤90时，设y与x之间的函数关系式为y＝mx+n，将（90，30），（60，120）代入得9030 60120m nm n+=⎧⎨+=⎩，解得：3300 mn=-⎧⎨=⎩，∴y＝﹣3x+300；综上所述，y＝180(4060) 3300(6090)x xx x-+≤≤⎧⎨-+<≤⎩；（2）当40≤x≤60时，W＝（x﹣30）y＝（x﹣30）（﹣x+180）＝﹣x2+210x﹣5400，当60＜x≤90时，W＝（x﹣30）（﹣3x+300）＝﹣3x2+390x﹣9000，综上所述，W＝222105400(4060) 33909000(6090)x x xx x x⎧-+-≤≤⎨-+-<≤⎩；（3）当40≤x≤60时，W＝﹣x2+210x﹣5400，∵﹣1＜0，对称轴x＝2102--＝105，∴当40≤x≤60时，W随x的增大而增大，∴当x＝60时，W最大＝﹣602+210×60﹣5400＝3600，当60＜x≤90时，W＝﹣3x2+390x﹣9000，∵﹣3＜0，对称轴x＝3906--＝65，∵60＜x≤90，∴当x ＝65时，W 最大＝﹣3×652+390×65﹣9000＝3675，∵3675＞3600，∴当x ＝65时，W 最大＝3675，答：这种商品的销售单价定为65元时，月利润最大，最大月利润是3675．【点睛】本题考查了把实际问题转化为二次函数，再利用二次函数的性质进行实际应用．根据题意分情况建立二次函数的模型是解题的关键．【变式4-1】（2019·山东中考真题）从地面竖直向上抛出一小球，小球的高度h (单位：m )与小球运动时间t (单位：s )之间的函数关系如图所示．下列结论：①小球在空中经过的路程是40m ；②小球抛出3秒后，速度越来越快；③小球抛出3秒时速度为0；④小球的高度30h m =时， 1.5t s =．其中正确的是( )A ．①④B ．①②C ．②③④D ．②③【答案】D【解析】【分析】根据函数的图象中的信息判断即可．【详解】①由图象知小球在空中达到的最大高度是40m ；故①错误；②小球抛出3秒后，速度越来越快；故②正确；③小球抛出3秒时达到最高点即速度为0；故③正确；④设函数解析式为：()2340h a t =-+，把()0,0O 代入得()200340a =-+，解得409a =-， ∴函数解析式为()2403409h t =--+，把30h =代入解析式得，()240303409t =--+，解得： 4.5t =或 1.5t =，∴小球的高度30h m =时， 1.5t s =或4.5s ，故④错误；故选D ．【点睛】本题考查了二次函数的应用，解此题的关键是正确的理解题意【变式4-3】（2019·江苏中考真题）如图，利用一个直角墙角修建一个梯形储料场ABCD ，其中∠C ＝120°．若新建墙BC 与CD 总长为12m ，则该梯形储料场ABCD 的最大面积是（）A ．18m 2B ．183m 2C ．243m 2D ．4532m 2 【答案】C【解析】【分析】过点C 作CE ⊥AB 于E ，则四边形ADCE 为矩形，CD=AE=x ，∠DCE=∠CEB=90°，则∠BCE=∠BCD-∠DCE=30°，BC=12-x ，由直角三角形的，性质得出11BE BC 6x 22==-得出311AD CE 3BE 63x,AB AE BE x 6x x 6222===-=+=+-=+，又梯形面积公式求出梯形ABCD 的面积S 与x 之间的函数关系式，根据二次函数的性质求解.【详解】解：如图，过点C 作CE ⊥AB 于E ，则四边形ADCE 为矩形，CD=AE=x ，∠DCE=∠CEB=90°，则∠BCE=∠BCD-∠DCE=30°，BC=12-x ，在Rt △CBE 中，∵∠CEB=90°，11BE BC 6x 22∴==- 311AD CE 3BE 63x,AB AE BE x 6x x 6222∴===-=+=+-=+ ∴梯形ABCD 面积211133333S (CD AB)CE x x 663x x 33x 1832222888⎛⎫⎛⎫=+⋅=++⋅-=-++=- ⎪ ⎪⎝⎭⎝⎭ 2(4)243x -+∴当x=4时，S 最大=243．即CD 长为4 m 时，使梯形储料场ABCD 的面积最大为243 m 2；故选C ．【点睛】此题考查了梯性质、矩形的性质、含30°角的直角三角形的性质、勾股定理、二次函数的运用,利用梯形的面积建立二次函数是解题的关键【变式4-3】（2019·湖南中考真题）某政府工作报告中强调，2019年着重推进乡村振兴战略，做优做响湘莲等特色农产品品牌．小亮调查了一家湘潭特产店,A B 两种湘莲礼盒一个月的销售情况，A 种湘莲礼盒进价72元/盒，售价120元/盒，B 种湘莲礼盒进价40元/盒，售价80元/盒，这两种湘莲礼盒这个月平均每天的销售总额为2800元，平均每天的总利润为1280元．（1）求该店平均每天销售这两种湘莲礼盒各多少盒？（2）小亮调査发现，A 种湘莲礼盒售价每降3元可多卖1盒．若B 种湘莲礼盒的售价和销量不变，当A 种湘莲礼盒降价多少元/盒时，这两种湘莲礼盒平均每天的总利润最大，最大是多少元？【答案】（1）该店平均每天销售A 礼盒10盒，B 种礼盒为20盒；（2）当A 种湘莲礼盒降价9元/盒时，这两种湘莲礼盒平均每天的总利润最大，最大是1307元．【解析】【分析】（1）根据题意，可设平均每天销售A 礼盒x 盒，B 种礼盒为y 盒，列二元一次方程组即可解题（2）根据题意，可设A 种礼盒降价m 元/盒，则A 种礼盒的销售量为：（103m +）盒，再列出关系式即可．【详解】解：（1）根据题意，可设平均每天销售A 礼盒x 盒，B 种礼盒为y 盒，则有(12072)(8040)1280120802800x y x y -+-=⎧⎨+=⎩，解得1020x y =⎧⎨=⎩ 故该店平均每天销售A 礼盒10盒，B 种礼盒为20盒．（2）设A 种湘莲礼盒降价m 元/盒，利润为W 元，依题意总利润(12072)108003m W m ⎛⎫=--++ ⎪⎝⎭化简得221161280(9)130733W m m m =-++=--+∵103a =-< ∴当9m =时，取得最大值为1307，故当A 种湘莲礼盒降价9元/盒时，这两种湘莲礼盒平均每天的总利润最大，最大是1307元．【点睛】本题考查了二次函数的性质在实际生活中的应用．最大销售利润的问题常利函数的增减性来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．【达标训练】1．（2019·广西中考真题）如图，抛物线2y ax bx c =++的对称轴为直线1x =，则下列结论中，错误的是（）A ．0ac <B ．240b ac ->C ．20a b -=D ．0a b c -+=【答案】C【解析】【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【详解】A 、由抛物线的开口向下知0a <，与y 轴的交点在y 轴的正半轴上，可得0c >，因此0ac <，故本选项正确，不符合题意；B 、由抛物线与x 轴有两个交点，可得240b ac ->，故本选项正确，不符合题意；C 、由对称轴为12b x a=-=，得2a b =-，即20a b +=，故本选项错误，符合题意； D 、由对称轴为1x =及抛物线过(3,0)，可得抛物线与x 轴的另外一个交点是(1,0)-，所以0a b c -+=，故本选项正确，不符合题意．故选：C ．【点睛】本题考查了二次函数图象与系数的关系．会利用对称轴的范围求2a 与b 的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．2．（2019·内蒙古中考真题）二次函数2y ax ＝与一次函数y ax a +＝在同一坐标系中的大致图象可能是（）A ．B ．C ．D ．【答案】D【解析】【分析】由一次函数y=ax+a 可知，一次函数的图象与x 轴交于点（-1，0），即可排除A 、B ，然后根据二次函数的开口方向，与y 轴的交点；一次函数经过的象限，与y 轴的交点可得相关图象进行判断．【详解】解：由一次函数y ax a +＝可知，一次函数的图象与x 轴交于点10-（，），排除A B 、；当a 0＞时，二次函数开口向上，一次函数经过一、三、四象限，当a 0＜时，二次函数开口向下，一次函数经过二、三、四象限，排除C ；故选D ．【点睛】本题主要考查一次函数和二次函数的图象，解题的关键是熟练掌握二次函数的图象和一次函数的图象与系数之间的关系．3．（2019·浙江中考真题）二次函数2(1)3y x =-+图象的顶点坐标是（）A ．(1,3)B ．(1,3)-C ．(1,3)-D ．(1,3)--【答案】A【解析】【分析】根据二次函数顶点式即可得出顶点坐标.【详解】∵2(1)3y x =-+，∴二次函数图像顶点坐标为：(1,3).故答案为：A.【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a （x-h ）2+k 中，对称轴为x=h ，顶点坐标为（h ，k ）．4．（2019·黑龙江中考真题）将抛物线22y x =向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为（）.A ．22(2)3y x =++；B ．22(2)3y x =-+；C ．22(2)3y x =--；D ．22(2)3y x =+-.【答案】B【解析】【分析】根据抛物线图像的平移规律“左加右减，上加下减”即可确定平移后的抛物线解析式.【详解】解：将抛物线22y x =向上平移3个单位长度，再向右平移2个单位长度，得到的抛物线的解析式为()2223y x =-+，故选：B ．【点睛】本题考查了二次函数的平移规律，熟练掌握其平移规律是解题的关键.5．（2019·福建中考真题）若二次函数y =|a |x 2+bx+c 的图象经过A(m ,n )、B(0,y 1)、C(3－m ,n )、D(2, y 2)、E(2,y 3)，则y 1、y 2、y 3的大小关系是( ).A ．y 1< y 2< y 3B ．y 1 < y 3< y 2C ．y 3< y 2< y 1D ．y 2< y 3< y 1 【答案】D【解析】【分析】由点A （m ，n ）、C （3−m ，n ）的对称性，可求函数的对称轴为x ＝32，再由B （0，y 1）、D （2，y 2）、E （2，y 3）与对称轴的距离，即可判断y 2< y 3< y 1；【详解】解答：解：∵经过A （m ，n ）、C （3−m ，n ），∴二次函数的对称轴x ＝32， ∵B （0，y 1）、D （2，y 2）、E （2，y 3）与对称轴的距离B 最远，D 最近，∵|a|＞0，∴y 2< y 3< y 1；故选：D ．【点睛】本题考查二次函数的图象及性质；熟练掌握函数图象上点的特征是解题的关键．6．（2019·辽宁中考真题）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc >；②930a b c ++=；③248b ac a -<；④50a b c ++>．其中正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据图象可直接判断a 、c 的符号，再结合对称轴的位置可判断b 的符号，进而可判断①；抛物线的图象过点（3，0），代入抛物线的解析式可判断②；根据抛物线顶点的位置可知：顶点的纵坐标小于－2，整理后可判断③；根据图象可知顶点的横坐标大于1，整理后再结合③的结论即可判断④.【详解】解：①由图象可知：0a >，0c <，由于对称轴02b a->，∴0b <，∴0abc >，故①正确； ②∵抛物线过(3,0)，∴3x =时，930y a b c =++=，故②正确； ③顶点坐标为：24,24b ac b aa ⎛⎫-- ⎪⎝⎭.由图象可知：2424acb a -<-，∵0a >，∴248ac b a -<-，即248b ac a ->，故③错误； ④由图象可知：12b a->，0a >，∴20a b +<， ∵930a b c ++=，∴93c a b =--，∴5593422(2)0a b c a b a b a b a b ++=+--=--=-+>，故④正确；故选：C ．【点睛】本题考查了抛物线的图象与性质和抛物线的图象与其系数的关系，熟练掌握抛物线的图象与性质、灵活运用数形结合的思想方法是解题的关键.7．（2019·四川中考真题）二次函数2y ax bx c ++＝的部分图象如图所示，有以下结论：①30a b ﹣＝；②240b ac ﹣＞；③520ab c +﹣＞；④430b c +＞，其中错误结论的个数是（）A ．1B ．2C ．3D ．4 【答案】A【解析】【分析】 ①对称轴为32x =-，得3b a ＝； ②函数图象与x 轴有两个不同的交点，得240b ac ∆＝﹣＞；③当1x ＝-时，0a b c +﹣＞，当3x ＝-时，930a b c +﹣＞，得520a b c +﹣＞；④由对称性可知1x ＝时对应的y 值与4x ＝-时对应的y 值相等，当1x ＝时0433333330a b c b c b b c b a c a b c +++++++++＜，＝＝＝（）＜【详解】解：由图象可知00a c ＜，＞，对称轴为32x =-， 322b x a∴=-=-， 3,b a ∴=，①正确；∵函数图象与x 轴有两个不同的交点，240b ac ∴∆＝﹣＞，， ②正确；当1x ＝﹣时，0a b c +-＞，当3x ＝-时，930a b c +﹣＞，10420a b c ∴+﹣＞，520a b c ∴+﹣＞，③正确；由对称性可知1x ＝时对应的y 值与4x ＝-时对应的y 值相等，∴当1x ＝时0a b c ++＜，3b a Q ＝，433333330b c b b c b a c a b c ∴+++++++＝＝＝（）＜，430b c ∴+＜，④错误；故选：A ．【点睛】考查二次函数的图象及性质；熟练掌握从函数图象获取信息，将信息与函数解析式相结合解题是关键．8．（2019·广东中考真题）已知2(0)y ax bx c a =++≠的图象如图，则y ax b =+和c y x=的图象为（）A ．B ．C ．D ．【答案】C【解析】【分析】根据二次函数y=ax 2+bx+c （a≠0）的图象可以得到a ＜0，b ＞0，c ＜0，由此可以判定y=ax+b 经过一、二、四象限，双曲线c y x =在二、四象限．【详解】根据二次函数y=ax 2+bx+c （a≠0）的图象，可得a ＜0，b ＞0，c ＜0，∴y=ax+b 过一、二、四象限，双曲线c y x=在二、四象限，∴C 是正确的．故选C ．【点睛】此题考查一次函数，二次函数，反比例函数中系数及常数项与图象位置之间关系．9．（2019·重庆中考真题）抛物线2362y x x =-++的对称轴是（）A ．直线2x =B ．直线2x =-C ．直线1x =D ．直线1x =-【答案】C【解析】【分析】将抛物线的一般式配方成为顶点式，可确定顶点坐标及对称轴．【详解】解：∵223623(1)5y x x x =-++=--+，∴抛物线顶点坐标为(1,5)，对称轴为1x =．故选：C ．【点睛】本题考查了二次函数的性质．抛物线2()y a x h k =-+的顶点坐标为（h ，k ），对称轴为x ＝h ． 10．（2019·浙江中考真题）已知,a b 是非零实数，a b >，在同一平面直角坐标系中，二次函数21y ax bx =＋与一次函数2y ax b =＋的大致图象不可能是（）A ．B ．C ．D ．【答案】D【解析】【分析】采用赋值法，选取符合图形条件的未知数的值，再采用排除法即可确定答案.【详解】解答本题可采用赋值法. 取2,1a b ==，可知A 选项是可能的；取2,1a b ==-，可知B 选项是可能的；取2,1a b =-=-，可知C 选项是可能的，那么根据排除法，可知D 选项是不可能的.故选：D.【点睛】本题考查二次函数的图象、一次函数的图象，解题的关键是明确二次函数与一次函数图象的特点．11．（2019·四川中考真题）如图，二次函数2y ax bx c =++的图象经过点()1,0A ，()5,0B ，下列说法正确的是（）A ．0c <B ．240b ac -<C ．0a b c -+<D ．图象的对称轴是直线3x =【答案】D【解析】【分析】根据二次函数的图像与性质即可求解.【详解】由图象可知图象与y 轴交点位于y 轴正半轴，故c>0. A 选项错误；函数图象与x 轴有两个交点，所以24b ac -＞0，B 选项错误；观察图象可知x ＝－1时y=a －b ＋c ＞0，所以a －b ＋c ＞0，C 选项错误；根据图象与x 轴交点可知，对称轴是（1,0）.（5,0）两点的中垂线，152x +=， x ＝3即为函数对称轴，D 选项正确；【点睛】此题主要考查二次函数的图像与性质，解题的关键是熟知二次函数的图像.12．（2019·浙江中考真题）在平面直角坐标系中，已知a b ¹，设函数()()y x a x b =++的图像与x 轴有M 个交点，函数()()11y ax bx =++的图像与x 轴有N 个交点，则（）A ．1M N =-或1M N =+B ．1M N =-或2M N =+C ．M N =或1M N =+D ．M N =或1M N =-【答案】C【解析】【分析】先根据函数()()y x a x b =++的图像与x 轴有M 个交点解得2M =，再对a ，b 分情况讨论，求得答案.【详解】对于函数()()y x a x b =++，当0y =时，函数与x 轴两交点为（－a ，0）、（－b ，0），∵a b ¹，所以有2个交点，故2M =对于函数()()11y ax bx =++ ①0a b ≠≠，交点为11(,0),(,0)a b--，此时2N M N =⇒= ②0,0a b =≠，交点为1(,0)b-，此时11N M N =⇒=+ ③0,0b a =≠，交点为1(,0)a -，此时11N M N =⇒=+ 综上所述，M N =或1M N =+故选C.【点睛】本题考查二次函数与坐标轴的交点，解题的关键是分情况讨论a ，b.13．（2019·四川中考真题）已知二次函数(1)(1)37y x a x a a =---+-+(其中x 是自变量)的图象与x 轴没有公共点，且当1x <-时，y 随x 的增大而减小，则实数a 的取值范围是( )A ．2a <B ．1a >-C ．12a -<≤D ．12a -≤<【答案】D【分析】由抛物线与x 轴没有公共点，可得∆<0，求得2a <，求出抛物线的对称轴为直线x a =，抛物线开口向上，再结合已知当1x <-时，y 随x 的增大而减小，可得1a ≥-，据此即可求得答案.【详解】(1)(1)37y x a x a a =---+-+22236x ax a a =-+-+，Q 抛物线与x 轴没有公共点，22(2)4(36)0a a a ∴∆=---+<，解得2a <，Q 抛物线的对称轴为直线 22a x a -=-=，抛物线开口向上，而当1x <-时，y 随x 的增大而减小，1a ∴≥-，∴实数a 的取值范围是12a -≤<，故选D ．【点睛】本题考查了二次函数图象与x 轴交点问题，抛物线的对称轴，二次函数图象的增减性，熟练掌握和灵活运用相关知识是解题的关键.14．（2019·四川中考真题）已知抛物线21y x =-与y 轴交于点A ，与直线y kx =（k 为任意实数）相交于B ，C 两点，则下列结论不正确的是（）A ．存在实数k ，使得ABC ∆为等腰三角形B ．存在实数k ，使得ABC ∆的内角中有两角分别为30°和60°C ．任意实数k ，使得ABC ∆都为直角三角形D ．存在实数k ，使得ABC ∆为等边三角形【答案】D【解析】【分析】通过二次函数和正比例函数图象，等边三角形和直角三角形的判定可解答．【详解】解：A 、如图1，可以得ABC ∆C 为等腰三角形，正确；∆的内角中有两角分别为30°和60°，正确；B、如图3，30ACB︒∠=，60ABC︒∠=，可以得ABC∆为直角三角形，正确；C、如图2和3，90BAC︒∠=，可以得ABC∆为等边三角形，不正确；D、不存在实数k，使得ABC本题选择结论不正确的，故选：D．【点睛】本题考查了二次函数和正比例函数图象，等边三角形和直角三角形的判定，正确画图是关键．。

2024年河南省中考数学一轮知识点复习专题+二次函数的图象与性质+课件

2024河南中考数学一轮知识点复习专题二次函数的图象与性质
第一节实数
考点1 二次函数表达式的确定及图象的变换
1.[2023江苏徐州] 在平面直角坐标系中，将二次函数的图象向右平移2个单位长度，再向下平移1个单位长度，所得抛物线对应的函数表达式为( )
B
A. B. C. D.
16.[2023浙江台州] 抛物线与直线交于，两点.若，则直线一定经过( )
D
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
17. ［原创新题］若对于二次函数，当时，随的增大而增大，则的值可以是__________________________________.
于点．设的长为，四边形的面积为，与的函数图象是如图（2）所示的一段抛物线，其顶点的坐标为，则的长为_ ____.
30.[2023郑州二模] 如图,抛物线与轴, 轴分别交于 , 两点,点的坐标为 ,抛物线的顶点为 ,点关于抛物线对称轴（直线）的对称点为点 .
[答案] .
考点2 二次函数与方程、不等式的关系
6.[2023许昌二模] 若抛物线与轴没有交点,则的值可以是( )
D
A. B.0 C.4 D.8
7.[2022浙江绍兴] 已知抛物线的对称轴为直线，则关于的方程的根是( )
D
A. ， B. ， C. ， D. ，
（1）求该抛物线的函数表达式.
[答案] 将代入，得，抛物线的对称轴为直线，即， . 抛物线的函数表达式为 .
（2）当时,求函数值的取值范围.
[答案] 当时，；当时，；当时， . 当时，的取值范围为 .

河南省2024年数学中考热点备考重难专题：二次函数图象与性质综合题对称性、增减性、最值问题(课件)

2
22
②t<－ 1 或t>3 .
2
2
方法总结
求抛物线上点的纵坐标最值或取值范围的一般步骤：
第一步画草图，求出对称轴（直线x=t）；第二步结合草图，判断两端点x1，x2（取值范围为x1≤x≤x2）与对称轴（直线x=t）
的位置：位于对称轴的同侧，还是异侧.若位于同侧，则只根据增减性确定确定最值的位置（即两端点处）；若为异侧，则顶点处为其中的一个最值点，另一个最值，根据离对称轴的距离确定（或根据对称性转移到同侧，根据增减性确定）；第三步取最值处的x值代入函数解析式，确定最值或取值范围.
当x1=t时， y1取最小值
(2)①∵y＝(x－t)2－t， ∴抛物线的对称轴为直线x＝t. ∵1>0，∴抛物线开口向上． ∵t－1≤x1≤t＋2，∴当x＝t时，y1的最小值为－t. ∵y1的最小值是－2，∴t＝2. ∵|t－1－t|＝1，|t＋2－t|＝2， ∴当x＝t＋2时，y1最大＝(t＋2－t)2－t＝4－t＝4－2＝2，即y1的最大值为2；
两端点在对称轴同侧 x1≤x≤x2
两端点在对称轴异侧 x1≤x≤x2
a＜0
y1＞y2
yt最大，y2最小
最大值：离对称轴越近端最大值：顶点纵坐标
点纵坐标
最小值：离对称轴越远
最小值：离对称轴越远端端点纵坐标
点纵坐标
利用对称性将将两点转化到同侧，根据增减性比较大小
课堂练兵
练习在平面直角坐标系中，抛物线y＝ax2－4ax＋c(a＜0)与x轴交于A(1，0)，
x2 x2
x1＞0 x1 2t＞0
或
x2 x2
x1＜0 x1 2t＜0
(t>Ⅰt＋)当2，xx22∴t＜xx11＞－102①t＞.由0②②知时，，x2＋由x①1>知2t，，x∵2>t－x1，1≤∵x1≤t－t＋12≤，x1≤xt2＋＝21，－xt，2＝∴1－0≤tx，2＋∴x11≤－3，

2020年全国中考数学试题分类(8)——二次函数

2020年全国中考数学试题分类（8）——二次函数一．二次函数的性质（共2小题）1．（2020•黔西南州）如图，抛物线y ＝ax 2+bx +4交y 轴于点A ，交过点A 且平行于x 轴的直线于另一点B ，交x 轴于C ，D 两点（点C 在点D 右边），对称轴为直线x =52，连接AC ，AD ，BC ．若点B 关于直线AC 的对称点恰好落在线段OC 上，下列结论中错误的是（）A ．点B 坐标为（5，4）B ．AB ＝ADC ．a =−16D ．OC •OD ＝162．（2020•长春）如图，在平面直角坐标系中，点A 的坐标为（0，2），点B 的坐标为（4，2）．若抛物线y =−32（x ﹣h ）2+k （h 、k 为常数）与线段AB 交于C 、D 两点，且CD =12AB ，则k 的值为．二．二次函数图象与系数的关系（共16小题）3．（2020•济南）已知抛物线y ＝x 2+（2m ﹣6）x +m 2﹣3与y 轴交于点A ，与直线x ＝4交于点B ，当x ＞2时，y 值随x 值的增大而增大．记抛物线在线段AB 下方的部分为G （包含A 、B 两点），M 为G 上任意一点，设M 的纵坐标为t ，若t ≥﹣3，则m 的取值范围是（）A ．m ≥32B ．32≤m ≤3C ．m ≥3D ．1≤m ≤34．（2020•日照）如图，二次函数y ＝ax 2+bx +c （a ≠0）图象的对称轴为直线x ＝﹣1，下列结论：①abc ＜0；①3a ＜﹣c ；①若m 为任意实数，则有a ﹣bm ≤am 2+b ； ①若图象经过点（﹣3，﹣2），方程ax 2+bx +c +2＝0的两根为x 1，x 2（|x 1|＜|x 2|），则2x 1﹣x 2＝5．其中正确的结论的个数是（）A ．4个B ．3个C ．2个D ．1个5．（2020•葫芦岛）如图，二次函数y ＝ax 2+bx +c （a ≠0）的图象的对称轴是直线x ＝1，则以下四个结论中：①abc ＞0，①2a +b ＝0，①4a +b 2＜4ac ，①3a +c ＜0．正确的个数是（）A ．1B ．2C ．3D ．46．（2020•眉山）已知二次函数y ＝x 2﹣2ax +a 2﹣2a ﹣4（a 为常数）的图象与x 轴有交点，且当x ＞3时，y 随x 的增大而增大，则a 的取值范围是（）A ．a ≥﹣2B ．a ＜3C ．﹣2≤a ＜3D ．﹣2≤a ≤37．（2020•鸡西）如图是二次函数y ＝ax 2+bx +c （a ≠0）图象的一部分，对称轴为x =12，且经过点（2，0）．下列说法：①abc ＜0；①﹣2b +c ＝0；①4a +2b +c ＜0；①若（−52，y 1），（52，y 2）是抛物线上的两点，则y 1＜y 2；①14b ＞m （am +b ）（其中m ≠12）．其中说法正确的是（）A ．①①①①B ．①①①C ．①①①D ．①①①8．（2020•丹东）如图，二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A ，B 两点，与y 轴交于点C ，点A 坐标为（﹣1，0），点C 在（0，2）与（0，3）之间（不包括这两点），抛物线的顶点为D ，对称轴为直线x ＝2．有以下结论：①abc ＞0；①若点M （−12，y 1），点N （72，y 2）是函数图象上的两点，则y 1＜y 2； ①−35＜a ＜−25； ①△ADB 可以是等腰直角三角形．其中正确的有（）A ．1个B ．2个C ．3个D ．4个9．（2020•东营）如图，已知抛物线y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A 、B 两点，其对称轴与x 轴交于点C ，其中A 、C 两点的横坐标分别为﹣1和1，下列说法错误的是（）A．abc＜0B．4a+c＝0C．16a+4b+c＜0D．当x＞2时，y随x的增大而减小10．（2020•威海）如图，抛物线y＝ax2+bx+c（a≠0）交x轴于点A，B，交y轴于点C．若点A坐标为（﹣4，0），对称轴为直线x＝﹣1，则下列结论错误的是（）A．二次函数的最大值为a﹣b+cB．a+b+c＞0C．b2﹣4ac＞0D．2a+b＝011．（2020•湘西州）已知二次函数y＝ax2+bx+c图象的对称轴为x＝1，其图象如图所示，现有下列结论：①abc＞0，①b﹣2a＜0，①a﹣b+c＞0，①a+b＞n（an+b），（n≠1），①2c＜3b．正确的是（）A．①①B．①①C．①①D．①①12．（2020•牡丹江）如图，抛物线y＝ax2+bx+c与x轴正半轴交于A，B两点，与y轴负半轴交于点C．若点B（4，0），则下列结论中，正确的个数是（）①abc＞0；①4a+b＞0；①M（x1，y1）与N（x2，y2）是抛物线上两点，若0＜x1＜x2，则y1＞y2；①若抛物线的对称轴是直线x＝3，m为任意实数，则a（m﹣3）（m+3）≤b（3﹣m）；①若AB≥3，则4b+3c＞0．A．5B．4C．3D．213．（2020•凉山州）二次函数y＝ax2+bx+c的图象如图所示，有如下结论：①abc＞0；①2a+b＝0；①3b﹣2c＜0；①am2+bm≥a+b（m为实数）．其中正确结论的个数是（）A．1个B．2个C．3个D．4个14．（2020•泸州）已知二次函数y＝x2﹣2bx+2b2﹣4c（其中x是自变量）的图象经过不同两点A（1﹣b，m），B（2b+c，m），且该二次函数的图象与x轴有公共点，则b+c的值为（）A．﹣1B．2C．3D．415．（2020•齐齐哈尔）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（4，0），其对称轴为直线x＝1，结合图象给出下列结论：①ac＜0；①4a﹣2b+c＞0；①当x＞2时，y随x的增大而增大；①关于x的一元二次方程ax2+bx+c＝0有两个不相等的实数根．其中正确的结论有（）A．1个B．2个C．3个D．4个16．（2020•德州）二次函数y＝ax2+bx+c的部分图象如图所示，则下列选项错误的是（）A．若（﹣2，y1），（5，y2）是图象上的两点，则y1＞y2B．3a+c＝0C．方程ax2+bx+c＝﹣2有两个不相等的实数根D．当x≥0时，y随x的增大而减小17．（2020•甘孜州）如图，二次函数y＝a（x+1）2+k的图象与x轴交于A（﹣3，0），B两点，下列说法错误的是（）A．a＜0B．图象的对称轴为直线x＝﹣1C．点B的坐标为（1，0）D．当x＜0时，y随x的增大而增大18．（2020•宁波）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线x＝﹣1．则下列选项中正确的是（）A．abc＜0B．4ac﹣b2＞0C．c﹣a＞0D．当x＝﹣n2﹣2（n为实数）时，y≥c三．二次函数图象上点的坐标特征（共1小题）19．（2020•河北）如图，现要在抛物线y＝x（4﹣x）上找点P（a，b），针对b的不同取值，所找点P的个数，三人的说法如下，甲：若b＝5，则点P的个数为0；乙：若b＝4，则点P的个数为1；丙：若b＝3，则点P的个数为1．下列判断正确的是（）A ．乙错，丙对B ．甲和乙都错C ．乙对，丙错D ．甲错，丙对四．二次函数图象与几何变换（共1小题）20．（2020•陕西）在平面直角坐标系中，将抛物线y ＝x 2﹣（m ﹣1）x +m （m ＞1）沿y 轴向下平移3个单位．则平移后得到的抛物线的顶点一定在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限五．待定系数法求二次函数解析式（共1小题）21．（2020•江西）已知抛物线y ＝ax 2+bx +c （a ，b ，c 是常数，a ≠0）的自变量x 与函数值y 的部分对应值如下表：x … ﹣2 ﹣1 0 1 2 …y … m 0 ﹣3 n ﹣3 …（1）根据以上信息，可知抛物线开口向，对称轴为；（2）求抛物线的表达式及m ，n 的值；（3）请在图1中画出所求的抛物线．设点P 为抛物线上的动点，OP 的中点为P '，描出相应的点P '，再把相应的点P '用平滑的曲线连接起来，猜想该曲线是哪种曲线？（4）设直线y ＝m （m ＞﹣2）与抛物线及（3）中的点P '所在曲线都有两个交点，交点从左到右依次为A 1，A 2，A 3，A 4，请根据图象直接写出线段A 1A 2，A 3A 4之间的数量关系．六．抛物线与x 轴的交点（共5小题）22．（2020•大连）抛物线y ＝ax 2+bx +c （a ＜0）与x 轴的一个交点坐标为（﹣1，0），对称轴是直线x ＝1，其部分图象如图所示，则此抛物线与x 轴的另一个交点坐标是（） A ．（72，0） B ．（3，0）C ．（52，0）D ．（2，0）23．（2020•呼和浩特）关于二次函数y =14x 2﹣6x +a +27，下列说法错误的是（）A．若将图象向上平移10个单位，再向左平移2个单位后过点（4，5），则a＝﹣5B．当x＝12时，y有最小值a﹣9C．x＝2对应的函数值比最小值大7D．当a＜0时，图象与x轴有两个不同的交点24．（2020•娄底）二次函数y＝（x﹣a）（x﹣b）﹣2（a＜b）与x轴的两个交点的横坐标分别为m和n，且m＜n，下列结论正确的是（）A．m＜a＜n＜b B．a＜m＜b＜n C．m＜a＜b＜n D．a＜m＜n＜b25．（2020•安顺）已知二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，关于x的方程ax2+bx+c+m ＝0（m＞0）有两个根，其中一个根是3．则关于x的方程ax2+bx+c+n＝0（0＜n＜m）有两个整数根，这两个整数根是（）A．﹣2或0B．﹣4或2C．﹣5或3D．﹣6或426．（2020•杭州）在平面直角坐标系中，已知函数y1＝x2+ax+1，y2＝x2+bx+2，y3＝x2+cx+4，其中a，b，c 是正实数，且满足b2＝ac．设函数y1，y2，y3的图象与x轴的交点个数分别为M1，M2，M3，（）A．若M1＝2，M2＝2，则M3＝0B．若M1＝1，M2＝0，则M3＝0C．若M1＝0，M2＝2，则M3＝0D．若M1＝0，M2＝0，则M3＝0七．二次函数的应用（共15小题）27．（2020•长沙）“闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”．在特定条件下，“可食用率”P与加工煎炸时间t（单位：分钟）近似满足的函数关系为：P＝at2+bt+c（a≠0，a，b，c 是常数），如图记录了三次实验的数据．根据上述函数关系和实验数据，可以得到加工煎炸臭豆腐的最佳时间为（）A．3.50分钟B．4.05分钟C．3.75分钟D．4.25分钟28．（2020•巴中）现有一“祥云”零件剖面图，如图所示，它由一个半圆和左右两支抛物线的一部分组成，且关于y轴对称．其中半圆交y轴于点E，直径AB＝2，OE＝2；两支抛物线的顶点分别为点A、点B．与x轴分别交于点C、点D；直线BC的解析式为：y=yy+34．则零件中BD这段曲线的解析式为．29．（2020•日照）如图，某小区有一块靠墙（墙的长度不限）的矩形空地ABCD，为美化环境，用总长为100m的篱笆围成四块矩形花圃（靠墙一侧不用篱笆，篱笆的厚度不计）．（1）若四块矩形花圃的面积相等，求证：AE＝3BE；（2）在（1）的条件下，设BC的长度为xm，矩形区域ABCD的面积为ym2，求y与x之间的函数关系式，并写出自变量x的取值范围．30．（2020•盘锦）某服装厂生产A品种服装，每件成本为71元，零售商到此服装厂一次性批发A品牌服装x件时，批发单价为y元，y与x之间满足如图所示的函数关系，其中批发件数x为10的正整数倍．（1）当100≤x≤300时，y与x的函数关系式为．（2）某零售商到此服装厂一次性批发A品牌服装200件，需要支付多少元？（3）零售商到此服装厂一次性批发A品牌服装x（100≤x≤400）件，服装厂的利润为w元，问：x为何值时，w最大？最大值是多少？31．（2020•朝阳）某公司销售一种商品，成本为每件30元，经过市场调查发现，该商品的日销售量y（件）与销售单价x（元）是一次函数关系，其销售单价、日销售量的三组对应数值如下表：销售单价x（元）406080日销售量y（件）806040（1）直接写出y与x的关系式；（2）求公司销售该商品获得的最大日利润；（3）销售一段时间以后，由于某种原因，该商品每件成本增加了10元，若物价部门规定该商品销售单价不能超过a元，在日销售量y（件）与销售单价x（元）保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求a的值．32．（2020•呼伦贝尔）某商店销售一种销售成本为每件40元的玩具，若按每件50元销售，一个月可售出500件，销售价每涨1元，月销量就减少10件．设销售价为每件x元（x≥50），月销量为y件，月销售利润为w元．（1）写出y与x的函数解析式和w与x的函数解析式；（2）商店要在月销售成本不超过10000的情况下，使月销售利润达到8000元，销售价应定为每件多少元？（3）当销售价定为每件多少元时会获得最大利润？求出最大利润．33．（2020•鄂尔多斯）某水果店将标价为10元/斤的某种水果．经过两次降价后，价格为8.1元/斤，并且两次降价的百分率相同．（1）求该水果每次降价的百分率；（2）从第二次降价的第1天算起，第x天（x为整数）的销量及储藏和损耗费用的相关信息如下表所示：时间（天）x销量（斤）120﹣x储藏和损耗费用（元）3x2﹣64x+400已知该水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜10）之间的函数解析式，并求出第几天时销售利润最大，最大利润是多少？34．（2020•随州）2020年新冠肺炎疫情期间，部分药店趁机将口罩涨价，经调查发现某药店某月（按30天计）前5天的某型号口罩销售价格p（元/只）和销量q（只）与第x天的关系如下表：第x天12345销售价格p （元/只）23 4 5 6 销量q （只） 7075 80 85 90 物价部门发现这种乱象后，统一规定各药店该型号口罩的销售价格不得高于1元/只，该药店从第6天起将该型号口罩的价格调整为1元/只．据统计，该药店从第6天起销量q （只）与第x 天的关系为q ＝﹣2x 2+80x ﹣200 （6≤x ≤30，且x 为整数），已知该型号口罩的进货价格为0.5元/只．（1）直接写出该药店该月前5天的销售价格p 与x 和销量q 与x 之间的函数关系式；（2）求该药店该月销售该型号口罩获得的利润W （元）与x 的函数关系式，并判断第几天的利润最大；（3）物价部门为了进一步加强市场整顿，对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m 倍的罚款，若罚款金额不低于2000元，则m 的取值范围为．35．（2020•丹东）某服装批发市场销售一种衬衫，衬衫每件进货价为50元．规定每件售价不低于进货价，经市场调查，每月的销售量y （件）与每件的售价x （元）满足一次函数关系，部分数据如下表：售价x （元/件）60 65 70 销售量y （件）1400 1300 1200 （1）求出y 与x 之间的函数表达式；（不需要求自变量x 的取值范围）（2）该批发市场每月想从这种衬衫销售中获利24000元，又想尽量给客户实惠，该如何给这种衬衫定价？（3）物价部门规定，该衬衫的每件利润不允许高于进货价的30%，设这种衬衫每月的总利润为w （元），那么售价定为多少元可获得最大利润？最大利润是多少？36．（2020•荆门）2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年，荆门市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第x 天（x 为正整数）的销售价格p （元/千克）关于x 的函数关系式为p ={25y +4(0＜y ≤20)−15y +12(20＜y ≤30)，销售量y （千克）与x 之间的关系如图所示．（1）求y 与x 之间的函数关系式，并写出x 的取值范围；（2）当月第几天，该农产品的销售额最大，最大销售额是多少？（销售额＝销售量×销售价格）37．（2020•潍坊）因疫情防控需要，消毒用品需求量增加．某药店新进一批桶装消毒液，每桶进价50元，每天销售量y （桶）与销售单价x （元）之间满足一次函数关系，其图象如图所示．（1）求y 与x 之间的函数表达式；（2）每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利润＝销售价﹣进价）38．（2020•营口）某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x （元），每天的销售量为y （瓶）．（1）求每天的销售量y（瓶）与销售单价x（元）之间的函数关系式；（2）当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？39．（2020•武汉）某公司分别在A，B两城生产同种产品，共100件．A城生产产品的总成本y（万元）与产品数量x（件）之间具有函数关系y＝ax2+bx．当x＝10时，y＝400；当x＝20时，y＝1000．B城生产产品的每件成本为70万元．（1）求a，b的值；（2）当A，B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？（3）从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D 两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（2）的条件下，直接写出A，B两城总运费的和的最小值（用含有m的式子表示）．40．（2020•青岛）某公司生产A型活动板房成本是每个425元．图①表示A型活动板房的一面墙，它由长方形和抛物线构成，长方形的长AD＝4m，宽AB＝3m，抛物线的最高点E到BC的距离为4m．（1）按如图①所示的直角坐标系，抛物线可以用y＝kx2+m（k≠0）表示．求该抛物线的函数表达式；（2）现将A型活动板房改造为B型活动板房．如图①，在抛物线与AD之间的区域内加装一扇长方形窗户FGMN，点G，M在AD上，点N，F在抛物线上，窗户的成本为50元/m2．已知GM＝2m，求每个B 型活动板房的成本是多少？（每个B型活动板房的成本＝每个A型活动板房的成本+一扇窗户FGMN的成本）（3）根据市场调查，以单价650元销售（2）中的B型活动板房，每月能售出100个，而单价每降低10元，每月能多售出20个．公司每月最多能生产160个B型活动板房．不考虑其他因素，公司将销售单价n（元）定为多少时，每月销售B型活动板房所获利润w（元）最大？最大利润是多少？41．（2020•鄂州）一大型商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元/件）（x为正整数）之间满足一次函数关系，下表记录的是某三周的有关数据：x（元/件）456y（件）1000095009000（1）求y与x的函数关系式（不求自变量的取值范围）；（2）在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？（3）抗疫期间，该商场这种商品售价不大于15元/件时，每销售一件商品便向某慈善机构捐赠m元（1≤m≤6），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．八．二次函数综合题（共9小题）42．（2020•柳州）如图①，在平面直角坐标系xOy中，抛物线y＝x2﹣4x+a（a＜0）与y轴交于点A，与x轴交于E、F两点（点E在点F的右侧），顶点为M．直线y=23y−y与x轴、y轴分别交于B、C两点，与直线AM交于点D．（1）求抛物线的对称轴；（2）在y轴右侧的抛物线上存在点P，使得以P、A、C、D为顶点的四边形是平行四边形，求a的值；（3）如图①，过抛物线顶点M作MN⊥x轴于N，连接ME，点Q为抛物线上任意一点，过点Q作QG ⊥x轴于G，连接QE．当a＝﹣5时，是否存在点Q，使得以Q、E、G为顶点的三角形与△MNE相似（不含全等）？若存在，求出点Q 的坐标；若不存在，请说明理由．43．（2020•济南）如图1，抛物线y ＝﹣x 2+bx +c 过点A （﹣1，0），点B （3，0），与y 轴交于点C ．在x 轴上有一动点E （m ，0）（0＜m ＜3），过点E 作直线l ⊥x 轴，交抛物线于点M ．（1）求抛物线的解析式及C 点坐标；（2）当m ＝1时，D 是直线l 上的点且在第一象限内，若△ACD 是以∠DCA 为底角的等腰三角形，求点D 的坐标；（3）如图2，连接BM 并延长交y 轴于点N ，连接AM ，OM ，设△AEM 的面积为S 1，△MON 的面积为S 2，若S 1＝2S 2，求m 的值．44．（2020•大连）在平面直角坐标系xOy 中，函数F 1和F 2的图象关于y 轴对称，它们与直线x ＝t （t ＞0）分别相交于点P ，Q ．（1）如图，函数F 1为y ＝x +1，当t ＝2时，PQ 的长为；（2）函数F 1为y =3y ，当PQ ＝6时，t 的值为；（3）函数F 1为y ＝ax 2+bx +c （a ≠0），①当t =√y y 时，求△OPQ 的面积；①若c ＞0，函数F 1和F 2的图象与x 轴正半轴分别交于点A （5，0），B （1，0），当c ≤x ≤c +1时，设函数F 1的最大值和函数F 2的最小值的差为h ，求h 关于c 的函数解析式，并直接写出自变量c 的取值范围．45．（2020•呼伦贝尔）如图，抛物线y =−12x 2+bx +c 与x 轴交于点A （﹣1，0）和点B （4，0），与y 轴交于点C ，连接BC ，点P 是线段BC 上的动点（与点B ，C 不重合），连接AP 并延长AP 交抛物线于点Q ，连接CQ ，BQ ，设点Q 的横坐标为m ．（1）求抛物线的解析式和点C 的坐标；（2）当△BCQ 的面积等于2时，求m 的值；（3）在点P 运动过程中，yy yy 是否存在最大值？若存在，求出最大值；若不存在，请说明理由．46．（2020•永州）在平面直角坐标系xOy 中，等腰直角△ABC 的直角顶点C 在y 轴上，另两个顶点A ，B在x 轴上，且AB ＝4，抛物线经过A ，B ，C 三点，如图1所示．（1）求抛物线所表示的二次函数表达式．（2）过原点任作直线l 交抛物线于M ，N 两点，如图2所示．①求△CMN 面积的最小值．①已知Q （1，−32）是抛物线上一定点，问抛物线上是否存在点P ，使得点P 与点Q 关于直线l 对称，若存在，求出点P 的坐标及直线l 的一次函数表达式；若不存在，请说明理由． 47．（2020•云南）抛物线y ＝x 2+bx +c 与x 轴交于A 、B 两点，与y 轴交于点C ，点A 的坐标为（﹣1，0），点C 的坐标为（0，﹣3）．点P 为抛物线y ＝x 2+bx +c 上的一个动点．过点P 作PD ⊥x 轴于点D ，交直线BC 于点E ．（1）求b 、c 的值；（2）设点F 在抛物线y ＝x 2+bx +c 的对称轴上，当△ACF 的周长最小时，直接写出点F 的坐标；（3）在第一象限，是否存在点P ，使点P 到直线BC 的距离是点D 到直线BC 的距离的5倍？若存在，求出点P 所有的坐标；若不存在，请说明理由．48．（2020•青海）如图1（注：与图2完全相同）所示，抛物线y =−12y 2+bx +c 经过B 、D 两点，与x 轴的另一个交点为A ，与y 轴相交于点C ．（1）求抛物线的解析式．（2）设抛物线的顶点为M ，求四边形ABMC 的面积．（请在图1中探索）（3）设点Q 在y 轴上，点P 在抛物线上．要使以点A 、B 、P 、Q 为顶点的四边形是平行四边形，求所有满足条件的点P 的坐标．（请在图2中探索） 49．（2020•通辽）如图，在平面直角坐标系中，抛物线y ＝﹣x 2+bx +c 与x 轴交于点A ，B ，与y 轴交于点C ．且直线y ＝x ﹣6过点B ，与y 轴交于点D ，点C 与点D 关于x 轴对称，点P 是线段OB 上一动点，过点P 作x 轴的垂线交抛物线于点M ，交直线BD 于点N ．（1）求抛物线的函数解析式；（2）当△MDB 的面积最大时，求点P 的坐标；（3）在（2）的条件下，在y 轴上是否存在点Q ，使得以Q ，M ，N 三点为顶点的三角形是直角三角形？若存在，直接写出点Q 的坐标；若不存在，说明理由．50．（2020•咸宁）如图，在平面直角坐标系中，直线y =−12x +2与x 轴交于点A ，与y 轴交于点B ，抛物线y =−23x 2+bx +c 过点B 且与直线相交于另一点C （52，34）．（1）求抛物线的解析式；（2）点P 是抛物线上的一动点，当∠P AO ＝∠BAO 时，求点P 的坐标；（3）点N （n ，0）（0＜n ＜52）在x 轴的正半轴上，点M （0，m ）是y 轴正半轴上的一动点，且满足∠MNC ＝90°．①求m 与n 之间的函数关系式；①当m 在什么范围时，符合条件的N 点的个数有2个？2020年全国中考数学试题分类（8）——二次函数参考答案与试题解析一．二次函数的性质（共2小题）1．【解答】解：∵抛物线y＝ax2+bx+4交y轴于点A，∴A（0，4），∵对称轴为直线x=52，AB∥x轴，∴B（5，4）．故A无误；如图，过点B作BE⊥x轴于点E，则BE＝4，AB＝5，∵AB∥x轴，∴∠BAC＝∠ACO，∵点B关于直线AC的对称点恰好落在线段OC上，∴∠ACO＝∠ACB，∴∠BAC＝∠ACB，∴BC＝AB＝5，∴在Rt△BCE中，由勾股定理得：EC＝3，∴C（8，0），∵对称轴为直线x=5 2，∴D（﹣3，0）∵在Rt△ADO中，OA＝4，OD＝3，∴AD＝5，∴AB＝AD，故B无误；设y＝ax2+bx+4＝a（x+3）（x﹣8），将A（0，4）代入得：4＝a（0+3）（0﹣8），∴a=−1 6，故C无误；∵OC＝8，OD＝3，∴OC•OD＝24，故D错误．综上，错误的只有D．故选：D．2．【解答】解：∵点A的坐标为（0，2），点B的坐标为（4，2），∴AB＝4，∵抛物线y=−32（x﹣h）2+k（h、k为常数）与线段AB交于C、D两点，且CD=12AB＝2，∴设点C的坐标为（c，2），则点D的坐标为（c+2，2），h=2y+22=c+1，∴2=−32[c﹣（c+1）]2+k，解得，k=7 2．二．二次函数图象与系数的关系（共16小题）3．【解答】解：当对称轴在y 轴的右侧时，{ 2y −6＜0−2y −62≤24(y 2−3)−(2y −6)24≥−3，解得32≤m ＜3，当对称轴是y 轴时，m ＝3，符合题意，当对称轴在y 轴的左侧时，2m ﹣6＞0，解得m ＞3，综上所述，满足条件的m 的值为m ≥32．故选：A ．4．【解答】解：由图象可知：a ＜0，c ＞0，−y 2y =−1， ∴b ＝2a ＜0，∴abc ＞0，故①abc ＜0错误；当x ＝1时，y ＝a +b +c ＝a +2a +c ＝3a +c ＜0，∴3a ＜﹣c ，故①3a ＜﹣c 正确；∵x ＝﹣1时，y 有最大值，∴a ﹣b +c ≥am 2+bm +c （m 为任意实数），即a ﹣b ≥am 2+bm ，即a ﹣bm ≥am 2+b ，故①错误；∵二次函数y ＝ax 2+bx +c （a ≠0）图象经过点（﹣3，﹣2），方程ax 2+bx +c +2＝0的两根为x 1，x 2（|x 1|＜|x 2|），∴二次函数y ＝ax 2+bx +c 与直线y ＝﹣2的一个交点为（﹣3，﹣2），∵抛物线的对称轴为直线x ＝﹣1，∴二次函数y ＝ax 2+bx +c 与直线y ＝﹣2的另一个交点为（1，﹣2），即x 1＝1，x 2＝﹣3，∴2x 1﹣x 2＝2﹣（﹣3）＝5，故①正确．所以正确的是①①；故选：C ．5．【解答】解：①根据抛物线开口向下可知：a ＜0，因为对称轴在y 轴右侧，所以b ＞0，因为抛物线与y 轴正半轴相交，所以c ＞0，所以abc ＜0，所以①错误；①因为抛物线对称轴是直线x ＝1，即−y 2y=1，所以b ＝﹣2a ，所以b +2a ＝0，所以①正确；①因为b ＝﹣2a ，由4a +b 2＜4ac ，得4a +4a 2＜4ac ，∵a ＜0，∴c ＜1+a ，根据抛物线与y 轴的交点，c ＞1，所以①错误；①当x ＝﹣1时，y ＜0，即a ﹣b +c ＜0，因为b ＝﹣2a ，所以3a +c ＜0，所以①正确．所以正确的是①①2个．故选：B ．6．【解答】解：∵二次函数y ＝x 2﹣2ax +a 2﹣2a ﹣4（a 为常数）的图象与x 轴有交点，∴△＝（﹣2a ）2﹣4×1×（a 2﹣2a ﹣4）≥0解得：a ≥﹣2；∵抛物线的对称轴为直线x =−−2y 2=a ，抛物线开口向上，且当x ＞3时，y 随x 的增大而增大， ∴a ≤3，∴实数a 的取值范围是﹣2≤a ≤3．故选：D ．7．【解答】解：①∵抛物线开口向下，∴a ＜0，∵抛物线对称轴为x =−y 2y =12，∴b ＝﹣a ＞0， ∵抛物线与y 轴的交点在x 轴上方，∴c ＞0，∴abc ＜0，所以①正确；①∵对称轴为x =12，且经过点（2，0），∴抛物线与x 轴的另一个交点为（﹣1，0），∴y y =−1×2＝﹣2，∴c ＝﹣2a ，∴﹣2b +c ＝2a ﹣2a ＝0所以①正确；①∵抛物线经过（2，0），∴当x ＝2时，y ＝0，∴4a +2b +c ＝0，所以①错误；①∵点（−52，y 1）离对称轴要比点（52，y 2）离对称轴远，∴y 1＜y 2，所以①正确；①∵抛物线的对称轴x =12，∴当x =12时，y 有最大值，∴14a +12b +c ＞am 2+bm +c （其中m ≠12）．∵a ＝﹣b ，∴14b ＞m （am +b ）（其中m ≠12），所以①正确．所以其中说法正确的是①①①①．故选：A ．8．【解答】解：∵二次函数y ＝ax 2+bx +c （a ≠0）的对称轴为：x =−y 2y ，∴−y 2y =2，∴b ＝﹣4a ，∵点A 坐标为（﹣1，0），点C 在（0，2）与（0，3）之间，且都在抛物线上，∴a ﹣b +c ＝0，2＜c ＜3，由二次函数图象可知，a ＜0，∴b ＞0，又∵c ＞0，∴abc ＜0，故①不正确；∵点N （72，y 2）关于对称轴x ＝2的对称点为（12，y 2），12＞−12，y 随x 的增大而增大，∴y 1＜y 2，故①正确；∵{y =−4yy −y +y =02＜y ＜3，解得：−35＜a ＜−25，故①正确；∵抛物线的顶点为D ，对称轴为直线x ＝2，∴点A 与点B 关于直线x ＝2对称，点D 在直线x ＝2上，∴AB ＝6，DA ＝DB ，∴△ADB 是等腰三角形，如果△ADB 是等腰直角三角形，则点D 到AB 的距离等于12AB ＝3，即D （2，3），则{y −y +y =0y =−4y 3=4y +2y +y ，解得：{ y =−13y =43y =53， ∴二次函数解析式为：y =−13x 2+43x +53，当x ＝0时，y =53，与点C 在（0，2）与（0，3）之间（不包括这两点）矛盾，∴△ADB 不可能是等腰直角三角形，故①不正确；∴正确的有2个，故选：B ． 9．【解答】解：抛物线开口向下，因此a ＜0，对称轴为x ＝1，即−y 2y =1，也就是2a +b ＝0，b ＞0，抛物线与y 轴交于正半轴，于是c ＞0，∴abc ＜0，因此选项A 不符合题意；由A （﹣1，0）、C （1，0）对称轴为x ＝1，可得抛物线与x 轴的另一个交点B （3，0），∴a ﹣b +c ＝0，∴a +2a +c ＝0，即3a +c ＝0，因此选项B 符合题意；当x ＝4时，y ＝16a +4b +c ＜0，因此选项C 不符合题意；当x ＞1时，y 随x 的增大而减小，因此选项D 不符合题意；故选：B ．10．【解答】解：当x ＝﹣1时，y ＝a ﹣b +c 的值最大，选项A 不符合题意；抛物线与x 轴的另一个交点为（2，0），当x ＝1时，y ＝a +b +c ＞0，因此选项B 不符合题意；抛物线与x 轴有两个不同交点，因此b 2﹣4ac ＞0，故选项C 不符合题意；抛物线y ＝ax 2+bx +c 过点A （﹣4，0），对称轴为直线x ＝﹣1，因此有：x ＝﹣1=−y 2y ，即2a ﹣b ＝0，因此选项D 符合题意；故选：D ．11．【解答】解：①由图象可知：a ＜0，b ＞0，c ＞0，abc ＜0，故①错误；①由于a ＜0，所以﹣2a ＞0．又b ＞0，所以b ﹣2a ＞0，故①错误；①当x ＝﹣1时，y ＝a ﹣b +c ＜0，故①错误；①当x ＝1时，y 的值最大．此时，y ＝a +b +c ，而当x ＝n 时，y ＝an 2+bn +c ，所以a +b +c ＞an 2+bn +c ，故a +b ＞an 2+bn ，即a +b ＞n （an +b ），故①正确；①当x ＝3时函数值小于0，y ＝9a +3b +c ＜0，且该抛物线对称轴是直线x =−y 2y =1，即a =−y 2，代入得9（−y 2）+3b +c ＜0，得2c ＜3b ，故①正确；故①①正确．故选：D ．12．【解答】解：如图，抛物线开口向下，与y 轴交于负半轴，对称轴在y 轴右侧，∴a ＜0，c ＜0，−y 2y ＞0，∴b ＞0， ∴abc ＞0，故①正确；如图，∵抛物线过点B （4，0），点A 在x 轴正半轴，∴对称轴在直线x ＝2右侧，即−y 2y ＞2， ∴2+y 2y =4y +y 2y ＜0，又a ＜0，∴4a +b ＞0，故①正确； ∵M （x 1，y 1）与N （x 2，y 2）是抛物线上两点，0＜x 1＜x 2，可得：抛物线y ＝ax 2+bx +c 在0＜y ＜−y 2y上，y 随x 的增大而增大，在y ＞−y 2y 上，y 随x 的增大而减小，∴y 1＞y 2不一定成立，故①错误；若抛物线对称轴为直线x ＝3，则−y 2y =3，即b ＝﹣6a ，则a （m ﹣3）（m +3）﹣b （3﹣m ）＝a （m ﹣3）2≤0，∴a （m ﹣3）（m +3）≤b （3﹣m ），故①正确；∵AB ≥3，则点A 的横坐标大于0或小于等于1，当x ＝1时，代入，y ＝a +b +c ≥0，当x ＝4时，16a +4b +c ＝0，∴a =4y +y −16，则4y +y−16+y +y ≥0，整理得：4b +5c ≥0，则4b +3c ≥﹣2c ，又c ＜0，﹣2c ＞0，∴4b +3c ＞0，故①正确，故正确的有4个．故选：B ．13．【解答】解：①∵对称轴在y 轴右侧，∴a 、b 异号，∴ab ＜0，∵c ＜0，∴abc ＞0，故①正确；①∵对称轴x=−y2y=1，∴2a+b＝0；故①正确；①∵2a+b＝0，∴a=−12 b，∵当x＝﹣1时，y＝a﹣b+c＞0，∴−12b﹣b+c＞0，∴3b﹣2c＜0，故①正确；①根据图象知，当x＝1时，y有最小值；当m为实数时，有am2+bm+c≥a+b+c，所以am2+bm≥a+b（m为实数）．故①正确．本题正确的结论有：①①①①，4个；故选：D．14．【解答】解：由二次函数y＝x2﹣2bx+2b2﹣4c的图象与x轴有公共点，∴（﹣2b）2﹣4×1×（2b2﹣4c）≥0，即b2﹣4c≤0 ①，由抛物线的对称轴x=−−2y2=b，抛物线经过不同两点A（1﹣b，m），B（2b+c，m），b=1−y+2y+y2，即，c＝b﹣1 ①，①代入①得，b2﹣4（b﹣1）≤0，即（b﹣2）2≤0，因此b＝2，c＝b﹣1＝2﹣1＝1，∴b+c＝2+1＝3，故选：C．15．【解答】解：抛物线开口向上，因此a＞0，与y轴交于负半轴，因此c＜0，故ac＜0，所以①正确；抛物线对称轴为x＝1，与x轴的一个交点为（4，0），则另一个交点为（﹣2，0），于是有4a﹣2b+c＝0，所以①不正确；x＞1时，y随x的增大而增大，所以①正确；抛物线与x轴有两个不同交点，因此关于x的一元二次方程ax2+bx+c＝0有两个不相等的实数根，所以①正确；综上所述，正确的结论有：①①①，故选：C．16．【解答】解：∵抛物线的对称轴为直线x＝1，a＜0，∴点（﹣1，0）关于直线x＝1的对称点为（3，0），则抛物线与x轴的另一个交点坐标为（3，0），点（﹣2，y1）与（4，y1）是对称点，∵当x＞1时，函数y随x增大而减小，故A选项不符合题意；把点（﹣1，0），（3，0）代入y＝ax2+bx+c得：a﹣b+c＝0①，9a+3b+c＝0①，①×3+①得：12a+4c＝0，∴3a+c＝0，故B选项不符合题意；当y＝﹣2时，y＝ax2+bx+c＝﹣2，由图象得：纵坐标为﹣2的点有2个，∴方程ax2+bx+c＝﹣2有两个不相等的实数根，故C选项不符合题意；∵二次函数图象的对称轴为x＝1，a＜0，∴当x≤1时，y随x的增大而增大；当x≥1时，y随x的增大而减小；。

中考数学压轴题河南·专题：二次函数压轴题

x＋3与y轴交于点
C，与x轴交于点D.点P是x轴上方的抛物线上一动点，过点
P作PF⊥x轴于点F，交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式；
(2)若PE＝5EF，求m的值；
专题பைடு நூலகம்析
聚焦河南
(3)若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．
点的四边形是平行四边形？请说明理由；
专题剖析
聚焦河南
(3)若存在点P，使∠PCF＝45°，请直接写出相应的点P的坐标．
∴0＜m＜5.
PE＝－m2＋4m＋5－(－ 3 m＋3)＝－m2＋ 19 m＋2.
4
4
分两种情况讨论：
专题剖析
聚焦河南
①当点E在点F上方时，EF＝－
3 4
m＋3.
∵PE＝5EF，
∴－m2＋ 19 m＋2＝5(－ 3 m＋3)，
4
4
即2m2－17m＋26＝0，
解得m1＝2，m2＝
13 2
(舍去)．
专题剖析
专题剖析
聚焦河南
(3)小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使 △PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标．
专题剖析
聚焦河南
【分析】 (1)利用待定系数法求出抛物线解析式即可； (2)首先表示出P，F点坐标，再利用两点之间距离公式得出 PD，PF的长，进而求出即可；(3)根据题意当P，E，F三点共线时，PE＋PF最小，进而得出P点坐标以及利用△PDE的面积可以等于4到13之间的所有整数，在面积为12时，a的值有两个，进而得出答案．【自主解答】 (1)抛物线的解析式为y＝－ 1 x2＋8.

2020年中考数学二模复习之二次函数中考压轴题(26张PPT)【精美版】

利用铅垂线求面积
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
四.逐问突破（2）→铅垂线
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
“类铅垂线”问题
利用铅垂线求面积
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
本题不直接考察，而是利用铅垂线与已知直线的“几何关联”来求解 2.16-17连续考察平行四边形存在性，18年等腰三角形存在性，19年再次考察“平行四边形存在性”的可能大，而且平行四边形难度也较大，正符合 “150分”下难度提升的大形势
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
四.逐问突破（3）→存在性
直接探讨“等腰三角形存在性”
等腰三角形
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
四.逐问突破（3）→存在性
利用“平行四边形”性质求解
平行四边形
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】
四.逐问突破（3）→存在性
利用“等腰三角形”求点
等腰三角形
2020年中考数学二模复习之二次函数中考压轴题（2 6张PPT ）【精美版】

2020年中考数学考前专题复习——二次函数压轴专题课件(共22张PPT)

类型三特殊三角形存在性问题
1. 如图，抛物线y＝x 2＋bx＋c（c＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为D，且OB＝OC＝3．点E为线段BD上的一个动点，EF⊥x轴于F．
（1）求抛物线的解析式；
（2）是否存在点E，使△ECF为直角三角形？若存在，求点E的坐标；若不存在，请说明理由．
当x b 时, y最大值为 4ac b2
2a
4a
3、求解析式的三种方法
1、一般式：已知抛物线上的三点，通常设解析式为
_y_=__a_x_2_+_b_x_+__c_(a__≠_0)
2,顶点式：已知抛物线顶点坐标（h, k），通常
设抛物线解析式为__y__=_a_(_x_-_h_)_2+__k_(_a≠0)
变式一：
2. 如图，抛物线y＝x²＋(m＋2)x＋4的顶点C在x轴正半轴上，直线y＝x＋2与抛物线交于A，B两点 (点A在点B的左侧)． (1)求抛物线的函数表达式； (2)点P是抛物线上一点，若S△PAB＝2S△ABC，求点P的坐标； (3)将直线AB上下平移，平移后的直线y＝x＋t与抛物线交于A′、B′两点(A′在B′的左侧)，当以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时，求t的值．
A： y (x 4)2 6 C: y (x 2)2 2
B: y (x 4)2 2 D： y (x 1)2 3
5.二次函数与一元二次方程和不等式的关系
当b2 4ac 0时,方程ax2 bx c 0a 0有两个不相等的实数根；
x1,2 b
b2 4ac .
2a
当b2 4ac 0时,方程ax2 bx c 0a 0有两个相等的实数根:

河南中考二次函数的实际应用复习课件

9 5
∴当运动时间为1秒时，△PBQ面积最大，最大
首页末页目录
9 面积为 . 10

中招考点清单
课堂过关检测河南三年中招常考类型剖析
（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK∶S△PBQ=5∶2,
, 解得：
,
故y=-2x+80.

（2）在商品不积压且不考虑其他因素的
中招考点清单
课堂过关检测河南三年中招常考类型剖析
条件下，每件服装的销售定价为多少时，该
小商场销售这种服装每天获得的毛利润最大？每天的最大毛利润是多少？（注：每件服装销售的毛利润=每件服装的销售价-每件服装的进货价）【思路分析】根据题意列出函数关系式，运用二次函数的最值解决问题.
再放进绝对值中，然后按动点在定点左或者右分类讨论.
备考试题演练
河南名师预测
首页末页目录

常考类型剖析
类型一二次函数实际应用题
中招考点清单
课堂过关检测河南三年中招常考类型剖析
例1（’14常州）某小商场以每件20元的价格购进一种服装，先试销一周，试销期间每天的销量t(件)与每件的销售价x(元/件)如下表所示：
wwwwanweieducom备考试题演练河南三年中招河南名师预测函数与几何知识的综合应用题型很多最常见的类型有存在性问题动点问题动手操作问题涉及的内容有方程函数等腰三角形直角三角形相似三角形平行四边形特殊的平行四边形等多种知识
中招考点清单
课堂过关检测河南三年中招常考类型剖析
第一部分教材知识梳理
题；
（2）结合动点计算几何图形的长度和面积的考题；（3）和其他函数相结合的考题；（4）其他类型.

2020年中考数学二次函数压轴题专题复习 (含答案)

2020年中考数学二次函数压轴题专题复习 (含答案)2020年中考数学二次函数压轴题专题复1.在平面直角坐标系中，抛物线$y=ax^2+bx+c$交$x$轴于$A、B$两点，交$y$轴于点$C(0,c)$，$OA=1$，$OB=4$，直线$l$过点$A$，交$y$轴$CD$于点$D$，交抛物线于点$E$，且满足$\tan∠OAD=$。

1）求抛物线的解析式；2）动点$P$从点$B$出发，沿$x$轴正方向以每秒$2$个单位长度的速度向点$A$运动，动点$Q$从点$A$出发，沿射线$AE$以每秒$1$个单位长度的速度向点$E$运动，当点$P$运动到点$A$时，点$Q$也停止运动，设运动时间为$t$秒。

①在$P、Q$的运动过程中，是否存在某一时刻$t$，使得$\triangleADC$与$\triangle PQA$相似，若存在，求出$t$的值；若不存在，请说明理由。

②在$P、Q$的运动过程中，是否存在某一时刻$t$，使得$\triangle APQ$与$\triangle CAQ$的面积之和最大？若存在，求出$t$的值；若不存在，请说明理由。

2.在平面直角坐标系中，抛物线$y=ax^2+bx+c$交$x$轴于$A、B$两点（$A$在$B$的左侧），且$OA=3$，$OB=1$，与$y$轴交于$C(0,3)$，抛物线的顶点坐标为$D(-1,4)$。

1）求$A、B$两点的坐标；2）求抛物线的解析式；3）过点$D$作直线$DE\parallel y$轴，交$x$轴于点$E$，点$P$是抛物线上$B、D$两点间的一个动点（点$P$不与$B、D$两点重合），$PA、PB$与直线$DE$分别交于点$F、G$，当点$P$运动时，$EF+EG$是否为定值？若是，试求出该定值；若不是，请说明理由。

3.二次函数$y=ax^2+bx+c$的图象与$x$轴交于点$A、B$，与$y$轴交于点$C$，点$A$的坐标为（$-4,0$），$P$是抛物线上一点（点$P$与点$A、B、C$不重合）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(3)点Q是线段BD上异于B，D的动点，过点Q作QF⊥x轴于点F，交抛物线于点G，当△QDG为直角三角形时，直接写出点Q的坐标．
2．(2019·洛阳三模)在平面直角坐标系中，直线y＝ x－2与x轴交于点B，与y轴交于点C，二次函数y＝ x2＋bx＋c的图象经过B，C两点，且与x轴的负半轴交于点A.
(1)求该抛物线的解析式；
(2)若直线y＝－ x＋m将△AOC的面积分成相等的两部分，求m的值；
(3)点B是该二次函数图象与x轴的另一个交点，点D是直线x＝2上位于x轴下方的动点，点E是第四象限内该二次函数图象上的动点，且位于直线x ＝2右侧．若以点E为直角顶点的△BED与△AOC相似，求点E的坐标．
1．(2020·原创)如图，抛物线y＝ax2＋bx＋c关于直线x＝1对称，
与坐标轴交于A，B，C三点，且AB＝4，点D
在抛物线上，直
线l是一次函数y＝kx－2(k≠0)的图象，点O是坐标原点．
(1)求抛物线的解析式；
(2)若直线l平分四边形OBDC的面积，求k的值；
(3)在抛物线上是否存在一点P，使得点Q在x轴上，点M在坐标平面内，四边形CQPM是正方形，若存在，求点P的横坐标；若不存在，请说明理由
(1)求b，c的值； (2)直线l与x轴交于点P. ①如图1，若l∥y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x＝1的对称点为D，求四边形CEDF面积的最大值； ②如图2，若直线l与线段BC相交于点Q，当△PCQ∽△CAP时，求直线l的表达式．
1．(2019·四川泸州)如图，在平面直角坐标系xOy中，已知二次函数y＝ ax2＋bx＋c的图象经过点A(－2，0)，C(0，－6)，其对称轴为直线x＝2.
(1)求抛物线的解析式；
(2)若抛物线的对称轴上存在一点M，使△AOM的周长最小，求点M的坐标；
(3)点F是x轴上一动点，过点F作x轴的垂线，交直线AB于点E，交抛物线于点P，且PE＝，直接写出点E的坐标(写出符合条件的两个点即可).
面积问题
例2、(2019·江苏常州)如图，二次函数y＝－x2＋bx＋3的图象与x轴交于点A，B，与y轴交于点C，点A的坐标为(－1，0)，点D为OC的中点，点P在抛物线上． (1)b＝____； (2)若点P在第一象限，过点P作PH⊥x轴，垂足为H，PH与BC，BD分别交于点M，N.是否存在这样的点P，使得PM＝MN＝NH，若存在，求出点P的坐标；若不存在，请说明理由； (3)若点P的横坐标小于3，过点P作PQ⊥BD，垂足为Q，直线PQ与x轴交于点R，且S△PQB＝2S△QRB，求点P的坐标．
2．(2020·原创)如图，矩形OABC的边OA，OC分别在x，y轴的正半轴
上，且OA＝1，OC＝2，以O为直角顶点作Rt△COD，OD＝3，已知二次
函数y＝ax2＋bx－的图象过D，B两点． (1)求二次函数的解析式； (2)如图1，连接BD，在BD下方的抛物线上是否存在点M，使得四边形 BCDM的面积S最大？若存在，请求出S的最大值及点M的坐标；若不存在，请说明理由； (3)如图2，E为射线DB上的一点，过E作EH⊥x轴于H，点P为抛物线对称轴上一点，且在x轴上方，点Q在第二象限的抛物线上，是否存在P， Q使得以P，O，Q为顶点的三角形与△DEH全等？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
(3)当矩形MNHG的周长最大时，能否在二次函数图象上找到一点P，使 △PNC的面积是矩形MNHG面积的，若存在，求出点P的横坐标；若不存在，请说明理由．
1．(2019·山东东营)已知抛物线y＝ax2＋bx－4经过点A(2，0)，B(－4，0)，与y轴交于点C.
(1)求这条抛物线的解析式；
(1)求二次函数的解析式；
(2)如图，点M是线段BC上的一动点，动点D在直线BC下方的二次函数图象上．设点D的横坐标为m.
①过点D作DM⊥BC于点M，求线段DM关于m的函数关系式，并求线段DM的最大值；
②若△CDM为等腰直角三角形，直接写出点M的坐标．
平行四边形的存在探究
例5、(2019·广西贵港)如图，已知抛物线y＝ax2＋bx＋c的顶点为A(4， 3)，与y轴相交于点B(0，－5)，对称轴为直线l，点M是线段AB的中点．
(3)在(2)的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由
相似三角形、全等三角形的存在探究
例7、(2019·四川攀枝花)已知抛物线y＝－x2＋bx＋c的对称轴为直线x＝1，其图象与x轴相交于A，B两点，与y轴交于点C(0，3).
(1)求抛物线的函数表达式；
(2)点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC′D，若点C′恰好落在抛物线的对称轴上，求点C′和点D的坐标；
(3)设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当 △CPQ为等边三角形时，求直线BP的函数表达式．
直角三角形、等腰直角三角形的存在探究
(1)求抛物线的表达式； (2)写出点M的坐标并求直线AB的表达式； (3)设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．
1．(2019·郑州三甲联考)如图，在矩形OABC中，OC＝8，OA＝10，分别以 OC，OA所在的直线为x轴，y轴建立如图所示平面直角坐标系，已知，点D 是线段AB上一点，沿直线CD折叠矩形OABC的一边BC使点B落在OA边上的点E 处，抛物线y＝－ x2＋bx＋c经过O，D，C三点． (1)求抛物线的表达式； (2)一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C 时，两点同时停止运动，设运动时间为t秒，当t为何值时，以P，Q，C为顶点的三角形与△ADE相似？ (3)点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．
例4、(2019·许昌一模)如图，二次函数y＝ax2＋bx＋c交x轴于点A(1，0) 和点B(3，0)，交y轴于点C，抛物线上一点D的坐标为(4，3).
(1)求该二次函数所对应的函数解析式；
(2)如图1，点P是直线BC下方抛物线上的一个动点，PE∥x轴，PF∥y轴，求线段EF的最大值；
(3)如图2，点M是线段CD上的一个动点，过点M作x轴的垂线，交抛物线于点N，连接CN，BN.当△CBN是直角三角形时，请直接写出所有满足条件的点M的坐标．
(3)在第四象限的抛物线上任取一点M，连接MN，MB.请问：△MBN 的面积是否存在最大值？若存在，求出此时点M的坐标；若不存在，请说明理由．
等腰三角形的存在探究
例3、(2019·山东菏泽)如图，抛物线与x轴交于A，B两点，与y轴交于点 C(0，－2)，点A的坐标是(2，0)，点P为抛物线上的一个动点，过点P作 PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝－1. (1)求抛物线的函数表达式； (2)若点P在第二象限内，且PE＝ OD，求△PBE的面积． (3)在(2)的条件下，若点M为直线BC上一点，在x轴的上方，是否存在点 M，使△BDM是以BD为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．
专题八二次函数压轴题
线段问题
例1、(2019·湖南常德)如图，已知二次函数图象的顶点坐标为A(1，4)，与坐标轴交于B，C，D三点，且点B的坐标为(－1，0).
(1)求抛物线的解析式；
(2)在二次函数图象位于x轴上方部分有两个动点M，N，且点N在点M的左侧，过M，N作x轴的垂线交x轴于点G，H两点，当四边形MNHG为矩形时，求该矩形周长的最大值；
2．(2019·濮阳一模)如图，抛物线y＝－ x2＋bx＋c与x轴交于A，B两点(点A在点B的左侧)，点A的坐标为(－1，0)，与y轴交于点C(0，2)，直线CD：y＝－x＋2与x轴交于点D.动点M在抛物线上运动，过点M作MP⊥x轴，垂足为P，交直线CD于点N. (1)求抛物线的解析式； (2)当点P在线段OD上时，△CDM的面积是否存在最大值，若存在，请求出最大值；若不存在，请说明理由； (3)点E是抛物线对称轴与x轴的交点，点F是x轴上一动点，点M在运动过程中，若以C， E，F，M为顶点的四边形是平行四边形时，请直接写出点F的坐标．
(2)如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点 P的坐标；
(3)如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE 上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．
2．(2019·河南模拟)如图，抛物线y＝ax2＋bx(a≠0)的图象过原点O和点 A(1， )，且与x轴交于点B，△AOB的面积为 .
1．(2019·江苏淮安)如图，已知二次函数的图象与x轴交于A，B两点， D为顶点，其中点B的坐标为(5，0)，点D的坐标为(1，3).
(1)求该二次函数的解析式；
(2)点E是线段BD上的一点，过点E作x轴的垂线，垂足为F，且ED＝EF，求点E的坐标；
(3)试问在该二次函数图象上是否存在点G，使得△ADG的面积是△BDG的面积的？若存在，求出点G的坐标；若不存在，请说明理由．
1．(2019·信阳一模)如图所示，已知抛物线y＝ax2＋bx＋c(a≠0)经过点 A(－2，0)，B(4，0)，C(0，－8)，与直线y＝x－4交于B，D两点．
(1)求抛物线的解析式并直接写出点D的坐标；
(2)点P为直线BD下方抛物线上的一个动点，试求出△BDP面积的最大值及此时点P的坐标；
矩形、菱形、正方形的存在探究