弱无穷小算子算法
【国家自然科学基金】_随机线性算子_基金支持热词逐年推荐_【万方软件创新助手】_20140802
2013年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 推荐指数 非自治 1 隐式交替方向格式 1 美式期权 1 线性互补问题 1 概周期解 1 时滞 1 收敛性 1 投影算法 1 heston随机波动率模型 1 acquistapace-terreni条件 1
2014年 序号 1 2 3 4
2014年 科研热词 渐近行为 最小q-函数 对偶分支q-矩阵 对偶 推荐指数 1 1 1 1
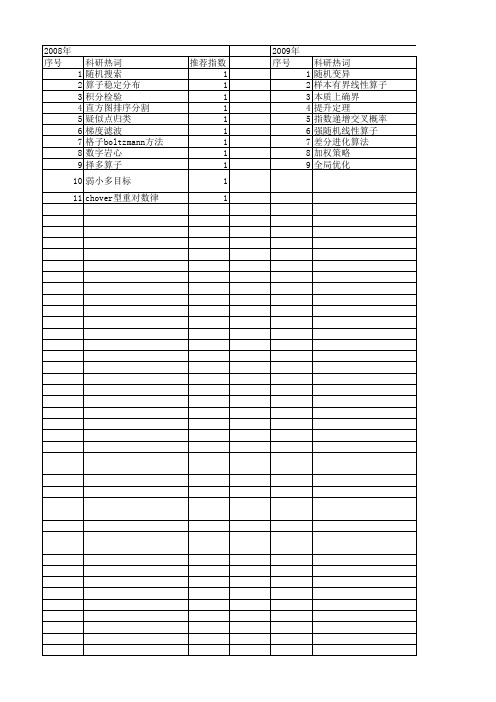
2008年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 随机搜索 算子稳定分布 积分检验 直方图排序分割 疑似点归类 梯度滤波 格子boltzmann方法 数字岩心 择多算子 弱小多目标 hover型重对数律
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9
科研热词 随机变异 样本有界线性算子 本质上确界 提升定理 指数递增交叉概率 强随机线性算子 差分进化算法 加权策略 全局优化
推荐指数 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9
科研热词 随机微分方程 随机吸引子 遗传算法 缓增随机集 组换装时间 线性规划 强阻尼 单机调度 wiener过程
科研热词 推荐指数 随机赋范模 3 随机线性算子的c0-半群 2 随机线性算子 2 随机无穷小生成元 2 (ε ,λ )一拓扑 1 (ε , λ )-topology 1 随机自反 1 配流 1 调机运用 1 自适应测量 1 统计自相关函数 1 约束等距常数 1 粒子群优化算法 1 稀疏解 1 离散粒子群优化算法 1 矩阵向量乘算子 1 正交杂交 1 欠定线性方程组 1 有偏随机键遗传算法 1 最佳线性估计 1 最佳s项逼近 1 整数非线性规划 1 数值预报 1 收敛分析 1 快速图像重建 1 平均遍历定理 1 子集选择 1 奇异值分解 1 图像处理 1 可预报分量 1 参数均匀交叉 1 单向编组站 1 分块压缩感知 1 几乎处处幂有界的随机线性算子 1 random normed module 1 random linear operator 1 random infinitesimal generator1 lorenz系统 1 c0-semigroupsof random linear 1 operators (ε ,λ )-拓扑 1
数学专业术语

数学
量
假设
定理
逆否命题
猜想
验证
充要条件
论证
恒等式
公式
小于
不等方程
常数
复合
完全的
肯定的
离散的
周期
族
子集
并
直积集
差集
n元组
值域
逆映射
恒同映射
映入
同构
对称性
超穷基数
幺拟群
连通代数群
代数群的有理表示
左函数平移
代数群的李代数
典范态射
半单元
抽象根系
幂幺根
抛物子群
代数群的外尔群
布吕阿分解
谢瓦莱群
算术子群
拓扑群的直积
左一致结构
局部紧群
零化子的互反性
紧阿贝尔群
紧群的群环
局部单连通
泛覆叠群
可数无穷的
数理逻辑
形式语言
合式的
矢列式
论题
命题演算
联结词
逻辑加法
否定词
析取范式
真值
重言式
谓词变元
个体变元
非标准量词
前束词
闭公式
全域
一阶理论
相容性
可定义性
斯科伦壳
初等等价的
初等子模型
进退构造
原子理论
对象的余积
终对象
自由对象
对偶函子
忠实函子
常数函子
自然等价
泛性质
表示函子
推出
无穷小计算

无穷小计算
无穷小计算是现在互联网技术发展的重要趋势之一,它是指在互联网时代利用
低成本的云计算技术、以及智能化的物联网技术等,将大规模的计算任务分解为多个可独立执行的任务,然后由不同计算机并行执行,从而实现的计算性能扩展。
无穷小计算对传统的计算机技术和运算使用方式实现了革命性的改变,它将计算任务拆分成大量离散的小任务,再分发到不同计算机或网络节点上,通过节点之间的协作,从而实现更高性能的计算。
无穷小计算主要应用于大规模、高性能的计算,如实时数据分析、桌面虚拟化、视频编辑等,极大地提高了系统的吞吐量和处理数据量,可以有效缩短计算任务的完成时间。
此外,无穷小计算还可以实现在网络上的分布式计算,使得不同的计算机可以使用网络上的资源,从而节省计算机成本和服务器的影响,并能够更有效地共享用户资源。
无穷小计算带来了巨大的社会变革,它大大改变了我们处理海量数据的方式,
使我们更容易得到更准确、更及时的信息,成为依托快速发展的互联网行业的重要助力和载体,同时也为更多用户提供了个性化、有价值的信息服务。
总之,无穷小计算的出现使得计算能力得到近乎无限的扩展,为互联网时代的
发展带来了新的机遇,它将发挥更大的作用,推动现代社会智能化进程,促进社会发展和生活提升。
一类随机非线性系统自适应跟踪的模块化设计

引理 3 』假设 "和P是定义在 R “: 上的实值 函数 ,, 是 6c
正常数。 如果 P ∈ L 并且 t满 足 微分 不 等式 ≤一C , , O+
6() , ( )≥ 0 则 有 pt vO ,
: ,
0) 川 ㈣1 2+ V )
其 中 。T , , , , P是 类 函数 , 则称系统关于 ( ,)是输 人 ~状态稳定 的(S ) IS 。
其中 是状态变量 , : ( , , ) ∈R是系统 x 。 …, ;
的输入 , R是系统 的输 出; ( Y 互)∈R 是 已知 的光滑非线 p 性函数向量 , 满足 ;0 ( )=0 ; R 是未知参数向量 , p 的估
对于系统 不确定 噪声采用 随机扰动抑 制控制的机制 , 对 不确定参数采用 自适应 机制 , 用于跟 踪控制设 计 , 应 使跟 踪
误差在概率意义下 收敛到一个任意小范围 。
计值是 () 则误差定义为 () t, t :=0 () 田 ( 一 t , 互)eR 是
已知的光滑非线性 函数 向量 , W是定 义在概率 空间 ( F, 力, 尸) 上的 r 维相互独立 的方差不确定 Wi e 过程向量 , 中 为 e r n 其
识器结合 , 控制模块镇定 被控 对象 , 辨识 器能保 证独 立于控 制器 的特定有界特性 。用来 描述扰 动抑制 问题 的输入 一状 态稳定 (S ) 念 最初 由 Sna 出 l 。Focigr在文 IS 概 ot g提 4 lrh e J n
踪 问题 。通过设计强参数鲁棒稳定特 性的控制器 , 实现控 制 模块镇定 被控 对象 , 并能 和任 意 的标 准辨 识器 结 合。运用
无穷小阶的运算

无穷小阶的运算“无穷小阶”是当今数学领域最重要的概念之一,也是数学发展的重要组成部分。
它是一种技术,可以用来评估数学表达式中复杂问题的解决方案。
它被广泛应用于各种数学领域,包括统计,计算机科学,运算论等等,影响着社会科学,医学,工程等学科的研究。
无穷小阶的定义是:“一个变量的无限次近似值,使得其在给定问题中得到求解的解”。
无限次近似的解决方法通常是利用无穷级数,及其特殊的函数,形成的解的近似值。
这些解的近似值在运算上被认为是无限次近似值,因此被称为无穷小阶。
无穷小阶运算在许多数学领域中得到广泛应用,如统计,机器学习等等,因此对于研究者来说,无穷小阶的具体原理及应用是十分重要的。
无穷小阶的理论涉及到极限理论,级数,函数拟合,以及各种数值分析技术,同时也涉及到随机数据分析,概率论等等。
在非线性方面,无穷小阶经常被用于求解非线性解,尤其是非线性方程组,以及非线性最优化问题。
比如,在逼近非线性函数中,可以使用无穷小阶算法来比较非线性函数的结果。
此外,在解决无穷维极值问题时,可以利用无穷小阶的定理来求解不可避免的极值问题。
无穷小阶的几何概念也被广泛应用于微分几何,几何拟合,及计算几何技术中,用于研究复杂曲面的几何特征,解决不可避免的表面和几何拟合问题。
此外,无穷小阶还被用于各种数值计算技术,如有限差分,拉格朗日插值,样条插值,以及基于微分方程的数值计算等。
最后,无穷小阶运算也被应用于统计分析中,用于检验分布及性质,估计未知参数,以及其他分析工作。
总而言之,无穷小阶运算是一个技术,可以用来解决复杂的数学问题,并且广泛应用于统计,计算机科学,几何,微分几何,及其他数值计算技术中。
因此,学习无穷小阶运算的理论及其应用是非常有必要的。
事件驱动Markov型网络系统的输出反馈H∞控制

周学德,张艳 . 事件驱动 Markov 型网络系统的输出反馈 H∞ 控制 . 计算机工程与应用,2019,55(6):231-236. ZHOU Xuede, ZHANG Yan.Event-triggered output feedback H∞ control for networked Markov type systems. Computer Engineering and Applications, 2019, 55(6):231-236.
Abstract:In order to solve the H∞ output feedback control problem of event-triggered Markov type systems, Wirtinger’s inequality is used to estimate the upper bound of the weak infinitesimal operator of Lyapunov function by constructing Lyapunov function containing event- triggered and quantized output information. The stability criterion of event-triggered Markov network closed-loop system is obtained, and the output feedback controller design method is given. It satisfies the level of H∞ disturbance suppression, which can effectively overcome the impact of disturbance on the system. Key words:event-triggered; Markov type network control system; time delay; Wirtinger’s inequality; H∞ output feedback control
中立型灰色随机分布时滞系统的指数鲁棒稳定性

中立型灰色随机分布时滞系统的指数鲁棒稳定性苏春华;刘思峰【摘要】为了得到一类中立型灰色随机分布时滞系统的指数鲁棒稳定性,本文利用LyapunovKrasovskii泛函法、灰矩阵的连续矩阵覆盖的分解技术和It(o)公式,分别得到了以非线性矩阵不等式和线性矩阵不等式(LMI)表示的该系统指数鲁棒稳定的时滞依赖性判据.对非线性矩阵不等式判据,我们给出了一般性算法,解决了非线性矩阵不等式判据不便于实际应用的问题.数值例子表明,本文所给判据是有效的,且系统的指数稳定性和时滞,随着绝对灰度矩阵的谱范数的增大而减小.【期刊名称】《工程数学学报》【年(卷),期】2010(027)003【总页数】12页(P403-414)【关键词】中立随机系统;分布时滞;指数鲁棒稳定性;灰矩阵;线性矩阵不等式【作者】苏春华;刘思峰【作者单位】信阳师范学院数学与信息科学学院,信阳,464000;南京航空航天大学经济与管理学院,南京,210016【正文语种】中文【中图分类】N941.5;O231.31 引言由于随机微分系统在自然、社会和科技等领域具有广泛的应用,所以,近三十多年来,关于随机微分系统的稳定与控制问题,一直是很多学者关注的焦点问题,并取得了许多有价值的成果[1]。
其间,在二十世纪八十年代,Kolmanovaskii和Nosov基于化学工程和航空理论发展的需要,还建立了一类中立型随机泛函微分系统,并研究了该系统解的存在性、唯一性[2]、稳定性和渐近稳定性[3]的问题。
此后,一些学者又利用Lyaponuv泛函和Razumikhin技术,研究了中立型随机系统的指数稳定问题,得到了一些指数稳定的代数判据[4-6]。
2007年,Randjelovic和Jankovic则基于一个关于向量范数的p-阶矩不等式,给出了中立型随机系统的p-阶矩指数稳定的代数判据[7],且该判据还是文献[8]的结果的推广。
然而,关于中立型不确定随机系统的研究,目前仅有少量的报道。
高阶无穷小计算规则

高阶无穷小计算规则
嘿,朋友们!今天咱们来聊聊高阶无穷小的计算规则。
啥是高阶无穷小呢?简单说,就是在某个变化过程中,一个无穷小
量比另一个无穷小量趋向于零的速度更快。
在计算的时候,有这么几个重要的规则得记住哈。
允许这样做:如果有两个无穷小量α和β,当α/β的极限等于0 时,那α就是β的高阶无穷小。
比如说,当 x 趋向于 0 时,x²就是 x 的高
阶无穷小。
为啥呢?因为 x 趋向于 0 时,(x²)/x 的极限是 0 呀,这就说
明 x²趋向于 0 的速度比 x 快得多。
禁止这样做:可别随便把不同阶的无穷小量直接相加减就认为还是
无穷小量哦。
比如说 x 是一个无穷小量,x²是比 x 高阶的无穷小量,
要是直接把它们相加,x + x²,可不能简单地认为它还是个无穷小量。
还有哦,如果有一串无穷小量α₁,α₂,α₃……,按照阶数从高到
低排列。
那在计算的时候,低阶的那些无穷小量在高阶无穷小量面前,影响就很小啦,可以忽略不计。
为啥要搞清楚这些规则呢?这可太重要啦!比如说在研究函数的极限、泰勒展开这些地方,搞清楚高阶无穷小,就能让咱们更准确地把
握函数的变化趋势,不会出错。
就像走迷宫,知道了这些规则,就等
于有了一张清晰的地图,能更快更准地找到出口。
总之,高阶无穷小的计算规则虽然有点复杂,但只要咱们用心去理解,多做几道题练练手,就一定能掌握好,让数学变得不再那么可怕,反而有趣起来!
好啦,今天关于高阶无穷小计算规则就说到这儿,希望对大家有帮
助哟!。
大学数学分析-关于无穷小量的研究王杰

大学数学分析-关于无穷小量的研究王杰学士学位论文关于无穷小量的研究目录1 引言...................................................................... .. (1)2 无穷小思想的由来...................................................................... ......................................2 3 无穷小量的性质...................................................................... ..........................................3 3.1 无穷小量的运算...................................................................... .. (3)3.2 无穷小量阶的比较...................................................................... . (6)3.2.1 高阶无穷小...................................................................... (6)3.2.2 等价无穷小...................................................................... (7)3.2.3 同阶无穷小...................................................................... .................................8 4 无穷小量的应用...................................................................... .........................................9 4.1 极限中的无穷小量...................................................................... ...............................9 4.2 微分中的无穷小量...................................................................... .............................11 4.3 积分中的无穷小量...................................................................... .............................13 4.4 级数中的无穷小量...................................................................... .............................14 5 结束语...................................................................... .. (18)参考文献...................................................................... .. (19)致谢...................................................................... . (20)关于无穷小量的研究关于无穷小量的研究摘要:无穷小量在数学分析中占有举足轻重的地位,无穷小量具有很好的性质,它使得一些复杂的极限问题、微积分问题、级数问题简单化(从无穷小的思想出发,追述历史发展过程到分析学中的应用(全文主要分为三个部分:第一部分是对无穷小量的发展过程进行概述;第二部分给出无穷小量的相关性质,其中主要对无穷个无穷小量的和与积运算后未必是无穷小量进行了详细证明;第三部分应用无穷小量的等价性、可加性、可乘性解决函数极限、微分、积分、级数问题;这些问题的解决对加深无穷小量概念的理解有很大的帮助(关键词:无穷小量;极限;微分;积分;正项级数Research on the InfinitesimalInfinitesimal in mathematical analysis in a pivotal position,the :Abstractnature of infinitesimals good, it makes the limits of some of the complexproblem of calculus problems, series simplification of the problem. From theinfinitely small idea, goes back to the analysis of the historical development ofscience. Full-text is divided into three parts, the first part of the infinite processof the development of a small overview, the second part gives the relevantproperties of infinitesimals, mainly on the infinitely infinitesimal and withproduct operation carried out after a small amount may not be infinite full proof.The third part of the application of the equivalence of infinitesimal, additive,multiplicative function to solve the limit, differentiation, integration, positiveseries problems the solution of the concept of deepening the understanding ofinfinitesimals of great help.Key words:Infinitesimal;Limit;Differential;Integration;Series1 引言无穷小思想历史悠久,源远流长, M.克莱因曾说过:“数学史上最使人惊奇的实事之一是实数系的逻辑基础竞迟至19世纪后叶才建立起来”(而这明显是由于人[7]们在理解无穷这个概念上所遇到的巨大困难造成的(二千多年来,人们一直没有放弃对无穷概念的思考探索,企图明白无穷思想的真谛,然而,诚如希尔伯特所说:“无穷是一个永恒的谜”要揭开这个谜底还有待时日(本文试图从无穷小的几个性质及其作用做一点探索(本文从无穷小的思想出发,首先给出无穷小数列的相关定义和关于函数为无穷小量的定义,明确在什么前提下才能谈无穷小量.其次谈无穷小量的性质,无穷小量是- 1 -关于无穷小量的研究有极限变量中最简单而且是最重要的一类,有其自身特殊的性质,两个(相同类型的)无穷小量之和、差、积仍为无穷小量,无穷小量与有界量的乘积为无穷小量,本文重点论证了无穷个无穷小量的和与积不一定是无穷小量(无穷小量是以0为极限的函数,而不同的无穷小量收敛于0的速度有快有慢(为此,本文考察两个无穷小量的比,以便对他们的收敛速度作出判断即无穷小量阶的比较(再次,无穷小量在高等数学中有着非常重要的地位,他是解决极限问题的基础,而且技巧性很强,掌握并充分利用好它的性质,往往会使一些复杂的问题简单化,可起到事半功倍的效果(最后本文运用无穷小量性质来解决求极限问题、微积分的证明、求级数的敛散性判别、级数的收敛域问题(2 无穷小思想的由来无穷小思想最初是在哲学范围内提出的,无论是在古希腊还是在中国都是如此,哲学家们对“无穷小”都进行了一定程度的论述(中国就曾有“一尺之棰,日取其半,万世不竭” ,并且我国第一个创造性地将无穷小思想运用到数学中的人是魏晋时期的著名数学家刘徽,他天才地提出了用增加圆内接正多边形的边数来逼近圆的“割圆术”,并阐述道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,7,而无所失矣”(可见刘徽对无穷小的认识已相当深刻(到17世纪六七十年代,牛顿和莱布尼茨以无穷小思想为依据,成功运用无限过程的运算,创立了微积分学,无穷小量才有一席之地(数学不再由几何学独占,而是支撑在几何学与微积分这两根支柱上(古希腊时期,哲学家,数学家就注意了无穷概念(达哥拉斯学派发现了无理数的存在,引起了古希腊数学的危机(稍后埃利亚学派的芝诺提出了四个悖论:二分说,阿基里斯追龟说,飞箭静止说,运动场悖论,使危机更加加深(这些悖论显然违背人们的常识,迫使更多哲学家和数学家思考无穷小的问题(亚里士多德考虑过无穷的问题,但他只承认潜无穷(阿基米德发明的“穷竭法”中引进了无穷小,无限分割的思想,他的这种类似今天求极限的方法被公认为微积分计算的鼻祖,正是芝诺提出的悖论使人们对无穷小有了最初的认识(人们从无穷小思想出发,进而想到无穷小量的问题(首先由无界单调增加数列引入无穷小概念,下面给出几个相关定义.xy定义1 设有数列,如果有一无界单调增加数列使 ,,,,nn1x,, nyn,2,x则称是无穷小数列( ,,nxa定义2 设有数列,如果有一个实数和一无穷小数列使得 a,,,,nn- 2 -关于无穷小量的研究, xaa,,nn,2,limxa,x则称以为极限,记作 ( a,,nn,,nx,,0N定义3 设有数列,是常数,若对于任意给定的,总存在一个整数,a,,n nN,使当一切时,都有xa,,,, n[14]limxa,x则称为数列的极限,记为( a,,nn,,nlim0a,定义4 若则称a为无穷小数列( ,,nnn,,与无穷小数列的概念相类似,我们给出关于函数为无穷小量的定义(0fUx定义5 设在某内有定义,若,,n, lim0fx,,,xx,0ff则称为当时的无穷小量(则称为当时的无穷小量( xx,xx,003 无穷小量的性质穷小量是有极限变量中最简单而且是最重要的一类,有其自身特殊的性质(下面通过所给无的定义和例题进一步剖析无穷小量理论(3.1 无穷小量的运算1. 两个(相同类型的)无穷小量之和、差、积仍为无穷小量(2. 无穷小量与有界量的乘积为无穷小量(12xx,0下面看这个例子,当时,是无穷小量,为有界量,故 sinx12. x,limsin0x,0x由函数极限与无穷小量的定义可立即推出如下结论:limfxAfxA,,,,,,,,,xx,0是当时的无穷小量( xx,03. 下面来研究一下无穷个无穷小量作和、作积运算后是否仍为无穷小量(在数学分析中,无穷小量及其运算起着非常重要的作用,由定义5可得,任意有限个无穷小量的积均为无穷小量,在接下来的例题中我们将证明,无限个无穷小量的乘积未必收敛即使收敛,也未必是无穷小量(Unk假设对每一个固定的,当时,为无穷小量,即 n,,,,k- 3 -关于无穷小量的研究k,1,2,3?, lim0Un,,,k,,n无限个无穷小量的乘积应理解为,mUnUnUnUn,,,limlim ,,,,,,,,,,kkmmm,,,,11kk,,mUnUn,其中,当时,的极限存在(否则,无限个无穷小量的乘积无m,,,,,,,kmk,1[5]意义(Un我们的问题是,当时,是否为无穷小量,即 n,,,,,,limlimlim0UnUn,, ,,,,m,,,,,,nnm,,是否成立(其实无限个无穷小量的乘积不一定是无穷小量,举一个“无限个无穷小量的乘积不是无穷小量”的例子(例1 设,,1,nk,,n,1 Unnnkk,1,2,3,,,,?,,,k,1,,nk,n,因为1 UnUn,,,limlimlim0,,,,kk,,,,,,nnnn,nkk,1,2,3,?Un所以,对于当时,为无穷小量( n,,,,k为了看出,mUnUnUnUn,,,limlim ,,,,,,,,,,kkmmm,,,,11kk,,Un我们将写成如下形式,,k11111Un:1,,,,,,…,,,1246351111Un:1,2,,,,,…,,,24635111Un:1,1, 9,,,,…,,,345611Un:1,1,1,64,,,…,,,456因为- 4 -关于无穷小量的研究mm111,1n UnUnUnn,,,,,,,,??limlimlim1111,,,,,,,,Kk,,,,,,mnmnnn,,11kk,mn所以, lim1Un,,,n,,[5]Un即无限个无穷小量的乘积不是无穷小量( ,,不仅如此,还可以举出无限个无穷小量的乘积为无穷大量的例子(只要将上例改写一下即可(例2 设,,1,nk,,n Unnnkk,,,,1,2,3,?,,,k,1,,nk,n,这里,k,1,2,3?, lim0Un,,,k,,k而mUnUnn,,lim, ,,,,,k,,m1,klimUn,,,,n,,Un即无限个无穷小量的乘积为无穷大量( ,,例1和例2表明,无穷小量的无穷乘积运算是非常复杂的,类似的计算也发生在无穷小量的无限求和运算中(,,1tt,0ftt,例如时的无穷小量,但并不收敛,下面的例子ft,为,,,,,,nnnn11nn,,表明,即使无限求和收敛,也未必是无穷小量( 例3 设1,0,1,,t,n,11,ftt,,,1, ,,,nnn,1,1,0,0,,t,n,1,,nftt,,2,0为t,0ft则对每个时的无穷小量(另一方面,不再是时的无,,,,,nn,n2穷小量(- 5 -关于无穷小量的研究 3.2 无穷小量阶的比较无穷小量是以0为极限的函数,而不同的无穷小量收敛于0的速度有快有慢(为此,我们考察两个无穷小量的比,以便对他们的收敛速度作出判断(3.2.1 高阶无穷小量fxgx与定义6 设均为无穷小量,若,,,,fx,,, lim0,xx,0gx,,时,则称当xx,fg为的高阶无穷小量。
无穷小阶的估计法的应用

无穷小阶的估计法的应用
无穷小阶的估计法是微积分中常用的一种方法,主要用于研究函数在某一点处的极限
行为。
它的基本思想是通过分析函数在该点处的性质,将函数的局部行为进行近似,进而
估计函数的极限值。
无穷小阶的估计法在微积分的各个领域中有着广泛的应用,下面将具体介绍几个常见
的应用场景。
1. 求函数极限:对于一个函数f(x),要求其在某一点a处的极限值,可以利用无穷
小阶的估计法。
首先找到函数在该点附近的一个无穷小阶h(x),使得f(x)与h(x)的差趋
于零。
然后利用无穷小阶的性质,对h(x)进行近似估计,得到f(x)的极限值。
2. 求函数的导数:导数是函数在某一点处的变化率,求导可以通过无穷小阶的估计
法来进行近似计算。
通过观察函数在该点附近的变化规律,取其局部行为与线性函数近似,得到导数的近似值。
4. 求定积分:定积分是计算函数在某一区间上面积的方法,可以通过无穷小阶的估
计法来进行近似计算。
将函数在该区间内划分为多个小区间,然后利用无穷小阶的性质,
对各个小区间内的函数进行近似估计,最后将所有小区间的近似值相加,得到定积分的近
似值。
以上仅是无穷小阶的估计法的一些常见应用场景,实际上无穷小阶的估计法在微积分
的各个领域中都有着广泛的应用。
通过对函数局部行为的近似估计,可以更好地理解函数
的性质和变化规律,进而解决与函数相关的各种问题。
弱闭对称算子公式

弱闭对称算子公式(原创版)目录1.弱闭对称算子公式的定义与性质2.弱闭对称算子公式的应用3.弱闭对称算子公式的例子与推导正文一、弱闭对称算子公式的定义与性质弱闭对称算子公式是数学领域中的一个概念,主要用于研究函数空间中的算子。
它可以描述一个函数在另一个函数作用下的变化规律。
弱闭对称算子公式具有以下几个基本性质:1.线性性:对于任意的函数 f(x) 和 g(x),以及任意的实数 a 和 b,有 T(af(x)+bg(x))=aT(f(x))+bT(g(x))。
2.弱闭性:对于任意的函数 f(x) 和 g(x),在 L^2 空间中,有T(f(x)g(x))=T(f(x))g(x)+f(x)T(g(x))。
3.对称性:对于任意的函数 f(x) 和 g(x),有T(f(x)g(x))=T(g(x)f(x))。
二、弱闭对称算子公式的应用弱闭对称算子公式在数学和物理学中有广泛的应用,例如在量子力学、统计力学、偏微分方程等领域。
它可以帮助我们解决许多实际问题,例如求解哈密顿算子、推导薛定谔方程等。
三、弱闭对称算子公式的例子与推导下面我们以一个简单的例子来说明如何推导弱闭对称算子公式。
假设有一个哈密顿算子 H,它作用在函数 f(x) 上,我们可以得到:Hf(x)=-f"(x) (1)其中 f"(x) 表示 f(x) 的导数。
现在我们考虑一个势能函数 V(x),并且假设哈密顿算子与势能函数之间的关系为:H=T+V(x) (2)其中 T 表示动能算子,它作用在函数 f(x) 上,我们可以得到:Tf(x)=f"(x) (3)将式 (1) 和式 (3) 代入式 (2),我们可以得到:-f"(x)=Tf(x)+V(x)这正是弱闭对称算子公式的形式,由此我们可以推导出弱闭对称算子公式。
总结:弱闭对称算子公式是一种重要的数学工具,它可以帮助我们解决许多实际问题。
通过理解其定义与性质,我们可以更好地应用它来解决实际问题。
弱几乎极限算子的一些性质

D u n f o r d—P e t t i s 眭。等价地 , 中的相对弱紧集都是极限集。
1 弱几乎极 限算子 的 一弱 紧性
首 先 给 出了在 空 间满 足什 么样 的条 件下 ,弱几乎极 限算 子 是 L一弱紧算 子 。 定理 1 设 是 自反 的 B a n a c h空 间 ,E是 具 有 序 连续 范 数 的 B a n a c h格 , : — E是 连 续线 性 算 子 。
第 2期
周玉莎等 :弱几 乎极限算子的一些性质
9 1
注 :若 将 定理 1中 E具 有 序 连 续 范 数 空 间改 为 E是 有 限 维 的 ,根 据 文献 中 的定 理 3 . 1结 论 仍 然
成立。
上 述 定理 在满 足 一定 的空 间条 件 理 根 据 算 子 之 间 的关 系 ,推
十
,
设 X中的有界子集 A ,如果满足在 X 中的任意_ 厂 n
,都有s u p I ( ) l 一0 ,则称 A为极限集。
易知 中的每一个相对紧集都是极限集 ,但反之不成立。事实上集合 { e : ∈ N}是 极限集不是相对紧 集 ,其中 e 是f 中的基。如果 中的极 限集都是相对紧集 ,则称 是 G e l f a n d —P h i l l i p s 空间 ( 简称 G P
第2 5卷
第 2期
洛 阳理 工 学 院学 报 ( 自然 科 学 版 )
J o u na r l o f L u o y a n g I n s t i t u t e o f S c i e n c e a n d T e c h n o l o g y ( N a t u r a l S c i e n c e E d i t i o n )
无穷小计算迪厄多内

无穷小计算迪厄多内
迪厄多内是一位杰出的数学家,他为无穷小的概念做出了重要的贡献。
无穷小是数学中一个非常有趣且重要的概念,它在微积分中扮演着重要的角色。
迪厄多内通过他的研究,帮助我们更好地理解了无穷小的概念。
无穷小可以被看作是无穷小于任何实数的数,它非常接近于零,但并不等于零。
通过无穷小,我们可以更好地理解函数的极限以及微积分中的各种概念。
无穷小在数学中有着广泛的应用。
在微积分中,我们可以使用无穷小来描述函数的变化率。
无穷小也可以用来描述一些物理现象,例如在物体运动中,我们可以使用无穷小来描述物体的速度变化。
迪厄多内的研究不仅推动了数学的发展,也对其他领域的研究产生了影响。
他的贡献帮助我们更好地理解了数学中的无穷小概念,并且为我们打开了更多探索的大门。
无穷小的概念在数学中扮演着重要的角色,它不仅帮助我们更好地理解了函数的极限,还在各个领域中有着广泛的应用。
迪厄多内通过他的研究,为我们解开了无穷小的奥秘,让我们能够更深入地探索数学的世界。
迪厄多内为无穷小的研究做出了重要的贡献。
他的研究帮助我们更好地理解了无穷小的概念,并且为我们打开了更多探索的大门。
无
穷小在数学中扮演着重要的角色,它不仅帮助我们理解函数的极限,还在各个领域中有着广泛的应用。
迪厄多内的研究影响深远,为我们提供了更多的思考和探索空间。
无穷小的运算法则

无穷小的运算法则在数学的广袤世界中,无穷小是一个极为重要的概念,而与之相关的运算法则更是我们理解和解决众多数学问题的关键工具。
首先,让我们来明确一下什么是无穷小。
简单地说,无穷小就是在某个变化过程中,以零为极限的变量。
想象一下,当一个变量不断地趋近于零,但永远不会真正达到零,这个变量就可以被称为无穷小。
无穷小的加法法则是比较直观的。
如果有两个无穷小量α和β,那么它们的和α +β 也是一个无穷小量。
这就好比两个非常非常小的数相加,结果仍然是一个非常小的数。
比如说,当 x 趋近于 0 时,x 是一个无穷小,2x 也是一个无穷小,那么 x + 2x = 3x 同样是一个无穷小。
再来看无穷小的减法法则。
若α和β是无穷小,那么α β 也是无穷小。
例如,当 x 趋近于 0 时,3x 是无穷小,x 也是无穷小,3x x = 2x 还是无穷小。
接着是无穷小的乘法法则。
两个无穷小的乘积依然是无穷小。
这是因为当两个非常小的数相乘时,得到的结果会更小。
比如,当 x 趋近于 0 时,x 是无穷小,x²也是无穷小。
然而,无穷小的除法法则就需要我们更加小心地去处理了。
当两个无穷小相除时,结果可能是一个常数、无穷小或者无穷大,这取决于这两个无穷小趋近于零的速度。
比如说,当 x 趋近于 0 时,x 是无穷小,2x 也是无穷小,那么 x /2x = 1/2 ,结果是一个常数。
但如果是 x 除以 x²,当 x 趋近于 0 时,结果就是无穷大。
在实际应用中,无穷小的运算法则常常用于求极限。
比如,我们在计算一些复杂函数的极限时,可以通过将其分解为若干个简单的无穷小的组合,然后运用相应的运算法则来求解。
另外,需要注意的是,无穷小之间也存在着阶的概念。
阶数越高,趋近于零的速度就越快。
比如,当 x 趋近于 0 时,x²相对于 x 就是更高阶的无穷小。
总之,无穷小的运算法则虽然看似简单,但却蕴含着深刻的数学思想,为我们解决各种数学问题提供了强大的工具。
无穷小阶的运算

无穷小阶的运算
无穷小阶的运算是数学中的一种重要技术,可以用来提高数学模型的准确性和精确性。
以下是一些关于无穷小阶的运算的详细介绍。
无穷小阶的运算是指在数值计算中,将某一变量进行极小变化,然后用于计算模型中的参数。
由于公式中所有变量都是极小的,这种运算又被称为“变分法”,其基本理论是取极小值来代替参数,使模
型的计算变得精确而可控。
这样,在一定范围内变量的值不会因为小变化而发生很大的变化。
无穷小阶的运算可以应用于解决复杂的数学模型中的问题,以提升模型的准确性与精确性。
例如,对于复杂的函数极限,通过对函数极限采取无穷小阶的运算,可以得出更加精确的结果。
无穷小阶的运算也被广泛应用于复杂的微分方程,可以更精确的求解出未知的参数。
另外,无穷小阶的运算也被应用于机器学习、深度学习中,用于计算神经网络的权重。
将参数设置成无穷小的数值,可以使训练的收敛速度得到提高,让神经网络可以更好地拟合模型。
总之,无穷小阶的运算是一种非常有用的数学技术,可以提高数学模型的准确性和精确性,不仅可以应用于数学理论,而且可以应用于机器学习和深度学习中,提高神经网络的性能。
- 1 -。
《D24B无穷小比较》课件

导数计算:用于计 算导数,如函数导 数、数列导数等
积分计算:用于计 算积分,如函数积 分、数列积分等
微分方程求解:用 于求解微分方程, 如常微分方程、偏 微分方程等
在数学分析中的应用
极限理论:用于证明极限的存在性和唯一性 连续性理论:用于证明函数的连续性和可微性 微积分理论:用于计算积分和微分 级数理论:用于分析级数的收敛性和求和方法
较的正确性
注意无穷小比 较的符号表示, 避免因符号错 误导致的错误
结果
掌握无穷小比较的重要性
理解无穷小比较的概念和原理
避免无穷小比较中的常见错误
添加标题
添加标题
掌握无穷小比较的方法和技巧
添加标题
添加标题
提高无穷小比较的准确性和效率
THANKS
汇报人:பைடு நூலகம்
D24B无穷小比较 的定义
定义及公式
D24B无穷小比较 的定义:比较两个 无穷小量的大小关 系
公式:D24B无穷 小比较的公式为 f(x)/g(x),其中f(x) 和g(x)为两个无穷 小量
比较方法:当 f(x)/g(x)的极限为 0时,f(x)为g(x)的 高阶无穷小
应用:D24B无穷 小比较在数学、物 理、工程等领域有 广泛应用
D24B无穷小与无穷 小量的关系:D24B 无穷小与无穷小量相 比,其大小关系是相 等的。
D24B无穷小与无穷 小量的关系:D24B 无穷小与无穷小量相 比,其大小关系是相 等的。
D24B无穷小与无穷 小量的关系:D24B 无穷小与无穷小量相 比,其大小关系是相 等的。
无穷小量的阶
无穷小量的阶是衡量无穷小量大小的标准 无穷小量的阶越高,表示无穷小量越小 无穷小量的阶是实数,可以是正数、负数或零 无穷小量的阶可以比较,例如a^n和b^n,如果n>m,则a^n>b^n
无穷小计算规则

无穷小计算规则
1. 哎呀,有限个无穷小的和还是无穷小呀!就好比你有一把沙子,再加上另一把沙子,那整体不还是一点点沙子嘛。
比如$\lim\limits_{x \to 0}
(x+x^2)=0$。
2. 嘿,有界函数与无穷小的乘积还是无穷小呢!这就好像是一个大箱子装着一个小小的东西,整体看还是主要是那个大箱子的特点呀。
像
$\lim\limits_{x \to 0} x \cdot \sin x=0$。
3. 哇塞,常量与无穷小的乘积当然也是无穷小啦!这不就跟大力士拎起一个小不点一样轻松嘛。
举个例子,$\lim\limits_{x \to 0} 5x=0$。
4. 咦,无穷小与无穷小的乘积仍旧是无穷小哦!你想想,两个超级超级小的东西乘在一起,那得多小呀。
例如$\lim\limits_{x \to 0} x \cdot x=0$。
5. 哈,有限个无穷小的乘积必然也是无穷小呀!就像很多个小芝麻粒聚在一起还是小小的。
比如$\lim\limits_{x \to 0} (x \cdot x^2)=0$。
6. 哟,无穷小的倒数是无穷大呀(但要注意零不能作分母哦)!这就像是把一个小东西倒过来看,突然就变得好大了。
比如当$x \to 0$时,$1/x
\to \infty$($x \neq 0$)。
我的观点结论就是:这些无穷小计算规则真的很神奇很有用,好好掌握它们对我们学习数学帮助太大啦!。
弱闭对称算子公式

弱闭对称算子公式
(实用版)
目录
1.弱闭对称算子公式的定义与性质
2.弱闭对称算子公式的应用领域
3.弱闭对称算子公式的优缺点分析
正文
一、弱闭对称算子公式的定义与性质
弱闭对称算子公式,是数学领域中一种描述线性算子性质的公式。
它可以用来描述在给定的希尔伯特空间中的线性算子,该算子具有一些特殊的性质,例如对称性、弱闭性等。
弱闭对称算子公式在物理学、工程学等领域中有着广泛的应用。
二、弱闭对称算子公式的应用领域
1.物理学:在量子力学中,弱闭对称算子公式可以用来描述系统的能量本征值和本征态。
这对于理解原子、分子等微观粒子的性质和行为具有重要意义。
2.工程学:在信号处理、图像处理等领域,弱闭对称算子公式可以用来设计和分析各种算法,例如傅里叶变换、小波变换等。
这些算法在实际应用中具有很好的性能,可以有效地提取信号的特征信息、去除噪声等。
三、弱闭对称算子公式的优缺点分析
1.优点:弱闭对称算子公式具有很好的理论性质,可以用来描述许多实际问题中的线性算子。
同时,它在实际应用中也表现出了很好的性能,可以为各种工程问题提供有效的解决方案。
2.缺点:弱闭对称算子公式在某些情况下可能存在数值稳定性问题,需要采用一定的技巧来加以解决。
此外,由于其理论性质较为复杂,对于
初学者来说可能难以理解和掌握。
总之,弱闭对称算子公式是一种具有重要意义的数学工具,在物理学、工程学等领域中都有着广泛的应用。
求00型极限在弱条件下的简便方法

求00型极限在弱条件下的简便方法
陈新明;杨逢建
【期刊名称】《高等数学研究》
【年(卷),期】2010(13)5
【摘要】利用洛必达法则与等价无穷小代换对抽象函数的00型极限可得结论:设当x→x0时f(x)与g(x)为无穷小,g(x)~(x-x0)β,取k为正实数,使得fk(x)=A(x-
x0)α+o[(x-x0)α],其中A>0,α≥2,β>0为实数,则有limx→x0f(x)g(x)=1.该方法对求常见的00型极限都适用.当使用洛必达法则求limx→x0f(x)g(x)很复杂时,使用该方法可简化计算.
【总页数】2页(P32-33)
【作者】陈新明;杨逢建
【作者单位】仲恺农业工程学院计算科学学院,广州,510225;仲恺农业工程学院计算科学学院,广州,510225
【正文语种】中文
【中图分类】O171
【相关文献】
1.一种求1∞型未定式极限的简便方法 [J], 王群智
2.求无穷大的零次方型极限在弱条件下的简便方法 [J], 陈新明;杨逢建
3.《求0^0型极限在弱条件下的简便方法》注记 [J], 李永利;何晓娜
4.求∞/∞型未定式极限的一种简便方法 [J], 梁海滨
5.运用重要极限lim x→0(1+x)<sup>?/x</sup>=e求极限时的一个简便方法[J], 陈书勤
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弱无穷小算子算法
简介
弱无穷小算子算法(Weak Infinitesimal Operator Algorithm)是一种用于解决
非线性优化问题的数值计算方法。
它通过将非线性问题转化为一系列线性问题的求解,从而有效地降低了计算的复杂度。
背景
在实际问题中,我们经常需要求解非线性优化问题,即最小化或最大化一个非线性目标函数的值。
这类问题通常无法直接应用传统的数值优化方法进行求解,因为非线性函数具有复杂的数学形式,难以找到全局最优解。
弱无穷小算子算法应运而生,为我们提供了一种有效且高效的求解非线性优化问题的方法。
基本思想
弱无穷小算子算法基于泰勒展开和牛顿迭代方法,并结合了弱收敛理论。
它将原始的非线性优化问题转化为一系列线性子问题来求解。
具体来说,该算法通过引入一个弱无穷小量(infinitesimal)来逐步逼近原始目标函数,并使用牛顿迭代方法
更新当前点的估计值,直到满足收敛准则为止。
算法步骤
1.初始化:选择初始点和收敛准则的阈值,设定迭代次数上限。
2.迭代更新:根据泰勒展开,将原始目标函数在当前点进行二阶近似,并引入
弱无穷小量。
3.线性子问题求解:将二阶近似后的目标函数转化为一个线性子问题,通过求
解线性子问题得到下一步的迭代点。
4.收敛判断:计算当前点与上一步迭代点之间的差异,并与收敛准则进行比较。
如果满足收敛准则,则停止迭代;否则返回第2步继续迭代。
5.输出结果:返回最终收敛的点作为最优解。
算法特点
•高效性:弱无穷小算子算法通过将非线性优化问题转化为一系列线性子问题来求解,大大降低了计算复杂度,提高了计算效率。
•全局收敛性:该算法基于牛顿迭代方法,具有全局收敛性。
在合理的初始点选择和适当的参数设定下,可以得到全局最优解。
•鲁棒性:弱无穷小算子算法对于非线性函数形式的要求相对较低,适用于各种类型的非线性优化问题。
•可扩展性:该算法可以与其他优化算法相结合,例如遗传算法、模拟退火等,形成一种混合优化方法,以解决更加复杂的问题。
应用领域
弱无穷小算子算法在许多领域都有广泛的应用,包括但不限于: - 机器学习:用
于求解非线性模型的参数优化问题。
- 金融工程:用于投资组合优化、风险管理
等问题。
- 工业工程:用于生产调度、物流规划等问题。
- 图像处理:用于图像分割、边缘检测等问题。
总结
弱无穷小算子算法是一种有效解决非线性优化问题的数值计算方法。
它通过将原始问题转化为一系列线性子问题来求解,在保证全局收敛性和高效性的同时,具有较好的鲁棒性和可扩展性。
该算法在实际应用中具有广泛的应用前景,可以帮助我们更好地解决各种复杂的非线性优化问题。
