立体几何综合试题
文科立体几何综合测试题

高三文科数学《立体几何》作业(20091121)一、 选择题(每道小题 5分,共 40分 )1. 如果平面α外一条直线 l 与α内的两条直线垂直,那么l 与α的位置关系是( )A .l ⊥αB . l ∥αC .l 与α斜交D .不能确定2. 如果a 、b 是异面直线,则a,b 的公垂线 ( )A .不一定存在B .有且只有一条C .可能有一条也可能有无数条D .一定有无数条3. 设a 、b 是异面直线,那么 ( )A .必然存在唯一的平面同时平行于直线a 和bB .必然存在唯一的平面同时垂直于直线a 和bC .过直线a 存在唯一的一个平面平行于直线bD .过直线a 存在唯一的一个平面垂直于直线b4. 如图,已知点A 在直线a 上,AB , AC 分别在平面βα,内,AB a AC a ⊥⊥,则以下结论不正确的( )A .BA 是AC 在α内的射影B .AC 是AB 在内的射影C .a ⊥平面ABCD .AB ⊥AC5. 若圆锥侧面展开图是半径为1的半圆,这个圆锥的体积是( )A B C D ....ππππ12243123246. 正方体ABCD -A 1B 1C 1D 1中,直线BC 1与直线A 1C 的位置关系是( ) A .相交且垂直 B .相交但不垂直 C .异面且垂直 D .异面但不垂直7 一个空间几何体的三视图,其中主视图和左视图的高为2,俯视图是边长为1的正六边形,那么这个几何体的体积为( )2361D C B A8 过圆锥顶点的一个截面与底面成60°的角,这截面截圆锥底面的圆所得劣弧是120°,底面圆心到截面距离是3cm ,则圆锥的侧面积是 ( )A 247cmB 12cmC 421cmD 821cm 222....ππππ72二、 填空(每题5分, 共20分)9. 过四条平行直线,最多可确定_______________个平面.10. 如果直线a ∥平面β,a ⊥平面α,则平面α与β的位置关系为________________.11 长方体ABCD -A'B'C'D'中棱AA'=5,AB=12,直线B'C'与平面A'BCD'的距离为___________ 12 E ,F 分别是边长为a 的正方形ABCD 的边BC 与CD 的中点,AC 交EF 于H ,现在沿AE ,EF ,AF 将正方形折成四面体,使D ,B ,C 重合,记重合后的点为G ,那么在四面体A-EFG中有:(1)AH 垂直平面EFG ;(2)AG 垂直平面EFG ;(3)四面体A-EFG 的体积为324a ;(4)四面体A-EFG 的体积为3232a 。
立体几何试题及解析

立体几何试题及解析第一题:求长方体的体积已知长方体的长为6cm,宽为4cm,高为3cm,求长方体的体积。
解析:长方体的体积公式为:体积 = 长 ×宽 ×高代入已知数据:体积 = 6cm × 4cm × 3cm = 72cm³所以长方体的体积为72立方厘米。
第二题:求正方体的表面积已知正方体的边长为5cm,求正方体的表面积。
解析:正方体的表面积公式为:表面积 = 6 ×边长²代入已知数据:表面积 = 6 × (5cm)² = 6 × 25cm² = 150cm²所以正方体的表面积为150平方厘米。
第三题:求圆柱体的体积已知圆柱体的底面半径为2cm,高度为8cm,求圆柱体的体积。
解析:圆柱体的体积公式为:体积= π × 半径² ×高度代入已知数据:体积= 3.14 × (2cm)² × 8cm ≈ 100.48cm³所以圆柱体的体积约为100.48立方厘米。
第四题:求球体的表面积已知球体的半径为3cm,求球体的表面积。
解析:球体的表面积公式为:表面积= 4π × 半径²代入已知数据:表面积= 4 × 3.14 × (3cm)² ≈ 113.04cm²所以球体的表面积约为113.04平方厘米。
总结:在几何学中,立体几何是其中的一个重要部分。
通过对不同类型立体的题目进行解析,可以加深对其体积、表面积等概念的理解。
掌握了基本的立体几何公式和计算方法,能够更好地解决与立体几何相关的问题。
在实际生活中,立体几何的应用广泛,例如建筑、工程、制造等领域。
因此,对立体几何的学习和理解具有重要的意义。
高一数学立体几何综合试题

高一数学立体几何综合试题1.正方体的棱长为1,为的中点,为线段的动点,过的平面截该正方体所得的截面记为,则下列命题正确的是①当时,为四边形②当时,为等腰梯形③当时,与的交点满足④当时,为六边形⑤当时,的面积为【答案】①②③⑤【解析】如图,当时,,即Q为CC1中点,此时可得,故可得截面APQD1为等腰梯形,故②正确;由上图当点Q向C移动时,满足,只需在DD1上取点M满足AM∥PQ,即可得截面为四边形APQM,故①正确;③时,如图,延长DD1至N,使,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,可证,由1,可得,故可、得,故正确;④由③可知当时,只需点Q上移即可,此时的截面形状仍然上图所示的APQRS,显然为五边形,故错误;⑤当时,Q与C1重合,取A1D1的中点F,连接AF,可证,可知截面为APC1F为菱形,故其面积为,故正确.【考点】空间图形与平面图形的关系2.下列说法正确的是( )A.三点确定一个平面B.平面和有不同在一条直线上的三个交点C.梯形一定是平面图形D.四边形一定是平面图形【答案】C【解析】A中应为不共线的三点确定一个平面,B与公理2矛盾,D中有空间四边形,而C中梯形有一组对边平行,是平面图形,所以选C.【考点】平面的基本性质.3.等腰梯形,上底,腰,下底,以下底所在直线为x轴,则由斜二测画法画出的直观图的面积为_______.【答案】【解析】如上图,,,,因为,所以,所以,在直观图中,【考点】斜二测画法4.如图,在五面体中,四边形是正方形,平面∥(1)求异面直线与所成角的余弦值;(2)证明:平面;(3)求二面角的正切值。
【答案】(1);(2)略;(3)。
【解析】(1)因为四边形ADEF是正方形,所以FA∥ED.故∠CED为异面直线CE与AF所成的角.因为FA⊥平面ABCD,所以FA⊥CD.故ED⊥CD.在Rt△CDE中,CD=1,ED=2, CE==3,故cos∠CED==.所以异面直线CE和AF所成角的余弦值为。
立体几何高考综合试题(含答案)

立体几何1.【云南省昆明市2019届高三高考5月模拟数学试题】已知直线l ⊥平面α,直线m ∥平面β,若αβ⊥,则下列结论正确的是A .l β∥或l β⊄B .//l mC .m α⊥D .l m ⊥ 【答案】A【解析】对于A ,直线l ⊥平面α,αβ⊥,则l β∥或l β⊂,A 正确;对于B ,直线l ⊥平面α,直线m ∥平面β,且αβ⊥,则//l m 或l 与m 相交或l 与m 异面,∴B 错误;对于C ,直线m ∥平面β,且αβ⊥,则m α⊥或m 与α相交或m α⊂或m α∥,∴C 错误; 对于D ,直线l ⊥平面α,直线m ∥平面β,且αβ⊥,则//l m 或l 与m 相交或l 与m 异面,∴D 错误.故选A .【名师点睛】本题考查了空间平面与平面关系的判定及直线与直线关系的确定问题,也考查了几何符号语言的应用问题,是基础题.2.【陕西省2019届高三年级第三次联考数学试题】已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为A B .34C D .54 【答案】B【解析】如图,设BC 的中点为D ,连接1A D 、AD 、1A B ,易知1A AB ∠即为异面直线AB 与1CC 所成的角(或其补角).设三棱柱111ABC A B C -的侧棱与底面边长均为1,则AD =112A D =,1A B =,由余弦定理,得2221111cos 2A A AB A B A AB A A AB +-∠=⋅111322114+-==⨯⨯. 故应选B.【名师点睛】本题主要考查了异面直线所成角的求解,通过平移找到所成角是解这类问题的关键,若平移不好作,可采用建系,利用空间向量的运算求解,属于基础题.解答本题时,易知1A AB ∠即为异面直线AB 与1CC 所成的角(或其补角),进而通过计算1ABA △的各边长,利用余弦定理求解即可. 3.【四川省宜宾市2019届高三第三次诊断性考试数学试题】如图,边长为2的正方形ABCD 中,,E F 分别是,BC CD 的中点,现在沿,AE AF 及EF 把这个正方形折成一个四面体,使,,B C D 三点重合,重合后的点记为P ,则四面体P AEF -的高为A .13B .23C .34D .1【答案】B 【解析】如图,由题意可知PA PE PF ,,两两垂直,∴PA ⊥平面PEF ,∴11111123323PEF A PEF V S PA -=⋅=⨯⨯⨯⨯=△, 设P 到平面AEF 的距离为h , 又2111321212112222AEF S =-⨯⨯-⨯⨯-⨯⨯=△, ∴13322P AEF h V h -=⨯⨯=, ∴123h =,故23h =, 故选B .【名师点睛】本题考查了平面几何的折叠问题,空间几何体的体积计算,属于中档题.折叠后,利用A PEF P AEF V V --=即可求得P 到平面AEF 的距离.4.【广东省深圳市高级中学2019届高三适应性考试(6月)数学试题】在三棱锥P ABC -中,平面PAB ⊥平面ABC ,ABC △是边长为6的等边三角形,PAB △是以AB 为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______.【答案】48π【解析】如图,在等边三角形ABC 中,取AB 的中点F ,设等边三角形ABC 的中心为O ,连接PF ,CF ,OP .由6AB =,得23AO BO CO CF OF ===== PAB △是以AB 为斜边的等腰角三角形,PF AB ∴⊥,又平面PAB ⊥平面ABC ,PF ∴⊥平面ABC ,PF OF ∴⊥,OP ==则O 为棱锥P ABC -的外接球球心,外接球半径R OC ==∴该三棱锥外接球的表面积为(24π48π⨯=,故答案为48π. 【名师点睛】本题主要考查四面体外接球表面积,考查空间想象能力,是中档题. 要求外接球的表面积和体积,关键是求出球的半径.求外接球半径的常见方法有:①若三条棱两两垂直,则用22224R a b c =++(,,a b c 为三条棱的长);②若SA ⊥面ABC (SA a =),则22244R r a =+(r 为ABC △外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径. 5.【2019北京市通州区三模数学试题】如图,在四棱柱1111ABCD A B C D -中,侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB =,12,5AC AA AD CD ,点E 为线段1AA 上的点,且12AE =.(1)求证:BE ⊥平面1ACB ;(2)求二面角11D AC B --的余弦值;(3)判断棱11A B 上是否存在点F ,使得直线DF ∥平面1ACB ,若存在,求线段1A F 的长;若不存在,说明理由.【答案】(1)见解析;(2;(3)见解析. 【解析】(1)因为1A A ABCD ⊥底面,所以1A A AC ⊥.又因为AB AC ⊥,所以AC ⊥平面11ABB A ,又因为BE ⊂平面11ABB A ,所以AC ⊥BE .因为112AE AB AB BB ==,∠EAB =∠ABB 1=90°, 所以1Rt Rt ABE BB A△∽△.所以1ABE AB B ∠=∠.因为1190BAB AB B ∠+∠=︒,所以190BAB ABE ∠+∠=︒.所以BE ⊥1AB .又1AC AB A =,所以BE ⊥平面1ACB .(2)如图,以A 为原点建立空间直角坐标系,依题意可得111(0,0,0),(0,1,0),(2,0,0),(1,2,0),(0,0,2),(0,1,2),(2,0,2),A B C D A B C 11(1,2,2),(0,0,)2D E .由(1)知,1(0,1,)2EB 为平面1ACB 的一个法向量, 设(,,)x y z =n 为平面1ACD 的法向量.因为1(1,2,2),(2,0,0)AD AC ,则10,0,AD AC ⎧⋅=⎪⎨⋅=⎪⎩n n 即220,20,x y z x -+=⎧⎨=⎩ 不妨设1z =,可得(0,1,1)=n . 因此10cos ,10||||EBEBEB n n n . 因为二面角11D AC B --为锐角,所以二面角11D AC B . (3)设1A F a ,则(0,,2)F a ,(1,2,2)DF a . 1(1,2,2)(0,1,)2102DF EB a a , 所以1a =-(舍). 即直线DF 的方向向量与平面1ACB 的法向量不垂直,所以,棱11A B 上不存在点F ,使直线DF ∥平面1ACB . 【名师点睛】本题主要考查线面垂直与平行、以及二面角的问题,熟记线面垂直的判定定理以及空间向量的方法求二面角即可,属于常考题型.(1)根据线面垂直的判定定理,直接证明,即可得出结论成立; (2)以A 为原点建立空间直角坐标系,由(1)得到1(0,1,)2EB 为平面1ACB 的一个法向量,再求出平面1ACD 的一个法向量,求两向量夹角的余弦值,即可得出结果;(3)先设1A Fa ,用向量的方法,由0DF EB 求出a 的值,结合题意,即可判断出结论.。
立体几何试题及答案

立体几何试题及答案一、选择题1. 已知一个正方体的体积为8立方厘米,那么它的棱长为多少厘米?A. 2B. 4C. 3D. 2√2答案:C2. 一个长方体的长、宽、高分别为3厘米、4厘米、5厘米,那么它的表面积是多少平方厘米?A. 62B. 94C. 96D. 100答案:B3. 一个圆锥的底面半径为3厘米,高为4厘米,那么它的体积是多少立方厘米?A. 36πB. 48πC. 72πD. 96π答案:B二、填空题4. 如果一个圆柱的底面半径为5厘米,高为10厘米,那么它的体积是_____立方厘米。
答案:7855. 一个球的体积是4/3π立方厘米,那么它的半径是_____厘米。
答案:16. 一个棱锥的底面是边长为4厘米的正方形,高为5厘米,那么它的体积是_____立方厘米。
答案:32三、解答题7. 已知一个圆锥的底面半径为3厘米,高为5厘米,求圆锥的体积。
解:圆锥的体积公式为V = 1/3πr²h,代入数据得:V = 1/3 × π × 3² × 5 = 15π(立方厘米)答:圆锥的体积为15π立方厘米。
8. 一个正四面体的棱长为a厘米,求它的体积。
解:正四面体的体积公式为V = a³√2/12,代入数据得:V = a³√2/12(立方厘米)答:正四面体的体积为a³√2/12立方厘米。
9. 一个长方体的长、宽、高分别为2a厘米、a厘米、a厘米,求它的体积。
解:长方体的体积公式为V = 长× 宽× 高,代入数据得:V = 2a × a × a = 2a³(立方厘米)答:长方体的体积为2a³立方厘米。
立体几何综合测试题

第七篇 检测试题(时间:120分钟 满分:150分)【选题明细表】一、选择题(本大题共12小题,每小题5分,共60分)1.已知a 、b 表示直线,α、β表示平面,则a ∥α的一个充分条件是( D ) (A)α∥β,a ∥β (B)α⊥β,a ⊥β (C)a ∥b,b ∥α (D)α∩β=b,a ⊄α,a ∥b解析:对于A 选项直线a 有可能在平面α内,B 选项可以推出a ∥α,或者a 在平面α内,对于C 选项直线a 有可能在平面α内,D 选项是正确的,故选D.2.(2012青岛第二次质检)已知直线l ⊥平面α,直线m ⊂平面β,则下列四个命题: ①α∥β⇒l ⊥m;②α∥β⇒l ∥m;③l ∥m ⇒α⊥β;④l ⊥m ⇒α⊥β 其中正确的是( C ) (A)①② (B)③④ (C)①③ (D)②④解析:①α∥β,l ⊥α,则l ⊥β,∵m ⊂β,∴l ⊥m,①正确,故②错.③l ∥m,l ⊥α,则m ⊥α,又m ⊂β,∴α⊥β,故③正确,④l ⊥m,l ⊥α,则m ∥α或m ⊂α,α,β可能平行,故④错.故①③正确,选C.3.已知某个几何体的三视图如图(正视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的表面积是( B )(A)(92+20π) cm 2 (B)(92+14π) cm 2 (C)(112+14π) cm 2 (D)(92+10π) cm 2 解析:如图,直观图S=4×5×3+4×4×2+21×2π×2×5+π×22=92+14π(cm 2),故选B.4.一个平面四边形的斜二测画法的直观图是一个边长为a 的正方形,则原平面四边形的面积等于( B )(A)42 a 2(B)22a 2(C)22 a 2(D)322a 2解析:根据斜二测画法画平面图形的直观图的规则,可以得出一个平面图形的面积S 与它的直观图的面积S'之间的关系是S'=42S,本题中直观图的面积为a 2,所以原平面四边形的面积等于422a =22a 2.故选B.5.已知各顶点都在一个球面上的正四棱柱的高为2,这个球的表面积为6π,则这个正四棱柱的体积为( B ) (A)1 (B)2 (C)3 (D)4解析:S 表=4πR 2=6π,∴R=26,设正四棱柱底面边长为x, 则(22x)2+1=R 2,∴x=1, ∴V 正四棱柱=2.故选B.6.平面α外有两条直线m 和n,如果m 和n 在平面α内的射影分别是直线m 1和直线n 1,给出下列四个命题:①m 1⊥n 1⇒m ⊥n;②m ⊥n ⇒m 1⊥n 1;③m 1与n 1相交⇒m 与n 相交或重合;④m 1与n 1平行⇒m 与n 平行或重合.其中不正确的命题个数是( D ) (A)1 (B)2 (C)3 (D)4解析:如图,在正方体中,AD 1,AB 1,B 1C 在底面上的射影分别是A 1D 1,A 1B 1,B 1C 1.由A 1D 1⊥A 1B 1,而AD 1不垂直AB 1,故①不正确;又因为AD 1⊥B 1C,而A 1D 1∥B 1C 1,故②也不正确;若m 1与n 1相交,则m 与n 还可以异面,③不正确;若m 1与n 1平行,m 与n 可以异面,④不正确.故选D.7.(2011承德模拟)下列四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出 AB ∥平面MNP 的图形的序号是( C )(A)①③ (B)②③ (C)①④ (D)②④解析:对于图形①:平面MNP 与AB 所在的对角面平行,即可得到AB ∥平面MNP,对于图形④:AB ∥PN,即可得到AB ∥平面MNP,图形②、③都不可以.故选C.8.已知m,n 是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的为( D ) (A)若α⊥γ,β⊥γ,则α∥β (B)若m ∥α,m ∥β,则α∥β (C)若m ∥α,n ∥α,则m ∥n (D)若m ⊥α,n ⊥α,则m ∥n解析:A 中,垂直于同一平面的平面可能平行或者相交;B 中,平行于同一直线的平面可能平行或者相交;C 中,平行于同一平面的直线可以是任意关系;D 中,垂直于同一平面的直线平行,正确.故选D.9.如图,正方体ABCD A 1B 1C 1D 1中,M,N 分别为AB,DC 中点,则直线MC 与D 1N 所成角的余弦值为( B )(A)21(B) 51 (C)-51 (D)-31解析:连接NA,D 1A(图略),则∠D 1NA 为所求,在三角形D 1NA 中由余弦定理可求得cos ∠D 1NA=51.故选B. 10.在二面角αl β的两个面α,β内,分别有直线a,b,它们与棱l 都不垂直,则( B )(A)当该二面角是直二面角时,可能a ∥b,也可能a ⊥b (B)当该二面角是直二面角时,可能a ∥b,但不可能a ⊥b (C)当该二面角不是直二面角时,可能a ∥b,但不可能a ⊥b (D)当该二面角不是直二面角时,不可能a ∥b,也不可能a ⊥b解析:当该二面角为直二面角时(如图),∵b 与l 不垂直,在b 上取点A,过A 作AB ⊥l,AB ∩b=A,假设a ⊥b,∵α⊥β,AB ⊥l,∴AB ⊥α,∴AB ⊥a. 又b ⊥a,∴a ⊥β,又l ⊂β,∴a ⊥l,与题设a 与l 不垂直矛盾,故不可能a ⊥b,故选B.11.三棱锥P ABC 的高为PH,若三个侧面两两垂直,则H 为△ABC 的( C ) (A)内心 (B)外心 (C)垂心 (D)重心解析:三个侧面两两垂直得AP ⊥面PBC,故BC ⊥PA.又BC ⊥PH,∴BC ⊥AH,同理BH ⊥AC,CH ⊥AB,故H 为垂心. 故选C.12.在空间中,给出下面四个命题:(1)过一点有且只有一个平面与已知直线垂直;(2)若平面外两点到平面的距离相等,则过两点的直线必平行于该平面;(3)两条相交直线在同一平面的射影必为相交直线;(4)两个相互垂直的平面,一个平面内存在一直线垂直于另一平面内的无数条直线. 其中正确的是( D ) (A)(1)(2) (B)(2)(3) (C)(3)(4) (D)(1)(4)解析:(1)正确;对于(2)该直线与平面可能相交即两点在平面异侧,故(2)错;对于(3)两相交直线的射影可能为一条直线,故(3)错;(4)正确.故选D.二、填空题(本大题共4小题,每小题5分,共20分)13.如图,一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为 .解析:设球的半径为r,则三个几何体的体积分别为V 1=πr 2·2r=2πr 3,V 2=31πr 2·2r=32πr 3,V 3=34πr 3,所以三个几何体的体积之比为3∶1∶2.答案:3∶1∶214.一条直线和一个平面所成的角为60°,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是 .解析:在平面内存在一直线和其垂直,所以此直线和平面内不经过斜足的所有直线所成的角中最大的角是90°.答案:90°15.将正方形ABCD 沿AC 折成直二面角后,∠DAB= .解析:取AC 中点E,连结BE 、DE.设原正方形ABCD 的边长为a, ∵AB=BC,AD=CD, ∴BE ⊥AC,DE ⊥AC, ∴∠BED=90°, 在Rt △ABC 和Rt △ACD 中,BE=DE=22a. 在Rt △BDE 中, ∴BD=22DE BE =a. ∴△ABD 为正三角形, ∴∠DAB=60°. 答案:60°16.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .解析:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”. 答案:36三、解答题(本大题共6小题,共70分) 17.(本小题满分10分)(2011温州模拟)如图,在长方体ABCD A 1B 1C 1D 1中,AA 1=AD=a,AB=2a,E 、F 分别为C 1D 1、A 1D 1的中点.(1)求证:DE ⊥平面BCE; (2)求证:AF ∥平面BDE.证明:(1)∵BC ⊥侧面CDD 1C 1, DE ⊂侧面CDD 1C 1,∴DE ⊥BC. 在△CDE 中,CD=2a,CE=DE=2a, 则有CD 2=CE 2+DE 2, ∴∠DEC=90°,∴DE ⊥EC,又BC ∩EC=C,∴DE ⊥平面BCE.(2)连接EF 、A 1C 1,连接AC 交BD 于O,连接OE, ∵EF21A 1C 1,AO 21A 1C 1, ∴四边形AOEF 是平行四边形, ∴AF ∥OE.又∵OE ⊂平面BDE,AF ⊄平面BDE, ∴AF ∥平面BDE. 18.(本小题满分12分)已知四面体ABCD(图(1)),沿AB 、AC 、AD 剪开,展成的平面图形正好是图(2)所示的直角梯形A 1A 2A 3D(梯形的顶点A 1、A 2、A 3重合于四面体的顶点A). (1)证明:AB ⊥CD;(2)当A 1D=10,A 1A 2=8时,求四面体ABCD 的体积.(1)证明:由图(2),A 1A 2A 3D 为直角梯形,得A 1B ⊥A 1D,A 2B ⊥A 2C.即图(1)中,AB ⊥AC,AB ⊥AD. 又AC ∩AD=A,∴AB ⊥平面ACD.∵CD ⊂平面ACD,∴AB ⊥CD.(2)解:在图(2)中, 作DE ⊥A 2A 3于E, ∵A 1A 2=8,∴DE=8, 又∵A 1D=A 3D=10, ∴EA 3=6,∴A 2A 3=10+6=16.而A 2C=A 3C,∴A 2C=8,即图(1)中AC=8,AD=10. 由A 1A 2=8,A 1B=A 2B,得图(1)中AB=4. S △ACD =CD A s 3∆=21×8×8=32. 由(1)知,AB ⊥平面ACD,∴ACD B V -=31×32×4=3128.19.(本小题满分12分)直棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.(1)求证:AC ⊥平面BB 1C 1C;(2)在A 1B 1上是否存在一点P,使得DP 与平面BCB 1与平面ACB 1都平行?证明你的结论. (1)证明: 直棱柱ABCD A 1B 1C 1D 1中, BB 1⊥平面ABCD,∴BB 1⊥AC. 又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2, ∴AC=2,∠CAB=45°,∴BC=2,∴ BC ⊥AC. 又BB 1∩BC=B,BB 1,BC ⊂平面BB 1C 1C, ∴ AC ⊥平面BB 1C 1C.(2)解:存在点P,P 为A 1B 1的中点.证明:由P 为A 1B 1的中点,有PB 1∥AB,且PB 1=21AB. 又∵DC ∥AB,DC=21AB,∴DC ∥PB 1且DC= PB 1, ∴四边形DCB 1P 为平行四边形,从而CB 1∥DP.又CB 1⊂平面ACB 1,DP ⊄平面ACB 1,∴DP ∥平面ACB 1. 同理,DP ∥平面BCB 1.20.(本小题满分12分)如图,在四棱台ABCD A 1B 1C 1D 1中,下底面ABCD 是边长为2的正方形,上底面A 1B 1C 1D 1是边长为1的正方形,侧棱DD 1⊥平面ABCD.(1)求证:B1B∥平面D1AC;(2)求证:平面D1AC⊥平面B1BDD1.证明:(1)设AC∩BD=E,连接D1E,∴B1D1∥BE, ∵B1D1=BE=2,∴四边形B1D1EB是平行四边形,∴B1B∥D1E.又因为B1B⊄平面D1AC,D1E⊂平面D1AC,所以B1B∥平面D1AC.(2)侧棱DD1⊥平面ABCD,AC⊂平面ABCD,∴AC⊥DD1.∵下底面ABCD是正方形,∴AC⊥BD.∵DD1与DB是平面B1BDD1内的两条相交直线,∴AC⊥平面B1BDD1.∵AC⊂平面D1AC,∴平面D1AC⊥平面B1BDD1.21.(本小题满分12分)(2011福州模拟)如图(1)所示,在边长为12的正方形AA'A'1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA'1分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A'A'1与AA1重合,构成如图(2)所示的三棱柱ABC A1B1C1.(1)求证:AB⊥PQ;(2)在底边AC上有一点M,AM∶MC=3∶4,求证:BM∥平面APQ.(1)证明:在图(2)中,∵AB=3,BC=4,∴AC=5,从而AC2=AB2+BC2,即AB⊥BC.又∵AB⊥BB1,而BC∩BB1=B,∴AB⊥平面BC1,又PQ⊂平面BC1,∴AB⊥PQ.(2)解:如图(3),过M 作MN ∥CQ 交AQ 于N,连接PN, ∵AM ∶MC=3∶4,∴AM ∶AC=MN ∶CQ=3∶7, ∴MN=PB=3,∵PB ∥CQ,∴MN ∥PB,∴四边形PBMN 为平行四边形, ∴BM ∥PN,∴BM ∥平面APQ. 22.(本小题满分12分)如图,四边形ABCD 为矩形,DA ⊥平面ABE,AE=EB=BC=2,BF ⊥平面ACE 于点F,且点F 在CE 上.(1)求证:AE ⊥BE;(2)求三棱锥D AEC 的体积;(3)设点M 在线段AB 上,且满足AM=2MB,试在线段CE 上确定一点N,使得MN ∥平面DAE. (1)证明:如题图,∵AD ⊥平面ABE,AD ∥BC, ∴BC ⊥平面ABE, ∴BC ⊥AE,又BF ⊥平面ACE, ∴BF ⊥AE, 又BF ∩BC=B, ∴AE ⊥平面BCE. 又BE ⊂平面BCE, ∴AE ⊥BE.解:(2)在△ABE 中,过点E 作EH ⊥AB 于点H, 则EH ⊥平面ABCD.由已知及(1)得EH=21AB=2,S △ADC =22.故AEC D V -=ADC E V -=31×22×2=34. (3)在△ABE 中过点M 作MG ∥AE 交BE 于点G,在△BEC 中过点G 作GN ∥BC 交EC 于点N,连接MN, ∵NG ∥BC ∥AD,MG ∥AE,AD ∩AE=A,MG ∩NG=G, ∴平面ADE ∥平面MGN, 又∵MN ⊂平面MGN, ∴MN ∥平面DAE.在线段CE 上存在点N,当CN=31CE 时,使得MN ∥平面DAE.。
立体几何试题及答案

立体几何试题及答案一、选择题1. 一个正方体的棱长为a,其表面积为:A. 3a²B. 4a²C. 6a²D. 8a²答案:C2. 一个长方体的长、宽、高分别为l、w、h,其体积为:A. lwhB. 2(lwh)C. l²wD. lw²答案:A3. 圆柱的底面半径为r,高为h,其体积为:A. πr²hB. 2πr²hC. πrhD. πr²答案:A二、填空题1. 一个球的体积公式为:_________________。
答案:\( V = \frac{4}{3}πr^3 \)2. 圆锥的体积公式为:_________________。
答案:\( V = \frac{1}{3}πr^2h \)3. 若一个棱锥的底面积为S,高为h,则其体积为:_________________。
答案:\( V = \frac{1}{3}Sh \)三、计算题1. 已知一个正四面体的棱长为a,求其表面积和体积。
解:正四面体的表面积为:\( S_{表} = 4 \times \frac{\sqrt{3}}{4}a^2 = \sqrt{3}a^2 \)正四面体的体积为:\( V = \frac{1}{3} \times \frac{\sqrt{3}}{4}a^2 \times\frac{\sqrt{2}}{2}a = \frac{\sqrt{2}}{12}a^3 \)2. 已知一个圆柱的底面半径为r,高为h,求其表面积和体积。
解:圆柱的表面积为:\( S_{表} = 2πr^2 + 2πrh \)圆柱的体积为:\( V = πr^2h \)四、证明题1. 证明:在一个球面上,任意两个大圆的弦所成的角都是直角。
证明:设球面上的两个大圆为O₁O₂和O₃O₄,弦AB和CD分别位于这两个大圆上,连接O₁A、O₁B、O₂A、O₂B、O₃C、O₃D、O₄C、O₄D。
高考数学总复习《立体几何》部分试题及答案

高考数学总复习试卷立体几何综合训练第I卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题正确的是()A.直线a,b与直线l所成角相等,则a//bB.直线a,b与平面α成相等角,则a//bC.平面α,β与平面γ所成角均为直二面角,则α//βD.直线a,b在平面α外,且a⊥α,a⊥b,则b//α2.空间四边形ABCD,M,N分别是AB、CD的中点,且AC=4,BD=6,则()A.1<MN<5 B.2<MN<10C.1≤MN≤5 D.2〈MN<53.已知AO为平面α的一条斜线,O为斜足,OB为OA在α内的射影,直线OC在平面α内,且∠AOB=∠BOC=45°,则∠AOC等于()A.30°B.45°C.60°D.不确定4.甲烷分子结构是:中心一个碳原子,外围四个氢原子构成四面体,中心碳原子与四个氢原子等距离,且连成四线段,两两所成角为θ,则cosθ值为()A.B.C.D.5.对已知直线a,有直线b同时满足下面三个条件:①与a异面;②与a成定角;③与a距离为定值d,则这样的直线b有()A.1条B.2条C.4条D.无数条6.α,β是不重合两平面,l,m是两条不重合直线,α//β的一个充分不必要条件是()A.,且l//β,m//βB.,且l//mC.l⊥α,m⊥β,且l//m D.l//α,m//β,且l//m7.如图正方体中,E,F分别为AB,的中点,则异面直线与EF所成角的余弦值为( )A.B.C.D.8.对于任一个长方体,都一定存在一点:①这点到长方体的各顶点距离相等;②这点到长方体的各条棱距离相等;③这点到长方体的各面距离相等,以上三个结论中正确的是()A.①②B.①C.②D.①③9.在斜棱柱的侧面中,矩形最多有几个?A.2 B.3 C.4 D.610.正六棱柱的底面边长为2,最长的一条对角线长为,则它的侧面积为()A.24 B.12 C.D.11.异面直线a,b成80°角,P为a,b外的一个定点,若过P有且仅有2条直线与a,b所成的角相等且等于α,则角α属于集合()A.{α|0°〈α〈40°} B.{α|40°<α〈50°}C.{α|40°〈α<90°}D.{α|50°<α〈90°}12.从水平放置的球体容器的顶部的一个孔向球内以相同的速度注水,容器中水面的高度与注水时间t之间的关系用图象表示应为()第II卷(非选择题共90分)二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中横线上)13.正四棱锥S—ABCD侧棱长与底面边长相等,E为SC中点,BE与SA所成角的余弦值为_____________。
高二数学立体几何综合试题

高二数学立体几何综合试题1.如图,点为斜三棱柱的侧棱上一点,交于点,交于点.(1) 求证:;(2) 在任意中有余弦定理:.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明【答案】(1)见解析 (2) 见解析【解析】(1)由题意和三棱柱的性质,证出 CC1⊥平面PMN,再证 CC1⊥MN.(2)利用类比推理边“对应侧面面积”得出结论,证明用到余弦定理平行四边形的面积公式和题中的垂直关系.试题解析:(1) 证:;(4分)(2) 解:在斜三棱柱中,有,其中为平面与平面所组成的二面角.上述的二面角为,在中,,由于,∴有(12分)【考点】空间中直线与直线之间的位置关系;归纳推理.2.在△ABC 中,∠C =90°,∠B =30°,AC=1,M 为 AB 中点,将△ACM 沿 CM 折起,使 A、B 间的距离为,则 M 到面 ABC 的距离为()(A)(B)(C)1(D)【答案】A【解析】由已知得AB=2,AM=MB=MC=1,BC=,由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,则AD=,DE=,CE=.折起后,由BC2=AC2+AB2,知∠BAC=90°,又cos∠ECA=,∴AE2=CA2+CE2-2CA•CEcos∠ECA=,于是AC2=AE2+CE2.∴∠AEC=90°.∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥A-BCM的高,AE=。
设点M到面ABC的距离为h,∵S△BCM =,∴由VA-BCM=VM-ABC,可得×=××1×h,∴h=。
故选A.【考点】折叠问题,体积、距离的计算。
点评:中档题,折叠问题,要特别注意折叠前后“变”与“不变”的几何量。
本题利用“等体积法”,确定了所求距离。
3.正四棱锥中,,点M,N分别在PA,BD上,且.(Ⅰ)求异面直线MN与AD所成角;(Ⅱ)求证:∥平面PBC;(Ⅲ)求MN与平面PAB所成角的正弦值.【答案】(1)90o(2)要证明线面平行,则主要证明线线平行即可,结合判定定理得到。
高二数学立体几何综合试题答案及解析

高二数学立体几何综合试题答案及解析1.以正方体的任意4个顶点为顶点的几何形体有①空间四边形;②每个面都是等边三角形的四面体;③最多三个面是直角三角形的四面体;④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.【答案】①②④【解析】①只要不在同一平面上的四个点连结而成的四边形都是空间四边形. ②从一个顶点出发与它的三个对角面的顶点连结所成的四棱锥符合条件.最多有四个直角四面体.由一个顶点和又该点出发的两条棱的端点及一个对角面的定点四点即可.所以③不成立. ④显然成立.故选①②④.【考点】1.空间图形的判断.2.空间中线面间的关系.2.下列关于用斜二测画法画直观图的说法中,错误的是()A.用斜二测画法画出的直观图是在平行投影下画出的空间图形B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C.水平放置的矩形的直观图是平行四边形D.水平放置的圆的直观图是椭圆【答案】B【解析】选项.用斜二测画法画出的直观图是在平行投影下画出的空间图形,正确;选项.斜二测画法的规则中,已知图形中平行于轴的线段,在直观图中保持原长度不变;平行于轴的线段,长度为原来的一半.平行于轴的线段的平行性和长度都不变.故几何体的直观图的长、宽、高与其几何体的长、宽、高的比例不相同;选项.水平放置的矩形的直观图是平行四边形,正确;选项.水平放置的圆的直观图是椭圆,正确.故选【考点】斜二测画法画直观图.3.如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=.(1)证明:平面A1BD∥平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.【答案】(1)证明见解析;(2)1.【解析】(1)设线段的中点为,易得四边形为平行四边形,得,又,,,所以平面平面;(2)因为平面,所以是三棱柱的高,所以三棱柱的体积,通过计算即可得出三棱柱的体积.试题解析:(1) 设线段的中点为.和是棱柱的对应棱同理,和是棱柱的对应棱且且四边形为平行四边形,,平面平面(2)平面是三棱柱的高在正方形中,.在中,,三棱柱的体积.所以,三棱柱的体积.【考点】1.面面平行的判定定理;2.棱柱的体积.4.如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.(1)求证:B1C∥平面AC1M;(2)求证:平面AC1M⊥平面AA1B1B.【答案】 (1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形,且∠ACB=90°.连结A1C,设A1C∩AC1=O,连结MO,由题意可知,得到MO∥B1C,进一步得到B1C∥平面AC1M.(2)利用已知得到C1M⊥A1B1,根据平面A1B1C1⊥平面AA1B1B,得到C1M⊥平面AA1B1B,达到证明目的:平面AC1M⊥平面AA1B1B.【解析】思路分析:首先,由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形。
高二数学立体几何综合试题

高二数学立体几何综合试题1.以正方体的任意4个顶点为顶点的几何形体有①空间四边形;②每个面都是等边三角形的四面体;③最多三个面是直角三角形的四面体;④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.【答案】①②④【解析】①只要不在同一平面上的四个点连结而成的四边形都是空间四边形. ②从一个顶点出发与它的三个对角面的顶点连结所成的四棱锥符合条件.最多有四个直角四面体.由一个顶点和又该点出发的两条棱的端点及一个对角面的定点四点即可.所以③不成立. ④显然成立.故选①②④.【考点】1.空间图形的判断.2.空间中线面间的关系.2.用斜二测画法作一个边长为2的正方形,则其直观图的面积为()A.B. 2C.4D.【答案】D【解析】用斜二测画法作一个边长为2的正方形,则其直观图与轴平行的长度不变其长度为2,与轴平行的一边长度变为原来其长度为1,相邻两边所成角是45°,所以其面积为.故选D【考点】斜二测画法3.如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=.(1)证明:平面A1BD∥平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.【答案】(1)证明见解析;(2)1.【解析】(1)设线段的中点为,易得四边形为平行四边形,得,又,,,所以平面平面;(2)因为平面,所以是三棱柱的高,所以三棱柱的体积,通过计算即可得出三棱柱的体积.试题解析:(1) 设线段的中点为.和是棱柱的对应棱同理,和是棱柱的对应棱且且四边形为平行四边形,,平面平面(2)平面是三棱柱的高在正方形中,.在中,,三棱柱的体积.所以,三棱柱的体积.【考点】1.面面平行的判定定理;2.棱柱的体积.4.已知四棱锥的底面是直角梯形,,,侧面为正三角形,,.如图所示.(1) 证明:平面;(2) 求四棱锥的体积.【答案】(1) 证明如下 (2)【解析】证明(1) 直角梯形的,,又,,∴.∴在△和△中,有,.∴且.∴.(2)设顶点到底面的距离为.结合几何体,可知.又,,于是,,解得.所以.【考点】直线与平面垂直的判定定理;锥体的体积公式点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。
数学立体几何测试题

数学立体几何测试题测试题一:立体图形的表示1. 画出一个正方体,并标注出各个面、边和顶点。
测试题二:计算立体图形的性质2. 一个立方体的棱长为10cm,求它的表面积和体积。
3. 一个正方体的对角线长为12cm,求它的棱长。
4. 一个正方体的棱长为8cm,求它的对角线长。
测试题三:计算截面图形的面积5. 一个圆柱体的底面半径为6cm,高为10cm,求它的体积。
6. 一个球的半径为5cm,求它的表面积。
7. 一个锥体的高为12cm,底面半径为8cm,求它的体积。
测试题四:判断立体图形的性质8. 判断以下说法是否正确:a) 一个正方体的每个面都是正方形。
b) 一个棱柱的底面和顶面都是正多边形。
9. 判断以下说法是否正确:a) 一个正方体的对角线长度等于它的体对角线的两倍。
b) 一个圆柱的高等于它的侧面积除以底面积。
10. 判断以下说法是否正确:a) 一个棱锥的底面是一个正多边形。
b) 一个正球的体积等于它的表面积乘以π倍。
测试题五:运用立体几何解决实际问题11. 一张纸片的形状是一个以边长为6cm的正方形,若将这张纸片折叠成一个正立方体,则每个小正方体的体积是多少?12. 一个长方体箱子的长、宽、高分别为8cm、6cm、10cm,请问这个箱子的体积是多少立方厘米?13. 一个蜡烛用圆柱体塑料包装,如果塑料包装的高度是12cm,底面直径为4cm,蜡烛的高度为10cm,并且蜡烛剩余部分的直径与底面直径相等,求蜡烛的剩余部分的高度。
测试题六:解答题14. 已知一个棱长为a的正方体,将它的每个面都截去边长为b的正方形,最后剩下的多面体的体积是多少?15. 一个高度为h的圆锥的底面半径为r,切一个与底面平行的截面得到一个半径为R的圆,若R>r,则这个圆锥的高度能使得截面圆的面积最大吗?为什么?答案测试题一:立体图形的表示1. 略。
测试题二:计算立体图形的性质2. 表面积 = 6 * 边长² = 6 * 10² = 600 cm²体积 = 边长³ = 10³ = 1000 cm³3. 对角线长 = 边长* √3 = 10 * √3 cm4. 对角线长 = 边长* √3 = 8 * √3 cm测试题三:计算截面图形的面积5. 体积= π * 半径² * 高度= π * 6² * 10 = 360π cm³6. 表面积= 4π * 半径² = 4π * 5² = 100π cm²7. 体积= (1/3) * π * 半径² * 高度= (1/3) * π * 8² * 12 = 256π cm³测试题四:判断立体图形的性质8. a) 正确b) 正确9. a) 错误,它们相等。
高一数学立体几何综合试题

高一数学立体几何综合试题1.如图是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在的直线是异面直线的有()A.1对B.2对C.3对D.4对【答案】C【解析】如图所示:把展开图再还原成正方体,由经过平面外一点和平面内一点的直线和平面内不进过该点的直线是异面直线可得,AB,CD,EF,GH这四条线段所在直线是异面直线的有:AB和 CD,AB 和 HG,EF 和 HC,共三对,故选 C.【考点】展开图还原几何体,异面直线.2.如图,三棱柱的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。
(I)求证:B1C//平面AC1M;(II)求证:平面AC1M⊥平面AA1B1B.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)由三视图还原为空间几何体的实际形状时,要从三视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体的实际形状时,一般以正视图和俯视图为主,结合侧视图进行综合考虑;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(3)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.试题解析:证明:(I)由三视图可知三棱柱为直三棱柱,底面是等腰直角三角形且,连结A1C,设。
连结MO,由题意可知A1O=CO,A1M=B1M,所以 MO//B1C.又平面;平面,所以平面 6分(II),又为的中点,平面,平面又平面所以平面AC1M⊥平面AA1B1B 12分【考点】(1)直线与平面平行的判定;(2)平面与平面垂直的判定.3.如图所示,直观图四边形是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A.B.C.D.【答案】A【解析】由题可得A¢D¢=A¢B¢=1,B¢C¢=1+,所以原平面图形中AD=1,AB=2,BC=1+,根据梯形的面积计算公式可得【考点】斜二测画法.4.在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形,则实数x的值为()A.-2B.2C.6D.2或6【答案】D【解析】因为在空间直角坐标系中,以点为顶点的是以为底边的等腰三角形.所以可得.有空间两点间的距离公式可得,解得.故选D.【考点】1.空间中的两点的距离公式.2.解二次方程的能力.5.如图,空间四边形的对棱、成的角,且,平行于与的截面分别交、、、于、、、.(1)求证:四边形为平行四边形;(2)在的何处时截面的面积最大?最大面积是多少?【答案】(1)利用线面平行的性质得到线线平行,然后再利用平行四边形的定义即可证明.(2)当E为AB的中点时,截面面积最大,,【解析】(1)平面,平面,平面平面,.同理,,同理,四边形为平行四边形.(2)与成角,或,当E为AB的中点时,截面面积最大,,【考点】本题考查了线面平行的性质及平行四边形的概念、面积点评:证明两直线平行的方法有:①依定义采用反证法;②利用公理4;③线面平行的性质定理;④面面平行的性质定理6.如图:是⊙的直径,垂直于⊙所在的平面,PA="AC," 是圆周上不同于的任意一点,(1) 求证:平面。
2023全国甲卷数学立体几何18题

(1)证明见解析.
(2) 13 13
【基本思路】 (1)根据线面垂直,面面垂直的判定与性质定理可得 A1O 平面 BCC1B1 ,再由勾股定理 求出 O 为中点,即可得证; (2)利用直角三角形求出 AB1 的长及点 A 到面的距离,根据线面角定义直接可得正弦值. 【详细解析】⑴如图,
第 4 页(共 5 页)
由 CM∥A1C1,CM A1C1知四边形 A1CMC1 为平行四边形, C1M∥A1C ,C1M 平面 ABC ,又 AM 平面 ABC ,
C1M AM 则在 Rt△AC1M 中, AM 2AC,C1M A1C , AC1 (2AC)2 A1C2 , 在 Rt△AB1C1 中, AC1 (2AC)2 A1C2 , B1C1 BC 3 ,
(1)证明见解析. (2)1
【基本思路】
(1)由 A1C 平面 ABC 得 A1C BC ,又因为 AC BC ,可证 BC 平面 ACC1A1 ,从而 证得平面 ACC1A1 平面 BCC1B1 ; (2) 过点 A1 作 A1O CC1 ,可证四棱锥的高为 A1O ,由三角形全等可证 A1C AC ,从而证 得 O 为 CC1 中点,设 A1C AC x ,由勾股定理可求出 x ,再由勾股定理即可求 A1O .
AB1 (2 2)2 ( 2)2 ( 3)2 13 , 又 A 到平面 BCC1B1 距离也为 1,
所以 AB1 与平面 BCC1B1 所成角的正弦值为
1 13
13
.
13
第 5 页(共 5 页)
【详细解析】 ⑴证明:因为 A1C 平面 ABC , BC 平面 ABC , 所以 A1C BC , 又因为 ACB 90o,即 AC BC ,
立体几何平行与垂直综合测试题
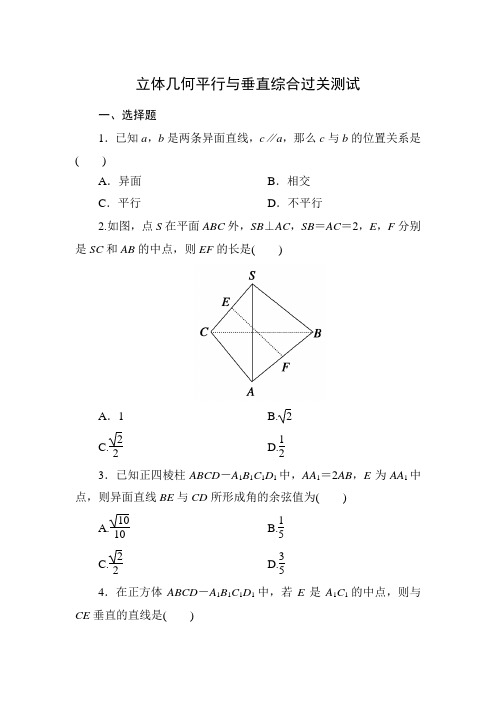
立体几何平行与垂直综合过关测试一、选择题1.已知a ,b 是两条异面直线,c ∥a ,那么c 与b 的位置关系是( )A .异面B .相交C .平行D .不平行2.如图,点S 在平面ABC 外,SB ⊥AC ,SB =AC =2,E ,F 分别是SC 和AB 的中点,则EF 的长是( )A .1 B. 2 C.22D.123.已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,E 为AA 1中点,则异面直线BE 与CD 所形成角的余弦值为( )A.1010B.15C.22D.354.在正方体ABCD -A 1B 1C 1D 1中,若E 是A 1C 1的中点,则与CE 垂直的直线是( )A.AC B.BDC.A1D D.A1D15.三棱锥P-ABC的高为PH,若三个侧面两两垂直,则H为△ABC的()A.内心B.外心C.垂心D.重心6.已知二面角α-l-β为60°,动点P,Q分别在面α,β内,P 到β的距离为3,Q到α的距离为23,则P,Q两点之间距离的最小值为()A.1 B.2C.2 3 D.47.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,错误的为()A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°8.如图所示,已知六棱锥P-ABCDEF的底面是正六边形,P A⊥平面ABC,P A=2AB,则下列结论正确的是()A.PB⊥ADB.平面P AB⊥平面PBCC.直线BC∥平面P AED.直线PD与平面ABC所成的角为45°9.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC10.正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是() A.线段B1CB.线段BC1C.BB1中点与CC1中点连成的线段D.BC中点与B1C1中点连成的线段二、填空题11.设平面α∥β,A,C∈α,B,D∈β,直线AB与CD交于点S,且S在α,β之间,AS=8,BS=9,CD=34,则CS=________.12.如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是________.13.直线l与平面α所成角为30°,l∩α=A,m⊂α,A∉m,则m 与l所成角的取值范围是________.14.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上述命题中,真命题的序号________(写出所有真命题的序号).三、解答题15.如图,棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是B1C1、C1D1的中点,(1)求证:E,F,B,D四点共面;(2)求四边形EFDB的面积.16、如图是一个正方体的表面展开图,MN和PQ是两条面对角线,请在图(2)的正方体中将MN,PQ画出来,并解答下列问题:(1)MN和PQ所成角的大小;(2)四面体M-NPQ的体积.17如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面P AD是等边三角形,且侧面P AD⊥底面ABCD,G为AD的中点.(1)求证:BG⊥平面P AD;(2)求证:AD⊥PB;(3)求二面角A-BC-P的大小.18如图,四棱锥P-ABCD的底面是正方形,PD⊥面ABCD,点E在棱PB上.(1)求证:平面AEC⊥平面PDB;(2)当PD=2AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.。
高三数学(理科)综合立体几何试题4个大题

立体几何复习试题1.如图甲所示,BO 是梯形ABCD 的高,∠BAD=45°,OB=BC=1,OD=3OA ,现将梯形ABCD 沿OB 折起如图乙所示的四棱锥P ﹣OBCD ,使得PC=,点E 是线段PB 上一动点.(1)证明:DE 和PC 不可能垂直;(2)当PE=2BE 时,求PD 与平面CDE 所成角的正弦值.2.如图,四棱锥P ABCD -中,底面ABCD 是矩形,面PAD ⊥底面ABCD ,且PAD ∆是边长为2的等边三角形,13,PC M =在PC 上,且PA 面MBD . (1)求证:M 是PC 的中点;(2)在PA 上是否存在点F ,使二面角F BD M --为直角?若存在,求出AFAP的值;若不存在,说明理由.3.如图,在四棱锥P -ABCD 中,BA ∥平面PCD ,平面P AD ⊥平面ABCD ,CD ⊥AD ,△APD 为等腰直角三角形,222PA PD CD ===. (1)证明:平面P AB ⊥平面PCD ; (2)若三棱锥B -P AD 的体积为13,求平面P AD 与平面PBC 所成二面角的余弦值.4.如图,在圆柱OO 1中,矩形ABB 1A 1是过OO 1的截面CC 1是圆柱OO 1的母线,AB=2,AA 1=3,∠CAB=.(1)证明:AC 1∥平面COB 1;(2)在圆O 所在的平面上,点C 关于直线AB 的对称点为D ,求二面角D ﹣B 1C ﹣B 的余弦值.PDCAB立体几何复习试题试卷答案1.【解答】(1)证明:如图甲所示,因为BO 是梯形ABCD 的高,∠BAD=45°,所以AO=O B…(1分) 因为BC=1,OD=3OA ,可得OD=3,OC=…(2分)如图乙所示,OP=OA=1,OC=,PC=,所以有OP 2+OC 2=PC 2,所以OP ⊥OC…(3分)而OB ⊥OP ,OB ∩OC=O ,所以OP ⊥平面OPD…(4分)又OB ⊥OD ,所以OB 、OD 、OP 两两垂直.故以O 为原点,建立空间直角坐标系(如图),则P (0,0,1),C (1,1,0),D (0,3,0)设E (x ,0,1﹣x ),其中0≤x ≤1,所以=(x ,﹣3,1﹣x ),=(1,1,﹣1),假设DE 和SC 垂直,则=0,有x ﹣3+(1﹣x )(﹣1)=0,解得x=2,这与0≤x ≤1矛盾,假设不成立,所以DE 和SC 不可能垂直…(6分) (2)解:因为PE=2BE ,所以 E (,0,)…(7分) 设平面CDE 的一个法向量是=(x ,y ,z ),因为=(﹣1,2,0),=(,﹣3,),所以取=(2,1,5)…(10分) 而=(0,3,﹣1),所以|cos <,>=,所以PD 与平面CDE 所成角的正弦值为.…(12分)2.解答:(1)证明:连AC 交BD 于E ,连.ME ABCD 是矩形,E ∴是AC 中点.又PA 面MBD ,且ME 是面PAC 与面MDB 的交线, ,PA ME M ∴∴是PC 的中点.(2)取AD 中点O ,由(1)知,,OA OE OP 两两垂直. 以O 为原点,,,OA OE OP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系(如图),则各点坐标为()()()()()1331,0,0,1,3,0,1,0,0,1,3,0,0,0,3,,,222A B D C P M ⎛⎫--- ⎪ ⎪⎝⎭.设存在F 满足要求,且AFAPλ=,则由AF AP λ=得:()1,0,3F λλ-,面MBD 的一个法向量为231,,33n ⎛⎫=- ⎪ ⎪⎝⎭,面FBD 的一个法向量为221,,33m λλ-⎛⎫=- ⎪⎝⎭,由·0n m =,得421093λλ-++=,解得38λ=,故存在F ,使二面角F BD M --为直角,此时38AF AP =. 3.解:(1)依题:CD ADPAD ABCD ⊥⎧⎨⊥⎩面面CD ⇒⊥面PAD CD AP ⇒⊥,又AP PD ⊥,AP ∴⊥平面PCD ,又AP ⊂平面PAB ,∴平面PAB ⊥平面PCD(2)ABCD PCD CD BA PCD⋂=⎧⎨⎩平面平面∥平面BA CD ⇒∥,由(1)知AB ⊥面PAD1132B PAD V AB PA PD -∴=⋅⋅113AB =⇒=, 取AD 中点O ,PO AD ⊥,平面PAD 平面ABCD ,PO ∴平面ABCD ,以过点O 且平行于AB 的直线为x 轴,如图建系,各点坐标如图.由(1)易知平面PAD 的一法向量为()1,0,0m =,设平面PBC 的法向量为(),,n x y z =.()1,1,1PB =-,()2,1,1PC =--.0n PB n PC ⎧⋅=⎪⎨⋅=⎪⎩020x y z x y z +-=⎧⇒⎨--=⎩,取2x =,()2,1,3n =. cos ,m n =147m n m n⋅=,故所求二面角的余弦值为147.4.【解答】证明:(1)连结B 1C 1、BC 1,设BC 1∩B 1C=M , ∵BB 1CC 1,∴四边形BB 1C 1C 为平行四边形,∴M 为BC 1的中点,在△ABC 1中,O 为AB 的中点,∴MO ∥AC 1,又AC 1⊄平面B 1CD ,MO ⊂平面B 1CD ,∴AC 1∥平面COB 1. 解:(2)如图,∵AB 是圆O 的直径,∴AC ⊥BC ,∵C 1C ⊥平面ABC ,∴C 1C ⊥AC ,C 1C ⊥BC ,又∠BAC=60°,AB=2,∴AC=1,BC=,AA1=3,以点C为坐标原点,分别以CA,CB,OC1为x轴,y轴,z轴,建立空间直角坐标系,则C(0,0,0),A(1,0,0),B(0,,0),C1(0,0,3),O(,0),B1(0,),在圆O上,C,D关于直线AB对称,△AOC为正三角形,且OA=1,∴CD=,∠ACD=30°,过点D作DP⊥x轴,DQ⊥y轴,垂足分别为P,Q,则CP=CD•cos=,CQ=CD•sin,∴D(,0),∴=(,0),设平面CDB1的一个法向量=(x,y,z),则,取y=﹣,得=(1,﹣,1),平面B1BC的一个法向量=(1,0,0),设二面角D﹣B1C﹣B的二面角为θ,则cosθ==.故二面角D﹣B1C﹣B的余弦值为.。
立体几何测试题(8套)

(B)若a与b相交,b与c相交,则a与c也相交
(C)若a//b,b//c,则a//c
(D)若a与b异面,b与c异面,则a与c也是异面直线
4.已知异面直线a、b分别在平面α、β内,且α∩β=c,那么直线c( )
(A)一定与a、b交于同一点
(B)至少与a、b中的一条相交
(C)至多与a、b中的一条相交
4.若a,b是两条平行直线,且都不垂直与平面 ,那么a,b在平面 内的射影为()。
(A)两条平行线 (B)相交的两直线
(C)两条平行线或同一直线 (D)相交的两直线或同一直线
5.相交的两直线都是平面 的斜线,那么这两斜线在平面 的设影是()。
(A)同一直线 (B)相交的两直线
(C)两条平行直线 (D)一直线或两相交直线
三、解答题
12、已知正方体ABCD-A`B`C`D`中,E,F分别是A`B`,B`C`的中点。
求证:EF∥面AD`C。
13、已知PA⊥正方形ABCD,PA=AB=2,M,N为BC,CD中点,
⑴求C到面PAM的距离,⑵求BD到面PMN的距离。
立体几何测试1
参考答案
一、选择题ADBCDCDC
二、填空题(每小题5分,共15分)
6.和两条异面直线都相交的两条直线是( )
(A)平行直线(B)异面直线(C)相交直线(D)异面直线或相交直线
7.在正方体ABCD-A1B1C1D1中,12条棱互成异面直线的对数有( )
(A) 48对(B) 36对(C) 24对(D) 12对
8.分别平行于两条异面直线的两条直线的位置关系是( )
(A)异面直线(B)平行直线
21.夹在直二面角 -MN- 内的线段PQ(P,Q MN)与 , 所成的角分别为 ,则 应满足的条件是。
立体几何测试题(共10篇)

立体几何测试题(共10篇)立体几何测试题(一): 立体几何问题立体几何试题已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.1.EF平行于B1D1,B1D1平行于BD,所以EF平行于BD,EFBD四点共面2.F,D,A,C1属于平面A1ACC1,且AC1与PQ不平行,所以AC1与PQ相交A1C交平面DBFE于R点,又因为PQ属于平面DBFE,所以AC1与PQ相交于R 所以R属于PQ,PQR共线立体几何测试题(二): 几个书后练习题立体几何1.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.是否正确2.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.为什么不对谢不对,因为a有可能在经过b的面上,不是平行关系立体几何测试题(三): 一道数学基本的立体几何的题目~在正方形ABCD-A"B"C"D"中,P、Q分别为A"B"、BB"的中点.(1)求直线AP与CQ所成的角的大小(2)求直线AP与BD所成的角的大小我还没学过空间向量,1.取DC中点E,连EC,证明EC平行AP,用余弦定理算2.取AB中点F,连接FB,用余弦定理算【立体几何测试题】立体几何测试题(四): 求大量立体几何难题!立体几何综合试题(自己画图)1、已知正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点.(1)求证:DE‖平面A1B1C1;(2)求二面角A1—DE—B1的大小.2、已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF =BC=2a.(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么证明你的结论3、在底面是直角梯形的四棱锥中,AD‖BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a.(I)求二面角P—CD—A的正切值;(II)求点A到平面PBC的距离.4、在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.5、已知四棱锥P—ABCD,底面ABCD是菱形,平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值6.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P 在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.7、在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明平面;(II)证明平面EFD;(III)求二面角的大小.8、已知在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(I)试确定点F的位置,使得D1E⊥平面AB1F;(II)当D 1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).9、直四棱柱ABCD-A1B1C1D1的底面是梯形,AB‖CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点.点P到直线AD1的距离为⑴求证:AC‖平面BPQ⑵求二面角B-PQ-D的大小10、已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心.(Ⅰ)证明:AF⊥平面FD1B1;(Ⅱ)求异面直线EB与O1F所成角的余弦值;这些题应该还可以!你来试试吧!题不要求多就精就可以了!不懂的或不会做的,我来帮你解答!立体几何测试题(五): 立体几何初步练习题已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱B1C1,C1D1,A1B1,D1A1的中点,求证(1)MN平行于DEF,(2)平面AMN平行于平面CEF(1)连接B1D1因为MN、EF为三角形A1B1D1、B1C1D1的中位线,所以MN平行于EF因为MN不属于面DEF,EF属于面DEF所以MN平行于面DEF(2)这题题目错了吧,应该是DEF吧立体几何测试题(六): 解析几何基础知识练习题靠!一楼的那么多废话那么多选择题:集合,函数(图像),立体几何,圆锥一、数学命题原则 1.普通高等学校招生数学科的考试,按照“考查基础知识的【立体几何测试题】立体几何测试题(七): 高一必修二立体几何习题1-7的题仓库的房顶呈正四棱锥形,量的地面的边长为2.6m,侧棱长2.1m,先要在房顶上铺一层油毡纸,问:需要油毡纸的面积多少运用海伦公式房顶为4个相同的三角形海伦公式a=2.6 b=2.1 c=2.1 p=a+b+c/2=3.4S=根号下p*(p-a)*(p-b)*(p-c)=2.1444S=2.144*4=8.576平方米立体几何测试题(八): 怎么根据题目画数学的立体几何图形搞懂了题目的要求,就照那意思去画,立体几何记住透视很重要.立体几何测试题(九): 求立体几何判断题的解题方法.①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直⑤……等等,诸如此类.见到很多这样的题目,但是却总找不到解题的方法,概念定理也经常记混.本人感激不尽!记一些模型,例如墙角模型什么的这个很重要.遇见不熟悉的题,用书本和笔(手指也可以)比划一下.这种题目主要是找反例!想象力也很重要啦……立体几何测试题(十): 一道高中立体几何的题目.已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,O1是底面A1B1C1D1的中心.E 是CO1上的点,设CE等于X,四棱锥E-ABCD的体积为y,求y关于X的函数关系式..图只有自己画一下了,做EF垂直于平面ABCD 垂足为F易得出CEF相似于O1CC1因为C1O1=根号2 CC1=4 得CO1=3根号2CE/CO1=EF/CC1 得出EF=4X/3根号2Y=底面积*EF/3=4*4X/9根号2Y=8根号2*X/9职高立体几何测试题空间立体几何测试题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何综合试题1.如图,在正三棱柱 ABC — A i B i C i 中,各棱长都相等,D 、 (i )求证:DE //平面 A i B i C i ; (2)求二面角 A i — DE — B i E 分别为AC i , BB i 的中点。
的大小。
4.在直三棱柱 ABC — A i B i C i 中,CA=CB=CC i =2, / ACB=90 ° , E 、F 分别是 BA 、BC 的中点,G 是 AA i 上一点,且AC i 丄EG.(I)确定点 (n)求直线 G 的位置;AC 1与平面EFG 所成角0的大小.5 .已知四棱锥 2.如图:已知直二棱柱 ABC — A i B i C i , AB = AC , F 为棱 BB i 上一点,BF: FB i = 2: I , BF = BC =2a 。
(I )若D 为BC 的中点,E 为AD 上不同于 A 、D 的任意一点,证明 EF 丄FC i ; (II )试问:若 AB = 2a ,在线段AD 上的E 点能否使EF 与平面BB i C i C 成60°角, 的结论 为什么?证明你3. / ADC (I )P —ABCD ,底面ABCD 是菱形,点E 为AB 中点,点F 为PD 中点.(1) 证明平面 PED 丄平面PAB ;(2) 求二面角P —AB — F 的平面角的余弦值如图,在底面是直角梯形的四棱锥P — ABCD 中,AD // BC , / ABC = 90。
,且= arcsi 』,又 PA 丄平面 ABCD , AD = 3AB = 3PA = 3a 。
5求二面角P — CD — A 的正切值;(II )求点A 到平面PBC的距离。
-D6.在棱长为4的正方体ABCD-A i B i C i D i 中,0是正方形A i B i C i D i 的中心,点P 在棱CC i 上,且CC i =4CP. (I )求直线AP 与平面BCC i B i 所成的角的大小(结果用反三角函数值表示) ; (n )设0点在平面D i AP 上的射影是H ,求证: (川)求点P 到平面ABD 1的距离. C iP C7、如图,在四棱锥P - ASCD中,底面ABCD是正方形,侧棱PDi底面ABCD,PD- DC,E 是PC 的中点,作EFLPB交PB于点F。
(I)证明F盘II平面EDB; (II)证明PBi 平面EFD ;(Ill)求二面角BP氏D 的大小。
9、如图,直四棱柱ABCD-A i B i C i D i的底面是梯形,AB // CD,AD 丄DC,CD=2,DD i=AB=i,P、Q 分别是CC i、C i D i 的中点。
点P 到直线AD i 的距离为迟2⑴求证:AC //平面BPQ⑵求二面角B-PQ-D的大小&如图,在棱长为1的正方体ABCD —A i B i C i D i中,点E是棱BC的中点,点F 是棱CD上的动点.(I)试确定点F的位置,使得D i E丄平面AB i F;(II )当D i E丄平面AB i F时,求二面角C i —EF —A的余弦值. io (本题满分i3分)已知长方体ABCD —A i B i C i D i中,AB=BC=4,AA i=8,E、F分别为AD和CC i的中点,O i为下底面正方形的中心。
(I)证明:AF丄平面FD i B i;(n)求异面直线EB与O i F所成角的余弦值;D1立体几何1、(1)取 A i C i 中点 F ,连结 B i F , DF ,••• D i E 分别为 AC i 和 BB i 的中点,DF // AA i ,DF= (1/2) AA i , B I E / AA i , B i E= (1/2) AA i ,: DF // B i E , DF=B i E ,.・. DEB i F 为平行四边形,二 DE // B i F ,又 B i F 在平面 A i B i C i 内,DE 不在平面 A i B i C i ,: DE //平面 A i B i C i (2)连结A i D , A i E ,在正棱柱ABC — A i B i C i 中,因为平面A i B i C i 丄平面ACC i A i , A i C i 是平面A i B i C i 与平面ACC i A i 的交线,又因为 B i F 在平面A i B i C i 内,且B i F 丄A i C i ,,所以B i F 丄平面ACC i A i ,又DE // B i F ,所以DE 丄平面ACC i A i 所以/ FDA i 为二面角设正三棱柱 42DCi =——,AiD 2 2. (I )连结DF , DC •••三棱柱 ABC — A i B i C i 是直三棱柱, 的棱长为 1 ,因为/42=——,N A i DC i =900「Z FDA i 2A i — DE —B i 的平面角。
并且/ FDA 1 = ( 1/2)/ A i DC i , 点,所以 AA i C i =900, D 是 AC i 的中 =45°,即为所求的二面角的度数。
3/ ••• CC i 丄平面ABC,...平面BB i C i C 丄平面ABC•/ AB = AC , D 为 BC 的中点,••• AD 丄 BC , AD 丄平面 BB iC iC••• DF 为EF 在平面BB i C i C 上的射影,在^ DFC i 中,••• DF 2= BF 2+ BD 2= 5a 2, DC ; = CC-2 + DC 2= 10a 2,2 2 0 2FC i = B i F + B iG = 5a ,• DC i2 = DF 2 + FC i 2,• DF 丄 FC iFC 」EF (II ) •/ AD 丄平面BB i C i C , ••• / DFE 是 EF 与平面 BB i C i C所成的角在^ EDF 中,若/ EFD = 60 ,贝U ED = DFtg60 °= • 75a = V isa ,•••勺T5a >, ••• E 在DA 的延长线上,而不在线段AD 故线段AD 上的E 点不能使EF 与平面BB i C i C成60°角。
12/3.解:(1)在底面ABCD 内,过A 作AE 丄CD ,垂足为E ,连结PEPHrA 「■ 」 ;.\ 一E C-D•/ PA 丄平面ABCD ,由三垂线定理知: PE 丄CD •••/ PEA 是二面角 P — CD — A 的平面角 .......在 RUAED 中,AD = 3a , N ADE = arcsinPA 在 R U PAE 中,tan N PEA =—AE■ pn 坐”•. AE = AD rsin N AD^^-5a 5 5面角P —CD — A 的正切值为 V !3(II )在平面 APB 中,过 A 作AH 丄PB ,又AB 丄BC ,• BC 丄平面 PAB.••平面PBC 丄平面PAB••• AH 丄平面PBC 故AH 的长即为点 A 到平面PBC 的距离 垂足为 H •/ PA 丄平面 ABCD ,••• PA 丄BC10分4,在等腰直角三角形 PAB 中, 14分)解法一:(I)以C 为原点,分别以0), E (1, 1, 0), A (0, 2,AC i = (0-2,2)J 2AH = —— a ,所以点 A 到平面PBC 的距离为2a 4.(本小题满分 2CB 、CA 、CC i 为X 轴、y 轴、z 轴建立空间直角坐标系,则 F ( 1 , 0, 0), C i (0, 0, 2),设 G (0, 2, h ),则 EG = (—i,i,h)匚 •••— ix 0+1 X(— 2) +2h=0. ••• h=i ,AC i 丄 EG,「. EG-AC i = 0.即G 是AA i 的中点. (n)设m=(X, y,z)是平面EFG 的法向量,则 m 丄FE,ml EG.所以* 0x X 中1X y + 0x z - 0,平面EFG 的一个法向量 m = (1, 0, 1) _ X + y+ z = 0.|m 'AC 1| ••• sin e =二■,二= 2L = 1|m|・|AC i |2 2兀 为一6• 8 =—,即AC i 与平面EFG 所成角06解法二:(I)取 AC 的中点D ,连结DE 、DG ,贝U ED//BC •/ BC 丄 AC ,• ED 丄 AC.又 CC i±平面 ABC ,而 EDU 平面 ABC , • CC i±ED. •••CC i QAC=C ,• ED 丄平面 A i ACC i . ……3 分又••• AC i±EG ,• AC i± DG. ......... 4 分连结 A i C,v AC i 丄A i C ,.・. A i C//DG.•/ D是AC 的中点,••• G 是AA 1的中点 .. ........ 6分(n)取 CC i 的中点 M ,连结 GM 、FM ,贝U EF//GM , ••• E 、F 、M 、G 共面作C i H 丄FM ,交FM 的延长线于H ,14分10分1分C1器 ........ ”A••• AC 丄平面 BB i C i C ,%iC 1H U 平面 BB 1C 1C ,A AC 丄 G 1H ,又 AC//GM , A GM 丄 GH. •/ GM n FM=M ,二C 1H 丄平面EFG ,设AC 1与MG 相交于N 点,所以/ G N H 为直线AC 1与平面EFG 所成角0 . .............. 12 分.5.本小题主要考查空间中的线面关系,四棱锥的有关概念及余弦定理等基础知识,考查空 间想象能力和推理能力.满分12分.(1)证明:连接BD.DE [PC ① 同样由 PDi 底面ABCD ,得T 底面ABCD 是正方形, 有DC 丄船鳥C 丄平面PDC而DE 匚平面PDC ,.',BC VDE.②2分丄面 ABCD , AB U 面 ABCD ,二 AB 丄 PD.匸面 PED , PD U 面 PED , DE n PD=D,”・. AB 丄面 PED.由①和②推得 Q&丄平面PBC 而PB C 平面PBC , :,DSLPB又EFiPB 且DEHEZE ,所以丹丄平面EFD因为GH ¥,C 1N=H si心梟寺14分(II)证明:、:PD 丄底在ABCD 且DC 匚底面ABCD ,二 PD i DC.AB U 面 PAB 面 PED 丄面 PAB.(III)解:由(II)知,PB LDF 故 ZSFD 是二面角C~ PB ~D 的平面角(2)解: 连接EF ,二 NPEF 丁 AB 丄平面 PED ,PE U 面 PED ,二 AB 丄 PE. EF U PED ,二 AB 丄 EF •为二面角P — AB — F 的平面角. 设 AD=2,那么 PF=FD=1,DE= J 3 . 在 APEF 中,PE = J7,EF =2, PF =1,•••cos N P EF ”)2节-52X 2J 7 145" 即二面角P — AB — F 的平面角的余弦值为 5—146、解(1) N APB =arctan 土17(2 )略 (3) 37227方法一:证明:连结 AC ,AC 交BD 于0。
