两条直线的平行与垂直课件
合集下载
两条直线的平行与垂直ppt课件

C.垂直
D.重合
3.若直线l过点(-1,2)且与直线2x-3y+4=0垂直,则直线l的方程是( C ) A.2x-3y+5=0 B.2x-3y+8=0 C.3x+2y-1=0 D.3x+2y+7=0
根据今天所学,回答下列问题: 1.怎样根据直线方程的特征判断两条直线的平行或垂直关系呢? 2.判断两条直线是否平行的步骤是哪些? 3.判断两条直线是否垂直的方法有哪些?
1.直线l1与l2为两条不重合的直线,则下列命题正确的是( BCD ) A.若l1∥l2,则斜率k1=k2 B.若斜率k1=k2,则l1∥l2 C.若倾斜角α1=α2,则l1∥l2 D.若l1∥l2,则倾斜角α1=α2
2.已知直线l1的倾斜角为60°,直线l2经过点A(1, 3),B(-2,-2 3),则 直线l1,l2的位置关系是( A ) A.平行或重合 B.平行
解:(1)由题意知,直线
<m>l1</m>的斜率
<m>k1
=
5−1 −3−2
=
−
45</m>,
直线
<m>l2</m>的斜率
<m>k2
=
−7+3 8−3
=
−
45</m>,
所以直线 <m>l1</m>与直线 <m>l2</m>平行或重合,
又
<mk>BC
=
5− −3 −3−3
=
−
4 3
≠
−
45</m>,所以
所以 <m>l1//l2</m>.
人教版四年级数学上册5.1平行与垂直(第2课时画垂线)课件(20张ppt)

画线标号
沿三角尺的另一条直 角边画一条直线,并 标出直角符号,这条 直线就是已知直线的 垂线。
二、学习新课
画垂线的步骤(过直线外一点)
边线重合
把三角尺的一 条直角边与已 知直线重合。
边点重合
沿直线移动三角 尺,使三角尺的 另一条直角边过 直线外的已知点。
画线标号
沿三角尺的另一条直 角边画一条直线,并 标出直角符号,这条 直线就是已知直线的 垂线。
(2)沿着左边三角尺的斜边和右边三角尺的直角 边分别画一条直线并标出直角符号。
二、学习新课
用量角器画两条互相垂直的直线。
二、学习新课
用量角器画两条互相垂直的直线。
二、学习新课
用量角器画两条互相垂直的直线的步骤
(1)先画一条直线,并在直线上任意标出一个点, 这个点就是垂足。
(2)将量角器的0°刻度线与所画直线重合,再 将量角器的中心与标出的点重合,最后在量角器 的90°处点上一个点。
平行四边形和梯形
1 平行与垂直 第2课时 画垂线
一、情境引入
找一找平行与 垂直。
二、学习新课
你能画出互相垂直的两条直线吗?
①
②
③
二、学习新课
用两把三角尺画两条互相垂直的直线。
二、学习新课
用两把三角尺画两条互相垂直的直线。
标出直 角符号
二、学习新课
用两把三角尺画两条互相垂直的直线的步骤
(1)先放好一把三角尺,再把另一把三角尺和第 一把三角尺其中的一条直角边重合。
(2)沿着直线移动三角尺,使三角尺的另一条 直角边过直线外的已知点。
(3)沿着三角尺的另一条直角边,画一条直线 并标出直角符号,这条直线就是已知直线的垂 线。
二、学习新课
两条直线的平行与垂直课件

判断两条不重合直线是否平行的步骤
[跟进训练] 1.已知直线 l1 经过点 A(2,a),B(a-1,3),直线 l2 经过点 C(1, 2),D(-3,a+2). (1)若 l1∥l2,求 a 的值; (2)若 l1⊥l2,求 a 的值.
[解] 设直线 l1,l2 的斜率分别为 k1,k2,若 a=3,则 k1 不存在, k2=-34,则 l1 与 l2 既不平行,也不垂直.
1234
2.直线 2x+y+m=0 和 x+2y+n=0 的位置关系是( )
A.平行
B.垂直
C.相交但不垂直
D.不能确定
C [直线 2x+y+m=0 的斜率 k1=-2,直线 x+2y+n=0 的斜 率为 k2=-12,则 k1≠k2,且 k1k2≠-1.]
1234
3.l1 过点 A(m,1),B(-3,4),l2 过点 C(0,2),D(1,1),且 l1∥l2, 则 m=________.
(2)根据题意,得(k-3)×(-2)-2(k-3)×(4-k)=0, 解得 k=3 或 k=5.经检验,均符合题意. ∴若这两条直线平行,则 k=3 或 k=5.
1.利用斜率研究两直线的平行和垂直关系时,要分斜率存在、 不存在两种情况进行讨论.
2.当直线是一般式方程时,也可利用以下结论研究两直线的平 行和垂直关系:
1.两条直线平行
设两条不重合的直线 l1,l2,倾斜角分别为 α1,α2,斜率存在时
斜率分别为 k1,k2.则对应关系如下:
类型
斜率存在
斜率不存在
前提条件 对应关系
α1=α2≠90° l1∥l2⇔_k_1=__k_2_
α1=α2=90° l1∥l2⇐两直线斜率都不存在
图示
高中数学选择性必修一(人教版)《2.1.2两条直线平行和垂直的判定》课件

图示
l1 与 l2 中的一条斜率不
对应 l1 与 l2 的斜率都存在, 存在(倾斜角为 90°),另
关系 分别为 k1,k2,则 l1⊥ 一条斜率 为零 (倾斜 角
l2⇔ k1·k2=-1
为 0°),则 l1 与 l2 的位置
关系是 l1⊥l2
(二)基本知能小试
1.已知直线 l1 的斜率 k1=2,直线 l2 的斜率 k2=-12,则 l1 与 l2
故选 A. 答案:A
2.已知定点 A(-1,3),B(4,2),以 A,B 为直径作圆,与 x 轴有 交点 C,则交点 C 的坐标是_______.
解析:以线段 AB 为直径的圆与 x 轴的交点为 C, 则 AC⊥BC.设 C(x,0),则 kAC=x-+31,kBC=x--24, 所以x-+31·x--24=-1.解得 x=1 或 2. 所以 C 的坐标为(1,0)或(2,0). 答案:(1,0)或(2,0)
解得ab= =- 6. 1,
所以 D(-1,6). (2)因为 kAC=43- -21=1,kBD=-6-1-05=-1,
所以 kAC·kBD=-1. 所以 AC⊥BD.故平行四边形 ABCD 为菱形.
二、应用性——强调学以致用 2.如图,一个矩形花园里需要铺两条笔直的小路,
已知矩形花园长 AD 为 5 m,宽 AB 为 3 m, 其中一条小路定为 AC,另一条小路过点 D,问如何在 BC 上 找到一点 M,使得两条小路所在直线 AC 与 DM 互相垂直?
解:由题意知 A,B,C,D 四点在坐标平面内的位置如图所示, 由斜率公式可得 kAB=2-5--34=13, kCD=-0-3-36=13,kAD=-30--3-4=-3, kBC=36- -52=-12.
《平行与垂直》课件

物的高度、柱子和横梁等元素可以保持垂直,以实现视觉上的突出和力
量感。
02
城市规划
在城市规划中,垂直线用于划分不同的功能区域和空间层次。例如,商
业区、住宅区和公园等区域可以沿着垂直轴线进行布局,以实现空间的
有效利用和城市的可持续发展。
03
交通工程
在道路和桥梁设计中,垂直线用于支撑和连接不同的交通层面。这样可
如果一条直线与平面内的一条直 线垂直,那么这条直线与该平面
垂直。
斜线与平面
如果一条直线与平面内的两条相交 的直线都垂直,那么这条直线与该 平面垂直。
三垂线定理
如果平面内的一条直线与平面的一 条斜线在平面内的射影垂直,那么 这条直线与斜线垂直。
04
平行与垂直的应用
平行的应用
建筑学
在建筑设计中,平行线可以用来 构建对称、平衡和和谐的外观。 例如,窗户、门和墙面的线条可 以保持平行,以实现视觉上的统
填空题:若直线a与直线b平 行,且被直线c所截,则同位 角____,内错角____,同旁内
角____。
答案
判断题:错。应该是两条平行线被第三条直线所截,同位角相等。
选择题:B。
填空题:相等,相等,互补。
THANKS
感谢观看
一和美感。
交通工程
在道路和轨道设计中,平行线用 于规划车辆行驶的方向和路线。 这样可以确保交通流畅,减少事
故风险,并提高运输效率。
艺术与设计
在绘画、摄影和图形设计中,平 行线可以用来创造平衡、稳定和 动态的效果。艺术家可以利用平 行线来表达特定的主题和情感。
垂直的应用
01
建筑学
在建筑设计中,垂直线用于构建高大、雄伟和稳定的外观。例如,建筑
《平行与垂直》课件

Q&A
1 答疑解惑
解答听众在学习过程中提出的问题。
2 互动交流
与听众进行互动,促进学习交流。
2
判定平行与垂直的方法
讨论如何相互判定两条线段是否平行或垂。
3
实例分析
通过实际案例,展示平行和垂直的联合应用。
总结
1 平行和垂直的作用与重要性
总结平行与垂直在几何与日常生活中的重要作用。
2 跨领域的应用实例
展示平行与垂直在不同领域中的实际应用示例。
3 总结和展望
总结课件内容,并展望平行与垂直的未来发展。
展示生活中常见的平行线的实际应用,如建筑、城市规划等。
垂直
垂直的定义与性质
讨论垂直线段的定义及其相关 性质。
垂直线的判定方法
讲解如何判断两条线段是否垂 直,如角度、斜率等。
垂直线的应用场景
展示垂直线在不同领域的应用, 如建筑设计、电子工程等。
平行与垂直的关系
1
平行和垂直的比较
对比平行和垂直的特点,探讨二者之间的异同。
《平行与垂直》PPT课件
这个PPT课件将介绍平行与垂直的概念和应用,以生动的方式帮助您理解并区 分二者之间的关系。
介绍
• 平行与垂直的概念 • 平行与垂直在生活和工作中的应用
平行
平行的定义与性质
解释什么是平行线以及它们的基本性质。
平行线的判定方法
介绍多种判定两条线段平行的方法,如角度、距离等。
平行线的应用场景
《平行与垂直》ppt课件
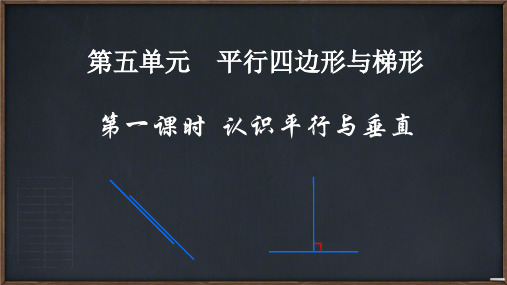
1.在同一个平面内不相交的两条直线叫做平行线,也可以
说这两条直线互相平行。
课 2.两条直线相交成直角,就说这两条直线互相垂直,其中
堂 概
一条直线叫作另一条直线的垂线,这两条直线的交点叫作 垂足。
念
小
结
第五单元 平行四边形与梯形
第二课时 垂线的画法
1.过直线上一点画垂线。
1.边线重合 2.移动靠点 3.画线标记
课 2.两条直线相交成直角,就说这两条直线互相垂直,其中
堂 概
一条直线叫作另一条直线的垂线,这两条直线的交点叫作
垂足。 3.画垂线步骤:一边线重合,二移动靠点,三画线标记。
念 4.经过直线外一点可以画1条已知直线的垂线。
小 5.从直线外一点到这条直线所画的垂直线段最短,它的长
结
度叫做这点到直线的距离。 6.端点分别在两条平行线上,且与平行线垂直的所有线段
第五单元 平行四边形与梯形
第一课时 认识平行与垂直
不 相 交
不 相 交
?
在同一个平面内不相交的 两条直线叫做平行线, 也可以说这两条直线 互相平行。
在同一个平面内不相交的 两条直线叫做平行线,也可以 说这两条直线互相平行。
左边这组相交直线组成的每 个角都是直角
两条直线相交成 直角,就说这两条直 线互相垂直,其中一 条直线叫作另一条直 线的垂线,这两条直 线的交点叫作垂足。
念 4.经过直线外一点可以画1条已知直线的垂线。
小
结
第五单元 平行四边形与梯形
第三课时 垂线和平行线的性质
A a
b
(1)从直线外一点A,到这条直线画几条线段。
量一量所画线段的长度,哪一条最短?
A 垂直线段最短。
两条直线平行与垂直的判定 课件

[典例精析] 已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点 C(2,3),D(-1,a-2),如果l1⊥l2,求a的值. [解] 设直线l1,l2的斜率分别为k1,k2. ∵直线l2经过点C(2,3),D(-1,a-2),且2≠-1, ∴l2的斜率存在. 当k2=0时,a-2=3,则a=5,此时k1不存在,符合题 意.当k2≠0时,即a≠5,此时k1≠0, 由k1·k2=-1,得a--32--a3·a--12--23=-1,解得a=-6. 综上可知,a的值为5或-6.
[典例精析] 根据下列给定的条件,判断直线l1与直线l2的位置关系. (1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7); (2)l1的倾斜角为60°,l2经过点M(3,2 3),N(-2,-3 3). [解] (1)由题意知k1=-5-3-12=-45,k2=-87-+33=-45. 因为k1=k2,且A,B,C,D四点不共线,所以l1∥l2. (2)由题意知k1=tan 60°= 3,k2=-3-32--23 3= 3. 因为k1=k2,所以l1∥l2或l1与l2重合.
[类题通法] 利用两条直线平行或垂直判定图形形状的步骤
[课堂归纳领悟] 1.本节课的重点是理解两条直线平行或垂直的判定条件,会利
用斜率判断两条直线平行或垂直,难点是利用斜率判断两条 直线平行或垂直. 2.本节课要重点掌握的规律方法 (1)判断两条直线平行的步骤,见探究点一. (2)利用斜率公式判断两条直线垂直的方法,见探究点二. (3)判断图形形状的方法步骤,见探究点三. 3.本节课的易错点是利用斜率判断含字母参数的两直线平行或 来自直时,对字母分类讨论,如探究点二.
2.两直线垂直的判定 (1)如果两条直线都有斜率,且它们互相垂直,那么它们的 斜率之积等于 -1;反之,如果它们的斜率之积等于-1, 那么它们 垂直 ,即 l1⊥l2⇔k1k2=-1 . (2)若两条直线中的一条直线没有斜率,另一条直线的斜率 为 0 时,它们互相垂直.
直线平行与垂直课件PPT课件

直线平行与垂直课件ppt课件
contents
目录
• 直线平行与垂直的基本概念 • 直线平行与垂直的判定定理 • 直线平行与垂直的应用 • 直线平行与垂直的作图方法 • 直线平行与垂直的习题及解析
01 直线平行与垂直的基本概 念
直线平行的定义
总结词
同一平面内,不相交的两条直线
详细描述
直线平行是指两条直线在同一平面内,且不相交。这意味着它们没有交点,并 且始终保持相同的距离。
05 直线平行与垂直的习题及 解析
基础习题
基础习题1:判断下列说法是否正确,并说明理由。如果 错误,请给出反例。
两条直线被第三条直线所截,如果内错角相等,则这两 条直线平行。
基础习题2:已知直线a和b平行,点A在直线a上,点B、 C、D在直线b上,且AB=BC=CD=DE,那么线段AE是点 A到直线b的什么线?
交通
在道路和交通标志的设计中,直线平行和垂直的性质也得到 了广泛应用。例如,在道路交叉口的设计中,需要确保各个 道路相互垂直或平行,以确保交通的顺畅和安全。
在工程设计中的应用
机械设计
在机械设计中,为了确保机器的稳定性 和功能性,常常需要利用直线平行和垂 直的性质。例如,在设计和制造机器零 件时,需要确保各个部分相互垂直或平 行,以确保机器的正常运转和安全性。
VS
电子工程
在电子工程中,直线平行和垂直的性质也 得到了广泛应用。例如,在电路板的设计 中,需要确保各个线路相互垂直或平行, 以确保电流的顺畅流通。
04 直线平行与垂直的作图方 法
平行线的作图方法
1. 确定一个点
选择一个已知点作 为起点。
3. 画出直线
根据确定的方向和 起点,画出直线。
平行线的定义
contents
目录
• 直线平行与垂直的基本概念 • 直线平行与垂直的判定定理 • 直线平行与垂直的应用 • 直线平行与垂直的作图方法 • 直线平行与垂直的习题及解析
01 直线平行与垂直的基本概 念
直线平行的定义
总结词
同一平面内,不相交的两条直线
详细描述
直线平行是指两条直线在同一平面内,且不相交。这意味着它们没有交点,并 且始终保持相同的距离。
05 直线平行与垂直的习题及 解析
基础习题
基础习题1:判断下列说法是否正确,并说明理由。如果 错误,请给出反例。
两条直线被第三条直线所截,如果内错角相等,则这两 条直线平行。
基础习题2:已知直线a和b平行,点A在直线a上,点B、 C、D在直线b上,且AB=BC=CD=DE,那么线段AE是点 A到直线b的什么线?
交通
在道路和交通标志的设计中,直线平行和垂直的性质也得到 了广泛应用。例如,在道路交叉口的设计中,需要确保各个 道路相互垂直或平行,以确保交通的顺畅和安全。
在工程设计中的应用
机械设计
在机械设计中,为了确保机器的稳定性 和功能性,常常需要利用直线平行和垂 直的性质。例如,在设计和制造机器零 件时,需要确保各个部分相互垂直或平 行,以确保机器的正常运转和安全性。
VS
电子工程
在电子工程中,直线平行和垂直的性质也 得到了广泛应用。例如,在电路板的设计 中,需要确保各个线路相互垂直或平行, 以确保电流的顺畅流通。
04 直线平行与垂直的作图方 法
平行线的作图方法
1. 确定一个点
选择一个已知点作 为起点。
3. 画出直线
根据确定的方向和 起点,画出直线。
平行线的定义
人教版四年级上册数学《平行与垂直》课件(共25张PPT)

b
记作:a /b/ 读作:a平行于b
d
记作:
f
记作:
读作:
读作:
平行线与摆放的方向无关。
活动六:判一判
相交
1
2
3 5
不相交
4 6
活动单 活动要求:自主学习数学书 P57,完成活动单。
一、量一量:
上面相交的两条直线组成的每个角都是(
)度,都是(
)角 。
二、填一填:
1、两条直线相交成直角,就说这两条直线( 互相垂直 ),其中一条直线叫做另一条
下面各组直Байду номын сангаас,哪一组互相平行?哪一组互相垂直?
互相平行
互相垂直
二、智慧闯关(找一找)
b
a
c
d 互相平行的有( 2 )组 互相垂直的有( 4 )组
三、智慧闯关(摆一摆)
a
通过平移可以达到平行 通过旋转可以达到垂直
平行、垂直现象在生活中很常见,你能举出一些例子吗?
既有平行现象又有垂直现象。
课堂小结 同学们:通过这节课,你有什么收获呢?
在同一平面
两条直线
相交
一般相交 互相垂直
不相交
互相平行
课后练习(书61页第2题)
(1)把两根小棒都摆成和第三根小棒互相平行, 这两根小棒平行吗?
(2)把两根小棒都摆成和第三根小棒互相垂直, 这两根小棒有什么关系?
谢谢聆听
拓展提升
1.把两根小棒都摆成和第三根小棒平行。看一 看,这两根小棒有什么关系?
直线的( 垂线 ),这两条直线的交点叫做( 垂足 )
a
2、请把垂直符号标在图中。
右图中直线a与b互相垂直,记作: ( a⊥b ),读作: ( a垂直于b
北师大高中数学选择性必修第一册1.1.4两条直线的平行与垂直【课件】

3
4
∴k=- .
3
又∵直线l过点(1,2),∴所求直线方程为y-2=- (x-1),
4
即3x+4y-11=0.
通法提炼
一般地,直线 Ax+By+C=0 的斜率可由系数 A,B 来确定. 因此在求过定点
且与已知直线平行的直线方程时,通常采用以下方法:
(1)先求已知直线的斜率,若已知直线斜率存在,则根据两直线平行的性质得
上的高所在的直线方程.
解:(1)①k1=
k2=
-(-)
-(-)
-(-)
=2,
-(-)
= .
∵k1k2=1≠-1,∴l1与l2不垂直.
-
②k1=-10,k2=
= ,
-
∴k1k2=-1,∴l1⊥l2.
③∵l1的倾斜角为90°,∴l1⊥x轴.
-
∵k2=
=0,
1. 与直线 y=kx+b 平行的直线可假设为 y=kx+m,m≠b.
2. 与直线 Ax+By+C=0 平行的直线可假设为 Ax+By+m=0(m≠C).
3. 与直线 Ax+By+C=0 垂直的直线可假设为 Bx-Ay+λ=0,然后再用待定
系数法求未知数.
变式训练 3
若直线 l 与直线 2x+3y+5=0 平行,且在两坐标轴上的
谢谢观赏!
Thanks!
验证.
变式训练 1
(1)l1 经过点 A(-1,-2),B(2,1),l2 经过点 M(3,
4),N(-1,-1),l1 与 l2 是否平行?
(2)求过点(1,1)且与直线 2x-4y+1=0 平行的直线 l 的方程.
-(-)
--
解:(1)k1=
4
∴k=- .
3
又∵直线l过点(1,2),∴所求直线方程为y-2=- (x-1),
4
即3x+4y-11=0.
通法提炼
一般地,直线 Ax+By+C=0 的斜率可由系数 A,B 来确定. 因此在求过定点
且与已知直线平行的直线方程时,通常采用以下方法:
(1)先求已知直线的斜率,若已知直线斜率存在,则根据两直线平行的性质得
上的高所在的直线方程.
解:(1)①k1=
k2=
-(-)
-(-)
-(-)
=2,
-(-)
= .
∵k1k2=1≠-1,∴l1与l2不垂直.
-
②k1=-10,k2=
= ,
-
∴k1k2=-1,∴l1⊥l2.
③∵l1的倾斜角为90°,∴l1⊥x轴.
-
∵k2=
=0,
1. 与直线 y=kx+b 平行的直线可假设为 y=kx+m,m≠b.
2. 与直线 Ax+By+C=0 平行的直线可假设为 Ax+By+m=0(m≠C).
3. 与直线 Ax+By+C=0 垂直的直线可假设为 Bx-Ay+λ=0,然后再用待定
系数法求未知数.
变式训练 3
若直线 l 与直线 2x+3y+5=0 平行,且在两坐标轴上的
谢谢观赏!
Thanks!
验证.
变式训练 1
(1)l1 经过点 A(-1,-2),B(2,1),l2 经过点 M(3,
4),N(-1,-1),l1 与 l2 是否平行?
(2)求过点(1,1)且与直线 2x-4y+1=0 平行的直线 l 的方程.
-(-)
--
解:(1)k1=
两条直线平行与垂直的判定 课件

第三章 3.1 直线的倾角与斜率
3.1.2 两条直线平行与垂直的判定
• ●知识衔接
• 1.直线的倾斜角与斜率. • 当直线倾斜角α≠90°时,斜率k=_____t_an_α___.当直线倾斜
角α=90°时,斜率k_不__存__在_____. • 直线倾斜角的范围是_0_°__≤_α_<_1_8_0_°______,直线斜率的取值
(4)l1 的斜率不存在,k2=12--11=0,画出图形,如下图所示,
则 l1⊥x 轴,l2⊥y 轴,∴l1⊥l2.
• 平面内两条直线相交,而且它们的夹角是___直__角_____,那 么这两条直线垂直.
• 4.已知直线l1的斜率为0,且直线l1⊥l2,则直线l2的倾斜角 为( )
• A.0° B.135° • C.90° D.180° • [答案] C • 5.直线l1的倾斜角为45°,l2∥l1,则l2的倾斜角为
[解析] 由题意知 A,B,C,D 四点在坐标平面内的位置, 如右图,
由斜率公式可得 kAB=2-5--34=13, kCD=-0-3-36=13, kAD=-30--3-4=-3, kBC=36--52=-12.
所以 kAB=kCD,由图可知 AB 与 CD 不重合, 所以 AB∥CD,由 kAD≠kBC,所以 AD 与 BC 不平行. 又因为 kAB·kAD=13×(-3)=-1, 所以 AB⊥AD, 故四边形 ABCD 为直角梯形.
两直线的倾斜角不相等,则一定 ③√
相交,故③正确
• 2.直线l1的斜率为k1=-3,直线l2的斜率为k2=-3,则l1与 l2( )
• A.平行 B.垂直
• C.重合 D.平行或重合
• [答案] D
3.已知直线 l1 的斜率为 a,l2⊥l1,则 l2 的斜率为( )
3.1.2 两条直线平行与垂直的判定
• ●知识衔接
• 1.直线的倾斜角与斜率. • 当直线倾斜角α≠90°时,斜率k=_____t_an_α___.当直线倾斜
角α=90°时,斜率k_不__存__在_____. • 直线倾斜角的范围是_0_°__≤_α_<_1_8_0_°______,直线斜率的取值
(4)l1 的斜率不存在,k2=12--11=0,画出图形,如下图所示,
则 l1⊥x 轴,l2⊥y 轴,∴l1⊥l2.
• 平面内两条直线相交,而且它们的夹角是___直__角_____,那 么这两条直线垂直.
• 4.已知直线l1的斜率为0,且直线l1⊥l2,则直线l2的倾斜角 为( )
• A.0° B.135° • C.90° D.180° • [答案] C • 5.直线l1的倾斜角为45°,l2∥l1,则l2的倾斜角为
[解析] 由题意知 A,B,C,D 四点在坐标平面内的位置, 如右图,
由斜率公式可得 kAB=2-5--34=13, kCD=-0-3-36=13, kAD=-30--3-4=-3, kBC=36--52=-12.
所以 kAB=kCD,由图可知 AB 与 CD 不重合, 所以 AB∥CD,由 kAD≠kBC,所以 AD 与 BC 不平行. 又因为 kAB·kAD=13×(-3)=-1, 所以 AB⊥AD, 故四边形 ABCD 为直角梯形.
两直线的倾斜角不相等,则一定 ③√
相交,故③正确
• 2.直线l1的斜率为k1=-3,直线l2的斜率为k2=-3,则l1与 l2( )
• A.平行 B.垂直
• C.重合 D.平行或重合
• [答案] D
3.已知直线 l1 的斜率为 a,l2⊥l1,则 l2 的斜率为( )
平行与垂直ppt课件

平行线和垂线的判定方法
利用平行线的性质和垂线的性质进行判定。例如,在同一平面内,如果两条直线都垂直于同一 条直线,那么这两条直线平行;或者如果一条直线与另外两条平行线中的一条垂直,那么它与 另外一条平行线也垂直。
02
平行四边形中平行与垂直
平行四边形中平行线性质
01 对边平行
平行四边形两组对边分别 平行。
03 对边相等
平行四边形的对边相等。
02 对角相等
平行四边形的对角相等。
04 邻角互补
平行四边形邻角互补。
平行四边形中垂直线性质
高与底垂直
从平行四边形一个顶点向对边作垂线,这条垂线 段就是高,高与底互相垂直。
高长度相等
任意一条高都将平行四边形分为两个面积相等的 三角形,因此,同底的高长度相等。
平行四边形对角线性质
平行于直径的弦是圆的另一条直径,且这两条直 径互相平分。
03 平行弦与圆心距
在同一圆内,两平行弦到圆心的距离相等。
圆中垂直弦性质
垂直弦性质
从圆心到弦的垂线平分该弦,并且平 分该弦所对的两条弧。
垂径定理
在圆内,垂直于弦的直径平分该弦, 并且平分该弦所对的两条弧。若过圆 内一点引两条互相垂直的弦,则它们 的中点连线段必过圆心。
在绘制工程图纸时,需要使用平 行线和垂直线来表示物体的轮廓 、尺寸和位置关系,以确保图纸 的准确性和可读性。
建筑设计
在建筑设计中,平行和垂直关系 对于确定建筑物的结构、立面和 平面布局至关重要,有助于实现 稳定、美观的建筑效果。
地理信息系统中平行和垂直线用于绘制等高线、道路、河流等地理 要素,以展示地形地貌、交通网络等空间信息。
对角线互相平分
平行四边形的对角线互相平分。
利用平行线的性质和垂线的性质进行判定。例如,在同一平面内,如果两条直线都垂直于同一 条直线,那么这两条直线平行;或者如果一条直线与另外两条平行线中的一条垂直,那么它与 另外一条平行线也垂直。
02
平行四边形中平行与垂直
平行四边形中平行线性质
01 对边平行
平行四边形两组对边分别 平行。
03 对边相等
平行四边形的对边相等。
02 对角相等
平行四边形的对角相等。
04 邻角互补
平行四边形邻角互补。
平行四边形中垂直线性质
高与底垂直
从平行四边形一个顶点向对边作垂线,这条垂线 段就是高,高与底互相垂直。
高长度相等
任意一条高都将平行四边形分为两个面积相等的 三角形,因此,同底的高长度相等。
平行四边形对角线性质
平行于直径的弦是圆的另一条直径,且这两条直 径互相平分。
03 平行弦与圆心距
在同一圆内,两平行弦到圆心的距离相等。
圆中垂直弦性质
垂直弦性质
从圆心到弦的垂线平分该弦,并且平 分该弦所对的两条弧。
垂径定理
在圆内,垂直于弦的直径平分该弦, 并且平分该弦所对的两条弧。若过圆 内一点引两条互相垂直的弦,则它们 的中点连线段必过圆心。
在绘制工程图纸时,需要使用平 行线和垂直线来表示物体的轮廓 、尺寸和位置关系,以确保图纸 的准确性和可读性。
建筑设计
在建筑设计中,平行和垂直关系 对于确定建筑物的结构、立面和 平面布局至关重要,有助于实现 稳定、美观的建筑效果。
地理信息系统中平行和垂直线用于绘制等高线、道路、河流等地理 要素,以展示地形地貌、交通网络等空间信息。
对角线互相平分
平行四边形的对角线互相平分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知直线l1⊥l2, ①若l1,l2的斜率均存在,设l1:y=k1x+b1,l2:y=k2x+b2
则k1·k2=-1;
②l1,l2中有一条直线斜率不存在,
则另一条斜率为0.
y
l2
l2 y
O
x
l1
学习交流PPT
O
x
l1
4
数学应用
例1.已知四点A(5,3),B(10,6),C(3,-4),D(-6,11). 求证:AB⊥CD.
学习交流PPT
11
回顾
1.利用两直线的斜率关系判断两直线的位置关系. ①斜率存在, l1∥l2 k1=k2,且截距不等;l1⊥l2 k1·k2 =-1, ②斜率不存在. 注:若用斜率判断,须对斜率的存在性加以分类讨论.
2.利用两直线的一般式方程判断两直线的平行关系. l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0, l1∥l2 A1B2-B1A2=0,且A1C2-C1A2≠0或B1C2-B2C1≠0. l1⊥l2 A1A2+B1B2=0.
变式练习:
(1)已知直线l1的斜率k1= 求实数a的值.
3 4
,直线l2经过点A(3a,-2),B(0,a2+1),且l1⊥l2,
(2)求过点A(0,-3),且与直线2x+y-5=0垂直的直线的方程.
学习交流PPT
5
数学建构
两直线垂直.
2.利用两直线的一般式方程判断两直线的平行关系. ③已知l1:A1x+B1y+C1 =0,l2:A2x+B2y+C2=0, 则l1⊥l2A1A2+B1B2=0 .
3.利用直线系解题 已知l1∥l2,且l1的方程为Ax+By+C1=0,则设l2的方程为Ax+By +C=0(C ≠C) ,
学习交流PPT
2
情境问题
能否利用两直线的斜率关系或直接利用直线的一般式方程来 判断两直线的垂直关系呢?如何判断,又如何利用这一关系解题 呢?
学习交流PPT
3
数学建构
两直线垂直. 1.利用两直线的斜率关系判断两直线的垂直关系.
两条直线的平行与垂直(2)
学习交流PPT
1
复习回顾
1.利用两直线的斜率关系判断两直线的平行关系 ①斜率存在, l1∥l2 k1=k2,且b1≠b2 ; ②斜率都不存在. 注:若用斜率判断,须对斜率的存在性加以分类讨论.
2.利用两直线的一般式方程判断两直线的平行关系 l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0, 则l1∥l2 A1B2-B1A2=0,且A1C2-C1A2≠0或B1C2-B2C1≠0 .
学习交流PPT
8
数学应用
例3.如图在路边安装路灯,路宽MN长为23米,灯杆AB长2.5米,且与灯 柱BM成120角,路灯采用锥形灯罩,灯罩轴线AC与灯杆AB垂直,当灯柱 BM高为多少米时,灯罩轴线AC正好通过道路路面的中线?(精确到0.01米) 分析 建立直角坐标系:以灯柱底端M为原点,灯柱BM为y轴,建立 直角坐标系。
A
B
N
M
C
学习交流PPT
9
y A
B
(M) O
C
x N
学习交流PPT
10
小结
1.利用两直线的斜率关系判断两直线的垂直关系.
2.利用直线的一般式方程判断两条直线的垂直关系. l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0, 则l1⊥l2 A1A1+B1B2=0. 3.利用直线系解题 已知l1⊥l2,若l1的方程为Ax+By+C=0,则l2的方程可设为 Bx-Ay+C=0或-Bx+Ay+C=0.
3.利用直线系解题 已知l1⊥l2 ,且l1的方程为Ax+By+ C =0,则设l2的方程可设为 Bx-Ay+ C =0
学习交流PPT
6
数学应用
(3)已知直线l 与直线l:3x+4y-12=0互相垂直,且与坐标轴围成的三角形 面积为6,求直线l 的方程.
学习交流PPT
7
数学Байду номын сангаас用
例2.已知三角形的三个顶点分别为A(2,4),B(1,-2),C(-2,3), 求:AC边上的高BE所在直线的方程.
学习交流PPT
12
