插值法与数据拟合
用拉格朗日插值法拟合数据

用拉格朗日插值法拟合数据步骤
以下是使用拉格朗日插值法拟合数据的基本步骤:
1. 收集已知数据点:首先,需要收集一组已知的数据点,这些数据点包括自变量和对应的因变量值。
2. 构造拉格朗日多项式:根据已知数据点,构造拉格朗日多项式。
拉格朗日多项式是一个关于自变量的多项式,通过已知数据点确定其系数。
3. 插值计算:利用构造的拉格朗日多项式,对未知数据点进行插值计算。
根据自变量值,计算出对应的因变量值。
注意事项
在使用拉格朗日插值法拟合数据时,需要注意以下几点:
1. 数据点的选择:已知数据点的选择对拟合结果有重要影响。
应选择具备代表性的数据点,并避免过分密集或过于稀疏的分布。
2. 插值误差:拉格朗日插值法是一种插值方法,而非外推方法。
因此,在进行插值计算时,应注意插值误差的范围,避免过大的误差。
3. 拟合复杂性:拉格朗日插值法是一种简单直观的拟合方法,
适用于一般性的数据拟合。
然而,对于复杂的数据拟合问题,可能
需要考虑其他更为复杂的插值方法。
总结
拉格朗日插值法是一种常用的数据拟合方法,可以通过已知的
数据点推测出未知数据点的值。
它基于拉格朗日多项式的概念,并
利用多项式的特性进行拟合。
在使用拉格朗日插值法时,需要注意
数据点的选择、插值误差的范围以及拟合复杂性。
第二章插值与拟合

1 不为零。
xn
n xn xn
实 用 测 量 数 据 处 理 方 法
中 南 大 学
三、线性插值
假定已知区间[xk, xk+1] 的端点处的函数值 yk=f(xk), yk+1=f(xk+1),要求线性插值多项式 L1(x),使它满足 L1(xk)=yk
L1(xk+1)=yk+1
则L1(x)的表达式可按下式给出:
实 用 测 量 数 据 处 理 方 法
中 南 大 学
l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k , k 1) l k ( x k ) 1, l k ( x j ) 0( j k 1, k 1) (28) l k 1 ( x k 1 ) 1, l k 1 ( x j ) 0( j k 1, k ) 满足(28 )式的插值基函数很容 易求出的,例如求 l k 1 ( x),因为它有两个零点 k 和x k 1,故可表达为: x l k 1 ( x) A( x x k )(x x k 1 ) 其中A为待定系数可由 k 1 ( x k 1 ) 1定出: l 1 A ( x k 1 x k )(x k 1 x k 1 ) ( x x k )(x x k 1 ) 于是l k 1 ( x)= ,同理可得 ( x k 1 x k )(x k 1 x k 1 ) ( x x k-1 )(x x k 1 ) ( x x k 1 )(x x k ) l k ( x)= ,l k 1 ( x)= ( x k x k-1 )(x k x k 1 ) ( x k+1 x k 1 )(x k 1 x k )
解:2、抛物插值
插值法和曲线拟合的主要差异

插值法和曲线拟合的主要差异
插值法和曲线拟合是数据处理和分析中常用的方法,它们的主要差异如下:
1. 目标不同:
- 插值法的主要目标是通过已知数据点的函数值推断未知数据点的函数值,以填充数据的空缺部分或者进行数据的重构。
- 曲线拟合的主要目标是通过已知数据点拟合出一条函数曲线,以描述数据点之间的趋势或模式。
2. 数据使用方式不同:
- 插值法使用已知数据点的函数值作为输入,通过构造插值函数来推断未知数据点的函数值。
- 曲线拟合使用已知数据点的函数值作为输入,并通过选择合适的拟合函数参数,使得拟合函数与数据点尽可能接近。
3. 数据点要求不同:
- 插值法要求已知数据点间的函数值比较准确,以保证插值函数的质量,并要求数据点间的间距不会过大,避免出现过度插值或者不稳定的现象。
- 曲线拟合对于数据点的要求相对较松,可以容忍噪声、异常值等因素,因为它不需要将函数曲线完全通过所有数据点。
4. 应用场景不同:
- 插值法常见应用于信号处理、图像处理等领域,可以用于填充缺失数据、图像重构等任务。
- 曲线拟合常见应用于数据分析、模型建立等领域,可以用
于描述数据间的趋势、拟合科学模型等。
综上所述,插值法和曲线拟合在目标、数据使用方式、数据点要求和应用场景等方面存在明显的差异。
数值计算插值法与拟合实验

dy0=-10.*(1-5.^4)./(1+5.^4).^2;dyn=10.*(1-5.^4)./(1+5.^4).^2;
m=maspline(x1,y1,dy0,dyn,xx);
plot(xx,m,'ok')
2、
程序:
x=[-1.5 -1.0 -0.5 0.0 0.5 1.0 1.5]';
plot(xx,m,'ok')
第二个方程
程序
x=-5:0.2:5;
y=atan(x);
plot(x,y,'r');
hold on
x1=-5:1:5;
y1=atan(x1);
xx=-4.5:0.5:4.5;
yy=malagr(x1,y1,xx);
plot(xx,yy,'+')
dy0=1./(1+25);dyn=1./(1+25);
实验报告三
一、实验目的
通过本实验的学习,各种插值法的效果,如多项式插值法,牛顿插值法,样条插值法,最小二乘法拟合(即拟合插值),了解它们各自的优缺点及插值。
二、实验题目
1、插值效果比较
实验题目:将区间 10等份,对下列函数分别计算插值节点 的值,进行不同类型的插值,作出插值函数的图形并与 的图形进行比较:
y=[-4.45 -0.45 0.55 0.05 -0.44 0.54 4.55]';
plot(x,y,'or');hold on
%三.2:1.5;
y1=p1(1)*x1.^3+p1(2)*x1.^2+p1(3)*x1+p1(4);
插值法和曲线拟合的主要差异

插值法和曲线拟合的主要差异引言在数学和统计学中,插值法和曲线拟合是两种常用的数据处理方法。
它们在数据分析、模型构建和预测等领域发挥着重要作用。
本文将详细介绍插值法和曲线拟合的定义、原理、应用以及它们之间的主要差异。
插值法定义插值法是一种通过已知数据点之间的函数关系来推断未知数据点的方法。
它基于一个假设,即已知数据点之间存在一个连续且光滑的函数,并且通过这个函数可以准确地估计其他位置上的数值。
原理插值法通过对已知数据点进行插值操作,得到一个近似函数,然后使用这个函数来估计未知数据点的数值。
常见的插值方法有拉格朗日插值、牛顿插值和样条插值等。
应用插值法在各个领域都有广泛应用,如地图制作中根据少量已知地理坐标点推算其他位置上的坐标;传感器测量中根据离散采样点推断连续时间序列上未采样到的数据;图像处理中通过已知像素点推测其他位置上的像素值等。
主要特点•插值法可以精确地通过已知数据点估计未知数据点的数值,适用于需要高精度估计的场景。
•插值法对输入数据的要求较高,需要保证已知数据点之间存在连续且光滑的函数关系。
•插值法只能在已知数据点之间进行插值,无法对整个数据集进行全局拟合。
曲线拟合定义曲线拟合是一种通过选择合适的函数形式,并调整函数参数来使得函数与给定数据集最为接近的方法。
它不仅可以对已知数据进行拟合,还可以根据拟合结果进行预测和模型构建。
原理曲线拟合首先选择一个适当的函数形式,如多项式、指数函数、对数函数等。
然后使用最小二乘法或最大似然估计等方法来确定函数参数,使得函数与给定数据集之间的误差最小化。
应用曲线拟合广泛应用于各个领域,如经济学中根据历史数据构建经济模型进行预测;物理学中通过实验数据来验证理论模型;生物学中根据实验测量数据拟合生长曲线等。
主要特点•曲线拟合可以对整个数据集进行全局拟合,能够更好地描述数据的整体趋势。
•曲线拟合可以选择不同的函数形式和参数,灵活性较高。
•曲线拟合可能存在过拟合或欠拟合的问题,需要通过模型评估和调整来提高拟合效果。
数值计算04-插值与拟合

二维插值的定义
第一种(网格节点):
y
O
x
已知 mn个节点 其中 互不相同,不妨设
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
第二种(散乱节点):
y
0
x
已知n个节点
其中 互不相同,
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
最邻近插值
y
( x1 , y2 ) ( x2 , y2 )
( x1 , y1 ) ( x2 , y1 )
x
O
注意:最邻近插值一般不连续。具有连续性的最简单 的插值是分片线性插值。
分片线性插值
速度最快,但平滑性差
linear
占有的内存较邻近点插值方法多,运算时间 也稍长,与邻近点插值不同,其结果是连续 的,但在顶点处的斜率会改变 运算时间长,但内存的占有较立方插值方法 要少,三次样条插值的平滑性很好,但如果 输入的数据不一致或数据点过近,可能出现 很差的插值结果 需要较多的内存和运算时间,平滑性很好 二维插值函数独有。插值点处的值和该点值 的导数都连续
x=0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 y=0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
海拔高度数据为: z=89 90 87 85 92 91 96 93 90 87 82 92 96 98 99 95 91 89 86 84 82 84 96 98 95 92 90 88 85 84 83 81 85 80 81 82 89 95 96 93 92 89 86 86 82 85 87 98 99 96 97 88 85 82 83 82 85 89 94 95 93 92 91 86 84 88 88 92 93 94 95 89 87 86 83 81 92 92 96 97 98 96 93 95 84 82 81 84 85 85 81 82 80 80 81 85 90 93 95 84 86 81 98 99 98 97 96 95 84 87 80 81 85 82 83 84 87 90 95 86 88 80 82 81 84 85 86 83 82 81 80 82 87 88 89 98 99 97 96 98 94 92 87
插值法与数据拟合法

第七讲插值方法与数据拟合§ 7.1 引言在工程和科学实验中,常常需要从一组实验观测数据(x i , y i ) (i= 1, 2, …, n) 揭示自变量x与因变量y 之间的关系,一般可以用一个近似的函数关系式y = f (x) 来表示。
函数f (x) 的产生办法因观测数据与要求的不同而异,通常可采用两种方法:插值与数据拟合。
§ 7.1.1 插值方法1.引例1 已经测得在北纬32.3︒海洋不同深度处的温度如下表:根据这些数据,我们希望能合理地估计出其它深度(如500米、600米、1000米…)处的水温。
解决这个问题,可以通过构造一个与给定数据相适应的函数来解决,这是一个被称为插值的问题。
2.插值问题的基本提法对于给定的函数表其中f (x) 在区间[a, b] 上连续,x0,x1,…,x n为[a, b] 上n + 1个互不相同的点,要求在一个性质优良、便于计算的函数类{P(x)} 中,选出一个使P(x i ) = y i,i= 0, 1, …, n(7.1.1) 成立的函数P(x) 作为 f (x) 的近似,这就是最基本的插值问题(见图7.1.1)。
为便于叙述,通常称区间[a, b] 为插值区间,称点x0,x1,…,x n为插值节点,称函数类{P(x)} 为插值函数类,称式(7.1.1) 为插值条件,称函数P(x) 为插值函数,称f (x) 为被插函数。
求插值函数P(x) 的方法称为插值法。
§ 7.1.2 数据拟合1.引例2 在某化学反应中,已知生成物的浓度与时间有关。
今测得一组数据如下:根据这些数据,我们希望寻找一个y = f (t) 的近似表达式(如建立浓度y与时间t之间的经验公式等)。
从几何上看,就是希望根据给定的一组点(1, 4.00),…,(16, 10.60),求函数y = f (t) 的图象的一条拟合曲线。
2.数据拟合问题的基本提法 对于给定的函数表x x 0 x 1 … x n y = f (x )y 0y 1…y n其中f (x ) 在区间 [a , b ] 上连续,x 0,x 1,…,x n 为 [a , b ] 上n + 1个互不相同的点,要求找一个简单合理的函数近似表达式 ϕ (x ),使 ϕ (x ) 与f (x ) 在某种准则下最为接近,这就是最基本的数据拟合问题(见图7.1.2)。
插值和拟合

插值和拟合都是函数逼近或者数值逼近的重要组成部分他们的共同点都是通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律的目的,即通过"窥几斑"来达到"知全豹"。
简单的讲,所谓拟合是指已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λ3), 使得该函数与已知点集的差别(最小二乘意义)最小。
如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。
表达式也可以是分段函数,这种情况下叫作样条拟合。
而插值是指已知某函数的在若干离散点上的函数值或者导数信息,通过求解该函数中待定形式的插值函数以及待定系数,使得该函数在给定离散点上满足约束。
插值函数又叫作基函数,如果该基函数定义在整个定义域上,叫作全域基,否则叫作分域基。
如果约束条件中只有函数值的约束,叫作Lagrange插值,否则叫作Hermite插值。
从几何意义上将,拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。
一、概念的引入1. 插值与拟合在现实生活中的应用l 机械制造:汽车外观设计l 采样数据的重新建构:电脑游戏中场景的显示,地质勘探,医学领域(CT)2.概念的定义l 插值:基于[a,b]区间上的n个互异点,给定函数f(x),寻找某个函数去逼近f(x)。
若要求φ(x)在xi处与f(xi)相等,这类的函数逼近问题称为插值问题,xi即是插值点l 逼近:当取值点过多时,构造通过所有点的难度非常大。
此时选择一个次数较低的函数最佳逼近这些点,一般采用最小二乘法l 光顾:曲线的拐点不能太多,条件:①二阶几何连续②不存在多余拐点③曲率变化较小l 拟合:曲线设计过程中用插值或通过逼近方法是生成的曲线光滑(切变量连续)光顾二、插值理论设函数y=f(x)在区间[a,b]上连续,在[a,b]上有互异点x0,x1,…,xn处取值y 0,y1,…,yn。
插值与拟合的实验报告心得

插值与拟合的实验报告心得1.引言1.1 概述插值与拟合是数值分析和数据处理领域中常见的重要技术方法,通过对已知数据点进行插值计算,得到未知点的数值估计。
插值方法可以帮助我们填补数据间的空缺、平滑曲线和预测未来趋势,因此在科学研究、工程建模和数据分析中具有广泛的应用价值。
本实验报告将对插值的基本概念进行介绍,探讨插值方法的分类和在实际应用中的意义。
同时,我们将总结实验结果,评述插值与拟合的优缺点,并提出对进一步研究的建议,希望通过本报告对插值与拟合的方法和应用有一个全面的了解。
1.2文章结构文章结构部分的内容可以包括:在本报告中,将包括以下几个部分的内容:1. 引言:介绍插值与拟合的基本概念,以及本实验的目的和意义。
2. 正文:包括插值的基本概念、插值方法的分类以及插值在实际应用中的意义。
我们将深入探讨这些内容,并解释它们在实验中的具体应用。
3. 结论:总结本次实验的结果,分析插值与拟合的优缺点,并提出对进一步研究的建议。
通过以上内容的分析和探讨,我们希望能够全面地了解插值与拟合的理论基础和实际应用,为进一步的研究和实践提供一定的参考和启发。
1.3 目的本实验的目的在于通过对插值和拟合的实验研究,探索和了解这两种数学方法在现实生活中的应用。
通过实验,我们将深入了解插值的基本概念和分类方法,以及插值在实际应用中的意义。
同时,我们还将对插值和拟合的优缺点进行分析,为进一步的研究提供建议和启示。
通过本实验,我们的目的是掌握插值与拟合方法的应用和特点,为实际问题的求解提供更多的数学工具和思路。
2.正文2.1 插值的基本概念插值是指通过已知数据点构建出一个函数,该函数经过这些数据点,并且在每个数据点上都有相应的函数值。
换句话说,插值是一种通过已知离散数据点来推断未知数据点的方法。
在数学上,插值可以用于近似未知函数的值,或者用于填补数据间的空隙。
在插值过程中,我们通常会选择一个合适的插值函数,比如多项式函数、三角函数或者样条函数等,来拟合已知的数据点。
数值计算方法CH插值法与最小二乘法数据拟合的最小二乘法
i0
(1,0 )
6
6
(1,1) i1(xi )1(xi ) xi2 3.64
i0
i0
6
6
( f ,0 ) i yi0 (xi ) yi 25.1
i0
i0
6
6
( f ,1) i yi1(xi ) yi xi 20.18
i0
i0
得法方程组:
7 4.2
34.6.24
a0 a1
2 2
m
i (S (xi ) yi )2
m
n
i (
a j j (xi ) yi )2
i0
i0
j0
为拟合系数 a j ( j 0,1的,函, n数) .因此,可设平方误差为:
m
n
(a0 , a1,, an ) i ( a j j (xi ) yi )2
i0
j0
第7页/共28页
求最小二乘解 S *(的x) 问题
第3页/共28页
一、最小二乘法的基本概念
根据上述实例图中测试点的分布情况,可以画出很多条靠 近这些点的直线,其方程都可表示为:
S(t) at b
(1)
其中: a, b 待定.要从形如(1)式的所有直线中,找出一条用某种 度量标准来衡量最靠近所有数据点 (ti , si ) (的i 直0,1线,...,.m)
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
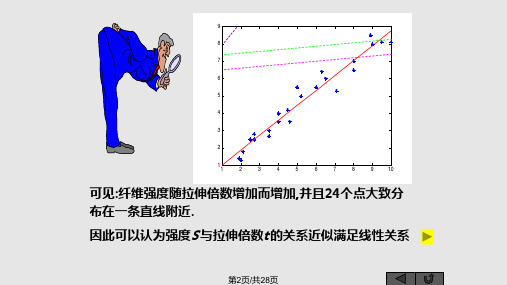
可见:纤维强度随拉伸倍数增加而增加,并且24个点大致分 布在一条直线附近.
因此可以认为强度S 与拉伸倍数t 的关系近似满足线性关系
插值法与数据拟合

x=0:3:9;
y=x.*cos(x);
xx=linspace(0,9);
plot(x,y,'o');%样本点
hold on;
plot(xx,interp1(x,y,xx,'spline'),'r');%interp1只能使用默认边界条件
plot(xx,spline(x,[0 y 0],xx),'r:');%spline可以使用第一类边界条件,这里y'(0)=y'(9)=0 pp=csape(x,y,'second');
>> yi=New_int(x,y,0.596)
yi =0.631914405504000
4、已知函数在下列各点的值为:
0.2
0.4
0.6
0.8
1.0
0.98
0.92
0.81
0.64
0.38
试用4次牛顿插值多项式 对数据进行插值,根据{ },画出图形。
解:X=[0.2:0.2:1.0]; y=[0.98,0.92,0.81,0.64,0.38];
解:a=-1;b=1;n=100;h=(b-a)/n;
>> x=a:h:b;y=1./(1+25.*x.^2);
>> plot(x,y,'k')
其函数原图形分别如下所示:
图二龙格函数的图形
用龙格函数的Lagrange()插值函数画图源程序
当n =10时,有:
functionRunge(10)
% Runge现象
xx=[0:0.5:64]; yy=sqrt(ห้องสมุดไป่ตู้x);
Matlab数学建模学习笔记——插值与拟合
Matlab数学建模学习笔记——插值与拟合⽬录插值与拟合插值和拟合的区别图⽚取⾃知乎⽤户yang元祐的回答插值:函数⼀定经过原始数据点。
假设f(x)在某区间[a,b]上⼀系列点上的值y_i=f(x_i),i=0,1,\dots,n。
插值就是⽤较简单、满⾜⼀定条件的函数\varphi(x)去代替f(x)。
插值函数满⾜条件\varphi(x_i)=y_i,i=0,1,\dots,n拟合:⽤⼀个函数去近似原函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最⼩。
插值⽅法分段线段插值分线段插值就是将每两个相邻的节点⽤直线连起来,如此形成的⼀条折线就是就是分段线性插值函数,记作I_n(x),它满⾜I_n(x_i)=y_i,且I_n(x)在每个⼩区间[x_i,x_{i+1}]上是线性函数(i=0,1\dots,n-1)。
I_n(x)可以表⽰为I_n(x)=\sum_{i=0}^n y_il_i(x),其中l_i(x)= \begin{cases} \frac{x-x_{i-1}}{x_i-x_{i-1}},&x\in [x_{i-1},x_i],i \neq 0,\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},&x\in [x_i,x_{i+1}],i \neq n,\\ 0,&其他 \end{cases}I_n(x)有良好的收敛性,即对x\in [a,b],有\lim _{n \rightarrow \infin}I_n(x)=f(x)⽤I_n(x)计算x点的插值的时候,只⽤到x左右的两个点,计算量与节点个数n⽆关。
但是n越⼤,分段越多,插值误差越⼩。
拉格朗⽇插值多项式朗格朗⽇(Lagrange)插值的基函数为\begin{aligned} l_i(x)&=\frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)}{(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)}\\ &= \prod_{j=0\\j\neq i}^{n} \frac{x-x_j}{x_i -x_j},i=0,1,\cdots,n。
数值分析插值法与拟合实验

实验报告
一、实验目的
感受插值效果的比较以及拟合多项式效果的比较。
二、实验题目
1.插值效果的比较
将区间[-5,5]5等分和10等分,对下列函数分别计算插值节点错误!未找到引用源。
的值,进行不同类型的插值,做出插值函数的图形并与错误!未找到引用源。
的图形进行比较:
做拉格朗日插值。
2.拟合多项式实验
分别对上述数据作三次多项式和五次多项式拟合,并求平方误差,作出离散函数错误!未找到引用源。
和拟合函数的图形。
三、实验原理
拉格朗日插值和多项拟合插值的通用程序
四、实验内容及结果
五、实验结果分析
(1)实验1中通过图象,可以很明显的辨别出拉格朗日插值并不是插值点越多图象就一定越精确,会有高阶插值的振荡现象。
(2)通过三个图象的对比,发现基本都是重合在一起的。
.三次多项式五次多项式拟合的平方误差分别为1.8571e-004和4.7727e-005,可知五次多项式拟合比三次多项式拟合更加准确。
但是后面去计算一下拟合所需要的时间,会发现拟合次数越大,时间越长,所以也不一定是次数越大越好,需要把时间也考虑进去。
插值与拟合方法

插值与拟合方法插值和拟合是数学中常用的方法,用于根据已知数据点的信息,推断出未知数据点的数值或函数的形式。
插值和拟合方法是经典的数学问题,应用广泛,特别是在数据分析、函数逼近和图像处理等领域。
1.插值方法:插值方法是通过已知数据点的信息,推断出两个已知数据点之间的未知数据点的数值。
插值方法的目的是保证插值函数在已知数据点处与实际数据值一致,并且两个已知数据点之间的连续性良好。
最常用的插值方法是拉格朗日插值法和牛顿插值法。
拉格朗日插值法根据已知数据点的横纵坐标,构造一个多项式函数,满足通过这些数据点。
拉格朗日插值法可以用于任意次数的插值。
牛顿插值法是使用差商的概念进行插值。
差商是指一个多项式在两个数据点之间的斜率。
牛顿插值法通过迭代计算得到与已知数据点一致的多项式。
插值方法的优点是可以精确地经过已知数据点,但是在两个已知数据点之间的插值部分可能会出现震荡现象,从而导致插值结果不准确。
2.拟合方法:拟合方法是通过已知数据点的信息,找出一个函数或曲线,使其能够最好地拟合已知数据点。
拟合方法的目标是寻找一个函数或曲线,尽可能地逼近已知数据点,并且能够在未知数据点处进行预测。
最常用的拟合方法是最小二乘法。
最小二乘法是通过求解最小化残差平方和的问题来进行拟合。
残差是指已知数据点与拟合函数的差异。
最小二乘法的目标是找到一个函数,使得所有数据点的残差平方和最小。
拟合方法的优点是可以得到一个光滑的函数或曲线,从而可以预测未知数据点的数值。
但是拟合方法可能会导致过拟合问题,即过度拟合数据点,导致在未知数据点处的预测结果不准确。
除了最小二乘法,还有其他的拟合方法,如局部加权回归和样条插值等。
局部加权回归是一种基于最小二乘法的拟合方法,它通过赋予不同的数据点不同的权重,来实现对未知数据点的预测。
样条插值是一种基于多项式插值的拟合方法,它将整个数据集分段拟合,并且在分段部分保持连续性和光滑性。
总结:插值和拟合方法是数学中的经典方法,用于根据已知数据点的信息,推断出未知数据点的数值或函数的形式。
数值分析实验报告插值与拟合
结果分析:高次插值稳定性差,而低次插值对于较大区间逼近精度又不够,而且,随着节点的加密,采用高次插值,插值函数两端会发生激烈震荡。解决这一矛盾的有效方法就是采用分段低次代数插值。
(2)
通过采用分段线性插值得到以下结果:
结果分析:通过采用分段线性插值,发现随着插值节点增多,插值计算结果的误差越来越小,而且分段线性插值的优点是计算简单,曲线连续和一致收敛,但是不具有光滑性。
拟合是指通过观察或测量得到一组离散数据序列 ,i=1,2,…,m,构造插值函数 逼近客观存在的函数 ,使得向量 与 的误差或距离最小。
可知当基函数的选择不同时,拟合函数的误差也会不同,所以在对数据进行拟合时应选择适合的基函数。
三、练习思考
整体插值有何局限性?如何避免?
答:整体插值的过程中,若有无效数据则整体插值后插值曲线的平方误差会比较大,即在该数据附近插值曲线的震动幅度较大。在插值处理前,应对原始数据进行一定的筛选,剔除无效数据。
②相同点:通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律目的
四、本次实验的重点难点分析
答:加强了对插值和拟合的认识,了解了其算法思想,并使用matlab将其实现。学会了观察插值拟合后的图形,并分析其问题。
画图进行比较:
通过观察图像,经比较可知两结果是很接近的。
2.区间 作等距划分: ,以 ( )为节点对函数 进行插值逼近。(分别取 )
(1)用多项式插值对 进行逼近,并在同一坐标系下作出函数的图形,进行比较。写出插值函数对 的逼近程度与节点个数的关系,并分析原因。
(2)试用分段插值(任意选取)对 进行逼近,在同一坐标下画出图形,观察分段插值函数对 的逼近程度与节点个数的关系。
数值分析拟合实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析方法对一组已知数据点进行拟合,掌握线性插值、多项式插值、样条插值等方法的基本原理和实现过程,并学会使用MATLAB进行数值拟合。
二、实验内容1. 线性插值线性插值是一种简单的插值方法,适用于数据点分布较为均匀的情况。
其基本原理是通过两个相邻的数据点,利用线性关系拟合出一条直线,然后通过该直线来估算未知的值。
2. 多项式插值多项式插值是一种较为精确的插值方法,通过构造一个多项式函数来逼近已知数据点。
其基本原理是利用最小二乘法求解多项式的系数,使得多项式在已知数据点上的误差最小。
3. 样条插值样条插值是一种更灵活的插值方法,通过构造一系列样条曲线来逼近已知数据点。
其基本原理是利用最小二乘法求解样条曲线的系数,使得样条曲线在已知数据点上的误差最小。
三、实验步骤1. 线性插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`linspace`生成插值点:xi = linspace(1, 5, 100);(3)使用MATLAB内置函数`interp1`进行线性插值:yi = interp1(x, y, xi, 'linear');(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');2. 多项式插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`polyfit`求解多项式系数:p = polyfit(x, y, 3);(3)使用MATLAB内置函数`polyval`进行多项式插值:yi = polyval(p, xi);(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');3. 样条插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`spline`进行样条插值:yi = spline(x, y, xi);(3)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');四、实验结果与分析1. 线性插值线性插值方法简单易行,但精度较低,适用于数据点分布较为均匀的情况。
数学建模-插值拟合的案例讲解

估计水塔的流量
内容
问题
解题思路
算法设计 与编程
表 1 水位测量记录 (符号//表示水泵启动)
y=0:400:4800;
z=[370 470 550 600 670 690 670 620 580 450 400 300 100 150 250;
510 620 730 800 850 870 850 780 720 650 500 200 300 350 320;
650 760 880 970 1020 1050 1020 830 900 700 300 500 550 480 350;
1600
1250 1450 1500 1200 1200 1550 1500
2000
1280 1420 1500 1100 1100 1600 1550
2400
1230 1400 1400 1350 1550 1550 1510
2800
1040 1300 900 1450 1600 1600 1430
162 117.5]; y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -
33.5]; z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];
cx=75:0.5:200; cy=-70:0.5:150; cz=griddata(x,y,z,cx,cy','cubic');
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6、下列数据点的插值01491625364964012345678 (1)可以得到平方根函数的近似,在区间[0,64]上作图。
(2)用这9个点作8次多项式插值。
四、实验结果1、用MATLAB编写独立的拉格朗日插值多项式函数Lagrange 插值多项式源代码function yi=Lagrange(x, y, xi)% Lagrange 插值多项式,其中% x --- 向量,全部的插值节点% y --- 向量,插值节点处的函数值% xi --- 标量,自变量x% yi --- xi 处的函数估计值n=length(x); m=length(y);if n~=merror('The lengths of X and Y must be equal');return;endp=zeros(1,n);% 对向量p赋初值0for k=1:nt=ones(1,n);for j=1:nif j~=kif abs(x(k)-x(j))<epserror('the DATA is error!');return;endt(j)=(xi-x(j))/(x(k)-x(j));endendp(k)=prod(t);endyi=sum(y.*p);2、用MATLAB编写独立的牛顿插值多项式函数function yi=New_Int(x, y, xi)% Newton 基本插值公式,其中% x --- 向量,全部的插值节点,按行输入% y --- 向量,插值节点处的函数值,按行输入% xi --- 标量,自变量x% yi --- xi 处的函数估计值n=length(x); m=length(y);if n~=merror('The lengths of X and Y must be equal');return;end% 计算均差表YY=zeros(n); Y(:,1)=y';% Y(:,1)表示矩阵中第一列的元素for k=1:n-1for i=1:n-kif abs(x(i+k)-x(i))<epserror('the DATA is error!');return;endY(i,k+1)=(Y(i+1,k)-Y(i,k))/(x(i+k)-x(i));endend% 计算Newton插值公式 N(xi)yi=0;for i=1:nz=1;for k=1:i-1z=z*(xi-x(k));endyi=yi+Y(1,i)*z;end3、利用编写好的函数计算本章P66例1、P77例1的结果并比较。
P66例1x=[144 169 225];y=[12 13 15];yi=Lagrange(x,y,175)yi = 13.230158730158733P77例1x=[0.40,0.55,0.65,0.80];>> y=[0.41075,0.57815,0.69675,0.88811];>> yi=New_int(x,y,0.596)yi =0.6319144055040004、已知函数在下列各点的值为:0.20.40.60.8 1.00.980.920.810.640.38试用4次牛顿插值多项式对数据进行插值,根据{},画出图形。
解: X=[0.2:0.2:1.0]; y=[0.98,0.92,0.81,0.64,0.38];xx=[0.2:0.08:1.0];m=length(xx); z=zeros(1,m);for i=1:mz(i)=Lagrange(x, y, xx(i));endhold onplot(x,y,'o');plot(xx,z,'r*');hold off得到如下图形:图一 练习4的图形5、在区间[-1,1]上分别取用两组等距节点对龙格函数作多项式插值,对不同值,分别画出插值函数及的图形。
解:a=-1;b=1;n=100;h=(b-a)/n;>> x=a:h:b;y=1./(1+25.*x.^2);>> plot(x,y,'k')其函数原图形分别如下所示:图二龙格函数的图形用龙格函数的Lagrange()插值函数画图源程序当n =10时,有:function Runge(10)% Runge现象% n --- 等距离节点a=-1; b=1; h=(b-a)/n;x=[a:h:b]; y=1./(1+25.*x.^2);xx=[a:0.01:b]; yy=1./(1+25.*xx.^2); m=length(xx); z=zeros(1,m);for i=1:mz(i)=Lagrange(x, y, xx(i));endhold onplot(x,y,'o');plot(xx,z,'r-');hold off当n =20时,有:function Runge(10)% Runge现象% n --- 等距离节点a=-1; b=1; h=(b-a)/n;x=[a:h:b]; y=1./(1+25.*x.^2);xx=[a:0.01:b]; yy=1./(1+25.*xx.^2); m=length(xx); z=zeros(1,m);for i=1:mz(i)=Lagrange(x, y, xx(i));endhold onplot(x,y,'o');plot(xx,z,'r-');hold off其图形分别如下所示:图三 Runge(10)图四 Runge(20)6、下列数据点的插值01491625364964012345678 (1)可以得到平方根函数的近似,在区间[0,64]上作图。
(2)用这9个点作8次多项式插值。
function L8%平方根函数的8次多项式插值x=[0 1 4 9 16 25 36 49 64]; y=sqrt(x);m=length(x); z=zeros(1,m);for i=1:mz(i)=Lagrange(x, y, x(i));endhold onplot(x,y,'o'); plot(x,y,'o');xlabel('x');ylabel('y');plot(x,z,'r-');hold off得到其图形如下所示:图五的图形x=[0 1 4 9 16 25 36 49 64];y=[0 1 2 3 4 5 6 7 8];xx=[0:0.5:64]; yy=sqrt(xx);m=length(xx);z=zeros(1,m);for i=1:mz(i)=Lagrange(x,y,xx(i));endplot(x,y,'o',xx,yy,'.',xx,z,'r-');的8次Lagrange插值函数图形图六的8次Lagrange插值函数图形五、讨论分析从下面这段代码可以看出,利用mathlab自带的增长型变量来作图,是一种在c语言学习中没有发现的方法。
而且,代码中还体现了一种比较作图和数据共用的思维方法。
例如:x=[0 1 4 9 16 25 36 49 64];y=[0 1 2 3 4 5 6 7 8];xx=[0:0.5:64]; yy=sqrt(xx);m=length(xx);z=zeros(1,m);for i=1:mz(i)=Lagrange(x,y,xx(i));endplot(x,y,'o',xx,yy,'.',xx,z,'r-');利用以上简单的程序,matble就可以做出图形,方便观察和研究。
我们知道,利用计算机则可以方便地增加曲线上样点的个数,随着样点的个数增加,让学生观察函数的图像性质,从而抽象出函数图像的形状。
当然,作图的话我们也可以利用z+z超级画板。
下面我们完成这个过程:(1)在坐标系的属性对话框中,选择“画坐标网格”和“显示刻度”选项。
(2)在作图区空白处单击鼠标右键,在快捷菜单中单击【函数或参数方程曲线…】命令,如下图所示弹出函数作图属性对话框,在“”对应的编辑框中输入:√x,然后在下面的曲线属性中,设置“曲线的点数”为:9,选择曲线以“折线段”方式显示,设置变量x的参数范围为:0到64,选择在折线段上“画点”,设置点的大小为:2;最后单击【确定】按钮完成,同样可以画出函数图像,通过改变曲线的点数,函数曲线越来光滑;六、改进实验建议三次样条插值直接用spline函数做。
边界条件加在y的首尾,第一个表示y'(x0),最后一个表示y'(xt)。
如果不加边界条件,默认是not-a-knot边界条件(注意不是自然边界条件)自然边界条件的插值要用csape函数才能得到。
如果用interp1,则只能使用spline 函数的默认边界条件,即not-a-knot条件。
下面是例子 :x=0:3:9;y=x.*cos(x);xx=linspace(0,9);plot(x,y,'o');%样本点hold on;plot(xx,interp1(x,y,xx,'spline'),'r');%interp1只能使用默认边界条件plot(xx,spline(x,[0 y 0],xx),'r:');%spline可以使用第一类边界条件,这里y'(0)=y'(9)=0 pp=csape(x,y,'second');plot(xx,fnval(pp,xx)) %第二类边界条件要用csape做,这里自然边界条件legend('样本点','默认边界条件','一阶导数为0','自然边界条件','location','south')hold off;另外,我们可以设: y=a0+a1*x+a2*x^2+…+a(n-1)*x^(n-1),则其 n次拉格朗日函数插值程序:function LagrangesNs() %用于求过n点的拉格朗日n-1次插值多项式options={'Name of data file'};title='Lagranges_points';lineNo=2;def={'Lagranges.dat'};outval=inputdlg(options,title,lineNo,def);if isempty(outval)==1,return,endfilename=outval{1};data=load(filename);x=data(:,1);y=data(:,2);lagrangesN(x,y);endfunction lagrangesN(x,y)%画出已知n个点的位置plot(x,y,'*');hold on%n次拉格朗日多项式为 y=a0+a1*x+a2*x^2+…+a(n-1)*x^(n-1) %其中a0 a1 a2…a(n-1)为待求系数n=length(x);X=Vandermonde(x,1);A=X\y;%绘制插值函数图象x1=linspace(0,max(x));x2=Vandermonde(x1',n);y1=x2*A;plot(x1',y1);hold on%显示公式func=['y= ',num2str(A(1))];for i=2:n;b=['+ ',num2str(A(i)),'*x^',num2str(i-1)];func=[func,b];endtext(0.8,0.8,func);end%创建一个Vandermonde行列式function XX=Vandermonde(x,m)%创建x的列向量if m==1n=length(x);XX=zeros(n);for i=1:nXX(:,i)=x.^(i-1);endelsen=length(x);XX=zeros(n,m);for i=1:mXX(:,i)=x.^(i-1);endendend观察以上程序,我们发现其相对较复杂,但最终结果是一致的,这也为我们提供了另外一种思路-插值法与数据拟合。
