MFC空间几何变换之图像平移、镜像、旋转、缩放详解
二维几何变换学习镜像平移和旋转等变换

二维几何变换学习镜像平移和旋转等变换在几何学中,二维几何变换是一种将平面上的点或形状进行改变的操作。
镜像、平移和旋转是常见的二维几何变换,它们不仅有着广泛的应用,而且在计算机图形学和图像处理等领域中扮演着重要的角色。
本文将分别介绍镜像、平移和旋转等变换的基本概念、性质与应用。
一、镜像变换镜像变换,又称翻转变换,是将平面上的点或形状沿着一条直线进行对称的变换。
在镜像变换中,我们可以定义一条直线作为镜像轴,对于沿轴线的点,它们在镜像后仍保持在轴上,而对于不在轴上的点,则沿垂直于轴线的方向移动相同的距离。
镜像变换可以分为对称镜像和中心镜像两种类型。
对称镜像是将平面上的点或形状沿着一条直线进行对称的变换。
对于对称镜像,镜像轴上的点保持不变,其他点关于轴线对称。
例如,在一个直角三角形中,如果将三角形沿着斜边的中垂线进行对称,那么三角形的形状将完全相同,但位置改变了。
中心镜像是将平面上的点或形状沿着一个点进行对称的变换。
对于中心镜像,镜像中心点保持不变,其他点关于镜像中心对称。
例如,在一个正方形中,如果将正方形沿着中心进行中心镜像,那么正方形的形状将保持不变。
镜像变换在现实生活和工程应用中有着广泛的应用。
例如,在建筑设计中,通过对称镜像可以快速获得相对称的结构,从而减少设计和施工的难度。
在计算机图形学中,镜像变换被广泛应用于图像处理和计算机游戏中,能够快速生成镜像效果。
二、平移变换平移变换是将平面上的点或形状沿着一个方向进行移动的变换。
在平移变换中,每个点的平移距离和方向相同,所有的点都保持相对位置不变。
平移变换可以用坐标表示为(x, y) → (x+dx, y+dy),其中(dx, dy)表示平移的距离和方向。
平移变换的一个重要性质是保持平行性,即平移后的平行线与原先的平行线依然平行。
这个性质在工程设计和计算机图形学中有着重要的应用。
例如,在工程设计中,通过平移变换可以方便地复制和粘贴结构,缩短设计和施工的时间。
编程实现一幅图像的平移、镜像、旋转、缩小和放大。

课程设计任务书学生姓名: zhh 专业班级: 通信1002班指导教师:徐文君工作单位:信息工程学院题目: 通信工程应用技术综合训练与实习初始条件:1。
数字图像处理课程相关知识。
2。
Matlab软件的软件编程应用与仿真.要求完成的主要任务:任务:编程实现一幅图像的平移、镜像、旋转、缩小和放大.要求:1。
给出所用算法的理论依据和必要的推导过程。
2.给出原始图像和处理后的图像。
时间安排:指导教师签名:年月日系主任签名:年月日目录摘要............................................................................ Abstract (I)1 图像的几何变换 01.1图像几何变换内容 01.2 Matlab仿真使用的主要函数 02图像的平移变换 (3)2。
1图像平移变换原理 (3)2.2图像平移变换的matlab实现 (4)3图像的镜像变换 (5)3.1 图像镜像变换原理 (6)3。
2 图像镜像变换的matlab实现 (7)4图像的旋转变换 (8)4。
1图像旋转变换原理 (9)4。
2 图像旋转变换的matlab实现 (10)5图像的比例变换................................................. 错误!未定义书签。
5.1 图像比例变换原理 (13)5。
2 图像比例变换的matlab实现 (13)6 心得体会 (17)参考文献 (18)附录 (19)摘要图像是对三维实际景物的平面投影,图形图像处理主要是通过计算机对图像进行处理,从而达到预期的效果的技术.为了观测需要,常常需要进行各种不同的几何变换,主要包括图像的平移变换,图像水平、垂直镜像变换,图像旋转变换,图像比例变换。
实际上,几何变换不改变像素值,而是改变像素所在的位置。
在图像处理中,可以通过Matlab来实现图像的几何变换,此软件的语法结构简单,并且具有极强的数值计算、图形文字处理、数据分析、图形绘制及图像处理等功能。
C++(MFC)金刚石图案的绘制平移缩放

//CBrush d(RGB(0,255,0));////////设置填充颜色
//pDC->SelectObject(d);/////////////////////
CView::OnRButtonDown(nFlags, point);
}
void CAaaaaView::On1()//缩放菜单
{
// TODO: Add your command handler code here
a=true;
}
void CAaaaaView::On2()//平移菜单
{
// TODO: Add your command handler code here
CPoint b=point;
pCurrentDC->DPtoLP(&b);
x0=x0-b.x;
y0=y0-b.y;
}
Invalidate();
CView::OnLButtonDown(nFlags, point);
}
int CAaaaaView::OnCreate(LPCREATESTRUCT lpCreateStruct)
{
if (CView::OnCreate(lpCreateStruct) == -1)
return -1;
// TODO: Add your specialized creation code here
pCurrentDC= new CClientDC(this);
return 0;
}
void CAaaaaView::OnRButtonDown(UINT nFlags, CPoint point)//缩放下的右击缩小
mfc空间几何变换之图像平移、镜像、旋转、缩放详解

MFC空间几何变换之图像平移、镜像、旋转、缩放详解一. 图像平移前一篇文章讲述了图像点运算(基于像素的图像变换),这篇文章讲述的是图像几何变换:在不改变图像容的情况下对图像像素进行空间几何变换的处理方式。
点运算对单幅图像做处理,不改变像素的空间位置;代数运算对多幅图像做处理,也不改变像素的空间位置;几何运算对单幅图像做处理,改变像素的空间位置,几何运算包括两个独立的算法:空间变换算法和灰度级插值算法。
空间变换操作包括简单空间变换、多项式卷绕和几何校正、控制栅格插值和图像卷绕,这里主要讲述简单的空间变换,如图像平移、镜像、缩放和旋转。
主要是通过线性代数中的齐次坐标变换。
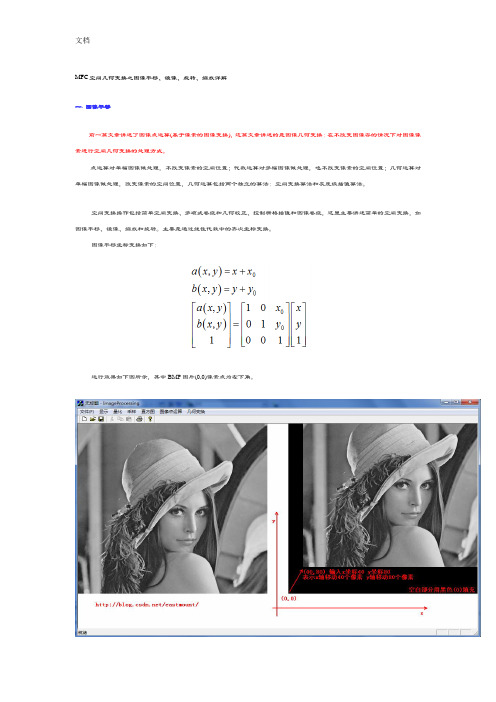
图像平移坐标变换如下:运行效果如下图所示,其中BMP图片(0,0)像素点为左下角。
其代码核心算法:1.在对话框中输入平移坐标(x,y) m_xPY=x,m_yPY=y2.定义Place=dlg.m_yPY*m_nWidth*3 表示当前m_yPY行需要填充为黑色3.新建一个像素矩阵ImageSize=new unsigned char[m_nImage]4.循环整个像素矩阵处理for(int i=0 ; i<m_nImage ; i++ ){if(i<Place) {ImageSize[i]=black;continue;}//黑色填充底部从小往上绘图else if(i>=Place && countWidth<dlg.m_xPY*3) {//黑色填充左部分ImageSize[i]=black;countWidth++; continue;}else if(i>=Place && countWidth>=dlg.m_xPY*3) {//图像像素平移区域ImageSize[i]=m_pImage[m_pImagePlace];//原(0,0)像素赋值过去m_pImagePlace++;countWidth++;if(countWidth==m_nWidth*3) {//一行填满m_pImagePlace走到(0,1)number++;m_pImagePlace=number*m_nWidth*3;}}}5.写文件绘图fwrite(ImageSize,m_nImage,1,fpw)第一步:在ResourceView资源视图中,添加Menu子菜单如下:(注意ID号)第二步:设置平移对话框。
编程实现一幅图像的平移、镜像、旋转、缩小和放大

课程设计任务书学生姓名:专业班级:通信1003班指导教师:郭志强工作单位:信息工程学院题目: 通信工程应用技术初始条件:(1)使用matlab软件进行操作(2)选择一个图像进行处理要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1)编程实现一幅图像的平移、镜像、旋转、缩小和放大。
(2)给出所用算法的理论依据和必要的推导过程,给出原始图像和处理后的图像。
时间安排:第15周:安排任务,布置题目;第15—18周:设计仿真,撰写报告第19周:完成设计,提交报告,答辩指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)Abstract ........................................................................................................................................................... I I 1 MA TLAB简介 .. (1)1.1 MA TLAB用途 (1)2图像选择及变换 (4)2.1 原始图像选择读取 (4)2.2 图像放大和缩小 (6)2.2.1 图像放大缩小的知识 (6)2.2.2 函数说明及参数选择 (8)2.2.3 源程序及运行结果 (8)2.3 图像任意角度的旋转 (10)2.3.1 函数说明及参数选择 (10)2.3.2 源程序及运行结果 (10)2.4 图像的平移 (12)2.4.1 函数说明及参数选择 (12)2.4.2 源程序及运行结果 (13)2.5 图像经过镜像 (13)3.5.1 函数说明及参数选择 (13)2.5.2 源程序及运行结果 (14)4 感悟体会小结 (17)5 参考文献 (18)附录 (19)全部源程序代码: (19)摘要MATLAB是—套高性能的数值计算和可视化软件,它集数值分析、矩阵运算、信号处理和图形显示于一体,构成—个方便的、界面友好的用户环境。
MFC空间几何变换之图像平移、镜像、旋转、缩放详解
MFC空间几何变换之图像平移、镜像、旋转、缩放详解一. 图像平移前一篇文章讲述了图像点运算(基于像素的图像变换),这篇文章讲述的是图像几何变换:在不改变图像容的情况下对图像像素进行空间几何变换的处理方式。
点运算对单幅图像做处理,不改变像素的空间位置;代数运算对多幅图像做处理,也不改变像素的空间位置;几何运算对单幅图像做处理,改变像素的空间位置,几何运算包括两个独立的算法:空间变换算法和灰度级插值算法。
空间变换操作包括简单空间变换、多项式卷绕和几何校正、控制栅格插值和图像卷绕,这里主要讲述简单的空间变换,如图像平移、镜像、缩放和旋转。
主要是通过线性代数中的齐次坐标变换。
图像平移坐标变换如下:运行效果如下图所示,其中BMP图片(0,0)像素点为左下角。
其代码核心算法:1.在对话框中输入平移坐标(x,y) m_xPY=x,m_yPY=y2.定义Place=dlg.m_yPY*m_nWidth*3 表示当前m_yPY行需要填充为黑色3.新建一个像素矩阵 ImageSize=new unsigned char[m_nImage]4.循环整个像素矩阵处理for(int i=0 ; i<m_nImage ; i++ ){if(i<Place) {ImageSize[i]=black; continue;} //黑色填充底部从小往上绘图else if(i>=Place && countWidth<dlg.m_xPY*3) {//黑色填充左部分ImageSize[i]=black; countWidth++; continue;}else if(i>=Place && countWidth>=dlg.m_xPY*3) {//图像像素平移区域ImageSize[i]=m_pImage[m_pImagePlace];//原(0,0)像素赋值过去m_pImagePlace++; countWidth++;if(countWidth==m_nWidth*3) { //一行填满 m_pImagePlace走到(0,1)number++; m_pImagePlace=number*m_nWidth*3;}}}5.写文件绘图fwrite(ImageSize,m_nImage,1,fpw)第一步:在ResourceView资源视图中,添加Menu子菜单如下:(注意ID号)第二步:设置平移对话框。
几何变换的基本概念和性质

几何变换的基本概念和性质几何变换是指平面或空间中的图形在不同的变化规则下发生的形态变化。
在数学和计算机图形学中,几何变换是一个重要的概念,它被广泛应用于各种领域,包括计算机视觉、机器人学、游戏开发和工程设计等。
几何变换包括平移、旋转、缩放和镜像四种基本类型。
每种变换都有其独特的性质和特点。
1. 平移(Translation)平移是指将图形沿着平行于原来位置的方向移动一定距离。
平移不改变图形的大小、形状和方向,只改变了其位置。
平移的变换规则是通过坐标的加减运算来实现的。
2. 旋转(Rotation)旋转是指将图形绕着某个点进行旋转运动。
旋转可以使图形沿着一个轴线旋转一定角度。
旋转不改变图形的大小和形状,但会改变其方向。
旋转的变换规则是通过坐标的旋转公式来实现的。
3. 缩放(Scaling)缩放是指将图形按照一定的比例进行放大或缩小。
缩放可以改变图形的大小和形状,但不改变其方向。
缩放的变换规则是通过坐标的乘除运算来实现的。
4. 镜像(Reflection)镜像是指将图形按照某条直线或平面进行对称反转。
镜像可以改变图形的方向,但不改变其大小和形状。
镜像的变换规则是通过坐标的变号来实现的。
这些几何变换具有一些重要的性质。
例如,平移和旋转是可逆的,即可以通过逆变换将图形恢复到原来的位置和方向;缩放和镜像也是可逆的,但镜像时需要注意选择合适的对称轴;任意两个几何变换都可以通过组合来实现更复杂的变换效果。
总之,几何变换是数学和计算机图形学中的重要概念,通过平移、旋转、缩放和镜像等变换可以实现对图形的形态变化。
掌握几何变换的基本概念和性质对于理解和应用相关领域的知识具有重要意义。
参考资料:。
图像的旋转缩放平移变换公式

图像的旋转缩放平移变换公式图像的旋转缩放平移变换公式在前两天的应⽤中,⽤Flex简单写了⼀个拖动图⽚缩放的ObjectHandler控件,当时的功能还⽐较简单,只有缩放功能,不能平移和旋转。
太不完整了!平移还好,旋转⼀来,就有点头疼了。
旋转必然要涉及旋转中⼼点的问题。
⼀般的情况是缩放的中⼼点是图⽚左上⾓,旋转的中⼼点是图⽚的中⼼,如果⽤户每操作⼀次就要⼿动去改变⼀下中⼼点,不仅逻辑上繁琐,也给调试带来很⼤的不便,最后不仅错在哪⼀步不知道,连怎么错的都不知道。
那么,⽐较好的解决办法是,指定中⼼点center,给定平移量shift,缩放量scale,旋转量rotate,及图⽚的原始宽⾼size 即可保证图⽚正确显⽰。
(图⽚默认缩放中⼼为左上⾓)⾸先,这⾥我们需要⼏个简单的数学变换,主要针对缩放和旋转:OK,想清楚了变换的过程,下⾯的⼯作就更加简单了,套⽤⼀下公式就⾏:/*** transforms:{* shift: {x:'', y:''}* rotate: '',* scale: ''* }* origin: {* originWidth:'',* originHeight: '',* originLeft: '',* originTop: ''* }***/private function fixTransformToCenter(center:Point, transforms:Object, origin:Object):Object{var result:Object = {left: 0,top: 0,r: 0,s: 1};var ow:Number = origin.originWidth;var oh:Number = origin.originHeight;var oleft: Number = origin.originLeft;var otop: Number = origin.originTop;// 平移result.left = oleft + transforms.shift.x;result.top = otop + transforms.shift.y;// 缩放result.s = transforms.scale;result.left = (result.left - center.x) * result.s;result.top = (result.top - center.y) * result.s;// 旋转result.r = tranfroms.rotate;var x:Number = (result.left - center.x) * cos(result.r) + (result.top - center.y) * sin(result.r);var y:Number = (result.top - center.y) * cos(result.r) - (result.left - center.x) * sin(result.r);result.left = x;result.top = y;reutrn result;}。
几何变换形的平移旋转缩放

几何变换形的平移旋转缩放几何变换形的平移、旋转、缩放几何变换是指在平面或者空间中对图形进行移动、旋转、缩放等操作,从而得到新的图形。
平移、旋转和缩放是几何变换中最基本的操作,它们在数学、计算机图形学、物理学等领域都有广泛的应用。
本文将详细介绍平移、旋转和缩放的定义、性质以及应用。
一、平移(Translation)平移是指将图形在平面上沿着一定的方向和距离移动。
在平移过程中,图形的形状、大小和方向都保持不变,只是位置发生了改变。
平移可以用向量来表示,即将图形中的每个点都沿着指定的向量进行平移。
平移操作可以应用于平面上的任意图形,例如点、线段、多边形等。
在计算机图形学中,平移常用于图形的移动、动画效果的实现等方面。
二、旋转(Rotation)旋转是指围绕某一点或某一轴线,图形按照一定的角度进行转动。
在旋转过程中,图形的形状、大小和位置都会发生变化,但是其内部结构和比例关系保持不变。
旋转可以用旋转矩阵或者旋转向量表示。
旋转操作可以使平面上的图形绕着任意一点或轴线旋转,也可以使图形绕着自身的中心旋转。
在数学、几何学和计算机图形学中,旋转广泛用于物体建模、仿真模拟等领域。
三、缩放(Scaling)缩放是指通过改变图形的大小,使其变得更大或者更小。
在缩放过程中,图形的形状、位置和方向都保持不变,只是大小发生了改变。
缩放可以通过乘以缩放因子的方式来实现。
缩放操作可以应用于平面上的任意图形,例如点、线段、多边形等。
在计算机图形学、地图制作和工程制图等领域,缩放是一个重要的操作,可以实现图像的放大和缩小,从而适应不同的尺寸和比例要求。
四、应用领域平移、旋转和缩放是几何变换中最常见也是最基础的操作,它们在许多领域都有广泛的应用。
在数学和几何学中,平移、旋转和缩放被用于解决各种图形的性质和形态问题,如图形的相似性、对称性等。
在计算机图形学中,平移、旋转和缩放是实现二维图形变换和三维物体变换的重要手段。
通过对图形进行平移、旋转和缩放,可以实现图形的移动、变形、旋转等效果。
图像的几何变换(平移、旋转、镜像)

一、图像平移strel %用来创建形态学结构元素translate(SE,[y x])%原结构元素SE上y和x方向平移imdilate%形态学膨胀代码:I=imread('Bluesky.jpg');se=translate(strel(1),[180 190]);B=imdilate(I,se);figure(1);subplot(1,2,1);subimage(I);title('原图像'); subplot(1,2,2);subimage(B);title('平移后图像');figure(2);subplot(1,2,1);imshow(I);title('原图像'); subplot(1,2,2);imshow(B);title('平移后图像');%显然subimage()命令可以显示图像轴而imshow()不可以结果:Figure1Figure2:二、图像镜像B=imtransform(A,TFORM,method);TFORM=makeform(transformtype,Matrix);%空间变换结构参数transformtype指定了变换的类型,常见的’affine’为二维或多维仿射变换,包括平移、旋转、比例、拉伸和错切等。
Matrix为相应的仿射变换矩阵。
代码:A=imread('Bluesky.jpg');[height,width,dim]=size(A);%计算图像尺寸tform=maketform('affine',[-1 0 0;0 1 0;width 0 1]);%空间变换结构,其中[-1 0 0;0 1 0;width 0 1]为水平翻转矩阵B=imtransform(A,tform,'nearest');tform2=maketform('affine',[1 0 0;0 -1 0;0 height 1]);%空间变换结构,其中[1 0 0;0 -1 0;0 height 1]为垂直翻转矩阵C=imtransform(A,tform2,'nearest');figure;subplot(1,3,1);imshow(A);title('原图');subplot(1,3,2);imshow(B);title('水平镜像');imwrite(B,'水平镜像.jpg');subplot(1,3,3);imshow(C);title('垂直镜像');imwrite(B,'垂直镜像.jpg');结果:加上代码tightfig 后如下(白边框变小了):Tightfig 函数代码如下:function hfig = tightfig(hfig)% tightfig: Alters a figure so that it has the minimum size necessary to % enclose all axes in the figure without excess space around them. %% Note that tightfig will expand the figure to completely encompass all % axes if necessary. If any 3D axes are present which have been zoomed, % tightfig will produce an error, as these cannot easily be dealt with. %% hfig - handle to figure, if not supplied, the current figure will be used% instead.原图水平镜像垂直镜像if nargin == 0hfig = gcf;end% There can be an issue with tightfig when the user has been modifying % the contnts manually, the code below is an attempt to resolve this, % but it has not yet been satisfactorily fixed% origwindowstyle = get(hfig, 'WindowStyle');set(hfig, 'WindowStyle', 'normal');% 1 point is 0.3528 mm for future use% get all the axes handles note this will also fetch legends and % colorbars as wellhax = findall(hfig, 'type', 'axes');% get the original axes units, so we can change and reset these again % laterorigaxunits = get(hax, 'Units');% change the axes units to cmset(hax, 'Units', 'centimeters');% get various position parameters of the axesif numel(hax) > 1% fsize = cell2mat(get(hax, 'FontSize'));ti = cell2mat(get(hax,'TightInset'));pos = cell2mat(get(hax, 'Position'));else% fsize = get(hax, 'FontSize');ti = get(hax,'TightInset');pos = get(hax, 'Position');end% ensure very tiny border so outer box always appearsti(ti < 0.1) = 0.15;% we will check if any 3d axes are zoomed, to do this we will check if% they are not being viewed in any of the 2d directionsviews2d = [0,90; 0,0; 90,0];for i = 1:numel(hax)set(hax(i), 'LooseInset', ti(i,:));% set(hax(i), 'LooseInset', [0,0,0,0]);% get the current viewing angle of the axes[az,el] = view(hax(i));% determine if the axes are zoomediszoomed = strcmp(get(hax(i), 'CameraViewAngleMode'), 'manual');% test if we are viewing in 2d mode or a 3d viewis2d = all(bsxfun(@eq, [az,el], views2d), 2);if iszoomed && ~any(is2d)error('TIGHTFIG:haszoomed3d', 'Cannot make figures containing zoomed 3D axes tight.')endend% we will move all the axes down and to the left by the amount% necessary to just show the bottom and leftmost axes and labels etc. moveleft = min(pos(:,1) - ti(:,1));movedown = min(pos(:,2) - ti(:,2));% we will also alter the height and width of the figure to just% encompass the topmost and rightmost axes and lablesfigwidth = max(pos(:,1) + pos(:,3) + ti(:,3) - moveleft);figheight = max(pos(:,2) + pos(:,4) + ti(:,4) - movedown);% move all the axesfor i = 1:numel(hax)set(hax(i), 'Position', [pos(i,1:2) - [moveleft,movedown],pos(i,3:4)]);endorigfigunits = get(hfig, 'Units');set(hfig, 'Units', 'centimeters');% change the size of the figurefigpos = get(hfig, 'Position');set(hfig, 'Position', [figpos(1), figpos(2), figwidth, figheight]);% change the size of the paperset(hfig, 'PaperUnits','centimeters');set(hfig, 'PaperSize', [figwidth, figheight]);set(hfig, 'PaperPositionMode', 'manual');set(hfig, 'PaperPosition',[0 0 figwidth figheight]);% reset to original units for axes and figureif ~iscell(origaxunits)origaxunits = {origaxunits};endfor i = 1:numel(hax)set(hax(i), 'Units', origaxunits{i});endset(hfig, 'Units', origfigunits);% set(hfig, 'WindowStyle', origwindowstyle);end三、图像转置代码段:A=imread('Bluesky.jpg');tform=maketform('affine',[0 1 0;1 0 0;0 0 1]);B=imtransform(A,tform,'nearest');figure;subplot(1,2,1);imshow(A);title('原图');subplot(1,2,2);imshow(B);title('转置后');tightfig;imwrite(B,'转置后图像.jpg');结果:原图转置后四、图像的中心旋转B=imrotate(A,angle,method,’crop’);angle为旋转角度,正值为逆时针旋转。
旋转、平移和镜像变换

旋转、平移和镜像变换旋转、平移和镜像变换是几种常见的图形变换方法,在计算机图形学、几何学以及艺术设计等领域都有广泛应用。
通过这些变换,我们可以改变图形的位置、形状和方向,从而达到我们想要的效果。
1. 旋转变换旋转变换是将一个图形按照某个点为中心点进行旋转,使得图形围绕这个中心点旋转一定角度。
旋转变换可以分为顺时针旋转和逆时针旋转两种。
旋转变换的公式为:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,(x, y)表示原始的点的坐标,(x', y')表示旋转后的点的坐标,θ表示旋转的角度。
2. 平移变换平移变换是将一个图形沿着平移向量的方向进行移动,使得图形整体平移一定距离。
平移变换是保持图形形状和方向不变的基本变换之一。
平移变换的公式为:x' = x + dxy' = y + dy其中,(x, y)表示原始的点的坐标,(x', y')表示平移后的点的坐标,(dx, dy)表示平移向量。
3. 镜像变换镜像变换是将一个图形按照某个镜像轴进行对称,使得图形在镜像轴两侧呈镜像关系。
镜像变换可以分为水平镜像和垂直镜像两种。
水平镜像变换的公式为:x' = xy' = y垂直镜像变换的公式为:x' = -xy' = y其中,(x, y)表示原始的点的坐标,(x', y')表示镜像后的点的坐标。
通过组合使用旋转、平移和镜像变换,我们可以实现更加复杂的变换效果。
例如,可以先将一个图形进行平移,然后再进行旋转和镜像变换,从而得到一个整体上更加生动和有趣的图形。
总结:旋转、平移和镜像变换是图形变换中常用的几种方法。
它们可以灵活地改变图形的位置、形状和方向,为计算机图形学、几何学和艺术设计等领域提供了丰富的工具和技术。
熟练掌握这些变换方法,对于创作和处理图形具有重要意义。
数学中的几何变换形的平移旋转缩放与镜像

数学中的几何变换形的平移旋转缩放与镜像几何变换是数学中研究空间中图形移动、旋转、缩放和镜像的重要概念。
它们不仅在几何学中广泛应用,还在计算机图形学、物理学、工程学等领域中发挥着重要作用。
本文将探讨数学中的几种常见几何变换:平移、旋转、缩放和镜像,并阐述它们的定义、性质和应用。
一、平移变换平移变换是指通过沿着特定的方向和距离将图形移动至新的位置。
在平面几何中,对于平移变换,原图形和变换后的图形具有相同的形状和大小,只是位置不同。
平移变换可以表示为:T(x,y) = (x+a, y+b)其中,(x,y)为原图形上某点的坐标,(x+a, y+b)为平移后图形上对应点的坐标,a和b分别表示平移的水平和垂直方向的距离。
平移变换具有以下性质:1. 保持形状不变:平移变换后,图形的各边和角度保持不变。
2. 保持大小不变:平移变换后,图形的面积和周长保持不变。
3. 保持平行关系:平移变换后,图形上任意两点之间的距离、平行线之间的距离和夹角大小保持不变。
4. 可叠加性:对于多个平移变换依次进行,结果等价于进行一个平移变换。
平移变换的应用:1. 地图标注:在地理信息系统中,通过平移变换可以实现地图上标注物体的位置调整。
2. 图像处理:在计算机图像处理中,通过平移变换可以实现图像的平移和移动。
3. 动画制作:在动画制作中,通过平移变换可以使图像或物体在屏幕上产生移动效果。
二、旋转变换旋转变换是指将图形绕某一固定点旋转一定角度得到新的图形。
在平面几何中,旋转变换可以围绕坐标原点进行,也可以围绕其他点或轴进行。
旋转变换可以表示为:R(x,y) = (xcosθ - ysinθ, xsinθ + ycosθ)其中,(x,y)为原图形上某点的坐标,(xcosθ - ysinθ, xsinθ+ ycosθ)为旋转后图形上对应点的坐标,θ表示旋转的角度。
旋转变换具有以下性质:1. 保持形状不变:旋转变换后,图形的各边和角度保持不变。
函数图像的平移 伸缩与翻转技巧

函数图像的平移伸缩与翻转技巧函数图像的平移、伸缩与翻转技巧函数图像的平移、伸缩与翻转是数学中常见的变换操作。
通过这些操作,我们可以改变函数图像的位置、形状和方向,从而更好地理解和分析函数的特点。
本文将介绍函数图像平移、伸缩与翻转的基本概念和相关技巧。
一、函数图像的平移函数图像的平移是指将整个函数图像沿横轴或纵轴方向上移动一定的距离。
平移分为水平平移和垂直平移两种。
1. 水平平移:函数图像沿横轴方向平移当给定函数f(x)时,若改变x的取值范围,即f(x+a),其中a为常数,可以实现函数图像在横轴方向上平移。
平移的距离和方向由a的正负决定。
当a>0时,函数图像向左平移;当a<0时,函数图像向右平移。
例如,若f(x) = x^2,若将x的取值范围改为x+a,即f(x+a) =(x+a)^2,函数图像将向左平移a个单位。
2. 垂直平移:函数图像沿纵轴方向平移当给定函数f(x)时,若改变f(x)整体的值,即f(x)+a,其中a为常数,可以实现函数图像在纵轴方向上平移。
平移的距离和方向由a的正负决定。
当a>0时,函数图像向上平移;当a<0时,函数图像向下平移。
例如,若f(x) = x^2,若将f(x)整体的值改为f(x)+a,即f(x)+a =x^2+a,函数图像将向上平移a个单位。
二、函数图像的伸缩函数图像的伸缩是指将整个函数图像在横轴或纵轴方向上拉长或收缩。
伸缩分为水平伸缩和垂直伸缩两种。
1. 水平伸缩:函数图像在横轴方向上的伸缩当给定函数f(x)时,若改变x的取值范围,即f(kx),其中k为常数,可以实现函数图像在横轴方向上的伸缩。
伸缩的程度由k的绝对值决定。
当0<k<1时,函数图像横轴方向上收缩;当k>1时,函数图像横轴方向上拉长。
例如,若f(x) = x^2,若将x的取值范围改为kx,即f(kx) = (kx)^2,函数图像将在横轴方向上收缩。
2. 垂直伸缩:函数图像在纵轴方向上的伸缩当给定函数f(x)时,若改变f(x)的值,即kf(x),其中k为常数,可以实现函数图像在纵轴方向上的伸缩。
C++3D图形变换(含源码,下载后可复制黏贴使用)

实验三 3D图形变换一.实验目的:掌握3D图像的变换,了解多数的3D变换,平移,旋转等几何变换,还有投影变换等知识。
二.实验原理:3D图像的移动,比例变化,旋转等几何变换算法原理及各种投影变换算法原理。
三.实验步骤:一.建立MFC单文档程序,用来编写3D变换。
二.建立Mainframe,并设计,添加相应的ID及映射函数。
三.实验的主要代码:1、设计3维图形平移变换算法的实现程序;void CMyView::OnTranslation(){m_Select=SEL_TS;m_str="平移";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[4][4]=1;my1.A[3][3]=1;my1.A[4][1]=20; //x轴方向上平移my1.A[4][2]=28; //y轴方向上平移my1.A[4][3]=28; //z轴方向上平移my1.Draw();}2、设计3维图形缩放变换算法的实现程序;void CMyView::OnScalingS(){m_Select=SEL_MO;m_str="整体变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[3][3]=1;my1.A[4][4]=0.5;my1.Draw();}void CMyView::OnScalingXyz(){m_Select=SEL_MO;m_str="XYZ变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=2; //x轴方向上比例my1.A[2][2]=1; //y轴方向上比例my1.A[3][3]=2; //z轴方向上比例my1.A[4][4]=1;my1.Draw();}3、设计3维图形旋转变换算法的实现程序。
vc实现图像的基本几何变换

Vc 实现图像的基本几何变换图像的几何变换,通常包括图像的平移、图像的镜像变换、图像的转置、图像的缩放和图像的旋转等。
程序基本框架如下:图1.1 程序基本框架图1.1 图像的平移图像的平移是几何变换中最简单的变换之一。
1.1.1 理论基础图像平移就是将图像中所有的点都按照指定的平移量水平、垂直移动。
设(x0,y0)为原图像上的一点,图像水平平移量为tx ,垂直平移量为ty ,则平移后点(x0,y0)坐标将变为(x1,y1)。
显然(x0,y0)和(x1,y1)的关系如下:⎩⎨⎧+=+=tyy y tx x x 0101用矩阵表示如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1001001001111y x ty tx y x对该矩阵求逆,可以得到逆变换:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1111001001100y x ty tx y x 即⎩⎨⎧-=-=tyy y tx x x 1010这样,平移后的图像上的每一点都可以在原图像中找到对应的点。
例如,对于新图中的(0,0)像素,代入上面的方程组,可以求出对应原图中的像素(-tx ,-ty )。
如果tx 或ty 大于0,则(- tx ,- ty )不在原图中。
对于不在原图中的点,可以直接将它的像素值统一设置为0或则255(对于灰度图就是黑色或白色)。
同样,若有点不在原图中,也就说明原图中有点被移出显示区域。
如果不想丢失被移出的部分图像,可以将新生成的图像宽度扩大|tx |,高度扩大| ty |。
1.1.2 Visual C++编程实现有了上面的理论基础,可以十分容易的用Visual C++来实现图像的平移。
在这里,只介绍灰度图像的平移,因为灰度图像每个像素位数正好是8位,即1个字节,这样,在进行图像处理时,可以不必考虑拼凑字节的问题。
而且由于灰度图调色板的特殊性,进行灰度图像处理时,不必考虑调色板的问题。
图像的几何变换的两种实现(旋转、平移、放大、缩小)

面向对象程序设计学号:2学生所在学院:信息工程学院学生姓名:邵丽群任课教师:熊邦书教师所在学院:信息工程学院2013级实现图像的几何变换电子信息工程信息工程学院摘要:几何变换是最常见的图像处理手段,通过对变形的图像进行几何校正,可以得出准确的图像。
常用的几何变换功能包括图像的平移、图像的镜像变换、图像的转置、图像的缩放、图像的旋转等等。
目前数字图像处理的应用越来越广泛,已经渗透到工业、航空航天、军事等各个领域,在国民经济中发挥越来越大的作用。
作为数字图像处理的一个重要部分,本文接受的工作是如何Visual C++编程工具设计一个完整的应用程序,实现经典的图像几何变换功能。
程序大概分为两大部分:读写BMP图像,和数字图像的几何变换。
即首先用Visual C++创建一个单文档应用程序框架,在实现任意BMP图像的读写,打印,以及剪贴板操作的基础上,完成经典的图像几何变换功能。
图像几何变换的Visual C++编程实现,为校课题的实现提供了一个实例。
关键字:图像处理;几何变换(图像的平移、缩放、转置、旋转和镜像变换);BMP图像;Visual C++一、引言图像几何变换是指用数学建模的方法来描述图像位置、大小、形状等变化的方法。
在实际场景拍摄到的一幅图像,如果画面过大或过小,都需要进行缩小或放大。
如果拍摄时景物与摄像头不成相互平行关系的时候,会发生一些几何畸变,例如会把一个正方形拍摄成一个梯形等。
这就需要进行一定的畸变校正。
在进行目标物的匹配时,需要对图像进行旋转、平移等处理。
在进行三维景物显示时,需要进行三维到二维平面的投影建模。
因此,图像几何变换是图像处理及分析的基础。
图像几何变换是计算机图像处理领域中的一个重要组成部分,也是值得深讨的一个重要课题。
在图像几何变换中主要包括图像的放缩、图像的旋转、图像的移动、图像的镜像、图像的块操作等容,几何变换不改变图像的像素值,只改变像素所在的几何位置。
从广义上说,图像是自然界景物的客观反映,是人类认识世界和人类本身的重要源泉。
10、图像的几何变换——平移、镜像、缩放、旋转、仿射变换

10、图像的⼏何变换——平移、镜像、缩放、旋转、仿射变换1.⼏何变换的基本概念 图像⼏何变换⼜称为图像空间变换,它将⼀副图像中的坐标位置映射到另⼀幅图像中的新坐标位置。
我们学习⼏何变换就是确定这种空间映射关系,以及映射过程中的变化参数。
图像的⼏何变换改变了像素的空间位置,建⽴⼀种原图像像素与变换后图像像素之间的映射关系,通过这种映射关系能够实现下⾯两种计算:原图像任意像素计算该像素在变换后图像的坐标位置变换后图像的任意像素在原图像的坐标位置对于第⼀种计算,只要给出原图像上的任意像素坐标,都能通过对应的映射关系获得到该像素在变换后图像的坐标位置。
将这种输⼊图像坐标映射到输出的过程称为“向前映射”。
反过来,知道任意变换后图像上的像素坐标,计算其在原图像的像素坐标,将输出图像映射到输⼊的过程称为“向后映射”。
但是,在使⽤向前映射处理⼏何变换时却有⼀些不⾜,通常会产⽣两个问题:映射不完全,映射重叠映射不完全输⼊图像的像素总数⼩于输出图像,这样输出图像中的⼀些像素找不到在原图像中的映射。
上图只有(0,0),(0,2),(2,0),(2,2)四个坐标根据映射关系在原图像中找到了相对应的像素,其余的12个坐标没有有效值。
映射重叠根据映射关系,输⼊图像的多个像素映射到输出图像的同⼀个像素上。
上图左上⾓的四个像素(0,0),(0,1),(1,0),(1,1)都会映射到输出图像的(0,0)上,那么(0,0)究竟取那个像素值呢?要解决上述两个问题可以使⽤“向后映射”,使⽤输出图像的坐标反过来推算改坐标对应于原图像中的坐标位置。
这样,输出图像的每个像素都可以通过映射关系在原图像找到唯⼀对应的像素,⽽不会出现映射不完全和映射重叠。
所以,⼀般使⽤向后映射来处理图像的⼏何变换。
从上⾯也可以看出,向前映射之所以会出现问题,主要是由于图像像素的总数发⽣了变化,也就是图像的⼤⼩改变了。
在⼀些图像⼤⼩不会发⽣变化的变换中,向前映射还是很有效的。
MFC下实现图形学之立方体平移、比例、旋转、投影变换算法

MFC下实现图形学之⽴⽅体平移、⽐例、旋转、投影变换算法//*********************************//绘制坐标系以及初始⽴⽅体//*********************************void CTransGraphicsView::OnDraw(CDC* pDC){CTransGraphicsDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);HBRUSH hbrush;CPen pen;HPEN hPen;// TODO: add draw code for native data herepen.CreatePen(PS_SOLID,3,RGB(255,0,0));hPen=(HPEN)pDC->SelectObject(pen);pDC->SetViewportOrg(cxClient/2,cyClient/2);pDC->MoveTo(-cxClient/2,0);pDC->LineTo(cxClient/2,0);pDC->MoveTo(0,-cyClient/2);pDC->LineTo(0,cyClient/2);pen.DeleteObject();pDC->SelectObject(hPen);this->ShadowTrans(-45);for(int i=0;i<4;i++){pDC->MoveTo(cpoints[i]);pDC->LineTo(cpoints[i+4]);}hbrush = (HBRUSH)pDC->SelectObject(GetStockObject(NULL_BRUSH)) ;pDC->Polygon(cpoints,4);pDC->Polygon(cpoints+4,4);}//********************//矩阵的乘法//*********************void CTransGraphicsView::MutiTransMarix(double a[1][4],double b[4][4],double MutiResult[1][4]){for(int i=0;i<4;i++) MutiResult[0][i] = 0;for(i=0; i<1;i++)for(int j=0;j<4;j++)for(int k=0;k<4;k++)MutiResult[i][j] += a[i][k]*b[k][j];}//******************************//将坐标转化为矩阵形式(向量)//******************************void CTransGraphicsView::TransPointToMarix(ThPoint &tp,double a[1][4]){a[0][0] = tp.x;a[0][1] = tp.y;a[0][2] = tp.z;a[0][3] = 1;}//******************************//将矩阵(向量)转化为三维坐标形式//******************************void CTransGraphicsView::TransMarixToPoint(double a[1][4],ThPoint &tp) {tp.x = a[0][0];tp.y = a[0][1];tp.z = a[0][2];}//******************************//⽴⽅体的平移算法//******************************void CTransGraphicsView::MoveTrans(double x,double y,double z){double a[8][4],result[1][4];double moveMarix[4][4] ={{1,0,0,0},{0,1,0,0},{0,0,1,0},{x,y,z,1}};for(int i=0;i<8;i++){TransPointToMarix(points[i],a+i);MutiTransMarix(a+i,moveMarix,result);TransMarixToPoint(result,points[i]);}ShadowTrans(-45);}//****************************************************//⽴⽅体的斜交投影算法(将三维坐标转化为⼆维在屏幕显⽰)//****************************************************void CTransGraphicsView::ShadowTrans(int degree){double a[8][4],result[1][4];ThPoint pts[8];for(int i=0;i<8;i++){pts[i].x = points[i].x;pts[i].y = points[i].y;pts[i].z = points[i].z;}double shadowMarix[4][4] ={{1,0,0,0},{0,1,0,0},{cos(degree),sin(degree),0,0},{0,0,0,1}};for(i=0;i<8;i++){TransPointToMarix(pts[i],a+i);MutiTransMarix(a+i,shadowMarix,result);TransMarixToPoint(result,pts[i]);}for(i=0;i<8;i++){cpoints[i].x = (int)pts[i].x;cpoints[i].y = (int)pts[i].y;}}//***************************************//⽴⽅体旋转算法,旋转中⼼可以是x,y或z轴//degree旋转的度数, rc旋转中⼼//****************************************void CTransGraphicsView::RotateTrans(double degree,CString rc) {double a[8][4],result[1][4];int i = 0;if(rc == "z"){double xRotateMarix[4][4] ={{cos(degree*3.14/180),sin(degree*3.14/180),0,0},{-sin(degree*3.14/180),cos(degree*3.14/180),0,0},{0,0,1,0},{0,0,0,1},};for(i=0;i<8;i++){TransPointToMarix(points[i],a+i);MutiTransMarix(a+i,xRotateMarix,result);TransMarixToPoint(result,points[i]);}}else if(rc == "x"){double yRotateMarix[4][4]={{1,0,0,0},{0,cos(degree*3.14/180),sin(degree*3.14/180),0},{0,-sin(degree*3.14/180),cos(degree*3.14/180),0},{0,0,0,1}};for(i=0;i<8;i++){TransPointToMarix(points[i],a+i);MutiTransMarix(a+i,yRotateMarix,result);TransMarixToPoint(result,points[i]);}}else if(rc == "y"){double zRotateMarix[4][4]={{cos(degree*3.14/180),0,-sin(degree*3.14/180),0},{0,1,0,0},{sin(degree*3.14/180),0,cos(degree*3.14/180),0},{0,0,0,1}};for(i=0;i<8;i++){TransPointToMarix(points[i],a+i);MutiTransMarix(a+i,zRotateMarix,result);TransMarixToPoint(result,points[i]);}}ShadowTrans(-45);}//*********************************//⽴⽅体的⽐例变换算法//*********************************void CTransGraphicsView::BigerOrSmallerTrans(double timeX,double timeY,double timeZ) {double a[8][4],result[1][4];double bsMarix[4][4] ={{timeX,0,0,0},{0,timeY,0,0},{0,0,timeZ,0},{0,0,0,1}};for(int i=0;i<8;i++){TransPointToMarix(points[i],a+i);MutiTransMarix(a+i,bsMarix,result);TransMarixToPoint(result,points[i]);}ShadowTrans(-45);}#endif //_DEBUG/// CTransGraphicsView message handlers//********************************//获取屏幕的⼤⼩//********************************void CTransGraphicsView::OnSize(UINT nType, int cx, int cy){CView::OnSize(nType, cx, cy);// TODO: Add your message handler code herecxClient = cx;cyClient = cy;}//*****************************************//根据对话框输⼊的参数进⾏⽐例变换//*****************************************void CTransGraphicsView::OnBgsm(){// TODO: Add your command handler code hereBGSMDialog B_dlg;if(IDOK == B_dlg.DoModal()){BiggerOrSmallerTrans(B_dlg.m_sx,B_dlg.m_sy,B_dlg.m_sz);}Invalidate();UpdateWindow();UpdateWindow();}//********************************//根据对话框输⼊的参数进⾏平移变换//********************************void CTransGraphicsView::OnMove(){// TODO: Add your command handler code hereCMoveDialog M_dlg;if(IDOK == M_dlg.DoModal()){MoveTrans(M_dlg.m_dx,M_dlg.m_dy,M_dlg.m_dz);}Invalidate();UpdateWindow();}//********************************//根据对话框输⼊的参数进⾏旋转变换//********************************void CTransGraphicsView::OnRotate(){// TODO: Add your command handler code hereRoateDialog BT_dlg;if(IDOK == BT_dlg.DoModal()){RotateTrans(BT_dlg.m_degree,BT_dlg.m_rc);}Invalidate();UpdateWindow();}//**************************************************// 根据键盘调⽤相应的算法//其中down向下平移⼀个单位,up向上平移⼀个单位,//left向左平移⼀个单位,right向右平移⼀个单位//***************************************************void CTransGraphicsView::OnKeyDown(UINT nChar, UINT nRepCnt, UINT nFlags) {// TODO: Add your message handler code here and/or call defaultswitch(nChar){case VK_DOWN:MoveTrans(0,1,0);break;case VK_UP:MoveTrans(0,-1,0);break;case VK_LEFT:MoveTrans(-1,0,0);break;case VK_RIGHT:MoveTrans(1,0,0);break;}Invalidate();UpdateWindow();CView::OnKeyDown(nChar, nRepCnt, nFlags);CView::OnKeyDown(nChar, nRepCnt, nFlags);}//******************************************************// 根据键盘字符键调⽤相应的算法//其中x以x轴为旋转中⼼旋转⼀度,y以y轴为旋转中⼼旋转⼀度,//z以z轴为旋转中⼼旋转⼀度,b变⼤,s缩⼩//*******************************************************void CTransGraphicsView::OnChar(UINT nChar, UINT nRepCnt, UINT nFlags) {// TODO: Add your message handler code here and/or call defaultswitch(nChar){case 'x':RotateTrans(1,"x");break;case 'y':RotateTrans(1,"y");break;case 'z':RotateTrans(1,"z");break;case 'b':BiggerOrSmallerTrans(1.1,1.1,1.1);break;case 's':BiggerOrSmallerTrans(0.9,0.9,0.9);break;}Invalidate();UpdateWindow();CView::OnChar(nChar, nRepCnt, nFlags);}。
相对任意方向的二维几何变换

相对任意方向的二维几何变换平面上的二维几何变换是指将平面上的一个点或一组点通过某种规则进行变换,得到新的点或点集的过程。
这些变换可以是平移、旋转、缩放、对称等。
在本文中,将分别介绍这些二维几何变换的定义、特点和应用。
一、平移变换平移变换是指将平面上的点沿着指定的方向进行移动,距离为指定的平移向量。
平移变换的特点是保持形状和大小不变,只改变位置。
平移变换可以用向量表示,即用平移向量将原始点的坐标进行平移,得到新点的坐标。
平移变换的应用非常广泛,比如在计算机图形学中,平移变换常用于图像的移动、平面的平移等。
此外,在几何学中,平移变换也可以用于解决平面图形的位置关系、求解线段的平移等问题。
二、旋转变换旋转变换是指将平面上的点绕着指定的旋转中心按照指定的角度进行旋转。
旋转变换的特点是保持形状和大小不变,只改变方向和位置。
旋转变换可以用旋转角度和旋转中心表示,即通过旋转矩阵将原始点的坐标进行旋转,得到新点的坐标。
旋转变换的应用也非常广泛,比如在航空航天中,旋转变换常用于描述飞机的姿态变化;在计算机图形学中,旋转变换常用于图像的旋转、三维模型的旋转等。
此外,在几何学中,旋转变换也可以用于解决线段的旋转、图形的对称等问题。
三、缩放变换缩放变换是指将平面上的点按照指定的比例进行放大或缩小。
缩放变换的特点是保持形状不变,只改变大小。
缩放变换可以用缩放因子表示,即通过缩放矩阵将原始点的坐标进行缩放,得到新点的坐标。
缩放变换的应用也非常广泛,比如在计算机图形学中,缩放变换常用于图像的放大、缩小、三维模型的缩放等。
此外,在几何学中,缩放变换也可以用于解决图形的相似性判断、线段的伸缩等问题。
四、对称变换对称变换是指将平面上的点按照指定的对称中心或对称轴进行镜像。
对称变换的特点是保持形状不变,只改变方向。
对称变换可以用对称中心或对称轴表示,即通过对称变换的公式将原始点的坐标进行镜像,得到新点的坐标。
对称变换的应用也非常广泛,比如在几何学中,对称变换常用于解决图形的对称性判断、线段的对称等问题。
镜像与旋转的变换

镜像与旋转的变换镜像和旋转是图形几何学中常见的变换方式,它们在多个领域中都有广泛应用。
本文将介绍镜像和旋转的基本概念、方法和应用。
一、镜像变换镜像变换是将原图形通过一条直线(称为镜像轴)对称重复出现的变换。
它分为水平镜像和垂直镜像两种类型。
1. 水平镜像水平镜像是指原图形沿着水平方向进行对称,图形上下翻转而左右保持不变。
应用实例包括制作对称的图案、设计、艺术创作等。
2. 垂直镜像垂直镜像是指原图形沿着垂直方向进行对称,图形左右翻转而上下保持不变。
它可以用于摄影修图、美容整形等领域,也常用于图案制作和艺术设计中。
二、旋转变换旋转变换是将原图形绕着某一点或某一直线旋转一定角度的变换。
根据旋转中心,旋转可以分为固定点旋转和任意点旋转两种形式。
1. 固定点旋转固定点旋转是指将原图形绕着某一点作为旋转中心进行旋转。
在数学中,这个旋转中心即为一个坐标点,旋转过程可以通过坐标变换公式实现。
固定点旋转常用于计算机图形学中的三维模型、动画制作等。
2. 任意点旋转任意点旋转是指将原图形绕着不是坐标原点的点作为旋转中心进行旋转。
这种旋转方式可以通过平移变换和固定点旋转相结合来实现。
任意点旋转广泛应用于游戏开发、虚拟现实等领域。
三、应用实例1. 图像处理镜像和旋转变换在图像处理中起着重要的作用。
通过镜像和旋转,可以实现图像的修复、裁剪、拼接等操作。
同时,还可以对图像进行艺术处理,增加图像的美感和创意。
2. 几何学应用在几何学中,镜像和旋转变换被广泛应用于计算机辅助设计、建模等方面。
通过镜像和旋转变换,可以生成对称的图形、构建立体几何模型等。
3. 游戏与动画制作镜像和旋转的变换在游戏开发和动画制作中也扮演着重要的角色。
通过对游戏角色、场景等元素进行镜像和旋转变换,可以实现丰富的游戏效果和动画效果。
四、总结镜像和旋转的变换是图形几何学中常见且有用的变换方式。
通过镜像变换可以实现图像的上下或左右翻转,而旋转变换可以使图像在平面中绕某一点或某一轴旋转。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MFC空间几何变换之图像平移、镜像、旋转、缩放详解一. 图像平移前一篇文章讲述了图像点运算(基于像素的图像变换),这篇文章讲述的是图像几何变换:在不改变图像内容的情况下对图像像素进行空间几何变换的处理方式。
点运算对单幅图像做处理,不改变像素的空间位置;代数运算对多幅图像做处理,也不改变像素的空间位置;几何运算对单幅图像做处理,改变像素的空间位置,几何运算包括两个独立的算法:空间变换算法和灰度级插值算法。
空间变换操作包括简单空间变换、多项式卷绕和几何校正、控制栅格插值和图像卷绕,这里主要讲述简单的空间变换,如图像平移、镜像、缩放和旋转。
主要是通过线性代数中的齐次坐标变换。
图像平移坐标变换如下:运行效果如下图所示,其中BMP图片(0,0)像素点为左下角。
其代码核心算法:1.在对话框中输入平移坐标(x,y) m_xPY=x,m_yPY=y2.定义Place=dlg.m_yPY*m_nWidth*3 表示当前m_yPY行需要填充为黑色3.新建一个像素矩阵ImageSize=new unsigned char[m_nImage]4.循环整个像素矩阵处理for(int i=0 ; i<m_nImage ; i++ ){if(i<Place) {ImageSize[i]=black;continue;}//黑色填充底部从小往上绘图else if(i>=Place && countWidth<dlg.m_xPY*3) {//黑色填充左部分ImageSize[i]=black;countWidth++; continue;}else if(i>=Place && countWidth>=dlg.m_xPY*3) {//图像像素平移区域ImageSize[i]=m_pImage[m_pImagePlace];//原(0,0)像素赋值过去m_pImagePlace++;countWidth++;if(countWidth==m_nWidth*3) {//一行填满m_pImagePlace走到(0,1)number++;m_pImagePlace=number*m_nWidth*3;}}}5.写文件绘图fwrite(ImageSize,m_nImage,1,fpw)第一步:在ResourceView资源视图中,添加Menu子菜单如下:(注意ID号)第二步:设置平移对话框。
将试图切换到ResourceView界面--选中Dialog,右键鼠标新建一个Dialog,并新建一个名为IDD_DIALOG_PY。
编辑框(X)IDC_EDIT_PYX 和 (Y)IDC_EDIT_PYY,确定为默认按钮。
设置成下图对话框:第三步:在对话框资源模板空白区域双击鼠标—Create a new class创建一个新类--命名为CImagePYDlg。
会自动生成它的.h和.cpp文件。
打开类向导(Ctrl W),选择类名:CImagePYDlg添加成员变量如下图所示,同时在Message Maps中生成ID_JHBH_PY实现函数。
第四步:在CImageProcessingView.cpp中添加头文件#include "ImagePYDlg.h",并实现平移。
[cpp]view plain copy1./********************************************************/2./*图像空间几何变换:图像平移ID_JHBH_PY(几何变换-平移)3./*使用平移对话框:CImagePYDlg dlg4./*算法:f(x,y)=f(x+x0,y+y0)图像所有点平移,空的补黑'0'5./*注意该图像平移方法只是从左上角(0,0)处开始平移6./*其他方向原理相同自己去实现7./********************************************************/8.9.void CImageProcessingView::OnJhbhPy()10.{11.if(numPicture==0){12.AfxMessageBox("载入图片后才能空间平移!",MB_OK,0);13.return;14.}15.//定义采样对话框也是用来空间变换平移的坐标16.CImagePYDlg dlg;17.if(dlg.DoModal()==IDOK)//显示对话框18.{19.//采样坐标最初为图片的自身像素20.if(dlg.m_xPY>m_nWidth||dlg.m_yPY>m_nHeight){21.AfxMessageBox("图片平移不能为超过原图长宽!",MB_OK,0);22.return;23.}24.AfxMessageBox("图片空间变换-平移!",MB_OK,0);25.26.//打开临时的图片读写文件27.FILE*fpo=fopen(BmpName,"rb");28.FILE*fpw=fopen(BmpNameLin,"wb+");29.fread(&bfh,sizeof(BITMAPFILEHEADER),1,fpo);30.fread(&bih,sizeof(BITMAPINFOHEADER),1,fpo);31.fwrite(&bfh,sizeof(BITMAPFILEHEADER),1,fpw);32.fwrite(&bih,sizeof(BITMAPINFOHEADER),1,fpw);33.fread(m_pImage,m_nImage,1,fpo);34.35./************************************************************/36./*图片空间变换-平移37./*坐标(dlg.m_xPY,dlg.m_yPY)表示图像平移的坐标38./*先用Plave计算出平移后的起始坐标,其他的坐标赋值为'0'黑色39./*然后依次平移坐标,空的赋为黑色,否则填充40./************************************************************/41.42./******************************************************************/43./*严重错误1:数组变量赋值相等44./*在View.h中定义变量BYTE*m_pImage读入图片数据后的指针45./*建立临时变量数组,让它平移变换unsigned char*ImageSize46./*ImageSize=m_pImage(错误)47./*会导致ImageSize赋值变换时m_pImage也产生了变换,所以输出全为黑色48./*因为它俩指向了相同的数组地址49./*解决方法:使用下面C++的new方法动态分配或for循环i=m_nImage赋值50./******************************************************************/51.52./*临时变量存储的像素与m_pImage相同,便于处理图像*/53.unsigned char*ImageSize;54.ImageSize=new unsigned char[m_nImage];//new和delete有效的进行动态内存的分配和释放55.56.int Place;//建立临时坐标记录起始坐标(0,0)平移过来的位置57.int m_pImagePlace;//原始图像平移为(0,0)图像把它平移到Place位置58.unsigned char black;//填充黑色='0'59.60./************************************************************/61./*for(int i=0;i<m_nHeight;i++)62./*for(int j=0;j<m_nWidth;j++)63./*不能使用的上面的因为可能图像的最后一行没有完整的一行像素64./*这样会出现exe报错,使用m_nImage读写所有像素比较正确65./************************************************************/66.67.Place=dlg.m_yPY*m_nWidth*3;//前m_yPY行都要填充为黑色68.black=0;//颜色为黑色69.m_pImagePlace=0;//图像处事位置为(0,0),把该点像素平移过去70.int countWidth=0;//记录每行的像素个数,满行时变回071.int number=0;//数字记录使用的像素行数,平移时使用72.73.for(int i=0;i<m_nImage;i++)74.{75./*如果每行的像素填满时清为0*/76.if(countWidth==m_nWidth*3){77.countWidth=0;78.}79.80./*第一部分:到平移后像素位置前面的所有像素点赋值为黑色*/81.if(i<Place){82.ImageSize[i]=black;//赋值为黑色83.continue;84.}85.86./*第二部分:平移区域的左边部分赋值为黑色*/87.else if(i>=Place&&countWidth<dlg.m_xPY*3){//RGB乘388.ImageSize[i]=black;//赋值为黑色89.countWidth++;90.continue;91.}92.93./****************************/94./*各部分如图所示:95./*00000000000000000000000096./*00000000000000000000000097./*0000000.................98./*0000000.................99./*0000000.................100./*0000000.................101./*点表示像素部分,0为黑色102./****************************/103.104./*重点错误提示:由于bmp图像显示是从左下角开始存储(0,0)点所以输出图像为*/ 105./*bmp图像是从左下角到右上角排列的*/106.107./****************************/108./*各部分如图所示:109./*0000000.................110./*0000000.................111./*0000000.................112./*0000000.................113./*000000000000000000000000114./*000000000000000000000000115./*点表示像素部分,0为黑色116./****************************/117.118./*第三部分:图像像素平移区域*/119.else if(i>=Place&&countWidth>=dlg.m_xPY*3)120.{121.ImageSize[i]=m_pImage[m_pImagePlace];122.m_pImagePlace++;123.countWidth++;124.if(countWidth==m_nWidth*3)125.{126.number++;127.m_pImagePlace=number*m_nWidth*3;128.}129.}130.}131.132.fwrite(ImageSize,m_nImage,1,fpw);133.fclose(fpo);134.fclose(fpw);135.numPicture=2;136.level=200;//200表示几何变换137.Invalidate();138.}139.}同时在ShowBitmap中添加level标记重新绘制图片,代码如下:[cpp]view plain copy1.else//图像几何变换2.if(level=200)3.{4.m_hBitmapChange=(HBITMAP)LoadImage(NULL,BmpNameLin,IMAGE_BITMAP,0,0,5.LR_LOADFROMFILE|LR_DEFAULTSIZE|LR_CREATEDIBSECTION);6.}运行时需要注意一点:BMP图像在处理过程中可能会出现一些斜线,而平移(40,60)位移量时可能出现如下。
