弯矩二次分配法(六层)

弯矩二次分配法(六层)弯矩二次分配法是一种常用的结构计算方法之一，可以有效地计算出结构中各部分的弯矩值和相应的受力情况。

这种方法具有计算简单、精度高、直观易懂等特点，被广泛应用于各类建筑结构的设计和分析中。

在本文中，我们将介绍弯矩二次分配法的基本原理、计算步骤和实例应用。

一、基本原理弯矩二次分配法的基本原理是通过叠加各种荷载的分布形态，逐步计算出结构中各个部分的受力情况。

具体来说，我们通过将荷载分解为若干小块，逐步计算每一块对结构的影响，并将计算结果叠加起来，最终得到整体的受力情况。

这种方法具有高精度、计算简单、可扩展性强等优点，通常被用于分析各种较为复杂的结构。

二、计算步骤弯矩二次分配法的计算步骤一般可以分为以下六层：1、确定结构模型和荷载模型首先，我们需要确定结构模型和荷载模型。

在确定结构模型时，应考虑结构的几何形状、材料特性、外部荷载等因素；在确定荷载模型时，应考虑荷载的大小、作用点、分布形态等因素。

这些因素的准确度决定了弯矩二次分配法的精度和可靠性。

2、绘制荷载图在确定好荷载模型后，我们需要将荷载分布情况用荷载图的形式表示出来。

荷载图一般采用坐标轴表示，将X轴和Y轴分别表示荷载和受力的距离，通过指定不同的坐标值来表示荷载的大小和作用点。

3、计算受力分布坐标接下来，我们需要根据荷载图和结构模型来计算出受力分布坐标，即测量出各个部位的受力位置和受力大小。

这一步骤需要注意测量的精度和准确性，以确保后续的计算能够得到准确的结果。

在测量出受力分布坐标后，我们需要根据受力分布的情况来计算初次的受力分布情况。

这个过程中，我们需要考虑各个部位的受力情况和相互之间的作用，以确定初次的受力分布。

在计算出初次的受力分布后，我们需要根据改变系经验公式来进行弯矩二次分配计算，用窗口法和直接交错法得到二次受力分布，这一步骤非常重要，因为它可以精确地计算出各个部分的弯矩值，从而为后续的结构分析提供参考。

6、计算最终反力分布通过计算得到二次受力分布后，我们就可以根据材料特性和式子进行最终的反力分布计算。

框架结构内力计算-竖向弯矩二次分配,水平D值法

现浇楼面
Ib=2.0I0
Ib=1.5I0
装配整体式楼面 Ib=1.5I0
Ib=1.2I0
为了简化计算,本例框架梁截面惯性矩增大系数均采用1.2。
半边结构
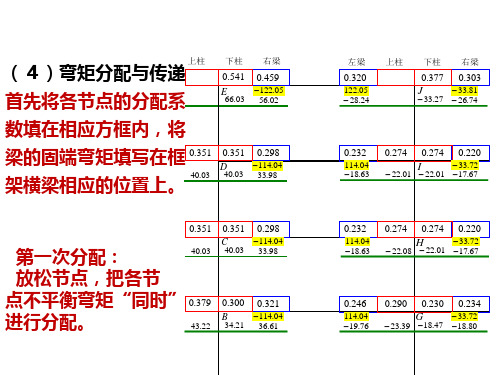
（４）弯矩分配与传递
上柱
下柱右梁
0.541 0.459
E
122.05
66.03 56.02
首先将各节点的分配系
数填在相应方框内，将梁的固端弯矩填写在框
0.274 0.274 0.220
H
33.72
22.08 22.01 17.67
0.246
114.04 19.76
0.290 0.230 0.234
G
33.72
23.39 18.47 18.80
A
F
（４）弯矩分配与传递上柱第一次分配
下柱右梁
0.541 E
66.03 20.02
43.22 34.21 36.61
左梁
0.320
122.05 28.24
上柱
下柱右梁
0.377 0.303
J
33.81
33.27 26.74
0.232
114.04 18.63
0.274 0.274 0.220
I
33.72
22.01 22.01 17.67
0.232
114.04 18.63
0.351
C
40.03
21.61
0.298
114.04 33.98 9.32
1/2）；
0.379
43.22 20.02
0.300 B
34.21
0.321
114.04 36.61 9.88

《弯矩二次分配法》课件

确定结构模型：选择合适的结构模型，如梁、
板、柱等
计算内力：根据结构模型和受力情况，计算内力，如弯
矩、剪力等
确定分配系数：根据结构模型和内力分布情况，确定分配
系数
计算分配弯矩：根据分配系数和内力，计算
分配弯矩
绘制分配弯矩图：将分配弯矩绘制成图，以便于分析和
设计
桥梁结构分析：利用弯矩二次分配法进行桥梁结构分析，提高计算精度
加强与建筑设计院的合作，推广弯矩二次分配法在建筑设计中的应用
开展弯矩二次分配法在桥梁、隧道等大型结构工程中的应
用研究
推广弯矩二次分配法在抗震设计中的应用，提高建筑物的
抗震性能
加强与高校、科研机构的合作，培养更多的弯矩二次分配法专业人才，提高市场
占有率
加强理论研究：深入研究弯矩二次分配法的原理和应用，提高理论水平
桥梁设计优化：利用弯矩二次分配法进行桥梁设计优化，提高桥梁承载能力和安全性
桥梁施工监控：利用弯矩二次分配法进行桥梁施工监控，确保施工质量和安全
桥梁健康监测：利用弯矩二次分配法进行桥梁健康监测，及时发现和修复桥梁缺陷，延长桥梁使用寿命
结构设计：用于计算结构构件的弯矩和剪
力
抗震设计：用于评估结构在地震作用下的
进行传递
确定结构类型：确定结构是静定结构还是超静定结构
计算各杆件的内力：根据结构类型，计算各杆件的内力
确定各杆件的杆端弯矩：根据内力，计算各杆件的杆端弯矩
计算各杆件的杆端弯矩：根据内力，计算各杆件的杆端弯矩
计算各杆件的杆端弯矩：根据内力，计算各杆件的杆端弯矩
计算各杆件的杆端弯矩：根据内力，计算各杆件的杆端弯矩

《弯矩二次分配法》课件

设计提供了有力支持。
02 弯矩二次分配法的基本原理
弯矩与应力的关系
弯矩是使梁产生弯曲变形的力矩，与梁的截面和跨度等因素有关。
应力是由于弯矩引起的梁截面上的正应力和剪应力，与弯矩的大小和梁的材料属性有关。
弯矩与应力的关系可以通过材料力学中的弯曲正应力公式和剪切应力公式来描述。
弯矩二次分配法的计算步骤
03 弯矩二次分配法的实现过程
建立模型
确定结构形式和支承条件
确定单元类型和节点
根据实际工程情况，确定结构的跨度、高度、材料等参数，分为若干个单元，确定节点位置和数量。
建立计算简图
根据结构形式和支承条件，建立计算简图，简化实际结构，便于计算分析。
内存占用减少
优化算法以降低内存占用，使其在处理大规模问题时更加高效。
精度控制
引入误差控制机制，确保计算结果在可接受的精度范围内。
应用范围拓展
多跨连续梁
将弯矩二次分配法应用于多跨连续梁，解决复杂结构的内力分析
问题。
考虑剪切变形
在方法中考虑剪切变形的影响，以更精确地模拟实际结构的受力
情况。
06 结论与展望
弯矩二次分配法的总结
弯矩二次分配法是一种有效的结构分析方法，适用于求解连续梁和刚架结构的弯矩分布情况。
弯矩二次分配法在工程实践中得到了广泛应用，为结构设计提供了重要的依据和支持。
该方法基于结构力学的基本原理，通过迭代计算，对结构的弯矩进行二次分配，得到更为精确的结果。
优化改进
根据对比分析结果，对计算方法进行优化改进，提高计算精度和可靠性。
04 弯矩二次分配法的应用实例
桥梁工程中的应用
总结词

竖向荷载计算(弯矩二次分配法)实例

03 在节点平衡条件中，考虑上下平衡，以更准确地计算弯矩。
05
结论
竖向荷载计算的重要性
确保结构安全
竖向荷载计算是结构设计中的重要环节，准确计算竖向荷载对于保证结构安全至关重要。
提高结构性能
合理的竖向荷载计算有助于优化结构设计，提高结构的承载能力、稳定性和抗震性能。
降低成本
竖向荷载计算的误差可能导致结构加固或重建，准确计算可降低不必要的成本。
弯矩二次分配法的限制条件
01
假定楼板为刚性，不考虑楼板的变形和位移。
ቤተ መጻሕፍቲ ባይዱ02
仅适用于规则的结构，对于不规则的结构需要进行特殊处理。
03
对于节点平衡条件，仅考虑节点左右两侧的平衡，不考虑上下平衡。
弯矩二次分配法的优化建议
01 考虑楼板的变形和位移，采用有限元法或其他数值方法进行计算。
02 对于不规则的结构，采用特殊处理方法，如引入弹性支座或采用有限元模型进行模拟。
弯矩二次分配法的优势与局限性
优势
局限性
弯矩二次分配法计算过程较为复杂，需要耗费较多时间和计算资源，对于大型复杂结构可能不适用。
弯矩二次分配法能够考虑各杆件之间的相互作用和影响，计算结果相对准确，适用于多种结构形式。
适用范围
弯矩二次分配法适用于梁、柱等杆系结构，但对于板、壳等连续介质，需要采用其他方法进行计算。
03
竖向荷载计算实例
实例一：简单框架结构
总结词
简单框架结构适用于跨度较小、层数较少的建筑，其竖向荷载计算相对简单。
详细描述
简单框架结构通常由梁和柱组成，竖向荷载通过梁传递至柱，再由柱传递至基础。弯矩二次分配法在此类结构中应用广泛，能够快速准确地计算出各构件的弯矩值。

弯矩二次分配法.docx

按弯矩二次分配法计算例题5-2钢筋混凝土框架的弯矩，并绘岀弯矩图。

屋面和楼面荷载标准值见下表7表7例题5-3框架屋面和楼面荷载荷载性质荷载类别屋面荷载(kN / n l )楼面荷tt(tπ∕m 5) 熬室走道活载使用荀载 0.70 2,00雷荷載 0.30 ——— 恒载地面材料重 2.93 1.10 1.10 誓合层重 1.00 1.001.00 预制板重2.602.602.60【解】⑴计算梁、柱转动刚度因为框架结构对称、荷载对称，又属奇数跨，故在对称轴上梁的截面只有竖向位移取如图4所示半边结构计算。

对称截面处可取为滑动端。

梁、柱转动刚度及相对转动刚度如表8所示。

图4 ［例题5 - 3］计算简图表8 粱、柱转动刚度及相对转动刚度⅞3 ~44.9QK7∣hQj=4Ξ. 12Wni ππππm誓严兰!牛Iy∏⅛¾ =44. 96kN∕m ⅛Hin y 丄山斛山HIIiTnrnlnlInhiimniiIii(沿对称轴方向)，没有转角。

所以可构件宕称转动刚度SM ・沁相对转动刚度F框架梁边跨4Xk 尸4X 24X 10⅛6・ 64X IO 11.072 中» Ξ×k b -2X½90X 10⅛l t BOXID l 1,019 框架柱首S4×k e =4×Ξ2. 53XlO 3=QO. 12×103 1.000 其他层4 Xk 尸4 × 28,48 X 1O 3=113,92× IO 31, 264(2)计算分配系数分配系数按下式计算:其中各节点杆件分配系数见表9-M- ⅛∑⅛d 左梁□右梁"上柱d 下柱5 1*O7Ξ÷L. 264=2. 336 --- 0.459 — 0. 541 4 1.072+1.204X2-3.6000. 293 0.351 0. 351 3 1.072+1. 264×S=3.600 — O T 298 0.351 0. 351 2 1.CW2+1. 264+1.00=3.336 — 0. 321 0.379 6 300 10 I i 072+1.019+1. 2^4=3. 355 0. 320 0. 303 — 0. 377 9 1.072+1.019+1. 2S4×2=4.619 0+ Ξ3≡ 0. 220 0*274 0. 274 8 1.072+1,019+1- 264× 2=4.619O t 232 Q,22O 0.274 0, 2741,072+1.019+1. Ξ64+l. Ooo=4. 3550. 2460. 2340.2900. 230(3)荷载分析1)屋面梁上线荷载设计值①×.5+0.25 ×0.60 ×25×1.2 ]=40.67kN∕m1.4×D.70×4.5=4.41 kN/m(①式中系数1.2为考虑梁挑檐及抹灰重的系数)q 1=45.08 kN/m2)楼面梁上线荷载设计值教室恒载：1.2[(2.93+1.00+2.60)活载:恒载：1.2[（1.10+1.00+2.60） ×.5+0.25 ×0.60 ×25×1.2]=30.78kN∕m 活载： 1.4χ2 00⅛4 5χ0.9s =11.34 kN/m（②系数0.9为屋面及楼而活荷载折减系数。

弯矩二次分配法

按弯矩二次分配法计算例题5-2钢筋混凝土框架的弯矩，并绘出弯矩图。

屋面和楼面荷载标准值见下表7。

表7 例题5-3框架屋面和楼面荷载【解】(1)计算梁、柱转动刚度因为框架结构对称、荷载对称，又属奇数跨，故在对称轴上梁的截面只有竖向位移(沿对称轴方向)，没有转角。

所以可取如图4所示半边结构计算。

对称截面处可取为滑动端。

梁、柱转动刚度及相对转动刚度如表8所示。

图4[例题5－3]计算简图表8粱、柱转动刚度及相对转动刚度(2)计算分配系数分配系数按下式计算：其中各节点杆件分配系数见表9。

表9分配系数(3)荷载分析1)屋面梁上线荷载设计值恒载：1.2[(2.93+1.00+2.60) ×4.5+0.25×0.60×25×1.2①]=40.67kN/m活载：（①式中系数1.2为考虑梁挑檐及抹灰重的系数）q1=45.08 kN/m2)楼面梁上线荷载设计值教室恒载：1.2[(1.10+1.00+2.60) ×4.5+0.25×0.60×25×1.2]=30.78kN/m活载：（②系数0.9为屋面及楼而活荷载折减系数。

）q2=42.12 kN/m走道. 恒载：=30.78kN/m活载：q3=44.96 kN/m(4)梁端固端弯矩M F顶层边跨梁（教室）：中跨梁（走道）：其他层边跨梁（教室）：中跨梁（走道）：(5)弯矩分配与传递弯矩分配与传递按图5的方法进行。

首先将各节点的分配系数填在相应方框内；将梁的固端弯矩填写在框架横梁相应位置上。

然后将节点放松，把各节点不平衡弯矩同时进行分配。

假定远端固定进行传递(不向滑动端传递)：右(左)梁分配弯矩向左(右)梁传递；上(下)柱分配弯矩向下(上)柱传递(传递系数均为1／2)。

第一次分配弯矩传递后，再进行第二次弯矩分配，然后不再传递。

实际上，弯矩二次分配法，只将不平衡弯矩分配两次，将分配弯矩传递一次。

弯矩二次分配法.doc

Excel在框架弯矩二次分配法中的应用ＰＫＰＭ只有计算结果没有计算过程但毕业设计需要有计算过程本人对弯矩二次分配法比较熟练毕业设计中反复用到１个下午就只能算一榀框架的恒荷载的弯矩２次分配如此繁琐的体力活应该可以交给电脑,我们不应该沦为计算的奴隶此文献给做毕业设计的土木人！土木人网在工程界弯矩二次分配法物理概念明确且易于掌握,是设计人员进行手算复核时的常用方法。

对于土木人来讲,由于在进行混凝土结构课程设计和毕业设计时须手算框架在竖向荷载作用下的弯矩,且要求有计算过程,这就意味着要反复利用弯矩二次分配法。

经过分析弯矩二次分配法的基本原理,同时充分利用Excel软件[3,4]中的公式编辑功能,编制了用于竖向荷载作用下框架结构弯矩分配的Excel模板。

该模板不仅能提高计算结果的准确性和计算速度,而且能够弥补结构计算软件只有结果而无过程的不足之处,可当作计算工具使用,避免了繁琐的反复手算过程。

用于不同节点的弯矩分配时,只需根据实际情况改动部分单元格中的数据,就可以准确快速地得到其弯矩分配的具体过程及计算结果,非常实用。

为方便大家使用,下面介绍在Excel界面所建立的通用模板,将表格中的表达式编辑到Excel中,即可进行杆端不平衡弯矩的分配。

表1计算节点2计算原理在进行弯矩分配时,为了简化计算,通常假定某一节点的不平衡弯矩只对与该节点相交的各杆件的远端有影响,而对其余杆件的影响忽略不计。

计算时,先将各节点不平衡弯矩进行第一次分配,并向远端传递（传递系数均取1/2）,再将因传递弯矩而产生新的不平衡弯矩进行二次分配。

进行图1所示的框架[5]弯矩分配时,在Excel界面的A1%Q17区域中依次相应输入表1%表5中的相关数据符号信息。

其中!为分配系数；!"为固端弯矩；!!"为分配弯矩,公式编辑过程中已取各杆件的传递系数为1/2,固端弯矩以对节点而言逆时针方向为正,顺时针方向为负。

在使用该工具时,表格中已输入公式的部分不需作任何改动,运算一次能得到一个节点的弯矩二次分配过程及结果,对于不同节点只需调整空白所代表的部分数据即可自动得到相应的正确结果。

二次弯矩分配法

33.27 11 .01
0.303
33 .81 26.74
E
66.03 20.02
J
0.351
0.351
0.298
114 .04 33.98 9.32
0.232
114 .04 18 .63 16 .99
0.274
0.274
0.220
33.72 17 .67
传递假定：远端固定进行传递；右（左）梁分配弯矩向左（右）梁传递；上（下）柱分配弯矩向下（上）柱传递（传递系数均为 1/2）；
0.290
23.39
0.230
0.234
33.72 18 .80
B
34 .21
G
18 .47
（４）弯矩分配与传递第一次分配
上柱上柱
下柱
右梁
0.541
0.459
122 .05 56.02 14 .12
0.320
122 .05 28.24 28.01
0.377
33.72 17 .67
40.03 21.61
22.08 22 .01 11 .01 11 .70
H
0.379
43.22 20.02
0.300
0.321
114 .04 36 .61 9.88
0.246
114 .04 19 .76 18 .31
0.290
0.230
0.234
0.232
114 .04 18 .63 16 .99 1.33 113 .73
0.274
0.274
0.220
33.72 17 .67
1.26 50.13

结构设计弯矩二次分配法计算(表格自带公式)

分配弯矩传递弯矩2次分配最终弯矩
分配弯矩传递弯矩2次分配最终弯矩
分配弯矩传递弯矩2次分配最终弯矩
分配弯矩传递弯矩2次分配最终弯矩
分配弯矩传递弯矩2次分配最终弯矩
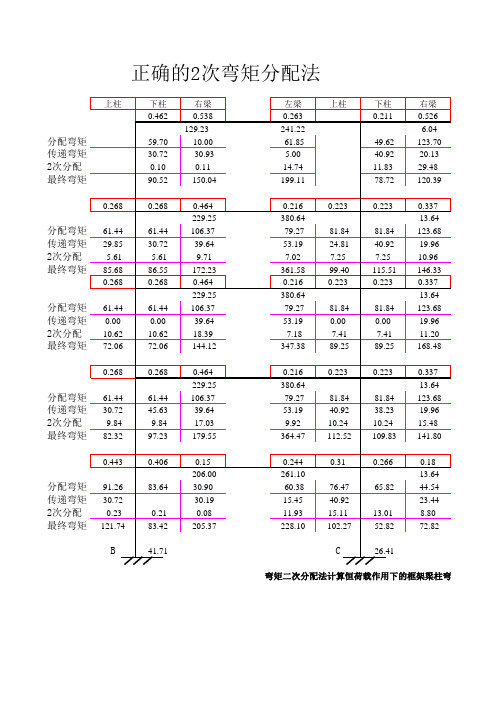
弯矩二次分配法计算恒荷载作用下的框架梁柱弯矩
正确的2次弯矩分配法
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
弯矩二次分配法计算活荷载作用下的框架梁柱弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
弯矩二次分配法计算重力荷载代表值作用下的框架梁柱
柱弯矩
滑动支座
柱弯矩
架梁柱弯矩。

弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法（Moment Distribution Method）是一种用于计算连续梁和框架结构内力的方法。

它的原理是通过数值迭代的方式来逐步分配弯矩，直到收敛为止。

这种方法在工程实践中广泛应用，其计算结果精确可靠。

弯矩二次分配法的基本步骤如下：1. 绘制结构的荷载图和剪力图首先，根据结构的几何形状和荷载情况，绘制出整个结构的荷载图和剪力图。

这些图用于确定结构中各个节点的边界条件和外力作用点。

2. 划分初始刚度矩阵将结构按照其自由度进行划分，建立初始的刚度矩阵。

每个节点的自由度包括水平位移和转角，而每个单元的自由度包括剪力和弯矩。

刚度矩阵记录了结构中各个单元之间的刚度关系。

3. 进行弯矩分配根据结构的初始刚度矩阵以及节点的边界条件，通过弯矩分配的方法来逐步计算每个单元的剪力和弯矩。

首先，将全局外力施加到结构上，然后根据初始刚度矩阵和外力计算出每个单元的初始剪力和弯矩。

接下来，按照一定的迭代顺序，将每个单元的剪力和弯矩按照一定的比例分配给相邻的单元，然后更新刚度矩阵。

直到满足一定的收敛条件，即剪力和弯矩的分配趋于稳定，这个过程称为弯矩分配。

4. 计算节点位移在进行了弯矩分配之后，根据节点边界条件和每个单元的位移，可以计算出每个节点的位移。

这里使用弯矩二次分配法的一个重要假设，即梁在弯曲作用下可以看作刚性倍增杆，因此弯曲刚度与柔度成反比。

5. 更新刚度矩阵根据已知的节点位移和单元位移，可以更新刚度矩阵。

通过多次迭代计算，直到满足一定的收敛条件。

6. 计算内力最后，在完成弯矩分配和节点位移计算之后，根据梁的基本原理和弯矩分配法的结果，可以得到结构中各个节点和单元的内力。

以上是弯矩二次分配法的基本步骤，通过这种方法可以计算得到结构中各个节点和单元的内力分布。

这种方法在实际工程中广泛应用，尤其是对于复杂结构的计算分析非常有用。

在Excel中，可以通过建立相应的计算模型和公式来实现弯矩二次分配法的计算。

弯矩二次分配法

梁端弯矩调幅
（1) 为何要进行调幅
框架构造梁端弯矩较大，配筋较多，因而不便施工。而框架中允许梁端出现塑性铰。所以，在梁中可考虑塑性内力重分布，一般是降低支座弯矩（梁端弯矩），以减小支座处旳配筋。
（2) 怎样进行调幅 ① 根据工程经验，对钢筋混凝土框架，可取
调幅系数：
钢筋混凝土装配式框架钢筋混凝土现浇式框架
因为框架构造对称、荷载对称，故可取如下图（b）所示半边构造计算。 ① 梁旳线刚度
其他层柱：
梁、柱转动刚度及相对转动刚度见表3.3。
（2）计算分配系数：分配系数按下式计算：
（4）弯矩分配与传递
弯矩分配与传递如图所示。首先将各节点旳分配系数填在相应方框内，将梁旳固端弯矩填写在框架横梁相应位置上，然后将节点放松，把各节点不平衡弯矩“同步”进行分配。
二、弯矩二次分配法
对六层下列无侧移旳框架，此法较为以便。
详细计算环节：
（1）计算框架各杆旳线刚度及分配系数。（2）计算框架各层梁端在竖向荷载作用下旳固端弯矩。（3）计算框架各节点处旳不平衡弯矩，并将每一节点处旳不平
衡弯矩同步进行分配并向远端传递，传递系数为1/2。（4）进行两次分配后结束（仅传递一次，但分配两次）（5）将各杆端旳固端弯矩、第一。这么，在支座出现塑性铰后来，不会造成跨中截面承载力不足。一般，跨中弯矩可乘以1.1～1.2旳调整系数（见下图）。
为了确保梁旳安全，跨中弯矩还必须满足下列条件：
图框架梁塑性调幅
M1' M1
M 2 ' M 2 M 0 ' M 0.5 (M1 M 2 )
二、弯矩二次分配法
对六层下列无侧移旳框架，此法较为以便。基本假定：
① 框架梁、柱正交； ② 框架梁连续且贯穿整个楼层； ③ 不考虑轴向变形； ④ 框架侧移忽视不计。

弯矩二次分配法(六层)

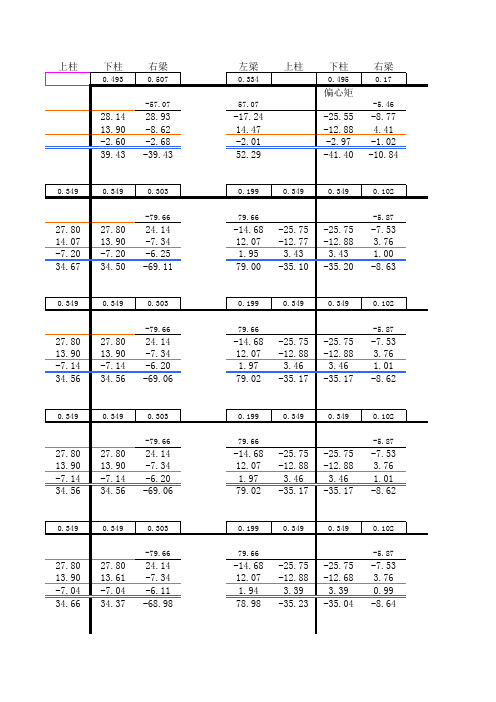
在计算竖向恒载和活载作用下框架结构弯矩时要多次使用弯矩二次分配法，此表为恒载作用下12轴线框输入每一层的各节点梁柱分配系数和各节点固端弯矩，即可自动计算生成所有其他数据，注意千万不要据，否则公式被取消了就无法得出正确结果！！！！（计算的各节点最终弯矩代数和均为0，有的为0.0
图5－29 恒载作用下的框架弯矩
此表为恒载作用下12轴线框架的计算过程，如果大家也是三跨的梁可以参用这个计算器，有其他数据，注意千万不要改动了表上除各节点梁柱分配系数和各节点固端弯矩以外的数矩代数和均为0，有的为0.01的是因为四舍五入造成的）
架弯矩内力二次分配图。

弯矩分配法——精选推荐

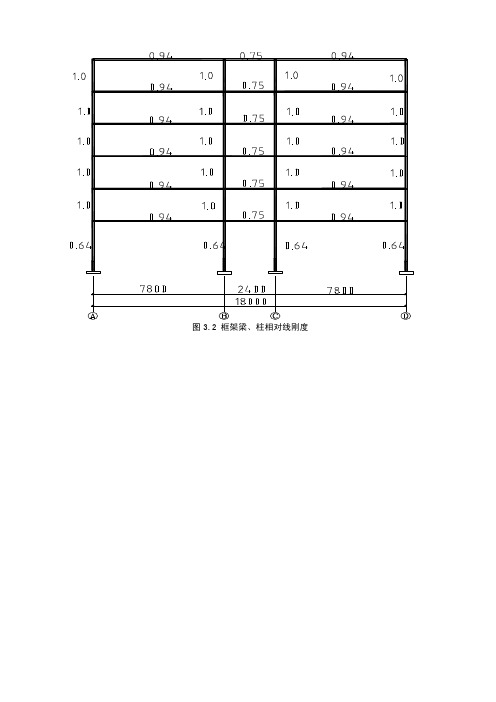
图3.2 框架梁、柱相对线刚度
图3.7 框架竖向受荷图（单位：kN，kN/m）
力矩二次分配法
力矩二次分配法是一种计算竖向荷载作用下框架结构内力的一种近似方法; 假定节点的不平衡弯矩值对于该节点相交的各杆件的远端有影响,对其余各杆件的影响忽略不计; 先对各节点的不平衡弯矩进行第一次分配,并向远端传递(传递系数为1/2); 在将传递弯矩产生的新的不平衡弯矩进行第二次分配, 整个弯矩分配和传递结束。

力矩二次分配法是房屋建筑中框架结构在竖向荷载作用下内力计算的常用方法，其原理是:
1)所有节点全部“锁住”，计算出固端力矩;
2)全部节点同时放松，计算第一次分配的力矩;
3)同时向远端传递力矩，传递系数一律1/2;
4)各节点将所有相邻节点传递来的力矩作一次分配;
5)对每个杆端各种力矩求和，即得杆端最后力矩。

显然力矩分配法是一种近似计算，舍去了一部分。

恒荷载作用下内力计算采用力矩二次分配法，计算过程见表3.4
表3.4恒荷载作用下内力计算分析
图3.8恒荷载作用下的弯矩、剪力图（单位：kN·m，kN）。