大物第二章课后习题答案

合集下载

大学物理习题答案解析第二章

第二章牛顿定律2 -1如图(a)所示,质量为m的物体用平行于斜面的细线联络置于圆滑的斜面上,若斜面向左方作加速运动 ,当物体刚离开斜面时,它的加快度的大小为()(A) gsin θ(B) gcos θ(C) gtan θ(D) gcot θ剖析与解当物体走开斜面瞬时 ,斜面对物体的支持力消逝为零,物体在绳索拉力 F Ｔ (其方向仍可认为平行于斜面 )和重力作用下产平生行水平面向左的加快度a,如图 (b) 所示 ,由其可解得合外力为 mgcot θ,应选 (D)．求解的重点是正确剖析物体刚走开斜面瞬时的物体受力状况和状态特点．2 -2 用水平力 F N把一个物体压着靠在粗拙的竖直墙面上保持静止．当 F N渐渐增大时 ,物体所受的静摩擦力 F f的大小 ()(A)不为零 ,但保持不变(B)随 F N成正比地增大(C)开始随 F N增大 ,达到某一最大值后 ,就保持不变(D)没法确立剖析与解与滑动摩擦力不一样的是 ,静摩擦力可在零与最大值μF N范围内取值．当F N增加时,静摩擦力可取的最大值成正比增加 ,但详细大小则取决于被作用物体的运动状态．由题意知 ,物体向来保持静止状态 ,故静摩擦力与重力大小相等 ,方向相反 ,并保持不变 ,应选 (A) ．2 -3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()(A)不得小于(C)不得大于μgR (B) 一定等于μgRμgR (D) 还应由汽车的质量m 决定剖析与解由题意知 ,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只好由路面与轮胎间的静摩擦力供给,能够供给的最大向心力应为μF N．由此可算得汽车转弯的最大速率应为 v＝μRg．所以只需汽车转弯时的实质速率不大于此值,均能保证不侧向打滑．应选 (C) ．2 -4 一物体沿固定圆弧形圆滑轨道由静止下滑,在下滑过程中 ,则 ( )(A)它的加快度方向永久指向圆心,其速率保持不变(B)它遇到的轨道的作使劲的大小不停增加(C)它遇到的合外力大小变化 ,方向永久指向圆心(D)它遇到的合外力大小不变 ,其速率不停增加剖析与解由图可知 ,物体在下滑过程中遇到大小和方向不变的重力以实时辰指向圆轨道中心的轨道支持力 F N 作用 ,其合外力方向并不是指向圆心 ,其大小和方向均与物体所在地点有关．重力的切向分量 (m g cos θ) 使物体的速率将会不停增加 ( 由机械能守恒亦可判断 ),则物体作圆周运动的向心力 (又称法向力 )将不停增大 ,由轨道法向方向上的动力学方程F Nmgsin θ mv 2可判断 ,随 θ 角的不停增R大过程 ,轨道支持力 F N 也将不停增大 ,因而可知应选 (B) ．2 -5 图 (a)示系统置于以 a ＝ 1/4 g 的加快度上涨的起落机内 ,A 、B 两物体质量相同均为 m,A 所在的桌面是水平的 ,绳索和定滑轮质量均不计 ,若忽视滑轮轴上和桌面上的摩擦,其实不计空气阻力 ,则绳中张力为 ( )(A) 58 mg (B) 12 mg (C) mg (D) 2 mg剖析与解此题可考虑对 A 、B 两物体加上惯性力后 ,以电梯这个非惯性参照系进行求解．此时 A 、B两物体受力状况如图 (b)所示 ,图中 a ′为 A 、B 两物体相对电梯的加快度 ,ma ′为惯性力．对 A 、B 两物体应用牛顿第二定律 ,可解得 F ＝ 5/8 mg ．应选 (A) ．Ｔ议论关于习题 2 -5 这种种类的物理问题 ,常常从非惯性参照系 (此题为电梯 )察看到的运动图像较为明确 ,但因为牛顿定律只合用于惯性参照系,故从非惯性参照系求解力学识题时,一定对物体加上一个虚构的惯性力．如以地面为惯性参照系求解,则两物体的加快度 a A 和a B 均应付地而言 ,此题中 a A 和 a 的大小与方向均不相同．此中 aA 应斜向上．对 a A 、a 、a 和a ′之间还要用到相对运动规律 ,求解BB过程较繁．有兴趣的读者不如自己试试试看．2 -6 图示一斜面 ,倾角为 α,底边 AB 长为 l ＝ 2.1 m,质量为 m 的物体从题 2 -6 图斜面顶端由静止开始向下滑动 ,斜面的摩擦因数为 μ＝ 0.14 ．试问 ,当 α为何值时 ,物体在斜面上下滑的时间最短？其数值为多少？剖析动力学识题一般分为两类：(1) 已知物体受力争其运动状况；(2) 已知物体的运动状况来剖析其所受的力．自然,在一个详细题目中,这两类问题并没有截然的界线,且都是以加快度作为中介,把动力学方程和运动学规律联系起来．此题重点在列出动力学和运动学方程后,解出倾角与时间的函数关系α＝ f(t),而后运用对 t 求极值的方法即可得出数值来．解取沿斜面为坐标轴Ox,原点 O 位于斜面极点,则由牛顿第二定律有mgsin α mgμcosαma(1) 又物体在斜面上作匀变速直线运动,故有l 1 at2 1g sin α μcosαt 2cosα 2 2则t2l(2) gcosαsin α μcosα为使下滑的时间最短,可令dt0 ,由式(2)有dα则可得此时sin αsin α μcosαcosαcosα μsin α0 tan 2α 1 , 49oμt 2l 0.99 sgcosαsin α μcosα2 -7 工地上有一吊车 ,将甲、乙两块混凝土预制板吊起送至高空．甲块质量为 m 2 k g,乙块＝ 2.00 10×1质量为 m2＝ 1.00 ×102 kg．设吊车、框架和钢丝绳的质量不计．试求下述两种状况下,钢丝绳所受的张力以及乙块对甲块的作使劲：(1) 两物块以 10.0 m ·ｓ-2的加快度上涨； (2) 两物块以 1.0 m ｓ·-2的加快度上涨．从此题的结果,你能领会到起吊重物时一定迟缓加快的道理吗？剖析预制板、吊车框架、钢丝等可视为一组物体．办理动力学识题往常采纳“隔绝体”的方法物体所受的各样作使劲 ,在所选定的惯性系中列出它们各自的动力学方程．依据连结体中物体的多少可列出相应数量的方程式．联合各物体之间的互相作用和联系 ,可解决物体的运动或互相作使劲．,剖析解按题意 ,可分别取吊车(含甲、乙 )和乙作为隔绝体,画示力争 ,并取竖直向上为Oy 轴正方向 (如图所示 )．当框架以加快度 a 上涨时 ,有FＴ-(m1 ＋ m )g ＝(m ＋ m )a (1)2 1 2FN2- m g ＝ m a (2)2 2解上述方程 ,得F ＝ 1 2 (3)ＴFN2 ＝m (g ＋ a) (4) 2(1)当整个装置以加快度 a ＝ 10 m ·ｓ-2上涨时 ,由式 (3) 可得绳所受张力的值为FＴ＝10×3 N乙对甲的作使劲为N2 N2 2(g ＋ a) ＝3F′＝-F ＝ -m 10× N(2)当整个装置以加快度 a ＝ 1 m·ｓ-2上涨时 ,得绳张力的值为FＴ＝10×3 N此时 ,乙对甲的作使劲则为F′ N2＝103× N由上述计算可见,在起吊相同重量的物体时,因为起吊加快度不一样 ,绳中所受张力也不一样,加快度大 ,绳中张力也大．所以,起吊重物时一定迟缓加快,以保证起吊过程的安全．2 -8 如图 (a)所示 ,已知两物体 A、 B 的质量均为 m ＝ 3.0kg 物体 A 以加快度 a ＝ 1.0 m ·ｓ-2 运动 ,求物体 B 与桌面间的摩擦力． (滑轮与连结绳的质量不计)剖析该题为连结体问题 ,相同可用隔绝体法求解．剖析时应注意到绳中张力大小到处相等是有条件的 ,即一定在绳的质量和伸长可忽视、滑轮与绳之间的摩擦不计的前提下成立．同时也要注意到张力方向是不一样的．解分别对物体和滑轮作受力剖析［图(b)］．由牛顿定律分别对物体 A 、B 及滑轮列动力学方程,有m A g -F Ｔ＝m A a (1)F′1 -Fｆ＝ m B a′(2)ＴF′ -2FＴ1＝ 0 (3)Ｔ考虑到 mＴＴＴ1 Ｔ,a ′＝ 2a,可联立解得物体与桌面的摩擦力A ＝mB ＝m, F ＝F′ ,F ＝ F′1F f mg m 4m a7.2 N2议论动力学识题的一般解题步骤可分为：(1) 剖析题意 ,确立研究对象,剖析受力 ,选定坐标； (2) 根据物理的定理和定律列出原始方程组； (3) 解方程组 ,得出文字结果； (4) 查对量纲 ,再代入数据 ,计算出结果来．2 -9 质量为m′的长平板 A 以速度v′在圆滑平面上作直线运动,现将质量为m 的木块 B 轻轻安稳地放在长平板上 ,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板获得共同速度？剖析当木块 B 安稳地轻轻放至运动着的平板 A 上时 ,木块的初速度可视为零,因为它与平板之间速度的差别而存在滑动摩擦力,该力将改变它们的运动状态．依据牛顿定律可获得它们各自相对地面的加快度．换以平板为参照系来剖析,此时 ,木块以初速度-v ′(与平板运动速率大小相等、方向相反)作匀减速运动 ,其加快度为相对加快度,按运动学公式即可解得．该题也可应用第三章所叙述的系统的动能定理来解．将平板与木块作为系统,该系统的动能由平板原有的动能变成木块和平板一同运动的动能,而它们的共同速度可依据动量定理求得．又因为系统内只有摩擦力作功,依据系统的动能定理,摩擦力的功应等于系统动能的增量．木块相对平板挪动的距离即可求出．解 1 以地面为参照系 ,在摩擦力 Fｆ＝μmg的作用下 ,依据牛顿定律分别对木块、平板列出动力学方程F ｆ＝μ mg＝ma1F ′ｆ＝-F ｆ＝ m′a2a1和 a2分别是木块和木板相对地面参照系的加快度．若以木板为参照系,木块相对平板的加快度 a ＝ a1＋ a2 ,木块相对平板以初速度- v ′作匀减速运动直至最后停止．由运动学规律有2- v′＝ 2as由上述各式可得木块有关于平板所挪动的距离为sm v 22 μg m m解 2 以木块和平板为系统 ,它们之间一对摩擦力作的总功为W ＝F ｆ(s ＋l ) -F ｆl＝μ mgs式中 l 为平板相对地面挪动的距离．因为系统在水平方向上不受外力,当木块放至平板上时,依据动量守恒定律,有m′v′＝ (m′＋ m) v″由系统的动能定理 ,有μmgs 1 m v 2 1 m m v 22 2由上述各式可得sm v 22 μg m m2 -10 如图 (a)所示 ,在一只半径为 R 的半球形碗内 ,有一粒质量为 m 的小钢球 ,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时 ,它距碗底有多高？剖析保持钢球在水平面内作匀角速度转动时,一定使钢球遇到一与向心加快度相对应的力(向心力 ), 而该力是由碗内壁对球的支持力 F N的分力来供给的 ,因为支持力 F N一直垂直于碗内壁,所以支持力的大小和方向是随ω而变的．取图示 Oxy 坐标 ,列出动力学方程 ,即可求解钢球距碗底的高度．解取钢球为隔绝体 ,其受力剖析如图 (b) 所示．在图示坐标中列动力学方程F N sin θ ma n mRω2sin θ(1)F N cosθ mg (2)且有由上述各式可解得钢球距碗底的高度为R h cos θ(3)Rgh Rω2可见 ,h 随 ω的变化而变化．2 -11 火车转弯时需要较大的向心力,假如两条铁轨都在同一水平面内 (内轨、外轨等高 ),这个向心力只好由外轨供给 ,也就是说外轨会遇到车轮对它很大的向外侧压力 ,这是很危险的．所以 ,对应于火车的速率及转弯处的曲率半径,一定使外轨适合地超出内轨,称为外轨超高．现有一质量为m 的火车 ,以速率 v 沿半径为 R 的圆弧轨道转弯 ,已知路面倾角为 θ,试求： (1) 在此条件下 ,火车速率 v 0 为多大时 ,才能使车轮对铁轨内外轨的侧压力均为零？(2) 假如火车的速率 v ≠v 0 ,则车轮对铁轨的侧压力为多少？剖析如题所述 ,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平重量F N sin θ 提供 (式中 θ角为路面倾角 )．从而不会对内外轨产生挤压．与其对应的是火车转弯时一定以规定的速率v 0行驶．当火车行驶速率 v ≠v 0 时,则会产生两种状况：如下图 ,如 v ＞ v 0 时 ,外轨将会对车轮产生斜向内的侧压力 F 1 ,以赔偿原向心力的不足,如 v ＜ v 0时 ,则内轨对车轮产生斜向外的侧压力F 2 ,以抵消剩余的向心力 ,不论哪一种状况火车都将对外轨或内轨产生挤压．由此可知 ,铁路部门为何会在每个铁轨的转弯处规准时速 ,从而保证行车安全．解 (1) 以火车为研究对象 ,成立如下图坐标系．据剖析 ,由牛顿定律有F N sin θ mv 2(1)RF N cos θ mg 0(2)解 (1)(2) 两式可得火车转弯时规定速率为v 0gRtan θ(2) 当 v ＞ v 0 时 ,依据剖析有F N sin θ F 1cos θ m v2(3)RF N cos θ F 1sin θ mg 0(4)解 (3)(4) 两式 ,可得外轨侧压力为F 1 m v 2cos θ gsin θR当 v ＜ v 0 时,依据剖析有2F N sin θ F 2cos θ mv(5)RF N cos θ F 2sin θ mg(6)解 (5)(6) 两式 ,可得内轨侧压力为F 2 m gsin θ v 2cos θR2 -12 一杂技演员在圆筒形建筑物内表演飞车走壁．设演员和摩托车的总质量为 m,圆筒半径为 R,演员骑摩托车在直壁上以速率 v 作匀速圆周螺旋运动 ,每绕一周上涨距离为 h,如下图．求壁对演员和摩托车的作使劲．剖析杂技演员 (连同摩托车 )的运动能够当作一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加．其旋转一周所形成的旋线轨迹睁开后,相当于如图 (b)所示的斜面．把演员的运动速度分解为图示的 v 1 和 v 2 两个重量 ,明显 v 1是竖直向上作匀速直线运动的分速度 ,而 v 2则是绕圆筒壁作水平圆周运动的分速度,此中向心力由筒壁对演员的支持力F N 的水平重量 F N2 供给 ,而竖直重量 F N1则与重力相均衡．如图 (c) 所示 ,此中 φ角为摩托车与筒壁所夹角．运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象 ,据 (b)(c)两图应有FN1mg 0(1) F N 2m v 2(2)Rv 2vcos θ v2πR(3)R 2 h 22πF NF N 21 F N 2 2(4)以式 (3) 代入式 (2),得22 22 2m4π R v4π RmF N 222222v2(5)RhR 4πRh 4π将式 (1) 和式 (5)代入式 (4),可求出圆筒壁对杂技演员的作使劲( 即支承力 )大小为2222224πRF NFN1F N 2 m g2 2 v2h4πR与壁的夹角 φ为FN 222arctan4πRv2arctan2 2FN 14πRh g议论表演飞车走壁时 , 演员一定控制好运动速度,行车路线以及摩托车的方向 ,以保证三者之间知足解题用到的各个力学规律．2 -13 一质点沿 x 轴运动 ,其受力如下图 ,设 t ＝ 0 时 ,v 0＝ 5m ·ｓ-1,x 0＝ 2 m, 质点质量 m ＝ 1kg, 试求该质点 7ｓ末的速度和地点坐标．剖析第一应由题图求得两个时间段的 F(t)函数 ,从而求得相应的加快度函数,运用积分方法求解题目所问 ,积分时应注意积分上下限的取值应与两时间段相应的时辰相对应．解由题图得F t2t, 0 t 5s 35 5t,5s t 7s由牛顿定律可得两时间段质点的加快度分别为a 2t , 0 t 5sa 35 5t , 5s t 7s对 0 ＜ t ＜ 5ｓ时间段 ,由 adv 得dtvd tv 0 adtv积分后得 v 5 t 2再由 vdx 得dtxt dxvdtx 0积分后得 x 2 5t1 t 33将 t ＝ 5ｓ代入 ,得 v 5＝ 30 m ·ｓ-1 和 x 5 ＝ 68.7 m 对 5ｓ＜ t ＜7ｓ时间段 ,用相同方法有vtdva 2dtv 0 5 s得v 35t2xt再由dx vdtx5 5 s得x ＝23 -82.5t ＋将 t ＝7ｓ代入分别得 v 7＝ 40 m ·ｓ -1 和 x 7 ＝ 142 m2 -14 一质量为 10 kg 的质点在力 F 的作用下沿 x 轴作直线运动 ,已知 F ＝120t ＋ 40,式中 F 的单位为 N, t 的单位的ｓ．在 t ＝ 0 时 ,质点位于 x ＝5.0 m 处 ,其速度 v 0 ＝6.0 m ·ｓ-1 ．求质点在随意时辰的速度和地点．剖析这是在变力作用下的动力学识题．因为力是时间的函数 ,而加快度 a ＝ dv/dt,这时 ,动力学方程就成为速度对时间的一阶微分方程 ,解此微分方程可得质点的速度v (t)；由速度的定义 v ＝dx /d t,用积分的方法可求出质点的地点．解因加快度 a ＝ dv/dt,在直线运动中 ,依据牛顿运动定律有120t40m dvdt依照质点运动的初始条件 ,即t 0 ＝ 0 时 v 0 ＝ 6.0 m ｓ·-1 ,运用分别变量法对上式积分,得vt4.0 dtdv 0 vv ＝2又因 v ＝ dx /dt,并由质点运动的初始条件： t 0 ＝ 0 时 x 0 ＝ 5.0 m,对上式分别变量后积分 ,有xt6.0t 2dtdxx 0x ＝2 +2.0 t 32 -15 轻型飞机连同驾驶员总质量为10×3 kg ．飞机以 55.0 m ｓ·-1 的速率在水平跑道上着陆后,驾驶员开始制动 ,若阻力与时间成正比 ,比率系数 α＝ 5.0 ×102 N ·ｓ -1,空气对飞机升力不计 ,求： (1) 10 ｓ后飞机的速率； (2) 飞机着陆后 10ｓ内滑行的距离．剖析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动．其水平方向所受制动力 F 为变力 ,且是时间的函数．在求速率和距离时,可依据动力学方程和运动学规律,采纳分别变量法求解．解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有 Fma mdvαtαt dtdtvdt vmv 0得v v 0α t 22m所以 ,飞机着陆 10ｓ后的速率为v ＝ 30 m ｓ· -1xt α t 2 dt又dxv 0x02m故飞机着陆后 10ｓ内所滑行的距离s x x 0 v 0tα t 3 467 m6m2 -16 质量为 m 的跳水运动员 ,从 10.0 m 高台上由静止跳下落入水中．高台距水面距离为 h ．把跳水运动员视为质点 ,并略去空气阻力．运动员入水后垂直下沉,水对其阻力为 bv 2 ,此中 b 为一常量．若以水面上一点为坐标原点O,竖直向下为Oy轴,求： (1)运动员在水中的速率v 与 y的函数关系；(2) 如 b/m＝-1 , 跳水运动员在水中下沉多少距离才能使其速率v 减少到落水速率v 0的1 /10？(假设跳水运动员在水中的浮力与所受的重力大小恰巧相等)剖析该题能够分为两个过程,入水前是自由落体运动,入水后 ,物体受重力 P、浮力 F 和水的阻力 F ｆ的作用 ,其协力是一变力 ,所以 ,物体作变加快运动．固然物体的受力剖析比较简单 ,可是 ,因为变力是速度的函数(在有些问题中变力是时间、地点的函数 ),对这种问题列出动力学方程其实不复杂 ,但要从它计算出物体运动的地点和速度就比较困难了．往常需要采纳积分的方法去解所列出的微分方程．这也成认识题过程中的难点．在解方程的过程中 ,特别需要注意到积分变量的一致和初始条件确实定．解 (1) 运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P -F ｆ-F ＝ma由题意 P ＝ F、 F ｆ＝ bv2 ,而a ＝ dv /dt ＝ v (d v /dy),代入上式后得-bv2＝ mv (d v /dy)考虑到初始条件 y0＝0 时 , v0 2gh ,对上式积分,有mv dvtdy0b v0 vv v0e by / m 2ghe by / m(2) 将已知条件 b/m ＝ 0.4 m -1 ,v ＝0 代入上式 ,则得y m ln v 5.76 mb v0*2 -17 直升飞机的螺旋桨由两个对称的叶片构成．每一叶片的质量m＝ 136 kg,长 l ＝ 3.66 m．求当它的转速 n＝ 320 r/min 时 ,两个叶片根部的张力．(设叶片是宽度必定、厚度平均的薄片)剖析螺旋桨旋转时 ,叶片上各点的加快度不一样,在其各部分双侧的张力也不一样；因为叶片的质量是连续散布的 ,在求叶片根部的张力时 ,可选用叶片上一小段 ,剖析其受力 ,列出动力学方程 ,而后采纳积分的方法求解．解设叶片根部为原点 O,沿叶片背叛原点 O 的方向为正向 ,距原点 O 为 r 处的长为 dr 一小段叶片 ,其双侧对它的拉力分别为 F Ｔ(r) 与 F Ｔ (r ＋ dr )．叶片转动时 ,该小段叶片作圆周运动 ,由牛顿定律有dF T F T rF T r drmω2 rdrl因为 r ＝l 时外侧 F Ｔ＝ 0,所以有t dF Tlm ω2F T rl r drrF T m ω2 2r 22πmn 22r 2rll2ll上式中取 r ＝0,即得叶片根部的张力F Ｔ 0 ＝10×5 N负号表示张力方向与坐标方向相反．2 -18 一质量为 m 的小球最先位于如图 (a)所示的 A 点 ,而后沿半径为 r 的圆滑圆轨道 ADCB 下滑．试求小球抵达点 C 时的角速度和对圆轨道的作使劲．剖析该题可由牛顿第二定律求解．在取自然坐标的状况下 ,沿圆弧方向的加快度就是切向加快度a ,ｔ与其相对应的外力 F 是重力的切向重量 mgsin α,而与法向加快度 a n 相对应的外力是支持力 F N 和重力ｔ的法向重量 mgcos α．由此 ,可分别列出切向和法向的动力学方程F ＝ mdv/dt 和F n ＝ma n ．因为小球在ｔ滑动过程中加快度不是恒定的 ,所以 ,需应用积分求解 ,为使运算简易 ,可变换积分变量．倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度 ,方法比较简易．但它不可以直接给出小球与圆弧表面之间的作使劲．解小球在运动过程中遇到重力 P 和圆轨道对它的支持力 F N ．取图 (b) 所示的自然坐标系,由牛顿定律得F tmgsin α mdv(1)dtF n F Nmgcos α mmv 2(2)R由 vdsr α r α运动到点 C 的始末条件 ,进行积分 ,有d ,得 dtd ,代入式 (1),并依据小球从点 Adtdtvvαv 0d90org sin αd αv v得v2rgcos α则小球在点 C 的角速度为ωv2 cos α/rr g由式 (2)得F Nm mv 2 mgcos α 3mgcos αr由此可得小球对圆轨道的作使劲为F NF N 3mgcos α负号表示 F ′N 与 e n 反向．2 -19 圆滑的水平桌面上搁置一半径为 R 的固定圆环 ,物体紧贴环的内侧作圆周运动 ,其摩擦因数为μ,开始时物体的速率为 v 0 ,求： (1) t 时辰物体的速率； (2) 当物体速率从 v 0减少到 12 v 0时 ,物体所经历的时间及经过的行程．剖析运动学与动力学之间的联系是以加快度为桥梁的,因此 ,可先剖析动力学识题．物体在作圆周运动的过程中,促进其运动状态发生变化的是圆环内侧对物体的支持力 F N和环与物体之间的摩擦力 F ｆ,而摩擦力大小与正压力 F N′成正比 ,且F N与F N′又是作使劲与反作使劲 ,这样 ,便可经过它们把切向和法向两个加快度联系起来了 ,从而可用运动学的积分关系式求解速率和行程．解 (1) 设物体质量为 m,取图中所示的自然坐标 ,按牛顿定律 ,有mv2F N ma nRdvF f ma tdt由剖析中可知,摩擦力的大小 Fｆ＝μF ,由上述各式可得N2μv dvR dt取初始条件 t ＝0 时 v ＝v 0 ,并对上式进行积分,有t R v dvdt20 μ v0 vv Rv0R v0μt(2)当物体的速率从 v 0减少到 1/2v 0时 ,由上式可得所需的时间为tRμv0物体在这段时间内所经过的行程t stRv0dt vdtv0μt0 RsRln 2μ2 -20 质量为 45.0 kg 的物体 ,由地面以初速 60.0 m·ｓ-1 竖直向上发射 ,物体遇到空气的阻力为 F r＝kv, 且 k ＝ 0.03 N/( m-1最大高度为多少？ｓ· )． (1) 求物体发射到最大高度所需的时间．(2)剖析物体在发射过程中 ,同时遇到重力和空气阻力的作用,其协力是速率v 的一次函数 ,动力学方程是速率的一阶微分方程,求解时 ,只需采纳分别变量的数学方法即可．可是,在求解高度时 ,则一定将时间变量经过速度定义式变换为地点变量后求解 ,并注意到物体上涨至最大高度时 ,速率应为零．解 (1) 物体在空中受重力 mg 和空气阻力 F r ＝ kv 作用而减速．由牛顿定律得mg k mdv(1)vdt依据始末条件对上式积分,有t vddtmvvv 0mg kvtmln 1 kv 06.11 skmgdv dv(2) 利用v 的关系代入式 (1),可得dtdydvmg kv mv分别变量后积分y 0dyv 0mvdvmgkv故m mg ln 1kv 0 v 0183 mykmgkv 0 和 y 2议论如不考虑空气阻力 ,则物体向上作匀减速运动．由公式tv 0 分别算得 t ≈ｓ和g2gy ≈184 m,均比实质值略大一些．2 -21 一物体自地球表面以速率 v 0 竖直上抛．假设空气对物体阻力的值为F r ＝ kmv 2 ,此中 m 为物体的质量 ,k 为常量．试求： (1) 该物体能上涨的高度； (2)物体返回地面时速度的值． (设重力加快度为常量． )剖析因为空气对物体的阻力一直与物体运动的方向相反 ,所以 ,物体在上抛过程中所受重力 P 和阻力 F r 的方向相同；而下落过程中 ,所受重力 P 和阻力 Fr 的方向则相反．又因阻力是变力 ,在解动力学方程时 ,需用积分的方法．解分别对物体上抛、下落时作受力剖析 ,以地面为原点 ,竖直向上为 y 轴 (如下图 ) ．(1) 物体在上抛过程中 ,依据牛顿定律有mg km 2 m dv m vdvv dt dy 依照初始条件对上式积分,有y 0 v ddy v2v0 g kvy 1ln g kv 2 2k g kv02物体抵达最高处时, v ＝ 0,故有hymax 1 ln g kv 022k g (2)物体下落过程中 ,有2vdvmg kmv m对上式积分 ,有ydy 0vdv0 v0 g k2vkv 2 1/ 2v则v0 1g2 -22 质量为 m 的摩托车 ,在恒定的牵引力 F 的作用下工作 ,它所受的阻力与其速率的平方成正比,它能达到的最大速率是 v m．试计算从静止加快到mv /2所需的时间以及所走过的行程．剖析该题依旧是运用动力学方程求解变力作用下的速度和地点的问题,求解方法与前两题相像,只是在解题过程中一定想法求出阻力系数k．因为阻力 Fr ＝ kv2 ,且 F r又与恒力 F 的方向相反；故当阻力随速度增加至与恒力大小相等时,加快度为零 ,此时速度达到最大．所以,依据速度最大值可求出阻力系数来．但在求摩托车所走行程时,需对变量作变换．解设摩托车沿 x 轴正方向运动 ,在牵引力 F 和阻力 F r同时作用下 ,由牛顿定律有F k 2 m dv(1)v dt当加快度 a ＝ dv/dt ＝ 0 时,摩托车的速率最大,所以可得k＝F/v m2 (2) 由式 (1) 和式 (2)可得依据始末条件对式(3)积分 ,有t mdtFF 1 v 2 m dv (3)v m2 dt1v m v2 12 dv1 2v m则tmv m ln3 dvmvdv 2F(3)积分 ,有又因式 (3) 中 m,再利用始末条件对式dtdxxmdxF 1v m v212 dv0 12v m则xmv m2ln40.144 mv m 22F3F*2 -23 飞机下降时 ,以 v 0 的水平速度下落伍自由滑行,滑行时期飞机遇到的空气阻力 F 1＝ -k 1 v 2, 升力F 2＝ k 2 v 2, 此中 v 为飞机的滑行速度 ,两个系数之比 k 1/ k 2 称为飞机的升阻比．实验表示,物体在流体中运动时 ,所受阻力与速度的关系与多种要素有关 ,如速度大小、流体性质、物体形状等．在速度较小或流体密度较小时有 F ∝ v,而在速度较大或流体密度较大的有 F ∝ v 2 ,需要精准计算时则应由实验测定．此题中因为飞机速率较大,故取 F ∝v 2 作为计算依照．设飞机与跑道间的滑动摩擦因数为μ,试求飞机从触地到静止所滑行的距离．以上计算实质上已成为飞机跑道长度设计的依照之一．剖析如下图 ,飞机触地后滑行时期遇到 5 个力作用 ,此中 F 1 为空气阻力 , F 2 为空气升力 , F 3 为跑道作用于飞机的摩擦力 , 很明显飞机是在合外力为变力的状况下作减速运动 ,列出牛顿第二定律方程后 ,用运动学第二类问题的有关规律解题．因为作用于飞机的合外力为速度 v 的函数 ,所求的又是飞机滑行距离 x,所以比较简易方法是直接对牛顿第二定律方程中的积分变量dt 进行代换 ,将 dt 用dx取代 ,获得一个有关 v 和 x 的微分方程 ,分别变量后再作积分．v解取飞机滑行方向为 x 的正方向 ,着陆点为坐标原点,如下图 ,依据牛顿第二定律有F N k 1v 2m dv(1)k 2v 2dtF Nmg 0(2)将式 (2)代入式 (1),并整理得μmg k μkv 2m dvm dv12dt v dx分别变量并积分 ,有vm dvv2dxμmgk 1 μk 2v 0v得飞机滑行距离xm ln μmg k 1 μk 2 v 2(3)2 k 1 μk 2 μmg考虑飞机着陆瞬时有 F N ＝ 0 和v ＝ v 0 ,应有 k 2v 02＝ mg,将其代入 (3)式 ,可得飞机滑行距离 x 的另一表达。

《大学物理》课后解答题第二章牛顿运动定律与守恒

解：（1）A、B系统弹性碰撞动量不守恒（水平方向
守恒，竖直方向不守恒）。受力分析如右图。
注意：斜劈在碰撞瞬间受到桌面的冲力。
（2）令斜劈左右位置互换，如右图
A、B系统弹性碰撞动量守恒。
4、如图4.1所示，质量为m的物体放在水平传送带上，与传送带一起以恒定的加速度前进，当物体被传送一段距离时，传送带对物体作功是多少？物体对传送带作功多少？请分别以地面和皮带为参照系考虑问题。在两个参照系中它们互相所做的功的总和是否改变？
（3）动量不守恒，对滑轮轴的角动量守恒，动能和机械能不守恒。
二、课堂练习
1、如图2.11所示，质量为m的物体A放在水平面上，已知滑动摩擦系数为μ，求：欲拉动A以恒定速度沿水平方向前进所需的最小的拉力。
图2.11
解：设拉力方向如图，受力分析得：
所以
令得：
又因为
所以得
2、如图2.12所示，水平桌面上有一块质量为M的木板，板上放一质量为m的物体，M、m与桌面彼此之间的滑动摩擦系数均为，静摩擦系数均为，今以水平方向的拉力作用于M，使M与m一起以加速度运动。
解：应采用系统综合法，即以静置于桌面的绳子和提起运动部分的绳子总体作为研究对象，系统所受合外力实际上只有提起运动部分的绳子所受重力与上提力。提起部分的质量为：，所受重力
由动量定理：
而：，故得：。
6、一根均匀的链条，总长为，一部分放在光滑的桌面上，另一部分从桌面边缘下垂，长为，如图4.6所示，设开始时链条静止，求链条刚好全部离开桌面时的速率。
图2.3
3）、A与B叠放在一起（如图2.3），分以下几种情况讨论：a、A、B静止；b、A、B一起自由下落；c、一起匀速上升。
解：对A和B分别分析分析受力如下图

大物习题答案第2章动量守恒定律与能量守恒定律

第2章动量守恒定律与能量守恒定律一基本要求1 理解冲量、动量等概念。

掌握动量定理及动量守恒定律，能运用它们解简单系统在平面内运动的力学问题。

2 理解功的概念，能计算变力做功的问题。

3 理解保守力做功的特点和势能的概念，会计算重力、弹性力和万有引力做的功及对应的势能。

4 理解动能定理、功能原理和机械能守恒定律，掌握运用守恒定律解问题的思想和方法。

二基本概念１质点的动量、冲量质点的动量定义：m =p υ，p 为矢量，也是状态量。

质点的冲量定义：21t t dt =⎰I F ，它也是矢量，是过程量。

2 冲力在解决冲击、碰撞问题时，将两个物体在碰撞瞬间的相互作用力称为冲力，冲力作用时间短，量值变化也很大，所以很难确定每一时刻的冲力，常用平均冲力的冲量来代替变力的冲量。

3内力和外力对于质点系，其内部各个质点之间的相互作用力称为内力，质点系以外的其他物体对其中的任一质点的作用力称为外力。

4功功率（1）功力对质点所作的功为力在质点位移方向的分量与位移大小的乘积。

cos BBAAW dW d F dr θ==⋅=⎰⎰⎰F r(2) 功率功随时间的变化率,反映的是做功的快慢。

dW P dt =cos d d P F dt dtυθ⋅==⋅=⋅=F r r F F υ5动能质量为m 的物体，当它具有速度υ时，定义212m υ为质点在速度为υ时的动能，用k E 表示。

6保守力和非保守力如果力F 对物体做的功只与物体初、末位置有关而与物体所经过的路径无关，我们把具有这种特点的力称为保守力，否则称为非保力。

保守力做功0ld ⋅=⎰F l ，非保守力作功 0ld ⋅≠⎰F l 。

重力、弹性力、万有引力均为保守力，而摩擦力、汽车的牵引力等都是非保守力。

7势能系统某点的势能等于在保守力作用下将物体从该点沿任意路径移动到零势能点保守力做的功，用p E 表示。

8机械能，系统的动能和势能统称为机械能，用E 表示。

大学物理课后习题答案第02章

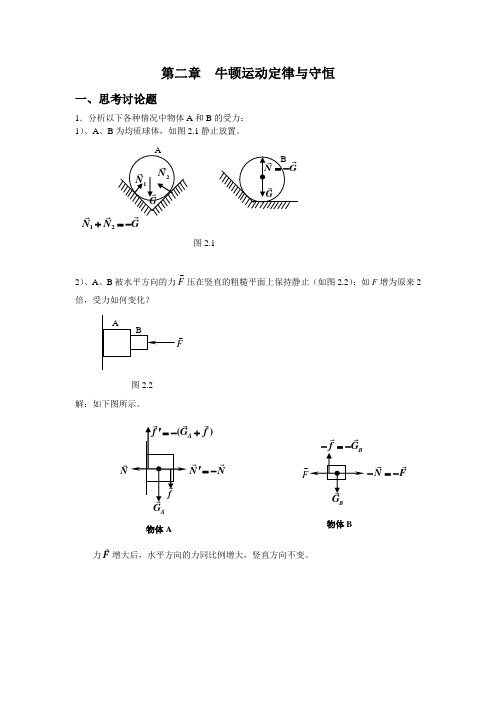
第2章质点和质点系动力学2.1 一斜面的倾角为α, 质量为m 的物体正好沿斜面匀速下滑. 当斜面的倾角增大为β时, 求物体从高为h 处由静止下滑到底部所需的时间.解：设斜面摩擦系数为μ。

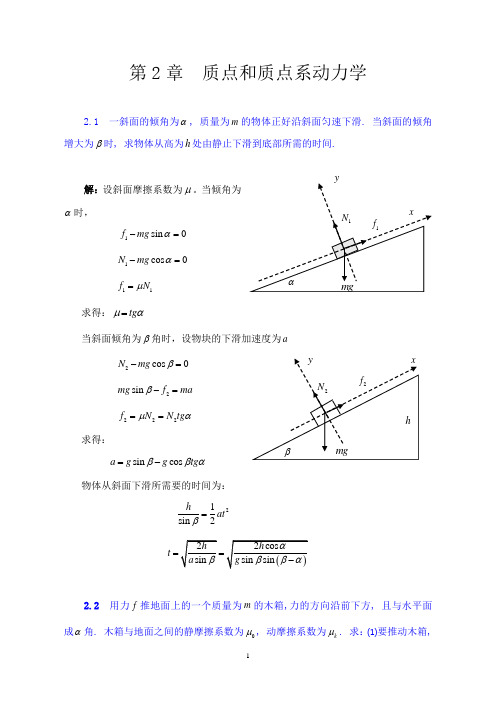
当倾角为α时，1sin 0f mg α-=1cos 0N mg α-= 11f N μ= 求得：tg μα=当斜面倾角为β角时，设物块的下滑加速度为a2cos 0N mg β-= 2sin mg f ma β-= 222f N N tg μα==求得：sin cos a g g tg ββα=- 物体从斜面下滑所需要的时间为：21sin 2h at β=t ==2.2 用力f 推地面上的一个质量为m 的木箱,力的方向沿前下方, 且与水平面成α角. 木箱与地面之间的静摩擦系数为0μ, 动摩擦系数为k μ. 求：⑴要推动木箱,f 最小为多少？使木箱作匀速运动, f 为多少？⑵证明当α大于某值时, 无论f 为何值都不能推动木箱, 并求α值.解：⑴当f 的水平分力克服最大静摩擦力时，木箱可以运动，即 ()0cos sin f mg f αμα≥+ 00cos sin mgf μαμα≥-0min 0cos sin mgf μαμα=-使木箱做匀速运动，则()cos sin k f mg f αμα=+ cos sin k k mgf μαμα=-⑵由能推动木箱的条件: ()0cos sin f mg f αμα≥+ 00cos sin f f mg αμαμ-≥若0cos sin 0f f αμα-<时,上式不可能成立,即不可能推动木箱的条件为: 01tg αμ>， 01arctgαμ>2.3 质量为5000kg 的直升飞机吊起1500kg 的物体, 以0.6m/s 2的加速度上升, 求：（1）空气作用在螺旋桨上的升力为多少. （2）吊绳中的张力为多少.解：（1）对飞机物体整体进行受力分析，得()()f M m g M m a -+=+()()4650010.2 6.8910f M m g a N =++=⨯=⨯ （2）对物体m 进行受力分析，得T mg ma -=()4150010.6 1.5910T m g a N =+=⨯=⨯2.4质量为m 汽车以速率0v 高速行驶, 受到2kv f -=的阻力作用, k 为常数.当汽车关闭发动机后, 求：（1）速率v 随时间的变化关系. （2）路程x 随时间的变化关系. （3）证明速率v 与路程x 之间的函数关系为x mke v v -=0．（4）若020/v m s =, 经过15s 后, 速率降为10/t v m s =, 则k 为多少？解：由题意， 2dvmkv dt =- 两边积分 020v tv dv k dt v m =-⎰⎰011kt v v m ⎛⎫-=- ⎪⎝⎭即 00001v mv v k m kv t v t m ==+⎛⎫+ ⎪⎝⎭（2）由上式两边积分 0000xtmv dx dt m kv t =+⎰⎰即 0ln m kv t m x k m +⎛⎫=⎪⎝⎭（3）由（1）中得 00mv kv t m v =-，代入（2）中的结果，得 00ln ln mv m m v m m v x k m k v ⎛⎫+- ⎪⎛⎫== ⎪ ⎪⎝⎭⎪⎝⎭即 0k x mv v e-=（4）020/v m s =,15t s =,10/t v m s =代入00mv v m kv t=+，求得300m k =2.5质量为m 的质点以初速度0v 竖直上抛, 设质点在运动中受到的空气阻力与质点的速率成正比, 比例系数为0>k ．试求：（1）质点运动的速度随时间的变化规律. （2）质点上升的最大高度.解：（1） dvm mg kv dt=--mdvdt mg kv=-+1()kd kv mg dt mg kv m+=-+两边积分 001()vtv k d kv mg dt mg kv m +=-+⎰⎰0lnkv mg kt kv mg m+=-+即 k mg e k mg v v t m k-⎪⎭⎫ ⎝⎛+=-0 （2）由（1）中方程得 dv dv dy dv mg kv mm mv dt dy dt dy--=== ()mg kv mg mvdv m dy dv mg kv k mg kv+--==-++两边积分 00(1)yv v m mgdy dv k mg kv=--+⎰⎰ ()2020ln m m g mg kvy v v k k mg kv +=-++当0v =时，有 20max02ln mg kv m m g y v k k mg ⎛⎫+=- ⎪⎝⎭2.6自动枪以每分钟发射120发子弹的速率连续发射. 每发子弹的质量为7.9g , 出口速率为735/m s . 求射击时枪托对肩部的平均压力.解：设肩部所受的平均作用力为F ，由动量定理得 Ft mv =∑即 31207.91073511.660mv F N t-⨯⨯⨯==≈∑2.7 质点在x 轴上受x 方向的变力F 的作用．F 随时间的变化关系为：在刚开始的0.1s 内均匀由0增至20N ，又在随后的0.2s 内保持不变，再经过0.1s 从20N 均匀地减少到0. 求：（1）力随时间变化的t F -图. （2）这段时间内力的冲量和力的平均值. （3）如果质点的质量为3kg , 初始速度为1/m s , 运动方向与力的方向相同. 当力变为零时, 质点速度为多少？解：（1）由题意得（2）由上图得11200.1200.2200.1622I N s =⨯⨯+⨯+⨯⨯=⋅0.5200.1200.20.5200.1150.4I F N t ⨯⨯+⨯+⨯⨯=== （3）由动量定理得 0t I mv mv =-0.10.30.4即 06313/3t I mv v m s m ++⨯===2.8子弹脱离枪口的速度为300/m s , 在枪管内子弹受力为5400410/3F t =-⨯（SI ）, 设子弹到枪口时受力变为零. 求：（1）子弹在枪管中的运行的时间. （2）该力冲量的大小. （3）子弹的质量.解：（1）由541040003tF ⨯=-=得3310t s -=⨯ （2）35310004104000.63tt I Fdt dt N s -⨯⎛⎫⨯==-=⋅ ⎪⎝⎭⎰⎰（3）由0I Ft mv ==-得 30.6210300I m kg v -===⨯2.9 自由电子在沿x 轴的振荡电场()0cos E t ωϕ=+E i中运动, 其中0E , ω,ϕ为常数. 设电子电量为e -, 质量为m , 初始条件为：0=t 时, 00v =v i, 00x =r i . 略去重力和阻力的作用, 求电子的运动方程.解：由()0cos F eE t ωϕ=-+得 0tvv Fdt mdv =⎰⎰解得()000sin sin eE eEv v t m m ϕωϕωω=+-+ 两边同乘dt 积分，()000sin sin eE eE dx v t dt m m ϕωϕωω⎛⎫=+-+ ⎪⎝⎭两边积分，()ϕωωϕωϕω++⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=t m eE t m eE v m eE x x cos sin cos 20002002.10 质量为m 的物体与一劲度系数为k 的弹簧连接, 物体可以在水平桌面上运动, 摩擦系数为μ. 当用一个不变的水平力拉物体, 物体从平衡位置开始运动. 求物体到达最远时, 系统的势能和物体在运动中的最大动能.解：分析物体水平受力，物体受外力、弹性力以及摩擦力，如图所示物体到达最远时，速度为0。

大学物理第二章习题答案

普通物理
1
第二章机械能及其守恒定律
——思考题与习题（2课时）
思考题

2
在驱动轮不发生滑动的条件下，一辆汽车从静止加速到速率V。汽车的动能是否由路面施于汽车的静摩擦力所作之功而获得的？

路面对汽车的静摩擦力并没有作功，汽车作用。
1 R 3
1 1 2 1 2 mgx k ( x x ) kx mv 2 2 2 2 (1)
O
A
x
F
x
B
mg
x
18
小球在 A 点时处于平衡状态，故
mg kx (2)
A
由以上二式可解出由静止释放小球后小球第一次经过点 A 时的速率为
v k x m
O
x
F
x
B
mg
x
注意，在此问题中，弹性势能 0 点不能选在 A 点，而必须选择弹簧自然伸长时的位置 O 点，因为弹性势能的定义 1 2 E p kx 2 只有选择弹簧自然伸长时的位置为势能 0 点时才成立。
3

一人逆水划船，使船相对于河岸静止。试问: 1）人是否要作功？ 2）停止划船，让船顺流而下，则流水对船是否作功？ 1）要作功，使被划的水获得动能增量。 2）略去空气阻力，略去船的海拔下降，人刚停下时流水做功，使船与水达到同速，此后流水对船不作功。

4

质点系的内力之和是否一定为零？内力作功之和是否一定为零？内力矩之和是否一定为零？为什么？质点系的内力之和一定为零，因为内力是成对出现的，每一对内力大小相等，方向相反。内力作功之和不一定等于零，因为一对内力的功与内力大小及发生作用的两部分之间的相对位移有关，例如爆炸的情况，内力做功大于零。内力矩之和一定为零，因为内力矩也是成对出现的，大小相等，方向相反。

大学物理答案第二章牛顿定律-习题解答

牛顿运动定律与实际问题的综合应用
将牛顿运动定律应用于各种实际问题中，如天体运动、弹性碰撞、摩擦力问题等，通过建立物理模型和运用数学工具解决实际问题。
解决复杂问题的思路与方法
01
02
03
04
建立物理模型
根据问题的实际情况，抽象出具体的物理模型，如质点、刚体、弹性碰撞等，为解决问题提供清晰的思路。
定律的应用场景与实例
总结词
牛顿第一定律在日常生活和科学研究中有着广泛的应用。例如，汽车安全带的设计、投掷物体的轨迹、行星的运动等都遵循这一规律。
详细描述
汽车安全带的设计依据了惯性定律，通过限制乘客在急刹车或碰撞时的运动，减少伤害风险。投掷物体时，出手的角度和力量会影响物体的运动轨迹，这也符合惯性定律。行星的运动规律是牛顿第一定律的重要应用之一，行星绕太阳的椭圆轨道运动可以由惯性定律推导出来。
05
习题解答
常见错误解析与纠正
01 02 03
错误1
混淆了牛顿第二定律中的力和加速度概念，将力误认为是加速度的原因，而实际上力是产生加速度的原因。纠正：正确理解力和加速度的关系，力是产生加速度的原因，加速度的大小和方向由力的三要素决定。
错误2
在分析多力作用下物体的运动时，未能正确分析合力和加速度的关系。纠正：在分析多力作用下物体的运动时，应先求出合力，再根据牛顿第二定律求出加速度，最后根据运动学公式求解速度和位移。
导出牛顿第三定律。
定律的应用场景与实例
要点一
总结词
牛顿第三定律在现实生活中有着广泛的应用，例如火箭发射、车辆行驶、体育运动等。
要点二
详细描述
在火箭发射中，火箭向下喷射高温高压气体，产生一个向上的反作用力，使火箭升空。在车辆行驶中，车辆发动机产生的力推动车辆前进，同时车辆也会给地面一个向后的反作用力，使地面产生磨损。在体育运动中，例如篮球投篮时，投篮的力量和手受到的反作用力大小相等、方向相反。

大学物理第2章课后答案

大学物理第2章课后答案(总34页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第二章质点动力学四、习题选解2-1 光滑的水平桌面上放有三个相互接触的物体，它们的质量分别为.4,2,1321kg m kg m kg m ===（1）如图a 所示，如果用一个大小等于N 98的水平力作用于1m 的左方，求此时2m 和3m 的左边所受的力各等于多少？（2）如图b 所示，如果用同样大小的力作用于3m 的右方。

求此时2m 和3m 的左边所受的力各等于多少？（3）如图c 所示，施力情况如（1），但3m 的右方紧靠墙壁（不能动）。

求此时2m 和3m 左边所受的力各等于多少？解：（1）三个物体受到一个水平力的作用，产生的加速度为a()a m m m F321++=232114-⋅=++=s m m m m Fa用隔离法分别画出32,m m 在水平方向的受力图（a ），题2-1（a ）图由a m F =a m f f23212=- a m f323= 2332f f =N f 5623= N f 8412=（2）由()a m m m F321++=232114-⋅=++=s m m m m Fa用隔离法画出321m m m 、、在水平方向的受力图（b ）由a m F = 得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧====-=-3223122112121232323f f f f am f a m f f a m f F解得： N f 1412= N f 4223=题2-1（b ）图（3）由于321m m m 、、都不运动，加速度0=a ，三个物体彼此的作用力都相等，都等于FN f f 982312==2-2 如图所示，一轻质弹簧连接着1m 和2m 两个物体，1m 由细线拉着在外力作用下以加速a 竖直上升。

问作用在细线上的张力是多大？在加速上升的过程中，若将线剪断，该瞬时1m 、2m 的加速度各是多大？解：（1）分别画出1m 、2m 受力的隔离体如图（a ），题2-2（a ）图取向上为正方向，由牛顿第二定律⎪⎩⎪⎨⎧='=-'=--f f a m g m f a m g m f T 2211故 ()()a g m m g m g m a m a m T ++=+++=212121 （2）将线剪断，画出21m m 、的隔离体图，如图（b ）题2-2（b ）图取竖直向上为正方向，由牛顿第二定律得⎪⎩⎪⎨⎧='=-'=--f f a m g m f a m g m f 222111 得⎪⎩⎪⎨⎧+--==-=)(/)'(121222a g m m g a a m g m f a1a 的方向向下，2a的方向向上。

大学物理课后习题2第二章答案

(B) aA>0 , aB<0.
(C) aA<0 , aB>0.
(D) aA<0 , aB=0. F
B
A
x
答案：(D)。
题 2.1(5)图
2.2 填空题 (1) 质量为 m 的小球，用轻绳 AB、BC 连接，如图所示，其中 AB 水平．剪断绳 AB 前后的瞬间，绳 BC 中的张力比 T : T′＝____________．
说
法
中
：
（）
(A)①、②是正确的。
(B)②、③是正确的。
(C)只有②是正确的。
(D)只有③是正确的。
答案：(C)。
(4) 一质量为 M 的斜面原来静止于水平光滑平面上，将一质量为 m 的木块轻
轻放于斜面上，如图．如果此后木块能静止于斜面上，则斜面将
（）
(A) 保持静止．
(B) 向右加速运动．
(C) 向右匀速运动． (D) 向左加速运动．
受的合力为 F =( a bt )N( a,b 为常数)，其中 t 以秒为单位：(1)假设子弹运行
到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的
冲量；(3)求子弹的质量．
解: (1)由题意，子弹到枪口时，有
F (a bt) 0 ,得 t a b
(2)子弹所受的冲量
，
物体与水平面间的摩擦系数为
。
答案： v2 ; 2s
v2 . 2gs
(5) 在光滑的水平面内有两个物体 A 和 B，已知 mA=2mB。（a）物体 A 以一定的动
能 Ek 与静止的物体 B 发生完全弹性碰撞，则碰撞后两物体的总动能

大学物理习题答案解答第二章牛顿运动定律

第二章牛顿运动定律一、填空题1、考察直线运动，设加速度为()a t ，初速度为00v =，则由dv a dv adt dt =⇒= 两边定积分，即 00v t v dv adt =⎰⎰ 得质点在任意时刻t 的速度为 110()()t v t a t dt =⎰ （2-1）再由ds v ds vdt dt =⇒= 两边定积分，即 00s t s ds vdt =⎰⎰ 得质点在任意时刻t 的路程为 0220()t s s s v t dt ∆=-=⎰ 把（2-1）式代入上式，得211200()tt s a t dt dt ∆=⎰⎰依题设可知两物体必做直线运动，设某时刻两物体间作用力为F ，则两物体的加速度分别为11F a m = 和 22F a m = 所以两物体在相同时间内发生的路程分别为：2221111121211200000011()1()()tt tt t t F t s a t dt dt dt dt F t dt dt m m ∆===⎰⎰⎰⎰⎰⎰ 2221221121211200000022()1()()t t t t t t F t s a t dt dt dt dt F t dt dt m m ∆===⎰⎰⎰⎰⎰⎰所以 11222111s m m s m m ∆==∆ 此即为所求。

2、箱子在最大静摩擦力的作用下，相对地面具有的最大加速度为2max 0max 00.49.8 3.92()F mg a g m s m mμμ-====⨯=⋅ （1）若设箱子相对卡车静止，即物体相对地面的加速度2max 2a m s a -=⋅<表明箱子与卡车底板间是静摩擦，摩擦力的大小为40280()F ma N ==⨯=（2）依然设箱子相对卡车静止，即物体相对地面的加速度2max 4.5a m s a -=⋅>表明箱子与卡车底板间是滑动摩擦，摩擦力的大小为0.25409.898()F mg N μ==⨯⨯=3、如图2-1(a)所示建立直角坐标系，再分析滑块的受力情况，如图2-1(b)所示，滑块受到三个力的作用，分别是地球施加的重力mg ，斜面对它的支持力1N 和滑动摩擦力1f ，并设其加速度为a 。

大学物理教程第2章习题答案

⼤学物理教程第2章习题答案思考题2.1 从运动学的⾓度看，什么是简谐振动？从动⼒学的⾓度看，什么是简谐振动？答：从运动学的⾓度看，弹簧振⼦相对平衡位置的位移随时间按余弦函数的规律变化，所作的运动就是简谐振动。

从动⼒学的⾓度看，如果物体受到的⼒的⼤⼩总是与物体对其平衡位置的位移成正⽐，⽽⽅向相反，那么该物体的运动就是简谐振动。

2.2 弹簧振⼦的振幅增⼤到2倍时，其振动周期、振动能量、最⼤速度和最⼤加速度等物理量将如何变化？答：弹簧振⼦的运动⽅程为0cos()x A t ω?=+，速度为0sin()v A t ωω?=-+，加速度的为)cos(02?ωω+-=t A a ，振动周期2T =221kA E =。

所以，弹簧振⼦的振幅A 增⼤到2倍时，其振动周期不变，振动能量为原来的4倍，最⼤速度为原来的2倍，最⼤加速度为原来的2倍。

2.3 下列运动是否为简谐振动？（1）⼩球在地⾯上作完全弹性的上下跳动；（2）⼩球在半径很⼤的光滑凹球⾯底部作⼩幅度的摆动；（3）曲柄连杆机构使活塞作往复运动；（4）⼩磁针在地磁的南北⽅向附近摆动。

答：（2）、（4）为简谐振动，（1）、（3）、不是简谐振动。

2.4 三只相同的弹簧（质量忽略不计）都⼀端固定，另⼀端连接质量为m 的物体，它们放置情况不同，其中⼀个平放，⼀个斜放，另⼀个竖直放。

如果它们振动起来，则三者是否均为简谐振动，它们振动的周期是否相同？答：三者均为简谐振动，它们振动的周期也相同。

2.5 当谐振⼦作简谐振动的振幅增⼤为原来的2倍时，谐振⼦的什么量也增⼤为原来的2倍？答：最⼤速度和最⼤加速度。

2.6 ⼀弹簧振⼦作简谐振动，其振动的总能量为E 1。

如果我们将弹簧振⼦的振动振幅增加为原来的2倍，⽽将重物的质量增加为原来的4倍，则新的振⼦系统的总能量是否发⽣变化？答：弹簧振⼦212E kA = ，所以新的振⼦系统的总能量增加为原来的4倍。

2.7 ⼀质点作简谐振动，振动频率为n，则该质点动能的变化频率是多少？答：该质点动能的变化频率是2n。

大学物理第二章习题及答案

第二章牛顿运动定律一、选择题1.下列说法中哪一个是正确的A 合力一定大于分力B 物体速率不变,所受合外力为零C 速率很大的物体,运动状态不易改变D 质量越大的物体,运动状态越不易改变2.用细绳系一小球,使之在竖直平面内作圆周运动,当小球运动到最高点时A 将受到重力,绳的拉力和向心力的作用B 将受到重力,绳的拉力和离心力的作用C 绳子的拉力可能为零D 小球可能处于受力平衡状态3.水平的公路转弯处的轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不致于发生侧向打滑,汽车在该处的行驶速率A 不得小于gRμ B 不得大于gRμ C 必须等于gRμ2 D 必须大于gRμ34.一个沿x 轴正方向运动的质点,速率为51s m -⋅,在0=x 到m 10=x 间受到一个如图所示的y 方向的力的作用,设物体的质量为1. 0kg,则它到达m 10=x 处的速率为A 551s m -⋅B 1751s m -⋅C 251s m -⋅D 751s m -⋅5.质量为m 的物体放在升降机底板上,物体与底板的摩擦因数为μ,当升降机以加速度a 上升时,欲拉动m 的水平力至少为多大A mgB mg μC )(a g m +μD )(a g m -μ6 物体质量为m ,水平面的滑动摩擦因数为μ,今在力F 作用下物体向右方运动,如下图所示,欲使物体具有最大的加速度值,则力F与水平方向的夹角θ应满足 A 1cos =θ B 1sin =θC μθ=tgD μθ=ctg 二、简答题1.什么是惯性系什么是非惯性系2.写出任一力学量Q 的量纲式,并分别表示出速度、加速度、力和动量的量纲式;三、计算题质量为10kg 的物体,放在水平桌面上,原为静止;先以力F 推该物体,该力的大小为20N,方向与水平成︒37角,如图所示,已知物体与桌面之前的滑动摩擦因数为,求物体的加速度;质量M=2kg 的物体,放在斜面上,斜面与物体之间的滑动摩擦因数2.0=μ,斜面仰角︒=30α,如图所示,今以大小为的水平力F 作用于m, 求物体的加速度;雨下降时,因受空气阻力,在落地前已是等速运动,速率为5m/s;假定空气阻力大小与雨滴速率的平方成正比,问雨滴速率为4m/s 时的加速度多大一装置,如图所示,求质量为1m 和2m 两个物体加速度的大小和绳子的张力,假设滑轮和绳的质量以及摩擦力可以忽略不计;题图桌面上叠放着两块木板,质量各为21,m m .如图所示, 2m 和桌面间的摩擦因数为2μ,1m 和2m 间静摩擦因数1μ,问沿水平方向用多大的力才能把下面的木块抽出来.如图所示,物体A,B 放在光滑的桌面上,已知B 物体的质量是A 物体质量的两倍,作用力1F 和2F 的四倍.求A,B 两物体之间的的相互作用力.北京设有供试验用高速列车环形铁路,回转半径9km,将要建设的京沪列车时速250km/h,若在环路上此项列车试验且铁轨不受侧压力,外轨应比内轨高多少设轨距为1.435m.在一只半径为R 的半球形碗内,有一个质量为m 的小钢球,当以角速度ω在水平面内沿碗内壁做匀速圆周运动时, 它距碗底又多高一质量为10kg 质点在力)(40120N t F +=作用下,沿x 轴作直线运动;在t=0时,质点位于05x m=处,其速度06/m sυ=;求质点在任意时刻的速度和位置;mg θFN fmgθFNfyx第二章牛顿运动定律答案一、选择题二、简答题1.什么是惯性系什么是非惯性系在这样的参照系中观察,一个不受力作用的物体将保持静止或匀速直线运动状态不变,这样的参照系称惯性系;简言之,牛顿第一定律能够成立的参照系是惯性系,反之,牛顿第一定律不成立的参照系是非惯性系;2.任一力学量Q 的量纲式：[]p q r Q L M T =;速度、加速度、力、动量的量纲式分别为：1221[],[],[],[]LT a LT F MLT P MLT υ----==== 三、计算题质量为10kg 的物体,放在水平桌面上,原为静止;先以力F 推该物体,该力的大小为20N,方向与水平成︒37角,如图所示,已知物体与桌面之前的滑动摩擦因数为,求物体的加速度; 解：研究对象是物体桌上面的运动情况：外力静止开始均速直线运动;隔离体讨论受力情况物体受右边所式的四种力的作用;它们是重力G ,弹力N,推力F,滑动摩擦力f 建立坐标系：左边图所示, 在x 轴上：)1(cos maf F =-θ轴上在y ：)2(0sin =--θF mg N滑动摩擦力为： )3(Nf μ=式 1,2,3结合求解a 可得：mg2υk f =a2/5.0)]6.02098(1.01.020[101)]37sin 208.910(1.037cos 20[101)]sin (cos [1)sin (cos s m F mg F m a maF mg F =⨯+-⨯=︒⨯+⨯-︒⨯=+-==+-θμθθμθ 答：该物体的加速度为 2/5.0s m质量M=2kg 的物体,放在斜面上,斜面与物体之间的滑动摩擦因数2.0=μ,斜面仰角︒=30α,如图所示,今以大小为的水平力F 作用于m, 求物体的加速度;解：以物体为研究对象;讨论物体的运动方向; 斜面向上的力：N F 38.930cos 6.19cos =︒⨯=α 斜面向下的力：N mg 8.930sin 8.92sin =︒⨯⨯=α ααsin cos mg F >∴ 物体沿斜面向上运动,对物体受力分析 )1(0sin cos =-+N F mg αα)3()2(cos sin N f maF f mg μαα==+--结合式 1,2,3可得：2/909.0)]sin cos (sin cos [1s m F mg mg F ma =+--=ααμαα 答：该物体加速度大小为2/909.0s m a =,方向沿斜面向上;雨下降时,因受空气阻力,在落地前已是等速运动,速率为5m/s;假定空气阻力大小与雨滴速率的平方成正比,问雨滴速率为4m/s 时的加速度多大解：根据牛顿第二定律雨滴等速运动时,加速度为零)1(021=-υk mgmg1FαF题图1ag m 11T2ag m 22T'1T '1T '2T 2a1 2 3222212221212221/53.38.9)541()1(s m g a mamgmg ma k mg mgk ≈⨯-=-==-=-=υυυυυυ一装置,如图所示,求质量为1m 和2m 两个物体加速度的大小和绳子的张力,假设滑轮和绳的质量以及摩擦力可以忽略不计; 解：假定1m 加速度竖直向上; 对1m 受力分析得)1(1111a m g m T =-对2m 受力分析得)2(2222a m T g m =-对动滑轮受力分析得 )0()3(02212===-m ma T T因为相同时间内1m 下落高度是2m 的2倍,所以)4(221a a =由1—4可得：21112244m m a g m m -=+ 2121224m m a g m m -=+ 1211234m m T g m m =+ 1221264m m T g m m =+桌面上叠放着两块木板,质量各为21,m m .如图所示, 2m 和桌面间的摩擦因数为2μ,1m 和2m 间静摩擦因数1μ,问沿水平方向用多大的力才能把下面的木块抽出来.解：隔离物体进行受力分析对图1：1111111a m g m N f ===μμ得 g a 11μ= 对图2：222222121212N f a m f f F g m g m g m N N μ==-'-+=+'=得])([12121122g m m g m F m a +--=μμ 将木块抽出的条件是 12a a > 得到g m m F ))((2121++>μμ如图所示,物体A,B 放在光滑的桌面上,已知B 物体的质量是A 物体质量的两倍,作用力1F 是2F 的四倍.求A,B 两物体之间的的相互作用力.解：条件是光滑的桌面,所以不考虑摩擦力再进行隔离体和受力分析：对物体A ：设其向右以加速度a 运动 )1(1a m F F A BA =-对图2：)3()2(2BAAB B AB F F a m F F ==-已知条件代入上面等式中可得：⎩⎨⎧=-=-)2(2)1(422am F F a m F F A AB A AB解此方程组： 23F F F BA AB ==∴北京设有供试验用高速列车环形铁路,回转半径9km,将要建设的京沪列车时速250km/h,若在环路上此项列车试验且铁轨不受侧压力,外轨应比内轨高多少设轨距为.解：根据列车受力的情况可得：根据牛顿第二定律BA F1N Ag m A1F12F2Ng m BAB F2Rm mg F mgF n n 2tan tan υθθ===解得2tan gRυθ=m gRl l l h 078.0tan sin 2==≈=υθθ 在一只半径为R 的半球形碗内,有一个质量为m 的小钢球,当以角速度ω在水平面内沿碗内壁做匀速圆周运动时, 它距碗底又多高解：取刚球为隔离体,其受力分析如图b)3()(cos )2(cos )1(sin sin 2Rh R mgF mR ma F n -====θθθωθ 由上述格式可解得刚球距碗底的高度为2ωgR h -=一质量为10kg 质点在力)(40120N t F +=作用下,沿x 轴作直线运动;在t=0时,质点位于05x m=处,其速度06/m s υ=;求质点在任意时刻的速度和位置;解：由牛顿第二定律F ma =,得124Fa t m ==+ 00002(124)646tt adtt dt t t υυυ=+=++=++⎰⎰0020032(646)2265ttx x dtx t t dtt t t υ=+=+++=+++⎰⎰mgmgxb。

大学物理学第二章课后答案

选择题(1) 一质点作匀速率圆周运动时，(A)它的动量不变，对圆心的角动量也不变。

(B)它的动量不变，对圆心的角动量不断改变。

(C)它的动量不断改变，对圆心的角动量不变。

(D)它的动量不断改变，对圆心的角动量也不断改变。

[答案：C](2) 质点系的内力可以改变(A)系统的总质量。

(B)系统的总动量。

(C)系统的总动能。

(D)系统的总角动量。

[答案：C](3) 对功的概念有以下几种说法：①保守力作正功时，系统内相应的势能增加。

②质点运动经一闭合路径，保守力对质点作的功为零。

③作用力与反作用力大小相等、方向相反，所以两者所作功的代数和必为零。

在上述说法中：(A)①、②是正确的。

(B)②、③是正确的。

(C)只有②是正确的。

(D)只有③是正确的。

[答案：C]填空题(1) 某质点在力i x F)54( （SI ）的作用下沿x 轴作直线运动。

在从x=0移动到x=10m的过程中，力F所做功为。

[答案：290J ](2) 质量为m 的物体在水平面上作直线运动，当速度为v 时仅在摩擦力作用下开始作匀减速运动，经过距离s 后速度减为零。

则物体加速度的大小为，物体与水平面间的摩擦系数为。

[答案：22;22v v s gs](3) 在光滑的水平面内有两个物体A 和B ，已知m A =2m B 。

（a ）物体A 以一定的动能E k 与静止的物体B 发生完全弹性碰撞，则碰撞后两物体的总动能为；（b ）物体A 以一定的动能E k 与静止的物体B 发生完全非弹性碰撞，则碰撞后两物体的总动能为。

[答案：2;3k k E E ]在下列情况下，说明质点所受合力的特点：（1）质点作匀速直线运动；（2）质点作匀减速直线运动；（3）质点作匀速圆周运动；（4）质点作匀加速圆周运动。

解：（1）所受合力为零；（2）所受合力为大小、方向均保持不变的力，其方向与运动方向相反；（3）所受合力为大小保持不变、方向不断改变总是指向圆心的力；（4）所受合力为大小和方向均不断变化的力，其切向力的方向与运动方向相同，大小恒定；法向力方向指向圆心。

大学物理(机械工业出版社)第二章课后答案

第二章质点动力学2－1一物体从一倾角为30︒的斜面底部以初速v 0=10m·s -1向斜面上方冲去，到最高点后又沿斜面滑下，当滑到底部时速率v =7m·s -1,求该物体与斜面间的摩擦系数。

解：物体与斜面间的摩擦力f ＝uN ＝umgcos30︒物体向斜面上方冲去又回到斜面底部的过程由动能定理得220112(1)22mv mv f s -=-⋅物体向斜面上方冲到最高点的过程由动能定理得2010sin 302mv f s mgh f s mgs -=-⋅-=-⋅-2(2)s ∴=把式（2）代入式（1）得，220.198u =2－2如本题图，一质量为m 的小球最初位于光滑圆形凹槽的A 点，然后沿圆弧ADCB 下滑，试求小球在C 点时的角速度和对圆弧表面的作用力，圆弧半径为r 。

解：小球在运动的过程中受到重力G 和轨道对它的支持力T.取如图所示的自然坐标系，由牛顿定律得22sin (1)cos (2)t n dv F mg mdtv F T mg m Rαα=-==-=由,,1ds rd rd v dt dt dt vαα===得代入式（）， A 并根据小球从点运动到点C 始末条件进行积分有，习题2－2图902n (sin )m cos 3cos '3cos ,e v vdv rg d v v rv mg mg rmg αααωααα=-===+==-=-⎰⎰得则小球在点C 的角速度为＝由式（2）得 T 由此可得小球对园轨道得作用力为T T 方向与反向2－3如本题图，一倾角为θ 的斜面置于光滑桌面上，斜面上放一质量为m 的木块，两者间摩擦系数为μ，为使木块相对斜面静止，求斜面的加速度a 应满足的条件。

解：如图所示()1212min max sin ,cos cos sin (1)sin cos 2(1)(2)(sin cos )(cos sin )(sin cos )()(cos sin )1(2)(1)(sin cos )(cos sin )(sin cos a a a a N mg ma ma mg uN m a ma u g u a u g u g tg u a u utg u g u a u g u a θθθθθθθθθθθθθθθθθθθθθ==∴-==±==⨯+-=+--∴==++-⨯+=-+∴=得，得，)()(cos sin )1()()11g tg u u utg g tg u g tg u a utg utg θθθθθθθθθ+=---+∴≤≤+- 2－4如本题图，A 、B 两物体质量均为m ，用质量不计的滑轮和细绳连接，并不计摩擦，则A 和B 的加速度大小各为多少。

大学物理课后习题答案第二章

大学物理教程课后习题答案第二章 2.1 两根轻弹簧与物体连接方式如题图 2.1，物体质量为m ，弹簧劲度系数为1k 和2k ，水平面光滑．证明系统可作简谐振动，并求振动的固有频率．题图2.1 解以物体m 的平衡位置为原点，建立坐标轴Ox 水平向右．设m 位于x 时，两弹簧分别伸长1x 和2x ，则12x x x =+．因两弹簧弹性力相等，所以物体m 所受合力1122F k x k x ==．设由两弹簧组合而成的“组合弹簧”的劲度系数为k ，于是12121212()()k k F F F kx k x x k kF k k k k +==+=+= 由此求得“组合弹簧”的劲度系数1212k k k k k =+为常量，可见物体m 所受合力为线性回复力，所以系统作简谐振动，振动的固有频率12121122()k k k m m k k νππ==+ 2.2 两根轻弹簧与物体连接方式如题图2.2，物体质量为m ，弹簧劲度系数为1k 和2k ，水平面光滑，物体静止时两弹簧均处于自由伸张状态．证明系统可作简谐振动，并求振动的圆频率和周期．题图2.2 解以物体m 的平衡位置为原点，建立坐标轴Ox 水平向右．m 位于x 时，弹簧1被拉长，弹簧2被压缩，m 所受合力1212()F kx k x k x k k x ==+=+由此求得“组合弹簧”的劲度系数12k k k =+为常量，可见物体m 所受合力为线性回复力，所以系统作简谐振动，振动的圆频率和周期分别为120k k m ω+= ， 122m T k k π=+ 2.3 弹簧振子的质点质量为42.510kg -⨯，运动学方程为0.06cos(5)(m)x t π=+．求：（1）振幅和周期；（2）质点的初始位置；（3）质点位于初始位置时所受合力；（4）质点在s t π=时的位置、速度和加速度．解（1）由运动学方程可见，振幅006m A .=，05ω=，周期0204(s)126(s)T ..ππω===（2）由运动学方程可见，0t =时，质点的初始位置0006cos 006(m)x ..π==-．（3）对运动学方程求时间导数可得d 0.3sin(5)d x x v t tπ==-+ d 1.5cos(5)d x x v a t t π==-+ 0t =时0 1.5cos 1.5x a π=-=，根据牛顿第二定律可知质点位于初始位置时所受合力440025101537510(N)x F ma ...--==⨯⨯=⨯（4）把t π=代入运动学方程和（3）中求得的x v 、x a 表达式，即可求得质点在t π=时的位置、速度和加速度分别为006cos(5+)006(m)x ..ππ==03sin(5)0(m )x v .ππ=-+=215cos(5) 1.5(m )x a .ππ=-+=-2.4 一质点作简谐振动，振幅为0.02m ，速度幅为0.03m s ，取速度为最大值时为0t =．求：（1）周期；（2）加速度幅；（3）运动学方程．解设运动学方程为00cos()002cos()x A t .t ωϕωϕ=+=+，则00002sin()x v .t ωωϕ=-+200002cos()x a .t ωωϕ=-+（1）由m 0002003v ..ω==，可知000315002...ω==，所以周期为 022419(s)15T ..ππω=== （2） 222m 0002002150045(m s )a ....ω==⨯=（3）由已知条件0t =时00x =、0m x v v =，可知0002cos .ϕ=、m m sin v v ϕ=-，即cos =0ϕ ，sin =1ϕ- 由以上二式求出2πϕ=-，所以运动学方程为002cos(15)2x ..t π=-2.5 一水平放置的弹簧振子，质点质量为0.1kg ，振幅为0.01m ，质点运动的最大加速度为20.04m s ．求：（1）系统的机械能；（2）质点通过平衡位置时的动能；（3）以0.01m x =时为0t =，动能与势能相等的时刻．解根据001m A .=和22m 0004m s a A .ω==，可以求出00040012..ω==．由0k m ω=，可知2001404k m ..ω==⨯=．（1）系统的机械能2251104001210(J)22E kA ..-==⨯⨯=⨯ （2）通过平衡位置时0x =，势能p 0E =，所以动能5k 210(J)E E -==⨯．（3）由已知条件0t =时0001m x .=、00x v =，可知cos 1ϕ= ， sin 0ϕ=由以上二式求出0ϕ=．于是2252k 01sin ()210sin 22E kA t t ωϕ-=+=⨯ 2252p 01cos ()210cos 22E kA t t ωϕ-=+=⨯ 动能与势能相等的时刻，k p E E =，即22sin 2cos 2t t =可求出2(21)244t kk πππ=+=+ ， 0123k ,,,...= 所以(21)8t k π=+，0123k ,,,...=2.6 题图2.6所示为振幅与频率相同的两个简谐振动的x t -图．求：（1）两个简谐振动的运动学方程；（2）哪个简谐振动的相位超前？超前多少？题图2.6解由x t -图可见01m A .=、4s T =，可知0205.Tπωπ==．对振动(1)，1101cos (05)x ..t πϕ=+，当0t =时101005201cos x ..ϕ== ， 101005sin 0x v .πϕ=-<可知14πϕ=．运动学方程为 101cos(05)4x ..t ππ=+ 振动(2)，2201cos (05)x ..t πϕ=+，当0t =时 202005201cos x ..ϕ== ， 202005sin 0x v .πϕ=->可知24πϕ=-．运动学方程为101cos(05)4x ..t ππ=- 两个简谐振动的的相位差 122πϕϕϕ∆=-=说明振动(1)比振动(2)超前2π． 2.7 有两个同方向同频率的简谐振动，它们的运动学方程分别为130.05cos(10)4x t π=+和210.05cos(10)4x t π=+（国际制单位）．求：（1）合振动的振幅和初相位；（2）若另有一振动30.08cos(10)x t ϕ=+，ϕ为何值13x x +的振幅最大？ϕ为何值13x x +的振幅最小？（利用旋转矢量图解题）解（1）分别作与0t =时刻的1x 和2x 对应的旋转矢量1A 和2A ，如题解图2.7．由旋转矢量图可见合矢量12A A +的长度为0.052，与Ox 轴夹角为90ο．于是可知合振动的振幅0.052m A =，初相位12ϕπ=合．题解图2.7（2）1x 和3x 同相，即34ϕπ=时，13x x +的振幅最大；1x 和3x 反相，即14ϕπ=-时，13x x +的振幅最小．2.8 有两个同方向同频率的简谐振动，其合振动的振幅为0.02m ，合振动与第一个分振动的相位差为30ο，第一个分振动的振幅为0.013m ．求：（1）第二个分振动的振幅；（2）两个分振动的相位差．（利用旋转矢量图解题）解根据已知条件作旋转矢量图，如题解图2.8．（1）由图可见，第二个分振动的振幅20.01m A =．（2）由图可见，两个分振动的相位差2190ϕϕο-=．题解图2.82.9 现在力学的学习暂时告一段落，请读者总结一下有何收获和体会？（牛顿质点力学的理论结构、数学和物理的关系、学习了哪些方法……）*2.10 某阻尼振动（弱阻尼状态）的振幅经一“周期”后变为原来的13，求振动的“周期”为振动系统固有周期的几倍．解弱阻尼振动()e cos t x A 't βωϕ-=+，由题意()e 1e 3e et T 't T'T'A A ββββ--+-=== lne ln3T'T 'ββ==所以22ln 3'T 'ππβω==根据'ω=0ω== 于是0022T ''T 'ωπωπωω===1015.= *2.11 质量为3310kg m -=⨯的质点，挂在劲度系数21.210N m k -=⨯的弹簧下端，沿Ox 轴运动．质点除线性回复力外，还受策动力0cos 2t(N)x F F =和阻力rx x F v γ=-作用．求当阻力系数γ增为原来的3倍时，质点稳态振幅减为原来的几分之几？解根据已知条件，22312104310k .m ω--⨯===⨯，2ω=．故弱阻尼受迫振动的稳态振幅004f A β== 由于00F f m =和2mγβ=，所以 002F A γ=当3'γγ=，00001263F F A A γγ'==='，因此当阻力系数γ增为原来的3倍时，质点稳态振幅减为原来的三分之一．*2.12 为什么说牛顿力学是“确定性”的？混沌的基本特征是什么？。

大学物理第二章质点动力学课后答案

势能零点在 z = 0处。
1 2 弹性势能：E p kx 势能零点在弹簧原长处。 2 Mm 引力势能：E p G0 势能零点在 r 处。 r
五、功能原理与机械能守恒定律
W W E2 E1 功能原理
ex in 非
Ek 2 Ep 2 Ek1 Ep1 机械能守恒定律
4 105 t 0.003s F 400 t0 3 t t 4 105 I Fdt [400 t ]dt 0.6 N s 0 0 3 I 0.6 0.002kg m I mv 0 v 300
2-7 两块并排的木块A和B，质量分别为m1和m2，静止地放置在光滑的水平面上。一子弹水平地穿过两木块，设子弹穿过两木块所用的时间分别为t1和t2，木块对子的阻力为恒力F，则子弹穿出后，木块A的速度大小为，木块B的速度大小为。
1 1 2 W mv2 mv12 2 2
质点的动能定理：在一个过程中，作用在质点上合外力的功，等于质点动能的增量。
四、保守力的功 F保 dr 0
l
势能
E p F保 dr (b为势能零点) a
b
W保 ( Epb Epa ) Ep
重力势能：Ep mgz
l
dx v 2ct dt
l
W 0 fdx 0 4kcxdx 2kcl 2
2-28 水平方向动量守恒
( P Q)v0 cos Pv Q(v u)
Qu ( P Q) v0 cos Qu v0 cos v PQ PQ
Δx vt v0 cos t
总
结
一、动量定理和动量守恒定律 t2 Fdt mv2 mv1

大学物理学(课后答案解析)第2章

第2章牛顿运动定律习题一选择题2-1 关于惯性有下面四种表述，正确的为[ ]（A）物体静止或作匀速运动时才具有惯性（B）物体受力作变速运动才具有惯性（C）物体受力作变速运动时才没有惯性（D）物体在任何情况下均有惯性解析：惯性是物体具有的固有特性，因此物体在任何情况下均有惯性，答案选D。

2-2 下列表述中正确的是[ ]（A）质点运动的方向和它所受的合外力方向相同（B）质点的速度为零，它所受的合外力一定为零（C）质点作匀速率圆周运动，它所受的合外力必定与运动方向垂直（D）摩擦力总是阻碍物体间的相对运动，它的方向总是与物体的运动方向相向解析：根据牛顿第二定律，质点所受的合外力等于动量随时间的变化率，因此A、B错误。

质点作匀速率圆周运动，合外力指向圆心，运动方向沿切线方向，二者垂直，因此选项C正确。

摩擦力总是阻碍物体间的相对运动或相对运动趋势，它的方向沿着物体运动或运动趋势的切线方向，但并不是总与物体的运动方向相向，因此选项D错误。

2-3 一质点在力5(52)()F m t SI =-的作用下，0t =时从静止开始作直线运动，式中，m 为质点质量，t 为时间。

则当5t s =，质点的速率为[ ]（A ）25m s （B ）50m s - （C ）0 （D ）50m s 解析：根据牛顿第二定律dv F ma mdt ==可得，5(52)dv Ft dt m==-，所以5(52)dv t dt =-，两边积分可得2255v t t =-，即得50v =。

答案选C 。

2-4 如图2-4（A ）所示，A B m m μ>时,算出B m 向右的加速度为a ，今去掉Am 而代之以拉力A T m g =，如图2-4(B)所示，算出B m 的加速度a '，则[ ]（A ）a a '> （B ）a a '< （C ）a a '= （D ）无法判断解析：去掉A m 前，{A A B Bm g T m a T m g m a μ-=-=，联立求得ABA B m m a g m m μ-=+；去掉A m 后，B A B B T m g m g m g m a μμ'-=-=，求得A BBm m a g a m μ-'=>。

大物上海交大课后答案第二章

⼤物上海交⼤课后答案第⼆章习题22-1质量为16kg 的质点在xOy 平⾯内运动，受⼀恒⼒作⽤，⼒的分量为6N x f =，7N y f =，当0t =时，0x y ==，2m /s x v =-，0y v =。

当2s t =时，求： (1) 质点的位⽮； (2) 质点的速度。

解：由x x f a m =，有：x a 263m /168s ==，27m /16y y f a s m -== （1）2003522m /84x x xv v a dt s =+=-+?=-?， 200772m /168y y y v v a dt s -=+=?=-?。

于是质点在2s 时的速度：57m /s 48v i j =--（2）22011()22x y r v t a t i a t j =++1317(224)()428216i j -=-?+??+?137m 48i j =--2-2 质量为2kg 的质点在xy 平⾯上运动，受到外⼒2424=- F i t j 的作⽤，t =0时，它的初速度为034=+v i j ，求t =1s 时质点的速度及受到的法向⼒n F 。

解：解：由于是在平⾯运动，所以考虑⽮量。

由：d v F m d t= ，有：24242d v i t j dt -=? ，两边积分有：0201(424)2v t v d v i t j dt =-?? ，∴3024v v t i t j =+- ，考虑到034v i j =+ ，s t 1=，有15v i =由于在⾃然坐标系中，t v ve = ，⽽15v i =（s t 1=时），表明在s t 1=时，切向速度⽅向就是i ⽅向，所以，此时法向的⼒是j ⽅向的，则利⽤2424F i t j =- ，将s t 1=代⼊有424424t n F i j e e =-=-，∴24n F N =-。

2-3．如图，物体A 、B 质量相同，B 在光滑⽔平桌⾯上．滑轮与绳的质量以及空⽓阻⼒均不计，滑轮与其轴之间的摩擦也不计．系统⽆初速地释放，则物体A 下落的加速度是多少？解：分别对A ，B 进⾏受⼒分析，可知：A A A m g T m a -=2B B T m a =12B A a a =则可计算得到：45A a g =。

大物第二章课后习题答案

简答题2.1 什么是伽利略相对性原理？什么是狭义相对性原理？答：伽利略相对性原理又称力学相对性原理，是指一切彼此作匀速直线运动的惯性系，对于描述机械运动的力学规律来说完全等价。

狭义相对性原理包括狭义相对性原理和光速不变原理。

狭义相对性原理是指物理学定律在所有的惯性系中都具有相同的数学表达形式。

光速不变原理是指在所有惯性系中，真空中光沿各方向的传播速率都等于同一个恒量。

2.2同时的相对性是什么意思？如果光速是无限大，是否还会有同时的相对性？答：同时的相对性是：在某一惯性系中同时发生的两个事件，在相对于此惯性系运动的另一个惯性系中观察，并不一定同时。

如果光速是无限的，破坏了狭义相对论的基础，就不会再涉及同时的相对性。

2.3什么是钟慢效应? 什么是尺缩效应?答：在某一参考系中同一地点先后发生的两个事件之间的时间间隔叫固有时。

固有时最短。

固有时和在其它参考系中测得的时间的关系，如果用钟走的快慢来说明，就是运动的钟的一秒对应于这静止的同步的钟的好几秒。

这个效应叫运动的钟时间延缓。

尺子静止时测得的长度叫它的固有长度，固有长度是最长的。

在相对于其运动的参考系中测量其长度要收缩。

这个效应叫尺缩效应。

2.4 狭义相对论的时间和空间概念与牛顿力学的有何不同? 有何联系?答：牛顿力学的时间和空间概念即绝对时空观的基本出发点是：任何过程所经历的时间不因参考系而差异；任何物体的长度测量不因参考系而不同。

狭义相对论认为时间测量和空间测量都是相对的，并且二者的测量互相不能分离而成为一个整体。

牛顿力学的绝对时空观是相对论时间和空间概念在低速世界的特例，是狭义相对论在低速情况下忽略相对论效应的很好近似。

2.5 能把一个粒子加速到光速c吗？为什么?答：真空中光速C是一切物体运动的极限速度，不可能把一个粒子加速到光速C。

从质速关系可看到，当速度趋近光速C 时，质量趋近于无穷。

粒子的能量为2mc ，在实验室中不存在这无穷大的能量。

2.6 什么叫质量亏损? 它和原子能的释放有何关系?答：粒子反应中，反应前后如存在粒子总的静质量的减少0m ∆，则0m ∆叫质量亏损。

大物第二章课后习题答案

大学物理习题答案解析第二章

《大学物理》课后解答题 第二章牛顿运动定律与守恒

大物习题答案第2章动量守恒定律与能量守恒定律

大学物理课后习题答案第02章

大学物理第二章习题答案

大学物理答案第二章牛顿定律-习题解答

大学物理第2章课后答案

大学物理课后习题2第二章答案

大学物理习题答案解答第二章牛顿运动定律

大学物理教程第2章习题答案

大学物理第二章习题及答案

大学物理学第二章课后答案

大学物理(机械工业出版社)第二章课后答案

大学物理课后习题答案 第二章

大学物理第二章质点动力学课后答案

大学物理学(课后答案解析)第2章

大物上海交大课后答案第二章

大物第二章课后习题答案

《大学物理》课后解答题第二章牛顿运动定律与守恒

大学物理课后习题答案第二章