量子遗传算法

合集下载

【国家自然科学基金】_遗传量子算法_基金支持热词逐年推荐_【万方软件创新助手】_20140802

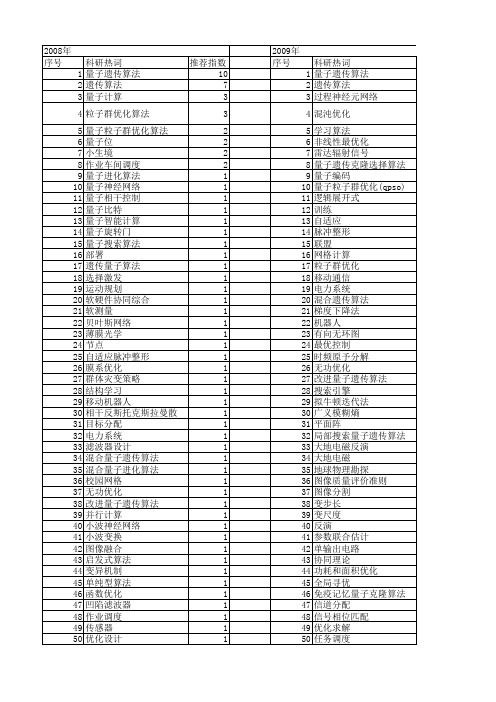
推荐指数 14 5 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57
人工势场中性分束镜三基因链编码 fir数字滤波器 bloch球面坐标
1 1 1 1 1
53 54 55 56
web搜索 sat问题 chirp1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

一种改进变尺度混沌优化的模糊量子遗传算法

中围分类号：Ｐ８ＴＩ
种改进变尺度混沌优化的模糊量子遗传算法
膝皓，曹爱增，杨炳儡
（．济南大学信息科学与工程学院，济南２０２；２１５０２．北京科技大学信息工程学院，北京１０８）００３
摘
要：针对量子遗传算法存在的易陷入局部极小等问题，提出一种模糊量子遗传算法。该算法采用一种变尺度混沌优化方法，只需设
第３卷第１期６３
ＶＬ３ｏ６
・
计
算
机
工
程
２１００年７月
Ｊｕｙ０１ｌ２０
Ｎｏ１．３
ＣｏｐｕｔｒＥｎｇｉｅｉｇｍｅｎｅｒｎ
人工智能及识别技术・
一
文章编号：１．４８ｏ０３＿７＿文献标识０－３２（ｌ１０５００２）— １ — ３码：Ａ
２ＳｈｏｆｎｒｔｎＥｇｎｅｉｇＵｎｖｒｉｔｃｅｃｎｅｈｏｏｙＢｉｎ，ｅｉｇｌ０８）．ｃｏｌｉｆｍａｉｎｉｅｒ，ｉｅｓｔｏ、ｉｎｅａｄＴｃｎｌｇｅｉｇＢｉｎ００３ｏｏｏｎｙＳｊｊ［ｓｒｃ］ＡｉｎｔｈｒｂｅｆａｔｍｎｔｇｒｈＱＧＡ）ｘｓａｉｅｔｇｉｔｏａｍｉｉｍ．ｈｓｐｐｒｒｓｎｓａｆｚｙＡｂｔａｔｍｉｇａｅｐｏｌｍｏｎｕＧｅｅｉＡｌｏｉｍ（ｔＱｕｃｔｅｉｓｅｓｌｇｔｎｏｌｃｌｎｍｕｔｉａｅｅｅｔｕｚｔｙｉｎｐ
关健词：量子遗传算法；混沌优化；收敛策略；变尺度；模糊控制

基于量子遗传算法的CDMA多用户检测技术

ａｖｎａｅｆｔｒｐｒｉｓｏｕｎｕｍｅｈｎｉｓｓｃｓｑａｔｍａａｌｌｓａｄｅｔｎｌｍｅｔｃｎｓｌｅｄａｔｇｓｏｈｅｐｏｅｔｆｑａｔｍｃａｃｕｈａｕｕｐｒｌｅｉｍｅｎｎｎａｇｅｎａｖｏｔｉｒｂｅｈｓｐｏｌｍｅｉｉｎｙ．ＡｍｕｔｕｅｄｔｃｉｎａｅＯｌｕａｔｍｇｎｔａｇｒｔｍｉｐｐｓｄ，ｗｈｃｆｃｅｔｌｌｉｓｒｅｅｔｂｄｉ — ｏｓｑｎｕｅｅｉｌｏｉｈｃｓｒｏｅｏｉｈｉｔｇａｅｅｅｃｌｇｒｔｍｔａｔｍｏｕｉｇｔｅｒＴｈｏｕｅｓｍｕａｉｎｒｓｌｓｓｏｔａｅｎｅｒｔｓｇｎｔａｏｈｗｉｑｎｕｃｍｐｔｎｏｙ．ｅｃｍｐｔｒｉｌｔｅｕｔｈｗｔｔｉｉｈｕｈｏｈｈｍｅｏａｒｏｒｒｐｒｉｓｔａｅｄｔｃｏａｅｎｃａｓｃｅｅｉｌｏｔｍｓａｄｈｗｅｆｌｈｔｄｈｍｏｅｐｗｅｆｐｏｅｔｅｎｔｅｅｔｒｂｓｄｏｌｉａｇｎｔｃａｇｒｈａｐｓｕｌｈｈｓｌｉｎｓｏｒｕｐｏｅｔｓｉｉｅＴｒｒｔｒｐｒｉｎｂｔＩｏａｅ．ｅＫｅｒｓ：ｇｎｔｌｏｉｍ；ｑａｔｅｅｃａｇｒｔｍ；ｍｕｔ— ｓｒｄｔｔｎｙｗｏｄｅｅｉａｇｒｔｃｈｕｎｕｇｎｔｌｏｉｍｉｈｌｉｕｅｅｅｉｃｏ

基于混沌优化的量子遗传算法

维普资讯
第２９卷第２期
２０
ＥＬＥＣＴＲ０ＮＩＭＥＡＳＣＵＲＥＥＮＴＴＥＣＨＮ０ＬＯＧＹＭ
基于混沌优化的量子遗传算法
郭海燕
（南科技大学绵阳６０２）西１０１
在式
Ｕ一
一
ｃｏｓＯ
．
－
ｓｎｉ０
—
－］
ｌＪ
（（）１
ｓ —ｌ（ｃｌＬｍＯｌｏｓ］
（）中０为旋转角。１
的一种算法。它是一种十分高效的优化方法，但它
有时也会陷入局部极值口。］
混沌能不重复地历经一定范围内的所有状态，具有遍历性，同时它的随机性和规律性，使它具有
ｅｇｄｃｔｆｃａｔｐｉｚｔｎｃｎａｏｄｉｆｏｄｏｐｎｔｃｌｐｉｍｓｌｒｏｉｉｏｈｏｉｏｔｍｉａｉａｖｉｔｒｍｒｐｉｇｉｏｌａｔｙｃｏｎｏｏｍｕｅｉａｙ；ｔｅｒｎｏｃｔｎｈｒｅｈａｄｍｉｉａｄｔｅｏｄｒｙ
２混沌优化方法简介
混沌运动具有遍历性、随机性、规律性等特
点，这使它能不重复地经历一定范围的所有状态，
所以，利用混沌变量进行优化搜索无疑比随机搜索更好。混沌搜索过程可分为两个阶段：首先用类似载波的方法将混沌状态引入到优化

改进的量子遗传算法及其在测试数据生成中的应用

ｐｏａｉｔａｐｉｄｆｕｎｕｉ．ＩＧａｐｌｄｉｏｔｔａｅｅｔｎｈｘｅｉｅｔｏｒｅｂｓｒｒｍｒｂｂｌｙｍｌｕｅｏｑａｔｍｂｓＱＡｗｓａｐｉｔｅｔｇｎｒｉ．Ｔｅｅｐｒｎｓｎｔｅａｉｐｏａｓｉｔｔｅｎｓｄａａｏｍｈｃｇ
ｅｏｕｉｎｓｃｎ，ｔｅｉａｉｄｖｄａｓｖｌｔ；ｅｏｄｏｈｂｎｒｎｉｉｕｌｙｗｅｅｒｍｕａｅａｔｒｔｔｄｆｅｍｅｓｒｍｅｔｉｓｅｄｆｔｅｔａｉｏａｘｈｎｅｆｔｅａｕｅｎ，ｎｔａｏｈｒｄｔｎｌｃａｇｏｈｉｅ
ＺＵＱＩＮｈ－ａ，ＺＯＸｅｆｎＨＯｉ，ＪＧＳｕｊｎＨＡｕ－ｇＡｕｅ
（ｃｏｌｆＣｍｕｅＳｉｃｎｅｈｏｏｙｈｎｎｖｒｔｎｎｎｅｈｏｇＸｚｏＳｈｏｏｏｐｔｃｎｅａｄＴｃｎｌ，ＣｉａＵｉｓｙｏＭｉｉｇａｄＴｃｎｌｙｕｈｕｒｅｇｅｉｆｏＭ２１，Ｃｉ）２１１６ｈｎａ
的方向进化，同时有效地避免了早熟现象，能以更快的速度搜索到目标解。
关键词：量子遗传算法；测试数据生成；取反指导更新；二进制变异；快速收敛
中图分类号：Ｔ３１５Ｐ１．２文献标志码：Ａ
Ｉｐｏｅｕａｔｍｅｅｃａｇｒｔｍｎｔｐｉａｏｎｔｓｔｅｒｔｏｍｒｖｄｑｎｕｇｎｔｌｏｉｈａｄｉｓａｐｌｃｔｎｉｅｔｄａａｇｎｅａｎｉｉｉ

量子遗传算法在多目标分配中的应用探讨

量子遗传算法在多目标分配中的应用探讨作者：叶茂章洁来源：《消费电子》2012年第12期摘要:多目标分配目前是最优化领域中的一个重要研究方向。

遗传算法是一种借鉴生物界自然选择和遗传机制的高度并行、随机、自适应的全局优化搜索算法,近年来,基于遗传算法的多目标分配应用研究在过程工程领域越来越受重视。

本论文提出了用量子遗传算法处理和解决多目标分配问题,有一定的工程价值。

关键词:量子遗传算法;多目标分配;最优化中图分类号:TP18 文献标识码:A 文章编号:1674-7712 (2012) 12-0176-01一、引言遗传算法不同于传统寻优算法的特点在于:遗传算法在寻优过程中,仅需要得到适应度函数的值作为寻优的依据;同时使用概率性的变换规则,而不是确定性的变换规则;遗传算法适应度函数的计算相对于寻优过程是独立的;算法面对的是参数的编码集合,而并非参数集合本身,通用性强。

它尤其适用于处理传统优化算法难于解决的复杂和非线性问题。

[1]目前,GA已经在很多领域得到成功应用,但随着问题规模的不断扩大和搜索空间的更加复杂,GA在求解很多具体问题时往往并不能表现出其优越性。

于是,近年来便出现了遗传算法与其它理论相结合的实践,其中遗传算法与量子理论的结合是一个崭新的、极富前景和创意的尝试。

量子遗传算法QGA是量子计算特性与遗传算法相结合的产物。

基于量子比特的叠加性和相干性,在遗传算法中借鉴量子比特的概念,引入了量子比特染色体。

由于量子比特染色体能够表征叠加态,比传统GA具有更好的种群多样性,同时QGA也会具有更好的收敛性,因此在求解优化问题时,QGA在收敛速度、寻优能力方面比GA都将有较大的提高。

QGA的出现结合了量子计算和遗传算法各自的优势,具有很高的理论价值和发展潜力。

本论文提出用量子遗传算法处理和解决多目标分配问题,为多目标问题的解决提供一种新的思路。

二、量子遗传算法在传统计算机中,信息存储是以二进制来表示,不是“0”就是“1”态,但是在量子计算机中,充当信息存储单元的物质是一个双态量子系统,称为量子比特(qubit),量子比特与比特不同之就在于它可以同时处在两个量子态的叠加态,量子进化算法建立在量子的态矢量表述基础上,将量子比几率幅表示应用于染色体的编码,使得一条染色体可以表示个态的叠加,并利用量子旋转门更新染色体,从而使个体进达到优化目标的目的。

一种新的量子遗传算法变异机制

３．ＪｉａｎｇｘｉＶｏｃａｔｉｏｎｌａＣｏｌｌｅｇｅｏｆＭｅｃｈａｎｉｃｌ＆ＥａｌｅｃｔｉｒｃｌａＴｅｃｈｎｏｌｏｇｙ，ＮａｎｃｈａｎｇＪｉａｎｇｘｉ３３００１３，Ｃｈｉｎａ）ＡＢＳＴＲＡＣＴ：Ｓｔｎｄａａｒｄｑｕｎｔａｕｍｇｅｎｅｔｉｃｌｇａｏｒｉｔｈｍ（ＱＧＡ）ａｐｐｌｉｅｄｔｏｎｕｍｅｉｒｃａｌｏｐｔｉｍｉｚａｉｔｏｎｉｓｅａｓｙｔｏｃｏｎｖｅｒｇｅｔｏ
ｂｅｄｄｅｄｉｎｔｈｅｑｕａｎｔｕｍｏｔｒａｔｉｏｎｐｏｌｉｃｙｔｂｌａｅｉｓｓｉｍｐｌｅｔｏｉｍｐｌｅｍｅｎｔａｎｄｉｔｉｓｈｉｇｈｌｙｅｉｃｆｉｅｎｔ．Ｔｙｐｉｃｌａｃｏｍｐｌｅｘｆｕｎｃｔｉｏｎ
２．华南农业大学信息学院，广东广州５１０６４２；
３．江西机电职业技术学院，江西南昌３３００１３）
摘要：针对标准的量子遗传算法（ＱＧＡ）应用于数值优化时容易早熟收敛而陷入局部最优的问题，引入ｋ位变异子空间概念
对Ｑ— ｂｉｔ变异概率分布进行了分析，传统随机变异机制和ＱＧＡ自蕴变异机制存在冲突。为此提出一种用观测状态的阶段
ｓｃｌａｅＶａｉｒａｔｉｏｎＭｅｃｈｎｉａｓｍＢａｓｅｄｏｎＯｂｓｅｒｖａｔｉｏｎ（ＳＬＶＭＢ００）ｗａｓｐｒｏｐｏｓｅｄ．ＭｕｔａｔｉｏｎｏｐｅｒａｔｏｒｏｆＳＬＶＭＢ００ｅｍ —

一种基于克隆选择的量子遗传函数优化算法

．
Ａｓａｔｎｏｄｒｔｏｅｃｍｅｓｏｃｍｎｆｈｕｎｕｅｅｃａｏｔｍ（Ｇ，ｈｃｈｅｕｔｂｔｃ：ＩｒｅｖｒｏｅｔｈａｏｉｇｏｔｅｑａｔｍｇｎｔｌｒｈＱＡ）ｉｗｉｈｔｅｒｌｒｏｈｉｇｉｎｓ
算法。
关键词：量子遗传算法；克隆选择；函数优化
中图分类号：Ｐ０．；Ｐ８Ｔ３１６Ｔ１文献标识码：Ａ
ＡＱｕｎｕＧｅｅｉＦｎｔｎＯｐｉｚｔｎＡｇｒｔｍａｔｍｎｔｕｃｉｔａｉｌｏｉｃｏｍｉｏｈ
ｍａｏｖｒｅｔｅｌｃｌｐｉｌａｕ，ｅｓｄｉｈｐｉｚｔｎｏｏｔｕｕｎｔｎｉｎｘｙｃｎｅｇｏｔｏａｔｈｏｍａｖｅｗｈｎｉｉｕｅｔｅｏｔａｉｆｎｉｏｓｆｃｉｓｗｔｍａｖｅ — ｌｔｓｎｍｉｏｃｎｕｏｈｔｍｅＶｕｓｔｅｃｎｅｔａｄｐｎｉｌｆｌｎｌｅｅｔｎｉｍｍｕｏｏｙｉｉｔｄｃｄＡｏｅｖｌｔｏａｙａ一ｒａｅ，ｈｏｃｐｎｒｃｐｅｏｏａｌｃｉｉｅｌｉｃｓｏｎｎｌｇｓｎｒｕｅｏｎｖｌｅｏｕｉｎｒ１
ｔｎａｄｔｅｑａｔｍｏａｅｇｔｔｅａｇｒｈｃｎｓａｃｈｅｓｂｅｓｌｔｎＴｅｐｒｏｍａｃｆｔｅｇｏａｉｎｈｕｎｕｒｔｔａｅ，ｏｔｍａｅｒｈｔｅｆａｉｌｏｕｉｏｈｌｉｏｈｅｆｒｎｅｏｈｌｂＩ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（2）在量子遗传算法中，用量子比特（由｜0〉和｜1〉两个量子态描述）来表示个体基因，即｜ψ 〉=α ｜0〉
+β｜1〉，式中α 和β的平方和为1，因此基因链比原始算法多一倍。根据叠加原理，该基因可以为“0”态或 “1”态，或他们的任意叠加状态。因此基因不在表达一确定信息，而是包含所有可能的信息。
2
量子遗传算法
2 3
4
缺点
1
设置不当，会造成迭代次数多，收敛速度慢，全局搜索能力不强,很容易陷入局部最优解。
量子遗传算法
2
量子遗传算法
基本概念
（1）量子遗传算法是量子计算与遗传算法相结合的智能优化算法，其将量子态、量子门、量子状态特性、概率幅等量子概念引入到遗传算法当中。量子遗传算法也是一种概率搜素算法，它采用量子位来表示基因。遗传算法的基因所表达的是某一确定的信息，而量子遗传算法中，由于量子信息的叠加性使量子位所表达的基因包含所有可能的信息。
索算法。它模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止。
1
遗传算法
基本过程
确定表示问题的编码
初始化染色体种群
计算每个个体适应度
是否满足终止条件否
根据适应度进行交叉运算
是
输出最优解变异
1
遗传算法
主要特点
优点 1
群体搜索，易于并行化处理；
不是盲目穷举，而是启发式搜索；适应度函数不受连续、可微等条件的约束，适用范围很广。容易实现。一旦有了一个遗传算法的程序，只需要改变一下适应度函数就可以应用于其他问题。
基本步骤
step1：初始化父代染色体
step2：对每个染色体基因位即量子位进行测量，得到一个状态，即二进制编码。对每个状态计算适应度，记录最佳个体及适应度。
step3：遗传进化设定的代数，其中采用量子旋转门对每一代染色体进行遗传变异。 step4：达到终止条件，输出最佳个体及适应度。
程序实现
3
遗传算法
量子遗传算法
程序实现
遗传算法
1
遗传算法
达尔文进化论：物竞天择，适者生存
达尔文认为，生物之间存在着生存争斗，适应者生存下来，不适者则被淘汰，这就是自然的选择。生物正是通过遗传、变异和自然选择，从低级到高级，从简单到复杂，种类由少到多地进化着、发展着。
遗传算法(Genetic Algorithms, GA)是一类借鉴生物界自然选择和自然遗传机制的随机化搜
QuantumMain函数：主函数，根据量子遗传算法的基本步骤，求解优化问题。
Байду номын сангаас
3
程序实现
执行结果分析
1、由于Collapse函数中存在随机数，故每次运行的过程都会有所不同。
2、本程序使用的时固定的旋转角，可调整为可变旋转角，可优化运行过程。
3、可以考虑加入交叉运算，使每个个体的进化收到其他个体的影响。 4、可加入变异操作，以防止程序陷入局部最优解。 5、可加入大灾变，引入大扰动，避免陷入局部最优解。
感谢聆听
程序实现
各子程序功能 InitPop函数：用量子比特矩阵表示初始种群，初始时，各情况是等概率的。 Collapse函数：对种群进行测量，把量子比特矩阵，转换成二进制编码矩阵。 Qgate函数：根据每个个体的适应度和最优适应度之间的关系，调整各个基因的量子比特值，使其向着有利于BEST 的方向演化 FitnessFunction函数：根据优化问题，计算各个个体的适应度。 Objfunction函数：把基因中的二进制编码转换，为公式中使用的十进制数。