南邮2013MATLAB数学实验答案(全)
数学实验(MATLAB)课后习题答案
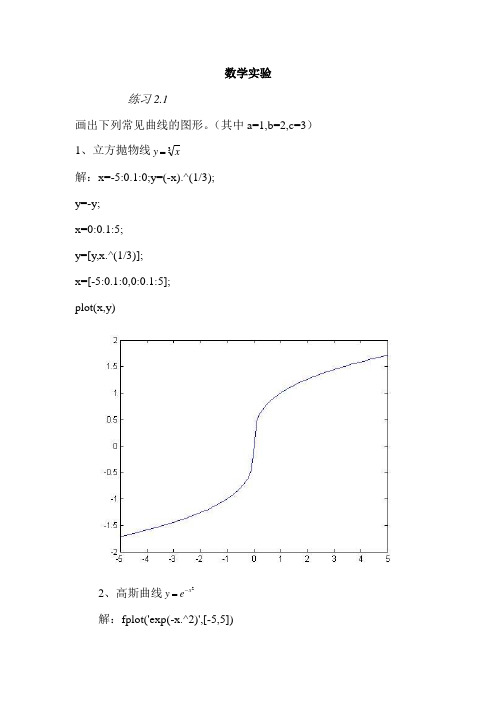
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
数学实验2013答案(全部)

A =
1 2 6
2 4 4
1 -5 7
>> B=[1 3 4;3 0 5;2 -1 1]
B =
1 3 4
3 0 5
2 -1 1
>> A+B,2*A-B,A*B,A.*B,A/B,A\B,A.^B
ans =
2 5 10
5 4 9
3 -6 8
ans =
1 1 8
(1) (2)
>> [X,Y]=eig(A)
X =
0 0.3015 0.3015
0 0.3015 0.3015
1.0000 -0.9045 -0.9045
Y =
2 0 0
0 1 0
0 0 1
A的特征值是2,1,1
特征向量是0和0.3015和0.3015
00.30150.3015
1.0000-0.9045-0.9045
>> a=5.3
a =
5.3000
>> b=[1 3; 2 5]
b =
1 3
2 5
>> who
Your variables are:
a b
>> whos
Name Size Bytes Class
a 1x1 8 double array
b 2x2 32 double array
Grand total is 5 elements using 40 bytes
%这是求从100米高空自由落下的皮球到最后静止经过总路程的程序
%其中s是总路程,h是弹起高度,n是弹起次数
南邮MATLAB数学实验答案(全)[精品文档]
![南邮MATLAB数学实验答案(全)[精品文档]](https://img.taocdn.com/s3/m/3d22b17eb307e87101f6963b.png)
第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin limx mx mxx →∞- syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf) ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2) ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100xy e dxdy +⎰⎰dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) ans = 2.13941.4 计算4224x dx m x +⎰ syms xint(x^4/(902^2+4*x^2)) ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).syms xtaylor(sqrt(902/1000+x),5,x) ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
MATLAB实验及答案详解

《MATLAB原理及应用》实验报告实验一MATLAB环境熟悉及基本操作一、实验目的熟悉MATLAB软件的工作环境和练习MATLAB命令窗口的基本操作。
二、实验内容1.命令窗口(Command Window)运行如入门【实验1-1】求23)]47(212[÷-⨯+的算术运算结果。
用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容:(12+2*(7-4))/(3^2)在上述表达式输入完成后,按【Enter】键,该命令被执行。
在命令执行后,MATLAB命令窗口中将显示结果。
ans =2【实验1-2】简单矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=15524974111415412869811105132316A的输入步骤。
(1)用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容:A=[16 3 2 13 -1 -4;5 10 11 8 7 9;9 6 8 12 -4 2;4 15 14 1 -5 15](2)按【Enter】键,该命令被执行。
(3)在命令执行后,MATLAB命令窗口中将显示结果.(4)采用分行输入,在命令窗口输入:A=[16 3 2 13 -1 -45 10 11 8 7 99 6 8 12 -4 24 15 14 1 -5 15]【实验1-3】用简短命令计算并绘制在0≤x≤6范围内的sin(Ax)、sinAx2、sin2(Ax)。
( A代表你的学号)在命令窗口输入:x=0:0.01:6;y=[sin(1*x);sin(1*x.^2);sin(1*x).^2];plot(x,y)(2) 按【Enter】键,该命令执行结果如图1图1 函数曲线图(3)在命令窗口输入:x=0:0.01:6;y1=sin(1*x);y2=sin(1*x.^2);y3=sin(1*x).^2; subplot(2,2,1),plot(x,y1),title('sin(1*x)') subplot(2,2,2),plot(x,y2),title('sin(1*x.^2)') subplot(2,2,3),plot(x,y3),title('sin(1*x) .^2') (4) 按【Enter】键,该命令执行结果如图2图2子图形式函数曲线图2.命令窗口(Command Window)常用的基本操作【实验1-4】命令行操作过程示例。
matlab实验内容答案

m a t l a b实验内容答案(总16页) -本页仅作为预览文档封面,使用时请删除本页-实验报告说明:matlab 课程实验需撰写8个实验报告,每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。
第一次实验内容:实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。
2.熟悉MATLAB 命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1)22sin8511z e ︒=+ (2)12ln(2z x =,其中2120.455i +⎡⎤=⎢⎥-⎣⎦(3)0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- 提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
(4)2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩,其中t =0::提示:用逻辑表达式求分段函数值。
2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值:(1) A+6=B 和A-B+I(其中I 为单位矩阵)。
(2) A*B 和A.*B 。
(3) A^3和A^.3 。
(4) A/B 和B\A 。
(5)[A ,B]和[A([1,3],;);B^2] 。
3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D(3) 查看MATLAB 工作空间使用情况。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/f6c08c5902d276a201292ece.png)
1 + e2 (2) z = 1 ln( x + 1 + x 2 ) ,其中 x = ⎡⎢ 2⎣-0.45 ⎦2 2 ⎪t 2 - 2t + 1 2 ≤ t <3 ⎨实验一MATLAB 运算基础1. 先求下列表达式的值,然后显示 MATLAB 工作空间的使用情况并保存全部变量。
(1) z = 2sin 8501221 + 2i ⎤5 ⎥(3) z = e 0.3a - e -0.3asin(a + 0.3) + ln 0.3 + a ,a = -3.0, - 2.9, L , 2.9, 3.03⎧t 2 0 ≤ t < 1 (4) z = ⎪t 2 - 11 ≤ t <2 ,其中 t=0:0.5:2.5 4⎩解:M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
(2)建立一个字符串向量,删除其中的大写字母。
解:(1)结果:m=100:999;n=find(mod(m,21)==0);length(n)ans=43(2).建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch=⎣O2⨯3⎥,其中E、R、O、S分别为单位矩阵、随机矩阵、零矩S⎦阵和对角阵,试通过数值计算验证A=⎢⎥。
Matlab实验习题集答案.docx

1:用以上两种形式计算56+sin^ + e 3算术运算结果。
» 5A 6+sin(pi)+exp(3)ans =1.5645e+004» x=5A 6+sin(pi)+exp(3)»A=[1 2;1 2];» B=[l 1;2 2];» C=(A<B)&(A==B)C =0 0 03:对数d = 5 + sin7用五位定点、十五位定点以及有理数形式表示出来。
»a=5+sin(7); format short,a 5.6570» a=5+sin(7);» format long,aa =» A=[l 2 3;4 15 60;7 8 9]A =12 3 415 60 7 8 9 n i n i i i5:输入矩阵U 1 1丿。
%利用MATLAB 命令直接输入矩阵OneMatrix=ones(33J)OneMatrix =8 10 9 101 1 11 1 11 1 1‘0 0 0 0 0、c养」0 0 0 0 0,» OneMatrix=ones(2,5;l);ZeroMatrix=zeros(size(OneMatrix)) ZeroMatrix =0 0 0 0 00 0 0 0 07:生成3阶魔方矩阵。
» magic(3) ans =8 1 63 5 749 28:操作符冒号”:”的应用a)步长为1的等差数列b)步长为2的等差数列c)步长为-2的等差、递减数列» 0:1:10 ans =» 0:2:10 ans =» 10:(-2):0C)取矩阵A 的A (2), A (3), A (4)d)取矩阵A的第一行e)取矩阵A的第三列D把矩阵A的第一行第三列元素赋值给变吊: g)把矩阵A的第二行第列元素修改为100» A=[l 23 56;sin(3) 7 9;log(2) 6 1]» A(2,3)fl 3 100) c 二,利用A 与B 生成矩阵V 6 9 0 A ans = ans =23 » A ⑵,A ⑶,A(4)ans =0.141120008059867ans =0.693147180559945 ans =23»A(1,:)ans =1 23 56» A(:,3)ans =5691» x=A(l,3)56 » A(2,1)=100L0000 100.0000 0.6931 23.0000 7.0000 6.000056.00009.00001.00001 3 A =6 9 io :己知矩阵 L° R _(A 0) D = (A B)曲=〔0 B 丿»A=[13;6 9];B=[1 5;0 8]; » C=[AB(:,1)];» C(l,3)=100c =1 3 1006 9 0» A=[l 3;6 9];B=[1 5;0 8];D=[A B]D =公比为10°" » A=[l 23 56;sin(3) 7 9;log(2) 6 1];»A(1,:)=[]A =0.1411 7.0000 9.00000.6931 6.0000 1.000012: 1 inspace(0, 1, 6) / %给出区间[0, 1]的6个等分点数据logspace(0, 1,6) / %给出区间的6个等比点数据,»linspace(0J,6) ans =» a=l:5 b=3:2:ll c=a>*a a = 1 2b = 3 5c = 1 4» a.*bans = 3 103 4 57 9 119 16 2521 36 55■兀 . sm(k ——),k = ±2, ±1,014:计算 2 的值。
MATLAB数学实验练习题附答案PPT课件

%2、求100~999之间的水仙花数
clear all;
clc;
for n=100:999
n1=floor(n/100); %取出百位数字n1
ቤተ መጻሕፍቲ ባይዱ
n2=mod(floor(n/10),10); %取出十位数字n2
2
n3=mod(n,10) ; %取出个位数字n3
if n1^3+n2^3+n3^3==n
fprintf('%d是“水仙花数”\n', n)
让我们共同进步
2021/3/9
5
===============================================================
%5.作xoy面上的曲线(x-a).^2+y.^2=r.^2绕z轴旋转所得到的图形(0<r<a),取r=1,a=2.
clear all,clc;
x=1:0.1:3;
3
[x,y,z]=cylinder(sqrt(1-(x-2).^2));
surf(x,y,z)
2021/3/9
%6. 作x2/2-y2/3=2z图形. clear,clf,clc; [X,Y,Z]=meshgrid(-1:0.1:1); V=X.^2./2+Y.^2./2-2*Z; fv=isosurface(X,Y,Z,V,0);%显示V=0等值面 p=patch(fv); set(p,'FaceColor','blue','EdgeColor','none');%设置图形的相关属性 view(3) hold on camlight
end
202e1n/3d/9
matlab实验指导答案详解(非常详细正确)

实验一MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条(Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-52⨯2-70)÷3 >>(365-52*2-70)/3 ans = 63.6667(2)>>area=pi*2.5^2 area = 19.6350(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= >>x=3 >>y=4>>z = x ^2 * y ^3 / (x - y) ^2 z = 576(4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1 =[16 2 3 13 ; 5 11 10 8 ; 9 7 6 12 ; 4 14 15 1 ] >>m1( 2 , 3 ) ans = 10 >>m1( 11 ) ans = 6>>m1( : , 3 ) ans =3 10 6 15>>m1( 2 : 3 , 1 : 3 ) ans =5 11 10 9 7 6>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) ans = 34(5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) (6)执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
MATLAB全部实验及答案

MATLAB全部实验及答案MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B 与A.*B?A*B就是线代里面的矩阵相乘A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9)写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、已知+?=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
matlab2013实验3参考答案

MATLAB 实验三MATLAB 计算可视化试验报告说明:1 做试验前请先预习,并独立完成试验和试验报告。
2 报告解答方式:将MATLAB 执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3 在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3 报告以Word 文档书写。
文档命名方式: 学号+姓名+_(下划线)+试验几.doc 如:110400220张三_试验1.doc 4 试验报告doc 文档以附件形式发送到maya_email@ 。
凡文档命名不符合规范,或者发送方式不正确,不予登记。
一 目的和要求(1)熟练掌握MATLAB 二维曲线的绘制(2)熟练掌握图形的修饰(3)掌握三维图形的绘制(4)熟练掌握各种特殊图形的绘制(5)掌握句柄图形的概念二 内容和步骤1 符号计算 (必做)1.1 已知725),(23+-=x y y x y x f ,求12=x dxdy f d 。
(必做) syms x yf=(x^3*y-5*y)/(2*x^2+7)g =diff(diff(f,x),y)%有同学调用方式:>> f1=diff(f,2) ,要注意这种调用方法其实是对第一自由变量x 求2阶导数。
subs(g,x,1)ans =0.53091.2计算二重积分⎰⎰-ππππy dx x x dy )sin(2。
(必做) >> f=sym('sin(x)/x');>> int(int(f,'x','y-pi',pi),'y',pi,2*pi) %注意对y 积分,要明确指定积分变量‘y ’ % 注意积分区间(a,b ),参数的前后顺序ans =21.3解方程组:221,2x y xy +== 。
(必做) >> S=solve('x^2+y^2=1','x*y=2',’x ’,’y ’);>> xx=double(S.x),yy=double(S.y)xx =1.1180 - 0.8660i1.1180 + 0.8660i-1.1180 - 0.8660i-1.1180 + 0.8660iyy =1.1180 + 0.8660i1.1180 - 0.8660i-1.1180 + 0.8660i-1.1180 - 0.8660i1.4 求微分方程022=+'+''y y y ,当0)0(=y ,1)0(='y 时的解。
MATLAB实验答案

2,(1)A=[1 2;3 4 ];B=[5 5;7 8 ];A^2*B(2) A=[1 2 3;4 5 6;7 8 9 ];B=[1 0 0;0 2 0;0 0 3 ];A\B,A/B(3) A=[5+1i,2-1i,1;6*1i,4,9-1i ]; A1=A.',A2=A'(4) A=[1 2 3;4 5 6;7 8 9 ];B=A([1,2],[3]),C=A(2:end, : )(5) M=magic(4),M(:,4)=[]3,(1) p1=[1 0 2 4];PS1=poly2str(p1,'x')r=roots(p1)(2) p=poly(A)polyval(p,20)poly2str(p,’A’)4,(1) t=0:.1:2*pi;y=cos(t);plot(t,y),grid(2) t=0:.1:2*pi;y1=cos(t-0.25);y2=sin(t-0.25);plot(t,y1,t,y2)gridt=0:.01:4*pi;y=10*sin(t);plot(t,y,'r:+')gridaxis([0,10,-15,15])xlabel('x','FontSize',16)ylabel('y','FontSize',16)title('正弦函数')6,(1)sum=0;i=1;while(sum<2000)sum=sum+i;i=i+1;endn=i-2{ n=0;s=0;while s<2000n=n+1;s=s+n;endn=n-1}(2)解法1:function [ s i ] = mitifang1(n)s=0;for i=0:ns=s+2^i; if(i>n), break;endends,n解法2:function [ s i ] = mitifang2(n)s=0;i=0;while(i<=n) ,s=s+2^i;i=i+1;ends,n(3)reply=input('ÇëÊäÈë:','s');while reply=='y'||reply=='Y'||reply=='n'||reply=='N'if (reply=='y'||reply=='Y')x=1;disp('x=')disp(x)elseif (reply=='n'||reply=='N')x=0;disp('x=')disp(x)elsedisp('shu ru you wu')endreply=input('ÇëÊäÈë:','s');enddisp('shu ru you wu ')试验二1,(1)num=5*[1 5 6];den=[1 6 10 8];G=tf(num,den)step(G)impulse(G)num=5*[1 5 6];den=[1 6 10 8];G=tf(num,den)[A B C D]=tf2ss(num,den)x=[1 1 0]'initial(A,B,C,D,x)(2)wn=[2:2:12];z=0.7;t=0:0.1:12;hold onfor i=1:length(wn)Gc=tf(wn(i)^2,[1,2*z*wn(i),wn(i)^2]); step(Gc,t)endgrid onhold on(3)z=[0.2:0.2:2.0];wn=6;t=0:0.1:12;hold onfor i=1:length(z)Gc=tf(wn^2,[1,2*z(i)*wn,wn^2]); step(Gc,t)endgrid onhold on2,(1)wn=[2:2:12];z=0.7;hold onfor i=1:length(wn)num=wn(i)^2;den=[1,2*z*wn(i),wn(i)^2]; bode(num,den);endgrid onhold on(2)z=[0.2:0.2:2.0];wn=6;hold onfor i=1:length(z)num=wn^2;den=[1,2*z(i)*wn,wn^2];bode(num,den);endgrid onhold on3,num=[1];den=conv([1 0],conv([1 1],[1 2])); sys=tf(num,den);rlocus(sys)[x,y]=ginput(3);p=x+i*yK=rlocfind(sys,p)实验三1,(1)k=100;p=[0,-1,-20];z=-2;sys=zpk(z,p,k)sys=tf(sys)G_c=feedback(sys,1);%转换为闭环传递函数roots(G_c.den{1})%求闭环特征方程的根[rtab,msg]=routh(G_c.den{1})(2)sys=tf([1,3],conv(conv([1,0],[1,5]),conv([1,6],[1,2,2]))) rlocus(sys)[K,poles]=rlocfind(sys)(3)sys1=tf(2.7,[1 5 4 0])margin(sys1);%画出波特图[Gm,Pm,Wcg,Wcp]=margin(sys1)G_c=feedback(sys,1)step(G_c)%验证阶跃响应是否稳定Grid2,[A,B,C,D]=tf2ss([1,-1],[1,10,27,18])%取0,1时同理Tc=ctrb(A,B)rank(Tc)To=obsv(A,C)rank(To)3, b=[2 3 4 0];a=[1 3 3 2];n=2^3;Fs=40;[h,f]=freqz(b,a,n,Fs);plot(f,abs(h))grid ontitle('离散系统幅频特性曲线')p=angle(h);ph=p*180/pi;plot(f,ph)grid ontitle('离散系统相频特性曲线')t=1;dbode(b,a,t)[mag,phase,w]=dbode(b,a,t)figure(7)[gm,pm,wg,wp]=margin(mag,phase,w) dnyquist(b,a,t)。
MATLAB)课后实验答案-精简版

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e=+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.52. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
解:. 运算结果:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
(2).建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果是: 实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 40 98 80 7 14 16 73 55 57 64 41 4 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 34 17 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37P 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1]; >> rank(A), rank([A,b])ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]'; >> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95]; >> x1=a*x, x2=a^2*x, x10=a^10*x >> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i -0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000 -41.0000 25.0000 10.0000 -6.0000 -17.0000 10.0000 5.0000 -3.0000 10.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286 -0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771 -0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628 -0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\b ans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3)) fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);1 6*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi;x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[ 4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小,x(2)最大。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
“”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根。
(先画图后求解)(要求贴图)>> ('(x)-3*x^2',0)=-2*(-1/6*3^(1/2))-2*(-11/6*3^(1/2))-2*(1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x->->> x;>> (((x))^3)=1/62) (10)cos ,x y e x y =求 >> x;>> ((x)*(x),10)=(-32)*(x)*(x)3)21/20(17x e dx ⎰精确到位有效数字)>> x;>> ((((x^2),0,1/2)),17)=0.544987104183622224)42254x dx x+⎰>> x;>> (x^4/(25^2))=125*(5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
>> t;>> ((1^2))(t);>> ()()=16)设函数(x)由方程e所确定,求y′(x)。
>> x y;*(y)(1);>> ()()=(x + (y))7)sin2xe xdx+∞-⎰>> x;>> ()*(2*x); >> (y,0)=2/58)08x =展开(最高次幂为)>> x(1);taylor(f,0,9)=- (429*x^8)/32768 + (33*x^7)/2048 - (21*x^6)/1024 + (7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + 2 + 19) 1sin (3)(2)x y e y =求>> x y;>> ((1));>> ((y,3),2)=-0.582610)求变上限函数x⎰对变量x的导数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin limx mx mxx →∞- syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf) ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2) ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +⎰⎰dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) ans = 2.13941.4 计算4224x dx m x +⎰ syms xint(x^4/(902^2+4*x^2)) ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).syms xtaylor(sqrt(902/1000+x),5,x) ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+= 用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
x=[1,1]; for n=3:20x(n)=x(n-1)+x(n-2); end x x=Columns 1 through 101 123 5 8 13 21 34 55 Columns 11 through 2089 144 233 377 610 987 1597 2584 4181 67651.8 对矩阵211020411000A m ⎛⎫ ⎪- ⎪= ⎪⎪- ⎪⎝⎭,求该矩阵的逆矩阵,特征值,特征向量,行列式,计算6A ,并求矩阵,P D (D 是对角矩阵),使得1A PDP -=。
A=[-2,1,1;0,2,0;-4,1,902/1000];inv(A)ans =0.4107 0.0223 -0.4554 0 0.5000 0 1.8215 -0.4554 -0.9107 eig(A) ans =-0.5490 + 1.3764i -0.5490 - 1.3764i 2.0000 det(A) ans =4.3920[P,D]=eig(A)P = %特征向量0.3245 - 0.3078i 0.3245 + 0.3078i 0.2425 0 0 0.9701 0.8944 0.8944 0.0000 D =-0.5490 + 1.3764i 0 0 0 -0.5490 - 1.3764i 0 0 0 2.0000 P*D^6*inv(P) %A^6的值 ans =15.3661 12.1585 + 0.0000i -5.8531 0 64.0000 0 23.4124 -5.8531 + 0.0000i -1.61961.9 作出如下函数的图形(注:先用M 文件定义函数,再用fplot 进行函数作图):1202()12(1)12x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩m 文件:function y=fenduan(x)if x<=1/2 y=2*xelse x<=1 y=2-2*xend end执行函数:fplot('fenduan',[0,1]); grid ontitle('第1.9题图') 得下图:0.0.0.0.0.0.0.0.0.第1.9题图1.10 在同一坐标系下作出下面两条空间曲线(要求两条曲线用不同的颜色表示)(1)cos sin x t y t z t =⎧⎪=⎨⎪=⎩ (2)2cos 2sin x t y t z t =⎧⎪=⎨⎪=⎩t=-10:0.01:10; x1=cos(t); y1=sin(t); z1=t;plot3(x1,y1,z1); hold onx2=cos(2*t); y2=sin(2*t); z2=t;plot3(x2,y2,z2,'m'); grid ontitle('第1.10题图') 得下图:第1.10题图1.11 已知422134305,203153211A B m -⎛⎫⎛⎫ ⎪ ⎪=-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,在MATLAB 命令窗口中建立A 、B 矩阵并对其进行以下操作:(1) 计算矩阵A 的行列式的值det()A(2) 分别计算下列各式:1122,*,.*,,,,T A B A B A B AB A B A A --- 解:A=[4,-2,2;-3,0,5;1,5*902,3]; B=[1,3,4;-2,0,3;2,-1,1];det(A) ans =-117288 2*A-B ans =7 -7 0-4 0 7 0 9021 5 A*B ans =12 10 127 -14 -7 -9013 0 13537 A.*B ans =4 -6 86 0 15 2 -4510 3 A*inv(B) ans =1.0e+003 *-0.0000 0 0.0020 0.0000 0.0016 0.0001 1.0311 -0.9016 -1.4167 inv(A)*B ans =0.3463 0.5767 0.5383 0.0005 -0.0006 -0.0005 -0.1922 0.3460 0.9230 A*A ans =24 9012 4-7 22556 9 -13523 13528 22561 A' ans =4 -3 1-2 0 4510 2 5 31.12已知22()2()x f x μσ--=分别在下列条件下画出)(x f 的图形:(1)/600m σ=,μ分别为0,1,1-(在同一坐标系上作图); (2)0μ=,σ分别为1,2,4,/100m (在同一坐标系上作图). (1)x=-5:0.1:5;h=inline('1/sqrt(2*pi)/s*exp(-(x-mu).^2/(2*s^2))'); y1=h(0,902/600,x);y2=h(-1,902/600,x);y3=h(1,902/600,x); plot(x,y1,'b',x,y2,'m',x,y3,'y')grid ontitle('第1.12题')第1.12题(2) z1=h(0,1,x);z2=h(0,2,x);z3=h(0,4,x); z4=h(0,902/100,x);plot(x,z1,x,z2,'y',x,z3,'m',x,z4, 'g') grid ontitle('第1.12题')z1=h(0,1,x);z2=h(0,2,x);z3=h(0,4,x); z4=h(0,902/100,x);第1.12题1.13 作出24z mx y =+的函数图形。
x=-10:0.2:10;y=x;[X Y]=meshgrid(x,y);Z=902*X.^2+Y.^4; mesh(X,Y,Z); title('第1.13题')第1.13题1.14对于方程50.10200mx x --=,先画出左边的函数在合适的区间上的图形,借助于软件中的方程求根的命令求出所有的实根,找出函数的单调区间,结合高等数学的知识说明函数为什么在这些区间上是单调的,以及该方程确实只有你求出的这些实根。
最后写出你做此题的体会。
解:作图程序:(注:x 范围的选择是经过试探而得到的)x=-1.7:0.02:1.7;y=x.^5-902/200*x-0.1;plot(x,y);grid on; title('第1.14题')第1.14题由图形观察,在x=-1.5,x=0,x=1.5附近各有一个实根 solve('x^5-902/200*x-0.1') ans =-1.4516870267499636199995749888894 -0.022172950190557703188753959027919 1.46277510594806546372292321961741.4573364935933870280941533926624*i + 0.0055424354962279297327028641499658 0.0055424354962279297327028641499658 - 1.4573364935933870280941533926624*i 三个实根的近似值分别为:-1.4517,-0.0222,1.4628由图形可以看出,函数在区间(,1)-∞-单调上升,在区间(1,1)-单调下降,在区间(1,)∞单调上升。
syms xdiff('x^5-902/200*x-0.1',x)结果为5*x^4-4.51solve('5*x^4-902/200') ans =-(451^(1/4)*500^(3/4))/500 (451^(1/4)*500^(3/4))/500 -(451^(1/4)*500^(3/4)*i)/500 (451^(1/4)*500^(3/4)*i)/500 vpa(ans) ans =-0.97454440927373918149075795211629 0.97454440927373918149075795211629 -0.97454440927373918149075795211629*i 0.97454440927373918149075795211629*i 得到两个实根:-0.9745与0.9745可以验证导函数在)9745.0,(--∞内为正,函数单调上升 导函数在)9745.0,9745.0(-内为负,函数单调下降 导函数在),9745.0(∞内为正,函数单调上升 根据函数的单调性,最多有3个实根。
