匝道计算
匝道车道数目计算

匝道车道数目计算
- 交通量:匝道基本路段的交通量是确定匝道车道数的重要因素之一。
在相同服务水平下,不同运行速度的车道具有不同的最大服务交通量。
- 运行速度:匝道设计速度从30km/h到80km/h有较大的变化幅度,因而当设计服务水平被选定之后,不同性质和不同运行速度的匝道容许通行能力将会有较大的差别。
- 超车需求:匝道上的超车需求也是确定车道数的重要因素之一。
- 车道平衡:车道平衡要求也是确定匝道车道数时需要考虑的因素之一。
在实际计算中,需要根据具体情况综合考虑这些因素,并结合相关规范和标准来确定匝道车道数。
如果需要详细的计算方法,建议咨询专业的交通规划师或工程师。
高速公路匝道偏距计算公式

高速公路匝道偏距计算公式在高速公路设计和建设中,匝道的偏距是一个非常重要的参数。
偏距是指匝道与主线之间的水平距离,它对于车辆的转弯半径、安全性和舒适性都有着重要的影响。
因此,正确计算匝道偏距是确保高速公路安全畅通的关键之一。
匝道偏距的计算需要考虑多个因素,包括车辆的设计参数、道路的设计速度、转弯半径等。
在实际工程中,匝道偏距的计算通常采用以下公式:偏距 = V^2 / (127 R)。
其中,V为设计速度(km/h),R为转弯半径(m)。
这个公式是根据车辆的侧向加速度和转弯半径来计算匝道偏距的,下面我们来详细解释一下这个公式的各个参数。
首先是设计速度V,设计速度是指匝道设计时考虑的车辆行驶速度。
在实际工程中,设计速度一般根据交通量、车辆类型、道路等级等因素来确定。
设计速度越高,匝道偏距也就越大,因为车辆在高速行驶时需要更大的转弯半径和侧向空间。
其次是转弯半径R,转弯半径是指车辆在匝道上进行转弯时所需要的最小曲线半径。
转弯半径的大小取决于车辆类型和设计速度,一般来说,转弯半径越小,匝道偏距也就越小。
公式中的127是一个经验系数,它是根据车辆的侧向加速度和转弯半径来确定的。
在实际工程中,这个系数可能会有所调整,以适应不同的道路和车辆情况。
通过这个公式,我们可以看到,匝道偏距的计算是与车辆的侧向加速度和转弯半径密切相关的。
因此,在设计匝道时,需要充分考虑车辆的行驶特性,以确保匝道的安全性和舒适性。
除了上述公式外,还有一些其他计算匝道偏距的方法,比如根据车辆的转弯半径和车辆轴距来确定匝道偏距,或者根据车辆的最大侧向位移和车辆速度来确定匝道偏距等。
这些方法都是根据车辆的行驶特性和道路的设计要求来确定匝道偏距的。
在实际工程中,匝道偏距的计算是一个复杂而又重要的工作。
它需要考虑到车辆的行驶特性、道路的设计要求、交通流量等多个因素,以确保匝道的安全性和舒适性。
因此,在进行匝道设计时,需要充分考虑这些因素,以确保匝道的设计符合实际要求。
匝道专用计算(两条)

一匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 二匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 K000+090.000 K000+160.000 K000+223.715 K000+271.881 K000+384.032 K000+444.032 K000+544.032 9987.403 9968.981 9910.603 9880.438 9922.316 9981.363 10081.363 10059.378 10125.341 10136.791 10100.904 10007.909 10000.000 10000.000 1.000 50.000 50.000 75.000 75.000 1.000 0.000 桩 号 坐 X(M) 标 Y(M) 半径R(M)
请输入中桩到 左 边桩垂距(M)= 3.50 请输入中桩到 右 边桩垂距(M)= 3.50
请输入自定义逐桩距
ห้องสมุดไป่ตู้ 切线方位角
备 注
输
入
说
明
匝道的组成:起点直线-缓和曲线(ZH)-圆 曲线(HY1)-卵形曲线(YH1)-圆曲线(HY2)缓和曲线(YH2)-直线(HZ)-终点。 1、切线方位角: 136°08′20.6″ 按 136.08206 格式输入。 2、半径输入:缓和曲线接直线端输入“1”, 其余按设计参数输入,直线不作规定。 3、起点或终点无直线段可不作输入,但ZH-HZ 间各行必须输入。如:接直线端无缓和曲线 92.17262 132.23516 205.24336 251.24185 337.04542 0.00000 0.00000 ,HY1、YH1输入同一点参数过度。 4、自定义逐桩距的取值:请按以下线性设计 逐桩点个数及线段长度选择 2、 2.5、5、 10、 20、25、50米7个级数。 直线、圆曲线50个逐桩点,如果自定义 逐桩距为5米,可计算250米长的直线和圆 曲线; 完整缓和曲线50个逐桩点; 不完整缓和曲线40个逐桩点,如果自定义 逐桩距为5米 ,可计算200米长的不完整 缓和曲线。 如果要同时计算两条匝道,请根据长匝道中 的最长线段自定义逐桩距,使其完整显示。
互通匝道超高计算方法

互通匝道超高计算方法摘要:一、互通匝道超高计算方法简介二、互通匝道超高计算公式及参数解释三、实例分析四、注意事项正文:互通匝道超高计算方法是高速公路设计中的一项重要内容。
互通匝道超高是指在互通立交中,由于道路线形的变化,使某一部位的纵断面具有较大的高差。
合理的互通匝道超高计算方法能够保证道路线形流畅,提高行驶安全性。
本文将详细介绍互通匝道超高计算方法、公式及实例分析,以期为设计师提供参考。
一、互通匝道超高计算方法简介互通匝道超高计算方法主要包括以下几个步骤:1.根据互通立交的类型,确定匝道的线形组合。
2.分析互通匝道的交通量、车速、路幅宽度等设计参数。
3.依据设计规范,确定互通匝道的最小半径、最大坡度等技术指标。
4.计算互通匝道的超高值,并进行相应的调整。
二、互通匝道超高计算公式及参数解释1.超高计算公式:h = (v^2)/127R其中,h为超高值(m),v为设计速度(km/h),R为曲线半径(m)。
2.参数解释:(1)设计速度:根据互通立交的交通量、车速等因素综合确定。
(2)曲线半径:根据互通立交的类型、地形地貌等因素综合确定。
(3)超高调整系数:根据道路等级、设计年限等因素确定。
三、实例分析以某一等级为高速公路的互通立交为例,已知设计速度为100km/h,曲线半径为150m。
根据公式计算,得到超高值为0.12m。
考虑到道路等级较高,超高调整系数取1.1,最终确定超高值为0.132m。
四、注意事项1.在计算互通匝道超高时,应充分考虑地形地貌、交通量、设计年限等因素,确保计算结果的合理性。
2.超高值不应过大,以免影响道路线形美观和行驶安全性。
3.超高调整系数应根据实际情况确定,以满足不同道路等级的设计要求。
4.在实际设计过程中,应充分了解设计规范,确保互通匝道超高的计算符合相关规定。
通过以上分析,我们可以了解到互通匝道超高计算方法的重要性。
匝道的计算公式与认识

18.有时设计院没有给出匝道最后一段缓和曲线的结束半径,那么在积木法计算前就需要计算最后一段缓和曲线的结束半径。
公式如下:其中 A 是缓和曲线参数、R 是半径ls 是缓和曲线长度。
回旋线是公路路线设计中最常见的一种缓和曲线。
我国的标准规定缓和曲线采用回旋线。
它的基本公式为:A*A=r*l其中:A是回旋线参数。
r是回旋线上某点的曲率半径(m)l是回旋线上某点到原点的曲线长在回旋线上的任意点上,r是随着l 的变化而变化的。
但是在缓和曲线的终点处,l=Ls,r=R,则上式可写为A*A=R*Ls则 -------A=√R*Ls在设计上可以由已知R和Ls计算A,也可以按各种条件选择R和A,再计算Ls.至于用于计算坐标,你可以综合所有的已知条件进行计算,它只是提供一个计算和你进行复核的条件。
对互通立交端部的一点认识随着经济和交通运输事业的飞速发展,高等级公路的普遍修建,作为高等级公路车辆出入门户的互通式立交也开始大量修建。
立体交叉中主线与交叉线处于不同高程上,需用道路将其互相联系,便于各方向车流四通八达,这些起联系作用的道路通常称为匝道。
匝道两端与主线、交叉线连接区域称之为匝道端部。
匝道端部范围,包括匝道出入口,三角区,变速车道等部分。
匝道的端部形式,就其出入口位置不同,有左出入口和右出入口;就其主线或交叉线几何形状不同,有直线和曲线等。
匝道端部形式多样,几何关系以及设计都较繁琐,而且都应满足各自不同的技术要求,如设计不当,将造成对车辆行驶不利,容易引发事故阻碍交通。
本文就结合自己的设计经验,针对匝道端部设计做一些探讨。
一、匝道端部路线平、纵面要求1、路线平面要求从主线流出的车辆,在进入匝道的短暂运行过程中,其驾驶过程较为复杂,分流、转向、减速对司机都有一定的操作要求,同时司机产生心理压力也有影响。
因此,出口处应为车辆行驶创造良好条件,对路线平面应有较高要求,入口处一般也应如此。
我国公路《规范》规定,驶入匝道的分流点应具有较大的曲率半径,并使曲率变化适应行驶速度的变化。
互通式立交匝道运行速度计算

互通式立交匝道运行速度计算
1. 相互通式立交匝道的定义
互通式立交匝道是由垂直交叉路口连接在一起的路口,它把两个平行受限的道路或街道互相连接起来,工程师和技术人员称之为立交或立体交叉路口。
相比较普通的交叉口,立交匝道可以使得道路交通更加顺畅,减少交通拥堵。
2. 相互通式立交匝道运行速度计算
(1)相互通式立交匝道的运行速度取决于许多因素,主要包括:道路状况、拥堵情况,车辆的速度限制和道路的坡度。
(2)正常情况下,当车辆进入交叉路口时,要减速驾驶,但是在立交匝道中,因为把交叉口的两边的路段分开,车的速度就可以保持一定的稳定值,例如,每小时可以保持50-60km/h的行驶速度,这样特定类型的路口就可以更加安全、快捷地实现交通流动。
(3)另外,在立交匝道中,根据国家及各地政策,可能规定更严格的限制,速度也要更低,通常要求保持30-40km/h的速度。
这样可以有效地减少事故风险,提高路况和其他重大事故的发生几率。
(4)最后,运营当局也可以利用摄像头、传感器等技术,对立交匝道的速度限制进行动态监测,如果有车辆超速行驶,可以立即阻挡住,
以确保安全。
3. 相互通式立交匝道运行速度计算结论
综上所述,相互通式立交匝道运行速度计算要考虑许多因素,在正常情况下,如果车辆遵守交通规则和道路标准,一般可以以50-60km/h的速度行驶;但如果国家及地方政策设置更严格的限制,则应保持30-40km/h的速度。
通过动态监测等技术,可以更有效地确保安全,避免事故的发生。
广东省高速公路匝道里程计算方法

广东省高速公路的收费里程计算方式
高速公路收费里程包含主线收费里程和匝道收费里程.主线收费里程直接等于主线的长度。
匝道收费里程按照匝道的平均长度折半计算。
一、收费站匝道里程计算
收费站的匝道收费里程等于收费站的所有匝道长度平均折半,每条匝道长度按照收费站中心桩号起计算至高速主线连接处(收费站与市政路相连的长度不计入收费里程)。
二、互通立交匝道里程计算
互通立交的匝道收费里程等于所有匝道长度平均折半(枢纽互通及T型互通的匝道取消收费)。
1.枢纽互通的高接高匝道取消收费。
高接高互通立交的主线桩号,取高速相交处的中心桩号(如遇特殊情况单独研究),高接高互通立交的匝道统一为0,不计入收费里程。
2.T型连接的互通立交匝道取消收费,互通立交的主线桩号调整至两条主线相交的虚拟点。
3.双喇叭互通的匝道可保留继续收费。
匝道8 一个很难计算的匝道2022

立交匝道计算案例——某高速公路立交F匝道的计算————————————————————————————————————————————————————————————分析F匝道,该匝道设计文件的特殊之处在于,没有标注缓和曲线参数A,同时匝道的起、终点的半径有待确定。
设计单位“偷懒”,但同时也为锻炼一线测量员的计算能力提供了又一个很好的实例。
F匝道共四个线元,为表达方便,分别用1~4来指代。
线元1、3、4为缓和曲线,线元2为圆曲线,其中线元1明显为不完整缓和曲线,线元3、4为完整缓和曲线,要顺利进行F匝道的逐桩坐标计算,需要确定的参数是:1.匝道起点的切线方位角;2.匝道起点的半径;3.匝道终点的半径。
幸运的是,这里,设计单位给出了各曲线的交点坐标,因此,很容易地根据线元1的交点(HJD1)坐标与线元1起点坐标,求得线元1起点切线方位角(也是匝道起点切线方位角)为:236°01′46.95″。
类似地,根据线元1的终点坐标与线元1的交点(HJD)坐标,求得线元1的终点切线方位角为:318°08′13.66″。
这样,线元1的起点、终点切线方位角之差即为线元1的转角:82°06′26.71″。
这里设线元1的起点半径为R1,终点半径为R2,线元1的长度为L,这里已知R2=40m,L=107.341m,根据缓和曲线的相关几何特性,可列方程组如下:根据以上方程组,可求解得:A=67.875m,R1=587.962m。
现在只剩下最后一个问题,就是计算线元4终点半径,即匝道终点半径。
终点半径的计算思路,完全可以参照线元1的起点半径的计算方法,而且由于线元4是完整缓和曲线,方程组更加简单,这里就不再赘述了。
我这里采用的是另一个计算方法,就是试算法,通过不断改变线元1的终点半径值,直到终点坐标与设计文件一致(或差值小于限差)。
这种方法的使用前提是:1.只有一个不确定的变量;2.必须有相关的计算软件或程序;3.必须知道变量的大致范围,并合理地确定一个初值;4.试算法的优点在于不必列出和求解繁杂的数学公式。
匝道坡度最大值

匝道坡度最大值匝道坡度是指匝道上坡或下坡的程度,是匝道设计中非常重要的一项参数。
匝道坡度的设计必须考虑车辆的性能,以及乘客的舒适感受。
在匝道设计中,坡度的最大值是需要考虑的重要因素之一。
一、坡度的定义和计算匝道坡度,是指匝道路面在水平方向的投影与垂直方向的距离之比,一般用百分比表示。
坡度计算公式如下:坡度=(匝道上升高度/匝道水平长度)×100%二、匝道坡度的分类按坡度程度可分为:平坡、缓坡和陡坡。
1. 平坡:坡度在1%-3%之间,起点和终点高程差较小,车辆通行顺畅,乘车舒适度高。
2. 缓坡:坡度在3%-5%之间,起点和终点高差适中,车辆通行相对较顺畅,但乘车舒适度会有所下降。
3. 陡坡:坡度在5%以上,起点和终点高差较大,车辆通行受阻,乘车舒适度较差。
三、匝道坡度的限制1.道路规划:匝道坡度的设定要符合道路规划要求。
根据道路设计标准,匝道上限坡度一般不应超过8%,下限坡度一般不应低于2%。
2.车辆性能:每种车型的性能限制不同,车辆所能承受的坡度也不尽相同。
匝道坡度必须根据车辆性能来设定。
3.环境因素:坡度还受到环境因素的限制,如雨雪天气对车辆行驶的影响等。
在匝道设计中,必须考虑到环境因素的影响。
四、匝道坡度的优化设计1.优化坡度:优化匝道坡度的设计,坡度应逐渐变化,起点和终点处应有平缓过渡,使车辆通过匝道时更加平稳舒适。
2.考虑车速:设计匝道坡度时还需考虑车速,根据车速设定合理的匝道坡度,确保车辆快速通过匝道。
3.防止侧翻:在设计陡坡时,需采取措施,防止因侧翻而影响车辆行驶安全。
结语匝道坡度是匝道设计中的一个重要参数。
合理的坡度设计能够提高车辆的通过能力、乘客的舒适度,更重要的是,确保车辆行驶的安全性。
在匝道设计中,必须根据道路规划、车辆性能以及环境因素等因素来设定匝道坡度,保证匝道的设计符合实际需求。
匝道的计算

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
立交匝道计算案例——又一个高速公路立交匝道的计算

立交匝道计算案例-又一个高速公路立交匝道的计算该问题是上个月网友“快乐的我”提出的,我一直未引起重视,今晚一细看,再次对设计单位无语了,真是:没有最“那个”,只有更“那个”。
设计文件图片质量较差,但绝对会很严重地挑战各位的计算能力,网友自己也声称:“叫了好几个哥们帮忙看都说有问题”,我今晚也暂时未能琢磨出来。
看各路高手有何良策?————————————————————————————————————————————————————————————现在是作一个总结的时候了。
分析F匝道,该匝道设计文件的特殊之处在于,没有标注缓和曲线参数A,同时匝道的起、终点的半径有待确定。
设计单位“偷懒”,但同时也为锻炼一线测量员的计算能力提供了又一个很好的实例。
F匝道共四个线元,为表达方便,分别用1~4来指代。
线元1、3、4为缓和曲线,线元2为圆曲线,其中线元1明显为不完整缓和曲线,线元3、4为完整缓和曲线,要顺利进行F匝道的逐桩坐标计算,需要确定的参数是:1.匝道起点的切线方位角;2.匝道起点的半径;3.匝道终点的半径。
幸运的是,这里,设计单位给出了各曲线的交点坐标,因此,很容易地根据线元1的交点(HJD1)坐标与线元1起点坐标,求得线元1起点切线方位角(也是匝道起点切线方位角)为:236°01′46.95″。
类似地,根据线元1的终点坐标与线元1的交点(HJD)坐标,求得线元1的终点切线方位角为:318°08′13.66″。
这样,线元1的起点、终点切线方位角之差即为线元1的转角:82°06′26.71″。
这里设线元1的起点半径为R1,终点半径为R2,线元1的长度为L,这里已知R2=40m,L=107.341m,根据缓和曲线的相关几何特性,可列方程组如下:根据以上方程组,可求解得:A=67.875m,R1=587.962m。
现在只剩下最后一个问题,就是计算线元4终点半径,即匝道终点半径。
某高速A匝道坐标计算讲解
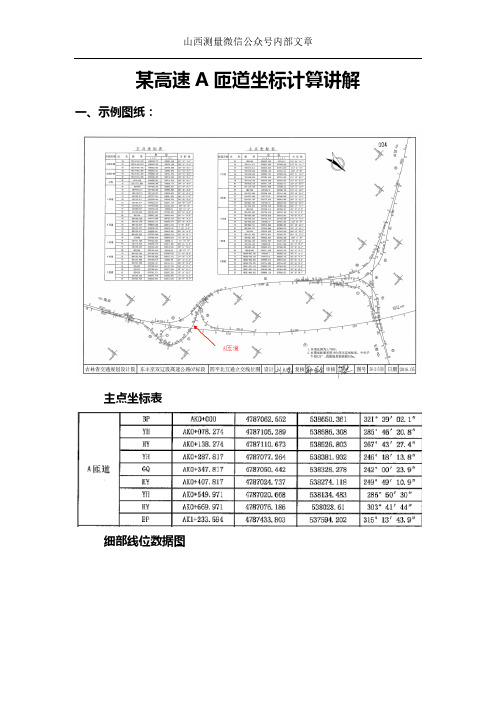
某高速A匝道坐标计算讲解一、示例图纸:
主点坐标表
细部线位数据图
二、数据分析
根据主点坐标表和线元数据平面图可以得出下图:
BP—YH为一段圆曲线,R=125;YH—HY为一段缓和曲线,参数
A=104.447,LS=60:HY—YH为一段圆曲线,R=400;可以知道这里是两段圆曲线之间插入一段缓和曲线,缓和曲线一定是非完整的,根据公式A^2=[ (R 大*R 小) ÷(R 大-R 小)]*Ls,
104.447^2=[ (400*125) ÷(400-125)]*60。
YH—GQ为一段缓和曲线,A=154.919,LS=60,GQ—HY为一段缓和曲线,A=114.891,LS=60,两端缓和曲线在半径相等处连接,半径为0,无穷大;HY—YH 为一段圆曲线,R=220;YH—HY为一段缓和曲线,A=169.267,
LS=120,HY—EP为一段圆曲线,R=2800,和起点处一致,也是两段圆曲线之间插入一段缓和曲线。
三、轻松测量输入界面
其中半径区分正反之分,曲线向左转为负,向右转为正。
四、中桩批量计算坐标表。
匝道验算

本计算以C匝道桥第1联30+32*2+30箱梁第2跨为例,对荷载进行计算及对支架体系进行验算。
该跨的验算具有代表性。
本方案设计均采用容许应力法计算,不计结构、荷载及材料等安全系数。
(1)、荷载计算1、荷载分析根据本工程现浇箱梁的结构特点,在施工过程中将涉及到以下荷载形式;1.1、q1—模板自重q1取1.5kn/m2;1.2、q2—箱梁自重荷载,新浇钢筋混凝土密度取26kn/m3;1.3、q3—施工人员、施工材料及设备荷载,一般按2kn/m2进行取值。
按分布荷载计算,计算模板及直接支承模板的小棱时取2.5kn/m2,计算直接支承小棱的梁时取1.2kn/m2,计算支架立柱时取1.0kn/m2;1.4、q4—振捣荷载,对水平面模板q4=2.0kn/m2;垂直于模板q4=4.0kn/m21.5、q5—新浇混凝土对侧模的压力(按规范要求每层浇筑高度控制在30cm 以内计算侧压力)。
1.6、q6—倾倒混凝土产生的水平荷载,查《路桥施工计算手册》表8-1,q6=2.0kn/m2;1.7、q7—支架自重,支架自重根据支架立杆设计间距、横杆步距、扣件、剪刀撑等钢管组合计算。
2、荷载组合模板、支架设计计算的荷载组合荷载组合受力结构强度计算(承载力)刚度验算(稳定性)底模q1+ q2+ q3+ q4 q1+ q2侧模q4+q 5+ q6 q6底模下纵桥向方木q1+ q2+ q3+ q4 q1+ q2立杆托顶横桥向方木q1+ q2+ q3+ q4 q1+ q2支架q1+ q2+ q3+ q4+ q7 q1+ q2 q3+ q4+ q7 地基q1+ q2+ q3+ q4+ q73、荷载计算3.1箱梁自重—q2计算根据工程现浇箱梁结构特点,通过认真分析,选取具有代表性及最不利荷载的断面,进行箱梁自重计算。
经分析:本段箱梁断面外尺寸相同,端横梁C1#、C2#、C30#、C5#、C6#墩梁高1.8m,部分为实心结构,混凝土结构自重最大。
匝道坐标计算实例(非常实用)

0
备注 弧度制 1.050259
R2*Ls1 =A12 8100
备注
值(左转“+”,右转“-”)
位角(左转“-”,右转“+”) 利用公式反算
坐标增量 △X 16.19957485 △Y 0.08747836
ZH
任一点 与ZH完整 点弧长 L0 16.2
16.19981 1.066459 1.061059
0.005399988
0.0162
-1
ZH完整点切线方位角β ZH完整-M0直线方位角β X完整 Y完整
切线方位角=M0点切线方位角±转角值(左转“+”,右转“-”)
第一段完整曲线要素 ZH完整坐标 X 3435389.441 Y 500174.9586 ZH完整桩号 K0+702.747
弦长C= 偏角= √△X2+△Y2 arctg(△Y/△X)
(切线)方位 角β 1 1.066458665
转角值= 2 L0 /2*R2*Ls1
参数g (左偏-1, 右偏+1)
直线
(适用正推)直线方位角=偏角±切线方位角(左转“-”,右转“+”) X0=X完整+C*COS(ZH完整-M0直线方位角) Y0=Y完整+C*SIN(ZH完整-M0直线方位角)
3435389.441 500174.9586
缓和曲线 完整性 不完整
备注 A12=Ls1*R2
整
不是直线方位角)
说明:①现以第一段曲线上任一点坐标和方位角反推ZH完整点坐标,切线方位角(不是直线方位角) ②不用改变坐标系 第一段缓和曲线上任一点曲线元素 任一点坐标M0 X0 Y0 3435397.346 500189.099 任一点M0桩号 K0+718.947 度 60 (切线)方位角β 0 分 秒 10 31.4
高速公路曲线、匝道的坐标、高程计算公式

高速公路曲线、匝道的坐标、高程计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
互通式立交匝道运行速度计算

互通式立交匝道运行速度计算
互通式立交匝道作为一种管理复杂路网系统的重要手段,其运行速度的计算和控制可以帮助改善路网的运行效率,提高交通出行的安全性。
因此,运行速度的计算就显得十分重要。
下面,我们将介绍一种适用于常见的互通式立交匝道的运行速度计算方法。
1、常见的互通式立交匝道的运行速度是基于路网系统中的基本元素来计算的,这包括车道、桥梁、信号灯及其他运行环境。
首先,我们需要确定匝道运行中每节点的最大速度,这个最大速度不同的情况可能会有所不同,受道路场景、交通流量等因素的影响。
2、接着,我们需要根据路网系统中的车辆数量和车道分布情况,基于最大速度确定一个基本的匝道运行速度,比如每张交叉口的基本速度不能超过每节点的最大速度的50%以上,以此来保证交通安全。
3、当路网系统出现拥堵情况时,我们还需要考虑路况因素,适当降低匝道的运行速度,以减少路网上的拥堵程度,并且避免发生交通事故。
4、此外,我们还需要根据道路的特征情况,做出相应的调整,比如在某些特殊的路口,如果需要车辆停靠特别久的时间,就需要将运行速度更多地降低,以避免发生交叉冲突的情况。
总的来说,互通式立交匝道的运行速度计算是一个复杂的系统,需要综合考虑路网系统中各种元素,避免发生交通拥堵和交通事故。
才能让公路网络更加安全、高效地运行。
在这里,我们介绍了如何计算互通式立交匝道的运行速度,以改
善路网的运行效率,提高交通出行的安全性。
在实际应用中,可以根据交通实际情况,结合分析结果,进一步优化匝道的运行速度,让交通出行更加安全可靠。
公路匝道点位坐标计算

匝道是组成高等及公路立交的基本单元,其形式千变万化,就线形而言,也是由直线段、回旋曲线段、圆曲线段组成。
但是,组成立交的匝道涉及线形的曲率变化特点,利用复化辛普森公式导证了计算公路匝道点位坐标的通用公式。
并利用卡西欧FX-4500P计算器编程计算公路匝道点位坐标。
二、公路匝道点位坐标计算1. 公路匝道中线形式公路匝道中线是由直线—回旋曲线—圆曲线(R1)—回旋曲线—圆曲线(R2)—回旋曲线—直线的顺序组成的,其中R1¹R2。
2. 回旋曲线上点位坐标方位角的计算如图1,设回旋曲线起点A的曲率为r A,其里程为DK A;回旋曲线终点B的曲率为,其里程为DK B,Ax¢y¢为以A为坐标原点,以A点切线为x¢轴的局部坐标系;AXY为线路坐标系。
由此回旋曲线上各点曲率半径为R i和该点离曲线起点的距离ﺎi成反比,故此任意点的曲率为(=R0为常数)(1)由式(1)可知,回旋曲线任意点的曲率按线性变化,由此回旋曲线上里程为DK i点的曲率为(2)当曲线右偏时,取正;当曲线左偏时取负。
在图1中有(3)将式(2)代入式(3)得(4)若已知回旋曲线起点A在线路坐标系下切线坐标方位角αA,则里程为Dk i点切线坐标方位角为(5)将式(4)代入式(5)得(6)对于式(6),当,时,,则a i=a A,式(6)变成计算直线段上任意点切线坐标方位角计算公式;当,时,,,则式(6)代表圆曲线上任意点切线坐标方位角计算公式。
可见,若已知曲线段起点和终点的曲率及起点的切线坐标方位角,式(6)便能计算任意线型点位切线坐标方位角。
3、回旋曲线点位坐标计算由图1可得回旋曲线上点位在坐标系下坐标计算公式:(7)(8)设回旋曲线起点A在线路坐标系下的坐标为将式(6)替代式(8)中的,便得回旋曲线上任意点在线路坐标系下的坐标:(9)对于式(9)的解算,由于后半部分是定积分,我们引入复化辛普森公式对其进行解算。
匝道计算

B值 = G值 =
0.326072577 0.330009478
C值= 0.00066823 H值= 0.93056816
D值= I值=
6.17282E6.17282E-05 0.069431844
E值=
57.29577951
249° 05′47.5″ 起点方位角 249° 05′47.5″
K0+000 3275092.037 533114.707 K0+020 3275085.181 533095.920 K0+040 3275079.518 533076.745 K0+060 3275076.038 533057.066 K0+080 3275075.767 533037.097 K0+100 3275079.68 533017.531
Hale Waihona Puke 3275092.037 533114.707 249°05′47.5″ 249.0965278 3275085.181 533095.92 251°16′37.1″ 251.2769644 3275079.518 533076.745 256°17′12.5″ 256.2868134 3275076.038 533057.066 264°07′33.9″ 264.1260748 3275075.767 533037.097 274°47′41.1″ 274.7947486 3275079.68 533017.531 288°17′34.2″ 288.2928348
3275092.037 533114.707 249
曲线、直线坐标计算 曲线、
说明:本程序适用于匝道坐标,可任意一段曲线内坐标及方位角(包括卵形曲线),也可算直线段坐标 当半径无穷大时输入=10的45次方(=10^45),运行直线时,Rq和Rz输=10^45,L输大于零的数就行 待求点 桩号 待求点中桩坐标 X Y 距起点 中桩0 左+,右- ,中桩0 距离 0 0 0 0 0 0 0 20 40 60 80 100 边距 待求点坐标 X Y 方位角转换 °′″ 方位角 百进制( 百进制( 度)
立交匝道计算案例——某高速公路立交匝道的计算

立交匝道计算案例——某高速公路立交匝道的计算王老师你好,我现在在一高速路遇上一难题。
在一互通式立交中,没有给线元起点方位角,怎么算啊。
A-D砸道起终点都没有直线段,所有线元只有坐标、桩号、半径。
特别是E匝道,全线都没有一条直线。
现将E匝道截图如下:————————————————————————————————————————————————————————————哈哈,各位网友已经发表了众多高见,我这里就做一个总结,以结束这篇日志。
本案例计算的关键,就是要准确确定E匝道的起点方位角,讲到这里,我忍不住要发个牢骚,这设计单位也太“那个”了,给出各节点的切线方位角这样的举手之劳都不做,再不济,给出各曲线交点(IP点)的坐标也行啊,也不做,纯粹就是想考验施工单位的测量员的计算水平。
不过,咱也不怕。
我先阐述一下我的解决方案。
网友们说得很对,对于E匝道起点方位角而言,的确可考虑参考A匝道的HY1点的切线方位角,因为从设计意图来看,E匝道的起点与A匝道的HY1点之间的几何关系应为:E匝道起点应为A匝道HY1点的一个右偏移点,其切线方位角应该是一致的。
先来看看A匝道的坐标数据:由于A匝道的第一条线元是直线,很容易求得A匝道起点的切线方位角:33°30′17.9″。
则计算验证各节点参数(与设计文件对照无误),如下:如此,可得A匝道HY1点的切线方位角为40°40′01.0″,就将这个角度假定为E匝道的起点方位角。
这里之所以说“假定”,是因为之前的所述的设计意图是推断的,“应该”的,但到底是否如此,还需计算验证确认,验证无误的参数如下:在进行以上计算时,起点半径的确定也是一个重点和难点,因为这个参数设计文件中没有直接标注,只能通过其它参数计算而得,这里的276就是通过计算而得的(根据缓和曲线参数A=95、缓和曲线长度L=57.551、缓和曲线终点半径R2=100三个数据,计算过程略),和推断的起点方位角一起,后面验证准确的各节点坐标证明了起点半径和方位角均是准确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ZD K+432.211 2778179.092 544115.375 306°56′31″
计算步骤
QD-YH曲线元,该段为圆曲线
运行程序,按照提示输入曲线元QD纵横坐标及方位角,QD和YH点桩号,再输入该曲线元内所求点桩号即可显示该中线坐标和切线方位角,可以输入YH点桩号K0+81.721验证计算出的结果,之后会提示输入“W”值,即边线宽度,左负右正,如不需要计算边线坐标或计算完毕后输入数值0即可计算下一个桩号坐标。
五、 总结
该程序最大的特点是输入参数少,程序本身简短,可以计算任何曲线元的坐标,当所求桩号大于该段终点桩号时(H>DKB),程序会自动判断处理,即把上一个曲线元的终点参数置换为下一个曲线元的起点参数,并提示输入下一个曲线元终点的半径和桩号,如此即可计算下一个曲线元的中线及边线坐标。
M=C+45 Q(I÷4+2D)÷(2π):N=C+135Q(3I÷4+2D)÷(2π)
K=C+45Q(I÷2+2D)÷π
Fix 3
X=A+Q÷12×(COS C+4(COS M+COS N)+2COS K+COS J)▲!该句中的“×”号不可省略,否则计算结果将不正确
Y=B+Q÷12×(SIN C+4(SIN M+SIN N)+2SIN K+SIN J)▲!该句中的“×”号不可省略,否则计算结果将不正确
XA:YA:CA―――曲线元起点X、Y坐标及起点切线方位角。
1÷RA:1÷RB―――曲线元起点及终点半径,以倒数输入,如起点、终点半径分别为60和40米则输入1/60,1/40,注意:遇ZH,HZ,GQ点时半径都输入0。
DKA:DKB―――曲线元起点和终点桩号。
DKI―――曲线元中待求点桩号
YH K0+081.721 2777900.604 544309.576 299°33′37″
HY K+122.038 2777921.779 544275.286 305°04′30″
YH K+277.085 2778043.376 544183.130 340°36′33″
GQ K+317.085 2778081.751 544171.883 345°11′34″
YH-HY曲线元,该段为回旋线
同前面一样运行程序,此时起点为YH点,终点为HY点,两点的半径是不一样的,YH点半径输入“1÷1291”,HY点半径输入“1÷250”。
YH-GQ曲线元,该段为缓和曲线
起点为YH点,终点为GQ点,输入相应参数,需要注意的是此时GQ点的半径要输入数值0,实际上把GQ点理解为HZH点就不难理解。
二、 程序清单
Lb1 0
{E G}
A“XA”:B“YA”:C“CA”:D“1÷RA”:E“1÷RB”:F“DKA”:G“DKB”
Lb1 1
Norm
Deg
{H}
H“DKI”:H>G?Goto 3⊿
P=(E-D)÷ABS(G-F):Q=ABS(H-F):I=PQ
J=C+90 Q(I+2D)÷π:J≥360?J=J-360:≠?J<0?J=J+360⊿
Fix 4
J“FWJ=”▲
Lb1 2
{W}
Fix 3
W=0?Goto 1⊿
W<0?Z=-Z:≠?Z=1⊿
U“XW”=X+ZWCOS(J+90Z)▲
V“YW”=X+ZWSIN(J+90Z)▲
Goto 2
Lb1 3
A=X:B=Y:D=E:F=G:C=J:Goto 0
三、 变量及符号说明说明 Fra bibliotekCASIO fx-4800匝道计算程序
摘要:匝道在立交工程中常常用到,由于其采用线型多样,计算复杂,因此一份适用的计算程序是不可缺少的,本文提供一份匝道计算程序,该程序简单,容易上手,输入参数少。
关键词:匝道;程序
一、 说明
在高速公路和城市建设中常常运用到互通式立交工程,互通式立交由于曲线元的复杂性和多样性,给施工中的测量定位工作带来困难,手工计算已经不能满足要求,时下CASIO系列计算器在土木工程中已经得到普遍运用,为便于对立交工程匝道的准确测量定位,本人根据多年的测量工作经验,编写出一份CASIO fx-4800匝道计算程序,该程序界面好,能计算出匝道各种线元的中线坐标和边线坐标。
X:Y:FWJ―――待求曲线元中线点X,Y坐标及切线方位角
W―――计算边桩距中线平距,左边输入负值,右边输入正值,退出输入0
XW:YW―――边桩X,Y坐标
四、 示例
如龙门互通立交D匝道线型及相关数据如下
D-D
点号 桩号 X(N) Y(E) 方位角
QD K0+000 2777862.564 544381.888 295°56′01″
