完整word版遗传算法求解TSP问题实验报告
TSP问题求解实验报告

TSP问题求解(一)实验目的熟悉和掌握遗传算法的原理,流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
(二)实验原理巡回旅行商问题给定一组n个城市和俩俩之间的直达距离,寻找一条闭合的旅程,使得每个城市刚好经过一次且总的旅行距离最短。
TSP问题也称为货郎担问题,是一个古老的问题。
最早可以追溯到1759年Euler提出的骑士旅行的问题。
1948年,由美国兰德公司推动,TSP成为近代组合优化领域的典型难题。
TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。
近年来,有很多解决该问题的较为有效的算法不断被推出,例如Hopfield神经网络方法,模拟退火方法以及遗传算法方法等。
TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。
在如此庞大的搜索空间中寻求最优解,对于常规方法和现有的计算工具而言,存在着诸多计算困难。
借助遗传算法的搜索能力解决TSP问题,是很自然的想法。
基本遗传算法可定义为一个8元组:(SGA)=(C,E,P0,M,Φ,Г,Ψ,Τ)C ——个体的编码方法,SGA使用固定长度二进制符号串编码方法;E ——个体的适应度评价函数;P0——初始群体;M ——群体大小,一般取20—100;Ф——选择算子,SGA使用比例算子;Г——交叉算子,SGA使用单点交叉算子;Ψ——变异算子,SGA使用基本位变异算子;Т——算法终止条件,一般终止进化代数为100—500;问题的表示对于一个实际的待优化问题,首先需要将其表示为适合于遗传算法操作的形式。
用遗传算法解决TSP,一个旅程很自然的表示为n个城市的排列,但基于二进制编码的交叉和变异操作不能适用。
路径表示是表示旅程对应的基因编码的最自然,最简单的表示方法。
它在编码,解码,存储过程中相对容易理解和实现。
例如:旅程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)(三)实验内容N>=8。
实验六:遗传算法求解TSP问题实验2篇

实验六:遗传算法求解TSP问题实验2篇第一篇:遗传算法的原理与实现1. 引言旅行商问题(TSP问题)是一个典型的组合优化问题,它要求在给定一组城市和每对城市之间的距离后,找到一条路径,使得旅行商能够在所有城市中恰好访问一次并回到起点,并且总旅行距离最短。
遗传算法作为一种生物启发式算法,在解决TSP问题中具有一定的优势。
本实验将运用遗传算法求解TSP问题,以此来探讨和研究遗传算法在优化问题上的应用。
2. 遗传算法的基本原理遗传算法是模拟自然界生物进化过程的一种优化算法。
其基本原理可以概括为:选择、交叉和变异。
(1)选择:根据问题的目标函数,以适应度函数来评估个体的优劣程度,并按照适应度值进行选择,优秀的个体被保留下来用于下一代。
(2)交叉:从选出的个体中随机选择两个个体,进行基因的交换,以产生新的个体。
交叉算子的选择及实现方式会对算法效果产生很大的影响。
(3)变异:对新生成的个体进行基因的变异操作,以保证算法的搜索能够足够广泛、全面。
通过选择、交叉和变异操作,不断迭代生成新一代的个体,遗传算法能够逐步优化解,并最终找到问题的全局最优解。
3. 实验设计与实施(1)问题定义:给定一组城市和每对城市之间的距离数据,要求找到一条路径,访问所有城市一次并回到起点,使得旅行距离最短。
(2)数据集准备:选择适当规模的城市数据集,包括城市坐标和每对城市之间的距离,用于验证遗传算法的性能。
(3)遗传算法的实现:根据遗传算法的基本原理,设计相应的选择、交叉和变异操作,确定适应度函数的定义,以及选择和优化参数的设置。
(4)实验流程:a. 初始化种群:随机生成初始种群,每个个体表示一种解(路径)。
b. 计算适应度:根据适应度函数,计算每个个体的适应度值。
c. 选择操作:根据适应度值选择一定数量的个体,作为下一代的父代。
d. 交叉操作:对父代进行交叉操作,生成新的个体。
e. 变异操作:对新生成的个体进行变异操作,以增加搜索的多样性。
实验六:遗传算法求解TSP问题实验3篇

实验六:遗传算法求解TSP问题实验3篇以下是关于遗传算法求解TSP问题的实验报告,分为三个部分,总计超过3000字。
一、实验背景与原理1.1 实验背景旅行商问题(Traveling Salesman Problem,TSP)是组合优化中的经典问题。
给定一组城市和每两个城市之间的距离,求解访问每个城市一次并返回出发城市的最短路径。
TSP 问题具有很高的研究价值,广泛应用于物流、交通运输、路径规划等领域。
1.2 遗传算法原理遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传机制的搜索算法。
它通过选择、交叉和变异操作生成新一代解,逐步优化问题的解。
遗传算法具有全局搜索能力强、适用于多种优化问题等优点。
二、实验设计与实现2.1 实验设计本实验使用遗传算法求解TSP问题,主要包括以下步骤:(1)初始化种群:随机生成一定数量的个体(路径),每个个体代表一条访问城市的路径。
(2)计算适应度:根据路径长度计算每个个体的适应度,适应度越高,路径越短。
(3)选择操作:根据适应度选择优秀的个体进入下一代。
(4)交叉操作:随机选择两个个体进行交叉,生成新的个体。
(5)变异操作:对交叉后的个体进行变异,增加解的多样性。
(6)更新种群:将新生成的个体替换掉上一代适应度较低的个体。
(7)迭代:重复步骤(2)至(6),直至满足终止条件。
2.2 实验实现本实验使用Python语言实现遗传算法求解TSP问题。
以下为实现过程中的关键代码:(1)初始化种群```pythondef initialize_population(city_num, population_size): population = []for _ in range(population_size):individual = list(range(city_num))random.shuffle(individual)population.append(individual)return population```(2)计算适应度```pythondef calculate_fitness(population, distance_matrix): fitness = []for individual in population:path_length =sum([distance_matrix[individual[i]][individual[i+1]] for i in range(len(individual) 1)])fitness.append(1 / path_length)return fitness```(3)选择操作```pythondef selection(population, fitness, population_size): selected_population = []fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]for _ in range(population_size):individual = random.choices(population, fitness_probability)[0]selected_population.append(individual)return selected_population```(4)交叉操作```pythondef crossover(parent1, parent2):index1 = random.randint(0, len(parent1) 2)index2 = random.randint(index1 + 1, len(parent1) 1)child1 = parent1[:index1] +parent2[index1:index2] + parent1[index2:]child2 = parent2[:index1] +parent1[index1:index2] + parent2[index2:]return child1, child2```(5)变异操作```pythondef mutation(individual, mutation_rate):for i in range(len(individual)):if random.random() < mutation_rate:j = random.randint(0, len(individual) 1) individual[i], individual[j] = individual[j], individual[i]return individual```(6)更新种群```pythondef update_population(parent_population, child_population, fitness):fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]new_population =random.choices(parent_population + child_population, fitness_probability, k=len(parent_population)) return new_population```(7)迭代```pythondef genetic_algorithm(city_num, population_size, crossover_rate, mutation_rate, max_iterations): distance_matrix =create_distance_matrix(city_num)population = initialize_population(city_num, population_size)for _ in range(max_iterations):fitness = calculate_fitness(population, distance_matrix)selected_population = selection(population, fitness, population_size)parent_population = []child_population = []for i in range(0, population_size, 2):parent1, parent2 = selected_population[i], selected_population[i+1]child1, child2 = crossover(parent1, parent2)child1 = mutation(child1, mutation_rate)child2 = mutation(child2, mutation_rate)parent_population.extend([parent1, parent2]) child_population.extend([child1, child2])population =update_population(parent_population, child_population, fitness)best_individual =population[fitness.index(max(fitness))]best_path_length =sum([distance_matrix[best_individual[i]][best_individual[i +1]] for i in range(len(best_individual) 1)])return best_individual, best_path_length```三、实验结果与分析3.1 实验结果本实验选取了10个城市进行测试,遗传算法参数设置如下:种群大小:50交叉率:0.8变异率:0.1最大迭代次数:100实验得到的最佳路径长度为:1953.53.2 实验分析(1)参数设置对算法性能的影响种群大小:种群大小会影响算法的搜索能力和收敛速度。
(完整word版)遗传算法求解TSP问题实验报告

人工智能实验报告实验六遗传算法实验II一、实验目的:熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
二、实验原理:旅行商问题,即TSP问题(Traveling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。
该问题可以被证明具有NPC计算复杂性。
因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。
它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。
后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程。
群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。
要求利用遗传算法求解TSP问题的最短路径。
三、实验内容:1、参考实验系统给出的遗传算法核心代码,用遗传算法求解TSP的优化问题,分析遗传算法求解不同规模TSP问题的算法性能。
2、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
3、增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
4、上交源代码。
四、实验报告要求:1、画出遗传算法求解TSP问题的流程图。
2、分析遗传算法求解不同规模的TSP问题的算法性能。
规模越大,算法的性能越差,所用时间越长。
3、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
TSP问题求解实验报告(word文档良心出品)

TSP问题求解(一)实验目的熟悉和掌握遗传算法的原理,流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
(二)实验原理巡回旅行商问题给定一组 n 个城市和俩俩之间的直达距离,寻找一条闭合的旅程,使得每个城市刚好经过一次且总的旅行距离最短。
TSP 问题也称为货郎担问题,是一个古老的问题。
最早可以追溯到 1759 年 Euler提出的骑士旅行的问题。
1948 年,由美国兰德公司推动, TSP成为近代组合优化领域的典型难题。
TSP 是一个具有广泛的应用背景和重要理论价值的组合优化问题。
近年来,有很多解决该问题的较为有效的算法不断被推出,例如 Hopfield 神经网络方法,模拟退火方法以及遗传算法方法等。
TSP搜索空间随着城市数n 的增加而增大 , 所有的旅程路线组合数为 (n-1)!/2。
在如此庞大的搜索空间中寻求最优解,对于常规方法和现有的计算工具而言,存在着诸多计算困难。
借助遗传算法的搜索能力解决TSP问题,是很自然的想法。
基本遗传算法可定义为一个8 元组:(SGA)=( C, E,P0, M,Φ,Г,Ψ ,Τ)C ——个体的编码方法,SGA 使用固定长度二进制符号串编码方法;E——个体的适应度评价函数;P0——初始群体;M ——群体大小,一般取20—100;Ф——选择算子,SGA使用比例算子;Г——交叉算子,SGA使用单点交叉算子;Ψ——变异算子,SGA使用基本位变异算子;Т——算法终止条件,一般终止进化代数为 100—500;问题的表示对于一个实际的待优化问题,首先需要将其表示为适合于遗传算法操作的形式。
用遗传算法解决 TSP,一个旅程很自然的表示为 n 个城市的排列,但基于二进制编码的交叉和变异操作不能适用。
路径表示是表示旅程对应的基因编码的最自然,最简单的表示方法。
它在编码,解码,存储过程中相对容易理解和实现。
例如:旅程( 5-1-7-8-9-4-6-2-3)可以直接表示为( 5 1 7 894623 )(三)实验内容N>=8。
基于遗传算法求解TSP问题

适应度函数
适应度函数用于评估每个染色体的优劣程 度,根据问题的不同,适应度函数需要进 行定制设计。
交叉操作
交叉操作将两个染色体的基因进行交换, 以产生新的个体。常见的交叉方法有单点 交叉、多点交叉等。
选择操作
选择操作根据适应度函数的评估结果,选 择优秀的个体进入下一代种群。常见的选 择方法有轮盘赌选择、锦标赛选择等。
通过选择操作,优秀的个体有更大的机会被选中并参与交叉和变异操作 。交叉操作将两个个体的染色体进行交换,以产生新的个体。变异操作 则对染色体的某些基因进行随机改变,以增加种群的多样性。
遗传算法构成要素
种群
种群是由一组染色体组成的集合,每个染 色体都是优化问题的潜在解。
变异操作
变异操作对染色体的某些基因进行随机改 变,以增加种群的多样性。常见的变异方 法有位点变异、倒位变异等。
04
基于遗传算法的TSP问题求解
TSP问题的遗传算法建模
编码方式
使用染色体编码方式,将TSP问题的解编码 为染色体。
适应度函数
使用距离作为适应度函数,评估染色体的优 劣。
解码方法
通过解码方式将编码后的染色体还原为TSP 问题的解。
遗传操作
包括选择、交叉和变异等操作,用于产生新 的染色体。
编码方式与解码方法
VS
实验环境
本次实验在Windows 10操作系统下进行 ,使用Python 3.8作为编程语言,并利用 NumPy和Matplotlib等库进行数据处理 和可视化。
实验结果展示
最优解
通过运行遗传算法程序,我们得到了最优解为207.9km,与TSPLIB中的最优解206.2km相TSP问题是一个NP-hard问题,它具有以下特征
(完整)用遗传算法求解TSP问题

用遗传算法求解TSP问题遗传算法(Genetic Algorithm——GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是由美国Michigan大学的J。
Holland教授于1975年首先提出的。
J.Holland 教授和它的研究小组围绕遗传算法进行研究的宗旨有两个:抽取和解释自然系统的自适应过程以及设计具有自然系统机理的人工系统。
遗传算法的大致过程是这样的:将每个可能的解看作是群体中的一个个体或染色体,并将每个个体编码成字符串的形式,根据预定的目标函数对每个个体进行评价,即给出一个适应度值。
开始时,总是随机的产生一些个体,根据这些个体的适应度,利用遗传算子-—选择(Selection)、交叉(Crossover)、变异(Mutation)对它们重新组合,得到一群新的个体.这一群新的个体由于继承了上一代的一些优良特性,明显优于上一代,以逐步向着更优解的方向进化.遗传算法主要的特点在于:简单、通用、鲁棒性强。
经过二十多年的发展,遗传算法已经在旅行商问题、生产调度、函数优化、机器学习等领域得到成功的应用。
遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法,与传统的优化算法相比,主要有以下特点:1、遗传算法以决策变量的编码作为运算对象.传统的优化算法往往直接决策变量的实际植本身,而遗传算法处理决策变量的某种编码形式,使得我们可以借鉴生物学中的染色体和基因的概念,可以模仿自然界生物的遗传和进化机理,也使得我们能够方便的应用遗传操作算子.2、遗传算法直接以适应度作为搜索信息,无需导数等其它辅助信息。
3、遗传算法使用多个点的搜索信息,具有隐含并行性。
4、遗传算法使用概率搜索技术,而非确定性规则。
遗传算法是基于生物学的,理解或编程都不太难。
下面是遗传算法的一般算法步骤:1、创建一个随机的初始状态初始种群是从解中随机选择出来的,将这些解比喻为染色体或基因,该种群被称为第一代,这和符号人工智能系统的情况不一样;在那里,问题的初始状态已经给定了。
TSP问题求解

TSP问题的遗传算法实验报告一、实验题目TSP问题的遗传算法实现二、实验目的1 熟悉和掌握遗传算法的基本概念和基本思想;2 加深对遗传算法的理解,理解和掌握遗传算法的各个操作算子;3 理解和掌握利用遗传算法进行问题求解的基本技能。
三、实验要求1 以10/个城市结点的TSP问题为例,用遗传算法加以求解;2 掌握遗传算法的基本原理、各个遗传操作和算法步骤;3能求出问题最优解,若得不出最优解,请分析原因;4要求界面显示每次迭代求出的局部最优解和最终求出的全局最优解。
四、实验代码Main函数%% 连续Hopfield神经网络的优化—旅行商问题优化计算% function main%% 清空环境变量、定义全局变量clear allclcglobal A D%% 导入城市位置load city_location%% 计算相互城市间距离distance=dist(citys,citys');%% 初始化网络N=size(citys,1);A=200;D=100;U0=0.1;step=0.0001;delta=2*rand(N,N)-1;U=U0*log(N-1)+delta;V=(1+tansig(U/U0))/2;iter_num=10000;E=zeros(1,iter_num);%% 寻优迭代for k=1:iter_num% 动态方程计算dU=diff_u(V,distance);% 输入神经元状态更新U=U+dU*step;% 输出神经元状态更新V=(1+tansig(U/U0))/2;% 能量函数计算e=energy(V,distance);E(k)=e;end%% 判断路径有效性[rows,cols]=size(V);V1=zeros(rows,cols);[V_max,V_ind]=max(V);for j=1:colsV1(V_ind(j),j)=1;endC=sum(V1,1);R=sum(V1,2);flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));%% 结果显示if flag==1% 计算初始路径长度sort_rand=randperm(N);citys_rand=citys(sort_rand,:);Length_init=dist(citys_rand(1,:),citys_rand(end,:)');for i=2:size(citys_rand,1)Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');end% 绘制初始路径figure(1)plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-') for i=1:length(citys)text(citys(i,1),citys(i,2),[' ' num2str(i)])endtext(citys_rand(1,1),citys_rand(1,2),[' 起点' ])text(citys_rand(end,1),citys_rand(end,2),[' 终点' ])title(['优化前路径(长度:' num2str(Length_init) ')'])axis([0 1 0 1])grid onxlabel('城市位置横坐标')ylabel('城市位置纵坐标')% 计算最优路径长度[V1_max,V1_ind]=max(V1);citys_end=citys(V1_ind,:);Length_end=dist(citys_end(1,:),citys_end(end,:)');for i=2:size(citys_end,1)Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');enddisp('最优路径矩阵');V1% 绘制最优路径figure(2)plot([citys_end(:,1);citys_end(1,1)],...[citys_end(:,2);citys_end(1,2)],'o-')for i=1:length(citys)text(citys(i,1),citys(i,2),[' ' num2str(i)])endtext(citys_end(1,1),citys_end(1,2),[' 起点' ])text(citys_end(end,1),citys_end(end,2),[' 终点' ])title(['优化后路径(长度:' num2str(Length_end) ')'])axis([0 1 0 1])grid onxlabel('城市位置横坐标')ylabel('城市位置纵坐标')% 绘制能量函数变化曲线figure(3)plot(1:iter_num,E);ylim([0 2000])title(['能量函数变化曲线(最优能量:' num2str(E(end)) ')']);xlabel('迭代次数');ylabel('能量函数');elsedisp('寻优路径无效');end% %=========================================== % function du=diff_u(V,d)% global A D% n=size(V,1);% sum_x=repmat(sum(V,2)-1,1,n);% sum_i=repmat(sum(V,1)-1,n,1);% V_temp=V(:,2:n);% V_temp=[V_temp V(:,1)];% sum_d=d*V_temp;% du=-A*sum_x-A*sum_i-D*sum_d;% %========================================== % function E=energy(V,d)% global A D% n=size(V,1);% sum_x=sumsqr(sum(V,2)-1);% sum_i=sumsqr(sum(V,1)-1);% V_temp=V(:,2:n);% V_temp=[V_temp V(:,1)];% sum_d=d*V_temp;% sum_d=sum(sum(V.*sum_d));% E=0.5*(A*sum_x+A*sum_i+D*sum_d);diff_u函数% % % % 计算dufunction du=diff_u(V,d)global A Dn=size(V,1);sum_x=repmat(sum(V,2)-1,1,n);sum_i=repmat(sum(V,1)-1,n,1);V_temp=V(:,2:n);V_temp=[V_temp V(:,1)];sum_d=d*V_temp;du=-A*sum_x-A*sum_i-D*sum_d;Energy函数% % % % % 计算能量函数function E=energy(V,d)global A Dn=size(V,1);sum_x=sumsqr(sum(V,2)-1);sum_i=sumsqr(sum(V,1)-1);V_temp=V(:,2:n);V_temp=[V_temp V(:,1)];sum_d=d*V_temp;sum_d=sum(sum(V.*sum_d));E=0.5*(A*sum_x+A*sum_i+D*sum_d);五、实验结果(图一、最优路径矩阵)(图二、优化前路线)(图三、优化后路线)(图三、能量函数)。
利用遗传算法解决TSP问题(DOC)

课程实验报告1.实验目的利用遗传算法获得TSP问题的近似解。
2.实验要求要求学生了解遗传算法解决问题的基本流程。
对TSP问题有所了解,知道TSP 问题的难点在什么地方,如何使用遗传算法来获得一个较好的近似解。
3.实验内容已知n个城市之间的相互距离,现有一个推销员必须遍访这n个城市,并且每个城市只能访问一次,最后又必须返回出发城市。
如何安排他对这些城市的访问次序,可使其旅行路线的总长度最短?用图论的术语来说,假设有一个图g=(v,e),其中v是顶点集,e是边集,设d=(dij)是由顶点i和顶点j之间的距离所组成的距离矩阵,旅行商问题就是求出一条通过所有顶点且每个顶点只通过一次的具有最短距离的回路。
4.实验软硬件环境基本Windows系统基本运行环境,VS20125.实验方案(1)遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法遗传算法的基本运算过程如下:a)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。
b)个体评价:计算群体P(t)中各个个体的适应度。
c)选择运算:将选择算子作用于群体。
选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
选择操作是建立在群体中个体的适应度评估基础上的。
d)交叉运算:将交叉算子作用于群体。
所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。
遗传算法中起核心作用的就是交叉算子。
e)变异运算:将变异算子作用于群体。
即是对群体中的个体串的某些基因座上的基因值作变动。
群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t 1)。
f)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
(2)用遗传算法模拟TSP问题TSP问题及旅行商问题,假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
人工智能实验三-TSP问题

【实验名称】人工智能实验三:遗传算法求解TSP问题遗传算法参数(SGA)=(C,E,P0,M,Φ,Г,Ψ,Τ)C ——个体的编码方法;E ——个体的适应度评价函数;P0——初始群体;M ——群体大小,一般取20—100;Ф——选择算子,SGA使用比例算子;Г——交叉算子,SGA使用单点交叉算子;Ψ——变异算子,SGA使用基本位变异算子;Т——算法终止条件,一般终止进化代数为100—500;实验代码:#include <cmath>#include <ctime>#include <vector>#include <map>#include <string>#include <iostream>#include <algorithm>using namespace std;float pcross = 0.80; //交叉率float pmutation = 0.1; //变异率int popsize = 300; //种群大小const int lchrom = 20; //染色体长度int gen; //当前世代int maxgen = 100; //最大世代数int run; //当前运行次数int maxruns =10; //总运行次数float max_var = 9 ; //路径最大连接开销//基因定义(一个城市)struct Gene{string name;map<Gene*,float> linkCost; //该城市到其它城市的路程开销};//染色体定义(到各城市顺序的一种组合)struct Chrom{vector<Gene*> chrom_gene; //染色体(到各城市去的顺序)float varible; //路程总开销float fitness; //个体适应度};//种群定义struct Pop{vector<Chrom> pop_chrom; //种群里的染色体组float sumfitness; //种群中个体适应度累计};Pop oldpop; //当前代种群Pop newpop; //新一代种群vector<Gene> genes(lchrom); //保存全部基因//产生一个随机整数(在low和high之间)inline int randomInt(int low,int high){if(low==high)return low;return low+rand()%(high-low+1);}//计算一条染色体的个体适应度inline void chromCost(Chrom& chr){float sum=0;for(int i=0;i<chr.chrom_gene.size()-1;i++){sum += (chr.chrom_gene[i])->linkCost[chr.chrom_gene[i+1]];}sum += (chr.chrom_gene.front())->linkCost[chr.chrom_gene.back()];chr.varible=sum;chr.fitness=max_var*(lchrom) - chr.varible;}//计算一个种群的个体适应度之和inline void popCost(Pop &pop){float sum=0;for(int i=0;i<pop.pop_chrom.size();i++){sum+=pop.pop_chrom[i].fitness;}pop.sumfitness = sum;}void outChrom(Chrom& chr);//随机初始化一条染色体inline void initChrom(Chrom& chr){vector<int> tmp(lchrom);for(int i=0;i<lchrom;i++)tmp[i]=i;int choose;while(tmp.size()>1){choose=randomInt(0,tmp.size()-1);chr.chrom_gene.push_back(&genes[tmp[choose]]);tmp.erase(tmp.begin()+choose);}chr.chrom_gene.push_back(&genes[tmp[0]]);chromCost(chr);}//随机初始化种群inline void initpop(Pop& pop){pop.pop_chrom.reserve(popsize);Chrom tmp;tmp.chrom_gene.reserve(lchrom);for(int i=0;i<popsize;i++){initChrom(tmp);pop.pop_chrom.push_back(tmp);tmp.chrom_gene.clear();}popCost(pop);}//轮盘赌选择,返回种群中被选择的个体编号inline int selectChrom(const Pop& pop){float sum = 0;float pick = float(randomInt(0,1000))/1000;int i = 0;if(pop.sumfitness!=0){while(1){sum += pop.pop_chrom[i].fitness/pop.sumfitness;i++;if( (sum > pick) || i==pop.pop_chrom.size()-1)return i-1; //??为什么返回29就会出错???}}elsereturn randomInt(0,pop.pop_chrom.size()-2);}//精英策略,返回最优秀的一条染色体inline int chooseBest(const Pop& pop){int choose = 0;float best = 0;for(int i = 0;i< pop.pop_chrom.size();i++){if(pop.pop_chrom[i].fitness > best){best = pop.pop_chrom[i].fitness;choose = i;}}return choose;}//染色体交叉操作,由两个父代产生两个子代(顺序交叉OX)inline void crossover(Chrom& parent1,Chrom& parent2,Chrom& child1,Chrom& child2){child1.chrom_gene.resize(lchrom);child2.chrom_gene.resize(lchrom);vector<Gene*>::iteratorv_iter,p1_beg,p2_beg,c1_beg,c2_beg,p1_end,p2_end,c1_end,c2_end;p1_beg = parent1.chrom_gene.begin();p2_beg = parent2.chrom_gene.begin();c1_beg = child1.chrom_gene.begin();c2_beg = child2.chrom_gene.begin();p1_end = parent1.chrom_gene.end();p2_end = parent2.chrom_gene.end();c1_end = child1.chrom_gene.end();c2_end = child2.chrom_gene.end();vector<Gene*> v1(parent2.chrom_gene), v2(parent1.chrom_gene); //用于交叉的临时表//随机选择两个交叉点int pick1 = randomInt(1,lchrom-3);int pick2 = randomInt(pick1+1,lchrom-2);int dist = lchrom-1-pick2; //第二交叉点到尾部的距离//子代保持两交叉点间的基因不变copy(p1_beg+pick1, p1_beg+pick2+1, c1_beg+pick1);copy(p2_beg+pick1, p2_beg+pick2+1, c2_beg+pick1);//循环移动表中元素rotate(v1.begin(), v1.begin()+pick2+1,v1.end());rotate(v2.begin(), v2.begin()+pick2+1,v2.end());//从表中除去父代已有的元素for(v_iter = p1_beg+pick1; v_iter!=p1_beg+pick2+1; ++v_iter) remove(v1.begin(),v1.end(),*v_iter);for(v_iter = p2_beg+pick1; v_iter!=p2_beg+pick2+1; ++v_iter) remove(v2.begin(),v2.end(),*v_iter);//把表中元素复制到子代中copy(v1.begin(), v1.begin()+dist, c1_beg+pick2+1);copy(v1.begin()+dist, v1.begin()+dist+pick1, c1_beg);copy(v2.begin(), v2.begin()+dist, c2_beg+pick2+1);copy(v2.begin()+dist, v2.begin()+dist+pick1, c2_beg);}//染色体变异操作,随机交换两个基因inline void mutation(Chrom& chr){vector<Gene*>::iterator beg = chr.chrom_gene.begin();int pick1,pick2;pick1 = randomInt(0,lchrom-1);do{pick2 =randomInt(0,lchrom-1);}while(pick1==pick2);iter_swap(beg+pick1, beg+pick2);}//世代进化(由当前种群产生新种群)void generation(Pop& oldpop,Pop& newpop){newpop.pop_chrom.resize(popsize);int mate1,mate2,j;float pick;float tmp;Chrom gene1,gene2,tmp1,tmp2;gene1.chrom_gene.resize(lchrom);gene2.chrom_gene.resize(lchrom);tmp1.chrom_gene.resize(lchrom);tmp2.chrom_gene.resize(lchrom);//将最佳染色体放入下一代mate1 = chooseBest(oldpop);newpop.pop_chrom[0] = oldpop.pop_chrom[mate1];j = 1;//产生两条新染色体do{int count = 0;mate1 = selectChrom(oldpop);mate2 = selectChrom(oldpop);pick = float(randomInt(0,1000))/1000;gene1= oldpop.pop_chrom[mate1];gene2= oldpop.pop_chrom[mate1];if(pick < pcross) //交叉操作{int count = 0;bool flag1 = false;bool flag2 = false;while(1){crossover(oldpop.pop_chrom[mate1],oldpop.pop_chrom[mate2],tmp1,tmp2) ;chromCost(tmp1); //计算适应度chromCost(tmp2);if(tmp1.fitness > gene1.fitness){gene1 = tmp1;flag1 = true;}if(tmp2.fitness > gene2.fitness){gene2 = tmp2;flag2 = true;}if((flag1==true && flag2==true) || count> 50){newpop.pop_chrom[j] = gene1;newpop.pop_chrom[j+1] = gene2;break;}count++;}}else{newpop.pop_chrom[j].chrom_gene = oldpop.pop_chrom[mate1].chrom_gene;newpop.pop_chrom[j+1].chrom_gene = oldpop.pop_chrom[mate2].chrom_gene;chromCost(newpop.pop_chrom[j]);chromCost(newpop.pop_chrom[j+1]);}pick = float(randomInt(0,1000))/1000;if(pick < pmutation) //变异操作{int count = 0;do{tmp = newpop.pop_chrom[j].fitness;mutation(newpop.pop_chrom[j]);chromCost(newpop.pop_chrom[j]); //计算适应度count++;}while(tmp > newpop.pop_chrom[j].fitness && count < 50);}pick = float(randomInt(0,1000))/1000;if(pick < pmutation) //变异操作{int count = 0;do{tmp = newpop.pop_chrom[j+1].fitness;mutation(newpop.pop_chrom[j+1]);chromCost(newpop.pop_chrom[j+1]); //计算适应度count++;}while(tmp > newpop.pop_chrom[j+1].fitness && count < 50);}//chromCost(newpop.pop_chrom[j]); //计算适应度//chromCost(newpop.pop_chrom[j+1]);j += 2;}while(j < popsize-1);popCost(newpop); //计算新种群的适应度之和}//输出一条染色体信息inline void outChrom(Chrom& chr){cout<<endl<<"路径:";for(int i=0;i<lchrom;i++){cout<<chr.chrom_gene[i]->name;}cout<<endl<<"回路总开销:"<<chr.varible<<endl;cout<<"适应度:"<<chr.fitness<<endl;}int main(){cout<<"*************用遗传算法解决TSP问题******************"<<endl;cout<<"*************** E01114336 朱蓉蓉******************"<<endl;stringnames[lchrom]={"A","B","C","D","E","F","G","H","I","J","K","L","M","N", "O","P","Q","R","S","T"};//基因(城市)名称//用矩阵保存各城市间的路程开销float dist[lchrom][lchrom] ={{0, 1, 4, 6, 8, 1, 3, 7, 2, 9, 7, 3, 4, 5, 8, 9, 2, 8, 2, 8},{1, 0, 7, 5, 3, 8, 3, 4, 2, 4, 4, 6, 2, 8, 2, 9, 4, 5, 2, 1},{4, 7, 0, 3, 8, 3, 7, 9, 1, 2, 5, 8, 1, 8, 9, 4, 7, 4, 8, 4},{6, 5, 3, 0, 3, 1, 5, 2, 9, 1, 3, 5, 7, 3, 4, 7, 3, 4, 5, 2},{8, 3, 8, 3, 0, 2, 3, 1, 4, 6, 3, 8, 4, 5, 2, 8, 1, 7, 4, 7},{1, 8, 3, 1, 2, 0, 3, 3, 9, 5, 4, 5, 2, 7, 3, 6, 2, 3, 7, 1},{3, 3, 7, 5, 3, 3, 0, 7, 5, 9, 3, 4, 5, 9, 3, 7, 3, 2, 8, 1},{7, 4, 9, 2, 1, 3, 7, 0, 1, 3, 4, 5, 2, 7, 6, 3, 3, 8, 3, 5},{2, 2, 1, 9, 4, 9, 5, 1, 0, 1, 3, 4, 7, 3, 7, 5, 9, 2, 1, 7},{9, 4, 2, 1, 6, 5, 9, 3, 1, 0, 3, 7, 3, 7, 4, 9, 3, 5, 2, 5},{7, 4, 5, 3, 3, 4, 3, 4, 3, 3, 0, 5, 7, 8, 4, 3, 1, 5, 9, 3},{3, 6, 8, 5, 8, 5, 4, 5, 4, 7, 5, 0, 8, 3, 1, 5, 8, 5, 8, 3},{4, 2, 1, 7, 4, 2, 5, 2, 7, 3, 7, 8, 0, 5, 7, 4, 8, 3, 5, 3},{5, 8, 8, 3, 5, 7, 9, 7, 3, 7, 8, 3, 5, 0, 8, 3, 1, 8, 4, 5},{8, 2, 9, 4, 2, 3, 3, 6, 7, 4, 4, 1, 7, 8, 0, 4, 2, 1, 8, 4},{9, 9, 4, 7, 8, 6, 7, 3, 5, 9, 3, 5, 4, 3, 4, 0, 4, 1, 8, 4},{2, 4, 7, 3, 1, 2, 3, 3, 9, 3, 1, 8, 8, 1, 2, 4, 0, 4, 3, 7},{8, 5, 4, 4, 7, 3, 2, 8, 2, 5, 5, 5, 3, 8, 1, 1, 4, 0, 2, 6},{2, 2, 8, 5, 4, 7, 8,3, 1, 2, 9, 8, 5, 4, 8, 8, 3, 2, 0, 4},{8, 1, 4, 2, 7, 1, 1, 5, 7, 5, 3, 3, 3, 5, 4, 4, 7, 6, 4, 0}};//初始化基因(所有基因都保存在genes中)int i,j;for(i=0;i<lchrom;i++){genes[i].name =names[i];for(j=0;j<lchrom;j++){genes[i].linkCost[&genes[j]] = dist[i][j];}}//输出配置信息cout<<"\n染色体长度:"<<lchrom<<"\n种群大小:"<<popsize<<"\n交叉率:"<<pcross<<"\n变异率:"<<pmutation;cout<<"\n最大世代数:"<<maxgen<<"\n总运行次数:"<<maxruns<<"\n路径最大连接开销:"<<max_var<<endl;//输出路径信息cout<<endl<<" ";for(i=0;i<lchrom;i++)cout<<genes[i].name<<" ";cout<<endl;for(i=0;i<lchrom;i++){cout<<genes[i].name<<":";for(j=0;j<lchrom;j++){cout<<genes[i].linkCost[&genes[j]]<<" ";}cout<<endl;}cout<<endl;int best;Chrom bestChrom; //全部种群中最佳染色体bestChrom.fitness = 0;float sumVarible = 0;float sumFitness = 0;//运行maxrns次for(run = 1;run<=maxruns;run++){initpop(oldpop); //产生初始种群//通过不断进化,直到达到最大世代数for(gen = 1;gen<=maxgen;gen++){generation(oldpop,newpop); //从当前种群产生新种群oldpop.pop_chrom.swap(newpop.pop_chrom);oldpop.sumfitness = newpop.sumfitness;newpop.pop_chrom.clear();}best = chooseBest(oldpop); //本次运行得出的最佳染色体if(oldpop.pop_chrom[best].fitness > bestChrom.fitness)bestChrom = oldpop.pop_chrom[best];sumVarible += oldpop.pop_chrom[best].varible;sumFitness += oldpop.pop_chrom[best].fitness;cout<<run<<"次"<<"Best:";outChrom(oldpop.pop_chrom[best]); //输出本次运行得出的最佳染色体cout<<endl;oldpop.pop_chrom.clear();}cout<<endl<<"一条最佳染色体:";outChrom(bestChrom); //输出全部种群中最佳染色体cout<<endl<<endl<<"最佳染色体平均开销:"<<sumVarible/maxruns;cout<<endl<<"最佳染色体平均适应度:"<<sumFitness/maxruns<<endl;system("PAUSE");return 0;}实验结果截图:。
tsp问题求解

计算机科学与工程学院
《进化计算》实验报告[2]
专业班级
智能二班
实验时间
学生学号
1205030219
实验地点
J523
学生姓名
谭龙顺
指导教师
赵彤洲
实验项目
用遗传算法解决TSP问题
实验类别
验证性
实验学时
4
实验目的及要求
实验目的:
1、掌握遗传算法的基本思想;
2、使用遗传算法解决实际问题的方法;
实验要求:
具体要求:
城市数=30;
最大迭代次数=500;
交叉概率=80%;
变异概率=5%;
编写代码并写出运算结果
熟练掌握:用VC开发程序的步骤
正确理解:遗传算法的基本思想
使用遗传算法解决TSP问题
成绩评定表
类别
评分标准
分值
得分
合计
上机表现
按时出勤、遵守纪律
认真完成各项实验内容
30分
报告质量
程序代码规范、功能正确
填写内容完整、体现收获
70分
说明:
评阅教师:
日期:2015年月日
实验内容
用遗传算法解决TSP问题。给定测试数据,并对测试结果进行分析。
遗传算法求解TSP问题报告

遗传算法求解TSP问题实验报告一、实验要求:以旅行商问题(TSP)为例做模拟进化搜索技术实验,并提交实验研究报告。
二、实验思路:bool fnCreateRandomGene(); //产生随机基因bool fnGeneAberrance(); //基因变异bool fnGeneMix(); //基因交叉产生新的个体测试并淘汰适应度低的个体bool fnEvalAll(); //测试所有基因的适应度int fnEvalOne(T &Gene); //测试某一个基因的适应度void Crossover( int nFatherA, int nFatherB);void fnDispProbability(); //显示每个个体的权值Crossover()——两染色体的交叉实现输入参数:1、nFatherA 父染色体A2、nFatherB 父染色体B3、nMode 交叉方式返回值:空注:现有交叉方式1、常规交叉方式,该方式比《现代计算方法》(邢文训等编著)p178给出的“非常规码的常规交配法”稍复杂些。
书中只随机选择一个交配位,两个后代交配位之前的基因分别继承双亲的交配位之前的基因。
本程序中,是随机选择两个不相同的交配位,后代在这两个交配位之间继承双亲在这两个交配位之间的基因如父A 1 2 3 | 4 5 6 7 | 8 9 10父B 4 7 8 | 3 2 5 9 | 1 6 10子A 8 3 2 | 4 5 6 7 | 9 1 10子B 1 4 6 | 3 2 5 9 | 7 8 102、贪心交叉方式(Greedy Crossover),具体算法可参见谢胜利,等.求解TSP问题的一种改进的遗传算法[J].计算机工程与应用,2002(8):58~245.三、实验代码:#include <fstream>#include<iostream>#include <vector>#include <algorithm>#include<math.h>#include <time.h>#include <stdlib.h>#include "def.h"#include "TSP.h"void main(){ifstream input_file;ofstream output_file;time_t time1,time2;int _GENERATION_AMOUNT;int times;int _CITY_AMOUNT=-1;int ii,j,k;std::vector<double> x;std::vector<double> y;char readfile[50];const char* writefile="tsp.txt";double tempx[10000],tempy[10000];cout<<"打开城市坐标文件:";cin>>readfile;input_file.open(readfile);if(!input_file){cout<<"打开错误!";return;}cout<<"读入城市坐标........"<<endl;while(1){if(!input_file.eof()){_CITY_AMOUNT++;input_file>>tempx[_CITY_AMOUNT]>>tempy[_CITY_AMOUNT];if(tempx[_CITY_AMOUNT]<0||tempy[_CITY_AMOUNT]<0){cout<<"文件格式有误!";return;}}elsebreak;}if( _CITY_AMOUNT==-1){cout<<"文件格式有误!";return;}input_file.close();_CITY_AMOUNT=_CITY_AMOUNT+1;x.reserve(_CITY_AMOUNT);y.reserve(_CITY_AMOUNT);lpCityDistance.reserve(_CITY_AMOUNT*_CITY_AMOUNT);for(k=0;k<_CITY_AMOUNT;k++){x[k]=tempx[k];y[k]=tempy[k];}cout<<"已存入的城市信息为:"<<endl;for(ii=0;ii<_CITY_AMOUNT;ii++)cout<<"第"<<ii+1<<"个城市"<<"("<<x[ii]<<","<<y[ii]<<")"<<endl;lpCityDistance.clear();for(k=0;k<_CITY_AMOUNT;k++){lpCityDistance[k*_CITY_AMOUNT+k]=0;for(j=k+1;j<_CITY_AMOUNT;j++){lpCityDistance[k*_CITY_AMOUNT+j]=lpCityDistance[j*_CITY_AMOUNT+k] =sqrt((x[k]-x[j])*(x[k]-x[j])+(y[k]-y[j])*(y[k]-y[j]));}}cout<<"输入进化代数:"<<endl;cin>>times;cout<<"输入种群大小:(大于城市个数小于10000)"<<endl;cin>> _GENERATION_AMOUNT;while(_GENERATION_AMOUNT>=10000||_GENERATION_AMOUNT<_CITY_AMOUNT){cout<<"种群数输入错误!请重新输入(大于城市个数小于10000)"<<endl;cin>> _GENERATION_AMOUNT;}Csga<_CONTAINER, _CONTAINER_P> CUnit(times,_GENERATION_AMOUNT,_CITY_AMOUNT); //初始化time1=time(NULL);//开始遗传算法if(!CUnit.fnCreateRandomGene()) //产生随机基因//产生随机的基因{exit(0);}//循环基因编译,杂交,淘汰过程CUnit.fnEvalAll(); //测试所有基因的适应度for ( int i = 0; i<times; ++i ){//CUnit.fnDispProbability();//显示每个个体的权值CUnit.fnGeneAberrance(); //基因变异//基因变异//CUnit.fnDispProbability();//显示每个个体的权值CUnit.fnGeneMix();//交叉产生新的个体测试并淘汰适应度低的个体//基因杂交CUnit.fnEvalAll(); //测试所有基因的适应度// 每隔_DISP_INTERV AL显示一次结果if ( (i+1)%_DISP_INTERV AL == 0 || i == 0){cout << "第" << i+1 << "代" <<endl;CUnit.fnDispProbability();CUnit.fnDispHistoryMin();}}CUnit.fnDispHistoryMin();time2=time(NULL);cout<<"\n\n计算用时为:"<<difftime(time2,time1)<<"s"<<endl;}四、实验结果:。
TSP的遗传算法程序实验报告
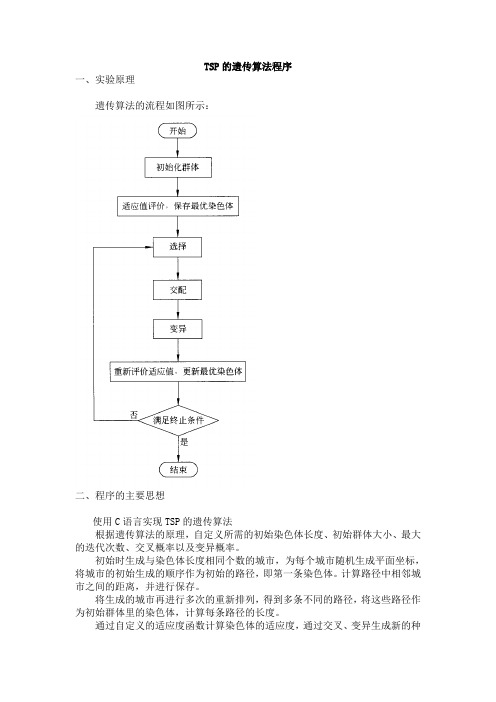
TSP的遗传算法程序一、实验原理遗传算法的流程如图所示:二、程序的主要思想使用C语言实现TSP的遗传算法根据遗传算法的原理,自定义所需的初始染色体长度、初始群体大小、最大的迭代次数、交叉概率以及变异概率。
初始时生成与染色体长度相同个数的城市,为每个城市随机生成平面坐标,将城市的初始生成的顺序作为初始的路径,即第一条染色体。
计算路径中相邻城市之间的距离,并进行保存。
将生成的城市再进行多次的重新排列,得到多条不同的路径,将这些路径作为初始群体里的染色体,计算每条路径的长度。
通过自定义的适应度函数计算染色体的适应度,通过交叉、变异生成新的种群。
对新种群继续迭代操作,直到达到初始定义的迭代次数,获得最终的路径及路径图。
三、程序的主要步骤①染色体初始化的子函数1)void initialize()2){int k,j,minx,miny,maxx,maxy;3)initdata();4)minx=0;5)miny=0;6)maxx=0;maxy=0;7)for(k=0;k<lchrom;k++)8){x[k]=rand();9)if(x[k]>maxx)maxx=x[k];10)if(x[k]<minx)minx=x[k];11)y[k]=rand();12)if(y[k]>maxy)maxy=y[k];13)if(y[k]<miny)miny=y[k];14)}15)if((maxx-minx)>(maxy-miny))16){maxxy=maxx-minx;}17)else {maxxy=maxy-miny;}18)maxdd=0.0;19)for(k=0;k<lchrom;k++)20)for(j=0;j<lchrom;j++)21){dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]);22)if(maxdd<dd[k*lchrom+j])maxdd=dd[k*lchrom+j];23)}24)refpd=dd[lchrom-1];25)for(k=0;k<lchrom;k++)26)refpd=refpd+dd[k*lchrom+k+2];27)for(j=0;j<lchrom;j++)28)dd[j*lchrom+j]=4.0*maxdd;29)ff=(0.765*maxxy*pow(lchrom,0.5));30)minpp=0;31)min=dd[lchrom-1];32)for(j=0;j<lchrom-1;j++)33){if(dd[lchrom*j+lchrom-1]<min)34){min=dd[lchrom*j+lchrom-1];35)minpp=j;36)}37)}38)initpop();39)statistics(oldpop);40)initreport();41)}7) for(k=0;k<lchrom;k++)8) {x[k]=rand();9) if(x[k]>maxx)maxx=x[k];10)if(x[k]<minx)minx=x[k];11)y[k]=rand();12)if(y[k]>maxy)maxy=y[k]13)if(y[k]<miny)miny=y[k];14)}此段程序是初始化多个城市的坐标值(x,y),其中(x[k],y[k])代表第k+1个城市的坐标值,也相当于初始染色体的第k+1个基因值。
用遗传算法解决TSP问题

用遗传算法解决TSP问题设计思路:1.初始化城市距离采用以城市编号(i,j=1代表北京,=2代表上海,=3代表天津,=4代表重庆,=5代表乌鲁木齐)为矩阵行列标的方法,输入任意两个城市之间的距离,用矩阵city表示,矩阵中的元素city(i,j)代表第i个城市与第j个城市间的距离。
2.初始化种群通过randperm函数,生成一个一维随机向量(是整数1,2,3,4,5的任意排列),然后将其赋给二维数组group的第一列,作为一个个体。
如此循环N次(本例生成了50个个体),生成了第一代种群,种群的每个个体代表一条路径。
3.计算适应度采用的适应度函数为个体巡回路径的总长度的函数。
具体为adapt(1,i)=(5*maxdis-dis) (1) 在式(1)中,adapt(1,i)表示第i个个体的适应度函数,maxdis为城市间的最大距离,为4077km,dis为个体巡回路径的总长度,这样定义的适应度,当路经越短时适应度值越大。
在适应度值的基础上,给出的计算个体期望复制数的表达式为adaptnum(1,i)=(N* adapt(1,i)/ sumadapt) (2) 其中,sumadapt为种群适应度之和。
4.复制采用优秀个体的大比例保护基础上的随机数复制法。
具体做法为在生成下一代个体时,先将最大适应度对应的路径个体以较大的比例复制到下一代,然后再用随机数复制法生成下一代的其他个体。
其中,有一个问题必须考虑,即若某一次生成的随机数过大,结果能复制一个或极少个样本。
为了避免这一情况,采用了限制措施,即压低了随机数的上限。
5.交叉采用的方法为按步长的单点交叉,为随机选择一对样本,再随机选择一个交叉点位置,按一定的步长进行交叉点的选择。
选择一个步长而不是将其设为1,是因为若某一位置处的城市代码因为进行了交叉而发生了改变,则其经过该处的两个距离都会改变。
这种交叉兼有遗传和变异两方面的作用,因为若交叉点处的城市编号都相同,则对两个个体而言交叉后样本无变化,否则样本有变化。
TSP问题遗传算法求解实验报告

一、旅行商问题所谓旅行商问题(Travelling Salesman Problem , TSP),即最短路径问题,就是在给定的起始点S到终止点T的通路集合中,寻求距离最小的通路,这样的通路成为S点到T点的最短路径。
在寻找最短路径问题上,有时不仅要知道两个指定顶点间的最短路径,还需要知道某个顶点到其他任意顶点间的最短路径。
遗传算法方法的本质是处理复杂问题的一种鲁棒性强的启发性随机搜索算法,用遗传算法解决这类问题,没有太多的约束条件和有关解的限制,因而可以很快地求出任意两点间的最短路径以及一批次短路径。
假设平面上有n个点代表n个城市的位置, 寻找一条最短的闭合路径, 使得可以遍历每一个城市恰好一次。
这就是旅行商问题。
旅行商的路线可以看作是对n个城市所设计的一个环形, 或者是对一列n个城市的排列。
由于对n个城市所有可能的遍历数目可达(n- 1)!个, 因此解决这个问题需要0(n!)的计算时间。
假设每个城市和其他任一城市之间都以欧氏距离直接相连。
也就是说, 城市间距可以满足三角不等式, 也就意味着任何两座城市之间的直接距离都小于两城市之间的间接距离。
二、遗传算法1 遗传算法介绍遗传算法是由美国J.Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的,它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
通过模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标从解群中选取较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行组合,产生新一代的候选解群,重复此过程,直到满足某种收敛指标为止。
遗传算法在本质上是一种不依赖具体问题的直接搜索方法,是一种求解问题的高效并行全局搜索方法。
其假设常描述为二进制位串,位串的含义依赖于具体应用。
搜索合适的假设从若干初始假设的群体集合开始。
当前种群成员通过模仿生物进化的方式来产生下一代群体,如随机变异和交叉。
2023年基于遗传算法求解TSP问题实验报告

基于遗传算法求解TSP问题班级, 学号, 姓名摘要: 巡回旅行商问题(TSP)是一种组合优化方面旳问题, 从理论上讲, 使用穷举法不仅可以求解TSP问题, 并且还可以得到最优解。
不过, 运用穷举法所花费旳时间巨大旳, 当问题旳规模很大时, 穷举法旳执行效率较低, 不能满足及时旳需要。
遗传算法是计算机科学人工智能领域中用于处理最优化旳一种搜索启发式算法, 是进化算法旳一种。
该算法通过模拟生物学交叉、变异等方式, 是目前向最优解旳方向进化, 因此使用于TSP问题旳求解。
关键词: 人工智能;TSP问题;遗传算法本组组员: 林志青, 韩会雯, 赵昊罡本人分工:掌握遗传算法旳基本原理, 编写遗传算法中部分匹配交叉、循环交叉和循序交叉旳详细实现过程。
1 引言旅行商问题, 即TSP问题, 是一种最优解旳求解问题。
假设有n个都市, 并且每个都市之间旳距离已知, 则怎样只走一遍并获得最短途径为该问题旳详细解释。
对于TSP问题旳处理, 有穷举法、分支限界法等求解方式, 该文章重要简介遗传算法求解过程。
遗传算法简称GA, 在本质上是一种求解问题旳高效并行全局搜索措施。
遗传算法从任意一种初始化旳群体出发, 通过随机选择、交叉和变异等遗传操作, 使群体一代一代旳进化到搜索空间中越来越好旳区域, 直至抵达最优解。
在遗传算法中, 交叉操作为重要操作之一, 包括部分匹配交叉、循环交叉和次序交叉等。
2 算法原理与系统设计执行遗传算法, 根据需要设定对应旳交叉因子、变异因子和迭代次数, 并选择对应旳交叉算法,当程序图形显示并运算时会得到目前旳最优解, 判断与否获得最终旳最优解, 若已得到所需成果, 则停止运行, 否则继续执行。
详细流程图如下所示:部分匹配交叉(PMX): 先随机生成两个交叉点, 定义这两点间旳区域为匹配区域, 并互换两个父代旳匹配区域。
如下图所示:父代A: 872 | 130 | 9546父代B: 983 | 567 | 1420互换后变为:temp A: 872 | 567 | 9546temp B: 983 | 130 | 1420对于 temp A.tempB中匹配区域以外出现旳数码反复, 要根据匹配区域内旳位置逐一进行替代。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人工智能实验报告
实验六遗传算法实验II
一、实验目的:
熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP
问题的流程并测试主要参数对结果的影响。
二、实验原理:
旅行商问题,即TSP问题(Traveling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。
该问题可以被证明具有NPC计算复杂性。
因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。
它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。
这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。
后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程。
群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。
要求利用遗传算法求解TSP问题的最短路径。
三、实验内容:
1、参考实验系统给出的遗传算法核心代码,用遗传算法求解TSP的优化问题,分析遗传算法求解不同规模TSP问题的算法性能。
2、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
3、增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
4、上交源代码。
四、实验报告要求:
1、画出遗传算法求解TSP问题的流程图。
开始初始化种群(随机产生城市坐标确定种群规模、迭代次数、个体选择式、交叉概率、变异概率计算染
色体适应度值(城市间的欧氏距离按某个选择概率选择个YE个体交个体变P迭代总次N输入适应度最高的结
2、分析遗传算法求解不同规模的TSP问题的算法性能。
规模越大,算法的性能越差,所用时间越长。
3、对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
(1)种群规模对算法结果的影响
x01.13.537844.592
2
2
4
4
9
5.1
y
4.5
1.1
8
3
实验次数:10
最大迭代步数:100
交叉概率:0.85
变异概率:0.15
种群规平均适应度最优路
1025.2644-5-8-7-6-3-1-0-9-2
2026.34282-9-1-0-3-6-7-5-8-4
3025.16521-3-6-7-5-8-4-2-9-0
50 25.1652 0-1-3-6-7-5-8-4-2-9
80 25.1652 9-0-1-3-6-7-5-8-4-2
100 25.1652 1-0-9-2-4-8-5-7-6-3
150 25.1652 5-8-4-2-9-0-1-3-6-7
200 25.1652 1-3-6-7-5-8-4-2-9-0
250 25.1652 3-1-0-9-2-4-8-5-7-6
300 25.1652 5-8-4-2-9-0-1-3-6-7
如表所示,显然最短路径为25.1652m,最优路径为1-0-9-1-3-6-7-5-8-4-2或
3-1-0-9-2-4-8-5-7-6,注意到这是一圈,顺时针或者逆时针都可以。
当种群规模为10,20时,并没有找到最优解。
因此并不是种群规模越小越好。
(2)交叉概率对算法结果的影响
x 9 1.1 3.5 3.5 7 8 4 4.5 3 2
1
3
1
9
8.5
y
1.1
3
1
4
5.1
实验次数:15
种群规模:25
最大迭代步数:100
变异概率:0.15
实验结果:
(注:红色表示非最优解)
在该情况下,交叉概率过低将使搜索陷入迟钝状态,得不到最优解。
(3)变异概率对算法结果的影响
x 9 1.1 3.5 3.5 7 8 4 4.5 3 2
1
1
1
4
5.1
9
3
y
1.1
8.5
3
实验次数:10
种群规模:25
最大迭代步数:100
交叉概率:0.85
实验结果:
变异概率最好适应度最差适应度平均适应度最优解
0-6-2-1-9-3-8-7-4-5 29.4717 32.4911 34.732 0.001
8-4-5-0-2-6-9-1-3-7 34.6591 32.3714 29.0446 0.01
5-0-2-6-9-1-3-8-7-4 30.9417 0.1 28.0934 34.011
6-0-5-4-7-8-3-1-9-2 27.0935 0.15 30.2568 32.093
8-7-4-5-0-6-2-9-1-3
30.3144
32.2349 27.0935
0.2
从该表可知,当变异概率过大或过低都将导致无法得到最优解。
4、增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
不同变异策略和不同个体选择分配策略几乎不影响算法运行的时间,但会影响适应度。
五、实验心得与体会
通过本实验,更加深入体会了参数设置对算法结果的影响。
同一个算法,参数值不同,获得的结果可能会完全不同。
同时通过本次实验,使自己对遗传算法有了更进一步的了解。
遗传算法是一种智能优化算法,它能较好的近似求解TSP问题,在问题规模比较大的时候,遗传算法的优势就明显体现出来,当然不能完全保证能得到最优解。
