信源熵值计算实验报告
信息论上机实验报告

信息论与编码实验报告实验一:计算离散信源的熵一、实验设备: 1、计算机2、软件:Matlab 二、实验目的:1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程; 三、习题:1. 甲地天气预报构成的信源空间为:1111(),,,8482X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦ 小雨云 大雨晴 乙地信源空间为:17(),88Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦小雨晴 求此两个信源的熵。
求各种天气的自信息量。
代码:x=[1/2,1/4,1/8,1/8]; y=[7/8,1/8];HX=sum(-x.*log2(x)) HY=sum(-y.*log2(y)) IX=-log2(x) IY=-log2(y) 答案:() 1.75;()0.5436H X H Y ==2、 某信息源的符号集由A 、B 、C 、D 、E 组成,设每一符号独立出现,其出现的概率分别为,1/4,1/8,1/8,3/16,5/16,试求该信源符号的平均信息量。
代码:x=[1/4,1/8,1/8,3/16,5/16]; HX=sum(-x.*log2(x))答案:H(X) = 2.2272bit/符号3、设有四个消息分别以概率1/4,1/8,1/8,1/2传送,每一消息的出现是相互独立的。
试计算其平均信息量。
代码:x=[1/4,1/8,1/8,1/2]; HX=sum(-x.*log2(x)) 答案:H(X) =1.75bit/符号4. 设一个二元信源(只有0和1两种符号)其概率空间为:(),1X p x p p ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦0 1编程画出H 与p 的关系,并说明当P 呈什么分布时,平均信息量达到最大值。
(说明:H=-p.*log2(p)-(1-p).log2(1-p);) 代码:p= 1/1000000:1/1000:1;H=-p.*log2(p)-(1-p).*log2(1-p); plot(p,H) grid on xlabel('p'); ylabel('HP'); 图:实验二:验证熵的可加性与强可加性1. 【例2.6】有一离散无记忆信源123111(),,244a a a X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦验证二次扩展信源2X 的熵等于离散信源X 的熵的2倍,即2()2()H X H X =代码:x=[1/2,1/4,1/4];hx=sum(x.*log2(1./x))x2=[1/4,1/16,1/16,1/8,1/8,1/8,1/16,1/8,1/16] hx2=sum(x2.*log2(1./x2)) 答案:2() 1.5;() 3.0H X H X ==2. 验证两个统计独立的信源,X Y ,验证:()()()H XY H X H Y =+其中:123111(),,244a a a X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦123111(),,333b b b Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦代码:x=[1/2,1/4,1/4]; y=[1/3,1/3,1/3];xy=[1/6,1/6,1/6,1/12,1/12,1/12,1/12,1/12,1/12] hx=sum(x.*log2(1./x)) hy=sum(y.*log2(1./y)) Hxy=sum(xy.*log2(1./xy)) 答案:() 1.5,() 1.585() 3.085H X H Y H XY ===3、条件熵的计算与熵的强可加性 验证离散二维平稳信源,满足:12121()()(|)H X X H X H X X =+某一离散二维平稳信源0121141(),,3694X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦12X X 其联合概率分布12()p X X 为:编程计算:1) 联合熵12()H X X 2) 条件熵21(|)H X X3) 验证:12121()()(|)H X X H X H X X =+代码:x1=[11/36,4/9,1/4]; x2=[11/36,4/9,1/4];b=[1/4,1/18,0;1/18,1/3,1/18;0,1/18,7/36]; HXY=0;for i=1:size(b,1) for j=1:size(b,2) if b(i,j)>0HXY=HXY-b(i,j).*log2(b(i,j)); end end end HXYHx1=sum(x1.*log2(1./x1)) Hx2=sum(x2.*log2(1./x2))b0=b(1,:); b1=b(2,:); b2=b(3,:);x1x2=[b0./x2;b1./x2;b2./x2]; Hx1x2=0;for i=1:size(x1x2,1) for j=1:size(x1x2,2) if x1x2(i,j)>0Hx1x2=Hx1x2-b(i,j).*log2(x1x2(i,j)); end end end Hx1x2 答案:12112121() 1.5426;(|)0.8717() 2.4144()(|) 2.4144H X H X X H X X H X H X X ===+=实验三:离散信道的平均互信息的计算1. 【习题3.1】 设信源12()0.6,0.4X x x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦通过一干扰信道,接收到符号为12[,]Y y y =,其信道矩阵为:516631,44P ⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1) 求信源X 中事件1x 和2x 分别含有的自信息;2) 收到消息(1,2)j y j =后,获得的关于(1,2)i x i =的信息量;3) 求信源X 和输出变量Y 的信息熵; 4) 信道疑义度(|)H X Y 和噪声熵(|)H Y X ; 5) 接收到消息Y 后获得的平均互信息;代码:x=[0.6,0.4];p=[5/6,1/6;3/4,1/4]; Ix1=log2(1./(x(1,1))) Ix2=log2(1./(x(1,2)))pxy=[x(1,1)*p(1,:);x(1,2)*p(2,:)]; py=[x*p(:,1),x*p(:,2)];px_y=[pxy(:,1)/py(1,1),pxy(:,2)/py(1,2)]; I=log2(p./[py;py]) Hx=sum(x.*log2(1./x)) Hy=sum(py.*log2(1./py))Hx_y=sum(sum(pxy.*log2(1./px_y))) Hy_x=sum(sum(pxy.*log2(1./p)))Ixy=sum(sum(pxy.*log2(p./[py;py])))答案:12111221221.()0.737() 1.32192.(;)0.0589,(;)0.263,(;)0.0931,(;)0.32193.()0.971,()0.72194.(|)0.9635(|)0.71455.(;)0.0074I x I x I x y I x y I x y I x y H X H Y H X Y H Y X I X Y ====-=-======2. 二元信道的互信息与信源分布的关系 有二元信源:01()1X p x ωω⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦有二元信道,其传递矩阵为:11p p P p p -⎡⎤=⎢⎥-⎣⎦, 其中0.2p =,即传递矩阵0.80.20.20.8P ⎡⎤=⎢⎥⎣⎦编程实现下面题目:1) 画出平均互信息(;)I X Y 随信源分布ω的关系曲线,并求出最大平均互信息。
信源熵值计算实验报告材料(成型)(2)

信息论与编码课程设计报告设计题目:专业班级学号学生指导教师教师评分年月日目录目录一、设计任务与要求 (1)二、设计思路 (1)三、设计流程图 (2)四、程序运行及结果 (3)五、心得体会 (3)参考文献 (3)附录:源程序 (4)设计一.信源熵值计算一、设计任务与要求任务与要求:统计任意文本文件中各字符(不区分大小写)数量,计算字符概率,并计算信源熵。
二、设计思路由于能力有限,该程序统计只含有字母文档与空格的文档,下面对程序进行讲解:第一步:打开一个名为“text”的TXT文档,并判断文档是否为空,读入一篇英文文章存入一个数组temp,为了程序准确性将所读容转存到另一个数组S,计算该数组中每个字母与空格的出现次数(遇到小写字母都将其转化为大写字母进行计数),每出现一次该字符的计数器+1;第二步:计算信源总大小计算出每个字母和空格出现的概率;第三步:通过统计数据和信息熵公式计算出所求信源熵值并计算文档长度。
三、设计流程图四、程序运行及结果建立文件夹,输入文字,编写好程序并运行,查看结果输入测试文档“text2”There is no hate without fear. Hate is crystallized fear, fears dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity and our dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.结果:五、心得体会信息论与编码是我们电子信息工程的一门重要的专业课,通过对本次课程设计,学习将学到的理论知识用于实践,同时也学习了用软件编写程序,进一步对本课程知识的巩固和理解。
实验二信源熵的计算及信源编码实验

⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 实验二 信源熵的计算及信源编码实验实验目的:1、掌握信源熵、疑义度、噪声熵、联合熵和信源的二次扩展信源的熵的计算。
2、掌握哈夫曼编码的Matlab 实现方法。
3、掌握香农编码的Matlab 实现方法。
实验内容与步骤:一、信源熵H(X)、疑义度H(X|Y)、噪声熵H(Y|X)、联合熵H(XY)和信源二次扩展信源的熵H(X 2)的计算已知信源:接到如图所示的信道上,求在该信道上传输信息的信源熵H(X)、疑义度H(X|Y)、噪声熵H(Y|X)、联合熵H(XY)和信源二次扩展信源的熵H(X 2)结果:联合概率:px1y1 =0.4500px1y2 =0.0500px2y1 = 0.1000px2y2 = 0.4000Y 的概率:py1 =0.5500py2 =0.4500疑义度:px1_y1=0.8182px2_y1 =0.1818px1_y2 =0.1111px2_y2 = 0.8889信源熵:HX =1HY = 0.9928HXY =1.5955疑义度:HX_Y = 0.6027噪声熵:HY_X = 0.5955二次扩展信源熵:H_X = 2二、 香农编码实验设信源共7个符号消息,其数学模型如下其香农编码过程如下:0.8 0.1 0.2 X1X2 y1 y2 0.9根据分析模型编写M文件进行仿真,记录结果。
结果:十进制转二进制:c =0 0 0c =0 0 1c =0 1 1c =1 0 0c =1 0 1c =1 1 1 0c =1 1 1 1 1 1 0三、Huffman编码实验1)编写计算信息熵的M文件求信源X=[x1,x2,X3,X4,X5,X6,X7,X8,x9],其相应的概率为p=[0.2,0.15,0.13,0.12,0.1,0.09,0.08,0.07,0.06];利用编写的程序计算信息熵,并记录数值。
离散信源熵信道容量实验报告

离散信源熵信道容量实验报告实验目的:通过模拟离散信源熵和信道容量的实验,掌握熵和信道容量的概念及计算方法。
实验原理:离散信源:离散信源是指其输出符号集合为有限的离散符号集合,通常用概率分布来描述其输出符号的概率分布,称为离散概率分布。
离散信源的熵是度量这一离散概率分布的不确定度的量度,其单位是比特。
离散信源的熵公式为:H(S)=-Σpi×log2pi其中,H(S)为离散信源的熵,pi为消息符号i出现的概率,log2为以2为底的对数。
信道容量:信道容量是指在某一固定的信噪比下,能够传送的最大信息速率。
信道容量的大小决定了数字通信系统的最高可靠传输速率。
离散无记忆信道的信道容量公式为:C=max{I(X;Y)}其中,X为输入符号,Y为输出符号,I为信息熵。
实验步骤:1. 生成随机概率分布对于3种不同的符号数量,生成随机的符号及其概率分布。
在生成时,要求概率之和为1。
2. 计算离散信源的熵根据所生成的随机概率分布计算离散信源的熵。
3. 构建离散无记忆信道构建一个离散的2进制对称信道,并存储在一个概率矩阵中,利用生成的概率分布对该矩阵进行初始化。
4. 计算信道容量根据所构建的离散无记忆信道计算其信道容量。
实验结果分析:以下是实验结果分析,其中H(S)表示离散信源的熵,C表示离散无记忆信道的信道容量。
符号数量为3时:符号概率a 0.2b 0.3c 0.5H(S) = 1.485构建的离散无记忆信道的概率矩阵为:| 0 | 1 |--------------------------a | 0.20 | 0.80 |--------------------------b | 0.60 | 0.40 |--------------------------c | 0.80 | 0.20 |--------------------------C = 0.823从实验结果可以看出,当符号数量增加时,熵的值也会随之增加,这是由于符号集合增加,随机性增强所导致的。
计算信息熵实验原理的应用

计算信息熵实验原理的应用1. 实验目的本实验旨在探究信息熵在计算机科学和信息论中的应用,通过实验验证信息熵的计算原理,并分析其在数据压缩、密码学以及机器学习等领域的实际应用。
2. 实验原理信息熵是信息论中度量信息不确定性的常用指标。
信息熵的计算公式如下:H(X) = -Σ(P(x) * log2(P(x)))其中,H(X)代表随机变量X的信息熵,P(x)表示随机变量X取值为x时的概率。
信息熵的单位是比特,表示所需的平均比特数来编码一组符号。
3. 实验步骤1.首先,收集一组待处理的数据,可以是文本、图像或其他形式的数据。
2.对数据进行预处理,例如去除噪声、归一化处理等,以确保数据质量和准确性。
3.根据数据的特点和需求,选择合适的编码方式。
常用的编码方式包括ASCII编码、Unicode编码、Huffman编码等。
4.对编码后的数据计算信息熵。
根据实验原理中给出的信息熵计算公式,计算数据的信息熵。
可以使用编程语言的计算函数或自行编写计算代码进行计算。
5.分析实验结果。
根据计算得到的信息熵结果,进行进一步的分析和讨论。
比较不同编码方式和不同数据集的信息熵结果,探讨其差异和潜在规律。
6.探究信息熵在数据压缩、密码学和机器学习等领域的应用。
通过查阅相关文献和资料,了解和讨论信息熵在不同领域中的具体应用方式和效果。
4. 实验结果与讨论通过实验计算得到的信息熵结果可以用于评估数据的不确定性和信息量。
信息熵越高,表示数据的不确定性越大,需要更多的比特数来进行编码。
在数据压缩中,可以利用信息熵的概念来设计压缩算法,减少数据存储和传输的成本。
在密码学中,信息熵可以用于生成随机密钥,增加密码的强度和安全性。
在机器学习中,信息熵可以作为衡量模型复杂度和决策效果的指标,帮助选择和优化模型。
5. 实验结论信息熵是计算机科学和信息论中的重要概念,具有广泛的应用价值。
通过实验可以验证信息熵的计算原理,并了解其在数据压缩、密码学和机器学习等领域的应用。
《信息论基础》实验报告-实验1

信息与通信工程学院实验报告(软件仿真性实验)课程名称:信息论基础实验题目:绘制信源熵函数曲线指导教师:班级:1605XXXX学号:XX 学生姓名:王小明一、实验目的和任务1.掌握离散信源熵的原理和计算方法。
2.熟悉Matlab软件的基本操作,练习应用Matlab软件进行信源熵函数曲线的绘制。
3.理解信源熵的物理意义,并能从信源熵函数曲线图上进行解释其物理意义。
二、实验内容及原理(1)离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
假定X是一个离散随机变量,即它的取值范围R={x1,x2,x3,…}是有限或可数的。
设第i个变量xi发生的概率为p i=P{X=x i}。
则:定义一个随机事件的自信息量I(x i)为其对应的随机变量x i出现概率对数的负值。
即:I(xi )= -log2p(xi)定义随机事件X的平均不确定度H(X)为离散随机变量x i出现概率的数学期望,即:∑∑-==i ii ii ixpxpxIxpXH)(log)()()()(单位为 比特/符号 或 比特/符号序列。
平均不确定度H (X )的定义公式与热力学中熵的表示形式相同,所以又把平均不确定度H (X )称为信源X 的信源熵。
必须注意以下几点:某一信源,不管它是否输出符号,只有这些符号具有某些概率特性,必有信源的熵值;这熵值是在总体平均上才有意义,因而是个确定值,一般写成H (X ),X 是指随机变量的整体(包括概率分布)。
信息量则只有当信源输出符号而被接收者收到后,才有意义,这就是给与信息者的信息度量,这值本身也可以是随机量,也可以与接收者的情况有关。
熵是在平均意义上来表征信源的总体特征的,信源熵是表征信源的平均不确定度,平均自信息量是消除信源不确定度时所需要的信息的量度,即收到一个信源符号,全部解除了这个符号的不确定度。
或者说获得这么大的信息量后,信源不确定度就被消除了。
信源熵和平均自信息量两者在数值上相等,但含义不同。
信源熵值计算实验报告
result=-result;
printf("信息熵为:%f",result);
printf("\n");
return 0;
}
运行结果如下:
其中guojia.txt中的文档如下:
There is no hate without fear. Hate is crystallized fear, fear’s dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity and our dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.
fread(temp,1, 486, f);}
fclose(f);
s[0]=*temp;
for(i=0;i<strlen(temBiblioteka );i++){
s[i]=temp[i];
}
for(i=0;i<strlen(s);i++)
{
if(s[i]==' ')
num[26]++;
else if(s[i]>='a'&&s[i]<='z')
5.程序优点:
本程序可以打开文档进行统计,不必运行程序时重新输入文档,节省时间并且避免了一定的输入错误。
实验三_信源熵及信道容量特性

实验三信源熵及信道容量极值性研究一、实验目的验证信源熵及信道容量的极值特性,理解相关参数的变化对信源熵及信道容量的影响。
二、实验原理二元信源的熵H(X)=[wlog2(1/w)+(1-w)log2(1/(1-w))]这时信息熵H(X)是w的函数,通常用H(w)表示,w取值[0,1]。
当固定某信道时,选择不同的信源(其概率分布不同)与信道连接,在信道输出端接收道每个符号获得的信息量是不同的。
而且对于每一个固定信道,一定存在有一种信源(某一种概率分布P(x)),使输出获得的平均信息量为最大。
当信源固定后,选择不同的信道传输同一信源符号时,在信道的输出端获得关于信源的信息量是不同的。
信道输出端获得关于信源的信息量是信道传递概率的U型凸函数。
三、程序信源熵的程序:w=[0.000001:0.01:1];H=w.*log2(1./w)+(1-w).*log2(1./(1-w));plot(w,H);title('信源熵函数H(w)');xlabel('w');ylabel('H(w)');固定二元对称信道的互信息和固定二元信源的互信息:w=[0:0.01:1];p=0.2;h=-p.*log2(1./p)-(1-p).*log2(1./(1-p));H=(w.*(1-p)+(1-w).*p).*log2(1./(w.*(1-p)+(1-w).*p))-(1-(w.*(1-p)+ (1-w).*p)).*log2(1-(w.*(1-p)+(1-w).*p));I=H+h;subplot(2,1,1);plot(w,I);title('固定二元对称信道的互信息');xlabel('w');ylabel('I(X;Y)');p=[0.000001:0.01:1];w=0.2;h=-p.*log2(1./p)-(1-p).*log2(1./(1-p));H=(w.*(1-p)+(1-w).*p).*log2(1./(w.*(1-p)+(1-w).*p))-(1-(w.*(1-p)+ (1-w).*p)).*log2(1-(w.*(1-p)+(1-w).*p));I=H+h;subplot(2,1,2);plot(p,I);title('固定二元信源的互信息'); xlabel('p');ylabel('I(X;Y)');四、实验结果图1图2五、实验分析由图1可知,如果二元信源的输出时确定的(~w=1-w=0或w=1),则该信源不提供任何信息。
信息论实验报告1--信息熵的计算
~
fori=1:5
forj=1:4
sum=sum+A(i,j);
end
A(i,:)=A(i,:)/sum;
,
sum=0;
end
y=A;
求H(x|y):
functiony=H_x_y(A)
"
sum=0;
fori=1:4
forj=1:5
sum=sum+A(j,i);
end
\
A(:,i)=A(:,i)/sum;
实验
总结
日
本次实验的收获、体会、经验、问题和教训:
\
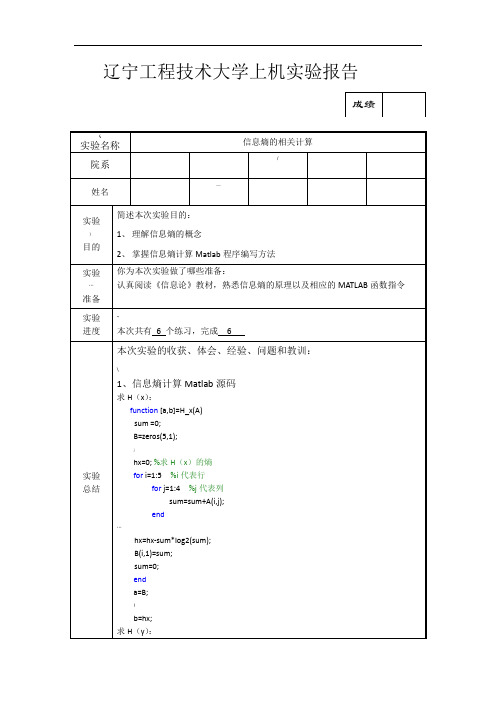
1、信息熵计算Matlab源码
求H(x):
function[a,b]=H_x(A)
sum =0;
B=zeros(5,1);
;
hx=0;%求H(x)的熵
fori=1:5%i代表行
forj=1:4%j代表列
sum=sum+A(i,j);
end
…
hx=hx-sum*log2(sum);
求H(x|y),H(y|x)
A=[ 0 0 0; 0 0;0 0;0 0 ;0 0 0];
H_x_y(A)
ans =
0 0 0
0 0
0 0
0 0
0 0 0
H_y_x(A)
ans =
0 0 0
0 0
0 0
0 0
0 0 0
教师
评语
成绩
辽宁工程技术大学上机实验报告
(
实验名称
信息熵的相关计算
院系
/
姓名
—
实验
)
目的
简述本次实验目的:
1、理解信息熵的概念
离散信源熵信道容量实验报告

计算离散信源熵、离散信道容量1 实验任务和目的实验任务:(1)简要总结信源的熵、信道容量的物理意义,概念;(2)写出离散信源熵、离散信道容量计算的基本步骤,画出实现离散信源熵、离散信道容量计算的程序流程图;(3)讨论信源的熵的大小与前后符号之间相关性的关系,讨论信道容量与信源先验概率及信道转移概率的关系。
实验目的:掌握信源的熵、信道容量的物理意义,概念;熟练掌握离散信源熵、离散信道容量的计算方法步骤;利用Matlab 编写离散信源熵、离散信道容量的计算程序;验证程序的正确性。
2 实验过程和结果 2.1 实验过程1、简要总结信源的熵、信道容量的物理意义,概念。
信源熵的物理意义是指信源中的各个符号的平均不确定性;熵是信源符号的平均信息量,是信源符号的平均不确定度。
信道容量 概念:在信道可以传输的基本前提下,对信源的一切可能的概率分布而言,信道能够传输的最大(接收)熵速率称为信道容量。
意义:求出了某个信道的信道容量,也就找到了信源的最佳概率分布。
从而指导人们改造信源,使之最大可能地利用信道的传输能力。
2、写出离散信源熵、离散信道容量计算的基本步骤,画出实现离散信源熵、离散信道容量计算的程序流程图;离散信源熵的计算步骤:()()()11log log ()qr r r i i i i H X E p a a p a =⎛⎫==- ⎪⎝⎭∑信道容量的计算步骤:()(){}()符号/;max bit Y X I C XP =3、(1)讨论信源的熵的大小与前后符号之间相关性的关系,讨论信道容量与信源先验概率及信道转移概率的关系。
信源的相关性是信源符号间的依赖程度的度量。
由于信源输出符号间的依赖关系也就是 信源的相关性使信源的实际熵减小。
信源输出符号间统计约束关系越长,信源的实际熵越小。
当信源输出符号间彼此不存在依赖关系且为等概率分布时,信源的实际熵等于最大熵。
(2)信道容量与信源先验概率及信道转移概率的关系。
信息论编码实验二熵的计算

实验二 熵的计算一、实验目的通过本次实验的练习,使学生进一步巩固熵的基本概念,掌握熵的统计方法,培养学生使用编程工具进行分析计算的基本能力。
二、实验仪器与软件1. PC 机 1台2. MATLAB7.0环境三、实验原理(一)信息熵的基本原理离散信源数学模型如下(设该信源可能取的符号有n 个):⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡)(,),(,),(),( ,, , , , )( 2121n i n i a p a p a p a p a a a a X P X 则该信源的信息熵为)(log )()(21i n i ix p x p X H ∑==H(X)是信源X 中每个事件出现的平均信息量,或者说H(X)表示了信源X 中各符号出现的平均不确定性。
图像的信息熵设数字图像的灰度级集合为{r 1,r 2,…,r m },其对应的概率分别为p (r 1),p (r 2),…,p (r m ),则图像的信息熵可以定义为:图像的信息熵表示像素各个灰度级位数的统计平均值,它给出了对此输入灰度级集合进行无失真图像编码时所需要的平均位数的下限。
(二)图像文件的读取(1)函数imread () MATLAB 通过函数imread 完成图像的读取,该函数语法格式如下:I = imread(filename,fmt)用于读取由filename 指定的图像数据到数组A 中,参数fmt 对应于所有图像处理工具所支持的图像文件格式。
如I=imread ('rice.tif');(2)函数imhist () 显示图像的直方图。
用法:imhist(I,n) 计算和显示图像I 的直方图,n 为指定的灰度级数目,默认为256。
如果I 是二值图像,那么n 仅有两个值。
[counts,x] = imhist(I) 返回直方图数据向量counts 或相应的色彩值向量x 。
(3)函数size(a) 表示矩阵a 每个维度的长度如size([1 2 3;4 5 6]),返回[2 3],表示该矩阵有2行3列(4)find 寻找非零元素下标如:x = [11 0 33 0 55];find(x)ans =135find(x == 0)ans =24(5)相关函数点运算在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。
信源熵的计算

桂林电子科技大学数学与计算科学学院实验报告 实验室: 实验日期: 2010年 11月 11日院(系) 数学与计算科学学院 年级、专业、班 0800710310 姓名 何帅 成绩课程名称 信息与编码 实验项目名 称 信源熵的计算 指导教师一 实验目的1、掌握香农编码的原理2、掌握二进制小数的输出方法二 实验内容与步骤Shannon 码编码步骤为:1、将信源S 的所有符号按概率从大到小排列:12q P P P ≥≥≥ 2、对第i 个信源符号i s 取整数码长[]1log 1,i i l P ⎡⎤=+⎢⎥⎣⎦为取整运算 3、计算累加概率111,0,(2)i i i k k R R R P i -===≥∑ 4、将i R 变换成二进制数12j i j j R x ∞-==∑,并按步骤2中计算的长度i l 取i R 的二进制系数j x ,组合起来即为i s的香农码字i W 程序:#include<stdio.h>#include<iostream.h>#include<math.h>double P[6]={0.25,0.1,0.2,0.25,0.15,0.05},Pax[6],machang[6];void main(){double temp;for(int a=1;a<6;a++){for(int i=0;i<6-a;i++)if(P[i]<P[i+1]){temp=P[i];P[i]=P[i+1];P[i+1]=temp;}}for(int i=0;i<6;i++)cout<<P[i]<<" ";cout<<endl;for(i=0;i<6;i++){Pax[0]=0.0;Pax[i+1]=Pax[i]+P[i];}cout<<"概率累加和为:"<<endl;for(i=0;i<6;i++)cout<<Pax[i]<<" ";cout<<endl;for(i=0;i<6;i++){double m=log(1/P[i]/log(2));if(m-int(m)==0)machang[i]=log(1/P[i])/log(2);elsemachang[i]=int(m)+1;cout<<P[i]<<"的码长为:"<<machang[i]<<endl;}for(i=0;i<6;i++){for(int j=0;j<machang[i];j++){int n=int(Pax[i]*2);cout<<n;if((Pax[i]*2-1)>0){Pax[i]=Pax[i]*2-1;continue;}if((Pax[i]*2-1)==0)Pax[i]=Pax[i]*2-1;elsePax[i]=Pax[i]*2;}cout<<endl;}}运行结果:三实验体会心得通过本次实验学习了求香农编码的基本步骤,同时学习了如何在C++下实现,在编程中主要是注意求二进制数是通过乘2取整得到的。
计算离散信源的熵matlab实现

实验一:计算离散信源的熵一、实验设备:1、计算机2、软件:Matlab二、实验目的:1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程;三、实验内容:1、写出计算自信息量的Matlab 程序2、写出计算离散信源平均信息量的Matlab 程序。
3、掌握二元离散信源的最大信息量与概率的关系。
4、将程序在计算机上仿真实现,验证程序的正确性并完成习题。
四、实验报告要求简要总结离散信源的特点及离散信源平均信息量的计算,写出习题的MATLAB 实现语句。
信息论基础:自信息的计算公式 21()log aI a p = Matlab 实现:I=log2(1/p) 或I=-log2(p) 熵(平均自信息)的计算公式22111()log log qq i i i i i i H x p p p p ====-∑∑ Matlab 实现:HX=sum(-x.*log2(x));或者h=h-x(i)*log2(x(i)); 习题:1. 甲地天气预报构成的信源空间为:1111(),,,8482X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦ 小雨 云 大雨晴 乙地信源空间为:17(),88Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦ 小雨晴 求此两个信源的熵。
求各种天气的自信息量。
案:() 1.75;()0.5436H X H Y ==运行程序:p1=[1/2,1/4,1/8,1/8];%p1代表甲信源对应的概率p2=[7/8,1/8];%p2代表乙信源对应的概率H1=0.0;H2=0.0;I=[];J=[];for i=1:4H1=H1+p1(i)*log2(1/p1(i));I(i)=log2(1/p1(i));enddisp('自信息量分别为:');Idisp('H1信源熵为:');H1for j=1:2H2=H2+p2(j)*log2(1/p2(j));J(j)=log2(1/p2(j));enddisp('自信息量分别为:');Jdisp('H2信源熵为:');H2。
实验1

《信息论与编码》实验1 离散信源熵实验一、实验目的熟悉工作环境及Matlab 软件 掌握绘图函数的运用 理解熵函数表达式及其性质 二、实验原理信息熵自信息量是针对信源的单个符号而言的,而符号是随机发生的,因此单个符号的不确定性不足于代表信源的不确定性性质,为此,可对所有符号的自信息量进行统计平均,从而得到平均不确定性。
熵的表示[]()()()()()log ()i i i i iiH X E I X p x I x p x p x ===-∑∑注意的问题熵是自信息量的统计平均,因此单位与自信息量的单位相同,与熵公式中所用对数的底有关:bit/符号、nat/符号、dit/符号、r 进制单位/符号。
特殊公式:某个pk=0时,0log0=0 (0lim log 0→=x x x )在熵的定义中忽略零概率事件。
平均互信息平均互信息量(I(X;Y))是统计平均意义下的先验不确定性与后验不确定性之 差,是互信息量的统计平均:()()()()()();/;/=-=-I X Y H X H X Y I Y X H Y H Y X三、实验内容1.用 Matlab 软件绘制二进熵函数曲线。
二元信源1011⎛⎫⎛⎫=≤≤ ⎪ ⎪-⎝⎭⎝⎭X p P p p二元信源的熵为(,1)log (1)log(1)-=----H p p p p p p绘制当p 从0到1之间变化时的二元信源的信息熵曲线.Matlab 程序: p=0.00001:0.001:1;h=-p.*log2(p)-(1-p).*log2(1-p); plot(p,h);title('二进熵函数曲线'); ylabel('H(p,1-p)') 2.绘制三元信源的熵三元信源1231212120,11()⎛⎫⎛⎫=≤≤ ⎪⎪--⎝⎭⎝⎭x x x X p p p p p p P x三元信源的熵为111111221212(,,1)log log (1)log(1)--=-------H p p p p p p p p p p p p 绘制当12,p p 从0到1之间变化时的三元信源的信息熵曲线.3.绘制平均互信息量图形对于二元对称信道的输入概率空间为0,1(),1ωωω⎡⎤⎡⎤=⎢⎥⎢⎥=-⎣⎦⎣⎦X P x平均互信息:根据:1()()(|)1===∑rj i j i i P b P a P b a所以:21(0)()(0|)(0)(0|0)(1)(0|1)ωω====+=+∑i i i P y P a P a P P P P p p21(1)()(0|)(0)(1|0)(1)(1|1)ωω====+=+∑i i i P y P a P a P P P P p p1111(;)()()()log ()log [log log ]()()()ωωωωωωωωωω=-=+++-+++=+-I X Y H Y H p p p p p p p p p p p p pH p p H p 绘制当,ωp 从0到1之间变化时的平均互信息熵曲线.(;)()(/)=-I X Y H Y H Y X 1()()(/)log(/)=-∑∑XYH Y P x P y x P y x 11()()[loglog ]=-+∑XH Y P x p p p p11()[loglog ]()()=-+=-H Y p p H Y H p p p四、实验报告要求简述实验目的;简述实验原理;分别绘制二元信源和三元信源的熵及平均互信息量图形。
关于信源熵的实验报告

实验报告实验名称关于信源熵的实验课程名称信息论与编码姓名xxx 成绩90班级电子信息1102学号0909112204日期2013.11.22地点综合实验楼实验一MATLAB完成离散信源熵的计算一、实验目的1. 通过信息论与编码学理论,掌握离散信源熵的原理和计算方法。
2. 熟悉matlab 软件的基本操作和基本工具以及使用,掌握利用matlab求解信息熵的原理和方法。
3. 练习使用matlab 求解信源的信息熵。
自学图像熵的相关概念,并应用所学知识,使用matlab 或其他开发工具求解图像熵。
4. 掌握Excel的绘图功能,使用Excel绘制散点图、直方图。
二、实验原理1.离散信源的基本概念、原理和信源熵相关计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号,因此离散离散消息可以看成是一种有限个状态的随机序列。
随机事件的自信息量I(xi)为其对应的随机变量xi 出现概率对数的负值。
即: I (xi )= -log2p ( xi)随机事件X 的平均不确定度(信源熵)H(X)为离散随机变量 xi 出现概率的数学期望,即:2.离散二元信源的信息熵设信源符号集X={0,1} ,每个符号发生的概率分别为p(0)= p,p(1)= q,p+ q =1,即信源的概率空间为:则该二元信源的信源熵为:H(X) = - p*logp–q*logq = - p*logp –(1 - p)*log(1- p)即:H (p) = - p*logp –(1 - p)*log(1- p) 其中 0 ≤ p ≤13.MATLAB二维绘图用matlab 中的命令plot( x , y) 就可以自动绘制出二维图来。
例:在matlab 上绘制余弦曲线图,y = cos x ,其中 0 ≤ x ≤ 2 。
>>x =0:0.1:2*pi; %生成横坐标向量,使其为 0,0.1,0.2,…,6.2>>y =cos(x ); %计算余弦向量>>plot(x ,y ) %绘制图形4.MATLAB求解离散信源熵求解信息熵过程:1) 输入一个离散信源,并检查该信源是否是完备集。
熵函数实验报告
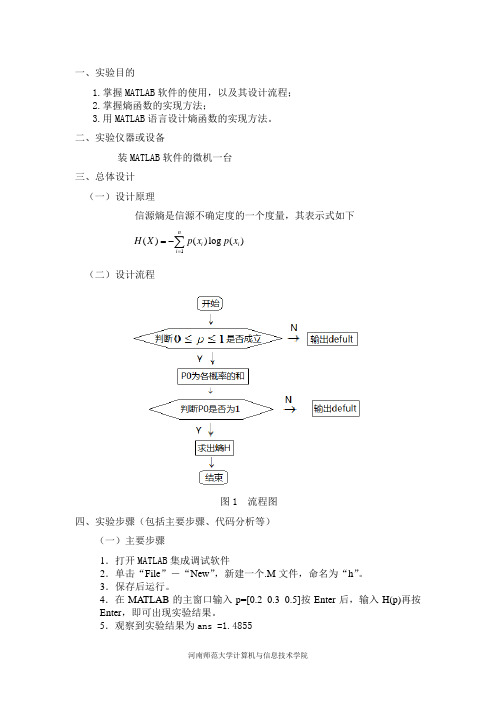
一、实验目的1.掌握MATLAB 软件的使用,以及其设计流程;2.掌握熵函数的实现方法;3.用MATLAB 语言设计熵函数的实现方法。
二、实验仪器或设备装MATLAB 软件的微机一台 三、总体设计 (一) 设计原理信源熵是信源不确定度的一个度量,其表示式如下1()()log ()ni i i H X p x p x ==-∑(二) 设计流程图1 流程图 四、实验步骤(包括主要步骤、代码分析等) (一)主要步骤1.打开MATLAB 集成调试软件2.单击“File ”-“New ”,新建一个.M 文件,命名为“h ”。
3.保存后运行。
4.在MATLAB 的主窗口输入p=[0.2 0.3 0.5]按Enter 后,输入H(p)再按Enter ,即可出现实验结果。
5.观察到实验结果为ans =1.48556.并分析实验结果 (二)主要代码分析function H=H(p)if((p>=0)&(p<=1)) %如果01p ≤≤,执行下列语句 P0=sum(p); %P0为各概率之和if (P0==1) %如果P0=1执行下列语句 H=-sum(p.*log2(p)); elsedisplay('defult') %P0为各概率之和不为1,输出defult end elsedisplay('defult') %如果不是01p ≤≤,输出defult end五、结果分析与总结通过本次实验,我进一步理解了熵函数的意义,通过MATLAB 编程,我进一步理解了熵函数的是对信源不确定度的度量。
但是,我发现自己在MATLAB 编程上还存在很大的欠缺,以后要加强在这方面的练习。
教师签名:年 月 日。
信息熵与图像熵的计算

实验一信息熵与图像熵计算一、实验目的1.复习MATL AB 的基本命令,熟悉MATL AB 下的基本函数。
2.复习信息熵基本定义, 能够自学图像熵定义和基本概念。
二、实验仪器、设备1.计算机-系统最低配置256M 内存、P4 CPU。
2.Matlab仿真软件- 7.0 / 7.1 / 2006a等版本Mat lab 软件。
三、实验内容与原理(1)内容:1.能够写出MATLAB源代码,求信源的信息熵。
2.根据图像熵基本知识,综合设计出M ATLAB程序,求出给定图像的图像熵。
(2)原理1. MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。
2.利用信息论中信息熵概念,求出任意一个离散信源的熵(平均自信息量)。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。
所发出的消息不同,它们所含有的信息量也就不同。
任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
不能作为整个信源的信息测度,因此定义自信息量的数学期望为信源的平均自信息量:信息熵的意义:信源的信息熵H是从整个信源的统计特性来考虑的。
它是从平均意义上来表征信源的总体特性的。
对于某特定的信源,其信息熵只有一个。
不同的信源因统计特性不同,其熵也不同。
3.学习图像熵基本概念,能够求出图像一维熵和二维熵。
图像熵是一种特征的统计形式,它反映了图像中平均信息量的多少。
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi 表示图像中灰度值为i的像素所占的比例,则定义灰度图像的一元灰度熵为:255log i iip p ==∑H图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征,为了表征这种空间特征,可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。
信息论与编码实验一

实验报告实验名称关于信源熵的实验课程名称信息论与编码姓名成绩班级电子信息1102学号日期2013.11.22地点综合实验楼实验一关于信源熵的实验一、实验目的1. 掌握离散信源熵的原理和计算方法。
2. 熟悉matlab 软件的基本操作,练习使用matlab 求解信源的信息熵。
3. 自学图像熵的相关概念,并应用所学知识,使用matlab 或其他开发工具求解图像熵。
4. 掌握Excel的绘图功能,使用Excel绘制散点图、直方图。
二、实验原理1. 离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
随机事件的自信息量I(xi)为其对应的随机变量xi 出现概率对数的负值。
即: I (xi )= -log2p ( xi)随机事件X 的平均不确定度(信源熵)H(X)为离散随机变量 xi 出现概率的数学期望,即:2.二元信源的信息熵设信源符号集X={0,1} ,每个符号发生的概率分别为p(0)= p,p(1)= q,p+ q =1,即信源的概率空间为:则该二元信源的信源熵为:H( X) = - plogp–qlogq = - plogp –(1 - p)log(1- p)即:H (p) = - plogp –(1 - p)log(1- p) 其中 0 ≤ p ≤13. MATLAB二维绘图用matlab 中的命令plot( x , y) 就可以自动绘制出二维图来。
例1-2,在matlab 上绘制余弦曲线图,y = cos x ,其中 0 ≤ x ≤2 。
>>x =0:0.1:2*pi; %生成横坐标向量,使其为 0,0.1,0.2,…,6.2>>y =cos(x ); %计算余弦向量>>plot(x ,y ) %绘制图形4. MATLAB求解离散信源熵求解信息熵过程:1) 输入一个离散信源,并检查该信源是否是完备集。
2) 去除信源中符号分布概率为零的元素。
BDPSK调制和平均信源熵的计算仿真(通信原理实验报告)

实验报告信息学院(院、系)电子信息工程专业班通信原理教程课BDPSK调制和平均信源熵的计算仿真一、编写BDPSK调制程序,任意给定一组二进制数,计算经过这种调制方式的输出信号。
1、实验目的(1)熟悉BDPSK调制原理。
(2)学会运用Matlab编写BDPSK调制程序。
(3)会画出原信号、BPSK和BDPSK调制信号的波形图。
(4)掌握数字通信的BDPSK的调制方式。
2、实验原理2DPSK方式即是利用前后相邻码元的相对相位值去表示数字信息的一种方式。
现假设用Φ表示本码元初相与前一码元初相之差,并规定:Φ=0表示0码,Φ=π表示1码。
则数字信息序列与2DPSK信号的码元相位关系可举例表示如2PSK信号是用载波的不同相位直接去表示相应的数字信号而得出的,在接收端只能采用相干解调,它的时域波形图如图1所示。
图1 2DPSK信号在这种绝对移相方式中,发送端是采用某一个相位作为基准,所以在系统接收端也必须采用相同的基准相位。
如果基准相位发生变化,则在接收端回复的信号将与发送的数字信息完全相反。
所以在实际过程中一般不采用绝对移相方式,而采用相对移例如,假设相位值用相位偏移x表示(x定义为本码元初相与前一码元初相之差),并设1数字信息“→=∆Φπ”0数字信息“→=∆Φ”则数字信息序列与2DPSK信号的码元相位关系可举例表示如下:数字信息:0 0 1 1 1 0 0 1 0 12DPSK信号相位: 0 0 0 π0 πππ0 0 π或:πππ0 π0 0 0 ππ0为了便于说明概念,我们可以把每个码元用一个如图2所示的矢量图来表示。
图中,虚线矢量位置称为基准相位。
在绝对移相中,它是未调制载波的相位;在相对移相中,它是前一码元载波的相位。
如果假设每个码元中包含有整数个载波周期,那么,两相邻码元载波的相位差既表示调制引起的相位变化,也是两码元交界点载波相位的瞬时跳变量。
图2(a)所示的移相方式,称为A方式。
在这种方式中,每个码元的载波相位相对于基准相位可取0、π。
实验一 信息熵与图像熵计算

实验一信息熵与图像熵计算(2 学时)一、实验目的1.复习MATLAB的基本命令,熟悉MATLAB下的基本函数;2.复习信息熵基本定义,能够自学图像熵定义和基本概念。
二、实验容1.能够写出MATLAB源代码,求信源的信息熵;2.根据图像熵基本知识,综合设计出MATLAB程序,求出给定图像的图像熵。
三、实验仪器、设备1.计算机-系统最低配置256M存、P4 CPU;2.MATLAB编程软件。
四实验流程图五实验数据及结果分析四、实验原理1.MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。
2.利用信息论息熵概念,求出任意一个离散信源的熵(平均自信息量)。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。
所发出的消息不同,它们所含有的信息量也就不同。
任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
不能作为整个信源的信息测度,因此定义自信息量的数学期望为信源的平均自信息量:1( ) 1 ( ) [log ] ( ) log ( ) i n i i p a i H E p a p a X信息熵的意义:信源的信息熵H是从整个信源的统计特性来考虑的。
它是从平均意义上来表征信源的总体特性的。
对于某特定的信源,其信息熵只有一个。
不同的信源因统计特性不同,其熵也不同。
3.学习图像熵基本概念,能够求出图像一维熵和二维熵。
图像熵是一种特征的统计形式,它反映了图像中平均信息量的多少。
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi表示图像中灰度值为i的像素所占的比例,则定义灰度图像的一元灰度熵为:2550 log i i i p p H图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征,为了表征这种空间特征,可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。
选择图像的邻域灰度均值作为灰度2分布的空间特征量,与图像的像素灰度组成特征二元组,记为(i,j),其中i表示像素的灰度值(0<=i<=255),j表示邻域灰度(0<=j<=255),2 ( , ) / ij p f i j N上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征,其中f(i,j)为特征二元组(i,j)出现的频数,N为图像的尺度,定义离散的图像二维熵为:2550 log ij ij i p p H构造的图像二维熵可以在图像所包含信息量的前提下,突出反映图像中像素位置的灰度信息和像素邻域灰度分布的综合特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fclose(f);
s[len(temp);i++)
{
s[i]=temp[i];
}
for(i=0;i<strlen(s);i++)
{
if(s[i]==' ')
num[26]++;
else if(s[i]>='a'&&s[i]<='z')
int main(void)
{
char s[N];
int i,n=0;
float num[27]={0};
double result=0,p[27]={0};
FILE *f;
char *temp=new char[485];
f=fopen("guojia.txt","r");
while (!feof(f)) {
n++;
if(n==3)
{
printf("\n");
n=0;
}
}
p[26]=num[26]/strlen(s);
printf("空格:%f\t",p[26]);
printf("\n");
for(i=0;i<27;i++)
{
if (p[i]!=0)
result=result+p[i]*log(p[i]);
5.程序优点:
本程序可以打开文档进行统计,不必运行程序时重新输入文档,节省时间并且避免了一定的输入错误。
}
result=-result;
printf("信息熵为:%f",result);
printf("\n");
return 0;
}
运行结果如下:
其中guojia.txt中的文档如下:
There is no hate without fear. Hate is crystallized fear, fear’s dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity and our dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.
第二步:计算信源总大小计算出每个字母和空格出现的概率;
最后,通过统计数据和信息熵公式计算出所求信源熵值(本程序中单位为奈特nat)。
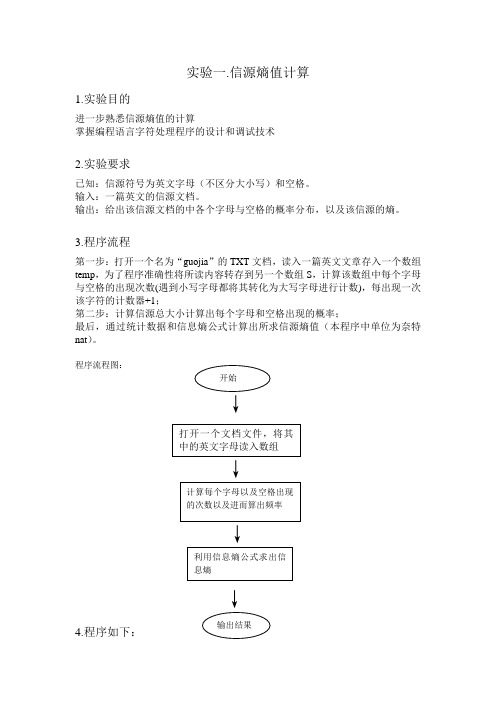
程序流程图:
↓
↓
↓
↓
4.程序如下:
#include"stdio.h"
#include <math.h>
#include <string.h>
#define N 1000
实验一.信源熵值计算
1.实验目的
进一步熟悉信源熵值的计算
掌握编程语言字符处理程序的设计和调试技术
2.实验要求
已知:信源符号为英文字母(不区分大小写)和空格。
输入:一篇英文的信源文档。
输出:给出该信源文档的中各个字母与空格的概率分布,以及该信源的熵。
3.程序流程
第一步:打开一个名为“guojia”的TXT文档,读入一篇英文文章存入一个数组temp,为了程序准确性将所读内容转存到另一个数组S,计算该数组中每个字母与空格的出现次数(遇到小写字母都将其转化为大写字母进行计数),每出现一次该字符的计数器+1;
num[s[i]-97]++;
else if(s[i]>='A'&&s[i]<='Z')
num[s[i]-65]++;
}
printf("文档中各个字母出现的频率:\n");
for(i=0;i<26;i++)
{
p[i]=num[i]/strlen(s);
printf("%3c:%f\t",i+65,p[i]);
