【习题第四章立体的投影】
合集下载
土木工程制图 教学课件 作者 张爽 第四章立体的投影
【例4-13】已知四棱柱体与三棱柱体相贯的水平 投影图和侧面投影图，求相贯线正投影。
平面立体与曲面立体相交
方梁和圆柱相贯
【例4-14】已知圆锥体薄壳基础的轮廓线，求其相贯线。
曲面立体与曲面立体相交
辅助平面法
表面取点
【例4-15】求两正交圆柱的相贯线。
【例4-16】求轴线正交的圆柱和圆锥的相贯线。
s″
z
z
k′ z n′
z
k″
z
z (n″)
a′
b′
c′ a″(c″)
b″
a
c
s
n z
z
k
z
b
【例4-2】完成三棱锥表面线条的各面投影。
曲面立体的投影
一、圆柱体
圆柱体
圆柱由圆柱面和上、 下两底面组成。
圆柱面可看成是由 直线AA1绕与它平行的 轴线旋转而成。
直线AA1称为母线。
圆柱面上与轴线平 行的任一直线称为圆柱 面的素线。
截切——用平面与立体相交，截去立体的一部分。
截交线
• 截平面 —— 用以截切物体的平面。 • 截交线 —— 截平面与物体表面的交线。 • 截断面 —— 因截平面的截切，在物体上形成的平面。
一、平面和平面立体的截交线
截交线的性质： • 截交线是一个由直线组成的封闭的平面多边形。 • 截交线的每条边是截平面与棱面的交线。
1、形体分析 2、投影选择 ⑴ 选择安放位置 ⑵ 选择正面投影方向 ⑶ 选择投影图的数量 3、先选比例、后定图幅或先定图幅、后选比例 4、画底稿线（布图、画基准线、逐个画出各基本形 体投影图，标注尺寸） 5、检查整理底稿、加深图线、书写文字 ，完成全图
1、形体分析的内容 1) 平面体相邻组成部分间的表面衔接与投 影图的关系
立体的投影
为斜面体，如棱锥、棱台等。建筑工程中把有坡屋顶的房子、有斜面的构件均看作是斜面体的
组合体、
各棱线和各顶点的投影，由
于点、直线和平面是构成平
面立体表面的几何元素，因
此绘制平面立体的投影，归
根结底是绘制点、直线和平
面的投影。在平面立体中，
可见棱线用实线表示，不可
见棱线用虚线表示，以区分
可见表面和不可见表面。
01 第一节 平面立体的投影
1.棱柱体
（1）形体特征 棱柱的各棱线互相平行，底面、顶面为多 边形。棱线垂直顶面时称为直棱柱，棱线倾斜 顶面时称为斜棱柱。图4-3a给出一个直三棱柱。 它是由上、下两个底面（三角形）和三个棱面 （长方形）组成的。
（2）安放位置 安放形体时要考虑两个因素：一要使形体
处于稳定状态，二要考虑形体的工作状况。为 了作图方便，应尽量使形体的表面平行或垂直 于投影面。
对于图4-3a中的直三棱柱，选上下底面平 行于H面，棱面AA1C1C平行于V面。
01 第一节 平面立体的投影
（3）投影分析 图4-3b是它的两面投影图。因为上、下两
底面是水 平面，棱面AA1C1C为正平面，其 余两个棱面是铅垂面，所以它的水平投影是一 个三角形，这个三角形是上、下底面的投影， 反映了实形，三角形的三个边即为三个棱面的 积聚投影，三角形的三个顶点分别是三条棱线 的水平积聚投影。三棱柱的后棱面是正平面， 它的正面投影反映实形，成为棱柱的外形轮廓 线，此外形轮廓线的上、下两边即为上、下两 底面的积聚投影，左、右两边是左、右两条棱 线的投影。b′b1′是棱线BB1的V面投影，它 把三棱柱的正面投影分为左、右两个线框，这 两个线框就是左、右两个棱面的投影 （ 不反映 实形）。
第二节 曲面立体的投影
04 立体的投影解析
1'
2'3'
4'5' 6'7' 5"
3"
1"
解题步骤
2" 4" 6"
1．分析 截平面为正垂面，截 交线的侧面投影为圆，水平投 影为椭圆； 2．求出截交线上的特殊点Ⅰ、 Ⅳ、 Ⅴ、 Ⅷ； 3．求出若干个一般点Ⅱ、Ⅲ、 Ⅵ、Ⅶ；
8'
7 8
5
7" 3 1
4．光滑且顺次地连接各点，作 出截交线，并且判别可见性； 5．整理轮廓线。
水平投影是一个圆， 这个圆是圆锥底圆和圆 锥面的重合投影，反映 底圆的实形，（通常用 细点画线画出十字对称 中心线） 。
正面投影和侧面投 影是两个相等的等腰三 角形，（回转轴的投影 用细点画线来表示） 。
3、 圆锥的投影特点
4、圆锥表面上取点
三、 圆球的投影
1、圆球的形成
2、 圆球的画法
3、 圆球的投影特点
[例题1] 求立体截割后的投影
(1) 2
1’’ 2’’
Ⅰ
(5)
3
4
5’’
4’’
Ⅴ
3’’
Ⅱ Ⅲ Ⅳ
5
1
4
3
2
[例题2] 求立体切割后的投影
4 5 1
（3）
3
6
4 5
（6）
2 1
（2）
Ⅲ
2
3 Ⅵ
Ⅳ
1
Ⅱ
6
Ⅴ Ⅰ
5
4
[例题3] 求四棱锥被截切后的俯视图和左视图。
(4) 3 1 2 1 ● 2 4 ● ● ● 3
3 ●
4 ● 1 ● ● 2
2'3'
4'5' 6'7' 5"
3"
1"
解题步骤
2" 4" 6"
1．分析 截平面为正垂面，截 交线的侧面投影为圆，水平投 影为椭圆； 2．求出截交线上的特殊点Ⅰ、 Ⅳ、 Ⅴ、 Ⅷ； 3．求出若干个一般点Ⅱ、Ⅲ、 Ⅵ、Ⅶ；
8'
7 8
5
7" 3 1
4．光滑且顺次地连接各点，作 出截交线，并且判别可见性； 5．整理轮廓线。
水平投影是一个圆， 这个圆是圆锥底圆和圆 锥面的重合投影，反映 底圆的实形，（通常用 细点画线画出十字对称 中心线） 。
正面投影和侧面投 影是两个相等的等腰三 角形，（回转轴的投影 用细点画线来表示） 。
3、 圆锥的投影特点
4、圆锥表面上取点
三、 圆球的投影
1、圆球的形成
2、 圆球的画法
3、 圆球的投影特点
[例题1] 求立体截割后的投影
(1) 2
1’’ 2’’
Ⅰ
(5)
3
4
5’’
4’’
Ⅴ
3’’
Ⅱ Ⅲ Ⅳ
5
1
4
3
2
[例题2] 求立体切割后的投影
4 5 1
（3）
3
6
4 5
（6）
2 1
（2）
Ⅲ
2
3 Ⅵ
Ⅳ
1
Ⅱ
6
Ⅴ Ⅰ
5
4
[例题3] 求四棱锥被截切后的俯视图和左视图。
(4) 3 1 2 1 ● 2 4 ● ● ● 3
3 ●
4 ● 1 ● ● 2
现代工程图学习题集答案 第四版 主编杨裕根 第4章
第4章 立体的投影
答案
现代工程图学习题集（第4版）
4-3.5.完成圆锥被截后的水平和侧面投影。
第4章 立体的投影
答案
现代工程图学习题集（第4版）
第4章 立体的投影
4-3.6、完成圆锥被截后的水平和侧面投影。
模型 答案
现代工程图学习题集（第4版）
第4章 立体的投影
4-4.1、完成圆锥被截后的水平和侧面投影。
现代工程图学习题集（第4版）
4-4.4、画出顶尖的水平投影
第4章 立体的投影
y1
y2
返回
y1 y2
现代工程图学习题集（第4版）
4-4.*5、求组合回转体的水平投影
第4章 立体的投影
返回
现代工程图学习题集（第4版）
4-5.1、补全侧面投影
第4章 立体的投影
y1
返回
y1
现代工程图学习题集（第4版）
返回
现代工程图学习题集（第4版）
第4章 立体的投影
4-6.1、完成圆柱与圆锥相贯后的正面投影和水平投影。
返回
现代工程图学习题集（第4版）
第4章 立体的投影
4-6.2、完成圆柱与半球相贯后的水平和正面投影。
返回
现代工程图学习题集（第4版）
第4章 立体的投影
4-6.3、补全三面投影(形体提示:带有轴线为铅垂线和侧垂线 的两个圆柱形通孔的球体)。
第4章 立体的投影
4-1.5、作四棱锥被正垂面截断后的侧面投影，并补全截断后 的水平投影。
y1
返回
y1
现代工程图学习题集（第4版）
4-1.6 作出立体的水平投影
第4章 立体的投影
返回
现代工程图学习题集（第4版）
第4章 立体的投影
二、曲面体的投影图 曲线是点按一定的运动规律运动形成的轨迹。 曲面是直线或曲线按一定规律运动形成的轨迹。运 动的线叫做母线，母线的任一位置称为素线。 旋转面：当母线绕一条固定轴回转所形成的曲面。 ——曲面体 母线上的任意一点的轨迹都是一个圆，称为纬圆， 其圆心在回转轴上。
2、棱柱体 ㈠棱柱体的组成 由两个底面和若干侧棱面 组成。侧棱面与侧棱面的 交线叫侧棱线，侧棱线相 互平行。 ㈡棱柱体的三视图 在图示位置时，六棱柱的 两底面为水平面，在俯视 图中反映实形。前后两侧 棱面是正平面，其余四个 侧棱面是铅垂面，它们的 水平投影都积聚成直线， 与六边形的边重合。
三棱锥
3、棱椎体 ㈠棱椎体的组成 由一个底面和若干侧棱面组成。 侧棱线交于有限远一点：锥顶。 s s ㈡棱椎体的三视图 S 棱锥处于 图示位置 b 时，其底 b c a(c) a C 面是水平 A 面，在俯 B a c s 视图上反映实形。 侧棱面SAC为侧垂面，另两个 b 侧棱面为一般位置平面。 上述可知，求平面体的投影 求其棱线的投影。
叠加式
章目录
返 回
切割式
综合式
粘合：指两部分有相互粘合的表面。
相切：指两部分间有光滑过渡的平面与 曲面或曲面与曲面。
相交：指两部分间有彼此相交的表面。
形体分析
第三节 剖视图与断面图
剖视图的概念 1、剖视图的形成 假想用一个剖切平面平行于某一个投影面， 把物体在某一位置剖开，将观察者和剖切平 面之间的部分移去，其余部分向投影面作投 影，所得到的图形为剖视图，如图所示。 注意：剖切平面是一个假想的平面，应平行 于投影面。在该投影面上是移去前面部分， 但其他视图仍应完整画出。
建筑工程制图第4章 曲线与曲面立体的投影
两圆柱位置不同时相贯线的变化趋势
(a)
(b)
(c)
(d)
4.5 旋转楼梯
平螺旋面
螺旋楼梯
4.5 旋转楼梯
1．平螺旋面
4.5 旋转楼梯
平螺旋面的应用— 螺旋楼梯
4.5 旋转楼梯
平螺旋面的应用— 螺旋楼梯
4.5 旋转楼梯
4.5 旋转楼梯
Thanks
5 3
4.3 平面与曲面立体截交
例3:圆锥被正平面截切，补全主视图。Fra bibliotek● ●
e′
●
c d′
′
●
●
a′
b′
截交线 的空间 E 形状？ 截交线 D C 的投影 特性？ A
B
a c
●
●
●
e
●
d
●
b
4.3 平面与曲面立体截交
例4:圆锥被正平面截切，补全主视图。
● ●
e′
●
c d′
′
●
●
a′
b′
截交线 的空间 E 形状？ 截交线 D C 的投影 特性？ A
底圆 母线 素线 顶圆 轴线
4.2 曲面立体及其表面上的点
例1：绘制圆柱的三视图。 O A
O1 A1
4.2 曲面立体及其表面上的点
例2：已知圆柱表面的点的投影1’、2’、3’、4，求其它两面投影。
4
1′
4″
1″
3
(2)
2″
3
利用投影的
积聚性 O A
2 1
4
3
O1 A1
相贯线 相贯线
第四章 立体的投影2.
例 求圆柱与圆锥的相贯线。
相贯线—— 闭合的空间曲线
例 求圆柱与圆锥 的相贯线。 a’
e’(f
？ c’’)(d
’) b’
d
f
(b) ？ a
e
c
a f” ’’ e”
d’’
c’’
b ’’
例 求圆柱与圆锥 的相贯线。
c’(d ’)
d’’
c’’
d
虚实分界点
c
关于圆柱相贯线的讨论
两圆柱轴线垂直相交，当两圆柱相对直径 变化时，对相贯线的影响。
§4-4 两回转体表面相交
相贯线: 两立体表面相交所得的交线。
两曲面立体相贯线的性质与类型
1.共有性: 相贯线是相交两立体表面的共有线，同 时也是两立体表面的分界线。
2.封闭性:两曲面立体的 相贯线一般是一闭合的空 间曲线。 3.相贯线的形状取决于曲面 的形状、大小及两曲面间的相对位置。
类型 两曲面立体的相贯线，一般是闭合的空间 曲线，特殊情况下，也可能是平面曲线或直线段 。
’ ’)
’
1”(3
”)
已知H、W投影
6
5
”
” 求正面投影
8 ”
2”(4 ”)
7 ”
找特殊点
闭合的空间曲线
6(8)
1(2)
3(4)
5(7)
闭合的空间曲线
例 圆筒与圆孔相贯
外交线
外内交线
外交线
例 圆筒与圆孔相贯
yy
yy
两圆柱相交的三种基本形式
不论是外圆柱面还是内圆柱面，实质都是圆柱面。因此， 只要相交两圆柱轴线的相对位置不变，如都是正交；直径的 大小不变，则相贯线的形状和作图方法完全相同。
第四章 立体投影(第四讲)
截交线的求法： 截交线的求法：
平面立体截交线是一个封闭的平面多边形， 平面立体截交线是一个封闭的平面多边形，多边形的 封闭的平面多边形 顶点是平面立体的棱线与截平面的交点，多边形的每条边 顶点是平面立体的棱线与截平面的交点，多边形的每条边 是平面立体的棱线与截平面的交点 是平面立体的棱面与截平面的交线。 是平面立体的棱面与截平面的交线。 棱面与截平面的交线 求截交线---归根到底是求截 求截交线 归根到底是求截 平面与立体表面（或棱线） 平面与立体表面（或棱线） 一系列交线（或交点） 一系列交线（或交点）的问 题。 交线 顶点
平面与平面立体相交
应用举例（单一截平面） 应用举例（单一截平面）
例1:已知立体的正面投影和水平投影, 求其侧面投影。 ★ 形体分析和投影分析
1、根据投影，判别立体形状 、根据投影， 2、根据截平面位置，判别截断面形状 、根据截平面位置， 3、判别截平面与投影面的相对位置 、
平面与平面立体相交
(5′ 3(5′) ′ (6′ (6′) 2′ 1′
4 3
作图: 检查、 作图: ③检查、完成
检查、 (e) 检查、完成 图3-22 正四棱锥被两平面截切
平面与平面相交画法
截平面
截交线
例题2 求立体截切后的投影
4′ 5′ 1′
（3′）
3″ 6″
4″ 5″
（6′）
2″ 1″
（2′）
2
3
Ⅲ Ⅳ
1
Ⅵ
6
Ⅱ Ⅰ
4
Ⅴ
5
例题5
求立体截切后的投影
1′（2′） 3′（4′） 4″
求水平面、 (c) 求水平面、正垂面与立体的交线
图3-22 正四棱锥被两平面截切
第四章立体的投影
③判别可见性。
❖ ㈡两平面立体的表面交线
相交形体的表面交线称为相贯线。
两平面立体相贯线的特征：一般情况为空间折线，特殊情况为平面折线，每 段折线是两立体棱面的交线，每个折点是一立体棱线与另一立体的贯穿点。 立体的相贯形式有两种：
一是全贯，即一个立体完全穿过另一个立体，相贯线有两组； 二是互贯，两个立体各有一部分参与相贯，相贯线为一组。 求两平面体相贯线的方法：有两种 （1）交点法——先作出各个平面体的有关棱线与另一立体的交点，再将所有交 点顺次连成折线，即组成相贯线。连点的规则是：只有当两个交点对每个立体 来说，都位于同一个棱面上时才能相连，否则不能相连。 （2）交线法——直接作出两平面立体上两个相应棱面的交线，然后组成相贯线。
（3）投影分析
（二）棱锥体 （1）形体特征: 底面是多边形，棱 线交于一点，侧棱面均为三角形。 （2）安放位置: 底面△ABC平行于H面。 （3）投影分析
【例4-1】 作四棱台的正投影图 解：（1）分析
1）四棱台的上、下底面都与H面平行， 前、后两棱面为侧垂面，左、右两棱面 为正 垂面。 2）上、下两底面与H面平行，其水平投 影反映实形；其正面、侧面投影积聚为 直线。 3）前、后两棱面与W面垂直，其侧面投影积聚为直线；与H、V面倾斜，投 影为缩小的类似形。 4）左、右两个面与V面垂直，其正面投影积聚为直线；与H、W面倾斜，投 影为缩小的类似形。 5）四根斜棱线都是一般位置直线，其投影都不反映实长。
3）连点。 4）判断可见性。
❖ 三、同坡屋面交线的画法
单坡屋面 坡屋面 双坡屋面
四坡屋面 同坡屋面：既屋檐高度相等、各屋面与水平面倾角相等的屋面。 同坡屋面交线的画法，其实 质是求两平面交线的问题。
同坡屋面上各种交线的名称
❖ ㈡两平面立体的表面交线
相交形体的表面交线称为相贯线。
两平面立体相贯线的特征：一般情况为空间折线，特殊情况为平面折线，每 段折线是两立体棱面的交线，每个折点是一立体棱线与另一立体的贯穿点。 立体的相贯形式有两种：
一是全贯，即一个立体完全穿过另一个立体，相贯线有两组； 二是互贯，两个立体各有一部分参与相贯，相贯线为一组。 求两平面体相贯线的方法：有两种 （1）交点法——先作出各个平面体的有关棱线与另一立体的交点，再将所有交 点顺次连成折线，即组成相贯线。连点的规则是：只有当两个交点对每个立体 来说，都位于同一个棱面上时才能相连，否则不能相连。 （2）交线法——直接作出两平面立体上两个相应棱面的交线，然后组成相贯线。
（3）投影分析
（二）棱锥体 （1）形体特征: 底面是多边形，棱 线交于一点，侧棱面均为三角形。 （2）安放位置: 底面△ABC平行于H面。 （3）投影分析
【例4-1】 作四棱台的正投影图 解：（1）分析
1）四棱台的上、下底面都与H面平行， 前、后两棱面为侧垂面，左、右两棱面 为正 垂面。 2）上、下两底面与H面平行，其水平投 影反映实形；其正面、侧面投影积聚为 直线。 3）前、后两棱面与W面垂直，其侧面投影积聚为直线；与H、V面倾斜，投 影为缩小的类似形。 4）左、右两个面与V面垂直，其正面投影积聚为直线；与H、W面倾斜，投 影为缩小的类似形。 5）四根斜棱线都是一般位置直线，其投影都不反映实长。
3）连点。 4）判断可见性。
❖ 三、同坡屋面交线的画法
单坡屋面 坡屋面 双坡屋面
四坡屋面 同坡屋面：既屋檐高度相等、各屋面与水平面倾角相等的屋面。 同坡屋面交线的画法，其实 质是求两平面交线的问题。
同坡屋面上各种交线的名称
机械制图习题答案
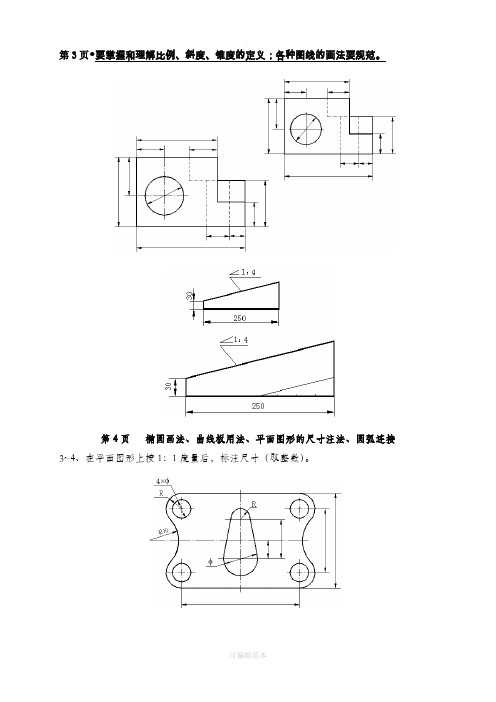
第3页●要掌握和理解比例、斜度、锥度的定义；各种图线的画法要规范。
第4页椭圆画法、曲线板用法、平面图形的尺寸注法、圆弧连接3~4、在平面图形上按1：1度量后，标注尺寸（取整数）。
第6页点的投影3、按立体图作诸点的两面投影。
●根据点的三面投影的投影规律做题。
4、作出诸点的三面投影：点A（25，15，20）；点B距离投影面W、V、H分别为20、10、15；点C在A之左，A之前15，A之上12；点D在A之下8，与投影面V、H等距离，与投影面W的距离是与H面距离的3.5倍。
●根据点的投影规律、空间点的直角坐标与其三个投影的关系及两点的相对位置做题。
各点坐标为：A（25，15，20）B（20，10，15）C（35，30，32）D（42，12，12）6、已知点A距离W面20；点B距离点A为25；点C与点A是对正面投影的重影点，y坐标为30；点D在A的正下方20。
补全诸点的三面投影，并表明可见性。
●根据点的三面投影的投影规律、空间点的直角坐标与其三个投影的关系、两点的相对位置及重影点判断做题。
各点坐标为：A（20,15,15）B（45,15，30）C（20,30,30）D（20,15,10）第7页直线的投影（一）2、作下列直线的三面投影：（1）水平线AB，从点A向左、向前，β＝30°，长18。
（2）正垂线CD，从点C向后，长15。
●该题主要应用各种位置直线的投影特性进行做题。
（具体参见教P73～77）3、判断并填写两直线的相对位置。
●该题主要利用两直线的相对位置的投影特性进行判断。
（具体参见教P77）AB、CD是相交线；PQ、MN是相交线；AB、EF是平行线；PQ、ST是平行线；CD、EF是交叉线；MN、ST是交叉线；5、分别在图（a）、（b）、（c）中，由点A作直线AB与CD相交，交点B距离H面20。
●图(c)利用平行投影的定比性作图。
6、作直线的两面投影：（1）AB与PQ平行，且与PQ同向，等长。
立体的投影习题答案
Part
03
中心投影
中心投影的定义
中心投影的定义
中心投影是一种投影方式， 其中物体通过一个固定点 （即投影中心）投射到投 影面上。
中心投影的原理
当光线通过一个固定点时， 物体的图像会呈现在该点 的对面平面上。
中心投影的特点
中心投影可以产生物体的 真实图像，且投影面与物 体的相对位置不影响图像 的形状和大小。
04
立体图形的投影
立方体的投影
01
02
03
立方体的正面投影
呈现一个正方形，其中包 含三个垂直交叉的线段， 分别代表立方体的长度、 宽度和高度。
立方体的侧面投影
呈现两个相同的长方形， 分别代表立方体的侧面和 顶面。
立方体的顶部投影
呈现一个正方形，代表立 方体的顶面。
圆柱体的投影
圆柱体的正面投影
呈现一个圆形，代表圆柱体的底面。
中心投影的应用
1 2
建筑设计
在建筑设计领域，中心投影常用于绘制建筑物的 三维效果图，以展示建筑物的外观和空间关系。
机械制图
在机械制图领域，中心投影用于绘制零件的三视 图，以准确表达零件的形状和尺寸。
3
艺术绘画
艺术家使用中心投影来创作具有立体感的画作， 通过调整光线和阴影来表现物体的立体形态。
Part
圆柱体的侧面投影
呈现一个矩形，其中包含两个平行的长方形，分 别代表圆柱体的高度和底面的宽度。
圆柱体的顶部投影
呈现一个圆形，代表圆柱体的顶面。
圆锥体的投影
圆锥体的正面投影
呈现一个等腰三角形，其中包含一个垂直的线段，代表圆锥体的 高度。
圆锥体的侧面投影
呈现一个扇形，其中包含一个弧形和两条相交的线段，分别代表圆 锥体的底面圆弧和侧面。
机械制图 第四章 立体及其表面交线的投影
作图步骤：
例：求作截平面平行圆锥轴线的截交线的投影 可在圆锥面上作辅助圆，或作辅助素线法 例：求作截平面斜切圆锥的截交线的投影
3. 切割球体
平面从任何方向截切球体所产生的截交线均为 圆。 截平面平行投影面时，截交线在该投影面上的 投影反映实形。 例：半球开槽的三面投影图
四. 综合举例
【例1】：求作顶针上的表面交线
求作顶针的表面交线
A
Ⅰ Ⅰ
Ⅴ Ⅴ B 求连杆头的表面交线
(a) 两平面立体 相交
(b) 平面立体与 曲面立体相 交
(c) 两曲面立体 相交
其相贯线可看成由平面立体上 有关表面分别切割另一基本体所产 生的截交线所围而成。
立体相交的三种情形
相贯线为两回转 体相交的表面交 线——本节讨论
(a) 两外圆柱面 相交（柱柱相贯）
特例：当截平面与圆柱轴线成450斜切时，截交 线的侧面投影为圆。
综合举例：
【例1】：联轴节的三面投影
【例2】：联轴套的三面投影
【例3】：轴销的三面投影
2. 切割圆锥体
可产生直线、圆、椭圆、双曲线和抛物线等 五种不同性质的截交线。
记忆口诀：
截在锥顶两直线，切去锥顶是椭圆； 保留锥顶双曲线；平行锥面抛物线。
【例2】：求作连杆头表面交线的投影
§4-3 立体相交表面交线的投影
一、概述 两个基本体相交（又叫相贯），在相交表面所产 生的交线，叫立体相交表面交线，又叫相贯线。 相贯线的基本性质：
是两相交回转体表面的共有线、分界线。 一般是闭合的空间曲线，特殊情况下是平面曲线 或直线。
可见，求作相贯线实质上是求作两相交回转体表 面上共有点的问题。 常用两种方法：
【机械制图】第4章 立体的投影
表面求点只
k”
能用辅助圆 法！
M
m
（3）圆球表面上取点
完成圆球表面指定点的另两投影。
m’ (n’)
注意：圆球
m”
表面求点只
k”
能用辅助圆 法！
M
m
（3）圆球表面上取点
完成圆球表面指定点的另两投影。
m’ k’ (n’)
m”
k” (n ”)
注意：圆球 表面求点只 能用辅助圆
法！
(n) M
m k
4.3 立体的截交线
截交线为平面几边形？
——平面七边形
2、投影分析：
截交线的正面投影？
——落在截平面的积聚性投 影上；
截交线的水平投影？
——其中六条边落在六棱柱 棱面的积聚性投影上，另一 条边为截平面与棱柱顶面相 交的一条正垂线。
3、投影作图：
4、整理图线：
【例题3】求正四棱锥被截切后的水平和侧面投影。
6′5′7′
4′8′
Y 可见；反之为不可见。
棱柱表面上取点和取线
已知正六棱柱表面上点M的正面投影及点N的 水平投影，分别求它们的其余两面投影。
a’ d’ n’ m’
a” n” d” m” 请同学们思考：
b’ c’
如果将已知点
b”
c” 加上括号，会是
什么结果？
a
(b)
n
m
d(c)
2. 棱锥的投影
V
a'
X
Z
s'
s” S
n”
请同学们思考：
m’
m”
如果将已知点
a’ 2’ b’ c’ a”(c”)
加上括号，会是 b” 什么结果？
第五讲第4章立体投影(一)
第五讲第4章立体的投影（一）本讲的学习目标：掌握平面立体（棱柱、棱锥）的形状特点，掌握曲面立体（圆柱、圆锥、圆球）的形成原理；熟练掌握基本形体的投影特征以及形体表面上点和线的求解方法。
学习的重点：基本形体的投影特征以及形体表面上点和线的求解方法4.1 平面立体的投影图4-1 房屋形体的分析图4-2 水塔形体的分析基本形体：组成形体的最简单但又规则的几何体，叫做基本形体。
基本形体的分类：根据表面的组成情况，基本形体可分为平面立体和曲面立体两种。
平面立体：表面由若干平面围成的基本体，叫做平面立体。
平面立体类型：有棱柱、棱锥、棱台等。
平面体的投影：作平面立体的投影，就是作出组成平面立体的各平面的投影。
4.1.1 棱柱4.1.1.1 棱柱的投影如图4-3所示，有两个三角形平面互相平行，其余各平面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些平面所围成的基本体称为棱柱。
图4-3 三棱柱体当底面为三角形、四边形、五边形……时，所组成的棱柱分别为三棱柱、四棱柱、五棱柱等。
（a）立体图（b）投影图图4-4 三棱柱的三面投影分析其三面投影图：W投影：投影为三角形。
H投影：投影为两个矩形。
V投影：投影为一个矩形。
4.1.1.2 棱柱表面定点和定线【例4-1】如图4-5所示，已知三棱柱上直线AB、BC的V投影，求另外两个投影。
（a）已知条件（b）作图图4-5 三棱柱表面上的点和线【例4-2】如图4-5所示，已知四棱柱表面上点K的V投影和点M的V投影，求它们的另外两投影。
（a）立体图（b）已知条件（c）作图图4-6 四棱柱表面上的点4.1.2 棱锥定义：由一个多边形平面与多个有公共顶点的三角形平面所围成的几何体称为棱锥。
如图4-6所示为三棱锥。
图4-7-1 三棱锥根据不同形状的底面，棱锥有三棱锥、四棱锥和五棱锥等。
当棱锥底面为正n边形时，称为正n棱锥。
4.1.2.1 棱锥的投影1. 棱锥如图4-7所示为一正三棱锥,三棱锥底面ABC是水平面，后棱面SAC是侧垂面，其它两个侧面都是一般面；棱线SB为侧平线，其它两条棱线为一般线。