计量经济学课程作业
计量经济学作业

计量经济学作业计量经济学作业(5-7)一、作业五1. 在存在异方差情况下,普通最小二乘法(OLS )估计量是有偏的和无效的。
()2. 当存在自相关时,OLS 估计量是有偏的并且也是无效的。
()3. 如果在多元回归模型中,根据通常的t 检验,全部回归系数分别都是统计上不显著的,那么该模型不会有一个高的R 2值。
()4. 在时间序列模型中,遗漏重要解释变量既有可能导致异方差问题,又有可能导致自相关问题。
()5. 变量是非线性的回归模型在计量经济学上不被称作线性回归模型。
()6. 随机误差项μi 与残差e i 是一回事。
()7. 给定显著性水平α及自由度,若计算得到的t 值超过临界的t 值,则接受原假设。
8. 蛛网现象可能会带来计量经济模型的自相关问题。
()9. 无论模型中包括多少个解释变量,总离差平方和(TSS )的自由度总为(n-1)。
()10. 在多元线性回归模型中,方差膨胀因子(VIF )一定是不小于1。
()11. 在存在异方差情况下,常用的OLS 法总是高估了估计量的标准差。
()12. 若假定自相关系数等于1,那么一阶差分变换能够消除自相关。
()13. 存在多重共线时,模型参数无法估计。
()14. 如果在多元回归模型中,根据通常的t 检验,全部回归系数分别都是统计上不显著的,那么该模型不会有一个高的R 2值。
()15. 当我们得到参数区间估计的上下限的具体数值后,就可以说参数的真实值落入这个区间的概率为1-α. ()16. p 值和显著性水平α是一回事。
()17. 只有当μi 服从正态分布时,OLS 估计量才服从正态分布。
()18. 多元回归模型的总体显著性意味着模型中任何一个变量都是统计显著的。
()19. 戈德菲尔德-夸特检验(GQ 检验)可以检验复杂性的异方差。
()20. 残差平方和除以自由度(n-k )始终是随机误差项μi 方差(2σ)的无偏估计量。
()21. 用一阶差分法消除自相关时,我们假定自相关系数等于-1。
计量经济学第一次作业

计量经济学第一次作业一、选择题1、在同一时间不同统计单位的相同统计指标组成的数据组合,是( D )A 、原始数据B 、时点数据C 、时间序列数据D 、截面数据2、同一统计指标按时间顺序记录的数据称为( B )。
A 、横截面数据B 、时间序列数据C 、修匀数据D 、原始数据3、下列模型中不属于线性模型的有( C )A 、u X Y ++=ln 10ββB 、u Z X Y +++=210βββC 、u X Y ++=10ββD 、Y=u X ++10ββ4、半对数模型μββ++=X Y ln 10中,参数1β的含义是( C )A .X 的绝对量变化,引起Y 的绝对量变化B .Y 关于X 的边际变化C .X 的相对变化,引起Y 的期望值绝对量变化D .Y 关于X 的弹性5、设OLS 法得到的样本回归直线为i i i e X Y ++=21ˆˆββ,以下说法不正确的是 ( )A .0=∑i eB .),(Y X 在回归直线上C .Y Y =ˆD .0),(≠i i e X COV6、根据样本资料估计得出人均消费支出Y 对人均收入X 的回归模型为i Y ∧ln =2.00+0.75lnXi ,这表明人均收入每增加1%,人均消费支出将增加( B )A 、0.2%B 、0.75%C 、2%D 、7.5%7、古典线性回归模型的普通最小二乘估计量的特性有A 、无偏性B 、线性性C.最小方差性 D 一致性 E. 有偏性8、利用普通最小二乘法求得的样本回归直线i i X Y 21ˆˆˆββ+=的特点( )A. 必然通过点),(Y XB. 可能通过点),(Y XC. 残差i e 的均值为常数D.i Y ˆ的平均值与i Y 的平均值相等 E. 残差i e 与解释变量i X 之间有一定的相关性二、判断正误(1) 随机误差项u i 与残差项e i 是一回事。
(×)1:Ui 为观察值Yi 围绕它的期望值E(Y|Xi)的离差(deviation ),是一个不可观测的随机变量.2:e 为残差,代表了其他影响Yi 的随机因素的集合,可看成Ui的估计量。
计量经济学第一次作业参考答案

1914
1998
2840 .6010563 .4897674
0
1
2840 4789.801 3361.39 176.1308 50725.66
2840 7.624296
2.9349
0
15
(3) 乌有大学的飘渺教授认为教育对于收入有着重要的影响,她建议估计下面这个回归 方程式:
empjob _ twage *schooling _ yr u
21.03976 133.0146
179.4049
t
7.64 -8.50
21.84ຫໍສະໝຸດ P>|t|0.000 0.000
0.000
[95% Conf. Interval]
119.535 202.0446 -1391.024 -869.3943
3567.096 4270.651
(b) 你能得到所有系数的估计值吗?如果不能,为什么?(提示:考虑上面这个回 归方程中,哪个假设不能成立。) (5 分) 不能,违背了假设: 解释变量不能存在多重共线性.
Variable
female male
birthyear marriage empjob_twage
schooling_yr
Obs
Mean Std. Dev.
Min
Max
2840 .3140845 .464232
0
1
2840 .6859155 .464232
0
1
2840 1974.865 11.2741
=
Adj R-squared =
Root MSE
=
2840 70.06 0.0000 0.0471 0.0464 3282.5
计量经济学课后作业

2.4以中国改革开放以来只能各国国民总收入为解释变量X 、最终消费为被解释变量Y ,建立线性回归方程利用Eviews 对模型进行OLS 估计得到结果如下图所示:由上图可得,线性回归方程为t 3044.3430.530112t Y X ∧=+t =(3.399965)(54.82076)回归估计的标准误差3580.903σ∧=,可决系数20.990769R =,修正后的可决系数20.990440R =,查表得t 的临界值为2.048,显然回归系数都能通过t 检验。
如果2008年全年国民总收入为300670亿元,预测可能达到的最终消费水平为: 2008ˆ3044.3430.530112300670162433.1180Y =+⨯=(亿元) 对最终消费的均值置信度为95%的预测区间为:2^^22()1f f iX X Y t n x ασ-+∑ 由Eviews 计算国民总收入X 变量样本数据的统计量得:68765.51x σ= 63270.07X = n=30则有 222(1)68765.51(301)137132165601.2429i x x n σ=-=⨯-=∑22()(30067063270.07)56358726764.0049f X X -=-=取0.05α=,2008ˆ162433.1180Y =,0.025(30-2)=2.048t ,已知 ˆ3580.903σ=,平均值置信度95%的预测区间为: 2^^22()1f f iX X Y t n x ασ-+∑ =156358726764.0049162433.1180 2.0483580.90330137132165601.2429⨯⨯+=162433.11884888.4110(亿元)2.5(1)航班正点率与投诉率的散点图如下图所示:(2)由上述散点图可得,航班正点率与投诉率呈负相关关系。
(3)以投诉率为解释变量,航班正点率为被解释变量建立回归方程,利用Eviews 对模型进行OLS 估计,得到结果如下图所示:即 i iX Y 070414.0017832.6ˆ-= (1.017832)(-0.014176)t=(5.718961) (-4.967254)R 2=0.778996 F=24.67361从检验结果可以看出, 航班正点到达比率对乘客投诉次数确有显著影响。
计量经济学作业1-4

作业一1、双对数模型01ln ln Y X u ββ=++中,参数β1的含义是( )A .X 的相对变化,引起Y 的期望值绝对量变化B .Y 关于X 的边际变化C .X 的绝对量发生一定变动时,引起因变量Y 的相对变化率D .Y 关于X 的弹性2、设OLS 法得到的样本回归直线为12i i i Y X e ββ=++,以下说法不正确的是 ( ) A .0i e =∑ B .(,)X Y 在回归直线上 C .Y Y = D .(,)0i i COV X e ≠3、下列说法正确的有( )A .时序数据和横截面数据没有差异B. 对总体回归模型的显著性检验没有必要C. 总体回归方程与样本回归方程是有区别的D. 判定系数R 2不可以用于衡量拟合优度4、在回归分析中,下列有关解释变量和被解释变量的说法正确的有( )A .被解释变量和解释变量均为随机变量B .被解释变量和解释变量均为非随机变量C .被解释变量为随机变量,解释变量为非随机变量D .被解释变量为非随机变量,解释变量为随机变量5、一元线性回归分析中的回归平方和ESS 的自由度是( )A 、nB 、n-1C 、n-kD 、16、对样本的相关系数γ,以下结论错误的是( )A .γ越接近1,X 与Y 之间线性相关程度高B .γ越接近0,X 与Y 之间线性相关程度高C .01γ≤≤D . X 与Y 相互独立,则γ=0,7、同一时间,不同单位相同指标组成的观测数据称为( )A .原始数据B .横截面数据C .时间序列数据D .修匀数据8、根据样本资料估计得出人均消费支出Y 对人均收入X 的回归模型为ln i Y =2.00+0.75lnXi ,这表明人均收入每增加1%,人均消费支出将增加( )A 、0.2%B 、0.75%C 、2%D 、7.5%9、利用OLS 估计得到的样本回归直线12i i Y X ββ=+ 必然通过点 ( )A 、(,)X YB 、(,0)XC 、(0,)YD 、(0,0)10、多元线性回归分析中的 RSS 反映了( )A .应变量观测值总变差的大小B .应变量回归估计值总变差的大小C .应变量观测值与估计值之间的总变差D .Y 关于X 的边际变化11、将内生变量的前期值作解释变量,这样的变量称为( )A 、虚拟变量B 、控制变量C 、政策变量D 、滞后变量12、回归分析中使用的距离是点到直线的垂直坐标距离。
计量经济学作业第5篇(含答案)

计量经济学作业第5篇(含答案)第5章习题一、单项选择题1.对于一个含有截距项的计量经济模型,若某定性因素有m个互斥的类型,为将其引入模型中,则需要引入虚拟变量个数为()A. mB. m-1C. m+1D. m-k2.在经济发展发生转折时期,可以通过引入虚拟变量方法来表示这种变化。
例如,研究中国城镇居民消费函数时。
1991年前后,城镇居民商品性实际支出Y 对实际可支配收入X的回归关系明显不同。
现以1991年为转折时期,设虚拟变量,数据散点图显示消费函数发生了结构性变化:基本消费部分下降了,边际消费倾向变大了。
则城镇居民线性消费函数的理论方程可以写作()A. B.C. D.3.对于有限分布滞后模型在一定条件下,参数可近似用一个关于的阿尔蒙多项式表示(),其中多项式的阶数m必须满足()A. B. C.D.4.对于有限分布滞后模型,解释变量的滞后长度每增加一期,可利用的样本数据就会( )A. 增加1个B. 减少1个C. 增加2个D. 减少2个5.经济变量的时间序列数据大多存在序列相关性,在分布滞后模型中,这种序列相关性就转化为()A.异方差问题 B. 多重共线性问题C.序列相关性问题 D. 设定误差问题6.将一年四个季度对因变量的影响引入到模型中(含截距项),则需要引入虚拟变量的个数为()A. 4B. 3C.2 D. 17.若想考察某两个地区的平均消费水平是否存在显著差异,则下列那个模型比较适合(Y代表消费支出;X代表可支配收入;D2、D3表示虚拟变量)()A. B.C. D.二、多项选择题1.以下变量中可以作为解释变量的有()A. 外生变量B. 滞后内生变量C. 虚拟变量D. 先决变量E. 内生变量2.关于衣着消费支出模型为:,其中Y i 为衣着方面的年度支出;Xi为收入,=女性男性12iD;=大学毕业及以上其他13iD则关于模型中的参数下列说法正确的是()A.表示在保持其他条件不变时,女性比男性在衣着消费支出方面多支出(或少支出)差额B.表示在保持其他条件不变时,大学毕业及以上比其他学历者在衣着消费支出方面多支出(或少支出)差额C.表示在保持其他条件不变时,女性大学及以上文凭者比男性和大学以下文凭者在衣着消费支出方面多支出(或少支出)差额D. 表示在保持其他条件不变时,女性比男性大学以下文凭者在衣着消费支出方面多支出(或少支出)差额E. 表示性别和学历两种属性变量对衣着消费支出的交互影响三、判断题1.通过虚拟变量将属性因素引入计量经济模型,引入虚拟变量的个数与样本容量大小有关。
计量经济学作业(三)
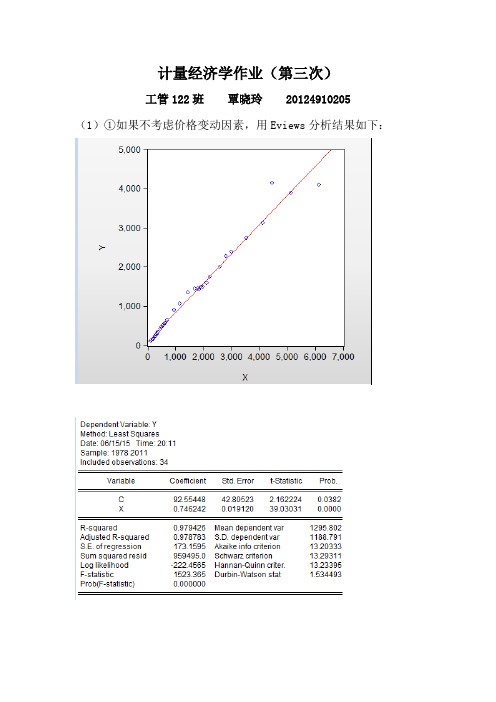
计量经济学作业(第三次)工管122班覃晓玲 20124910205(1)①如果不考虑价格变动因素,用Eviews分析结果如下:设Y表示农村人均生活消费支出,X表示农村人均纯收入,则建立样本回归函数如下:Y=92.55448+0.746242X(42.80523)(0.019120)t=(2.162224)(39.03031)R2=0.979426 F=1523.365 n=34②用White检验是否存在异方差由上图可知,nR2=13.62708,由White检验可知,在a=0.05下,查X2分布表,得临界值X20.05(2)=5.9915,而nR2=13.62708> X20.05(2)=5.9915,所以拒绝原假设,表明模型存在异方差。
③运用WLS法对异方差性进行修正由上图可知,运用WLS消除了异方差性后,参数t检验均显著,F检验也显著,即估计结果为:Y=17.69310+0.821014X(6.283235)(0.016865)t=(2.815922)(48.68011)R2=0.986676 DW=0.605854 F=2369.753(2)①如果考虑价格变动因素,用Eviews分析结果如下:设Y表示农村人均生活消费支出,X表示农村人均纯收入,P表示商品零售价格指数,则建立样本回归函数如下:Y=43.41668+0.741684X+0.235028P(71.22936)(0.019905)(0.271701)t=(0.609534)(37.26101)(0.865026)R2=0.979911 F=756.0650 n=34②运用White检验是否存在异方差由上图可知,nR2=19.25463,由White检验可知,在a=0.05下,查X2分布表,得临界值X20.05(5)=11.0705,而nR2=19.25463> X20.05(2)=11.0705,所以拒绝原假设,表明模型存在异方差。
计量经济作业题参考答案

X
0.0814545454545 0.0112158879832 7.26242501502 8.69975385378e-05
R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
1328.09375 393.649455929 14.1216750946 14.2132835885 34.1723395787 2.14765879739e-06
∑ Y = n Yi =683939.1, i=1 n
∑ 方差 SY2
=
n i =1
(Yi − Y )2 n −1
=
41167.492
≈ 1, 694, 762, 233
2)求 X 的均值和方差。
∑ X = n Xi =67857.58, i=1 n
∑ 方差
S
2 X
=
n i =1
(Xi − X )2 n −1
Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
14.5 19.6914956263
4.15406062604 4.19788830989 1002.04709591 8.11447150656e-09
解:如上表所示,回归结果如下:(格式参见课本 P137—7.7 回归分析结果的报
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1269.4
44888.1
1981
32502.01
15679
1334.9
44574
1982
35450.01
16614.3
1513.4
44177
1983
38727.98
18022.1
1659.8
44644.1
1984
40731.02
19497.2
1739.8
44453
1985
广东
2415.5
31084.4
山西
430.5
5733.4
广西
282.7
5955.7
内蒙古
347.9
6091.1
海南
88.0
1223.3
辽宁
815.7
11023.5
重庆
294.5
4122.5
吉林
237.4
5284.7
四川
629.0
10505.3
黑龙江
335.0
7065.0
贵州
211.9
2741.9
上海
普通最小二乘法建立一元线性回归模型:
将Y作为被解释变量,GDP作为解释变量利用eviews6.0的Equation进行模型估计,输出结果报告如下:
Ss
ssa
由上表可知货物运输量随国内生产总值变化的一元线性回归方程为: Y = 12596.27++ 26.9542* GDP
其中斜率26.95415表示国内生产总值每增加一元,货物运输量平均增长26.9542万辆。
山东
1308.4
25965.9
新疆
220.6
3523.2
河南
625.0
15012.5
以Eviews软件完成以下问题:
(1)作出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义;
散点图如图所示:
建立如下的回归模型
根据Eviews软件对表中数据进行回归分析的计算结果知:
R^2 = 0.760315 F=91.99198
F统计量=42.79505,其伴随概率0.000028<0.05,在5%的显著性水平下,拒绝原假设,接受备择假设,即方程总体是显著的。
所有系数的t统计量伴随概率均小于0.05,在5%的显著性水平下,拒绝原假设。说明系数显著,GDP对货物运输量有显著影响。
(4)加入2000年某市以1980年为不变价的国内生产总值为620亿元,求2000年货物运输量预测值及预测区间。
广东石油化工学院2015—2016学年第二学期
《计量经济学》作业
班级:
作业1
1、下表是中国2007年各地区税收 和国内生产总值GDP的统计资料。
单位:亿元
地区
Y
GDP
地区
Y
G9353.3
湖北
434.0
9230.7
天津
438.4
5050.4
湖南
410.7
9200.0
河北
618.3
13709.5
1993
21640
276.8
1987
18400
184.07
1994
23783
316.38
1988
16693
194.75
1995
24040
363.52
1989
15543
197.86
1996
24133
415.51
1990
15929
208.55
1997
25090
465.78
1991
18308
221.06
1998
3、已知我国粮食产量Q(万吨)、农业机械总动力X1(万千瓦)、化肥施用量X2(万吨)、土地灌溉面积X3(千公顷)1978年-1998年赝本观测值见下表。
年份
Q
X1
X2
X3
1978
30477.01
11749.9
884
44965.3
1979
33212
13379.6
1086.3
45003
1980
32055.99
24505
509.1
资料来源:《天津统计年鉴》,1999年。
(1)估计一元线性回归模型;
建立货物运输量Y随国内生产总值GDP的一元线性回归模型
从图中可以看出Y与GDP之间可能存在线性相关关系。但是我们无法得出Y与GDP之间精确的计量关系,因此用普通最小二乘法进行一元线性回归模型的估计。
(2)对估计结果作结构分析;
(3)若2008年某地区国内生产总值为8500亿元,求该地区税收收入的预测值和预测区间。
由上图可得知该地区国内生产总值的预测值:
Yi= -10.63+0.071*8500=592.87(亿元)
下面给出国内生产总值90%置信度的预测区间
E(GDP)=8891.126
Var(GDP)=57823127.64
在90%的置信度下,某地区E(Y0)的预测区间为(60.3,1125.5)。
2、已知某市货物运输总量Y(万吨),国内生产总值GDP(亿元,1980不变价)1985年-1998年的样本观测值见下表。
年份
Y
GDP
年份
Y
GDP
1985
18249
161.69
1992
17522
246.92
1986
18525
171.07
假如2000年某市以1980年为不变价的国内生产总值为620亿元,求2000年货物运输量预测值及预测区间。
国内生产总值为620亿元,货物运输量的预测值=12596.27++ 26.9542* 620 =29307.84万吨。经计算
故货物运输量的预测区间为:(28873.08746万辆,29742.59254万辆)。
1975.5
12188.9
云南
378.6
4741.3
江苏
1894.8
25741.2
西藏
11.7
342.2
浙江
1535.4
18780.4
陕西
355.5
5465.8
安徽
401.9
7364.2
甘肃
142.1
2702.4
福建
594.0
9249.1
青海
43.3
783.6
江西
281.9
5500.3
宁夏
58.8
889.2
(3)对估计结果进行统计检验;
对所建立建立的回归方程进行检验(t(12)=2.18)
1经济学意义上的检验
从回归方程来看,国内生产总值每增加一元,货物运输量平均增长26.9542万辆。系数为正,符合经济发展规律,是具有经济意义的模型。
2计学意义上的检验
可决系数R-squared=0.762752,说明被解释变量的变异中有76%以上。可由方程解释,模型总体拟合程度还不错。
斜率的经济意义:国内生产总值GDP每增加1亿元,国内税收增加0.071亿元。
(2)对所建立的方程进行检验;
从回归估计的结果看,模型拟合较好。可决系数R2=0.760315,表明国内税收变化的76.03%可由国内生产总值GDP的变化来解释。从斜率项的t检验值看,大于10%显著性水平下自由度为n-2=29的临界值t0.05(29)=1.699,且该斜率值满足0<0.071<1,符合经济理论中税收乘数在0与1之间的说法,表明2007年,国内生产总值GDP每增加1亿元,国内税收增加0.071亿元。
