结构力学第四章
合集下载
《结构力学》第四章静定拱

受力特点概述
静定拱在荷载作用下,拱身主要承受 压力作用,这使得拱具有较好的受压 性能。
拱身受压力作用
由于拱的曲线形状和荷载作用位置的 不同,拱身内力分布通常不均匀,需 要进行详细的内力分析。
内力分布不均匀
静定拱在荷载作用下,其变形主要以 压缩变形为主,弯曲变形相对较小。
变形以压缩为主
影响因素分析
面内失稳
1
拱在面内发生屈曲,导致承载力急剧下降。
面外失稳
2
拱在面外方向发生侧倾或扭转,失去原有形状。
局部失稳
3
拱的局部区域发生失稳,如拱脚的局部压曲等。
提高稳定性的措施
合理选择拱的轴线形式 使拱在受力时能够均匀分布荷载,避 免应力集中。
加强拱的横向联系
通过设置横撑、横系梁等构件,增强 拱的横向稳定性。
贰
静定拱的受力特点
受力分析基本假设
拱身是理想弹性体 在分析中,假设拱身材料符合胡克定律, 即应力与应变成正比关系。 荷载作用在拱的节点上 为简化计算,通常将荷载(如均布荷载、 集中力等)作用在拱的节点上进行分析。 忽略拱身自重影响 在分析中,通常忽略拱身自重对受力的影 响,或将其简化为等效荷载进行处理。
增加拱的刚度
采用高强度材料、增加截面尺寸等措 施,提高拱的整体刚度。
考虑施工方法和顺序
合理的施工方法和顺序可以有效减少 拱在施工过程中的变形和应力,有利 于提高稳定性。
陆
静定拱的工程应用
桥梁工程中的应用
拱桥
静定拱是拱桥的主要结构形式,能够承受较大的竖向荷载和水平推 力,具有良好的经济性和美观性。
习题一
某静定拱的跨度为L,矢高为f,承受均布 荷载q作用,试求其拱脚处的水平推力H和 竖向反力V。
结构力学第四章

M
(2将)虚位移X 与/ 实C 际 力a /状b 态代无入关得,故:可设
B
X X
0
X
P
x
b1P
/
a
C
0
(3通)求常解取时关键一步X 是找1出虚位x 移状态的位移关系。
(4)用单几位何位法移来解法静(U力n平it-衡D问isp题lacement Method)
2、虚功原理用于虚设的平衡力状态与实际的协 调位移状态之间。
微段外力功 dW= dWg+dWi
所有微段的外力功之和:
所有微段的外力功之和:
Wex =∫dWe+∫dWn =∫dWe =δWe
Ude =∫dWi =δWi
故有Wex = Ude成立。
几个问题:
1. 虚功原理里存在两个状态: 力状态必须满足平衡条件;位移状态必须满足协调
条件。
2. 原理的证明表明:原理适用于任何 (线性和非线性)的 变形体,适用于任何结构。
二、结构的虚变形功 平面杆系结构k状态微段外力、m状态的变形为
微段受力 微段拉伸
微段剪切
微段弯曲
整个平面杆系结构,结构的虚变形功为 Ude =Σ∫[FNkδεm+FQkδγm+Mkδθm]ds
§4-3. 虚功原理
一、变形体的虚功原理
原理的表述:
任何一个处于平衡状态的变形体,当 发生任意一个虚位移时,变形体所受外力 在虚位移上所作的总虚功Wex,恒等于变 形体各微段外力在微段变形位移上作的虚
例. 求 A 端支座发生竖向位移 c 时引起C点的竖向位移 . A
c
BC
1
A
B
A
C
a
b C
YA
结构力学 第四章 三铰拱

杆轴线为曲线 在竖向荷载作 用下不产生水 平反力。 平反力。
FP
曲梁
三铰拱
第四章 三铰拱
三、拱常用的形式
静定拱
三铰拱
两铰拱
超静定拱
无铰拱
第四章 三铰拱
四、拱的有关概念
顶铰 拱轴线 平拱 拱趾铰 跨度 拱趾铰 拱轴线 拱(矢)高
斜拱
拉杆拱
第四章 三铰拱 §4-2 三铰拱的支座反力和内力 一、支反力 1、竖向反力 A ∑ M A = 0, VB l − M ABP = 0 H A
第四章 三铰拱
第四章 三铰拱
§4-1 概述 §4-2 三铰拱的支座反力和内力 §4-3 压力线与合理拱轴
第四章 三铰拱
§4-1 概述 实例——拱桥 一、实例 拱桥 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承受轴向压力为主 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。
第四章 三铰拱 [例4-1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: 1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: 三铰拱及其所受荷载如图所示 y=4fx(l-x)/l2,求支座反力,并绘制内力图。 求支座反力,并绘制内力图。 解: (1) 反力计算
4 × 4 + 1× 8 ×12 0 VA = VA = 16 = 7kN ( ↑ ) 7kN
M ABP VB = l l 同跨度同荷载简支梁(代 同跨度同荷载简支梁( 的支座反力: 梁)的支座反力:
i i
P
q
C
f
B
l1
l − l1
HB VB
∑ Pa =
VA
结构力学第四章

Wex =∫dWe+∫dWn =∫dWe =δWe
2.利用平衡条件计算 所有微段的外力虚功之和 Ude 微段位移分 刚体位移 ab ab 为两部分 变形位移 ab ab 微段外力功 在刚体位移上的功dWg 分为两部分 在变形位移上的功dWi 微段外力功 dW= dWg+dWi 所有微段的外力功之和:
1 YA c 0
bc / a
(1)所建立的虚功方程, 实质上是几何方程。 (2)虚设的力状态与实际位移状 态无关,故可设单位广义力 P=1 (3)求解时关键一步是 找出虚力状态的静力 平衡关系。 (4)是用静力平衡法来解几何问题。
单位位移法的虚功方程 单位荷载法的虚功方程
三、图形分解 求 B
20 A
MP
20
A
B
40
B
20 kN m
A
20 kN m
EI
40 B
40 kN m 10 m
1
40 kN m
Mi
1/ 3
2/3
1 1 2 B ( 10 40 EI 2 3 1 1 500 10 20 ) ( ) 2 3 3EI
三、图形分解
微段受力
微段拉伸
微段剪切
微段弯曲
整个平面杆系结构,结构的虚变形功为
Ude =Σ∫[FNkδεm+FQkδγm+Mkδθm]ds
§4-3. 虚功原理
一、变形体的虚功原理
原理的表述:
任何一个处于平衡状态的变形体,当 发生任意一个虚位移时,变形体所受外力 在虚位移上所作的总虚功Wex,恒等于变 形体各微段外力在微段变形位移上作的虚 功之和Ude。也即恒有如下虚功方程成立
求 B
2.利用平衡条件计算 所有微段的外力虚功之和 Ude 微段位移分 刚体位移 ab ab 为两部分 变形位移 ab ab 微段外力功 在刚体位移上的功dWg 分为两部分 在变形位移上的功dWi 微段外力功 dW= dWg+dWi 所有微段的外力功之和:
1 YA c 0
bc / a
(1)所建立的虚功方程, 实质上是几何方程。 (2)虚设的力状态与实际位移状 态无关,故可设单位广义力 P=1 (3)求解时关键一步是 找出虚力状态的静力 平衡关系。 (4)是用静力平衡法来解几何问题。
单位位移法的虚功方程 单位荷载法的虚功方程
三、图形分解 求 B
20 A
MP
20
A
B
40
B
20 kN m
A
20 kN m
EI
40 B
40 kN m 10 m
1
40 kN m
Mi
1/ 3
2/3
1 1 2 B ( 10 40 EI 2 3 1 1 500 10 20 ) ( ) 2 3 3EI
三、图形分解
微段受力
微段拉伸
微段剪切
微段弯曲
整个平面杆系结构,结构的虚变形功为
Ude =Σ∫[FNkδεm+FQkδγm+Mkδθm]ds
§4-3. 虚功原理
一、变形体的虚功原理
原理的表述:
任何一个处于平衡状态的变形体,当 发生任意一个虚位移时,变形体所受外力 在虚位移上所作的总虚功Wex,恒等于变 形体各微段外力在微段变形位移上作的虚 功之和Ude。也即恒有如下虚功方程成立
求 B
结构力学第四章知识讲解

位移协调系(位移状态m):在结构的边界和内部都必须是分段光滑 连续的,在边界上满足位移边界条件且是微小的位移系。
虚功原理:
设有一变形体系,分布存在两个独立无关的静力平衡系和位移协调 系,则力系中的外力经位移系中的位移所作的虚功恒等于变形体系 各微段外力在变形位移上虚功和。即:
以平面刚架为例证明虚功原理: 静力平衡力系k: 截面内力分量:
求解步骤:
(1)解除所求约束力的约束,代之以约束力,得k状态。 (2)沿所求约束力的方向给以一位虚位移,得m状态。 (3)由虚位移原理建立虚功方程,求解约束力。
例 利用单位位移法求两跨静定梁在图示荷载下的支座D的反力和截面E的 弯矩。 解 : 1.求支座反力 :
(1)解除D支座,代之一约束力 ,得 静力状态k;
恒等于变形体系各微段外力在变形位移上的虚功和。
静力平衡系
位移协调系
(虚拟)
(真实)
单位荷载法:
在应用虚力原理时,特别的假设单位荷载。
求解步骤:
(1)沿所求位移的方向加上对应的单位虚力,得静力状态k。 (2)实际位移状态m,建立虚功方程。
例 试用单位荷载法求图示两跨静定梁,由于中间支座B向下移动 , 中间铰C的竖向位移 。 解: 1.建立静力状态k: 2.建立虚功方程:
静力状态k的集中力 在位移状态m的位移Δkm 上所作的虚功:
2.力偶虚功: 静力状态k的力偶 在位移状态m的角位移θkm 上所作的虚功:
3.均布力虚功: 静力状态k的均布力在位移状态m 上所作的虚功:
4.等量反向共线的两集中力的虚功:
静力状态k的力在位移状态m 上所作的虚功: 平衡力系在刚体位移上的虚功=?
解:(1)桁架各杆的剪力和弯矩为零,轴力为常数,建立虚力方程,位移公式简 化为
虚功原理:
设有一变形体系,分布存在两个独立无关的静力平衡系和位移协调 系,则力系中的外力经位移系中的位移所作的虚功恒等于变形体系 各微段外力在变形位移上虚功和。即:
以平面刚架为例证明虚功原理: 静力平衡力系k: 截面内力分量:
求解步骤:
(1)解除所求约束力的约束,代之以约束力,得k状态。 (2)沿所求约束力的方向给以一位虚位移,得m状态。 (3)由虚位移原理建立虚功方程,求解约束力。
例 利用单位位移法求两跨静定梁在图示荷载下的支座D的反力和截面E的 弯矩。 解 : 1.求支座反力 :
(1)解除D支座,代之一约束力 ,得 静力状态k;
恒等于变形体系各微段外力在变形位移上的虚功和。
静力平衡系
位移协调系
(虚拟)
(真实)
单位荷载法:
在应用虚力原理时,特别的假设单位荷载。
求解步骤:
(1)沿所求位移的方向加上对应的单位虚力,得静力状态k。 (2)实际位移状态m,建立虚功方程。
例 试用单位荷载法求图示两跨静定梁,由于中间支座B向下移动 , 中间铰C的竖向位移 。 解: 1.建立静力状态k: 2.建立虚功方程:
静力状态k的集中力 在位移状态m的位移Δkm 上所作的虚功:
2.力偶虚功: 静力状态k的力偶 在位移状态m的角位移θkm 上所作的虚功:
3.均布力虚功: 静力状态k的均布力在位移状态m 上所作的虚功:
4.等量反向共线的两集中力的虚功:
静力状态k的力在位移状态m 上所作的虚功: 平衡力系在刚体位移上的虚功=?
解:(1)桁架各杆的剪力和弯矩为零,轴力为常数,建立虚力方程,位移公式简 化为
结构力学第四章静定结构总论

2008年10月13日星期一9时35分12秒
§4-6
2)三角形桁架
FP FP
各种桁架的受力特点
FP FP/2 h 4d
C
FP/2
简支梁C 点的弯 矩
(1)上弦杆
0 2.5FP 2d FP d 0.5FP 2d MC FN r r
在往下的竖向荷载作用下,三角形桁架的上弦杆受压,并 且抵抗弯矩。由于简支梁的弯矩是按抛物线变化的,而r是按三 角形变化的,因此上弦杆的内力中间小,两边大。
2008年10月13日星期一9时35分12秒
§4-6
FP FP/2
D
各种桁架的受力特点
FP FP FP FP FP/2 h 简支梁D 点的弯 矩
3)抛物线形桁架
6d (2)下弦杆
0 3FP 2d FP d 0.5FP 2d M D FN r r
在往下的竖向荷载作用下,抛物线形桁架的下弦杆受拉, 并且抵抗弯矩。由于简支梁的弯矩是按抛物线变化的,r也是按 抛物线变化的,因此下弦杆的内力相同。
2008年10月13日星期一9时35分12秒
2008年10月13日星期一9时35分12秒
§4-6
FP FP/2
各种桁架的受力特点
FP FP FP FP FP/2 h
3)抛物线形桁架
6d (3)腹杆
可以证明抛物线形桁架腹杆的内力等于零,剪力由上 弦杆受承受。
2008年10月13日星期一9时35分12秒
§4-6
各种桁架的受力特点
通过上述分析可以得出以下结论: 1、平行弦桁架 由于杆件内力分布不均匀,会造成材料的浪费。但构造 简单,经常应用于小跨度结构。 2、三角形桁架 在支座处,桁架的夹角小,内力大,构造复杂,因此一 般用于小跨度的屋架。 3、抛物线形桁架 由于上下弦杆的内力基本相同,因此最节省材料,但是 结点构造复杂,一般用于大跨度结构。
§4-6
2)三角形桁架
FP FP
各种桁架的受力特点
FP FP/2 h 4d
C
FP/2
简支梁C 点的弯 矩
(1)上弦杆
0 2.5FP 2d FP d 0.5FP 2d MC FN r r
在往下的竖向荷载作用下,三角形桁架的上弦杆受压,并 且抵抗弯矩。由于简支梁的弯矩是按抛物线变化的,而r是按三 角形变化的,因此上弦杆的内力中间小,两边大。
2008年10月13日星期一9时35分12秒
§4-6
FP FP/2
D
各种桁架的受力特点
FP FP FP FP FP/2 h 简支梁D 点的弯 矩
3)抛物线形桁架
6d (2)下弦杆
0 3FP 2d FP d 0.5FP 2d M D FN r r
在往下的竖向荷载作用下,抛物线形桁架的下弦杆受拉, 并且抵抗弯矩。由于简支梁的弯矩是按抛物线变化的,r也是按 抛物线变化的,因此下弦杆的内力相同。
2008年10月13日星期一9时35分12秒
2008年10月13日星期一9时35分12秒
§4-6
FP FP/2
各种桁架的受力特点
FP FP FP FP FP/2 h
3)抛物线形桁架
6d (3)腹杆
可以证明抛物线形桁架腹杆的内力等于零,剪力由上 弦杆受承受。
2008年10月13日星期一9时35分12秒
§4-6
各种桁架的受力特点
通过上述分析可以得出以下结论: 1、平行弦桁架 由于杆件内力分布不均匀,会造成材料的浪费。但构造 简单,经常应用于小跨度结构。 2、三角形桁架 在支座处,桁架的夹角小,内力大,构造复杂,因此一 般用于小跨度的屋架。 3、抛物线形桁架 由于上下弦杆的内力基本相同,因此最节省材料,但是 结点构造复杂,一般用于大跨度结构。
01 第四章 空间力系(结构力学)

§4–3 空间力偶
4.3.1 力偶矩以矢量表示--力偶矩矢
F1 F2 F1 F2
⑴空间力偶的三要素 a.大小:力与力偶臂的乘积; b.方向:由转动方向依据右手定则确定 c.作用面方位:力偶作用面。
⑵力偶矩矢 M BA F
a.大小:由矢的长短表示; b.方位:与力偶作用面的法向方位相同; c.指向:与力偶转向的关系服从右手定则。
⑵力偶系的平衡条件 空间力偶系平衡的充分必要条件是 :
合力偶矩矢等于零 即
M 0
M ( M x )2 ( M y )2 ( M z )2 0
Mx 0 My 0 Mz 0
称为空间力偶系的平衡方程。
求:工件所受合力偶矩在 x, y, z 轴上的投影。
解:把力偶用 力偶矩矢表示, 平行移到点A。
M x Mix M3 M 4 cos 45 M5 cos 45 193.1N m M y Miy M 2 80N m M z Miz M1 M 4 cos 45 M5 cos 45 193.1N m
Mx Mx , M y M y , Mz Mz
a.合力偶矩矢的大小
M ( M x )2 ( M y )2 ( M z )2
b.方向余弦 cos M x
M cos M y
M
cos M z
M
例4-6 已知:在工件四个面上同时钻5个孔,每个孔 所受切削力偶矩均为80N·m。
4.3.1 力偶矩以矢量表示--力偶矩矢
F1 F2 F1 F2
⑴空间力偶的三要素 a.大小:力与力偶臂的乘积; b.方向:由转动方向依据右手定则确定 c.作用面方位:力偶作用面。
⑵力偶矩矢 M BA F
a.大小:由矢的长短表示; b.方位:与力偶作用面的法向方位相同; c.指向:与力偶转向的关系服从右手定则。
⑵力偶系的平衡条件 空间力偶系平衡的充分必要条件是 :
合力偶矩矢等于零 即
M 0
M ( M x )2 ( M y )2 ( M z )2 0
Mx 0 My 0 Mz 0
称为空间力偶系的平衡方程。
求:工件所受合力偶矩在 x, y, z 轴上的投影。
解:把力偶用 力偶矩矢表示, 平行移到点A。
M x Mix M3 M 4 cos 45 M5 cos 45 193.1N m M y Miy M 2 80N m M z Miz M1 M 4 cos 45 M5 cos 45 193.1N m
Mx Mx , M y M y , Mz Mz
a.合力偶矩矢的大小
M ( M x )2 ( M y )2 ( M z )2
b.方向余弦 cos M x
M cos M y
M
cos M z
M
例4-6 已知:在工件四个面上同时钻5个孔,每个孔 所受切削力偶矩均为80N·m。
结构力学第4章静定拱(f)

FH
FH
由边界条件
x 0, y 0 : x 0, y 0 :
A qc
B0
合理拱轴线的方程为
y qc (cosh x 1)
FH
§4-3 三铰拱的合理拱轴线
例4-3 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
解:由图a,荷载为非竖向荷载。
思路:假定拱处于无弯矩状态,根据平衡 条件推求合理拱轴线方程。
Fi ai l
Fx 0 FAH FBH FH
相应简支梁
取左半拱为隔离体
MC 0
FH
FAV l1 F1(l1 a1) f
可 得
FAV FBV
FA0V FB0V
FH
M
0 C
f
三铰拱的反力只与 荷载及三个铰的位置有 关,与拱轴线形状无关;
推力FH 与拱高 f 成反比。
§4-2 三铰拱的计算
§4-2 三铰拱的计算
2、内力的计算
压力为正
任一截面的轴力等于该截面一 侧所有外力在该截面法线方向 上的投影代数和。
FN FAV sin FH cos F1 sin (FAV F1) sin FH cos FS0 sin FH cos
相应简支梁
§4-2 三铰拱的计算
2、内力的计算
区别拱与梁的主要标志:推力的存在与否。
§4-1 概述
拉杆拱: 拱两支座间的拉杆代替支座承受水平推力
拉杆做成折线形可获得较大空间
高跨比:f/l
平拱: 两拱趾在同一水平线上 斜拱: 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算
由拱的整体平衡
M B 0 FAV
Fibi l
M A 0 FBV
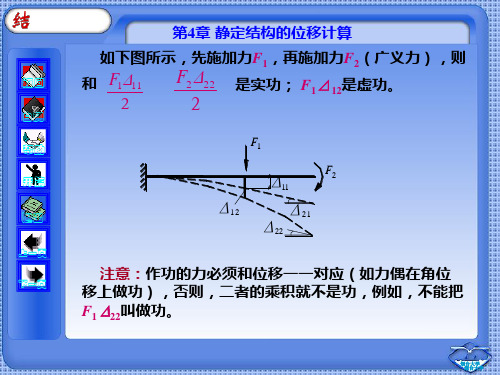
结构力学第4章

自测
静定结构当支座产生移动时,整个结构发生刚体位移, 静定结构当支座产生移动时,整个结构发生刚体位移, 因而不产生变形,应用刚体的虚功原理W =0, 因而不产生变形,应用刚体的虚功原理 e=0,得
帮助 开篇
退出
上一页
下一页
∆ ×1 + ∑ Rc = 0
式中, 为虚单位力引起的支座反力 为虚单位力引起的支座反力, 式中,R为虚单位力引起的支座反力,c 为实际支座 位移,当二者方向一致时,其乘积取正值,相反时取负值。 位移,当二者方向一致时,其乘积取正值,相反时取负值。 若结构是超静定的,则当支座移动时, 若结构是超静定的,则当支座移动时,将会产生内力和变 形,故 Wi≠0,因此应该用变形体的虚功原理求位移。 ,因此应该用变形体的虚功原理求位移。 4.温度作用时的位移计算 4.温度作用时的位移计算 静定结构在温度变化时,杆件不产生切应变, 静定结构在温度变化时,杆件不产生切应变,而轴向 线应变和曲率分别为 / ε =α t0, κ=α∆t/h
A B
帮助 开篇
退出
上一页
下一页
c
烟台大学 烟台大学
第4章 静定结构的位移计算 章
返回
自测
若结构发生位移时,结构内部也同时产生应变, 若结构发生位移时,结构内部也同时产生应变,则 此时结构的位移计算问题属于变形体的位移计算问题 变形体的位移计算问题。 此时结构的位移计算问题属于变形体的位移计算问题。 例如,图中简支梁由于温度变化产生了应变, 例如,图中简支梁由于温度变化产生了应变,就属于 变形体的位移计算问题。 变形体的位移计算问题。 -t
烟台大学 烟台大学
帮助 开篇
退出
上一页
下一页
第4章 静定结构的位移计算 章
静定结构当支座产生移动时,整个结构发生刚体位移, 静定结构当支座产生移动时,整个结构发生刚体位移, 因而不产生变形,应用刚体的虚功原理W =0, 因而不产生变形,应用刚体的虚功原理 e=0,得
帮助 开篇
退出
上一页
下一页
∆ ×1 + ∑ Rc = 0
式中, 为虚单位力引起的支座反力 为虚单位力引起的支座反力, 式中,R为虚单位力引起的支座反力,c 为实际支座 位移,当二者方向一致时,其乘积取正值,相反时取负值。 位移,当二者方向一致时,其乘积取正值,相反时取负值。 若结构是超静定的,则当支座移动时, 若结构是超静定的,则当支座移动时,将会产生内力和变 形,故 Wi≠0,因此应该用变形体的虚功原理求位移。 ,因此应该用变形体的虚功原理求位移。 4.温度作用时的位移计算 4.温度作用时的位移计算 静定结构在温度变化时,杆件不产生切应变, 静定结构在温度变化时,杆件不产生切应变,而轴向 线应变和曲率分别为 / ε =α t0, κ=α∆t/h
A B
帮助 开篇
退出
上一页
下一页
c
烟台大学 烟台大学
第4章 静定结构的位移计算 章
返回
自测
若结构发生位移时,结构内部也同时产生应变, 若结构发生位移时,结构内部也同时产生应变,则 此时结构的位移计算问题属于变形体的位移计算问题 变形体的位移计算问题。 此时结构的位移计算问题属于变形体的位移计算问题。 例如,图中简支梁由于温度变化产生了应变, 例如,图中简支梁由于温度变化产生了应变,就属于 变形体的位移计算问题。 变形体的位移计算问题。 -t
烟台大学 烟台大学
帮助 开篇
退出
上一页
下一页
第4章 静定结构的位移计算 章
结构力学第4章(2024版)
1 qa 2 2
MP
1
8
qa
2
qa
(2) 在C 截面加单位力偶作 M图1 ,如图b所示。
2
m =1 (c)
2
1 1
3
2
1
a
M1
烟台大学 烟台大学
第4章 静定结构的位移计算
返回
c
M 1MP ds EI
RM
RM P
1 k1
R
N
RNP
1 k2
自测
1 [ 2 1 qa2 a 1 1 2a qa2 ( 2 3 1 1)
烟台大学 烟台大学
第4章 静定结构的位移计算
5. 具有弹性支撑或弹性约束的结构的位移计算
返回
弹性支承或弹性约束有以下几种类型:
自测
(a)
(b)
(c)
(d)
帮助
开篇
已知弹簧的刚度系数为k(或已知柔度系数为f,其中
退出 f=1/k)
图a和图b的弹簧会产生线位移⊿,从而产生反力k⊿。
上一页
注意:弹簧的反力与位移⊿方向相反。
第4章 静定结构的位移计算
3. 支座移动时的位移计算
返回
静定结构当支座产生移动时,整个结构发生刚体位移,
自测 因而不产生变形,应用刚体的虚功原理We=0,得
Δ1 Rc 0
帮助
式中,R为虚单位力引起的支座反力,c 为实际支座位
开篇 移,当二者方向一致时,其乘积取正值,相反时取负值。若
结构是超静定的,则当支座移动时,将会产生内力和变形,
应的位移影响系数21等于由荷载F2引起的与荷载F1相应
上一页 的位移影响系数12。
这里的荷载可以是广义荷载,而位移则是相应的广义位
结构力学-第4章影响线

简要介绍某大桥的工程背景,包括桥梁类型、跨度、设计荷载等。
影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程,包括影响线和包络图的绘制、最不利位置的确定、最大内力的计 算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价,包括结构安全性、经济性等方面的评估。同时,可以与其他设计方 案进行对比分析,以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图,可以找到结构在地震作用下的最大变形和位移,为结构的刚 度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图,可以对建筑结构进行优化设计,如调整结构布置、改变构件截面等 ,以提高结构的抗震性能和经济效益。
工程案例分析:某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布,对结 构进行优化设计,以改善结构的 受力性能。
80%
工程实例分析
结合具体工程实例,利用影响线 理论进行结构分析和设计,验证 理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取 基本体系和基本未知量,利用力法方程 求解多余未知力,并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线,可以确定移动荷载在桥梁上的最不利位置,从而进行结构分析和设 计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图,可以找到桥梁在移动荷载作用下的最大内力,为桥梁的强度设计和 稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用
影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程,包括影响线和包络图的绘制、最不利位置的确定、最大内力的计 算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价,包括结构安全性、经济性等方面的评估。同时,可以与其他设计方 案进行对比分析,以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图,可以找到结构在地震作用下的最大变形和位移,为结构的刚 度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图,可以对建筑结构进行优化设计,如调整结构布置、改变构件截面等 ,以提高结构的抗震性能和经济效益。
工程案例分析:某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布,对结 构进行优化设计,以改善结构的 受力性能。
80%
工程实例分析
结合具体工程实例,利用影响线 理论进行结构分析和设计,验证 理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取 基本体系和基本未知量,利用力法方程 求解多余未知力,并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线,可以确定移动荷载在桥梁上的最不利位置,从而进行结构分析和设 计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图,可以找到桥梁在移动荷载作用下的最大内力,为桥梁的强度设计和 稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用
结构力学-4精选全文

注意到 ch2 x sh2x 1,则上式变为
cos k chk 1
这是一个频率方程,其中 k=0 的解对应于静止状态。
超越方程的数值解或作图法,得一系列 ki 的值
i
1
2
3
4
5
i kil 4.73 7.853 10.996 14.137 17.279
ki2
i
a
i
ki2
a
i
2
a
i2
1 l2
纵向刚性位移。
4.2 圆轴扭转 假设: 1)每一横截面,绕通过截面形心的轴线转动 一个角度,截面保持平面; 2)截面上每一个点都转 动相同的角度。扭转振动位移用 表示。 由材料力学可知
Mt GJ p x G ——剪切弹性模量,
J p ——截面的极惯性矩 由达朗贝尔原理
Mt
M t x
dx
Mt
Jp
则微元段上的惯性力为
2 y x,t
t 2
m x dx
f
x,t
,
且在微段上可认为惯力是均布的。
外载和惯性力均可认为是作用在中点上
达朗贝尔原理:
Q(x,t) q(x,t)dx (Q(x,t) Q dx) f (x,t) 0 x
q(x,t)dx Q dx f (x,t) x
Q x
第四章 连续弹性体的振动
实际的工程结构实质都是由连续分布的质量和连续分布的刚 度所组成,在一定条件下简化成离散的多自由度系统,是必要的 合理的。但在某些条件下用连续模型描述更合理。例如细长飞行 器(导弹,火箭结构),细长比大于 4 时可用连续的变截面梁模型 描述,小于 4 时可用弹簧质量块模型描述。
Yi x
Yi x 为梁上第 x 点的振幅,称为第 i 阶振型函数
cos k chk 1
这是一个频率方程,其中 k=0 的解对应于静止状态。
超越方程的数值解或作图法,得一系列 ki 的值
i
1
2
3
4
5
i kil 4.73 7.853 10.996 14.137 17.279
ki2
i
a
i
ki2
a
i
2
a
i2
1 l2
纵向刚性位移。
4.2 圆轴扭转 假设: 1)每一横截面,绕通过截面形心的轴线转动 一个角度,截面保持平面; 2)截面上每一个点都转 动相同的角度。扭转振动位移用 表示。 由材料力学可知
Mt GJ p x G ——剪切弹性模量,
J p ——截面的极惯性矩 由达朗贝尔原理
Mt
M t x
dx
Mt
Jp
则微元段上的惯性力为
2 y x,t
t 2
m x dx
f
x,t
,
且在微段上可认为惯力是均布的。
外载和惯性力均可认为是作用在中点上
达朗贝尔原理:
Q(x,t) q(x,t)dx (Q(x,t) Q dx) f (x,t) 0 x
q(x,t)dx Q dx f (x,t) x
Q x
第四章 连续弹性体的振动
实际的工程结构实质都是由连续分布的质量和连续分布的刚 度所组成,在一定条件下简化成离散的多自由度系统,是必要的 合理的。但在某些条件下用连续模型描述更合理。例如细长飞行 器(导弹,火箭结构),细长比大于 4 时可用连续的变截面梁模型 描述,小于 4 时可用弹簧质量块模型描述。
Yi x
Yi x 为梁上第 x 点的振幅,称为第 i 阶振型函数
结构力学第4章

定义:单位移动荷载作用下描述某物理 量随荷载位置变化规律的图形称 影响线。 确定影响线通常有两者方法: 静力法 机动法
§4-2 静力法做简支梁 影响线
将描述荷载位置的量作为固定值,通 过静力平衡的方式确定某物理量与荷 载位置的关系的方法称静力法。 正确的影响线应该具有“正确的外形、 必要的控制点纵座标值和正负号”等 基本特征。
FP=1
a a
b Nc b 1 c1
N1
d 上承 e d e
ff
g g h h
方法:结点法与截面法 1、I.L RA及RG MC 0 2、 I .L N1
P 1在Ⅰ Ⅰ以左 , 取右隔离体
A A
RA
C B C B C P=1
P=1 C
D D
E F E 下承 F
G G
N 1 h RG 4 d 0
lx l
a
bl 1 l
ab l
b
al 2
( a x l l2 )
4
l
MC
I.L M C
P=1
x
D
B
P=1
A
d
l2
l1
伸臂部分影 响线
(5 ) M x,
l
RA
RB
D
I .L M
d
D
0
x d
(6) Q D 1
1
I .L Q D
0
x d
影响线座标的意义:横座标表示单位荷载的位置; 纵座标表示单位荷载作用在本位置时指定位置物理 量的反应。 简支梁弯矩影响线与弯矩图的区别
x 1
由比例可得: y C
5d 8
, yE
结构力学第四章虚功原理和结构的位移计算

N N Pl EA
杆件 NP
A 1.50 1/2
E
N
-1.58
l 0.263l
N N P l EA
1.97Pl/AbEb 1.84Pl/AbEb 0 0 0.63Pl/AgEg 0.5Pl/AgEg
AD
-4.74P
Ab Ab 0.75Ab
Ag 3Ag 2Ag
钢筋 混凝土
CD DE CE
-4.42P
-1.58
2
§4· 位移计算概述 1
a)验算结构的刚度; 1、计算位移目的: b)为超静定结构的内力分析 打基础; a)荷载作用; 2、产生位移的主要原因: b)温度改变和材料胀缩; c)支座沉降和制造误差
↓↓↓↓↓↓↓↓↓ -t +t
d w dx
2 2
l β Δ
/l
M ,Q, N
, ,
A
Δ
B
6
4、刚体虚功原理 刚体在外力作用下处于平衡的充分必要条件是, 对于任意微小的虚位移,外力所作的虚功之和等于零。 W=0 二、虚功原理的应用 1)虚设位移求未知力(虚位移原理) 2)虚设力系求位移(虚力原理) P 1、需设位移求静定结构的未知力(虚位移原理)
X X P P 0
19
l/2
(a+l)/3 (b+l)/3
一、变形体虚功原理 状态 1 是满足平衡条件的力状 ≠ T12 = 0 态,状态2是满足变形连续条件 的位移状态,状态1的外力在状 态2的位移上作的外虚功等于状 态1的各微段的内力在状态2 各 微段的变形上作的内虚功之和 即:T12= V 12
变
10
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
ds
结构力学 第4章 静定结构的位计算

例如,图1(a)所示两个梯形应用图乘法,可不必求 梯形的形心位置,而将其中一个梯形(设为MP图)分成 两个三角形,分别图乘后再叠加。
图1
对于图2所示由于均布荷载q所引起的MP图,可以 把它看作是两端弯矩竖标所连成的梯形ABDC与相应简
支梁在均布荷载作用下的弯矩图叠加而成。
四、几种常见图形的面积和形心的位置
零。
P
2Δ
PP2P30
22
2
YA P/2
YB P/2
2.变形体系的虚功原理 We Wi
体系在任意平衡力系作用下,给体系以几何可能的
位移和变形,体系上所有外力所作的虚功总和恒等于体
系各截面所有内力在微段变形位移上作的虚功总和。
说明: (1)虚功原理里存在两个状态:力状态必须满足平衡条件;位移状态
PR3 PRk PR
4EI 4EA 4GA
M N Q
P θ
P=1
钢筋混凝土结构G≈0.4E 矩形截面,k=1.2,I/A=h2/12
Q M
kGEAI2R14Rh2
N M
I AR2
1 h2 12R
如 h 1 , 则Q 1 , N 1
1
EA 2(1 2)Pa()
1 2
1
EA
2
1
例3.求图示1/4圆弧曲杆顶点的竖向位移Δ。
解:1)虚拟单位荷载
2)实际荷载
虚拟荷载
ds
M P PR sin
M R sin
QP P cos
Q cos
dθ
N P P sin
N sin
d d ds d
d dd sd sN Pds
结构力学(第四章)-力矩分配法

C M AB = CM BA = 28.6
C M CB = 0
0 0
配 传 递
最终杆端弯矩: 最终杆端弯矩 M AB = 100 28.6 = 128.6 q = 12kN / m 42.9 M BA = 100 57.1 = 42.9 M BC = 0 42.9 = 42.9 128 .6 M CB = 0
C d M AB = CM BA = 0.5 × ( 57.1) = 28.6 C d M CB = CM BC = 0 × ( 42.9) = 0
传递弯矩
与远端支承 情况有关
固定状态: 固定状态 F M AB = ql 2 / 12 = 100kN .m F M BA = 100kN .m F F M BC = M CB = 0 放松状态: 放松状态 d u M BA = BA ( M B ) = 57.1 d u M BC = BC ( M B ) = 42.9
1
ql / 8
2
12
2
100 0 -57.1 -42.9 -6.1 3.5 2.6
0 0 0
28.6
100
-28.6 -57.1 -42.9
21.4 6.1 -9.2 -12.2 -6.1 1.8 6.1 1.8 3.5 2.6
分 配 传 递
0
M 0
A
0
q = 12 kN / m
40.3
2
B
… … ...
A
M
d BA
B
u MB
B
u MB
C
u d d M B + M BA + M BC = 0 1 u ( M B ) B = S BA + S BC
B
C M CB = 0
0 0
配 传 递
最终杆端弯矩: 最终杆端弯矩 M AB = 100 28.6 = 128.6 q = 12kN / m 42.9 M BA = 100 57.1 = 42.9 M BC = 0 42.9 = 42.9 128 .6 M CB = 0
C d M AB = CM BA = 0.5 × ( 57.1) = 28.6 C d M CB = CM BC = 0 × ( 42.9) = 0
传递弯矩
与远端支承 情况有关
固定状态: 固定状态 F M AB = ql 2 / 12 = 100kN .m F M BA = 100kN .m F F M BC = M CB = 0 放松状态: 放松状态 d u M BA = BA ( M B ) = 57.1 d u M BC = BC ( M B ) = 42.9
1
ql / 8
2
12
2
100 0 -57.1 -42.9 -6.1 3.5 2.6
0 0 0
28.6
100
-28.6 -57.1 -42.9
21.4 6.1 -9.2 -12.2 -6.1 1.8 6.1 1.8 3.5 2.6
分 配 传 递
0
M 0
A
0
q = 12 kN / m
40.3
2
B
… … ...
A
M
d BA
B
u MB
B
u MB
C
u d d M B + M BA + M BC = 0 1 u ( M B ) B = S BA + S BC
B
4结构力学(李廉锟第五版)

q( x) p( x) ds dx
dx p(x) ds x
y
中南大学
退出
返回
18:50
§4-3 三铰拱的合理拱轴线
将 q( x) p( x)
2
结构力学
ds dx
代入方程(4-5),得
2
d y q( x) p( x) ds p( x) dy 1 2 dx FH FH dx FH dx
由于规定y 向上为正, x 向右为正,q 向下为 正,故上式右边为正号。
中南大学
退出
返回
18:50
§4-3 三铰拱的合理拱轴线
或
结构力学
d dy dx dx dy 1 dx
1
2
p( x) FH
p ( x) dy sh dx. FH dx 如p(x)=常数=p ,则
中南大学
退出
返回
18:50
§4-2 三铰拱的数值解
(3) 求内力 由水平推力 FH 82.5 kN 得 0
结构力学
(2) 求支座反力,结果为: FVA 105 kN , FVB 115 kN
FSD 105 kN 100 kN 5 kN
FSD FS0D cos D FH sin D
返回
中南大学
退出
18:50
§4-2 三铰拱的数值解
与代梁相比较有:
0 FVA FV A 0 FVB FVB 0 MC FH f
结构力学
F F K A x x l/ 2 FVA f B l/ 2 FVB FHB C F
y
F HA
F1 A
dx p(x) ds x
y
中南大学
退出
返回
18:50
§4-3 三铰拱的合理拱轴线
将 q( x) p( x)
2
结构力学
ds dx
代入方程(4-5),得
2
d y q( x) p( x) ds p( x) dy 1 2 dx FH FH dx FH dx
由于规定y 向上为正, x 向右为正,q 向下为 正,故上式右边为正号。
中南大学
退出
返回
18:50
§4-3 三铰拱的合理拱轴线
或
结构力学
d dy dx dx dy 1 dx
1
2
p( x) FH
p ( x) dy sh dx. FH dx 如p(x)=常数=p ,则
中南大学
退出
返回
18:50
§4-2 三铰拱的数值解
(3) 求内力 由水平推力 FH 82.5 kN 得 0
结构力学
(2) 求支座反力,结果为: FVA 105 kN , FVB 115 kN
FSD 105 kN 100 kN 5 kN
FSD FS0D cos D FH sin D
返回
中南大学
退出
18:50
§4-2 三铰拱的数值解
与代梁相比较有:
0 FVA FV A 0 FVB FVB 0 MC FH f
结构力学
F F K A x x l/ 2 FVA f B l/ 2 FVB FHB C F
y
F HA
F1 A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
恭喜,交卷操作成功完成!你本次进行的《结构力学》第04章在线测试的得分为20分(满分20分),本次成绩已入库。
若对成绩不满意,可重新再测,取最高分。
测试结果如下:
∙ 1.1 [单选] [对] 悬臂梁固定端截面的弯矩影响线的最大竖标在
∙ 1.2 [单选] [对] 悬臂梁固定端截面的剪力影响线
∙ 1.3 [单选] [对] 简支梁的弯矩影响线是
∙ 1.4 [单选] [对] 简支梁AB,跨度为6m,C为跨间一截面,AC长为2m,则C截面弯矩影响线中的最大竖标是
∙ 1.5 [单选] [对] 外伸梁支座反力影响线形状特征是
∙ 2.1 [多选] [对] 外伸梁伸臂上的截面剪力影响线是
∙ 2.2 [多选] [对] 下列哪些量值的影响线是无量纲的?
∙ 2.3 [多选] [对] 下列哪些量值的影响线是长度量纲?
∙ 2.4 [多选] [对] 伸臂梁的影响线的特点是
∙ 2.5 [多选] [对] 下列关于影响线的论述正确的是
∙ 3.1 [判断] [对] 静定结构的内力和反力影响线是直线或折线组成。
∙ 3.2 [判断] [对] 若有一集中力作用在影响线顶点,必为荷载临界位置。
∙ 3.3 [判断] [对] 悬臂梁固定端截面的弯矩影响线的最大竖标(绝对值)在自由端截面。
∙ 3.4 [判断] [对] 静定结构基本部分上的某量值的影响线在附属部分上的影响线竖标为零。
∙ 3.5 [判断] [对] 简支梁的反力影响线是一条直线。
